|
Базисы
|
x0
|
x1
|
x2
|
x4
|
x5
|
|
х5
|
1
|
0
|
0
|
3/8
|
7/8
|
1
|
|
х2
|
3
|
0
|
1
|
1/8
|
5/8
|
0
|
|
х1
|
2
|
1
|
0
|
1/4
|
1/4
|
0
|
|
f
|
8
|
0
|
0
|
1/2
|
1
1/2
|
0
|
В Таблице №4 все элементы индексной
строки не отрицательные (положительные и нули), значит задача решена. Так оно и
есть, значит, план является оптимальным, а значение, стоящее в индексной строке
столбца х0 есть максимальное значение целевой функции. Вычисления
прекращаем и получаем: 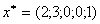 ,
, 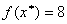 .
.
Так же было проведена проверка с
помощью MS Excel, встроенной
функции «Поиск решения». На Рисунке 1 - Заполнение требуемых параметров, мы
видим заданную систему; изменяемые ячейки, которые являются базисами; целевую
ячейку, которая отображает максимальное значение целевой функции; сохраняемые
модели, которые необходимы для хранения временных данных.
линейное программирование функция
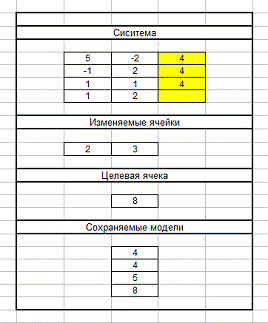
Рисунок 1 - Заполнение требуемых параметров
На Рисунке 1 изображено не все, так же имеются
формулы, которые написаны для расчета целевой функции и сохраняемых моделей.
Формула для расчета целевой ячейки: произведение сумм коэффициентов перед
неизвестными в целевой функции на изменяемые ячейки соответственно. Для
сохраняемых моделей: сумма произведений коэффициентов перед неизвестными
соответствующего уравнения на изменяемые ячейки.
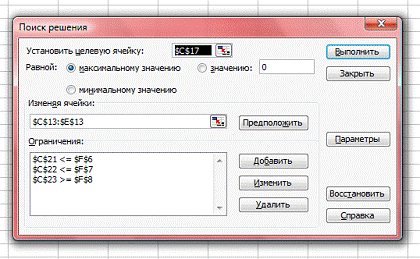
Рисунок 2 - Выполняемая программа
После выполнения программы, изображенной на
Рисунке 2, появиться правильный ответ, то есть максимальное значение целевой
функции, изображенной на Рисунке 1.
Задание №1. Построить графическое решение:
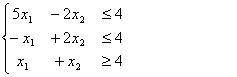 (1.1)
(1.1)
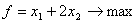 (1.2)
(1.2)
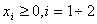 (1.3)
(1.3)
Система линейных ограничений (1.1) -
(1.3), представлена в виде прямых, определим точки для построения прямых на
плоскости:
) 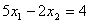
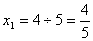 ;
; 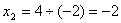
) 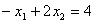
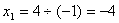 ;
; 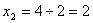
) 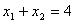
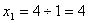 ;
; 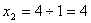
Постоим получившиеся прямые на
плоскости. Каждая прямая делит декартову плоскость на две полуплоскости:


Рисунок 3 - График
Так как изначально нам были даны неравенства то,
следовательно, решение неравенства является множество точек, а решение системы
является область, включающая точки, удовлетворяющие всем неравенствам.
Для определения интервала точек для каждого
неравенства достаточно взять любую точку из первой полуплоскости и подставить в
неравенство, отвечающее за данную прямую, и проверить условия. Если точка
удовлетворяет условию тогда эта полуплоскость является решением неравенства.
Теперь построим вектор нормали из
коэффициентов целевой функции (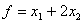 ;
;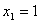 ,
,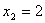 ), находим точку направления
вектора, соединяем начало координат с этой точкой, указываем направление
вектора. Вектор нормали указывает направление передвижения функции по многоугольнику.
), находим точку направления
вектора, соединяем начало координат с этой точкой, указываем направление
вектора. Вектор нормали указывает направление передвижения функции по многоугольнику.
Теперь построим целевую функцию.
Целевую функцию можно изобразить в виде сетки параллельных прямых, достаточно
для построения приравнять целевую функцию к любому значению и построить прямую
(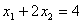 ; (4;0);
(0;2)). Та точка, через которую пройдет целевая функция при перемещении вдоль
вектора нормали окажется последней в многоугольнике будет ответом. Эта тоска с
координатами (2;3). Получаем ответ:
; (4;0);
(0;2)). Та точка, через которую пройдет целевая функция при перемещении вдоль
вектора нормали окажется последней в многоугольнике будет ответом. Эта тоска с
координатами (2;3). Получаем ответ: 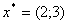 . Для получения оптимального плана
подставим координаты в целевую функцию и получим:
. Для получения оптимального плана
подставим координаты в целевую функцию и получим: 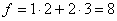 ,
оптимальный план:
,
оптимальный план: 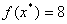 .
.
Задание №2. Решить транспортную
задачу
Решить транспортную задачу. Заданы
мощности поставщиков аi (i=1,2,3),
емкости потребителей bj (j=1,2,3) и
матрица стоимостей перевозок единицы продукции от каждого поставщика каждому
потребителю. Требуется найти план перевозок, при котором суммарные транспортные
затраты будут наименьшими.
Исходные данные:
Таблица №5 - Исходные данные
|
Потребители
|
B1
|
B2
|
B3
|
|
Поставщики
|
|
14
|
20
|
22
|
|
A1
|
50
|
3
|
8
|
|
A2
|
18
|
3
|
4
|
5
|
|
А3
|
12
|
2
|
7
|
6
|
Решить задачу можно в том случае
если задача закрыта, то есть должно выполнять равенство: 50+18+12=14+20+22,
получается 80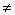 56; введем
дополнительного потребителя
56; введем
дополнительного потребителя
-56=24.
Таблица №6 - Ввод дополнительного
потребителя
|
Потребители
|
B1
|
B2
|
B3
|
Вф
|
|
Поставщики
|
|
14
|
20
|
22
|
24
|
|
A1
|
50
|
3
|
8
|
9
|
0
|
|
A2
|
18
|
3
|
4
|
5
|
0
|
|
А3
|
12
|
2
|
7
|
6
|
0
|
Составим исходный план перевозок Х1 (Рисунок
4) методом «северо-западного угла», распределяя мощности поставщиков по порядку
между потребителями, так чтобы каждая перевозка была максимально возможной.
План перевозок оформим в виде
таблицы, разделенной на клетки. В центре каждой клетки плана поместим перевозки
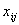 , а в правом
верхнем углу - стоимость перевозки единицы продукции. В клетки, соответствующие
нулевым перевозкам, нули не вписываем, оставляя их пустыми. В таком случае план
Х1 будет содержать не больше, чем m+n-1
положительных перевозок или занятых клеток, где m - число
поставщиков, n - число
потребителей. Остальные компоненты плана Х1, соответствующие нулевым
перевозкам, будем называть свободными клетками. Если число занятых клеток K = m + n -1, то план
перевозок называется невырожденным, если K < m + n - 1, то
вырожденным.
, а в правом
верхнем углу - стоимость перевозки единицы продукции. В клетки, соответствующие
нулевым перевозкам, нули не вписываем, оставляя их пустыми. В таком случае план
Х1 будет содержать не больше, чем m+n-1
положительных перевозок или занятых клеток, где m - число
поставщиков, n - число
потребителей. Остальные компоненты плана Х1, соответствующие нулевым
перевозкам, будем называть свободными клетками. Если число занятых клеток K = m + n -1, то план
перевозок называется невырожденным, если K < m + n - 1, то
вырожденным.
Подсчитаем суммарную стоимость
перевозок по плану Х1:
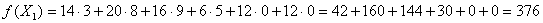
Проверим план Х1 (Рисунок
4) на оптимальность. Найдем потенциалы 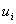 поставщиков и потенциалы
поставщиков и потенциалы 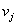 потребителей.
потребителей.
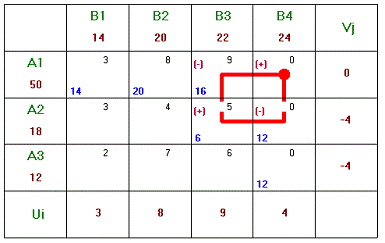
Рисунок 4 - План Х1 (План
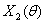 )
)
По условию для занятых клеток:
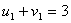
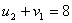
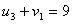
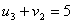
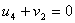
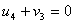
Один из потенциалов всегда задается
произвольно, зададим 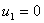 . Тогда из
системы получим
. Тогда из
системы получим 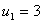 ,
, 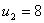 ,
, 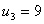 ,
, 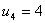 ,
,  ,
,  ,
, 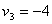 . Эти
потенциалы полезно записать справа и снизу от плана
. Эти
потенциалы полезно записать справа и снизу от плана 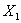 .
.
По условию для свободных клеток:

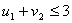
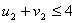

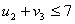
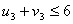
Подставим потенциалы в неравенства,
получим:
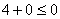 ; 4 > 0
; 4 > 0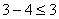 ; -1 < 3
; -1 < 3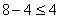 ; 4 = 4
; 4 = 4
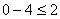 ; -4 < 2
; -4 < 2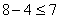 ; 4 < 7
; 4 < 7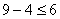 ; 5 < 6
; 5 < 6
Мы видим, что не выполняется одно
неравенство
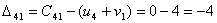
Следовательно, план 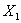 можно
улучшить, введя в план перевозку
можно
улучшить, введя в план перевозку 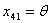 . С этой целью составим цикл,
имеющий начало в свободной клетке (4, 1), а остальные вершины - в занятых
клетках, последовательно увеличивая и уменьшая перевозки, попавшие в цикл, на
величину
. С этой целью составим цикл,
имеющий начало в свободной клетке (4, 1), а остальные вершины - в занятых
клетках, последовательно увеличивая и уменьшая перевозки, попавшие в цикл, на
величину 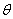 . Цикл и
последовательность увеличения и уменьшения перевозок изображено на рисунке 5.
. Цикл и
последовательность увеличения и уменьшения перевозок изображено на рисунке 5.
Важно отметить, что при составлении
цикла следует двигаться только по горизонтали или вертикали, так что бы в каждую
строку и каждый столбец плана перевозок, охваченных циклом, попали только две
перевозки.
Выбираем 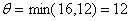 , то есть в
качестве
, то есть в
качестве 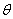 выбирается
наименьшая из перевозок, из которых
выбирается
наименьшая из перевозок, из которых 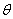 вычитается. При включении в план
вычитается. При включении в план 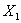 перевозки
перевозки 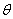 =12
суммарная стоимость перевозок изменится на
=12
суммарная стоимость перевозок изменится на 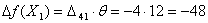 , то есть уменьшится на 48 ед. и для
нового плана составит:
, то есть уменьшится на 48 ед. и для
нового плана составит:
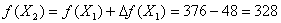
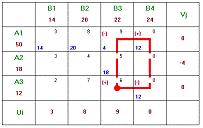
Рисунок 6 - План Х2 (План
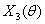 )
)
По условию для занятых клеток:
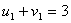
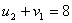
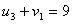
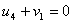
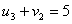
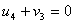
По условию для свободных клеток:

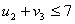
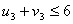
Подставим потенциалы в неравенства,
получим:
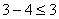 ; -1 < 3
; -1 < 3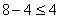 ; 4 = 4
; 4 = 4 ; -4 > 0
; -4 > 0
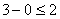 ; 3 > 2
; 3 > 2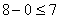 ; 8 >
7
; 8 >
7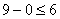 ; 9 >
6
; 9 >
6
Мы видим, что не выполняются три
неравенство причем
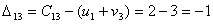 ;
;
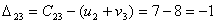 ;
;
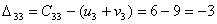 .
.
Следовательно, план 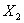 можно
улучшить, введя в план перевозку
можно
улучшить, введя в план перевозку 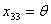 , для которой разность
, для которой разность 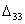 оказалась
меньше разностей
оказалась
меньше разностей 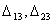 . С этой
целью составим цикл, имеющий начало в свободной клетке (3, 3), а остальные
вершины - в занятых клетках, последовательно увеличивая и уменьшая перевозки,
попавшие в цикл, на величину
. С этой
целью составим цикл, имеющий начало в свободной клетке (3, 3), а остальные
вершины - в занятых клетках, последовательно увеличивая и уменьшая перевозки,
попавшие в цикл, на величину 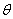 . Цикл и последовательность
увеличения и уменьшения перевозок изображено на рисунке 6.
. Цикл и последовательность
увеличения и уменьшения перевозок изображено на рисунке 6.
Выбираем 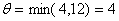 , то есть в
качестве
, то есть в
качестве 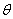 выбирается
наименьшая из перевозок, из которых
выбирается
наименьшая из перевозок, из которых 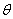 вычитается. При включении в план
вычитается. При включении в план 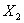 перевозки
перевозки 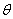 =4 суммарная
стоимость перевозок изменится на
=4 суммарная
стоимость перевозок изменится на 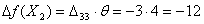 , то есть уменьшится на 12 ед. и для
нового плана составит:
, то есть уменьшится на 12 ед. и для
нового плана составит:
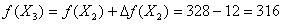
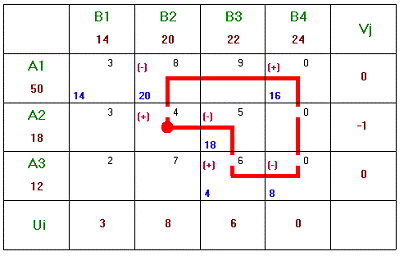
Рисунок 7 - План Х3 (План
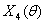 )
)
По условию для занятых клеток:
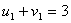
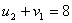
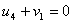
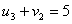
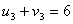
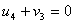
По условию для свободных клеток:
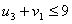
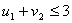
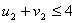
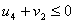

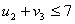
Подставим потенциалы в неравенства,
получим:
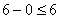 ; 6 = 6
; 6 = 6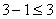 ; 2 < 3
; 2 < 3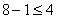 ; 7 >
4
; 7 >
4
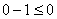 ; -1 < 0
; -1 < 0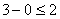 ; 3 >
2
; 3 >
2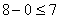 ; 8 >
7
; 8 >
7
Мы видим, что не выполняются три
неравенство причем
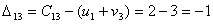 ;
;
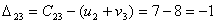 ;
;
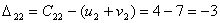 .
.
Следовательно, план 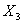 можно
улучшить, введя в план перевозку
можно
улучшить, введя в план перевозку 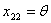 , для которой разность
, для которой разность 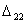 оказалась
меньше разностей
оказалась
меньше разностей 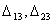 . С этой
целью составим цикл, имеющий начало в свободной клетке (2, 2), а остальные
вершины - в занятых клетках, последовательно увеличивая и уменьшая перевозки,
попавшие в цикл, на величину
. С этой
целью составим цикл, имеющий начало в свободной клетке (2, 2), а остальные
вершины - в занятых клетках, последовательно увеличивая и уменьшая перевозки,
попавшие в цикл, на величину 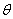 . Цикл и последовательность
увеличения и уменьшения перевозок изображено на рисунке 7.
. Цикл и последовательность
увеличения и уменьшения перевозок изображено на рисунке 7.
Выбираем 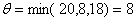 , то есть в
качестве
, то есть в
качестве 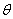 выбирается
наименьшая из перевозок, из которых
выбирается
наименьшая из перевозок, из которых 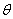 вычитается. При включении в план
вычитается. При включении в план 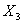 перевозки
перевозки 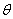 =8 суммарная
стоимость перевозок изменится на
=8 суммарная
стоимость перевозок изменится на 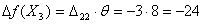 , то есть уменьшится на 24 ед. и для
нового плана составит:
, то есть уменьшится на 24 ед. и для
нового плана составит:
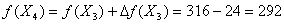

Рисунок 8 - План Х4
По условию для занятых клеток:
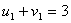
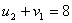
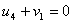
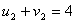
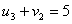
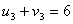
По условию для свободных клеток:
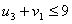
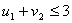
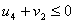

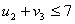
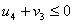
Подставим потенциалы в неравенства,
получим:
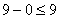 ; 9 = 9
; 9 = 9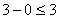 ; 3 = 3
; 3 = 3 ; -4 < 4
; -4 < 4
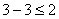 ; 0 < 2
; 0 < 2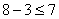 ; 5 < 7
; 5 < 7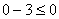 ; -3 < 0
; -3 < 0
Из уравнений и неравенств следует,
что они выполняются оба условия критерия оптимальности плана перевозок.
Следовательно, план перевозок Х4 является оптимальным планом
закрытой задачи, а 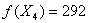 представляет
собой наименьшую стоимость перевозок. Отбросив последний столбец плана Х4,
получим оптимальный план Х* исходной открытой задачи, для которой
представляет
собой наименьшую стоимость перевозок. Отбросив последний столбец плана Х4,
получим оптимальный план Х* исходной открытой задачи, для которой 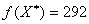 есть
наименьшая стоимость перевозок.
есть
наименьшая стоимость перевозок.
Отброшенный столбец означает, что
первые два поставщика вывезут всю имеющуюся у них продукцию, а у третьего
поставщика останутся не вывезенными 24 ед. продукции.