Преодоление психологических барьеров при изучении математики в 5-6 классах

МОСКОВСКИЙ ГОРОДСКОЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ

Математический факультет

ДИПЛОМНАЯ РАБОТА

По теме: "ПРЕОДОЛЕНИЕ ПСИХОЛОГИЧЕСКИХ БАРЬЕРОВ ПРИ ИЗУЧЕНИИ МАТЕМАТИКИ В 5-6 КЛАССАХ"

Студентки 5 курса д/о

Барс Е.В.

Научный руководитель:

доктор физ.-мат. наук,

профессор Дорофеев

Георгий Владимирович

Москва, 2011

Содержание

Введение

Глава 1. Особенности преподавания математики в средней школе

.1 Познавательные процессы в обучении школьников математике

.2 Психологические барьеры в обучении школьников математике

Глава 2. Методика преподавания математики в 5 классе средней школы с преодолением психологических барьеров

.1 Описание методики

.2 Апробация методики в классе 5.3 средней школы №1605 г. Москвы

.3 Результаты

Заключение

Список литературы

Приложение

Введение

познавательный математика школьник психологический

Математика является инструментом, без которого в настоящее время невозможно полноценное развитие никакой науки, с помощью которого наиболее эффективно производятся многочисленные исследования во многих науках. Математика проникает почти во все области деятельности человека, что положительно сказалось на темпе роста научно-технического прогресса. В связи с этим стало жизненно необходимым усовершенствовать математическую подготовку подрастающего поколения.

Ребенок с первых дней обучения в школе встречается с математикой. Изучение почти любого предмета в школе предполагает хорошее знание математики, и без нее учащиеся не могут освоить эти предметы. С начала и до конца обучения в школе математика неизменно помогает ученику вырабатывать правильные понятия и глубже выяснять различные стороны взаимосвязей в окружающей его жизни, дает возможность применять изучаемые теоретические положения. В то же время математика способствует развитию школьников.

Если недавно основной задачей, стоящей перед учителем, была передача ученикам определенной суммы знаний, то в данный момент согласно современной концепции математического образования, его важнейшей задачей является интеллектуальное развитие учащихся, формирование качеств мышления, характерных для математической деятельности и необходимых человеку для полноценной жизни в обществе.

В данный момент наблюдается повышенный интерес учителей к психолого-педагогическим проблемам, к психологическим знаниям. Этот интерес можно объяснить тем, что учителя в своей повседневной практической деятельности сталкиваются с такими проблемами, которые возможно разрешить только опираясь на психолого-педагогические знания.

Исследованию как общих, так и частных проблем взаимодействия психологии и педагогики, математики и системного подхода посвящены работы Г.Н. Александрова, С.И. Архангельского, В.П. Беспалько, Г.В. Воробьева, В.Ф. Венды, Б.С. Гершунского, Л.В. Занкова, Л.Б. Ительсона, Л.Н. Ланды, В.С. Леднева, В.И. Михеева, Е.И. Машбица, Н.Д. Никандрова, В.Н. Пушкина, А.П. Свиридова, А.А. Столяра, О.К.Тихомирова, Л.М. Фридмана и других.

Психологические проблемы обучения, управления познавательной деятельностью учащихся, без которых невозможно продвижение в обучении математики, исследовались в работах Г.Н. Александрова, П.Я. Гальперина, В.В. Дробышева, Л.В. Занкова, В.П. Зинченко, И.П. Калошиной, Г.С. Костюка, Ю.Н. Кулюткина, А.М. Матюшкина, Н.А. Менчинской, Ю.А. Самарина, Н.Ф. Талызиной, О.К. Тихомирова, А.Ф. Эсаулова.

Несмотря на большое количество литературы по данному вопросу, хочется отметить, что конкретного материала, позволяющего построить обучение школьников с учетом особенностей преодоления психологических барьеров, нет. Существует множество методических пособий по курсу математики в средней школе, но в ходе исследования литературы не встретилось ни одного, где были бы собраны и обобщены данные, позволяющие преодолевать психологические барьеры, возникающие у школьников при изучении математики. Поэтому, исходя из выше сказанного, хочется отметить, актуальность исследования данного вопроса.

Барьер от французского barriere - преграда, препятствие. Какие преграды, препятствия, трудности могут возникнуть у школьников при изучении математики и как им помочь справиться с ними? На этот вопрос необходимо ответить.

В психологической литературе выделяют несколько определений понятия психологического барьера.

Психологический барьер - совокупность взаимосвязанных и взаимообусловленных действий, суждений, понятий, умозаключений, ожиданий, эмоциональных переживаний, в которых осознанно и/или неосознанно, скрыто или явно, преднамеренно или непреднамеренно выражается негативное отношение индивида и/или различных групп к разработке и внедрению нововведений в различных сферах жизни.

Другое определение: внутреннее препятствие психологической природы (нежелание, боязнь, неуверенность и т.п.), мешающее человеку успешно выполнить некоторое действие. Часто возникает в деловых и личных взаимоотношениях людей и препятствует установлению между ними открытых и доверительных отношений. Третье определение: психическое состояние, проявляющееся в неадекватной пассивности человека, препятствующая выполнению им тех или иных действий. При наличии психологического барьера усиливаются отрицательные эмоциональные переживания и установки, ассоциированные с задачей - стыд, чувство вины, страх, тревога, низкая самооценка.

Еще одно определение: субъективная реакция, обусловленная негативным отношением или предубеждением. Возникает из-за несовпадения интереса личности с требованиями ситуации или условиями выполняемой работы. Такого вида барьер в психологии называют "смысловым".

Термином "смысловой барьер" в психолого-педагогической литературе называют такое явление, заключающееся в том, что в силу разного отношения школьника и взрослого к одному и тому же явлению, поступку, поведению в целом ребенок оказывается, совершенно невосприимчив к педагогическим воздействиям. В результате ученик, хорошо понимая и умея выполнить то, что от него требует педагог, не "принимает" это требование и упорно его не выполняет.

Психологический барьер является серьезным тормозом на пути той или иной деятельности человека. В случае неудовлетворения потребности включаются в работу защитные механизмы.

Психологические барьеры могут возникнуть вследствие слабой воли, лени, неуверенности в себе, нетребовательности в работе.

Успешному "преодолению" барьера, или снижению количества возможных трудностей, им вызванных, могут способствовать своевременная и полная информация о предстоящих нововведениях, индивидуальная работа, организация обучения, направленного на снижение возникновения психологических барьеров и т. п.

Первоначальные математические знания усваиваются в определенной, приспособленной к пониманию системе, в которой отдельные положения логически связаны одно с другим, вытекают одно из другого. При сознательном усвоении математических знаний учащиеся пользуются основными операциями мышления в доступном для них виде: анализом и синтезом, сравнением, абстрагированием и конкретизацией, обобщением; ученики делают индуктивные выводы, проводят дедуктивные рассуждения. Сознательное усвоение учащимися математических знаний развивает математическое мышление учащихся. Овладение мыслительными операциями в свою очередь помогает учащимся успешнее усваивать новые знания.

Объектом исследования в работе является процесс обучения школьников математике.

Предметом исследования является методика преодоления психологических барьеров на уроках математики в средней школе.

Цель работы исследовать методику преодоления психологических барьеров в процессе обучения математике в средне школе, выявить новые подходы к обучению.

После анализа литературы по интересующему вопросу была выдвинута гипотеза, что продуктивная учебная деятельность школьников на уроках математики, заинтересованность их математикой возможна только при условии использования на уроках определенных психологических приемов, направленных на снятие и преодоление психологических барьеров.

В связи с этим были выделены следующие задачи, которые определили содержание и структуру исследования в его теоретической и экспериментальной частях:

. Исследовать вопрос теории обучения: существо проблемы и её историко-теоретический аспект.

. Проанализировать вопрос, что есть понятие "психологический барьер".

. Изучить основные особенности процесса обучения математике в средней школе.

. Рассмотреть некоторые психолого-педагогические принципы преодоления психологических барьеров.

. Выявить уровень сформированности психологических барьеров на уроках математики в условиях современной школы (5 класс).

. Определить способы и конкретные приемы преодоления психологических барьеров на уроках математики у учащихся 5-х классов.

Методы с помощью которых проводилось исследование:

Метод теоретического анализа, синтеза, обобщения и конкретизации;

Метод эксперимента с помощью внедрения методики преподавания математики с целью преодоления психологических барьеров;

Методы количественного анализа и качественной обработки данных исследования.

Работа состоит из введения, двух глав, заключения, списка литературы и приложения.

Глава 1. Особенности преподавания математики в средней школе

.1 Познавательные процессы в обучении школьников математике

Большое влияние на совершенствование традиционной системы обучения оказала созданная в трудах отечественных психологов и педагогов теория деятельности. Концепция деятельностного подхода к обучению по-новому поставила вопросы о соотношении знаний, умений и навыков учащихся и их развитие в учебной деятельности. По этой причине многочисленные исследования психологов и педагогов посвящены теории активизации учебно-познавательной деятельности школьников (М. А. Данилов, Б. П. Есипов, А. М. Матюшкин, И. Я. Лернер, М. Н. Скаткин, Т. И. Шамова и др.). Такие качества личности, как любознательность, целеустремленность, а также овладение знаниями и способами учения: интеллектуальными умениями, общими навыками учебного труда и специальными умениями, формируются только в учебно-познавательной деятельности ребенка. Такое понимание познавательной деятельности включает в себя понятие познавательной самостоятельности.

Деятельность является самостоятельной, если ее составляющими элементами являются такие действия, как установление нового факта, явления и его характеристика; формулирование проблемы, задачи; выдвижение гипотезы; установление существенных связей и закономерностей развития явления; определение путей поиска новых фактов, выявление их сущности на основе сравнения, сопоставления и противопоставления фактов; выделение общего положения в конкретном случае; оценка решения, значимости полученного результата.

Говоря о механизмах взаимодействия учителя и ученика, а также о том как происходит механизм усвоения знаний, формирования умственных и предметных действий, можно выразить их с помощью такой структуры:

механизмы формирования личности в деятельности; понимание процесса обучения как включение обучаемого в систему деятельностей, отношений и общения; механизмы взаимодействий знаний, деятельности и перестраивающихся установок в умственном развитии обучаемых;

механизмы познавательной деятельности в обучении: взаимодействия видов познавательной деятельности;

механизмы ориентировочной основы действий, как механизмы взаимодействия алгоритмических и эвристических процессов;

механизмы самих психических процессов, умственных и предметных действий.

Область применения тех или иных механизмов определяется целями обучения, дидактическими задачами, особенностями логической структуры знаний, индивидуальными характеристиками учащихся и возможностями совместной деятельности; условиями обучения. Одной из основных закономерностей развития учащихся в процессе обучения является взаимодействие видов познавательной деятельности при ведущей роли продуктивной. В структуру познавательной деятельности выделяют следующие виды: репродуктивную, репродуктивно-преобразовательную и продуктивную. Каждый из видов познавательной деятельности, в свою очередь описывается соответствующей совокупностью интеллектуальных действий и умений.

Вопрос о взаимодействии репродуктивной и продуктивной познавательной деятельности исследовался в работах советских психологов и педагогов (Л.С.Выготский, П.П.Блонский, М.Пистрак, И.С.Якиманская, П.М.Эрдниев, ЛМ.Фридман и др.). Воспроизводящая познавательная деятельность позволяет наиболее экономным путем вооружить большим количеством сведений; продуктивная познавательная деятельность способствует развитию познавательных возможностей, но требует большего времени для изучения материала (М.А.Данилов, В.И. Загвязинский, Б.П.Есипов, И.Я.Лернер, М.И.Махмутов, П.И.Пидкасистый и др.).

В процессе обучения математике непосредственно участвуют с одной стороны - учитель, с другой - ученик. Роли их в этом процессе представляются, по крайней мере, на первый взгляд, достаточно ясными: учитель организует, направляет и руководит процессом обучения математике, а ученик должен учиться, выполнять все требования учителя.

Обучением называется двусторонний процесс, состоящий из деятельности учителя, когда он ученикам объясняет, рассказывает, показывает, заставляет их выполнять упражнения, исправляет их ошибки и т.д., и из деятельности учеников, которые под руководством учителя усваивают знания и соответствующие умения и навыки. Обучение, есть основная форма психического развития.

А вот как определяется процесс обучения математике.

"Обучение в частности математике - сложный процесс управления, осуществляемый учителем с использованием вспомогательных средств (учебников, наглядных пособий, технических средств обучения)… Учитель перерабатывает информацию, получаемую им из программы, научной, учебной и методической литературы, а так же осведомительную информацию, об уровне и возможностях мыслительной деятельности ученика и передает, пользуясь определенными средствами, обучающую информацию, ученику.

Ученик воспринимает и перерабатывает информацию полученную им от учителя, из учебника и других источников и по требованию педагога передает ему информацию в качестве усвоения учебного материала и достигнутом развитии мыслительной деятельности в виде ответов на вопросы, решений упражнений и задач.

Основная роль учителя математики в современных условиях - это воспитание личности учащихся, формирование их потребностно-мотивационной сферы, воспитание их способностей, нравственных идеалов и убеждений. Обучение знаниям умениям и навыкам по математике является составной частью этого воспитания и тем процессом, в котором это воспитание осуществляется.

Процесс обучения математике более сложный, более противоречивый, чем это описано в приведенных определениях.

В психолого-педагогической литературе постоянно обсуждается проблема учета индивидуальных психологических особенностей школьников. Естественно возникает вопрос о том, какие же именно особенности должен учитывать учитель. Их очень много качественные особенности восприятия (предметность, осознанность, структурность и т.д.); преобладающие виды памяти (зрительная, слуховая, двигательная и т.д.); виды мышления (наглядно-образное, словесно-логическое и т.д.), его качества (гибкость, глубина, широта и т.д.). Между тем, необходимо иметь в виду, что возрастные особенности - это не нечто неизменное и вечное, то, что присуще ученикам определённого возраста. Сами эти особенности довольно резко меняются со временем. Рассмотрим некоторые психологические особенности ученика, которые важно учитывать в процессе обучения математике.

Ученик - это растущий, развивающийся человек. Придя в школу в семь лет, он заканчивает её в 17 лет вполне сложившимся человеком юношеского возраста. За эти десять лет обучения ученик проходит огромный путь физического, психического и социально-нравственного развития.

Подростковый возраст - это весьма сложный, таящий в себе опасность кризисных явлений, период в жизни ученика. В этот период организм ребёнка претерпевает кардинальные изменения. Развёртывается процесс полового созревания. С этим процессом связано возникновение у подростка физического ощущения собственной взрослости. У него возникает представление о себе уже не как о ребёнке, он стремится быть и считаться взрослым. Отсюда у подростка возникает новая жизненная позиция "Я-концепция" по отношению к себе, к окружающим людям, к миру. Он становится социально активным, восприимчивым к усвоению норм ценностей и способов поведения, которые существуют среди взрослых.

Период подросткового возраста характерен тем, что здесь начинается формирование морально-нравственных и социальных установок личности ученика, намечается общая направленность этой личности.

Подросток стремится к активному общению со своими сверстниками, и через это общение он активно познаёт самого себя, овладевает своим поведением, ориентируясь на образцы и идеалы, почерпнутые из книг, кинофильмов, телевидения.

Подросток становится более независимым от взрослых ещё и потому, что у него возникают такие потребности, которые он должен удовлетворить только сам (потребность в общении со сверстниками, в дружбе, в любви).

Родители и вообще взрослые при всём их желании не могут решить проблемы, встающие перед подростками в связи с возникновением у них новых потребностей, между тем как удовлетворение всех основных потребностей младших школьников зависит в основном от родителей. Всё это зачастую болезненно сказывается на отношении учащихся к учению. Вот как характеризует это известный психолог Н.С. Лейтес: "Дети 12-13 лет в подавляющем большинстве своём относятся к учению в основном благодушно: не утруждают себя излишними раздумьями, выполняют только уроки в пределах заданного, часто находят поводы для развлечения… Ослабление связи с учителем, снижение его влияния особенно дают о себе знать в недостатках поведения учеников на уроках. Теперь учащихся не только иногда позволяют себе игнорировать получаемые замечания, но могут и активно им противостоять. В средних классах можно столкнутся с изобретательными шалостями и проявлением самого легкомысленного поведения".

Общая картина работы учащихся-подростков на уроках по сравнению с младшими классами ухудшается. Ранее примерные и аккуратные ученики позволяют себе не выполнять задания. Тетради ведутся неряшливо. У многих учащихся меняется почерк, он становится неразборчивым и небрежным. При решении математических задач многие подростки не проявляют нужной настойчивости и прилежания. Попытки учителя заинтересовать учеников занимательностью формы изложения или какими-либо другими способами зачастую не приносят ожидаемого результата.

В то же время эти же подростки весьма охотно участвуют в работе различных кружков, где, казалось бы, наиболее трудные подростки охотно выполняют все указания взрослого руководителя кружка, с интересом и усердием овладевают теоретическими знаниями, нужными для выполнения практических работ.

Подростковый возраст есть начало внутреннего перехода ученика от положения объекта обучения воспитания, которым он был в младшем школьном возрасте, к положению субъекта этого процесса.

В подростковом возрасте происходит совершенствование таких познавательных процессов как память, речь и мышление.

Подростки уже могут мыслить логически, заниматься теоретическими рассуждениями и самоанализом. Они относительно свободно рассуждают на нравственные, политические другие темы, практически недоступные интеллекту младшего школьника. У старшеклассников наблюдается способность делать общие выводы на основе частных посылок и, напротив переходить к частным умозаключениям на базе общих посылок, т. е. способность к индукции и дедукции. Важнейшее интеллектуальное приобретение подросткового возраста - это умение оперировать гипотезами.

Если подростковый возраст есть начало внутреннего перехода ученика от положения объекта обучения и воспитания, которым он был в младшем школьном возрасте, к положению субъекта этого процесса, то в юношеском возрасте ученик становится (во всяком случае, должен становиться) уже подлинным субъектом своей деятельности в учебно-воспитательном процессе.

В то же время ученики ещё сохраняют материальную зависимость от родителей. Главным в их жизни становится подготовка к будущей самостоятельной, взрослой жизни, подготовка к труду, выбор жизненного пути, профессии.

В эти годы особую значимость для учеников приобретает ценностно-ориентационная деятельность. Ученик пытается произвести глубокую самооценку своей личности, своих способностей. Растёт и развивается рефлексия, познавательный интерес к философским проблемам, юноша пытается выяснить смысл жизни; оценить наблюдаемые явления с этой точки зрения.

Подросток весьма податлив влиянию сверстников. Внутренне отойдя от родителей, он ещё не пришёл к своей индивидуальности, которая обретается в юношеском возрасте. Если подростка волнует вопрос: "Неужели я не такой, как все?", то юношу: "Неужели я такой, как все?".

Учителю всё это надо иметь в виду и учитывать в своей работе.

Выше мы установили, что ученик в процессе обучения математике из объекта этого обучения постепенно становится его субъектом. Что это значит? В чём выражается различие между объектом и субъектом обучения? Ведь в том и в другом случае ученик как-то учится, приобретает знания, умения.

Действительно, и когда ученик является лишь объектом обучения математике, и когда он становится субъектом этого процесса он выполняет задания учителя, решает задачи, повторяет изученный материал и т.д., т.е. он учится. Все различия между учением ученика в роли объекта и его же учением в роли субъекта состоят в том, ради чего он это делает.

Человек, ученик есть деятельное существо. Он всегда что-то делает, участвует в какой-то деятельности. Но ученик участвует во многих различных деятельностях, совершает разные действия. Для того чтобы ученик эффективно учился, он должен совершать не любые действия, а вполне определённые. Встаёт вопрос: почему ученик совершает именно эти действия, а не другие, что побуждает совершать эти действия, что направляет и регулирует его деятельность в процессе обучения? Иными словами, что мотивирует - побуждает и направляет - деятельность ученика.

Все, что мы делаем, мы делаем из интереса, хотя бы из отрицательного интереса - боязни неприятностей. Таким образом, интерес - естественный двигатель детского поведения, он является верным выражением инстинктивного стремления, указанием на то, что деятельность ребенка совпадает с его органическими потребностями.

Эта потребность состоит, в частности, в том, что каждому ребенку от природы присуще стремление что - либо делать самостоятельно и получать от этого удовольствие. Психологическая точка зрения требует признать, что в учебно - воспитательном процессе личный опыт ученика представляет из себя все. Воспитание и обучение должны быть организованы так, чтобы не ученика обучали и воспитывали, а ученик воспитывался и обучался сам.

Только разобравшись в этом, мы сможем понять, в чём различия между объектом и субъектом процесса обучения. Кроме того, в этом надо разобраться ещё и потому, а может быть главным образом потому, что учитель должен научиться управлять деятельностью учащихся в процессе обучения, а для этого он должен формировать у них нужную мотивацию.

Поэтому учитель должен вызвать у учащихся такое желание, а это значит, что он должен формировать у них соответствующую мотивацию.

Под мотивацией понимают побуждения, вызывающие активность организма и определяющие ее направленность.

Однако когда деятельность уже началась, то она имеет определённую цель. Цель - это то, чего сознательно хочет достигнуть человек в результате своей деятельности. Но между целью деятельности и её побуждениями не всегда существует полное соответствие. Когда оно имеется, то говорят, что эта деятельность имеет смысл; в противном случае, когда цель деятельности и вызвавшие эту деятельность побуждения не соответствуют друг другу, то говорят, что деятельность не имеет смысла, лишена для данного человека смысла.

Например, когда ученики решают задачу перед ними стоит одна цель - научиться решать подобные задачи. Побуждения же могут быть самые различные. Так, одни из них решают задачу потому, что привыкли выполнять требования учителя, у них ещё имеется достаточно стойкая установка на выполнение требований учителя, но некоторые из них, кроме того, хотят получить хорошую отметку, похвалу. Для других главное - получить хорошую отметку; третьи решают задачу ещё и потому, что их интересует сам процесс решения, он приносит эмоциональное удовольствие; наконец, есть и такие, у которых, кроме перечисленных побуждений, есть ещё и стремление овладеть общим способом решения подобных задач. Возможно, что у некоторых учащихся и другие побуждения.

Однако независимо от мотивов, которые побуждают учащихся решать задачу, объективно их деятельность направлена на учебные цели, например, на то, чтобы каждый из них научился решать подобные задачи. Заметим, что сама задача с психологической точки зрения выступает лишь как материал, как средство этой деятельности.

Итак, ученик всегда является объектом деятельности в процессе обучения, а субъектом этой деятельности он становится тогда, когда сознательно принимает объективные цели деятельности за свои личные цели. В последнем случае обучение является наиболее эффективным, только в этом случае учитель может полностью осуществить цели и задачи обучения.

Учителю необходимо стремиться к тому, чтобы каждый ученик становился субъектом деятельности в процессе обучения. А для этого нужно, чтобы все стороны учебно-воспитательного процесса, его содержание, организация и методы содействовали такому становлению, были прямо направлены на воспитание ученика - субъекта своей деятельности.

Также большое значение в обучении школьников математики имеет тип их мышления и обучаемость.

Рассматривая индивидуальные компоненты мышления, нужно ставить перед собой задачу выделить те его особенности, от которых зависит легкость овладения однородными знаниями, темп продвижения в них, т. е. связывали его с понятием общих способностей. У школьников эти свойства их психики обуславливают успешность учебной деятельности, быстроту и легкость в овладении новыми знаниями, широту их переноса, т. е. выступают как их общие способности к учению. Для их обозначения в психологии широко используют термин "обучаемость".

Чем выше обучаемость, тем быстрей и легче приобретает человек новые знания, тем свободнее оперирует ими в относительно новых условиях, тем выше, следовательно, и темп его умственного развития. Вот обучаемость, наряду с фондом действенных знаний, т. е. тех, которые человек применяет на практике, входит в структуру умственного развития.

Об умственных способностях человека судят не потому, что он может сделать на основе подражания, усвоить в результате подробного, развернутого объяснения. Ум проявляется в относительно самостоятельном приобретении, "открытии" новых для себя знаний, в широте переноса этих знаний в новые ситуации, при решении нестандартных, новых для него задач. В этой стороне психики находит свое выражение продуктивное мышление, его особенности проявляются в формирующихся у человека качествах ума, определяя уровень и специфику обучаемости личности. Эти особенности, свойства мыслительной деятельности учащихся, качества их ума и есть компоненты обучаемости, они входят в ее структуру, а своеобразие их сочетаний определяет многообразие индивидуальных различий в обучаемости учащихся.

Одно из важнейших качеств ума - его глубина. Это качество проявляется в степени существенности признаков, которые человек может абстрагировать при овладении новым материалом, при решении проблем, и в уровне их обобщенности. Противоположное качество - поверхностность ума. Оно видно по выделению внешних, лежащих как бы на поверхности наблюдаемых явлений признаков, по установлению случайных связей между ними, что отражает низкий уровень их обобщенности.

Продуктивное мышление предполагает не только широкое использование усвоенных знаний, но и преодоление барьера прошлого опыта, отхода от привычных ходов мысли, разрешение противоречий между актуализированными знаниями и требованиями проблемной ситуации, оригинальность решений, их своеобразие. Эту сторону мышления чаще всего обозначают как гибкость ума, динамичность, подвижность и т. д. При гибком уме человек легко переходит от прямых связей к обратным, от одной системы действий к другой, если этого требует решаемая задача, он может отказаться от привычных действий и т. д. Инертность ума проявляется в противоположном: в склонности к шаблону, в трудности переключения от одних действий к другим, в длительной задержке на уже известных действиях, несмотря на наличие отрицательного подкрепления и т. д.

Г. П. Антонова, исследуя гибкость мышления при решении разнообразных математических задач, отмечает устойчивость этого качества и наличие весьма существенных различий по суммарному "показателю гибкости" мышления школьников одного и того же возраста.

Для творческого решения проблем важно не только выделить требуемые ситуацией существенные признаки, но и, удерживая в уме всю их совокупность, действовать в соответствии с ними, не поддаваясь на влияние внешних, случайных признаков анализируемых ситуаций. Эту сторону мыслительной деятельности обозначали как устойчивость ума. Она проявляется в ориентации на совокупность выделенных ранее значимых признаков, несмотря на провоцирующее действие случайных признаков новых задач того же типа. Трудности в ориентации на ряд признаков, входящих в содержание нового понятия или закономерности, необоснованная смена ориентации, переход от одних действий к другим под влиянием случайных ассоциаций - показатель неустойчивости ума.

Открытие принципиально новых знаний, столь характерное для мышления, представляет собой циклический процесс, в котором в противоречивом единстве выступают как хорошо осознанные, словесно-логические компоненты, так и не находящие адекватного отражения в слове, подсознательные, интуитивно-практические компоненты. Включение интуиции в процесс поиска нового закономерно. Однако, чтобы найденные таким образом знания приобрели действенную силу, т. е. могли быть переданы другим, использованы для решения широкого круга задач, должны быть хорошо осознаны как их существенные признаки, так и способы оперирования этими знаниями. Вот почему одним из основных качеств ума, входящих в обучаемость, мы считаем осознанность своей мыслительной деятельности, возможность сделать ее предметом мысли самого решающего проблему субъекта. В близком значении употребляется термин "рефлексия".

Это качество ума проявляется в возможности выразить в слове или в других символах (в графиках, схемах, моделях) цель и продукт, результат мыслительной деятельности (существенные признаки вновь сформированных понятий, закономерностей), а также те способы, с помощью которых этот результат был найден, выявить ошибочные ходы мысли и их причины, способы их исправления и т. п. Неосознанность мыслительной деятельности проявляется в том, что человек не может провести анализ решенной задачи (даже если она решена верно), не замечает своих ошибок, не может указать те признаки, на которые он опирался, давая тот или иной ответ, и т. д.

Внешне хорошо выраженная особенность продуктивного мышления - самостоятельность при приобретении и оперировании новыми знаниями. Это качество ума проявляется в постановке целей, проблем, выдвижении гипотез и самостоятельном решении этих задач, причем существенные индивидуальные различия по этому параметру экспериментально обнаружены уже у младших школьников.

На высшем уровне развития этого качества человек не только решает сложные для себя проблемы, но и сам, без внешней стимуляции, ищет наиболее совершенные, более высокого уровня обобщенности способы их решения.

В то же время на низшем уровне, при невозможности самостоятельного решения поставленной задачи, различия в продуктивности мышления проявляются в чувствительности к помощи: чем меньше помощь, которая необходима для решения, тем выше продуктивность мышления. Вот почему мы предпочитаем разграничивать самостоятельность и чувствительность к помощи.

Таковы основные особенности ученика, от которых зависит успешность обучения математике.

Следует лишь отметить, что выделение данных личностных свойств ученика в процессе обучения математике является весьма условным. Ведь психика представляет собой чрезвычайно сложное динамическое целое.

1.2 Психологические барьеры в обучении школьников математике

В соответствии с требованиями, предъявляемыми современной школой, обучение в ней должно ориентироваться на развитие продуктивного, творческого мышления, обеспечивающего возможность самостоятельно приобретать новые знания, применять их в многообразных условиях окружающей действительности.

Воспитание и обучение должны быть организованы так, чтобы не ученика обучали и воспитывали, а ученик воспитывался и обучался сам.

"Обучение путем "делания" в 6 - 7 раз продуктивнее обучения путем "слушания" (И.П. Подласый. Педагогика. 1996).

"Поэтому вся наша система обучения и воспитания, которая весь процесс сводила к пассивному восприятию учеником предначертаний и поучений учителя, является верхом педагогической несуразности" (Л.С. Выготский. Педагогическая психология, стр 82.)

Основной формой работы на уроке должна стать системная самостоятельная работа учащихся под руководством учителя, так как развитие происходит только через самостоятельную деятельность учащегося.

Возможности развития учащихся скрываются в специально отобранном содержании учебного материала, то есть в познавательных заданиях. Однако это лишь предпосылка для развития. Для того, чтобы обучение проявило свой развивающий эффект, необходимо выполнять условие: развиваемый ученик должен быть вовлечен в активную деятельность и общение. Это вытекает из того, что ученик в учебном процессе не только объект, но и субъект процесса собственного учения. Эффективность обучения зависит не только от характера предъявляемых заданий, но, прежде всего, от активности самого ученика.

Необходима реализация системы принципов, звенья которой определяются спецификой самого продуктивного мышления, особенностями его развития у школьников.

Проблема развития самостоятельности учащихся в процессе обучения математике является острой, ещё не разрешённой проблемой методики математики.

Анализ характера умственной деятельности учеников на различных уроках, в разных классах показал, что лишь 15-20% учебного времени тратится на самостоятельную работу, чем старше класс, тем самостоятельных работ меньше.

Если в числе тренировочных упражнений преобладают однотипные, при решении которых ученик ограничивается лишь получением ответа и сверкой его с готовым ответом, то такие упражнения не направляют усилия ученика на разрешение иных нешаблонных заданий, с чем ему придётся встречаться в жизни.

Знания ученика будут прочными, если они приобретены не одной памятью, не заучены механически, а являются продуктом собственных размышлений и закрепились в результате его собственной творческой деятельности над учебным материалом.

Под обобщением будем понимать распространение какого-либо суждения от частого понятия к общему

Суждения, полученные по аналогии, будут проблематическими и подлежат дальнейшему исследованию и доказательству.

Умозаключения по аналогии являются непременной составной частью творческого мышления, так как этим путём мысль человека выходит за пределы известного, пролагая путь к неизвестному.

Умственное развитие учащихся, которые должны подготавливаться уже в период школьного обучения к роли творчески мыслящих активных деятелей, не может быть полноценным, если их не научат в школе специально применению приёма аналогии.

Простое применение аналогии даёт упражнение подобное, однопорядковое с исходным. От него следует отличать составление задачи обобщением, когда новая задача оказывается в том или ином отношении сложнее исходной.

Процесс обобщения основывается на применении аналогии, но не сводится полностью к ней.

Применение обобщения связано с преобразованием мыслей, с умственным экспериментированием; оно есть одно из самых важных средств самообучения, то есть, самостоятельного расширения и углубления имеющихся знаний.

Для достижения усвоения нового понятия, способа решения нельзя обходиться задачами одного уровня трудности, а нужно предложить обобщённую задачу, а ещё лучше дать учащимся возможность самим обобщить решённую задачу, чтобы затем решить такую же, видоизменяя ее, если нужно прежний способ.

В практике обучения общее классное задание рассчитано на среднего ученика, а для расширения познавательных способностей более сильных учащихся необходимы дополнительные задания по самостоятельному обобщению и решению составленных задач.

Если, скажем готовую задачу, решают все учащиеся в основном одинаковой последовательностью рассуждений, то с обобщением уже справляется не всякий. Результат обобщения зависит не столько от суммы знаний, примерно одинаковой для всех учащихся класса, а от умения комбинировать, связывать эти знания по-новому, заглядывать дальше обычных пределов.

Характер упражнений, выполняемых в классе, должен отразиться и на характере контрольных и проверочных работ; чему обучают, то и следует проверять.

Всякая математическая задача неисчерпаема в своих связях с другими задачами; после решения задачи почти всегда можно найти предмет размышления, найти несколько направлений, в которых удаётся обобщить задачу, и найти затем решение созданных таким образом новых проблем.

Время и усилия, затраченные на обобщение знаний, окупаются той большой экономией мышления, в последующем, которые достигаются благодаря единообразным методам усвоения материала.

Умственное развитие - сложная динамическая система количественных и качественных изменений, происходящих в интеллектуальной деятельности субъекта в связи с овладением им человеческим опытом в соответствии с общественно-историческими условиями, в которых он живет, и возрастными и индивидуальными особенностями его психики. Фонд усвоенных знаний (включая и приемы, методы познания) и обучаемость как способность к их приобретению являются основными компонентами умственного развития.

Как показали многочисленные эксперименты, весьма существенны индивидуальные различия в уровне усвоения знаний. Школьники, находящиеся в идентичных условиях обучения, усваивают новый для них материал по-разному: одни на высоком, другие на среднем, третьи на низком уровне. При этом показатель уровня усвоения, характерный для того или иного учащегося, довольно устойчив (колебания хотя и имеют место, но обычно в пределах ближайшего уровня). В уровнях усвоения знаний проявляются типичные для учащихся устойчивые особенности психики, от которых зависит успешность учебной деятельности, возможность решать проблемы, требующие предусмотренных программой знаний. Школьники, усвоившие эти знания на низком уровне, не смогут их использовать при решении таких проблем.

Возможно ли доведение каждого учащегося массовой школы до высшего уровня овладения определенными знаниями?

Эксперименты показали, что возможно достижение высшего уровня овладения новым для них понятием всеми учениками, но различным путем. Одни достигают этого уровня уже на основе первичного знакомства с новым для них понятием; для других требуется в среднем решение от 10 до 20 задач с опорой при затруднении на помощь экспериментатора. Третьим необходимо было решить около сотни задач для полного овладения новым для них понятием.

Таким образом, в условиях индивидуализации обучения различия в уровнях знаний (по тому или иному разделу программы) могут быть сняты. В массовой школе, где обычно нет реального учета индивидуальных различий, к концу изучения определенного раздела программы разница в уровнях его усвоения несколько сглаживается, но все же остается весьма значительной.

В еще большей мере, чем от уровня знаний, продуктивность самостоятельной деятельности учащихся при усвоении новых знаний зависит от обучаемости. Среди учащихся разных возрастов имеются школьники с высоким, средним и низким уровнем развития их как практического, так и словесно-логического компонентов продуктивного мышления, практики с относительным преобладанием интуитивно-логического мышления над словесно-логическим и небольшое число теоретиков.

Исследования показали, что индивидуально-типические особенности развития продуктивного мышления школьников значительно перекрывают возрастные.

В современной психологии мышление понимается как социально-обусловленный, неразрывно связанный с речью психологический процесс поисков и открытия существенно нового, т. е. процесс опосредствованного и обобщенного отражения действительности в ходе ее анализа и синтеза.

Под математическим мышлением понимается прежде всего форма, в которой проявляется мышление в процессе познания конкретной науки - математики. Математическое мышление имеет свои черты и особенности, которые обусловлены спецификой изучаемых при этом объектов, а также спецификой методов их изучения.

Математическому мышлению свойственны те качества, которые присущи научному мышлению.

В условиях ориентации на "среднего" ученика, т. е. без реальной индивидуализации обучения, замедляется темп развития тех, кто пришел в школу значительно более развитым, чем их сверстники. Но в особенно тяжелые условия попадают школьники с замедленным темпом умственного развития. Условия обучения в массовой школе настолько не соответствуют их возможностям, что такие учащиеся с возрастом не приближаются в своем развитии к сверстникам, а все больше и больше отстают от них.

На успешность учебной деятельности, связанной с продвижением в развитии, большое влияние оказывают и другие стороны психики учащихся, и прежде всего - их умственная работоспособность, которая может в некоторой степени компенсировать наличие относительно невысокой общей успеваемости.

На продуктивность мыслительной деятельности весьма существенно влияет такое качество личности как интеллектуальная активность или интеллектуальная инициатива. Как показывают исследования наличие высоких умственных способностей не гарантирует проявление высокого уровня инициативы; нередко весьма способные люди ограничиваются и удовлетворяются решением той или иной поставленной проблемы более элементарным способом, хотя, при соответствующем побуждении со стороны, решают ту же проблему на самом высоком уровне.

Нельзя не учитывать при работе со школьниками и значительных различий в их интересах: от полного отсутствия, до наличия глубокого, устойчивого, разностороннего, активного познавательного интереса к тому или иному изучаемому в школе предмету или к их группе. Существенное влияние на успешность и специфику учебной деятельности оказывают и индивидуальные различия в ее мотивации.

В любом классе нет двух учащихся, идентичных друг другу по особенностям своей психики; каждый по-своему усваивает учебный материал. Естественно, возникает мысль о том, что в условиях массового обучения принцип его индивидуализации не может быть реализован. Это не так. Экспериментально доказана не только возможность, но и высокая эффективность реализации в школе принципа проблемно-индивидуального обучения. При данной форме работы, более развитые школьники имеют возможность работать над материалом повышенной трудности, самостоятельно решать посильные им задачи. Более слабые учащиеся получаются подробные инструкции от учителя, решая задачи с постепенно увеличивающейся трудностью, тем самым преодолевают трудности с некоторой помощью от учителя. Усваивают новый материал постепенно, постепенно продвигаются в своем развитии. Нередко такие ученики переходят в группы с более высоким уровнем.

В психологических работах уделяется внимание описанию отрицательной роли прошлого опыта, который может препятствовать, тормозить движение в принципиально новом направлении, тем самым подчеркивается необходимость преодоления "барьера прошлого опыта".

Под психологическим барьером прошлого опыта понимаются затруднения, испытываемые человеком при избирательной актуализации знаний в процессе решения творческих задач. Процесс включения (воспоминания) элементов прошлого опыта не всегда обеспечивает появления новообразований в творческом мышлении, а в каких-то случаях это даже может затруднить поиск правильного решения.

Одной из причин появления психологических барьеров прошлого опыта является наличие в задании таких условий, которые актуализируют ранее сложившиеся стереотипные действия, не позволяющие обнаружить новые условия, требуемые для разрешения творческого задания.

Исследования отражают известный прогресс в решении проблемы продуктивного мышления и путей его развития и оказывают свое положительное влияние на практику обучения. Однако, как это нередко бывает, усиленное внимание к одной стороне мыслительной деятельности (продуктивному мышлению) в практике обучения может привести к недооценке другой ее стороны - репродуктивного мышления и неразрывно связанной с ней мнемической деятельности, обеспечивающей прочность знаний, их готовность к актуализации в соответствии с требованиями задачи. В результате этого у школьников подчас не формируется прочной системы знаний основ изучаемого материала, из-за чего тормозится и интеллектуальное развитие.

Прямая установка на запоминание повышает уровень мыслительной активности при работе над подлежащим усвоению материалом, степень ее саморегуляции и самоконтроля, что значительно увеличивает эффект усвоения. Этому же способствует сознательное применение рациональных приемов мнемической деятельности (таких как группировка, классификация, составление плана, выделение смысловых опор и т. д.). Продуктивное мышление предполагает выход за пределы имеющихся знаний. Однако именно эти знания - опора в открытии нового. Чтобы открывать новое, неизвестное, отвергать уже известное, необходимо владеть этим старым, иметь достаточно широкий объем знаний (включая и их операционную сторону), достаточных для движения вперед и находящихся в состоянии готовности к актуализации в соответствии с поставленной перед субъектом целью. Чтобы выполнить это чрезвычайно важное требование, нужно предусмотреть специальную организацию мнемической деятельности, обеспечивающую прочность усваиваемых знаний и их готовность к актуализации при решении проблем. Эта специальная организация - один из важнейших принципов развития продуктивного мышления.

Однако, чем больше объем знаний, тем труднее обеспечить прочность их усвоения. Поэтому, необходимо ограничить тот круг знаний, которые подлежат усвоению, и искать пути организации знаний в такую систему высокого уровня обобщения, в которой по относительно немногим прочно закрепленным ее звеньям на основе рассуждений ученик мог бы найти дополнительные звенья, необходимые для оперирования приобретенными знаниями.

Важно четко ограничить обязательный минимум знаний от второстепенного материала и ориентировать учащихся на тщательное закрепление именно основных знаний и способов оперирования ими, что лучше делать сразу же при введении нового материала.

Ориентация на выделение и обобщение существенного в материале, классификацию в зависимости от его значимости содействует формированию одного из важнейших качеств продуктивного мышления - глубины ума.

В связи с большим объемом подлежащих усвоению знаний необходимо по возможности "сжать", "уплотнить" их, что может быть осуществлено на основе более раннего введения обобщенных знаний - теорий, законов, общих методов решения широкого класса задач. Такие знания позволяют учащимся не запоминать множество отдельных частных закономерностей, способов решения, а самим на основе логических рассуждений "выводить" их из общих положений.

Развивающее обучение - это обучение, которое целенаправленно обеспечивает развитие и активно использует его для усвоения знаний, умений и навыков. Развивающее обучение отдает приоритет развивающей функции обучения по отношению к информационной.

Развивающее обучение, в отличие от традиционного, характеризуется стремлением сделать развитие мышления школьников управляемым процессом, а основные приемы мышления - специальным предметом усвоения.

Проблемным называется такое обучение, при котором усвоение знаний и начальный этап формирования интеллектуальных навыков происходят в процессе относительно самостоятельного решения задач-проблем, протекающего под общим руководством учителя.

Проблемными называются, только те задачи, решение которых предполагает хотя и управляемый учителем, но самостоятельный поиск еще неизвестных школьнику закономерностей, способов действия, правил. Такие задачи возбуждают активную мыслительную деятельность, поддерживаемую интересом, а сделанное самими учащимися "открытие" приносит им эмоциональное удовлетворение и гораздо прочнее закрепляется в их памяти, чем знания, преподнесенные в "готовом" виде. Эта активная самостоятельная мыслительная деятельность приводит к формированию новых связей, свойств личности, положительных качеств ума и тем самым - к сдвигу в их умственном развитии (Н. А. Менчинская, А. М. Матюшкин).

Степень сложности задачи, как об этом пишет А. М. Матюшкин, определяется числом существенных взаимосвязей в ее условии, числом опосредований и преобразований, приводящих к нахождению искомого. Зависит она и от уровня самостоятельности при постановке и решении проблемы (В. А. Крутецкий). Наименьшая самостоятельность требуется от учащихся тогда, когда преподаватель сам ставит проблему и намечает основные этапы для ее решения, включая школьников лишь в отдельные звенья рассуждения, приводящего к определению искомого. Обычно так идет урок проблемного типа на начальном этапе работы над принципиально новым для школьников разделом программы, когда базис для решения такого рода проблем у них еще очень мал. Поставив проблему, учитель должен дать школьникам самим попытаться ее решить на основе имеющихся знаний и убедиться, что этих знаний для достижения цели явно недостает, а затем принять участие в построении доступных для них звеньев рассуждения, приводящих к новому знанию.

По мере накопления исходных знаний степень самостоятельности поисков решения должна нарастать. Учитель, поставив проблему, предоставляет школьникам самим искать путь ее решения, давая теперь лишь самые общие указания о направлении поиска. Далее он только ставит проблему и ограничивается критикой ложных ходов мысли при попытках школьников найти решение. Наконец, когда у школьников в изучаемой области накопились необходимые знания и навыки, следует предоставить им возможность самим увидеть в предполагаемых исходных ситуациях новую для себя проблему, сформулировать ее и найти способ решения, а педагог лишь в крайнем случае, если сами учащиеся в рассуждениях зашли в тупик, оказывает им минимальную помощь, намекая, как можно выйти из него.

Однако следует особо подчеркнуть, что даже полностью отвечающая указанным условиям задача может не стать для школьников проблемной, если при ознакомлении с ней учителю не удастся создать у них "проблемной ситуации". Проблемная ситуация отражает субъективное принятие задачи, реальное участие каждого школьника (хотя бы мысленно) в процессе ее решения. Важно, чтобы ученик сам задумался над сформулированной в классе проблемой, сам себе задал тот же вопрос и попытался дать на него ответ.

Наиболее эффективное средства для создания у школьников проблемных ситуаций - использование противоречий, конфликта между усвоенными знаниями, знакомыми способами решения определенного класса задач и теми требованиями, которые предъявляет новая задача; школьники должны убедиться в том, что решение задач на основе уже имеющихся знаний приводит к ошибкам. Учителю необходимо заострить внимание учеников на данной проблеме, подчеркнуть возникающее противоречие, стимулировать учащихся на поиски выхода из создавшегося проблемной ситуации, разрешить противоречие.

Проблемные ситуации у школьников могут быть созданы тем, что в задачах с недостающими и избыточными данными им будет предложено найти ряд возможных вариантов решения и обоснованно выбрать наиболее эффективный; часть данных в них определяется по таблицам, на основе дополнительных измерений и т. д. Решение таких задач приближает школьное обучение к жизненной практике, повышает действенность знаний, поскольку последние приобретены в процессе более или менее самостоятельной активной мыслительной деятельности.

Конфликтные ситуации, используемые в проблемном обучении, как бы наталкивают учащихся на ошибки. В проблемном обучении при создании конфликтных ситуаций обычно используется материал, в основе усвоения которого лежит углубленное понимание основных отношений между его существенными признаками, закономерностей, общих принципов решения целого класса задач и т. д. Задачи-проблемы ставят ученика в условия неопределенности, и возникновение здесь ошибок вполне возможно. Такие ошибки не страшны, если преподаватель обратит на них внимание школьников и добьется понимания тех причин, которые породили ошибки, и способов их преодоления.

Основной путь открытия нового для человека способа решения проблем - "анализ через синтез". Он предполагает включение содержащихся в условии задачи основных и выводимых из них промежуточных данных во все новые и новые системы связей, благодаря чему в них выявляются не выделенные ранее свойства, отношения, раскрываются их возможности для достижения цели.

Возникнет ли в условиях обучения у того или иного учащегося проблемная ситуация, обратится ли он для ее решения к наиболее эффективному приему продуктивного мышления - "анализ через синтез" или же к механической манипуляции данными - зависит не только от объективных факторов, но и от факторов субъективных, и прежде всего - от умственного развития школьников. Поскольку школьники одного и того же возраста имеют весьма существенные различия в достигнутом ими уровне умственного развития, полная реализация принципа проблемности не может быть осуществлена без индивидуализации обучения.

Проблемность и другие принципы развития творческого мышления не могут быть реализованы без учета возрастных и индивидуально-типических особенностей мышления. Возрастным особенностям интеллектуального развития посвящено немало исследований. В них выявлена стадиальность развития интеллекта, дана характеристика каждой стадии в зависимости от ведущего вида мыслительной деятельности.

На первой стадии ведущим является наглядно-действенное, практическое мышление, которое осуществляется в конкретной ситуации, в процессе практических действий с реальными предметами.

На второй стадии преобладает наглядно-образное мышление; оно позволяет решать задачи на основе оперирования уже не реальными предметами, а образами восприятия и представлений, содержащимися в детском опыте. Связь мышления с практическими действиями хоть и сохраняется, но не является такой прямой, непосредственной, как раньше. чтобы решать задачи ребенок должен отчетливо воспринимать, наглядно представлять рисуемую в них ситуацию.

На третьей, высшей, ступени развития ведущую роль в мыслительной деятельности приобретает отвлеченное, абстрактно-теоретическое мышление. Мышление выступает здесь в форме отвлеченных понятий и рассуждений, отражающих существенные стороны окружающей действительности, закономерные связи между ними. Овладение в ходе усвоения основ наук понятиями, законами, теориями оказывает значительное влияние на умственное развитие школьников. Оно раскрывает возможности самостоятельного творческого приобретения знаний и широкого применения их на практике.

Под влиянием всевозрастающих требований к школьному образованию психологи начали исследовать "зону ближайшего развития" детей. Была поставлена задача выяснить, каковы возможности мышления детей, если так изменить содержание и методы обучения, чтобы они активизировали развитие отвлеченного, абстрактно-теоретического мышления (В. В. Давыдов, С. Ф. Жуйков, Л. В. Занков, А. В. Запорожец, А. А. Люблинская, Н. А. Менчинская, А. В. Скрипченко, Д. Б. Эльконин и др.).

Вместе с тем установка на более раннее развитие отвлеченного, понятийного мышления, на его формировании на основе движения "от абстрактного к конкретному" - вероятно, вследствие подчас ошибочного понимания сущности этого процесса - на практике нередко приводит к недооценке роли наглядности, конкретизации знаний, а также к значения деятельности и других видов мышления. Нельзя забывать о том, что и отвлеченное, абстрактно-теоретическое мышление, далеко выходя за пределы чувственного опыта, только тогда обладает действенной силой, позволяет проникать в суть познаваемой действительности, когда оно неразрывно связано с наглядно-чувственными данными. Развитие отвлеченного мышления, без достаточной конкретизации усваиваемого материала, без связи с наглядно-практическим и наглядно-образным мышлением может привести к формальному усвоению знаний, к образованию пустых абстракций, оторванных от живой действительности.

Гармоничное развитие личности предполагает активизацию всех видов мышления, их совершенствование.

Необходимость развивать различные виды мыслительной деятельности вытекает из специфики продуктивного, творческого мышления. Процесс открытия новых знаний и у ребенка, впервые познающего давно открытые человечеством истины, и у ученого, впервые проникающего за пределы известного, не происходят в виде строгих логических рассуждений, непосредственно опирающихся на знакомые закономерности. Решение проблемы нередко происходит интуитивно, и в этом процессе существенную роль играют и практическое и образное мышление, непосредственно связанное с чувственной опорой.

В практической жизни у детей не реализуются те знания, умения, навыки, которые они не знают для чего применять. "Навык возникает как сознательно автоматизируемое действие и затем функционирует как автоматизированный способ выполнения действия" (С.Л. Рубинштейн, 2000). Сознательный же акт направлен на осуществление определенной цели. Если навык формируется в отрыве от самого действия, тогда его невозможно реализовать в жизни. Поэтому необходимо, чтобы дети при социальных взаимодействиях знали, какое действие, к какому результату приводит. Поэтому необходимо разработать методику, по которой можно формировать цель действий у учащихся.

Осуществляя целенаправленное математическое развитие школьников, следует помнить, что задачи являются здесь наиболее естественным и наиболее эффективным средством.

Мышление психологически выступает как деятельность по решению задачи. А. В. Брушлинский пишет, что развитие мышления происходит "именно в ходе решения задач, когда человек сам наталкивается на посильные для него проблемы и вопросы, формулирует их и затем решает".

С. Л. Рубинштейн, характеризуя психическую природу мыслительного процесса, указывал: "Всякий мыслительный процесс является по своему внутреннему строению действием, направленным на разрешение определенной задачи. Задача эта заключает в себе цель для мыслительной деятельности индивида, соотнесенную с условиями, которыми она задана. Начальным моментом мыслительного процесса обычно является проблемная ситуация. Мыслить человек начинает, когда у него появляется потребность что-то понять. Мышление обычно начинается с проблемы или вопроса, с удивления или недоумения, с противоречия".

Развитие математического мышления и творческих способностей осуществляется в ходе размышлений учащихся над задачами. Самостоятельная деятельность учащихся по решению задач занимает главное место в обучении математике. Умение решать задачи - критерий успешности обучения математике.

Задача в теории обучения понимается в широком смысле. В это понятие можно включить любое задание, требующее осуществления какого-либо познавательного акта, любой учебный текст, подлежащий усвоению. Согласно А.Н.Леонтьеву, задача - это есть цель, данная в определенных условиях.

Рассмотрим систематизацию задач в зависимости от их функций. К. И. Нешков и А. Д. Семушин выделяют следующие типы задач: задачи с дидактическими функциями, задачи с познавательными функциями, задачи с развивающими функциями. Характеристика функций задач дана в работах Ю. М. Колягина и Е. И. Лященко. По мнению Ю. М. Колягина, функции задач должны соответствовать основным компонентам образования: обучению, воспитанию и развитию. Е. И. Лященко, анализируя требования к задачам, исходит из деления задач на дидактические, познавательные, развивающие.

К развивающим задачам, или задачам с развивающими функциями относятся:

) задачи, для решения которых не требуются новые знания по предмету, надо применять имеющиеся знания в иной комбинации;

) задачи, с помощью и на основе которых приобретаются знания по предмету.

Развивающие задачи, или задачи с развивающими функциями, - это задачи, содержание которых может отходить от основного курса математики с посильным осложнением некоторых из изученных ранее вопросов школьной программы; запоминание и усвоение этого материала всеми учащимися необязательно. При решении этих задач ученику недостаточно применять изученные теоретические сведения или уже известные методы решения задач, а необходимо проявить выдумку, сообразительность.

Задачи с развивающими функциями не должны быть объектом изучения. Это не означает, что они превращаются в задачи, необязательные для решения. Таких задач должно быть достаточно много в учебнике для каждого класса, начиная с 1-го. Задачи, несущие развивающие функции, в основном предназначены для развития мышления учащихся. Однако способности учащихся различны, и поэтому их успехи в решении таких задач, естественно, неодинаковы. Необходимо исходить из того, что не каждый ученик может решить любую задачу, не каждый ученик сумеет достаточно глубоко разобраться в некоторых готовых решениях. Задачи с развивающими функциями не должны быть случайными. Они должны быть связаны с изучаемым материалом и представлять посильные для учащихся трудности. Наибольшую пользу эти задачи приносят тогда, когда они решаются без предварительной подготовки и достаточно разнообразны по содержанию и способам решения. Если же, как это часто делается, решать с целью "развития" несколько однородных задач подряд до тех пор, пока учащиеся не усвоят способ решения, то эти задачи потеряют свои ценные развивающие качества.

Решение задач с развивающими функциями не доводится до навыка. Учащиеся - каждый по мере своих возможностей - должны просто решать эти задачи. И все же при их решении учащиеся будут получать не только знания, но и развитие, что непременно отразится на усвоении ими всего курса математики. При решении задач с развивающими функциями создаются благоприятные условия для проявления самостоятельности учащихся, особое значение приобретает индивидуальный подход к учащимся.

Задачи с развивающими функциями не пользуются популярностью у многих учителей по ряду причин. Обучение их решению требует большого напряжения со стороны учителя и не сразу дает внешне заметные результаты. Кроме того, эти важные результаты обучения довольно трудно выявить самому учителю (одну задачу решила одна группа учащихся, с другой справилась другая группа, и учитель постоянно испытывает тревогу, что решение не оставит следа в сознании всех учащихся).

Решение проблемы в словесном плане, на основе теоретических рассуждений развертывается постепенно, звено за звеном. человеку невозможно при этом охватить все необходимые звенья, что затрудняет установление взаимосвязи между ними. Включение в этот процесс наглядно-образного мышления дает возможность сразу, "одним взглядом" охватить все входящие в проблемную ситуацию компоненты, а практические действия позволяют установить взаимосвязь между ними, раскрыть динамику исследуемого явления и тем самым облегчают поиск решения.

Преобладание практических, образных или понятийных видов мыслительной деятельности определяется не только спецификой решаемой проблемы, но и индивидуальными особенностями самих людей.

Одним из важнейших принципов развития творческого мышления является оптимальное (отвечающее целям обучения и психическим особенностям индивида) развитие разных видов мыслительной деятельности: абстрактно-теоретического, наглядно-образного, наглядно-действенного, практического мышления.

Как обучать детей нахождению способа решения математической задачи? Этот вопрос - центральный в методике преподавания математики. Для ответа на него в литературе предложено немало практических приемов, облегчающих поиск способа решения задачи. Однако теоретические положения относительного нахождения пути решения задачи остаются мало разработанными.

Особенности текста задачи могут определить ход мыслительного процесса при ее решении. Как сориентировать детей на эти особенности? Знание ответов на них составляют теоретико-методические положения, на основе которых можно строить конкретную методику обучения; они помогут определить методические приемы поиска способов решения задачи, в том числе решения различными способами.

Решение задач занимает в математическом образовании огромное место. Умение решать задачи является одним из основных показателей уровня математического развития, глубины освоения учебного материала.

Математику любят в основном те ученики, которые умеют решать задачи. Если научить детей владеть умением решения задачи, тем самым мы повысим интерес к предмету, на развитие мышления и речи.

Математические знания усваиваются детьми в определенной, приспособленной к их пониманию системе, в которой отдельные положения логически связаны одно с другим, вытекают одно из другого. При сознательном усвоении математических знаний учащиеся пользуются основными операциями мышления в доступном для них виде: анализом и синтезом, сравнением, абстрагированием и конкретизацией, обобщением; ученики делают индуктивные выводы, проводят дедуктивные рассуждения. Сознательное усвоение учащимися математических знаний развивает математическое мышление учащихся. Овладение мыслительными операциями в свою очередь помогает учащимся успешнее усваивать новые знания.

В процессе решения задачи ученик под руководством учителя, прежде всего, анализирует содержание задачи, расчленяя его на числовые данные, условия и вопрос.

При решении составных арифметических задач требуется применить более сложный и более тонкий анализ и синтез. Анализ содержания составной задачи, так же как и простой, сводится к расчленению его на числовые данные, условия и вопрос. Однако сами данные, условие и искомое должны подвергнутся дополнительно анализу, расчленению на составляющие их элементы.

В процессе обучения математике находит своё применение приём сравнения, то есть выделение сходных и различных признаков у рассматриваемых чисел, арифметических примеров, арифметических задач.

Основную часть времени на уроке ученик проводит, решая задачи, и во многом от их особенностей (сложности, многогранности, сюжетной формы, последовательности и др.) и зависит, насколько успешным будет процесс обучения математике. Но что же мы имеем на самом деле? На практике получается, что чаще всего процесс решения задач на уроке обладает некоторой рутинностью и оставляет ученику мало возможностей для творчества . Со временем такая специфика задач вырабатывает у ученика некоторый неправильный стереотип мышления, относящийся к решению задач. Ученик просто ищет стандартную ситуацию, к которой можно было бы применить известные формулы и теоремы, и теряется, когда предложенная задача требует даже несложного нестандартного подхода.

По мнению Л.Фридмана, одной из основных в обучении математике функций задач является функция формирования и развития у учащихся общих умений решений любых математических (в том числе и прикладных) задач.

Учащиеся же в настоящее время не получают никаких специальных знаний, на базе которых возможно такое формирование. Более того, в настоящее время эти общие умения формируются чисто стихийно, а не в результате целенаправленного, систематического обучения. Считается, что эти умения могут возникнуть лишь благодаря решению большого числа математических задач.

После решения задач учащиеся сравнивают, каким действием решается та или другая задача: одна сложением, другая умножением, а затем сопоставляют способы решения с различиями в условиях задач. Такое сопоставление помогает учащимся лучше осознать смысл выражений "больше на несколько единиц" и "больше в несколько раз" и прочнее установить связь между условием каждой задачи и способом её решения.

Сравнение основано на анализе и синтезе: необходимо расчленить каждую задачу на составляющие её элементы, а затем мысленно соединить сходные элементы, выделив при этом существенные различия.

При объяснении учащимся новой для них по способам решения задачи с многозначными числами часто используется приём аналогии: учитель предлагает решить аналогичную задачу с небольшими числами, вычисления над которыми можно выполнить устно.

Используя в обучении математике различные методы, учитель применяет их так, чтобы они содействовали активизации мышления учащихся, и тем самым способствовали его развитию.

Одним из эффективных средств преодоления психологических барьеров учащихся является решение математических задач. Математические задачи отражают различные стороны жизни, несут много полезной информации, поэтому их решение является одним из звеньев в системе воспитания вообще, патриотического, нравственного и трудового в частности.

Хорошо подобранные и правильно методически расположенные задачи помогают ученику усвоить теоретический материал, делают курс математики более интересным, вызывают потребность в новых знаниях и умении самостоятельно их приобретать. Приступая к решению задачи, ученик сначала знакомится с ее формулировкой, решение же пока остается вне поля его деятельности. Поэтому очень важно, чтобы содержание задачи вызывало живой интерес. Полезно, когда тексты задач обращены не только к уму, но и к эмоциям детей, вызывая у них чувство причастности к решению актуальных проблем, стоящих перед нашей страной. При этом воспитательное воздействие содержания задач осуществляется не только через условие задачи, но и непроизвольно, через подтекст материала. С усвоением любой информации связано формирование отношения к ней. Отсюда понятно значение содержания решаемой задачи.

Учебная работа школьников на уроках математики, наряду с рассмотренными направлениями усиления воспитательной направленности школьного обучения, также очень важна. Необходимость убедительной аргументации по ходу решения задач способствует развитию таких волевых качеств, как настойчивость, самостоятельное преодоление трудностей, критическое отношение к себе и к окружающему. Поиски и нахождение самостоятельных путей решения задач и доказательства теорем способствуют развитию творческого подхода к выполняемой работе, духа новаторства. Поэтому учащиеся не должны выступать на уроках в роли пассивных слушателей. На уроке должны использоваться разнообразные виды самостоятельной учебной работы, рациональные приемы учебы. Такая организация обучения математике способствует пониманию того, что смысл жизни человека состоит в труде, что только творческий труд дает удовлетворение всегда, будь то деятельность ученого или ученика.

Тексты задач должны не только давать материал для ума, но и вызывать у детей чувство сопричастности к текущим событиям, желание преодолевать трудности. Однако в учебных пособиях число задач, действующих на эмоции ученика, создающих проблемную ситуацию, невелико.

В процессе решения математических задач учащиеся усваивают конкретный смысл арифметических действий, знакомятся со знаками для записи выполняемых действий; изучаемые правила сразу же подтверждаются в решении задач. Такие задачи предусмотрены программой каждого года обучения.

В школе невозможно рассматривать все виды математических задач. Сколько бы задач ни решали в школе, всё равно учащиеся в своей будущей работе встретятся с новыми видами задач. Поэтому школа должна вооружать учащихся общим подходом к решению любых задач.

Система в подборе задач и расположении их по времени построена с таким расчетом, чтобы обеспечить наиболее благоприятные условия для сопоставления, сравнения, противопоставления задач, сходных в том или ином отношении, а также задач взаимно обратных. При этом имеется в виду, что в процессе изучения математики дети все время будут встречаться с задачами различных видов. Это исключает возможность выработки штампов и натаскивания в решении задач: дети с самого начала будут поставлены перед необходимостью каждый раз производить анализ задачи, устанавливая связь между данными и искомым, прежде чем выбрать то или иное действие для ее решения.

Математические задачи являются тем материалом, на котором будет решаться важнейшая задача преподавания математики - развитие мышления и творческой активности учащихся.

Важно научить всех детей самостоятельно находить путь решения предложенной задач, применять общие подходы к их решению. Дети учатся анализировать содержание задачи, точно объясняя, что известно в решаемой задаче и что неизвестно, что следует из условия задачи, какие арифметические действия и в какой последовательности должны быть выполнены для получения ответа на вопрос задачи; обосновывать выбор каждого действия и пояснять полученные результаты; составлять по задаче выражение и вычислять его значение; устно давать полный ответ на вопрос задач и проверять правильность решения задачи. Необходимо, чтобы учащиеся знали о возможности различных способов решения некоторых задач и сознательно выбирали наиболее рациональный из них.

В процессе работы над задачами дети упражняются в самостоятельном составлении задач по различным заданиям учителя. Числовой и сюжетный материал для составления задач берется из окружающей действительности с использованием особенностей той местности, в которой живут дети. Составление и решение такого рода задач способствует не только лучшему осознанию особенностей структуры и хода решения задач различных видов, но и развитию творческой самостоятельности детей, расширению их кругозора, усилению связи обучения с жизнью.

Таким образом, в процессе решения математических задач реализуются образовательные, воспитательные и развивающие цели. Решение задач способствует формированию у детей полноценных знаний, определяемых программой. Задачи дают возможность связать теорию с практикой, обучение с жизнью. Решение задач позволяет углубить и расширить представления детей о жизни, формирует у них практические умения (подсчитать стоимость покупки, ремонта квартиры).

Однако своеобразным психологическим барьером в решении задач будет то, что при предложении учителем новой задачи после решения предыдущей, ученик, зная алгоритм решения предыдущей задачи, не будет стараться найти новые способы решения и подходы к осмыслению задачи. Барьером будет и необходимость отказа от старых алгоритмов решения задач при переходе к новым видам задач (психологический барьер прошлого опыта).

Поэтому проблему математического образования в школе нельзя сводить только к передаче учащимся определенной суммы знаний и навыков по этому предмету. Перед учителями математики стоит и другая, не менее важная задача Если в недавнем прошлом основной задачей, стоящей перед учителем, была передача ученикам определенной суммы знаний, то в настоящее время на первый план выдвигается задача развития учащихся в процессе обучения.

Глава 2. Методика преподавания математики в 5 классе средней школы с преодолением психологических барьеров

2.1 Описание методики

С целью практического обоснования выводов, полученных в ходе наблюдения за деятельностью учащихся пятых классов средней школы № 1605 г. Москвы, было проведено исследование.

Работа велась с ноября 2010 г. по апрель 2011 г. и включала несколько этапов. На первом этапе проводилось исследование, которое позволило выявить наличие психологических барьеров у учащихся данного класса в процессе обучения математике. Вторым этапом работы было проведение экспериментальных занятий, направленных на формирование у учащихся рациональных приемов познавательной деятельности и преодоление барьеров. Заключительный этап исследования, проводился теми же методами, что и первый. Целью этого этапа было - выявить какие-либо индивидуальные изменения у учащихся класса в преодолении барьеров.

После чего были подведены итоги исследования.

В методике моделировалось обучение, непосредственно направленное на преодоление психологических барьеров. Эта методика была построена в виде обучающего эксперимента, в котором школьники включаются в проблемные ситуации, рассчитанные на самостоятельное решение новых для них учебных задач. Остановимся кратко на характеристике структуре экспериментов и способов обработки получаемых на их основе данных.

Первый этап - выявление у учащихся психологических барьеров при обучении. Изучение проходило во время занятий, когда упомянутые выше барьеры проявлялись при выполнении определенных заданий учителя или при самостоятельной работе. Во время наблюдения было зафиксировано несколько таких барьеров:

) трудность преодоления имеющихся комплексов от неудачных решений предыдущих задач;

) отсутствие мотивации к решению задач и упражнений по математике, отсутствие мотивации к познавательной деятельности вообще;

) боязнь выглядеть хуже других перед одноклассниками;

) трудности в решении новых задач из-за использования алгоритмов решения, применявшихся к старым задачам;

) несамостоятельность в переходе от старых алгоритмов решения задач к новым.

Так же во время наблюдения были выявлены некоторые причины возникновения тех или иных трудностей:

·        Несформированность мыслительной операции "анализ через синтез"

·        Недостаточное развитие анализа пространственных отношений

·        Несформированность понятий "больше", "меньше"

·        Несформированность умения перехода из конкретного плана действий в абстрактный

·        Недостаточное развитие смысловой памяти

·        Недостаточная гибкость мыслительной деятельности

·        Недостаточная отдифференцированность понятий "сложения", "вычитания", "умножения", "деления"

·        Недостатки в развитии процессов произвольного внимания

·        Низкий уровень сформированности внутреннего плана действий

·        Сниженный уровень интеллектуальной деятельности

·        Сниженная работоспособность

В исследовании принимало участие 24 ученика класса 5.3 средней школы № 1605 г.Москвы. Психологические барьеры среди них распределились следующим образом (см. приложение 1):

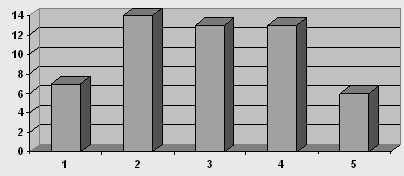
Рис. 1 Распределение психологических барьеров среди учащихся класса 5.3 средней школы №1605 г.Москвы

На этом этапе все наблюдаемые барьеры фиксировались, каждому ученику присваивался индивидуальный номер.

После завершения первого этапа была проведена обучающую часть исследования, которая заключалась в проведение со школьниками ряда занятий по методике решения математических задач.

.2 Апробация методики преодоления психологических барьеров в классе 5.3 средней школы № 1605 г. Москвы

Обучающий эксперимент включал три этапа: предварительный, основной и вспомогательный. На предварительном этапе экспериментатор обеспечивал школьникам исходный минимум знаний; т.е. устранение тех причин, которые вызвали тот или иной психологический барьер, создавалась установка на решение новой проблемы, вызывалось желание решить ее как можно лучше, без боязни ошибиться при поисках решения. С этой целью на ряде простых арифметических задач экспериментатор напоминал школьникам о прямой и обратной зависимости.

Для дальнейшего эффективного преодоления психологических барьеров при изучении математики на предварительном этапе школьникам предлагалось решить задачи, которые помогли бы им устранить причины, которые повлекли за собой возникновение того или иного психологического барьера (см.приложение 3).

Остановимся теперь на характеристике тех показателей, по которым при анализе собранного экспериментального материала мы судили о преодолении психологических барьеров школьников, давая их качественную характеристику.

Самостоятельность (преодоление барьера № 5) учащихся определялась по тому, как справился он с решением проблемы на основном этапе, или ему дополнительная помощь со стороны учителя. По степени помощи, необходимой испытуемому для выделения искомой закономерности определялись потенциальные возможности учащегося в решении проблемы.

Преодоление трудностей в решении новых задач из-за использования алгоритмов решения, применявшихся к старым задачам (барьер № 4), отражающее степень существенности абстрагируемых признаков и степени их обобщенности, определялась на основе анализа суждений испытуемых при их попытках сформулировать искомую закономерность для каждого нового цикла задач.

О преодолении боязни выглядеть хуже других перед одноклассниками, "смелости" мыслительной деятельности и характере ее реализации можно судить по соотношению хода практического решения задач с высказываниями испытуемых вслух о тех закономерностях, по которым, по их мнению, можно решить задачу. Отсутствие боязни дает основание для утверждения о преодолении барьера № 3; присутствие боязни говорит об осознанности этой деятельности. Примером данного психологического барьера может служить боязнь учащегося решать задачу у доски. Преодоление данного психологического барьера было разделено на несколько этапов. В начале ученику, имеющий психологический барьер данного типа предлагалось решить задачу у доски, естественно он отказывался выходить к доске из-за боязни выглядеть хуже других, аргументируя это тем, что он не знает, как решить данную задачу. Тогда ему предлагалась помощь, но не со стороны учителя, а со стороны учащихся и сообщалось, что за неправильное решение плохая оценка ставиться не будет. Помощь со стороны класса состояла в том, что они помогали найти верный ход решения задачи, предлагая различные варианты (в том числе свой вариант предлагал и ученик у доски). Далее ученик мог остановиться на том варианте, который предлагали одноклассники или на том, который предложил он. Наблюдения показали, что в дальнейшем у учеников, имеющих психологический барьер данного вида, при совместной деятельности пропала боязнь. Но при совместной деятельности может возникнуть другая проблема несамостоятельность. Для этого ученикам , имеющим этот барьер предлагалась инструкция, которая могла бы помочь им при решении задачи.

Алгоритм решения для ученика:

. Пользуясь "деревом рассуждения", составь и запиши план решения задачи.

2. Выполни модель задачи.

. Составь к задаче "дерево рассуждения".

. Пользуясь "деревом рассуждения", составь план решения.

. Измени задачу так, чтобы она имела разные способы решения и отрази это на модели задачи.

Преодоление имеющихся комплексов от неудачных решений предыдущих задач (барьер № 2) проявляется в возможности формулировки двух вариантов искомой закономерности в совершенствовании раз сформулированного суждения, в переходе к суждениям более высокой степени обобщенности, введении в них новых научных терминов вместо житейских, в легкости отказа от ошибочности суждений и т. д.

Мотивация к решению задач и к познавательной деятельности вообще (барьер № 1) найдет свое выражение в воспроизведении и целесообразной ориентации на найденный в процессе анализа значимый признак закономерности для решения задачи.

В работе не приводиться описание каждого проведенного урока. Хочу обратить внимание, лишь на некоторые методические приемы, использованные на уроках математики для активизации познавательной, творческой и мыслительной деятельности учащихся, и их теоретическом обосновании.

Воспитание в процессе обучения, развитие мотивации и интереса к обучению у учащихся в процессе изучения ими математики является одной из актуальных задач, стоящих перед учителями математики в современной школе. Основным средством такого воспитания и развития математических способностей учащихся являются задачи. Не случайно известный современный математик и методист Д. Пойа пишет: "Что значит владение математикой? Это есть умение решать задачи, причем не только стандартные, но и требующие известной независимости мышления, здравого смысла, оригинальности, изобретательности".

При обучении математике на решение задач отводится большая часть учебного времени. Можно сделать вывод, что учебное время, отводимое на решение задач в школе, используется неэффективно, а это отрицательно сказывается на качестве обучения математике в целом.

Одна из главных причин затруднений учащихся, испытываемых ими при решении задач, заключается в том, что математические задачи, содержащиеся в основных разделах школьных учебников, как правило, ограничены одной темой. Их решение требует от учащихся знаний, умений и навыков по какому-нибудь одному вопросу программного материала и не предусматривает широких связей между различными разделами школьного курса математики. Роль и значение таких задач исчерпываются в течении того непродолжительного периода, который отводится на изучение (повторение) того или иного вопроса программы. Функция таких задач прежде всего сводится к иллюстрации изучаемого теоретического материала, к разъяснению его смысла. Поэтому учащимся нетрудно найти метод решения данной задачи. Метод решения иногда подсказывается названием раздела учебника или задачника, темой, изучаемой на уроке, указаниями учителя и т. д. Самостоятельный поиск метода решения учеником здесь минимален. При решении задач на повторение, требующих знания нескольких тем, у учащихся, как правило, возникают определенные трудности.

К сожалению, в практике обучения математике решение задач чаще всего рассматривается лишь как средство усвоения школьниками программного материала. Задачи повышенной трудности из дидактических материалов, сборников задач, в основном закрепляют умения и навыки учащихся в решении стандартных задач, задач определенного типа. А между тем функции задач очень разнообразны: обучающие, развивающие, воспитывающие, контролирующие. В связи с этим задачи могут использоваться и как средство преодоления психологических барьеров.

Любая предлагаемая учителем задача для решения учащимся должна служить конкретным целям обучения. И все же главная цель задач - развить творческое мышление учащихся, заинтересовать их математикой, привести к "открытию" математических фактов.

Достичь этой цели с помощью одних стандартных задач невозможно, хотя стандартные задачи, безусловно, полезны и необходимы, если они даны вовремя и в нужном количестве. Следует избегать большого числа стандартных задач как на уроке, так и во внеклассной работе, так как в этом случае сильные ученики могут потерять интерес к предмету, а у слабых учеников выработаться шаблонность.

Ознакомление учащихся лишь со специальными способами решения отдельных типов задач создают, опасность того, что учащиеся ограничатся усвоением одних шаблонных приемов и не приобретут умения самостоятельно решать незнакомые задачи. При первом знакомстве с задачей они будут говорить, что такие задачи в классе не решали.

В системе задач школьного курса математики, необходимы задачи, направленные на отработку того или иного математического навыка, задачи иллюстративного характера, тренировочные упражнения, выполняемые по образцу. Но не менее необходимы задачи, направленные на воспитание у учащихся устойчивого интереса к изучению математики, творческого отношения к учебной деятельности математического характера. Необходимы специальные упражнения для обучения школьников способам самостоятельной деятельности, обучение общим приемам решения задач, для овладения ими методами научного познания реальной действительности и приемам продуктивной умственной деятельности Такими задачами могут служить задачи различного типа.

Осуществляя целенаправленное обучение школьников решению задач, с помощью специально подобранных упражнений, можно научить их наблюдать, пользоваться аналогией, индукцией, сравнениями, и делать соответствующие выводы. Так же прививать учащимся прочные навыки творческого мышления.

В школьных учебниках математики мало задач, с помощью которых можно показать учащимся роль наблюдения, аналогии, индукции, эксперимента.

Такого типа задачи необходимо решать на уроке со всеми учащимися, а не только с отдельными учениками. Решение проводить в процессе изучения или повторения учебного материала предусмотренного программой. Для развития навыков преодоления психологических барьеров необходимо несколько изменять условия задач, встречающихся в школьных и других учебниках.

Полезно предложить учащимся самим установить с помощью наблюдений и индукции формулы для решения задач.

На уроках математики необходимо систематически использовать задачи, способствующие целенаправленному развитию творческого мышления учащихся, их математическому развитию, формированию у них познавательного интереса и самостоятельности. Такие задачи требуют от школьников наблюдательности, творчества и оригинальности.

Эффективное развитие математических способностей у учащихся и преодоление психологических барьеров невозможно без использования в учебном процессе задач на сообразительность, задач-шуток, математических ребусов.

Как показывают исследования, рассмотрение на уроке задач такого типа, для решения которого недостаточно известного учащимся материала, вызывает естественный интерес к новой теме, осознание необходимости ее изучения и соответствующий настрой к преодолению предстоящих на пути приобретения новых знаний трудностей.

Процесс обучения предполагает целенаправленное управление мыслительной деятельностью учащихся, что приводит к продвижению учеников в их умственном развитии. Чтобы развить мышление учащихся, нужно показать им как функционирует мышление на практике. Развитие происходит в деятельности, поэтому необходимо создавать ученикам условия соответствующей деятельности, нужно демонстрировать сложную картину поиска решения, всю трудность этой работы. В этом случае ученики становятся активными участниками процесса поиска решения, начинают понимать источники возникновения решения. Как результат - ими легче осваиваются причины ошибок, затруднений, оценивается найденный способ решения и ход логических мыслей, а без этого знания не могут перейти в убеждения.

Системное развитие логического мышления должно быть неотрывно от урока, каждый ученик должен принимать участие в процессе решения не только стандартных заданий, но и задач развивающего характера (активно или пассивно).

На уроках учитель должен моделировать ту умственную деятельность, которая нужна на данном этапе развития (учить анализировать задачи, делать чертежи, выявлять отношения объектов и т.д.). Это имеет обучающее и воспитывающее значение: учащиеся приобщаются к методу поиска, ориентируются не только на результат, но и на процесс его достижения, т.е. учатся мыслить логически.

Можно выделить два подхода к формированию и становлению логико-математического мышления:

. традиционное обучение, приводящее в зависимости от воздействия и других объективных причин к формированию либо эмпирического, либо теоретического мышления.

. специально организованное обучение, ориентированное на формирование учебной деятельности, приводящее к становлению теоретического мышления.

Для формирования логического мышления приоритетным является второй подход, который и был положен в основу формирования технологии.

Для осуществления формирования логического мышления учащихся 5-6 классов была составлена система развивающих заданий по темам:

· аналогия;

· исключение лишнего;

· "в худшем случае";

· классификация;

· логические задачи;

· перебор;

· задачи с геометрическим содержанием;

· задачи "на переливание";

· задачи-шутки;

· ребусы и кросснамберы;

· занимательные задания.

Эти задачи можно разделить на группы, учитывая их воздействие на мыслительную деятельность учащихся.

Формирование гибкости ума, освобождение мышления от шаблонов происходит при решении задач-шуток, занимательных заданий, задач на перебор вариантов, т.к. в большинстве своем эти задачи не привязаны к темам и не требуют особой теоретической подготовки.

Задачи на переливание, логические задачи, ребусы, задачи на классификацию учат школьников умению рассуждать, формируют математический стиль мышления, развивают логико-лингвистические способности детей, которые приводят к умению четко мыслить, полноценно логически рассуждать и ясно излагать свои мысли.

Задачи на аналогию и исключение лишнего используются для формирования умений поиска решения задач, интуиции, требуют знания теории и нешаблонного подхода к решению.

Задачи с геометрическим содержанием нацелены на знание геометрических фигур и их свойств как основы для формирования пространственных и изобразительных умений школьников, на расширение кругозора.

Учитель, преподающий в 5-6 классах, может развивать логическое мышление учащихся с помощью созданной системы заданий. Для этого необходимо учитывать следующее:

. выбранные задания должны быть посильными для детей;

. задания, отобранные для одного урока, должны быть разнообразными для воздействия на различные компоненты мышления;

. если ученики не справляются с заданием, то целесообразно оставить его на обдумывание до следующего урока;

. ученикам можно дать необязательное домашнее задание по составлению аналогичных задач;

Система развивающих заданий

Аналогия

Аналогия - это сходство между объектами в некотором отношении. Использование аналогии в математике является одной из основ поиска решения задач. Задачи этой серии направлены на отработку таких познавательных приемов, как проведение словесных аналогий и нахождение аналогий между фигурами.

Например:

. уменьшаемое - разность, множитель - …?

. продолжите ряд: 1, 5, 13, 29, …

, 19, 37, 61, …

Исключение лишнего

В каждой задаче этой серии указаны четыре объекта, из которых три в значительной мере сходны друг с другом, и только один отличается от всех остальных.

Например,

. Сумма, разность, множитель, частное

. 9, 12, 8, 15

. см, дм, м², км.

В худшем случае

Это прием решения задачи, где для доказательства какого-либо утверждения можно рассмотреть самый неудобный, худший случай, в котором утверждение выполняется. Если мы докажем утверждение для худшего случая, то тем более оно будет верно и в остальных случаях. Главное - правильно определить этот худший случай.

Например:

.В классе 37 человек. Докажите, что среди них найдутся четыре человека, родившиеся в один и тот же месяц.

.Есть три ключа от трех замков. Какое наименьшее количество проб нужно осуществить, чтобы подобрать ключи к замкам?

Классификация

Классификация - это общепознавательный прием мышления, суть которого заключается в разбиении данного множества объектов на попарно непересекающиеся подмножества (классы). Число таких подмножеств, а также их состав зависит от основания классификации (т.е. признака, существенного для данных объектов), которое может принимать различные значения.

Например:

Что объединяет слова длина, площадь, масса? Какое слово к ним подходит: секунда, центнер, величина, метр?

Логические задачи

Логические задачи - это задачи, требующие умения проводить доказательные рассуждения, анализировать.

Например:

.Ира, Даша, Коля и Митя собирали ягоды. Даша собрала ягод больше всех, Ира - не меньше всех. Верно ли, что девочки собрали ягод больше, чем мальчики?

.Наташа произнесла истинное утверждение. Лена повторила его дословно и оно стало ложным. Что сказала Наташа?

Перебор

Сущность этого приема заключается в проведении организованного разбора и анализа всех случаев, которые потенциально возможны в ситуации, описанной в задаче.

Например:

. Сколько имеется двузначных чисел, у которых среди цифр есть хотя бы одна пятерка?

. В числе 48352 зачеркните такие две цифры, чтобы число, образованное оставшимися цифрами в том же порядке было наибольшим (наименьшим).

Задачи с геометрическим содержанием

. Нарисуйте два треугольника так, чтобы их общей частью были: а) шестиугольник; б) пятиугольник; в) четырехугольник; г) отрезок; д) точка.

. Разрезать квадрат на две равные фигуры (10 способов).

. Деревянный куб покрасили со всех сторон, потом распилили на 27 одинаковых кубиков. Сколько кубиков имеют 3 окрашенные грани, 2 окрашенные грани? Сколько кубиков не окрашено?

Задачи на переливание

. В первый сосуд входит 10 литров воды. Как, используя еще два пустых сосуда по 5 и 7 литров, разделить воду на две части?

. Восьмилитровый бидон наполнен водой. Как с помощью трехлитровой и пятилитровой банок отлить 1л воды?

Задачи-шутки

. Гусь стоит 20 рублей и еще половину того, сколько он на самом деле стоит. Сколько стоит гусь?

. Сколько концов у двух палок, у трех палок, у пяти с половиной палок?

. Какой математический знак нужно поставить между 5 и 6, чтобы полученное число было больше 5, но меньше 6?

. Один поезд отправляется из Москвы в Пермь, одновременно с ним выходит поезд из Перми в Москву, скорость которого в два раза больше. Какой из поездов в момент встречи будет находиться дальше от Москвы?

. Крышка стола имеет 4 угла. Один угол отпилили. Сколько углов осталось?

Занимательные задачи

1. Чему равно произведение ?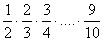

. Вдоль всей траектории забега поставили 15 столбов. После начала забега спортсмен был у третьего столба через три минуты. За сколько минут он пробежит весь путь? (Скорость спортсмена считать постоянной).

Проведенная работа по формированию логического мышления у учащихся 5-6 классов позволяет сделать следующие выводы:

· логическое мышление развивается интенсивнее, если создавать на уроке атмосферу уважения, поощрять инициативу и стимулировать творчество учащихся;

· система развивающих заданий позволяет привить интерес к предмету, дает более глубокое и полное понимание изучаемых тем, развивает мышление учащихся, помогает преодолеть трудности при решении

Результативность. Система заданий является средством повышения уровня логического мышления учащихся 5-6 классов, развивает интеллект. Повышается успеваемость учащихся, прививается интерес к предмету, помогает учащимся справиться с трудностями при решении нестандартных задач.

Нестандартные задачи - это такие задачи, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения".

Однако следует заметить, что понятие "нестандартная задача" является относительным. Одна и та же задача может быть стандартной и нестандартной, в зависимости от того, знаком решающий со способами решения задач такого типа или нет. Задача является для учащихся нестандартной до тех пор, пока учащиеся не познакомились со способами решения таких задач. Но если после решения этой задачи учащимся предложить несколько аналогичных задач, такие задачи становятся для них стандартными.

Можно сделать вывод, что нестандартная задача - это задача, алгоритм решения которой учащимся неизвестен, то есть учащиеся не знают заранее ни способа ее решения, ни того, на какой учебный материал опирается решение.

К сожалению, иногда учителя единственным способом обучения решению задач считают показ способов решения определенных видов задач, после чего следует отработка учащимися алгоритмов решения. Нельзя не согласиться с мнением известного американского математика и методиста Д. Пойа, что, если преподаватель математики "заполнит отведенное ему учебное время натаскиванию учащихся в шаблонных упражнениях, он убьет их интерес, затормозит их умственное развитие и упустит свои возможности".

Как же помочь учащимся научиться решать нестандартные задачи? Как помочь им преодолевать психологические барьеры в решении этих задач? Универсального метода, позволяющего решить любую нестандартную задачу, к сожалению, нет, так как нестандартные задачи в какой-то степени неповторимы. Однако опыт работы многих передовых учителей, добивающихся хороших результатов в математическом развитии учащихся как у нас в стране, так и за рубежом, позволяет сформулировать некоторые методические приемы обучения учащихся способам решения нестандартных задач.

Хочется сказать, что научить учащихся решать задачи (в том числе и нестандартные) можно только в том случае, если у учащихся будет желание их решать, то есть если задачи будут содержательными и интересными с точки зрения ученика. Поэтому проблема первостепенной важности, стоящая перед учителем, - вызвать у учащихся интерес к решению той или иной задачи. Необходимо тщательно отбирать интересные задачи и делать их привлекательными для учащихся. Как это сделать - решать самому учителю. Наибольший интерес вызывают у учащихся задачи, взятые из окружающей их жизни, задачи, естественным образом связанные со знакомыми учащимся вещами, опытом, служащие понятной ученику цели.

Учитель должен уметь находить интересные для учащихся задачи и своевременно предлагать их. Приведем примеры.

Конечно, нельзя приучать учащихся решать только те задачи, которые вызывают у них интерес. Так же нельзя забывать, что такие задачи учащийся решает легче и свой интерес к решению одной или нескольких задач он может в дальнейшем перенести и на "скучные" разделы, неизбежные при изучении любого предмета, в том числе и математики. И можно будет достигнуть полного преодоления психологических барьеров.

Таким образом, учитель, желающий научить школьников решать задачи, должен вызвать у них интерес к задаче.

Задачи не должны быть слишком легкими, но и не должны быть слишком трудными, так как учащиеся, не решив задачу или не разобравшись в решении, предложенном учителем, могут потерять веру в свои силы. Не следует предлагать учащимся задачу, если нет уверенности, что они смогут ее решить.

Ну а как же помочь учащемуся научиться решать задачи, если интерес к решению задач у него есть, и трудности решения его не пугают? В чем должна заключаться помощь учителя ученику, не сумевшего решить интересную для него задачу? Как эффективным образом направить усилия ученика, затрудняющегося самостоятельно начать или продолжить решение задачи?

Не следует идти по самому легкому в этом случае пути - познакомить ученика с готовым решением. Не следует и подсказывать, к какому разделу школьного курса математики относится предложенная задача, какие известные учащимся свойства и теоремы нужно применить при решении.

Решение нестандартной задачи - очень сложный процесс, для успешного осуществления которого учащийся должен уметь думать, догадываться. Необходимо также хорошее знание фактического материала, владение общими подходами к решению задач, опыт в решении нестандартных задач.

В процессе решения каждой задачи и ученику, решающему задачу, и учителю, обучающему решению задач, целесообразно четко разделять четыре этапа:

) изучение условия задачи;

) поиск плана решения и его составление;

) осуществление плана, то есть оформление найденного решения;

) изучение полученного решения - критический анализ результата решения и отбор полезной информации.

Даже при решении несложной задачи учащиеся много времени тратят на рассуждения о том, за что взяться, с чего начать. Чтобы помочь учащимся найти путь к решению задач, учитель должен уметь поставить себя на место решающего задачу, попытаться увидеть и понять источник его возможных затруднений, направить его усилия в наиболее естественное русло. Умелая помощь ученику, оставляющая ему разумную долю самостоятельной работы, позволит учащемуся развить математические способности, накопить опыт, который в дальнейшем поможет находить путь к решению новых задач.

"Лучшее, что может сделать учитель для учащегося, состоит в том, чтобы путем неназойливой помощи подсказать ему блестящую идею… Хорошие идеи имеют своим источником прошлый опыт и ранее приобретенные знания. Таким образом, хорошим средством обучения решению задач, средством для нахождения плана решения являются вспомогательные задачи. Умение подбирать вспомогательные задачи свидетельствует о том, что учащийся уже владеет определенным запасом различных приемов решения задач. Если этот запас не велик (что вполне очевидно для учащихся 5-6 классов), то учитель, видя затруднения учащегося, должен сам предложить вспомогательные задачи. Умело поставленные вспомогательные вопросы, вспомогательная задача или система вспомогательных задач помогут понять идею решения. Необходимо стремиться к тому, чтобы учащийся испытал радость от решения трудной для него задачи, полученного с помощью вспомогательных задач или наводящих вопросов, предложенных учителем.

Безусловно, учащихся следует приучать самим составлять вспомогательные задачи, или упрощать условия предложенных задач так, чтобы без помощи учителя найти способы их решения.

Умение находить вспомогательные задачи, как и вообще умение решать задачи, приобретается практикой. Предлагая учащимся задачу, следует посоветовать выяснить, нельзя ли найти связь между данной задачей и какой-нибудь задачей с известным решением или с задачей, решающейся проще.

Для приобретения навыков решения довольно сложных задач нужно приучать школьников больше внимания уделять изучению полученного решения. Для этого можно предлагать учащимся видоизменять условия задачи, чтобы закрепить способ ее решения, придумывать задачи аналогичные решенным, более или менее трудные, с использованием найденного при решении основной задачи способа решения.

Систематическая работа по изучению способов решения задач помогает учащимся не только научиться решать задачи, но и самим их составлять.

Конструирование задач - интересное занятие, один из верных способов решать задачи.

Умение учащихся составлять нестандартные задачи, решаемые нестандартными способами, свидетельствует о культуре их мышления, хорошо развитых математических способностях.

При анализе решения задачи полезно сопоставить решение данной задачи с ранее решенными, установить возможность ее обобщения.

Очевидно, что учитель должен постоянно помнить, что решение задач является средством обучения. Обсуждение найденного решения, поиск других способов решения, закрепление в памяти тех приемов, которые были использованы, выявление условий возможности применения этих приемов, обобщение данной задачи - все это дает возможность школьникам учиться на задаче.

Именно через задачи учащиеся могут узнать и глубоко усвоить новые математические факты, овладеть новыми математическими методами, накопить определенный опыт, сформировать умения самостоятельно, и творчески применять полученные знания.

Поэтому уже в младших классах школы при обучении математике (да и другим предметам) надо учить школьников наблюдениям, прививать им навыки исследовательской творческой работы, которые могут пригодиться в дальнейшем, какой бы вид деятельности они не избрали после окончания школы.

При отыскании различных способов решения задач у школьников формируется познавательный интерес, развиваются творческие способности, вырабатываются исследовательские навыки. После нахождения очередного метода решения задачи учащийся, как правило, получает большое моральное удовлетворение. Учителю, важно поощрять учащихся поиск различных способов решения задач, а не стремиться навязывать свое решение. Общие методы решения задач должны стать прочным достоянием учащихся, но наряду с этим необходимо воспитывать у них умение использовать индивидуальные особенности каждой задачи, позволяющие решить ее проще. Именно отход от шаблона, конкретный анализ условий задачи являются залогом успешного ее решения.

Особое внимание, следует обратить на решение задач арифметическим способом, так как именно решение задач арифметическим способом способствует развитию оригинальности мышления, изобретательности.

Часто учащиеся, ознакомившись со способом решения задач с помощью уравнения, не обременяют себя глубоким анализом условия задачи, стараются побыстрее составить уравнение и перейти к его решению. При этом и введение обозначений, и схема решений, как правило, соответствуют определенному шаблону.

В этом случае задача учителя - показать учащимся на примерах, что решение задач по шаблону часто приводит к значительному увеличению объема работы, а иногда и к усложнению решения, в результате чего увеличивается возможность появления ошибок. Поэтому учащимся полезно предложить, прежде чем составлять уравнение для решения задачи, внимательно изучить условие задачи, подумать над тем, какой способ решения наиболее соответствует ее условию, попытаться решить задачу без использования уравнений, арифметическим способом.

Широко распространено мнение, что решение задач повышенной трудности арифметическими методами излишне ввиду существования метода решения задач с помощью составления уравнения.

Существует и другое мнение, опирающееся на наблюдения за учащимися, согласно которому решение задач только алгебраическим методом ведет к одностороннему математическому развитию учащихся. Следует учитывать и то, что для составления уравнения следует использовать определенные арифметические навыки, понимание зависимостей между величинами. Кроме того, существует ряд задач, решение которых арифметическими методами проще, чем с помощью уравнений.

Арифметический способ решения задач, когда шаблонный метод не легко приводит к результату, является, как свидетельствуют наблюдения, одним из лучших средств развития самостоятельного, творческого решения учащихся. С помощью специально подобранных задач, которые могут заинтересовать учащихся своей кажущейся простотой и тем, что их решение не сразу дается в руки, можно показать учащимся красоту, простоту и изящество логического рассуждения, приводящего к решению задачи. Рассматривая решение задач несколькими способами, учитель на уроке и во внеклассной работе должен ориентировать учащихся на поиски красивых, изящных решений. Тем самым учитель будет способствовать эстетическому воспитанию учащихся и повышению их математической культуры.

Решая с учащимися ту или иную задачу, учитель должен стремиться к достижению двух целей. Первая - помочь ученику решить именно данную задачу, научить его решать задачи, аналогичные рассматриваемой; вторая - так развить способности ученика, чтобы он мог в будущем решить любую задачу школьного курса самостоятельно. Эти две цели, безусловно, связаны между собой, так как, справившись с заданной достаточно трудной для него задачей, учащийся несколько развивает свои способности к решению задач вообще.

Отметим, что частое использование одного и того же метода при решении задач иногда приводит к привычке, которая становится вредной. У решающего задачу ученика вырабатывается склонность к так называемой психологической инерции. Поэтому, как бы ни казался учащимся простым найденный способ решения задачи, всегда полезно попытаться найти другой способ решения, который обогатит опыт решающего задачу. Кроме того, в некоторых случаях, получение того же результата другим способом служит лучшей проверкой правильности результата.

Определяющее условие количественной оценки результатов экспериментов исследуемых барьеров - адекватность этой оценки, качественной ее характеристики.

Качественный анализ механизма преодоления психологических барьеров в обучении школьников решению математических задач привел к выводу, что наиболее общим, суммарным показателем уровня его развития могут служить скорость мышления и связанная с этой скоростью самооценка, как краткость пути к самостоятельному решению проблемы.

В определении показателя скорости мышления при решении проблемы исходят из следующих показателей: чем раньше ученик выделит закономерность в решении задач и будет ориентироваться на нее, тем вернее он будет решать задачи. Следовательно, о скорости и об уровне связанной с ней самооценки можно судить по совокупности баллов, начисленных за верно решенные задачи.

2.3 Результаты эксперимента

В ходе проведения эксперимента были получены следующие результаты. 11 человек класса показали достаточно высокие результаты и были отнесены к высшему уровню скорости мышления.

Большая часть испытуемых была отнесена к среднему уровню: 13 человек

Следовательно, исходя из вышеперечисленных данных, общий уровень скорости мышления можно считать достаточно высоким. При этом допускается наличие возможных погрешностей в исполнении, обработке и трактовке данных.

В заключение было проведено вторичное тестирование. Результаты вторичного испытания отражены в таблице.

Рис.2.Анализ предварительных результатов класса 5.3

Улучшение показателей класса дает основание считать гипотезу, выдвинутую нами в начале нашей работы, подтвердившейся и конкретные методические приемы по преодолению психологических барьеров в обучении математике школьников заслуживающими внимания.

Нельзя считать этот результат окончательным. Так могут возникать новые психологические барьеры, поэтому необходимо и далее разрабатывать и совершенствовать приемы и методы преодоления психологических барьеров в обучении математике, в зависимости от индивидуальных свойств и особенностей каждого отдельно взятого учащегося. Многое также будет зависеть от педагога-предметника, от того, будет ли он учитывать особенности познавательных процессов школьников и применять приемы активизации мышления в ходе объяснения и закрепления материала, будет ли он строить свои уроки на ярком, эмоционально окрашенном рассказе или чтении текста учебника; а также от многих других фактов.

Анализируя проделанную работу можно сделать ряд выводов:

1.           Экспериментальные занятия по курсу математики в классе 5.3 средней школы № 1605 г. Москвы были достаточно эффективны. Удалось достичь основной цели данного исследования - выработать ряд методических приемов, включенных в обычные программные уроки, позволяющих овладевать приемами преодоления психологических барьеров, а, следовательно, облегчать усваиваемость материала и активизировать познавательные и творческие способности школьников.

2.       Анализ учебного материала, предшествующий практической части работы, позволил структурировать отобранный материал наиболее логичным и приемлемым способом, в соответствии с целями исследования.

.        Результатом проведенной работы являются несколько методических рекомендаций к курсу математики:

1 В целях совершенствования преподавания математики целесообразно разрабатывать новые методики использования нестандартных задач, связанных с приемами преодоления психологических барьеров.

2 Систематически использовать на уроках задачи развивающего характера, способствующие формированию у учащихся познавательного интереса и самостоятельности.

3 Осуществляя целенаправленное обучение школьников решению задач, с помощью специально подобранных упражнений, учить их наблюдать, пользоваться аналогией, индукцией, сравнениями и делать соответствующие выводы.

4 Целесообразно использование на уроках задач на сообразительность, задач-шуток, математических ребусов, софизмов, с целью релаксации учащихся.

5 Учитывать индивидуальные особенности школьника, дифференциацию познавательных процессов у каждого из них, используя задания различного типа.

Таким образом, проведенное исследование позволяет утверждать, что работа над формированием навыков преодоления психологических барьеров в обучении математике учащихся - дело важное и необходимое. Поиск новых путей активизации познавательной и творческой деятельности школьников является одной из задач современной психологии и педагогики.

Заключение

Обучаясь и преодолевая психологические барьеры, учащиеся приобретают новые математические знания, готовятся к практической деятельности. Новые нестандартные задачи способствуют развитию их логического мышления. Большое значение имеет решение задач и в воспитании личности учащихся. Поэтому важно, чтобы учитель имел глубокие представления о математической задаче, о ее структуре, умел решать такие задачи различными способами.

Математические знания служат также одним из важнейших средств ознакомления детей с математическими отношениями, выражаемыми словами "быть на столько-то больше (меньше)", "быть на столько-то раз больше (меньше)". Они используются и в целях уяснения понятия доли (задачи на нахождение доли величины и искомого значения величины по доле). Математические знания помогают и при формировании ряда геометрических понятий, а также при рассмотрении элементов алгебры.

Если мы хотим сформировать у школьников правильное понятие о предмете математики и уменьшить их психологические барьеры, необходимо, чтобы дети решили достаточное количество простых задач, практически выполняя каждый раз решение самостоятельно, поднимая тем самым собственную самооценку. Выступая в роли конкретного материала для формирования знаний, такие задачи также дают возможность связать теорию с практикой, обучение с жизнью. Их решение формирует у детей практические умения, необходимые каждому человеку в повседневной жизни. Например, подсчитать стоимость покупки, вычислить в какое время надо выйти, чтобы не опоздать на поезд и т.п.

Сам процесс решения задач при определенной методике оказывает весьма положительное влияние на умственное развитие школьников, поскольку он требует выполнения умственных операций: анализа и синтеза, конкретизации и абстрагирования, сравнения, обобщения. Так, при решении любой задачи ученик выполняет анализ: отделяет вопрос от условия, выделяет данные и искомые числа; намечая план решения, он выполняет синтез, пользуясь при этом конкретизацией (мысленно рисует условие задачи), а затем абстрагированием (отвлекаясь от конкретной ситуации, выбирает арифметические действия); в результате многократного решения задач какого-либо вида ученик обобщает знания связей между данными и искомым в задачах этого вида, в результате чего обобщается способ решения задач этого вида.

Решение задач - это не только преодоление психологических барьеров в обучении математике, но и упражнения, развивающие мышление. Мало того, решение задач способствует воспитанию терпения, настойчивости, воли, способствует пробуждению интереса к самому процессу поиска решения, дает возможность испытать глубокое удовлетворение, связанное с удачным решением.

Нельзя забывать, что решение задач воспитывает у детей многие положительные качества характера и развивает их эстетически.

Изучена методика работы над математической задачей: понятие и виды задач, способы ее решения, этапы, задачи, общие вопросы методики обучения решению задач.

Проведена работа по диагностике исходных психологических барьеров в обучении математике, что позволило сравнить уровень развития психики у учащихся.

Данный вопрос не закрыт, необходимо искать новые формы, подходы, направления, новые методические обоснования для более успешного преодоления психологических барьеров в обучении школьников математике.

Список литературы

1. Аверченко Л.К., Андрюшина Т.В. и др., Психология и педагогика, Москва-Новосибирск, Инфра-М-НГАЭиУ, 2008

2. Антонова И.И. Обучаем математике: Книга для учителя. М.: Просвещение, 2010.

3. Аракелян О.А. Некоторые вопросы изучения математики в средней школе. М.: Учпедгиз, 1960.

4. Бондаренко, С.М., Почему детям бывает трудно учиться?, серия "Педагогика и психология", М. Знание №2, 1975"

5. Безруких М.М, Каких детей называют медлительными и отчего им трудно учиться, Тула ,1997

6. Давыдов В. В. Проблемы развивающего обучения: Опыт теоретического и экспериментального психологического исследования. М.: Педагогика, 1986.

7. Дубровина И.В. Психология: Учебник для студентов средних педагогических учебных заведений. М.: Издательский центр "Академия", 2009.

8. Еникеев М.И. Психологическая диагностика. Стандартизированные тесты. М.: Приор, 2002.

9. Зинченко С.И., Почему детям бывает трудно учиться. М.: Знание, 1984.

10. Калмыкова З. И. Продуктивное мышление как основа обучаемости. М.: Педагогика, 1981.

11.  Калмыкова З.И., Отстающие в учении школьники. М: Знание,1986

12.  Калмыкова З.И., Проблема преодоления неуспеваемости глазами психолога, М: Знание, 1982.

13. Кожабаев К.Б. О воспитательной направленности обучения математике в школе: Книга для учителя. М.: Просвещение, 1988.

14. Колягин Ю. М., Оганесян В. А. Учись решать задачи. М.: Просвещение, 1980.

15. Кордемский Б.А. Математическая смекалка. М.: ГИФМЛ, 1958.

16. Кордемский Б.А. Увлечь школьников математикой. (Материал для классных и внеклассных занятий). М.: Просвещение, 1981.

17. Краткий психологический словарь / Под общей ред. А.В. Петровского и М.Г. Ярошевского; ред.-составитель Л.А. Карпенко. - 2-е изд. - Ростов-на-Дону: Феникс, 1998. / Электронная версия / М.Э. Шпилевский, 2002 // #"534864.files/image004.gif">

Е. Задание на понимание связи между компонентами сложение и вычитании, умножения и деления

.Ученику нужно соединить линиями разного цвета слова, одинаковые по смыслу. Эти же слова учитель может написать на отдельных карточках и попросить ученика разложить их на группы:

2. Ученику дан пример с ответом. Учитель записывает новые примеры, которые "один ученик" якобы составил на основе исходного примера. Учащемуся предлагается оценить их правильность и выписать только те из них, которые составлены правильно, а у неправильно составленных в качестве ответа ставить вопросительный знак.

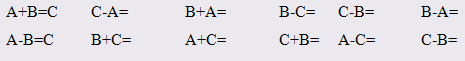
Приложение 3

Таблица результатов итогового этапа исследования