Подбор торгового персонала
Введение
Цель курсовой работы получить навыки расчета
линейных стационарных САУ с микропроцессорными регуляторами.
В первой половине работы применить метод расчета
последовательного корректирующего устройства, основанного на использовании
логарифмических частотных характеристик, а также исследовать динамику САУ
моделированием ее на ПЭВМ в системе ''MATLAB ~ Simulink.
Во второй половине работы на основании полученной
передаточной функции корректирующего устройства рассчитывается дискретная
передаточная функции регулятора. Далее производится исследование динамики уже
дискретной системы.
В связи с
использованием в контуре управления Микропроцессорного регулятора, помимо
обычных требований по обеспечению устойчивости, точности и качества
проектируемой САУ, учитываются требования к шагам квантования сигналов по
уровню и по времени. Частоты квантования по уровню и времени выбираются так,
что система приближенно может рассматриваться как линейная непрерывная САУ. Это
позволяет использовать для расчета закона управления простой и эффективный
аппарат логарифмических частотных характеристик. Затем закон управления
представляется в дискретной форме для получения переходного процесса уже в
дискретной системе.
В качестве
критерия правильности расчета можно поставить идентичность переходных процессов
в линейной и микропроцессорной системе, выбирая соответствующий период
квантования по времени.
1. Неизменяемая часть системы
Проектирование САУ всегда начинается с анализа
объекта, формулировки задачи функционирования проектируемой системы, выбора
критерия качества системы или задания требований к системе.
Будем считать, что этап анализа объекта,
получения уравнений объекта и их линеаризация, выбор исполнительного механизма
и датчиков уже решен, Полученные данные будут составлять так называемую
неизменяемую часть системы.
Получим, что передаточная функция такой
неизменяемой части системы имеет вид
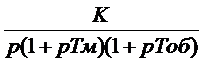
2. Структурная схема САУ с микропроцессорным регулятором
Поскольку микропроцессорный регулятор построен на
базе Микро-ЭВМ и может обрабатывать сигналы только дискретной формы" а
сигнал на выходе объекта Ux и регулирующий сигнал Ur - непрерывны, то
необходимо использовать преобразователи сигналов. АЦП - аналогово-цифровой
преобразователь осуществляет кодирование непрерывного сигнала Ux дискретным сигналом 1х-
ЦАП -цифро-аналоговый преобразователь преобразовывает дискретный сигнал регулирования
1г в непрерывный Ur. В процессе аналого-цифрового преобразования
осуществляется квантование сигнала по времени и по уровню и это оказывает
серьёзное влияние на динамические процессы в САР.
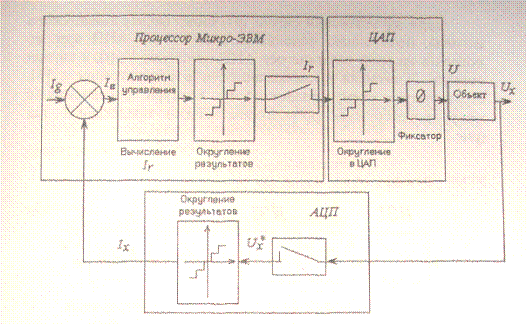
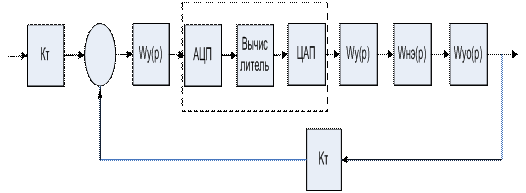
Рис. 2
На рис. 2 представлена в общем виде структурная
схема САР с микропроцессорным регулятором и форма используемых в такой системе
сигналов [1]. Непрерывный сигнал Ux(t) с выхода объекта поступает сначала в АЦП, где производится
квантование сигнала по времени с постоянным шагом То в моменты t - 0, То, 2То, ... , кТо.
В результате этого будет получен дискретный
сигнал u*x(k)<. д^^ производится квантование
сигнала по уровню путём округления Ух Д° ближайшего стандартного значения
Полученный при этом сигнал 1г представляет собой последовательность
цифровых двоичных кодов, которые в дискретные моменты времени передаются в
процессор и Микро-ЭВМ вырабатывает дискретный сигнал ошибки на основе которого
в каждый тактовый момент времени 0' Т 2Т0,.... кТо вычисляется в
соответствии с выбранным законом регулирования регулирующий сигнал Щ), Тх в процессе вычисления регулирующего воздействия могут использоваться операции умножения или другие арифметические операции, приводящие к переполнению разрядной сетки Микро-ЭВМ, полученный сигнал вновь подвергается округлению, а затем в дискретные моменты
времени выдаётся в ЦАП. Если число разрядов микропроцессора и ЦАП не совпадают, в ЦАП вновь производится округление. На выходе ЦАП имеется экстраполятор, который превращает цифровой код в аналоговый кусочно линейный сигнал. В Микро-ЭВМ чаще
всего используются экстраполяторы нулевого порядка,
которые носят название фиксаторов и превращают
цифровой код в аналоговый ступенчатый сигнал. Этот
сигнал воздействует на исполнительный механизм,
осуществляя процесс регулирования. В
приведённой на рис.2 схеме САР задающей сигнал Ig имеет цифровую форму.
Такой сигнал
может быть получен от специального цифрового датчика или другой Микро-ЭВМ.
Функциональная схема
линейной САУ

1 – датчик входного сигнала
2 - согласующий усилитель
3 - последовательное КУ
4 – исполнительный
элемент (двигатель)
5 - управляемый объект
6 – датчик выходного
сигнала (температуры)
g – заданное значение температуры
Ux – температура на выходе системы
E – ошибка
U – управляющее воздействие
Функциональная схема МП
САУ
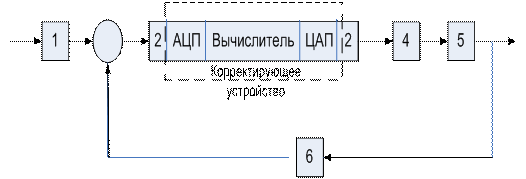
Структурная схема
линейной САУ
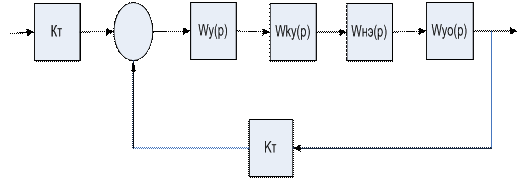
Структурная схема МП САУ
В рассматриваемой системе
регулирования температуры технологического процесса учтем исходные данные,
характеризующие неизменяемую часть системы.
Кроме этого к системе предъявляются следующие
требования:
·
максимальное
перерегулирование σ = 30 %;
·
максимальное
время регулирования: t = 55 сек;
·
запас
устойчивости по фазе Δφ (Град) должен лежать в пределах 35° - 65° в
соответствии с диапазоном изменения σ % от 40% до 20% в исходных данных
·
Коэффициенты
ошибок Do = 0 D = 0,058
В нашем
случае передаточная функция неизменной части системы имеет вид:
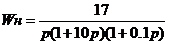
Для
построения ЛЧХ на оси частот выбираем точку 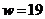 1/с и
проводим асимптоту с наклоном -20 дБ/дек
1/с и
проводим асимптоту с наклоном -20 дБ/дек
Построение
необходимо проводить в соответствии с выражением ЛЧХ
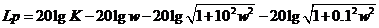
Фазочастотную
характеристику строим по формуле:

|
 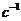
|
0.1
|
0.2
|
0.5
|
0.8
|
1
|
|
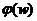
|
-135,57
|
-154,3
|
171,56
|
176,5
|
180
|
В рассматриваемой РГР σ = 30 %
и t
= 55 сек.
Из таблицы находим B = 11,3; Wср=0,2 1/с
Найдем
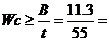 0.2
0.2
L1=15 дБ
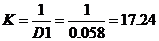
Синтез линейной САУ
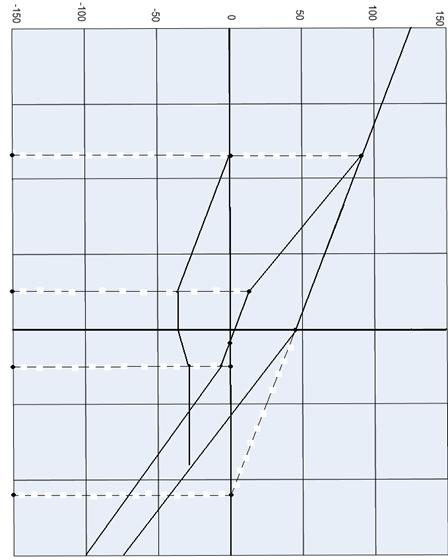
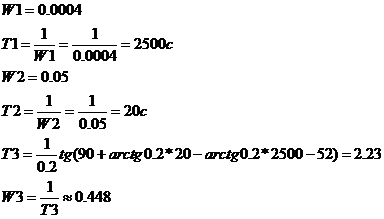
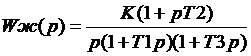
Определим передаточную
функцию корректирующего устройства
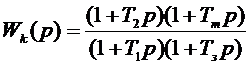
Передаточная функция
замкнутой системы имеет вид:

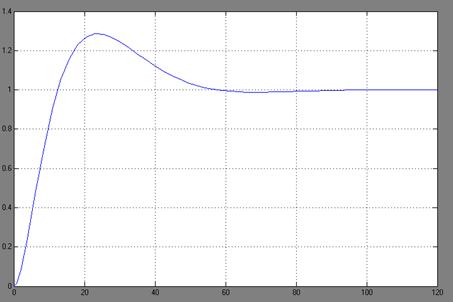
Получим переходный
процесс в системе моделированием её на ЭВМ.
Переходный процесс в
линейной САУ
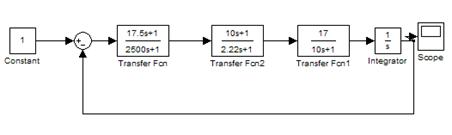
Определение дискретной
передаточной функции корректирующего звена.
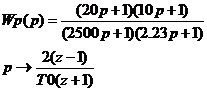
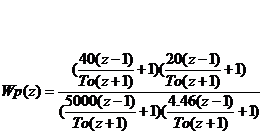
При T0 = 0.35
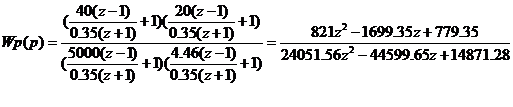
При T0 = 0.25
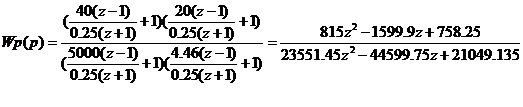
При T0 = 0.1
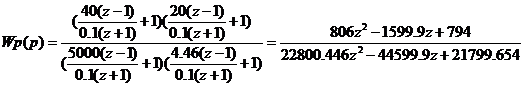
Для моделирования САУ в
пакете "ДИСПАС" соответствующее уравнение имеет вид:
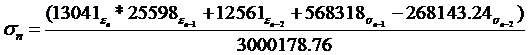
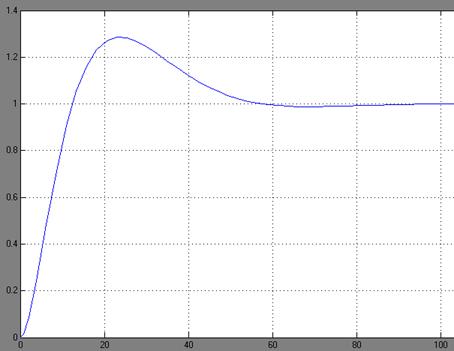
Переходный процесс в
дискретной САУ при шаге квантования
Т=0.35
Схема моделирования при
Т0=0.35
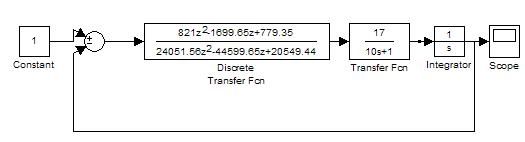
Переходный процесс в
дискретной САУ при шаге квантования
Т=0.25
Схема моделирования при
Т0=0.25
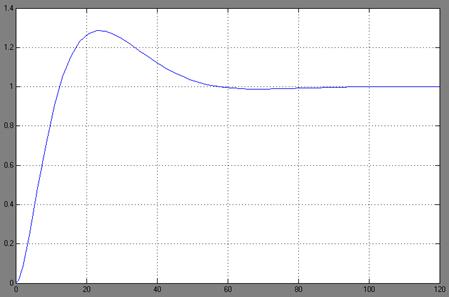
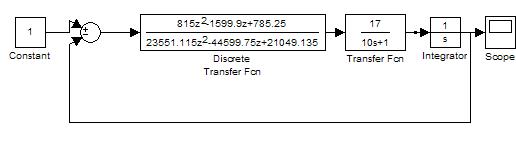
Переходный процесс в
дискретной САУ при шаге квантования
Т=0.1
Схема моделирования при
Т0=0.1

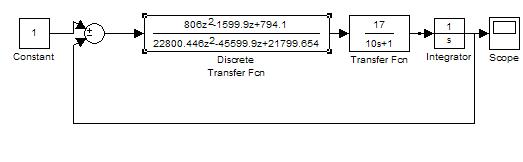
Выводы
В результате проделанной
работы было выяснено, что независимо от того, каким способом анализировать
результаты разработки САУ с микропроцессорным регулятором, в результате анализа
необходимо получить график переходного процесса.
Вывели дискретную
передаточную функцию регулятора, для того чтобы исследовать динамику САУ с
микропроцессорным регулятором, так же выбрали шаг квантования Т0. Для
исследования системы и решения задачи можно использовать пакет "MATLAB" и др. По полученному графику
убедились в устойчивости системы. Убедились, что процессы в линейной и
дискретной САУ идентичны, следовательно расчеты произведены верно и задачу
можно считать выполненой.