Расчёт и проектирование воздушной линии электропередач напряжением 500кВ и механической передачи

Министерство образования РФ

НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙЙ УНИВЕРСИТЕТ

Расчётно-пояснительная записка к курсовой работе

по прикладной механике

на тему

расчёт и проектирование ВЛЭП напряжением 500кВ и механической передачи

Tехническое задание

Напряжение 500кВ

Количество цепей ЛЭП -1

Район гололёдности III

Скорость ветра 25м/с

Длина пролёта 340м

Сечение провода 3*500/64

Температура воздуха

t_min=-50°C ,t_ср=-7°C ,t_mах=35°C

Кинематическая схема механизма:

для натяжения провода n_вх=96об/мин

(цилиндрический косозубый n_б=8 об/мин

редуктор и открытая D_б=0,3 м

коническая передача). P_б=85 кН

Общая характеристика воздушной линии электропередач

Воздушная линия электропередачи (ВЛ) -устройство для передачи и распределения электрической энергии по проводам,расположенным на открытом воздухе и прикрепленным к опорам или кронштейнам и стойкам на инженерных сооружениях при помощи изоляторов и арматуры.Ответвления к вводам в здания относятся к ВЛ.

Трасса ВЛ -положении оси линии электропередачи на земной поверхности.

Опоры ВЛ- сооружения ,поддерживающие провода с помощью изоляторов и арматуры на заданном расстоянии между собой и от поверхности земли

Пролет или , точнее , длина пролета -измеренное по горизонтали расстояние между двумя опорами, на которых подвешен провод.

Стрела провеса провода- вертикальное расстояние от горизонтальной прямой ,соединяющей точки подвеса провода,до низшей точки провода в пролете.

Запас прочности или коэффициент запаса прочности отдельных элементов ВЛ(проводов,изоляторов, арматуры и др.)-отношение величины нагрузки, разрушающей данный элемент ,к величине нормально действующей нагрузки, полученной по расчету для наиболее тяжелых условий.

[3] Основными элементами воздушных линий являются провода ,изоляторы, линейная арматура, опоры и фундаменты.Дополнительными элементами, необходимыми на некоторых линиях для обеспечения надежности их работы, являются грозозащитные тросы ,заземления ,разрядники ,виброгасители и т.д.

На ВЛ переменного трехфахного тока подвешивается не менее трех проводов, составляющих одну цепь По числу цепей линии электропередачи делятся на одноцепные двухцепные и многоцепные Число цепей зависит от передаваемой мощности напряжения линии электропередачи и необходимости резервирования.

На рисунке показаны основные элементы ВЛ:

                                           2-траверсы

                                       1-ствол опоры;

      ;                     

                                            3-гирлянды изоляторов;

                                           4-провода;

                                             5-фундамент;

                                   6-грозозащитный трос.

Опоры, в зависимости от способа подвески проводов ,делятся:

На опоры промежуточные,на которых провода закрепляются и поддерживаются зажимами;

На опоры анкерного типа,служащие для натяжения проводов.

ВЛ может находится в трех режимах: нормальном,аварийном,монтажном.

Нормальный режим-состояние ВЛ при необорванных проводах и тросах.

Аварийный режим- состояние при оборванных одном или нескольких проводах или тросах

Монтажный режим- состояние в условиях монтажа опор, проводов и тросов.

[2] Промежуточные опоры устанавливаются на прямых участках трассы и ,как правило,не воспринимают тяжения (усилия,направленные по оси провода или троса,с которыми они натягиваются и закрепляются на анкерных опорах) от проводов и тросов в нормальном режиме работВЛ.Допускается установка промежуточных угловых опор на углах ,не превышающих 10-20⁰.

Анкерные опоры устанавливаются на прямых участках трассы и полностью воспринимают тяжение проводов и тросов в аварийном и монтажном режимах и разность тяжений по проводам и тросам в смежных пролетах вдоль ВЛ в нормальном режиме работы ВЛ.

Опоры ВЛ 500кВ выполняются металлическими,деревянными и железобетонными.

Опоры ВЛ должны размещаться так ,чтобы не загораживались входы в здания,въезды во дворы и не затруднялось движение транспорта и пешеходов.

В местах, где имеется опасность наезда транспорта, опоры ВЛ необходимо защищать железобетонными отбойными тумбами. Опоры ВЛ следует устанавливать по возможности в отдалении от размываемых берегов рек с учетом возможных перемещений русл и затопляемости района, а также вне мест,где могут быть потоки дождевых и других вод, ледоходы и др.

В курсовом проекте рассматривается только нормальный режим с учетом профилактических работ.

1. Расчёт механики проводов воздушной линии электропередач

.1 Характеристика провода (А:С=7,71 ¸8,04) [1];

площадь сечения провода 3*500/64 мм² (аллюминий/сталь);

диаметр провода 30,6 мм;

масса провода 1852 кг/км;

приведенный модуль упругости Е=7,7*10³ даН/мм²;

температурный коэффициент линейного удлинения a=19,8*10^-6град^-1

.2Определение удельных нагрузок:

1)удельная нагрузка от собственного веса провода

[4]

G-вес(масса провода)

F(площадь сечения)=553,5 мм²

)удельная нагрузка от веса гололеда:

с-толщина стенки гололеда (III зона гололедности), с=15мм

d=30,6мм (диаметр провода)

)удельная нагрузка от веcа провода и гололеда

4)удельная нагрузка от горизонтального ветрового напора:

Выбираю опору ПС 330-7 -промежуточная стальная одноцепная опора для напряжения 500кВ (район гололедности III-IV) H=31м[1]

К_n=1,35; K_l=1;

a-коэффициент, учитывающий неравномерность скоростного напора; при 25м/с (скорость ветра)

Чтобы найти значение коэффициента a, надо воспользоваться линейной интерполяцией.

С_x -коэффициент лобового сопротивления

С_x =(d=30,6мм³20мм)=1,2 (т.к. провод покрыт льдом)

q_max-максимальный скоростной напор

q_max=V²_max/16 , V_max-максимальная скорость ветра

V_max=25м/с ;q_max=(25)²/2=39,06даН/м²

          5) Горизонтальная ветровая нагрузка на провод, покрытый гололедом:

C_x=1,2_г=V²/16 , V=0.5V_max [4]

6) Результирующая удельная нагрузка от веса провода без гололеда и ветрового напора:

)Результирующая удельная нагрузка от веса провода,покрытого гололедом, и ветрового напора:

.3 Нахождение исходного режима работы провода

Исходный режим работы провода определяется по заданной величине пролёта и характеризуется действующим напряжением.

N	Расчетные условия				Расчетная  нагрузка, даН_  м×мм2	Допускаемые напряжения, даН мм2
		V, м/с	С, мм	t,°C
I	t°min	0	0	-50	g1=3,345×10-3	[s]I=0,3sв=8,1
IIa IIb	gmax	Vmax=35 0,5Vmax =17,5	0 Cmax=20	-5 -5	g6=4,498×10-3 g7=7,274×10-3	[s]II=0,45sв=12,15
III	tэкспл. сред.темп	0	0	-7	g1=3,345×10-3	[s]III=[s]IV=0,45sв=12,15
IV	tmax	0	0	35	g1=3,345×10-3

(зависит от типа провода)

Первый критический пролёт (определяется с помощью I и III режима):

I

III

Второй критический пролёт (определяется с помощью I и II режима):

I

a II  b

Третий критический пролёт (определяется с помощью I и II режима):

 I              

a  II b

Определение исходного режима. Сравнение действующего пролёта с критическими и получаем:

          L_крI> L_крII> L_крIII

№		исходный режим
1. 2. 3. 4.	L<Lкр I;  L>Lкр II;  Lкр I<L<Lкр III;  Lкр I>Lкр II>Lкр III;  L<Lкр II;  L>Lкр II;	1) 2) 3)  2б) 2a)

 

Выбираю 2a) температурный режим - режим минимальных температур.

.4 Расчёт промежуточной опоры

.4.1 Подбор изоляторов и определение длины подвесной гирлянды

Определяем коэффициент запаса нагрузки для ветрового режима при гололеде.

 

P- гарантированная нагрузка на изолятор

F- площадь поперечного сечения провода

k- число проводов в фазе, k=1

L_{весовое}=1,25L действующей - весовой пролёт, L_b =425м

G- вес гирлянды изоляторов

Выбираем изоляторы ПС-70Д

.4.2 Определение коэффициента запаса нагрузки без воздействия ветра и гололеда

 

1.4.3 Определение максимальной величины провеса провода

 

f- величина провеса

i- расчетный режим эксплуатации

L- длина пролета

g- удельная нагрузка (примем = , т.к. режим - 2а))

d- нормальное напряжение (=)

Максимальное значение величины провеса 8,251м.

1.4.4 Определение высоты опоры

Определение длины подвесной гирлянды

n- число изоляторов

H- высота изолятора

- длина монтажного инструмента

Высота траверсы:

 

f_max- максимальный провес

h_o=0,02L=6,8м- опускание центра тяжести провода от обрыва в соседнем пролете

h_Г - габаритная высота (зависит от напряжения: 500кВ - 7м)

.4.5 Определение вертикальных нормативных нагрузок

1)  - от веса опоры

) - от веса изоляторов

)  - от веса провода без гололеда

)  - от веса гололеда

)  - моментальная нагрузка

1.4.6 Определение расчетных вертикальных нагрузок

)

)

)

)

)

.4.7 Определение горизонтальных нормативных нагрузок

1)Нагрузка от веса свободно стояще опоры:

C_x=0.52

 

q_b- нормальный скоростной напор

 

K_П - коэффициент скоростного напора на высоте H/2

- коэффициент, учитывающий воздействие динамического ветрового напора

S- площадь проекции опоры по наружному контуру, перпендикулярному направлению ветрового потока

)Нормативная нагрузка от ветра на провода без гололеда:

)Нормативная нагрузка от ветра на провод, покрытый гололедом:

.4.8 Горизонтальные расчётные нагрузки

1)

)

)

.4.9 Определение реакций в опорах башмаках:

1)Составление расчётной схемы:

Наибольшее опасное сочетание нагрузок с учётом гололёда:

G^p=G_из^p+G_п^p+G_г^p+G_м^p =96,25+2596,66+4928,7+325=7946,61 даН

Р^р=Р^р _п+г=2453,2даН

Опирание опорных секций рассматривается как шарнирное.Реакции на одноименные башмаки одинаковы.

)Определение горизонтальных реакций по приближенным формулам:

горизонтальная реакция в точке А:

горизонтальная реакция в точке В:

)Определение вертикальных реакций:

åM(B)=0

2V_A×C₁-P₀^p×H/2-3×P^p×H+G₀^p×C₁/2+G^p(C₁/2-a₂)+G^p×C₁/2+ G^p(C₁/2+a₁)=0₁=5,42м ; H=31м ; a₁=5,75м ;a₂=5,75м ; - для опор ПC 330-7 [1]

10.84V_a+23046.11-48797.1+64605.94-236902.62=0

V_a=18270,08 даН ;

åМ(А)=0

V_В×C₁-P₀^p×H/2-3P^p×H-G₀^p×C₁/2-G^p(a₂+C₁/2)-G^p×C₁/2-G^p(C₁/2-a₁)=0

10.84V_B-23046.11-48797.1-64605.94-236902.62=0

V_B=34442.05 даН ;

Проверка:

G^p+G_o^p=-2V_A+2V_B

3×7946,61+8504.1=-2×18270,08+2×34442,05

,93=32343,94

.5 Определение расчётных усилий в раскосах опорной секции

.5.1 Составление расчётной схемы опорной секции.

C=(0,75…0,5)C₁=0,625×5.42=3,387 м

h=(0,25…0,4)H= 0,3×31= 9,3 м

l£(0,8…1) м = 0,9 м

                                                               

Определим a и b исходя из геометрии нижней опорной секции:

.5.2 Определяем расчётное усилие, действующее в точке А

åP_x=0 åP_y=0 a=83.76° b=64.64°

-H_A+N₁cosa- N₂cosb=0

-V_A-N₂sinb+ N₁sina=0

 -1838,86+N₁cos83.76°-N₂cos64.64°=0

 -18270,08- N₂sin64.64°+ N₁sin83.76°=0

₁=18817.06 даН ;₂=481.97 даН ;

1.5.3 Определение расчётных усилий, действующих в точке В

åP_x=0 åP_y=0 a=83.76° b=64.64°

-H_B+N₄cosa - N₃cosb=0

V_B+N₄sina-N₃sinb=0

-3415.03-N₃cos64.64°+N₄cos83.76°=0

.05-N₃sin64.64°+N₄sin83.76°=0₄=35615.4даН ;₃=1064.96 даН ;

Проверка путём построения силовых многоугольников (1 см = 1000 даН):

.5.4 Таблица расчётных усилий

Наименование	Усилия	Значение	Вид деформации
Наружные раскосы	N1	18817,06даН	max растяжение
	N4	35615,4даН	max сжатие
Внутренние раскосы	N2	481,97даН	сжатие
	N3	1064,96даН	растяжение

1.6 Подбор сечения стержней опорной секции

.6.1 Расчёт на сжатие с учётом продольного изгиба

1) Задаёмся гибкостью l=80 для стали 10Г2С1 j₁=0,637 (j- коэффициент понижения сжимающих усилий).

l	110	85	55
j	0,4	0,6	0,8

2) Определяем величину минимального радиуса инерции:

l=0,9 м r_min=0,9/80=0,01125 м = 1,125 см

) Определяем № стандартного однобокого уголка и соответствующую площадь сечения

F₁=4,38 см² уголок №5,6 [5]

) Проверить уголок на устойчивость:

[R]=2900 даН/см² - расчётное сопротивление стали

перегрузка более 5%

Так как перегрузка более 5%, выберем следующее по величине r_min2=1.58см, тогда номер уголка 8, сечение F₂=10.8 см²

) Определить гибкость l₂

Проверяем действующее значение напряжения

перегрузка превышает 5%

Выберем уголок сномером 10, у которого F=15.6 см², r_min=1.98 см, тогда

Проверяем действующее значение напряжения:

недогрузка на 8,46% < 10%

Сечение уточняется при недогрузке более чем на 10% и при перегрузке более чем на 5%. Принимаем уголок №10, F=15,6 см², r_min=1,98 см.

1.6.2 Расчёт на сжатие с учётом ослабления сечения:

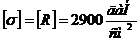
,8-коэффициент ослабления (дырки под болты).

Выбираем стандартный уголок номер 10, у которого F=15.6 см²

 

Недогрузка 1,6%

1.6.3 Расчёт на растяжение с учётом ослабления сечения

Выбираем стандартный уголок номер №8, у которого F=8.63 см²

Недогрузка 6%

Вывод: окончательно принимаем уголок №10, площадь сечения F=15.6см², с толщиной стенки d=8мм

.6.4 Подбор сечения стержня внутренней решетки опорной секции

Стержни внутренней решётки не воспринимают усилий от нагрузки.

l₃=1,12 м

) Принимаем для внутреннего нерабочего стержня l₃ предельную гибкость l_пр=200

) Определяем минимальный радиус инерции:

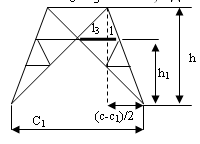
l₃ - наиболее длинный стержень решетки

l₃=C/2+l, где l=[(h-h₁)/h]*[(C-C₁)/2] (по подобию треугольника)

h₁=tgb*C₁/2=tg64.64*5.42/2=5.71 м, тогда

l₃=3.387/2+[(9.3-5.71)/9.3]*[(5.42-3.38)/2]=2.08 м

С учетом r_min=1.04 выбираем уголок №5

.7 Расчёт и конструирование узлов опорной секции

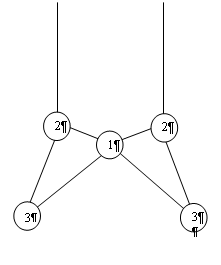
.7.1 Характеристика узлов опорной секции

-центральный узел выполняется

в болтовом варианте;

болтовом варианте;

-нижние опорные узлы

выполняются сварными.

.7.2 Расчёт центрального узла опорной секции

1)   В центральном узле появляются внутренние уравновешивающиеся силы.

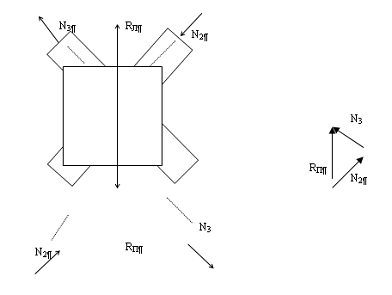
R²= N² ₂+N₃²-2 N₂N₃cos2b =±Ö(N²₂+N₃²-2N₂N₃cos2b)=±Ö[(481,97)²+(1064,96)²-2×481,97×1064,96×cos129,28]= ±1419,98даН

2)Расчет болтового соединения на срез

Количество болтов из условия на срез

[t] =500 даН/см² - касательное напряжение на срез.

d_б=10 мм =1 см

) Определение количества болтов из условия на смятие.

d_min=0,8…1 см - линейная толщина наименьшей накладки.

С учётом расчёта на срез и смятие принять количество болтов для центрального узла опорной секции- 4штуки с диаметром равным 10 мм.

) Расчёт сварного соединения для нижнего опорного узла.

aⁿ=0,3 коэффициенты,учитывающие распределение усилий на сварные швы

a^°=0,7

b= коэффициент ,учитывающий вид сварки

а) ручная b=0,7

б)машинная b=1

[t]_СВ=15даН/мм²

h_ш=d=8мм=0,8см (уголок №10)

2. Проектирование механического привода

2.1 Назначение и сравнительная характеристика привода

Редуктором называют механизм, состоящий из зубчатых или червячных передач, выполненный в виде отдельного агрегата и служащий для передачи вращения от вала двигателя к валу рабочей машины. Кинематическая схема привода может включать, помимо редуктора, открытые зубчатые передачи, цепные или ременные.

Назначение редуктора - понижение угловой скорости и соответственно повышения вращающего момента ведомого вала по сравнению с ведущим. Механизм для повышения угловой скорости, выполненные в виде отдельных агрегатов, называют ускорителями или мультипликаторами.

Редуктор состоит из корпуса (литого чугунного или сварного стального), в котором помещают элементы передачи - зубчатые колеса, валы, подшипники и т.д. В отдельных случаях в корпусе редуктора размещают также устройства для смазывания зацеплений и подшипников (например, внутри корпуса редуктора может быть помещен шестеренный масляный насос) или устройства для охлаждения (например, змеевик с охлаждающей водой в корпусе червячного редуктора).

Редуктор проектируют либо для привода определенной машины, либо заданной нагрузке (момент на выходном валу) и передаточному числу без указания конкретного назначения. Второй случай характерен для специализированных заводов, на которых организовано серийное производство редукторов.

Редукторы классифицируют по следующим основным признакам: типу передачи (зубчатые, червячные или зубчаточервячные); числу ступеней (одноступенчатые, двухступенчатые и т.д.); типу зубчатых колес (цилиндрические, конические, коническо-цилиндрические и т.д.); относительному расположению валов редуктора в пространстве (горизонтальные, вертикальные); особенностям кинематической схемы (развернутая, соосная, с раздвоенной ступенью и т.д.).

Возможности получения больших передаточных чисел при малых габаритах обеспечивают планетарные и волновые редукторы.

Одноступенчатые цилиндрические редукторы могут иметь колеса с прямыми, косыми или шевронными зубьями. Корпуса чаще выполняют литыми чугунными, реже - сварными стальными. Максимальное передаточное число одноступенчатого цилиндрического редуктора по ГОСТ 2185-66 U_max=12,5. Высота одноступенчатого редуктора с таким или близким к нему передаточным числом больше, чем двухступенчатого с тем же значением U. Поэтому практически редукторы с передаточными числами, близкими к максимальному, применяют редко, ограничиваясь U£6.

Одноступенчатые конические редукторы применяют для передачи движения между валами, оси которых пересекаются обычно под углом 90°. Передачи с углами, отличными от 90°, встречаются редко. Передаточное число U одноступенчатых конических редукторов с прямозубыми колесами, как правило, не выше трех; в редких случаях U=4. При косых или криволинейных зубьях U=5 (в виде исключения U=6,3).

У редукторов с коническими прямозубыми колесами допускаемая окружная скорость (по делительной окружности среднего диаметра) V£5м/с. При более высоких скоростях рекомендуют применять конические колеса с круговыми зубьями, обеспечивающими более плавное зацепление и большую несущую способность.

          Двухступенчатые цилиндрические редукторы

Наиболее распространены двухступенчатые горизонтальные редукторы. Эти редукторы отличаются простотой, но из-за несимметричного расположения колес на валах повышается концентрация нагрузки по длине зуба. Поэтому в этих редукторах следует применять жесткие валы.

В отношении типа зубьев и подшипников в двухступенчатых редукторах справедливо сказанное относительно одноступенчатых цилиндрических редукторов; часто быстроходную ступень выполняют косозубой, а тихоходную - прямозубой.

Редуктор с раздвоенной быстроходной ступенью может иметь либо шевронные колеса, либо прямозубые. При раздвоенной быстроходной (или тихоходной) ступени колеса расположены симметрично относительно опор, что приводит к меньшей концентрации нагрузки по длине зубьев, чем при применении обычной развернутой или соосной схемы. Это позволяет иметь в рассматриваемом случае менее жесткие валы.

Двухступенчатые цилиндрические редукторы обычно применяют в широком диапазоне передаточных чисел: по ГОСТ 2185-66 U=6,3¸63.

От целесообразной разбивки общего передаточного числа двухступенчатого редуктора по его отдельным ступеням в значительной степени зависят габариты редуктора, удобство смазывания каждой ступени, рациональность конструкции корпуса и удобство компоновки всех элементов передачи.

          Коническо-цилиндрические редукторы

В двухступенчатых коническо-цилиндрических редукторах коническая пара может иметь прямые, косые или криволинейные зубья. Цилиндрическая пара также может быть либо прямозубой, либо косозубой. Наиболее употребительный диапазон передаточных чисел для таких редукторов U=8¸15. Наибольшие значения при прямозубых конических колесах с круговыми зубьями U_max=34.

Червячные редукторы

Червячные редукторы применяют для передачи движения между валами, оси которых перекрещиваются.

По относительному положению червяка и червячного колеса различают три основные схемы червячных редукторов: с нижним, верхним и боковым расположением червяка. При нижнем расположении червяка условия смазывания зацепления лучше, при верхнем хуже, но меньше вероятность попадания в зацепление металлических частиц - продуктов износа.

Выбор схемы редуктора обусловлен удобством компановки привода в целом : при окружных скоростях червяка до 4-6 м/с предпочтительно нижнее расположение червяка. Передаточные числа червячных редукторов обычно колеблются в пределах U=8¸80.Т.к. КПД червячных редукторов невысок ,то для передачи больших мощностей и в установках, работающих непрерывно, проектировать их нецелесообразно. Практически червячные редукторы применяют для передачи мощности до 45 кВТ и в виде исключения до 150кВТ.

 

2.2 Кинематический и силовой расчет привода

.2.1 Определить момент сопротивления барабана

T_З=Р_Б×(D_Б/2)

Р_б=85кН -усилие на барабане;

D_б=0,3м-диаметр барабана;

.2.2 Опредилить угловую скорость на барабане (выходном валу)

n_вых= n_б=8 об/мин (число оборотов барабана)

.2.3 Определить мощность привода

N₃=T₃×w₃=12750Н×м×0,838с^-1=10685Вт»10,685кВт

2.2.4 Определить КПД привода

h_Р-КПД редуктора,

h_0П-КПД открытой передачи,

h_n-КПД пары подшипников,

h₃-КПД закрытой передачи.

h=h_Р ×h_0П×h_n

h_Р=h₃×h_n² .

Выбираем средние значения КПД механических передач:

h_0П=0,95;

h_n=0,99;

h_Р =0,97;

h_Р=0,97×(0,99)²=0,95

h=0,95×0,95×0,99=0,89 [6]

.2.5 Определить передаточное отношение привода

U=n_вх/n_вых

n_вх, n_вых- частота вращения входного и выходного валов соответственно

n_вх=96 об/мин,

n_вых=8 об/мин

U =96/8=12

.2.6 Передаточное отношение открытой передачи:

Выбираем U_0П=3,81 (ГОСТ 2185-66) [6] стр.7

.2.7 Определение передаточного отношения редуктора

U_р= U/ U_0П=12/3,81=3,15;

Полученное значение входит в стандартный ряд по ГОСТ 2185-66.

2.2.8 Определить момент сопротивления на промежуточном валу

T₂=T₃/U_0П×h_0П=12750 Н×м/(3,81×0,95)=3522,6Н×м

.2.9 Определить угловую скорость на входе

w₁=p×n_вх/30=3,14×96об/мин/30=10,05с^-1

2.3 Геометрический прочностной расчёт цилиндрических закрытых передач (редукторов)

 

2.3.1 Выбор материала

Выбираем материал: сталь 45

[s]_н =550 МПа -допускаемое напряжение на контактную прочность.

.3.2 Расчет геометрических параметров зубчатой передачи

1)Примем, z₁=18 - количество зубьев на шестерне, тогда

z₂= z₁× U_р=18×3,15=56,7»57 - число зубьев на колесе.

)Межосевое расстояние :

Для косозубых передач

          К_Нα=1,1(примем)- коэффициент, учитывающий неравномерность

распределения нагрузки между зубьями.

К_Нb=1,11 - учитывает неравномерность распределения нагрузки по

ширине венца.

К_Нu=1,02 - учитывает влияние динамической нагрузки, возникающей в

зацеплении.

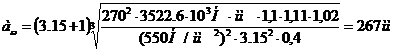
y_ва=0,4 коэффициент ширины венца по межосевому расстоянию для косозубых колёс [6]табл. 3.1,3.6

          Ближайшее стандартное значение а_w=250мм

)Определение нормального модуля зацепления:

β=26⁰ - угол наклона линии зуба (примем), тогда

Входит в ряд стандартных значений [6].

)Определим основные размеры для шестерни и колеса:

А)диаметры делительные:

- на шестерне

на колесе

Проверка:

Б)диаметры вершин зубьев:

на шестерне

d_a1=d₁+2m_n=120мм+2×5мм=130мм

на колесе

d_a2=d₂+2m_n =380мм+2×5мм=390мм

В) диаметры впадин

на шестерне

d_f1=d₁-2,5m_n=120мм-2,5×5мм=107,5мм

на колесе

d_f2=d₂+2,5m_n=380мм-2,5×5мм=367,5мм

Г)ширина венца колеса

b₂=y_ba×a_w=0,4×250=100мм;

Д)ширина венца шестерни

b₁= b₂+5мм=105мм

Е)длина зуба

b_з2= b₂/cos β=100мм/cos 26⁰=111,26мм

b_з1= b₁/cos β=105мм/cos 26⁰=116,82мм

Окружная скорость колёс:

При такой скорости для косозубых колёс следует принять восьмую степень точности ([6] табл.3.4)

Уточняем коэффициенты :К_H= К_Hb× К_Ha× ×К_HV

К_Ha=1,06;

К_Hb=1,15;

К_HV=1,0; при условии, что y_bd=b₁/d₁=105мм/120мм=0,875 и симметричном рясположении колёс

К_H=1,06×1,15×1,0=1,219

.3.3 Проверка зубчатой передачи на контактную прочность

,24Н/мм²<550 Н/мм²=[s]_H

 

2.3.4Определение усилий зацепления

- окружные:

радиальные:

α=20⁰ - угол защепления зубьев, тогда

- осевые:

2.4 Расчёт открытой конической передачи

.4.1 Выбор материала

Принимаем для шестерни и колеса одну и ту же марку стали .

Сталь 45 с твёрдостью НВ 190 Н/мм²

Допускаемое напряжение при проверке зубьев на выносливость по напряжению изгиба

Коэффициент запаса прочности [n]_f определяют как произведение двух коэффицитов [n]_f=[n]_f^¢×[n]_f^¢¢ [6]

[n]_f^¢ - учитывает нестабильность свойств материала зубчатых колёс ([6],табл. 3.9)

[n]_f^¢=1,75-учитывает нестабильность свойств материала зубчатых колес;

[n]_f^¢¢ - учитывает способ получения заготовки зубчатого колеса

[n]_f^¢¢ =1,0- для поковок и штамповок, тогда

[n]_f=1,75

s_f°_limb=1,8×HB=1,8×190 Н/мм²=342 Н/мм²

2.4.2 Геометрические параметры конической передачи

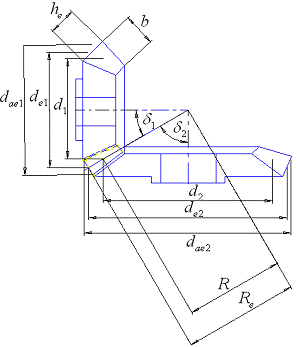
) Примем количество зубьев на

шестерне

Z₁=20, тогда

Z₂= Z₁ ×U_ОП=20×3,81=76,2»77 - количество

зубьев на колесе.

) Угол делительного конуса колеса:

d₂=arctg(U_0П)=75,3°;

угол делительного конуса шестерни:

d₁=90-d₂=14,7°

3)Расчёт среднего окружного модуля:

y_bm - коэффициент ширины венца по отношению к среднему

модулю.

K_F - коэффициент нагрузки при расчёте на изгиб

K_F=K_Fb×K_FV;

K_Fb=1,34 - учитывает неравномерность распределения нагрузки по длине зуба;

K_FV=1,45 - коэффициент динамичности; [6] стр.35

K_F=1,943 .

Y_F - коэффициент формы зубьев, выбираемый в зависимости от эквивалентного числа зубьв Z_v:

Расчёт ведём по тому колесу, у которого отношение [s_F]/ Y_F меньше,

т.к. материал одинаковый, то выбираем шестерню.

q_F=0,85 - опытный коэффициент нагрузочной способности.

Т= Т₂=3522,6×10³ Н×мм-вращающий момент на промежуточном валу.

)Расчёт внешнего окружного модуля:

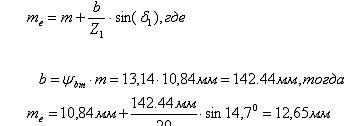
b - ширина зубчатого венца:

)Определение среднего делительного диаметра:

шестерни: d₁=m×Z₁=10,84×20=216,8 мм

колеса: d₂=m×Z₂=10,84×77=834,68 мм

)Определение внешнего делительного диаметра:

шестерни: d_е1= m_е×Z₁=12,65×20=253 мм

колеса: d_е2= m_е×Z₂=12,65×77=974,05 мм

)Внешнее конусное расстояние:

)Среднее конусное расстояние:

R=R_е - 0,5×b=503,5мм - 0,5×142,44мм=432,3 мм

)Внешняя высота головки зуба:

h_ae = m_е =12,65 мм

)Внешний диаметр вершин зубьев:

шестерни: d_ае1= d_е1+2× h_ae×cos(s₁)=253+2×12,65×cos14.7°=277,2 мм

колеса: d_ае2= d_е2+2× h_ae× cos(s₂)=974,05+2×12,65×соs75,3°=980,4мм

2.4.3 Определение усилий, действующих в зацеплении

 окружное:

радиальные и осевые усилия:

P_r2 = P_a1=P×tg(α) ×cos(s₁)=32500Н×tg20°×cos14.7°=11441,8Н

P_a2= P_r1= P×tg(α) ×cos(s₂)=32500Н×tg20°×cos75,3°=3001,7Н

2.4.4 Проверка зубьев на выносливость по напряжению изгиба

2.5 Конструирование деталей и эскизная компоновка редуктора

 

2.5.1 Ориентировочный расчёт валов из условия на кручение:

Определить диаметры выходного конца ведущего и ведомого валов:

Материал - сталь 45, тогда [t]_k - допускаемое касательное напряжение

при кручении,причем:

[t]_{kР ведущего вала}=25Н/мм² ; [6]

[t]_{k ведомого вала}=20 Н/мм².

T - крутящий момент, действующий на валу, тогда:

Принимаем стандартные значения:

d_В1=60мм; d_В2=95мм.

2.5.2 Определение основных конструктивных размеров валов

1) диаметры под подшипник:

А) ведущий вал: d_n1 = d_В1+(2…5)мм=60мм+5мм=65мм,

Б) ведомый вал: d_n2 = d_В2+(2…5)мм=95мм+5мм=100мм

Принять за основу ступенчатую конструкцию вала.

Шарикоподшипники радиально-упорные (ГОСТ 831-75)

А)№46313 d=65мм - диаметр внутреннего кольца;

D=140мм - диаметр внешнего кольца подшипника;

В=33мм - ширина подшипника;

С=113кН - динамическая грузоподъемность;

С₀=75 кН - статическая грузоподъемность;(средняя узкая серия)

Б) №46320, где d=100мм, D=215мм, В=47мм,

С=213кН, С₀=177кН.(тяжелая серия)

Шестерню выполняем за одно целое с валом, где

d_ш =d₁ =120мм

d_a1=130мм

b_ш= b₁=105мм,

(2…2,5) d_в1=2,4×60=144мм

Ведомый вал:

b₂=100мм-ширина колеса

d_k2=d_n2+(2…5)мм=100мм+5мм=105мм - размер под колесо;

d_S=d_k2+(2…5)мм=110мм - размер под бортик.

продольные размеры:

L_K=(1,2…1,5)×d_k2=1,4×105=147мм - длина ступицы колеса;

S=5мм - длина под бортик;

(2…2,5) d_в2=2,4×95=228мм.

Входной вал:

Выходной вал:

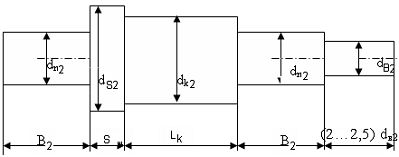
2.5.3 Конструирование колеса:

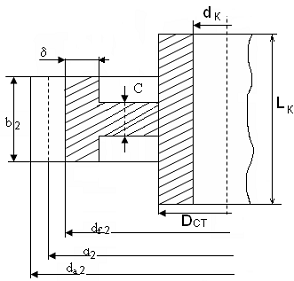
D_ст=1,6×d_k=168 мм - диаметр ступицы;

d =(2,5…4)×m_n=4×5=20 мм-толщина обода;

b₂=100мм - ширина венца колеса;

d_f2=367,5мм;

d₂=380мм;

d_а2=390мм;

L_к=147мм;

С=0,3×b₂=30мм - толщина диска.

2.5.4 Определение конструктивных размеров корпуса редуктора

- Толщина стенки корпуса редуктора:

d=0,025a_w+1мм=0,025×250мм+1мм=7,25 мм

Толщина стенки крышки редуктора:

d₁=0,02a_w+1мм=0,02×250мм+1мм=6 мм.

Первый этап компоновки редуктора: служит для приближённого определения положения зубчатых колёс относительно опор для

последующего определения опорных реакций и подбора подшипников.

Очерчиваем внутреннюю стенку корпуса:

а) принимаем зазор между торцом колеса и внутренней стенкой корпуса А=1,2d=1,2×7,25мм=8,7мм

б) принимаем зазор от окружности вершин зубьев шестерни до внутренней

стенки корпуса А=8,7мм

 

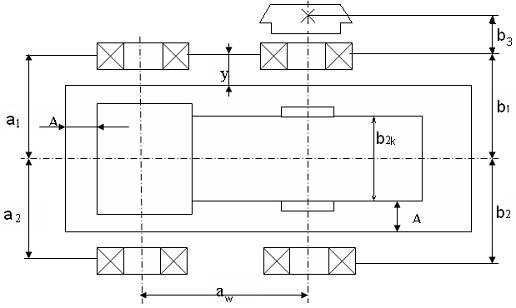
Причем:

у=8…10мм=8мм;

а₁= а₂=А+ b₂/2+y+ b_n1/2=8,7+100/2+8+33/2=83,2мм.₁= b₂=А+ b₂/2+y+ b_n2/2=8,7+100/2+8+47/2=90,2мм.₃ = (2…2,5) d_в2+ b_n2/2=237,5+47/2=261мм.

2.6 Расчет долговечности подшипников

Расчет вала на усталостную прочность.

.6.1 Ведущий вал

2.6.1.1 Определение сил и моментов

Р=18540Н (окружная сила )

Р_a=5316Н (радиальная сила)

Р_r=7020Н (осевая сила)

М=Р_а×(d₁/2)=5316Н×(120мм/2)= 319000Н×мм

 

.6.1.2 Определение реакций в опорах

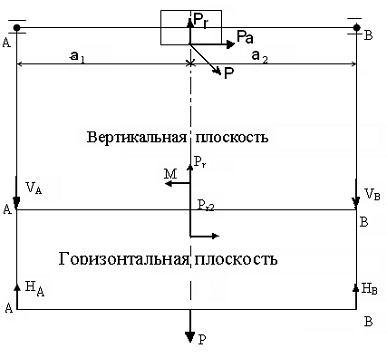
Вертикальная плоскость:

åМ(А)=0

P_r×а₁+M-V_B2а₁=0

V_B= (P_r×а₁+M)/2а₁=(7020Н×83,2мм+319000 Н×мм )/2×83,2мм=5427H

åM(B)=0

V_A2а₁ -P_r×а₁+M=0

V_A= (P_r×а₁-M)/2а₁=(7020Н×83,2-319000Н×мм)/2×83,2мм=1593H

Проверка: V_A-P_r+V_B=0

Горизонтальная плоскость:

åМ(А)=0

P×а₁+Н_В ×2×а₁=0

Н_В= H_A=P×а₁/ 2×а₁=Р/2=18540Н/2=9270Н.

åM(B)=0

H_A ×2 ×a₁+P ×a₁=0

H_A=P/2=9270H

2.6.1.3 Определение эквивалентной нагрузки

Р_Э=(х×К_V×F_r+y×F_a)×K_Б×К_Т [4]

х,у-коэффициенты радиальной и осевой нагрузки;

К_V=1-коэффициент, учитывающий вращение колец подшипника

K_Б=1,2 -коэффициент безопасности

К_Т=1 ,если t<100°C -температурный коэффициент

F_r=R_max=R_B;

F_а= Р_а=5316Н - осевая нагрузка;

отношение F_a/C₀=5316/75000=0,071, этой велечине соответствует l»0,68 [6]

Отношение P_a/R_B=5316/10740=0,495<l ,следовательно х=1,у=0.

Р_Э=(1×10740Н+0) ×1,2×1=12888Н

 

.6.1.4 Определение расчетной долговечности

 

- в миллионах оборотов:

 - в часах:

Оставляем данную серию подшипников.

.6.2 Ведомый вал

2.6.2.1.Определение сил и моментов

Р=18540Н, Р₁=32500Н - окружная сила;

Р_a=5316Н, Р_a1=11441.8Н - осевая сила;

Р_r=7020Н, Р_r1=3001.7Н - радиальная сила;

М_а=Р_а×(d₂/2)=5316Н×(380мм/2)=1010000Н×мм; М_а1=Р_а1×(d_1оп/2)=11441.8Н×(216,8мм/2)=1240000 Н×мм.

b₁=b₂=90.2мм; b₃=261мм

2.6.2.2 Определение реакций в опорах.

Вертикальная плоскость:

åМ(А)=0

P_r×b₁+M_a-V_B×2×b₁+P_r1(2×b₁+b₃)-M_a1=0

V_B= (P_r×b₁+M_a+P_r1(2×b₁+b₃)-M_a1)/2×b_1B=(7020Н×90,2мм+1010000Н×мм+3001.7Н(2×90,2мм+261мм)-1240000Н×мм)/ 2×90,2мм=9580H

åM(B)=0_A×2×b₁-P_r×b₂+M_a -M_a1+P_r1b₃=0_A= (P_r×b₂-M_a +M_a1-P_r1b₃)/2×b_1A=(7020Н×90,2мм-1010000Н×мм+1240000Н×мм-3001.7Н×261мм)/ 2×90,2мм =442H

Проверка: V_A-P_r+V_B-P_r1=0

Горизонтальная плоскость:

åМ(А)=0

P×b₁-Н_В 2×b₁ +P₁(2×b₁+b₃)=0

Н_В=( P₁(2×b₁+b₃)- P×b₁)/ 2×b₁=(32500Н×(2×90,2мм+261мм)-18540Н×90,2мм)/

2×90,2мм=70251H

åM(B)=0

H_A×2b₁-P×b₂-P₁×b₃=0_A=( P×b₂+P₁×b₃)/2b₁=(18540Н×90,2мм+32500Н×261мм)/2×90,2мм= 56291Н

Проверка: Н_А+Р₁-Н_В-Р=0

2.6.2.3 Построение эпюр

Вертикальная плоскость.

)-V_A×x=M(x) 0£x£b₁

M(0)=0 (b₁)=-442H×0.0902м=-39.86Н×м

) b₁£x£b₂+b₁ M(x)=-V_A×x-M_a+P_r(x-b₁)(b₁)= -V_A× b₁-M_a=-39.86Н×м-1010H×м= -1049.86Н×м

M(2b₁)=-V_A×2b₁-M_a +P_r×b₁=-39.86Н×2×0,0902м-1010Н×м+7020Н×0,0902м=

=-383.98Н×м

) b₁+b₂£x£b₂+b₁+b₃ M(x)= -V_A×x-M_a+P_r(x-b₁) -V_B(x-2b₁)(2b₁)= -383.98H×м(2b₁ +b₃)= -V_A×(2b₁+b₃)- M_a +P_r×(b₂+b₃) -V_B×b₃= -1240H×м

Горизонтальная плоскость

)М(х)=Н_А×х 0£x£b₁

M(0)=0

M(b₁)=Н_А×b₁=56291H×0,0902м=5077Н×м

) b₁£x£b₂+b₁ M(x)=Н_A×x-P_r(x-b₁)

М(b₁)= 5077Н×м

М(b₁+b₂)=H_A×2b₁-P×b₁=56291Н×2×0.0902м-18540Н×0,0902м=8483Н×м

) b₁+b₂£x£b₂+b₁+b₃ M(x)=Н_A×x-P_r(x-b₁)-Н_B(x-2b₁)

М(b₁+b₂)=8483Н×м

М(b₁+b₂ +b₃)=H_A×(2b₁+b₃)-P_r×(b₂+b₃)-H_B×b₃=56291Н×(2×0,0902м+0,261м)-

Н×(0,0902м+0,261м) -70251Н×0,261м= 0,088»0 Н×м

Построение эпюр:

2.6.2.4 Определение эквивалентной нагрузки

Р_Э=(х×К_V×F₂+y×F_a)×K_Б×К_Т

F₂=R_max=R_B

F_a= Р_a =2650Н

К_V=1-коэффициент учитывающий вращение колец подшипника

K_Б=1,2 -коэффициент безопасности

К_Т=1 ,если t<100°C -температурный коэффициент

F_a/C₀=5316Н/177000Н=0,03, этой величине соответствует l»0,68

( [6],стр.119 )

Отношение P_a/R_B=5316Н/70901Н=0,075<l ,следовательно

х=1,у=0

Р_Э=1×1×70901Н×1,2×1=85081Н

 

.6.2.5 Определение расчетной долговечности

- в млн. об.

в часах:

Оставляем данную серию подшипников.

2.7 Уточнённый расчет валов

 

.7.1 Выбрать материал вала

Примем для вала углеродистую сталь 30ХГС.

Предел временного сопротивления s_в=1020МПа.

 

.7.2 Определить изгибающие моменты

вертикальная плоскость: М_{из А-А}=-1050Н×м; М_{из В-В}=-457Н×м

горизонтальная плоскость: М_{из А-А}=5077Н×м; М_{из В-В}=8483Н×м

Наиболее опасное сечение : В-В

 

.7.3 Полярный момент сопротивления

W_ρ=0,2d_n2³ =0,2×(100мм)³=200×10³×мм³

 

.7.7Определение амплитуды касательных напряжений:

t_а=T₂/W_ρ=(3522,6×10³Н×мм)/200×10³мм³=17,613Н/мм².

Т₂=3522,6Н×м - момент сопротивления на промежуточном валу.

2.7.8Определение коэффициентов запаса прочности по нормальным и касательным напряжениям:

 

s_-1 ,τ_-1 - пределы выносливости при симметричном цикле для нормальных и касательных напряжений.

s_-1=0,43s_в=0,43×1020=438,6МПа;

τ_-1=0,58s_-1=0,58×438,6=254,4МПа;

ε_s ,ε_τ - масштабные коэффициенты;

Считая,что диаметр вала в сечении В-В равен 100мм,тогда:

ε_s=0,70;

ε_τ=0,59; [6]

β - коэффициент, учитывающий влияние шероховатости поверхности;

β=0,97, если шероховатость R_a=0,32мкм;

к_s, к_τ - эффективные коэффициенты концентрации напряжений.

Концентрация напряжений обусловлена переходом от диаметра 100мм к диаметру 95мм,и считая что,

d_n2/d_в2=100мм/95мм=1,05 и r/d_в2=2,5мм/95мм=0,026 примем:

к_s=2,35-0,54×0,016/0,02=1,9

к_t=1,45-0,16×0,016/0,02=1,32 /используя интерполяцию/ [6]

2.7.9 Результирующий коэффициент запаса прочности:

 

 

Этот коэффициент возможен только при расчете вала на жесткость.

 

.7.10 Расчет вала на жесткость:

 

 

 

[φ₀]=[5-22]×10^-3рад/м - допускаемый угол закручивания;

М_КР - крутящий момент, действующий в расчетном сечении:

М_КР= М=8495,3×10³Н×мм;

G - модуль сдвига /для стали G=8×10⁴Н/мм²/;

I_ρ - полярный момент инерции расчетного сечения:

 

 

                          

 

Проверка на жесткость выполнена.

2.8 Выбор и анализ посадок

 

.8.1 Выбор посадок для основных сопрягаемых деталей

1)   Æ65К6, Æ100К6-соединение внутренних колец подшипников качения на

валы, /отклонение вала/.

2)   Æ140Н7, Æ215Н7- соединение наружных колец подшипников качения в корпусе,/отклонение отверстия/.

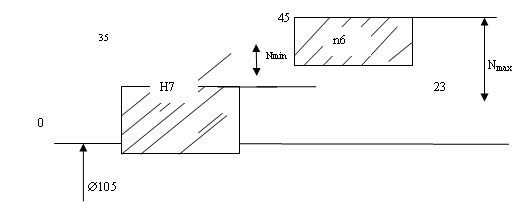
3)   Æ105Н7/6 - зубчатое колесо на вал, в случае частого демонтажа /переходная посадка/.

2.8.2 Анализ посадок

1)Определение предельного отклонения основного отверстия Æ105Н7/n6:

Для основного отверстия Н7:

верхнее отклонение Æ105 ЕS=+35мкм

нижнее отклонение Æ105 ЕI=0мкм

Для вала таблица 10.12.[6] n6

верхнее отклонение es=+45

нижнее отклонение ei=+23

Предельные размеры, мм:

Отверстие Н7 D_max=105,035 D_min=105,000

Вал n6 d_max=105.045мм, d_min=105.023мм

.Определение минимального значения натяга

N_min=ES-ei=0,035-0,023=0,012мм

.Определение максимального значения натяга

N_max=es-EI=45-0=0.045мм

.Определить допуск на отверстие и на вал:

Т_Д=ES=EI=0,035мм

Т_d=es-ei=0,022мм

4. Построим схему допусков:

Cписок использованной литературы

провод воздушная линия коническая передача

1. Справочник по проектированию линий электропередачи /М.Б. Вязьменский, В.Х. Ишкин, К.П. Крюков и др. Под ред.М.А. Реута и С.С. Рокотяна.-2-е изд.,перераб. и доп.-М.:Энергия,1980.-296 с.,ил.

2. Кастанович М.М. Монтаж воздушных линий электропередачи до 110кВ. М.,”Энергия”,1976. 272 с. ил. (Справочник электромонтажника).

3. Выбор исходного режима и построение монтажных графиков при расчете ЛЭП с применением ЭВМ. Методические указания к выполнению курсового проекта по курсу “Прикладная механика “ для студентовЭЭФ II курса всех форм обучения. НЭТИ Новосибирск 1987.

4. Конспект лекций и практика . Козлов А.Г.

5. Сопротивление материалов, Н.М. Беляев, Главная редакция физико-математической литературы изд-ва “Наука “,1976г., стр.608 с ил.

6. Курсовое проектирование деталей машин:

Учебное пособие для учащихся машиностроительных специальностей техникумов/ С.А. Чернавский, К.Н. Боков, И.М. Чернин и др.-2-е изд., перераб. и доп.-М.: Машиностроение,1988.-416 с.: ил.