Самосопряженные расширения симметрических операторов в гильбертовом пространстве
СОДЕРЖАНИЕ
Введение
1. Индексы
дефекта
2. Преобразование
Кэли и формулы Неймана
3. Формула
Крейна для резольвент самосопряженных расширений заданного симметрического
оператора
Литература
ВВЕДЕНИЕ
Чтобы получить симметрическое
расширение заданного оператора А нужно найти изометрическое расширение его
преобразования Кэли V. Для этого выберем в дефектных
подпространствах 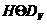 ,
, 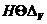 два
подпространства, F и G, равных
размерностей и построим произвольный изометрический оператор V1 c областью
определения F и областью
значений G.
два
подпространства, F и G, равных
размерностей и построим произвольный изометрический оператор V1 c областью
определения F и областью
значений G.
Определим, далее, линейный оператор 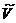 с областью
определения
с областью
определения 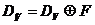 и областью
значений
и областью
значений 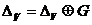 формулами
формулами
при 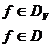 .
.
Очевидно, 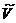 есть
изометрическое расширение V и при всевозможных изменениях F, G, V1 мы получим
все изометрические расширения
есть
изометрическое расширение V и при всевозможных изменениях F, G, V1 мы получим
все изометрические расширения 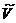 оператора V и каждое по
одному разу.
оператора V и каждое по
одному разу.
Итак, чтобы найти некоторое
симметрическое расширение 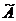 оператора
А, следует перейти к преобразованию Кэли оператора А, найти по описанному выше
методу некоторое расширение
оператора
А, следует перейти к преобразованию Кэли оператора А, найти по описанному выше
методу некоторое расширение 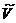 оператора V и, наконец,
вернуться к
оператора V и, наконец,
вернуться к 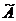 , выполнив
преобразование Кэли над
, выполнив
преобразование Кэли над 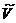 .
.
1. ИНДЕКСЫ ДЕФЕКТА
Определение: Всякую функцию 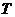 , которая
каждому элементу
, которая
каждому элементу 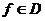 относит
некоторый элемент
относит
некоторый элемент 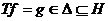 , называют
оператором в пространстве Н с областью определения
, называют
оператором в пространстве Н с областью определения 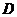 и областью
значений
и областью
значений 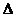 , состоящей
из всех
, состоящей
из всех 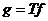 , где
, где 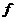 пробегает
все
пробегает
все 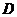 .
.
Тождественный оператор, т.е.
оператор, переводящий каждый вектор сам в себя, будем обозначать 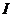 . Область
определения и область значение оператора будем обозначать
. Область
определения и область значение оператора будем обозначать 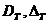 ,
соответственно.
,
соответственно.
Если оператор 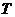 двум
различным элементам из
двум
различным элементам из 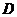 относит
различные элементы, то
относит
различные элементы, то 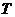 имеет
обратный оператор, который элементам из
имеет
обратный оператор, который элементам из 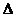 относит элементы из
относит элементы из 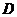 . Обратный
оператор обозначают символом
. Обратный
оператор обозначают символом 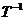 , таким образом,
, таким образом,
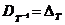 ,
, 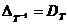 .
.
Определение: Оператор 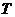 называется непрерывным
в точке
называется непрерывным
в точке 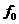 (
( ), если
), если 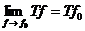 (
(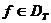 ); это
означает, что при любом
); это
означает, что при любом 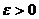 существует
такое
существует
такое 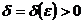 , что из
, что из 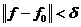 ,
, 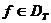
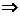
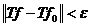 .
.
Если область определения 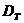 оператора
оператора 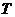 шире
области определения
шире
области определения 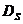 оператора
оператора 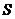 , т.е.
, т.е.  , и если
, и если 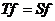 для любого
элемента
для любого
элемента 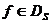 , то
оператор
, то
оператор 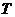 называют
расширением оператора
называют
расширением оператора 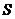 (
(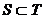 ).
).
Определение. Оператор Т называется
линейным, если его область определения D есть
линейное многообразие и 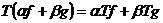 для любых
для любых 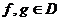 и любых
комплексных
и любых
комплексных 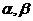 .
.
Определение. Оператор V, заданный
на всем пространстве Н1(DV=H1) и
отображающий его на все пространство Н2 (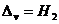 ),
называется изометрическим, если для любых
),
называется изометрическим, если для любых 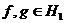
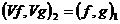 .
.
Определение. Линейный оператор А
называется симметрическим, если
1) область определения DA
плотна
в Н и
2) для любых двух элементов f, g из DA имеет место
равенство 
Определение. Значения параметра 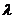 , для
которых обратный оператор
, для
которых обратный оператор 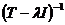 существует,
определен всюду в
существует,
определен всюду в 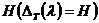 и
ограничен, называют регулярными значениями оператора Т. Все остальные точки
комплексной плоскости образуют спектр оператора Т.
и
ограничен, называют регулярными значениями оператора Т. Все остальные точки
комплексной плоскости образуют спектр оператора Т.
Определение. Резольвентой оператора
Т называют зависящий от параметра 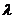 оператор
оператор  ,
рассматриваемый на множестве всех тех значений
,
рассматриваемый на множестве всех тех значений 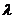 , для которых он существует и для
которых его область определения, т.е.
, для которых он существует и для
которых его область определения, т.е. 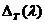 плотна в Н.
плотна в Н.
Пусть 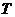 - произвольный линейный оператор.
- произвольный линейный оператор.
Определение: число 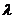 назовем
точкой регулярного типа оператора
назовем
точкой регулярного типа оператора 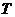 , если существует такое
, если существует такое 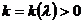 , что при
всех
, что при
всех 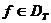
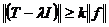 .
.
Поэтому собственные значения
оператора 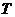 не являются
для него точками регулярного типа.
не являются
для него точками регулярного типа.
Если 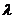 точка регулярного типа оператора
точка регулярного типа оператора 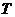 , то
оператор
, то
оператор 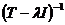 существует
и ограничен, и обратно, если оператор
существует
и ограничен, и обратно, если оператор 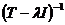 существует и ограничен, то
существует и ограничен, то 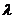 есть точка
регулярного типа.
есть точка
регулярного типа.
Если 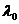 есть точка регулярного типа, то при
есть точка регулярного типа, то при
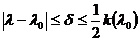 и любом
и любом 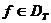 имеет место
неравенство
имеет место
неравенство
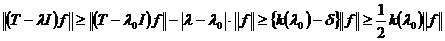 .
.
Оно показывает, что множество точек
регулярного типа всегда открыто. Это множество точек называется полем
регулярности оператора 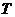 .
.
Если 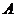 есть симметрический оператор и
есть симметрический оператор и 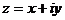
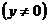 , то при
любом
, то при
любом 
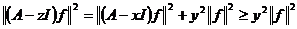 .
.
Отсюда видно, что верхняя и нижняя
половины 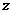 -плоскости
являются связными компонентами поля регулярности любого симметрического
оператора.
-плоскости
являются связными компонентами поля регулярности любого симметрического
оператора.
Теорема: если 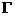 есть
связная компонента поля регулярности линейного оператора
есть
связная компонента поля регулярности линейного оператора 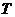 , то
размерность подпространства
, то
размерность подпространства 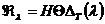 одинакова для всех
одинакова для всех 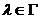 .
.
Условимся называть дефектным числом
линейного многообразия 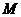 размерность
его ортогонального дополнения
размерность
его ортогонального дополнения 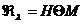 и будем писать
и будем писать
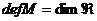 .
.
Определение: дефектное число
линейного многообразия 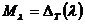 для точек
для точек 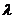 ,
принадлежащих данной связной компоненте поля регулярного оператора
,
принадлежащих данной связной компоненте поля регулярного оператора 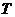 , называется
дефектным числом оператора
, называется
дефектным числом оператора 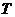 в этой компоненте поля
регулярности. При этом
в этой компоненте поля
регулярности. При этом 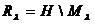 называется
дефектным подпространством оператора
называется
дефектным подпространством оператора 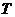 для точки
для точки 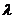 , а любой
отличный от нуля элемент дефектного подпространства называется дефектным
элементом.
, а любой
отличный от нуля элемент дефектного подпространства называется дефектным
элементом.
Каждый симметрический оператор 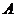 имеет два
дефектных числа, а именно одно (
имеет два
дефектных числа, а именно одно (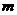 ) в нижней, другое (
) в нижней, другое (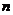 ) в верхней
полуплоскости. Их называют также индексами дефекта оператора
) в верхней
полуплоскости. Их называют также индексами дефекта оператора 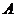 :
:
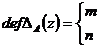
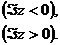
Индексы дефекта симметрического
оператора образуют упорядоченную пару чисел 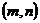 .
.
Из приведенной выше теоремы вытекают
следующие три предложения.
°. Если симметрический оператор
имеет вещественную точку регулярного типа, то его дефектные числа равны:  . То же
справедливо относительно изометрического оператора, если он имеет точку
регулярного типа на единичной окружности.
. То же
справедливо относительно изометрического оператора, если он имеет точку
регулярного типа на единичной окружности.
°. Если 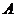 -
симметрический оператор, то любое невещественное число
-
симметрический оператор, то любое невещественное число 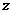 является для
сопряженного оператора
является для
сопряженного оператора 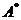 собственным
значением: кратности
собственным
значением: кратности 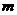 , если
, если 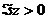 , и
кратности
, и
кратности 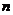 , если
, если 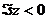 .
.
°. Дефектные числа изометрического
оператора 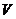 могут быть
определены с помощью следующих равенств:
могут быть
определены с помощью следующих равенств:
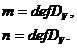
2. ПРЕОБРАЗОВАНИЕ КЭЛИ И ФОРМУЛЫ НЕЙМАНА
Пусть 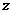 - какое-нибудь вещественное число, а
- какое-нибудь вещественное число, а
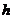 пробегает
пробегает 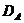 . Будем
полагать, что
. Будем
полагать, что 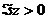 . Тогда
. Тогда
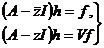 (1)
(1)
преобразование Кэли 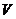 замкнутого
симметрического оператора
замкнутого
симметрического оператора 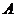 . Оператор
. Оператор 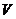 выражается
через оператор
выражается
через оператор 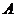 формулой
формулой 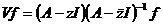 . При этом
областью определения
. При этом
областью определения 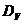 оператора
оператора 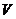 является
является 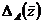 .
.
В силу формул (1) 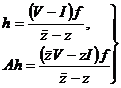 (2)
(2)
и поэтому 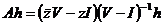 . (2’)
. (2’)
Утверждение. Индексы дефекта 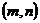 оператора
оператора 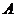 совпадают с
индексами дефекта оператора
совпадают с
индексами дефекта оператора 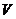 .
.
Действительно, по определению, 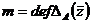 . Но
. Но 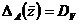 ,
следовательно,
,
следовательно, 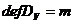 . С другой
стороны, снова по определению,
. С другой
стороны, снова по определению, 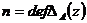 и
и 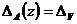 , так что
, так что 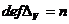 .
.
Теорема 1. Если оператор V -
изометрический и многообразие 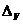 плотно в Н, то определяемый
формулой (2’) оператор А - симметрический, а оператор V есть его
преобразование Кэли.
плотно в Н, то определяемый
формулой (2’) оператор А - симметрический, а оператор V есть его
преобразование Кэли.
Теорема 2. Пусть А1 и А2
- симметрические операторы, а V1 и V2 - их
преобразования Кэли. Для того чтобы оператор А2 был расширением
оператора А1, необходимо и достаточно, чтобы оператор V2 был
расширением оператора V1.
Таким образом теорема 2 сводит
вопрос о симметрических расширениях заданного оператора А к вопросу об
изометрических расширениях его преобразования Кэли.
Известно, что замкнутые линейные
многообразия F и G могут
служить соответственно областью определения и изменения изометрического
оператора тогда и только тогда, когда равны их размерности, тогда
изометрические расширения оператора V могут быть
получены следующим образом.
Выберем в дефектных подпространствах
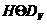 ,
, 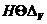 два
подпространства, F и G, равных размерностей
и построим произвольный изометрический оператор V1 c областью
определения F и областью
значений G.
два
подпространства, F и G, равных размерностей
и построим произвольный изометрический оператор V1 c областью
определения F и областью
значений G.
Определим, далее, линейный оператор 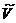 с областью
определения
с областью
определения 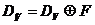 и областью
значений
и областью
значений 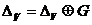 формулами
формулами
при 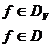 .
.
Очевидно, 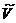 есть
изометрическое расширение V и при всевозможных изменениях F, G, V1 мы получим
все изометрические расширения
есть
изометрическое расширение V и при всевозможных изменениях F, G, V1 мы получим
все изометрические расширения 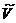 оператора V и каждое по
одному разу.
оператора V и каждое по
одному разу.
Из приведенных выше рассуждений
следует, в частности, что оператор А является максимальным симметрическим
(самосопряженным) тогда и только тогда, когда его преобразование Кэли V является
максимальным изометрическим оператором.
Поэтому имеют место следующие
теоремы.
Теорема 3. Для того чтобы
симметрический оператор был максимальным, необходимо и достаточно, чтобы одно
из его дефектных чисел равнялось нулю. Для того чтобы симметрический оператор
был самосопряженным, необходимо и достаточно, чтобы оба его дефектных числа
равнялись нулю.
Теорема 4. Пусть А - произвольный
симметрический оператор с индексами дефекта 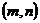 . Оператор А всегда можно расширить
до максимального. Если
. Оператор А всегда можно расширить
до максимального. Если 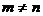 , то среди
таких расширений нет самосопряженных; если
, то среди
таких расширений нет самосопряженных; если  и
и 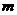 ,
, 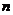 конечны, то любое максимальное
расширение оператора А является самосопряженным; если же дефектные числа
конечны, то любое максимальное
расширение оператора А является самосопряженным; если же дефектные числа 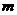 ,
, 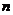 бесконечны
и равны, то среди максимальных расширений имеются как самосопряженные, так и
несамосопряженные.
бесконечны
и равны, то среди максимальных расширений имеются как самосопряженные, так и
несамосопряженные.
Теорема. Пусть А - произвольный
симметрический оператор с областью определения DA, a 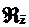 и
и 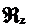 (
(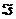 >0) -
какая-нибудь пара его дефектных подпространств. Для области определения DA* оператора А*
имеет место следующее определение в виде прямой суммы трех линейных
многообразий:
>0) -
какая-нибудь пара его дефектных подпространств. Для области определения DA* оператора А*
имеет место следующее определение в виде прямой суммы трех линейных
многообразий:
Доказательство. Покажем, что любой
элемент f из DA* представим в
виде
f = f0 + g + g
+ g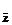 , (1)
, (1)
где f0  DA, gz
DA, gz 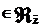 , g
, g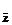
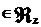 ; при этом
следует заметить, что вместе с (1) будет иметь место формула
; при этом
следует заметить, что вместе с (1) будет иметь место формула
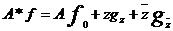 . (1’)
. (1’)
Пусть 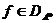 . Разложим элемент
. Разложим элемент 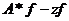 на
составляющие в ортогональных подпространствах
на
составляющие в ортогональных подпространствах 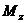 и
и 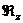 :
:
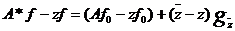 .
.
но  ; поэтому
; поэтому
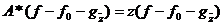 ,
,
откуда заключаем, что
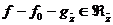 ,
,
т.е. 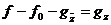
или 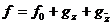 .
.
Для окончания доказательства теоремы
осталось установить, что представление (1) каждого элемента 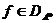 единственно.
Допуская противное, примем, что
единственно.
Допуская противное, примем, что
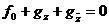 . (2)
. (2)
Применяя к обеим частям этого
равенства оператор А*, получаем
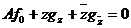 . (2’)
. (2’)
Умножая далее (2) на z и вычитая
из (2’), получаем
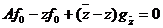 ,
,
откуда, вследствие ортогональности
слагаемых, следует, что 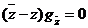 ; точно
также получим, что
; точно
также получим, что 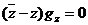 ;
;
следовательно, 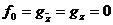 .
.
Теорема доказана.
Найдем теперь 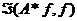 при любом
при любом 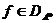 . В
соответствии с (1) и (1’), имеем
. В
соответствии с (1) и (1’), имеем 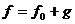 , где
, где 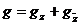 , и
, и
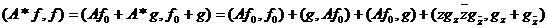 .
.
Так как сумма первых трех слагаемых
вещественна, то
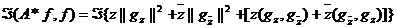 ,
,
где в квадратных скобках снова стоит
вещественная величина, а потому окончательно находим
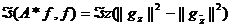 . (3)
. (3)
В соответствии с формулой (3)
область DA* состоит из
трех (нелинейных) многообразий Г+ (совокупность элементов f, для
которых 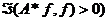 , Г-
((совокупность элементов f, для которых
, Г-
((совокупность элементов f, для которых 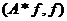 вещественно).
Элемент
вещественно).
Элемент
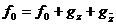
принадлежит Г+, Г-
или Г0, смотря потому, будет ли
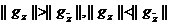 или
или 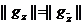 (если
(если 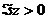 ).
).
Найдем теперь для области
определения 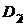 любого
симметрического расширения
любого
симметрического расширения 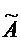 оператора А представление,
аналогичное формуле (1).
оператора А представление,
аналогичное формуле (1).
Чтобы подчеркнуть зависимость
подпространств F и G от z, будем
писать Fz и Gz. Таким
образом,
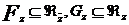 .
.
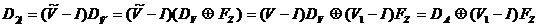
или, полагая
1= - V',
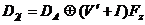 .
.
Из 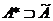 следует, что при
следует, что при
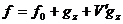
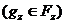 (4)
(4)
будет 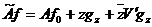 . (4')
. (4')
Формулы (1) и (4) будем называть
соответственно первой и второй формулой Неймана.
Из первой формулы Неймана
непосредственно следует для размерности DA* по модулю DA формула:
 . (5)
. (5)
Вторая формула Неймана совместно с
равенством (4’) описывает все симметрические расширения 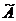 заданного
оператора А. Если, в частности, оператор А имеет равные дефектные числа и
заданного
оператора А. Если, в частности, оператор А имеет равные дефектные числа и 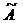 есть его
самосопряженное расширение, то в формуле (4) элемент
есть его
самосопряженное расширение, то в формуле (4) элемент 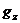 будет
пробегать все подпространство
будет
пробегать все подпространство 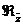 , а
, а 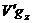 - все
- все 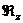 . Обратно,
если в (4) элемент
. Обратно,
если в (4) элемент 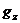 пробегает
все
пробегает
все 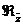 , а
, а 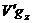 - все
- все 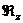 , то
оператор
, то
оператор 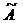 будет
самосопряженным расширением оператора А. Если индексы дефекта оператора А и его
симметрического расширения
будет
самосопряженным расширением оператора А. Если индексы дефекта оператора А и его
симметрического расширения 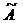 суть (m, n) и (m-p, n-p), где
суть (m, n) и (m-p, n-p), где 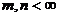 , то из
второй формулы Неймана вытекает соотношение
, то из
второй формулы Неймана вытекает соотношение
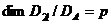
. ФОРМУЛА КРЕЙНА ДЛЯ РЕЗОЛЬВЕНТ
САМОСОПРЯЖЕННЫХ РАСШИРЕНИЙ ЗАДАННОГО СИММЕТРИЧЕСКОГО ОПЕРАТОРА
Теорема 1. Все самосопряженные
расширения оператора с равными и конечными дефектными числами имеют один и тот
же непрерывный спектр.
Теорема 2. При произвольном
расширении оператора с равными и конечными индексами дефекта (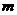 ,
,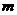 ) до
самосопряженного оператора кратность собственных значений повышает не более чем
на
) до
самосопряженного оператора кратность собственных значений повышает не более чем
на 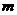 единиц (в
частности, новые собственные значения имеют кратность, не превосходящую
единиц (в
частности, новые собственные значения имеют кратность, не превосходящую 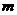 ).
).
Теорема3. Если 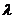 -
вещественная точка регулярного типа симметрического оператора А с индексом
дефекта
-
вещественная точка регулярного типа симметрического оператора А с индексом
дефекта 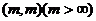 , то
существует самосопряженное расширение
, то
существует самосопряженное расширение 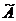 оператора А, для которого число
оператора А, для которого число 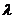 является
собственным значением кратности
является
собственным значением кратности 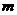 .
.
Доказательство. Пусть 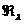 означает
линейное многообразие всех решений уравнения
означает
линейное многообразие всех решений уравнения
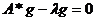 .
.
В силу теоремы об инвариантности
дефектного числа в поле регулярности число измерений многообразия 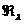 линейно
независимы, ибо в противном случае число
линейно
независимы, ибо в противном случае число 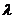 было бы собственным значением оператора
А.
было бы собственным значением оператора
А.
Положим
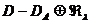 (1)
(1)
и пусть 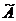 означает
оператор, совпадающий с оператором А* на
означает
оператор, совпадающий с оператором А* на 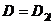 , так что число
, так что число 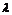 будет
собственным значением оператора
будет
собственным значением оператора 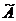 кратности
кратности 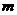 .
.
Покажем, что оператор 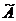 самосопряженный.
самосопряженный.
Для этого достаточно установить, что
оператор 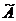 симметрический,
ибо из (1) следует, что
симметрический,
ибо из (1) следует, что
 .
.
Если 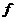 и
и 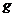 - произвольные элементы из
- произвольные элементы из 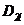 и
и
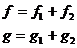
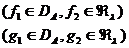
то
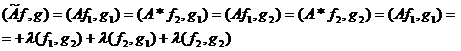
откуда следует симметричность
оператора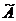 .
.
В заключении отметим еще одну
теорему, относящуюся к числу решений уравнения
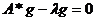
при вещественных 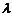 .
.
Теорема. Если А - симметрический
оператор с индексами дефекта 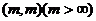 и
и 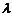 - вещественное число, не
принадлежащее точечному спектру оператора А, то число
- вещественное число, не
принадлежащее точечному спектру оператора А, то число 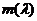 решений
уравнения
решений
уравнения
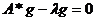 (2)
(2)
не превосходит дефектного числа 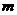 .
.
Для доказательства достаточно
построить с помощью многообразия 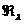 решения уравнения (2) область
решения уравнения (2) область 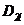 по формуле
(1), где основа
по формуле
(1), где основа 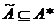 .
.
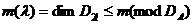 .
.
Теорема доказана.
Пусть А1 и А2
- два самосопряженных расширения симметричного оператора А с индексом дефекта 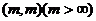 ,
,
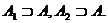
Всякий оператор С, удовлетворяющий
условиям
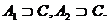 (3)
(3)
естественно называть общей частью
операторов А1 и А2.
Среди операторов С, удовлетворяющих
условиям (3), существует, очевидно, такой, который является расширением любой
общей части операторов А1 и А2; такой оператор назовем
максимальной общей частью операторов А1 и А2.
Максимальная общая часть либо является расширением оператора А, либо совпадает
с А; в последнем случае расширения А1 и А2 будем называть
взаимно простыми.
Для того чтобы расширения А1 и
А2 были взаимно простыми, необходимо и достаточно, чтобы
одновременное выполнение условий
 (4)
(4)
вело принадлежность 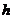 к
к 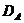 .
.
Если максимальное число линейно
независимых по модулю 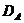 векторов,
удовлетворяющих условиям (4), равно
векторов,
удовлетворяющих условиям (4), равно  , то максимальная общая часть А0
операторов А1 и А2 имеет индексы дефекта
, то максимальная общая часть А0
операторов А1 и А2 имеет индексы дефекта 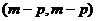 . В этом
случае операторы А1 и А2 могут рассматриваться как взаимно
простые самосопряженные расширения оператора А0.
. В этом
случае операторы А1 и А2 могут рассматриваться как взаимно
простые самосопряженные расширения оператора А0.
Задачей настоящего пункта является
вывод формулы, связывающей резольвенты двух самосопряженных расширений
оператора А. Пусть 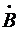 - фиксированное
самосопряженное расширение, а
- фиксированное
самосопряженное расширение, а 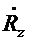 и
и  - их резольвенты. Пусть, далее
- их резольвенты. Пусть, далее 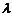 - любая
общая точка регулярности операторов
- любая
общая точка регулярности операторов 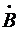 и В (в частности,
и В (в частности, 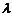 может быть
произвольным невещественным числом).
может быть
произвольным невещественным числом).
Чтобы не выделять случая, когда 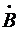 и В не
являются взаимно простыми расширениями оператора А, будем рассматривать их как
взаимно простые расширения их максимальной общей части А0, имеющей
индексы (r, r), где
и В не
являются взаимно простыми расширениями оператора А, будем рассматривать их как
взаимно простые расширения их максимальной общей части А0, имеющей
индексы (r, r), где 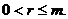
Положим 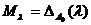 и
и 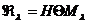 . Для
разности резольвент будем иметь
. Для
разности резольвент будем иметь
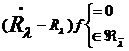
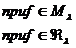 (5)
(5)
Последнее вытекает из того, что при
любом 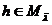
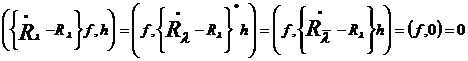 .
.
Выберем как-нибудь 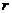 линейно
независимых векторов
линейно
независимых векторов 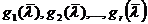 из
из 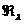 и
и 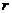 линейно
независимых векторов
линейно
независимых векторов 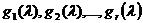 из
из 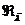 . Из (3) для
любого
. Из (3) для
любого 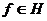 следует
следует
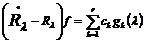 . (6)
. (6)
Согласно (4) константы 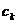 являются
линейными функционалами от
являются
линейными функционалами от 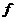 , и можно положить
, и можно положить 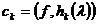
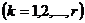 .
.
Так как, в силу (5) и линейной
независимости векторов  , при любом
, при любом 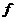 ,
ортогональном к
,
ортогональном к 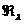 , должно
быть
, должно
быть
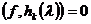
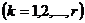 ,
,
то 
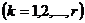 ,
,
т.е. 
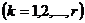 , (7)
, (7)
и (4) принимает вид
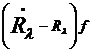 =
=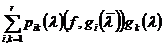 . (8)
. (8)
Заметим, что матричная функция 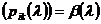 ,
определенная на множестве общих точек регулярности операторов
,
определенная на множестве общих точек регулярности операторов  и
и 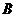 , является
неособенной.
, является
неособенной.
Предположение 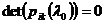 влечет в
силу (7) линейную зависимость векторов
влечет в
силу (7) линейную зависимость векторов 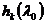
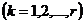 , что означает существование вектора
, что означает существование вектора
 ,
удовлетворяющего условиям
,
удовлетворяющего условиям 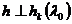 ,
, 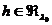
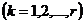 .
.
Для вектора 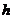 получаем из
(6)
получаем из
(6) 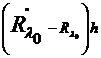 =0, а это
противоречит взаимной простоте операторов
=0, а это
противоречит взаимной простоте операторов 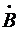 и
и 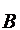 , как расширений оператора
, как расширений оператора 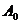 .
.
Опуская в (8) элемент 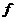 и
рассматривая
и
рассматривая 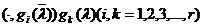 как
операторы, получаем для любого значения
как
операторы, получаем для любого значения 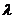 из множества общих точек
регулярности операторов
из множества общих точек
регулярности операторов 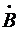 и В формулу
и В формулу
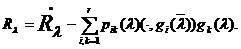 (9)
(9)
Левая и правая части формулы (8)
являются регулярными аналитическими вектор-функциями от 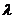 . Покажем,
что
. Покажем,
что 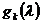
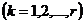 могут быть
определены как регулярные аналитические вектор-функции от
могут быть
определены как регулярные аналитические вектор-функции от 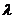 , и получим
соответствующую этому выбору формулу для матричной функции
, и получим
соответствующую этому выбору формулу для матричной функции 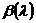 .
.
С этой целью возьмем какое-нибудь
фиксированное значение 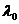 и введем
оператор
и введем
оператор 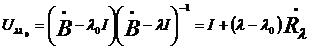 с областью
определения
с областью
определения 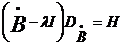 и областью
значений
и областью
значений 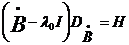 .
.
Оператор 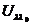 определяется
формулами
определяется
формулами
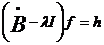 ,
, 
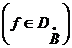 ,
,
из которых следует, что
осуществляемое им отображение Н на Н взаимно однозначно.
В частном случае, при 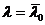 оператор
оператор 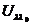 приводит к
преобразованию Кэли оператора
приводит к
преобразованию Кэли оператора 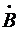 и отображает дефектное
подпространство
и отображает дефектное
подпространство 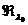 . Покажем,
что вообще
. Покажем,
что вообще 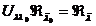 .
.
Выберем произвольный базис 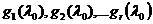 и докажем,
что
и докажем,
что 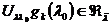 .
.
Имеем
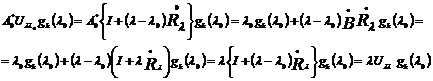
т.е. 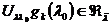
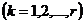 . При этом в силу взаимной
однозначности отображения, осуществляемого оператором
. При этом в силу взаимной
однозначности отображения, осуществляемого оператором 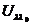 , векторы
, векторы 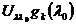 образуют
базис в
образуют
базис в 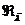 , и мы можем
принять, что векторы
, и мы можем
принять, что векторы 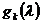 в любой
точке регулярности оператора
в любой
точке регулярности оператора  определены формулами
определены формулами
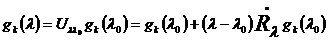
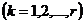 ,
,
и, следовательно, являются
регулярными аналитическими вектор-функциями от 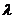 .
.
С помощью функционального уравнения
резольвенты легко проверить, что в таком случае для любых двух регулярных точек
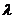 и
и 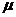 оператора
оператора  имеют место
равенства
имеют место
равенства
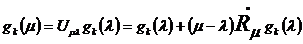 . (10)
. (10)
Теперь значение матричной функции 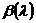 при любом
при любом 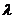 (регулярном
для
(регулярном
для  и
и 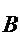 )
определяется по ее значению
)
определяется по ее значению 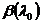 ; для нахождения соответствующей
формулы воспользуемся функциональным уравнением резольвенты
; для нахождения соответствующей
формулы воспользуемся функциональным уравнением резольвенты
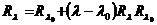 . (11)
. (11)
С другой стороны, в силу (7)
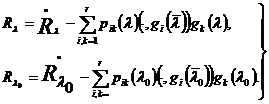 (12)
(12)
Подставляя правые части (12) в (11),
получаем (13):
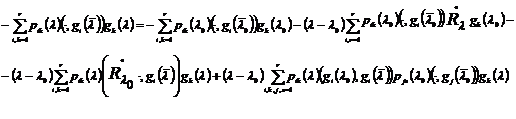
Если с помощью (10) приведем сумму
второго и третьего слагаемого в правой части к виду
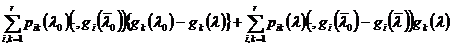 ,
,
и после этого приведем в (13)
подобные члены, то получим
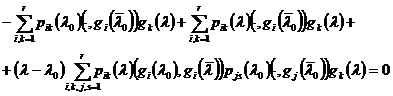
Отсюда, в силу линейной
независимости векторов 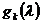 ,
,
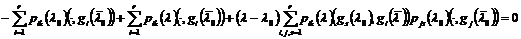
и, далее, в силу линейной
независимости 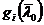
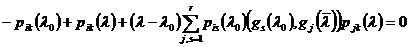
или, в матричном виде,
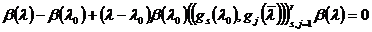 .
.
Умножая последнее равенство справа
на 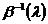 и слева на
и слева на 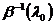 , получаем
искомое соотношение
, получаем
искомое соотношение
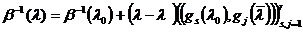 (14)
(14)
Нетрудно проверить, что из (14) для
любых двух общих регулярных точек 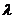 и
и 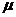 операторов
операторов  ,
, 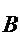 следует
следует
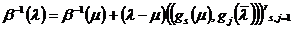 .
.
пространство симметрический оператор
СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ
1. Н.И.
Ахиезер, И.М. Глазман. Теория линейных операторов в гильбертовом пространстве.
- М., 1966. - 544 с.
2. Треногин
В.А. Функциональный анализ: Учебник. - 4-е изд., испр. - М. ФИЗМАТЛИТ, 2007. -
488с.