Тепловые явления
Как вычисляется и почему не зависит от характера процесса
изменение внутренней энергии тела?
Вну́тренняя эне́ргия тела (обозначается как E или U)
- полная энергия этого тела за вычетом кинетической энергии тела как целого и
потенциальной энергии тела во внешнем поле сил. Следовательно, внутренняя
энергия складывается из кинетической энергии хаотического движения молекул,
потенциальной энергии взаимодействия между ними и внутримолекулярной энергии.
Внутренняя энергия является однозначной функцией состояния системы. Это
означает, что всякий раз, когда система оказывается в данном состоянии, её
внутренняя энергия принимает присущее этому состоянию значение, независимо от
предыстории системы. Следовательно, изменение внутренней энергии при переходе
из одного состояния в другое будет всегда равно разности между ее значениями в
конечном и начальном состояниях, независимо от пути, по которому совершался
переход.
Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только
изменение внутренней энергии:
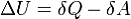
где
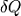 - подведённая к телу теплота, измеренная в джоулях
- подведённая к телу теплота, измеренная в джоулях
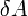 -
работа, совершаемая телом против внешних сил, измеренная в джоулях
-
работа, совершаемая телом против внешних сил, измеренная в джоулях
Эта формула является математическим выражением первого начала
термодинамики
Согласно закону Джоуля, выведенному эмпирически, внутренняя энергия
идеального газа не зависит от давления или объёма. Исходя из этого факта, можно
получить выражение для изменения внутренней энергии идеального газа. По
определению молярной теплоёмкости при постоянном объёме 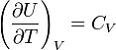 ак как внутренняя энергия идеального
газа является функцией только от температуры, то
ак как внутренняя энергия идеального
газа является функцией только от температуры, то Эта же формула верна и для вычисления
изменения внутренней энергии любого тела, но только в процессах при постоянном
объёме (изохорных процессах); в общем случае CV(T,V) является функцией и
температуры, и объёма. Если пренебречь изменением молярной теплоёмкости при
изменении температуры, получим:
Эта же формула верна и для вычисления
изменения внутренней энергии любого тела, но только в процессах при постоянном
объёме (изохорных процессах); в общем случае CV(T,V) является функцией и
температуры, и объёма. Если пренебречь изменением молярной теплоёмкости при
изменении температуры, получим:
ΔU = νCVΔT,
где ν - количество вещества, ΔT - изменение температуры.
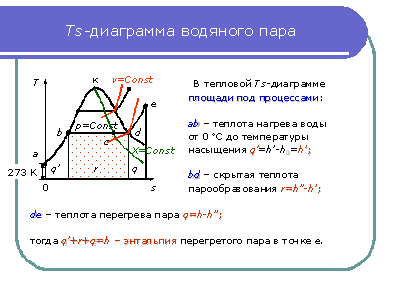
Покажите на диаграмме T-S энтальпию перегретого пара
Вода и водяной пар нашли широкое применение в качестве рабочих тел в
паровых турбинах тепловых машин, атомных установках и в качестве теплоносителей
в различного рада теплообменных аппаратах химико-технологических производств.
Газообразное тело, сосуществующее с кипящей жидкостью называется паром и
значительно отличается по своим термодинамическим свойствам от свойств
идеального газа.
Парообразованием называется процесс превращения вещества из жидкого
состояния в парообразное.
Кипением называется процесс превращения жидкости, кипящей во всем её
объеме, в пар при подводе к ней теплоты, а при отводе от пара теплоты
происходит обратный процесс - конденсация.
Процессы кипения и конденсации протекают при постоянной температуре и при
неизменном давлении, то есть tКП = tН.
Пар, соприкасающейся с жидкостью, из которой он получается и находящейся
с ней в термодинамическом равновесии называется насыщенным.
Сухой насыщенный пар - пар, не содержащий в себе жидкость.
Влажным паром называется механическая смесь, состоящая из сухого пара и
мельчайших капелек жидкости и характеризуется степенью сухости - Х или степенью
влажности - (1 - Х).
Перегретым паром называется пар, полученный из сухого насыщенного пара
при подводе к нему при P =
Const некоторого количества теплоты и вызванного этим повышением его
температуры. Разность между температурами перегретого пара - tП и сухого насыщенного
- tН называется степенью перегрева. Для технически важных веществ, например,
для водяного пара разработаны довольно точные уравнения, с помощью которых
рассчитаны параметры и функции состояния в широкой области температур и
давлений и сведены в таблицы и на их основе эти характеристики графически
представлены в виде диаграмм в P - V, T - S и h - S координатах. Эти диаграммы дают возможность наглядно
представить процессы и их энергетические особенности.
Фазовая P - V диаграмма системы, состоящей из жидкости и пара,
представляет собой график зависимости удельных объемов кипящей воды - v' и
сухого насыщенного пара - v" от давления (см. рис.).
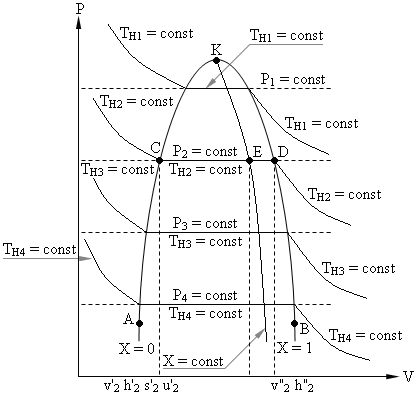
Рис.
График зависимости v' = f(P)
представлен на рис. кривой АК, которая называется нижней пограничной кривой или
линией кипящей жидкости и характеризуется степенью сухости Х = 0.
График зависимости v" = f(P) представлен на рис. кривой ВК, которая называется верхней пограничной
кривой или линией сухого насыщенного пара и характеризуется степенью сухости Х
= 1.
Обе кривые АК и ВК делят P - V диаграмму на три части: влево от
линии АК - область жидкости; между линиями АК и КВ - двухфазная система,
состоящая из смеси кипящей воды и сухого пара - область влажного пара характеризуется
степенью сухости 0 < X < 1; вправо от линии КВ и вверх от точки
"K" располагается область перегретого пара.
Процесс парообразования в области влажного пара, линия CD, является
одновременно изобарным (P =
Const) и изотермическим (T = Const).
Обе кривые АК и КВ сливаются в точке К, которая называется критической
точкой и характеризуется параметрами: РКР = 221,29 бар, tКР = 374,15 °C и vКР = 0,00326 м3/кг.
В критической точке исчезает различие между жидкостью и паром, выше её
существование вещества в двухфазном состоянии невозможно.
Состояние воды и водяного пара аналогичным образом может быть
представлено на T - S и h - S диаграммах (см. рис.). - S диаграмма широко
используется при исследовании термодинамических процессов и циклов, так как
позволяет видеть изменения температуры рабочего тела и находить количество
тепла в процессе. Недостатком данной диаграммы является то, что при определении
количества теплоты приходится измерять соответствующие площади.
Достоинством h - S диаграммы является то, что техническая работа и
количество тепла в процессах, изображаются отрезками линий.
Согласно объединённому уравнению первого и второго законов термодинамики:
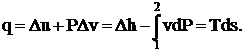
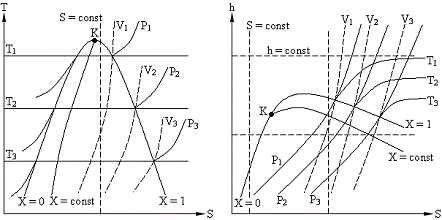
Рис.
В расчетах состояний вещества и процессов в области влажного пара с
помощью таблиц (см. таблицу №4 приложения) используются формулы вида:
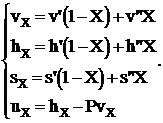
Более простым и наглядным, но менее точным, является графический метод
расчета процессов по h - S диаграмме, как в области насыщенных, так и в области
перегретых паров.
Процессы движения газа, происходящие в различных теплосиловых установках,
связаны с преобразованием энергии в газовом потоке.
Уравнение первого закона термодинамики для газового потока при отсутствии
сил тяжести и сил трения в газе примет вид:
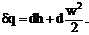
При адиабатном течении газа (δq = 0) уравнение после интегрирования будет:
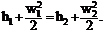
Из сравнения уравнений и следует, что для обратимого процесса течение
газа:
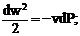
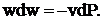
Равенство показывает, что при движении рабочего тела по каналу знаки dw и
dp противоположны. Если dP >
0, то газ сжимается, а его скорость будет уменьшаться dw < 0 и устройства, в
которых такие процессы проходят, называются диффузорами. Если dP < 0, a dw > 0, то такие
устройства (каналы) называются соплами. Из уравнения при условии, что w1
<< w2, можно определить скорость на выходе из канала:
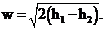
Некоторые качественные заключения могут быть сделаны на основании анализа
уравнений массового расхода и скорости при стационарном течении газа:
χ = Gv = Fw = const.
Так, для получения максимального расхода газа G, необходимо в уравнение
подставить значение располагаемой работы для идеального газа и найти экстремум,
в результате чего получается соотношение, называемое критическим и его значение
зависит только от свойств газа, и для двухатомных газов оно равно:
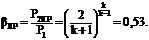
Оно показывает, что в суживающемся канале давление газа на выходе не
может быть меньше, чем P2 ≥ 0,53P1, а из этого следует, что скорость газа будет критической, равной
местной скорости звука.
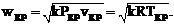
Скорость потока газа может быть больше скорости звука (сверхзвуковой) при
условии, что P2 < 0,53P1, если канал будет комбинированный (Сопло Ловаля), состоящий
из суживающейся и расширяющейся частей. В суживающейся части канала поток газа
движется с дозвуковой скоростью, в узком сечении скорость равна местной
скорости звука и в расширяющейся части она становится сверхзвуковой.
Расчет процесса истечения паров производят, используя h - S диаграмму.
Дросселированием (или мятием) называется необратимый процесс при δq
= 0, в котором давление
уменьшается при прохождении газа через суживающееся отверстие, а полезной
работы не производится. Уравнение процесса дросселирования получается из
уравнения (8.4) при условии w1 = w2, тогда h1 = h2. В
процессе дросселирования всегда dP <
0, а dT < или > 0 что следует из
анализа уравнения для эффекта Джоуля - Томсона:
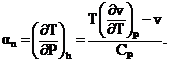
и
это явление широко используется в холодильной технике.
Задача
В помещении компрессорной станции объемом V произошла разгерметизация трубопровода, по которому
транспортируется горючий газ под давлением P1 при температуре Т1. через образовавшееся в трубопроводе
сквозное отверстие площадью f газ
выходит в помещение. Рассчитать, через какое время τ во всем объеме компрессорной станции
может образоваться взрывоопасная смесь, а также среднюю молекулярную массу,
плотность, удельный объем и изобарную удельную массовую теплоемкость смеси,
если ее температура Т = 293 К, а давление Р = 100 кПа. Коэффициент расхода
отверстия ξ = 0,7. воздухообмен не учитывается. Рассчитаем время образования
взрывоопасной концентрации по формуле:
τ = М1/G1,
где М1 - масса газа в помещении при концентрации, равной нижнему
концентрационному пределу воспламенения (НКПВ), кг;
G1 -
расход газа через отверстие в трубопроводе, кг/с
τ =3\1,61
τ = 1,863
Из уравнения состояния:
М1 = pr1V/R1T
Здесь p, V, T -
соответственно, давление, объем и температура смеси (данные по условию); r1 - значение НКПВ газа в объемных
долях; R1
= 8314/μ1 - газовая
постоянная, Дж/(кг*К); μ1 = молекулярная масса газа.
G1 = ξf√2kp21[(p/p)2/k - (p/p1)(k+1)/k]/(k-1)R1T1
если
p/p1 > β = [2/(k+1)]k/(k-1)
G1 = ξf√kp21[2/(k+1)](k+1)/(k-1)/R1T1
если
p/p1 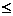 β = [2/(k+1)]k/(k-1)
β = [2/(k+1)]k/(k-1)
где
, k - показатель адиабаты G1= 0,86
Тогда молекулярная масса смеси будет равна :
μсм = rμ + r1μ1,
где μ - молекулярная масса воздуха;
r = 1-
r1 - объемная доля воздуха в смеси
μсм=28,995
Удельная газовая постоянная смеси будет равна:
Rсм =
8314\28,995=286,73
Плотность смеси:
ρсм = p/RсмT
ρсм=0,011
Удельный объем смеси
νсм = RсмT/p
νсм =286,73*293\100=838,59
Изобарная теплоемкость смеси
Сpсм = Cpg - Cp1g1
где Cp и Cp1 - соответственно, массовая удельная теплоемкость воздуха и
газа, Дж/(кг*К); g и g1 - соответственно, массовые доли
воздуха и газа (§ 1.4/1/)
g = μr/μсм;
g
=28,05*285,73\28,995=276,41
g1 = μ1r1/ μсм
g1 =
243,67
Сp = μCp/μ;
Сp = 28,05*43,56\28,05=43,46
Сp1 = μ1Cp1/μ1
Сp1 = 45,56
μCp и μ1Cp1 - соответственно, мольная теплоемкость воздуха и газа,
Дж/(моль*К) .
Сpсм = 43,46
*276,41-45,56*243,67=910,39
Задача
Рукавная линия диаметром d
поперечно обдувается воздухом со скоростью ωв. Температура воздуха tв. По рукавной линии со скоростью ωж движется вода, температура которой
на входе в рукавную линию t'ж.
рассчитать максимальную длину рукавной линии из условия, чтобы температура на
выходе из рукавной линии была t''ж ≥
10С. Толщина стенки рукавной линии δ = 4мм. эквивалентный коэффициент
теплопроводности материала рукава принять λ = 0,115 Вт/(м∙К).
|
|
|
ωв, м/с tв, 0С
|
6 -40
|
|
|
|
ωж, м/с t'ж, 0С d, мм
|
3,8 6 60
|
- Максимальная длина рукавной линии
l = Q/kπdср(tж - tв)
где Q - количество теплоты, отдаваемое
водой воздуху в единицу времени, Вт (равно изменению энтальпии воды ∆Y § 2.4); k - коэффициент теплопередачи от воды к воздуху, Вт/(м2∙К)
(§ 23.1 /1/); tж = (t'ж + t"ж)/2
- средняя температура воды, 0С; tв -
температура воздуха, 0С; dср = d
+ δ - средний
диаметр рукава, м.
l
=27200\6,69*3.14+65=313
∆ Ј = СжGж(t'ж - t"ж)
где Сж - теплоемкость воды, Дж/(кг∙К); Gж = πd2ωжρж/4 - массовая подача подача воды по
рукаву, кг/с; ρж - плотность воды, кг/м3
∆ Ј= 75,73*10719,4=811775,47
k = 1/(1/α1 + δ/λ +
1/α2)
где α1 - коэффициент теплоотдачи от воды к поверхности рукава, Вт/(м2∙К);
α2
- коэффициент
теплоотдачи от поверхности рукава к воздуху, Вт/(м2∙К).
Значение α1 рассчитывают по одной из следующих формул. Вид формулы
зависит от величины комплекса ωжd/νж = Re, называемого числом Рейнольдса. Если Re>104, то коэффициент теплоотдачи
находят из формулы (20.15), которую можно представить так:
α1 = 0,021λ0,57жω0,8ж(Сжρж)0,43/ν0.,37жd0,2
значение α2 также рассчитывают по одной из в зависимости от
величины комплекса ωвd/Vв. Эти формулы в явном виде можно
записать, соответственно, следующим образом:
α2 = 0,5ω0,5вλ0,62в(Свρв)0,38/ν0,18жd0,5
α2 = 0.25ω0,6вλ0,62в(Свρв)0,38/ν0,22жd0,4н
α2 = 0.23ω0,8вλ0,63в(Свρв)0,37/ν0,43жd0,2н
значения параметров воды λж, Сж, ρж, νж выписать из приложения УIII /2/ при средней температуре воды.
Значения параметров воздуха λв, Св, ρв, νв выписать из приложения УI /2/ при температуре воздуха. В
указанных формулах для условий данной задачи сомножитель (Рrж/Prс)1/4 ≈ 1, и поэтому не учитывается расчет сведем в
таблицу.
|
Точки T-S диаграммы
|
Ti °K, ti °C
|
hi кДж/кг
|
Si кДж/кг*К
|
|
3
|
353 80
|
335
|
0,7035
|
|
S
|
494,8 221,6
|
953
|
2,5207
|
|
S*
|
523 250
|
1085,8
|
2,7936
|
573 300
|
2961
|
6,3634
|
|
0
|
823 550
|
3512
|
6,82
|
|
2
|
373 100
|
2676,5
|
7,3628
|
Задача
Определить минимальное расстояние, обеспечивающее безопасность соседнего
с горящим объекта, при исходных данных: проекция факела пламени горящего
объекта имеет прямоугольную форму размером d ∙ l, его
температура Тф, а степень черноты εф. На поверхности не горящего
объекта: допустимое значение температуры Тдоп, допустимое значение плотности
теплового потока (критическая плотность) qкр, степень черноты поверхности ε.
Кроме того, оценить безопасное расстояние от факела для личного состава,
работающего на пожаре без средств защиты, от теплового воздействия при условии:
а) кратковременного пребывания; б) длительной работы. При кратковременном
тепловом воздействии для кожи человека qкр = 1120 Вт/м2, при длительном qкр = 560 Вт/м2. При решении задачи учитывать только
теплообмен излучением. Коэффициент безопасности принять равным β.
|
d, м
l, м Тф∙10-2, К εф
|
18 12 14 0,6
|
|
Тдоп, К ε qкр∙10-2 Вт/м2 β
|
680 0,85 120 1,4
|
Условия безопасности будут соблюдаться тогда, когда результирующая
плотность теплового потока излучением между факелом и поверхностью соседнего
объекта qфп будкт меньше значения допустимой qкр
qфп≤qкр
с учетом коэффициента безопасности
βqфп≤qкр
Результирующая плотность теплового потока между факелом и поверхностью тела
рассчитываем по формуле
q п = εпрС0[(Тф/100)4 - (Тдоп/100)4]φ
где С0 = 5,77 - коэффициент излучения абсолютно черного тела, Вт/(м2∙К);
εпр = 1/(1/εф + 1/ε - 1) - приведенная степень черноты
системы факел-поверхность; φ- средний по поверхности полный коэффициент
облученности факелом поверхности объекта.
q п
=15600
Коэффициент облученности является геометрической характеристикой системой
двух взаимноизлучающих поверхностей. Его величина зависит от формы, размеров и
взаимного расположения этих поверхностей. Полагаем, что загорание облучаемой
поверхности начинается с элементарной площадки dF. По условию проекция факела на вертикальную поверхность
имеет форму прямоугольника конечных размеров. В таком случае взаимное
расположение в пространстве факела и облучаемой поверхности является
плоскопараллельным - элемента поверхности и площадки конечных размеров.
Минимальное безопасное расстояние будет при соблюдении условия
Βqфп = qkp
При кратковременном тепловом воздействии для кожи человека qкр = 1120 Вт/м2, безопасное
расстояние от факела для личного состава, работающего на пожаре без средств
защиты будет равно 15м.
При длительной работе и тепловом воздействии для кожи человека qкр = 560 Вт/м2 безопасное расстояние
от факела для личного состава, работающего на пожаре без средств защиты будет
равно 40м.
Как
определить 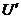 и
и 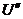 для
вычисления внутренней энергии влажного пара по формуле
для
вычисления внутренней энергии влажного пара по формуле 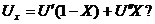
Определить
можно с помощью формулы :

Напишите
выражение закона действующих масс для следующих реакций: 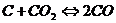 и
и 
Закон
действующих масс (основное уравнение кинетики) устанавливает соотношение между
массами реагирующих веществ в химических реакциях при равновесии. Закон
действующих масс сформулирован в 1864-1867 гг. К. Гульдбергом и П. Вааге.
Согласно этому закону при постоянной температуре скорость химической реакции
прямо пропорциональна произведению концентраций реагирующих веществ.
Закон
действующих масс используют при различных расчетах химических процессов. Он
позволяет решить вопрос, в каком направлении возможно самопроизвольное течение
рассматриваемой реакции при заданном соотношении концентраций реагирующих
веществ, какой выход нужного продукта может быть получен.
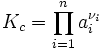
ai - активности веществ, выраженные через концентрации, парциальные
давления либо мольные доли;
νi - стехиометрический коэффициент (для
исходных веществ принимается отрицательным, для продуктов - положительным); -
константа химического равновесия
На практике в расчётах, не требующих особой точности, значения активности
обычно заменяются на соответствующие значения концентраций (для реакций в
растворах) либо парциальных давлений (для реакций между газами).

С
+ Н2О = СО + Н2
В продуктах реакции кроме углерода имеется кислород и водород, причём в
тех количествах, в которых они могут взаимодействовать между собой с
образованием воды по реакции:
½ О2 + Н2 = Н2О (2)
Процесс горения водяного газа описывается двумя реакциями:
CO +
1/2 О2 ----> CO2 (2)+ 1/2 О2
----> Н2О (3)
При этих реакциях тепло выделяется, поэтому укажем их количество в правой
части реакций:
+ 1/2 О2 ----> CO2 + 67,6 ккал (282.56 кдж) (2а)+ 1/2 О2 ----> Н2О
+ 57,8 ккал (241.6 кдж) (3а)
H2О + C ----> CO + H2 (1)+
1/2 О2 ----> CO2 (2)2 + 1/2 O2 ----> H2O (3)
Суммарное уравнение
C + O2 ----> CO2 (4)
 +42кДж+ C
↔ 2CO↑
(ΔH=172 кДж, ΔS=176 Дж/К).
+42кДж+ C
↔ 2CO↑
(ΔH=172 кДж, ΔS=176 Дж/К).
Эта
реакция часто происходит при печной топке, когда слишком рано закрывают печную
заслонку (пока окончательно не прогорели угли). Образующийся при этом монооксид
углерода, вследствие своей ядовитости, вызывает физиологические расстройства («угар»)
и даже смерть, отсюда и одно из тривиальных названий - «угарный газ». Картина
протекающих в печи реакций приведена на схеме.
Реакция
восстановления диоксида углерода обратимая, влияние температуры на состояние
равновесия этой реакции приведено на графике. Протекание реакции вправо
обеспечивает энтропийный фактор, а влево - энтальпийный. При температуре ниже
400 °C равновесие практически полностью сдвинуто влево, а при температуре выше
1000 °C вправо (в сторону образования CO). При низких температурах скорость
этой реакции очень мала, поэтому монооксид углерода при нормальных условиях
вполне устойчив. Это равновесие носит специальное название равновесие Будуара.

С + 1/2О2 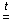 CO + Q1,
CO + Q1,
СO + 1/2О2 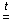 CO2 + Q2,
CO2 + Q2,
С + О2 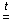 CO2 + Q3;= Q1 + Q2.
CO2 + Q3;= Q1 + Q2.
Задача
внутренний энергия теплоемкость пар
Производство, связанное с обращением ГЖ, размещено в помещении размерами
в плане a*b, м. и высотой Н, м. при аварии технологических аппаратов
возможны и розлив жидкости на пол и возникновение пожара. Предусмотрены
устройства, ограничивающие растекание жидкости на полу на площади квадрата f, м2 расстояние от границы горения до
стены с оконными и дверными проемами, через которые будет происходить газообмен
при пожаре в помещении с внешней средой, l, м.
Механическая вентиляция при возникновении пожара выключается. За счет
естественного газообмена в помещение поступает такое количество воздуха, что на
1 кг горящей жидкости в среднем приходится VА, м3 воздуха.
Рассчитайте возможную температуру среды в помещении при возникновении
пожара:
а) среднеобъемную через 5, 15 и 30 мин его развития;
б) локальную в точке над факелом под перекрытием через 5, 15 и 30 мин его
развития;
в) локальную в точках, находящихся на высоте 1,5 м от пола и расстояниях
от границы горения 0,25 l, 0,5
l, 0.75 l и l,
через 2 мин его развития.
Постройте графики:
а) изменения среднеобъемной температуры среды в помещении при пожаре во
времени;
б) изменения температуры среды в точке над факелом под перекрытием во
времени;
в) изменения температуры среды на высоте 1,5 м в зависимости от
расстояния от границы горения для 2 мин развития пожара.
|
А,м
|
b, м
|
l, м
|
f, м2
|
VА, м3/кг
|
Qp
|
V0,
|
V0
|
|
52
|
54
|
9
|
25
|
64
|
12
|
42355
|
10,46
|
11,94
|
|
|
|
|
|
|
|
|
|
|
Рассчитаем среднеобъемную температуру среды в помещении при пожаре для
любого заданного момента времени τ от начала его развития:
Tm,τ = 0,66 Ta(ηBcpVг/σ0εпрFT3a)0,17,
где Ta - температура продуктов горения, К
Ta = (ηQpн/cpVг) + 273
Здесь η - коэффициент полноты горения (η = 1); Qpн - теплота сгорания жидкости, Дж/кг;
Vг - приведенный действительный объем
продуктов горения, образующихся при сгорании 1 кг жидкости и коэффициенте
избытка воздуха αm, м³/кг.
Vг = V°г +V0(αm -1),
V°г -
объем продуктов горения, образующихся при сгорании 1 кг горючей жидкости и
теоретически необходимом количестве воздуха, м³/кг ; V0 - количество воздуха, необходимого для полного сгорания 1
кг горючей жидкости, м³/кг ; αm - коэффициент избытка воздуха, вычисляется по формуле
αm = Vд/Vо,
В - масса жидкости, сгорающей при пожаре за секунду (расход горючей
жидкости) кг/с
В = Мо(0,3+0,7√τ/30 )ƒ,
где Мо - массовая скорость выгорания жидкости, кг/(м²∙с); τ - время, отсчитываемое от начала
пожара, мин; Ср - удельная объемная изобарная теплоемкость продуктов горения
при постоянном давлении, Дж/(м³∙К)
Ср = 1250 + [0,12 + 0,1/(0,25 + αm)]Тm,τ.
σ0 = 5,7∙10-8 - константа излучения
абсолютного черного тела, Вт/(м²∙К); Епр - приведенная степень черноты
системы «среда - поверхность ограждения»
Епр = 1/[1 + 0,0022(Тm,τ - 273)],
F -
площадь поверхностей теплообмена, м²
F = 2(α + b)H + 2ab.
Локальное значение температуры среды в помещении при пожаре для любого
момента времени τ
Тх,у, τ - Тm,τ (0,8 + 0,2У/0,5Н) [1,33 - χ/(2χ
+ 0,5l)].
Над факелом под перекрытием (χ = 0, у = Н)
То,н,τ = 1,6 Тm,τ.
На высоте от пола (у = 1,5) и на любом расстоянии от границы горения
Тχ,1,5,
τ = Тm,τ(0,8 + 0,6/Н)
[1,33 - χ/(2χ + 0,5 l)].
αm = Vд/Vо,
αm = 4049,23
Vг = V°г +V0(αm -1),
Vг =
90680,35
В = Мо(0,3+0,7√τ/30 )ƒ,
В =7,552
Ср = 1250 + [0,12 + 0,1/(0,25 + αm)]
Ср = 0,120
Ta = (ηQpн/cpVг) + 273
Ta =
(1*42355\0,120*90680)+273=276,89
Tm,τ = 0,66 Ta(ηBcpVг/σ0εпрFT3a)0,17,
Tm,τ = 0,66*276,89(1*7,552*0,120\5,7∙10-8*0,567)0,17=182,74*0,025∙10-8=4,709∙10-8
Задача
Рассчитайте температурное поле по толщине перекрытия через 0,5 ч после
начала пожара, используя полученные при решении задачи 2.1 результаты расчета
температуры среды над факелом под перекрытием . Перекрытие представляет собой
сплошную железобетонную плиту толщиной 18 см. Толщина слоя бетона λ
= 1,2 Вт/(м∙К).
Начальная температура перекрытия 200С, такую же температуру имеет воздух над
перекрытием.
Задачу решить методом конечных разностей графически.
В теории теплообмена при решении задач теплопроводности известными могут
быть: температура на внешней поверхности тела, плотность теплового потока на
поверхности тела, температура среды, омывающей поверхность тела, и закон
теплообмена между средой и поверхностью тела (коэффициент теплоотдачи).
Первый тип задач называют задачами с граничными условиями 1 рода. Второй
- задачами с граничными условиями 2 рода. Третий - задачами с граничными
условиями 3 рода.
Исходные данные в рассматриваемый период могут изменяться или иметь
постоянные значения. В соответствии с этим граничные условия называют
изменяющимися или постоянными. Во время пожара, как правило, температура среды
и коэффициент теплоотдачи имеют переменные значения.
Δχ = 2λ / α1max,
где α1max - максимальное значение коэффициента теплоотдачи на обогреваемой
поверхности за период нагревания ( τ = 30 мин), Вт/(м2 ∙ 0С)
Основными факторами, влияющими на предел огнестойкости конструкций,
являются влага, коэффициент теплопроводности и прочность арматуры.
Влага в бетоне играет двоякую роль. Во-первых, при действии на бетон
высоких температур вода, испаряясь, замедляет темп прогрева, увеличивая тем
самым предел огнестойкости. Во-вторых, вода способствует взрывообразному
разрушению бетона при интенсивном прогреве вследствие образования пара.
Необходимым условием взрыва бетона является быстрое повышение температуры, т.е.
прогрев по стандартному температурному режиму или непосредственное воздействие
огня на конструкцию.
При пожарах через 10 - 20 мин после воздействия огня на конструкцию бетон
взрывообразно разрушается, откалываясь от обогреваемой поверхности пластинами
площадью 200 см2 и толщиной 0,5 - 1см. куски бетона отлетают на расстояние до
15м. Такое разрушение происходит по всей поверхности, приводя к быстрому
уменьшению сечения конструкции и, как следствие, к потере несущей способности и
огнезащитных свойств. При влажности бетона выше 5% и температуре 160 - 200°С,
что способствует максимальному давлению пара в порах, бетон разрушается почти
во всех случаях. При влажности 3,5 - 5% разрушение носит местный характер. При
влажности менее 3% взрывы не наблюдаются. При нагревании по растянутому во
времени режиму (с достижением стандартных температур через промежуток времени,
увеличенный вдвое) бетон не взрывается, несмотря на его повышенную влажность (5
- 6%). При этом вид заполнителя бетона заметно не влияет на его разрушение.
Повышение температуры окружающей среды при пожаре сопровождается
переносом теплоты в материал конструкции. Её тепло стремится к тепловому
равновесию. Поэтому температура внутренних точек будет изменяться не только в
зависимости от координат и их взаимного расположения, но и от времени. Такие
процессы теплопередачи принято называть нестационарными.
Незащищенные конструкции в процессе воздействия огня
прогреваются равномерно по сечению. Предел их огнестойкости характеризуется
временем прогрева металла до критической температуры, которая составляет в
среднем для стали 500°С, для алюминиевых сплавов - 250°С.
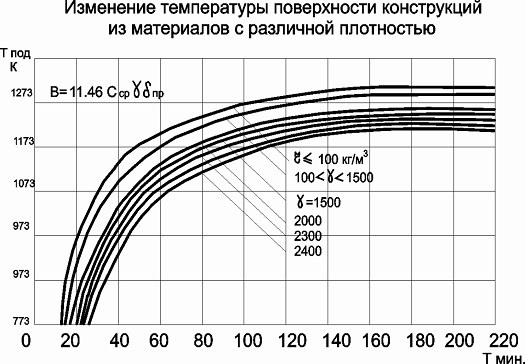
Среднее значение коэффициента удельной теплоемкости С
ср находится с учетом средней температуры:
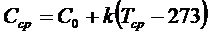 ,
,
где Со - начальное значение коэффициента удельной
теплоемкости кДж/(кг∙К); k
-коэффициент пропорциональности. Сср=0,120
Рассчитывается значение параметра β:
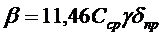 ,
,
где γ - плотность металла, кг/м3. β
= 0,33
По номограмме (рисунок) для известных значений Ткр и β
определяется значение τ.
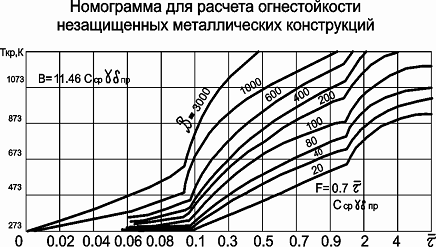


Распределение относительной избыточной температуры в
теплоизолированной железобетонной конструкции при развитие пожара.
По распределение относительной избыточной температуры
в теплоизолированной железобетонной конструкции при развитие пожара с учетом
выбранного интервала времени и плотности материала определяем значение
температуры поверхности Тпов и среднее значение температуры Тср для каждого
вида материала:
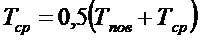 ,
,
Расчет по пунктам повторяется с учетом новых интервалов времени до того
момента, когда температура конструкции достигнет критического значения Т кр все
выносим на график.

Задача
Железобетонная плита перекрытия толщиной δ обогревается с одной стороны средой с
температурой tг в течение τ
мин. Коэффициент
теплообмен а на обогреваемой поверхности плиты α = 11,63 е0,0023tг. Начальная температура перекрытия t0 = 200C.
Коэффициент теплопроводности железобетона λ = 1,2 Вт/(м∙К), коэффициент
температуропроводности α = 5,6∙10-7 м2/с.
Рассчитать температуру на расстоянии s от обогреваемой поверхности плиты: а) принимая перекрытие за
неограниченную пластину; б) принимая перекрытие, как полуограниченное тело.
а) принимая плиту как плоскую стенку
Математическая постановка задачи для конструкции стены или покрытия имеет
вид:
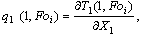 (1)
(1)
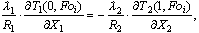 (2)
(2)
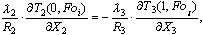 (3)
(3)
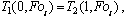 (4)
(4)
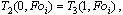 (5)
(5)
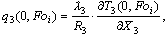 (6)
(6)
Краевые условия:
 (7)
(7)
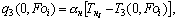 (8)
(8)
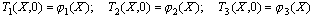
Температурное поле несимметричного нагрева (охлаждения) j-слоя с
использованием принципа суперпозиции полей по методу ДУКУ имеет вид [1,2]:
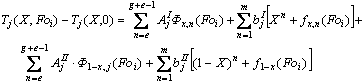
где первый и второй полиномы в правой части уравнения определяются
граничными и начальными условиями полей, у которых 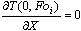 а третий и четвёртый - граничными и
начальными условиями полей, у которых
а третий и четвёртый - граничными и
начальными условиями полей, у которых 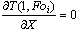 ; Фр,n, fp,n - специальные
табулированные функции, учитывающие влияние на температурное поле граничных и
начальных условий [1]; g - число моментов времени, в которые удовлетворяются
граничные условия;
; Фр,n, fp,n - специальные
табулированные функции, учитывающие влияние на температурное поле граничных и
начальных условий [1]; g - число моментов времени, в которые удовлетворяются
граничные условия; 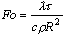 - число Фурье;
- число Фурье;  - время этапа расчёта; R,
- время этапа расчёта; R, 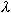 , с,
, с, 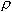 - соответственно толщина, коэффициент
теплопроводности, удельная массовая теплоемкость и плотность материала слоя.
- соответственно толщина, коэффициент
теплопроводности, удельная массовая теплоемкость и плотность материала слоя.
Подставляя в систему уравнения (1)-(9) значение краевых условий по методу
ДУКУ получаем систему 6g уравнений, которая решается относительно коэффициентов
аппроксимации 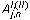 , при известных начальных условиях в каждом слое, заданных
теплофизических свойствах, толщинах слоев и коэффициентах теплоотдачи на
наружной и внутренней поверхности (
, при известных начальных условиях в каждом слое, заданных
теплофизических свойствах, толщинах слоев и коэффициентах теплоотдачи на
наружной и внутренней поверхности ( н,
н, в).
в).
Коэффициенты аппроксимации 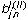 определяются в начале этапа расчёта
по параметрам температурного поля, связанным полиномом m-ой степени [2].
определяются в начале этапа расчёта
по параметрам температурного поля, связанным полиномом m-ой степени [2].
Температурная волна от наружной поверхности к внутренним слоям
перемещается в течение 12 часов.
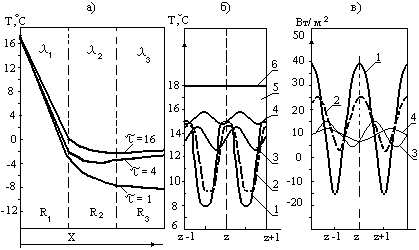
Рис. 1. Распределение температур по толщине многослойного ограждения а) в
течение 1 часа (а) и изменение температуры (б). (1 - Тн,i; 2 - Т3(0,Foi); 3 -
Т3(1,Foi)=Т2(0,Foi); 4 - Т2(1,Foi)=Т1(0,Foi); 5 - Т1(1,Foi); 6-Тв,i) и тепловых
потоков (в) по толщине ограждения (1 - q3(0,Foi); 2 - q2(0,Foi)= q3(1,Foi); 3 -
q1(0,Foi)= q2(1,Foi); 4 - q1(1,Foi)).
Для варианта полуограниченного тела расположение изоляционного слоя
снаружи, внутри и в середине конструкции вызывает различные законы изменения
температуры и теплового потока по толщине ограждения.
При этом следует отметить, что количество теплоты, теряемое ограждением,
практически остаётся неизменным. Однако для исключения конденсации влаги
целесообразно располагать изоляционный слой снаружи или ближе к наружной части
ограждения.
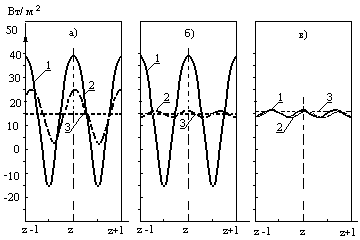
Рис. 2. Изменение тепловых потоков по толщине ограждающей конструкций: а)
изоляция внутри; б) изоляция в середине; в) изоляция снаружи; 1 - q3(0,Foi); 2
- q2(0,Foi)=q3(1,Foi); 3 - q1(1,Foi).
Список
использованной литературы
1. Безопасность
жизнедеятельности: Конспект лекций: Пособие для подготовки к экзаменам. Басаков
М.И., авт. -сост., 2003. - 135 с.
2. Безопасность
в чрезвычайных ситуациях: Учебник под ред. Н.К. Шишкина. - М., ГУУ, 2000. - 90
с.
3. Основы
безопасности жизнедеятельности. Алексеенко В.А., Матасова И.Ю., 2001. - 187 с.
. Пожарная
безопасность и предупреждение чрезвычайных ситуаций: Словарь терминов и
определений. Бариев Э. Р., ред., 2004. - 200 с. Теплотехника: Учебник для
втузов/ А.М. Архаров, И.А. Архаров, В.Н. Афанасьев и др.; Под общ. ред. А.М.
Архарова, В.Н. Афанасьева. - 2-е изд., перераб. и доп. - М.: Изд-во МГТУ им.
Н.Э. Баумана, 2004. - 712 с.: ил.
. Теплотехника:
Учебник для вузов/ В.Н. Луканин, М.Г. Шатров, Г.М. Камфер и др.; Под ред. В.Н.
Луканина. - 5-е изд., стер. - М.: Высшая шк., 2006. - 617 с.: ил.
. Теплотехника:
Учебник для вузов/ А.П. Баскаков, Б.В. Берг, О.К. Витт и др.; Под ред. А.П.
Баскакова. - 2-е изд., перераб. - М.: Энергоатомиздат, 1991. - 224 с.: ил.
7. Электронный ресурс www.firemen.ru
<http://www.firemen.ru>