Разработка обучающей программы по теме 'Обыкновенные дифференциальные уравнения'
Введение
В последнее время немалая роль в обучении отводится компьютерным
информационно-коммуникационным технологиям (ИКТ), так как с их помощью можно
по-новому представить содержание учебного материала и организовать его
изучение. При этом ИКТ выступают как новые интерактивные средства обучения,
обладающие целым рядом дидактических достоинств и позволяющие качественно
изменить методы, формы и содержание обучения [15], [26].
В Мурманском государственном техническом университете (МГТУ) внедрение
информационных технологий обучения активно происходит в Институте
дистанционного обучения (ИДО - это структурное подразделение МГТУ) и в
начальной стадии на специальностях очной формы обучения. Использование
электронных учебно-методических материалов (УММ), таких как конспект лекции
(ЭКЛ), обучающие программы (ОП), модули поддержки изучения отдельных тем,
наряду с классическими методами преподавания заметно усиливает учебный процесс
и повышает его эффективность. Однако подготовка электронных УММ является
трудоемким процессом, требующим совместного участия, как минимум,
преподавателей-методистов и программистов-разработчиков программных продуктов.
Кроме этого, при проектировании и разработке электронных учебных ресурсов
часто возникают технологические проблемы автоматизации решения учебных задач
как следствие небольшого количества разработок в сфере высшего технического
образования. Поэтому тема данной дипломной работы является актуальной
как для кафедры ПО ВТ и АС МГТУ, так и для выпускника специальности «ПО ВТ и
АС», так как в техническом задании к ней поставлена прикладная задача
образовательного назначения, для решения которой требуется широкое
использование знаний, полученных при изучении ряда дисциплин программистского
курса.
Проблемой для разработки электронных учебных материалов по ряду тем
дисциплины «Высшая математика» является автоматическое распознавание
основных математических структур (выражений, функций, уравнений, неравенств
и т.д.) и соотнесение их типа с позициями некоторого списка. Так в теме
«Обыкновенные дифференциальные уравнения» выбор метода получения общего решения
дифференциального уравнения (ДУ) предваряет позиционирование заданной
математической фразы как обыкновенного дифференциального уравнения, определение
его порядка, отнесение к одному или нескольким из известных типов ДУ. Эти
вспомогательные задачи имеют важное методическое значение для процесса
обучения, поэтому программируемый модуль их автоматического решения является
основным в данной дипломной работе. Для его проектирования потребовалось
решение следующих вопросов:
а) анализ методов распознавания лексических особенностей текста,
математического выражения или другого объекта и их доступность для решения
задач символьного анализа;
б) выбор и реализация метода синтаксического анализа математического
выражения или равенства на основе бинарных деревьев;
в) создание специализированного лексико-грамматического анализатора
математических выражений для обеспечения корректного ввода ДУ в обучающую
программу.
Цель дипломной работы сформулирована в техническом задании к ней как разработка
программного продукта «Обучающая программа по теме «Обыкновенные ДУ»,
предназначенного для методической поддержки средствами ИКТ учебного процесса в
МГТУ по дисциплине «Высшая математика». Обучающие программы (ОП) являются
основной формой современных электронных учебных ресурсов по математике, поэтому
их структуру можно считать установившейся [5] и обычно включающей в себя
следующие компоненты:
а) теоретический - чаще всего это электронный конспект лекций как совокупность
структурированной информации с системой навигации и интерактивными обучающими
элементами;
б) практический - включает в себя разбор примеров и задач по теме, а
также самопроверку и контролирующие тесты;
в) экспериментальный - представляет собой некоторую креативную среду
в виде программных модулей, обеспечивающих творческую работу студента с
объектами изучения [4].
Для создания заявленной обучающей программы в соответствии с техническим
заданием следовало разбить её на следующий комплекс задач:
а) разработка программного модуля распознавания математической
информации для синтаксического разбора дифференциального уравнения с целью
автоматического определения его порядка, типа, канонической формы и её
параметров, метода решения;
б) разработка программного модуля, реализующего в символьном виде
решение ДУ сведением их к интегралам;
в) создание программной оболочки, для отображения содержания ЭКЛ и
для проведения тренинга и тестирования по основным задачам, связанным с
решением ДУ;
г) разработка программного модуля автоматической генерации ДУ для
тренинга и тестирования;
д) разработка справочной системы обучающей программы.
Результатом решения этого комплекса задач является программный продукт
«Обучающая программа «Обыкновенные ДУ»», в которую теоретический компонент
введен как готовый ЭКЛ, а практически-экспериментальный компонент создан
полностью в рамках разработки дипломного проекта.
Таким образом, объектом исследования в дипломной работе является
процесс создания обучающих программ для применения информационно-компьютерных
технологий в изучении дисциплины «Высшая математика» в МГТУ, а предметом
исследования является автоматизация решения основных задач, связанных с
обыкновенными дифференциальными уравнениями.
К использованным методам анализа объекта исследования можно
отнести:
а) знакомство с предметной областью применения ИКТ в изучении
математических дисциплин (изложено в пункте 1.3-1.5);
б) обобщение и описание программных продуктов автоматизации решения
задач, связанных с обыкновенными дифференциальными уравнениями (изложено в
1.6);
в) сравнение поставленных задач по распознаванию типов ДУ с
известными задачами создания интеллектуальных систем распознавания образов и
методами их решения (описано в 2.1);
г) методы специальных программистских дисциплин, таких как теория
языков программирования, структуры и алгоритмы обработки данных,
программирование на языках высокого уровня, теория разработки программного
обеспечения и других.
1. Постановка задачи
1.1 Общая постановка задачи
Необходимо разработать программный продукт «Обучающая программа по теме
«Обыкновенные дифференциальные уравнения»», предназначенный для использования
студентами и курсантами 1-2 курсов технических специальностей МГТУ различных
форм обучения в рамках дисциплин «Высшая математика» или «Математический
анализ».
Обучающая программа состоит двух частей: теоретической и практической с
включением в последнюю экспериментальных компонентов.
Теоретическая часть содержит готовый электронный конспект лекций (ЭКЛ) по
теме, который необходимо включить в программную оболочку обучающей программы
(ОП); описание ЭКЛ следует включить в «Инструкцию пользователя ОП».
Практическая часть включает в себя автоматическое решение следующих
учебных задач.
Задача A. Задание
обыкновенного ДУ и определение его порядка: первый второй или выше второго;
задание ДУ можно осуществлять как с клавиатуры, так и генерировать
автоматически;
Задача Б. Определение типа ДУ первого или второго порядков, определения его
канонической формы и её параметров, указание метода решения в
соответствии с таблицей признаков этих качеств (Приложение A).
Для ЛНДУ (2.2.1) с постоянными коэффициентами нужно провести анализ
правой части f(x) на её принадлежность к специальному виду:
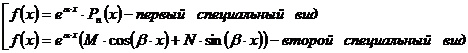
где 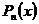 - полином степени
- полином степени 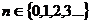 ;
;
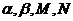 - числа.
- числа.
Все обозначенные задачи должны решаться в общем рабочем поле и в двух
режимах:
а) режим тренинга - студент задает или получает автоматически генерированием
ДУ, решает вручную задачи определения его порядка, типа, осознанного выбора
канонической формы с указанием её параметров, выбора метода получения общего
решения, а затем по своему запросу получает ответы обучающей программы на те же
вопросы; эффект обучения создается сравнением ответов и анализом ошибок ручного
решения;
б) режим тестирования - студент получает автоматически генерированием
последовательно несколько ДУ и для каждого из них последовательно отвечает на
следующие вопросы:
- определите тип ДУ;
- определите каноническую форму ДУ;
- укажите параметры канонической формы (если ответ на
предыдущий вопрос был верным);
- укажите метод решения ДУ;
По каждому ДУ контрольного тестирования студенту представляется обучающей
программой протокол проверки его ответов; в конце тестирования выводится
количество заданных вопросов и количество набранных баллов (по одному за каждый
верный ответ).
Задача В. Получение общего решения или общего интеграла ДУ в символьном виде с
пояснением хода решения. Эта задача обучающей программы относится к её
экспериментальным компонентам, хотя и может иметь большое практическое значение
в случае её успешной апробации в учебном процессе. В данной дипломной работе
задачу нужно решить для ДУ I
порядка четырех основных типов, обозначенных в Приложении A, при этом считать ДУ решенным, если
оно сведено к интегралам.
1.2 Формальная постановка задачи. Функциональные требования
На основании сформулированной в пункте 1.1 постановки задачи рассмотрим
основные компоненты, которые необходимо реализовать при выполнении задания:
- анализ и создание модуля распознавания вводимых математических выражений
и равенств;
- анализ и создание модуля распознавания типа ДУ, привязка к
его типу метода решения и канонической формы;
- создание модуля выделения параметров канонической формы;
- задание функциональной возможности решения ДУ первого порядка
в символьном виде сведением их к интегралам;
- создание интерфейса и модуля отображения ЭКЛ;
- создание интерфейса и модуля тестирования.
Данные задачи являются комплексными, каждая из них может быть разбита на
составные части.
Так для создания модуля распознавания вводимых математических
выражений необходимо провести работу по разработке лексико-грамматического
анализатора, позволяющего проводить анализ корректности ввода и принадлежность
вводимого выражения к языку. В рамках данной работы необходимо произвести
выделение основных лексем математического языка, используемого при вводе
дифференциальных уравнений, построить лексический анализатор, позволяющий по
введенной строке производить разбиение выражения на лексемы и для дальнейшей
работы создавать бинарное дерево вершинами которых являются операции, функции,
переменные или константы.
Создание модуля распознавания типа ДУ требует разработки такого
окружения, которое позволит производить лексический анализ введенного ДУ,
выделять некоторые характерные для каждого типа части, на основании присутствия
или отсутствия которых производится соотнесение введенного ДУ с одной из
канонических форм ДУ I или II порядка.
Разрабатываемый программный продукт должен соответствовать следующим
стандартным критериям: наличие интуитивно понятного интерфейса, выполнение
основного функционала, удовлетворение основным требованиям надежности,
сопровождаемости и мобильности.
Иерархическая структура интерфейса ПС приведена в Приложении Б.
1.3 Информационные технологии в создании обучающих программ
В начале анализа любой предметной области особое внимание уделяется
терминологии. Создание программных продуктов, позволяющих осуществлять
различного рода поддержку процесса обучения, является такой же областью знаний,
как и любая тематика по техническим или гуманитарным дисциплинам, а,
следовательно, имеет свой «фундамент», основу: понятия, определения, классификации.
Основными понятиями предметной области в данной работе выступают как аспекты,
связанные с педагогикой, так и определения и классификации, связанные с
разработкой программных продуктов.
Прежде чем подойти к определению обучающей программы необходимо определить
область, в которой производится постановка понятий и определений. В
рассматриваемом проекте основой выступают информационные технологии
как совокупность методов, производственных и программно-технологических
средств, объединенных в технологическую цепочку, обеспечивающую сбор, хранение,
обработку, вывод и распространение информации [22],[26].
В настоящее время не выработано и тем более не закреплено законодательно
определение обучающей программы. Большинство авторов, осуществляющих попытки
определить данное понятие, сходится лишь в том, что это некоторое программное
средство, ориентированное на решение педагогических задач, связанных с
определенной тематикой или отраслью знаний. При этом различия в определениях
носят зачастую чисто субъективный характер, так как оценка определения
производится с позиции применимости его к конкретной области знаний либо
дисциплине [13],[7],[16]. Наиболее общее определение обучающей программы
приводится авторами Рижского технического университета, где под обучающей
программой понимается комплекс информационных, методических и программных
средств, предназначенных для изучения отдельного предмета, и обычно включающие
вопросы и задачи для самоконтроля и проверки знаний, а также обеспечивающих
обратную связь [13]. Однако данное определение несколько скупо затрагивает
начальное определение понятия обучение, под которым понимается процесс
получения знаний и компетенций (умений) в определенной предметной области, где знания
- это результат процесса познания действительности, адекватный ее отображению в
сознании человека в виде представлений, суждений, умозаключений, теорий [11].
Таким образом, для реализации любого программного комплекса,
ориентированного на поддержку процесса обучения, предполагается использование в
ПС возможностей ознакомления с теоретическими аспектами изучаемой тематики
посредством использования элементов мультимедиа (рисунков, формул,
видеороликов), задач для проверки и самоконтроля и системы обеспечения обратной
связи с обучаемым. В целом все перечисленные компоненты представляют собой
отдельные учебные элементы или, другими словами, объекты, конкретные методы,
отобранные соответственно программе учебной дисциплины [15].
Рассмотренные определения задают базу для классификации обучающих
программ. Так в рамках информационных технологий можно выделить несколько
классификаций обучающих программ, описанных различными авторами, как
зарубежными, так и отечественными [3],[7],[26].
С учетом особенностей учебной деятельности принято выделять следующие
четыре типа современных обучающих программ [26]: тренировочные и
контролирующие призванные для решения прикладных задач по теоретической и
практической части, наставнические - помогающие в освоении материала,
путем представления его в удобном виде, с адаптацией по скорости выдачи
обучающемуся, подсказывающие наиболее важные, опорные моменты теории и
практики; имитационные и моделирующие - демонстрирующие процессы
происходящие в некоторых системах; развивающие игры - требующие
непосредственного участия обучаемого в ходе игры: при этом действия
пользователя приводят к развитию игровой ситуации различными путями.
Также принято выделять системы, a) ориентированные на работу в локальных системах, и
предназначенные для индивидуального обучения одного человека, не требующие
ресурсов подключения к локальным или глобальным сетям, б) сетеориентированные
приложения, работающие через глобальные сети, требующие подключения к
источнику данных, работающие под управлением Web-серверов, реализуя при этом модель клиент-сервер, и
предназначенные для большого количества людей, подразумевающие свободный или
ограниченный различными критериями доступ к учебно-методическим пособиям,
практическим и лабораторным заданиям.
1.4 Принципы создания обучающих программ
Констатируя очевидную потребность в новых гибких образовательных
структурах и технологиях, которые способны своевременно, качественно и
адекватно предоставлять образовательные услуги, авторы электронных обучающих
ресурсов отмечают, что «использование компьютера преобразует деятельность как учителя,
так и учащихся, изменяя ее содержание, операциональную структуру, оказывая
значительное влияние на мотивы участников этой деятельности, в значительной
мере перестраивая систему взаимоотношений между ними. Передача части обучающих
функций техническому устройству, анализ проблем обучения с учетом возможностей
компьютера не просто выдвигают новые психологические проблемы, они требуют
критического пересмотра фундаментальных положений педагогической и
психологической теорий обучения» [18].
При разработке дидактических методов, применение которых в компьютерных
технологиях обучения формировало бы профессиональную компетентность при
подготовке специалистов для различных сфер деятельности, требуется
разрабатывать подходы, учитывающие специфику требований к профессиональной
деятельности [17]. Так при подготовке специалистов по прикладной математике
одним из главных квалификационных требований являются знание и умение применять
методы математических дисциплин, в частности, численные методы и символьные
методы решения различных задач. Одним из наиболее эффективных средств поддержки
изучения этих дисциплин являются обучающие системы, учитывающие специфику
предметов [16]. При проектировании программно-методического комплекса согласно
теории инструкций Дж. Брунера, следует учитывать, прежде всего, четыре
важнейших момента [15]:
а) необходимые условия возможности обучения (стартовый уровень знаний,
уровень и структура мотивации);
б) способы структурирования материала, которые облегчали бы его
целостное понимание обучаемым;
в) способы предоставления материала;
г) способы оценки результатов, подкрепления и наказания.
Учет этих важных сторон организации учебного процесса помогает обучаемому
упрощать материал и генерировать новые предположения, а также увеличивает
динамичность работы с информацией.
На начальном этапе проектирования программно-методического комплекса
планируемый для изучения учебный материал разбивается на отдельные учебные
элементы (УЭ) [25]. Под учебным элементом будем понимать объекты -
конкретные методы, отобранные соответственно программе учебной дисциплины.
Совокупность УЭ представляют в виде структурной схемы - древовидного графа,
который называется графом содержания учебного материала и строится по
иерархическому принципу. Узлами (вершинами) графа являются УЭ, ребрами -
иерархические связи между ними. Систематизированный учебный материал, в котором
четко обозначены структурно-функциональные связи между его фрагментами, лучше
воспринимается и легче усваивается обучающимися. Располагая таким учебным материалом,
студент имеет возможность многократного и легкого обращения к отдельным
фрагментам и к системе в целом. При этом обращение к тому или иному фрагменту
может осуществляться различными путями, что способствует лучшему пониманию и
усвоению взаимных связей между отдельными понятиями, алгоритмами, методами и
т.д.
Последовательность действий, с которой обучающийся проходит по
определенной теме, составляет так называемый педагогический сценарий
обучения. Он является одной из форм описания и представления технологии
обучения [23].Педагогический сценарий включает описание связей между его
составными частями, текстами теоретического материала и практическими заданиями
различного уровня трудностей, переходами между обучающими элементами и т.д.
Содержание педагогического сценария определяется содержанием учебной
дисциплины, формами, целями и задачами обучения. В состав типового фрагмента
программно-методического комплекса, построенного по единой модели
педагогического сценария [15], могут входить такие части как: идея метода
решения задачи; алгоритм решения задачи; примеры решения задач; упражнения для
решения; тестовое упражнение с запланированными ошибками; сравнительный анализ;
тест.
Кроме того, по необходимости могут быть поставлены дополнительные примеры
и упражнения вспомогательного и исследовательского типов.
1.5 Принципы построения тестирующих программ
Одним из важных направлений совершенствования процесса обучения является
разработка оперативной системы контроля знаний, умений и навыков, позволяющей
объективно оценивать знания обучающихся, выявлять текущие пробелы и определять
способы их ликвидации. Обычно принято выделять пять этапов эволюции контроля
знаний [19]: традиционный контроль, контроль знаний с использованием бумажных
средств, контроль знаний с использованием технических средств, компьютерный
контроль знаний, удаленный контроль знаний.
Проблемы компьютерного контроля знаний обычно рассматриваются в двух
аспектах [14]: методическом и техническом.
К методическим аспектам относятся:
а) выбор заданий для проверки знаний, умений и навыков обучаемого («что
контролировать»); задача контроля позволяет определить соответствие
подготовленности обучающегося к тому или иному уровню усвоения учебного
материала;
б) планирование проведения контроля знаний («когда
контролировать?»);
б.1 исходный контроль знаний - проводится непосредственно перед
обучением;
б.2 текущий контроль - осуществляется в ходе обучения, позволяет
оценить уровень усвоения обучающимся материала;
б.3 рубежный контроль - проводится по завершении определенного этапа
обучения;
б.4 итоговый контроль - позволяет оценить уровень знаний и навыков
студента;
в) определение требований к формированию набора контрольных заданий
(«как контролировать?»); существует ряд методов для формирования контрольных заданий:
в.1 случайная последовательность вопросов и заданий разной
сложности;
в.2 специальный набор заданий различной сложности (для комплексной
проверки уровня подготовки), предъявляемый в строгой последовательности;
в.3 набор заданий, предъявляемых в порядке нарастания уровня
сложности;
в.4 группа заданий, последовательность выполнения которых выбирает
обучающийся.
Технические аспекты контроля знаний связаны, прежде всего, с проблемами
реализации планируемого контроля; к ним принято относить:
а) формирование набора контрольных заданий на основе выбранного подхода,
подразумевающее автоматическую подготовку набора заданий для контроля;
б) выбор и использование в системе контроля параметров контроля
знаний; принято выделять три основные группы параметров контроля:
б.1 параметры, характеризующие выполнение одного задания и
выполнение теста (количество обращений к справочной информации, время
выполнения задания, тип задания);
б.2 параметры, характеризующие работу обучаемого с набором контрольных
заданий (количество заданий, количество ответов и т.д.);
б.3 параметры, используемые для настройки алгоритма, обычно задаются
преподавателем, но могут иметь и заранее установленные значения (максимальный
балл или оценка; граничные значения для выставления оценки и др.);
в) выбор алгоритма для оценки знаний студентов; любой алгоритм оценки
знаний предусматривает сбор, анализ и/или преобразование данных, получаемых в
процессе контроля, и непосредственно формирование самой оценки [19]; выделяют
алгоритмы, которые применяются для:
в.1 выставления оценки по завершению контроля;
в.2 выставление оценки за отдельно взятое задание.
Для проведения компьютерного контроля знаний необходимо наличие методов
проведения контроля, а также методов оценки знаний, умений и навыков студентов
по результатам выполнения контрольных заданий. В литературе выделяется, как
правило, следующие методы проведения контроля знаний, которые получили
наибольшее распространение [12]:
а) неадаптивные методы компьютерного контроля знаний (КЗ); в процессе
контроля все студенты проходят одну и ту же, заранее определенную автором,
последовательность кадров; эта последовательность не зависит от действий
обучаемого во время контроля; всем студентам выдаются контрольные вопросы
одинаковой трудности либо в виде фиксированного набора, либо случайным образом;
число заданий является постоянным для всех студентов, независимо от их уровня
подготовленности;
б) частично адаптивные методы, в которых последовательность и число
контрольных заданий различны для сильных, средних и слабых студентов;
количество проверочных вопросов зависит от уровня подготовленности студентов и
всегда будет переменным числом [1];
в) полностью адаптивные методы компьютерного контроля знаний,
которые используют данные из модели студента (например, уровень
подготовленности студента, уровень беспокойства-тревоги, правильность ответа и
др.) и/или модели учебного материала (например, взаимосвязи между проверяемыми
понятиями) и позволяют организовать контроль индивидуально для каждого
студента, поддерживая, например, оптимальный для студента уровень трудности
выдаваемых контрольных заданий или формируя индивидуальные стратегии контроля
по отдельной теме, разделу или курсу в целом [9].
Проверка знаний может быть осуществлена с учетом различных критериев
формирования оценки. Методы оценки знаний можно разделить на три основных
класса [2]:
а) на основе количественных критериев (простейшая модель; модели,
учитывающие типы заданий; модели, учитывающие характеристики заданий; модели,
учитывающие характеристики заданий и параметры контрольных заданий).
б) на основе вероятностных критериев (модели, учитывающие
вероятность правильного ответа; модели, учитывающие неопределенность ответа)
в) на основе классификационных критериев (модели на основе
алгоритма вычисления оценок; модели на основе нечетких множеств).
Таким образом, для проверки знаний студентов применяются разнообразные
модели и алгоритмы оценивания [20], а также большое количество методов
проведения компьютерного контроля знаний, часть из которых в той или иной мере
можно считать адаптивными.
.6 Программы по высшей математике
В настоящее время на рынке программных продуктов, предоставляющих
возможности решения математических задач из курса высшей школы, имеется широкий
спектр различных программ, которые условно можно подразделить на категории по
сложности использования, стоимости распространения, функциональным возможностям
и многим другим критериям. Выделим несколько пакетов, которые предназначены
именно для поддержки обучения конкретным темам, не относящихся к универсальным
программным средствам символьной математики наподобие систем Mathematica, MathLab и другим продуктам крупных фирм.
1.6.1 Программа ODE
Программа ODE - это предметно ориентированная среда, предназначенная для
решения и исследования решений обыкновенных дифференциальных уравнений. Данный
программный продукт разработан на кафедре высшей математики МЭИ (ТУ) авторами
которой являются Кириллов А.И., Морозов К.А., Сливина Н.А.[17].
К основным возможностям данного учебного пакета относятся:
- возможность численно решать обыкновенные ДУ и системы до шестого порядка;
- строить графики численного решения;
- выбирать численный метод решения задачи и его параметры;
- для уравнений и систем высших порядков можно строить проекции
интегральных кривых на координатные плоскости.
Таким образом, программный продукт ODE предназначен для автоматизации сложных вычислительных
задач, связанных с вычислением и построением иллюстраций, показывающих решение
обыкновенных дифференциальных уравнений. Специализация данного продукта не
позволяет проводить тестирование и обучение студентов начальным теоретическим
сведениям: определению типа, канонической формы, параметров канонической формы
и метода решения. Недостатком данного программного средства является отсутствие
пояснений к решению, что связано с использованием численных методов, которые не
отражают сути решения, описанной в теории дифференциальных уравнений.
1.6.2 Программа ФОРМУЛА
ФОРМУЛА - компьютерная программа учебного назначения, предназначенная
помочь при изучении математического анализа. Основными возможностями программы
являются следующие:
- вводить произвольные аналитические выражения в общепринятой
математической нотации;
- производить всевозможные вычисления, дифференцировать функцию
в аналитической форме, численно интегрировать, вычислять значения многих
специальных функций и т.п.;
- а также предоставляет возможности для построения линии уровня
функции нескольких переменных и поля направлений обыкновенного ДУ первого
порядка;
Программный продукт разработан лабораторией кафедры высшей математики МЭИ
(ТУ) авторами Сливиной Н.А., Морозовым А.А., Морозовым К.А., Вороновым Р.С.
[24], работает под управлением операционной системы MS-DOS, использует
режимы отображения VGA и SVGA, и
имеет интерфейс, сходный с интерфейсом программного средства ODE.
Программный продукт ФОРМУЛА является менее ориентированным на решение
задач, связанных с дифференциальными уравнениями, однако предоставляет широкий
спектр возможностей численного решения различных подзадач, связанных с дифференциальными
уравнениями. Сложность использования данного продукта в рамках обучения теме
«ДУ» состоит в необходимости не только численно решить задачу, но и
предоставить студентам возможность пользоваться справочным материалом,
поясняющим ход решения некоторой задачи. Таким образом, данный продукт может
применяться на более поздних этапах для решения сложных вычислительных задач.
1.6.3 Программа «Математика»
Авторами данного программного продукта являются Грутовой А.В., Нелюбин
С.В., Строков А.В., Кремнёв М.В., Тверьянович Д.Ю., правообладателем
программного средства является компания Mentor Soft Ltd [8]. Система
предназначена для приобретения навыков решения задач по курсу «Высшая
математика». Данное ПС может работать в двух режимах: обучения и контроля;
предоставляет возможности работы с тремя уровнями знаний: школа, абитуриент,
студент. Программный продукт разработан на основе системы Computer Mentor, позволяющей осуществлять генерацию заданий на
выбранную пользователем тему.
Программный продукт позволяет решать генерируемые задачи выбранного типа.
Система автоматически решает сгенерированное задание и может предоставить
пользователю ход решения задачи.
В режим контроля преподаватель формирует билет, выбирая, сколько заданий
на какую тему должно в него войти, и задает необходимое количество билетов.
Программа генерирует билеты, каждый из которых отличается от остальных, при
этом типы и сложность заданий везде одинаковы.
Заложенные в данный продукт возможности позволяют производить
тестирование и обучение методам решения, так как поставленная задача может быть
решена пользователем самостоятельно, а полученный ответ введен для контроля.
Режим обучения предполагает, что программа автоматически генерирует задание из
выбранного раздела и осуществляет вывод хода решения ДУ. Однако подход
генерации заданий значительно сокращает возможности исследования хода решения
ДУ, заданного пользователем. С методической точки зрения получаемые пояснения
характеризуются запутанной структурой материала, решение задач осуществляется с
некоторыми ограничениями в решении, например, отсутствие возможностей
нахождения коэффициентов.
Для решения задачи обучения студентов по теме «Обыкновенные ДУ» нужно
разработать локально-ориентированное приложение, предназначенное для использования
в аудиториях и на домашних компьютерах. Это обусловлено тем, что в соответствии
с заданием разрабатываемый ПП не предназначен для доступа к информации по
локальным или глобальным сетям, не требует отправки результата тестирования
преподавателю по сети и рассчитан на высокую степень мотивации обучающегося.
При реализации системы тестирования будет использоваться модуль
автоматической генерации тестовых заданий с использованием частично адаптивных
методов контроля. В качестве модели оценивания знаний используем метод на
основе количественных критериев с выполнением пяти заданий, в каждом из которых
выделяется четыре подзадачи.
Адаптивный метод контроля подразумевает создание вложенности заданий.
Такой подход позволяет при верном выборе канонической формы перейти к решению
задачи о выделении её параметров, в противном случае данный этап не доступен
для пользователя.
В целом разрабатываемый программный продукт предоставит возможности:
- изучения теоретического материала;
- проведения тренинга и тестирования;
- обучение методам решения вводимых дифференциальных уравнений;
- поддержку в освоении выявления параметров канонической формы;
- предоставит возможности генерации тестовых заданий и многие
другие.
Такие возможности позволяют охватить большое количество выделяемых в
литературе классов обучающих программ. Данные системы принято называть
автоматизированные обучающие комплексы.
2. Обоснование метода решения (аналитическая часть)
2.1 Методы распознавания типа ДУ
В настоящее время решение задач, связанных с анализом любой текстовой
информации, является одним из новых направлений в компьютерных технологиях.
Именно по этой причине не существует открытых на общее ознакомление методов,
используемых для такого анализа. Фирмы-разработчики ПП не распространяются о
технологиях анализа, используемых при реализации своих программных продуктов.
Таким образом, данные технологии являются своеобразным «know how» фирм-разработчиков. Так, например, широко
распространенные математические пакеты реализуют решения многих математических
задач в аналитическом виде, при этом использование данных программных продуктов
не позволяет понять принципы, заложенные для их функционирования.
Задачи распознавания лексических особенностей текста, математического
выражения или другого объекта относятся к задачам создания интеллектуальных
систем распознавания образов. Известно несколько методов, которые доступны
для решения задач символьного анализа: методы с использованием бинарных
деревьев, методы построения нейронных сетей и методы, использующие экспертные
самообучающиеся системы. Рассмотрим, каким образом используются данные методы
для распознавания математических выражений.
Методы на основе анализа бинарных деревьев предоставляют возможности для
анализа за счет их структуры. Как известно, бинарное дерево состоит из вершин и
отношений между вершинами. Данный метод используется, как правило, для
построения систем автоматизации вычислений по вводимому математическому
выражению; при этом вершинами дерева являются переменные, операции и функции, а
связи между вершинами позволяют, используя процедуры обхода бинарного дерева,
получить различные записи математического выражения и вычислить значение
введенной функции. Принято выделять три способа, позволяющих произвести обход
дерева:
- рекурсивный обход с посещением и анализом вершины, после чего
производится переход к левой вершине, и только после этого - к правому
поддереву; использование такой процедуры позволят получить префиксную форму
записи математического выражения;
- рекурсивный обход с предварительным спуском в левое поддерево, анализ
вершины и спуск в правое поддерево; в результате получается инфиксная форма
записи математического выражения;
- рекурсивный обход посредством посещения левого поддерева,
затем правого и только после этого производится анализ вершины; такой метод
позволяет получить постфиксную форму записи выражения.
Данный метод в целом позволяет производить анализ математического
выражения на выявление частей, характеризующих данное выражение как
принадлежащее к одному из следующих типов: функция нескольких переменных,
функция одной переменной, линейная функция, тригонометрическая функция и многие
другие признаки для классификации математического выражения. В целом данный
метод можно назвать как рекурсивный синтаксический анализ частей бинарного
дерева.
Следующим методом, который применим для решения задач, связанных с
распознаванием типа ДУ, являются методы, основанные на построении нейронных
сетей. Под нейронной сетью понимается вычислительная или логическая схема,
построенная из однородных процессорных элементов, являющихся упрощенными
функциональными моделями нейронов. Каждый из нейронов призван выполнять
определенные функции анализа объекта и передавать информацию о результате
центральной системе, которая производит отождествление полученной совокупности
информации на основе предшествующего опыта с некоторым классом объектов. В
качестве данного объекта могут выступать и математические выражения. Однако для
реализации программных продуктов такого ранга (относящегося к рангу искусственного
интеллекта), потребуется достаточно длительный период времени, так как
достижения современных технологий не позволяют однозначно судить о принципах
работы нейронов, хотя данное направление и является достаточно многообещающим.
Методы, основанные на построении экспертных систем, позволяют делать выводы о
принадлежности объекта к конкретному классу или выявления его характеристик,
используя специализированные базы знаний. Такой подход широко применяется в
медицине для анализа и выявления заболеваний, установки диагноза и методов
лечения больного. В качестве реализации поставленной задачи данный подход может
быть использован следующим образом:
- обучение автоматизированной системы посредством участия групп
программистов и экспертов области;
- выявление взаимосвязей, характеризующих типы дифференциальных уравнений и
частей вводимого выражения, указывающих на принадлежность к типу;
- создание программных модулей для дальнейшего обучения
системы.
Таким образом, данный подход предполагает включение в работу над
созданием программного продукта широкого спектра специалистов, требует
предварительного обучения системы, а также не предоставляет возможностей
достаточного строгого выявления типа, так как данные системы призваны
осуществлять лишь поддержку новых специалистов, не являющихся экспертами в
области, и выносят решение, носящее рекомендательных характер. Такое решение не
может быть использовано в рамках создания обучающих программ, так как
вероятность правильно принятого решения при обучении должна быть достаточно
высока в районе 90 процентов от общего числа случаев.
Из рассмотренных методов наиболее простым в реализации и вполне
удовлетворяющим требованиям задач А и Б из постановки задачи (пункт 1.1)
является использование синтаксического анализа бинарного дерева. Дополнительным
основанием в пользу использования данного метода решения является его
ориентированность на работу с математическими выражениями и равенствами, а
также предоставление данным методом средств для анализа в виде хорошо
зарекомендовавших себя методов обхода.
2.2 Методы решения ДУ в символьном виде
В данной области также не существует открытых методов решения с целью
получения точного решения с использованием алгоритмов, преподаваемых в теории
дифференциальных уравнений.
В целом методы решения математических задач можно разделить на два
подтипа: точные и численные методы решения. Особенностью точных методов
решения ДУ является необходимость задания таких последовательностей и
алгоритмов работы программного средства, которые на основании установленного
типа ДУ будут выбирать наиболее адекватный метод решения, описанный в теории
дифференциальных уравнений. Аналоги решения данной задачи существуют в таких
математических пакетах как Mathematica, MatLab и других пакетах символьной
математики. Однако главным недостатком, который затрудняет использование данных
программных продуктов при обучении студентов по теме, является тот факт, что в
качестве решения приводится только ответ, и студент не имеет возможности
освоить метод, приводящий к такому ответу.
Численные методы позволяют также построить символьное решение за счет
выполнения процедур приближенного решения дифференциальных уравнений методами
Эйлера, Рунге-Кутта и другими. Программа, позволяющая задать возможности
вычисления широкого набора таких решений, может быть использована с той точки
зрения, что полученные численные решения являются численными значениями
некоторой функции. Построение аналитического выражения по заданному набору
значений этой функции можно производить посредством использования
интерполяционных методов Ньютона или Лагранжа, аппроксимирующих данную функцию,
методов сплайн-интерполяции и других методов, приводящих к символьной записи
функции, заданной точками. Хотя данный метод и позволяет построить символьное
приближенное решение поставленной задачи, однако не позволяет прийти к точному
решению, и тем более полученная в результате функция не будет являться
результатом применения метода решения, преподаваемого в теории.
Для получения решения задачи В из общей постановки задачи (пункт 1.1),
удовлетворяющего целям обучения, можно предложить способ заполнения
параметризированных шаблонов. Суть данного метода сводится к тому, что для
решения ДУ ранее определенного типа необходимо выполнить ряд следующих шагов:
- выявить параметры канонической формы ДУ установленного типа;
- заполнить шаблон решения ДУ указанного типа параметрами
рассматриваемого ДУ;
- считать ДУ решенным, если оно сведено к интегралам.
Таким образом, для решения поставленной задачи необходимо произвести
формирование шаблонов, предназначенных для вывода общего решения или общего
интеграла заданного ДУ. Параметрами шаблона являются параметры канонической
формы, которые могут быть выявлены в ходе синтаксического анализа частей ДУ.
Подставляя в шаблон выявленные параметры канонической формы, можно получить
достаточно подробный алгоритм решения ДУ.
Однако остается проблема вывода математических знаков и формул. В данном
случае наиболее целесообразным оказалось использование HTML подмножества MathML, позволяющего отобразить формулы таким образом, как
это будет привычным для студентов, т.е. с использованием дробей, верхних
индексов для отображения степеней и т.д.
3. Описание программного решения
3.1 Обоснование выбора программной среды и инструментов
разработки
Начиная разработку программного продукта, необходимо определить основной
инструментарий, призванный помочь программисту в выполнении поставленной
задачи. В настоящее время для разработки локально-ориентированных приложений
используются такие среды разработки как Visual Studio, JAVA, Borland C++.
Рассмотрим преимущества и недостатки использования каждого из данных
средств разработки программных продуктов.
Среда разработки С++ Builder
предназначена для визуальной разработки приложений в сочетании с высокой
степенью соответствия стандарту ANSI C++. Использование широкого спектра
компонентов для визуального оформления интерфейса разрабатываемых продуктов
позволяет сконструировать интерфейс при помощи технологии Drag-and-Drop.
Отладка сложных приложений осуществляется за счет использования возможностей
системы CodeGuard, установки точек останова, просмотра локальных переменных в
любой момент исполнения программы. Studio.NET - это среда разработчика,
позволяющая значительно существенно увеличить производительность труда разработчиков,
предоставляя им широкий выбор средств для автоматизации рутинных операций и
минимизации написания кода. Для создания клиентских приложений в Visual
Studio.NET используются Windows-формы, поддержку котроых обеспечивает ядро.NET
[27].Java Studio Enterprise 8 компании Sun - это унифицированная
инструментальная платформа для разработки приложений масштаба предприятия,
интегрированная с серверами Sun Java Enterprise System.Java Studio представляет
собой полное решение для разработчиков, включающее интегрированные инструменты,
наборы для разработки ПО (SDK, software development kit), интерфейсы создания
приложений (API), библиотеки и сервисы для разработчиков. Java Studio позволяет
быстро создавать приложения и Web-сервисы для различных платформ и сред.
При разработке приложений среда разработки предоставляет средства
аналогичные средствам представленным в двух ранее описанных средах: выделение
синтаксических конструкций и их подсветка, редакторы интерфейса посредством
использования стандартных компонент и многие другие.
Таким образом, необходимо отметить, что современные средства,
специализированные для разработки приложений, в целом используют одинаковые
методы ускорения работы программиста. Для ускорения разработки немаловажен факт
наличия открытых библиотек и простота их использования и освоения для различных
подзадач, а также наличие специализированных визуальных компонентов вывода HTML-шаблонов (TCppWebBrоwser). Такими свойствами и компонентами обладает среда
разработки С++ Builder, с помощью которой разработан программный продукт.
В качестве вспомогательного инструмента разработки шаблонов функции и
наглядного вывода на экран математических выражений широко используются XML подмножества, в частности MathML. MathML - это утвержденное W3C расширение языка HTML,
разработанное для кодирования математических выражений. Использование связки HTML и MathML позволяет использовать различные элементы оформления
страниц: рисунки, таблицы, формулы.
Для корректного и отображения формул в браузере Internet Explorer различных версий необходимо
установить специализированный пакет MathPlayer, разработанный компанией Design Science и позволяющий
браузеру трактовать теги MathML.
Данный программный продукт распространяется бесплатно, не требуя
лицензирования.
3.2 Описание входной и выходной информации
Использование программного средства предполагает взаимодействие
пользователя с ПП посредством использования различных манипуляторов и систем
ввода информации.
Разработанный ПП посредством взаимодействия пользователя с интерфейсом
позволяет осуществлять ввод информации с помощью следующих средств:
использование манипуляторов типа мышь; использование средств ввода символов,
например, с клавиатуры; использование средств взаимодействия с элементами
управления: кнопки, переключатели, раскрывающиеся списки; использование средств
автоматической генерации тестовых заданий в режиме тренинга и контроля;
использование файлов шаблонов для воспроизведения алгоритма решения ДУ.
Таким образом, основными типами входной информации являются:
- внешняя информация, исходящая от пользователя путем манипуляции мыши или
с использованием клавиатуры;
- внутренняя информация в виде набора HTML документов, средств генерации дифференциальных
уравнений, средств формирования шаблонов для генерации хода решения.
В качестве средств вывода информации для данного продукта характерно
использование интерфейса пользователя. Таким образом, единственным средством
вывода является экран монитора.
3.3 Архитектура и модульность программного средства
Разработка программного продукта предполагает создание специальной
иерархии объектов и способов взаимодействия интерфейса пользователя с
программными модулями. Разработанный ПП представляет собой совокупность двух
частей: теоретической и практической, в которой используются экспериментальные
компоненты. При дальнейшей разработке этой обучающей программы
экспериментальные модули могут быть выделены в самостоятельную часть.
Таким образом, общая структура программно средства может быть
представлена в виде изображенном на Рисунке 1.

Рисунок 1 - Общая структура программного средства
Теоретическая часть представляет собой модуль, предназначенный для вывода
и отображения конспекта лекций и его обучающих элементов на экране монитора.
Данный модуль использует HTML
файлы, содержащие страницы электронного конспекта лекций (ЭКЛ). Основными
обучающими элементами данного модуля являются такие характерные для ЭКЛ
средства, как структурированное изложение материала, краткое содержание,
контрольные вопросы самопроверки, глоссарий, список формул, элементы навигации
и гиперссылки.
Следующим элементом обучающей программы является «Практическая часть»,
которая дает возможность использования полученных при изучении ЭКЛ
теоретических знаний на практике за счет использования таких обучающих
элементов, как возможность ввода любого ДУ, тренинг и тестирование по задачам
определения типа, канонической формулы и её параметров, указания метода решения
заданного ДУ.
Такую возможность предоставляет набор модулей практической части (рисунок
2).

Рисунок 2 - Набор модулей практической части обучающей программы.
Функциональные диаграммы данных модулей и теоретической части ОП будут
приведены в Приложении В «DFD-диаграмма
программного средства».
Для лучшего понимания принципов функционирования и алгоритмов работы
данных модулей рассмотрим их более подробно.
3.3.1 Модуль лексико-грамматического анализа выражения и
равенства
Модуль лексико-грамматического анализа выражения или равенства позволяет
проверять корректность ввода ДУ. Данный модуль в качестве входной информации
принимает значение строки с формулой в виде равенства, производит её разбиение
на лексемы, каждая из которых представляет собой знак «=», один из знаков
арифметических операций, обозначение переменной или константы. Это необходимо
для дальнейшего проведения анализа корректности ввода ДУ, в котором
используются автоматные грамматики, построенные на идее построении КС-грамматик
языка, а также построении на их основе LL(1)-грамматик языка и построение модели нисходящего LL(1)-анализатора [10]. Процесс
разработки нисходящего LL-анализатора
можно подразделить на следующие этапы:
- формальное описание синтаксиса с помощью нормальных форм
Бекуса-Наура;
- формальное описание синтаксиса конструкции языка
программирования в форме КС-грамматик;
- выполнение эквивалентных преобразований КС-грамматики с целью
устранения недостижимых и бесплодных нетерминалов;
- описание множества классов лексем исходной конструкции и
построение модели лексического анализатора;
- составление тестовых данных для проверки правильности работы
лексического анализатора;
- приведение КС-грамматики к виду LL(1)-грамматики;
- построение нисходящего LL(1)-анализатора.
Прохождение данных этапов позволило разработать лексико-грамматический
анализатор, обрабатывающий такие характерные ошибки ввода, как
использование недопустимых лексем и неправильный синтаксис математического
выражения или равенства; этапы разработки LL(1)-анализатора, используемого в программном средстве
приведены в приложении В «Построение LL(1)-анализатора».
Выходной информацией к данному модулю является допуск или запрет
построения бинарного дерева, состоящего из вершин и связей между ними.
Вершинами дерева являются математические операции переменные, константы и
функции. Примером такого дерева может служить рисунок, изображающий дерево
характерное для формулы 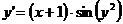 .
.
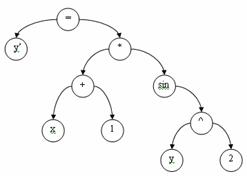
Рисунок 3 - Пример бинарного дерева
Сохранение такой структуры в памяти компьютера осуществляется за счет
создания пользовательского типа TTree
с использованием перечисленных ниже полей.
TTree *left,*right - поля,
предназначенные для хранения указателя на левую и правую вершины соответственно.
Указатель характеризуется шестнадцатеричным кодом участка памяти, в котором
расположена следующая вершина дерева. Данные указатели соответствуют связям
между вершинами бинарного дерева.
double data - данное поле предназначено для хранения констант, встречающихся
в выражении, что значительно упрощает вычисление значения функции и анализ ДУ.
AnsiString symbol - данное строковое поле предназначено для сохранения
информации о функции, операции или переменной, используемой в математическом
выражении.
Определение порядка следования операций при построении бинарного дерева,
является достаточно важным моментом. Как видно из рисунка 3, наименьшим
приоритетом обладают операции сложения/вычитания, далее идут операции умножения
и деления, а также возведения в степень. Полная таблица приоритетов операций,
используемых при построении корректного бинарного дерева по введенному ДУ,
приведена в таблице 1.
Таблица 1 - Приоритеты операций
|
Знак, операция, функция
|
Степень приоритета*
|
|
|
= (знак равества)
|
1
|
|
|
+ (сложение)
|
2
|
|
|
- (вычитание)
|
2
|
|
* (умножение)
|
4
|
|
/ (деление)
|
3
|
|
^ (возведение в степень)
|
5
|
|
cos
(косинус)
|
6
|
|
sin (синус)
|
6
|
|
ln (натуральный логарифм)
|
6
|
|
tg (такнгенс)
|
6
|
|
atan
|
6
|
|
acos
|
6
|
|
asin
|
6
|
|
|
|
|
Для выделения лексем, проверяемых на корректность, используется
специализированный массив типа, заданного пользователем. Данный
пользовательский тип имеет следующие поля:
AnsiString handle - строковое поле для хранения
лексемы;
short int priority - текущий приоритет лексемы для разбора;
bool useLec - признак того что данная лексема занесена в дерево;
TTree *rootLT- в случаях, когда лексема уже занесена в дерево, необходимо
сохранить указатель на данную вершину, чтобы в дальнейшем производить
связывание более приоритетных операций с менее приоритетным; в противном случае
лексема не была занесена в дерево, данное поле принимает значение NULL.
Множество лексем хранится в массиве. Данный массив представляет собой 255
элементов (лексем). Процедура построения бинарного дерева работает таким
образом, что в выражении не может присутствовать более 255 лексем.
В целом алгоритм работы программного модуля лексико-грамматического
анализатора выражения или равенства представлен в виде блок схемы изображенной
на рисунке 4.

Рисунок 4 - Блок-схема алгоритма работы модуля лексико-грамматического
анализатора
В случаях возникновения ошибок на этапах лексического и грамматического
анализа производится остановка работы лексико-грамматического анализатора с
указанием места возникновения и возможной ошибки.
3.3.2 Модуль определения типа ДУ, канонической формы и метода
решения
Как говорилось выше (пункт 2.1), для решения задачи, связанной с
распознаванием типа ДУ, будем использовать метод рекурсивного
синтаксического анализа частей бинарного дерева. Для проведения анализа
необходимо определить основные признаки, используемые для анализа.
В ходе изучения темы «Обыкновенные ДУ» студенты знакомятся с типами
дифференциальных уравнений, приведенными в Приложении A. В этой приложении, выделяются 6 основных типов (4 первого
порядка и 2 второго), 5 различных подтипов (с разделяющимися переменными, не
содержащие явно переменную «x»,
не содержащие явно переменную «y», ЛОДУ, ЛНДУ), 2 характеристики линейных ДУ второго порядка (с
постоянными и непостоянными коэффициентами) и два специальных вида правой части
ЛНДУ с постоянными коэффициентами.
Для выявления признаков каждого из данных типов были составлены таблицы
основных признаков, позволяющих при рекурсивном синтаксическом анализе выявить
части, характеризующие принадлежность к введенному ДУ (см. приложения Д, E).
Рассмотрим данные признаки в таблицах отдельно для ДУ первого и второго
порядков. При этом введем специализированное понятие уровень уточнения.
Уровень представляет собой совокупность условий, проверяемых при рекурсивном
синтаксическом анализе бинарного дерева. Далее используем следующие три уровня:
а) нулевой уровень соответствует основным теоретическим аспектам;
б) первый уровень используется для частных случаев, указывает на признаки
канонической формы, проверяемые после удовлетворения условий нулевого уровня;
в) второй уровень уточнения содержит признаки отрицания принадлежности
ДУ к конкретному типу; наличие данных признаков однозначно говорит о непринадлежности
ДУ к типу.
Наибольшим приоритетом обладает второй уровень уточнения. Если признаки
данного уровня отсутствуют в распознаваемом ДУ, то происходит переход к
проверке признаков первого и нулевого уровней уточнения. Признаки первого и
нулевого уровней проверяются в рамках одной рекурсивной процедуры, в результате
работы которой устанавливается наличие признаков для левого и правого
поддерева. Если признаки удовлетворяют обоим уровням уточнения для левого и
правого поддерева, то процедура распознавания типа принимает решение о
принадлежности ДУ к данному типу. Если хотя бы один из признаков нулевого или
первого уровня не удовлетворяется или удовлетворяются признаки второго уровня
уточнения для любого из поддеревьев (правого или левого), то процедура выносит
решение о несоответствии ДУ распознаваемому в текущий момент типу.
Основные признаки, используемые в рекурсивном синтаксическом
анализе ДУ первого порядка, указанны в Приложении Д.
В целом для определения типа ДУ первого порядка используются как методы
синтаксического анализа, так и численный метод определения принадлежности
правой части канонической формы ДУ к однородной функции нулевой степени
однородности. Необходимость использования численного метода несколько
снижает надежность распознавания однородных ДУ. Однако заменить его методом
синтаксического анализа дерева не удалось, так как при определении однородного
ДУ необходимо произвести такое преобразование, которое выделит признак
однородности: функция 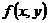 правой части канонической формы является зависимостью от
отношения
правой части канонической формы является зависимостью от
отношения 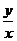 . Используемое решение строится на том признаке, что исходная
функция
. Используемое решение строится на том признаке, что исходная
функция 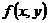 может быть записана в виде отношения
может быть записана в виде отношения
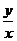 только в том случае, если при замене
«x» на «
только в том случае, если при замене
«x» на «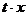 », а «y» на «
», а «y» на «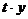 », где «t» - произвольная постоянная, не равная нулю
значение функции не меняется, т.е.
», где «t» - произвольная постоянная, не равная нулю
значение функции не меняется, т.е. 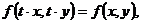 при любых
при любых 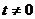 . Однако при таком решении возникает проблема сравнения,
которая заключается в том, что сравнение результатов вычисления двух функций от
двух переменных на одинаковых наборах данных может привести к различным
значениям, так как компьютер не умеет производить сокращение дробей в привычном
для человека виде. Таким образом, основным недостатком этого метода является
то, что при сравнении вычисленных значений двух функций используется не точное
сравнение двух чисел, а приближенное, характеризуемое малым отклонением
полученных значений. В качестве критерия достаточно хорошо показал себя
критерий сравнения чисел с точностью до 4-го знака дробной части.
. Однако при таком решении возникает проблема сравнения,
которая заключается в том, что сравнение результатов вычисления двух функций от
двух переменных на одинаковых наборах данных может привести к различным
значениям, так как компьютер не умеет производить сокращение дробей в привычном
для человека виде. Таким образом, основным недостатком этого метода является
то, что при сравнении вычисленных значений двух функций используется не точное
сравнение двух чисел, а приближенное, характеризуемое малым отклонением
полученных значений. В качестве критерия достаточно хорошо показал себя
критерий сравнения чисел с точностью до 4-го знака дробной части.
Признаки, используемые при определении типов дифференциальных уравнений
второго порядка, приведены в приложении Е. Для функций определения типов
второго порядка характерны только методы рекурсивного синтаксического анализа
дерева.
Рассмотрим идею алгоритма, заложенного в методы рекурсивного
синтаксического анализа бинарного дерева для определения типа ДУ.
Общая идея алгоритма состоит в том, что перед распознаванием выражения
используется одна их двух процедур:
- представление исходного выражения на в виде произведения нескольких
скобок;
- раскрытие скобок для получения развернутой формы выражения.
Так, например, для анализа на принадлежность к типу «ДУ с разделяющимися
переменными» необходимо представить правую часть в виде произведения двух
функций: функции с зависимостью только от переменной «x» и функции зависящей только от
переменной «y». Такое
представление возможно только за счет преобразования исходного выражения правой
части, а, следовательно, и построенного по нему бинарного дерева, к виду
произведения. Полного автоматического решения этой задачи добиться не удалось;
по этой причине предполагается, что пользователь будет либо самостоятельно
преобразовывать выражение к произведению, либо при попытке определения типов, в
качестве решения будет предложено отнесение ДУ к «прочим типам», распознавание
которых не предусмотрено программным средством. Однако на практике при
выполнении задач в рамках обучения пользователю редко предлагаются задачи, тип
которых не вписывается в изучаемый список типов. Поэтому при получении ответа о
принадлежности ДУ к «прочим типам» пользователь должен задуматься о том, что
для корректного определения типа можно осуществить ручное преобразование его
правой части к произведению, которое приведет к выявлению «ДУ с разделяющимися
переменными».
Для всех типов дифференциальных уравнений, отличных от ДУ с
разделяющимися переменными, наиболее удобна процедура разложения имеющихся скобок.
Выполнение данного преобразования для дерева сводится к выполнению следующей
последовательности шагов:
а) выявление признака возможности раскрытия скобок; в данном случае
возможны два варианта:
а.1. после вершины умножения в правом и левом поддереве стоит
операция сложения или вычитания;
а.2. после вершины со знаком умножения в левом или правом поддереве
стоит операция сложения или вычитания, а в другом поддереве хранится
окончательная вершина со значением константы или некоторой переменной;
б) разложение скобки путем добавления вместо вершины умножения вершины с
текущей операцией правого поддерева, добавление двух вершин со знаком
умножения, копирование правого поддерева, связывание вершин левого и правого
поддерева (скопированного или исходного) с вершиной умножения и связывание
вершины, в которой производилась замена знака умножения на знак сложения.
Рассмотрим пример выполнения описанной процедуры для ДУ 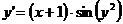 .
.
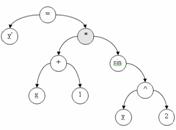

Рисунок 5 - Пример разложения скобок
На рисунке 5.а серым цветом обозначена вершина, в которой выполняются
признаки, указывающие на возможность разложения скобок: текущая вершина
содержит знак умножения, а в левом поддереве первая встречающаяся вершина
является сложением. На рисунке 5.б черным цветом обозначены вершины с
изменённым знаком и созданные заново, а в штриховой прямоугольник обведена
скопированная часть правого поддерева исходного состояния. Также для вершин,
обозначенных черным цветом, показан алгоритм соединения частей поддерева.
После обработки дерева ДУ процедурой преобразования математического
выражения вызываются функции определения типа ДУ. В качестве параметров данные
функции принимают корень бинарного дерева, а возвращают логическое значение,
указывающее на принадлежность ДУ к распознаваемому в данный момент типу.
Последовательно вызывая функции определения каждого типа ДУ, заполняется
массив, в дальнейшем передаваемый через параметр общей функции определения типа
ДУ в основную программу.
Каждая отдельно взятая функция распознавания типа реализует общий
алгоритм синтаксического анализа бинарного дерева с помощью использования
рекурсии. Алгоритм работы одного этапа рекурсии данных процедур состоит в
следующем:
- анализ вершины и поддеревьев на выявление признаков, характерных для
определяемого типа ДУ;
- если результат выявления признаков выполнился для правого и
левого поддерева, то процедура возвращает значение «истина» на предыдущий
уровень рекурсии, либо в функцию, её вызвавшую;
- если результат анализа левого или правого поддерева
отрицателен, то функция вызывает себя рекурсивно путем перехода от текущей
вершины к вершине левого или правого поддерева, соответственно результату левой
или правой части;
- в случае когда процедура сталкивается с признаками,
указывающими на бессмысленность дальнейшего анализа, происходит возврат ложного
значения анализа текущей вершины и её поддеревьев в более высокий уровень
рекурсии, происходит разложение стека вызовов с возвратом ложного результата, и
вызывающая процедура получает ложное значение, указывающее на непринадлежность
ДУ к заданному типу. К таким признакам относятся, например, признак того, что
вершина дерева является последней и не имеет левого и правого поддеревьев, а
также некоторые математические операции в вершине. Для ДУ с разделяющимися
переменными к последнему признаку относится вершина с аддитивной операцией.
Общая для всех процедур распознавания типа блок-схема одного этапа
рекурсии представлена на рисунке 6.

Рисунок 6 - Общая блок-схема одного этапа рекурсии
Использование данной процедуры синтаксического анализа применяется не
только к ДУ первого порядка, но и для определения типов ДУ второго порядка.
В целом данная процедура пригодна и для выявления, например, линейных,
тригонометрических и других зависимостей при изменении условий анализа вершины
и поддеревьев.
На основании определенного типа ДУ можно произвести определение
канонической формы и метода решения ДУ. Определение строится путем
использования условий устанавливающих соответствие между типом ДУ и его
канонической формой, либо между типом ДУ и его методом решения. Следовательно
для решения задач определения канонической формы и метода решения необходимо
составить таблицы соответствия (таблицы 2 и 3) и запрограммировать условные
конструкции выявляющие это соответствие.
Таблица 2 - Соответствие типов ДУ каноническим формам
|
Порядок ДУ
|
Тип ДУ
|
Каноническая форма
|
|
I
|
С разделяющимися
переменными
|
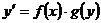
|
|
Линейное
|
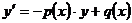
|
|
Бернулли
|
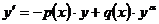 где где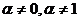
|
|
Однородное
|
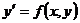 , , 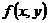 -однородная
функция нулевой степени однородности -однородная
функция нулевой степени однородности
|
|
II
|
Простейшее
|
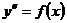
|
|
Не содержит явно «y»
|
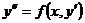
|
|
Не содержит явно «x»
|
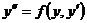
|
|
Линейное однородное с
постоянными коэффициентами
|
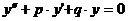
|
|
Линейное однородное с
переменными коэффициентами
|
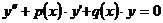
|
|
Линейное неоднородное с
постоянными коэффициентами
|
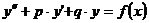
|
|
Линейное неоднородное с
переменными коэффициентами
|
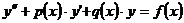
|
Таблица 3 - Соответствие типов ДУ методам решения
|
Порядок ДУ
|
Тип ДУ
|
Метод решения
|
|
I
|
С разделяющимися
переменными
|
Разделить переменные
|
|
Линейное
|
Выполнить замену 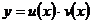
|
|
Бернулли
|
|
|
Однородное
|
Выполнить замену 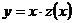
|
|
II
|
Простейшее
|
Двукратное интегрирование
|
|
Не содержит явно «y»
|
Выполнить замену 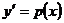
|
|
Не содержит явно «x»
|
Выполнить замену 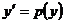
|
|
Линейное однородное с
постоянными коэффициентами
|
Решить характеристическое
уравнение 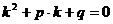
|
|
Линейное однородное с
переменными коэффициентами
|
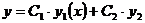 , ,  -ФСЧР -ФСЧР
|
|
Линейное неоднородное с
постоянными коэффициентами
|
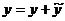
|
|
Линейное неоднородное с
переменными коэффициентами
|
|
.3.3 Модуль определения параметров канонической формы
В процессе тренинга пользователю необходимо предоставлять не только
полученные ответы, но и пояснять, почему было принято решение о принадлежности
данного ДУ к определенному типу. В классическом варианте обучения в результате
общения преподавателя и студента выясняется, что в данном дифференциальном
уравнении необходимо выделить такие части, которые будут его согласовывать с
канонической формулой ДУ того или иного типа. Таким образом, процесс пояснения
осуществляется сопровождением выделенных для данного ДУ параметров канонической
формы.
Процесс выделения параметров, как и процесс распознавания, осуществляется
за счет процедуры синтаксического рекурсивного анализа с тем отличием, что
вместо признака результата анализа (обнаружен или нет признак принадлежности),
составляется новое бинарное дерево, содержащее конкретный параметр канонической
формы. Таким образом, для построения деревьев, содержащих параметры канонической
формы, необходимо использовать признаки, приведенные в Приложениях Д и Е, а
также осуществлять выделение дополнительных математических выражений,
являющихся искомыми параметрами, и при необходимости создавать бинарное дерево
выделенного параметра канонической формы.
Дерево, характеризующее параметр канонической формы, может состоять из
нескольких частей ДУ, причем данные части могут располагаться в различных
местах в дереве, построенном по исходному ДУ. Данное обстоятельство
обуславливает два возможных варианта:
- если дерево параметра канонической формы пусто, то производится
копирование найденной части;
- если дерево параметра канонической формы не пусто,
производится объединение старой и новой частей характерным знаком.
Один шаг рекурсии функции выделения параметра канонической формы работает
следующим образом:
- анализ текущей вершины и поддеревьев левого и правого на соответствие
признаку;
- если корень дерева параметра канонической формы пуст, то
копируем дерево, начиная с рассматриваемой вершины;
- если корень параметра канонической формы не пуст, проверяем,
какая операция была сохранена;
- объединяем новое найденное дерево с деревом, найденным на
предыдущих шагах рекурсии, операцией, найденной на предыдущем шаге;
- запоминаем операцию текущей вершины для возможного
дальнейшего объединения частей параметра канонической формы;
- рекурсивный спуск в левое поддерево, начиная от текущей
вершины;
- рекурсивный спуск в правое поддерево, начиная от текущей
вершины;
- если вершина является конечной или встретилась операция,
указывающая на прекращение анализа, происходит возврат по стеку рекурсии или
выход в процедуру, вызвавшую функцию выделения параметра канонической формы, с
возвратом корня дерева, характеризующего найденный параметр.
На рисунке 7 приведена блок-схема работы данного алгоритма для нахождения
параметра канонической формы в виде функции зависящей только от переменой «y», ДУ с разделяющимися переменными.

Рисунок 7 - Блок-схема выделение части g(y)
ДУ с разделяющимися переменными
Таким образом, в начале процедуры проверяется, не является ли текущая
вершина пустой. Если вершина Root
исходного дерева не пуста, то производим проверку (вызовом функции onlyYF) наличия в дереве только зависимости
только от одной переменной «y».
В случае, когда такая зависимость присутствует, производится копирование части
с зависимостью только от «y»
и возврат на более высокий уровень рекурсии. На практике данное условие
позволяет выявить параметр g(y) в том случае, если правая часть ДУ
является только зависимостью от «y». В противном случае производится проверка вершины на соответствие
операциям умножения или деления. Если данная операция отсутствует, то анализ
прекращается, иначе производится анализ вызовом функций onlyYF(Root®left) и onlyYF(Root®right) левого и правого соответственно
поддерева на наличие зависимости только от переменной «у». Если одна из
функций onlyYF(Root®left)
или onlyYF(Root®right)
находит такую зависимость, то производится копирование левого или правого
поддерева соответственно, начиная от текущей вершины вызовом функции copyTree. При этом после выполнения
копирования устанавливаются признаки, указывающие на остановку дальнейшего
рекурсивного спуска в данные поддеревья.
При проверке факта, является ли созданное на предыдущих этапах рекурсии
дерево параметра канонической формы пустым, происходит разделение процесса
анализа по двум ветвям:
- дерево пусто, следовательно, необходимо произвести сохранение
найденной части путем присвоения указателя на вершину дерева, а также
необходимо сохранить знак текущей вершины для возможного дальнейшего
объединения;
- дерево не пусто, следовательно, необходимо произвести
объединение созданного ранее дерева и только что найденного в соответствии со
знаком умножения или деления.
Процессы, обозначенные RootGY
=addRoot+”/”+ RootGY и RootGY
= addRoot + ”*” + RootGY, характеризуют второй случай и позволяют создать
новое дерево с вершиной «*» или «/», присоединяя к ней левое поддерево addRoot (новое найденное) и правое поддерево
RootGY (выявленное ранее).
Следующим этапом является выявление части, которая еще не была
подвергнута анализу, что характеризуется логическими переменными lpart и rpart. В случае, когда данные переменные принимают значение
«истина», анализ будет прерван, а функция вернет значение текущего найденного
корня параметра канонической формы. В противном случае будет рекурсивно вызвана
рассматриваемая процедура OnlyYDiff. Рекурсия состоит в использовании в
качестве первого параметра указателя на левое или правое поддерево.
В случае, когда пользователь выбирает тип ДУ неверно, вместо шаблона решения
выводится информация о том, что введенное ДУ не соответствует выбранному типу.
В случаях верного выбора типа ДУ выполняется следующая последовательность
операций: выявление параметров канонической формы; открытие соответствующего
шаблона решения; заполнение шаблона решения вставками MathML кода; закрытие шаблона; вывод хода решения.
Для решения задачи по заполнению шаблона решения и вывода решения для
конкретного ДУ необходимо создать как сами шаблоны с незаполненными
параметрами, указывающим место для вставки параметров канонической формы, так и
процедуру генерации MathML кода,
используемого для вставки вместо параметра.
Для создания параметрического шаблона используется комбинация HTML и MathML. HTML в
данном случае призван выполнять функции вывода пояснений и выделения из общего
текста поясняемых формул. MathML
позволяет, используя специализированные теги, получить такую форму записи,
которая наиболее просто трактуется пользователем системы.
MathML
формирует свои теги либо в форме префиксной записи, либо в форме инфиксной
записи. Смысл префиксной записи состоит в том, что для оформления используются
специализированные теги, причем сначала выводятся теги с операциями, внутри
которых следуют теги констант и переменных. Однако такой способ записи более сложен,
так как использует для обозначения каждой из лексем широкий спектр тегов.
Второй метод, используемый для отображения, заключается в выводе формулы
последовательно, применяя специфичные теги к каждому из символов или лексем.
Данный способ более предпочтителен, так как для обозначения, например, операции
и вывода её ненаклонным шрифтом используется всего одна пара тегов <mo>операция</mo>. Последовательность тегов
формируется таким образом, что получаемый код MathML соответствует инфиксной форме записи.
Стандарт позволяет использовать и смешанные формы записи выражения, что
позволяет достаточно гибко изобразить такие элементы как степень, деление и
скобки, разделяя выражение на подвыражения, что значительно повышает скорость и
эффективность разработки шаблонов заполнения.
Таким образом, для формирования корректного выбора выражения (частей
канонической формы) бил применен смешанный формат представления тегов MathML.
Процедура формирования тегов по выражению осуществляется за счет обхода
дерева, построенного по параметру канонической формы, и предусматривает
выполнение ряда шагов:
- определение текущего параметра шаблона;
- построение дерева по вставляемому параметру канонической
формы;
- рекурсивный обход дерева с целью генерации вставляемого кода MathML; данный код представляет собой
строку текста, в которой использованы теги MathML и лексемы бинарного дерева (параметра канонической
формы);
- вставка полученной строки вместо указанного параметра.
Рекурсивный обход дерева осуществляется с помощью использования метода,
предназначенного для получения инфиксной формы записи математического выражения
по дереву, т.е. посещение левого поддерева, генерация тега MathML по значению вершины, посещение
правого поддерева.
Рассмотрим основные теги, использованные для генерации вставок MathML:
а) <m:math>выражение</m:math> - данная
пара тегов указывает браузеру, что далее следует объект MathML;
б) <m:mrow>выражение</m:mrow> - данная пара тегов указывает компилятору MathML, что между ними заключено некоторое
математическое выражение;
в) m:mi>переменная</m:mi> - данная пара тегов предназначена для вывода переменных;
сформированная переменная выводится наклонным шрифтом, что позволяет произвести
её выделение среди констант и операций;
г) <m:mo>операция</m:mo> - данный тег используется для вывода знаков, не
требующих специального оформления: сложения, вычитания, умножения, интегралов,
тригонометрических функций и логарифма;
д) <m:mn>константа</m:mn> - данный тег предназначен для обозначения символьных и
числовых констант; константа выводится прямым шрифтом, без наклона;
е) <m:mfrac>выражение1 выражение2</m:mfrac> - указывает
компилятору и специализированным шаблонам оформления, что далее идет два
выражения для формирования дроби следующего вида 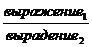 ;
;
ж) <m:mfenced>выражение</m:mfenced> - данная пара указывает компилятору и
специализированным шаблонам оформления о необходимости взятия выражения в
круглые скобки;
з) <m:msub>выражение1 выражение2</m:msub> - данная пара тегов
позволяет вывести выражение1 в степени выражениие2 в следующем общем виде 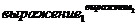 ;<m:msup></m:msup> - данная пара тегов позволяет формировать нижние
индексы.
;<m:msup></m:msup> - данная пара тегов позволяет формировать нижние
индексы.
Блок-схема алгоритма заполнения шаблона представлена на рисунке 8.

Рисунок 8 - Блок-схема алгоритма заполнения шаблона решения ДУ
3.3.5 Модуль генерации тестовых заданий
Данный модуль позволяет автоматически сгенерировать задачу для решения на
распознавание типа ДУ, его канонической формы, параметров канонической формы и
указание метода решения. Преимуществами использования данного модуля по
сравнению с использованием базы заданий заключается в том, что:
- контрольное тестирование может осуществляться с
использованием неограниченного числа заданий;
- позволяет обеспечить гибкость тестирования, невозможность
списывания за счет невозможности точного повторения заданий;
- облегчает работу преподавателя при подготовке тестовых
заданий, так как необходимость их создания отпадает;
- пользователю доступно для ознакомления неограниченное число
случайным образом сгенерированных заданий, что приводит к лучшему усвоению
материала в ходе тренинга.
Модуль генерации позволяет составить ДУ в соответствии с выбираемым шаблоном
генерации задания. Данный модуль выполняет также работу по созданию неверных
ответов для параметров канонических форм, используемых при проведении
контрольного тестирования.
Таким образом, данный модуль использует для генерации тестовых заданий
следующие две части:
- подмодуль генерации ДУ;
- подмодуль генерации неверных параметров канонических форм.
Рассмотрим основные операции и принципы, заложенные в работу данных
частей описываемого модуля.
Для генерации тестовых зданий на выполнение используется принцип, сходный
с работой автоматной грамматики. В основу данного принципа положено то
утверждение, что, имея набор правил автоматной грамматики и начальный
нетерминал, можно привести выражение к виду, который будет соответствовать тому
или иному выражению, принадлежащему исходному языку. В качестве языка в данном
случае подразумевается множество дифференциальных уравнений первого и второго
порядка. Начальный нетерминал - это строка, указывающая на то, что необходимо
произвести генерацию ДУ. Правила представляют набор функций следования и
позволяют производить разложение начального нетерминала, путем замены
нетерминальных символов грамматики на другие последовательности, состоящие из
нетерминалов и/или терминалов. Множество терминальных символов определяет
функции, операции и константы, позволяющие сформировать математическое
выражение, а в случае использования разработанных правил и дифференциальное
уравнение.
Таким образом, необходимо разработать автоматную грамматику, позволяющую
производить генерацию ДУ первого и второго порядка с записью его в канонической
форме. Основными правилами данной грамматики являются правила приведенные в
таблице 4.
Таблица 4 - Исходные правила генерации тестовых зданий
|
№ правила
|
Форма правила
|
|
1
|
<ДУ> ® <первого порядка> | <второго порядка>
|
|
2
|
<первого порядка> ® y' = <выражение>
|
|
3
|
<второго порядка> ® y'' = <выражение>
|
|
4
|
<выражение> ® <выражение> <бинарная операция> <выражение>
|
|
5
|
<выражение> ® (<выражение>)
|
|
6
|
<выражение>® <унарная операция> (<выражение>)
|
|
7
|
<выражение>® <константа>
|
|
8
|
<выражение>®<переменные первого порядка>
|
|
9
|
<выражение>® <переменные второго порядка>
|
|
10
|
<переменные первого
порядка>® x | y
|
|
11
|
<переменные второго
порядка> ® x | y | y’
|
|
12
|
<бинарная операция> ® + | - | * | / | ^
|
|
13
|
<унарная операция> ® sin | cos | tg | asin| acos | atan | ln
|
|
14
|
<константа> ® CONST
|
Однако при решении поставленной задачи использование описанных правил
приводит к генерации таких ДУ, которые не изучаются в рамках дисциплины, так
как количество классов в общем случае значительно превышает тот базис знаний,
который студенты получают в высших учебных заведениях. Поэтому приведенная выше
автоматная грамматика не может быть использована в чистом виде для генерации
тестовых заданий и требует преобразования, следствием которого будет автоматная
грамматика, генерирующая ДУ, попадающее хотя бы в один их изучаемых типов.
Это преобразование исходной автоматной грамматики позволяет прийти к
системе правил приведенной в таблице5, удовлетворяющей описанным ограничениям.
Таблица 5 - Результирующие правила генерации тестовых заданий
|
№
|
Форма правила
|
Назначение
|
|
1
|
<ДУ> ® <I порядка> | <II порядка>
|
начальный нетерминал
|
|
2
|
<I
порядка> ® y' = <EXP1>
|
ДУ первого порядка
|
|
3
|
<II
порядка> ® y'' = <EXP2>
|
ДУ второго порядка
|
|
4
|
<EXP1> ® (<EXPX>)<OP2>(<EXPY>)
|
ДУ I порядка с
раздел. переменными
|
|
5
|
<EXP1>
®(< EXPX >)*y<OP1><EXPX>
|
ДУ I порядка
линейное
|
|
6
|
<EXP1>
® (<EXPX>)*y<OP1>(<EXPX>)*y^<CONST>
|
ДУ I порядка
Бернулли
|
|
7
|
<EXP1>
® (<CONST>*x< OP1><
CONST >*y)/ /(< CONST> *x <OP1>
<CONST >*y)
|
однородное ДУ I порядка
|
|
8
|
<EXP2> ® < EXPX>
|
ДУ II порядка
простейшее
|
|
9
|
<EXP2>
®<CONST>*x<OP1><CONST><OP1><CONST>*
*y'<OP1> <CONST >
|
ДУ II порядка не
сод. явно «y»
|
|
10
|
<EXP2>
® < CONST >*y'< OP1>C<OP1><
CONST >* *y<OP1>< CONST >
|
ДУ II порядка не
сод. явно «x»
|
|
11
|
<EXP2>
® < CONST >*y'<OP1><CONST>*y
|
ЛОДУ II
порядка с постоянными коэффициентами
|
|
12
|
<EXP2>
® < CONST>*y'<OP1><
CONST >*y<OP1>< CONST >*x<OP1><
CONST >
|
ЛНДУ II
порядка с постоянными коэффициентами
|
|
13
|
<EXP2>
® (<CONST>*x<OP1><CONST>)*y'<OP1>(<
CONST>*x<OP1>< CONST>) *y
|
ЛОДУ II
порядка с переменными коэффициентами
|
|
14
|
<EXP2>
® (<CONST>*x<OP1><CONST>)*y'<OP1>(
<CONST> * x <OP1> <CONST>)*y<OP1><CONST>*
*x<OP1><CONST>
|
ЛНДУ II
порядка с переменными коэффициентами
|
|
15
|
<EXPX> ®<CONST>*x<OP1><CONST>
|
выражение от «x»
|
|
16
|
<EXPX> ®x<OP><CONST>
|
|
|
17
|
<EXPX> ®<UO>(<EXPX>)
|
|
|
18
|
<EXPY> ®<CONST>*y<OP1><CONST>
|
выражение от «y»
|
|
19
|
<EXPY> ®y<OP><CONST>
|
|
|
20
|
<EXPY> ®<UO>(<EXPY>)
|
|
|
21
|
<UO>
® sin | cos | tg | asin| acos | atan | ln
|
тригонометрическая/логарифмическая
функция
|
|
22
|
<OP> ® <OP1>|
<OP2> | <OP3>
|
бинарная операция
|
|
23
|
<OP1>
® + | -
|
«+» или «-»
|
|
24
|
<OP2>
® * | /
|
«*» или «/»
|
|
25
|
<OP3>
® ^
|
возведение в степень
|
|
26
|
<CONST>® CONST
|
генерация константы
|
В данной таблице введены дополнительные обозначения нетерминалов, т.е.
значений между треугольными скобками. Расшифровка обозначений нетерминалов
приведена в таблице 6.
Таблица 6 - Расшифровка обозначений нетерминалов
|
Нетерминале
|
Расшифровка
|
|
ДУ
|
дифференциальное уравнение
|
|
EXP1
|
правая часть ДУ первого
порядка;
|
|
EXP2
|
правая часть ДУ второго
порядка;
|
|
EXPX
|
функция от переменной «х»;
|
|
EXPY
|
функция от переменной «y»;
|
|
UO
|
унарная операция;
|
|
OP
|
бинарная операция (любая);
|
|
OP1
|
бинарная операция «+» или
«-»;
|
|
OP2
|
бинарная операция «*» или
«/»;
|
|
OP3
|
бинарная операция «^».
|
|
CONST
|
константа
|
Однако прямое использование данного метода приводит к достаточно сложным
выражениям, неоднозначно трактуемым при автоматическом определении типа.
Уменьшение количества вложенности нетерминалов до трех уровней с начального
нетерминала позволяет избежать ошибок работы модуля автоматического
распознавания типа ДУ.
Использование данной автоматной грамматики с наложенными ограничениями
позволяет сгенерировать ДУ при условии, что задан алгоритм выбора правил для
генерации. Для выбора правил генерации используется генератор случайных чисел C++ Builder random.
Алгоритм работы модуля для выбора правил осуществляется следующими
этапами:
- генерация порядка ДУ; так как порядков всего два, то вероятность
генерации ДУ первого порядка составляет 50 процентов, оставшиеся 50 процентов
сгенерированных выражений относятся к дифференциальным уравнениям второго
порядка;
- в соответствии с порядком ДУ выбирается тип канонической
формы для генерации; вероятность генерации каждого из типов ДУ второго порядка
составляет 1/8 из общего числа генерируемых дифференциальных уравнений, а
вероятность генерации ДУ каждого из типов второго порядка 1/14 из общего числа
генерируемых дифференциальных уравнений;
- выполнение процедуры заполнения правил EXPX и EXPY если таковые имеются;
- последовательно заполняются правила OP, OP1, OP2, OP3, UO, для генерации используемых операций, при выборе правил с
несколькими операциями используется генерация числового значения указывающего
на подставляемую операцию; например, при замене нетерминала OP1 возможен вариант выбора либо операции «сложение»,
обозначаемой генерируемым числом 1, или операции «вычитание» - 2;
- генерируются константы для замены нетерминалов CONST.
Полученное выражение последовательно из каждой функции замены
возвращается в процедуру, вызвавшую данную. В конце работы модуля на выходе
получаем строку, содержащую сгенерированное ДУ, тип которого может быть
определен модулем распознавания типа ДУ. Таким образом, сгенерированные задания
соответствуют только тем типам дифференциальных уравнений, которые изучаются в
рамках курса, а, следовательно, могут быть использованы как для функций
тренинга, так и в целях проведения контрольного тестирования.
Второй частью данного модуля является генерация неверных ответов для
выполнения в рамках тестирования задачи определения параметров канонической
формы. Особенность создания неверных вариантов состоит в том, что если
генерировать неверные варианты ответов использованием алгоритма генерации
дифференциальных уравнений, то значительно упрощается задача для студента, так
как она легко решается методом исключения. Для проведения адекватного
тестирования на задачу выделения параметров канонической формы необходимо таким
образом генерировать предлагаемые ответы, чтобы решение не являлось
элементарным. Для данный целей предлагается следующий набор действий:
а) выбор того или иного параметра канонической формы;
б) преобразование данного параметра путем изменения всех знаков на
противоположенные;
в) преобразование самого левого знака на противоположенный;
г) сокращение выражения отбрасыванием одной из его частей.
Данные преобразования позволяют сгенерировать неверные ответы, сходные с
теми выражениями, которые присутствуют в дифференциальном уравнении, выданном
для решения. В общем случае при тестировании пользователю предлагается четыре
варианта параметров, а также списки с перечислением специализированных
обозначений параметров канонических форм, приводимых в теории. При этом
максимально возможное количество параметров три (соответствует неоднородному ДУ
второго порядка), а минимальное количество параметров один (для простейших
дифференциальных уравнений второго порядка). Следовательно, для генерации
потребуется только три варианта генерации ответов, и поэтому предлагаемых
способов генерации неверного ответа будет достаточно для полного заполнения
ответов, предоставляемых на выбор.
3.3.6 Модуль проверки тестовых заданий
Основанием для модуля проверки задания служит результат, получаемый в
ходе работы модуля определения типа ДУ. Так как каждому типу ДУ можно поставить
в соответствие его каноническую форму и метод решения, то процедура проверки
строится именно на сопоставлении. Такой подход позволяет значительно снизить
сложности, связанные с определением метода решения и определения канонической
формы ДУ, приведенного в задании.
Для определения правильности введенного ответа на задание «определить тип
ДУ» установлено, что каждый тип ДУ имеет свой собственный индекс в массиве
ответов. Производя выбор варианта ответа, пользователь задает программе
значение данного элемента массива; используя процедуру адресного доступа к
элементу массива, можно получить значение, указывающее на принадлежность или не
принадлежность к данному типу. В случае правильного ответа пользователю
начисляется один балл, а результат фиксируется в протоколе тестирования. В
противном случае балл не начисляется и протокол тестирования остается
неизменным.
Используя входной массив значений, характеризующий принадлежность ДУ к
некоторому типу, можно составить условия соответствия номера выбранной канонической
формы и типа ДУ. Данные соответствия устанавливаются согласно таблице 2.
В случае, если пользователь выбирает такую каноническую форму, которая
соответствует типу с признаком истинности принадлежности, то ответ пользователя
считается верным; за верный ответ пользователю начисляется балл; сумма баллов,
полученная в ходе контрольного тестирования, дает оценку за выполнения теста.
При правильном выборе канонической формы пользователю, кроме начисления
дополнительного балла, предоставляется возможность указать параметры
канонической формы.
Для решения задачи, связанной с выбором параметров канонической формы,
необходимо воспользоваться модулем определения параметров канонической формы и
информацией о типе ДУ. Также при генерации тестового задания данного вида
используется процедура генерации неверных ответов. Сложность прямого введения
параметров канонической формы заключается в том, что ответ пользователя может
быть неоднозначным, и добиться решения данной задачи прямыми способами
сравнения строк невозможно, так как пользователь может ввести выражение,
например, переставив слагаемые. Эта особенность значительно усложняет создание
программного решения. Поэтому использовался метод, при котором варианты ответов
предоставляются пользователю заранее. Такой метод в совокупности с
использованием ниспадающих списков, хранящих обозначения параметров
канонической формы, позволяет добиться снижения вероятности угадывания верного
ответа. Так как в общем случае количество вариантов обозначений равно 10,
количество ответов, доступных для выбора равно 4, а количество верных ответов
равно 1, то вероятность угадывания верного ответа в данном случае составит
порядка 2,5 процентов. Для сравнения выбранной формы используется массив
соответствия используемой для вывода параметра метке и индекса выбранного в
ниспадающем списке обозначения данного параметра. При верном указании
количество баллов пользователя увеличивается на единицу, верный ответ
фиксируется в протоколе, и пользователю предоставляется возможность выбора метода
решения ДУ.
На практике при решении дифференциальных уравнений студент должен
корректно выбирать метод решения данного ДУ. Как упоминалось выше, метод
решения определяется исходя из типа ДУ. Для выполнения автоматической проверки
корректности выбора метода решения используется таблица соответствия типа ДУ и
методов решения (таблица 3).
Проверка соответствия аналогична процедуре, выполняемой при проверке
соответствия типа решения его канонической форме.
4. Экономическое обоснование
Программный продукт предназначен для внедрения в учебный процесс МГТУ для
студентов первого, второго курса технических специальностей различных форм
обучения. Приложение рекомендуется при изучении студентами темы «Обыкновенные
ДУ» в рамках дисциплины «Высшая математика» или «Математический анализ».
Разработка приложения была инициирована заказчиком в лице кафедры высшей
математики и программного обеспечения ЭВМ МГТУ. Руководитель (аналитик) стоит
во главе проекта. Он осуществляет постановку задачи и распределяет время.
Программист выполняет поставленные задачи, используя наиболее эффективные
алгоритмы и вычислительные модели, вносит дополнения и корректировки в
поставленные задачи.
Календарный план разработки программного продукта.
Для максимизации темпов разработки и повышения качества программного
обеспечения, а также для отражения основных фаз жизненного цикла программного
обеспечения используется календарный план разработки.
Жизненный цикл программы - это весь цикл от принятия решения о проведении
разработок до полного отказа конечного пользователя от применения данного
программного продукта; этот цикл включает в себя:
- этап работы над программным продуктом (составил 6 месяцев);
- этап введения программного продукта;
- этап зрелости: полный переход к автоматизированной системе;
- этап упадка: появление новых технологий и моральное
устаревание программного продукта.

Рисунок 9 - Календарный план разработки
информационный технология программа математика
На рисунке 9 представлен календарный план разработки дипломного ПП в
днях, где:
- предпроектное исследование (1),
- техническое задание (2)
- разработка и отладка программного продукта (3),
- тестирование (4),
- техническая отчетность (5),
- сдача темы (6).
Оценка стоимости программного продукта.
Основными источниками затрат при разработке данного программного
комплекса являются капитальные предпроизводственные затраты (таблица 7),
которые в некоторых рамках могут быть учтены и минимизированы. Расчет
осуществляется по статьям расходов. Данные по окладам работающего персонала и
процентные составляющие (таблица 8), используемые в этой части, были взяты
исходя из рыночной конъюнктуры.
Таблица 7 - Затраты на расходные материалы
|
№
|
Наименование материала
|
расход, шт.
|
цена, руб./шт.
|
сумма, руб.
|
|
1
|
Аппаратное обеспечение
|
1
|
20 500
|
20 500
|
|
2
|
операционная система
Windows XP SP2
|
1
|
4239,31
|
4239,31
|
|
3
|
среда разработки Builder
C++ v.6.0.
|
1
|
10653,8
|
10653,8
|
|
4
|
Office 2003 Box
For teacher and Student
|
1
|
3010
|
3010
|
|
5
|
Internet, ADSL
|
3
|
320
|
960
|
|
6
|
Прочее (бумага,
диски, картриджи)
|
--
|
--
|
790
|
|
Итого
|
40153,11
|
Таблица 8 - Основная заработная плата разработчиков программного
обеспечения
|
№
|
наименование этапа
|
исполнитель
|
Трудо-емкость, чел.дней
|
Трудо-емкость, чел.мес.
|
оклад, руб.
|
затраты
|
|
1
|
подготовительный
|
программист
|
14
|
0,67
|
4275
|
6633,98
|
|
2
|
техническое задание
|
руководитель
|
8
|
0,39
|
5200
|
4611,08
|
|
3
|
основной
|
программист
|
48
|
2,31
|
4275
|
22745,06
|
|
4
|
тестирование
|
программист
|
14
|
0,67
|
4275
|
6633,98
|
|
5
|
технический отчет
|
программист
|
22
|
1,06
|
4275
|
10424,82
|
|
6
|
сдача темы
|
руководитель
|
8
|
0,39
|
5200
|
4611,08
|
|
|
программист
|
8
|
0,39
|
4275
|
3790,84
|
|
Итого
|
59450,84
|
Дополнительная заработная плата разработчиков программного продукта
составляет 20 % от основной заработной платы:
,2 ´ 59450,84
= 11890,17 руб.
Фонд заработной платы представляет собой сумму основной и дополнительной
заработной платы:
,84+ 11890,17 = 71341,01 руб.
Отчисления на единый социальный налог составляет 26 % от фонда оплаты
труда. Тут же учтем еще и страхование жизни 1%:
,27 ´ 71341,01
= 19262,07325 руб.
Организации, занимающиеся разработкой и внедрением программного
обеспечения, имеют коэффициент накладных расходов, как правило, равным 1,2.
Поэтому накладные расходы составляют 150 % от величины основной заработной
платы:
,5 ´ 59450,84
= 89176,27 руб.
Прочие расходы включают расходы на машинное время (порядка 4-ёх месяцев
на разработку, отладку и тестирование программного продукта: 480 часов
стоимостью 10 руб./час):
´ 10 = 4800 руб.
Таблица 9 - Итоговые затраты
|
№
|
наименование статей
расхода
|
затраты, руб.
|
|
1
|
расходные материалы
|
40153,11
|
|
2
|
основная заработная плата
разработчиков
|
59450,84
|
|
3
|
дополнительная заработная
плата разработчиков
|
11890,17
|
|
4
|
отчисления на единый соц.
Налог, 26%
|
19262,07
|
|
5
|
накладные расходы
|
89176,27
|
|
6
|
прочие расходы
|
4800
|
|
Итого
|
224732,46
|
Рассчитаем предполагаемую прибыль.
Заработная плата преподавателя составляет 6 000 рублей в месяц.
Соответственно, за два месяца преподавания темы три преподавателя заработают:
Тогда экономическая эффективность разработанного программного продукта
вычисляется следующим образом:
E = 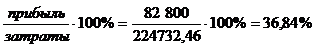 (1)
(1)
Таким образом, разработанный программный продукт позволит:
- Студенту сэкономить время на изучение темы «Дифференциальные
уравнения»
- Сэкономить время преподавателя на подготовку, проверку и
исправление ошибок тестовых заданий, сократить время консультирования
студентов.
5. Охрана труда
Анализ опасных и вредных производственных факторов.
В соответствии с ГОСТ 12.0.003-74 опасные и вредные производственные
факторы по природе действия подразделяются на четыре группы: физические,
химические, биологические и психофизиологические Пользователь персонального
компьютера подвергается следующим опасным и вредным факторам: повышенные уровни
шума; повышенные уровни электромагнитных излучений (радиочастотного и
инфракрасного диапазона); недостаточная освещенность рабочих мест; повышенная
яркость света; неблагоприятные микроклиматические условия; выделения вредных
веществ; психофизиологические факторы (физические перегрузки;
нервно-психические перегрузки: умственное перенапряжение, перенапряжение
анализаторов слуха, зрения, монотонность труда).
Безопасность труда при эксплуатации видеодисплейных
терминалов и персональных электронно-вычислительных машин.
Эксплуатация видеодисплейных терминалов (ВДТ) и персональных
электронно-вычислительных машин (ПЭВМ) определяются СанПиН 2.2.2.542-96
"Гигиенические требования к видеодисплейным терминалам, персональным
электронно-вычислительным машинам и организации работы». Основными требованиями
являются: площадь на одно рабочее место с ВДТ и ПЭВМ должна составлять не менее
6 м2, а объем - не менее 20 м3. Оптимальные параметры
микроклимата для помещений составляют: температура 21-25°С, относительная
влажность воздуха 40-60%, скорость движения воздуха 0,1-0,2 м/с. Уровень шума в
компьютерных классах учебных учреждений не должны превышать 50 дБА.
Освещенность на поверхности стола в зоне размещения рабочего документа должна
быть 300-500 лк. При использовании местного освещения оно не должно создавать
бликов на поверхности экрана и увеличивать освещенность экрана более 300 лк.
Естественное освещение должно обеспечить коэффициент естественной освещенности
(КЕО) не ниже 1,2 %. Экран видеомонитора должен находиться от глаз пользователя
на расстоянии 600-700 мм, но не ближе 500 мм. Уровень глаз при вертикально
расположенном экране ВДТ должен приходиться на центр или 2/3 высоты экрана.
Линия взора должна быть перпендикулярна к центру экрана.
Эргономические требования к рабочему месту пользователя
программного продукта. Рабочий стол: его высота должна составлять 720 мм, оптимальные размеры
рабочей поверхности столешницы - 1600х900 мм. Под столешницей рабочего стола
должно быть свободное пространство для ног. Размеры: по высоте - не менее 600
мм, по ширине - 500 мм.
Рабочий стул: высота должна составлять 400-500 мм, ширина - не менее 400
мм, глубина - не менее 380 мм. Поверхность сидения и спинки должна быть
полумягкой, с нескользящим, неэлектризующим и воздухонепроницаемым покрытием.
На рабочем месте необходимо предусматривать подставку для ног. Ее
размеры: длина - 400 мм, ширина - 350 мм, высота - 150 мм. Угол наклона
подставки - в пределах 0-20 градусов. Она должна иметь рифленое покрытие и
бортик высотой 10 мм по нижнему краю.
Режимы труда и отдыха. Для программного продукта «Обучающая программа
«Дифференциальные уравнения»» применимы требования группы «В» (творческая
работа в режиме диалога с ЭВМ). В зависимости от длительности работы
подразделяются на три категории: первая группа ( длительность работы до 2-х
часов) при 8-ой рабочей смене суммарное время регламентированных перерывов не
менее 30 минут и не менее 70 минут при 12-часовой; вторая группа
(продолжительность работы до 4-х часов) при 8-ой рабочей смене время
регламентированных перерывов не менее 50 минут и не менее 90 минут при
12-часовой; третья группа - длительность работы до 6-х часов, при 8-ой рабочей
смене суммарное время регламентированных перерывов не менее 70 минут и не менее
120 минут при 12-часовой смене.
Продолжительность непрерывной работы с ВДТ без регламентированного
перерыва не должна превышать 2 часов.
Профессиональные пользователи ВДТ и ПЭВМ должны проходить обязательные
предварительные и периодические медицинские осмотры не менее 1 раза в год.
Заключение
В ходе выполнения дипломной работы был разработан программный продукт
«Обучающая программа по теме «Обыкновенные дифференциальные уравнения»»,
предназначенный для методической поддержки средствами ИКТ учебного процесса в
МГТУ по дисциплине «Высшая математика».
Разработка программного продукта состояла из следующих этапов:
- исследование предметной области применения ИКТ в изучении математических
дисциплин, обобщение и описание программного продукта автоматизации решения
задач, связанных с обыкновенными дифференциальными уравнениями;
- проектирование программного продукта;
- разработка программных модулей для задания требуемого
функционала;
- опытная эксплуатация.
На этапе исследования предметной области были:
- определены основные понятия предметной области, связанные с применением
ИКТ при построении обучающих программ, осуществлена классификация обучающих
программ;
- выявлены основные компоненты обучающих программ по
математическим дисциплинам;
- определены основные подходы к проведению тестирования с
использованием электронных учебно-методических ресурсов;
- рассмотрены имеющиеся на рынке программные продукты,
позволяющие осуществлять поддержку учебного процесса по теме.
В результате исследования разработанный программный продукт позволяет
решать широкий спектр задач, связанных с обучением. Этап исследования
предметной области позволил уточнить требования к основным компонентам
разработанного программного продукта, определить подход и методы проведения
тестирования.
Рассмотрение аналогичных программных решений позволяет сделать вывод, что
большинство программных продуктов предназначено для решения сложных
вычислительных задач, связанных с ДУ, при этом в некоторых из них отсутствует
возможность ручного задания ДУ и элементы обучения.
Разработанный ПП содержит элементы новизны, позволяющие:
- осуществлять ввод и распознавание введенного ДУ за счет использования
разработанного модуля лексико-грамматического анализа выражений и равенств;
- автоматизировать решение основных задач предшествующих
получению решения ДУ, с целью проведения тренинга и тестирования;
- производить решение ДУ в символьном виде сведением к
интегралам с пояснением хода решения на основе разработанного метода заполнения
параметризированных шаблонов.
На этапе проектирования решен следующий ряд задач:
- определен набор функциональных требований преподавателя-методиста к
программному продукту;
- составлено техническое задание на выполнение;
- спроектирован интерфейс приложения;
- определены методы распознавания порядка, типа, канонической
формы и её параметров, методов решения ДУ;
- построена функциональная диаграмма программного продукта,
выявлены основные модули, требующие реализации.
К творческим элементам проектирования следует отнести:
- метод рекурсивного синтаксического анализа частей бинарного дерева с
использованием трех уровней уточнения признаков;
- создание логической схемы распознавания 12 типов, отнесенных
к четырем уровням вложенности;
- построение узкоспециализированного лексико-грамматического
анализатора для определения корректности ввода ДУ;
- построение автоматной грамматики с ограничениями для
генерации тестовых заданий.
На этапе разработки:
- осуществлен выбор среды разработки, удовлетворяющей наиболее эффективному
решению поставленной задачи;
- уточнены алгоритмы решения основных задач, связанных с ДУ;
- созданы семь основных программных модулей (модуль
лексико-грамматического анализатора выражения и равенства, модуль определения
типа ДУ, канонической формы и его метода решения, модуль проверки тестовых
заданий, модуль определения параметров канонической формы, модуль решения ДУ I порядка в символьном виде для
заполнения шаблонов и генерации для него MathML вставок по бинарному дереву, модель поддержки и
отображения ЭКЛ, модуля генерации тестовых заданий для тренинга и
тестирования);
- разработаны шаблоны решения ДУ первого порядка для
последующего их заполнения;
- разработана справочная система программного продукта и
руководство пользователя (Приложение Ж).
Итогом проделанной работы является программный продукт «Обучающая
программа по теме «Обыкновенные дифференциальные уравнения» удовлетворяющий
требованиям функциональности.
В ходе разработки проведено модульное тестирование, выявлены наиболее
критичные ошибки и произведено их исправление. А также проведено
экспериментальное тестирование при участии преподавателей-методистов.
Разработанный программный продукт рекомендуется для студентов и курсантов
МГТУ очного или заочного обучения 1-го и 2-го курсов технических
специальностей, изучающих в рамках дисциплины «Высшая математика» или «Математический
анализ» тему «Обыкновенные дифференциальные уравнения».
Список использованных источников
1. Артемов
А., Павлова Н., Сидорова Т. Модульно-рейтинговая система // Высшее образование
в России. - 1999. -№4. -с. 121 - 125.
2. Белоус
Н.В., Войтович И.В., Пархоменко С.А. Модель обучения на основе тестовых заданий
произвольных форм // Образование и виртуальность - 2003. Сборник научных трудов
6-й Международной конференции. - Харьков - Ялта: УАДО, 2003. - с.71.-74.
. Беспалько
В.П. Основы теории педагогических систем. Проблемы и методы
психолого-педагогического обеспечения технических обучающих систем. - Воронеж,
1977, 303с.
. Возженников
А.П. Разработка обучающих программ по высшей математике. - Открытое образование
и информационные технологии: материалы ВНМК, 17-20 октября 2005г., Пенза,
2005г. (стр.62-64).
. Возженников
А.П., Кацуба В.С. Приложение программного обеспечения к процессу обучения. -
Материалы XVII Международной конференции
«Применение новых технологий в образовании», 28 - 29 июня 2006 г. г.Троицк,
Московской области - ГОУ ДПО «Центр новых педагогических технологий» Московской
области, МОО Фонд новых технологий в образовании «Байтик» (стр. 441 - 442).
. Возженников
А.П., Кацуба В.С. Разработка инструментов для создания электронного конспекта лекций
по высшей математике. - Математическое моделирование, численные методы и
комплексы программ: межвузовский сборник статей. СПб, 2006 г. (стр. 10 - 15)
. Гершунский
Б.С. Компьютеризация в сфере образования: проблемы и перспективы. - М.:
Педагогика, 1987. - 264 с.
. Грутовой
А.В., Нелюбин С.В., Строков А.В., Кремнёв М.В., Тверьянович Д.Ю. Использование
программы «Математика» #"526123.files/image045.gif">
Приложение Б
DFD-диаграмма программного средства
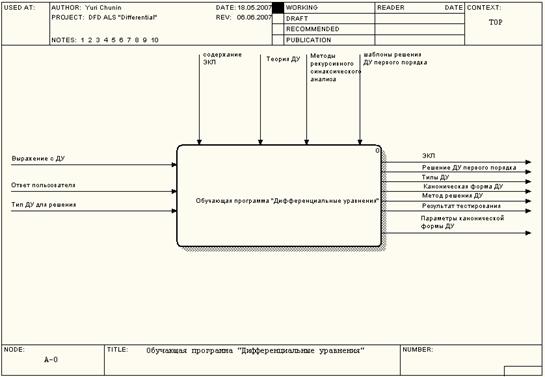

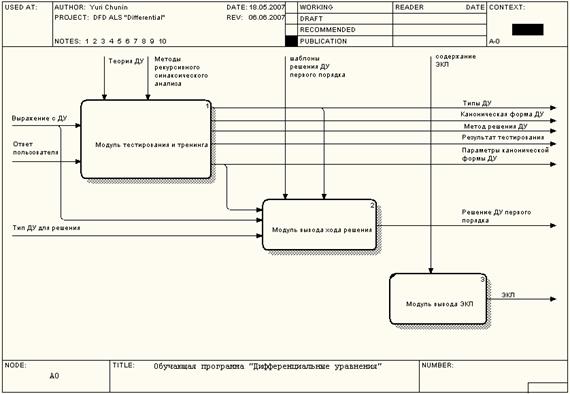

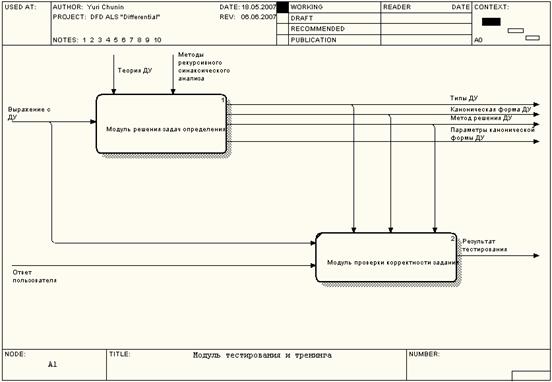

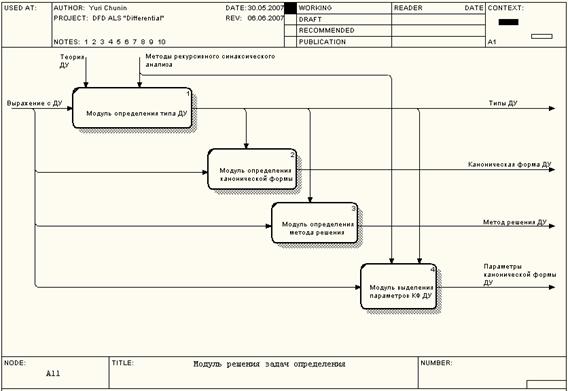

Приложение В
Построение LL(1)-анализатора
Формальное описание с помощью форм Бекуса-Наура.
1. <раздел описаний>::=<переменная порядка> =
<выражение>
2. <переменная порядка>::=y' | y''
. <выражение>::=<выражение><бинарная
операция><выражение>
. <выражение>::=<унарная операция>(<выражение>)
. <выражение>::=(<выражение>)
. <выражение>::=<переменная>
. <выражение>::=<константа>
8. <переменная>::=VARIABLE
9. <константа>::=CONST
10. <бинарная операция>::=SO
11. <унарная операция>::=UO
Множество терминалов/нетерминалов.
Множество нетерминалов
|
Нетерминалы
|
Индекс
|
|
раздел описаний
|
1001
|
|
переменная порядка
|
1002
|
|
Выражение
|
1003
|
|
бинарная операция
|
1004
|
|
унарная операция
|
1005
|
|
переменная
|
1006
|
|
константа
|
1007
|
Множество терминалов
|
ТерминалыИндекс
|
|
|
Пустая цепочка
|
0
|
|
VARIABLE
|
1
|
|
CONST
|
2
|
|
SO
|
3
|
|
UO
|
4
|
|
VARPOW
|
5
|
|
(
|
6
|
|
)
|
7
|
|
=
|
8
|
Правила грамматики
Начальный нетерминал S.
|
1.
|
1001 →
1002 8 1003
|
7.
|
1003 →
1007
|
|
2.
|
1002 → 5
|
8.
|
1006 → 1
|
|
3.
|
1003 →
1003 1004 1003
|
9.
|
1007 → 2
|
|
4.
|
1003 →
1005 6 1003 7
|
10.
|
1004 → 3
|
|
5.
|
1003 → 6
1003 7
|
11.
|
1005 → 4
|
|
6.
|
1003 →
1006
|
|
|
Эквивалентные преобразования грамматики
Цепных правил не имеется, недостижимых нетерминалов не имеется.
Имеется левокурсивное правило 3.
Введем дополнительный нетерминал <доп.1 > - 1008
После преобразований имеем следующие правила грамматики:
. 1001 → 1002 8 10037. 1003 → 1007 1008
. 1002 → 58. 1006 → 1
. 1008 → 1004 1003 10089. 1007 → 2
. 1003 → 1005 6 1003 7 100810. 1004 → 3
. 1003 → 6 1003 7 100811. 1005 → 4
. 1003 → 1006 100812. 1008 → 0
Построение модели лексического анализатора
Множество допустимых для конструкции слов разбито на классы лексем.
Ключевые слова: =
Разделители (, )
Константы: целые, действительные
Переменные: x,
y
Переменные порядка: y', y'', y'''.
Внутренние таблицы лексического анализатора:
1) таблица лексем «ключевые слова»
2) таблица лексем разделителей
3) лексема «константа»
4) лексема «переменная»
5) лексема «унарная операция»
6) лексема «бинарная операция»
6) лексема «переменные степени»
Построение таблиц лексического анализатора.
Лексема «константа».
1. <константа> → n <последовательность цифр><десятичная часть>
2. <последовательность цифр> → n <последовательность цифр>
3. <последовательность цифр> →
ε
4. <десятичная часть> →
<разделитель><последовательность цифр>
5. <десятичная часть> →
ε
6. <разделитель> →, |.
Обозначения:
A -
<константа>, C- <десятичная
часть>,
B -
<последовательность цифр>, E - ошибка.
Таблица переходов лексемы «константа»
|
|
n
|
,
|
.
|
ε
|
кон. цеп
|
|
A
|
B
|
E
|
E
|
E
|
0
|
|
B
|
B
|
E
|
E
|
E
|
1
|
|
C
|
E
|
B
|
B
|
E
|
0
|
|
E
|
E
|
E
|
E
|
E
|
0
|
Лексема «бинарная операция».
|
Лексема
|
Назначение
|
|
+
|
сложение
|
|
-
|
вычитание
|
|
*
|
умножение
|
|
/
|
деление
|
|
^
|
возведение в степень
|
Лексема «унарная операция»
Таблица переходов*
|
s
|
c
|
t
|
a
|
l
|
i
|
o
|
g
|
n
|
кон.цеп.
|
|
s
|
|
|
|
|
|
si
|
|
|
|
0
|
|
c
|
|
|
|
|
|
|
co
|
|
|
0
|
|
t
|
|
|
|
|
|
|
|
tg
|
|
0
|
|
a
|
as
|
ac
|
at
|
|
|
|
|
|
|
0
|
|
l
|
|
|
|
|
|
|
|
|
ln
|
0
|
|
si
|
|
|
|
|
|
|
|
|
sin
|
0
|
|
co
|
cos
|
|
|
|
|
|
|
|
|
0
|
|
tg
|
|
|
|
|
|
|
|
|
|
1
|
|
as
|
|
|
|
|
|
asi
|
|
|
|
0
|
|
ac
|
|
|
|
|
|
|
aco
|
|
|
0
|
|
at
|
|
|
|
ata
|
|
|
|
|
|
0
|
|
ln
|
|
|
|
|
|
|
|
|
|
1
|
|
sin
|
|
|
|
|
|
|
|
|
|
1
|
|
cos
|
|
|
|
|
|
|
|
|
|
1
|
|
ata
|
|
|
|
|
|
|
|
|
atan
|
0
|
|
aco
|
acos
|
|
|
|
|
|
|
|
|
0
|
|
asi
|
|
|
|
|
|
|
|
|
asin
|
0
|
|
atan
|
|
|
|
|
|
|
|
|
|
1
|
|
acos
|
|
|
|
|
|
|
|
|
|
1
|
|
asin
|
|
|
|
|
|
|
|
|
|
1
|
*Пустая ячейка в таблице соответствует обозначению ошибки.
Тестовые данные для проверки.
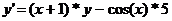
Таблица дескрипторов.
|
лексема
|
обозначение
|
код
|
|
y'
|
VARPOW
|
5
|
|
=
|
=
|
8
|
|
(
|
(
|
6
|
|
x
|
VARIABLE
|
1
|
|
+
|
SO
|
3
|
|
1
|
CONST
|
2
|
|
)
|
)
|
7
|
|
*
|
*
|
3
|
|
y
|
VARIABLE
|
1
|
|
-
|
-
|
3
|
UO
|
4
|
|
(
|
(
|
6
|
|
x
|
VARIABLE
|
1
|
|
)
|
)
|
7
|
|
*
|
SO
|
3
|
|
5
|
CONST
|
2
|
Дескрипторный текст:
8 6 1 3 2 7 3 1 3 4 6 1 7 3 2
Приведение грамматики к виду LL(1)-грамматики.
ВЫБОР(1) = {5}
ВЫБОР(2)= {5}
ВЫБОР(3)= {3}
ВЫБОР(4)= {4}
ВЫБОР(5)= {6}
ВЫБОР(6)= {1}
ВЫБОР(7)= {2}
ВЫБОР(8)= {1}
ВЫБОР(9)= {2}
ВЫБОР(10)= {3}
ВЫБОР(11)= {4}
ВЫБОР(12)= {1,2,7}
ВЫБОР(4)∩ВЫБОР(6) ∩ВЫБОР(1) ∩ВЫБОР(2)= {4}∩{6}∩{1}∩{2}=Æ
ВЫБОР(3) ∩ВЫБОР(12)={3}∩{1,2,7}=Æ
Таблица переходов.
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
-|
|
|
1001
|
|
|
|
|
1
|
|
|
|
|
|
1002
|
|
|
|
|
2
|
|
|
|
|
|
1003
|
6
|
7
|
|
4
|
|
5
|
|
|
|
|
1004
|
|
|
2
|
|
|
|
|
|
|
|
1005
|
|
|
|
2
|
|
|
|
|
|
|
1006
|
2
|
|
|
|
|
|
|
|
|
|
1007
|
|
2
|
|
|
|
|
|
|
|
|
1008
|
8
|
8
|
3
|
|
|
|
8
|
|
|
|
6
|
|
|
|
|
|
2
|
|
|
|
|
7
|
|
|
|
|
|
|
2
|
|
|
|
8
|
|
|
|
|
|
|
|
2
|
|
|
▼
|
|
|
|
|
|
|
|
|
Доп.
|
Обозначения значений ячеек таблицы переходов.
1. ЗАМЕН(1003 8 1002)
2. ВЫТОЛК; СДВИГ
. ЗАМЕН (1008 1003 1004); ДЕРЖ
. ЗАМЕН (1008 7 1003 6 1005); ДЕРЖ
. ЗАМЕН (1008 7 1003); СДВИГ
. ЗАМЕН(1008 1006); ДЕРЖ
. ЗАМЕН(1008 1007);ДЕРЖ
. ВЫТОЛК; ДЕРЖ.
Приложение Г
Признаки для определения типов ДУ первого порядка
|
Уровень
|
Типы дифференциальных
уравнений первого порядка
|
|
С разделяющимися
переменными
|
Линейные
|
Бернулли
|
Однородные
|
|
Нулевой уровень
|
Правая часть КФ ДУ содержит
две функции f(x) и g(y), объединенные знаком умножить или делить
|
Зависимая переменная «y»
присутствует в виде умножения на некоторую константу или выражение с
независимой переменной «x» (наличие линейной части)
|
Зависимая переменная «y»
присутствует в виде умножения на некоторую константу или выражение с
независимой переменной «x» (наличие линейной части)
|
Осуществление замены в
дереве всех переменных «x» и «y» на произведение «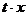 »
или « »
или «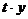 » соответственно не изменяет значения правой части » соответственно не изменяет значения правой части
|
|
Первый уровень уточнения
|
ДУ содержит в правой части
канонической формы только одну переменную
|
Может присутствовать
аддитивная часть с зависимостью только от переменной «х»
|
Должна присутствовать
аддитивная часть являющаяся произведением функции только от переменной «x»
и функции «yС», где
С - константа не равная 1.
|
Значения правой части
исходного ДУ и с произведенной заменой на наборе из 100 сгенерированных
случайным образом значений, принадлежащих области определения ДУ, должны быть
равны для каждого из 100 случаев генерации.
|
|
Второй уровень уточнения
|
|
Зависимая переменная «y»
не может быть использована при вычислении логарифмических, тригонометрических
и степенных функций
|
Зависимая переменная «y»
не может быть использована при вычислении логарифмических и тригонометрических
функций
|
|
Приложение Д
Признаки для определения типов ДУ второго порядка
|
Уровень
|
Типы дифференциальных
уравнений второго порядка
|
|
Решаемые понижением порядка
|
Линейные
|
|
Простейшие
|
Не содержат «y»
в явном виде
|
Не содержат «x»
в явном виде
|
Однородные
|
Неоднородные
|
|
Нулевой уровень
|
Правая часть ДУ состоит из
функции зависящей только от независимой переменной «x»
|
Содержит в левой части ДУ
производную второго порядка.
|
Содержит в левой части
канонической формы ДУ вторую производную
|
Содержат линейную зависимость
переменной «y» и производной первого порядка.
|
Содержат линейную
зависимость переменной «y» и производной первого порядка (признаки
однородного).
|
|
Первый уровень
|
|
Содержит в правой части
только зависимость от переменной «x» и производной первого порядка.
|
Содержит в правой части
канонической формы зависимость только от переменной «y» и
производные первого порядка
|
Коэффициенты линейных
зависимостей могут быть постоянными (с постоянными коэффициентами) или
являться зависимостью от переменной «x» (с непостоянными
коэффициентами)
|
Должна присутствовать
аддитивная часть, зависящая только от переменной «x». Выделенная
правая часть проверяется на наличие или отсутствие специального вида.
|
Приложение Е
Руководство пользователя
Системные требования
- процессор класса Pentium II или выше (рекомендуется Pentium III);
- оперативная память: 32MB (рекомендуется 64MB и более);
- 2MB свободного дискового пространства;
- SVGA монитор (1024x768);
- мышь;
- операционная система Microsoft Windows 98, ME, 2000, XP;
- установленный MS Internet Explorer 6.0 (или выше);
- установленный для IE plug-in Math Player.
2 Установка
Установка программного продукта осуществляется запуском инсталляционного
файла setup.exe. В ходе установки производится копирование рабочих
каталогов программы и исполняемого файла в пользовательский директорий с
сохранением структуры хранения файлов необходимых для работы программы.
Дистрибутив программного продукта представляет собой следующий набор
файлов и каталогов:
- parserDiff.exe - исполняемый файл программы;
- папка lect содержит
теоретические данные в формате HTML,
математические формулы и рисунки в формате GIF;
- папка xmltemplates содержит каскадные таблицы стилей
для оформления выражений MathML;
- папка dsolvetemplate
хранит шаблоны оформления решений в виде HTML с инкапсулированными вставками MathML шаблонов для вывода хода решения
заданного ДУ.
Программа может работать в трех режимах:
- режим обучения, в котором пользователю доступны возможности
просмотра ЭКЛ, включающего основные положения теории дифференциальных
уравнений;
- режим тренинга и тестирования позволяет пользователю путем
ввода любого ДУ, с использованием набора заданных функций, самостоятельно
решать ДУ, осуществляя самоконтроль полученных знаний, а также предоставляет
возможность прохождения контрольного тестирования с выводом результата;
- экспериментальная часть предоставляет возможности вывода
подробного алгоритма решения ДУ введенного пользователем.
Программный продукт представляет собой многооконное приложение. Главное окно
программы позволяет открывать дочерние окна позволяющие задействовать различную
функциональность.
Рисунок Е.1 - Основное окно программы
Рисунок Е.1 демонстрирует главное окно программы. «Главное меню»
программы позволяет открывать дочерние окна, осуществлять выход из программы и
вызывать справку (1). Действия по открытию окон программ могут выполняться как
комбинациями клавиш, так и с помощью панели «Быстрый доступ» (2). Остальную
часть главного окна занимает рабочая область для отображения дочерних окон
программы (3).
Панель «Быстрый доступ» имеет в наличии три основные кнопки позволяющие
открыть дочерние окна:
- «Электронный конспект лекций»;
- «Тренинг и тестирование»;
- «Решение ДУ первого порядка».
3 Режим обучения
Режим обучения предполагает использование ЭКЛ. Для вызова окна
отображающего конспект лекций, необходимо воспользоваться кнопкой «Конспект
лекций» на панели «Быстрый доступ».
Рисунок Е.2 - Иллюстрация работы ЭКЛ
Просмотр конспекта лекций осуществляется аналогично использованию
браузеров с помощью перехода по страницам, формулам, определениям
использованием гиперссылок на элементы электронного конспекта лекций.
4. Режим тренинга и тестирования
Режим тренинга и тестирования осуществляется в рамках единого окна,
предназначенного для осуществления функций тренинга (с выводом пояснений
решенной задачи) и тестирования (с ведением протокола тестирования). Вызов окна
«Тренинг и тестирование» осуществляется нажатием кнопки «Тест» на панели
«Быстрый доступ».
Интерфейс окна «Тренинга и тестирования» состоит из следующих составных
частей:
- меню выбора режима работы (1);
- область отображения задания или ввода ДУ (2);
- рабочая область для выбора типа (3), вида канонической формы
(5), метода решения ДУ (6) для всех режимов и области пояснения решений для
режима работы «Тренинг» (4);
- область отображения протокола тестирования (4);
- область управления ходом тренинга и тестирования, включающая
кнопки «Генерация задания» и «Показать ответы»(5).
Рабочая область окна приложения состоит из четырех основных частей:
- вывода верных типов решения и указания ответа
пользователя(3);
- вывода верных канонических форм ДУ и их указания в случае
тестирования пользователем (5);
- вывода верных ответов к задаче определения метода решения и
возможностей указания пользователем ответов на указанную задачу (6);
- поле вывода параметров канонической формы в режиме тренинга
при наведении на каноническую форму указателя мыши (4).
В процессе работы в режиме тренинга пользователь используя функции,
переменные, операции и константы (таблица Ж.1) формирует ДУ, нажимая кнопку
показать ответы на экране розовым цветом обозначаются тип, каноническая форма и
метод решения характерный для заданного ДУ. Наведение на подсвеченную
каноническую форму позволяет увидеть параметры канонической формы и тем самым
понять принцип решения задачи.
В режиме тренинга пользователь может кроме самостоятельного задания ДУ
сгенерировать новое ДУ нажатием кнопки «Следующее ДУ».
В таблице Е.1 приведены применимые для ввода операции, функции и символы
которые называются в программе лексемами.
Таблица Е.1 - Допустимые лексемы для ввода ДУ
|
Символы/
операции/функции
|
Назначение
|
|
(
|
Открывающая скобка
|
|
)
|
Закрывающая скобка
|
|
=
|
знак равенства
|
|
+
|
бинарная операция
«сложение»
|
|
-
|
бинарная операция
«вычитание»
|
|
*
|
бинарная операция
«умножение»
|
|
/
|
бинарная операция «деление»
|
|
^
|
бинарная операция
возведения в степень
|
|
cos
|
тригонометрическая функция
«косинус»
|
|
sin
|
тригонометрическая функция
«синус»
|
|
tg
|
тригонометрическая функция
«тангенс»
|
|
ln
|
натуральный логарифм
|
|
atan
|
обратная тригонометрическая
функция «тангенс»
|
|
acos
|
обратная тригонометрическая
функция «косинус»
|
|
asin
|
обратная тригонометрическая
функция «синус»
|
|
0-9
|
числа для ввода констант
|
|
«,» или «.»
|
разделитель целой и дробной
части константы
|
Кроме перечисленных лексем (операции и функций) допустимо использование в
программе переменных «x», «y», «y'», «y''», «y'''».
Для переключения в режим контрольного тестирования необходимо в главном
меню окна «Тренинг и тестирование» выбрать пункт «Контрольное тестирование».
После осуществления выбора предлагается первое дифференциальное уравнение.
Программа ожидает от пользователя указания типа ДУ. Указание типа производится
щелчком левой кнопки мыши на типе ДУ в иерархической схеме (3). Программа
производит проверку ответа пользователя и в случае корректного выбора
устанавливает «галочку» в протоколе тестирования (7).
Следующим шагом программа требует указать каноническую форму ДУ. Указание
канонической формы производится щелчком мыши по одной из форм в поле
«Канонические формы ДУ (5).
В случае неверного ответа пользователь переходит к задаче определения
метода решения (см. ниже).
При верном ответе результат заносится в протокол тестирования, а пользователю
предлагается решить задачу выделения параметров канонической формы ДУ, для чего
открывается окно «Параметры канонической формы» (рисунок Е.3).
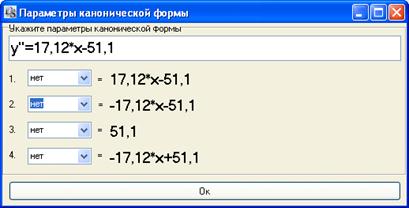
Рисунок Е.3 - Окно «Выбор параметров канонической формы»
Окно «Параметры канонической формы» представляет собой совокупность трех
частей. Первая верхняя часть окна предназначена для вывода задания пользователю
(1). В данной области приводится задание для решения, а именно надпись «Укажите
параметры канонической формы» и формула с заданным ДУ.
Пользователю в рабочей области окна (2) предлагается ряд вариантов
ответов, среди которых присутствуют как правильные, так и неправильные ответы.
Решение задачи осуществляется путем выбора из ниспадающего списка обозначения
параметра канонической формы. Для выбора неверных вариантов предусмотрен
специальный пункт «нет» ниспадающего списка.
Принятие ответов пользователя осуществляется нажатие кнопки «Ок». Нажатие
данной кнопки приводит к проверке выбранных вариантов. В случае корректного
указания, результат заносится в протокол тестирования. После проверки
пользователь переходит к окну «Тестирование и тренинг».
В окне «Тестирование и тренинг» пользователю предлагается для решения
следующий тип задачи: выбор метода решения предложенного ДУ. Выбор метода
решения осуществляется путем нажатия клавиши мыши на одном из перечисленных
методов. Выбор варианта приводит к процедуре проверки его корректности.
После указания метода решения пользователю предоставлена возможность
изучить и проанализировать свои ответы. Переход к следующему дифференциальному
уравнению осуществляется путем нажатия кнопки «Следующее ДУ».
Последовательно проходя этапы теста, состоящего из пяти вопросов,
пользователь получает результат тестирования, в котором отображается количество
верных ответов из общего числа заданных вопросов.
5 Вывод хода решения ДУ
Обучение студентов алгоритму решения ДУ первого порядка на конкретных
примерах осуществляется за счет использования окна «Решение ДУ». В программном
продукте реализовано решение ДУ первого порядка в квадратурах. Решение ДУ
осуществляется на основании указанного пользователем типа.
Окно разбито на три составные части: главное меню окна (1), поле для
ввода ДУ (2) и поле для вывода алгоритма решения ДУ указанного типа (3).
Работа с данным окном программы подразумевает, что пользователь в главном
меню указывает тип ДУ первого порядка. На основании указанного типа будет
проводиться решение введенного ДУ.
Далее пользователь, используя операции, функции, константы и переменные
(таблица Ж.1), вводит в специализированное поле (2) ДУ, представленное в
каноническом виде.
Нажимая кнопку «Решить ДУ сведением к интегралам» пользователю в рабочее
поле выводится подробный ход решения заданного ДУ в соответствии с указанным
ранее типом. Решение сопровождается пояснением его основных этапов. В случае, когда пользователь ошибочно указывает тип
ДУ в главном меню, программа сообщает о невозможности решения введенного ДУ
методами доступными для указанного типа.