Линейная алгебра и аналитическая геометрия
Линейная алгебра и аналитическая
геометрия
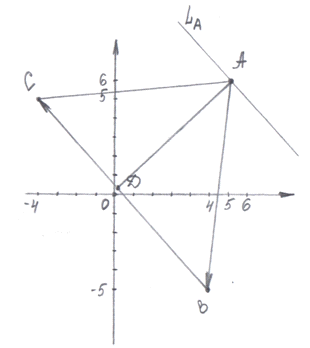
Задание № 1. Даны точки А, В, С: А(5;6),
В(4;-5), С(-4;5).
Построить: векторы 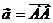 и
и 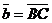 .
.
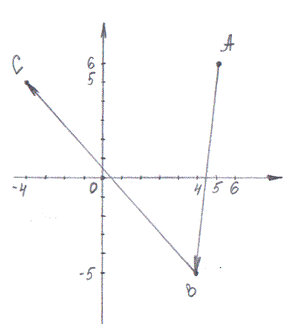
Найти: 1) векторы 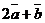 и
и 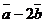 ;
;
) модули векторов 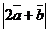 и
и 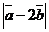 ;
;
) скалярное произведение 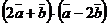 .
.
Решение:
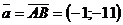
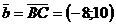
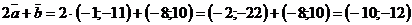 .
.
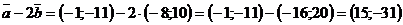 .
.
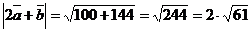
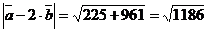
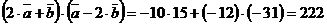 .
.
Ответ: 1) 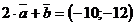 ;
; 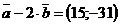 ;
;
) 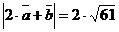 ;
; 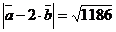 ;
;
) 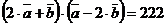 .
.
Задание № 2. Даны точки А, В, С: А
(5;6), В (4;-5), С (-4;5).
Найти: а) уравнение прямой АВ;
б) уравнение высоты АD;
в) уравнение прямой, проходящей
через точку А параллельно прямой ВС.
Решение:
а) уравнение АВ:
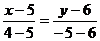
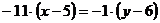
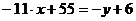
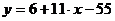
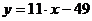 .
.
б) уравнение высоты АD:
. уравнение ВС:
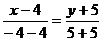
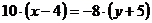
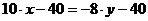
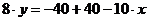
 .
.
. угловой коэффициент 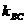 :
:
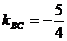 .
.
. угловой коэффициент 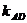 :
:
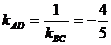 .
.
. уравнение AD:
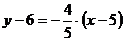
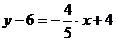
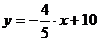 .
.
в) уравнение прямой 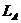 :
:
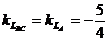
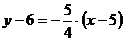
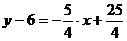
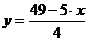 .
.
Ответ: а) 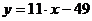 ; б)
; б) 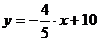 ; в)
; в) 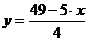 .
.
Задание № 3. Дана система линейных
уравнений:
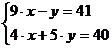
Найти: а) определитель основной
матрицы системы А;
б) обратную матрицу А-1;
в) решить систему линейных уравнений
методом Крамера.
Решение: а) 
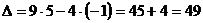 .
.
б) А-1:
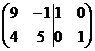 ~
~
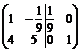 ~
~ 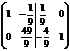 ~
~ 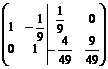 ~
~ 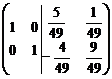
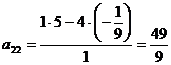 ,
, 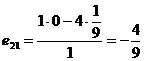 ,
, 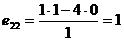 .
.
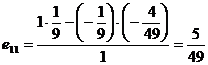 ,
, 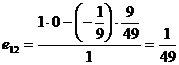 .
.
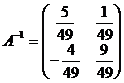 .
.
в) 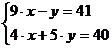
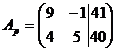
 ,
,
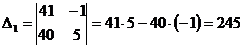 ,
,
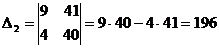 .
.
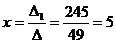 ,
,
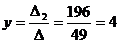 .
.
Ответ: а)  ; б)
; б) 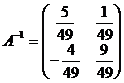 ; в)
; в) 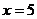 ,
, 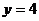 .
.
Задание № 4. Решить систему линейных
алгебраических уравнений
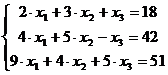
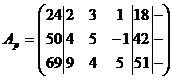 ~
~
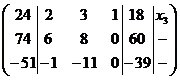 ~
~
Пусть 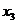 в 1-ом уравнении базисная, тогда
элемент
в 1-ом уравнении базисная, тогда
элемент 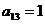 -
разрешающий. Первая строка, третий столбец - разрешающие. Разделим элементы
разрешающей строки на разрешающий элемент (
-
разрешающий. Первая строка, третий столбец - разрешающие. Разделим элементы
разрешающей строки на разрешающий элемент (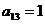 ). Запишем разрешающую строку после
этого преобразования.
). Запишем разрешающую строку после
этого преобразования.
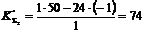 ,
, 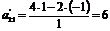 ,
, 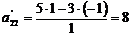 ,
, 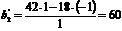 .
.
 ,
, 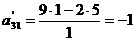 ,
, 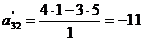 ,
, 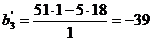 .
.
Пусть 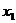 в 3-ем уравнении базисная, тогда
элемент
в 3-ем уравнении базисная, тогда
элемент  -
разрешающий. Третья строка, первый столбец - разрешающие. Разделим элементы
разрешающей строки на разрешающий элемент (
-
разрешающий. Третья строка, первый столбец - разрешающие. Разделим элементы
разрешающей строки на разрешающий элемент ( ). Запишем разрешающую строку после
этого преобразования.
). Запишем разрешающую строку после
этого преобразования.
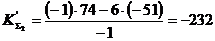 ,
,  ,
, 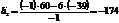 .
.
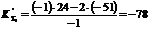 ,
, 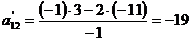 ,
, 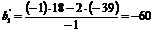 .
.
~
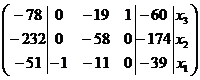
Запишем эквивалентную систему
линейных уравнений:
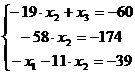
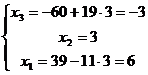
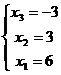
Ответ: 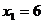 ,
, 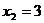 ,
, 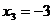 .
.
Задание № 5. Выполнить действия с
матрицами:
а) 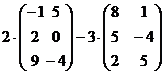 ; б)
; б) 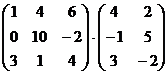 .
.
Решение:
а)  .
.
б) 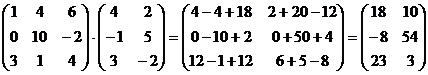 .
.
Ответ: а) 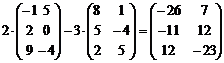 ; б)
; б) 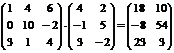 .
.
Задание № 6. Решить задачу линейного
программирования:
Предприятие планирует выпуск двух
продукций I и II, на производство которых расходуется три вида сырья А, В, С.
Потребность 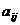 на каждую
единицу
на каждую
единицу 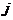 -го вида
продукции
-го вида
продукции 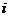 -го вида
сырья, запас
-го вида
сырья, запас  соответствующего
вида сырья и прибыль
соответствующего
вида сырья и прибыль 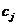 от реализации
единицы
от реализации
единицы 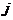 -го вида
продукции заданы таблицей:
-го вида
продукции заданы таблицей:
|
Виды
сырья
|
Виды
продукции
|
Запасы
сырья
|
|
I
|
II
|
|
|
А
|
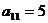 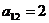 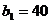
|
|
|
|
В
|
 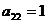 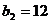
|
|
|
|
С
|
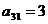 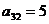 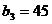
|
|
|
|
Прибыль
|
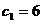 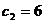
|
|
|
|
План,
ед.
|
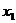 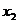
|
|
|
Для производства двух видов
продукции I и II с планом 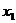 и
и 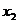 единиц
составить целевую функцию прибыли
единиц
составить целевую функцию прибыли 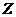 и соответствующую систему
ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не
менее n единиц обоих видов продукции.
и соответствующую систему
ограничений по запасам сырья, предполагая, что требуется изготовить в сумме не
менее n единиц обоих видов продукции.
В условиях задачи 1 составить
оптимальный план (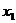 ,
,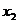 )
производства продукции, обеспечивающей максимальную прибыль
)
производства продукции, обеспечивающей максимальную прибыль 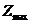 . Определить
остатки каждого вида сырья. (Задачу решить симплекс-методом).
. Определить
остатки каждого вида сырья. (Задачу решить симплекс-методом).
Построить по полученной системе
ограничений многоугольник допустимых решений и найти оптимальный план
производства геометрическим путем. Определить соответствующую прибыль 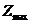 .
.
Решение:
Пусть предприятие производит 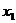 единиц
продукции I и
единиц
продукции I и 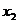 единиц продукции
II. Тогда задачу линейного программирования на максимум можно записать
следующим образом:
единиц продукции
II. Тогда задачу линейного программирования на максимум можно записать
следующим образом:
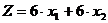 →
→  - целевая
функция.
- целевая
функция.
Ограничения по ресурсам:
А: 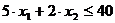
В: 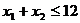
С: 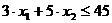
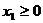
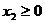
Введем в каждое неравенство
дополнительную балансовую переменную со знаком «+», получим систему ограничений
в виде системы линейных уравнений:
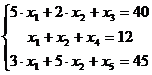
Для нахождения первоначального
базисного решения разобьем переменные на основные (базисные) и неосновные
(свободные):
Запишем расширенную матрицу системы
размером 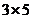 .
.
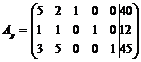
На первом этапе за основные можно
принять 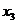 ,
, 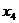 ,
, 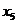 . Если
выбранные по этому правилу базисные переменные имеют те же знаки, что и соответствующие
им свободные члены, то полученные базисные решения будут допустимыми.
. Если
выбранные по этому правилу базисные переменные имеют те же знаки, что и соответствующие
им свободные члены, то полученные базисные решения будут допустимыми.
Основные переменные: 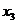 ,
, 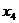 ,
, 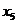 .
.
Неосновные переменные: 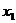 ,
, 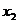 .
.
Выразим основные переменные через
неосновные
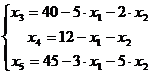
Запишем первое базисное решение,
приравняв неосновные переменные к 0, т. е. 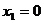 ,
, 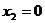 .
.
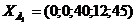 - это решение является допустимым.
- это решение является допустимым.
Выразим целевую функцию через
неосновные переменные
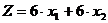 →
→ 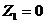
Функцию 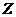 можно
увеличить за счет увеличения любой из неосновных переменных, входящих в
выражение для
можно
увеличить за счет увеличения любой из неосновных переменных, входящих в
выражение для 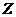 с
положительными коэффициентами. Для определенности выберем
с
положительными коэффициентами. Для определенности выберем 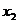 . Исходя из
условия неотрицательности переменных, из системы можно выбрать наиболее
возможное значение переменной
. Исходя из
условия неотрицательности переменных, из системы можно выбрать наиболее
возможное значение переменной 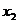 :
:
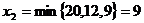
При 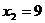 переменная
переменная 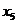 обращается
в 0 и переходит в неосновные переменные, а
обращается
в 0 и переходит в неосновные переменные, а 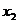 - в основные.
- в основные.
Основные: 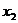 ,
, 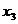 ,
, 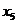 .
.
Неосновные: 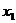 ,
, 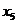 .
.
Выразим новые основные переменные
через новые неосновные, начиная с разрешающего уравнения для 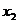 :
:
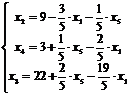
Таким образом, получим новую
систему:
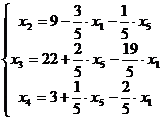
Запишем второе базисное решение:
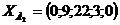 - допустимое решение.
- допустимое решение.
Выразим целевую функцию через новые
неосновные переменные:
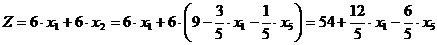 →
→ 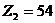
Полученное базисное решение 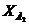 не является
оптимальным, поскольку возможно дальнейшее увеличение целевой функции
не является
оптимальным, поскольку возможно дальнейшее увеличение целевой функции 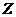 за счет
переменной
за счет
переменной 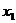 , имеющей
положительный коэффициент. Из системы следует, что наиболее возможное значение
для
, имеющей
положительный коэффициент. Из системы следует, что наиболее возможное значение
для 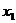 :
:
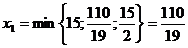
Второе уравнение системы является
разрешающим, при этом переменная 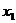 переходит в основные, а
переходит в основные, а 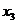 - в
неосновные.
- в
неосновные.
Основные: 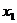 ,
, 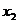 ,
, 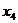 .
.
Неосновные: 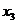 ,
, 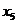 .
.
Выразим новые основные переменные
через новые неосновные, начиная с разрешающего для 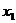 :
:
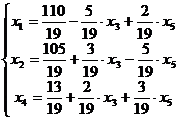
Таким образом получим систему.
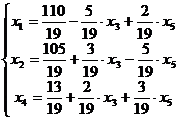
Запишем третье базисное решение:
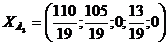
Выразим целевую функцию через новые
неосновные переменные:
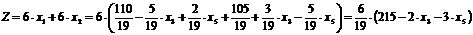 →
→ 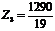 .
.
Это выражение не содержит
положительных коэффициентов при неосновных переменных, поэтому значение функции
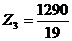 максимальное.
максимальное.
Экономический смысл полученного
решения: прибыль предприятия максимальна при реализации 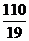 единиц
продукции I и
единиц
продукции I и  единиц
продукции II. Дополнительные переменные
единиц
продукции II. Дополнительные переменные 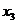 ,
, 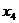 ,
, 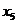 показывают остатки ресурсов. При
оптимальном плане производства
показывают остатки ресурсов. При
оптимальном плане производства 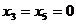 , т. е. остатки ресурсов А и В равны
0, а остатки ресурса С равны 3 и 5 единицам соответственно.
, т. е. остатки ресурсов А и В равны
0, а остатки ресурса С равны 3 и 5 единицам соответственно.
. Поскольку переменные 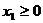 ,
, 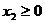 ,то
допустимые планы будут располагаться в I четверти координатной плоскости.
,то
допустимые планы будут располагаться в I четверти координатной плоскости.
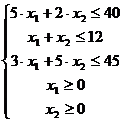
Ограничение определяет
полуплоскость. Для ее определения построим прямую 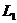 :
:  . Определим
координаты 2-х точек на этой прямой.
. Определим
координаты 2-х точек на этой прямой.
|
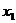 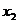
|
|
|
Т.
1
|
0
|
20
|
|
Т.
2
|
8
|
0
|
Для определения полуплоскости
задаваемой неравенством возьмем произвольную точку не лежащую на прямой. Удобно
взять точку О (0;0). Координаты этой точки удовлетворяют неравенству: 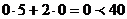 . Таким
образом, неравенство задает полуплоскость содержащую т. О (0;0).
. Таким
образом, неравенство задает полуплоскость содержащую т. О (0;0).
Рассмотрим неравенство. Прямая 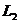 :
: 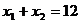 .
.
|
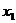 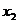
|
|
|
Т.
1
|
0
|
12
|
|
Т.
2
|
12
|
0
|
Для определения полуплоскости
выберем т. О (0;0), которая удовлетворяет неравенству: 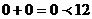 .
.
Рассмотрим ограничение. Прямая 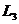 :
: 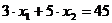 .
.
|
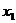 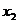
|
|
|
Т.
1
|
0
|
9
|
|
Т.
2
|
15
|
0
|
Для определения полуплоскости
выберем т. О (0;0), которая удовлетворяет неравенству: 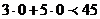 .
.
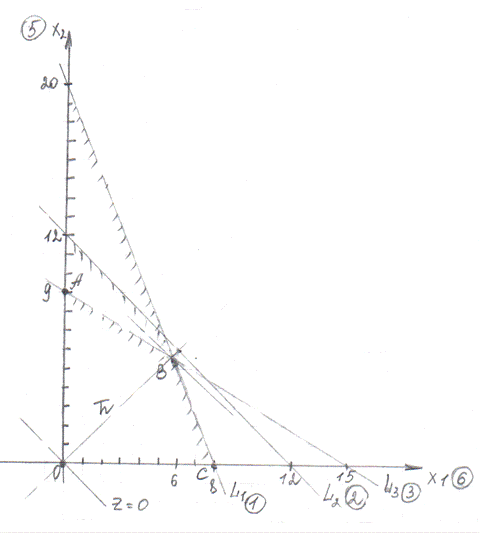
Таким образом, получена замкнутая
область, замкнутый четырехугольник ОАВС - область допустимых планов или область
допустимых решений.
Рассмотрим целевую функцию 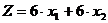 . Известно,
что данная функция задает прямую линию, а само выражение представляет собой
скалярное произведение вектора
. Известно,
что данная функция задает прямую линию, а само выражение представляет собой
скалярное произведение вектора 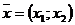 и перпендикулярного ему вектора
и перпендикулярного ему вектора 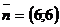 . Для всех
точек какой-либо прямой перпендикулярной
. Для всех
точек какой-либо прямой перпендикулярной 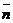 целевая функция имеет одно и то же
значение. Возрастание целевой функции происходит в положительном направлении
целевая функция имеет одно и то же
значение. Возрастание целевой функции происходит в положительном направлении 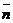 . Построим
вектор
. Построим
вектор 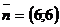 и
перпендикулярную ему прямую
и
перпендикулярную ему прямую 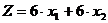 . Так как в задаче необходимо найти
. Так как в задаче необходимо найти  целевой
функции, то последней общей точкой (точкой выхода) прямой
целевой
функции, то последней общей точкой (точкой выхода) прямой 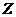 из ОДР
будет являться точка В. Таким образом, оптимальное решение находится в вершине
В, находящейся на пересечении прямых
из ОДР
будет являться точка В. Таким образом, оптимальное решение находится в вершине
В, находящейся на пересечении прямых 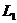 и
и 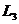 , т. е. координаты точки В
определяются решением системы уравнений:
, т. е. координаты точки В
определяются решением системы уравнений:
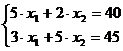
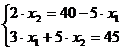
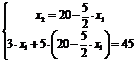
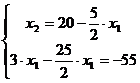
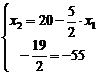
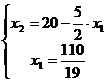
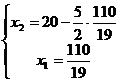
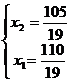
Решение этой системы 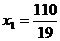 ,
, 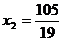 . При этом
. При этом  значение
целевой функции
значение
целевой функции 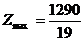 . Таким
образом, максимальная прибыль в размере
. Таким
образом, максимальная прибыль в размере 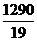 денежных единиц может быть
достигнута при производстве
денежных единиц может быть
достигнута при производстве 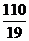 единиц продукции I и
единиц продукции I и  единиц
продукции II.
единиц
продукции II.
Задание № 7. Решить транспортную
задачу.
На складах  ,
, 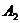 ,
, 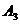 хранится
хранится 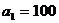 ,
, 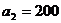 ,
, 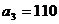 единиц
одного и того же груза. Этот груз требуется доставить трем потребителям
единиц
одного и того же груза. Этот груз требуется доставить трем потребителям 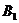 ,
, 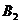 ,
, 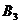 , заказы
которых составляют
, заказы
которых составляют 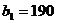 ,
, 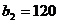 ,
, 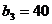 единиц
груза соответственно. Стоимости перевозок
единиц
груза соответственно. Стоимости перевозок 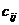 единицы груза с
единицы груза с 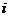 -го склада
-го склада 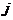 -му
потребителю указаны в соответствующих клетках транспортной таблицы:
-му
потребителю указаны в соответствующих клетках транспортной таблицы:
Суммарная мощность поставщиков равна:
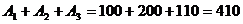
Суммарный спрос потребителей равен:

Модель данной транспортной задачи -
открытая. Введем фиктивного потребителя со спросом 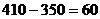 единиц.
Стоимость перевозки единицы груза до фиктивного потребителя равна 0. Получаем
закрытую модель.
единиц.
Стоимость перевозки единицы груза до фиктивного потребителя равна 0. Получаем
закрытую модель.
|
Поставщики
|
Потребители
|
|
190
|
120
|
40
|
60
|
|
100
|
4
|
2
|
4
|
0
|
|
200
|
5
|
5
|
3
|
0
|
|
110
|
1
|
5
|
6
|
0
|
Решаем ее распределительным методом.
Воспользуемся методом минимальной стоимости.
Шаг № 1. Заполняем клетку с нулевой
стоимостью, например, клетку (1, 4). 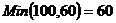 . Исключаем четвертый столбец.
. Исключаем четвертый столбец.
Шаг № 2. Заполняем клетку (3, 2). 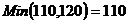 . Исключаем
третью строку.
. Исключаем
третью строку.
Шаг № 3. Заполняем клетку (1, 1). 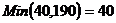 . Исключаем
первую строку.
. Исключаем
первую строку.
Шаг № 4. Заполняем клетку (2, 1). 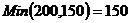 . Исключаем
первый столбец.
. Исключаем
первый столбец.
Шаг № 5. Заполняем клетку (2, 3). 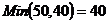 . Исключаем
третий столбец и вторую строку.
. Исключаем
третий столбец и вторую строку.
Проверяем выполнение условия 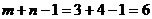 .
.
|
Тогда
начальный опорный план имеет вид:Поставщики
|
Потребители
|
|
190
|
120
|
40
|
60
|
|
100
|
4
40
|
2
|
4
|
0
60
|
|
200
|
5
150
|
5
10
|
3
40
|
0
|
|
110
|
1
|
5
110
|
6
|
0
|
Для этого плана находим оценки строк и столбцов.
|
Поставщики
|
Потребители
|
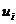
|
|
190
|
120
|
40
|
60
|
|
|
100
|
4
40
|
2
|
4
|
0
60
|
-4
|
|
200
|
5
150
|
5
10
|
3
40
|
0
|
-5
|
|
110
|
1
|
5
110
|
6
|
0
|
-5
|
|
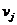 00-2-4- 00-2-4-
|
|
|
|
|
|
Затем получим матрицу оценок клеток:
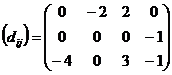
План является неоптимальным, так как
имеются клетки с отрицательными оценками. Выбираем клетку (3, 1), имеющую
большую по абсолютной величине оценку, и строим для нее цикл пересчета: (3, 1)
- (2, 1) - (2, 2) - (3, 2).
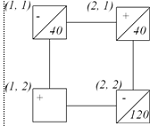
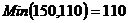 . Клетка (3, 1) становится
отмеченной, а клетка (3, 2) становится пустой. Составим новый план поставок,
для которого находим оценки строк и столбцов.
. Клетка (3, 1) становится
отмеченной, а клетка (3, 2) становится пустой. Составим новый план поставок,
для которого находим оценки строк и столбцов.
|
Поставщики
|
Потребители
|
|
|
190
|
120
|
40
|
60
|
|
|
100
|
4
40
|
2
|
4
|
0
60
|
-4
|
|
200
|
5
40
|
5
120
|
3
40
|
0
|
-5
|
|
110
|
1
110
|
5
|
6
|
0
|
-1
|
|
 00-2-4- 00-2-4-
|
|
|
|
|
|
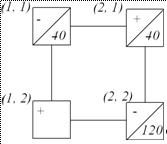
Получим матрицу оценок клеток:
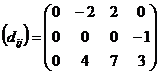
План является неоптимальным, так как
имеются клетки с отрицательными оценками. Выбираем клетку (1, 2), имеющую
большую по абсолютной величине оценку, и строим для нее цикл пересчета: (1, 2)
- (1, 1) - (2, 1) - (2, 2).
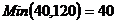 . Клетка (1, 2) становится
отмеченной, а клетка (1, 1) становится пустой. Составим новый план поставок,
для которого находим оценки строк и столбцов.
. Клетка (1, 2) становится
отмеченной, а клетка (1, 1) становится пустой. Составим новый план поставок,
для которого находим оценки строк и столбцов.
|
Поставщики
|
Потребители
|
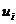
|
|
190
|
120
|
40
|
60
|
|
|
100
|
4
|
2
40
|
4
|
0
60
|
-2
|
|
200
|
5
80
|
5
80
|
3
40
|
0
|
-5
|
|
110
|
1
110
|
5
|
6
|
-1
|
|
 00-2-2- 00-2-2-
|
|
|
|
|
|
Получим матрицу оценок клеток:
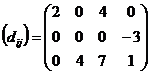
План является неоптимальным, так как
имеются клетки с отрицательными оценками. Выбираем клетку (2, 4), имеющую
большую по абсолютной величине оценку, и строим для нее цикл пересчета: (2, 4)
- (1, 4) - (1, 2) - (2, 2).
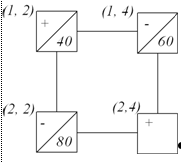
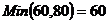 . Клетка (2, 4) становится
отмеченной, а клетка (1, 4) становится пустой. Составим новый план поставок,
для которого находим оценки строк и столбцов.
. Клетка (2, 4) становится
отмеченной, а клетка (1, 4) становится пустой. Составим новый план поставок,
для которого находим оценки строк и столбцов.
|
Поставщики
|
Потребители
|
|
|
190
|
120
|
40
|
60
|
|
|
100
|
4
|
2
100
|
4
|
0
|
-2
|
|
200
|
5
80
|
5
20
|
3
40
|
0
60
|
-5
|
|
110
|
1
110
|
5
|
6
|
0
|
-1
|
|
 00-2-5- 00-2-5-
|
|
|
|
|
|
Получим матрицу оценок клеток:
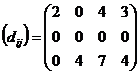
Матрица оценок не содержит
отрицательных чисел. Таким образом, получен оптимальный план поставок, который
окончательно можно представить в виде таблицы
|
Поставщики
|
Получатели
|
|
190
|
120
|
40
|
|
100
|
|
2
100
|
|
|
200
|
5
80
|
5
20
|
3
40
|
|
110
|
1
110
|
|
|
Суммарные затраты на перевозку груза равны:
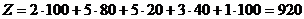 ден. ед.
ден. ед.
При этом поставщик 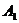 должен
поставить 100 единиц груза потребителю
должен
поставить 100 единиц груза потребителю 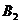 . Поставщик
. Поставщик 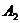 должен
поставить 80 единиц груза потребителю
должен
поставить 80 единиц груза потребителю 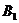 , 20 единиц груза потребителю
, 20 единиц груза потребителю 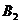 , 40 единиц
груза потребителю
, 40 единиц
груза потребителю 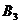 . Поставщик
. Поставщик 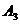 должен
поставить 110 единиц груза потребителю
должен
поставить 110 единиц груза потребителю 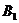 . 60 единиц груза останется на
складе у поставщика
. 60 единиц груза останется на
складе у поставщика 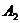 .
.
Задание № 8. Найти производные 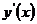 функций:
функций:
а) 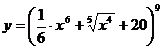
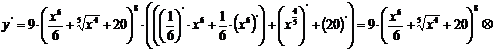
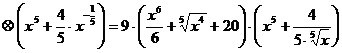 .
.
б) 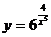
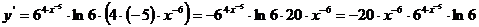 .
.
в) 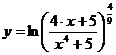
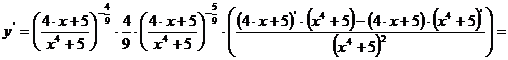
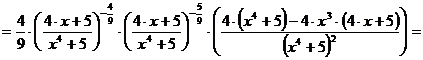
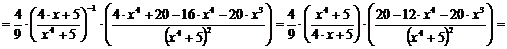
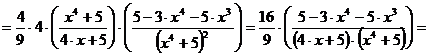
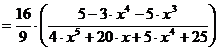 .
.
Задание № 9. Для функции 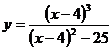
Найти: а) интервалы монотонности,
локальные экстремумы;
б) интервалы выпуклости вверх
(вниз), точки перегиба;
в) построить эскиз графика;
г) написать уравнение касательной к
графику в точке с абсциссой 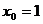 .
.
Решение:
Область определения функции
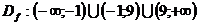
Область значений функции
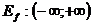
Нули функции и интервалы
знакопостоянства:
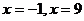
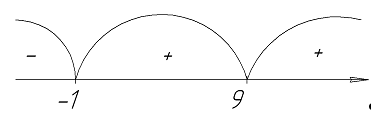
Определить четность, нечетность
функции
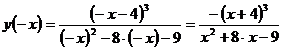 - функция общего вида.
- функция общего вида.
Непериодическая
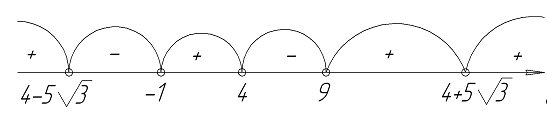
Исследование функции на монотонность
Первая производная функции:
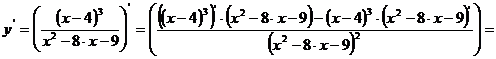
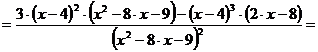
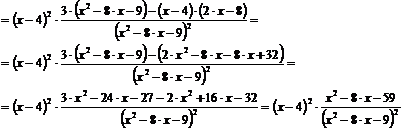
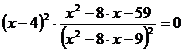
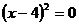 или
или 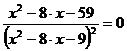
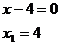
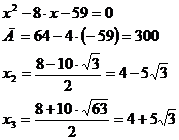
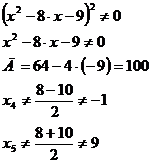
вектор матрица
транспортный задача
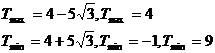
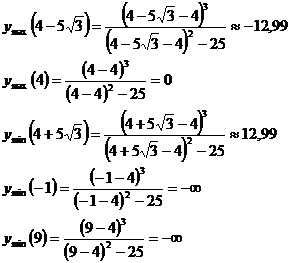
Исследование функции на выпуклость,
вогнутость.
Вторая производная:
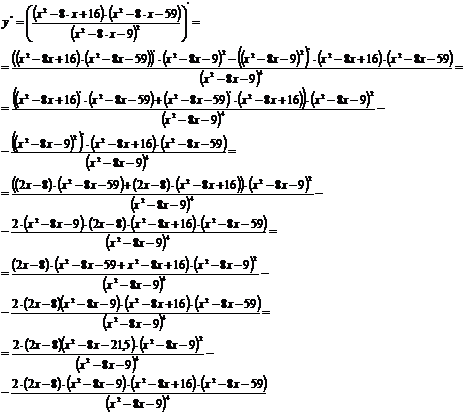
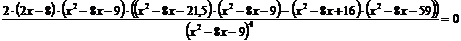
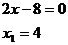 или
или 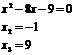 или
или 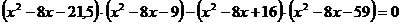
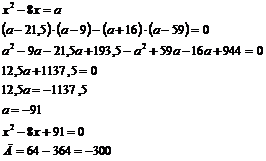
Нет решений.
Выпуклая книзу при 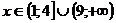
Выпуклая кверху при 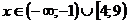 .
.
уравнение касательной к графику в
точке с абсциссой 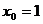 .
.
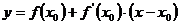
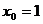
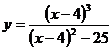
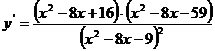
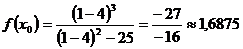
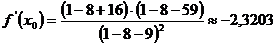
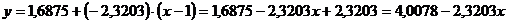
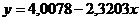
Эскиз графика
|
x
|
0
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
10
|
11
|
12
|
|
y
|
7,1
|
1,7
|
0,38
|
0,04
|
0
|
-0,04
|
-0,38
|
-1,7
|
-7,1
|
19,6
|
14,3
|
13,1
|
|
13
|
14
|
15
|
-2
|
-3
|
-4
|
-5
|
-6
|
-7
|
-8
|
-9
|
|
|
13,01
|
13,3
|
13,9
|
-19,6
|
-14,3
|
-13,1
|
-13,01
|
-13,3
|
-13,9
|
-14,52
|
-15,26
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
