Геометрические свойства кривых второго порядка
Исследовать и изучить геометрические свойства кривых
второго порядки (эллипса, гиперболы и параболы), представляющих собой линии
пересечения кругового конуса с плоскостями, не проходящими через его вершины, а
также научиться строить графики данных кривых в канонической и прямоугольной
декартовой системах координат.
Постановка задачи
Дано уравнение кривой
второго порядка:
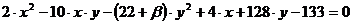 . (1)
. (1)
Задание. Для данного уравнения кривой
второго порядка с параметром 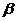 :
:
I. Определить зависимость типа кривой
от параметра 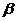 с помощью
инвариантов.
с помощью
инвариантов.
II. Привести уравнение кривой при 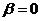 к каноническому виду,
применяя преобразования параллельного переноса и поворота координатных осей.
к каноническому виду,
применяя преобразования параллельного переноса и поворота координатных осей.
III. Найти фокусы, директрисы,
эксцентриситет и асимптоты (если они есть) данной кривой второго порядка.
IV. Получить уравнения канонических
осей в общей системе координат.
V. Построить график кривой в
канонической и общей системах координат.
Получение
канонической системы координат. Построение графиков
I. Тип кривой второго порядка в
зависимости от параметра 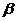
В прямоугольной
декартовой системе координат 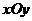 кривая второго порядка задается в общем виде
уравнением:
кривая второго порядка задается в общем виде
уравнением:
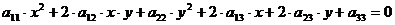 ,
,
если хотя бы один из
коэффициентов 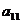 ,
, 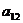 ,
, 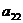 отличен от нуля.
отличен от нуля.
Для уравнения кривой
второго порядка (1) имеем:
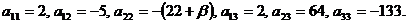
Теперь определим тип
данной нам кривой (1) с помощью инвариантов. Инварианты кривой второго порядка
вычисляются по формулам:
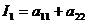 ;
;
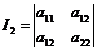 ;
;
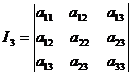 .
.
Для данной кривой они
равны: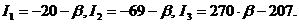
1). Если 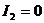 , то уравнение кривой (1) определяет
кривую параболического типа, но
, то уравнение кривой (1) определяет
кривую параболического типа, но 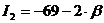 . Таким образом, если
. Таким образом, если 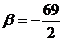 , то уравнение (1) определяет кривую параболического
типа. При этом
, то уравнение (1) определяет кривую параболического
типа. При этом 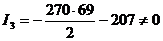 ,
то есть: если
,
то есть: если 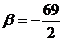 , то
уравнение (1) определяет параболу.
, то
уравнение (1) определяет параболу.
2). Если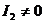 , то данная кривая — центральная.
Следовательно, при
, то данная кривая — центральная.
Следовательно, при 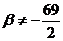 данная
кривая — центральная.
данная
кривая — центральная.
·
Если 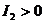 , то уравнение (1)
определяет кривую эллиптического типа. Следовательно, если
, то уравнение (1)
определяет кривую эллиптического типа. Следовательно, если 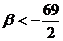 , то данная кривая есть кривая эллиптического
типа. Но при этом
, то данная кривая есть кривая эллиптического
типа. Но при этом 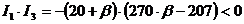 .
В соответствии с признаками кривых второго порядка получим: если
.
В соответствии с признаками кривых второго порядка получим: если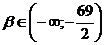 , то уравнение (1) определяет эллипс.
, то уравнение (1) определяет эллипс.
·
Если 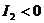 , то уравнение (1)
определяет кривую гиперболического типа. Следовательно, если
, то уравнение (1)
определяет кривую гиперболического типа. Следовательно, если 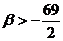 , то уравнение (1) определяет кривую гиперболического
типа.
, то уравнение (1) определяет кривую гиперболического
типа.
а) Если 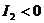 и
и 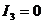 , то уравнение (1) определяет две
пересекающиеся прямые. Получим:
, то уравнение (1) определяет две
пересекающиеся прямые. Получим:
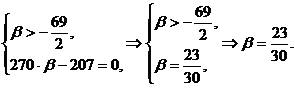
Следовательно, если 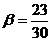 , то уравнение (1)
определяет две пересекающиеся прямые.
, то уравнение (1)
определяет две пересекающиеся прямые.
б) Если 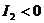 и
и 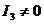 , то данная кривая — гипербола. Но
, то данная кривая — гипербола. Но 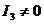 при всех
при всех 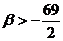 за исключением точки
за исключением точки 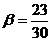 . Следовательно, если
. Следовательно, если 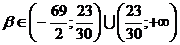 , то уравнение (1) определяет гиперболу.
, то уравнение (1) определяет гиперболу.
Используя полученные результаты,
построим таблицу:
|
Значение
параметра β
|
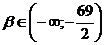
|
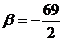
|
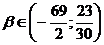
|
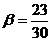
|
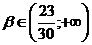
|
|
Тип кривой
|
Эллипс
|
Парабола
|
Гипербола
|
Две
пересекающиеся прямые
|
Гипербола
|
II. Переход от общего уравнения кривой к
каноническому
Рассмотрим теперь случай,
когда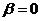 , и исследуем
данное уравнение кривой второго порядка с помощью инвариантов. Из
вышеприведенной таблицы видим, что при
, и исследуем
данное уравнение кривой второго порядка с помощью инвариантов. Из
вышеприведенной таблицы видим, что при  уравнение (1) определяет гиперболу и принимает
вид:
уравнение (1) определяет гиперболу и принимает
вид:
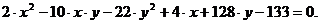 (2.1)
(2.1)
Приведем уравнение кривой
(2.1) к каноническому виду, применяя преобразования параллельного переноса и
поворота координатных осей.
Мы установили, что данная
кривая — центральная, поэтому используем методику приведения к каноническому
виду для уравнения центральной кривой. Совершим параллельный перенос начала
координат в точку 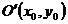 . При
этом координаты
. При
этом координаты 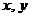 произвольной
точки
произвольной
точки 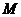 плоскости в
системе координат
плоскости в
системе координат 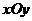 и
координаты
и
координаты 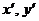 в новой
системе координат
в новой
системе координат 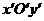 связаны
соотношениями
связаны
соотношениями
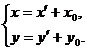
Подставляя эти выражения
в уравнение (2.1), получим:
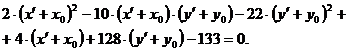 (2.2)
(2.2)
Раскрывая скобки и
приводя подобные члены, получим:
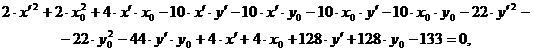
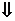
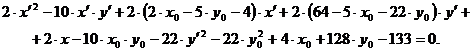 (2.3)
(2.3)
В уравнении (2.3)
коэффициенты при 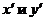 приравняем
к нулю. Получим систему уравнений относительно
приравняем
к нулю. Получим систему уравнений относительно 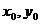
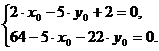 (2.4)
(2.4)
Решив систему (2.4),
получим:
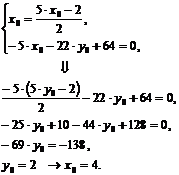
Центр кривой 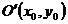 имеет координаты
имеет координаты 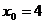 ,
,  . Поставим найденные значения
. Поставим найденные значения 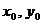 в уравнение (2.3). В новой системе
координат
в уравнение (2.3). В новой системе
координат 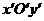 в уравнении
(2.3) коэффициенты при
в уравнении
(2.3) коэффициенты при 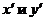 равны
нулю и уравнение примет вид
равны
нулю и уравнение примет вид
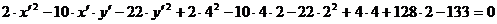 ,
,
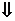
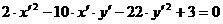 . (2.5)
. (2.5)
Так как 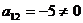 , то дальнейшее упрощение уравнения (2.5)
мы достигаем при помощи поворота осей координат на угол
, то дальнейшее упрощение уравнения (2.5)
мы достигаем при помощи поворота осей координат на угол 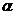 . При повороте осей координат на угол
. При повороте осей координат на угол
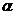 координаты
координаты 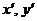 произвольной точки
произвольной точки 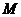 плоскости в системе
координат
плоскости в системе
координат 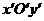 и координаты
и координаты
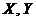 в новой системе
координат
в новой системе
координат 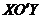 связаны
соотношениями
связаны
соотношениями
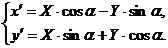 (2.6)
(2.6)
Подставляя (2.6) в
уравнение (2.5), получим
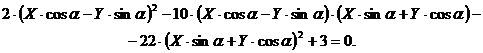
Раскроем скобки и
приведем подобные члены
Приводя подобные члены,
получим уравнение
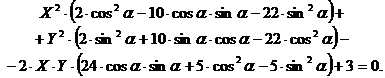 (2.7)
(2.7)
Теперь выберем такой угол
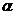 , что в уравнении (2.7)
коэффициент при произведении
, что в уравнении (2.7)
коэффициент при произведении 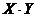 равен нулю. Получим уравнение относительно
синуса и косинуса угла
равен нулю. Получим уравнение относительно
синуса и косинуса угла 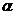 :
:
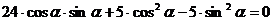 . (2.8)
. (2.8)
Разделим правую и левую
части данного уравнения почленно на 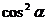 . Мы можем это сделать, так как
. Мы можем это сделать, так как 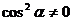 , потому что если
, потому что если 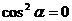 (то есть
(то есть 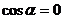 ), то при подстановке
), то при подстановке 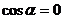 в уравнение (2.8) получим, что и
в уравнение (2.8) получим, что и 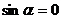 , что противоречит основному
тригонометрическому тождеству
, что противоречит основному
тригонометрическому тождеству 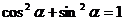 . Получим уравнение
. Получим уравнение
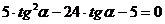 . (2.9)
. (2.9)
Решая уравнение (2.9),
получим
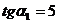 ,
, 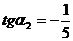 .
.
Зная значение тангенса,
можно вычислить значения синуса и косинуса по следующим формулам: 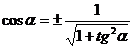 ,
, 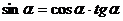 . Подставляя соответствующие значения тангенса,
получаем:
. Подставляя соответствующие значения тангенса,
получаем:
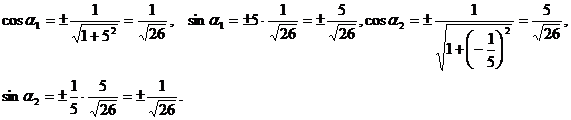
Возьмем для определенности
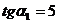 . Тогда соответствующие
значения синуса и косинуса есть
. Тогда соответствующие
значения синуса и косинуса есть
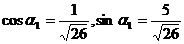 , (2.10)
, (2.10)
Подставляя (2.10) в
уравнение (2.7), получаем:
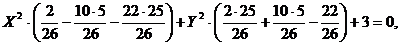
и преобразовав данное
уравнение, получим уравнение вида:
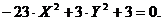
И, соответственно,
уравнение
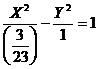 (2.11)
(2.11)
— это каноническое
уравнение исходной гиперболы.
III. Фокусы, директрисы, эксцентриситет и
асимптоты кривой
Пусть 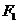 и
и 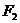 — фокусы,
— фокусы, 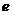 — эксцентриситет,
— эксцентриситет, 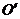 — центр, а
— центр, а 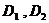 — директрисы данной гиперболы. Известно, что
фокусы имеют координаты:
— директрисы данной гиперболы. Известно, что
фокусы имеют координаты: 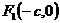 ,
,
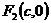 , где
, где 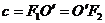 и
и 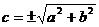 . Для данного уравнения гиперболы (2.11)
получаем, что
. Для данного уравнения гиперболы (2.11)
получаем, что 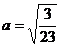 ,
, 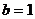 , и значит
, и значит 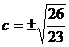 . Отсюда получаем
. Отсюда получаем 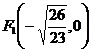 ,
, 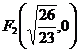 .
.
Эксцентриситет гиперболы
(2.11)
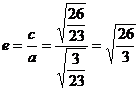 .
.
Директрисы гиперболы
задаются уравнениями: 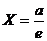 и
и
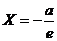 . Подставляя найденные
значения
. Подставляя найденные
значения 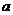 и
и 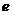 , получаем:
, получаем:
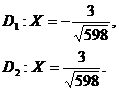
Прямые 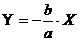 и
и 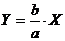 в канонической системе координат
в канонической системе координат 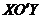 называются асимптотами
гиперболы. Для данной гиперболы (2.11) асимптоты имеют вид:
называются асимптотами
гиперболы. Для данной гиперболы (2.11) асимптоты имеют вид:
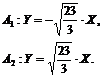
IV. Уравнения осей гиперболы в общей системе координат
Теперь напишем уравнения
осей новой системы 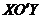 в
исходной системе координат
в
исходной системе координат 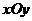 .
.
Так как система 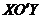 — каноническая для данной
гиперболы, то ее центр находится в центре кривой —
— каноническая для данной
гиперболы, то ее центр находится в центре кривой — 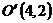 , то есть оси
, то есть оси 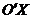 и
и 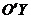 проходят через точку
проходят через точку 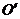 .
.
В пункте II было установлено, что угловой
коэффициент оси 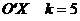 .
.
Уравнение прямой,
проходящей через данную точку 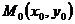 с заданным угловым коэффициентом
с заданным угловым коэффициентом 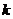 , имеет вид
, имеет вид 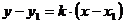 . Следовательно, ось
. Следовательно, ось 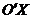 в системе координат
в системе координат 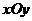 задана уравнением
задана уравнением 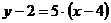 , или
, или 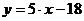 , где в роли точки
, где в роли точки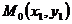 выступает центр гиперболы точка
выступает центр гиперболы точка 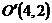 .
.
Так как ось 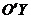 перпендикулярна оси
перпендикулярна оси 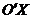 , то ее угловой коэффициент
, то ее угловой коэффициент 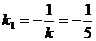 . Следовательно, ось
. Следовательно, ось 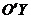 в системе координат
в системе координат 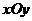 задана уравнением
задана уравнением 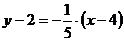 , или
, или 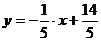 .
.
V. Построение графиков гиперболы
Используя полученные в
ходе выполнения задания данные, построим гиперболу (2.1) в исходной системе
координат  (см. рис. 1)
и гиперболу (2.11) в канонической системе координат (см. рис. 2).
(см. рис. 1)
и гиперболу (2.11) в канонической системе координат (см. рис. 2).
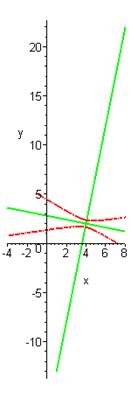
Рисунок 1.
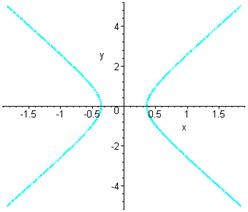
Рисунок 2.
Вывод
Таким образом, из
вышеприведенного решения видим, что с помощью инвариантов можно отследить тип
кривой второго порядка с параметром 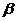 , а используя параллельный перенос и поворот
осей координат, можно привести кривую второго порядка от общего вида к
каноническому.
, а используя параллельный перенос и поворот
осей координат, можно привести кривую второго порядка от общего вида к
каноническому.
Список используемой литературы
1. Л.В. Бобылева, Л.С. Брюхина. Линейная алгебра и
аналитическая геометрия. Исследование кривых второго порядка.— Дубна:
Международный университет природы, общества и человека «Дубна», 2003.
2. Ильин В. А., Позняк Г. Д. Аналитическая геометрия. — М.:
Физматлит , 2002.
3. М.Я. Выгодский. Справочник по высшей математике.— М:
Наука, 1966.
4. А.В. Ефремов, Б.П. Демидович. Сборник задач по математике
для втузов. Линейная алгебра и основы математического анализа (Ч. 1). — М.:
Наука, 1993.