Теория упругости
Российский
государственный университет
нефти и газа
им. И.М.Губкина
Кафедра
технической механики
РЕФЕРАТ
«Теория
упругости»
Выполнил: Поляков А. А.
МИ-09- 1
Проверил: Евдокимов А.П.
Москва 2011
СОДЕРЖАНИЕ
теория
упругость уравнение
1. Введение
. Теория напряженно-деформированного
состояния в точке тела
2.1 Теория напряжений
.2 Теория деформаций
.3 Связь между напряженным и
деформированным состоянием для упругих тел
. Основные уравнения теории
упругости . Типы задач теории упругости
.1 Основные уравнения теории
упругости
.2 Типы задач теории упругости
.3 Прямая и обратная задачи теории
упругости
.4 Уравнения теории упругости в
перемещениях(уравнения Ламе)
. Вариационные принципы теории
упругости
.1 Принцип возможных перемещений
(принцип Лагранжа)
.2 Принцип возможных состояний
(принцип Кастильяно)
.3 Соотношение между точным решением
и решениями, получаемыми на основе принципов Лагранжа и Кастильяно
. Список использованной литературы
1. Введение
Теории напряжений и деформаций были созданы О.
Коши. Они изложены в работе, представленной в Парижскую академию наук в 1822
г., краткое содержание которой опубликовано в 1823 г. и ряде последующих
статей. О.Коши вывел три уравнения равновесия элементарного четырехгранника,
доказал закон парности касательных напряжений, ввел понятия главных осей и
главных напряжений и вывел дифференциальные уравнения равновесия (обычно они в
курсе сопротивления материалов не выводятся). Им же введена поверхность
нормальных напряжений (квадрика Коши), на которой располагаются концы
радиус-векторов, направления которых совпадают с направлением нормалей к
площадкам, а величина обратно пропорциональна корню квадратному из абсолютной
величины нормального напряжения в этой площадке, и доказано, что эта
поверхность является поверхностью второго порядка с центром в начале координат.
Возможность преобразования поверхности нормальных напряжений к главным осям
свидетельствует о существовании в каждой точке трех взаимно главных
перпендикулярных площадок.
Аналогичная поверхность касательных напряжений
была введена русским механиком Г.В. Колосовым в 1933 г.
Геометрическая интерпретация напряженного
состояния в пространстве в виде эллипсоида напряжений была дана Г. Ламе и Б.
Клапейроном в их мемуарах, представленных в Парижскую академию наук в 1828 г. и
опубликованных в 1833 г.
Геометрическое изображение напряженного
состояния на плоскости для одной серии площадок, проходящих через главную ось,
в виде окружности напряжений было предложено К. Кульманом в его книге в 1866 г.
Для общего случая напряженного состояния очень
наглядная геометрическая интерпретация его на плоскости дана О. Мором (так
называемая круговая диаграмма Мора) в 1882 г. Из нее можно сделать ряд важных
заключений об экстремальности главных напряжений, положении площадок, в которых
касательные напряжения максимальны, и о величинах этих максимальных касательных
напряжений.
О.Коши дал определение деформаций, вывел
зависимость их от перемещений в частном случае малых деформаций (эти
зависимости, как правило, в курсе сопротивления материалов не выводятся),
определил понятия главных напряжений и главных деформаций и получил зависимости
компонентов напряжений от компонентов деформаций, как для изотропного, так и
для анизотропного упругого тела. В сопротивлении материалов обычно устанавливаются
зависимости компонентов деформаций от компонентов напряжений для изотропного
тела. Они называются обобщенным законом Гука, хотя, конечно, это название
условно, так, как Р. Гуку понятие напряжения известно, не было.
В указанных зависимостях Коши вначале ввел две
постоянных и записал зависимости напряжений от деформаций в виде
m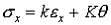
,
, 
, 
,
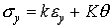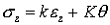
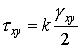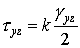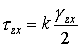
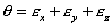
где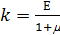 
,
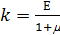Однако в дальнейшем О.Коши принял
концепцию Л. Навье. Согласно ей упругие тела состоят из молекул, между которыми
при деформировании возникают силы, действующие по направлениям прямых линий,
соединяющих молекулы, и пропорциональные изменению расстояний между молекулами.
Тогда число упругих постоянных для общего случая анизотропного тела равно 15, а
для тела изотропного получаем одну упругую постоянную. Этой гипотезы
придерживался С. Пуассон, а вначале - Г. Ламе и Б. Клапейрон. На основании ее
Пуассон установил, что коэффициент поперечной деформации равен 1/4.
Д. Грин в 1839 г. вывел зависимость
между деформациями и напряжениями без использования гипотезы о молекулярном
строении упругих тел . Он получил их на основе принципа сохранения энергии,
введя понятие упругого потенциала, и показал, что при использовании линейных
зависимостей шести компонентов деформаций от шести компонентов напряжений из 36
коэффициентов независимыми являются 21, т.е.в общем случае анизотропного тела
число упругих постоянных равно 21. Для изотропного тела число упругих
постоянных снижается до двух. Теория, в которой число упругих постоянных для
анизотропного тела равно 15, а для изотропного 1, иногда называлась «рариконстантной»
или «униконстантной», а теория, в которой число упругих постоянных для
анизотропного тела равно 21, а для изотропного 2 - «мультиконстантной».
Спор между сторонниками этих теорий
побудил физиков к экспериментальным исследованиям.
Г. Вертгейм на основании замеров
внутренних объемов стеклянных и металлических труб при осевом растяжении
установил в 1848 г., что коэффициент поперечной деформации не равен 1/4. Он
считал его различным для различных материалов, но для многих материалов близким
к 1/3.
А.Я. Купфер, испытывая в 1853 г. на
растяжение и кручение, металлические стержни, также получил, что отношение
модулей при сдвиге и растяжении не соответствует величине поперечной
деформации, равной 1/4.
Ф. Нейманн испытывал в 1855 г. на
изгиб образцы прямоугольного поперечного сечения и измерял при этом углы
поворота двух граней балки, (перечное сечение принимает трапецеидальную форму).
В результате он показал, что коэффициент поперечной деформации не равен 1/4. К
такому же выводу пришел Г. Кирхгоф, ученик Ф.Неймана, на основании проведенных
в 1859 г. испытаний на совместный изгиб и кручение круглых латунных стержней,
заделанных одним концом и нагруженных на другом сосредоточенной силой, с
замером угла закручивания стержня и угла поворота сечения.
Большое экспериментальное
исследование коэффициентов поперечной деформации для различных сортов стали,
провел один из учеников Г.Кирхгофа М.Ф. Окатов в 1865 - 1866 гг. Результаты
приведены в его докторской диссертации .Испытания на кручение и изгиб тонких
призм, вырезанных из монокристаллов, а также испытания сжимаемости кристаллов
при всестороннем равном сжатии были проведены В.Фойгтом и описаны в его
многочисленных статьях, объединенных в дальнейшем в книге, опубликованной в
1910 г. Они подтвердили правильность мультиконстантной теории.
Глубокое исследование математической
структуры закона Гука для анизотропных тел было проведено механиком и инженером
Яном Рыхлевским в 1984 г. на основе введенного им понятия собственного упругого
состояния. В частности, им показано, что 21 упругая постоянная представляет
собой шесть истинных модулей жесткости, 12 дистрибуторов жесткости и три угла.
2. Теория напряженно-деформированного состояния
в точке тела
.1 Теория напряжений
Внутренние силовые факторы, возникающие при нагружении
упругого тела, характеризуют состояние того или иного сечения тела, но не дают
ответа на вопрос о том, какая именно точка поперечного сечения является
наиболее нагруженной, или, как говорят, опасной точкой. Поэтому необходимо
ввести в рассмотрение какую-то дополнительную величину, характеризующую
состояние тела в данной точке.
Если тело, к которому приложены внешние силы,
находится в равновесии, то в любом его сечении возникают внутренние силы
сопротивления. Обозначим через 
внутреннее усилие,
действующее на элементарную площадку 
,
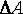а нормаль к этой площадке через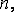 
тогда величина
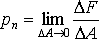(1)
называется полным напряжением.
В общем случае полное напряжение не совпадает по
направлению с нормалью к элементарной площадке, поэтому удобнее оперировать его
составляющими вдоль координатных осей -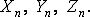 
Если внешняя нормаль совпадает с какой-либо координатной
осью, например, с осью Х, то составляющие напряжения примут вид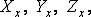 
при
этом составляющая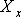 
оказывается
перпендикулярной сечению и называется нормальным напряжением, а составляющие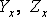 
будут
лежать в плоскости сечения и называются касательными напряжениями.
Чтобы легко различать нормальные и касательные
напряжения обычно применяют другие обозначения: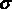 
-
нормальное напряжение, 
- касательное.
Выделим из тела, находящегося под действием
внешних сил, бесконечно малый параллелепипед, грани которого параллельны
координатным плоскостям, а ребра имеют длину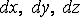 
.
На каждой грани такого элементарного параллелепипеда действуют по три
составляющие напряжения, параллельные координатным осям. Всего на шести гранях
получим 18 составляющих напряжений.
Нормальные напряжения обозначаются в виде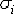 
,
где индекс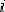 
обозначает нормаль
к соответствующей грани (т.е. может принимать значения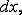 
).
Касательные напряжения имеют вид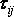 
;
здесь первый индекс соответствует нормали к той площадке, на которой действует
данное касательное напряжение, а второй указывает ось, параллельно которой это
напряжение направлено (рис.1).
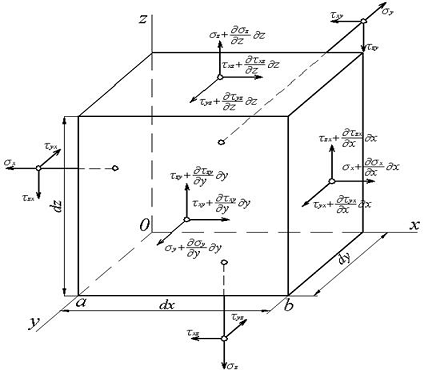
Рис.1. Нормальные и касательные напряжения
Для этих напряжений принято следующее правило
знаков. Нормальное напряжение считается положительным при растяжении, или, что
то же самое, когда оно совпадает с направлением внешней нормали к площадке, на
которой действует. Касательное напряжение считается положительным, если на
площадке, нормаль к которой совпадает с направлением параллельной ей
координатной оси, оно направлено в сторону соответствующей этому напряжению
положительной координатной оси.
Составляющие напряжений являются функциями трех
координат. Например, нормальное напряжение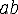 
в
точке с координатами 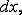можно обозначать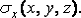 
В точке, которая отстоит от рассматриваемой на
бесконечно малом расстоянии, напряжение 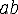с
точностью до бесконечно малых первого порядка можно разложить в ряд Тейлора:
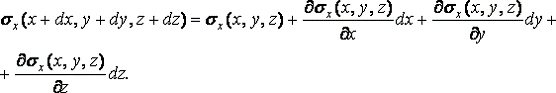
Для площадок, которые параллельны плоскости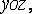 
изменяется
только координата х, а приращения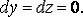 
Поэтому
на грани параллелепипеда, совпадающей с плоскостью 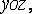нормальное
напряжение будет 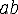, а на параллельной
грани, отстоящей на бесконечно малом расстоянии 
,
- 
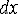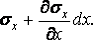Напряжения
на остальных параллельных гранях параллелепипеда связаны аналогичным образом.
Следовательно, из 18 составляющих напряжения неизвестными являются только
девять.
В теории упругости доказывается закон парности
касательных напряжений, согласно которому по двум взаимно перпендикулярным
площадкам составляющие касательных напряжений, перпендикулярные линии
пересечения этих площадок, равны друг другу:
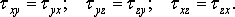(2)
Равенства (2) приводят к тому, что из девяти
составляющих напряжений, характеризующих напряженное состояние в точке тела,
остаются только шесть:
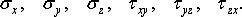(3)
Можно показать, что напряжения (3) не просто
характеризуют напряженное состояние тела в данной точке, но определяют его
однозначно. Совокупность этих напряжений образует симметричную матрицу, которая
называется тензором напряжений:
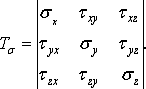(4)
Тензоры можно складывать и вычитать, при этом
суммой двух тензоров является тензор, компоненты которого представляют собой
сумму соответствующих компонентов слагаемых тензоров.
При умножении тензора на скалярную величину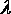 
получится
новый тензор, все компоненты которого в 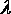раз
больше компонентов исходного тензора.
.2 Теория деформаций
Под действием внешних нагрузок упругое тело
изменяет свою форму, деформируется. При этом точки тела принимают какое-то
новое положение. Для определения деформации упругого тела сравним положения
точек тела до и после приложения нагрузки.
Рассмотрим точку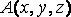 
ненагруженного
тела и ее новое положение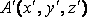 
после приложения
нагрузки. Вектор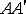 
называется
вектором перемещения точки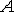 
(рис.2).
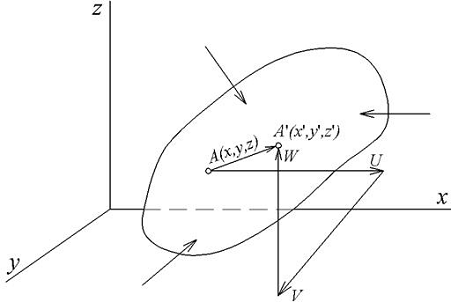
Рис.2. Вектор перемещения точки
Возможны два вида перемещений: перемещение всего
тела как единого целого без деформирования - такие перемещения изучает
теоретическая механика как перемещения абсолютно твердого тела, и перемещение,
связанное с деформацией тела - такие перемещения изучает теория упругости.
Обозначим проекции вектора перемещения точки 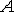на
координатные оси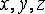 
через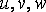 
соответственно.
Они равны разности соответствующих координат точек 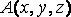и
:
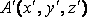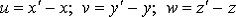
и являются функциями координат:
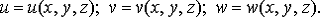
Деформирование тела вызвано разницей в
перемещениях различных его точек. Бесконечно малый параллелепипед с ребрами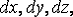 
вырезанный
из упругого тела около произвольной точки ,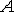
вследствие различных перемещений его точек деформируется таким образом, что
изменяется длина его ребер и искажаются первоначально прямые углы между
гранями.
На рис.3.3 показаны два ребра этого
параллелепипеда: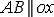 
и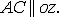 
длина
ребр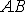а 
равн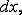а
а
ребра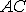 
-
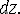
После деформации точки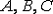 
принимают
положение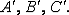 
При этом точка 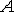получит
перемещение, составляющие которого в плоскости чертежа равны 
и 
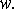Точка
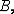отстоящая
от точки 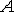на
бесконечно малом расстоянии 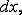получит
перемещение, составляющие которого будут отличаться от составляющих перемещения
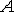точки на
бесконечно малую величину за счет изменения координаты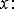 
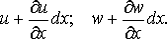
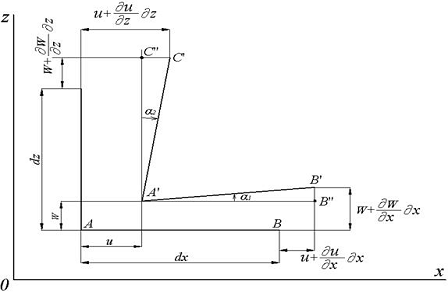
Рис.3. Линейные и угловые деформации
Составляющие перемещения точки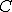 
будут
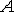отличаться от составляющих перемещения точки на
бесконечно малую величину за счет изменения координаты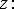 
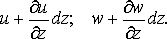
Длина проекции ребра 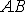на
ось 
после
деформации:
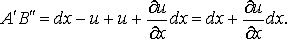(5)
Проекция абсолютного удлинения ребра 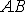на
ось
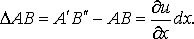
Относительное удлинение вдоль оси
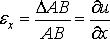(6)
называется линейной деформацией по направлению
оси .
Аналогично определяются линейные деформации по
направлениям осей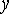 
и
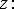
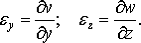(7)
Рассмотрим изменение углов между ребрами
параллелепипеда (рис.3). Тангенс угла поворота ребра 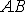в
плоскости 
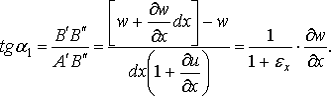
Вследствие малости деформаций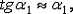 
а
линейной деформацией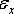 
можно пренебречь
ввиду ее малости по сравнению с единицей, и тогда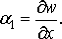 
Аналогичным образом можно определить угол
поворота ребра 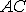в той же
плоскости:
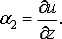
Искажение прямого угла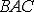 
называется
угловой деформацией и определяется как сумма углов поворота ребер 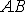и
:
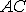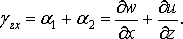(8)
Таким же образом определяются угловые деформации
в двух других координатных плоскостях:
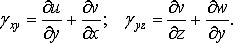(9)
Формулы (6)-(9) дают шесть основных зависимостей
для линейных и угловых деформаций от составляющих перемещения. Эти зависимости
называются уравнениями Коши:
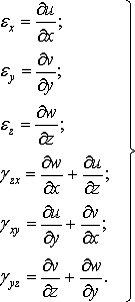(10)
В пределе, когда длины ребер параллелепипеда
стремятся к нулю, соотношения Коши определяют линейные и угловые деформации в
окрестности точки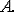 
Положительным линейным деформациям соответствуют
удлинения, а отрицательным - укорочения. Угол сдвига считается положительным
при уменьшении угла между положительными направлениями соответствующих
координатных осей и отрицательным - в противном случае.
Аналогично тензору напряжений, деформированное
состояние тела в данной точке описывается тензором деформаций
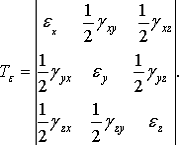(11)
Как и тензор напряжений, тензор деформаций
является симметричной матрицей, которая содержит девять компонентов, шесть из
которых являются различными.
2.3 Связь между напряженным и деформированным
состоянием для упругих тел
Зависимости между напряжениями и деформациями
носят физический характер. Ограничиваясь малыми деформациями, связь между
напряжениями и деформациями можно считать линейной.
При испытании стержня на растяжение (о
механических испытаниях материалов будет подробно рассказано в следующем
разделе) установлена пропорциональная зависимость между нормальным напряжением
и линейной деформацией в одном направлении, которая называется законом Гука:
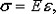(12)
где упругая постоянная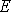 
называется
модулем продольной упругости.
Тем же экспериментальным путем установлена связь
между линейными деформациями в продольном и поперечном направлениях:
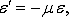(13)
где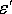 
-
линейная деформация в поперечном направлении,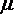 
-
вторая упругая постоянная, называемая коэффициентом Пуассона.
При механических испытаниях на чистый сдвиг
установлена прямо пропорциональная зависимость между касательным напряжением и
угловой деформацией в плоскости действия этого напряжения, которая получила
название закона Гука при сдвиге:
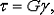(14)
где величина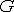 
является
третьей упругой постоянной и называется модулем сдвига. Однако эта упругая
постоянная не является независимой, т.к. связана с первыми двумя зависимостью
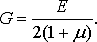(15)
Чтобы установить зависимости между деформациями
и напряжениями, выделим из тела бесконечно малый параллелепипед (рис.1) и
рассмотрим действие только нормальных напряжений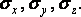 
Разницей
напряжений на противоположных гранях параллелепипеда можно пренебречь, т.к. она
приводит к деформациям более высокого порядка малости.
Определим удлинение ребра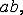 
параллельного
напряжению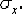 
При действии этого
напряжения согласно закону Гука (3.12) произойдет относительное удлинение ребра
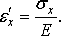
Напряжение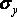 
вызывает
аналогичное удлинение в направлении, перпендикулярном ребру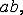
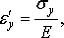
а в направлении ребра - укорочение, которое
согласно (13) составляет
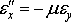
или, с учетом выражения деформации
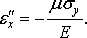
Аналогично определяется относительное укорочение
ребра 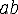при
действии напряжения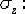 
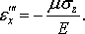
На основании принципа независимости действия сил
полное относительное удлинение ребра 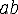можно
определить как сумму удлинений от действия каждого напряжения:
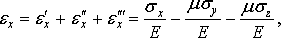
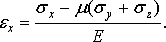
Аналогично можно определить линейные деформации
по направлениям двух других осей:
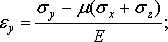
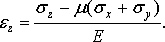
В соответствии с законом Гука при сдвиге (14)
связь между угловыми деформациями и касательными напряжениями можно представить
независимо для каждой из трех плоскостей, параллельных координатным плоскостям:
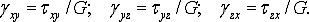
Таким образом, получены шесть формул, которые
выражают линейную зависимость между составляющими деформации и напряжений в
изотропном упругом теле и называются обобщенным законом Гука:
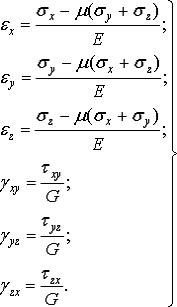(16)
3. Основные уравнения теории упругости . Типы
задач теории упругости
Основная задача теории упругости - определение
напряженно-деформированного состояния по заданным условиям нагружения и
закрепления тела.
Напряженно-деформированное состояние
определено, если найдены компоненты тензора напряжений {s} и вектора перемещений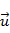 
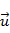, девять функций.
3.1 Основные уравнения теории упругости
Для того, чтобы найти эти девять функций надо
записать основные уравнения теории упругости, или:
Дифференциальные Коши
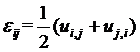(17)
где - компоненты тензора линейной
части деформаций Коши;
компоненты тензора производной
перемещения по радиусу.
Дифференциальные уравнения
равновесия
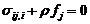(18)
где - компоненты тензора напряжений; - проекция
объемной силы на ось j.
Закон Гука для линейно-упругого изотропного тела
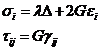(19)
где - константы Ламе; для изотропного тела.
Здесь - нормальные и касательные напряжения; деформации и углы сдвига
соответственно.
Вышеперечисленные уравнения должны удовлетворять
зависимостям Сен-Венана
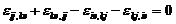(20)
В теории упругости задача решена, если
выполняются все основные уравнения.
.2 Типы задач теории упругости
Граничные условия на поверхности тела должны
выполняться и в зависимости от типа граничных условий различают три типа задач
теории упругости.
Первый тип. На поверхности тела заданы силы.
Граничные условия
Второй тип. Задачи, в которых на поверхности
тела задано перемещение. Граничные условия
Третий тип. Смешанные задачи теории упругости.
На части поверхности тела заданы силы, на части поверхности тела задано
перемещение. Граничные условия
.3 Прямая и обратная задачи теории упругости
Задачи, в которых на поверхности тела заданы
силы или перемещения, а требуется найти напряженно-деформированное состояние
внутри тела и то, что не задано на поверхности, называют прямыми задачами. Если
же внутри тела заданы напряжения, деформации, перемещения и т.д., а требуется
определить то, что не задано внутри тела, а также перемещения и напряжения на
поверхности тела (то есть найти причины, вызвавшие такое
напряженно-деформированное состояние) ), то такие задачи называются обратными.
.4 Уравнения теории упругости в перемещениях
(уравнения Ламе)
Для определения уравнений теории упругости в
перемещениях запишем: дифференциальные уравнения равновесия (18)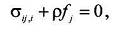 
закон
Гука для линейно-упругого изотропного тела (19)
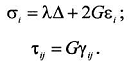
Если учесть, что деформации выражаются через
перемещения (17), запишем:
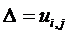(22)
Следует также напомнить, что угол сдвига связан
с перемещениями следующим соотношением (17):
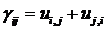(23)
Подставив в первое уравнение равенств (19)
выражение (22), получим, что нормальные напряжения
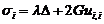(24)
Отметим, что запись иц в данном случае не
подразумевает суммирования по i.
Подставив во второе уравнение равенств (19)
выражение (23), получим, что касательные напряжения
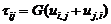(25)
Запишем уравнения равновесия (18) в
развернутом виде для j = 1
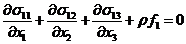(26)
Подставив в уравнение (26) выражения
для нормальных (24) и касательных (25) напряжений, получим
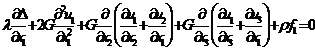(27)
где λ- константа
Ламе, которая определяется по выражению:
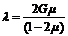(28)
Подставим выражение (28) в уравнение
(27) и запишем,
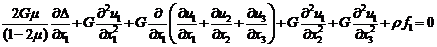(29)
где определяется по выражению (22), или в
развернутом виде
Разделим выражение (29) на G
и приведем подобные слагаемые и получим первое уравнение Ламе:
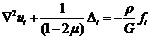(30)
где - оператор Лапласа
(гармонический оператор), который определятся как
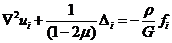(31)
Аналогично можно получить:
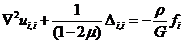(32)
Уравнения (30) и (32) можно записать
в следующем виде:
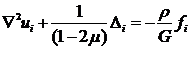(33)
Уравнения (33) или (30) и (32)
являются уравнениями Ламе. Если объемные силы равны нулю или постоянны, то
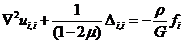(34)
причем запись в данном случае не подразумевает
суммирования по i. Здесь
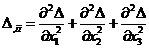(35)
или, с учетом (31)
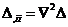(36)
Подставив (22) в (34) и проведя преобразования,
получим
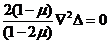
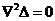(37)
где - функция, удовлетворяющая
данному равенству. Если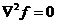 
следовательно, f - функция
гармоническая. Значит и объемная деформация также функция гармоническая.
Считая верным предыдущее предположение, возьмем
гармонический оператор от i
-ой строчки уравнения Ламе
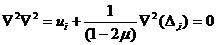(38)
где
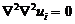(39)
Если объемные силы равны нулю или
постоянны, то компоненты перемещения есть бигармонические функции.
Известны различные формы представления
бигармонических функций через гармонические (удовлетворяющие уравнениям Ламе).
где k
= 1,2,3. Причем
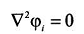и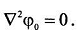 
Можно показать, что такое представление
перемещений через гармоническую функцию обращает в тождество уравнения Ламе
(33). Часто их называют условиями Попковича-Гродского. Четыре гармонические
функции не обязательны, ведь ф0 можно приравнять нулю.
4. Вариационные принципы Теории упругости.
.1 Принцип возможных перемещений (принцип
Лагранжа)
Принцип Лагранжа. Для тела, находящегося в
равновесии, работа внешних и внутренних сил на любых возможных бесконечно малых
приращениях перемещений равна нулю.
Используя теорему Клапейрона ,что для
упругодеформированного тела варьируя перемещением, получаем принцип Лагранжа
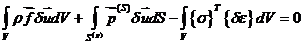(40)
Возможными в механике деформируемых тел называют
такие перемещения, которые удовлетворяют внешним и внутренним связям,
наложенным на тело.
Внешние связи - это условия закрепления,
внутренние связи - условие сплошности.
Чтобы удовлетворить внутренним связям, надо,
чтобы приращения перемещений были непрерывными однозначными функциями
координат.
В такой форме принцип Лагранжа справедлив для
любых деформируемых тел.
Для упругих тел было получено, что
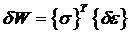(41)
Тогда (40) с учетом (41) запишется как
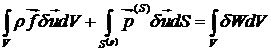(42)
где W - удельная
деформация, а
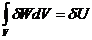(43)
Здесь U
- вариация всей потенциальной энергии тела.
Подставим в (42) выражение (43), и, поскольку
силы не варьируются, запишем, что
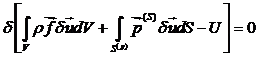(44)
Уравнение (44) является вариационным уравнением
Лагранжа.
Если силы консервативны, то первые два интеграла
представляют собой изменение потенциала внешних сил при переходе из
недеформирован-ного состояния в деформированное.
Потенциал внешних сил
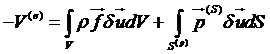(45)
где - возможная работа внешних сил
при переходе из недеформирован-ного в деформированное состояние вычислена в
предположении, что внешние силы остаются неизменными. Полная энергия системы
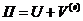(46)
Тогда с учетом выражений (44) - (46) принцип
Лагранжа запишется:
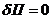(47)
то есть вариация полной энергии системы в
положении равновесия на возможных перемещениях равна нулю. Выражение (47)
является вариационным уравнением Лагранжа в случае действия только
консервативных сил.
В положении устойчивого равновесия полная
энергия П минимальна,
когда
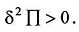
Принцип Лагранжа - принцип минимальной энергии.
.2 Принцип возможных состояний (принцип
Кастильяно)
Будем называть возможными состояниями такие,
которые находятся в соответствии с внешними и внутренними силами, то есть
удовлетворяющие уравнениям равновесия.
Удельная дополнительная работа в случае
линейно-упругого тела записывается по выражению,
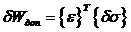(49)
Тогда, взяв вариацию дополнительной энергии тела
и подставив в выражение (48) уравнение (49), получаем
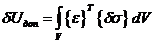
или, используя уравнение (50), можно записать
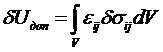(51)
Рассмотрим возможные напряженные состояния при
действии на тело объемных сил. Так как рассматриваются возможные напряженные
состояния, то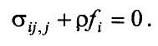 
Следовательно,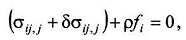 
откуда
следует, что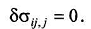
При действии поверхностных сил связь напряжений
и усилий можно записать
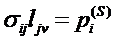(52)
Рассмотрим возможные напряженные состояния. В
этом случае
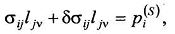
Откуда также следует, что
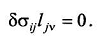
Вернемся к подинтеральному выражению уравнения
(51). Выразим деформации через перемещения (17) и запишем или
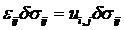(53)
Продифференцировав выражение (53), получим
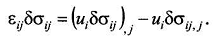
Подставим в выражение (51) уравнение
(53). Тогда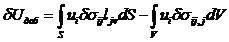
(54) причем
на поверхности ,на которой заданы силы
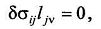
и, следовательно, второй интеграл
выражения (54)
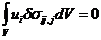(55)
Подынтегральное выражение первого
интеграла выражения (54) может быть записано как
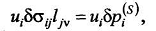
или в векторной форме
где - силы, действующие по той части
поверхности, на которой заданы перемещения (незаданные поверхностные силы).
Подставив выражения (55) и (56) в (54), получим,
что
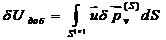(57)
Уравнение (57) записывает Принцип Кастильяно.
При возможных изменениях напряженного состояния тела вариация равна интегралу
по той части поверхности тела, на которой заданы перемещения от произведений
возможных поверхностных сил на перемещения.
.3 Соотношение между точным решением и
решениями, получаемыми на основе принципов Лагранжа и Кастильяно
На основе принципа Лагранжа, выбирая какие-то
функции, или их набор, и так как набор функций ограниченный, то получаем
меньшее число степеней свободы системы, таким образом, уменьшаем и степени
свободы конструкции. То есть в энергетическом смысле решение получается жестче,
чем точное.
Если брать интегральные характеристики, то
приближенное решение более жестко интегрально.
При решении задачи о нагружении шарнирно опертой
балки поперечной силой в середине пролета (рис. 1), то приближенное решение
даст меньшее перемещение под силой, чем при точном решении.
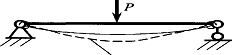
точное решение
Рис.1
При решении той же задачи при помощи
вариационного принципа Кастильяно, так как не выполняется условие сплошности,
система получает большую свободу, чем в действительности.
Точное решение находится между этим двумя
приближенными способами (Лагранжа и Кастильяно). Иногда разница между
полученными решениями невелика.
5. Список использованной литературы
1. Александров А.В., Потапов В.Д.
Основы теории упругости и пластичности. 400 стр.Высшая школа.1990г.
2. Веретимус Д.К. Основы теории
упругости.Часть I.Теория
напряжений .Методическое пособие по курсу «Основы теории упругости и
пластичности». 2005.-37с.
. Веретимус Д.К. Основы
теории упругости.Часть II
.Теория деформаций. Связь между напряженным и деформированным
состоянием.Методическое пособие по курсу «Основы теории упругости и
пластичности»,2005.-53с.
. Веретимус Д.К. Основы
теории упругости.Часть III
.Основные уравнения теории упругости.Типы задач теории упругости.Методическое
пособие по курсу «Основы теории упругости и пластичности»,2005.-45с.