Системы с открытым ключом: алгоритм шифрования RSA

Системы с открытым ключом: алгоритм шифрования RSA

Нижегородский государственный университет им. Н. И. Лобачевского

Факультет вычислительной математики и кибернетики

Кафедра информатизации и автоматизации научных исследований

Курсовая работа

Системы с открытым ключом: алгоритм шифрования RSA

Выполнил: Скульский М. А.

Научный руководитель: Фомина И. А.

Н. Новгород, 1997 г.

Оглавление

Введение

Понятие криптосистемы с открытым ключом

Описание алгоритма RSA

Возможные атаки на RSA

Практическая реализация RSA

Обоснование алгоритма

Комментарии к программе

Текст программы

Литература

Введение

Основной целью построения криптографических систем всегда была защита информации при ее передаче и хранении. Эта проблема остается актуальной и до сегодняшнего дня, однако же развитие вычислительных систем придало ей новое качество: вопрос уже не просто в том, чтобы, скажем, Александр мог послать письмо Борису, не опасаясь, что оно будет прочитано Сергеем. Сетевые компьютерные системы могут включать в себя сотни и даже тысячи пользователей; в такой ситуации классическая симметричная схема оказывается неэффективной. Новым требованием к криптосистемам также является обеспечение аутентификации сообщения - доказательство того, что Борис получил именно то сообщение, которое ему отправил Александр, и что оно не было подделано или изменено злоумышленником в процессе передачи. Кроме того, приходится мириться с тем, что к зашифрованной информации потенциально может иметь доступ довольно большое количество людей - например, маршрут любого сообщения, проходящего через Internet, в принципе невозможно предсказать, оно может пройти через несколько десятков узлов прежде чем попадет к своему адресату. Так что, если прежде наиболее надежным подходом к защите информации был все-таки амбарный замок, то теперь задача все более усложняется противоречивыми требованиями одновременно надежности и секретности передачи и легкости доступа к информации.

Традиционная криптографическая схема выглядит следующим образом. Александр и Борис оба знают некий ключ, с помощью которого они могут обмениваться зашифрованными сообщениями так, что любое третье лицо, даже если ему удастся перехватить шифровку, не сможет ничего в ней понять. Такая схема называется симметричной, так как и адресат, и отправитель используют один и тот же ключ для шифрования и дешифрования. Давайте попробуем применить ее к какой-нибудь простой распределенной задаче. Пусть у нас есть некое сетевое устройство - например, ядерная ракетная установка, - принимающая команды по сети. Конечно, не от всех, а только от имеющих соответствующие права доступа. Пусть у нашего устройства есть некий ключ, которым должны быть зашифрованы все команды, подаваемые на него. Этот ключ, так как систему мы предполагаем симметричной, необходимо сообщить всем пользователям. Теперь предположим, что Александр зашифровал сообщение “Стреляй в Бориса” и отправил его нашему устройству. Другой пользователь, Сергей, подкупленный Борисом, перехватил это сообщение и, зная ключ, с легкостью расшифровал его, сообщив о содержании Борису. Казалось бы, проблема легко решается введением разных паролей для разных пользователей. Ну а если доступ к данному устройству должен быть более или менее свободным?

Теперь давайте представим себе сеть из, например, ста пользователей и сервера баз данных. Между пользователями и сервером происходит некий обмен информацией, причем всем пользователям совершенно необязательно и, более того, нежелательно знать информацию, хранимую и запрашиваемую на сервере другими пользователями. Разумеется, необходимо защитить сам сервер - так, чтобы каждый пользователь имел доступ только к своей информации. Но ведь все это происходит в одной сети, и все данные передаются по одним и тем же проводам, а если это, скажем, что-нибудь типа Token Ring, то информация от сервера до владельца последовательно проходит через все станции, находящиеся между ними в кольце. Следовательно, ее необходимо шифровать. Можно опять ввести для каждого пользователя свой пароль, которым и шифровать весь информационный обмен с сервером. Но как отличить одного пользователя от другого? Один вариант - перед началом работы спрашивать у пользователя этот самый пароль и сверять с хранящимся на сервере. Но тогда он с легкостью может быть перехвачен в том же самом канале связи. Другой вариант - пароль не спрашивать, а верить тому, что пользователь говорит о себе. Так как пароль секретный, то даже сказав серверу “Я - Александр!”, злоумышленник не сможет расшифровать получаемые данные. Но зато он сможет получить столько материала для взлома шифра, сколько ему захочется - при этом часто можно предсказать ответ сервера на какой-то специфический вопрос и получить сразу шифр и соответствующий оригинальный текст. Согласитесь, это очень продвигает нас в взломе сервера.

Данная проблема носит название проблемы распределения ключей. Ее наличие делает симметричную схему неприспособленной для задач обмена данными с большим количеством пользователей, так как в ней для шифрования и дешифрования используется один и тот же ключ.

Понятие криптосистемы с открытым ключом

Концепция криптосистем с открытым ключом была предложена в 1976 г Уайтфилдом Диффи и Мартином Хеллманом в качестве решения проблемы распределения ключей. В соответствии с ней, каждая сторона получает пару ключей - открытый и закрытый. Открытый ключ распространяется свободно, в то время как закрытый держится в тайне. Исходный текст шифруется открытым ключом адресата и передается ему. Обратный процесс в принципе не может быть выполнен с помощью открытого ключа, для расшифровки получатель использует закрытый ключ, который известен только ему. Таким образом, кто угодно может посылать шифрованные сообщения, для этого ему не надо знать ничего тайного, но при этом только владелец закрытого ключа сможет их прочитать.

Системы с открытым ключом базируются на использовании так называемых односторонних функций - функций, вычислить значения которых во много раз проще, чем значения их обратной функции. Особенно важен подкласс односторонних функций-ловушек - так называются односторонние функции, вычисление которых в обратную сторону возможно при наличии некоторой дополнительной информации, и очень трудно иначе. Открытый ключ является параметром при вычислении односторонней функции; закрытый же представляет информацию, необходимую для вычисления обратной. Хорошая односторонняя функция должна обладать следующими очевидными свойствами:

Обратную функцию очень сложно вычислить, не зная закрытого ключа;

Закрытый ключ невозможно найти из открытого;

Сложность вычисления должна катастрофически возрастать с возрастанием длины ключа.

Существует большое количество функций, которые считаются односторонними, однако отсутствие полиномиального решающего алгоритма ни для одной не доказана. Поэтому при использовании любой системы с открытым ключом всегда остается риск того что в будущем обнаружится быстрый алгоритм нахождения обратной функции без закрытого ключа. На самом деле, корнем любой такой функции является какая-нибудь математическая проблема, традиционно считающаяся трудной. Если удается доказать, что раскрытие шифра эквивалентно разрешение этой проблемы, то проблема надежности шифра зависит от справедливости гипотезы P ¹ NP. Наиболее часто используются:

Разложение больших чисел на простые множители - RSA;

Вычисление дискретного логарифма (логарифма в конечном поле) - система Эль-Гамаля;

Вычисление квадратных корней в конечном поле - система Рабина;

Вычисление дискретного логарифма над эллиптическими кривыми;

Задача о камнях;

Таким образом, с развитием криптографии все более размывается граница между ней и другими областями математики. Новейшие достижения в решении сложных математических проблем сразу же находят применения в криптографии и наоборот, наличие такого лакомого куска подвигает многих математиков на исследования в смежных областях.

Описание алгоритма RSA

Выберем достаточно большие простые числа p и q;

Вычислим n=pq, называемый модулем;

Выберем e<n взаимно простое с j=(p-1)(q-1); е называется открытой экспонентой;

Найдем d | res(p-1)(q-1)(ed)=1 (то есть, ed=1 mod ); d называется закрытой экспонентой;

Теперь (n, d) - закрытый ключ; (n, e) - открытый ключ;

Шифрование: ;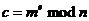

Дешифрование: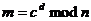

Здесь m - целое число, .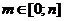

Ниже я сделаю некоторые комментарии к сказанному, а также приведу полное обоснование данного алгоритма, а сейчас обсудим вопрос о его потенциальной криптостойкости.

Возможные атаки на RSA

Главным и наиболее очевидным способом сломать RSA является отыскание закрытого ключа по данному открытому. Это позволило бы злоумышленнику читать все сообщения, зашифрованные этим ключом. Сделать это можно, например, разложив n на простые множители p и q. После этого отыскание d является тривиальной задачей. Надежность RSA основывается на трудности разложения n.

Лучшим алгоритмом, применяемым для факторизации на сегодняшний день, является NFS (Number Field Sieve - числовое решето), вычислительная сложность которого оценивается как O(exp(1.9223(ln n)1/3 (ln ln n)2/3)). Алгоритм этот сравнительно новый - при разложении знаменитого числа RSA-129, полученного в марте 1994, еще использовалось менее эффективное квадратичное решето, а не NFS. RSA-129 - это 129-значное число, разложение которого считалось весьма желательным с 1977 года. Для осуществления этого проекта через Internet было задействовано 1600 компьютеров (в том числе два факса), работавших в течение восьми месяцев. По некоторым оценкам использование NFS могло бы сократить этот срок в три-четыре раза. Таким образом, если 130 знаков примерно составляют предел для квадратичного решета, то использование NFS поднимает планку до 140-150 знаков. Модуль длиной 512 бит содержит около 155 знаков, поэтому для практически большинства приложений этого достаточно. По мнению фирмы RSA Data Security разложение такого числа будет стоить порядка $1,000,000 и займет около восьми месяцев. Также по ее мнению ключ длиной 768 бит останется неразложимым примерно до 2004 года.

Другим способом сломать RSA является отыскание способа вычисления корней степени e по модулю n. Так как , то даст нам исходное сообщение m. Этот способ не является эквивалентным разложению n, так как он не дает нам закрытого ключа d. Тем не менее само по себе вычисление корней над полями Галуа представляет собой сложную задачу. Известна теорема Рабина о том, что вычисление эквивалентно факторизации n, так что на самом деле практически не предпринималось попыток раскрытия шифра в этом направлении.

Все прочие способы не дают возможности раскрытия всех сообщений, зашифрованных данным ключом. Однако существуют подходы, иногда дающие возможность взломать данное конкретное сообщение. Простейший из них - угадывание оригинала. Злоумышленник видит шифр, догадывается, что в сообщении написано “Стреляй в Бориса”, зашифровывает свою версию известным открытым ключом и сравнивает с шифровкой. Еще один подход основан на свойствах преобразования RSA. Если одно и то же сообщение посылается e разным получателям (где е не основание натурального логарифма, а открытая экспонента), то злоумышленник, перехвативший все е шифровок, сможет восстановить исходное сообщение.

Практическая реализация RSA

Практическая реализация RSA сопряжена с определенными проблемами. Первая и, пожалуй, главная из них - вычислительная сложность алгоритма. По сравнению с большинством симметричных криптосистем RSA работает в несколько сот раз медленнее. При обычной реализации генерация ключа длины k требует O(k4) операций; шифрование - O(k2), а расшифровывание- O(k3) операций. Наиболее быстрая из чисто программных реализаций (bSafe 3.0, RSA Data Security) осуществляет шифрование со скоростью 21.6 Kбит/сек для 512-битного ключа. Это очень быстро если представить себе операции с числами из 150 знаков, но само по себе это конечно же медленно. Поэтому обыкновенно системы с открытым ключом используют в сочетании с какой-нибудь симметричной системой - например, DES. Допустим, Александр хочет послать Борису сообщение. Для этого он генерирует случайный ключ DES и шифрует им текст сообщения. После этого он берет открытый ключ Бориса и шифрует им ключ DES. То, что получается в результате, носит название “двоичного конверта”(digital envelope) и сочетает в себе лучшее из обоих принципов - скорость симметричных систем и удобство использования систем с открытым ключом. Двоичный конверт можно безопасно передавать по линиям связи - используя свой закрытый ключ, Борис сначала восстановит ключ DES, а соответственно и текст исходного сообщения.

Обычной практикой является выбор не слишком большого e - это не отражается на криптостойкости алгоритма, но существенно ускоряет шифрование. Тем не менее, d почти всегда оказывается велико. Поэтому возводить при дешифровании cd обычно оказывается не самой лучшей идеей. К счастью, использование Китайской теоремы об остатках позволяет существенно понизить порядок возведения в степень, а также свести вычисления по модулю n к вычислениям по модулю p и q. Подробнее об этом см. у Е. Бубновой [2]. Результаты несложного теста, проведенного нами с помощью нашей (весьма медленной) реализации RSA приведены в таблице и позволяют наглядно увидеть, почему надо пользоваться Китайской теоремой об остатках и не надо ничего возводить в степень “в лоб”.

При шифровании мы использовали метод последовательного возведения в квадрат, а при дешифровании - теорему об остатках. В результате шифрование оказалось примерно в 2.5 раза медленнее дешифрования!! То есть, грубо говоря, возведение в степень 30-40 занимает втрое больше времени, чем в степень 1,000,000,000.

Еще одна сложная проблема, связанная с реализацией алгоритма - это генерация p и q. Самый примитивный вариант - решето Эратосфена - хорошо работает для чисел длиной знаков 10, не более. Для генерации пригодного к использованию ключа в 150 знаков этот метод не работает. Фирма RSA Data Security рекомендует использовать вероятностный подход - то есть, генерировать не на самом деле простые числа, а те, для которых вероятность того, что они составные, меньше наперед заданной малой величины. Существуют хорошие алгоритмы, позволяющие доказать это для заданного числа - или показать, что оно составное. Однако если тестируемое число на самом деле окажется составным, криптостойкость RSA падает. Поэтому альтернативой этому является использование намного более медленных тестов, позволяющих абсолютно точно сказать простое это число или составное. Классическая группа таких тестов основана на знании простых множителей для p-1 или p+1; если их можно найти, то появляется возможность доказать или опровергнуть простоту p. Вообще проблема доказательства простоты достаточно сложна, но совершенно не эквивалентна разложению чисел на множители, так что за приемлемое время всегда можно найти нужные p и q.

Обоснование алгоритма

Сначала выведем некоторые важные свойства остатков. Через a=resnx будем обозначать остаток от деления n на x; эквивалентная этому запись x=a mod n. Все числа считаются целыми и неотрицательными.

Свойства остатков

Пусть x = a mod n; y = b mod n; Тогда resnxy = resnab

x=un+a; y=vn+b;

Следовательно,

 xy=(un+a)(vn+b)=uvn2+avn+bun+ab;

resnxy=resnab

Пусть x = a mod n; y = b mod n; Тогда resn(x+y) = resn(a+b)

Пусть x = a mod n; 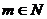Тогда resn(xm) = resn(am)

= resn(x*x*…*x) = resn(a*a*…*a) = resn(am)

Пусть x<n. Тогда resnx=x (resn(x)) = resnx

Пусть n=pq; Тогда resp(resnx) = respx

Следующие два утверждения приводятся без доказательства.

Теорема Эйлера

Пусть p - простое, a<p. Тогда 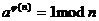, где 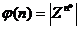 - к-во чисел < n и вз. простых с n; криптосистема открытый ключ

Лемма

Если n = pq, p и q простые, то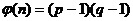

Функция 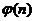называется функцией Эйлера. Следующая теорема использует эти результаты для доказательства возможности найти d; ее доказательство представляет практический способ его нахождения.

Теорема

Пусть e взаимно просто с 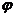. Тогда уравнение 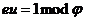имеет единственное решение u <

Существование.

Так как НОД(e, )=1, то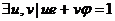

Возможны два случая:>0, v<0. Тогда ue=1+(-v)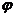; Следовательно ue = 1 mod 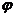<0, v>0.

Рассмотрим

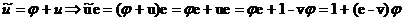
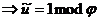
Пусть u >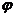, тогда

Единственность

Пусть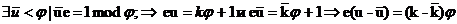

Следовательно,

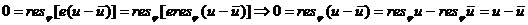
Отсюда окончательно имеем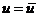

Наконец, последняя теорема доказывает корректность самого алгоритма.

Теорема

При соответствующем условиям алгоритма выборе e и d,

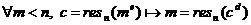
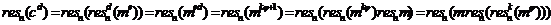
Обозначим это выражение за (*).

Если m взаимно просто с n, то по теореме Эйлера 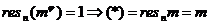что и требовалось. В противном случае либо m=tp, либо m=tq, так как у n нет других делителей; без ограничения общности будем предполагать m=tp. При этом t необходимо меньше q, так как m<n=pq

.

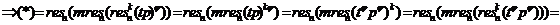
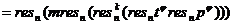Но 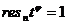(т. Эйлера); следовательно, это равно

 (+)

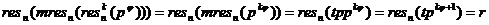Найдем r. Выражение (+) на самом деле означает, что t*p*…*p = Apq+r. Так как это равенство в целых числах, то отсюда следует, что r делится на p. То есть, t*p*…*p=Aq+r/p=r1;

Теперь 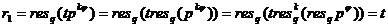 т.к. по т.Эйлера .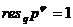

Следовательно, (*)=r=tp=m и в этом случае.

Комментарии к программе

В качестве иллюстрации предлагается реализация алгоритма RSA с длиной модуля 32 бита. В программе используются настоящие простые числа, генерируемые с помощью решета Эратосфена. Для возведения в степень при шифровании используется последовательное возведение в квадрат; при дешифровании - Китайская теорема об остатках. В программе реализован аппарат длинной 64-битной арифметики.

Текст программы

#include <dos.h>

#include <stdio.h>

#include <iostream.h>

#include <string.h>

#include "compcl.cpp"

/*************************************/

/** The following global variables **/

/** are required for all encryption **/

/** and decryption operations. **/

/*************************************/

/* The modulus */long modulus=0;

/* The primes; n=pq */int prime1=0, prime2=0;

/* The public exponent */int pub_exp=0;

/* The private exponent */long priv_exp;

/* The Euler Phi = (p-1)(q-1) */

unsigned long phi=0;

#include "math.cpp"

/*************************************/

/** RSA functions follow. **/

/*************************************/

/* Generate the keys for the first time*/

void InitRSA(void);

/* Initialize RSA for encryption */InitRSAe(unsigned int apub_exp, unsigned long amodulus);

/* Initialize RSA for decryption */InitRSAd (unsigned int aprime1, unsigned int aprime2, comp apriv_exp);

/* Encrypt one LONG of data */

unsigned long encrypt (unsigned long data);

/* Decrypt one LONG of ciphertext */

unsigned long decrypt (unsigned long cipher);

/*************************************/

/** Hehe - the actual function **/

/** instances follow **/

/*************************************/InitRSA(void)

{

get_primes(&prime1,&prime2);

modulus=((unsigned long)prime1)*((unsigned long)prime2);

phi=((unsigned long)(prime1-1))*((unsigned long)(prime2-1));

get_exponents(&pub_exp, &priv_exp);

}

void InitRSAe(unsigned int apub_exp, unsigned long amodulus)

{

modulus=amodulus; pub_exp=apub_exp;

}

void InitRSAd (unsigned int aprime1, unsigned int aprime2, unsigned long apriv_exp)

{

prime1=aprime1; prime2=aprime2;

phi=((unsigned long)prime1-1)*((unsigned long)prime2-1);

modulus=(unsigned long)prime1*(unsigned long)prime2;

priv_exp=apriv_exp;

}

#include "encr.cpp"ErrCommand(char *Msg)

{

cout << "Error: ";

cout << Msg;

cout << "\n";

exit(1);

}

/************************************************************/

/************************** M A I N *************************/

/****************888***********************888***************/main()

{

char name[128];

FILE *f, *fi, *fo;

time_t st=time(NULL);int i, j;

unsigned long l;

cout << "\nRSA implementation (c) 1997 M.Skulsky & K.Bubnova.\n";

cout << "Special thanks to Rivest, Shamir, Aldeman for their invaluable help, to\n";

cout << "Euclid, Euler, Fermat and Galois for having provided a bunch of very useful\n";

cout << "theorems and to V.N. Shevchenko for having made us able to understand them.\n\n";

switch (_argc) {

case 4:

case 2:

case 1:

cout << "Usage: rsa -k <key file name>\n";<< " - for generating random keys\n";<< " rsa -e <plain file> <encrypted file> <public key file>\n";

cout << " - for encryption\n";

cout << " rsa -d <encrypted file> <plain file> <private key file>\n";<< " - for decryption\n\n";<< "Public and private key files have .PBK and PVK respectively, so these are \n";<< "added to the <key file name> that you specify.\n";

exit(0);

case 3:

if (strcmp(strlwr(_argv[1]),"-k")) ErrCommand("Command not recognized.\n");();(name, _argv[2]);(name, ".pbk");=fopen(name, "wb");(f==NULL) ErrCommand("Invalid path.");(&modulus, sizeof(modulus), 1, f);(&pub_exp, sizeof(pub_exp), 1, f);(f);(name, _argv[2]);(name, ".pvk");=fopen(name, "wb");(&prime1, sizeof(prime1), 1, f);(&prime2, sizeof(prime2), 1, f);(&priv_exp, sizeof(priv_exp), 1, f);(f);<< "Private and public keys successfully created.\n";

break;5:

if (!strcmp(strlwr(_argv[1]),"-e")) { /* encrypting */

f=fopen (_argv[4], "rb");

if (f==NULL) ErrCommand ("Can't open public key!");

fread (&l, sizeof(l), 1, f);

fread (&i, sizeof(i), 1, f);

fclose(f);

InitRSAe (i, l);((fi = fopen(_argv[2], "rb"))==NULL)

ErrCommand ("Can't open plaintext file!");

if ((fo = fopen(_argv[3], "wb"))==NULL)

ErrCommand ("Can't create ciphertext file!");=0;

while (!feof(fi)) {

l=0;

i=fread (&l, 1, 3, fi);

if (i==0) break;

l=encrypt(l);

fwrite (&l, 1, sizeof (long), fo);

if (j++==50) {j=0; cout << "+"; }

} /* while */

printf ("\n");

fclose (fi);

fclose (fo);

printf ("Successfully encrypted %s\n", _argv[2]);

break;

}if (!strcmp(strlwr(_argv[1]),"-d")) { /* decrypting */

f=fopen (_argv[4], "rb");

if (f==NULL) ErrCommand ("Can't open private key!");

fread (&i, sizeof(i), 1, f);

fread (&j, sizeof(j), 1, f);

fread (&l, sizeof(l), 1, f);

fclose(f);

InitRSAd (i, j, l);((fi = fopen(_argv[2], "rb"))==NULL)

ErrCommand ("Can't open ciphertext file!");

if ((fo = fopen(_argv[3], "wb"))==NULL)

ErrCommand ("Can't create plaintext file!");

j=0;

while (!feof(fi)) {

i=fread (&l, 1, sizeof (long), fi);

if (i==0) break;

if (i==sizeof(long)) {

l=decrypt(l);

fwrite (&l, 1, 3, fo);

}

else /* unexpected end of file encountered */

ErrCommand ("Broken ciphertext!");

if (j++==50) {j=0; cout <<"+";}

} /* while */

printf ("\n");(fi);

fclose (fo);

printf ("Successfully decrypted %s\n", _argv[2]);

break;

} else ErrCommand("Command not recognized.\n");

}; /* switch */

st = time(NULL)-st;

printf ("Time running: %lu seconds.\n", st);

}

/************************ ENCR.CPP ************************/

/************ This file contains the encryption **************/

/*************** and decryption procedures *******************/

/************************************************************/

unsigned long encrypt (unsigned long data)

{

comp c, res, cmod;

int i;=modulus;

c=data;

c=(c*c)%cmod;

res=c;

for (i=1; i<pub_exp/2; i++)

res = (res*c)%cmod;=data;

res=(res*c)%cmod;

return res.lo();

}

unsigned long crt (unsigned long c, unsigned int m);long decrypt (unsigned long cipher)

{

comp a, b, M, u, Cp, Cq, Bmp;= crt (cipher, prime1);

b = crt (cipher, prime2);

u = inverse (prime2, prime1);= (unsigned long) prime1;

Cq = (unsigned long) prime2;= b%Cp;(a >= Bmp)

M=(((a-Bmp)*u)%Cp)*Cq+b;

else

M=(((a+Cp-Bmp)*u)%Cp)*Cq+b;M.lo();

}

unsigned long crt (unsigned long c, unsigned int m)

{

unsigned long dmm;

unsigned int i;

unsigned long res=1, cmm;= c%m;

dmm = (unsigned long) (m-1);

dmm = priv_exp%dmm;(i=0; i<dmm; i++) {

res*=cmm%m;

if (res>=m) res %= m;

}res;

}

/*************************************** MATH.CPP *************************************/

#include <stdlib.h>

#include <mem.h>

#include <time.h>

/**************************************/

/************* Prototypes *************/

/**************************************/long inverse(unsigned int x, unsigned long iModulus);get_primes(unsigned int *p1, unsigned int *p2);get_exponents(unsigned int *pbe, unsigned long *pve);

/**************************************/

/********** Function bodies ***********/

/**************************************/

int iter;inv (unsigned int x, unsigned long n, unsigned long *a, unsigned long *b)

{

 unsigned long q, r, t;

q = n/x;

r = n%x;(r==1) { *b=q; *a=1; }

else {

inv(r, x, a, b);

iter++;= *a;

*a = *b;

*b = t+q*(*b);

}

}

unsigned long inverse (unsigned int x, unsigned long n)

{

unsigned long a,b;=0;

inv (x, n, &a, &b);

if (iter%2==0) return n-b; else return b;

}

unsigned long rnd(unsigned long upto)

{

unsigned long t=time(NULL);=t*rand();

return t%upto;

}

#define MaxE 32767get_primes(unsigned int *p1, unsigned int *p2)

{

char *c;

unsigned long i=1, j, k;=(char *)malloc(MaxE+1);

if (c==NULL) {

cout<<"Error: Out of memory!\n";

exit(1);

};

memset (c, 0, MaxE);

while (i<MaxE) {

for(j=3;(k=(j*(2*i+1)-1)/2)<MaxE;j+=2) *(c+k)=1;

i++;

while ((i<MaxE) && *(c+i)) i++;

}

while (((i=rnd(MaxE))<MaxE/2) || *(c+i));

*p1=2*i+1;

j=i;

while (((i=rnd(MaxE))<MaxE/2) || *(c+i) || (i==j));

*p2=2*i+1;(c);

}

void get_exponents(unsigned int *pbe, unsigned long *pve)

{

unsigned int n=random(10);{

n=random(10);

*pbe=n*n-n+41;

} while ((phi%*pbe)==0);

*pve=inverse(*pbe, phi);

}

/********************************* COMP.CPP *********************************/comp

{

unsigned long a,b; /* a-high, b-lower */:

comp(unsigned long lo=0, unsigned long hi=0);&operator =(comp c);

comp &operator =(unsigned long c);

comp operator +(comp c);

comp operator -(comp c);

comp operator *(comp c);

comp operator /(comp c);

comp operator %(comp c);

comp operator <<(int i);

int operator >(comp c);

int operator >=(comp c);

int operator ==(unsigned long l);

int operator ==(comp c);long lo(void);

unsigned long hi(void);

/*private:*/

void set1(int where);

int is1(int where);

int pow(void);

};

/**** Results of the last division op ****/

comp lastdiv, lastmod;

comp::comp(unsigned long lo, unsigned long hi)

{

a=hi;

b=lo;

}

comp &comp::operator =(comp c)

{

a=c.a; b=c.b;

return (*this);

}

comp &comp::operator =(unsigned long c)

{

a=0; b=c;

return (*this);

}

comp comp::operator +(comp c)

{

comp res;

int i;

int was, is;

unsigned long l;

res=*this;=b&(1ul<<31);

for (i=0;i<=31;i++) {

res.b+=c.b & (1ul<<i);

is=(res.b & (1ul<<31))!=0;

if (was && !is) res.a++;

was=is;

}

res.a+=c.a;

return res;

}

comp comp::operator +(unsigned long l)

{

comp t=l;*this+t;

}

comp comp::operator -(comp c)

{

comp res;

if (a<c.a || (a==c.a && b<c.b))

res=0;

else if (a>=c.a && b>=c.b) {

res.a=a-c.a;

res.b=b-c.b;

}

else {

res.b=(0xffffffff)-(c.b-b)+1;

res.a=a-c.a-1;

}

return res;

}

comp comp::operator *(comp c)

{

comp res=0;

int i, llen;=c.pow();

for(i=0;i<=llen;i++)

if (c.is1(i)) res=res+(*this<<i);res;

}

comp comp::operator /(comp t)

{

comp th, r, result=0, rt;

int s1, s2;=pow(); s2=t.pow();

if (s1<s2) {

lastdiv=0l;

lastmod=*this;

return 0;

}=*this;

while (s1>s2) {

r=0;

r.set1(s1-s2);

if(th>=(rt=r*t)) th=th-rt; else {r=0; r.set1(s1-s2-1); th=th-r*t;}

result=result+r;

s1=th.pow();

}(s1==s2 && th>=t) {

result=result+1l;

th=th-t;

}=result;

lastmod=th;

return result;

}

comp comp::operator %(comp c)

{

*this/c;

return lastmod;

}

void comp::set1(int where)

{

unsigned long *l;(where>31) {

l=&a;

where-=32;

}

else l=&b;

*l=*l|(1l<<where);

}comp::pow(void)

{

int i,j;

unsigned long *l;(a==0) {

l=&b;

j=0;

}

else {

l=&a;

j=32;

}(*l==0) return 0;

for (i=31;!(*l>>i);i--);

return i+j;

}

comp comp::operator <<(int i)

{

comp t=*this;(;i>0;i--) {

t.a=(t.a)<<1;

if(t.b & (1ul<<31)) (t.a)++;

t.b=(t.b)<<1;

}t;

}

int comp::operator >(comp c)

{

comp t=*this-c;

return (t.a!=0) || (t.b!=0);

}

int comp::operator >=(comp c)

{

return (*this==c) || (*this>c);

}

int comp::is1(int where)

{

unsigned long *l;

unsigned long res;

if (where>31) {where-=32; l=&a; }

else l=&b;

res = *l & (1ul<<(unsigned long)where);

return res!=0;

}

int comp::operator ==(unsigned long l)

{

return ((a==0) && (b==l));

}

int comp::operator ==(comp c)

{

return ((a==c.a) && (b==c.b));

}

unsigned long comp::lo(void)

{

return b;

}

unsigned long comp::hi(void)

{

return a;

}

Литература

1. Баричев С., Криптография без секретов

2. Е.Бубнова, Системы с открытым ключом: алгоритм дешифрования RSA

. RSA Laboratories, Frequently Asked Questions About Today’s Cryptography, 1995

. Д.Сяо, Д. Керр, С.Мэдник, Защита ЭВМ

. Л.Дж.Хоффман, Современные методы защиты информации

. James Nechvatal, Public key cryptography, 1991

. Chris K.Caldwell, Finding Primes and proving primality