Банаховы пространства. Метрические и нормированные пространства

Одесский национальный политехнический университет

Банаховы пространства

Метрические и нормированные пространства

По дисциплине "Функциональный и выпуклый анализ"

Выполнила:

Студентка группы РИ-101 Козлюк Е.О.

Проверил: Бардай В.В.

Одесса 2011

Метрические и нормированные пространства

Именно в этих пространствах были первоначально исследованы фундаментальные понятия сильной и слабой сходимости, компактности, линейного функционала, линейного оператора и др. Банаховы пространства названы по имени С. Банаха, к-рый в 1922 начал систематич. изучение этих пространств на основе введенной им аксиоматики и получил глубокие результаты.

Множество M называется метрическим пространством, если каждым двум элементам x, y этого множества поставлено в соответствие действительное число, обозначаемое 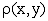и называемое расстоянием между элементами x и y, причем выполнены следующие аксиомы:

1. 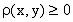     для любых 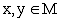, причем 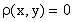в том и только в том случае, когда ;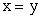

2. 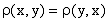     для любых ;

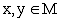3. 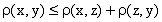     для любых .

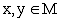Если x, y - два фиксированных элемента множества M, то 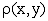есть действительное число, однако, полагая x и y равными всевозможным элементам множества M, получим, что 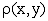является функцией двух переменных x, y. Эта функция называется метрикой данного пространства.

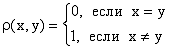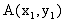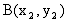Множество можно наделить метрикой: например, достаточно положить . Примером метрического пространства может также служить множество точек плоскости, где расстояние между точками и определяется как 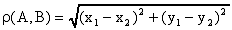. При этом третья аксиома, принимающая вид 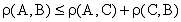 (где A, B, C - произвольные точки плоскости) имеет наглядную интерпретацию: длина любой из сторон треугольника не превосходит суммы двух других сторон (равенство достигается, если треугольник "вырожден": точка C лежит на отрезке AB). В связи с этим третью аксиому метрического пространства часто называют неравенством треугольника.

Приведем теперь менее тривиальный пример. В пространстве непрерывных на отрезке 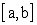функций (действительных или комплексных) введем метрику

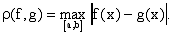
Выполнение первых двух аксиом метрического пространства при этом очевидно, а выполнение третьей аксиомы следует из тривиальных свойств модуля и того факта, что максимум суммы не превосходит суммы максимумов:

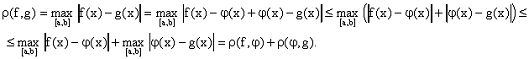
Разумеется, на одном и том же множестве метрику можно ввести по-разному. Рассмотренная только что метрика в пространстве непрерывных функций называется равномерной метрикой (пространство с этой метрикой обозначают 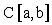). Однако на том же самом множестве непрерывных функций можно ввести и так называемую среднеквадратичную метрику

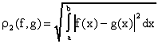
(пространство с этой метрикой обозначают 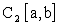), и некоторые другие метрики. Выполнение неравенства треугольника для среднеквадратичной метрики будет доказано несколько позже.

В линейных пространствах наряду с метрикой используют понятие нормы элемента.

Определение. Линейное пространство называется нормированным, если каждому элементу x этого пространства поставлено в соответствие действительное число 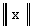 (норма x), причем выполнены следующие аксиомы:

1. 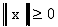     для любого x, причем 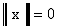тогда и только тогда, когда ;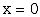

2. 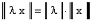     для любого x и любого комплексного;

3. 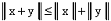     для любых x, y из данного пространства.

Для линейных пространств над полем действительных чисел также вводится понятие нормированного пространства с теми же аксиомами.

Неравенство, фигурирующее в третьей аксиоме, называется неравенством Минковского. Простейшими примерами нормированных пространств могут служить множества действительных чисел R и комплексных чисел C, где в качестве нормы числа рассматривается его модуль, а также пространство векторов на плоскости (или в пространстве) с нормой, равной длине вектора. В пространстве непрерывных функций на 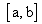 (действительном или комплексном) норму можно ввести, например, следующими способами:

, .

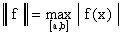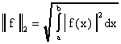Отметим теперь следующий важный факт. В любом линейном нормированном пространстве можно ввести метрику следующим образом:

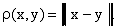
При этом выполнение первой аксиомы метрического пространства следует из первой аксиомы нормированного пространства. Выполнение второй аксиомы также очевидно:

.

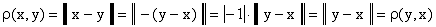Наконец, выполнение третьей аксиомы метрического пространства следует из неравенства Минковского:

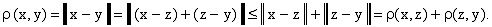
Итак, любое линейное нормированное пространство можно сделать метрическим пространством указанным выше естественным способом (так, указанные нами нормы в пространстве непрерывных функций порождают соответственно равномерную и среднеквадратичную метрику, т.е. порождают пространства и 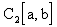соответственно). Обратное утверждение, вообще говоря, неверно: не в любом метрическом пространстве можно ввести норму, поскольку понятие нормы вводится лишь в линейном пространстве, а метрическое пространство может не быть наделено линейной структурой. Однако, если метрическое пространство наделено линейной структурой (является линейным пространством), то его всегда можно сделать нормированным, введя норму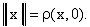

Всюду в дальнейшем мы будем рассматривать исключительно линейные нормированные пространства, причем всюду (в случае необходимости) будем подразумевать, что пространство снабжено естественной (индуцированной) метрикой .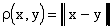

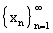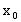Пусть теперь  - некоторая последовательность элементов линейного нормированного пространства L, а  - некоторый фиксированный элемент L. Для каждого номера n найдем 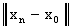. Тем самым получим числовую последовательность .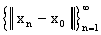

Определение. Элемент 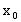линейного нормированного пространства L называется пределом последовательности элементов 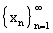, ес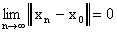ли

 (или ).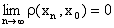

Обозначение: 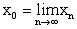 (если необходимо, то указывают, по какой норме рассматривается предел).

Если последовательность 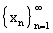имеет предел, то она называется сходящейся (по норме данного пространства), в противном случае - расходящейся.

Пример. Рассмотрим последовательность функций 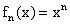в пространстве 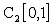. Функция 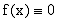является ее пределом, т.к.

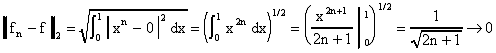при .

Однако в пространстве 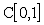эта же самая последовательность расходится. Действительно, допустим, что 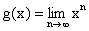в равномерной метрике. Тогда

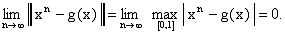
При каждом фиксированном

,

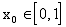очевидно,

,

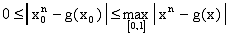и, следовательно,

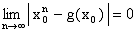, т.е.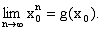

Но .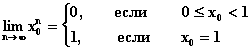

Итак, .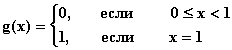

Однако такая функция 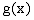не является непрерывной на 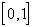, т.е. вообще не принадлежит рассматриваемому пространству. Таким образом, в 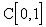данная последовательность предела не имеет.

Как видим, одна и та же последовательность может иметь предел в одной метрике и не иметь в другой.

Если последовательность имеет предел, то этот предел единственен. В самом деле, пусть 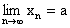и 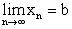. Тогда

.

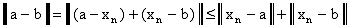При 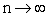правая часть стремится к нулю, следовательно, левая часть также стремится к нулю. Но 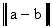 - константа, поэтому 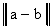=0, а значит, .

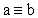Определение предела последовательности элементов нормированного пространства основано на понятии предела числовой последовательности. Используя определение предела числовой последовательности, "расшифруем" более подробно понятие предела в нормированном пространстве.

Элемент 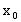линейного нормированного пространства L является пределом последовательности элементов 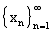, если для любого (сколь угодно малого) 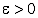найдется номер N, такой, что для всех номеров n, больших N, выполнено неравенство 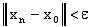. Или, в символьной записи,

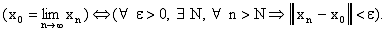
Рассмотрим теперь понятие фундаментальной последовательности, тесно связанные с понятием предела.

Определение. Последовательность элементов 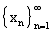линейного нормированного пространства называется фундаментальной, если

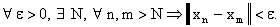
Очевидно, что любая сходящаяся последовательность фундаментальна: если

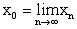, то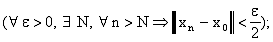

тогда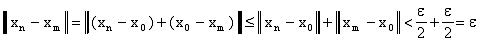

для всех номеров 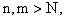что и доказывает фундаментальность последовательности .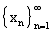

Определение. Линейное нормированное пространство называется полным, если в нем любая фундаментальная последовательность сходится.

Банахово пространство

Полное линейное нормированное пространство называют также банаховым пространством (по имени выдающегося польско-украинского математика Стефана Банаха (1892-1945)).

Пространства R и C - банаховы, а пространство Q - нет.

Рассмотренное выше пространство 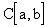 - банахово. В самом деле, пусть 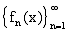 - фундаментальная последовательность в .

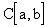Тогда (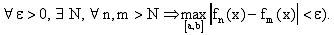 Тогда для любого фиксированного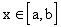 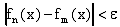, причем номер N не зависит от x. По критерию Коши равномерной сходимости это означает равномерную сходимость последовательности .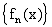

Переходя в неравенстве 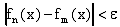к пределу при 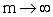, получим: 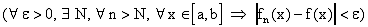, откуда следует, что 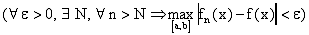, что означает сходимость последовательности 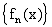к 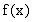по норме 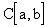. Таким образом, пространство 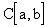 - полное, а значит - банахово.

Любопытно, что пространство 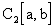полным не является. В качестве примера рассмотрим в 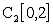последовательность 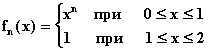. Предположим, что некоторая непрерывная функция f (x) является пределом этой последовательности в метрике .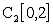

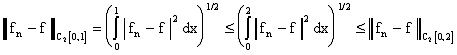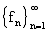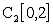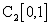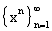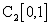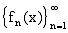Очевидно, , а следовательно, если сходится к f (x) в метрике , то сходится и в метрике . Однако, на отрезке [0, 1] рассматриваемая последовательность совпадает с рассмотренной выше последовательностью и имеет своим пределом в функцию, тождественно равную нулю. Аналогично, f (x) является пределом в 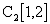, а поскольку 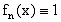на [1, 2], то и предел этой последовательности в 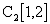тождественно равен 1.

В силу единственности предела, получаем, что 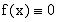на [0, 1] и 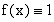на [1, 2] и при этом f (x) непрерывна на [0, 2]. Очевидно, таких функций не существует.

метрическое линейное банахово пространство

Следовательно, последовательность 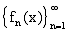в 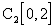расходится. Вместе с тем

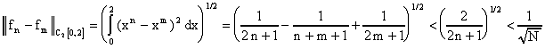 при n, m > N.

Выбирая для произвольного фиксированного 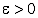номер 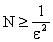, убеждаемся в фундаментальности данной последовательности в .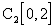

Построенный пример легко обобщается с отрезка [0, 2] на произвольный отрезок [a, b]. Итак, пространство 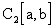неполно.

Примеры. Встречающиеся в математич. анализе Б. п. - это чаще всего множества функций или числовых последовательностей, подчиненные нек-рым условиям:

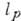) , , - пространство числовых последовательностей 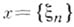, для к-рых

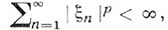
с нормой

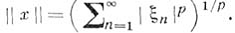
) т - пространство ограниченных числовых последовательностей с нормой

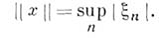
) с - пространство сходящихся числовых последовательностей с нормой

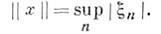
) с ₀ - пространство сходящихся к нулю числовых последовательностей с нормой

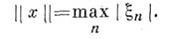
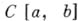)  - пространство непрерывных на 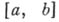функций 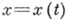с нормой

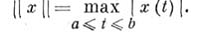
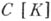)  - пространство непрерывных функций на компакте 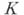с нормой

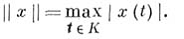
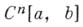)  - пространство функций, имеющих непрерывные производные до порядка пвключительно, с нормой

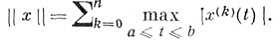
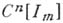)  - пространство всех непрерывно дифференцируемых до порядка пфункций, определенных в т - мерном кубе, с равномерной нормой по всем производным порядка не выше п.

9) 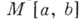 - пространство ограниченных измеримых функций с нормой

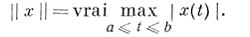
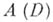)  - пространство функций, аналитических в открытом единичном круге Dи непрерывных в замкнутом круге 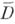, с нормой