Приближенные решения дифференциальных уравнений
Курсовая работа
по дисциплине:
Высшая математика
на тему: Приближенные решения
дифференциальных уравнений
Введение
При анализе режимов работы
электроэнергетических объектов и разработке новых технологических процессов
инженеру часто приходится сталкиваться с дифференциальными уравнениями, т.к.
большая часть законов электротехники и теплотехники формулируется в виде
дифференциальных уравнений. При этом нередко приходится иметь дело с
уравнениями, общее решение которых не выражается в квадратурах. Например, общее
решение очень простого уравнения 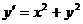 нельзя записать в конечном виде
через элементарные функции. Класс задач, для которых можно найти явное решение,
весьма узок. В связи с интенсивным применением дифференциальных уравнений в
качестве математических моделей широкого круга естественнонаучных задач и с
появлением высокопроизводительных ЭВМ важное значение приобрели численные
методы их решения. Численные методы - это алгоритмы вычисления приближенных
значений искомого решения в точках конечного множества значений аргумента
(узлах сетки). Решение при этом получается в виде таблицы. Рассмотрим два таких
метода: метод Рунге-Кутта и вытекающий из него метод Эйлера.
нельзя записать в конечном виде
через элементарные функции. Класс задач, для которых можно найти явное решение,
весьма узок. В связи с интенсивным применением дифференциальных уравнений в
качестве математических моделей широкого круга естественнонаучных задач и с
появлением высокопроизводительных ЭВМ важное значение приобрели численные
методы их решения. Численные методы - это алгоритмы вычисления приближенных
значений искомого решения в точках конечного множества значений аргумента
(узлах сетки). Решение при этом получается в виде таблицы. Рассмотрим два таких
метода: метод Рунге-Кутта и вытекающий из него метод Эйлера.
Метод Рунге-Кутта.
Рассматриваем задачу Коши для дифференциального
уравнения первого порядка
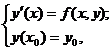 (1)
(1)
решение которой
находится на отрезке [x0,
x0+ H], h > 0. Считаем, что задача (1) имеет единственное решение у(х),
определяемое на этом отрезке. Выбираем на отрезке [х0, x0
+ H] сетку значений аргумента хд= х0 + nh
, n=0,1,...,N;
h= h/n. Разложим решение у (х) в ряд Тейлора в окрестности точки хn, полагая при этом уn=у(хn), у`= y`(xn) и т.д.
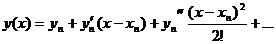 (2)
(2)
Подставим в разложение
(2) значение х = xn+1, получая
равенство 
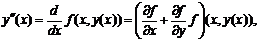
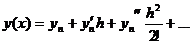 (3)
(3)
Стоящие в правой части
равенства (3) производные можно найти, последовательно дифференцируя
уравнение (1):
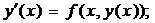 (4)
(4)
так что
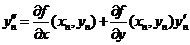 (5)
(5)
с учетом формул (5)
равенство (3) можно записать последовательно в виде
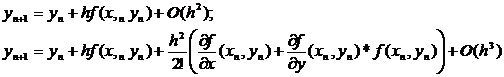 (6)
(6)
Пренебрегая в правых
частях формул (6) слагаемыми О(h2),О(h3), малыми при малых h,
получаем соответственно формулы
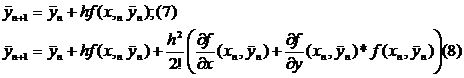
Каждая из формул
(7),(8),... позволяет по известному значению y0
решения задачи (1) в начальной точке xо
последовательно вычислять приближенные значения этого решения в узлах сетки
х1,х0,...,xn; в отличие от точных значений обозначим их 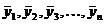
Формулу (8) и тем более,
формулы с большим числом членов в практических расчетах не используют, так как
если функция f(х,у) правой части имеет несложное выражение, то выражения (4) для
ее производных могут оказаться громоздкими. Если функция f(х,у) известна лишь приближенно, то процесс вычислений по этим
формулам усложняется еще и из-за необходимости использовать формулы численного,
дифференцирования.
Расчет приближенных значений уn задачи Коши (1) по формуле (7) называется методом Эйлера, или
схемой ломаных. Геометрическая интерпретация этой схемы дана на рис.1, где
изображено поле интегральных кривых.

При удалении от
точки (хо,уо) ломаная Эйлера может заметно отклоняться от графика точного
решения. Известна следующая оценка погрешности метода Эйлера. Пусть в D={(х,у): |х-хo |<а ; |у-уо|<b}-прямоугольник с центром в точке (xо,yo), в котором задача Коши
(1) однозначно разрешима (так что проекция d на ось
абсцисс содержит отрезок [xo,xo+H] ), и пусть в D выполняются неравенства
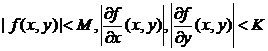
Тогда
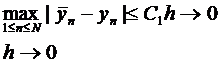
Где С1=(1+М)
(еКН-1)
При отсутствии ошибок
округлений локальная погрешность метода Эйлера, т.е. погрешность на одном шаге h , возникающая за счет перемещения по касательной к интегральной
кривой, проходящей через точку (хn,уn), а не по самой интегральной кривой, есть величина O(h2). Глобальная погрешность или, точнее, максимальная погрешность
решения на сетке {х1,x2,...,хN} в целом равна O(h), как следует из неравенства (9). В связи с этим говорят, что
метод Эйлера имеет первый порядок точности. С другой стороны в учебнике «Краткий
курс математического анализа» А.Ф.Бермант, И.Г.Араманович, М. 1973 г этот метод
описывается иначе. Известно, что уравнение 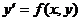 задает в некоторой области поле
направлений. Решение этого уравнения с некоторыми начальными условиями дает
кривую, которая касается поля направлений в любой точке. Если взять
последовательность точек х0, х1, х2, …. и заменить на получившихся
отрезках интегральную кривую на отрезки касательных к ней, то получим ломаную
линию.
задает в некоторой области поле
направлений. Решение этого уравнения с некоторыми начальными условиями дает
кривую, которая касается поля направлений в любой точке. Если взять
последовательность точек х0, х1, х2, …. и заменить на получившихся
отрезках интегральную кривую на отрезки касательных к ней, то получим ломаную
линию.
При подстановке заданных начальных
условий (х0, у0) в дифференциальное уравнение 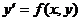 получаем
угловой коэффициент касательной к интегральной кривой в начальной точке
получаем
угловой коэффициент касательной к интегральной кривой в начальной точке
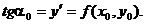 Заменив на отрезке [x0, x1]
интегральную кривую на касательную к ней, получаем значение
Заменив на отрезке [x0, x1]
интегральную кривую на касательную к ней, получаем значение
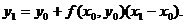 Производя аналогичную операцию для
отрезка [x1, x2],
получаем:
Производя аналогичную операцию для
отрезка [x1, x2],
получаем:
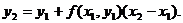 Продолжая подобные действия далее,
получаем ломаную кривую, которая называется ломаной Эйлера. Можно записать
общую формулу вычислений:
Продолжая подобные действия далее,
получаем ломаную кривую, которая называется ломаной Эйлера. Можно записать
общую формулу вычислений:

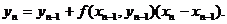
Если последовательность точек хi выбрать
так, чтобы они отстояли друг от друга на одинаковое расстояние h, называемое
шагом вычисления, то получаем формулу:
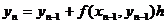
Следует отметить, что точность
метода Эйлера относительно невысока. Увеличить точность можно, конечно,
уменьшив шаг вычислений, однако, это приведет к усложнению расчетов. Поэтому на
практике применяется так называемый уточненный метод Эйлера или формула
пересчета.
Суть метода состоит в том, что в
формуле 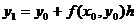 вместо
значения
вместо
значения 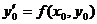 берется
среднее арифметическое значений f(x0, y0) и f(x1, y1). Тогда
уточненное значение:
берется
среднее арифметическое значений f(x0, y0) и f(x1, y1). Тогда
уточненное значение:
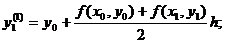
Затем находится значение производной
в точке 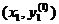 . Заменяя f(x0, y0) средним
арифметическим значений f(x0, y0) и
. Заменяя f(x0, y0) средним
арифметическим значений f(x0, y0) и 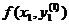 , находят
второе уточненное значение у1.
, находят
второе уточненное значение у1.
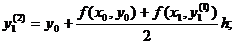
Затем третье:
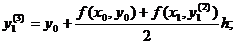
и т.д. пока два последовательных
уточненных значения не совпадут в пределах заданной степени точности. Тогда это
значение принимается за ординату точки М1 ломаной Эйлера.
Аналогичная операция производится
для остальных значений у. Подобное уточнение позволяет существенно
повысить точность результата. Одним из методов,
позволяющих для решения задачи Коши (1) строить вычислительные схемы более
высоких порядков точности, является метод, предложенный Рунге и
усовершенствованный Кутта и другими математиками. Схемы метода Рунге-Кутта
удобны как, для расчетов на ЭВМ, так и для ручных расчетов.
С основной идеей
метода ознакомимся на примере построения вычислительных схем второго порядка
точности. Воспользуемся теперь второй из формул (6)
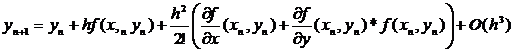 (10)
(10)
Покажем, что можно
правильно передать члены ряда Тейлора, указанные в формуле (10), избежав
дифференцирования, функция f(x,y), С этой целью полагаем
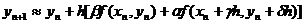 , (11)
, (11)
где 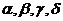 -некоторые постоянные По формуле Тейлора первого порядка находим
-некоторые постоянные По формуле Тейлора первого порядка находим
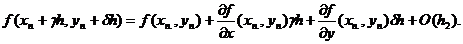
Подставляя это выражение
для значения 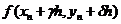 в
равенство (11) получаем
в
равенство (11) получаем
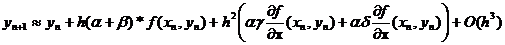 (12)
(12)
Выбираем параметры 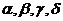 так,
чтобы правые части разложений (10) и (12) совпадали с точностью до слагаемых
порядка О(h3). Для этого достаточно положить:
так,
чтобы правые части разложений (10) и (12) совпадали с точностью до слагаемых
порядка О(h3). Для этого достаточно положить:
Эта система трех
уравнений с четырьмя неизвестными имеет бесконечно много решении. Выразим через 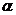 остальные параметры:
остальные параметры:
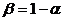 ,
,
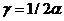 ,
,
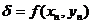
и подставим их в формулу
(12), пренебрегая при этом слагаемыми О(h3).
B результате
получаем
однопараметрическое семейство двучленных схем
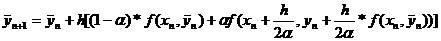 (13)
(13)
Локальная погрешность
формулы (13) равна О(h3).
Для максимальной погрешности на сетке выполняется оценка
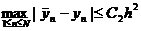
где С2 - некоторая постоянная, не
зависящая от h. Вычислительная схема расчета приближенных значений решения
задачи Коши (1) по формуле (13) называется схемой Рунге-Кутта второго порядка
точности. Эти схемы нередко используются в практических вычислениях. При этом
полагают, либо 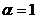 ,
либо
,
либо 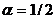 .
В первом случае получается схема особенно простого вида
.
В первом случае получается схема особенно простого вида
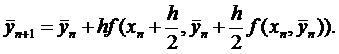 (14)
(14)
Для 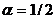 схема
(13) имеет вид
схема
(13) имеет вид
Методом Рунге-Кутта
можно строить схемы различного порядка точности. Например, схема ломаных (7)
есть схема Рунге-Кутта первого порядка точности, двучленные схемы (13) имеют
второй порядок точности. Наибольшее распространение получили схемы четвертого
порядка точности, при построении которых в записи ряда Тейлора (2) удерживаются
все члены, включая h4. Приведем без вывода
ту из них, которая записана в большинстве стандартных программ для ЭВМ:
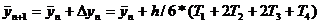 , (16)
, (16)
где
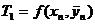 ,
,
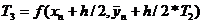 ,
,
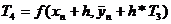
Для схемы (16)
выполняется следующая оценка погрешности: если в прямоугольнике d существуют непрерывные частные производные четвертого порядка
функции f (x,у), то
Схемы Рунге-Кутта более
высокого порядка точности практически не употребляются, так как расчетные
формулы становятся слишком громоздкими. Одним из
важных достоинств метода Рунге-Кутта является простота алгоритма вычислений.
Для начала вычислений достаточно выбрать сетку {хо, х1, ..., xN} и задать начальное значение у (хо) = уо. Далее вычисления
производят последовательно по одним и тем же формулам. Это свойство схем метода
Рунге-Кутта очень ценно при расчетах на ЭВМ, программирование расчетных формул
метода не представляет труда.
Выбор шага. Апостериорная
оценка погрешности. Правило Рунге
Правильный выбор шага
сетки h является одним из главных практических вопросов, которые
возникают при численном решении дифференциальных уравнений. Как получить
требуемую точность? Если шаг выбран слишком большим, то значительной будет
локальная погрешность и накопившаяся глобальная погрешность может быть
недопустимо большой. Если же шаг слишком мал, то расчет потребует неоправданно
много времени работы вычислителя или ЭВМ. При этом наблюдается следующий отрицательный
эффект: суммарное действие ошибок округления, малых при выполнении каждой
операции, может оказаться столь значительным, что полученный ответ становится
бесполезным.
Априорные оценки типа
(9) мало полезны для получения информации о точности вычислений ввиду их
сложности (особенно для схем высокого порядка); при этом они, как правило, во
много раз превосходят фактическую ошибку расчета. Основным
практическим приемом является апостериорная оценка погрешности. Для ее
получения проводят вычисления на двух или более сгущающихся сетках и применяют
так называемое правило Рунге, которое заключается в следующем. Пусть 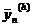 обозначает
приближенное значение решения задача Коши (1) в точке х =
x(h) = xo + nh, вычисленное
по некоторой схеме Рунге-Кутта p-го
порядка точности, а
обозначает
приближенное значение решения задача Коши (1) в точке х =
x(h) = xo + nh, вычисленное
по некоторой схеме Рунге-Кутта p-го
порядка точности, а 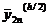 приближенное
значение для y(x), вычисленное
по той же схеме и в той же точке, являющейся узлом более густой сетки с
шагом h/2, так что
приближенное
значение для y(x), вычисленное
по той же схеме и в той же точке, являющейся узлом более густой сетки с
шагом h/2, так что 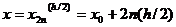 .
.
При некоторых
предположениях относительно гладкости функции правой части f(x,y) погрешность схемы Рунге-Кутта р-го порядка точности имеет вид
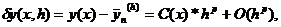 (17)
(17)
где С зависит от
точки х, но не от h. Применяя формулу (17) для оценки погрешности на сетке с шагом h/2 , получаем
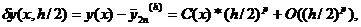 18)
18)
Сохраняем в равенствах
(17) и (18) только главную часть погрешности, пренебрегая слагаемыми 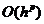 и
и
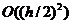 , и вычитаем почленно из первого равенства второе. В итоге
приходим к приближенному равенству
, и вычитаем почленно из первого равенства второе. В итоге
приходим к приближенному равенству
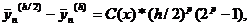
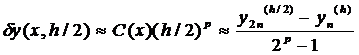
откуда определяем, что
погрешность 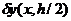 на сетке с меньшим шагом составляет
на сетке с меньшим шагом составляет  частности, оценка (19) имеет вид:
частности, оценка (19) имеет вид:
для схемы ломаных
(7)
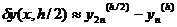 (19 а)
(19 а)
для схемы (13)
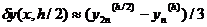 (19 б)
(19 б)
для схемы (16)
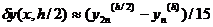 (19в)
(19в)
Информацию о погрешности
вычислений в виде (19) можно использовать для того, чтобы уточнить приближенные
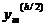 значения на сетке с меньшим шагом, внося в них поправки
следующим образом.
значения на сетке с меньшим шагом, внося в них поправки
следующим образом.
В точке 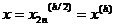 , являющейся
общим узлом двух сеток,, полагаем в соответствии о формулами (18) и (19):
, являющейся
общим узлом двух сеток,, полагаем в соответствии о формулами (18) и (19):
дифференциальный
уравнение точность погрешность
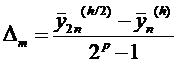
Значения поправок, в
узлах 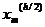 с нечетными номерами m=2n-1 находим, применяя линейную интерполяцию;
с нечетными номерами m=2n-1 находим, применяя линейную интерполяцию;
Можно ожидать, что исправленные
значения 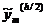 будут
более
точными, чем
будут
более
точными, чем 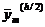 .
.
Пример практического расчета
Используя метод Эйлера, а затем схему Рунге-Кутта
второго порядка точности составить таблицу приближенных значений решения задачи
Коши
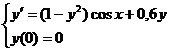
на отрезке [0,1] с шагом h=0,2 и h=0,1.
Результат округлить до 10-4. Оценить погрешность на сетке с шагом h=0,1 по
методу Рунге. Сравнить полученные результаты с результатами вычислений по схеме
четвертого порядка точности на сетке с шагом h=0,1.
В таблицах 2 и 3:
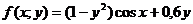 ,
,
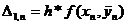 ,
,
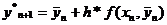 ,
,
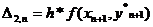 ,
,
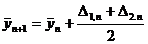
По методу Эйлера 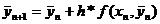 (табл.1)
(табл.1)
Таблица 1
|
n
|
xn
|
h
|
h*f(xn, 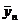 ) )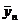
|
|
|
0
|
0,0
|
0,1
|
0,1000
|
0,0000
|
|
1
|
0,1
|
0,1
|
0,1045
|
0,1000
|
|
2
|
0,2
|
0,1
|
0,1062
|
0,2045
|
|
3
|
0,3
|
0,1
|
0,1050
|
0,3107
|
|
4
|
0,4
|
0,1
|
0,1011
|
0,4156
|
|
5
|
0,5
|
0,0953
|
0,5168
|
|
6
|
0,6
|
0,1
|
0,0883
|
0,6121
|
|
7
|
0,7
|
0,1
|
0,0810
|
0,7004
|
|
8
|
0,8
|
0,1
|
0,0740
|
0,7814
|
|
9
|
0,9
|
0,1
|
0,0680
|
0,8554
|
|
10
|
1,0
|
0,1
|
0,0634
|
0,9234
|
Таблица приближенных значений по схеме
Рунге-Кутта второго порядка точности шаг h=0,2
Таблица 2
|
n
|
xn
|
h
|
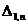 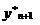 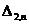 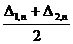 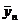
|
|
|
|
|
|
0
|
0,0
|
0,2
|
0,2000
|
0,2000
|
0,2122
|
0,2061
|
0,0000
|
|
1
|
0,2
|
0,2
|
0,2124
|
0,4185
|
0,2022
|
0,2073
|
0,2061
|
|
2
|
0,4
|
0,2
|
0,2023
|
0,6157
|
0,1764
|
0,1894
|
0,4134
|
|
3
|
0,6
|
0,2
|
0,1774
|
0,7802
|
0,1481
|
0,1628
|
0,6027
|
|
4
|
0,8
|
0,2
|
0,1495
|
0,9151
|
0,1385
|
0,7655
|
|
5
|
1,0
|
0,2
|
0,1282
|
1,0322
|
0,1108
|
0,1195
|
0,9040
|
Таблица приближенных значений по схеме Рунге-Кутта
второго порядка точности шаг h=0,1
Таблица 3
|
n
|
xn
|
h
|
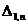 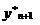 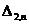 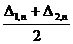 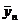
|
|
|
|
|
|
0
|
0,0
|
0,1
|
0,1000
|
0,1000
|
0,1045
|
0,1023
|
0,0000
|
|
1
|
0,1
|
0,1
|
0,1046
|
0,2069
|
0,1062
|
0,1054
|
0,1023
|
|
2
|
0,2
|
0,1
|
0,1062
|
0,3140
|
0,1050
|
0,1056
|
0,2077
|
|
3
|
0,3
|
0,1
|
0,1050
|
0,4183
|
0,1011
|
0,1030
|
0,3133
|
|
4
|
0,4
|
0,1
|
0,1011
|
0,5175
|
0,0953
|
0,0982
|
0,4163
|
|
5
|
0,5
|
0,1
|
0,0954
|
0,6099
|
0,0884
|
0,0919
|
0,5145
|
|
6
|
0,6
|
0,1
|
0,0886
|
0,6950
|
0,0812
|
0,6065
|
|
7
|
0,7
|
0,1
|
0,0814
|
0,7728
|
0,0744
|
0,0779
|
0,6914
|
|
8
|
0,8
|
0,1
|
0,0746
|
0,8439
|
0,0685
|
0,0716
|
0,7693
|
|
9
|
0,9
|
0,1
|
0,0687
|
0,9095
|
0,0639
|
0,0663
|
0,8408
|
|
10
|
1,0
|
0,1
|
0,0640
|
0,9711
|
0,0640
|
0,0640
|
0,9071
|
Оценим погрешность на сетке с шагом h=0,1
по методу Рунге. В таблице 4:
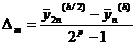
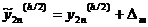
Таблица 4
|
n
|
m
|
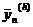 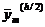 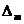 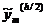
|
|
|
|
|
0
|
0
|
0,0000
|
0,0000
|
0,0000
|
0,0000
|
|
-
|
1
|
-
|
0,1023
|
0,0003
|
0,1025
|
|
1
|
2
|
0,2061
|
0,2077
|
0,0005
|
0,2082
|
|
-
|
3
|
-
|
0,3133
|
0,0008
|
0,3141
|
|
2
|
4
|
0,4134
|
0,4163
|
0,0010
|
0,4173
|
5
|
-
|
0,5145
|
0,0011
|
0,5156
|
|
3
|
6
|
0,6027
|
0,6065
|
0,0013
|
0,6078
|
|
-
|
7
|
-
|
0,6914
|
0,0013
|
0,6927
|
|
4
|
8
|
0,7655
|
0,7693
|
0,0013
|
0,7706
|
|
-
|
9
|
-
|
0,8408
|
0,0011
|
0,8419
|
|
5
|
10
|
0,9040
|
0,9071
|
0,0010
|
0,9081
|
Таблица приближенных значений по методу
Рунге-Кутта четвертого порядка точности h=0,1.
Здесь
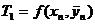 ,
,
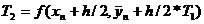 ,
,
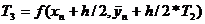 ,
,
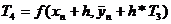 ,
,
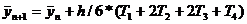
Таблица 5
|
n
|
xn
|
h
|
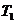 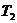 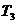 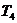 
|
|
|
|
|
|
0
|
0,0
|
0,1
|
1,0000
|
1,0263
|
1,0269
|
1,0461
|
0,0000
|
|
1
|
0,1
|
0,1
|
1,0461
|
1,0580
|
1,0581
|
1,0625
|
0,1025
|
|
2
|
0,2
|
0,1
|
1,0625
|
1,0595
|
1,0595
|
1,0495
|
|
3
|
0,3
|
0,1
|
1,0495
|
1,0331
|
1,0332
|
1,0110
|
0,3141
|
|
4
|
0,4
|
0,1
|
1,0111
|
0,9841
|
0,9844
|
0,9536
|
0,4173
|
|
5
|
0,5
|
0,1
|
0,9536
|
0,9200
|
0,9206
|
0,8852
|
0,5156
|
|
6
|
0,6
|
0,1
|
0,8852
|
0,8489
|
0,8497
|
0,8135
|
0,6076
|
|
7
|
0,7
|
0,1
|
0,8135
|
0,7782
|
0,7791
|
0,7454
|
0,6926
|
|
8
|
0,8
|
0,1
|
0,7454
|
0,7140
|
0,7148
|
0,6861
|
0,7705
|
|
9
|
0,9
|
0,1
|
0,6861
|
0,6608
|
0,6613
|
0,6396
|
0,8419
|
|
10
|
1,0
|
0,1
|
0,6396
|
0,6219
|
0,6222
|
0,6087
|
0,9081
|
По результатам таблиц построим 4 графика yn=f(xn)
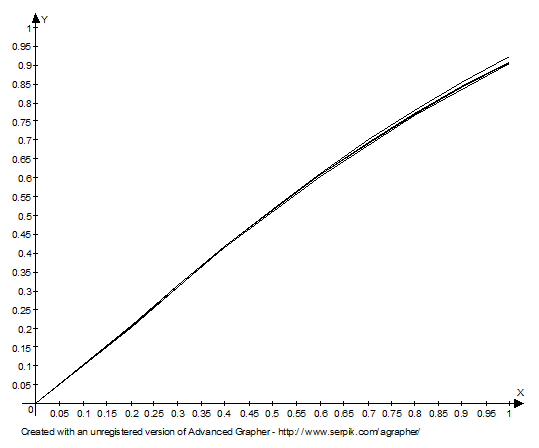
Как видно из графика более точные значения
решения задачи Коши (полученные по схеме Рунге-Кутта второго и четвертого
порядка точности с шагом h=0,1
графики 2 и 3) лежат между менее точными значениями (полученные методом Эйлера
и по схеме Рунге-Кутта второго порядка точности с шагом h=0,2
графики 1 и 4)
Литература
1. Методическое указание к
лабораторной работе «Метод сеток. II.
Решение задачи Коши для обыкновенного дифференциального уравнения первого
порядка». Архангельск 1985
2. «Краткий курс
математического анализа» А.Ф.Бермант, И.Г.Араманович, М. 1973 г. Хемминг Р.В.,
«Численные методы», «Наука».