Искусственные нейронные сети

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ

ГЛАВА 1 ИСКУССТВЕННЫЕ НЕЙРОННЫЕ СЕТИ

1.1   Возникновение искусственных нейронных сетей

1.2     Основные виды искусственных нейронных сетей

.3       Применение искусственных нейронных сетей

ГЛАВА 2 ПЕРСЕПТРОН РОЗЕНБЛАТТА

.1 Задачи, решаемые при помощи Персептрона Розенблатта

.2 Методика обучения Персептрона Розенблатта

.3 Пример использования Персептрона Розенблатта

ГЛАВА 3 КОМПЬЮТЕРНАЯ ИМИТАЦИОННАЯ МОДЕЛЬ ПЕРСЕПТРОНА РОЗЕНБЛАТТА

.1 Ограничения, накладываемые на имитационную модель

3.2 Схема имитационной модели Персептрона Розенблатта в среде Delphi

3.3 Описание сеанса работы с компьютерной программой

ЗАКЛЮЧЕНИЕ

ПРИЛОЖЕНИЕ. Исходные коды программы Perseptron

ВВЕДЕНИЕ

Человеческий мозг содержит триллионы особых клеток, называемых нейронами. Все они связаны друг с другом сотнями триллионов нервных нитей, называемых синапсами. Получившаяся таким образом огромная сеть нейронов отвечает за все те явления, которые мы привыкли называть мыслями и эмоциями, а также за все многообразие сенсомоторных функций [6,9,16,18,19,24,27,28,29]. До сих пор нет четкого ответа на вопрос, каким образом биологическая нейросеть осуществляет управление всеми этими процессами, хотя уже исследовано достаточно много аспектов ее работы. Из-за технической невозможности создания биологических нейронных сетей, в настоящее время создаются их неодушевленные аналоги - искусственные нейронные сети [6,7,9,12,13,20,21,22,25,26,27,28,29]. Актуальность исследований в этом направлении подтверждается массой различных применений нейронных сетей. Это автоматизация процессов распознавания образов, адаптивное управление, аппроксимация функционалов, прогнозирование, создание экспертных систем, организация ассоциативной памяти и многие другие приложения. С помощью нейронных сетей можно, например, предсказывать показатели биржевого рынка, выполнять распознавание оптических или звуковых сигналов, создавать самообучающиеся системы, способные управлять автомашиной при парковке или синтезировать речь по тексту [4,9,15,20,27,29].

По своей организации и функциональному назначению искусственная нейронная сеть с несколькими входами и выходами выполняет некоторое преобразование входных стимулов - сенсорной информации о внешнем мире - в выходные управляющие сигналы.

Возвращаясь к общим чертам, присущим всем нейронным сетям следует отметить принцип параллельной обработки сигналов, который достигается путем объединения большого числа нейронов в так называемые слои и соединения определенным образом нейронов различных слоев, а также, в некоторых конфигурациях, и нейронов одного слоя между собой, причем обработка взаимодействия всех нейронов ведется послойно [6,13,15,20,22,29].

Теоретически число слоев и число нейронов в каждом слое может быть произвольным, однако фактически оно ограничено ресурсами компьютера или специализированной микросхемы, на которых обычно реализуется НС. Чем сложнее нейронная сеть, тем масштабнее решаемые ей задачи.

Широкий круг задач, решаемый нейронными сетями, не позволяет в настоящее время создавать универсальные, мощные сети, вынуждая разрабатывать специализированные нейронные сети, функционирующие по различным алгоритмам. Тип используемой нейросети во много диктуется поставленной задачей. Так, для задачи классификации удобными могут оказаться многослойный персептрон [6,9,20,28,29] и сеть Липпмана-Хемминга [13,20,29]. Персептрон также применим и для задач идентификации систем и прогноза. При решении задач категоризации потребуются карта Кохонена [14,28,29], архитектура встречного распространения [20,27,28,29] или сеть с адаптивным резонансом [28,29]. Задачи нейроматематики обычно решаются с использованием различных модификаций модели Хопфилда [6,9,13,21,27,28,29]. На выбор конкретной нейронной сети может повлиять наличие или отсутствие соответствующих задаче программ.

Объектом данной дипломной работы являются нейронные сети.

Предметом данной дипломной работы является искусственная нейронная сеть на базе классической модели нейрона.

Целью данной дипломной работы является разработка элективного курса по теме «Введение в нейронные сети».

В соответствии с объектом, предметом и целью в данной дипломной работе были успешно решены следующие задачи:

1.     Изучена история возникновения нейронных сетей.

2.       Приведены архитектуры простейших нейронных сетей.

.        Рассмотрены прикладные программы для создания моделей искусственных нейронных сетей.

Дипломная работа состоит из введения, трех глав, заключения, библиографического списка использованной литературы и приложения.

В первой главе дипломной работы рассматривается история возникновения нейронных сетей, модели живого и искусственного нейронов, архитектуры простейших нейронных сетей, дается классификация нейронных сетей..

Во второй главе дипломной работы рассматриваются наиболее часто используемые для создания моделей нейронных сетей компьютерные программы.

В третьей главе дипломной работы рассматривается процесс разработки имитационной модели Персептрона Роземблатта.

В заключении сделаны выводы и подведен итог проделанной работы.

Приложение содержит разработанные автором дипломной работы исходный текст компьютерной программы

ГЛАВА 1. ИСКУСТВЕННЫЕ НЕЙРОНЫЕ СЕТИ

.1 Возникновение искусственных нейронных сетей

После двух десятилетий почти полного забвения, интерес к искусственным нейронным сетям быстро вырос за последние несколько лет. Специалисты из таких далеких областей, как техническое конструирование, философия, физиология и психология, заинтригованы возможностями, предоставляемыми этой технологией, и ищут приложения им внутри своих дисциплин.

Это возрождение интереса было вызвано как теоретическими, так и прикладными достижениями. Неожиданно открылись возможности использования вычислений в сферах, до этого относящихся лишь к области человеческого интеллекта, возможности создания машин, способность которых учиться и запоминать удивительным образом напоминает мыслительные процессы человека, и наполнения новым значительным содержанием критиковавшегося термина «искусственный интеллект».

Лучшее понимание функционирования нейрона и картины его связей позволило исследователям создать математические модели для проверки своих теорий. Эксперименты теперь могут проводиться на цифровых компьютерах без привлечения человека или животных, что решает многие практические и морально-этические проблемы. В первых же работах выяснилось, что эти модели не только повторяют функции мозга, но и способны выполнять функции, имеющие свою собственную ценность. Поэтому возникли и остаются в настоящее время две взаимно обогащающие друг-друга цели нейронного моделирования: первая - понять функционирование нервной системы человека на уровне физиологии и психологии и вторая - создать вычислительные системы (искусственные нейронные сети), выполняющие функции, сходные с функциями мозга.

Параллельно с прогрессом в нейроанатомии и нейрофизиологии психологами были созданы модели человеческого обучения. Одной из таких моделей, оказавшейся наиболее плодотворной, была модель Д. Хэбба, который в 1949г. предложил закон обучения, явившийся стартовой точкой для алгоритмов обучения искусственных нейронных сетей. Дополненный сегодня множеством других методов он продемонстрировал ученым того времени, как сеть нейронов может обучаться.

И все же, что такое искусственные нейронные сети? Что они могут делать? Как они работают? Как их можно использовать? Эти и множество подобных вопросов задают специалисты из разных областей. Найти вразумительный ответ нелегко Наиболее емким представляется следующее определение искусственных нейронных сетей, как адаптивной машины, данное в [2]:

Искусственная нейронная сеть - это существенно параллельно распределенный процессор, который обладает способностью к сохранению и репрезентации опытного знания. Она сходна с мозгом в двух аспектах:

- знание приобретается сетью в процессе обучения;

- для сохранения знания используются силы межнейронных соединений, называемые также синаптическими весами.

Имеется много впечатляющих демонстраций возможностей искусственных нейронных сетей: сеть научили превращать текст в фонетическое представление, которое затем с помощью уже иных методов превращалось в речь [3]; другая сеть может распознавать рукописные буквы [1]; сконструирована система сжатия изображений, основанная на нейронной сети [4]. Все они используют сеть обратного распространения - наиболее успешный, по-видимому, из современных алгоритмов. Обратное распространение, независимо предложенное в трех различных работах [5, 6, 7,], является систематическим методом для обучения многослойных сетей, и тем самым преодолевает ограничения, указанные Минским.

Обратное распространение не свободно от проблем. Прежде всего нет гарантии, что сеть может быть обучена за конечное время. Много усилий, израсходованных на обучение, пропадает напрасно после затрат большого количества машинного времени. Когда это происходит, попытка обучения повторяется - без всякой уверенности, что результат окажется лучше. Нет также уверенности, что сеть обучится наилучшим возможным образом.

Разработано много других сетевых алгоритмов обучения, имеющих свои специфические преимущества. Следует подчеркнуть, что никакая из сегодняшних сетей не является панацеей, все они страдают от ограничений в своих возможностях обучаться и вспоминать.

Мы имеем дело с областью, продемонстрировавшей свою работоспособность, имеющей уникальные потенциальные возможности, много ограничений и множество открытых вопросов. Такая ситуация настраивает на умеренный оптимизм. Авторы склонны публиковать свои успехи, но не неудачи, создавая тем самым впечатление, которое может оказаться нереалистичным. Те, кто ищет капитал, чтобы рискнуть и основать новые фирмы, должны представить убедительный проект последующего осуществления и прибыли. Существует, следовательно, опасность, что искусственные нейронные сети начнут продавать раньше, чем придет их время, обещая функциональные возможности, которых пока невозможно достигнуть. Если это произойдет, то область в целом может пострадать от потери кредита доверия и вернется к застойному периоду семидесятых годов. Для улучшения существующих сетей требуется много основательной работы. Должны быть развиты новые технологии, улучшены существующие методы и расширены теоретические основы, прежде чем данная область сможет полностью реализовать свои потенциальные возможности.

         1.2 Основные виды искусственных нейронных сетей

Развитие искусственных нейронных сетей вдохновляется биологией. То есть рассматривая сетевые конфигурации и алгоритмы, исследователи мыслят их в терминах организации мозговой деятельности. Но на этом аналогия может и закончиться. Наши знания о работе мозга столь ограничены, что мало бы нашлось руководящих ориентиров для тех, кто стал бы ему подражать. Поэтому разработчикам сетей приходится выходить за пределы современных биологических знаний в поисках структур, способных выполнять полезные функции. Во многих случаях это приводит к необходимости отказа от биологического правдоподобия, мозг становится просто метафорой, и создаются сети, невозможные в живой материи или требующие неправдоподобно больших допущений об анатомии и функционировании мозга.

Несмотря на то что связь с биологией слаба и зачастую несущественна, искусственные нейронные сети продолжают сравниваться с мозгом. Их функционирование часто напоминает человеческое познание, поэтому трудно избежать этой аналогии. К сожалению, такие сравнения неплодотворны и создают неоправданные ожидания, неизбежно ведущие к разочарованию. Исследовательский энтузиазм, основанный на ложных надеждах, может испариться, столкнувшись с суровой действительностью, как это уже однажды было в шестидесятые годы, и многообещающая область снова придет в упадок, если не будет соблюдаться необходимая сдержанность.

Несмотря на сделанные предупреждения, полезно все же знать кое-что о нервной системе млекопитающих, так как она успешно решает задачи, к выполнению которых лишь стремятся искусственные системы.

Нервная система человека, построенная из элементов, называемых нейронами, имеет ошеломляющую сложность. Около 1011 нейронов участвуют в примерно 1015 передающих связях, имеющих длину метр и более. Каждый нейрон обладает многими качествами, общими с другими элементами тела, но его уникальной способностью является прием, обработка и передача электрохимических сигналов по нервным путям, которые образуют коммуникационную систему мозга.

На рисунке 1.1 показана структура пары типичных биологических нейронов. Дендриты идут от тела нервной клетки к другим нейронам, где они принимают сигналы в точках соединения, называемых синапсами. Принятые синапсом входные сигналы подводятся к телу нейрона. Здесь они суммируются, причем одни входы стремятся возбудить нейрон, другие - воспрепятствовать его возбуждению. Когда суммарное возбуждение в теле нейрона превышает некоторый порог, нейрон возбуждается, посылая по аксону сигнал другим нейронам. У этой основной функциональной схемы много усложнений и исключений, тем не менее большинство искусственных нейронных сетей моделируют лишь эти простые свойства.

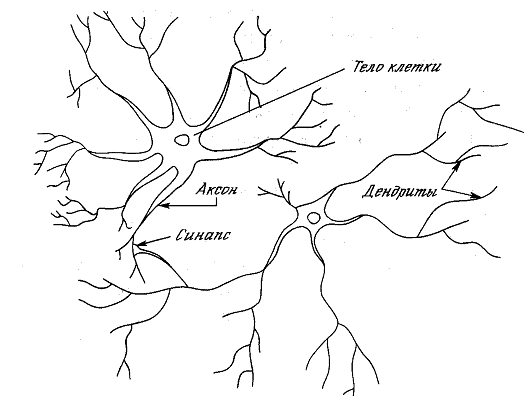
Рисунок 1.1 - Биологический нейрон

Искусственный нейрон имитирует в первом приближении свойства биологического нейрона. На вход искусственного нейрона поступает некоторое множество сигналов, каждый из которых является выходом другого нейрона. Каждый вход умножается на соответствующий вес, аналогичный синаптической силе, и все произведения суммируются, определяя уровень активации нейрона. На рисунке 1.2 представлена модель, реализующая эту идею. Хотя сетевые парадигмы весьма разнообразны, в основе почти всех их лежит эта конфигурация. Здесь множество входных сигналов, обозначенных x1, x2,…, xn, поступает на искусственный нейрон. Эти входные сигналы, в совокупности обозначаемые вектором X, соответствуют сигналам, приходящим в синапсы биологического нейрона. Каждый сигнал умножается на соответствующий вес w1, w2,…, wn, и поступает на суммирующий блок, обозначенный Σ. Каждый вес соответствует «силе» одной биологической синаптической связи. (Множество весов в совокупности обозначается вектором W.) Суммирующий блок, соответствующий телу биологического элемента, складывает взвешенные входы алгебраически, создавая выход, который мы будем называть NET. В векторных обозначениях это может быть компактно записано следующим образом

NET = XW. (1.1)

Рисунок 1.2 - Искусственный нейрон

Сигнал NET далее, как правило, преобразуется активационной функцией F и дает выходной нейронный сигнал OUT. Активационная функция может быть обычной линейной функцией

OUT = K(NET), (1.2)

где К - постоянная, пороговой функции

OUT = 1, если NET > T,

OUT = 0 в остальных случаях,

где Т - некоторая постоянная пороговая величина, или же функцией, более точно моделирующей нелинейную передаточную характеристику биологического нейрона и представляющей нейронной сети большие возможности.

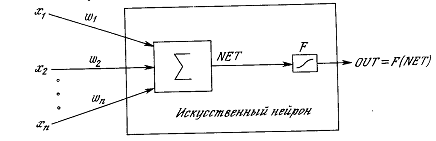
Рисунок 1.3 - Искусственный нейрон с активационной функцией

На рисунке 1.3 блок, обозначенный F, принимает сигнал NET и выдает сигнал OUT. Если блок F сужает диапазон изменения величины NET так, что при любых значениях NET значения OUT принадлежат некоторому конечному интервалу, то F называется «сжимающей» функцией. В качестве «сжимающей» функции часто используется логистическая или «сигмоидальная» (S-образная) функция, показанная на рисунке 1.4. Эта функция математически выражается как F(x) = 1/(1 + е-x). Таким образом

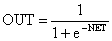. (1.3)

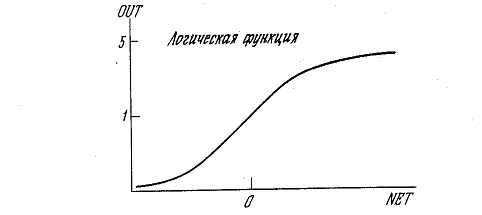
Рисунок 1.4 - Сигмоидальная логистическая функция

По аналогии с электронными системами активационную функцию можно считать нелинейной усилительной характеристикой искусственного нейрона. Коэффициент усиления вычисляется как отношение приращения величины OUT к вызвавшему его небольшому приращению величины NET. Он выражается наклоном кривой при определенном уровне возбуждения и изменяется от малых значений при больших отрицательных возбуждениях (кривая почти горизонтальна) до максимального значения при нулевом возбуждении и снова уменьшается, когда возбуждение становится большим положительным. Таким образом, нейрон функционирует с большим усилением в широком диапазоне уровня входного сигнала

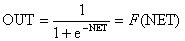. (1.4)

Другой широко используемой активационной функцией является гиперболический тангенс. По форме она сходна с логистической функцией и часто используется биологами в качестве математической модели активации нервной клетки. В качестве активационной функции искусственной нейронной сети она записывается следующим образом

OUT = th(x). (1.5)

Как показано на рисунке 1.5 подобно логистической функции гиперболический тангенс является S-образной функцией, но он симметричен относительно начала координат, и в точке NET = 0 значение выходного сигнала OUT равно нулю. В отличие от логистической функции гиперболический тангенс принимает значения различных знаков, что оказывается выгодным для ряда сетей.

Рисунке 1.5 - Функция гиперболического тангенса

Хотя один нейрон и способен выполнять простейшие процедуры распознавания, сила нейронных вычислений проистекает от соединений нейронов в сетях. Простейшая сеть состоит из группы нейронов, образующих слой, как показано в правой части рисунка 1.6.

Рисунок 1.6 - Однослойная нейронная сеть

В искусственных и биологических сетях многие соединения могут отсутствовать, все соединения показаны в целях общности. Могут иметь место также соединения между выходами и входами элементов в слое.

Удобно считать веса элементами матрицы W. Матрица имеет т строк и п столбцов, где m - число входов, а n - число нейронов. Например, w2,3 - это вес, связывающий третий вход со вторым нейроном. Таким образом, вычисление выходного вектора N, компонентами которого являются выходы OUT нейронов, сводится к матричному умножению N = XW, где N и Х - векторы-строки.

Более крупные и сложные нейронные сети обладают, как правило, и большими вычислительными возможностями.

Многослойные сети могут образовываться каскадами слоев. Выход одного слоя является входом для последующего слоя. Подобная сеть показана на рисунке 1.7 и снова изображена со всеми соединениями.

Рисунок 1.7 - Двухслойная нейронная сеть

Многослойные сети не могут привести к увеличению вычислительной мощности по сравнению с однослойной сетью лишь в том случае, если активационная функция между слоями будет нелинейной. Вычисление выхода слоя заключается в умножении входного вектора на первую весовую матрицу с последующим умножением (если отсутствует нелинейная активационная функция) результирующего вектора на вторую весовую матрицу (XW1)W2. Так как умножение матриц ассоциативно, то X(W1W2).

Это показывает, что двухслойная линейная сеть эквивалентна одному слою с весовой матрицей, равной произведению двух весовых матриц. Следовательно, любая многослойная линейная сеть может быть заменена эквивалентной однослойной сетью. Однослойные сети весьма ограниченны по своим вычислительным возможностям. Таким образом, для расширения возможностей сетей по сравнению с однослойной сетью необходима нелинейная активационная функция.

1.3 ПРИМЕНЕНИЕ ИСКУСТВЕННЫХ НЕЙРОННЫХ СЕТЕЙ

Нейронные сети могут все. Но точно также «все» могут машины Тьюринга, интерполяционные многочлены, схемы Поста, ряды Фурье, рекурсивные функции, дизъюнктивные нормальные формы, сети Петри. С помощью нейронных сетей можно сколь угодно точно аппроксимировать любую непрерывную функцию и имитировать любой непрерывный автомат. Это и слишком много - никому не нужен столь широкий класс функций, и слишком мало, так как далеко не все важные задачи ставятся как задачи аппроксимации.

Другое дело, что в конечном итоге решение практически любой задачи можно описать, как построение некоторой функции, перерабатывающей исходные данные в результат, но такое очень общее описание не дает никакой информации о способе построения этой функции. Мало иметь универсальные способности - надо для каждого класса задач указать, как применять эти способности. Именно здесь, при рассмотрении методов настройки нейронных сетей для решения задач должны выявиться реальные рамки их применимости. Конечно, такие реальные рамки изменяются со временем из-за открытия новых методов и решений.

Начнем с систем, состоящих из одного элемента.

Даже системы из одного адаптивного сумматора находят очень широкое применение. Вычисление линейных функций необходимо во многих задачах. Вот неполный перечень «специальностей» адаптивного сумматора:

линейная регрессия и восстановление простейших закономерностей [13-14];

линейная фильтрация и адаптивная обработка сигналов [15];

линейное разделение классов и простейшие задачи распознавания образов [16-18].

Задача линейной регрессии состоит в поиске наилучшего линейного приближения функции, заданной конечным набором значений: дана выборка значений вектора аргументов x1 , ..., xm, заданы значения функции F в этих точках: F(xi)=fi, требуется найти линейную (неоднородную) функцию j(x)=(a,x)+a0, ближайшую к F. Чтобы однозначно поставить задачу, необходимо доопределить, что значит «ближайшую». Наиболее популярен метод наименьших квадратов, согласно которому j ищется из условия

.                                      (1.6)

Необходимо особенно подчеркнуть, что метод наименьших квадратов не является ни единственным, ни наилучшим во всех отношениях способом доопределения задачи регрессии. Его главное достоинство - квадратичность минимизируемого критерия и линейность получаемых уравнений на коэффициенты j.

Явные формулы линейной регрессии легко получить, минимизируя квадратичный критерий качества регрессии. Обозначим

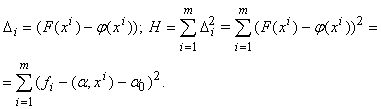 (1.7)

Найдем производные минимизируемой функции H по настраиваемым параметрам:

, (1.8)

где xij - j-я координата вектора xi.

Приравнивая частные производные H нулю, получаем уравнения, из которых легко найти все aj (j=0,...,n). Решение удобно записать в общем виде, если для всех i=1,...,m обозначить 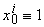 и рассматривать n+1-мерные векторы данных xi и коэффициентов a. Тогда

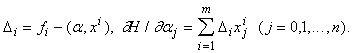
Обозначим p n+1-мерный вектор с координатами

,

 - матрицу размером (n+1)´(n+1) с элементами

.

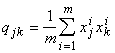В новых обозначениях решение задачи линейной регрессии имеет вид:

j(x)=(a,x), a=Q-1p.                        (1.9)

Приведем это решение в традиционных обозначениях математической статистики. Обозначим Mо среднее значение j-й координаты векторов исходной выборки:

.

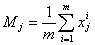Пусть M - вектор с координатами Mо. Введем также обозначение sj для выборочного среднеквадратичного отклонения:

.

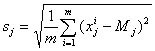Величины sj задают естественный масштаб для измерения j-х координат векторов x. Кроме того, нам потребуются величина sf и коэффициенты корреляции f с j-ми координатами векторов x - rfj:

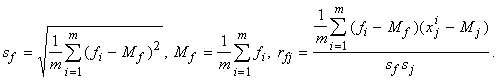 (1.10)

Вернемся к n-мерным векторам данных и коэффициентов. Представим, что векторы сигналов проходят предобработку - центрирование и нормировку и далее мы имеем дело с векторами yi

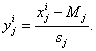
Это, в частности, означает, что все рассматриваемые координаты вектора x имеют ненулевую дисперсию, т.е. постоянные координаты исключаются из рассмотрения - они не несут полезной информации. Уравнения регрессии будем искать в форме: j(y)=(b,y)+b0. Получим

b0=Mf, b=sfR-1Rf,                                            (1.11)

где Rf - вектор коэффициентов корреляции f с j-ми координатами векторов x, имеющий координаты rfj, R - матрица коэффициентов корреляции между координатами вектора данных:

В задачах обработки данных почти всегда возникает вопрос о последовательном уточнении результатов по мере поступления новых данных (обработка данных «на лету»). Существует, как минимум, два подхода к ответу на этот вопрос для задачи линейной регрессии. Первый подход состоит в том, что изменения в коэффициентах регрессии при поступлении новых данных рассматриваются как малые и в их вычислении ограничиваются первыми порядками теории возмущений. При втором подходе для каждого нового вектора данных делается шаг изменений коэффициентов, уменьшающий ошибку регрессии D2 на вновь поступившем векторе данных. При этом «предыдущий опыт» фиксируется только в текущих коэффициентах регрессии.

В рамках первого подхода рассмотрим, как будет изменяться a при добавлении нового вектора данных. В первом порядке теории возмущений найдем изменение вектора коэффициента a при изменении вектора p и матрицы Q:

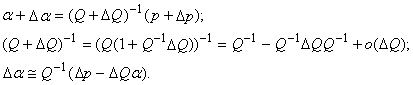
Пусть на выборке  вычислены p, Q, Q-1. При получении нового вектора данных xm+1 и соответствующего значения F(xm+1)=f m+1 имеем

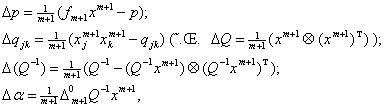                 (1.12)

где 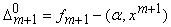 - ошибка на векторе данных xm+1 регрессионной зависимости, полученной на основании выборки .

Пересчитывая по приведенным формулам p, Q, Q-1 и a после каждого получения данных, получаем процесс, в котором последовательно уточняются уравнения линейной регрессии. И требуемый объем памяти, и количество операций имеют порядок n2 - из-за необходимости накапливать и модифицировать матрицу Q-1. Конечно, это меньше, чем потребуется на обычное обращение матрицы Q на каждом шаге, однако следующий простой алгоритм еще экономнее. Он вовсе не обращается к матрицам Q, Q-1 и основан на уменьшении на каждом шаге величины - квадрата ошибки на векторе данных xm+1 регрессионной зависимости, полученной на основании выборки .

Вновь обратимся к формуле (1.10) и будем рассматривать n+1-мерные векторы данных и коэффициентов. Обозначим . Тогда

.                                         (1.13)

Последняя элементарная формула столь важна в теории адаптивных сумматоров, что носит «именное название» - формула Уидроу. «Обучение» адаптивного сумматора методом наискорейшего спуска состоит в изменении вектора коэффициентов a в направлении антиградиента D2: на каждом шаге к a добавляется h´D´x, где h - величина шага.

Если при каждом поступлении нового вектора данных x изменять a указанным образом, то получим последовательную процедуру построения линейной аппроксимации функции F(x). Такой алгоритм обучения легко реализуется аппаратными средствами (изменение веса связи aj есть произведение прошедшего по ней сигнала xj на ошибку D и на величину шага). Возникает, однако, проблема сходимости: если h слишком мало, то сходимость будет медленной, если же слишком велико, то произойдет потеря устойчивости и сходимости не будет вовсе.

Задача четкого разделения двух классов по обучающей выборке ставится так: имеется два набора векторов x1 , ..., xm и y1,...,ym . Заранее известно, что xi относится к первому классу, а yi - ко второму. Требуется построить решающее правило, то есть определить такую функцию f(x), что при f(x)>0 вектор x относится к первому классу, а при f(x)<0 - ко второму.

Координаты классифицируемых векторов представляют собой значения некоторых признаков (свойств) исследуемых объектов.

Эта задача возникает во многих случаях: при диагностике болезней и определении неисправностей машин по косвенным признакам, при распознавании изображений и сигналов и т.п.

Строго говоря, классифицируются не векторы свойств, а объекты, которые обладают этими свойствами. Это замечание становится важным в тех случаях, когда возникают затруднения с построением решающего правила - например тогда, когда встречаются принадлежащие к разным классам объекты, имеющие одинаковые признаки. В этих случаях возможно несколько решений:

искать дополнительные признаки, позволяющие разделить классы;

примириться с неизбежностью ошибок, назначить за каждый тип ошибок свой штраф (c12 - штраф за то, что объект первого класса отнесен ко второму, c21 - за то, что объект второго класса отнесен к первому) и строить разделяющее правило так, чтобы минимизировать математическое ожидание штрафа;

перейти к нечеткому разделению классов - строить так называемые "функции принадлежности" f1(x) и f2(x) - fi(x) оценивает степень уверенности при отнесении объекта к i-му классу (i=1,2), для одного и того же x может быть так, что и f1(x)>0, и f2(x)>0.

Линейное разделение классов состоит в построении линейного решающего правила - то есть такого вектора a и числа a0 (называемого порогом), что при (x,a)>a0 x относится к первому классу, а при (x, a)<a0 - ко второму.

Поиск такого решающего правила можно рассматривать как разделение классов в проекции на прямую. Вектор a задает прямую, на которую ортогонально проектируются все точки, а число a0 - точку на этой прямой, отделяющую первый класс от второго.

Простейший и подчас очень удобный выбор состоит в проектировании на прямую, соединяющую центры масс выборок. Центр масс вычисляется в предположении, что массы всех точек одинаковы и равны. Это соответствует заданию a в виде

a= (y1+ y2+...+ym)/m -(x1+ x2+...+ x n)/n.                  (1.14)

Во многих случаях удобнее иметь дело с векторами единичной длины. Нормируя a, получаем:

a= ((y1+ y2+...+ym)/m -(x1+ x2+...+ x n)/n)/(y1+ y2+...+ym)/m -(x1+ x2+...+ +xn)/n.

Выбор a0 может производиться из различных соображений. Простейший вариант - посередине между центрами масс выборок:

a0= (((y1+ y2+...+ym)/m,a) + ((x1+ x2+...+ x n)/n,a))/2.

Более тонкие способы построения границы раздела классов a0 учитывают различные вероятности появления объектов разных классов, и оценки плотности распределения точек классов на прямой. Чем меньше вероятность появления данного класса, тем более граница раздела приближается к центру тяжести соответствующей выборки.

Можно для каждого класса построить приближенную плотность вероятностей распределения проекций его точек на прямую (это намного проще, чем для многомерного распределения) и выбирать a0, минимизируя вероятность ошибки. Пусть решающее правило имеет вид: при (x, a)>a0 x относится к первому классу, а при (x, a)<a0 - ко второму. В таком случае вероятность ошибки будет равна

где p1, p2 - априорные вероятности принадлежности объекта соответствующему классу,

r1(c), r2(c) - плотности вероятности для распределения проекций c точек x в каждом классе.

Приравняв нулю производную вероятности ошибки по a0, получим: число a0, доставляющее минимум вероятности ошибки, является корнем уравнения:

p1r1(c) = p2r2(c),                                              (1.15)

либо (если у этого уравнения нет решений) оптимальным является правило, относящее все объекты к одному из классов.

Если принять гипотезу о нормальности распределений:

,

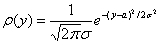то для определения a0 получим:

,

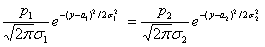Если это уравнение имеет два корня y=a1, a2, (a1<a2) то наилучшим решающим правилом будет: при a1<(x, a)<a2 объект принадлежит одному классу, а при a1>(x, a) или (x, a)>a2 - другому (какому именно, определяется тем, которое из произведений piri(c) больше). Если корней нет, то оптимальным является отнесение к одному из классов. Случай единственного корня представляет интерес только тогда, когда s1=s2. При этом уравнение превращается в линейное и мы приходим к исходному варианту - единственной разделяющей точке a0.

Таким образом, разделяющее правило с единственной разделяющей точкой a0 не является наилучшим для нормальных распределений и надо искать две разделяющие точки.

Если сразу ставить задачу об оптимальном разделении многомерных нормальных распределений, то получим, что наилучшей разделяющей поверхностью является квадрика (на прямой типичная «квадрика» - две точки). Предполагая, что ковариационные матрицы классов совпадают (в одномерном случае это предположение о том, что s1=s2), получаем линейную разделяющую поверхность. Она ортогональна прямой, соединяющей центры выборок не в обычном скалярном произведении, а в специальном: , где S - общая ковариационная матрица классов.

Важная возможность усовершенствовать разделяющее правило состоит с использовании оценки не просто вероятности ошибки, а среднего риска: каждой ошибке приписывается «цена» ci и минимизируется сумма c1p1r1(c)+c2p2r2(c). Ответ получается практически тем же (всюду pi заменяются на cipi), но такая добавка важна для многих приложений.

Требование безошибочности разделяющего правила на обучающей выборке принципиально отличается от обсуждавшихся критериев оптимальности. На основе этого требования строится персептрон Розенблатта.

Возьмем за основу при построении гиперплоскости, разделяющей классы, отсутствие ошибок на обучающей выборке. Чтобы удовлетворить этому условию, придется решать систему линейных неравенств:

(xi, a)>a0 (i=1,...,n)

(yj , a)<a0 (j=1,...,m).

Здесь xi (i=1,..,n) - векторы из обучающей выборки, относящиеся к первому классу, а yj (j=1,..,n) - ко второму.

Удобно переформулировать задачу. Увеличим размерности всех векторов на единицу, добавив еще одну координату -a0 к a, x0 =1 - ко всем x и y0 =1 - ко всем y . Сохраним для новых векторов прежние обозначения - это не приведет к путанице.

Наконец, положим zi =xi (i=1,...,n), zj = -yj (j=1,...,m).

Тогда получим систему n+m неравенств

(zi,a)>0 (i=1,...,n+m),

которую будем решать относительно a. Если множество решений непусто, то любой его элемент a порождает решающее правило, безошибочное на обучающей выборке.

Итерационный алгоритм решения этой системы чрезвычайно прост. Он основан на том, что для любого вектора x его скалярный квадрат (x,x) больше нуля. Пусть a - некоторый вектор, претендующий на роль решения неравенств (zi,a)>0 (i=1,...,n+m), однако часть из них не выполняется. Прибавим те zi, для которых неравенства имеют неверный знак, к вектору a и вновь проверим все неравенства (zi,a)>0 и т.д. Если они совместны, то процесс сходится за конечное число шагов. Более того, добавление zi к a можно производить сразу после того, как ошибка ((zi,a)<0) обнаружена, не дожидаясь проверки всех неравенств - и этот вариант алгоритма тоже сходится [2].

Перейдем от одноэлементных систем к нейронным сетям. Пусть aij - вес связи, ведущей от j-го нейрона к i-му (полезно обратить внимание на порядок индексов). Для полносвязных сетей определены значения aij при всех i,j, для других архитектур связи, ведущие от j-го нейрона к i-му для некоторых i,j не определены. В этом случае положим aij=0.

В данном разделе речь пойдет в основном о полносвязных сетях. Пусть на выходах всех нейронов получены сигналы xj (j-номер нейрона). Обозначим x вектор этих выходных сигналов. Прохождение вектора сигналов x через сеть связей сводится к умножению матрицы (aij) на вектор сигналов x. В результате получаем вектор входных сигналов нелинейных элементов нейронов:

.

Это соответствие «прохождение сети º умножение матрицы связей на вектор сигналов» является основой для перевода обычных численных методов на нейросетевой язык и обратно. Практически всюду, где основной операцией является умножение матрицы на вектор, применимы нейронные сети. С другой стороны, любое устройство, позволяющее быстро осуществлять такое умножение, может использоваться для реализации нейронных сетей.

В частности, вычисление градиента квадратичной формы  может осуществляться полносвязной сетью с симметричной матрицей связей:

 ().

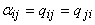Соответственно, можно методом наискорейшего спуска искать точку минимума многочлена второго порядка. Пусть задан такой многочлен:

.

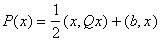Его градиент равен . Этот вектор может быть получен при прохождении вектора x через сеть с весами связей 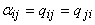 при условии, что на входной сумматор каждого нейрона по дополнительной связи веса b подается стандартный единичный сигнал.

Зададим теперь функционирование сети формулой

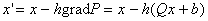                                   (1.16)

Каждый (j-й) нейрон имеет входные веса  для связей с другими нейронами (i¹j), вес  для постоянного единичного входного сигнала и вес  для связи нейрона с самим собой. Выбор шага h>0 может вызвать затруднение т.к. он зависит от коэффициентов минимизируемого многочлена. Есть, однако, простое решение: в каждый момент дискретного времени T выбирается свое значение . Достаточно, чтобы шаг стремился со временем к нулю, а сумма шагов - к бесконечности (например,  ).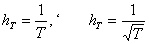

Итак, простая симметричная полносвязная сеть без нелинейных элементов может методом наискорейшего спуска искать точку минимума квадратичного многочлена.

Решение системы линейных уравнений  сводится к минимизации многочлена

Поэтому решение системы может производиться нейронной сетью. Простейшая сеть, вычисляющая градиент этого многочлена, не полносвязна, а состоит из двух слоев: первый с матрицей связей , второй - с транспонированной матрицей 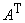. Постоянный единичный сигнал подается на связи с весами 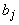 на первом слое. Минимизация этого многочлена, а значит и решение системы линейных уравнений, может проводиться так же, как и в общем случае, в соответствии с формулой 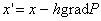. Усовершенствованные варианты алгоритма решения можно найти в работах Сударикова [8].

Небольшая модификация позволяет вместо безусловного минимума многочлена второго порядка P искать точку условного минимума с условиями , то есть точку минимума P в ограничении на аффинное многообразие, параллельное некоторым координатным плоскостям. Для этого вместо формулы

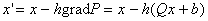
следует использовать:

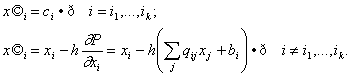               (1.17)

Устройство, способное находить точку условного минимума многочлена второго порядка при условиях вида  позволяет решать важную задачу - заполнять пробелы в данных (и, в частности, строить линейную регрессию).

Предположим, что получаемые в ходе испытаний векторы данных подчиняются многомерному нормальному распределению:

,

где Mx - вектор математических ожиданий координат, 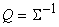ковариационная матрица, n - размерность пространства данных,

.

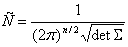Напомним определение матрицы :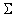

,

где M - символ математического ожидания, нижний индекс соответствует номеру координаты.

В частности, простейшая оценка ковариационной матрицы по выборке дает:

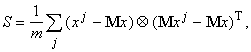
где m - число элементов в выборке, верхний индекс j - номер вектора данных в выборке, верхний индекс Т означает транспонирование, а Ä - произведение вектора-столбца на вектор-строку (тензорное произведение).

Пусть у вектора данных x известно несколько координат: . Наиболее вероятные значения неизвестных координат должны доставлять условный максимум показателю нормального распределения - многочлену второго порядка  (при условии ). Эти же значения будут условными математическими ожиданиями неизвестных координат при заданных условиях.

Таким образом, чтобы построить сеть, заполняющую пробелы в данных, достаточно сконструировать сеть для поиска точек условного минимума многочлена  при условиях следующего вида: . Матрица связей Q выбирается из условия 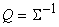, где S - ковариационная матрица (ее оценка по выборке).

На первый взгляд, пошаговое накопление 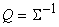 по мере поступления данных требует слишком много операций - получив новый вектор данных требуется пересчитать оценку S, а потом вычислить 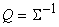. Можно поступать и по-другому, воспользовавшись формулой приближенного обрашения матриц первого порядка точности:

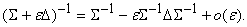
Если же добавка D имеет вид , то

                       (1.18)

Заметим, что решение задачи (точка условного минимума многочлена) не меняется при умножении Q на число. Поэтому полагаем:

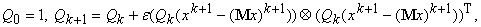
где 1 - единичная матрица, e>0 - достаточно малое число, 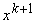 - k+1-й вектор данных,  - среднее значение вектора данных, уточненное с учетом :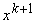

=

В формуле для пошагового накопления матрицы Q ее изменение DQ при появлении новых данных получается с помощью вектора y=, пропущенного через сеть: , где z=Qy. Параметр e выбирается достаточно малым для того, чтобы обеспечить положительную определенность получаемых матриц (и, по возможности, их близость к истинным значениям Q).

Описанный процесс формирования сети можно назвать обучением. Вообще говоря, можно проводить формальное различение между формированием сети по явным формулам и по алгоритмам, не использующим явных формул для весов связей (неявным). Тогда термин «обучение» предполагает неявные алгоритмы, а для явных остается название «формирование». Здесь мы такого различия проводить не будем.

Если при обучении сети поступают некомплектные данные 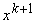 с отсутствием значений некоторых координат, то сначала эти значения восстанавливаются с помощью имеющейся сети, а потом используются в ее дальнейшем обучении.

Во всех задачах оптимизации существенную роль играет вопрос о правилах остановки: когда следует прекратить циклическое функционирование сети, остановиться и считать полученный результат ответом? Простейший выбор - остановка по малости изменений: если изменения сигналов сети за цикл меньше некоторого фиксированного малого d (при использовании переменного шага d может быть его функцией), то оптимизация заканчивается.

До сих пор речь шла о минимизации положительно определенных квадратичных форм и многочленов второго порядка. Однако самое знаменитое приложение полносвязных сетей связано с увеличением значений положительно определенных квадратичных форм. Речь идет о системах ассоциативной памяти [4-7,9,10,12].

Предположим, что задано несколько эталонных векторов данных  и при обработке поступившего на вход системы вектора x требуется получить на выходе ближайший к нему эталонный вектор. Мерой сходства в простейшем случае будем считать косинус угла между векторами - для векторов фиксированной длины это просто скалярное произведение. Можно ожидать, что изменение вектора x по закону

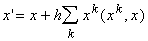,                                             (1.19)

где h - малый шаг, приведет к увеличению проекции x на те эталоны, скалярное произведение на которые 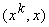 больше.

Ограничимся рассмотрением эталонов, и ожидаемых результатов обработки с координатами 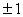. Развивая изложенную идею, приходим к дифференциальному уравнению

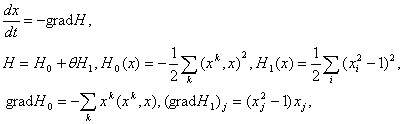     (1.20)

где верхними индексами обозначаются номера векторов-эталонов, нижними - координаты векторов.

Функция H называется «энергией» сети, она минимизируется в ходе функционирования. Слагаемое  вводится для того, чтобы со временем возрастала проекция вектора x на те эталоны, которые к нему ближе, слагаемое 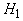 обеспечивает стремление координат вектора x к 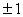. Параметр q определяет соотношение между интенсивностями этих двух процессов. Целесообразно постепенно менять q со временем, начиная с малых q<1, и приходя в конце концов к q>1.

Матрица связей построенной сети определяется функцией , так как  вычисляется непосредственно при j-м нейроне без участия сети. Вес связи между i-м и j-м нейронами не зависит от направления связи и равен

.                                             (1.21)

Эта простая формула имеет чрезвычайно важное значение для развития теории нейронных сетей. Вклад k-го эталона в связь между i-м и j-м нейронами () равен +1, если i-я и j-я координаты этого эталона имеют одинаковый знак, и равен -1, если они имеют разный знак.

В результате возбуждение i-го нейрона передается j-му (и симметрично, от j-го к i-му), если у большинства эталонов знак i-й и j-й координат совпадают. В противном случае эти нейроны тормозят друг друга: возбуждение i-го ведет к торможению j-го, торможение i-го - к возбуждению j-го (воздействие j-го на i-й симметрично). Это правило образования ассоциативных связей (правило Хебба) сыграло огромную роль в теории нейронных сетей.

Построение отношений на множестве объектов - одна из самых загадочных и открытых для творчества областей применения искусственного интеллекта. Первым и наиболее распространенным примером этой задачи является классификация без учителя. Задан набор объектов, каждому объекту сопоставлен вектор значений признаков. Требуется разбить эти объекты на классы эквивалентности.

Для каждого нового объекта мы должны сделать два дела:

найти класс, к которому он принадлежит;

использовать новую информацию, полученную об этом объекте, для исправления (коррекции) правил классификации.

Отнесение объекта к классу проводится путем его сравнения с типичными элементами разных классов и выбора ближайшего. Правила, использующие типичные объекты и меры близости для их сравнения с другими, очень популярны и сейчас.

Простейшая мера близости объектов - квадрат евклидового расстояния между векторами значений их признаков (чем меньше расстояние - расстояние - тем ближе объекты). Соответствующее определение признаков типичного объекта - среднее арифметическое значение признаков по выборке, представляющей класс.

Другая мера близости, естественно возникающая при обработке сигналов, изображений и т.п. - квадрат коэффициента корреляции (чем он больше, тем ближе объекты). Возможны и иные варианты - все зависит от задачи.

Если число классов m заранее определено, то задачу классификации без учителя можно поставить следующим образом.

Пусть {xp } - векторы значений признаков для рассматриваемых объектов и в пространстве таких векторов определена мера их близости r{x,y}. Для определенности примем, что чем ближе объекты, тем меньше r. С каждым классом будем связывать его типичный объект. Далее называем его ядром класса. Требуется определить набор из m ядер y1 , y2 , ... ym и разбиение {xp} на классы:

минимизирующее следующий критерий

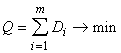,                                         (1.22)

где для каждого (i-го) класса  - сумма расстояний от принадлежащих ему точек выборки до ядра класса:

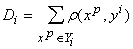.                                      (1.23)

Минимум Q берется по всем возможным положениям ядер 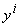 и всем разбиениям {xp}на m классов Yi.

Если число классов заранее не определено, то полезен критерий слияния классов: классы Yi и Yj сливаются, если их ядра ближе, чем среднее расстояние от элемента класса до ядра в одном из них.

Использовать критерий слияния классов можно так: сначала принимаем гипотезу о достаточном числе классов, строим их, минимизируя Q, затем некоторые Yi объединяем, повторяем минимизацию Q с новым числом классов и т.д.

Существует много эвристических алгоритмов классификации без учителя, основанных на использовании мер близости между объектами. Каждый из них имеет свою область применения, а наиболее распространенным недостатком является отсутствие четкой формализации задачи: совершается переход от идеи кластеризации прямо к алгоритму.

Сетевые алгоритмы классификации без учителя строятся на основе итерационного метода динамических ядер. Опишем его сначала в наиболее общей абстрактной форме. Пусть задана выборка предобработанных векторов данных {xp}. Пространство векторов данных обозначим E. Каждому классу будет соответствовать некоторое ядро a. Пространство ядер будем обозначать A. Для каждых xÎE и aÎA определяется мера близости d(x,a). Для каждого набора из k ядер a1,...,ak и любого разбиения {xp} на k классов {xp}=P1ÈP2È...ÈPk определим критерий качества:

                (1.24)

Требуется найти набор a1,...,ak и разбиение {xp}=P1ÈP2È...ÈPk, минимизирующие D.

Шаг алгоритма разбивается на два этапа:

-й этап - для фиксированного набора ядер a1,...,ak ищем минимизирующее критерий качества D разбиение {xp}=P1ÈP2È...ÈPk; оно дается решающим правилом: xÎPi, если d(x ,ai )<d(x ,aj ) при i¹j, в том случае, когда для x минимум d(x,a) достигается при нескольких значениях i, выбор между ними может быть сделан произвольно;

-й этап - для каждого Pi (i=1,...,k), полученного на первом этапе, ищется aiÎA, минимизирующее критерий качества (т.е. слагаемое в D для данного i -

Начальные значения a1,...,ak, {xp}=P1ÈP2È...ÈPk выбираются произвольно, либо по какому-нибудь эвристическому правилу.

На каждом шаге и этапе алгоритма уменьшается критерий качества D, отсюда следует сходимость алгоритма - после конечного числа шагов разбиение {xp}=P1ÈP2È...ÈPk уже не меняется.

Если ядру ai сопоставляется элемент сети, вычисляющий по входному сигналу x функцию d(x,ai), то решающее правило для классификации дается интерпретатором "победитель забирает все": элемент x принадлежит классу Pi, если выходной сигнал i-го элемента d(x,ai) меньше всех остальных

Единственная вычислительная сложность в алгоритме может состоять в поиске ядра по классу на втором этапе алгоритма, т.е. в поиске aÎA, минимизирующего

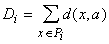
В связи с этим, в большинстве конкретных реализаций метода мера близости d выбирается такой, чтобы легко можно было найти a, минимизирующее D для данного P .

В простейшем случае пространство ядер A совпадает с пространством векторов x, а мера близости d(x,a) - положительно определенная квадратичная форма от x-a, например, квадрат евклидового расстояния или другая положительно определенная квадратичная форма. Тогда ядро ai, минимизирующее Di, есть центр тяжести класса Pi :

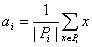,                                              (1.25)

где |Pi| - число элементов в Pi.

В этом случае также упрощается и решающее правило, разделяющее классы. Обозначим d(x,a)=(x-a,x-a), где d(x,a)- билинейная форма (если d - квадрат евклидового расстояния между x и a, то d(x,a) - обычное скалярное произведение). В силу билинейности

(x,a)=(x-a,x-a)=(x,x)-2(x,a)+(a,a).

Чтобы сравнить d(x,ai) для разных i и найти среди них минимальное, достаточно вычислить линейную неоднородную функцию от x:

(x,ai) = (ai, ai)-2(x, ai).

Минимальное значение d(x,ai) достигается при том же i, что и минимум d1(x,ai), поэтому решающее правило реализуется с помощью k сумматоров, вычисляющих d(x,a) и интерпретатора, выбирающего сумматор с минимальным выходным сигналом. Номер этого сумматора и есть номер класса, к которому относится x.

Пусть теперь мера близости - коэффициент корреляции между вектором данных и ядром класса:

где - координаты векторов, 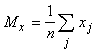 (и аналогично 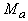), n - размерность пространства данных, (и аналогично ).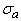

Предполагается, что данные предварительно обрабатываются (нормируются и центрируются) по правилу:

.

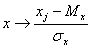Точно также нормированы и центрированы векторы ядер a. Поэтому все обрабатываемые векторы и ядра принадлежат сечению единичной евклидовой сферы (||x||=1) гиперплоскостью (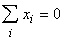). В таком случае

.

Задача поиска ядра для данного класса P имеет своим решением

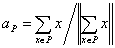.                                          (1.26)

В описанных простейших случаях, когда ядро класса точно определяется как среднее арифметическое (или нормированное среднее арифметическое) элементов класса, а решающее правило основано на сравнении выходных сигналов линейных адаптивных сумматоров, нейронную сеть, реализующую метод динамических ядер, называют сетью Кохонена. В определении ядер a для сетей Кохонена входят суммы 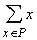. Это позволяет накапливать новые динамические ядра, обрабатывая по одному примеру и пересчитывая ai после появления в Pi нового примера. Сходимость при такой модификации, однако, ухудшается.

Закончим раздел рассмотрением различных способов использования полученных классификаторов.

. Базовый способ: для вектора данных xi и каждого ядра ai вычисляется yi=d(x, ai) (условимся считать, что правильному ядру отвечает максимум d, изменяя, если надо, знак d); по правилу «победитель забирает все» строка ответов yi преобразуется в строку, где только один элемент, соответствующий максимальному yi, равен 1, остальные - нули. Эта строка и является результатом функционирования сети. По ней может быть определен номер класса (номер места, на котором стоит 1) и другие показатели.

. Метод аккредитации: за слоем элементов базового метода, выдающих сигналы 0 или 1 по правилу "победитель забирает все" (далее называем его слоем базового интерпретатора), надстраивается еще один слой выходных сумматоров. С каждым (i-м) классом ассоциируется q-мерный выходной вектор zi с координатами zij . Он может формироваться по-разному: от двоичного представления номера класса до вектора ядра класса. Вес связи, ведущей от i-го элемента слоя базового интерпретатора к j-му выходному сумматору определяется в точности как zij . Если на этом i-м элементе базового интерпретатора получен сигнал 1, а на остальных - 0, то на выходных сумматорах будут получены числа zij.

. Нечеткая классификация. Пусть для вектор данных x обработан слоем элементов, вычисляющих yi=d(x, ai). Идея дальнейшей обработки состоит в том, чтобы выбрать из этого набора {yi} несколько самых больших чисел и после нормировки объявить их значениями функций принадлежности к соответствующим классам. Предполагается, что к остальным классам объект наверняка не принадлежит. Для выбора семейства G наибольших yi определим следующие числа:

где число a характеризует отклонение "уровня среза" s от среднего значения 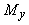 aÎ[-1,1], по умолчанию обычно принимается a=0.

Множество J={i|yiÎG} трактуется как совокупность номеров тех классов, к которым может принадлежать объект, а нормированные на единичную сумму неотрицательные величины

 (при iÎJ и f = 0 в противном случае)

интерпретируются как значения функций принадлежности этим классам.

. Метод интерполяции надстраивается над нечеткой классификацией аналогично тому, как метод аккредитации связан с базовым способом. С каждым классом связывается q-мерный выходной вектор zi. Строится слой из q выходных сумматоров, каждый из которых должен выдавать свою компоненту выходного вектора. Весовые коэффициенты связей, ведущих от того элемента нечеткого классификатора, который вычисляет fi, к j-му выходному сумматору определяются как zij. В итоге вектор выходных сигналов сети есть

В отдельных случаях по смыслу задачи требуется нормировка fi на единичную сумму квадратов или модулей.

ГЛАВА 2. ПЕРСЕПТРОН РОЗЕНБЛАТТА

.1 Задачи, решаемые при помощи Персептрона Розенблатта

В качестве научного предмета искусственные нейронные сети впервые заявили о себе в 40-е годы. Стремясь воспроизвести функции человеческого мозга, исследователи создали простые аппаратные (а позже программные) модели биологического нейрона и системы его соединений. Когда нейрофизиологи достигли более глубокого понимания нервной системы человека, эти ранние попытки стали восприниматься как весьма грубые аппроксимации. Тем не менее, на этом пути были достигнуты впечатляющие результаты, стимулировавшие дальнейшие исследования, приведшие к созданию более изощренных сетей [4].

Рисунок 2.1- Персептронный нейрон

Одной из первых искусственных сетей, способных к перцепции (восприятию) и формированию реакции на воспринятый стимул, явился PERCEPTRON Розенблатта (F.Rosenblatt, 1957). Персептрон рассматривался его автором не как конкретное техническое вычислительное устройство, а как модель работы мозга. Нужно заметить, что после нескольких десятилетий исследований современные работы по искусственным нейронным сетям редко преследуют такую цель.

Персептрон можно представлять себе как прибор для распознавания образов, который построен не для того, чтобы узнавать специфическое множество образов, а скорее для того, чтобы «научиться» после конечного числа испытаний узнавать образы из некоторого множества.

В персептрон образ поступает через сетчатку, состоящую из чувствительных элементов (например, фотоэлементов). Хотя любое воспринимаемое изображение может быть закодировано в форме, подходящей для входа, состоящего из набора чувствительных элементов, однако наиболее естественно (о чем и говорит термин «сетчатка») представлять образ как наблюдаемый вход, состоящий из света и тени. Фотоэлемент, который воспринимает относительно светлую часть образа, возбуждается, а фотоэлемент, воспринимающий относительно темную часть образа, не возбуждается.

После рассмотрения сетчатки лягушки становится ясным, что эта двоичная реакция, связанная с освещением сетчатки, имеет мало сходства с физиологической деятельностью. Чувствительные элементы соединены с промежуточными элементами (формальными нейронами), которые в свою

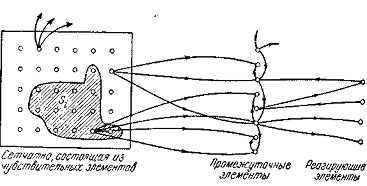
Рисунок 2.2 - Схематическое изображение персептрона

очередь могут быть соединены с реагирующими элементами (рисунок 2.2).

В терминах нейрофизиологического рассмотрения нервной системы как трехступенчатой системы сетчатка является рецептором персептрона; промежуточные элементы охватывают собственно нервную систему, а реагирующие элементы являются эффекторами или, скорее, соответствуют нейронам, выходы которых управляют эффекторами. С такими рассмотрением совместимо также и то, что когда на сетчатку персептрона действует изображение, то импульсы передаются от возбужденных чувствительных элементов к промежуточным элементам. Если сигнал, поступающий на промежуточный элемент, превосходит его порог, то этот элемент становится активным и посылает импульсы к элементам, с которыми он связан.

Перваночально персептрон являлся просто воплощением сильно упрощенных нейрофизиологических данных о нервной системе, снабженной зрительными рецепторами. Однако конструкторы персептрона пошли дальше этого, так что здесь стоит обсудить дополнительные свойства сети.

Существует, по-видимому, много подтверждений того, что люди имеют два вида памяти: «кратковременную» и «долговременную». Кроме того, кажется, что люди сначала должны запомнить мысль в кратковременной памяти, прежде чем передать ее в долговременную память. Время, необходимое для этой передачи, оценивается по-разному; в частности, одна из таких оценок равна 20 минутам. По-видимому, если кто-то впадает в бессознательное состояние, то его воспоминания о только что прошедших 20 минутах потеряны навсегда, так как они не были переданы в долговременную память. В настоящее время общепринято считать, что кратковременная память представляет собой в точности тот же тип памяти, которой мы снабдили модульную сеть, т. е. является прохождением по сети сложных конфигураций электрических импульсов. Далее, если такая временная активность продолжается довольно долго, то она фактически изменяет сеть. Это хорошо иллюстрируется простым примером (рисунок 2.3).

Рисунок 2.3 - Гипотетический пример долговременной памяти

Модуль, показанный на рисунке 2.3, хранит в кратковременной памяти информацию о том, был ли когда-нибудь возбужден его вход. Эта память сохраняется за счет образовавшегося в петле импульса. Модуль имел бы долговременную память, если бы кратковременная память могла, например, понизить его порог с 1 до 0, ибо в этом случае память сохранилась бы даже после исчезновения в петле импульса.

Один из возможных механизмов долговременной памяти заключается в образовании в нейронах специальных протеинов, которые изменяют их пороги в ответ на конфигурации кратковременной памяти. Другой механизм основан на росте концевых луковиц при повторном использовании и, таким образом, увеличивается вес соответствующего синапсического входа и, вероятно, облегчается восстановление конфигураций импульсов, использующих этот синапс. Это облегчает воспоминание прежней информации! Но истинный механизм все еще неизвестен. Поэтому физиология, гистология и анатомия, поддерживающие пока многие гипотезы, должны еще установить это).

Персептрон снабжен долговременной памятью. Это достигается изменением весов входов нейронов, или - на языке конструкторов персептрона - изменением величины импульса, поступающего от раздражителя. Эти изменения зависят от прошлой активности окончаний. Закон этой зависимости называется законом поощрения, так как он служит для поощрения правильных реакций персептрона на действие раздражителя. Сведения из физиологии настолько расплывчаты, что конструкторы персептрона выбрали такие правила поощрения, которые были удобны в теоретическом и экспериментальном отношениях. Их выбор дает персептрону возможность демонстрировать некоторые виды обучения.

Конструкторы персептрона должны были решить, каким образом надо соединить чувствительные элементы с промежуточными элементами. Первый подход заключался в том, чтобы соединения были многозначными и случайными. Позднее они включили в схему некоторые подсети, например подсети для линейного распознавания, подобные тем, которые нашли в кошке Хюбель и Визель.

Но подобно тому, как весьма упрощенная модульная сеть все же была способна хранить информацию и производить вычисления, так и первые персептроны, несмотря на все ограничения, проявляли простые свойства обучения.

Конструкторы персептрона провели три основных вида исследований: математический анализ, моделирование на цифровой вычислительной машине и построение действующей машины. Каждый метод имеет свои преимущества. Одним из важных результатов использования действующей машины является выяснение того, что ни точность, ни надежность компонент не имеют большого значения, а соединения не обязаны быть точными.

Другой интересный результат заключается в том, что персептрон может «учиться», несмотря на ошибки учителя.

Простым персептроном является такой персептрон, в котором промежуточные элементы не соединены между собой. Это означает, что у него нет кратковременной памяти.

Пусть имеются чувствительные элементы sh, промежуточные элементы am и n образов Si. В этой простой модели соединения между sh и ат не меняются (рисунок 2.4). Следовательно, множество промежуточных элементов, возбужденных образом S*, остается неизменным.

Пусть emi=1 тогда и только тогда, когда промежуточный элемент ат не возбужден образом Si-. Если Vm есть вес входа реагирующего элемента, подключенного к промежуточному элементу ат, когда перед сетчаткой находится образ Si, то вес входа реагирующего элемента равен

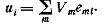
Предположим, что мы разбили имеющиеся образы на два класса: +1 и -1. Пусть ri - один из классов, содержащий образ Si. Мы хотим, чтобы реагирующий элемент возбуждался тогда и только тогда, когда данный образ принадлежит классу +1.

Одним из правил поощрения является процедура исправления ошибки, которая заключается в следующем. Персептрону показывается образ Si он дает ответ. В случае правильного ответа никакого подкрепления не делается.

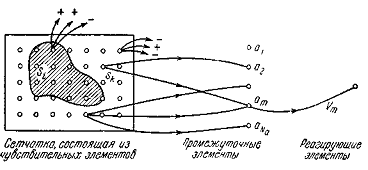
Рисунок 2.4.- Схематическое изображение простого персептрона

Если ответ неправильный, то Vm для возбужденных промежуточных элементов увеличивается на ηri (η - фиксированное положительное число). Невозбужденные промежуточные элементы остаются неизменными. Начальные значения произвольны, скажем,

 .... Vm, . . ., V N-

Предположим, что образы показываются в произвольном порядке так, что каждый образ повторяется достаточно часто. После некоторого конечного числа шагов машина будет давать правильные ответы на все образы, так что никаких дальнейших изменений не произойдет.

Порядок числа исправлений равен числу различных образов, подаваемых на сетчатку. Этот результат показал, что машина может выучивать наизусть, но использование простого персептрона в качестве прибора для распознавания образов нежелательно.

Персептрон «Марк-1» является простым персептроном. Он имеет сетчатку размером 20x20 фотоэлементов. Рассмотрим случай, когда в качестве образов используется 26 букв (английского) алфавита (каждая буква задается в стандартной форме), а выход состоит из пяти двоичных реагирующих элементов (25 = 32>',->26).

Рисунок 2.5 - Изображение буквы Е, которое может восприниматься чувствительными элементами персептрона

В проведенном эксперименте, как сообщалось, машина научилась правильно распознавать буквы после 15 показов каждой буквы, т. е. общее число показов было равно 390. Но обычно требуется от системы для распознавания нечто большее, чем только выделение образов в стандартной форме. Нужна машина, которая может распознавать каждую букву, помещенную на сетчатку, даже если она напечатана слегка искаженно и показана на пестром фоне. Но если мы допускаем это, то число образов катастрофически возрастает. В этом можно убедиться при рассмотрении различных вариантов стандартной буквы Е, образ которой представлен в виде точек, как показано на рисунке 2.5.

Следовательно, сделанный выше вывод о том, что для заучивания наизусть достаточно произвести некоторое число опытов, по порядку равное числу различных образов, является не столь значительным. Простой персептрон оказывается слишком простым. Этот простой персептрон мы обсуждаем из методических соображений; он полезен при рассмотрении вопроса о памяти нейронных сетей. На самом деле конструкторы персептрона проделали более сложную работу. Так как для своих сетей они ставили более трудные задачи, то и строили их с более сложной структурой. Их работа даже включает нейрохимическое исследование памяти и описание сопутствующих моделей [9].

Анатомия и физиология той части нашего мозга, работа которой относится к высшей нервной деятельности, мало изучена. Хотя макроскопическая анатомия мозга обнаружила сложную структуру, микроскопическая анатомия дает смутную картину, по-видимому, случайных взаимосвязей. Кажется невозможным, чтобы наши гены определяли точную структуру нашего мозга. Гораздо более вероятно, что они определяют некоторые схемы роста, более или менее подверженные меняющимся влияниям опыта. Кроме того, если бы связи были даже строго детерминированы, мы все равно не знаем механизма, посредством которого мозг может распознавать понятия, например узнавать букву А в разных видах и при некоторых искажениях. Поэтому конструкторы персептрона допускают, чтобы первоначальная структура была случайной, а та структура, которая необходима для распознавания образов, возникала в результате изменений, вызванных правилами поощрения.

Рассматривая зрительную систему лягушки можно обнаружить подтверждение того, что, по крайней мере, в лягушке некоторая очень важная структура предопределена генетически. В теории Винограда - Кована (Winograd - Cowan),можно убедимся, что если модульную сеть, предназначенную для определенной цели, преобразовать таким образом, чтобы уменьшить ее чувствительность к ошибкам, появляющимся вследствие неправильного функционирования или гибели нейронов, то в результате получится сеть, имеющая микроскопическую случайность, очень похожую на ту, которая обнаружена микроскопической анатомией мозга. В качестве последнего аргумента против использования полной случайности укажем на то, что имеются умственные акты, доступные ребенку, но совершенно недоступные для гориллы. Это происходит, возможно, вследствие генетически детерминированных различий в структуре. Дарвиновской эволюции понадобились тысячелетия, чтобы сделать наш мозг способным узнавать образы. Было бы крайне удивительно, если бы случайная сеть приобрела такую способность за несколько часов обучения.

Однако нужно признаться, что все вышеприведенные аргументы сводятся к следующему утверждению: адекватная модель человеческого мозга должна быть богата различными специфическими структурами, вроде той, которая обеспечивает восприятие прямых линий. Но это не помогает ответить на вопрос: необходима ли структура для обучения? Другими словами, если допустить, что человеческий мозг обладает структурой, то мы не достигнем еще никакого прогресса в выяснении следующих двух противоположных точек зрения:

человек разумен потому, что эволюция снабдила его мозгом с очень сложной структурой. Эта структура выполняет различные функции и, в частности, дает ему возможность учиться. Требуется некоторая критическая степень сложности структуры, чтобы сеть могла изменять себя (независимо от сложности ее правил поощрения) таким способом, который мы могли бы считать разумным;

человек - разумен потому, что эволюция снабдила его мозгом с очень сложными взаимосвязями. Схема взаимосвязей не имеет отношения к истинно разумному обучению, которое является результатом действия правил поощрения на достаточно большую, но существенно случайную сеть.

Рисунок 2.6 - Элементарный персептрон Розенблатта

Возможно, что истина заключается в искусном соединении этих точек зрения.

         2.2 Методика обучения персептрона

Способность искусственных нейронных сетей обучаться является их наиболее интригующим свойством. Подобно биологическим системам, которые они моделируют, эти нейронные сети сами моделируют себя в результате попыток достичь лучшей модели поведения.

Используя критерий линейной разделимости, можно решить, способна ли однослойная нейронная сеть реализовывать требуемую функцию. Даже в том случае, когда ответ положительный, это принесет мало пользы, если у нас нет способа найти нужные значения для весов и порогов. Чтобы сеть представляла практическую ценность, нужен систематический метод (алгоритм) для вычисления этих значений. Розенблатт [4] сделал это в своем алгоритме обучения персептрона вместе с доказательством того, что персептрон может быть обучен всему, что он может реализовывать.

Обучение может быть с учителем или без него. Для обучения с учителем нужен «внешний» учитель, который оценивал бы поведение системы и управлял ее последующими модификациями. При обучении без учителя сеть путем самоорганизации делает требуемые изменения. Обучение персептрона является обучением с учителем.

Алгоритм обучения персептрона может быть реализован на цифровом компьютере или другом электронном устройстве, и сеть становится в определенном смысле самоподстраивающейся. По этой причине процедуру подстройки весов обычно называют «обучением» и говорят, что сеть «обучается». Доказательство Розенблатта стало основной вехой и дало мощный импульс исследованиям в этой области. Сегодня в той или иной форме элементы алгоритма обучения персептрона встречаются во многих сетевых парадигмах.

Персептрон обучают, подавая множество образов по одному на его вход и подстраивая веса до тех пор, пока для всех образов не будет достигнут требуемый выход. Допустим, что входные образы нанесены на демонстрационные карты. Каждая карта разбита на квадраты и от каждого квадрата на персептрон подается вход. Если в квадрате имеется линия, то от него подается единица, в противном случае - ноль. Множество квадратов на карте задает, таким образом, множество нулей и единиц, которое и подается на входы персептрона. Цель состоит в том, чтобы научить персептрон включать индикатор при подаче на него множества входов, задающих нечетное число, и не включать в случае четного.

Рисунок 2.7 - Персептронная система распознавания изображений

искусственный нейронный сеть персептрон

На рисунке 2.7 показана такая персептронная конфигурация. Допустим, что вектор Х является образом распознаваемой демонстрационной карты. Каждая компонента (квадрат) Х - (x1, x2, …, xn) - умножается на соответствующую компоненту вектора весов W - (w1, w2, ..., wn). Эти произведения суммируются. Если сумма превышает порог Θ, то выход нейрона Y равен единице (индикатор зажигается), в противном случае он - ноль. Эта операция компактно записывается в векторной форме как Y = XW, а после нее следует пороговая операция.

Для обучения сети образ Х подается на вход и вычисляется выход Y. Если Y правилен, то ничего не меняется. Однако если выход неправилен, то веса, присоединенные к входам, усиливающим ошибочный результат, модифицируются, чтобы уменьшить ошибку.

Чтобы увидеть, как это осуществляется, допустим, что демонстрационная карта с цифрой 3 подана на вход и выход Y равен 1 (показывая нечетность). Так как это правильный ответ, то веса не изменяются. Если, однако, на вход подается карта с номером 4 и выход Y равен единице (нечетный), то веса, присоединенные к единичным входам, должны быть уменьшены, так как они стремятся дать неверный результат. Аналогично, если карта с номером 3 дает нулевой выход, то веса, присоединенные к единичным входам, должны быть увеличены, чтобы скорректировать ошибку.

Этот метод обучения может быть подытожен следующим образом:

1.       Подать входной образ и вычислить Y.

         а.       Если выход правильный, то перейти на шаг 1;

б.      Если выход неправильный и равен нулю, то добавить все входы к соответствующим им весам; или

в.       Если выход неправильный и равен единице, то вычесть каждый вход из соответствующего ему веса.

.        Перейти на шаг 1.

За конечное число шагов сеть научится разделять карты на четные и нечетные при условии, что множество цифр линейно разделимо. Это значит, что для всех нечетных карт выход будет больше порога, а для всех четных - меньше. Отметим, что это обучение глобально, т. е. сеть обучается на всем множестве карт. Возникает вопрос о том, как это множество должно предъявляться, чтобы минимизировать время обучения. Должны ли элементы множества предъявляться - последовательно друг за другом или карты следует выбирать случайно? Несложная теория служит здесь путеводителем.

Важное обобщение алгоритма обучения персептрона, называемое дельта-правилом, переносит этот метод на непрерывные входы и выходы. Чтобы понять, как оно было получено, шаг 2 алгоритма обучения персептрона может быть сформулирован в обобщенной форме с помощью введения величины δ, которая равна разности между требуемым или целевым выходом T и реальным выходом Y

δ = (T - Y).           (2.1)

Случай, когда δ=0, соответствует шагу 2а, когда выход правилен и в сети ничего не изменяется. Шаг 2б соответствует случаю δ > 0, а шаг 2в случаю δ <0.

В любом из этих случаев персептронный алгоритм обучения сохраняется, если δ умножается на величину каждого входа хi и это произведение добавляется к соответствующему весу. С целью обобщения вводится коэффициент «скорости обучения» η), который умножается на δхi, что позволяет управлять средней величиной изменения весов.

В алгебраической форме записи

Δi = ηδxi,             (2.2)

w(n+1) = w(n) + Δi,                                                                  (2.3)

где Δi - коррекция, связанная с i-м входом хi; wi (n+1) - значение веса i после коррекции; wi{n) -значение веса i до коррекции.

Дельта-правило модифицирует веса в соответствии с требуемым и действительным значениями выхода каждой полярности, как для непрерывных, так и для бинарных входов и выходов. Эти свойства открыли множество новых приложений.

Может оказаться затруднительным определить, выполнено ли условие разделимости для конкретного обучающего множества. Кроме того, во многих встречающихся на практике ситуациях входы часто меняются во времени и могут быть разделимы в один момент времени и неразделимы в другой. В доказательстве алгоритма обучения персептрона ничего не говорится также о том, сколько шагов требуется для обучения сети. Мало утешительного в знании того, что обучение закончится за конечное число шагов, если необходимое для этого время сравнимо с геологической эпохой. Кроме того, не доказано, что персептронный алгоритм обучения более быстр по сравнению с простым перебором всех возможных значений весов, и в некоторых случаях этот примитивный подход может оказаться лучше.

На эти вопросы никогда не находилось удовлетворительного ответа, они относятся к природе обучающего материала. Эти проблемы являются важной областью современных исследований.

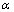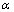Обучение сети состоит в подстройке весовых коэффициентов каждого нейрона. Пусть имеется набор пар векторов (x,y), a=1..p, называемый обучающей выборкой. Будем называть нейронную сеть обученной на данной обучающей выборке, если при подаче на входы сети каждого вектора xa на выходах всякий раз получается соответствующий вектор y.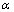

Предложенный Ф.Розенблаттом метод обучения состоит в итерационной подстройке матрицы весов, последовательно уменьшающей ошибку в выходных векторах. Алгоритм включает несколько шагов:

Шаг 0.       Начальные значения весов всех нейронов 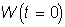 полагаются случайными.

Шаг 1.       Сети предъявляется входной образ xa, в результате формируется выходной образ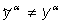  

Шаг 2.       Вычисляется вектор ошибки , делаемой сетью на выходе.

Шаг 3.       Вектор весов модифицируется по следующей формуле: 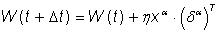. Здесь  - темп обучения.

Шаг 4.       Шаги 1-3 повторяются для всех обучающих векторов. Один цикл последовательного предъявления всей выборки называется эпохой. Обучение завершается по истечении нескольких эпох, а) когда итерации сойдутся, т.е. вектор весов перестает изменяться, или б) когда полная просуммированная по всем векторам абсолютная ошибка станет меньше некоторого малого значения.

Используемая на шаге 3 формула учитывает следующие обстоятельства:

         - модифицируются только компоненты матрицы весов, отвечающие ненулевым значениям входов;

знак приращения веса соответствует знаку ошибки, т.е. положительная ошибка (d>0, значение выхода меньше требуемого) проводит к усилению связи;

обучение каждого нейрона происходит независимо от обучения остальных нейронов, что соответствует важному с биологической точки зрения, принципу локальности обучения.

Данный метод обучения был назван Ф.Розенблаттом «методом коррекции с обратной передачей сигнала ошибки». Позднее более широко стало известно название «d - правило». Представленный алгоритм относится к широкому классу алгоритмов обучения с учителем, поскольку известны как входные вектора, так и требуемые значения выходных векторов (имеется учитель, способный оценить правильность ответа ученика).

Доказанная Розенблаттом теорема о сходимости обучения по d - правилу говорит о том, что персептрон способен обучится любому обучающему набору, который он способен представить.

Каждый нейрон персептрона является формальным пороговым элементом, принимающим единичные значения в случае, если суммарный взвешенный вход больше некоторого порогового значения:

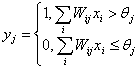
Таким образом, при заданных значениях весов и порогов, нейрон имеет определенное значение выходной активности для каждого возможного вектора входов. Множество входных векторов, при которых нейрон активен (y=1), отделено от множества векторов, на которых нейрон пассивен (y=0) гиперплоскостью.

. (2.4)

Следовательно, нейрон способен отделить (иметь различный выход) только такие два множества векторов входов, для которых имеется гиперплоскость, отсекающая одно множество от другого. Такие множества называют линейно разделимыми. Проиллюстрируем это понятие на примере.

Пусть имеется нейрон, для которого входной вектор содержит только две нулевые компоненты , определяющие плоскость. На данной плоскости возможные значения векторов отвечают вершинам единичного квадрата. В каждой вершине определено требуемое значение активности нейрона 0 (на рисунке 2.8 - белая точка) или 1 (черная точка). Требуется определить, существует ли такое такой набор весов и порогов нейрона, при котором этот нейрон сможет отделить точки разного цвета.

На рисунке 2.8 представлена одна из ситуаций, когда этого сделать нельзя вследствие линейной неразделимости множеств белых и черных точек.

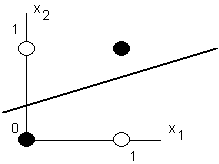
Рисунке 2.8 - Белые точки не могут быть отделены одной прямой от черных

Требуемая активность нейрона для этого рисунка определяется таблицей, в которой не трудно узнать задание логической функции “исключающее или”.

Линейная неразделимость множеств аргументов, отвечающих различным значениям функции означает, что функция “исключающее или”, широко использующаяся в логических устройствах, не может быть представлена формальным нейроном.

При возрастании числа аргументов ситуация еще более катастрофична: относительное число функций, которые обладают свойством линейной разделимости резко уменьшается. А значит и резко сужается класс функций, который может быть реализован персептроном (так называемый класс функций, обладающий свойством персептронной представляемости).

Нужно отметить, что позднее, в начале 70-х годов, это ограничение было преодолено путем введения нескольких слоев нейронов, однако критическое отношение к классическому персептрону сильно заморозило общий круг интереса и научных исследований в области искусственных нейронных сетей.

В завершении остановимся на тех проблемах, которые остались открытыми после работ Ф. Розенблатта. Часть из них была впоследствии решена, некоторые остались без полного теоретического решения [5].

) Практическая проверка условия линейной разделимости множеств. Теорема Розенблатта гарантирует успешное обучение только для персептронно представимых функций, однако ничего не говорит о том, как это свойство практически обнаружить до обучения.

) Сколько шагов потребуется при итерационном обучении? Другими словами, затянувшееся обучение может быть как следствием не представимости функции (и в этом случае оно никогда не закончится), так и просто особенностью алгоритма.

) Как влияет на обучение последовательность предъявления образов в течение эпохи обучения?

) Имеет ли вообще d - правило преимущества перед простым перебором весов, т.е. является ли оно конструктивным алгоритмом быстрого обучения?

) Каким будет качество обучения, если обучающая выборка содержит не все возможные пары векторов? Какими будут ответы персептрона на новые вектора?

Последний вопрос затрагивает глубокие пласты вычислительной нейронауки, касающиеся способностей искусственных систем к обобщению ограниченного индивидуального опыта на более широкий класс ситуаций, для которых отклик был заранее не сообщен нейросети. Ситуация, когда системе приходится работать с новыми образами, является типичной, так как число всех возможных примеров экспоненциально быстро растет с ростом числа переменных, и поэтому на практике индивидуальный опыт сети всегда принципиально не является полным.

.3 Примеры использования персептронов

Предсказание псевдослучайных последовательностей. Существуют простые рекуррентные зависимости, генерирующие псевдослучайные последовательности чисел. Например, модель, называемая логистической картой, в которой следующее значение последовательности x(t+1) связано с текущим x(t):

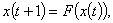
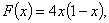 (2.5)

где 0£ x £1.

График функции F(x) показан на рисунке 2.9. Она имеет максимум F(0,5)=1.

Рисунок 2.9 - Функция, порождающая псевдослучайную последовательность

Если задать x(0) в интревале (0, 1), то по рекуррентной формуле получим псевдослучайную последовательность, элементы которой лежат в интервале (0, 1). Пример такой последовательности, для начального значения x(0)=0,2 представлен на рисунке 2.10.

Рисунок 2.10 - Псевдослучайная последовательность, полученная по формуле (2.5).

Задача состоит в том, чтобы по конкретной реализации случайной последовательности x(t) (рисунок 2.10), получить нейронную сеть, способную генерировать правильные псевдослучайные последовательности, т.е. для любого x, поданного на вход сети, давать x(t+1) на выходе.

Для решения задачи использовалась сеть с одним входом и одним выходом. Сеть содержала один скрытый слой из 5 нейронов. Применялась аналогичная сигмоидальной функция активации:

. (2.6)

Проводилось обучение методом обратного распространения с обучающим множеством, содержащим 1000 точек, т.е. 1000 известных отображений хt®хt1. Сеть также имела прямые синапсы со входа на выход, минуя скрытый слой.

В результате обучения сеть создала следующее отображение со входа на выход:

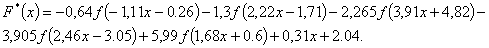 (2.7)

Созданное сетью отображение аналитически совсем не похоже на исходную функцию F(x). Тем не менее, отклонение F от F* в рабочем интервале (0, 1) оказывается малым. Графики функций F(x) (пунктир) и F*(x) (непрерывная линия) представлены на рисунке 2.11.

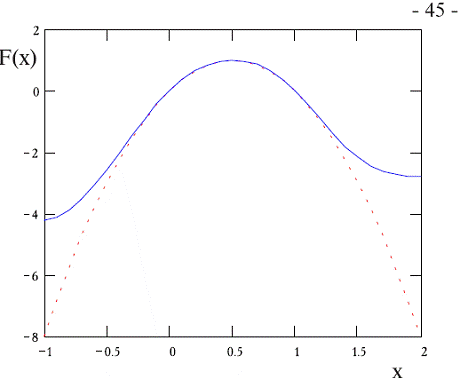
Рисунок 2.11 - Созданная сетью (непр. линия) и исходная функция F(x) (пунктир).

Из графиков рисунка 2.11 следует:

на рабочем участке сеть правильно выделила закономерность из входных данных; график F практически совпадает с F*; разумеется, при правильно изученной функции F* сеть способна правильно прогнозировать последовательность с любым x(0);

на основании неявных предположений о функции F (непрерывность и дифференцируемость) сеть адекватно прогнозировала функцию F, т.е. проявила способность к обобщению. Эта способность не присуща сети самой по себе, а определяется выбором функции активации. Если бы в качестве функции активации была выбрана, к примеру, ступенька с линейной частью, функция F* оказалась бы недифференцируемой.

Предсказание вторичной структуры белков. Молекулы белков построены из аминокислотных остатков. В живых белковых молекулах встречаются 20 различных аминокислот.

Различают три уровня структуры белковой молекулы. Первичная структура - порядок аминокислотных остатков в белковой молекуле, когда она растянута в линейную цепь. Аминокислотные остатки обозначаются трехбуквенными сочетаниями. Пример первичной структуры:

Лиз-Глу-Тре-Ала-Ала

соответствует цепи, состоящей из аминокислотных остатков: лизил-глутаминил-треонил-аланил-аланил.

Структура белковой молекулы в виде линейной цепи оказывается энергетически не самой выгодной. Благодаря изменению формы молекулы близкие участки цепи формируют несколько характерных структур: α*спираль и β*формы: параллельную и антипараллельную. Эти формы образуют вторичную структуру белковой молекулы. Она зависит от порядка аминокислотных остатков в молекуле. Третичная структура - дальний порядок в молекуле, определяет, в каком порядке вторичные структуры образуют клубок или глобулу - общий вид молекулы.

Задача ставится так: предсказать участки белковой цепи, имеющие определенную вторичную структуру, в данном случае α*спираль. Для предсказания используется только информация о последовательности аминокислотных остатков в молекуле.

Для кодирования информации об одном аминокислотном остатке в нейросети используется 20 двоичных входов, например:

Глицил 00000010...0;

Аланил 0.........01000.

Одновременно в сеть вводится информация о 51 последовательном аминокислотном остатке, со сдвигом. Всего получается 51 * 20 = 1020 входов. Сеть формирует единственный выход - вероятность того, что участок молекулы, заданный последовательностью из 51 входных аминокислотных остатков, имеет вид α* спирали. В экспериментах сеть состояла из 40 скрытых нейронов в одном слое, всего 40 000 весов и пороговых уровней. Для обучения бралась известная информация о 56 белках. Для ускорения начального этапа обучения, когда ошибка очень высока, сначала обучающее множество состояло из данных лишь об одном (n=1) белке из 56. Остальные 55 использовались для контроля качества обучения. Когда ошибка немного снижалась, в обучающее множество добавлялась информация еще об одной молекуле и т.д.

На завершающем этапе в обучении участвовали все 56 (n=56) белков [11].

В результате обучения сеть стала давать лучшую точность, чем известные математические методы для предсказания вторичной структуры. Это редкий случай, когда нейросети превосходят математические методы по точности.

Синтез речи: NET7talk. В 1987 г. Сейновский, Розенберг провели эксперименты по преобразованию текста из английских букв в фонемы. Задача синтеза речевого сигнала из фонем гораздо проще, чем преобразование текста в фонемы. Полученное нейронной сетью фонетическое представление затем «прочитывалось» вслух одним из многочисленных коммерческих синтезаторов речи.

Для преобразования текста в фонемы применялся многослойный перцептрон с одним скрытым слоем из 80 нейронов. На вход одновременно подавалась последовательность из 7 букв, каждая из которых кодировалась группой из 29 входов (26 букв алфавита + знаки препинания). Сеть имела 26 выходов для представления одной из 26 фонем с различной окраской звучания, сюда же относились фонемы-паузы.

Сеть прошла 50 циклов обучения по обучающему множеству из 1024 английских слов, и достигла 95% вероятности правильного произношения для слов из этого множества, и вероятности 80% на неизвестных сети словах. Если учесть скромность затрат на реализацию эксперимента, по сравнению с коммерческими синтезаторами, то этот результат очень хорош [19].

ГЛАВА 3. КОМПЬЮТЕРНАЯ ИМИТАЦИОНАЯ МОДЕЛЬ ПЕРСЕПТРОНА РОЗЕНБЛАТТА

.1 Ограничения, накладываемые на имитационную модель

Один из самых пессимистических результатов Минского показывает, что однослойный персептрон не может воспроизвести такую простую функцию, как ИСКЛЮЧАЮЩЕЕ ИЛИ. Это функция от двух аргументов, каждый из которых может быть нулем или единицей. Она принимает значение единицы, когда один из аргументов равен единице (но не оба). Проблему можно проиллюстрировать с помощью однослойной однонейронной системы с двумя входами, показанной на рисунке 3.1. Обозначим один вход через х, а другой через у, тогда все их возможные комбинации будут состоять из четырех точек на плоскости х-у, как показано на рис. 2.8. Например, точка х = 0 и у = 0 обозначена на рисунке как точка А Таблица 3.1 показывает требуемую связь между входами и выходом, где входные комбинации, которые должны давать нулевой выход, помечены А0 и А1, единичный выход - В0 и В1.

Рисунок 3.1 - Однослойная однонейронная система с двумя входами

В сети на рисунке 3.1 функция F является обычным порогом, так что OUT принимает значение ноль, когда NET меньше 0,5, и единица в случае, когда NET больше или равно 0,5. Нейрон выполняет следующее вычисление

NET = xw1 + yw2.                                                                   (3.1)

Никакая комбинация значений двух весов не может дать соотношения между входом и выходом, задаваемого таблице 3.1 Чтобы понять это ограничение, зафиксируем NET на величине порога 0,5. Сеть в этом случае описывается уравнением (3.2). Это уравнение линейно по х и у, т. е. все значения по х и у, удовлетворяющие этому уравнению, будут лежать на некоторой прямой в плоскости х-у.

xw1 + yw2 = 0,5.  (3.2)

Таблица 3.1. Таблица истинности для функции «ИСКЛЮЧАЮЩЕЕ ИЛИ»

Любые входные значения для х и у на этой линии будут давать пороговое значение 0,5 для NET. Входные значения с одной стороны прямой обеспечат значения NET больше порога, следовательно, OUT=1. Входные значения по другую сторону прямой обеспечат значения NET меньше порогового значения, делая OUT равным 0. Изменения значений w1, w2 и порога будут менять наклон и положение прямой. Для того чтобы сеть реализовала функцию ИСКЛЮЧАЮЩЕЕ ИЛИ, заданную таблицей 3.1, нужно расположить прямую так, чтобы точки А были с одной стороны прямой, а точки В - с другой. Попытавшись нарисовать такую прямую на рисунке 3.2, убеждаемся, что это невозможно. Это означает, что какие бы значения ни приписывались весам и порогу, сеть неспособна воспроизвести соотношение между входом и выходом, требуемое для представления функции «ИСКЛЮЧАЮЩЕЕ ИЛИ».

Рисунок 3.2 - Проблема ИСКЛЮЧАЮЩЕЕ ИЛИ

Взглянув на задачу с другой точки зрения, рассмотрим NET как поверхность над плоскостью х-у. Каждая точка этой поверхности находится над соответствующей точкой плоскости х-у на расстоянии, равном значению NET в этой точке. Можно показать, что наклон этой NET-поверхности одинаков для всей поверхности х-у. Все точки, в которых значение NET равно величине порога, проектируются на линию уровня плоскости NET (рисунок 3.3).

Рисунок 3.3 - Персептронная NET-плоскость

Ясно, что все точки по одну сторону пороговой прямой спроецируются в значения NET, большие порога, а точки по другую сторону дадут меньшие значения NET. Таким образом, пороговая прямая разбивает плоскость х-у на две области. Во всех точках по одну сторону пороговой прямой значение OUT равно единице, по другую сторону - нулю.

Как мы видели, невозможно нарисовать прямую линию, разделяющую плоскость х-у так, чтобы реализовывалась функция ИСКЛЮЧАЮЩЕЕ ИЛИ. К сожалению, этот пример не единственный. Имеется обширный класс функций, не реализуемых однослойной сетью. Об этих функциях говорят, что они являются линейно неразделимыми, и они накладывают определенные ограничения на возможности однослойных сетей.

Линейная разделимость ограничивает однослойные сети задачами классификации, в которых множества точек (соответствующих входным значениям) могут быть разделены геометрически. Для нашего случая с двумя входами разделитель является прямой линией. В случае трех входов разделение осуществляется плоскостью, рассекающей трехмерное пространство. Для четырех или более входов визуализация невозможна и необходимо мысленно представить n-мерное пространство, рассекаемое «гиперплоскостью» - геометрическим объектом, который рассекает пространство четырех или большего числа измерений.

Так как линейная разделимость ограничивает возможности персептронного представления, то важно знать, является ли данная функция разделимой. К сожалению, не существует простого способа определить это, если число переменных велико.

Нейрон с п двоичными входами может иметь 2n различных входных образов, состоящих из нулей и единиц. Так как каждый входной образ может соответствовать двум различным бинарным выходам (единица и ноль), то всего имеется 22n функций от n переменных.

Таблица 3.2 - Линейно разделимые функции

Как видно из таблицы 3.2, вероятность того, что случайно выбранная функция окажется линейно разделимой, весьма мала даже для умеренного числа переменных. По этой причине однослойные персептроны на практике ограничены простыми задачами.

         Эффективность запоминания. Серьезные вопросы имеются относительно эффективности запоминания информации в персептроне (или любых других нейронных сетях) по сравнению с обычной компьютерной памятью и методами поиска информации в ней. Например, в компьютерной памяти можно хранить все входные образы вместе с классифицирующими битами. Компьютер должен найти требуемый образ и дать его классификацию. Различные хорошо известные методы могли бы быть использованы для ускорения поиска. Если точное соответствие не найдено, то для ответа может быть использовано правило ближайшего соседа.

Число битов, необходимое для хранения этой же информации в весах персептрона, может быть значительно меньшим по сравнению с методом обычной компьютерной памяти, если образы допускают экономичную запись. Однако Минский [2] построил патологические примеры, в которых число битов, требуемых для представления весов, растет с размерностью задачи быстрее, чем экспоненциально. В этих случаях требования к памяти с ростом размерности задачи быстро становятся невыполнимыми. Если, как он предположил, эта ситуация не является исключением, то персептроны часто могут быть ограничены только малыми задачами. Насколько общими являются такие неподатливые множества образов? Это остается открытым вопросом, относящимся ко всем нейронным сетям. Поиски ответа чрезвычайно важны для исследований по нейронным сетям.

3.2 Схема имитационной модели Персептрона Розенблатта в среде Delphi

Теперь мы можем обратиться непосредственно к программированию нейронных сетей. Следует отметить, что число публикаций, рассматривающих программную реализацию сетей, ничтожно мало по сравнению с общим числом работ на тему нейронных сетей, и это при том, что многие авторы апробируют свои теоретические выкладки именно программным способом, а не с помощью нейрокомпьютеров и нейроплат, в первую очередь из-за их дороговизны. Возможно, это вызвано тем, что многие к программированию относятся как к ремеслу, а не науке. Однако в результате такой дискриминации остаются неразобранными довольно важные вопросы. Сложным и очень неприятным является вопрос лицензирования сред разработки нейронных сетей. Пожалуй, наилучшим средством для создания нейронных сетей является программа MatLab и встроенный в нее пакет создания нейронных сетей Neural Networks Toolbox, однако цена легального приобретения этой программы непомерно высока. Поэтому большинство программ моделирования нейронных сетей создается при помощи более дешевых универсальных языков программирования (Pascal, C, C++).

Как видно из рассмотренных в первой главе дипломной работы формул, описывающих алгоритм функционирования и обучения нейронных сетей, весь этот процесс может быть записан и затем запрограммирован в терминах и с применением операций матричной алгебры. Судя по всему, такой подход обеспечивает более быструю и компактную реализацию нейросети, нежели ее воплощение на базе концепций объектно-ориентированного программирования. Однако в последнее время преобладает именно объектно-ориентированный подход, что связано, скорее всего, с широким распространением визуальных средств разработки, таких как Visual Studio, Borland Builder, Borland Delphi и др. Программирование нейронных сетей с применением объектно-ориентированного подхода имеет свои плюсы. Во-первых, оно позволяет создать гибкую, легко перестраиваемую иерархию моделей нейронных сетей. Во-вторых, такая реализация наиболее прозрачна для программиста, и позволяет конструировать нейросети даже непрограммистам. В-третьих, уровень абстрактности программирования, присущий объектно-ориентированным языкам, в будущем будет, по-видимому, расти, и реализация нейросетей с объектно-ориентированным подходом позволит расширить их возможности [20,21,29].

Для формирования модели однослойного персептрона в MatLab предназначена функция newp

net = newp(PR, S) со следующими входными аргументами: PR - массив минимальных и максимальных значений для R элементов входа размера Rx2; S - число нейронов в слое.

В качестве функции активации персептрона по умолчанию используется функция hardlim.

Пример:

Функция

net = newp([0 2],l); создает персептрон с одноэлементным входом и одним нейроном; диапазон значений входа- [0 2].

Определим некоторые параметры персептрона, инициализируемые по умолчанию.

Веса входов:

inputweights = net.inputweights{1,1}

inputweights =

del'ays :       0:       'initzero':      1:       'learnp':       []:      [1 1]:  [lxl struct]:   'dotprod'.

Заметим, что функция настройки персептрона по умолчанию learnp; вход функции активации вычисляется с помощью функции скалярного произведения dotprod; функция инициализации initzero используется для установки нулевых начальных весов.

Смещения:

biases = net.biases{1}

biases =

initFcn:        'initzero':      1:       'learnp':       []:      1

userdata:      [lxl struct]

Нетрудно увидеть, что начальное смещение также установлено в 0.

Моделирование персептрона. Рассмотрим однослойный персептрон с одним двухэлементным вектором входа, значения элементов которого изменяются в диапазоне от -2 до 2:

 = newp([-2 2;-2 2],1); % Создание персептрона net

По умолчанию веса и смещение равны 0, и для того, чтобы установить желаемые значения, необходимо применить следующие операторы:

.IW{l, l}= [-1 1]; net.b{l} = [1];

В этом случае разделяющая линия имеет вид:

: -p1 +р2 + 1 =0.

Структурная схема модели персептрона показана на рисунке 3.4

Рисунок 3.4 - Структурная схема модели персептрона

Теперь определим, как откликается сеть на входные векторы р1и р2, расположенные по разные стороны от разделяющей линии:

1 =     [1; 13];

1 =     sim(net,pl) % Моделирование сети net с входным вектором p1

al       =       1

р2      =       [1; -1];

а2      =       sim(net,p2) % Моделирование сети net с входным вектором р2

а2      =       О.

Персептрон правильно классифицировал эти 2 вектора.

Заметим, что можно было бы ввести последовательность двух векторов в виде массива ячеек и получить результат также в виде массива ячеек:

% Последовательность двух векторов в виде массива ячеек

рЗ = {[1; 1][1; -1]>;

аЗ = sim(net,p3) % Моделирование сети net при входном сигнале рЗ

аЗ = [1] [0].

Инициализация параметров. Для однослойного персептрона в качестве параметров нейронной сети в общем случае выступают веса входов и смещения. Допустим, что создается персептрон с двухэлементным вектором входа и одним нейроном:

 = newp([-2 2;-2 2],1); Запросим характеристики весов входа:

net.inputweights{l, 1}=

delays:        0:       'initzero':      1:       'learnp':       [ ]:     [1 2]:  [lxl struct]:   'dotprod'.

Из этого перечня следует, что в качестве функции инициализации по умолчанию используется функция initzero, которая присваивает весам входа нулевые значения. В этом можно убедиться, если извлечь значения элементов матрицы весов и смещения:

= net.iw{l,l}=00= net.b{l} = 0.

Теперь переустановим значения элементов матрицы весов и смещения:

.lW{l,l} = [3, 4] net.b{l} = 5 =34 bias =5.

Для того, чтобы вернуться к первоначальным установкам параметров персептрона, и предназначена функция init:

= init(net); wts=00 bias = 0.

Можно изменить способ, каким инициализируется персептрон с помощью функции init. Для этого достаточно изменить тип функций инициализации, которые применяются для установки первоначальных значений весов входов и смещений. Например, воспользуемся функцией инициализации rands, которая устанавливает случайные значения параметров персептрона.

Задать функции инициализации весов и смещений:

.inputweights{l,1}.initFcn = 'rands';.biases{1}.initFcn = 'rands';

% Выполнить инициализацию ранее созданной сети с новыми функциями

= init(net);= net.IW{l,l>

wts = -0.96299   0.64281

bias = net.b(l) = -0.087065

Видно, что веса и смещения выбраны случайным образом.

Для создания более мощной программы с графическим использовательским интерфейсомиспользовалась среда быстрого проектирования и создания программ - Delphi 5. Эта среда очень удобна для программирования, поэтом была выбрана для реализации компьютерной программы Persrptron.

Программа Perseptron моделирует однослойную нейронную сеть из искусственных нейронов Мак-Каллока - персептрон. Программно предусмотрено создание персептронов, содержащих до 100 нейронов, однако из-за ограниченности площади экрана компьютера отображается и активируется только 3 нейрона. Персептрон содержит:

          Совокупность входов сell - массив до 100 специальных объектов TCell, отображаемых на экране компьютера в виде «флажков», включая и выключая которые можно подавать или отключать сигналы на входах соответствующих нейронов. Каждый вход соединен с каждым нейроном персептрона.

Совокупность искусственных нейронов Мак-Каллока - массив до 100 специальных объектов TNeuron, отображаемых на экране компьютера в виде прямоугольников, содержащих комбинированные линейки прокрутки для ручной настройки «весовых» коэффициентов нейрона.

Любое изменение входов или весовых коэффициентов любого из нейронов приводит к полному перерасчету сети и, соответственно, изменению содержимого выходов персептрона. В данной программе настройка «весов» нейрона производится «вручную».

Для корректного выхода из программы предусмотрена специальная кнопка «выход», нажатие на которую прервет работу персептрона.

Исходные коды главного модуля программы Perseptron приведены в приложении.

3.3 Описание сеанса работы с компьютерной программой

Определим процесс обучения персептрона как процедуру настройки весов и смещений с целью уменьшить разность между желаемым (целевым) и истинным сигналами на его выходе, используя некоторое правило настройки (обучения). Процедуры обучения делятся на 2 класса: обучение с учителем и обучение без учителя.

При обучении с учителем задается множество примеров требуемого поведения сети, которое называется обучающим множеством

 {P1t1,},{p2.t2},..,{PQ,tQ}.                                            (3.3)

Здесь р1 р2, ..., pq - входы персептрона, a t1 t2, ..., tQ -требуемые (целевые) выходы.

При подаче входов выходы персептрона сравниваются с целями. Правило обучения используется для настройки весов и смещений персептрона так, чтобы приблизить значение выхода к целевому значению. Алгоритмы, использующие такие правила обучения, называются алгоритмами обучения сучителем. Для их успешной реализации необходимы эксперты, которые должны предварительно сформировать обучающие множества. Разработка таких алгоритмов рассматривается как первый шаг в создании систем искусственного интеллекта.

В этой связи ученые не прекращают спора на тему, можно ли считать алгоритмы обучения с учителем естественными и свойственными природе, или они созданы искусственны. Например, обучение человеческого мозга на первый взгляд происходит без учителя: на зрительные, слуховые, тактильные и прочие рецепторы поступает информация извне и внутри мозга происходит некая самоорганизация. Однако нельзя отрицать и того, что в жизни человека немало учителей -и в буквальном, и в переносном смысле, - которые координируют реакции на внешние воздействия. Вместе с тем, как бы ни развивался спор приверженцев этих двух концепций обучения, представляется, что обе они имеют право на существование. И рассматриваемое нами правило обучения персептрона относится к правилу обучения с учителем.

При обучении без учителя веса и смещения изменяются только в связи с изменениями входов сети. В этом случае целевые выходы в явном виде не задаются. Главная черта, делающая обучение без учителя привлекательным, - это его самоорганизация, обусловленная, как правило, использованием обратных связей. Что касается процесса настройки параметров сети, то он организуется с использованием одних и тех же процедур. Большинство алгоритмов обучения без учителя применяется при решении задач кластеризации данных, когда необходимо разделить входы на конечное число классов.

Что касается персептронов, рассматриваемых в этой главе, то хотелось бы надеяться, что в результате обучения может быть построена такая сеть, которая обеспечит правильное решение, когда на вход будет подан сигнал, который отличается от тех, которые использовались в процессе обучения.

Правила настройки. Настройка параметров (обучение) персептрона осуществляется с использованием обучающего множества. Обозначим через р вектор входов персептрона, а через t - вектор соответствующих желаемых выходов. Цель обучения - уменьшить погрешность е = а -1, которая равна разности между реакцией нейрона а и вектором цели t.

Правило настройки (обучения) персептрона должно зависеть от величины погрешности е. Вектор цели t может включать только значения 0 и 1, поскольку персептрон с функцией активации hardlim может генерировать только такие значения.

При настройке параметров персептрона без смещения и с единственным нейроном возможны только 3 ситуации:

- для данного вектора входа выход персептрона правильный (а = t и е = t - а = 0) и тогда вектор весов w не претерпевает изменений;

выход персептрона равен 0, а должен быть равен 1 (а = 0, t = 1 и е = t - 0=1). В этом случае вход функции активации wTp отрицательный и его необходимо скорректировать. Добавим к вектору весов w вектор входа р, и тогда произведение (wT + рт) р = = w р + р р изменится на положительную величину, а после нескольких таких шагов вход функции активации станет положительным и вектор входа будет классифицирован правильно. При этом изменятся настройки весов.

Выход нейрона равен 1, а должен быть равен 0 (а - 0, t = 1 и е = t - а -1). В этом случае вход функции активации wTp положительный и его необходимо скорректировать. Вычтем из вектора весов w вектор входа р, и тогда произведение (wT - рт) р = = wTp - pTp изменится на отрицательную величину, а после нескольких шагов вход функции активации станет отрицательным и вектор входа будет классифицирован правильно. При этом изменятся настройки весов.

Теперь правило настройки (обучения) персептрона можно записать, связав изменение вектора весов Aw с погрешностью e-t - а:

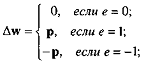 (3.4)

Все 3 случая можно описать одним соотношением:

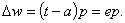 (3.5)

Можно получить аналогичное выражение для изменения смещения, учитывая, что смещение можно рассматривать как вес для единичного входа

 (3.6)

В случае нескольких нейронов эти соотношения обобщаются следующим образом:

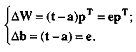 (3.7)

Тогда правило настройки (обучения) персептрона можно записать в следующей форме:

 (3.8)

Описанные соотношения положены в основу алгоритма настройки параметров персептрона, который реализован в ППП Neural Network Toolbox в виде М-функции leamp. Каждый раз при выполнении функции learnp будет происходить перенастройка параметров персептрона. Доказано, что если решение существует, то процесс обучения персептрона сходится за конечное число итераций. Если смещение не используется, функция learnp ищет решение, изменяя только вектор весов w. Это приводит к нахождению разделяющей линии, перпендикулярной вектору w и которая должным образом разделяет векторы входа.

Рассмотрим простой пример персептрона с единственным нейроном и двухэлементным вектором входа

 = newp([-2 2;-2 2],1);

Определим смещение b равным 0, а вектор весов w равным [1 -0.8]:

.b{l} = 0; w = [1 -0.8] ; net.IW{l,l} = w;

Обучающее множество зададим следующим образом

р = [1; 2]; t = [1];

Моделируя персептрон, рассчитаем выход и ошибку на первом шаге настройки (обучения)

а = sim(net,p)

а = 0

е = t-a

е = 1

Наконец, используя М-функцию настройки параметров learnp, найдем требуемое изменение весов

learnp(w,p,[ ],[ ],[ ],[ ],е,[ ],[ ],[ ]) = 1 2

Тогда новый вектор весов примет вид:

 = w + dw

w = 2.0000 1.2000

Заметим, что описанные выше правило и алгоритм настройки (обучения) персептрона гарантируют сходимость за конечное число шагов для всех задач, которые могут быть решены с использованием персептрона. Это в первую очередь задачи классификации векторов, которые относятся к классу линейно отделимых, когда все пространство входов можно разделить на 2 области некоторой прямой линией, в многомерном случае - гиперплоскостью.

Процедура адаптации. Многократно используя М-функции sim и learnp для изменения весов и смещения персептрона, можно в конечном счете построить разделяющую линию, которая решит задачу классификации, при условии, что персептрон может решать ее. Каждая реализация процесса настройки с использованием всего обучающего множества называется проходом или циклом. Такой цикл может быть выполнен с помощью специальной функции адаптации adapt. При каждом проходе функция adapt использует обучающее множество, вычисляет выход, погрешность и выполняет подстройку параметров персептрона.

Заметим, что процедура адаптации не гарантирует, что синтезированная сеть выполнит классификацию нового вектора входа. Возможно, потребуется новая настройка матрицы весов W и вектора смещений b с использованием функции adapt.

Чтобы пояснять процедуру адаптации, рассмотрим простой пример. Выберем персептрон с одним нейроном и двухэлементным вектором входа (рисунок 3.5).

Рисунок 3.5 - Персептрон с одним нейроном и двухэлементным вектором

Эта сеть и задача, которую мы собираемся рассматривать, достаточно просты, так что можно все расчеты выполнить вручную.

Предположим, что требуется с помощью персептрона решить задачу классификации векторов, если задано следующее обучающее множество

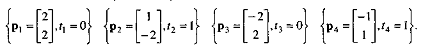 (3.9)

Используем нулевые начальные веса и смещение. Для обозначения переменных на каждом шаге используем индекс в круглых скобках. Таким образом, начальные значения вектора весов wT(0) и смещения b(0) равны соответственно wT(0) = [0 0] и Ь(0) = 0.

Вычислим выход персептрона для первого вектора входа p1, используя начальные веса и смещение

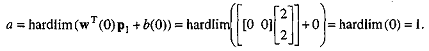 (3.10)

Выход не совпадает с целевым значением t1 и необходимо применить правило настройки (обучения) персептрона, чтобы вычислить требуемые изменения весов и смещений

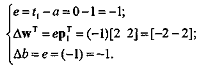 (3.11)

Вычислим новые веса и смещение, используя введенные ранее правила обучения персептрона.

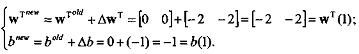 (3.12)

Обратимся к новому вектору входа р2, тогда

 (3.13)

В этом случае выход персептрона совпадает с целевым выходом, так что погрешность равна 0 и не требуется изменений в весах или смещении. Таким образом,

 (3.14)

Продолжим этот процесс и убедимся, что после третьего шага настройки не изменились

 (3.15)

а после четвертого приняли значение

 (3.16)

Чтобы определить, получено ли удовлетворительное решение, требуется сделать один проход через все векторы входа, чтобы проверить, соответствуют ли решения обучающему множеству. Вновь используем первый член обучающей последовательности и получаем:

 (3.17)

Переходя ко второму члену, получим следующий результат

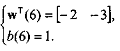 (3.18)

Этим заканчиваются ручные вычисления.

Теперь выполним аналогичные расчеты, используя М-функцию adapt. Вновь сформируем модель персептрона, изображенного на рисунке 3.2:

 = newp([-2 2;-2 2],1);

Введем первый элемент обучающего множества Р = {[2; 2]>; t = {0};

Установим параметр passes (число проходов) равным 1 и выполним 1 шаг настройки: net.adaptParam.passes =1; [net,a,e] = adapt(net,p,t);

a = [1]

e

e = [-1]

Скорректированные вектор весов и смещение равны twts = net.lW{l,l}

twts = -2 -2 tbiase = net.b{l} = -1

Это совпадает с результатами, полученными при ручном расчете. Теперь можно ввести второй элемент обучающего множества и т. д., т. е. повторить всю процедуру ручного счета и получить те же результаты.

Но можно эту работу выполнить автоматически, задав сразу все обучающее множество и выполнив 1 проход:

net = newp([-2 2;-2 2],1);.trainParam.passes = 1;

Р = {[2;2] [1;-2] [-2;2] [-1;1]};= <0 1 0 1);

Теперь обучим сеть:

[net,a,e] = adapt(net,p,t);

Возвращаются выход и ошибка: а

а = [1] [1] [0] [0]

е

е = [-1] [0] [0] [1].

Скорректированные вектор весов и смещение равны

= net.iw{l,l} twts = -3 -1 tbiase = net.b{l} tbiase = 0

Моделируя полученную сеть по каждому входу, получим:

= sim(net,p)= [0] [0] [1] [1]

Можно убедиться, что не все выходы равны целевым значениям обучающего множества. Это означает, что следует продолжить настройку персептрона. Выполним еще 1 цикл настройки:

[net,a,e] = adapt(net,p,t); а

а = [0]  [0]      [0]      [1]

е

е = [0]  [1]      [0]      [0]

twts = net.IW{l,l}

twts =2  -3

tbiase = net.b{l}= 1= sim(net,p)

al = [0]   [1]      [0]      [1]

Теперь решение совпадает с целевыми выходами обучающего множества и все входы классифицированы правильно.

Если бы рассчитанные выходы персептрона не совпали с целевыми значениями, то необходимо было бы выполнить еще несколько циклов настройки, применяя М-функцию adapt и проверяя правильность получаемых результатов.

Как следует из сказанного выше, для настройки (обучения) персептрона применяется процедура адаптации, которая корректирует параметры персептрона по результатам обработки каждого входного вектора. Применение М-функции adapt гарантирует, что любая задача классификации с линейно отделимыми векторами будет решена за конечное число циклов настройки.

Для настройки (обучения) персептрона можно было бы воспользоваться также М-функцией train. В этом случае используется все обучающее множество и настройка параметров сети выполняется не после каждого прохода, а в результате всех проходов обучающего множества. К сожалению, не существует доказательства того, что такой алгоритм обучения персептрона является сходящимся. Поэтому использование М-функции train для обучения персептрона не рекомендуется.

ЗАКЛЮЧЕНИЕ

Современные искусственные нейронные сети представляют собой устройства, использующие огромное число искусственных нейронов и связей между ними. Несмотря на то, что конечная цель разработки нейронных сетей - полное моделирование процесса мышления человека так и не была достигнута, уже сейчас они применяются для решения очень многих задач обработки изображений, управления роботами и непрерывными производствами, для понимания и синтеза речи, для диагностики заболеваний людей и технических неполадок в машинах и приборах, для предсказания курсов валют и т.д. Если перейти к более прозаическому уровню, то нейронные сети - это всего-навсего сети, состоящие из связанных между собой простых элементов - формальных нейронов. Ядром используемых представлений является идея о том, что нейроны можно моделировать довольно простыми автоматами, а вся сложность мозга, гибкость его функционирования и другие важнейшие качества определяются связями между нейронами.

Следует отметить, что основное назначение персептронов - решать задачи классификации. Они великолепно справляются с задачей классификации линейно отделимых векторов; сходимость гарантируется за конечное число шагов. Длительность обучения чувствительна к выбросам длины отдельных векторов, но и в этом случае решение может быть построено. Однослойный персептрон может классифицировать только линейно отделимые векторы. Возможные способы преодолеть эту трудность предполагают либо предварительную обработку с целью сформировать линейно отделимое множество входных векторов, либо использование многослойных персептронов. Можно также применить другие типы нейронных сетей, например линейные сети или сети с обратным распространением, которые могут выполнять классификацию линейно неотделимых векторов входа.

В ходе выполнения данной дипломной работы было сделано:

изучена история возникновения нейронных сетей;

приведены задачи решаемые при помощи Персептрона Розенблатта.

разработана программа для создания моделей искусственных нейронных сетей.

Таким образом, можно утверждать, что была достигнута цель дипломной работы и успешно решены все задачи дипломной работы.

ПРИЛОЖЕНИЕ

Исходные коды программы Perseptron

unit Unit1;

Windows, Messages, SysUtils, Classes, Graphics, Controls, Forms, Dialogs,

ExtCtrls, StdCtrls, Spin;

TNeuron=class

ndendro:integer;

w:array[1..100] of real;

x:array[1..100] of integer;

s:real; a:integer;

vw:array[1..100] of TSpinEdit;

vx:array[1..100]of TCheckBox; va:TCheckBox;

pb:TPaintBox;

function act:integer;

procedure tick(Sender: TObject);

procedure modify(Sender: TObject);

procedure draw;

end;

TInCell=class

n:integer; cb:TCheckBox;

nrn:array[1..100] of TNeuron;

pnt:array[1..100,1..2] of integer;

procedure tick(sender: TObject);

procedure draw;

end;

TPersForm = class(TForm)

Button1: TButton;

Label1: TLabel;

Label2: TLabel;

procedure FormCreate(Sender: TObject);

procedure FormPaint(Sender: TObject);

procedure Button1Click(Sender: TObject);

private

{ Private declarations }

nrn:array[1..100] of TNeuron;

cell:array[1..100] of TInCell;

public

{ Public declarations }

n,cells:integer;

end;PersForm: TPersForm;

{$R *.DFM}TNeuron.act:integer;

if s>=0 then act:=1 else act:=0;;TNeuron.tick(Sender: TObject);i:integer;

s:=0; for i:=1 to ndendro do s:=s+x[i]*w[i];

a:=act;

if (a=1) then va.checked:=true else va.checked:=false;;TNeuron.modify(Sender: TObject);i:integer;

for i:=1 to ndendro do

begin

if vx[i].checked then x[i]:=1 else x[i]:=0;

w[i]:=vw[i].Value;

end;

tick(self);;TNeuron.draw;.canvas.pen.color:=clBlack;.canvas.rectangle(1,1,pb.width-1,pb.height-1);;TInCell.tick(sender: TObject);i:integer;

for i:=1 to n do

begin

nrn[pnt[i][1]].vx[pnt[i][2]].checked:=cb.checked;

nrn[pnt[i][1]].modify(self);

end;;TInCell.draw;i:integer;

for i:=1 to n do

begin

PersForm.Canvas.Pen.Color:=clBlack;

PersForm.Canvas.MoveTo(cb.left,cb.top+10);

PersForm.Canvas.LineTo(nrn[pnt[i][1]].vx[pnt[i][2]].left,

nrn[pnt[i][1]].vx[pnt[i][2]].top+10);

end;;TPersForm.FormCreate(Sender: TObject);i,j:integer;:=3; cells:=3;i:=1 to n do

nrn[i]:=TNeuron.Create;

nrn[i].pb:=TPaintBox.Create(PersForm); nrn[i].pb.parent:=PersForm;

nrn[i].ndendro:=3;

nrn[i].pb.width:=50; nrn[i].pb.height:=nrn[i].ndendro*22;

nrn[i].pb.left:=150; nrn[i].pb.top:=30+(i-1)*(nrn[i].pb.height+10);

for j:=1 to nrn[i].ndendro do

begin

nrn[i].vw[j]:=TSpinEdit.Create(PersForm);

nrn[i].vw[j].parent:=PersForm; nrn[i].vw[j].tag:=j;

nrn[i].vw[j].OnChange:=nrn[i].modify;

nrn[i].vw[j].left:=nrn[i].pb.left+2;

nrn[i].vw[j].top:=nrn[i].pb.top+(j-1)*20+2;

nrn[i].vw[j].width:=nrn[i].pb.width-5; nrn[i].vw[j].height:=15;

nrn[i].vx[j]:=TCheckBox.Create(PersForm); nrn[i].vx[j].parent:=PersForm;

nrn[i].vx[j].enabled:=false;

nrn[i].vx[j].left:=nrn[i].pb.left-15;

nrn[i].vx[j].top:=nrn[i].pb.top+(j-1)*20+3;

nrn[i].vx[j].width:=10;

end;

nrn[i].va:=TCheckBox.Create(PersForm);

nrn[i].va.parent:=PersForm; nrn[i].va.enabled:=false;

nrn[i].va.left:=nrn[i].pb.left+nrn[i].pb.width+2;

nrn[i].va.top:=nrn[i].pb.top+nrn[i].pb.height div 2 - 8;

nrn[i].va.width:=10;

nrn[i].tick(self);;i:=1 to cells do

cell[i]:=TInCell.Create;

cell[i].cb:=TCheckBox.Create(PersForm); cell[i].cb.parent:=PersForm;

cell[i].cb.left:=30; cell[i].cb.top:=30+(i-1)*90;

cell[i].cb.width:=10;

cell[i].cb.OnClick:=cell[i].tick;

cell[i].n:=n;

for j:=1 to cell[i].n do cell[i].nrn[j]:=nrn[j];

for j:=1 to cell[i].n do

begin

cell[i].pnt[j][1]:=j;

cell[i].pnt[j][2]:=i;

end;

cell[i].tick(self);;;TPersForm.FormPaint(Sender: TObject);i:integer;i:=1 to n do nrn[i].draw;i:=1 to cells do cell[i].draw;;TPersForm.Button1Click(Sender: TObject);;;.