Функция Дирихле и ее свойства

Функция Дирихле и ее свойства

Министерство образования и науки РФ

Федеральное агентство по образованию

Сибирский Федеральный Университет

Институт математики

Курсовая работа

по математическому анализу

Функция Дирихле и ее свойства

Выполнила: студентка гр. М-26

Матузова В.В.

Красноярск 2008 г.

Функция, принимающая значение 1, если аргумент рационален, и 0, если аргумент иррационален:

D(x) =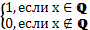

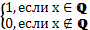
функция дирихле математический анализ

была введена немецким математиком П.В. Дирихле как пример функции, свободной от аналитического задания значения.

Свойства:

Область определения - (-∞; +∞); область значения - 0,1;

Функция Дирихле не имеет предела ни в одной точке, так как в любой окрестности любой точки вещественной прямой содержатся как рациональные, так и иррациональные числа (а значит, как нули, так и единицы функции).

Это в свою очередь значит, что функция разрывна на всей числовой прямой (причём все точки разрыва - второго рода), и ее график изобразить невозможно.

Также ни в одной точке вещественной оси для данной функции не существует производной.

Функция Дирихле служит примером функции, не интегрируемой в смысле Римана, но интегрируемой по Лебегу. Интеграл Лебега от функции Дирихле на любом числовом промежутке может быть легко найден, он всегда равен нулю. Это следует из того, что мера Лебега множества рациональных чисел равна нулю.

Функция Дирихле не имеет предела ни в одной точке:

Воспользуемся отрицанием критерия Коши: функция D не имеет предела в точке а, если либо функция не определена в окрестности точки а, либо найдется число ε > 0 и в любой окрестности U(а) найдутся точки x’, x’’ ∈ U(а), x’, x’’ ≠ a такие, что будет выполнено неравенство: |D(x’) - D(x’’)| ≥ ε.

Первое условие не выполнено, т.к. область определения функции Дирихле - вся числовая прямая.

Так как в любой окрестности любой точки а находятся как рациональные, так и иррациональные числа, то положим x’ ∈ ℚ, x’’ ∉ ℚ. Тогда D(x’) =1, D(x’’) = 0. Возьмем ε - любое число, принадлежащее полуотрезку (0, 1], получим:

|D(x’) - D(x’’)| = 1 ≥ ε.

Так как точка a - произвольна, то ни в одной точке числовой прямой не существует предела для функции Дирихле.

Аналогично можно показать отсутствие предела справа и слева.

Функция разрывна в каждой точке

По определению непрерывности D(x) непрерывна в точке а, если 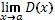 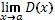= D(a), но функция Дирихле не имеет предела, а следовательно разрывна в каждой точке.

Или по прямому определению разрывности: функция D(x) разрывна в точке а, если существует число ε₀ > 0, что для любого δ > 0 найдется точка х_δ такая, что

|a - х_δ | < δ, |D(a) - D(х_δ)| < ε₀

Если точка а рациональна, то х_δ возьмем иррациональное и наоборот, если а ∈ ℚ, то пусть х_δ ∉ ℚ. Тогда |D(x’) - D(x’’)| = 1. При ε₀ ∈ (0, 1] видим, что D(x) разрывна в точке а; в силу произвольности а она разрывна в каждой точке. А так как не существует предела функции справа и слева, то все точки разрыва - II рода.

Очевидно, что функция Дирихле также не является равномерно непрерывной, потому что можно подобрать как угодно близкие числа x’, x’’ такие, что x’ ∈ ℚ, x’’ ∉ ℚ. Таким образом будет выполняться |D(x’) - D(x’’)| = 1 ≥ ε, если, например, ε ∈ (0,1].

Не существует производной функции Дирихле ни в одной точке.

Производная функции в точке - это предел отношения:

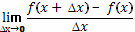
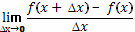
Покажем, что его не существует, то есть:

∃ε > 0 ∃ x’, x’’ ∈ U(0), x’, x’’ ≠ 0 : |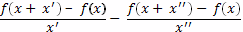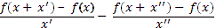| ≥ ε.

Подберем такие x’, x’’, что x’, x’’ < 1 и f(x + x’) - рационально, а f(x + x’’) - иррационально. Тогда в любом случае одна из дробей обращается в нуль, а вторая по модулю больше единицы. Остается положить ε = 1.

Функция Дирихле не интегрируема по Риману.

Пусть а = x₀ < x₁ < … < x_n = b - некоторое разбиение R отрезка [a,b]. Для любого такого разбиения

s_R = Σm_j∆х_j = 0 - очевидно;

S_R = ΣM_j∆х_j = (b - a) - длина отрезка [a,b]

(здесь 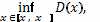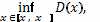m_j =  M_j = 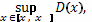 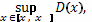∆х_j - длина отрезка [a,b]).

Пусть ε < b - a, тогда S_R - s_R ≥ ε, что и требовалось.

Функция Дирихле имеет жорданову меру нуль и лебегову меру нуль.

Множество G называется измеримым по Жордану, если его внутренняя и внешняя меры равны между собой: m_jG = m_eG = mG.

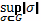
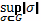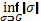
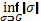Так как функция Дирихле принимает только два значения - 0 и 1, то будем множество ее значений рассматривать как объединение {0} ⋃ {1}. И для {0}, и для {1} внутренняя мера равна m_jG =  = |∅| = 0. Внешняя мера для обоих этих множеств также равна 0: m_eG =  = 0, потому что σ - отрезки, покрывающие {0} и {1} - имеют как угодно малую меру.

Таким образом, множество значений функции Дирихле имеет жоданову меру нуль как объединение множеств меры нуль.

Функция f называется измеримой по Лебегу на отрезке [a,b], если для любого А ∈ ℝ множество {х: х ∈ [a,b] ; f(x) < A} измеримо по Лебегу. Для функции Дирихле если А < 0 то множество таких х пустое, а значит измеримое. Если 0 < A < 1 или А > 1, то мера множества таких х равна длине отрезка [a,b] - также существует. Значит функция Дирихле измерима по Лебегу. А так как установлено, что ее жорданова мера равна 0, то и лебегова мера тоже будет равна 0.

Функция Дирихле интегрируема по Лебегу.

Удобно воспользоваться определением интеграла Лебега для ступенчатой функции. Функция f называется ступенчатой, если она принимает не более, чем счетное число значений С_j, j=1,2… и все множества α_j = {x: f(x) = С_j} - измеримы. Тогда интеграл Лебега ступенчатой функции равен ∫fdx = Σ С_j mα_j, если этот ряд сходится абсолютно.

Для функции Дирихле С₁ = 1, С₂ = 0, α₁ = {x: x ∈ ℚ }, α₂ = {x: x ∉ ℚ }. Множества α₁ и α₂ измеримы на любом отрезке [a,b], причем mα₁ = 0, так как это множество счетное, а mα₂ равна длине отрезка [a,b]. ∫D(x)dx = С₁ * 0 + С₂ * 1 = 0.

Литература

1. Никольский С.М. «Курс математического анализа», ФИЗМАТЛИТ, М., 2000.