Течение вязкой жидкости в канале прямоугольной формы
Министерство образования и науки
Российской Федерации
Новокузнецкий филиал-институт
Кемеровского государственного
университета
Кафедра математики и математического
моделирования
Курсовая работа
по дисциплине: Математическое
моделирование в естествознании и методы их исследования
на тему: Течение вязкой жидкости в
канале прямоугольной формы
Выполнил:
студент группы ПМИ-071
Черная Ю.А.
Проверил:
преподаватель кафедры МиММ
Седова Е.А.
Новокузнецк, 2011
Содержание
1. Введение
. Постановка задачи
. Решение
. Заключение
. Список литературы
1. Введение
Идеальная жидкость, т. е. жидкость без внутреннего трения, является
абстракцией. Всем реальным жидкостям и газам в большей или меньшей степени
присуще внутреннее трение, называемое также вязкостью. Вязкость проявляется, в
частности, в том, что возникшее в жидкости или газе движение, после прекращения
действия причин, его вызвавших, постепенно прекращается. Сопротивление жидкости
к изменению формы характеризуют динамической вязкостью (внутренним трением).
Сила внутреннего трения в жидкости τ на единицу площади, определяют по
закону Ньютона:
, (1)
где
-
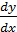
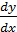градиент скорости в направлении перпендикулярном течению, 
абсолютная
и динамичная вязкость жидкости. Кинематическая вязкость - отношение
динамической вязкости к плотности: 
. Одной
из целей расчёта течения является нахождение поля давлений в зависимости от
координат и времени. В вязкой жидкости в каждой точке геометрической области
существует три компоненты давления, для несжимаемой жидкости:
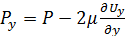
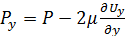
(2)
Среднее
давление находится в результате решения системы Навье-Стокса.
Движение
жидкости в канале называется безнапорным движением. Особенностью его является
наличие свободной поверхности с одинаковым давлением по всей ее длине. С точки
зрения гидравлики безнапорные потоки можно разделить на установившиеся потоки с
равномерным движением жидкости и неустановившиеся потоки, часто называемые
быстротоками.
Русла
подразделяют по параметрам, определяющим изменение площади сечения по длине
потока, на непризматические и призматические (и цилиндрические). У
непризматических русел, форма и (или) геометрические размеры поперечного
профиля меняются по длине русла. Поэтому площадь сечения потока является
функцией длины русла и функцией глубины потока вдоль русла. В таком русле
движение неравномерное. В призматических руслах форма и размеры элементов
поперечного профиля по длине сохраняются неизменными. Площадь живого сечения
потока может изменяться только в связи с изменением глубины потока. По форме
профиля поперечного сечения русла могут быть правильной и неправильной формы.
Призматические русла имеют правильную форму. Они могут быть прямоугольные,
треугольные, трапецеидальные. В нашем случае русло прямоугольной формы. Для
решения системы дифференциальных уравнений (уравнения движения жидкости и
уравнение неразрывности) необходимо задать начальные и граничные условия.
Начальные условия задают поле скоростей и давлений в жидкости в начальный
момент времени. Граничные условия бывают двух типов: кинематические (условия
для скорости на границах жидкости) и динамические (связанные с давлением).
2.
Постановка задачи
Составить
краевую задачу, включающую кинематические соотношения, уравнения движения,
определяющие соотношения и решить ее.
Будем
рассматривать установившееся движение вязкой и несжимаемой жидкости. Пусть в
расчетной области течения D, ограниченной свободной поверхностью С1 и твердыми
стенками С2, С3, С4 решается уравнение Лапласа. Ширина канала l,
высота h. Предположим что жидкость вязкая, несжимаемая.
Течение стационарное, установившееся, не турбулентное.
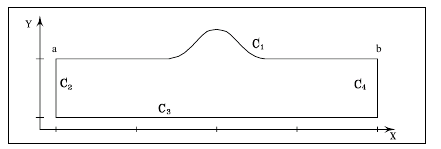
Рис.
1. Течение вязкой жидкости в канале прямоугольной формы
3.
Решение
Общая
задача гидродинамики сводится к решению совместной системы из четырёх
дифференциальных уравнений Навье-Стокса:
(3)
Система
уравнений складывается из уравнений движения по трём направлениям и уравнения
неразрывности (вязкости). Раз жидкость не сжимаема то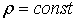 
. Так как движение установившееся:
. (4)
Тогда,
задача (3) примет вид:
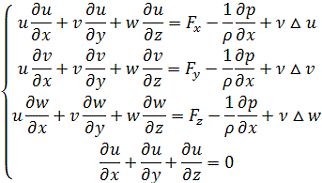(5)
Так
как движение жидкости безвихревое, траектории движения всех частиц будут строго
прямолинейными и параллельными между собой, а значит, компоненты скорости: v=0,
w=0.
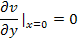
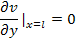
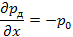
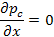(6)
Так
как движение прямолинейное и параллельное то единственная проекция вектора
скорости u будет оставаться постоянной и может изменяться только
в поперечном к траекториям направлении:
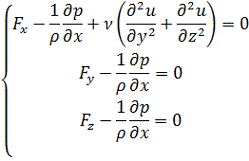(7)
, так как
в нашем случае синус равен единице то все силы по направлениям приравниваются к
ускорению свободного падения.
Представим
давление в виде суммы двух составляющих статической и динамической:
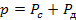.(8)
Статическое
давление определяется из уравнения равновесия:
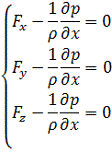.(9)
Используя
выражение для кинематического коэффициента вязкости:
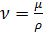
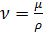,(10)
подставив
в нашу систему полное давление, получим:
(11)
Легко
догадаться, что динамическое давление не будет зависеть от y и z.
Левая часть уравнения зависит только от x, значит, левые
и правые части должны быть равны одной и той же величине:
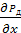
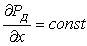. (12)
Это
означает, что перепад давления на единицу длины в направлении движения
постоянен. Таким образом, наша задача сводится к решению дифференциального
уравнения Пуассона:
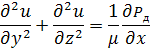,(13)
где
правая часть есть постоянная величина, границы, вдоль которых течёт вода, не
деформируются и остаются не подвижными, что удовлетворяет условию
прямолинейного параллельного движения. Используя условие прилипания, мы сводим
нашу задачу к задаче Пуассона при нужных нам граничных условиях. Так как правая
часть остаётся постоянной, то уравнение сводится к уравнению Лапласа заменой:
.(14)
При
такой замене рассматриваемая задача о прямолинейном параллельном движении
вязкой жидкости внутри канала прямоугольной формы, будет сводиться к решению
уравнения Лапласа для функции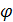 
:
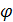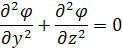(15)
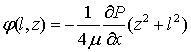
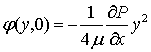(16)
на
свободной границе:
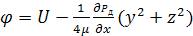
(U=const)(17)
С
помощью известного из математической физики метода Фурье, получим решение
полученной системы. Данный метод широко применяется для решения уравнений
математической физики. Его суть заключается в том, что мы функцию 
из уравнения (15) представляем в виде произведения
двух функций, каждая из которых зависит только от одной переменной:
(18)
Подставляем
данную замену в уравнение (15) и разделим переменные:
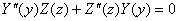(19)
Разделим
переменные: 
В
(19) левая часть зависит только от y, а правая - только от z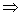 
равенство между ними возможно, только если обе части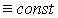 
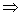
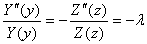(знак
при 
выбран для удобства) (20)
Отсюда:
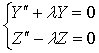(21)
Полученная
пара уравнений может быть решена стандартным способом. Дополним уравнения
условиями (16) и (17).
Требуется
указать такие и такую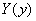 
,
тождественно не равную нулю, чтобы (6) имело решение.
Рассмотрим
три случая для :
. 
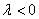
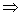ищем решение в виде: 
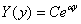, где С -
const, 
= -
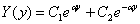
(находится
из граничных условий)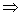 
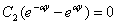, а по условию: , 
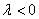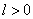
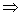
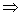
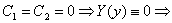не подходит
. 
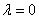
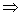
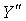=0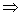 
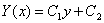(аналогично
получаем, что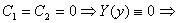 
не подходит)
. 
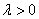
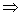характеристическое уравнение 
имеет два корня: 
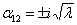, решение
имеет вид: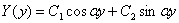 
. Подставив граничные условия (16) и (17), получаем
что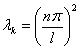 
, а решение примет вид:
.(22)
Решим
уравнение системы (21) относительно z, с уже найденным :
где
,
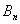- произвольные постоянные.
Тогда,
решение уравнение Лапласа имеет вид:
.(18)
Подставив
полученное решение в уравнение (14) получим искомое значение давления:
. (20)
4.
Заключение
Когда
речь заходит о построении математической модели какого-либо явления,
принадлежащего к физике, социологии, экономике или другой области знаний,
встаёт вопрос о правильном построении системы дифференциальных уравнений и её
решения, исходя из начальных или граничных условий.
Современную
физику невозможно представить без математики, и с появлением новых областей
исследования, новых теорий, встаёт необходимость в пополнении математической
базы, исследовании новых методов. Многие задачи современной физики могут быть
решены только с помощью численных методов. В интенсивном взаимодействии
теоретической физики и современной математики создаются качественно новые
классы моделей современной математической физики.
В данной работе представлен аналитический метод решения стационарного
уравнения Навье-Стокса в трехмерной геометрии. Решение получено для несжимаемой
жидкости. Решение нелинейных уравнений ищется методом последовательных
приближений. Метод последовательных приближений позволяет свести задачу к
решению последовательности систем линейных дифференциальных уравнений для
неизвестной функции с учетом нелинейной части, в которую входят известные
функции. Затем используется преобразование Лапласа для временной переменной и
преобразование Фурье - для пространственных переменных.
5. Список использованной литературы:
1. Сборник задач по уравнениям математической физики \
Под ред. В. С. Владимирова. - М.:ФИЗМАТЛИТ, 2003. - 288 с.
. Динамика вязкой не сжимаемой жидкости \ Слёзкин Н.А.
-М.:1955.- 519с.
. КМГЭ для решения плоских задач Гидродинамики \
Учебное пособие \ К.Е. Афанасьев, С.В. Стуколов -Кемерово:2001.