Функциональные уравнения на оси и полуоси
ДИПЛОМНАЯ
РАБОТА
Функциональные уравнения на оси и полуоси
СОДЕРЖАНИЕ
Введение
.Функциональные уравнения. Их
свойства и методы решения
.1 Определение и примеры
функциональных уравнений
.2 Методы решения функциональных
уравнений
. Решение функциональных уравнений
Коши на множестве Q рациональных чисел
.1 Решение уравнения вида
f(x+y)=f(x)+f(y) на Q
.2 Решение уравнения вида
f(x+y)=f(x)∙f(y) на Q
.3 Решение уравнения вида f(x∙y)=f(x)+f(y)
на Q
.4 Решение уравнения вида f(x∙y)=f(x)∙f(y)
на Q
. Решение функциональных уравнений
Коши на оси R
.1 Решение уравнения вида
f(x+y)=f(x)+f(y) на оси R
.2 Решение уравнения вида
f(x+y)=f(x)∙f(y) на оси R
. Решение функциональных уравнений
Коши на полуоси R+
.1 Решение уравнения вида
f(x+y)=f(x)+f(y) на полуоси R+
.2 Решение уравнения вида
f(x+y)=f(x)∙f(y) на полуоси R+
.3 Решение уравнения вида f(x∙y)=f(x)+f(y)
на полуоси R+
.4 Решение уравнения вида f(x∙y)=f(x)∙f(y)
на полуоси R+
. Решение функциональных уравнений
Коши в измеримых функциях
.1 Решение уравнения вида
f(x+y)=f(x)+f(y) в измеримых функциях
.2 Решение уравнения вида
f(x+y)=f(x)∙f(y) в измеримых функциях
.3 Решение уравнения вида f(x∙y)=f(x)+f(y)
в измеримых функциях
.4 Решение уравнения вида f(x∙y)=f(x)∙f(y)
в измеримых функциях
. Некоторые обобщения и приложения
.1 Функциональная характеристика
тригонометрического и гиперболического косинусов
.2 Решение уравнения для синуса на
оси R
.3 Класс уравнений типа Коши
Заключение
Список использованных источников
Введение
Настоящая
дипломная работа посвящена изучению функциональных уравнений, весьма
общему классу уравнений, в которых искомой является некоторая функция.
К
функциональным уравнениям по существу относятся дифференциальные
уравнения, интегральные уравнения, уравнения в конечных разностях; следует,
однако, отметить, что название функциональные уравнения обычно не
относят к уравнениям этих типов. Под функциональными уравнениями в узком
смысле слова понимают уравнения, в которых искомые функции связаны с известными
функциями одного или нескольких переменных при помощи операции образования
сложной функции. Функциональные уравнения можно также рассматривать как
выражение свойства, характеризующего тот или иной класс функций.
В первой главе настоящей работы вводятся основные понятия,
определения, свойства, приводятся примеры функциональных уравнений.
Рассматриваются функциональные уравнения с одной переменной, описываются
некоторые методы их решения, в частности, метод решения некоторых
функциональных уравнений с помощью групп функций, приводятся примеры. В главе 8
страниц.
Во второй главе рассматриваются уравнения вида
f(x+у) = f (x) + f (y),
f (x + у)
= f (x) f (y), (1)(xy) = f (x) + (y),
f (xy) = f (x) f (y),
находятся их решения в классе функций, заданных на множестве
рациональных чисел. Глава состоит из 10 страниц.
В третьей главе рассматриваются уравнения вида f(x+у)=f
(x) + f (y) и f
(x
+ у) = f
(x)
f
(y),
для функций, непрерывных на всей оси R. Глава содержит 7 страниц
В четвертой главе рассматриваются уравнения вида (1) для функций,
непрерывных на полуоси R+. Глава содержит 8
страниц.
В пятой главе рассматриваются решения уравнений вида (1) в классе
измеримых функций. В главе 9 страниц.
В шестой главе делается обобщение уравнений вида (1) и их решений.
Рассматривается также функциональное уравнение f(y+x)+f(y-x)=2f(x)∙f(y),
являющееся
функциональной характеристикой тригонометрического и гиперболического косинусов. Находится решение функционального уравнения f′(x-
y)-f′(x
+ y)=2λf(x)∙f(y). В главе 7 страниц
В заключении делаются выводы о том, что функциональные
уравнения могут служить для определения многих
элементарных функций, применяться для введения новых классов функций. Основным
же результатом работы станет решение уравнений (1) в классе измеримых функций.
решение функциональное уравнение множество ось полуось
1. Функциональные
уравнения. Их свойства и методы решения
.1
Определение и примеры функциональных уравнений
Функциональные уравнения - весьма
общий класс уравнений, в которых искомой является некоторая функция. К функциональным
уравнениям, по существу, относятся дифференциальные уравнения
<#"514664.files/image001.gif">
+t,
y=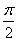 ;
x=
;
x=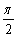 ,
y=
,
y=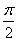 +t,
+t,
из (1.2) получают соответственно уравнения
f(t)
+ f(-t)
= 2a
cos
t,
f(π
+ t)
+ f(t
)= 0
и
f(π + t) + f(-t)= 2b cos(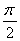 + t) = -2b sin t,
+ t) = -2b sin t,
где обозначено f(0)
= a,
f(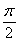 )
= b.
Отсюда
путем вычитания из суммы первых двух уравнений третьего, получают 2 f(t)=2a
cos
t
+ 2b
sin
t.
Общим
решением исходного функционального уравнения (1.2) является функция f(x)=a
cos x
+ и sin
x. Этот метод
применим также и к другим уравнениям типа
)
= b.
Отсюда
путем вычитания из суммы первых двух уравнений третьего, получают 2 f(t)=2a
cos
t
+ 2b
sin
t.
Общим
решением исходного функционального уравнения (1.2) является функция f(x)=a
cos x
+ и sin
x. Этот метод
применим также и к другим уравнениям типа
H [ f(x + y), f(x - y), f(x),
x, y ] = 0
при некоторых предположениях относительно функции
Н. К уравнениям других типов применяются различные другие подстановки.
Метод подстановок применяется и для сведения
одних функциональных уравнений к другим уравнениям того же типа, в частности к
функциональным уравнениям с известными решениями. Например, функциональное
уравнение
f((x
+ y)/2)
= f(x)/2
+ f(y)/2
(1.3)
может быть приведено к функциональному уравнению
Коши
f
(x
+ y)
= f(x)
+ f(y)
(1.4)
с непрерывным решением f(x)=Cx.
С этой целью в (1.3) подставляют x+y
вместо х и 0 вместо у:
f((x
+ y)/2)
= f(x
+у)/2 + а/2 , где a=f(0)
Сравнивая это с исходным функциональным
уравнением (1.3) получают функциональное уравнение вида f
(x
+ y)
= f(x)
+ f(y)
- а, откуда φ(x+y)=
φ(x)+
φ(y),
φ(x)=f(x)-a
и φ(x)
= Сх. Решением является
функция f(x)
= Cx+a.
Для сведения к другим функциональным уравнениям
того же типа применяют также логарифмирование и другие приемы. Например,
решение функционального уравнения
f
(x
+ y)
= f
(x)
∙ f
(y)
(1.5)
путем логарифмирования можно свести к решению
уравнения (1.4).
b)
Метод замены переменной:
Для того чтобы проиллюстрировать этот метод
рассмотрим уравнение:
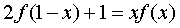 (1.6)
(1.6)
Предположим,
что существует функция f(x),
удовлетворяющая данному уравнению. Заменив x
на 1-x, получим
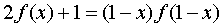
Из (1.6) находим 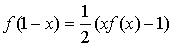 .
Подставляя значение во второе уравнение, получим:
.
Подставляя значение во второе уравнение, получим:
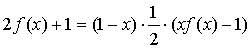 откуда
откуда 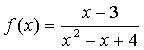
В рассмотренном уравнении под знаком уравнении
под знаком неизвестной функции стоят функции f1=x
и f2=1-x.
Замена x на 1-x
переводит функции f1
и
f2
друг в друга. В результате замены переменной получено еще одно уравнение,
содержащие f(x)
и f(1-x).
Решение функционального уравнения сводится к решению системы двух линейных
уравнений с двумя неизвестными.
Рассмотрим еще одно уравнение:
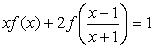 (1.7)
(1.7)
Выполним замену х→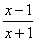 ,
получаем
,
получаем
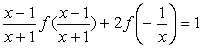 (1.8)
(1.8)
появилось новое «неизвестное» выражение 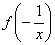 .
Применим еще одну подстановку:
.
Применим еще одну подстановку: 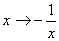 , имеем
, имеем
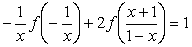 (1.9)
(1.9)
Кроме 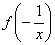 ,
в уравнении появилось «нежелательное» выражение
,
в уравнении появилось «нежелательное» выражение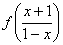 ,
выполним в (1.7) подстановку
,
выполним в (1.7) подстановку 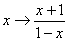 . И получаем
уравнение
. И получаем
уравнение
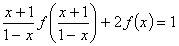 (1.10)
(1.10)
построена система линейных уравнений
(1.7)-(1.10) с четырьмя неизвестными 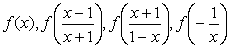 .
Последовательно исключая переменные, получим
.
Последовательно исключая переменные, получим 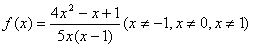 .
.
c)
Метод решения функциональных уравнений с помощью понятия группы
Пусть в функциональном уравнении
a1f(g1)+a2f(g2)+…+anf(gn)=b
(1.11)
выражения, стоящие под знаком неизвестной
функции f(x)
являются элементами группы G,
состоящей из n функций: g1(x)=x,
g2(x),…gn(x),
причем
коэффициенты уравнения (1.11) a1,
a2,
…an,
b - некоторые
функции от x. Предположим, что
уравнение (1.11) имеет решение. Заменим x→g2(x).
В результате последовательность функций g1(x),
g2(x),…gn(x),
перейдет
в последовательность g1º
g2,
g2º
g2,…gnº
g2,
состоящую
из всех элементов группы.
Поэтому «неизвестные» f(g1),
f(g2),…
f(gn),
переставятся и мы получим новое линейное уравнение того же вида, что и (1.11),
далее заменим x→g3(x),…
x→gn(x),
после чего получим систему из n
линейных уравнений, которую следует решить. Если решения есть, то проверкой
нужно убедиться в том, что они удовлетворяют уравнению.
Группой называется множество G
функций, обладающее следующими свойствами:
1. Для любых двух функций 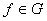 и
и
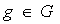 их
композиция
их
композиция 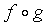 также принадлежит G.
также принадлежит G.
. Функция e(x)=x
принадлежит G.
. Для всякой функции 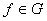 существует
обратная функция f-1,
которая также принадлежит G.
существует
обратная функция f-1,
которая также принадлежит G.
Из важных методов решения функциональных и
функционально-дифференциальных уравнений следует отметить также метод
дифференцирования <#"514664.files/image024.gif">
Q
удовлетворяет
уравнению
f
(x
+ у) = f
(x)
+ f
(y),
(2.1)
тождественно
относительно х и у, то она имеет вид f(t)
= Ct.
Где C
- постоянное число.
Доказательство:
►Прежде всего, с помощью метода математической
индукции легко обобщить соотношение (2.1) на случай любого числа (=n)
слагаемых :
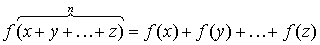 (2.2)
(2.2)
Действительно, если допустить его верность для
какого-либо числа (n
≥
2) слагаемых , то оно окажется верным и для n
+ 1 слагаемых:
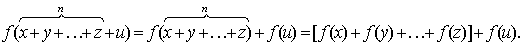
Полагая в (2.2) x=y=…=z,
найдем:
f(nx)=n∙f(x)
(2.3)
Заменив здесь n
на
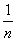 ,
получим
,
получим
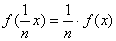 (2.4)
(2.4)
а затем, если
подставить mx (m-натуральное)
вместо х и использовать предыдущее равенство, придем к соотношению
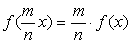 (2.5)
(2.5)
Положим теперь в основном уравнении (2.1) x=y=0;
получим
f(0)=2f(0),
так что f(0)=0. (2.6)
Если же взять y=-x,
то, с учетом (3.7), найдем:
f(-x)
= - f(x)
так что функция f(x)
меняет знак при изменении знака x.
А тогда из (2.3) и (2.5) легко вывести:
f(-nx)=-f(nx)=
-n∙f(x)
(2.7)
и, аналогично, вообще
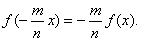 (2.8)
(2.8)
Полученные соотношения (2.3) - (2.8) могут быть
объединены в равенстве f(rx)=r∙f(x)
справедливом
для любого вещественного значения x,
каково бы ни было рациональное число r.
Если здесь взять х=1, и обозначить f(1)=C,
то получим
f®=Cr.
(2.9)
Теорема доказана. ▲ [4]
Таким образом, мы установили вид функции f
, принадлежащей классу функций, заданных на Q
(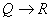 ).
При этом мы использовали только тот факт, что функция удовлетворяет условию
(2.1).
).
При этом мы использовали только тот факт, что функция удовлетворяет условию
(2.1).
2.2 Решение уравнений вида f(x+y)=f(x) ∙ f(y)
на Q
Следующей задачей будет нахождение всех заданных
на Q функций f(x),
удовлетворяющих условию:
f(x+y)=f(x)∙f(y),
(2.10)
каковы бы ни были значения х и у. Уравнение
(2.10) выражает общеизвестное правило умножения степеней:
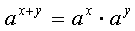
Теорема 2.2.
Если функция f(t),
заданная для всех значений t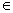 Q
удовлетворяет
уравнению
Q
удовлетворяет
уравнению
f
(x
+ у) = f
(x)∙f
(y),
тождественно
относительно х и у, то она имеет вид f(t)
= аt,
где а - неотрицательная постоянная. Доказательство:
►C
помощью метода математической индукции легко обобщить соотношение (2.10) на
случай любого числа (=n)
слагаемых :
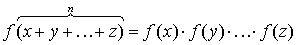 (2.11)
(2.11)
Действительно, если допустить его верность для
какого-либо числа (n
≥
2) слагаемых, то оно окажется верным и для n
+ 1 слагаемых
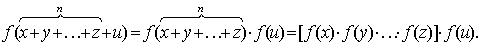
Полагая в (2.2) x=y=…=z,
найдем:
f(nx)=
f(x)n
(2.12)
Заменив здесь n
на
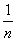 ,
получим
,
получим
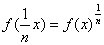 (2.13)
(2.13)
а затем, если подставить mx
(m-натуральное)
вместо х и использовать предыдущее равенство, придем к соотношению
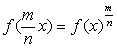 (2.14)
(2.14)
Положим теперь в основном уравнении (2.1) x=x,
y=0; получим
f(x+0)=
f(x)∙f(0),
так что
f(0)=1. (2.15)
Если же взять y=-x,
то, с учетом (2.15), найдем:
= f(0)
= f(x-x)=f(x)
∙f(-x)
,
откуда
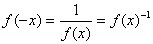 (2.16)
(2.16)
А тогда из (2.14) и (2.16) легко вывести:
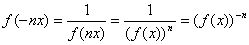 (2.17)
(2.17)
и, аналогично, вообще
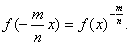 (2.18)
(2.18)
Полученные соотношения (2.14) - (2.18) могут
быть объединены в равенстве
f(rx)=
f(x)r
справедливом для любого рационального значения x,
каково бы ни было рациональное число r.
Если здесь взять х=1, и обозначить f(1)=a,
то получим
f(r)=ar.
(2.19)
Теорема доказана.▲
Таким образом, мы установили вид функции f,
принадлежащей классу функций, заданных на Q
(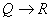 ).
При этом мы использовали только тот факт, что функция удовлетворяет условию
(2.10).
).
При этом мы использовали только тот факт, что функция удовлетворяет условию
(2.10).
2.3 Решение уравнений вида f(x∙y)=f(x)+ f(y)
на Q
Функциональное уравнение
f(xy)
= f(x)+f(y).
(2.20)
Есть запись логарифмирования произведения:
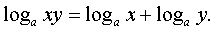
Теорема
2.3.
Если функция f(t),
заданная для всех положительных значений t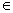 Q,
притом не сводящаяся к нулю, удовлетворяет уравнению (2.20)
тождественно относительно всех положительных значений х и у, то она имеет
вид f(t)=logat,
где а - положительная постоянная.
Q,
притом не сводящаяся к нулю, удовлетворяет уравнению (2.20)
тождественно относительно всех положительных значений х и у, то она имеет
вид f(t)=logat,
где а - положительная постоянная.
Доказательство:
►Как и в двух предыдущих случаях,
воспользуемся методом математической индукции. Обобщим соотношение (2.20) на
случай любого числа (=n)
переменных :
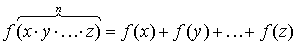 (2.21)
(2.21)
Действительно, если допустить его верность для
какого-либо числа (n
≥
2) сомножителей , то оно окажется верным и для n
+ 1 сомножителей :
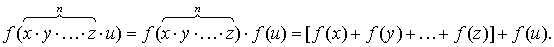 Полагая в (2.21) x=y=…=z,
найдем:
Полагая в (2.21) x=y=…=z,
найдем:
f(xn)=
n∙f(x)
(2.22)
Заменив здесь n
на
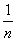 ,
получим
,
получим
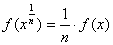 (2.23)
(2.23)
а затем, если
подставить mx (m-натуральное)
вместо х и использовать предыдущее равенство, придем к соотношению
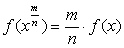 (2.24)
(2.24)
Положим теперь в основном уравнении (2.20) x=x,
y=1; получим
f(x∙1)=
f(x)+f(1),
так что f(1)=0.
(2.25)
Если же взять y=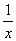 ,
то, с учетом (2.25), найдем:
,
то, с учетом (2.25), найдем:
= f(1)
= f(x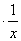 )=f(x)+f(
)=f(x)+f(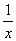 )
,
)
,
откуда 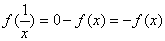 (2.26)
(2.26)
А тогда из (2.24) и (2.26) легко вывести:
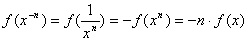 (2.27)
(2.27)
и, аналогично, вообще
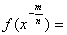
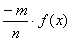 (2.28)
(2.28)
Полученные соотношения (2.23) - (2.28) могут
быть объединены в равенстве
f(xr)=r∙f(x)
(2.29)
справедливом для любого положительного
рационального значения x,
каково бы ни было рациональное число r.
Рассмотрим равенство (2.29) при натуральных
значениях r
и
положительных рациональных значениях x:
Не нарушая общности, можно записать x
в виде 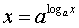 ,
где a>0,
a≠1
тогда для целого r
можно
записать:
,
где a>0,
a≠1
тогда для целого r
можно
записать:
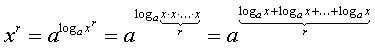
и переписать равенство (2.29) в виде:
f(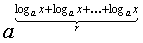 )=r∙f(
)=r∙f(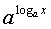 )
(2.30)
)
(2.30)
введем функцию φ(t)=f(at)
на
всей области определения функции f(x),
тогда
(2.30) примет вид:
φ(t+t+…+t)=φ(r∙t)=r∙φ(t)
(2.31)
функция φ(t)
очевидно удовлетворяет уравнению (2.3), а значит и 2.1. то есть
φ(t)
= Сt.
φ(log
a t) = С
log a t, тогда(a
log a t) = С
log a t и окончательно:
f(t)= С
log a t (2.32)
Теорема доказана. ▲
Таким образом, мы установили вид функции f
, принадлежащей классу функций, заданных на Q
(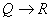 )
и удовлетворяющей (2.20)
)
и удовлетворяющей (2.20)
2.4 Решение уравнений вида f(x∙y)=f(x) ∙ f(y) на Q
Наконец, рассмотрим функциональное уравнение
f(x∙y)
= f(x)
∙ f(y).
(2.33)
(при рациональных положительных x
и y), это ничто
иное, как правило возведения в степень произведения двух чисел:
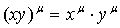 ,
,
Теорема
2.4.
Если функция f(t),
заданная для всех положительных значений t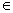 Q
,
притом не сводящаяся к нулю, удовлетворяет уравнению (2.33)
тождественно относительно всех положительных значений х и у, то она имеет
вид f(t)=tμ,
где μ
- постоянное
число.
Q
,
притом не сводящаяся к нулю, удовлетворяет уравнению (2.33)
тождественно относительно всех положительных значений х и у, то она имеет
вид f(t)=tμ,
где μ
- постоянное
число.
Доказательство:
►Воспользуемся методом математической
индукции. Обобщить соотношение (2.33) на случай любого числа (=n)
переменных :
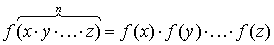 (2.34)
(2.34)
Действительно, если допустить его верность для
какого-либо числа (n
≥
2) сомножителей , то оно окажется верным и для n
+ 1 сомножителей :
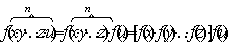 Полагая в (2.21) x=y=…=z,
найдем:
Полагая в (2.21) x=y=…=z,
найдем:
f(xn)=
f(x)n
(2.35)
Заменив здесь n
на
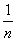 ,
получим
,
получим
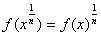 (2.36)
(2.36)
а затем, если
подставить mx (m-натуральное)
вместо х и использовать предыдущее равенство, придем к соотношению
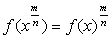 (2.37)
(2.37)
Положим теперь в основном уравнении (2.33) x=x,
y=1; получим f(x∙1)=
f(x)∙f(1),
так что f(1)=1.
(2.38)
Если же взять y=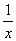 ,
то, с учетом (2.38), найдем:
,
то, с учетом (2.38), найдем:
1= f(1)
= f(x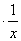 )=f(x)∙f(
)=f(x)∙f(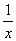 ),
откуда
),
откуда
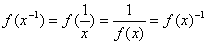 (2.39)
(2.39)
А тогда из (2.37) и (2.39) легко вывести:
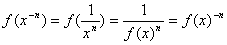 (2.40)
(2.40)
и, аналогично, вообще
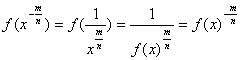 (2.41)
(2.41)
Полученные соотношения (2.36) - (2.41) могут
быть объединены в равенстве
f(xr)=f(x)r
(2.42)
В самом деле, если дана определенная
положительных для х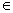 Q
функция f(x),
удовлетворяющая условию (2.33), то прибегнув к той же подстановке,
Q
функция f(x),
удовлетворяющая условию (2.33), то прибегнув к той же подстановке,
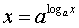 , где a>0,
a≠1
тогда для целого r
можно
записать:
, где a>0,
a≠1
тогда для целого r
можно
записать:
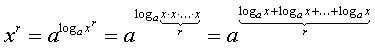
и переписать равенство (2.29) в виде:
f(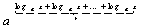 )=
)=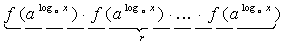 (2.43)
(2.43)
введем функцию φ(t)=f(at)
на
всей области определения функции f(x),
тогда
(2.30) примет вид:
φ(t+t+…+t)=φ(r∙t)=
φ(t)r
(2.44)
функция φ(t)
очевидно удовлетворяет уравнению (2.12), а значит и 2.10. то есть
φ(t)
= ct.
φ(log
a t) = c log a t, тогда(a
log
a
t)
= c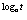 =
=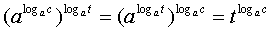
и окончательно:
f(t)=
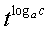 =tμ
(2.45)
=tμ
(2.45)
(если
положить μ=loga
c), что и требовалось
доказать. ▲[2][3]
Таким
образом, мы установили вид функции f
, принадлежащей классу функций, заданных на Q
(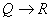 )
и удовлетворяющей (2.33)
)
и удовлетворяющей (2.33)
3. Решение Функциональных уравнений Коши на оси R
Полученные в предыдущей главе
результаты, могут быть продолжены для функций, непрерывных на всей числовой оси
R.
Если в дополнение к
функциональным уравнениям (2.1), (2.10), потребовать еще и непрерывности, то
формулировки и доказательства теорем (2.1-2.2) несколько изменятся (даже
упростятся), результат же (то есть сами решения уравнений) останется тем же.
Покажем это, решив уравнения.
3.1 Решение уравнений вида f(x+y)=f(x)+f(y) на оси R
Найти все непрерывные в промежутке (-∞, +∞)
функции f(x),
удовлетворяющие условию:
f(x+y)=f(x)+f(y),
(3.1)
каковы бы ни были значения х и у.
Легко видеть, что линейные однородные функции
вида
f(x)=c∙x (c=const) (3.2)
удовлетворяют этому уравнению:
с(x+y)=cx+cy,
Для того чтобы установить, что
это единственные непрерывные функции, удовлетворяющие (3.1), предположим, что
некоторая непрерывная функция f(x)
удовлетворяет (3.1), покажем, что она непременно имеет вид (3.2).
Теорема 3.1.
Если функция f(t),
заданная и непрерывная для всех значений t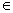 (-
∞; + ∞). Удовлетворяет уравнению (3.1) тождественно
относительно х и у, то она имеет вид f(t)
= Ct.
Где C
- постоянное число.
(-
∞; + ∞). Удовлетворяет уравнению (3.1) тождественно
относительно х и у, то она имеет вид f(t)
= Ct.
Где C
- постоянное число.
Доказательство:
►По Теореме 2.1 функция f
, принадлежащей классу разрывных функций (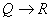 )
и удовлетворяющая условию (3.1), имеет вид f®=cr
,
)
и удовлетворяющая условию (3.1), имеет вид f®=cr
, 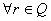
Пусть теперь s
будет любое иррациональное значение аргумента. Легко построить стремящуюся к
нему последовательность рациональных чисел.
R1,
r2,
…, rn,
…
(можно, например, взять отрезки соответствующей
бесконечной десятичной дроби).
F(rn)=crn
(n=1,2,3…)
Перейдем к пределу при n→+∞;
справа получим cs,
слева же, именно ввиду предположенной непрерывности функции f,
получится
lim
f(rn)=f(s),
так что окончательно,
f(s)=cs.▲
Таким образом, действительно, наша функция при
всех вещественных значениях аргумента выражается формулой (3.2). Эта формула
дает решение уравнения (3.1) в классе непрерывных функций.
3.2 Решение
уравнений вида f(x+y)=f(x) ∙f(y) на
оси R
Найти все непрерывные в промежутке (-∞, +∞)
функции f(x),
удовлетворяющие условию:
f(x+y)=f(x)∙f(y),
(3.3)
каковы бы ни были значения х и у.
Оказывается, что функциональным свойством (3.3),
вместе со свойством непрерывности, вполне определяется показательная функция
f(x)=а
x
(a > 0) (3.4)
Точнее говоря, единственной функцией,
определенной и непрерывной во всем промежутке (-∞, +∞) и
удовлетворяющей в нем условию (3.3), является показательная функция (если
не считать функции тождественно равной 0).
Иными словами, формула (3.4) - за указанным
исключением - дает самое общее решение функционального уравнения (3.3) в
непрерывных функциях.
Теорема
3.2.
Если функция f(t),
заданная и непрерывная для всех значений t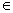 (-
∞; + ∞). удовлетворяет уравнению (3.3) тождественно
относительно х и у, то она имеет вид f(t)
= аt,
где а - неотрицательная постоянная.
(-
∞; + ∞). удовлетворяет уравнению (3.3) тождественно
относительно х и у, то она имеет вид f(t)
= аt,
где а - неотрицательная постоянная.
Доказательство:
►Для доказательства этого рассмотрим
произвольную функцию f(x),
Определенную и непрерывную при всех х, удовлетворяющую условию (3.3).
Исключается тривиальный случай, когда f(x)≡0.
Итак, при некотором значении x=x0
эта функция отлична от 0. Полагая в (3.3) y=x0-x,
получим
f(x)∙f(x0-x)
= f(x0)
≠ 0;
отсюда ясно, что f(x)
отлично от нуля при всяком x.
Более того, заменяя в (3.3) x
и y через 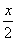 ,
найдем:
,
найдем:
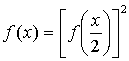 ,
,
так что f(x)
всегда строго положительна.
Пользуясь этим, прологарифмируем равенство
(3.3), например, по натуральному основанию е:
ln f(x+y) = ln f(x)+ln
f(y).
Если положить
φ(x)
= ln
f(x),
то φ(x)
есть
непрерывная функция (как результат суперпозиции непрерывных) и удовлетворяющая
условию:
φ (x+y)
= φ (x)+
φ (y),
аналогичному (3.1). В таком случае, как мы
установили, необходимо
φ(x)
= ln f(x) = cx (c=const)
откуда, наконец,
f(x)=ecx=ax
(если положить a=ec),
что и требовалось доказать. ▲
Таким образом, мы показали, что уравнения f(x+y)=f(x)+f(y)
и
f(x+y)=f(x)∙f(y),
имеют одинаковые решения среди функций, определенных на множестве рациональных
чисел и на множестве всех действительных чисел. Эти решения имеют вид: f(x)=C∙x
и f(x)=ax
соответственно.
4. Решение Функциональных уравнений Коши на полуоси R+
Рассмотрим теперь решения уравнений среди
функций, определенных, непрерывных и удовлетворяющих этим уравнениям лишь на
положительной полуоси R+.
Сформулируем соответствующие теоремы для
уравнений
f(x
+ y)
= f(x)
∙ f(y)
(4.2)
f(x∙y)
= f(x)
+ f(y)
(4.3)
f(x
∙
y)
= f(x)
∙ f(y)
(4.4)
требуя от функций определенности и непрерывности
только на (0; +∞)
4.1 Решение уравнений вида f(x+y)=f(x)+f(y)
на полуоси r+
Теорема 4.1.
Если функция f(t),
заданная и непрерывная для всех значений t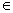 (0;+
∞). Удовлетворяет уравнению f(x+y)
= f(x)
+ f(y)
тождественно относительно х и у, то она имеет вид f(t)
= Ct.
Где C
- постоянное число.
(0;+
∞). Удовлетворяет уравнению f(x+y)
= f(x)
+ f(y)
тождественно относительно х и у, то она имеет вид f(t)
= Ct.
Где C
- постоянное число.
Доказательство:
►Доказательство проведем аналогично
теоремам (2.1) и (3.1), с учетом требования положительной области определения
функции f.
C помощью метода
математической индукции легко обобщить соотношение (4.1) на случай любого числа
(=n) слагаемых :
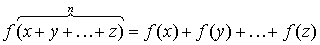 (4.5)
(4.5)
Действительно, если допустить его верность для
какого-либо числа (n
≥
2) слагаемых , то оно окажется верным и для n
+ 1 слагаемых :
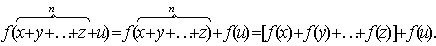 Полагая в (4.3) x=y=…=z,
найдем:
Полагая в (4.3) x=y=…=z,
найдем:
f(nx)=n∙f(x)
(4.6)
Заменив здесь n
на
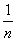 ,
получим
,
получим
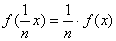 (4.7)
(4.7)
а затем, если
подставить mx (m-натуральное)
вместо х и использовать предыдущее равенство, придем к соотношению
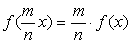 (4.8)
(4.8)
или
f(rx)=r∙f(x)
справедливом для любого положительного значения x,
каково бы ни было положительное рациональное число r.
Если здесь взять х=1, и обозначить f(1)=C,
то получим
f(r)=Cr.
(4.9)
Пусть теперь s
будет любое положительное иррациональное значение аргумента. Легко построить
стремящуюся к нему последовательность рациональных чисел.
R1,
r2,
…, rn,
…
(можно, например, взять отрезки соответствующей
бесконечной десятичной дроби).
F(rn)=crn
(n=1,2,3…)
Перейдем к пределу при n→+∞;
справа получим cs,
слева же, ввиду предположенной непрерывности функции f,
получится
lim
f(rn)=f(s),
так что окончательно,
f(s)=cs,
s>0▲
4.2 Решение уравнений
вида f(x+y)=f(x)∙f(y) на
полуоси r+
Теорема
4.2.
Если функция f(t),
заданная и непрерывная для всех значений t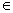 (0;
+ ∞). удовлетворяет уравнению (4.2) тождественно относительно х
и у, то она имеет вид f(t)
= аt,
где а - неотрицательная постоянная.
(0;
+ ∞). удовлетворяет уравнению (4.2) тождественно относительно х
и у, то она имеет вид f(t)
= аt,
где а - неотрицательная постоянная.
Доказательство:
►Для доказательства этого рассмотрим
произвольную функцию f(x),
Определенную и непрерывную при всех х, удовлетворяющую условию (4.2).
Исключается тривиальный случай, когда f(x)≡0.
Итак, при некотором значении 0<x=x0
эта функция отлична от 0. Полагая в (4.2) 0<x<x0
и 0<y=x0-x,
получим
f(x)∙f(x0-x)
= f(x0)
≠ 0; (4.10)
отсюда ясно, что f(x)
отлично от нуля при всяком 0<x<x0.
C другой стороны,
f(2∙x0)=
f(x0)
∙ f(x0)
≠ 0
и вообще
f(n∙x0)=
f(x0)n
≠
0. (4.11)
Равенство (4.11) легко
доказывается по индукции (см. теорему 2.2). Из (4.10) и (4.11) имеем:
если 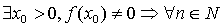 ,
,
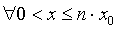 ,
,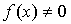 .
.
Следовательно, функция f
всюду
на R+
отлична от 0.
Более того, заменяя в (4.2) x
и y через 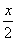 ,
найдем:
,
найдем:
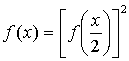 ,
,
так что f(x)
всегда
строго положительна.
Пользуясь этим, прологарифмируем равенство (4.2),
например, по натуральному основанию е:
ln f(x+y) = ln f(x)+ln
f(y).
Если положить
φ(x)
= ln
f(x),
то φ(x)
есть
непрерывная функция (как результат суперпозиции непрерывных) и удовлетворяющая
условию:
φ (x+y)
= φ (x)+
φ (y),
аналогичному (4.1). В таком случае, как
мы установили, необходимо
φ(x)
= ln f(x) = cx (c=const)
откуда, наконец,
f(x)=ecx=ax,
x>0
(если положить a=ec),
что и требовалось доказать. ▲
4.3 Решение уравнений вида f(x∙y)=f(x)+f(y)
на полуоси r+
Если
f(x) = logax (a>0, a≠1)
(4.12)
то при любых положительных значениях x
и y f(x)
будет удовлетворять уравнению (4.3)
И здесь это равенство, совместно с
непрерывностью, вполне характеризует именно логарифмическую функцию.
Теорема
4.3. Если функция f(t),
заданная и непрерывная для всех положительных значений t,
притом не сводящаяся к нулю, удовлетворяет уравнению (4.2)
тождественно относительно всех положительных значений х и у. то она имеет
вид f(t)=logat,
где а - положительная постоянная.
Доказательство:
►Для доказательства возьмем произвольную
функцию f(x),
непрерывную для x>0
и удовлетворяющую этому уравнению. Введем новую переменную ξ,
изменяющуюся
в промежутке (-∞; +∞), и положим
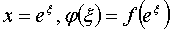 ,
,
откуда
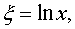
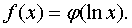
Непрерывная (как суперпозиция непрерывных)
функция φ(ξ)
удовлетворяет условию
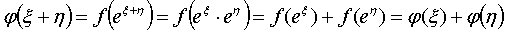
типа (3.1), значит,
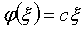 и
и 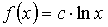
если исключить случай с=0 (тогда f(x)≡0),
то полученный результат может быть написан в виде
где 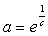 .
Этим все доказано ▲.
.
Этим все доказано ▲.
4.4 Решение уравнений вида f(x∙y)=f(x) ∙ f(y) на полуоси R+
Наконец, обратимся к функциональному уравнению
(4.4) (при любых положительных x
и y)
Уравнение это, в соединении с непрерывностью, в
данном случае характеризует степенную функцию.
Теорема
4.4. Если функция f(t),
заданная и непрерывная для всех положительных значений t,
притом не сводящаяся к нулю, удовлетворяет уравнению (4.4)
тождественно относительно всех положительных значений х и у, то она имеет
вид f(t)=tμ,
где μ
- постоянное
число.
Доказательство:
►В самом деле, если дана непрерывная для
х>0 функция f(x),
удовлетворяющая условию (4.4), то прибегнув к той же подстановке, что и в
Теореме 4.3).
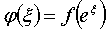 , получим:
, получим:
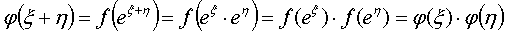
φ(ξ)
удовлетворяет уравнению (4.2), тогда (если исключить тривиальный случай)
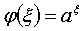 ,
(a>0)
,
(a>0)
Отсюда 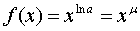
(если положить μ=ln
a), что и
требовалось доказать. ▲
Из вышеизложенного можно сделать вывод о том,
что рассматриваемые уравнения f(x+y)
= f(x)
+ f(y),
f(x
+ y)
= f(x)
∙ f(y),
f(x∙y)
= f(x)
+ f(y),
f(x
∙
y)
= f(x)
∙ f(y)
будут
иметь решения f(x)=C∙x,
f(x)=ax,
f(x)=logax,
f(x)=xμ
даже
если требовать от функции f
непрерывности только на положительной полуоси.
5. Решение Функциональных уравнений Коши в измеримых
функциях
Для того чтобы рассматривать решения уравнений
коши на множестве измеримых функций, дадим несколько необходимых определений
[5,с.300]:
Определение 1: Пусть
X - множество, на
котором задана σ-аддитивная
мера μ,
определенная
на σ-алгебре
Gμ.
Действительная функция f(x)
на X называется μ-измеримой,
если для всякого борелевского множества А числовой прямой
f-1(A)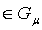 .
.
Иначе: функцию f(x)
называют
измеримой, если все множества {x:f(x)<c}
измеримы при любом действительном с.
Важнейшие свойства измеримых функций:
- Измеримая функция от измеримой функции есть
измеримая функция.
Сумма, разность, произведение двух измеримых
функций измеримы.
Частное двух измеримых функций, при условии,
что знаменатель не обращается в нуль, тоже измеримо.
Предел сходящейся при каждом 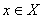 последовательности
измеримых функций измерим
последовательности
измеримых функций измерим
Функция f(x),
определенная на некотором измеримом множестве Е и эквивалентная на нем
некоторой измеримой функции g(x),
тоже
измерима (функции называют эквивалентными, если μ{x:f(x)≠g(x)}=0).
Определение измеримой функции, данное в начале
главы, относится к функциям на произвольных множествах и в общем случае никак
не связано с понятием непрерывной функции. Однако, если речь идет о функциях на
отрезке, то имеет место следующая важная теорема, установленная в 1913 г. Н.Н.
Лузиным.
Теорема 5.1. (Теорема
Лузина). Для того, чтобы функция f(x),
заданная на отрезке [a,
b], была
измерима, необходимо и достаточно, чтобы для любого ε
> 0, существовала такая непрерывная на [a,
b] функция
φ(x),
что
μ{x
: f(x)
≠
φ
(x)}
< ε.[5, c.309]
С помощью свойств измеримых функций и
воспользовавшись теоремой Лузина, будем искать решения функциональных уравнений
Коши в классе измеримых функций:
5.1
Решение уравнения вида f(x+y)=f(x)+f(y) в измеримых
функциях
Сформулируем и
докажем следующую теорему:
Теорема 5.2. Если
измеримая, ограниченная функция φ(x),
удовлетворяет условию
ψ(x)+
ψ(y)
=
ψ(x+y)
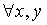 ,
(5.1)
,
(5.1)
то она имеет вид
С∙x,
где C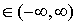 .
.
Доказательство:
►Покажем,
что всякая измеримая функция, удовлетворяющая (5.1) является непрерывной.
Так как ψ
измерима, то она измерима на произвольном отрезке I
длины l>0. По
теореме Лузина для любого числа ε > 0 найдется
замкнутое множество 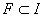 , такое, что
сужение ψ на F
является
непрерывной функцией и мера
, такое, что
сужение ψ на F
является
непрерывной функцией и мера 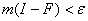 . Тогда существует
последовательность замкнутых множеств
. Тогда существует
последовательность замкнутых множеств 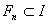 ,
для которых
,
для которых 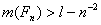 , а сужение ψ
на
Fn
непрерывно,
и более того, в силу компактности Fn
равномерно непрерывно. Значит, найдется число
, а сужение ψ
на
Fn
непрерывно,
и более того, в силу компактности Fn
равномерно непрерывно. Значит, найдется число 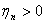 ,
обеспечивающее выполнение неравенства
,
обеспечивающее выполнение неравенства
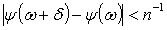
при 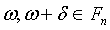 и
и
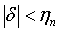 .
Зафиксируем число δn,
удовлетворяющее неравенствам 0 < δn<
ξn
=
min(ηn,
n-2).
Очевидно, что множество точек
.
Зафиксируем число δn,
удовлетворяющее неравенствам 0 < δn<
ξn
=
min(ηn,
n-2).
Очевидно, что множество точек 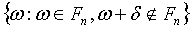 измеримо и мера не
превосходит n-2 +
δn<
2∙n-2.
Тогда
измеримо и мера не
превосходит n-2 +
δn<
2∙n-2.
Тогда 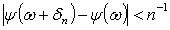 для
для
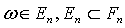 ,
если по построению
,
если по построению 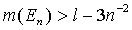 . Обозначим через
. Обозначим через 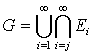 множество
точек ω,
принадлежащих
всем кроме конечного числа Ei
/
Если ввести множества Кi=I-Ei,
H=I-G,
то
множество
точек ω,
принадлежащих
всем кроме конечного числа Ei
/
Если ввести множества Кi=I-Ei,
H=I-G,
то 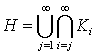 будет
множеством точек из I,
принадлежащих бесконечно многим Ki:
значит,
будет
множеством точек из I,
принадлежащих бесконечно многим Ki:
значит,
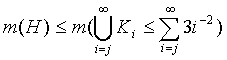
для всех j=1,2…,
поэтому m(H)=0,
a m(G)=l.
Следовательно,
для произвольной последовательности { δn
}, удовлетворяющей ограничениям 0 < δn<
ξn,
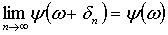 (5.2)
(5.2)
для почти всех 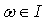 .
.
Пусть теперь I-это
отрезок [ω1
, ω2], а числа ω0,
ω
подчинены неравенствам: ω1
< ω < ω0
<ω2 .
Тогда, взяв x=
ω0 -ω,
y=
ω+ δn,
из (5.1) получаем
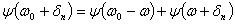 ,
,
если же точка берется из множества G,
то, согласно (5.2)
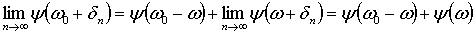 т.е.
т.е.
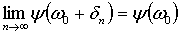 (5.3)
(5.3)
для всех 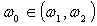 .
Последовательность положительных чисел { δn
} здесь не произвольна, поскольку зависит от интервала I
и
δn
.
Последовательность положительных чисел { δn
} здесь не произвольна, поскольку зависит от интервала I
и
δn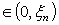 .
Пусть {θn
}- любая последовательность положительных чисел, сходящаяся к нулю.
Предположим, что
.
Пусть {θn
}- любая последовательность положительных чисел, сходящаяся к нулю.
Предположим, что
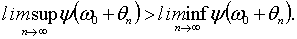 (5.4)
(5.4)
Тогда из {θn
} можно выбрать подпоследовательность {θni
} чисел 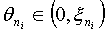 ,
для которой в силу (5.3) имеем
,
для которой в силу (5.3) имеем
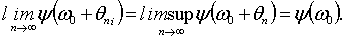
Аналогичные рассуждения приводят нас к равенству
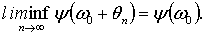
что противоречит (5.4).Значит, верхний и нижний
пределы совпадают, и каждый из них равен ψ(ω0).
Так как от последовательности {θn}требуется
лишь положительность, то функция ψ(ω)
непрерывна
справа в произвольной точке ω, поскольку
отрезок может быть выбран произвольно.
Для доказательства непрерывности слева положим  Ψ(x)=
ψ(-x);
тогда из (5.1) следует равенство Ψ(x)+
Ψ(y)=
Ψ(x+y).
Далее, аналогично тому, как это делалось выше, доказывается непрерывность Ψ
справа в произвольной точке x0.
Отсюда вытекает непрерывность ψ слева
в произвольной точке ω=-x0.
Итак,
мы доказали, что произвольная измеримая функция ψ,
удовлетворяющая уравнению (5.1) непрерывна. Тогда, по теореме (3.3) она имеет
вид ψ(x)=
С∙x.
Теорема
доказана. ▲ [6, c.18-20]
Ψ(x)=
ψ(-x);
тогда из (5.1) следует равенство Ψ(x)+
Ψ(y)=
Ψ(x+y).
Далее, аналогично тому, как это делалось выше, доказывается непрерывность Ψ
справа в произвольной точке x0.
Отсюда вытекает непрерывность ψ слева
в произвольной точке ω=-x0.
Итак,
мы доказали, что произвольная измеримая функция ψ,
удовлетворяющая уравнению (5.1) непрерывна. Тогда, по теореме (3.3) она имеет
вид ψ(x)=
С∙x.
Теорема
доказана. ▲ [6, c.18-20]
5.2
Решение уравнения вида f(x+y)=f(x)∙f(y)
в
измеримых функциях
Доказав, что
измеримая функция ψ,
удовлетворяющая уравнению (5.1) имеет вид ψ(x)=
С∙x,
мы
можем найти также решение уравнения
φ(λ)
∙φ(γ) =φ(λ∙
γ)
в измеримых
функциях.
Сформулируем и
докажем теорему
Теорема 5.3. Если
измеримая, ограниченная функция φ(λ),
λ>0,
удовлетворяет
условию
φ(λ) ∙φ(γ)
=φ(λ∙ γ)
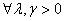 (5.5)
(5.5)
то она имеет вид
λρ, где
ρ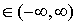 .
.
Доказательство:
►
Для доказательства этого рассмотрим произвольную измеримую функцию φ(x),
удовлетворяющую условию (5.5). Исключается тривиальный случай, когда φ(x)≡0.
Покажем, что если 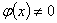 хотя
бы в одной точке, то она свюду положительна. Положим в уравнении (5.5) γ=λ,
тогда
хотя
бы в одной точке, то она свюду положительна. Положим в уравнении (5.5) γ=λ,
тогда
≤ φ(λ)2
=φ(λ2)
(5.6)
то есть φ(x)
≥ 0, если х представим в виде квадрата некоторого числа, но по условиям
теоремы φ определена
на положительной полуоси, а любое положительное число представимо в виде
квадрата некоторого числа.
Пусть далее при некотором λ0>0
φ(λ0)=0,
тогда любое число γ>0 представимо
в виде: 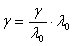 и
(5.5) принимает вид:
и
(5.5) принимает вид:
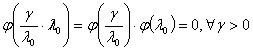 (5.7)
(5.7)
Противоречие с тем что φ
не равна нулю тождественно.
Таким образом, φ
всюду положительна, а значит, ее можно логарифмировать по любому основанию.
После преобразования ψ(x)=log
φ(ex)
(5.5) переходит в функциональное уравнение Коши
ψ(x)+
ψ(y)
=
ψ(x+y)
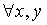 ,
,
где ψ конечна
и измерима, а по теореме (5.2) непрерывна и имеет вид ψ(x)=
С∙x.
Значит φ(x)=xρ.
Теорема доказана. ▲
Аналогично проведем доказательства для двух
оставшихся уравнений:
5.3
Решение уравнения вида f(x∙y)=f(x)+f(y)
в измеримых функциях
Теорема 5.4. Если
измеримая, ограниченная функция φ(x),
x>0, удовлетворяет
условию
φ(x)
+φ(y) =φ(x∙
y) 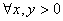 (5.8)
(5.8)
то она имеет вид
log a
x, где a>0,
a≠1.
Доказательство:
►После
преобразования 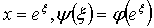 ,откуда
,откуда
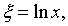
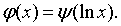
измеримая (как суперпозиция измеримых) функция ψ(ξ)
удовлетворяет условию
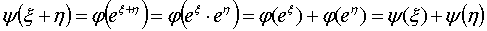
типа (5.1), значит она непрерывна и имеет вид:
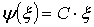 и
и 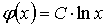
если исключить случай С=0 (тогда φ(x)≡0),
то полученный результат может быть написан в виде
где 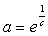 .
Этим все доказано ▲.
.
Этим все доказано ▲.
5.4
Решение уравнения вида f(x∙y)=f(x)∙f(y)
в измеримых функциях
Теорема 5.5. Если
измеримая, ограниченная функция φ(x),
удовлетворяет условию
φ(x)
∙ φ(y)
=φ(x +y)
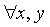 (5.9)
(5.9)
то она имеет вид
ax, где
a>0.
Доказательство:
►
Для доказательства этого рассмотрим произвольную измеримую функцию φ(x),
удовлетворяющую условию (5.9). Исключается тривиальный случай, когда φ(x)≡0.
Итак, при некотором значении x=x0
эта функция отлична от 0. Полагая в (5.9) y=x0-x,
получим
φ(x)∙
φ(x0-x)
= φ(x0)
≠ 0;
отсюда ясно, что φ
(x) отлично от нуля
при всяком x. Более того,
заменяя в (5.9) x и y
через 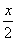 ,
найдем:
,
найдем:
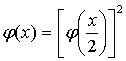 ,
,
так что φ(x)
всегда строго положительна.
Пользуясь этим, прологарифмируем равенство
(5.9), например, по натуральному основанию е:
ln φ(x+y)
= ln φ(x)+ln
φ(y).
Если положить
ψ(x)
= ln φ(x),
то ψ (x)
есть
измеримая функция (как результат суперпозиции измеримых) и удовлетворяющая
условию:
ψ (x+y)
= ψ (x)+
ψ
(y),
аналогичному (5.1). В таком случае, как мы
установили, необходимо
ψ
(x) = ln φ
(x) = Сx
(С=const)
откуда, наконец,
φ (x)=ecx=ax
(если положить a=ec),
что и требовалось доказать. ▲
Таким образом, мы установили, что функциональные
уравнения Коши:
f (x + у) = f (x) + f (y), f (x + у)
= f (x) f (y), f (xy) = f (x) + f (y), f (xy) = f (x) f (y) имеют
решения соответственно вида Cx, eCx, <#"514664.files/image130.gif"> (6.3)
Функциональное уравнение (6.2)
вместе с требованием непрерывности функции, и на этот раз полностью
характеризует оба косинуса:
Единственными функциями,
определенными и непрерывными в промежутке (-∞, +∞) и
удовлетворяющими в нем уравнению (6.2), являются тригонометрический и
гиперболический косинусы (6.1) (если, не считать
функции, тождественно равной нулю).
►Итак, пусть f(x)
будет непрерывная для всех x
функция, удовлетворяющая условию (6.2). Полагая x=0 и принимая
за у какое либо из значений, для которого f(y)≠0,
заключаем, что
f(0)=1.
(6.4)
При y=0
в таком случае получается
f(-x)=f(x)
(6.5)
так что функция f(x)
оказывается
четной.
Поскольку непрерывная функция f(x)
при x=0 будет
положительна, то найдется такое, скажем, положительное число с, что f(x)
будет положительна на всем промежутке [0, c].
В дальнейшем исследование пойдет по разным путям, в зависимости от того, будет
ли а) f(c)
≤ 1 или б) f(c)
> 1. Займемся случаем а).
Так как 0 < f(c)
≤ 1, то найдется такое θ 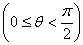 ,
что
,
что
f(c)
= cos θ.
(6.6)
Приведя затем основное
соотношение (6.2) к виду :
f(y +x) = 2 f(x)∙f(y)
- f(y - x),
станем в нем последовательно
полагать
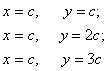
и т.д. Мы получим (с учетом
(6.4) и (6.6))
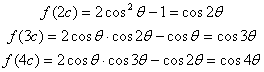
и т.д. Пользуясь методом
математической индукции, легко докажем для любого натурального m
формулу
f(mc)=cos
mθ
(6.7)
если же в (6.2) положить 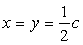 ,
то получим (снова с учетом (6.4) и (6.6)):
,
то получим (снова с учетом (6.4) и (6.6)):
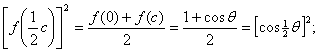
так как f(x)
остается положительной между 0 и с, а функция cos
x - между 0 и θ,
то,
извлекая положительные корни в обеих частях, придем к равенству:
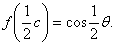
совершенно также, полагая в
(6.2) x=y=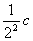 ,
найдем , что
,
найдем , что
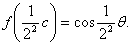
и т.д. Так, последовательно
(математическая индукция!), получим и общее соотношение
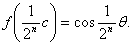 (n=1,
2,3,…) (6.8)
(n=1,
2,3,…) (6.8)
Наконец, повторяя тот процесс,
с помощью которого мы, отправляясь от (6.6) к (6.7), мы из (6.8) придем к
равенству:
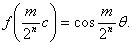
Итак, для положительных
значений x вида 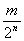 имеем:
имеем:
f(cx)
=cos θx
(6.9)
Но так как любое положительное
число x можно представить
как предел значений этого вида, то, с помощью предельного перехода (и опираясь
на непрерывность функций f(x)
и cos(x)),
установим справедливость формулы (6.9) для всех x>0.
Для x<0 она будет
верна в силу (6.5), а для x=0
- в силу (6.4).
Если заменить в (6.9) x
на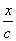 и положить
и положить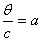 , то и получим
окончательно:
, то и получим
окончательно:
f(x)=cos
ax.
В случае б) имеем: f(c)>1;
тогда найдется такое θ, что
f(c)
= ch
θ.
Повторяя дословно все
проведенные только что рассуждения и опираясь на соотношения для
гиперболического косинуса, совпадающие по форме с соответствующими
соотношениями для тригонометрического косинуса, мы для рассматриваемого случая
найдем, что
f(x)=ch
ax.
(a>0)
При a=0,
по обеим формулам получили бы: f(x)≡1.▲
6.2
Решение уравнения для синуса на оси R
Наряду с уравнением (6.2), определяющим функции cos
ax и сh
ax, рассмотрим
дифференциальное функциональное уравнение
f′(x
- y)-f′(x
+ y)=2λf(x)∙f(y)
λ≠0
(6.10)
и покажем, что при дополнительном требовании
дважды дифференцируемости f(x)
оно характеризует функции С sin
αx
и
С sh
αx
(если
не считать функции, тождественно равной 0)
► 1. при у=0, имеем
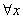 , f′(
x)-f′(x)=2λf(x)∙f(0)=0
, f′(
x)-f′(x)=2λf(x)∙f(0)=0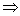 f(0)=0
(6.11)
f(0)=0
(6.11)
2. при х=0, имеем
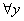 , f′(-у)-f′(у)=2λf(0)∙f(у)=0
, f′(-у)-f′(у)=2λf(0)∙f(у)=0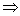 f′(х)-четная
f′(х)-четная
. продифференцируем (6.10) по у:
-f′′(x-y)-f′′(x+y)=2λf(x)∙f′(y)
при у=0 имеем
-2f′′(x)=2λf(x)∙f′(0)
f′(0)=с
f′′(x)+λ∙с∙f(x)=0
f(0)=0
f′(0)=с
для λ>0,
будем рассматривать случаи, когда с=0, с<0, c>0
a) c=0:
f′′(x)=0
f′′(x)=C1x+C2
f(0)=f′(0)=0
C1=C2=0.
f(x)≡0
b) c<0:
f(x)=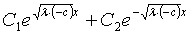 (0)=C1+C2=0
(0)=C1+C2=0
C1=-C2
f(x)=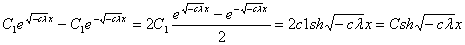 ′(x)=
′(x)=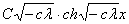 ′(0)=
′(0)=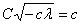 =
=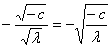 (x)=
(x)=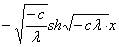 ;
;
положив α=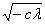
f(x)=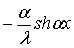 =-β
sh
λβx ;
=-β
sh
λβx ;
b) c >
0:
f(x)=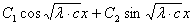 (0)=C1
=0
(0)=C1
=0
f(x)=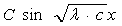 ′(x)=
′(x)=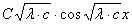 ′(0)=
′(0)=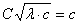
C=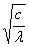
f(x)=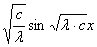 ;
;
положив α=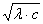
f(x)=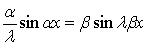 ,
▲
,
▲
6.3
Класс уравнений типа Коши
Сделаем далее еще одно обобщение. Классические
функциональные уравнения Коши [8] f(x+y)=f(x)+f(y), f(x+y)=f(x)∙f(y),
f(x∙y)=f(x)+f(y), f(x∙y)=f(x)∙f(y), имеющие непрерывные
решения соответственно с∙x, 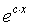 ,
с∙lnx, xс, связывают основные
смежные (в смысле распределительного закона) арифметические операции сложения +
и умножения ∙ .
,
с∙lnx, xс, связывают основные
смежные (в смысле распределительного закона) арифметические операции сложения +
и умножения ∙ .
В [9] указаны примыкающие к ним: «снизу» -
операция x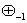 y = ln(ex+ey),
«сверху»
- операция x
y = ln(ex+ey),
«сверху»
- операция x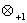 y=e(lnx∙lny).
Все
эти операции являются звеньями «естественной цепи арифметических операций»
y=e(lnx∙lny).
Все
эти операции являются звеньями «естественной цепи арифметических операций» 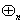 [10],
в которой +=
[10],
в которой +=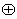 0,
∙ =
0,
∙ =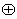 +1,
так
что
+1,
так
что 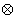 +1=
+1=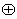 +2 (и вообще
+2 (и вообще 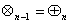 ).
Их
связывает класс функциональных уравнений типа Коши (название указывает на связь
различных арифметических операций)
).
Их
связывает класс функциональных уравнений типа Коши (название указывает на связь
различных арифметических операций)
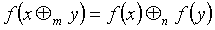
где m,n - целые числа.
Решения некоторых уравнений (с малыми индексами) таковы:
|
m
|
n
|
Решение
|
m
|
n
|
Решение
|
|
-1
|
-2
|
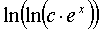
|
+1
|
-2
|
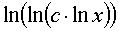
|
|
-1
|
-1
|
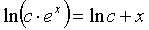
|
+1
|
-1
|
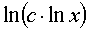
|
|
-1
|
0
|
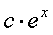
|
+1
|
0
|
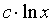
|
|
-1
|
+1
|
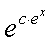
|
+1
|
+1
|
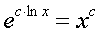
|
|
-1
|
+2
|
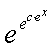
|
+1
|
+2
|
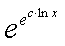
|
|
0
|
-2
|
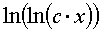
|
+2
|
-2
|
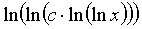
|
|
0
|
-1
|
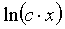
|
+2
|
-1
|
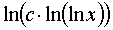
|
|
0
|
0
|
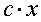
|
+2
|
0
|
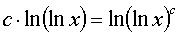
|
|
0
|
+1
|
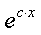
|
+2
|
+1
|
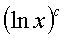
|
+2
|
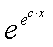
|
+2
|
+2
|
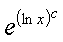
|
Наблюдающиеся
здесь закономерности справедливы в общем случае.[7]
Заключение
В данной дипломной работе, посвященной решению
некоторых функциональных уравнений на оси, был рассмотрен важнейший класс
уравнений - класс уравнений Коши.
Были
приведены некоторые методы решения функциональных уравнений, с помощью которых
впоследствии были решены важнейшие функциональные уравнения элементарной
математики,
f(x+у)
= f (x) + f (y),
f
(x + у) = f
(x) f
(y),
f
(xy) = f
(x) + (y),(xy)
= f (x) f (y),
показано,
что найденные решения могут служить для определения функции f(x)=Cx,
а также показательной, логарифмической, степенной функций.
Утверждения
были сформулированы в виде теорем для функций, определенных на Q,
функций непрерывных на R
и R+,
а также для любых измеримых функций. Все теоремы были доказаны и сделан вывод о
том что решения имеют один и тот же вид для функций, определенных на Q,
функций непрерывных на R
и R+,
а также для любых измеримых функций.
Были решены уравнения, определяющие функции
тригонометрический и гиперболический косинус. Также решено уравнение f′(x-y)-f′(x+y)=2λf(x)∙f(y),
решения которого имеют вид f(x)=-β
sh
λβx,
,
и f(x)=β
sin
λβx.
Было
приведено также важное обобщение свойств уравнений типа Коши и сделан вывод:
Список использованных источников
1. Энциклопедия элементарной
математики. Т.3. Под ред. П.С. Александрова, А.И. Маркушевича, А.Я. Хинчина.
Государственное издательство технико-теоретической литературы. М.: 1952.-560 с.
. Функциональные уравнения. Квант,
1985.-- № 7.
. Прасолов, В. В. Задачи по алгебре,
арифметике и анализу. М.: МЦНМО, 2005. - 545 с.
. Фихтенгольц, Г. М., Курс
дифференциального и интегрального исчисления. Т.1. М. : Наука, 1970.-616 с.
. Колмогоров, А. Н., Фомин, С. В.
Элементы теории функций и функционального анализа. М.: Физматлит, 2006. - 572
с.
. Сенета, Е. Правильно меняющиеся
функции. М. : Наука, 1985.-143 с.
. Блюмин, С. Л. Класс уравнений типа
Коши / Научный журнал "Фундаментальные исследования"// Российская
Академия Естествознания [Электронный ресурс]. - Электрон. журн. - 2008. - №2 -
Режим доступа: http://www.rae.ru
. Нечепуренко, М. И. Итерации
вещественных функций и функциональные уравнения. - Новосибирск: ИВМиМГ СО РАН,
1997.- 228 c.
9. Арнольд, И. В. Теоретическая
арифметика. - М.: ГУПИ, 1938. - 480 с.
10. Carroll, M. The Natural
Chain of Binary Arithmetic Operations and Generalized Derivatives
[arXiv.org/math.HO/0112050]