Математическое моделирование
МИНИСТЕРСТВО ВЫСШЕГО И СРЕДНЕГО
СПЕЦИАЛЬНОГО
ОБРАЗОВАНИЯ РЕСПУБЛИКИ УЗБЕКИСТАН
Кафедра «Информатика и математика»
КОНСПЕКТ ЛЕКЦИЙ
По дисциплине «математическое
моделирование»
для студентов направления
«Информатика и информационные технологии»
Составитель:
Сапаев. У
УРГЕНЧ-2008
АННОТАЦИЯ
В данном сборнике лекций представлены современные принципы, подходы и
методы моделирования сложно формализуемых объектов. Описаны задачи структурной
и параметрической идентификации. Рассмотрены практические задачи управления
сложными объектами. Для усвоения материалов лекций достаточно знания основ
высшей математики в объеме обычного курса ВТУЗа. Курс рассчитан для подготовки
бакалавров по направлению образования "Информатика и информационные технологии".
Курс рассчитан на 64 часов аудиторных занятий, из них:
32 асов - лекционных занятий;
16 часов - практических занятий;
часов - лабораторных занятий.
Лекция 1. ОБЩИЕ ВОПРОСЫ ТЕОРИИ
МОДЕЛИРОВАНИЯ (2 часа)
1.
Предмет теории моделирования
.
Роль и место моделирования в исследованиях систем
.
Классификация моделей
.
Моделирование в процессах познания и управления
.
Классификация объектов моделирования
.
Основные этапы моделирования
1. Предмет теории моделирования
Мысленные модели как форма теоретического осмысления и отражения
действительности играют большую роль в физическом познании. В этой связи важное
теоретико-познавательное и методологическое значения приобретает вопрос о
формировании моделей, использовании их в познании, возможности их включения в более
общие представления и их связи с другими формами познавательной деятельности,
мысленным и реальным экспериментами, гипотезой, теорией.
Модели, как научные гипотезы, мы можем рассматривать как форму развития
науки, неокончательно разработанные теории, согласно мнениям некоторых
представителей конкретных наук, можно рассматривать в качестве моделей будущих
совершенных теорий.
Представляется, что можно дать следующее рабочее определение мысленным и
материальным моделям.
Моделирование - это замещение одного объекта (оригинала) другим (моделью)
и фиксация или изучение свойств оригинала путем исследования свойств модели.
Замещение производится с целью упрощения, удешевления, ускорения фиксации или
изучения свойств оригинала.
В общем случае объектом-оригиналом может быть любая естественная или
искусственная, реальная или воображаемая система.
Метод моделирования применяется все большим числом ученых.
Примеры из механики, физики (твердого тела), химии, биологии, медицины,
экономии и др.
Концепция моделирования прежде всего преследует цель включения моделей в
процесс создания теорий, поскольку идеальные модели могут быть предварительной
ступенью в построении или моделью интерпретации теории.
Гипотезы отличаются от идеальных моделей, являющихся идеализированными объектами
теории, и могут быть представлены как предварительная ступень или модель
интерпретации теории, прежде всего благодаря своей функции в процессе познания
в качестве научно обоснованного предложения о до сих пор неизвестных и
недоступных явлениях. Гипотезы могут рассматриваться как предварительные
ступени формирующихся моделей.
При разработке исходной модели интуиция исследователя играет
большую роль. В начале может выдвигаться большое число моделей, однако в ходе
исследования их число сокращается.
Формой работы с моделью является мысленный эксперимент. Иногда он
называется идеализированным, что вскрывает тесную его связь с реальными
экспериментами и основное различие между ними. В известной мере мысленный
эксперимент представляет образное мысленное реконструирование определенных
сторон реального эксперимента «мышление есть не более чем продукт опыта в уме »
, -«мысленный опыт, безусловно удобнее, чем действительный опыт: мысли у нас
всегда имеются, и легче накопить опыт в уме, чем в действительности » [по
Энгельмайеру].
Эксперимент остается критерием адекватности отражения в модели
определенных сторон объекта оригинала. Эксперимент играет роль судьи, который
выносит решение, жить или не жить представлению, полученному с помощью модели.
Представление изучаемого явления, процесса или объекта с помощью
математических соотношений и формул называется математической моделью. При
моделировании объекта исследования дело начинается с формализации объекта, т.е.
с построения соответствующей математической модели. Для этого выделяются его
наиболее существенные черты и свойства и описываются с помощью математических
соотношений.
После того, как построена математическая модель, т.е. задача придана
математическая форма, мы можем воспользоваться для ее изучения математическими
методами.
Примеры математических моделей.
Рис.1. x2+y2=r2-уравнение (модель) окружности.
Рис.2 y=ax2-уравнение (модель) параболы.
Рис.3. 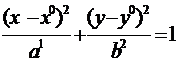 -
уравнение (модель) эллипса.
-
уравнение (модель) эллипса.
Задача
1. Необходимо определить площадь поверхности письменного стола.
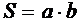
Это
означает, реальный объект (письменный стол) заменяется абстрактной
математической моделью прямоугольника. Прямоугольнику присваиваются размеры,
полученные в результате измерения, и площадь такого прямоугольника приближенно
принимается за искомую площадь.
Выбор
модели прямоугольника для поверхности стола мы обычно делаем, полагаясь на свое
зрительное восприятие. Однако, человеческий глаз как измерительный инструмент
не отличается высокой точностью. Поэтому при более серьезном подходе к задаче,
прежде чем воспользоваться моделью прямоугольника для определения площади, эту
модель, т.е. объект исследования, нужно проверить на предмет описания его
моделью прямоугольника. Для этого можно измерить противоположные стороны и обе
диагонали прямоугольника. Если они попарно равны, то поверхность стола
действительно можно рассматривать как прямоугольник. В противном случае от
модели прямоугольника надо отказаться, и следует перейти к модели
четырехугольника общего вида.
Моделирование
целесообразно, когда у модели отсутствуют те признаки оригинала, которые
препятствуют его исследованию, или имеются отличные от оригинала параметры,
способствующие фиксации или изучению свойств модели.
Теория
моделирования представляет собой взаимосвязанную совокупность положений,
определений, методов и средств создания и изучения моделей. Эти положения,
определения, методы и средства, как и сами модели, являются предметом теории
моделирования.
Основная
задача теории моделирования заключается в том, чтобы вооружить исследователей
технологией создания таких моделей, которые достаточно точно и полно фиксируют
интересующие свойства оригиналов, проще или быстрее поддаются исследованию и
допускают перенесение его результатов на оригиналы.
Теория
моделирования является основной составляющей общей теории систем -
системологии, где в качестве главного принципа постулируются осуществимые
модели: система представима конечным множеством моделей, каждая из которых
отражает определенную грань ее сущности.
В
данной книге в качестве объектов-оригиналов рассматриваются ВС, т. е. ВС составляют
предметную область моделирования. Понятие ВС здесь трактуется в широком
смысле-от однопроцессорных систем обработки данных до распределенных сетей ЭВМ
с различным программным обеспечением и функциональным назначением.
Поскольку
ВС - это искусственные, инженерные системы, все их параметры известны, по
крайней мере, они известны создателям ВС, а значит могут быть изучены, познаны
их исследователями. Это предопределяет принципиальную возможность моделирования
ВС.
2. Роль и место моделирования в исследованиях систем
Трудно переоценить роль моделирования в научных изысканиях, инженерном
творчестве и, вообще, в жизни человека. Познание любой системы сводится, по
существу, к созданию ее модели. Перед изготовлением каждого устройства или
сооружения разрабатывается его модель-проект. Любое произведение искусства
является моделью, фиксирующей действительность. Человек, прежде чем совершить
что-либо, обдумывает возможную последовательность действий или интуитивно
руководствуется определенными установившимися апробированными моделями
поведения.
Особую ценность имеют конструктивные модели, т. е. такие, которые
допускают не только фиксацию свойств, но и исследование зависимостей
характеристик от параметров системы. Такие модели позволяют оптимизировать
функционирование систем. Оптимизационные модели - основа теории сложных
систем.
Роль моделирования как метода научного познания и метода решения
технических задач всегда оценивалась достаточно высоко. С развитием техники
нашло широкое применение физическое моделирование сооружений, машин и
механизмов.
Достижения математики привели к распространению математического
моделирования различных объектов и процессов. Подмечено, что динамика
функционирования разных по физической природе систем описывается однотипными
зависимостями, т.е. может быть представлена одинаковыми моделями. Расчетные
формулы, которые используют инженеры для анализа и синтеза всевозможных систем,
зачастую выведены из математических моделей этих систем.
На качественно новую ступень поднялось моделирование в результате
разработки методологии имитационного моделирования. Это обусловлено тем,
что существенно расширился класс систем, которые могут быть исследованы с
помощью моделирования.
Появление вычислительных машин способствовало углублению и расширению сфер
применения моделирования. Особое значение приобретает моделирование в
современных условиях всемерного ускорения научно-технического прогресса, при
требованиях достижения больших эффектов с ограниченными материальными,
трудовыми, энергетическими и временными ресурсами.
Сейчас трудно указать область человеческой- деятельности, где не
применялось бы моделирование. Разработаны, например, модели производства
автомобилей, выращивания пшеницы, функционирования отдельных органов человека,
жизнедеятельности Азовского моря, последствий атомной войны. В перспективе для
каждой системы могут быть созданы свои модели, перед реализацией каждого
технического или организационного проекта. должно проводиться моделирование.
Специалисты считают, что моделирование становится основной функцией
вычислительных систем. Действительно, в настоящее время основные усилия
направлены на внедрение вычислительной техники в автоматизированные системы
управления технологическими процессами, организационно-экономическими
комплексами и процессами проектирования, для создания банков данных и знаний.
Но любая система управления нуждается в информации об управляемом объекте или
процессе. Поэтому справочные системы, банки данных и знаний следует
рассматривать как подспорье для управляющих систем. В свою очередь, любая
система управления нуждается в модели управляемого объекта или процесса, в
моделировании последствий тех или иных управляющих решений. В связи с этим
применение вычислительных систем для моделирования приобретает первостепенное
значение.
Сами ВС как сложные и дорогостоящие технические системы могут и должны
стать объектами моделирования. Моделирование целесообразно использовать на
этапе проектирования ВС, и для анализа функционирования действующих систем в
экстремальных условиях или при изменении их состава, структуры, способов
управления или рабочей нагрузки. Применение моделирования на этапе
проектирования позволяет анализировать варианты проектных решений, определять
работоспособность и производительность, выявлять дефицитные и малозагруженные
ресурсы, вычислять ожидаемые времена реакции и принимать решения по
рациональному изменению состава и структуры ВС или по способу организации
вычислительного процесса.
В том случае, когда не удается создать модель, допускающую использование
аналитических методов оптимизации, процесс разработки ВС принимает итерационный
характер. Предварительно выбранный вариант проектного решения анализируют путем
моделирования. Это дает возможность определить ожидаемые характеристики будущей
системы, выявить ее сильные и слабые стороны. Если характеристики не
удовлетворяют предъявляемым требованиям, по результатам анализа выполняют
корректировку проекта, затем снова проводят моделирование. Этот процесс
повторяется до достижения требуемого качества функционирования разрабатываемой
ВС.
При анализе действующих систем с помощью моделирования определяют границы
работоспособности системы, выполняют имитацию экстремальных условий, которые
могут возникнуть в процессе функционирования системы. Искусственное создание
таких условий на действующей системе затруднено и может привести к
катастрофическим последствиям, если система не справится со своими
функциональными обязанностями. Применение моделирования может быть полезным при
разработке стратегии развития ВС, ее усовершенствовании и образовании связей с
другими ВС при создании многомашинных комплексов и сетей ЭВМ, при изменении
количества, номенклатуры или частоты решаемых задач.
Целесообразнее использовать моделирование для действующих ВС, поскольку
можно опытным путем проверить адекватность модели и оригинала и более точно
определить те параметры системы и внешних воздействий на нее, которые служат
исходными данными для моделирования. Моделирование реальной ВС позволяет
выявить ее резервы и прогнозировать качество функционирования при любых
изменениях, поэтому полезно иметь модели всех развивающихся систем.
. Классификация моделей
Физические модели. В основу классификации положена степень абстрагирования
модели от оригинала. Предварительно все модели можно подразделить на две
группы: материальные (физические) и абстрактные (математические).
Физической моделью обычно называют систему, которая
эквивалентна или подобна оригиналу, либо у которой процесс функционирования
такой же, как у оригинала, и имеет ту же или другую физическую природу. Можно
выделить следующие виды физических моделей: натурные, квазинатурные, масштабные
и аналоговые.
Натурные модели - это реальные исследуемые системы. Их называют макетами и опытными
образцами. Натурные модели имеют полную адекватность с системой-оригиналом, что
обеспечивает высокую точность и достоверность результатов моделирования.
Процесс проектирования ВС завершается зачастую испытанием опытных образцов.
Квазинатурные модели представляют собой совокупность натурных
и математических моделей. Этот вид моделей используется в случаях, когда математическая модель
части системы не является удовлетворительной (например, модель
человека-оператора) или когда часть системы должна быть исследована во
взаимодействии с остальными частями, но их еще не существует, либо их включение
в модель затруднено или дорого. Примерами квазинатурных моделей могут служить
вычислительные полигоны, на которых отрабатывается программное обеспечение
различных систем, или реальные АСУ, исследуемые совместно с математическими
моделями соответствующих производств.
Масштабная модель - это система той же физической природы,
что и оригинал, но отличающаяся от него масштабами. Методологической основой масштабного
моделирования является теория подобия, которая предусматривает соблюдение
геометрического подобия оригинала и модели и соответствующих масштабов для их
параметров. При проектировании ВС масштабные модели могут использоваться для
анализа вариантов компоновочных решений по конструкции системы и ее элементов.
Аналоговыми моделями называются системы, имеющие физическую
природу, отличающуюся от оригинала, но сходные с оригиналом процессы
функционирования. Обязательным
условием при этом является однозначное соответствие между параметрами
изучаемого объекта и его модели, а также тождественность безразмерных
математических описаний процессов, протекающих в них. Для создания аналоговой
модели требуется наличие математического описания изучаемой системы.
В качестве аналоговых моделей используются механические, гидравлические,
пневматические системы, но наиболее широкое применение получили электрические и
электронные аналоговые модели, в которых сила тока или напряжение являются
аналогами физических величин другой природы. Особенностью аналоговых моделей
является их гибкость и простота адаптации к изменению и измерению
количественных значений параметров и характеристик моделируемой системы.
Аналоговые модели используют при исследовании средств вычислительной
техники на уровне логических элементов и электрических цепей, а также на
системном уровне, когда функционирование системы описывается, например,
дифференциальными или алгебраическими уравнениями.
Математические модели. Математическая модель представляет собой формализованное
описание системы с помощью абстрактного языка, в частности с помощью
математических соотношений, отражающих процесс функционирования системы. Для
составления модели можно использовать любые математические средства -
алгебраическое, дифференциальное и интегральное исчисление, теорию множеств,
теорию алгоритмов и т. д. По существу вся математика создана для составления и
исследования моделей объектов или процессов.
К средствам абстрактного описания систем относятся также
языки химических формул, схем, чертежей, карт, диаграмм и т. п. Выбор вида модели определяется особенностями
изучаемой системы и целями моделирования, так как исследование модели позволяет
получить ответы на определенную группу вопросов. Для получения другой
информации может потребоваться модель другого вида.
Цели моделирования и характерные черты оригинала определяют в конечном
счете ряд других особенностей моделей и методы их исследования. Например,
математические модели можно классифицировать на детерминированные и
вероятностные (стохастические). Первые устанавливают однозначное соответствие
между параметрами и характеристиками модели, а вторые - между статистическими
значениями этих величин. Выбор того или иного вида модели обусловлен степенью
необходимости учета случайных факторов. Среди математических моделей можно
выделить по методу их исследования аналитические, численные и имитационные
модели.
Аналитической моделью называется такое формализованное
описание системы, которое позволяет получить решение уравнения в явном виде,
используя известный математический аппарат.
Численная модель характеризуется зависимостью такого вида,
который допускает только частные численные решения для конкретных начальных
условий и количественных параметров модели.
Имитационная модель - это совокупность описания системы и
внешних воздействий, алгоритмов функционирования системы или правил изменения
состояния системы под влиянием внешних и внутренних возмущений. Эти алгоритмы и правила не дают
возможности использования имеющихся математических методов аналитического и
численного решения, но позволяют имитировать процесс функционирования системы и
производить измерения интересующих характеристик.
Имитационные модели могут быть созданы для гораздо более широкого класса
объектов и процессов, чем аналитические и численные модели. Поскольку для
реализации имитационных моделей используются, как правило, ВС, средствами
формализованного описания имитационных моделей служат зачастую универсальные
или специальные алгоритмические языки. Имитационные модели в наибольшей степени
подходят для исследования ВС на системном уровне.
. Моделирование в процессах познания и управления
С проблемой моделирования мы сталкиваемся в двух случаях: во-первых, в
процессах познания, когда стараются познавательные модели объектов и явлений, с
которыми приходится сталкиваться человеку, и во-вторых, в процессах управления,
связанных с целенаправленным изменением объекта, т.е. с достижением целей,
поставленных человеком.
Рассмотрим оба типа моделирования подробнее.
В процессах познания создается познавательная модель объекта,
отображающая в необходимой мере механизм его функционирования. Примером такого
рода моделирования является изучение окружающей нас природы. Объяснение
феноменов природы, их взаимная увязка и обусловленность, анализ механизмов и
т.д. - вот основные задачи моделирования этого рода. Такое моделирование по
сути дела мало чем отличается от познания вообще, целью которого, как известно,
является синтез моделей; отражающих важную для человека специфику объектов
окружающего его мира. Эта специфика отражается в своеобразии причинно-
следственных связей каждого объекта или явления, которые удобно представить в
виде некоторого «преобразователя» причины в следствие (рис 4.)
Рис 1. Представление объекта познания.
Описание «работы» такого преобразователя на каком-либо языке мы будем
подразумевать моделью.
Таким образом под моделью мы будем подразумевать рассуждения (на любом
языке - математическом, графическом, алгоритмическом, разговорном и т.д.),
позволяющие имитировать наблюдаемое явления. Очевидно, что конкретные цели
конкретизируют и язык на котором описывается модель. Так, языком большого числа
физических и технических моделей является математика.
Формализуем сказанное. Будем обозначать причину буквой Х, а следствие-Y. Связь между ними запишем условно в
виде
Y=F(X),
где F-правило преобразования причины Х в
следствие Y. Это и есть модель. Назовем F оператором модели.
На рис.5 показано взаимодействие моделируемого объекта со средой.
Рис.5. Взаимодействие объекта со средой.
Это взаимодействие происходит по каналом Х иY. По каналу Х среда воздействует на объект, а по какому Y объект воздействует на среду.
Задача моделирования сводится к определению оператора F, связывающего вход и выход объекта.
Пусть x1,x2, ... ,xN - наблюдения входа объекта, y1,y2, ... yN -соответствующие им наблюдения его
выхода в дискретные моменты времени 1,2, ... , N эти наблюдения связаны неизвестным оператором объекта F0 , т.е.
Yi=F0(xi) (i=1,2,...,N)
задача моделирования заключается в построении (синтезе) модельного
оператора F, т.е. в получении оценки F0 по наблюдениям хi и yi. Естественно потребовать, чтобы F был близок к F0 в смысле некоторого критерия, т.е. F~F0.
Существенной особенностью познавательных моделей является отражения
механизма объекта или явления в структуре оператора F, т.е. всех причинно - следственных связей, имеющихся у
объекта и выявленных в процессе моделирования. При не учете этих связей
познавательная сторона модели существенно пострадала бы, так как для познания
необходимо представлять не только как, но и почему это происходит. Мы эти вопросы
не будем затрагивать.
Другой тип моделирования, который мы будем изучать связан непосредственно с
потребностями управления объектом и по отношению к управлению имеет
вспомогательный характер. Действительно, чтобы управлять, нужно прежде всего
знать, чем управляешь, т.е. иметь модель объекта, на которой можно
«разыгрывать» последствия предполагаемого управления и выбрать наилучшее.
Поэтому в процессе моделирования такого рода должна быть создана модель,
которая прежде всего обязана удовлетворять потребностям управления.
Следует отметить, что такая модель, синтезированная специально для
потребностей управления, может и не отражать внутренних механизмов явления, что
совершенно необходимо для познавательной модели. Ей достаточно лишь
констатировать наличие определенной формальной связи между входом и выходом
объекта.
В связи с этим целесообразно выяснить, что следует подразумевать под
понятием «управление» и какие требования оно накладывает на модель управляемого
объекта, получаемую в процессе моделирования.
Под управлением будем понимать процесс такого
целенаправленного воздействия на объект, в результате которого объект
оказывается в определенном смысле «ближе» к выполнению поставленных целей , чем
до управления. На
рис.6. показана общая схема управления объектом.
Здесь Х - неуправляемая, но контролируемая составляющая;
U-управляемая составляющая; Y-информация о состоянии объекта, доступная управляющему устройству.
Для синтеза управления необходимо прежде всего определить цель Z, т.е. то, к чему должно «стремиться
» управляющее устройство при воздействии на объект, каким должен быть объект с
точки зрения управления. Однако, этого мало, необходимого еще иметь алгоритм
управления А, который указывает, как достигнуть этой цели.
Таким образом управление реализуется четверкой
<U,I=<X,Y>,A,Z>,
где U-управляющее воздействие; I=<X,Y> - информация о состоянии среды и объекта; А-
алгоритм; Z-цель управления.
Цель Z определяет требования, выполнение
которых обеспечивается и организацией управляющего воздействия U с помощью алгоритма А и
сбором информации по каналу Y.
Не зная, как X
и U влияют на состояние Y, т.е. не имея модели Y=F(X,U), нельзя определить управление U, достаточно лишь констатировать
наличие определенной формальной связи.
5. Классификация объектов моделирования
Задача моделирования, как задача построения оператора модели, отражающего
качественные и количественные стороны объекта, может быть сформулирована и
соответственно решаться по схеме, приведенной на рис 7. Исторически эти подходы
возникли независимо друг от друга и в связи с решением различных задач.
Классификационных задач, породивших эти методы, удобно произвести на основе
понятий динамического и статического объектов.
Рис. 7. Классификация объектов моделирования.
Первыми и простейшими объектами, которые были подвергнуты процедуре
модулирования, оказались статические детерминированные (не стохастические)
объекты, т.е. регулярные функции, связывающие вход и выход объекта. Это
обстоятельство и породило первый подход в теории моделирования, который
известен в математическом анализе в виде теории приближения функций
многочленами и ведет свое начало от работ П.Л. Чебышева. Это направление
связано с представлением функции в виде разложения по некоторой системе функций
(чаще всего по системе полиномов). В этой теории известны два направления -
теория аппроксимации и теория интерполяции. Для идентификации стохастических
объектов используются методы математической статистики. В этом направлении
известны две теории - теория оценивания и планирования эксперимента. Основной
задачей теории оценивания является оценка неизвестных параметров статического
объекта по наблюдениям в обстановке помех и случайных возмущений. В теории
планирования экспериментов рассматриваются активные эксперименты в целях
определения неизвестных параметров стохастического объекта.
Третьим подходом моделирования динамических объектов являются методы
теории систем автоматического управления. В этой теории разработаны специальные
методы моделирования динамических объектов управления в режиме нормальной
эксплуатации, т.е. в обстановке помех и случайных возмущений.
. Основные этапы моделирования
Для моделирования необходимо создать модель и провести ее исследование.
Перед созданием модели требуется конкретизировать цели моделирования. После
исследования надо выполнить анализ результатов моделирования. Процесс
создания модели проходит несколько стадий. Он начинается с изучения объекта и
внешних воздействий и завершается разработкой или выбором математической модели
или программы для ВС, если моделирование будет проводиться с ее помощью.
Некоторые математические модели могут быть исследованы без применения средств
вычислительной техники, но в дальнейшем, как правило, рассматриваются такие
модели, исследование которых надо проводить с помощью ВС. Таким образом,
моделирование на ВС предполагает наличие следующих укрупненных этапов:
формулировка целей, изучение объекта, описательное моделирование,
математическое моделирование, выбор (или создание) метода решения задачи, выбор
или написание программы для решения задачи на ЭВМ, решение задачи на ЭВМ,
анализ получаемого решения.
Этапы моделирования объектов (процессов, явлений)
1. Формулировка целей. В основе всякой задачи, проблемы
моделирования лежит информация о том, чего собственно добывается, что хочет
субъект от объекта, т.е. каковы его цели {Z}. Именно эта информация определяет объект. Существует
своеобразный парадокс: цель определяется объектом, а объект целью. Этот
парадокс разрешается довольно просто. Субъект, формулируя цель, всегда имеет
какие-то представления об объекте. Эти представления могут быть очень
приближенными, но всегда отражают некоторые его свойства, достаточные для
эффективной формулировки целей моделирования. Обычно в задачах моделирования
цель достигается путем максимизации или минимизации некоторого критерия,
задаваемого в виде целевой функции.
2. Изучение объекта. При этом требуется понять
происходящий процесс, определить границы объекта с окружающей его средой, если
таковые имеются. Кроме того, на данном этапе определяются перечень всех входных
и выходных параметров объекта исследования и их влияние на достижение целей
моделирования.
3. Описательное моделирование - установление и словесная фиксация
основных связей входных и выходных параметров объекта.
4. Математическое моделирование - перевод описательной модели на
формальный математический язык. Цель записывается в виде функции, которую
обычно называют целевой. Поведение объекта описывается с помощью соотношений,
входные и выходные параметры объекта на данном этапе в зависимости от сложности
исследуемой проблемы могут возникать ряд задач чисто математического характера.
Такими задачами являются задачи математического программирования, линейной
алгебры, задачи дифференциального и интегрального исчисления и многие другие.
5. Выбор (или создание) метода решения
задачи. На данном
этапе для возникшей математической задачи подберется подходящий метод. При
выборе такого метода необходимо будет обратить внимание на сложность метода и
потребляемые вычислительные ресурсы. Если подходящего метода по предъявленным
критериям не окажется, то требуется разработать новый метод решения задачи. Мы
делаем упор на разработку новых эффективных методов, не уступающих известным
методам по основным вычислительным характеристикам.
6. Выбор или написание программы для
решения задачи на ЭВМ. На данном этапе выбирается подходящая программа, реализующая выбранный
метод решения. Если такая программа отсутствует, то необходимо написать такую
программу.
7. Решение задачи на ЭВМ. Вся необходимая информация для
решения задачи вводится в память ЭВМ вместе с программой. С использованием
подходящей программы производится обработка целевой информации и получение
результатов решения задач в удобной форме.
8. Анализ получаемого решения. Анализ решения бывают двух видов:
формальный (математический), когда проверяется соответствие полученного решения
построенной математической модели (в случае несоответствия проверяется
программа, исходные данные, работа ЭВМ и др.) и содержательный (экономический,
технологический и т.п.), когда проверяется соответствие полученного решения
тому объекту, который моделировался. В результате такого анализа в модель могут
быть внесены изменения или уточнения, после чего весь рассмотренный процесс
повторяется. Модель считается построенной и завершенной, если она с достаточной
точностью характеризует деятельность объекта по выбранному критерию. Только
после этого модель можно использовать при расчетах.
Перечисленные этапы вытекают из общей методологии моделирования систем.
При моделировании различных систем трудоемкости одних и тех же этапов могут
быть разными. В процессе моделирования конкретной системы могут иметь место
некоторые изменения технологии. В частности, может быть заранее предопределен
метод моделирования или выбрано конкретное средство моделирования.
Математическая модель окажется настолько простой, что не потребуется проведения
машинных экспериментов, разработка программной модели исключит необходимость
создания математической модели.
Следует обратить внимание на первоочередную необходимость постановки,
формулирования цели моделирования. В этом вопросе должно быть достигнуто
взаимопонимание между заказчиком, ответственным за создание или модернизацию
системы, и разработчиком модели. Важность корректного выполнения этого этапа
определяется тем, что все последующие этапы проводятся с ориентацией на
определенную цель моделирования.
На этом же этапе конкретизируется, в каких единицах измерения
(относительных или абсолютных) должны быть представлены результаты моделирования.
Под относительными единицами здесь понимаются качественные градации,
сравнительные оценки разных вариантов системы (типа «лучше-хуже», «больше-
меньше»). При необходимости представления результатов в абсолютных единицах
должен быть решен вопрос о точности измерения. Этот вопрос зачастую не имеет
однозначного ответа, но крайне важен для выполнения всех этапов моделирования.
Проверка адекватности указана выше в виде одного из этапов моделирования.
Не надо это понимать буквально, так как на адекватность модели оказывает
влияние качество выполнения практически всех этапов. Поэтому проверка
адекватности должна проводиться в том или ином виде, начиная от разработки
концептуальной модели и кончая анализом результатов моделирования.
Под разработкой математической модели подразумевается создание полностью
формализованного описания динамики функционирования системы. Однако не для всех
систем, внешних условий и целей моделирования может быть подобран известный
метод формализации или конструктивный математический аппарат. Тем не менее и
для таких систем следует разработать однозначные зависимости выходных
характеристик от параметров и воздействий для каждой составляющей системы,
алгоритмы взаимодействия между составляющими, логические условия изменения состояний.
Результаты машинного моделирования должны быть проанализированы с целью
проверки их достоверности и выработки рекомендаций о способах повышения
качества исследуемой системы. На всех этапах моделирования следует обратить
особое внимание на документирование принимаемых решений, допущений, ограничений
и выводов.
Из организационных аспектов моделирования следует выделить необходимость
непосредственного участия в работе квалифицированных представителей заказчика
на первых этапах (вплоть до разработки математической модели) и на этапе
анализа результатов моделирования. Ответственный за систему заказчик должен
четко понимать цели моделирования, разработанную концептуальную модель,
программу исследований и полученные результаты. Это будет способствовать внедрению
выработанных рекомендаций.
Контрольные вопросы
. В чем заключается сущность моделирования?
. Роль и место моделирования в процессах познания.
. Какие разновидности моделей используются в исследованиях систем?
. Классификация моделей.
. Определение модели.
. Определение математической модели.
. Роль моделирования в задачах управления.
. Классификация объектов моделирования.
. Основные этапы моделирования объектов (процессов, явлений).
Литература
1. Альянах И.Н. Моделирование вычислительных систем, Л.:
Машиностроение, 1988 г. - 223 стр.
2. Растригин Л.А. Современные принципы управления
сложными объектами , М.: Советское радио, 1980 г. - 232 стр.
3. Растригин Л.А., Маджаров Н.Е. Введение в идентификацию объектов
управления, М.: Энергия, 1977 г. - 216 стр.
Лекция 2. ТЕХНОЛОГИЯ МОДЕЛИРОВАНИЯ (2 часа)
План
1.
Создание концептуальной модели
.
Подготовка исходных данных
.
Разработка математической модели
.
Выбор метода моделирования
1. Создание концептуальной модели
Определение и ориентация. В процессе разработки модели можно условно выделить
такие этапы описания, как концептуальный, математический и программный. На этих
этапах создается соответствующая модель.
Концептуальная (содержательная) модель - это абстрактная модель,
определяющая состав и структуру системы So, свойства элементов и причинно-следственные связи,
присущие исследуемой системе и существенные для достижения цели моделирования.
В концептуальной модели обычно в словесной форме приводятся сведения о природе
и параметрах элементарных явлений исследуемой системы, о виде и степени
взаимодействия между ними, о месте и значении каждого элементарного явления в
общем процессе функционирования системы.
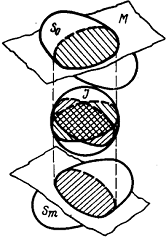
Рис. 1. Отображение оригинала So и модели Sm в сознании исследователя
Первоначально концептуальная модель системы So возникает в сознании исследователя j (рис. 1). Модель ориентируется на
выявление определенных свойств системы в соответствии с целями моделирования.
Для этого исследователь делает как бы мысленный срез системы в «плоскости» той
метасистемы М, в качестве элемента которой представляет интерес система So, т. е. выполняет M-ориентацию. Затем исследователь выявляет основные признаки
ориентированной модели и может добавить некоторые признаки и условия, которые
облегчат исследование модели или позволят представить ее в виде некоторого
среза моделирующей системы Sm. Концептуальная модель - это субстрат системы с позиций достижения целей
моделирования.
Разработка концептуальной модели требует достаточно глубоких знаний
системы So, так как надо обосновать не только
то, что должно войти в модель, но и то, что может быть отброшено без
существенных искажений результатов моделирования. Последнее является наиболее
проблематичным, поскольку возникает замкнутый круг: для точного определения
влияния исключения какого-либо элемента или явления из модели на степень
искажения результатов необходимо создать и исследовать две модели - с учетом и
без учета этого элемента или явления. Выполнить это по каждому сомнительному
элементу и явлению не представляется возможным в связи со значительным
увеличением объема работ.
Основная проблема при создании модели заключается в нахождении
компромисса между простотой модели и ее адекватностью с исследуемой системой.
Имеются теоретические проработки решения данной проблемы, но практически их
трудно реализовать. Поэтому разработчик модели, руководствуясь своими знаниями
системы, оценочными расчетами, опытом, должен принять решение об исключении
какого-то элемента или явления из модели без достаточно полной уверенности в
том, что это не внесет существенных погрешностей в результаты моделирования.
Процесс создания концептуальной модели, очевидно, никогда не может быть
полностью формализован. Именно в связи с этим иногда говорят, что моделирование
является не только наукой, но и искусством. При создании ориентированной модели
уточняются множества полезных и возмущающих внешних воздействий.
Стратификация. Следующим шагом на пути создания концептуальной модели
служит выбор уровня детализации модели (рис. 2).
Рис. 2. Уровни модели
Известно, что любая система, в том числе и вычислительная, - это прежде
всего целостная совокупность элементов. Непременным свойством каждой системы
является ее членимость. Модель системы представляется в виде совокупности
частей (подсистем, элементов) (рис. 2). В эту совокупность включаются все
части, которые обеспечивают сохранение целостности системы. Исключение
каких-либо элементов из модели не должно приводить к потере основных свойств
системы при выполнении функций по отношению к метасистеме.
С другой стороны, каждая часть системы тоже состоит из совокупности
элементов, которые, в свою очередь, могут быть расчленены на элементы. С учетом
этого проблема выбора уровня детализации может быть разрешена путем построения
иерархической последовательности моделей. Система представляется семейством
моделей, каждая из которых отображает ее поведение на различных уровнях
детализации (рис. 2). На каждом уровне существуют характерные особенности
системы, переменные, принципы и зависимости, с помощью которых описывается
поведение системы.
Уровни детализации иногда называются стратами, а процесс выделения
уровней-стратификацией. Выбор страт зависит от целей моделирования и степени
предварительного знания свойств элементов. Для одной и той же системы могут
быть использованы различные страты. Обычно в модель включаются элементы одного
уровня детализации - K-страта.
Однако может представлять интерес построение модели из элементов разных страт.
В том случае, когда общесистемные (функциональные) свойства отдельных элементов
мало известны или вызывает затруднение их описание, можно для каждого такого
элемента включить в модель его детализированное описание из нижестоящего (К
- 1)-страта. Некоторые элементы и этого уровня можно расчленить, т. е.
использовать их описание из следующего уровня - (К - 2)-страта.
При построении ориентированной и стратифицированной концептуальной модели
необходимо руководствоваться следующим. В модель должны войти все те параметры
системы Sok и, в первую очередь, параметры {soj}, допускающие варьирование в
процессе моделирования, которые обеспечивают определение интересующих
исследователя характеристик Yok при конкретных внешних воздействиях {xon} на заданном временном интервале Т
функционирования системы. Остальные параметры должны быть, по возможности,
исключены из модели.
Детализация. При расчленении системы на элементы можно поступать
следующим образом. Функционирование любой системы представляет собой выполнение
одного или нескольких технологических процессов преобразования вещества,
энергии или информации. Каждый процесс складывается из последовательности
элементарных операций. Выполнение каждой элементарной операции обеспечивается
определенным ресурсом - элементом. Поэтому в модели должны присутствовать все
элементы, которые реализуют выполнение всех технологических процессов. Кроме
них в модель могут быть включены элементы, которые служат для управления
ресурсами и процессами и для хранения объектов преобразования в промежутках
времени между выполнением элементарных операций, а также для хранения
информации, необходимой для управления. Применение этого правила требует
предварительного определения понятия элементарной операции.
Детализация системы должна производиться до такого уровня, чтобы для
каждого элемента были известны или могли бы быть получены зависимости
параметров выходных воздействий элемента, существенных для функционирования
системы и определения ее выходных характеристик, от параметров воздействий,
которые являются входными для этого элемента.
Если по результатам ориентации, стратификации и расчленения получается
модель большой размерности, т. е. с большим числом параметров, в частности, с
большим числом элементов (несколько сотен или даже тысяч), то ее следует
упростить, поскольку с громоздкой моделью работать неудобно. Это можно сделать
разными способами изоморфных преобразований модели без снижения степени
адекватности, в том числе путем декомпозиции системы на подсистемы, интеграции
элементарных операций и соответствующей интеграции элементов, исключения или
усечения второстепенных технологических процессов с исключением обеспечивающих
эти процессы элементов.
Локализация. Последующий шаг создания концептуальной модели - ее
локализация, которая осуществляется путем представления внешней среды в виде
генераторов внешних воздействий, включаемых в состав модели в качестве
элементов. При необходимости они дифференцируются на генераторы рабочей
нагрузки, поставляющие на вход системы основные исходные объекты - вещество
(сырье, полуфабрикаты, комплектующие), энергию для энергетических систем или
данные для информационных систем, в том числе для ВС; генераторы дополнительных
обеспечивающих объектов и энергии; генераторы управляющих и возмущающих
воздействий. Генераторы возмущающих воздействий нарушают процесс
функционирования системы (рис.3).
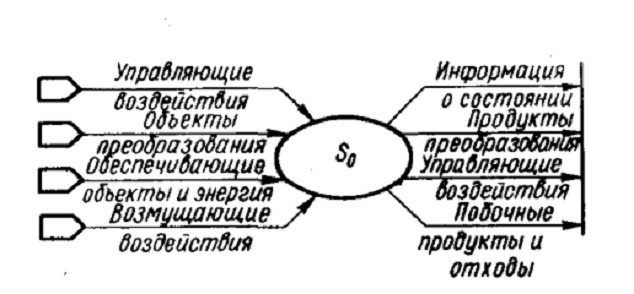
Приемники выходных воздействий системы обычно не включают в модель.
Считается, что результаты функционирования системы,
Рис. 3. Локализованная модель
включая основные продукты преобразования, побочные продукты и отходы,
информацию о состоянии системы и управляющие воздействия на другие системы,
внешняя среда потребляет (принимает) полностью и без задержек.
Структуризация. Управление. Завершается построение структуры модели указанием
связей между элементами. Связи могут быть подразделены на вещественные
и информационные. Вещественные связи отражают возможные пути перемещения
продукта преобразования от одного элемента к другому. Информационные связи
обеспечивают передачу между элементами управляющих воздействий и информации о
состоянии. Отметим, что как информационные, так и вещественные связи не
обязательно должны быть представлены в системе некоторым материальным каналом
связи. В простых системах, составленных из одно-функциональных элементов,
имеющих не более чем по одной выходной вещественной связи, информационные связи
могут вообще отсутствовать. Управление процессом функционирования в таких
системах определяется самой структурой, т. е. в них реализован принцип
структурного управления. Примерами таких систем могут служить логические
элементы и аналоговые вычислительные машины.
В более сложных системах, включающих многофункциональные элементы или
элементы, которые имеют больше чем по одной выходной вещественной связи,
имеются управляющие средства (решающие элементы) и соответствующие
информационные связи. Управление требуется для указания, какому элементу какой
исходный объект когда и откуда взять, какую операцию по преобразованию
выполнить и куда передать. О таких системах можно говорить, что они
функционируют в соответствии с программным или алгоритмическим принципом
управления. В концептуальной модели должны быть конкретизированы все решающие
правила или алгоритмы управления рабочей нагрузкой, элементами и процессами.
Выделение процессов. Рассмотренные выше действия направлены на создание модели,
отражающей статику системы - состав и структуру. Поскольку основной интерес
представляют динамические системы, следует дополнить эту модель описанием
работы системы.
Функционирование системы заключается в выполнении технологического
процесса преобразования вещества, энергии или информации. В сложных системах
зачастую одновременно протекает несколько технологических процессов. В
частности, все современные универсальные ВС рассчитаны на мультипрограммный
режим работы. Технологический процесс представляет собой определенную
последовательность отдельных элементарных операций. Часть операций может
выполняться параллельно разными элементами (ресурсами) системы. Задается технологический
процесс маршрутной картой, путевым листом, программой и т. п., другими словами
- одним из видов изображения алгоритма.
Алгоритм однозначно определяет, какие ресурсы системы, в какой
последовательности и какие операции должны выполнить для достижения некоторого
целевого назначения системы. В системах с программным принципом управления,
обеспечивающих параллельное выполнение нескольких технологических процессов,
имеются алгоритмы управления совокупностью процессов. Их основное назначение
заключается в разрешении конфликтных ситуаций, возникающих, когда два или более
процесса претендуют на один и тот же ресурс. Совокупность алгоритмов управления
А0 совместно с параметрами входных воздействий Х0
и элементов S0 отражают динамику функционирования системы.
Обычно алгоритмы преобразовываются к виду Am, удобному для моделирования. Данный
подход к описанию динамики работы системы особенно удобен для имитационного
моделирования и является естественным способом определения множества
характеристик системы:
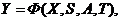 (1)
(1)
где Ф - множество операторов вычисления выходных характеристик (здесь и в
дальнейшем индексы о, т,k множеств, указывающие на интересующие (k) элементы оригинала (о) и модели (т), опущены в целях упрощения
записи).
Отражение
состояний. В ряде случаев, в
частности для систем со структурным принципом управления, получил
распространение другой подход. Для каждого элемента выбирается определенный
параметр s (иногда несколько параметров), значение которого
изменяется в ходе функционирования элемента и отражает его состояние в текущий
момент времени z(t). Множество
таких параметров по всем п =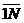 элементам системы {zn} отражает состояние системы Z (t). Функционирование системы представляется в виде
последовательной смены состояний: Z(t0), Z(t1) .... Z(Т).
Множество {Z} возможных
состояний системы называют пространством состояний. Текущее состояние системы в
момент времени t(
элементам системы {zn} отражает состояние системы Z (t). Функционирование системы представляется в виде
последовательной смены состояний: Z(t0), Z(t1) .... Z(Т).
Множество {Z} возможных
состояний системы называют пространством состояний. Текущее состояние системы в
момент времени t(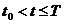 ) отражается в виде координаты точки в n-мерном
пространстве состояний, а вся реализация процесса функционирования системы за
время Т - в виде некоторой траектории.
) отражается в виде координаты точки в n-мерном
пространстве состояний, а вся реализация процесса функционирования системы за
время Т - в виде некоторой траектории.
Если
известно начальное состояние системы Z°= Z (t0), то можно
определить ее состояние в любой момент t, принадлежащий интервалу Т, когда известна
зависимость
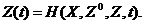 (2)
(2)
Тогда выходные характеристики определятся по формуле
V =G(Z, Т}. (3)
Созданная концептуальная модель должна быть проверена на адекватность
исследуемому объекту. Поскольку на данном этапе возможен только умозрительный
анализ и эксперимент, желательно, чтобы такую проверку выполняли эксперты, а не
разработчик модели.
2. Подготовка исходных данных
Сбор фактических данных. При создании концептуальной модели выявляются
качественные (функциональные) и количественные параметры объекта и внешних
воздействий X. Для количественных параметров необходимо определить их конкретные
значения, которые будут использованы в виде исходных данных при моделировании.
Это трудоемкий и ответственный этап работы. Он существенно влияет на успех
моделирования. Очевидно, что достоверность результатов моделирования однозначно
зависит от точности и полноты исходных данных.
На ранней стадии создания концептуальной модели зачастую выявляется часть
параметров, которые определенно войдут в модель. По этим параметрам сбор
исходных данных можно вести параллельно с разработкой концептуальной модели. По
мере уточнения концептуальной модели определяются остальные параметры. Сбор
исходных данных осложняется по следующим причинам. Во-первых, значения
параметров могут быть не только детерминированными, но и стохастическими.
Во-вторых, не все параметры оказываются стационарными. Особенно это относится к
параметрам внешних воздействий. В-третьих, всегда идет речь о моделировании
несуществующей (проектируемой, модернизируемой) системы или системы, которая
должна функционировать в новых условиях.
Большая часть параметров - это случайные величины по своей природе.
Однако в целях упрощения модели часто многие из них представляются
детерминированными средними значениями. Это можно делать, если случайная
величина имеет небольшой разброс, или в случае, когда для достижения цели
моделирования достаточно вести расчет по средним значениям. Например,
производительность процессора может быть задана определенным количеством
операций, выполняемых в единицу времени. Но это количество детерминировано
только для определенной смеси операций, которые может выполнять процессор.
Подмена в расчетах случайных значений параметров детерминированными величинами
должна производиться обдуманно, так как она может привести к погрешностям
моделирования. Под воздействием случайных факторов результаты функционирования
системы не только подвергаются рассеиванию, но могут также получить смещение
своих средних значений.
При создании модели может иметь место и обратное явление -
детерминированные параметры представляются случайной величиной. Делается это
при интеграции элементов системы или внешних воздействий с целью сокращения
размерности модели. Например, при выполнении программы ВС обрабатывается вполне
определенное количество данных. При следующем выполнении этой программы может
обрабатываться другое, но тоже определенное количество данных. Для
моделирования многократного выполнения программы можно задать всю совокупность
количеств данных или подменить это множество значений случайной величиной с
определенным законом распределения.
Подбор закона распределения. Для случайных параметров
организуется сбор статистики и последующая ее обработка. В процессе обработки
выявляется возможность представления параметра некоторым теоретическим законом
распределения. Это необходимо в связи с тем, что при определенных законах
распределения основных параметров системы и нагрузки появляется возможность
создания аналитической модели, а при имитационном моделировании может оказаться
проще задать вид закона распределения и основные статистические характеристики,
чем представлять случайную величину, например, в виде таблицы.
Процедура подбора вида закона распределения заключается в следующем. По
совокупности численных значений параметра строится гистограмма относительных
частот - эмпирическая плотность распределения. Гистограмма аппроксимируется
плавной кривой. Полученная кривая последовательно сравнивается с кривыми
плотности распределения различных теоретических законов распределения.
Выбирается один из законов по наилучшему совпадению вида сравниваемых кривых.
По эмпирическим значениям вычисляют параметры этого распределения. Затем
выполняют количественную оценку степени совпадения эмпирического и
теоретического распределения по тому или другому критерию согласия, например,
Пирсона (хи-квадрат), Колмогорова, Смирнова, Фишера или Стьюдента. Вопросы
подбора вида закона распределения детально разработаны в математической
статистике.
Особую сложность представляет сбор данных по случайным параметрам,
которые являются функциями времени. В первую очередь такие параметры характерны
для внешних воздействий. Пренебрежение фактами нестационарности параметров,
которое зачастую имеет место в практике моделирования, приводит к существенным
нарушениям адекватности модели.
Аппроксимация функций. Для каждого элемента системы существует функциональная связь
между параметрами входных воздействий на этот элемент и его выходными
характеристиками. Вид функциональной зависимости для одних элементов бывает
очевиден, для других может быть легко выявлен исходя из природы
функционирования. Однако для некоторых элементов может быть получена только
совокупность экспериментальных данных о количественных значениях выходных
характеристик при различных значениях параметров. В этом случае возникает
необходимость ввести некоторую гипотезу о характере функциональной зависимости,
т. е. аппроксимировать ее определенным математическим уравнением. Поиск
математических зависимостей между двумя или более переменными по собранным
опытным данным- может выполняться с помощью методов регрессионного,
корреляционного или дисперсионного анализа.
Предварительно для описания определенного элемента вид уравнения задает
исследователь. При двух переменных это делается достаточно просто по
результатам сравнения графика, на который нанесены экспериментальные точки, с
графиками наиболее распространенных аппроксимирующих функций, таких как прямая,
парабола, гипербола, экспонента и т. д. Затем методами регрессионного анализа
вычисляются константы выбранного уравнения таким образом, чтобы обеспечить
наилучшее приближение кривой к экспериментальным данным независимо от того,
насколько хорошо выбран вид кривой. Зачастую приближение оценивается по
критерию наименьших квадратов.
Для выяснения того, насколько точно выбранная зависимость согласуется с
опытными данными, используется корреляционный анализ. Коэффициент корреляции
лежит в пределах от 0 до ±1, что соответствует изменению степени согласования
от полного отсутствия корреляции до случая, когда все экспериментальные точки
лежат точно на кривой.
Выдвижение гипотез. По части параметров, которые отражают новые
элементы будущей системы или новые условия функционирования, отсутствует
возможность сбора фактических данных. Для таких параметров выдвигаются гипотезы
об их возможных значениях. Важно, чтобы гипотезы выдвигали эксперты-специалисты,
которые достаточно хорошо представляют создаваемую систему или новые внешние
воздействия на систему. Больший успех может быть достигнут, если представляется
возможность получить сведения от группы специалистов. В этом случае можно
уменьшить степень субъективности и воспользоваться хорошо отработанными
методиками экспертных оценок. При проведении данной работы определенные
сведения можно получить в результате анализа функционирования аналогичных,
систем или прототипов будущей системы.
Заканчивается этап сбора и обработки исходных данных классификацией на
внешние и внутренние, постоянные и переменные, непрерывные и дискретные,
линейные и нелинейные, стационарные и нестационарные, детерминированные и
стохастические. Для переменных количественных параметров, которыми может
варьировать исследователь в ходе моделирования, определяются границы их
изменений, а для дискретных - возможные значения.
3. Разработка математической модели
Обобщенные модели. Концептуальная модель и количественные исходные данные
служат основой для разработки математической модели. Создание математической
модели преследует две основные цели: 1) дать формализованное описание структуры
и процесса функционирования системы для однозначности их понимания; 2)
попытаться представить процесс функционирования в виде, допускающем
аналитическое исследование системы.
Разработка единой методики создания математических моделей, очевидно, не
представляется возможной. Это обусловлено большим разнообразием классов систем.
Системы могут быть статические и динамические, со структурным или программным
управлением, с постоянной или переменной структурой, с постоянным (жестким) или
сменным (гибким) программным управлением. По характеру входных воздействий и
внутренних состояний системы подразделяются на непрерывные и дискретные,
линейные и нелинейные, стационарные и нестационарные, детерминированные и
стохастические. При исследовании ВС может быть получено такое же разнообразие
моделей в зависимости от ориентации, а также от степени стратификации и
детализации.
Для определенных классов систем разработаны формализованные схемы и
математические методы, которые позволяют описать функционирование системы, а в
некоторых случаях-выполнять аналитические исследования.
Средствами формализованного описания процессов функционирования систем с
программным принципом управления служат определенные языки и системы
имитационного моделирования. Некоторые из них описаны ниже.
Агрегативные системы. Одной из наиболее общих формализованных схем является
описание в виде агрегативных систем. Этот метод позволяет представить
функционирование непрерывных и дискретных, детерминированных и стохастических
систем. Он в наибольшей мере приспособлен для описания систем, у которых
характерно представление входных и выходных воздействий в виде «сообщений»,
составленных из совокупностей «сигналов».
В основе метода лежит понятие агрегата как элемента системы.
Математическая модель агрегата выражается в виде зависимостей с конкретизацией
входных воздействий, состояний и операторов переходов и выходов. В частности,
выделяют особые состояния агрегата, к которым относятся состояния в моменты
получения входного или управляющего сигнала либо выдачи выходного сигнала. Из
особого состояния агрегат скачкообразно может переходить в новое состояние.
Агрегативная система образуется при расчленении системы на элементы, каждый из
которых представляет собой агрегат.
Единообразное математическое описание исследуемых объектов в виде
агрегативных систем позволяет использовать универсальные средства имитационного
моделирования.
Кусочно-линейные агрегаты. Дальнейшая конкретизация структуры пространств
состояний, входных и выходных воздействий, а также операторов переходов и
выходов приводит к понятию кусочно-линейных агрегатов, удобных для формализации
широкой совокупности разнообразных процессов и явлений материального мира. В
основе подхода лежит кусочно-линейный закон изменения состояния системы, что
обеспечивает простоту вычисления опорных моментов времени и, как следствие,
простоту реализации модели кусочно-линейного агрегата и системы, составленной
из таких агрегатов. В частных случаях для кусочно-линейных агрегативных систем
результаты могут быть получены аналитическим методом.
Совместно с формализованным описанием системы в виде совокупности
кусочно-линейных агрегатов может применяться метод управляющих
последовательностей. Суть метода заключается в том, что функционирование
системы определяется управляющими последовательностями, которые имеют
определенный физический смысл, а также алгоритмами, описывающими управление системой
с помощью введенных последовательностей. Управляющие последовательности и
алгоритмы позволяют составлять рекуррентные соотношения для описания
функционирования кусочно-линейного агрегата.
Стохастические сети. Для описания стохастических систем с дискретными множествами
состояний, входных и выходных воздействий, функционирующих в непрерывном
времени, широко используются стохастические сети. Стохастическая сеть
представляет собой совокупность систем массового обслуживания, в которой
циркулируют заявки, переходящие из одной системы в другую.
Большая группа языков имитационного моделирования основана на
формализованном представлении систем в виде стохастических сетей. При
определенных условиях стохастическая сеть может рассматриваться как
совокупность независимых систем массового обслуживания. Это открывает
возможность применения достижений теории массового обслуживания для проведения
аналитического моделирования.
Системы массового обслуживания. В основе системы массового
обслуживания лежит понятие прибора, который может выполнять конечное множество
операций. Прибор выполняет операцию, когда возникает заявка - требование на
выполнение операции. Если прибор выполняет любую операцию, то считается, что он
занят (работает), в противном случае прибор свободен. Ограничение числа
состояний прибора приводит к большей степени абстрактности, чем понятие
агрегата.
Временная последовательность заявок называется потоком заявок. Общий
поток заявок может состоять из нескольких потоков. В случаях независимости
потоков, случайных моментов поступления или завершения обслуживания заявок в
системе могут возникать очереди. Очередь - это заявки, ожидающие обслуживания,
когда прибор занят. Прибор может состоять из нескольких элементов (каналов),
каждый из которых способен обслужить любую заявку. Совокупность прибора,
потоков заявок и очередей к нему называют системой массового обслуживания
(СМО).
Теория массового обслуживания хорошо разработана. Поэтому она нашла
широкое применение для создания математических моделей, в частности, при
моделировании ВС. Применение теории марковских процессов и теории диффузионных
процессов для исследования СМО при определенных ограничениях и допущениях
позволило получить ряд важных аналитических зависимостей.
Непрерывные детерминированные системы. Если в модели системы не учитывается
воздействие случайных факторов, а операторы переходов и выходов непрерывны (это
означает, что малые изменения входных воздействий приводят к такого же порядка
малым изменениям выходного воздействия и состояния системы), то состояния
системы и выхода соответственно могут быть представлены в виде дифференциальных
уравнений
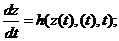 (4)
(4)
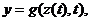 (5)
(5)
где h, g - вектор функции состояний и выходов соответственно;
х, z, у - векторы входных воздействий,
состояний и выходных воздействий соответственно.
В случае линейности таких систем, когда операторы переходов и выходов
обладают свойствами однородности и аддитивности, вид уравнений (4) и (5)
упрощается, что дает возможность аналитического решения или исследования
известными методами с помощью вычислительных машин.
Построение математических моделей непрерывных линейных детерминированных
систем в виде дифференциальных уравнений используется при анализе
функционирования элементов и электрических цепей ВС.
Автоматы. Рассмотренные выше формализованные математические
схемы применимы для систем, функционирующих в непрерывном времени. Системы,
состояния которых определены в дискретные моменты времени 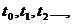 получили название автоматов. Если за единицу времени
выбран такт
получили название автоматов. Если за единицу времени
выбран такт 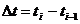 , то просто пишут: О, 1, 2, .... В каждый дискретный
момент времени, за исключением <е> в автомат поступает входной сигнал х
(t), под действием которого автомат переходит в новое
состояние в соответствии с функцией переходов
, то просто пишут: О, 1, 2, .... В каждый дискретный
момент времени, за исключением <е> в автомат поступает входной сигнал х
(t), под действием которого автомат переходит в новое
состояние в соответствии с функцией переходов
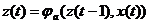 (6)
(6)
и выдает выходной сигнал, определяемый функцией выходов
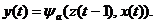 (7)
(7)
Если автомат характеризуется конечными множествами состояний z, входных сигналов х и выходных сигналов у,
он называется конечным автоматом. Функции переходов и выходов конечного
автомата задаются таблицами, матрицами или графами.
Стохастические системы, функционирующие в дискретном времени, можно
представлять вероятностными автоматами. Функция переходов вероятностного автомата
определяет не одно конкретное состояние, а распределение вероятностей на
множестве состояний, а функция выходов - распределение вероятностей на
множестве выходных сигналов. Функционирование вероятностных автоматов изучается
при помощи аппарата цепей Маркова. Для оценки характеристик систем,
представляемых в виде автоматов, могут использоваться аналитические или
имитационные методы.
Кроме приведенных математических схем для формализованного описания
функционирования систем используются исчисление высказываний, тензорная
алгебра, сети Петри, Е-сети и др..
Таким образом, построение математической модели предусматривает анализ
концептуальной модели и исходных данных в целях выбора одной из подходящих
формализованных схем, подбора необходимых множеств и конкретизации операторов.
Если это не удается сделать для всей системы, то формализованные схемы могут
быть применены для описания отдельных элементов, а вся система описывается с
использованием программного или структурного подхода.
. Выбор метода моделирования
Аналитические методы. Разработанная математическая модель функционирования системы
может быть исследована различными методами - аналитическими или имитационными.
С помощью аналитических методов анализа можно провести наиболее полное
исследование модели. В некоторых случаях наличие аналитической модели делает
возможным применение математических методов оптимизации. Для использования
аналитических методов необходимо математическую модель преобразовать к виду
явных аналитических зависимостей между характеристиками и параметрами системы и
внешних воздействий. Однако это удается лишь для сравнительно простых систем.
Применение аналитических методов для более сложных систем связано с большей по
сравнению с другими методами степенью упрощения реальности и абстрагирования.
Поэтому аналитические методы исследования используются обычно для
первоначальной грубой оценки характеристик всей системы или отдельных ее
подсистем, а также на ранних стадиях проектирования систем, когда недостаточно
информации для построения более точной модели. Они могут использоваться для
анализа параллельных процессов в сложных системах.
Ряд аналитических моделей не поддается аналитическим решениям
известными математическими методами. Для их исследования могут быть
использованы численные методы. Они применимы к более широкому классу систем, для которых
математическая модель представляется в виде системы уравнений, допускающей
решение численными методами. Использование численных методов особенно
эффективно с помощью быстродействующих ВС. Для исследования ВС,
функционирование которых описывается марковскими процессами, разработано,
например, программное средство для автоматизированного составления уравнений и
их решения на ВС. Результатом исследования систем численными методами являются
таблицы значений искомых величин для конечного набора значений параметров
системы и нагрузки.
Если полученные уравнения не удается решить аналитическими или численными
методами, то прибегают к качественным методам. Качественные методы
позволяют в ряде случаев оценить асимптотические значения искомых величин,
устойчивость, а также судить о поведении траектории системы в целом. Перечисленные
свойства относятся к поведению отдельных траекторий. Рассматриваются и такие
качественные свойства, которые характеризуют поведение совокупностей
траекторий. Примером такого свойства является непрерывность, наличие которой
говорит о том, что при малых изменениях параметров характеристики системы также
мало изменяются. Следует отметить, что для сложных систем важность качественных
методов возрастает.
Имитационные методы. Имитационное моделирование является наиболее универсальным
методом исследования систем и количественной оценки характеристик их
функционирования. При имитационном моделировании динамические процессы
системы-оригинала подменяются процессами, имитируемыми в абстрактной модели, но
с соблюдением таких же соотношений длительностей и временных
последовательностей отдельных операций. Поэтому метод имитационного
моделирования мог бы называться алгоритмическим или операционным. В процессе
имитации, как при эксперименте с оригиналом, фиксируют определенные события и
состояния или измеряют выходные воздействия, по которым вычисляют
характеристики качества функционирования системы.
Имитационное моделирование позволяет рассматривать процессы, происходящие
в системе, практически на любом уровне детализации. Используя алгоритмические
возможности ВС, в имитационной модели можно реализовать любой алгоритм
управления или функционирования системы. Модели, которые допускают исследование
аналитическими методами, также могут анализироваться имитационными методами.
Все это является причиной того, чтo имитационные методы моделирования становятся основными методами
исследования сложных систем.
Методы имитационного моделирования различаются в зависимости от класса
исследуемых систем, способа продвижения модельного времени и вида
количественных переменных параметров системы и внешних воздействий.
В первую очередь можно разделить методы имитационного моделирования
дискретных и непрерывных систем. Если все элементы системы имеют конечное
множество состояний и переход из одного состояния в другое осуществляется
мгновенно, то такая система относится к системам с дискретным изменением
состояний, или дискретным системам. Если переменные всех элементов системы
изменяются постепенно и могут принимать бесконечное множество значений, то
такая система называется системой с непрерывным изменением состояний, или
непрерывной системой. Системы, у которых имеются переменные того и другого
типа, считаются дискретно-непрерывными. У непрерывных систем могут быть
искусственно выделены определенные состояния элементов. Например, некоторые
характерные значения переменных фиксируются как достижение определенных
состояний. При моделировании ВС на системном уровне их зачастую удобно
рассматривать как системы с дискретным изменением состояний.
Одним
из основных параметров при имитационном моделировании является модельное время,
которое отображает время функционирования реальной системы. В зависимости от
способа продвижения модельного времени методы моделирования подразделяются на
методы с приращением временного интервала и методы с продвижением времени до
особых состояний. В первом случае модельное время продвигается на некоторую
величину 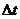 . Определяются изменения состояний элементов и
выходных воздействий системы, которые произошли за это время. После этого
модельное время снова продвигается на величину
. Определяются изменения состояний элементов и
выходных воздействий системы, которые произошли за это время. После этого
модельное время снова продвигается на величину 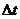 , и
процедура повторяется. Так продолжается до конца периода моделирования Tm,. Шаг приращения времени
, и
процедура повторяется. Так продолжается до конца периода моделирования Tm,. Шаг приращения времени 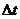 зачастую
выбирается постоянным, но в общем случае он может быть и переменным. Этот метод
называют "принципом
зачастую
выбирается постоянным, но в общем случае он может быть и переменным. Этот метод
называют "принципом 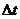 ".
".
Во
втором случае в текущий момент модельного времени t сначала анализируются те будущие особые состояния -
поступление дискретного входного воздействия (заявки), завершение обслуживания
и т. п., для которых определены моменты их наступления 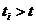 . Выбирается
наиболее раннее особое состояние, и модельное время продвигается до момента
наступления этого состояния. Считается, что состояние системы не изменяется
между двумя соседними особыми состояниями. Затем анализируется реакция системы
на выбранное особое состояние. В частности, в ходе анализа определяется момент
наступления нового особого .состояния. Затем анализируются будущие особые
состояния, и модельное время продвигается до ближайшего. Процедура повторяется
до завершения периода моделирования Тm. Данный
метод называют «принципом особых состояний», или «принципом
. Выбирается
наиболее раннее особое состояние, и модельное время продвигается до момента
наступления этого состояния. Считается, что состояние системы не изменяется
между двумя соседними особыми состояниями. Затем анализируется реакция системы
на выбранное особое состояние. В частности, в ходе анализа определяется момент
наступления нового особого .состояния. Затем анализируются будущие особые
состояния, и модельное время продвигается до ближайшего. Процедура повторяется
до завершения периода моделирования Тm. Данный
метод называют «принципом особых состояний», или «принципом 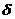 z». Благодаря
его применению экономится машинное время моделирования. Однако он используется
только тогда, когда имеется возможность определения моментов наступления
будущих очередных особых состояний.
z». Благодаря
его применению экономится машинное время моделирования. Однако он используется
только тогда, когда имеется возможность определения моментов наступления
будущих очередных особых состояний.
Количественные
параметры системы и внешних воздействий могут быть детерминированными или
случайными. По этому признаку различают детерминированное и статистическое
моделирование. При статистическом моделировании для получения достоверных
вероятностных характеристик процессов функционирования системы требуется их
многократное воспроизведение с различными конкретными значениями случайных
факторов и статистической обработкой результатов измерений. В основу
статистического моделирования положен метод статистических испытаний, или метод
Монте-Карло.
Особое
значение имеет стационарность или нестационарность случайных независимых
переменных системы и внешних воздействий. При нестационарном характере
переменных, в первую очередь - внешних воздействий, что часто наблюдается на
практике, должны быть использованы специальные методы моделирования, в
частности метод повторных экспериментов.
Еще
одним классификационным параметром следует считать схему формализации, принятую
при создании математической модели. Здесь прежде всего необходимо
разделить методы, ориентированные на алгоритмический (программный) или
структурный (агрегатный) подход. В первом случае процессы управляют элементами
(ресурсами) системы, а во втором - элементы управляют процессами, определяют
порядок функционирования системы.
Из
вышеизложенного следует, что выбор того или иного метода моделирования
полностью определяется математической моделью и исходными данными.
Контрольные вопросы
. Что понимается под сбором факальных данных для построения модели?
. Как решается подбор вида закона распределения?
. Что понимается под аппроксимацией функций?
. Какие виды средств используются для формализации описания
функционирования систем?
. Что вы понимаете под системой массового обслуживания?
Литература
1. Альянах И.Н. Моделирование вычислительных систем,
Л.: Машиностроение, 1988 г. - 223 стр.
2. Растригин Л.А. Современные принципы управления
сложными объектами, М.: Советское радио, 1980 г. - 232 стр.
3. Адлер Ю.П., Маркова Е.В., Грановский
Ю.В. - Планирование
эксперимента при поиске оптимальных условий, М.: Наука, 1976 г. -278 стр.
Лекция 3. ТЕХНОЛОГИЯ МОДЕЛИРОВАНИЯ (2 часа)
План
1.
Выбор средств моделирования
.
Проверка адекватности и корректировка модели
.
Планирование экспериментов с моделью
.
Анализ результатов моделирования
1. Выбор средств моделирования
Технические средства моделирования. После выбора метода
моделирования необходимо выбрать технические и программные средства для-
проведения исследования модели с помощью ВС. В качестве программных средств
могут быть использованы процедурно-ориентированные алгоритмические языки,
проблемно-ориентированные языки или автоматизированные системы моделирования.
Для исследования моделей применяются универсальные или специализированные
ВС. Для проведения аналитического моделирования с помощью универсальных ВС
зачастую не предъявляется каких-либо особых требований к техническим средствам.
Основным требованием к универсальным ВС, которые используются для имитационного
моделирования, является наличие оперативной памяти достаточно большой емкости.
Это объясняется тем, что в процессе модельного эксперимента постоянно
производятся чередующиеся обращения к параметрам элементов и воздействий (к
атрибутам статических и динамических составляющих), поэтому все они должны
находиться в оперативной памяти.
Каждый модельный эксперимент при статистическом моделировании требует
существенных затрат машинного времени, поэтому желательно использовать для
моделирования высокопроизводительные ВС. Остальные требования к составу и
техническим характеристикам универсальных ВС не являются существенными.
К специальным техническим средствам аналитического моделирования
относятся аналоговые вычислительные машины, используемые для исследования
непрерывных детерминированных систем.
В связи с широким применением имитационного моделирования в различных
областях все более актуальными становятся разработка и выпуск
специализированных ВС. К таким средствам относятся стохастические машины,
машины имитационного моделирования и гибридные моделирующие комплексы. Наиболее
мощными специализированными техническими средствами моделирования призваны
стать распределенные системы моделирования.
Алгоритмические языки. Для создания программных моделей могут использоваться
универсальные процедурно-ориентированные алгоритмические языки высокого уровня
такие, как Pascal, Delphi, C++, Java и др. Известны примеры применения
алгоритмических языков для составления программ имитационного моделирования ВС.
При создании имитационных моделей на языках общего назначения возникает ряд
трудностей, не типичных для практики программирования традиционных задач
обработки данных. Эти трудности связаны с двумя основными особенностями
алгоритмов имитационного моделирования.
Первая особенность заключается в том, что алгоритмы поведения сложных
систем относятся к параллельным алгоритмам, т. е. предполагающим выполнение
более чем одного преобразования в каждый момент времени. Трудности
программирования параллельных алгоритмов состоят в том, что алгоритмические
языки ориентированы на описание чисто последовательных процессов. Программная
имитация параллельных процессов при использовании языков высокого уровня
сводится к Организации псевдопараллельного развития параллельных процессов, что
достаточно сложно для программирования.
Вторая особенность состоит в том, что в процессе моделирования необходима
обработка данных, объем которых весьма трудно оценить априорно. Это обусловлено
динамическим характером имитационных моделей и их направленностью на изучение
массовых процессов в системах. При программировании таких алгоритмов
первостепенное внимание уделяется динамическому распределению оперативной
памяти.
Достоинства применения процедурно-ориентированных языков для составления
программ имитационного моделирования состоят в возможности использования
стандартного программного обеспечения ВС, написания экономичных по затратам
памяти и быстродействующих программ, учета детальных особенностей
функционирования моделируемых систем.
Языки моделирования. При создании программ имитационного моделирования возникают
задачи, общие для широкого класса моделей. Это - организация
псевдопараллельного выполнения алгоритмов; динамическое распределение памяти;
операции с модельным временем, отображающим астрономическое время
функционирования оригинала; имитация случайных процессов; ведение массива
событий; сбор и обработка результатов моделирования. Для облегчения решения
этих и некоторых других задач созданы специальные проблемно-ориентированные
средства (программные системы), которые называют языками моделирования. Решение
перечисленных выше задач осуществляется полностью или частично внутренними
средствами языка.
Описательные средства языков моделирования позволяют идентифицировать и
задавать параметры моделируемой системы и внешних воздействий, алгоритмы
функционирования и управления, режимы и требуемые результаты моделирования. По
структуре и правилам программирования языки моделирования подобны
процедурно-ориентированным алгоритмическим языкам высокого уровня. Они имеют
тот или иной набор операторов, сопровождаемых соответствующими • операндами. Но
операторы языков моделирования предопределяют выполнение более сложных
процедур, поэтому языки моделирования имеют более высокий уровень по сравнению
с уровнем алгоритмических языков, что упрощает составление программ. Языки
моделирования следует рассматривать как формализованный базис создания
математических моделей.
В настоящее время известно более 500 языков моделирования. Такое
множество языков частично обусловлено разнообразием классов моделируемых
систем, методов их формализованного математического описания, целей и методов
моделирования. По классу систем языки подразделяются на семейства,
ориентированные на моделирование дискретных, непрерывных и комбинированных
систем. В отдельное семейство выделяются языки, предназначенные для автоматизированного
составления схем соединения блоков аналоговых ЭВМ. Другим классификационным
признаком может служить алгоритмический или структурный подход к описанию
процессов функционирования систем. Можно подразделить языки и по другим
признакам.
Автоматизированные системы моделирования. Желание дальнейшего упрощения и
ускорения процесса создания машинных моделей привело к реализации идей по
автоматизации программирования имитационных моделей. Создан ряд систем, которые
избавляют исследователя от программирования. Программа создается автоматически
по одной из формализованных схем на основании задаваемых исследователем
параметров системы, внешних воздействий и особенностей функционирования.
Исходные данные представляются в той или иной канонической форме или в ходе
диалога с ВС. По результатам машинного эксперимента основные выходные данные
вычисляются и выводятся автоматически, дополнительные - по указанию
исследователя. Такие системы называют еще универсальными автоматизированными
имитационными моделями, или генераторами имитационных программ.
Перед исследователями систем, использующими имитационное моделирование,
неизбежно возникает задача выбора соответствующих программных средств
моделирования. Обилие этих средств, в большинстве своем реализованных на разнотипных
ВС, отсутствие исчерпывающей документации, единой методики сравнения
существующих систем значительно усложняет решение этой задачи. Усилиями рабочей
группы Международной ассоциации по применению математических методов и
вычислительных машин в имитационном моделировании разработаны единые
классификационные таблицы для представления средств программного обеспечения
машинного моделирования, которые позволяют в компактной форме описать различные
системы моделирования, особенности их реализации и применения.
Программные и технические средства моделирования выбираются с учетом ряда
критериев. Непременное условие при этом - достаточность и полнота средств для
реализации концептуальной и математической модели. Среди других критериев можно
назвать доступность средств, наличие у исследователя информации о тех или
других средствах. Немаловажное значение имеет простота и легкость освоения
программных средств моделирования, скорость и корректность создания программной
модели, существование методики использования средств для моделирования систем
определенного класса.
После выбора языка разрабатывают программную модель. Этот процесс
включает разработку алгоритма, конкретизацию форм представления входных данных
и результатов, написание и отладку программы. Это важный и трудоемкий этап, но
по технологии он практически не отличается от всякого другого программирования
и поэтому здесь детально не рассматривается.
. Проверка адекватности и корректировка модели
Проверка адекватности. Проверка адекватности модели системе заключается в анализе
ее соразмерности с исследуемой системой, а также равнозначности системе. Однако
модель не должна быть полным отображением системы, иначе теряется смысл ее
создания. Адекватность нарушается из-за идеализации внешних условий и режимов
функционирования, исключения тех или других параметров, пренебрежения
некоторыми случайными факторами. Отсутствие точных сведений о внешних
воздействиях, определенных нюансах структуры системы, принятые аппроксимации,
интерполяции, предположения и гипотезы тоже ведут к уменьшению соответствия
между моделью и системой. Перечисленные и другие факторы могут стать причиной
того, что результаты моделирования будут существенно отличаться от реальных.
Естественной простейшей мерой адекватности может служить отклонение
некоторой характеристики y0 оригинала и ym модели:
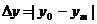
или,
что лучше, отношение отклонения к характеристике оригинала
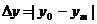 /y0
/y0
Тогда
можно считать, что модель адекватна с системой, если вероятность того, что
отклонение  у не превышает предельной величины
у не превышает предельной величины  , больше допустимой вероятности Р
, больше допустимой вероятности Р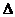 :
:
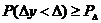
Однако
практическое использование данного критерия адекватности зачастую невозможно по
следующим причинам.
Во-первых,
для проектируемых или модернизируемых систем отсутствует информация о значении
характеристики У0, а моделируются, как правило, именно такие
системы. Можно сравнивать характеристики модели и некоторой системы-аналога, но
тогда будет одинаковая степень недоверия к этим характеристикам. Во-вторых,
система оценивается не по одной, а по множеству характеристик, у которых может
быть разная величина отклонения. В-третьих, характеристики могут быть
случайными величинами и функциями, а часто и нестационарными функциями. Для
стохастических систем может оказаться, что статистические характеристики,
полученные на модели с высокой степенью адекватности, более точны, чем
соответствующие характеристики, вычисленные по результатам измерений на
реальной системе Это объясняется тем, что результаты моделирования определяются
по большому числу реализации, в то время как количества измерений на реальной
системе всегда ограничены. В-четвертых, отсутствует возможность априорного
точного задания предельных . отклонений 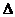 и
допустимых вероятностей Р
и
допустимых вероятностей Р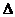 .
.
Тем не менее проверять адекватность необходимо, так как по неверным
результатам моделирования могут быть приняты неправильные решения. На практике
оценка адекватности обычно проводится путем экспертного анализа разумности
результатов моделирования. Можно выделить следующие виды проверок:
· проверка моделей элементов (в сомнительных случаях следует
детализировать элемент или провести дополнительный анализ);
· проверка модели внешних воздействий (принятые предположения,
аппроксимации и гипотезы необходимо оценить математическими методами);
· проверка концептуальной модели функционирования системы
(выявляются ошибки постановки задачи);
· проверка формализованной и математической модели;
· проверка способов измерения и вычисления выходных
характеристик; выявляются ошибки решения;
· проверка программной модели (анализируется соответствие
операций и алгоритмов функционирования программной и математической модели,
проводятся контрольные расчеты при типовых и предельных значениях переменных,
выявляются инструментальные ошибки программирования).
Корректировка модели. Если по результатам проверки адекватности выявляется
недопустимое рассогласование модели и системы, возникает необходимость в
корректировке или калибровке модели. При этом могут быть выделены следующие
типы изменений:
глобальные, локальные и параметрические.
Необходимость в глобальных изменениях возникает в случае обнаружения
методических ошибок в концептуальной или математической модели. Устранение
таких ошибок приводит к разработке новой модели. Локальные изменения связаны с
уточнением некоторых параметров или алгоритмов. Они выполняются, например,
путем замены моделей компонентов системы и внешних воздействий на
эквивалентные, но более точные модели. Локальные изменения требуют частичного
изменения математической модели, но могут привести к необходимости разработки
новой программной модели. Для уменьшения вероятности таких изменений
рекомендуется сразу разрабатывать модель с большей степенью детализации, чем
это необходимо для достижения цели моделирования.
К параметрическим относятся изменения некоторых специальных параметров,
называемых калибровочными. Для обеспечения возможности повышения адекватности
модели путем параметрических изменений следует заранее выявить калибровочные
параметры и предусмотреть простые способы варьирования ими.
Стратегия корректировки модели должна быть направлена на первоочередное
введение глобальных изменений, затем - локальных и, наконец, параметрических
изменений. Общая методика корректировки приведена в работе. Для выработки
тактики параметрических изменений большое значение имеет анализ
чувствительности модели к вариациям ее параметров.
Завершается этап проверки адекватности и корректировки модели
определением и фиксацией области пригодности модели. Под областью пригодности
понимается множество условий, при соблюдении которых точность результатов
моделирования находится в допустимых пределах.
. Планирование экспериментов с моделью
Стратегическое планирование. Цели моделирования достигаются путем
исследования разработанной модели. Исследования заключаются в проведении
экспериментов, в результате которых определяются выходные характеристики
системы при разных значениях управляемых переменных параметров модели.
Эксперименты следует проводить по определенному плану. Особую важность
приобретает планирование экспериментов при численном и статистическом
имитационном моделировании на универсальных ВС. Это обосновывается большим
числом возможных сочетаний значений управляемых параметров, а каждый машинный
эксперимент проводится при определенном сочетании значений параметров.
Например, при пяти управляемых параметрах, каждый из которых может иметь три
значения, количество сочетаний параметров равно 243, при десяти параметрах (по
пять значений каждого) число сочетаний приближается к 10 млн. При ограниченных
вычислительных и временных ресурсах обычно не представляется возможным провести
все эксперименты. Возникает необходимость в выборе определенных сочетаний
параметров и последовательности проведения экспериментов. Это называется
стратегическим планированием.
Разработка плана начинается на ранних этапах создания модели, когда
выявляются характеристики качества и параметры, с помощью которых
предполагается управлять качеством функционирования системы. Эти параметры
называют в теории планирования экспериментов факторами. Затем выделяются
возможные значения количественных параметров и варианты качественных
(функциональных) параметров. Их называют уровнями q. При этом число сочетаний
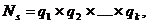
где
k - число факторов.
Если
число факторов велико, то для проведения исследований системы используется один
из методов составления плана по неполному факторному анализу. Эти методы хорошо
разработаны в теории планирования экспериментов и частично рассмотрены в книге.
Особую важность приобретает тщательное планирование экспериментов при
исследовании нестационарных систем в связи с необходимостью существенного
увеличения общего количества экспериментов.
Тактическое
планирование. Совокупность методов
уменьшения длительности машинного эксперимента при обеспечении статистической
достоверности результатов имитационного моделирования получила название
тактического планирования. На длительность одного .эксперимента (периода
моделирования Тm) влияет
степень стационарности системы, взаимозависимости характеристик и значения
начальных условий моделирования.
Данные,
собранные в эксперименте, можно рассматривать как временные ряды, состоящие из
замеров определенных характеристик. Ряд замеров характеристики у может
рассматриваться как выборка из стохастической последовательности. Если эта
последовательность стационарна, ее среднее у не зависит от времени.
Оценкой 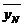 является среднее по временному ряду y1, .... уN. Для
эргодической последовательности точность этой оценки возрастает с ростом N.
является среднее по временному ряду y1, .... уN. Для
эргодической последовательности точность этой оценки возрастает с ростом N.
Если
заданы максимальная допустимая ошибка оценки (доверительный интервал) и
минимальная вероятность того, что истинное среднее у лежит внутри этого
интервала, то существует минимальный размер исследуемой выборки. Этот размер
соответствует минимальной длительности эксперимента. Для оценки нескольких
характеристик период моделирования определяется по максимальному значению.
Требуемый
размер выборки существенно зависит от дисперсии оцениваемой характеристики. Чем
больше дисперсия, тем больше должен быть размер выборки. Для коррелированных
случайных характеристик следует оценивать дисперсии. Имеются специальные приемы
обработки результатов моделирования, которые получили название методов уменьшения
дисперсии. Они используют априорную информацию о системе и позволяют уменьшить
размер выборки при сохранении заданной точности оценок. К ним относятся методы
коррелированных, стратифицированных выборок и др.
Большинство
имитационных моделей используются для изучения установившихся равновесных
режимов функционирования. Но в начальный период работы системы или модели
существует переходный режим даже при неизменных значениях параметров входных
воздействий. Как показали исследования, длительность переходного режима может
быть весьма большой. Значения выходных характеристик, измеренные в переходный
период, смещают их общие оценки.
Существует
три основных метода уменьшения ошибки, обусловленной начальными условиями.
Первый состоит в достаточном увеличении периода моделирования. С увеличением
числа замеров влияние начального смещения на статистическую оценку стремится к
нулю. Второй метод состоит в том, чтобы начинать сбор статистики не с
начального момента, а по истечении некоторого времени. Третий метод заключается
в инициализации модели не с «нулевого», а специально заданного состояния,
близкого к установившемуся.
Первые
два метода приводят к увеличению длительности эксперимента и не дают гарантии
уменьшения ошибки, так как априорно неизвестна длительность переходного режима.
Третий метод можно применять при наличии информации о подходящем начальном
состоянии. В последующих экспериментах для задания начальных состояний могут
использоваться уточненные сведения из предшествующих экспериментов.
При
моделировании нестационарных систем установившийся. режим может полностью
отсутствовать. Естественным методом определения характеристик имитационного
моделирования нестационарных систем является метод повторных экспериментов. В
этом случае число экспериментов существенно увеличивается, что приводит к
особым требованиям по их планированию.
. Анализ результатов моделирования
Обработка измерений имитационного эксперимента. При статистическом
моделировании в ходе имитационного эксперимента измеряются множества значений
по каждой выходной характеристике. Эти выборки необходимо отрабатывать для
удобства последующего анализа и использования. Поскольку выходные
характеристики зачастую являются случайными величинами или функциями, обработка
заключается в вычислении оценок математических ожиданий, дисперсий и
корреляционных моментов. Оценки, полученные в результате статистической
обработки измерений, должны быть состоятельными, несмещенными и эффективными.
Для того чтобы исключить необходимость хранения в машине всех измерений,
обработку проводят по рекуррентным формулам, когда оценки вычисляют в процессе
эксперимента методом нарастающего итога по мере появления новых измерений.
Для стохастических характеристик можно построить гистограмму
относительных частот - эмпирическую плотность распределения. С этой целью
область предполагаемых значений характеристики Y разбивается на интервалы. В ходе эксперимента по мере
измерений определяют число попаданий характеристики в каждый интервал и
подсчитывают общее число измерений. После завершения эксперимента для каждого
интервала вычисляют отношение числа попаданий характеристики к общему числу
измерений и длине интервала. Для построенной гистограммы можно попытаться
подобрать теоретический закон распределения. Делается это так же, как и при подготовке
исходных данных моделирования.
Если искомая характеристика является стационарной случайной функцией
времени y(t) и обладает свойством эргодичности, то для ее оценки
вычисление среднего по времени заменяется вычислением среднего по множеству
измерений при одном достаточно продолжительном эксперименте.
Для случайных нестационарных характеристик период моделирования T разбивается на отрезки с постоянным
шагом Tm (прогоны или сечения), и
запоминаются значения характеристики в конце каждого прогона. Проводится серия
экспериментов с разными последовательностями случайных параметров модели. Затем
измерения каждого сечения обрабатываются как при оценке случайных величин. В
книге рассмотрена методика этих вычислений.
Процессы обработки измерений имитационного эксперимента направлены на
получение интегральных характеристик, т. е. на сжатие данных.
Определение зависимостей характеристик от параметров системы. По результатам статистического
моделирования может быть проведен анализ зависимостей характеристик от параметров
системы и внешних воздействий. Для этого можно воспользоваться корреляционным,
дисперсионным или регрессионным методами.
С помощью корреляционного анализа можно установить наличие связи между
двумя или более случайными величинами. Оценкой связи служит коэффициент
корреляции при наличии линейной связи между величинами и нормальном законе их
совместного распределения. Коэффициент корреляции, равный единице по абсолютной
величине, свидетельствует о наличии функциональной нестохастической линейной связи
между анализируемыми величинами. При равенстве нулю коэффициента корреляции
связь отсутствует. Промежуточные значения коэффициента корреляции соответствуют
наличию линейной связи с рассеянием или нелинейной корреляции.
Дисперсионный анализ можно использовать для установления относительного
влияния различных факторов на значения выходных характеристик. При этом общая
дисперсия характеристики разлагается на компоненты, соответствующие
рассматриваемым факторам. По значениям отдельных компонентов делают вывод о
степени влияния того или другого фактора на анализируемую характеристику.
Когда все факторы в эксперименте являются количественными, можно найти
аналитическую зависимость между характеристиками и факторами. Для этого
используются методы регрессионного анализа. Найденная зависимость называется
эмпирической моделью. Регрессионный анализ заключается в том, что выбирается
вид соотношения между зависимыми и независимыми переменными, по
экспериментальным данным вычисляются параметры выбранной зависимости и оценивается
качество аппроксимации экспериментальных данных моделью. Если качество
неудовлетворительное, берется зависимость другого вида, и процедура
повторяется.
К анализу результатов моделирования можно отнести задачу анализа
чувствительности модели к вариациям ее параметров. Под анализом
чувствительности понимают проверку устойчивости характеристик процесса
функционирования системы к возможным отклонениям значений параметров.
Анализ результатов моделирования позволяет уточнить множество
информативных параметров модели, что может привести к существенному изменению
первоначального вида концептуальной модели; найти функциональные зависимости
характеристик и параметров, что иногда дает возможность создать аналитические
модели системы, или определить весовые коэффициенты критерия эффективности.
Использование результатов моделирования. В конечном счете результаты
моделирования используются для принятия решения о работоспособности системы,
для выбора лучшего проектного варианта или для оптимизации системы. Решение о
работоспособности принимается по тому, выходят или не выходят характеристики
системы за установленные границы при любых допустимых изменениях параметров.
При выборе лучшего варианта из всех работоспособных вариантов выбирается тот, у
которого максимальное значение критерия эффективности. Наиболее общей и сложной
является оптимизация системы: требуется найти такое сочетание значений
переменных параметров системы или рабочей нагрузки из множества допустимых,
которое максимизирует значение критерия эффективности:
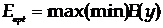
при
соблюдении ограничений на все п характеристик
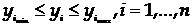
Если
выходная характеристика yi, является случайной величиной с некоторой плотностью
распределения f(yi), целесообразно ввести в задачу оптимизации
стохастические ограничения следующего вида:
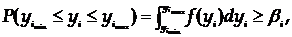
где
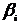 - минимально допустимая вероятность того, что
конкретные значения у, не выйдут за ограничивающие пределы.
- минимально допустимая вероятность того, что
конкретные значения у, не выйдут за ограничивающие пределы.
Для
нестационарных систем выходная характеристика уi зачастую является
случайной функцией с плотностью распределения, изменяющейся во времени f(yi,t). В этом случае можно задать ограничения следующим
образом:
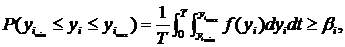
где
Т - длительность анализируемого периода функционирования системы.
Приведенная
постановка задачи оптимизации стохастических систем допускает выход за
установленные границы не только отдельных значений характеристики yi, но и ее математического ожидания M[yi,t] в пиковые моменты даже при величинах 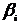 , близких к единице. Это показано на рис. 1. для
случая ограничения yi только сверху.
, близких к единице. Это показано на рис. 1. для
случая ограничения yi только сверху.
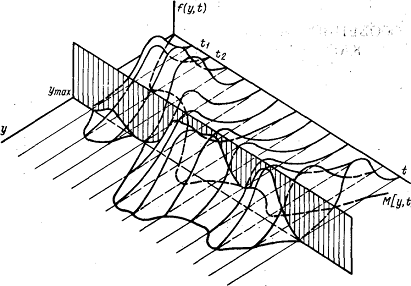
Рис. 1. Ограничение на выходную характеристику, представленную
нестационарным случайным процессом
При статистическом моделировании вычисление приведенного двойного
интеграла, которое часто оказывается невыполнимой. задачей в случае
использования других методов исследования, сводится к вероятностной оценке,
которая выполняется путем подсчета числа реализации уi, не выходящих за допустимые
значения, и его деления на величину выборки за время эксперимента Tm
В случае большого количества сочетаний независимых переменных поиск
оптимального варианта требует использования специальных процедур, например,
методов математического программирования, в частности, метода наискорейшего
спуска и др. Значительно сократить затраты машинного времени на моделирование
позволяет проведение зависимых, экспериментов. Применение этих методов следует
учитывать на этапе планирования экспериментов.
После создания системы целесообразна апостериорная проверка результатов
моделирования и измерения характеристик функционирования. Такая проверка
помогает уточнить модель и повысить эффективность системы. Наличие, модели
.действующей системы дает возможность прогнозирования качества функционирования
при развитии системы или изменении внешних воздействий.
Контрольные вопросы
1. Какие виды методов используются для
иследования сложных систем?
2. Предмет имитационного моделирования.
3. Что вы понимаете под средствами
моделирования и какие виды знаете?
5. Что означает планирование
экспериментов с моделью?
Литература
1. Альянах И.Н. Моделирование вычислительных систем,
Л.: Машиностроение, 1988 г. - 223 стр.
2. Растригин Л.А. Современные принципы управления
сложными объектами, М.: Советское радио, 1980 г. - 232 стр.
3. Адлер Ю.П., Маркова Е.В., Грановский
Ю.В. - Планирование
эксперимента при поиске оптимальных условий, М.: Наука, 1976 г. -278 стр.
Лекция 4. ПРОБЛЕМА МОДЕЛИРОВАНИЯ (2 часа)
План
1.
Объект моделирования
.
Сведения об объекте
.
Априорная информация
.
Апостериорная информация
При
постановке и решении проблемы моделирования исследователь сталкивается с
различными вопросами, одним из основных является вопрос - что называть объектом
моделирования и какие общие свойства, черты модели объекта? Поэтому проблему
моделирования начнем с изучения объекта моделирования.
1. Объект моделирования
Объект моделирования удобно представлять в виде
многополюсника,
изображенного на рис.1.а, где х1, ..., хп -наблюдаемые
входы объекта, e1, ..., еk- его ненаблюдаемые входы; у1,
..., ут-наблюдаемые выходы объекта.
Рис. 1. Изображение объекта моделирования.
Многомерный объект удобно описывать в векторной форме (рис. 1.б), где
X=(x1, . . . xn);=(y1,
. . . ym);=(e1, . . . ek);
Все входы объекта представляют собой воздействия внешней среды на объект
и являются какими-то определенными функциями состояния среды и времени. Так как
отсутствует модель среды, воздействующей на объект моделирования, то входы
объекта естественно рассматривать как случайные функции времени, т. е.
X=X(t), E=E(t),
статистические свойства которых в общем случае неизвестны. Однако
известны наблюдения входа и выхода объекта, т. е. реализации функций X(t) и Y(t) в непрерывной или дискретной форме. Относительно
ненаблюдаемого входа Е(t)
предполагается известной его структура, т. е. характер этой случайной функции.
В рамках данного курса мы ограничимся случаем, когда E(t) является нормальным случайным процессом,
непосредственное наблюдение которого невозможно.
Объект связывает входы Х и Е с выходом Y некоторым априори неизвестным оператором F0
Y=F0(X, E).
Однако идентифицируется не он, а оператор модели F, связывающий наблюдаемые входы и выходы:
Y=F(X).
Ненаблюдаемый фактор Е(t) рассматривается как случайная помеха, затрудняющая
определение оператора F.
Резюмируя, можно сказать, что объект идентификации в общем случае
представляется в виде многополюсника, часть входов которого ненаблюдаема (это и
есть Е)
. Сведения об объекте
Все сведения об объекте, которые необходимо иметь для того, чтобы начать
процедуру идентификации, как сказано выше, подразделяются на два вида:
априорные А и апостериорные B. Так, что
двойка
<А, B> (1)
характеризует всю информацию об объекте. Рассмотрим оба вида сведений в
отдельности.
3. Априорная информация
Априорная информация, которой необходимо располагать еще до
наблюдения входов и выходов объекта, должна ответить на вопрос, что
представляет собой структура идентифицируемого объекта. Структуру прежде всего мы будем
характеризовать значениями четырех признаков:
A =<α,
β, γ, δ>, (2)
которые кодируют объект по четырем признакам. Следует сразу отметить, что
структура объекта полностью далёко не исчерпывается этими четырьмя признаками.
Рассмотрим указанные признаки вида объекта подробнее и уточним их смысл.
. Признак динамичности α. Будем объект называть динамическим (α=1),
если поведение
его выхода зависит не только от значений входа в текущий момент времени, но и
от предыдущих значений входа. Это означает, что объект обладает памятью (или
инерционностью), которая и определяет зависимость выхода от предыстории входа.
В противном случае объект будем называть статическим (α=0).
2. Признак стохастичности β. Будем объект называть стохастическим
(β=1),
если поведение
его выхода зависит от неконтролируемых входов объекта или (что то же) сам
объект содержит неконтролируемый источник случайных факторов возмущений. В
противном случае будем объект называть детерминированным (β=0).
Заметим, что, строго говоря, нестохастических объектов не существует в
природе, так как всякое измерение неизбежно вносит свою погрешность в результат
наблюдения. Поэтому правильнее говорить о “малой” и “большой” стохастичности
объекта, подразумевая, что с малой стохастичностью можно не считаться и
называть такой объект детерминированным.
. Признак нелинейности γ. Объект будем называть нелинейным (γ=1),
если его реакция
на два различных возмущения входа не эквивалентна сумме реакций на каждое из
этих возмущений в отдельности. Для случая без помех нелинейность определяется
условием
F0(X1 + X2) ≠ F0(X1) + F0(X2).
При невыполнении этого условия, т. е. при равенстве в этом
выражении, объект будем называть линейным (γ=0).
4. Признак дискретности δ. Будем объект называть дискретным (δ=1),
если состояние
его входов и выходов изменяется или измеряется лишь в дискретные моменты
времени t=1, 2,
..., п. Если же вход и выход изменяются или измеряются непрерывно, то
объект назовем непрерывным (δ=0). Таким образом, способ измерения
может изменит этот признак объекта.
Как видно, A в значительной
степени проясняет вид модели, а для ее полной определенности следует сказать о
характере динамики (при α=1), вероятностных свойствах
стохастичности (при, γ=1) и виде нелинейности (при β=1).
Естественно, что представления о виде модели, определяемые A, могут измениться после анализа апостериорной
информации, т. е. после наблюдения за поведением входа и выхода объекта.
. Апостериорная информация
Если априорная информация A имеет качественный характер, то
апостериорная-количественный, т. е. результат (протокол) наблюдений входа и выхода
объекта. Этот
протокол имеет вид:
B=<X, Y>,
где X - результаты всех измерений 'входов объекта; Y - результаты этих измерений его выходов за тот же период
наблюдений.
Для непрерывных объектов (A=αβγ0) имеем записи непрерывных данных X=X(t), Y=Y(t) в интервале 0≤t≤T. Таким образом, получаем:
B0=(<X(t), Y(t)> ( 0 ≤ t ≤ T ).
Это означает, что поведение объекта зарегистрировано в виде n+m различных кривых: x1(t), ..., xn(t),
y1(t),
..., ym(t) в этом интервале.
Заметим, что X и X(t) в данном случае не тождественны, так как X представляет собой всю зависимость Х(t) в заданном интервале, a X(t)
может выражать только конкретное значение этой зависимости в момент t. Аналогична не тождественность Y и Y (t).
В дискретном случае (A=αβγl) имеем X=(X1, .... XN), Y= (Y1, ..., YN) и протокол записывается в виде
B1=(<Xi, Yi> (i=1, ..., N)),
который представляет собой таблицу чисел из п+т столбцов и N строк:
B1=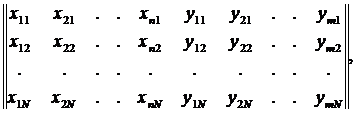
Очевидна
преемственность этих двух форм записи. Так, .протокол B1 может быть получен из B0 путем фиксации дискретных моментов времени t=0, δ, 2δ, ..., (N-1) δ, где δ - интервал
дискретности (δ=T/N).
(Заметим,
что обратный переход возможен далеко не всегда.)
Таким
образом двойка (1) достаточно полно характеризует объект для целей его
идентификации. Она и будет использоваться при изложении соответствующих идей,
методов и подходов идентификации.
Контрольные вопросы
1. Общее представление объекта
моделирования в виде многополюсника.
2. Априорная и апостериорная информация
об объекте моделирования.
3. По каким признакам классифицируются
объекты моделирования?
Литература
1. Растригин Л.А. Современные принципы управления
сложными объектами, М.: Советское радио, 1980 г. - 232 стр.
2. Растригин Л.А., Маджаров Н.Е. Введение в идентификацию объектов
управления, М.: Энергия, 1977 г. - 216 стр.
3. Адлер Ю.П., Маркова Е.В., Грановский
Ю.В. - Планирование
эксперимента при поиске оптимальных условий, М.: Наука, 1976 г. -278 стр.
Лекция 5. ЗАДАЧА ИДЕНТИФИКАЦИИ (2 часа)
План
1.
Постановка задачи идентификации.
.
Трудности идентификации
1. Постановка задачи идентификации.
Задачей идентификации является определение оператора F0 объекта, т.е. построения такого
оператора модели F, которой был определенном смысле близок к оператора объекта F0 т.е.
F»F0 (1)
(Заметим, что указанная «близость» весьма относительно, так как оператора
F0 и F
могут иметь разные структуру, могут быть сформулированы на разных языках и
иметь разные число входов. Именно поэтому близость операторов непосредственно
оценить трудно или просто невозможно, тем более что часто об операторе объекта F0 мало что известно.) В связи с этим естественно оценивать
близость операторов по их реакциям на одно и тоже входное воздействие Х , т.е.
по выходом объекта Y(t)=F0[X, E(t)] и модели YM=F(X). Степень
близости этих реакций в каждый момент времени можно оценить, например,
значением квадрата модуля разности векторов выхода:
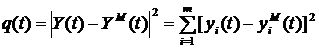 , (2’)
, (2’)
где
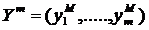
 векторов выхода модели.
векторов выхода модели.
В общем случае близость объекта и модели оценивается так называемой
функцией невязки ρ. Это скалярная функция двух векторных аргументов -
выходов объекта и модели:
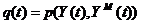 , (3)
, (3)
которая обладает следующими свойствами:
1) не отрицательна для любых Y(t) и YM (t), т.е.
ρ(Y(t), YM (t)) ≥ 0
2) равно нулю при Y(t) ≡ YM (t), т.е.
ρ(Y(t), YM (t))=0;
3) непрерывна и выпукла вниз по обоим
аргументам, т.е.
ρ((1-λ)Y1+λY2, YM) ≤ (1-λ)ρ(Y1, YM)+λρ(Y2, YM) ρ(Y(1-λ)YM1+λYM2) ≤ (1-λ)ρ(Y, YM1)+λρ(Y, YM2)
где 0 ≤ λ ≤ 1.
Говоря проще, эта функция всегда лежит ниже отрезка прямой , соединяющей
две любые точки (Y1, YM1) и (Y2, YM2), где Yi , YM i -
произвольные векторы . Удовлетворить этим требованиям не сложно. Так,
соотношение (2') соответствует им. Именно оно и будет чаще всего применяться в
дальнейшим.
Теперь сформулируем задачу идентификации. Она заключается в том, чтобы
построит такой оператор модели F,
которой бы реагировал на возмущение Х аналогично реакции объекта У . Реакция
оператора модели на вход Х имеет вид:
УМ=F(X)
Следовательно
модельный оператор F должен быть
таким, чтобы:
УМ
~ У
где ~ знак эквивалентности, т.е. выходы модели и объекта при одинаковых
входных воздействиях Х должен быть эквивалентны Этого можно добиться,
если ввести единую меру близости на всем интервале наблюдения, а не только в
каждой точке, как (3).
Такой мерой в непрерывном случае (объект А=αβγ0) может быть интеграл
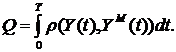
Действительно, в соответствии с определениям функции ρ(., .) величина Q выражает степень близости функций Y(t) и YM (t) в интервале 0 ≤ t ≤ T.
Значение явно зависит от F:
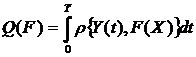
и задача идентификации заключается в ее минимизации путем
соответствующего выбора оператора модели F. Если по физическому смыслу задачи важность информации В в
различные моменты времени не одинакова, то целесообразно введение переменного
веса h(t)>0:
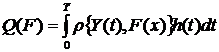 (5)
(5)
с естественным нормированием
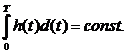 (6)
(6)
Выбор функции h(t) определяется ценностью информации.
Например, для стохастического непрерывного объекта (А=αβγ0)
при неравноточных
наблюдениях, т.е. когда дисперсия ошибки наблюдения выхода зависит определённым
образом от времени
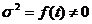 ,
,
где f(t) - заданная функция, вес h(t) должен
изменяться следующим образом:
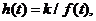
где, k - нормирующий член, обеспечивающий
выполнение условия (6) . Это означает, что ценность информации обратно
пропорционально уровняю дисперсии случайных помех.
Величину
Q(F) часто называют невязкой выходов объекта и модели. Эта невязка является функционалом, зависящим от
оператора модели F. По своей конструкции эта невязка неотрицательно и
равно нулю при 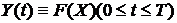 , т. е. при совпадение выходов объекта и модели на
исследуемом интервале.
, т. е. при совпадение выходов объекта и модели на
исследуемом интервале.
Если
объект является статическим и непрерывным А=0βγ0 т. е. , F(·) есть функция то невязка (5)
принимает вид:
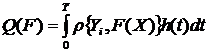
Для
дискретного объекта ( 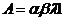 ) функционал невязки записывается в очевидной форме:
) функционал невязки записывается в очевидной форме:
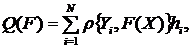 (7)
(7)
а
статическим дискретный объект (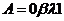 ) имеет
функционал невязки в виде:
) имеет
функционал невязки в виде:
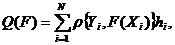
где,
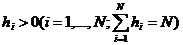 - вес информация в i-й момент
времени. Если объект стохастический и дискретный (
- вес информация в i-й момент
времени. Если объект стохастический и дискретный (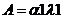 ) и измерения , например, зашумлены случайной помехой
с изменяющейся дисперсией σ2i(i=1,
. . . , N), то вес следует определять как
) и измерения , например, зашумлены случайной помехой
с изменяющейся дисперсией σ2i(i=1,
. . . , N), то вес следует определять как
hi=k/σ2i,
где
k - нормирующий член.
Таким
образом степень несоответствия (степень невязки) операторов модели и объекта
можно выразить в виде функционалов типов (5) и (7), зависящих явно от оператора
модели F.
Естественно,
процесс идентификации, т. е. процесс определения оператора модели, строит так,
чтобы минимизировать указанную невязку, т. е. решать задачи минимизации
функционала Q(F) по оператору F:
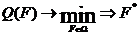 (8)
(8)
Эта символическая запись выражает следующую простую мысль: нужно минимизировать
функционал Q(F), варьируя оператором (или в простейшим случае функцией ) F не произвольно , а в некотором
определенном классе операторов (или функцией) Ω. Это обозначается с отношение F ÎΩ , т. е. F принадлежит классу Ω, где Ω - заданный класс операторов или
функций. Результатом процедуры минимизации является некоторый оператор (или
функция) F* (не обязательно единственно), обладающий свойством:
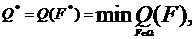 (9)
(9)
т. е. невязка Q* на этом операторе минимально (точнее,
не превышает всех возможных невязок, которые можно получить в классе Ω).
Говоря еще проще, для идентификации в заданном классе надо найти оператор
F, минимизирующий функционал невязки Q(F) на этом классе.
Утверждения, что идентификация всегда сводиться к операции отыскания
минимума, естественно, преувеличено. Действительно легко представить себе
статический объект , который идентифицируется путем решения системы линейных
или в общем случае нелинейных уравнений. Однако утверждения о сведении задания
идентификации к задаче минимизации имеют общий характер для всех случаев
идентификации с любыми классами допустимых операторов и функций .
Таким образом, использование процедуры минимизация для решение задачи
идентификации объектов является принципиальным и важным обстоятельством,
свойственным обычно решению сложных задач идентификации.
2. Трудности идентификации
Отметим две трудности постановки и решения задачи идентификации.
Первая трудность заключается в определении класса оператора Ω, в котором ищется это решение.
Преодоление этой трудности едва ли в настоящая время возможно формальным
образом.
Действительно, на стадии определение класса Ω
должна быт использована
априорная информации об объекте как предмета идентификации для целей
управления. Этот этап крайне трудно формализуем и нуждается в эвристических
решениях. Пока такие решения может принимать только человек.
Для принятия решения о классе Ω необходимо учесть следующее:
1) структур объекта управления ;
2) механизм работы объекта ;
3) цель управления ;
4) алгоритм управления.
Последние два пункта связывают класс Ω с будущим управлением, для которого и
идентифицируется объект.
Вторая трудность, которую нужно преодолевать при идентификации,
заключается в решении поставленной задачи минимизации (8) с наименьшим ущербом
для потребителя . дело в том, что процесс решения всякий задачи связан с
определенными потерями ( времени, средств, оборудование, энергии и т. д. ). Это
обстоятельство накладывает определенные ограничение на выбор алгоритма
идентификации.
Действительно, это алгоритм должен решать поставленную задачу в
определенном смысле наилучшим образом. Например, задачи идентификации должна
быть решена за минимальное время или затраты средств на ее решение должны быть
минимальные и т. д.
Как видно, всегда должен быть определен критерий эффективности процесса
решение задачи идентификации. Чаше всего это будет ущерб, наносимый в процессе
решение задачи идентификации, т. е. потери на идентификацию. Очевидно, что эти
потери зависят от сложности задачи (8), необходимого объема экспериментальных
данных и способа решения задачи, т. е. от алгоритма минимизации функционала Q(F).
Обозначим через А - алгоритм решения задачи идентификации (9), а I - потери на идентификацию, которые
представляют собой функционал, зависящий от алгоритма А. Очевидно, что алгоритм
следует выбирать таким, чтобы потери на идентификацию I были минимальны. Отсюда очевидным образом следует задача
определения алгоритма как задача минимизации:
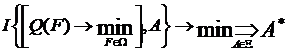 (10)
(10)
где I{B, A} - потери на
идентификацию, т. е. на решение задачи B=[Q((F)à minFÎΩ] с помощью алгоритма А. Этот
функционал должен быть задан. К примеру это может быть временно или стоимость
решения задачи идентификации, сложность ее программирования, сложность
применяемой при этой операторе, ее амортизация в процессе работе и
т.д.
Задача (10) формулируется следующим образом: нужно в классе Ξ
найти алгоритме
идентификации А*, которой минимизирует потери на идентификацию I заданного объекта. Такой алгоритм А*
естественно называть оптимальном в указанном смысле. Класс Ξ
алгоритмов идентификации
при этом должен быть задан. Если множество Ξ состоит из конечного и не слишком
большого числа алгоритмов т. е.
Ξ 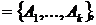
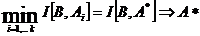
Заметим сразу, что, как правило, для идентификации выбирается не
оптимальный алгоритм А*, а некоторый рациональный алгоритм Ã*, который обеспечивает решения задачи
при допустимых потерях на идентификацию. Пусть I - допустимые потери. Тогда задача отыскание рационального
алгоритма сводится к следующей:
 (11)
(11)
Любой алгоритм из множества Ξ, удовлетворяющий этому неравенству,
следует считать рациональным.
Таким образом, вторая трудность решение задачи идентификации сводиться к
отысканию алгоритма решения этой задачи. При этом искомый алгоритм не может
быть любым и должен удовлетворять определенным требованиям - оптимальности (10)
или рациональности (11). Не последнюю роль здесь играет задание класса
алгоритмов идентификации Ξ. процесс определение класса Ξ
является эвристическим и
пока доступным лишь человеку.
Контрольные вопросы
1. Определение задачи идентификации.
2. Как ставиться задача идентификация?
3. Что понимается под функцией невязки
выходов объекта и модели?
4. Сведение задачи идентификация к
задаче оптимизации?
5. Какие трудности возникают в задачах
идентификации?
Литература
1. Растригин
Л.А. Современные
принципы управления сложными объектами, М.: Советское радио, 1980 г. - 232 стр.
2. Растригин
Л.А., Маджаров Н.Е. Введение
в идентификацию объектов управления, М.: Энергия, 1977 г. - 216 стр.
Лекция 6. ЗАДАЧИ ИДЕНТИФИКАЦИИ И КЛАССИФИКАЦИЯ МЕТОДОВ
ИДЕНТИФИКАЦИИ (2 часа)
План
1.
Идентификация структуры и параметров объекта
.
Классификация методов идентификации
1. Идентификация структуры и параметров объекта
Будем называть структурной идентификацией процесс определения
структуры оператора модели F. Если
же структура этого оператора F
определена или априори известно, то процесс идентификации сводится к
определению параметров этой структуры, т. е. задаче более простой чем
предыдущая. Назовем ее параметрической идентификацией (иногда первый процесс
называет идентификацией широком смысле, а второй - в узком).
Таким образом , идентификация структуры связана прежде всего с
предварительном выбором структуры модели, а идентификация параметров - лишь с
определением параметров этой модели при заданной структуре. Как видно,
первый этап структурной идентификации предшествует второму и часто включает в
себя второй как составную часть.
К сожалению, понятия «структура» не имеет четкого определения, хотя по
видимому, интуитивно понимается всеми примерно одинаково. Будем под структурой
модели понимать вид оператора с точностью до его коэффициентов. Заметим, что
структура объекта , кодируемая А, вообще говоря, может не совпадать со
структурой модели . Так, стохастический свойства объекта обычно не отражаются
модели, а лишь определяют выбор метода идентификации ее параметров. Кроме того,
модель может заведомо иметь меньше входов и выходов, чем их имеет объект. Это
часто делает при малом объеме наблюдений (иначе не определить параметры
модели).
Теперь уточным задачу идентификации. Пусть структура модели известна , т.
е. задача структурной идентификации решена. Тогда оператор F(х) может быть представлен в виде
F(x)=f(x, c),
где f(., . ) - заданный оператор, а С=(с1,
. . . , ск) -вектор неизвестных параметров модели. В этом случае
задача идентификации параметров модели может быть записана, вообще говоря в
виде задачи минимизации функции (а не функционала) невязки:
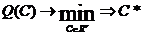 (12)
(12)
решением которой является вектор С*=(с*1, . . . с*к).
Здесь
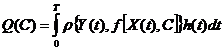
функция
невязки выходов объекта и модели ; Rk - k-
мерное евклидово пространства векторов С . Здесь трудности решения задачи
заключается в организации эффективного процесса минимизации заданных функций
многих (к) переменных. Заметим, что так, как структура модели известна, то
число переменных k определено заранее.
Очень
часто структуру можно закодировать, введя структурный параметры. Такими
структурными параметрами является числа k и l в
примере 2. В общем случае обозначим эти параметры вектором.
D=(d1, . . . , dq),
Это
означает, что структура кодируется q величинами d1, . . . , dq. Оператор модели теперь представляется в виде
F(X) = f(X, C, D),
Где f-заданный оператор. Здесь оператор
модели определяется двумя типами параметров структурными D и параметрами объекта С. Функция
невязки выходов объекта и модели (5) здесь принимает вид:
Тогда задачи идентификации в широком смысле сведется к решению следующий
задачи минимизации функции k+q переменных:
Здесь S - область определения структурных
параметров.
В заключение отметим, что сведение общей задачи идентификации (8) к
параметрический идентификации (12) и (13) естественно имеет условный характер.
Целью такого представления является упрощения задачи и сведение ее к известно
ранее с хорошо разработанными методами решения. Такой задачей является задача
математической программирования: минимизация функции многих переменных,
принадлежащих заданному множеству. Именно так мы сформулируем задачи параметрических
идентификации.
Однако не следует думать, что такое сведение задачи идентификации к
задаче математического программирование решает все проблемы идентификации.
Здесь возникает ряд новых проблем, например как это сведение сделать в
конкретном случае как решить полученную задачу минимизации? Эти проблемы
порождают другие и т. д. Но связь идентификации с математическим
программированием, отмеченную выше, следует всегда иметь виду.
2. Классификация методов идентификации
Будем различать методы идентификации по трем классификационным признакам
и характеризовать метод значениями этих признаков:
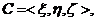 (14)
(14)
которые кодируют метод. Здесь ξ
, η, ς
- структурные признаки, которые могут принимать два значения. Естественно, что
структура метода никак не исчерпывается этими тремя признаками. Тройка (14)
служит, скорее, для обозначения метода , чем для его описания. Рассмотрим и
охарактеризуем эти признаки.
1.
Признак
активности. ξ. Будем метод идентификации называть активным (ξ=1), если при его реализации возможно
задавать и изменять определенным образом состояния входов объекта и т. е. как
бы изменять состояние среды. Это типичное управление объектом, но для
достижения целей идентификации. Если объект не позволяет управлять
состоянием его входа, то метод его идентификации мы будем называть пассивным (ξ=0), т. е. опирающийся на данные β, полученные в режиме нормальной
эксплуатации объекта. Блок-схема реализации активного метода показана на рис 1.
Здесь вход объекта управляется в процессе идентификации так, чтобы повысить ее
эффективность.
Рис 1. Блок-схема активного метода идентификации
2. Признак адаптивности η. Если информация β
о поведении
объекта используется в процессе идентификация не сразу, а по мере ее
поступления или циклически и при этом значения идентифицируемых параметров
корректируется на каждом шаге или непрерывно, то такой метод будем называть
адаптивным. В противном случае метод будем называть неадаптивным (η=0).
Если адаптивный метод параметрической идентификации применяет в реальном
масштабе времени использую непосредственно измерения входа и выхода объекта то
в этом случае его называют методов самонастраивающейся модели. Суть этого
метода состоит в следующим (рис 2).
Рис 2. Блок-схема реализации метода самонастраивающейся модели.
В каждый момент времени сопоставляются выходы объекта и модели, при этом
квадрат разности выходов минимизируется путем соответствующего выбора
параметров с оператора модели. Для повышения эффективности процесса минимизация
используется информация о состояния среды Х. Как видно модель таким образом все
время подстраивается к объекту, чтобы их реакции на один и тот же вход в каждый
момент времени различались минимально.
Адаптивный метод для дискретных объектов всегда описывается рекуррентной
формулой вида
Сi=I(Ci-1, Xi, Yi), (15)
Где Сi - вектор
идентифицируемых параметров на i-m шаге адаптации; I-алгоритм адаптации. Выражение (15)
удобно записать в виде
Ci=Ci-1+∆ Сi (16)
Где ∆ Сi
- приращение, реализуемое алгоритмом адаптации
∆ Сi=φ(Сi-1, Xi, Yi).
В k-мерном пространстве идентифицируемых
параметров С = (с1, ...., сk) процесс адаптации иллюстрируется ломаной С0
... Сi-1 Сi Сi+1. . . ,
которая стремится к С*=(с*1, . . . . , с*k) - точному значению параметров (рис.
3).
Рис. 3. Пример работы адаптивного метода
Для прерывного объекта (A=αβγ0) процесс адаптивной идентификации
реализуется дифференциальным уравнением
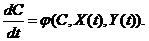 (17)
(17)
Однако режим адаптивной идентификации может реализоваться не только по
схеме самонастраивающейся модели, т. е. в режиме реального масштаба времени .
Если объем наблюдений мал, т. е. малы N(в дискретном случае) и Т(в непрерывном), то однократное использование
информации β может не решит задачи идентификации. В этом случае
целесообразно образовать цикл
B’=BBB. . . ,
которые решает поставленную задачу .
Следуют отметить такую особенность адаптивного метода. Он почти никогда
не решает задачу идентификации абсолютно точно, во всяком случае в пассивном
варианте. Но зато он позволяет все время улучшать значения идентифицируемых
параметров. По этому его целесообразно применять для идентификации “дрейфующих”
объектов параметры которых медленно изменяются. В этом случае адаптивной метод
позволяет отслеживать медленные изменения.
1.
Признак
шаговости ξ. Если идентифицируемые параметры в процессе
адаптивной идентификации изменяются дискретно, то такой метод будем называть
шаговым (ξ=1). В противном случае метод непрерывный
(ξ=0). Так, адаптивный метод (15) имеет
шаговый характер, а (17) - непрерывный.
Как видно, хотя этими тремя признаками метод идентификации описать проста
невозможно, они характеризирует структурные особенности метода которые
определяются спецификой объекта.
Контрольные вопросы
1. Что понимается под структурной
идентификацией?
2. Как решается задача параметрической
идентификации?
3. По каким признакам можно
классифицировать методы идентификации?
4. Адаптивный метод идентификации.
Литература
1. Растригин
Л.А. Современные
принципы управления сложными объектами, М.: Советское радио, 1980 г. - 232 стр.
2. Растригин
Л.А., Маджаров Н.Е. Введение
в идентификацию объектов управления, М.: Энергия, 1977 г. - 216 стр.
Лекция 7. СТРУКТУРНАЯ ИДЕНТИФИКАЦИЯ (2 часа)
План
1.
Выделение объекта из среды
.
Ранжирование входов и выходов объекта (Метод экспертных оценок)
.
Метод непосредственного ранжирования
К
задачам идентификации структуры объекта будем относить следующие:
1) выделенные объекта из среды.;
2) ранжирование входов и выходов
объекта, по степени их влияния на выполнение целей управления в объекте;
3) определение рационального числа
входов и выходов объекта, учитываемых в модели;
4) определения характера связи между
входом и выходом модели объекта, т. е. определение вида оператора F (это есть собственно структура
объекта .)
Рассмотрим каждую из этих задач в отдельности и укажем возможные пути их
решения.
1. Выделение объекта из среды
Как указано выше, процесс выделения объекта из среды полностью
определяется целями и алгоритмом управления. Это утверждение , однако,
нуждается пояснении. Действительно, если процесс определения объекта зависит от
целей, которые будут реализоваться в нем, то естественно спросить, а от чего
зависят эти цели? Цель по отношению к управлению имеет внешний характер. Она
формулируется на более высоком иерархическим уровне и выражает требования этого
уровня, предъявляемые к объекту управления. Однако формулировка и определения
множества целей связано с представлениями об объекте, в котором должны
реализовать эту цель. Действительно, нельзя эффективно сформулировать цель,
если не иметь какой-то модели объекта управления. Поэтому еще до формулировки
цели некоторая модель объекта должна быть. Естественно, что эта первая модель очень
приближенна, но именно она должна лечь в основу определения объекта управления,
т. е. процесса выделения объекта из среды.
Пусть цель Т в виде множества состояний T={Y*}, которые
должны быть достигнуты в процессе управления. Какую именно цель Y*Î{Y*} необходимо будет реализовать в определенный момент времени
определит верхний уровень управления . это означает , что управляющее
воздейтвие U в этот момент должно быть таким ,
чтобы состояние объекта Y
совпало с заданным целевым, т. е.
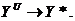
Однако
всякое управляющее воздействие U ограничено определенным ресурсом R.
Пусть {U}R - ресурсное множество управлений, которым располагает
управлений т. е.
UÎ{UR}
Таким
образом, для определения объекта необходимо знать множества целей {Y*} и
располагаемых управляющих воздействий {U}R.
Рассмотрим
теперь процесс выделение объекта из среды как последовательный переход от
простейших форм объекта к более сложным.
Простейшей
формой объекта назовем такую минимальную часть среды, которая несет информацию,
необходимую для проверки выполнимости поставленной цели. Эта минимальная часть F
показана на рис. 1, причем
Y=F(X, U).
Рис.
1. Блок-схема процедуры оценки выполнимости целей управления
Если
этот объект и среда Х таковы, что для любой цели Y*Î{Y*} и любого состояние среды ХÎ{Х} всегда найдется управление U*Î{U}R такое, что
Y*=F(X, U*), (1)
то этот объект удовлетворяет целям управления и процесс его определения
можно считать законченным.
В противном случае, когда ресурса R не хватает для обслуживания всех целей ввиду того, что среда
Х при этом слишком сильно изменяется, приходится расширять рамки объекта,
включая в него ту часть среды, которой можно управлять. Так, как воздействие Х
в значительной степени образуется каким-то определенным элементом среды, то
естественно попытаться этот элемент присоединить к объекту и управлять им с
тем, чтобы изменить в нужную сторону Х. Это расширение объекта показано на рис.
2.
Рис. 2. Структурная схема присоединения части среды к объекту
Если сделанное расширение объекта не удовлетворят целям управления, то
следует воздействовать на X’’ или X’’ , т. е. далее расширять объект.
Легко себе представить, что для любого множества заданных целей {Y*} описанный процесс расширения
объекта может либо закончится на каком - то шаге, либо никогда не закончится .
В первом случае мы получаем объект управления, во втором - констатируем, что
поставленная цель Т={Y*} не
достижима вообще, т. е. сформулирована ошибочна , без учета возможностей
объекта и среды. Такую цель надо менять или увеличить ресурс R.
Таким образом, процесс расширения объекта при его выделении должен
подчиняться следующему принципу: присоединять к объекту лишь те элементы среды,
которые воздействует на реализацию цели и которыми можно эффективно управлять
для достижения этой цели.
Заметим, что формальные реализации описанной процедуры выделения объекта
возможно лишь в том случае, если для каждого варианта выделения объекта
идентификация проводиться до конце т. е. до составления полной модели объекта.
Но для этого необходимо располагать измерениями В, которые производятся
при выбранной структуры (иначе не известно что именно измерять .) Столь
громоздкую процедуру с выходом на эксперимент едва ли в ближайшее время удастся
формализовать. По этому на стадии структурной идентификации широко пользуются
методом экспертного опроса, по результатам которого и принимаются решения о
структура объекта, его взаимоотношения со средой, возможным состоянием среды и
т.д.
2. Ранжирование входов и выходов объекта (Метод экспертных
оценок)
Для определения структуры модели объекта, представленного в виде
многополюсника, прежде всего необходимо выяснить, какие именно входы и выходы
объекта будут включены в его модель. Для этого прежде всего выявляет всех
возможных реальных «претендентов» на роль входов и выходов и из них выделяют
наиболее существенные, которые и образуют многополюсник модели n ´ m. Но здесь сразу возникает вопрос о том, какие входы называть
существенными. Ответь здесь однозначный. Так как модель создается для целей
управления, то существенным является тот фактор, который наибольшим образом
оказывает влияние на осуществление цели управление в объекте, а значит, и в его
модели. Это связано с тем, что при формировании структуры системы управления
прежде всего необходимо знать, какие воздействия может и будет испытывать
объект управления и как результаты этого воздействия связаны с достижением цели
управление в объекте. Поэтому при выборе структуры приходится варьировать числом
учитываемых входов и оценивать эффективность выбранной комбинации. Для этого
следует проранжировать выбираемые факторы. В этом случае выбор наиболее
существенных факторов очевиден - они должны быть расположены в начале
ранжированного ряда.
Поэтому первым этапом в задаче идентификации объекта следует считать
задачу ранжирования его входов . Так как модели объекта еще нет, то
ранжирование его можно сделать, например, методом экспертных оценок.
Для этого прежде всего определяются все входы и выходы, состояния которых
в какой-то степени можно влиять на выполнение цели в объекте
Как и выше будем различать два вида входных переменных - воздействие
среды Х и управления U и
выход Y. Рассмотрим их подробнее.
Входы Х=(х1, . . . , хn) подразумеваются прежде всего контролируемыми. В
противном случае их не имеет смысла вводить в модель. Отбор «претендентов» на
входы Х должен подчинятся следующим требованиям:
1) отбираются те и только те входы х1,
. . . , хn, состояние которых влияет на
реализацию цели в объекте;
2) состояния каждого входов хi должно эффективно, т. е. легко и
надежно, контролироваться (измеряться);
Исходя из этих соображений, составляется ряд «претендентов». Однако это
совсем не означает , что все они войдут в модель. Действительно некоторые из
них почти не влияют на цель и ими можно пренебречь. А другие хотя и влияют на
цель, но трудно измеряемы и поэтому также могут быть отброшены.
Однако прежде, чем производить селекцию входов необходимо их
проранжировать по степени их влияние на реализацию цели управления в объекте.
Это означает что каждому входу xi(i=1, . . . , n) следует постановить в соответствие
некоторое целое число ki - его ранг:
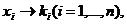
где
единичный ранг (k=1) имеет вход, влияющие наибольшим образом на
реализацию цели в объекте. Второй ранг (ki=2) и т. д. имеют входы, влияющие не столь существенно, как единичный. Здесь как видно, индексы при рангах определяют номер
ранжированного входа от первого до n-го.
Расположим
теперь входы в порядке возрастания их рангов
xi1, xi2 , . . . , xin, (2)
где индекс ij
равен номеру фактора с рангом j.
Этот ряд будем называть ранжированным рядом. Здесь на первом месте стоит самый
существенный вход, а далее следуют остальные в порядке уменьшение их влияния на
цели управления. Теперь, если в модели следует по каким-то соображениям
оставить лишь q входов, ими будет факторы с номерами
от i1 до iq т. е. имеющие первые q рангов.
Составить ранжированную последовательность при отсутствии модели объекта
можно например, с помощью специалистов - экспертов, хорошо осведомленных об
особенностях среды объекта F0 а также цели и способах ее
достижения, т. е. имеющих представление о будущем алгоритме управления этим
объектом.
Таким образом с помощью экспертов составляется последовательность:
k1, k2, . . . , kn, (3)
где ki- ранг i-го входа хi . Построить из нее ранжированный ряд (2) не представляет
труда. Например, при n=5
последовательность рангов (3) может иметь вид:
, 1, 5, 4, 2.
Это означает, что для данной задачи наибольшее влияния на цели управления
с учетом возможности измерения имеет второй вход х2 . Ему
приписывается единичный ранг (k2=1). Второй ранг имеет пятый вход (k5=2)и т. д. , т. е. k1=3, k4=4, k3=5.
Теперь рассмотрим входы управления U=(u1, . . . , uq). Эти входы также нужно
проранжировать, учитывая степени их влияния на достижения целей управления и
простоту организации изменения этих входов, т. е. простоту реализация
управления. Этот последний фактор управляемости очень важен, так как далеко не
всегда желание управлять каким-то определенным входом согласуется с
возможностями. Поэтому ранжирования входов управления должно производиться
экспертами, не только осведомленными об особенностях объекта управления, но
знакомыми со способами организации управляющих воздействий.
Аналогично каждому входу управления uj(j=1, . . . , q)
экспертно ставиться в соответствие ранг kj целое число в интервале [1, q]):
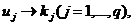
причем
единичный ранг соответствует самому существенному и легко изменяемого входу
управления, а самому не существенному и самому трудноизменяемо приписываться
ранг q.
Выходы
объекта также должны быть проранжированы. Здесь критерием может служит
количество информации который несет данный выход о близости к реализации целей
управления в объекте. Не имя модели объекта, это может сделать экспертно,
получить соотношения
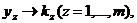
где
kz - ранг выхода yz.
Как
видно, все три случае, по сути дело одинаковы. Нужно путем опроса
экспертов-специалистов присвоить определенным параметрам (входа и выхода
будущего объекта управления ) различные ранги по степени их влияния на один или
несколько различных критериев. Это процедура получила названия метода
экспертных оценок. Рассмотрим только две модификации этого метода :
1) метод непосредственного ранжирования;
2) метод парных сравнений.
В первом случае эксперта сразу присваивают ранги фактором, которые
представлены для ранжирования. Второй метод использует парное ранжирование
факторов, что упрощает задачу эксперта, но требует дальнейшей обработки доля
получения ранжированного ряда.
3. Метод непосредственного ранжирования
Пусть N экспертов ранжируют n факторов. Каждому фактору каждый эксперт
присваивает ранг - целое число от 1 до n. Так, i-му
фактору j-й
эксперт присваивает ранг kij. В результате получается матрица N Х n
мнений экспертов где номера строк соответствуют номерам экспертом, а номера
столбец - номером ранжируемых факторов. Это означает что j-я строка представляет собой имени j-го эксперта, а i-й столбец - мнений всех экспертов по
поводу i-го фактора.
При назначении рангов экспертами нужно соблюдать следующие условия:
1. Сумма рангов, назначенных всем
факторам, должна быть одинакова для каждого эксперта и равна:
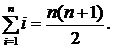
Это означает, что сумма элементов любой строки матрицы (4)
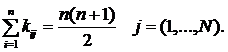
.
Если эксперт какие-то q факторов считает одинаковыми, то он присваивает им
один ранг. Этот ранг равен .среднему из q целых рангов, которые получены
при условии, что эксперту удалось их проранжировать. Например, равноценность
четырех факторов (q=4):
x1,x2,x3,x4, стоящих на пятом месте в ранжированном ряду,
приводит к тому, что их ранги равны:
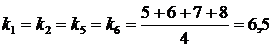
Как
видно, в этом случае ранги могут быть дробными. Как легко убедиться, дробные
ранги кратны 1/2.
Для
определения результирующих рангов следует вычислить средние ранги каждого
фактора

Эти
ранги и дают возможность проранжировать факторы. На первом месте ставится
фактор, имеющий минимальный средний ранг
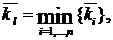
т.
е. фактор xl , на втором
- фактор, имеющий следующий по малости средний ранг, и т. д. Полученные ранги
позволяют построить ранжированный ряд факторов, который и будет осредненным
мнением коллектива из N экспертов.
Очевидно,
что далеко не всякий результат экспертного опроса следует считать
удовлетворительным. Действительно, если эксперты сильно противоречат друг другу
(например, половина экспертов фактору xi присвоила первый
ранг, а другая половина-последний), то такое ранжирование не может быть
положено в основу решающих процедур. Поэтому для оценки всякого экспертного
опроса вводится критерий, характеризующий согласованность экспертов. Чем выше
эта согласованность, тем более можно “верить” результатам экспертного опроса, и
наоборот.
Согласованность
экспертов удобно определять как степень рассеяния средних рангов 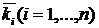 . Действительно, если эксперты полностью согласованы,
то средние ранги представляют собой целые, не равные друг другу числа (случай
одинаковых рангов пока не рассматриваем). Графически это проиллюстрировано на
рис. 3. а), где точками показано расположение средних рангов на числовой оси.
. Действительно, если эксперты полностью согласованы,
то средние ранги представляют собой целые, не равные друг другу числа (случай
одинаковых рангов пока не рассматриваем). Графически это проиллюстрировано на
рис. 3. а), где точками показано расположение средних рангов на числовой оси.
Если
же эксперты полностью не согласованы, то средние ранги примерно равны (n+1)/2.
В промежуточном случае (при частично согласованных экспертах) ранги
сгруппируются вокруг среднего значения (n+1)/2 (это
проиллюстрировано на рис. 3. б).
Рис.
3. Средние ранги на числовой оси при полностью (а) и частично (б) согласованных
экспертах
Вычислим
дисперсию средних рангов. Она, по определению, равна:
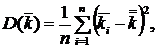
Где
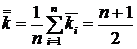
математическое
ожидание среднего ранга. Определим максимальную дисперсию (она бывает при
полностью согласованных экспертах)
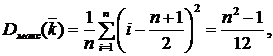
Критерий
согласованности экспертов удобно представить в виде отношения
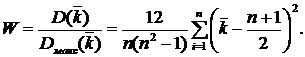
Легко
заметить, 0≤W≤1. При W=0 эксперты полностью не согласны, а при W=l
они высказываются как один, т. е. единогласно. Таким образом, значение W
характеризует степень согласованности экспертов.
Чем
ближе W к единице, тем более единодушны эксперты и тем более достоверен
результат ранжирования. (Следует отметить, что эксперты должны высказывать свое
мнение независимо друг от друга, т. е. до ранжирования они -не должны знать
мнение других экспертов. В противном случае возможно появление корреляции
мнений, что повышает критерий согласованности W, хотя в действительности
эксперты не столь единодушны).
Для
того чтобы знать, велико или мало конкретное значение критерия согласованности,
который никогда не бывает равным ни нулю, ни единице, можно 'предложить
следующий подход. Предположим, что т из N экспертов абсолютно
компетентны, а остальные N-т совершенно некомпетентны, т. е. принимают
свое решение чисто случайно (хотя такого, как правило, не бывает). Тогда
дисперсия средних рангов
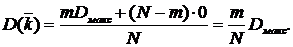
Разделив
все на Dмакс,
получим:
W=m/N.
Это
значит, что W выражает долю абсолютно компетентных экспертов. Так, при W=0,3 можно считать, что 30% экспертов были вполне
компетентны, а остальные 70% принимали свое решение случайно, что, естественно,
могло оказать роковое влияние на окончательную ранжировку (а могло и не
оказать!).
Отсутствие
согласованности мнений экспертов может иметь двоякое объяснение. Во-первых, это
возможно из-за некомпетентности экспертов, связанной с новизной или слабой
изученностью объекта идентификации. Во-вторых сложность объекта затрудняют
эксперта в ответах о рангах факторов. Эксперту в этом случае проще сопоставить
важность некоторых факторов попарно, т. е. указать, чей ранг одного из двух
факторов будет больше. Именно в таких ситуациях обращаются к методу парных
сравнений, который мы и рассмотрим ниже.
Контрольные вопросы
1. Какие задачи структурной
идентификация вы знаете?
2. Что понимается под ранжированием
входов и выходов объекта?
3. В чем заключается сущность метода
непосредственного ранжирования?
Литература
1. Растригин
Л.А. Современные
принципы управления сложными объектами, М.: Советское радио, 1980 г. - 232 стр.
2. Растригин
Л.А., Маджаров Н.Е. Введение
в идентификацию объектов управления, М.: Энергия, 1977 г. - 216 стр.
Лекция 8. ИССЛЕДОВАНИЕ ЗАДАЧ СТРУКТУРНОЙ ИДЕНТИФИКАЦИИ (2
часа)
План
1.
Метод парных сравнений
.
Определение рационального числа входов и выходов объекта, учитываемых в модели
.
Определение характера связи между входом и выходом модели объекта
1. Метод парных сравнений
Эксперту предлагается проранжировать факторы попарно, т. е. каждой паре
факторов хi и xl поставить в соответствие число qil:
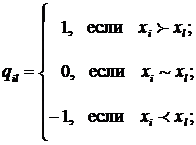
где
знак “ ” обозначает предпочтительность. Так, выражение хi
” обозначает предпочтительность. Так, выражение хi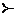 xl следует читать: “i-й фактор более предпочтителен при ранжировании, чем l-и”.
Знак ~ является знаком эквивалентности факторов с точки зрения ранжирования. Числа
qil обладают очевидным свойством
xl следует читать: “i-й фактор более предпочтителен при ранжировании, чем l-и”.
Знак ~ является знаком эквивалентности факторов с точки зрения ранжирования. Числа
qil обладают очевидным свойством
qil + 0 = qil.
Таким
образом, каждый (j-и) эксперт свое мнение представляет в виде таблицы п×п (табл. 1)
Или
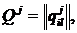
где
верхний индекс определяет номер эксперта.
Таблица
2-1
|
x1
|
X2
|
. . .
|
xn
|
0
|
qj12
|
. . .
|
qj1n
|
|
x2
|
qj21
|
0
|
. . .
|
qj2n
|
|
. . .
|
. . .
|
. . .
|
. . . . . . . .
.
|
. . .
|
|
xn
|
qjn1
|
qjn2
|
. . .
|
0
|
Осредним мнение экспертов. Для этого достаточно построить осредненную
таблицу (n×n)
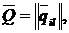
Где
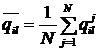
среднее
предпочтение i-го фактора перед l-м. Это и
есть мнение экспертов. Определим согласованность экспертов. В качестве меры
согласованности аналогично предыдущему естественно выбрать дисперсию величин 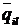 . В силу
того, что среднее значение
. В силу
того, что среднее значение 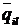 равно
нулю, для дисперсии получаем:
равно
нулю, для дисперсии получаем:
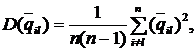
где
суммирование производится по всей таблице 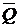 .
Максимальное значение дисперсии будет иметь место при полной согласованности
экспертов и равно:
.
Максимальное значение дисперсии будет иметь место при полной согласованности
экспертов и равно:
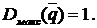
Тогда,
вводя критерий согласованности как отношение дисперсии средних предпочтений к
максимальной дисперсии, получаем:

Однако
эксперты могут противоречить. Примером такой таблицы 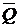 может служить табл. 2, где противоречие имеет вид
может служить табл. 2, где противоречие имеет вид 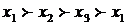 , т.е. оказалось что
, т.е. оказалось что 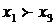 и
и 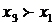 одновременно.
одновременно.
Таблица
2
|
x1
|
x2
|
x3
|
|
x1
|
0
|
1
|
-1
|
|
x2
|
-1
|
0
|
1
|
|
x3
|
1
|
-1
|
0
|
Выявление подобных противоречий совершенно необходимо не только в
осредненной таблице, но и в мнении каждого эксперта. Это можно сделать на
основе. следующего, довольно очевидного правила, которое называется правилом
транзитивности.
Для предпочтений оно имеет вид:
если
х1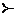 х2 и x2
х2 и x2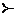 х3, то
х1
х3, то
х1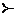 х3. (5)
х3. (5)
Для эквивалентности:
если х1 ~ х2 и x2 ~ х3, то х1 ~ х3
Таблицы, представляющие собой мнение каждого эксперта, должны
удовлетворять указанной транзитивности и при обнаружении противоречий
возвращаются соответствующему эксперту для разрешения отмеченных противоречий.
Для определения рангов ранжируемых факторов следует определить правило
назначения рангов по таблице Q. Таких правил может быть много. Рассмотрим два
из них,
Правило 1. Определим суммарные предпочтения каждого фактора
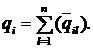
Естественно
считать, что первый ранг имеет фактор, суммарное предпочтение которого
максимально, т. е. при
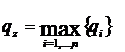
первый
ранг имеет фактор xz, т. е. kz=1.
Аналогично образуются ранги остальных факторов.
Рассмотренное
правило, однако, излишне осредняет предпочтения. Так, фактор, имеющий ряд явных
предпочтений, которые легко обнаруживают эксперты, получит первый ранг только
потому, что его второстепенность по отношению к другим факторам будет не столь
ярко выражена. Именно в этом случае часто приходится обращаться к другому
правилу.
Правило
2. Основная мысль этого правила
опирается на идею усиления контраста. Для этого вводится порог δ. Если предпочтение выше этого порога, то оно имеет
явный характер, а если ниже, то оно сомнительно, т. е. больше соответствует
эквивалентности. Получаем следующее преобразование матрицы средних предпочтений
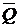 в контрастную матрицу U, которую легко преобразовать в ранжированный ряд:
в контрастную матрицу U, которую легко преобразовать в ранжированный ряд:
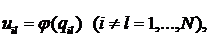
Где
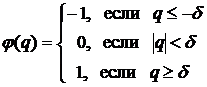
Как видно, это преобразование целиком и полностью определяется порогом δ
(0<δ<1). При δ=1
контрастная матрица U
становится нулевой и все факторы эквивалентны. При δ=0
она полностью
заполняется единицами, но при этом почти неизбежно появление противоречий в
виде нарушений транзитивности предпочтений (5).
Поэтому при выборе порога δ следует помнить, что его увеличение
приводит к отказу от ранжирования, а уменьшение-к увеличению числа явных
предпочтении и к опасности появления противоречий.
Одной из возможных рекомендаций по определению оптимального порога
является выбор порога δ на “пороге противоречий”, т. е. такого значения δ,
незначительное
уменьшение которого приводит к противоречиям.
2. Определение рационального числа входов и выходов объекта,
учитываемых в модели
Описанным выше образом получаются ранжированные ряды всех претендентов на
входы и выходы модели:
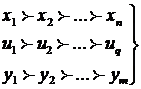 (6)
(6)
(здесь для удобства произведена перенумерация ранжированных факторов
таким образом, чтобы их номер стал равен рангу, т. е. ki=i).
Выбор рациональных чисел n*, q* и m*, характеризующих
модель, т. е. размерность ее входов и выходов, следует также производить
экспертно. Для этого нужно начать с минимального числа входов и выходов (n1, q1, m1, т. е. с простейшей модели, например, с n1=0; q1=m1=1). Назовем эту модель F1 [характер связи Y=F1 (X, U), где Y=(y1, ..., ym1);
X=(x1, ..., xn1);
U=(u1, ..., uq1):
при этом выяснять .не нужно, модель рассматривается как “черный ящик”]. Таким
образом, первая, простейшая модель характеризуется тройкой F1=<n1, q1, т1>. Вторая модель F2=<n2, q2, m2> должна быть выбрана экспертами
из трех:
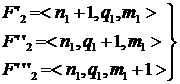 (7)
(7)
Здесь мы воспользовались ранжированными рядами (6), что позволяет
усложнять объект введением фактора, имеющего очередной ранг.
Эксперты ранжируют тройки (7) по критериям, заранее оговоренным. Тройка,
получившая первый ранг, образует F2.
Аналогично (i+1)-я модель Fi+1 определяется ранжированием трех
полученных из Fi троек:
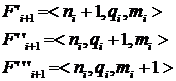
Таким
образом, получим последовательность моделей объекта F1, F2, ..., Fl, расположенных в порядке их
уточнения и усложнения. Теперь остается в этом ряду установить предпочтение, т.
с. выбрать ту модель, которая и будет идентифицироваться. Это можно также
сделать с помощью экспертов. Пусть в результате получен ряд предпочтений:
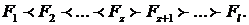
Это
означает, что следует остановиться на модели
Fz=(nz, qz, mz)
и таким образом n*=nz, q*=qz, m*=mz.
. Определение характера связи между входом и выходом модели
объекта
Мы уже говорили, что структура модели определяется видом оператора модели
F. Этот оператор, прежде всего, характеризуется кодом A. C него
и следует начинать.
Определение кода A
требует четырех двоичных выборов:
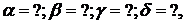
где
каждый из признаков может принимать одно из двух значений: 0 или 1. Анализ
следует начинать с простейшего (нулевого) случая. Действительно, код А построен
так, что наличие трудностей в процессе идентификации отражается единицами кода.
Так, динамический объект (α=1)
труднее идентифицировать, чем статический (α=0); стохастический (β=1) труднее детерминированного (β=0), нелинейный (γ=1) сложнее линейного (γ=0) и т. д.
В
процессе выбора кода A модели следует иметь в виду, что, учитывая эти
трудности, вполне можно намеренно “снизить” модель, т.е. сделать ее значительно
проще объекта. Так, поведение заведомо динамического объекта можно описывать
статической моделью, если динамика объекта не слишком ярко выражена; нелинейный
объект можно аппроксимировать линейным и т. д. Разумеется, что при этом
эффективность управления, построенного на основе такой модели, снизится. Но если
это снижение невелико, а выигрыш в идентификации значителен, то такой выбор
следует считать оптимальным.
После
выбора кода A модели следует определить конкретную форму ее
оператора F.
Контрольные вопросы
1. Чем различается два правила для
определения рангов ранжируемых факторов в методе парных сравнений?
2. Как определяется рациональное число
входов в выходов объекта?
3. Как определяется характер связи между
входом и выходом модели объекта?
Литература
1. Растригин
Л.А. Современные
принципы управления сложными объектами, М.: Советское радио, 1980 г. - 232 стр.
2. Растригин
Л.А., Маджаров Н.Е. Введение
в идентификацию объектов управления, М.: Энергия, 1977 г. - 216 стр.
Лекция 9. АНАЛИТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ
(2 часа)
План
1.
Потоки заявок
.
Марковские модели
1. Потоки заявок
Простейший поток. При аналитическом моделировании характеристики системы
вычисляются наиболее просто для потока заявок, называемого простейшим.
Простейший поток - это поток заявок, который обладает следующими свойствами: 1)
стационарность; 2) отсутствие последействия; 3) ординарность.
Стационарность означает постоянство вероятности того, что в
течение определенного временного интервала поступит одинаковое количество
заявок вне зависимости от расположения интервала на оси времени.
Отсутствие последействия заключается в том, что поступившие
заявки не оказывают влияния на будущий поток заявок, т. е. заявки поступают в
систему независимо друг от друга.
Ординарность - это значит, что в каждый момент времени в систему
поступает не более одной заявки.
Любой
поток, обладающий этими свойствами,  является
простейшим.
является
простейшим.
У
простейшего потока интервалы времени 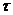 между
двумя последовательными заявками - независимые случайные величины с функцией
распределения:
между
двумя последовательными заявками - независимые случайные величины с функцией
распределения:
F(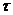 )=l-e -
)=l-e -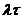 . (1)
. (1)
Такое распределение называется экспоненциальным (показательным) и имеет
плотность
f(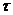 )=
)=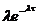 , (2)
, (2)
математическое ожидание длины интервала
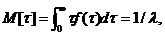 (3)
(3)
дисперсию
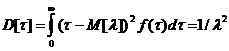 (4)
(4)
и среднеквадратическое отклонение, равное математическому ожиданию. Экспоненциальное
распределение характеризуется одним количественным параметром - интенсивностью.
Простейшие потоки заявок обладают следующими особенностями:
1.
Сумма М независимых, ординарных, стационарных потоков с интенсивностями 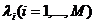 сходятся к простейшему потоку с интенсивностью
сходятся к простейшему потоку с интенсивностью
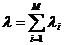 (5)
(5)
при условии, что складываемые потоки оказывают примерно одинаковое малое
влияние на суммарный поток.
2.
Поток заявок, полученный в результате случайного разрежения исходного
стационарного ординарного потока, имеющего интенсивность 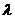 , когда каждая заявка исключается из потока с
определенной вероятностью р независимо от того, исключены другие заявки
или нет, образует простейший поток с интенсивностью р
, когда каждая заявка исключается из потока с
определенной вероятностью р независимо от того, исключены другие заявки
или нет, образует простейший поток с интенсивностью р .
.
.
Интервал времени между произвольным моментом времени и моментом поступления
очередной заявки имеет экспоненциальное распределение с таким же математическим
ожиданием 1/ , что и интервал времени между двумя последовательными
заявками.
, что и интервал времени между двумя последовательными
заявками.
.
Простейший поток создает тяжелый режим функционирования системы, поскольку,
во-первых, большее число (63 %) промежутков времени между заявками имеет длину
меньшую, чем ее математическое ожидание 1/ , и,
во-вторых, коэффициент вариации,
, и,
во-вторых, коэффициент вариации,
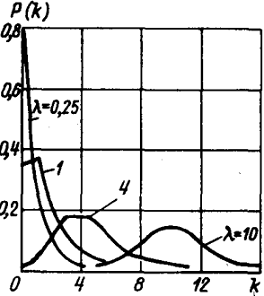
Рис. 1. Распределение Пуассона
равный отношению среднеквадратического отклонения к математическому
ожиданию:
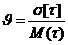
и
характеризующий степень нерегулярности потока, равен единице, в то время как у
детерминированного потока коэффициент вариации 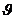 = 0, а
для большинства законов распределения 0<
= 0, а
для большинства законов распределения 0< <1.
<1.
Простейший
поток имеет широкое распространение не только из-за аналитической простоты
связанной с ним теории, но и потому, что большое количество реально наблюдаемых
потоков статистически неотличимы от простейшего. Этот эмпирический факт
подтвержден рядом математических моделей, в которых при довольно общих условиях
доказывается, что поток близок к простейшему.
Пуассоновский
поток. Пуассоновским потоком
называется ординарный поток заявок с отсутствием последействия, у которого
число заявок, поступивших в систему за промежуток времени τ, распределено по закону Пуассона:
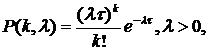 (6)
(6)
где
Р (k, 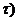 -
вероятность того, что за время τ в систему поступит точно k заявок;
-
вероятность того, что за время τ в систему поступит точно k заявок; 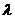 - интенсивность потока заявок.
- интенсивность потока заявок.
Математическое
ожидание и дисперсия распределения Пуассона равны 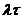 . Вид зависимостей этого распределения при
. Вид зависимостей этого распределения при 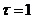 для разных
для разных 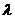 , показан
на рис. 1.
, показан
на рис. 1.
Следует
подчеркнуть, что распределение Пуассона дискретно. Стационарный пуассоновский
поток является простейшим.
Если
нестационарный поток, интенсивность которого представляет собой функцию времени
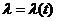 ,
описывается законом распределения Пуассона, то такой поток называется
пуассоновским, но не простейшим. В
распределении Пуассона длительности интервалов между двумя последовательными
заявками - это случайные величины с экспоненциальным распределением.
,
описывается законом распределения Пуассона, то такой поток называется
пуассоновским, но не простейшим. В
распределении Пуассона длительности интервалов между двумя последовательными
заявками - это случайные величины с экспоненциальным распределением.
Эрланговский
поток. В общем случае интервалы
времени между поступлением заявок могут иметь функцию распределения общего вида
G (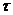 ). Если
интервалы независимы, то говорят, что заявки образуют рекуррентный поток или
поток с ограниченным последействием.
). Если
интервалы независимы, то говорят, что заявки образуют рекуррентный поток или
поток с ограниченным последействием.
Поток
называется рекуррентным (потоком Пальма), если он стационарен, ординарен, а
интервалы времени между заявками представляют собой независимые случайные
величины с одинаковым произвольным распределением. Тогда простейший поток рассматривается как частный
случай рекуррентного потока. Примером рекуррентного потока может служить поток
Эрланга.
Рис. 2. Потоки Эрланга
Потоком
Эрланга 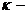 го порядка называется поток, у которого интервалы
времени между моментами поступления двух последовательных заявок представляют
собой сумму k независимых случайных величин, распределенных по
экспоненциальному закону с параметром
го порядка называется поток, у которого интервалы
времени между моментами поступления двух последовательных заявок представляют
собой сумму k независимых случайных величин, распределенных по
экспоненциальному закону с параметром 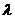 . Поток Эрланга получается из простейшего путем
исключения (k - 1) заявок с сохранением каждой k-й заявки (рис.
2). Плотность распределения интервала времени между двумя соседними заявками в
потоке Эрланга k-го порядка
. Поток Эрланга получается из простейшего путем
исключения (k - 1) заявок с сохранением каждой k-й заявки (рис.
2). Плотность распределения интервала времени между двумя соседними заявками в
потоке Эрланга k-го порядка
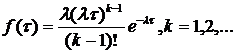 (7)
(7)
Поток Эрланга превращается в простейший при k = 1. Приведенные
потоки наиболее широко используются в теории массового обслуживания, в том
числе при аналитическом моделировании ВС.
. Марковские модели
Общие сведения. В теории массового обслуживания к наиболее изученным и
исследованным относятся модели, у которых случайный процесс функционирования
относится к классу марковских процессов, т. е. марковские модели.
Случайный процесс, протекающий в системе, называется
марковским, если для любого момента времени вероятностные характеристики
процесса в будущем зависят только от его состояния в данный момент и не зависят
от того, когда и как система пришла в это состояние.
При исследовании ВС аналитическим моделированием наибольшее значение
имеют марковские случайные процессы с дискретными состояниями и непрерывным
временем.
Процесс называется процессом с дискретными состояниями, если
его возможные состояния z1, z2,... можно заранее перечислить, т. е.
состояния системы принадлежат конечному множеству, и переход системы из одного
состояния в другое происходит мгновенно.
Процесс называется процессом с непрерывным временем, если
смена состояний может произойти в любой случайный момент.
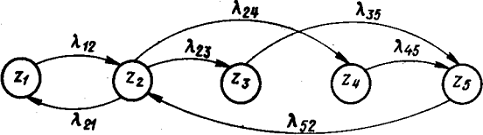
Рис. 3. Пример графа состояний
Описание
марковской модели. Для описания
поведения системы в виде марковской модели следует определить понятие состояния
системы; выявить все состояния, в которых может находиться система; указать, в
каком состояний находится система в начальный момент; построить граф состояний,
т. е. изобразить все состояния, например, кружками и возможные переходы из
состояния в состояние - стрелками, соединяющими состояния (на рис. 3 выделено
пять состояний); разметить граф, т. е. для каждого перехода указать
интенсивность 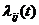 потока событий, переводящих систему из состояния zi в состояние zj
потока событий, переводящих систему из состояния zi в состояние zj
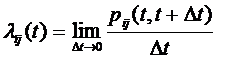 (8)
(8)
где
pij (t, t
+ 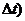 -
вероятность перехода из состояния zi в состояние zj за время от t до t +
-
вероятность перехода из состояния zi в состояние zj за время от t до t + 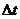 .
.
Для
стационарных марковских процессов интенсивности переходов не зависят от
времени: 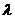 ij (t) =
ij (t) = 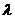 ij,
тогда pij (t, t
+
ij,
тогда pij (t, t
+ 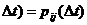 .
.
Понятие
состояния зависит от целей моделирования. В одном случае, например, оно может
быть определено по состояниям элементов, каждый из которых может быть
"свободен" или "занят" в другом случае состояние системы
определяется числом заявок, находящихся на обслуживании и в очередях.
Уравнения
Колмогорова для вероятностей
состояний. Исчерпывающей количественной характеристикой марковского
процесса является совокупность вероятностей состояний, т. е. вероятностей pi (t) того, что в момент t процесс будет находиться
в состоянии zi (t
= 1, ..., n).
Рассмотрим,
как определяются вероятности состояний по приведенному на рис. 3 графу
состояний, считая все потоки простейшими. В случайный момент времени t
система может находиться в одном из состояний zi
с вероятностью pi (t). Придадим t малое приращение 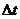 и найдем, например, p2 (t +
и найдем, например, p2 (t + 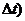 ) -
вероятность того, что в момент t +
) -
вероятность того, что в момент t + 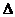 t система будет в состоянии z2. Это может произойти, во-первых, если система в
момент t была в состоянии z2 и за
время
t система будет в состоянии z2. Это может произойти, во-первых, если система в
момент t была в состоянии z2 и за
время 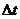 не вышла из него; во-вторых, если в момент t
система была в состоянии z1 или z5 и за время
не вышла из него; во-вторых, если в момент t
система была в состоянии z1 или z5 и за время 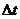 перешла
в состояние z2.
перешла
в состояние z2.
В
первом случае надо вероятность р2(t) умножить на вероятность
того, что за время 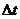 система не перейдет в состояние z1, z3 или z4. Суммарный поток событий, выводящий систему из
состояния z2, имеет
интенсивность
система не перейдет в состояние z1, z3 или z4. Суммарный поток событий, выводящий систему из
состояния z2, имеет
интенсивность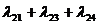 . Значит, вероятность того, что за время
. Значит, вероятность того, что за время 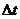 система выйдет из состояния z2, равна
система выйдет из состояния z2, равна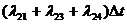 . Отсюда
вероятность первого варианта
. Отсюда
вероятность первого варианта
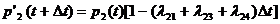
Найдем
вероятность перехода в состояние z2. Если в
момент t система находилась в состоянии z1 с вероятностью p1 (t), то вероятность перехода в состояние z1 за время 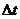 равна
равна
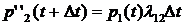
Аналогично
для состояния z5
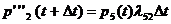
Складывая
вероятности 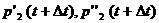 и
и 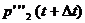 , получим
, получим
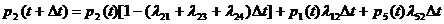 ,
,
Раскроем
квадратные скобки, перенесем p2 (t) в
левую часть и разделим обечасти на 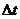 :
:
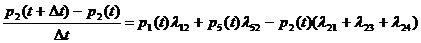 .
.
Если
устремить 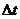 к нулю, то слева получим производную функции
к нулю, то слева получим производную функции 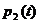 :
:
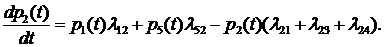
Аналогичные
уравнения можно вывести для всех остальных состояний. Получается система
дифференциальных уравнений:
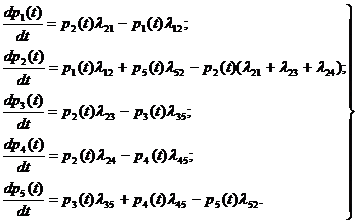 (8)
(8)
Эта система линейных дифференциальных уравнений дает возможность найти
вероятности состояний, если задать начальные условия. В левой части каждого
уравнения стоит производная вероятности i-го состояния, а в правой - сумма произведений вероятностей
всех состояний, из которых ведут стрелки в данное состояние, на интенсивности
соответствующих потоков событий, минус суммарная интенсивность всех потоков,
выводящих систему из данного состояния, умноженная на вероятность i-гo состояния.
Представим уравнения Колмогорова в общем виде:
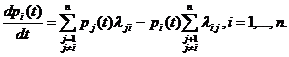 (9)
(9)
Здесь
учтено, что для состояний, не имеющих непосредственных переходов, можно
считать 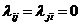
Предельные
вероятности состояний. В теории
случайных процессов доказывается, что если число п состояний системы
конечно и из каждого состояния можно перейти в любое другое за конечное число
шагов, то существуют предельные (финальные) вероятности состояний:
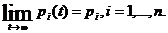 (10)
(10)
Сумма
вероятностей всех возможных состояний равна единице. При 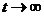 в системе S устанавливается стационарный
режим, в ходе которого система случайным образом меняет свои состояния, но их
вероятностные характеристики уже не зависят от времени. Предельную вероятность
состояния zi можно трактовать как среднее относительное время
пребывания системы в этом состоянии.
в системе S устанавливается стационарный
режим, в ходе которого система случайным образом меняет свои состояния, но их
вероятностные характеристики уже не зависят от времени. Предельную вероятность
состояния zi можно трактовать как среднее относительное время
пребывания системы в этом состоянии.
Для
вычисления предельных вероятностей нужно все левые части в уравнениях
Колмогорова (9) положить равными нулю и решить полученную систему линейных
алгебраических уравнений:
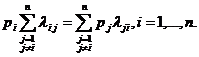 (11)
(11)
В связи с тем, что эти уравнения однородные, т. е. не имеют свободного
члена и, значит, позволяют определить неизвестные только с точностью до
произвольного множителя, следует воспользоваться нормировочным условием
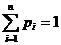 (12)
(12)
и с его помощью решить систему уравнений.
Модель размножения и гибели. Разновидностью марковской модели с
дискретным числом состояний и непрерывным временем является модель размножения
и гибели. Она характерна тем, что ее граф состояний имеет вид цепи (рис. 4).
Особенность этого графа состоит в том, что каждое из средних состояний z1, ..., zn-1 связано прямой и обратной стрелками с каждым из соседних состояний - zj правым и левым, а крайние состояния z0 и zn - только с одним соседним состоянием.

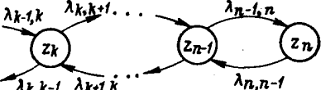
Рис.
4. Граф состояний модели размножения и гибели
В
этой модели формулы для определения вероятностей состояний, полученные в
результате решения уравнений Колмогорова, имеют вид:
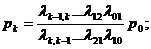 (13)
(13)
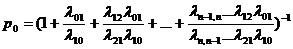 (14)
(14)
Эти формулы часто, используют при решении задач теории массового
обслуживания.
Контрольные вопросы
1. Простейший поток и его свойства.
2. Основная характеристика
экспоненциального распределения.
3. Пуассоновский поток.
4. Поток Эрланга и его основные
свойства.
5. Какой процесс называется Марковским,
описание Марковской модели?
6. Для чего используется уравнение
Колмогорова?
7. Граф состояний модели размножения и
гибели и основные формулы.
Литература
1. Альянах
И.Н. Моделирование
вычислительных систем, Л.: Машиностроение, 1988 г. - 223 стр.
2. Вентцель
Е.С. Исследование
операций: задачи, принципы, методология. М.: Наука, 1980 г. - 208 стр.
3. Зобов
Б.И., Сурков А.В. Основы
моделирования вычислительных систем. М.: МЛТИ, 1982 г. -32 стр.
4. Масков
А.И. моделирование
вычислительных систем. Пермь: ПГУ, 1982 г. - 95 стр.
Лекция 10. ХАРАКТЕРИСТИКИ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ (2 часа)
План
1.
Характеристики вычислительных систем как систем массового обслуживания
.
Характеристики вычислительных систем как сложных систем массового обслуживания
.
Методы приближённой оценки характеристик вычислительных систем
. Характеристики вычислительных систем как систем массового
обслуживания
Описание
системы. Предположим, что моделью ВС
является одноканальная СМО с однородным бесконечным простейшим потоком заявок и
неограниченной очередью. Интенсивность потока заявок равна 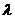 .
Длительность обслуживания заявки - это случайная величина с математическим
ожиданием
.
Длительность обслуживания заявки - это случайная величина с математическим
ожиданием 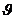 .
.
Наряду
с понятием средней длительности обслуживания используется понятие интенсивности
обслуживания 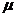 - величины, обратной
- величины, обратной 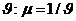 , и характеризующей число заявок, которое может
обслужить прибор в единицу времени.
, и характеризующей число заявок, которое может
обслужить прибор в единицу времени.
Поток
обслуживания тоже будем считать простейшим с интенсивностью 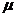 . В
соответствии с символикой, принятой в теории массового обслуживания, такая
система обозначается М/М/1.
. В
соответствии с символикой, принятой в теории массового обслуживания, такая
система обозначается М/М/1.
Выделим
состояния СМО по числу заявок, находящихся в системе:
z0 - прибор свободен, очереди нет;
z1 - прибор занят (обслуживает заявку), очереди нет;
z2 - прибор занят, одна заявка в очереди;
zk -
прибор занят, (k - 1) заявок
стоит в очереди.
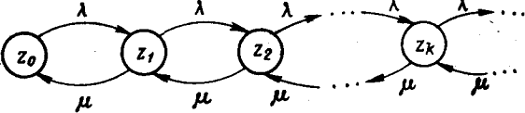
Рис. 1. Граф
состояний СМО
Граф состояний такой системы изображен на рис. 1. Это модель размножения
и гибели, но с бесконечным количеством состояний, поскольку, очередь
неограниченна.
Коэффициент загрузки. Предельная вероятность состояния
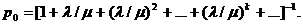 (1)
(1)
Обозначая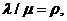 получаем
получаем
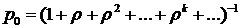 . (2)
. (2)
Ряд
в этой формуле представляет собой геометрическую прогрессию. Известно, что при ρ < 1 ряд сходится. Сумма членов прогрессии при этом равна
1/(1 - ρ),
откуда 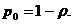
Это
вероятность того, что прибор свободен и очередь отсутствует. Значит,
вероятность того, что прибор занят обслуживанием заявки,
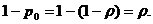
Это
означает, что отношение
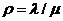 (3)
(3)
служит
мерой загрузки СМО и является коэффициентом загрузки. Тогда 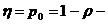 коэффициент простоя.
коэффициент простоя.
Число
заявок в СМО. Вероятности состояний z1, ..., zk, ... определяются из общей формулы размножения и гибели:
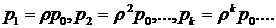
Определим
среднее число заявок в системе п. В текущий момент времени в системе
может быть 0, 1, 2, .... k, ... заявок
с вероятностями p0, p1, p2,…, pk… Математическое ожидание количества заявок равно
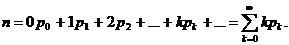
Подставим
значение рk и р0, исключив первое слагаемое,
равное нулю:
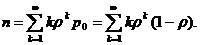
Вынесем
за знак суммы ρ
(1 - р):
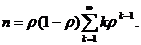
Но
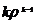 - это производная по
- это производная по 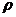 от
от 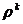 :
:
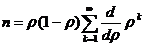 .
.
Меняя
местами операции дифференцирования и суммирования, получим
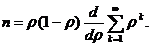 (4)
(4)
Сумма
в этой формуле - это сумма бесконечно убывающей прогрессии при 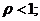 она равна ρ/(1-ρ), а ее производная 1/(1- ρ)2.
Следовательно, число заявок в системе в установившемся стационарном режиме
она равна ρ/(1-ρ), а ее производная 1/(1- ρ)2.
Следовательно, число заявок в системе в установившемся стационарном режиме
п = ρ/(1 - ρ). (5)
Длина очереди. Найдем среднее число заявок в очереди к обслуживающему
прибору - среднюю длину очереди l. Она равна среднему числу заявок в системе за вычетом среднего числа
заявок, находящихся под обслуживанием. Число заявок под обслуживанием может
быть равно нулю, если прибор свободен, или единице, если прибор занят. В
установившемся режиме математическое ожидание такой случайной величины равно
вероятности того, что прибор занят. А эта вероятность определена ранее - ρ.
Откуда получается
средняя длина очереди в СМО:
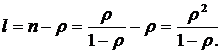 (6)
(6)
Зависимость
средней длины очереди от коэффициента загрузки изображена на рис. 2. При ρ >
0,6-0,7 очередь стремительно
увеличивается и при ρ
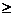 1 уходит в бесконечность. У детерминированной системы
коэффициенты вариации интенсивностей потоков заявок и обслуживания равны нулю,
при ρ
< 1 очередь отсутствует, а при ρ
1 уходит в бесконечность. У детерминированной системы
коэффициенты вариации интенсивностей потоков заявок и обслуживания равны нулю,
при ρ
< 1 очередь отсутствует, а при ρ 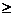 1 - уходит в бесконечность. Для систем, которые имеют
промежуточные коэффициенты вариации 0 <v < 1, зависимости средней длины очереди от коэффициента
загрузки лежат в области, заштрихованной на рис. 2.
1 - уходит в бесконечность. Для систем, которые имеют
промежуточные коэффициенты вариации 0 <v < 1, зависимости средней длины очереди от коэффициента
загрузки лежат в области, заштрихованной на рис. 2.
Время
реакции. Для определения среднего
времени реакции рассмотрим поток заявок, прибывающих в СМО, и поток заявок,
покидающих систему. Если в системе устанавливается предельный стационарный
режим при ρ<1,
то среднее число заявок, прибывающих в
единицу времени, равно среднему числу заявок, покидающих ее: оба потока имеют
интенсивность 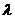 .
.
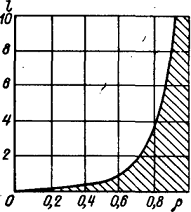
Рис.
2. Зависимость средней длины очереди от коэффициента загрузки для простейшей
СМО
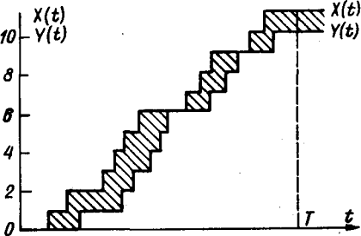
Рис.
3. Временная диаграмма процессов поступления и ухода заявок
Обозначим
через Х (t) число
заявок, поступивших в СМО до момента времени t, а через Y
(t) - число
заявок, покинувших СМО до момента t. Та и. другая функции являются
случайными и меняются скачком - увеличиваются на единицу в моменты прихода или
ухода заявок (рис. 3).
Очевидно,
что для любого момента времени t разность функций п (t)=Х (t) - Y (t)
есть число заявок, находящихся в СМО. Рассмотрим большой промежуток времени Т
и вычислим среднее число заявок, находящихся в системе:
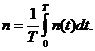
Интеграл
изображен в виде заштрихованной фигуры на рис. 3. Она состоит из
прямоугольников, каждый из которых имеет высоту, равную единице, и основание,
равное времени пребывания в системе i-й заявки ti:
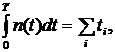
где
сумма распространяется на все заявки, поступившие в систему за время Т.
Разделим
правую и левую части на Т.
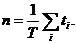
Разделим
и умножим правую часть на 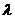 :
:
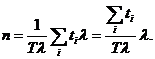
Произведение
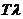 ,-это среднее количество заявок, пришедших за время Т.
Если разделить сумму всех времен ti на среднее
число заявок, то получится среднее время пребывания заявки в системе, т. е.
среднее время реакции и:
,-это среднее количество заявок, пришедших за время Т.
Если разделить сумму всех времен ti на среднее
число заявок, то получится среднее время пребывания заявки в системе, т. е.
среднее время реакции и:
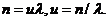 (7)
(7)
Это формула Литтла: для каждой СМО при любом характере потока
заявок и при любом распределении времени обслуживания среднее время реакции
равняется среднему числу заявок в системе, деленному на интенсивность потока
заявок. Отсюда
получается:
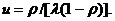 (8)
(8)
Вторая формула Литтла связывает среднее время пребывания заявки в очереди
и среднее число заявок в очереди подобным соотношением:
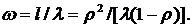 (9)
(9)
Среднее время реакции равняется сумме среднего времени
пребывания заявки в очереди и средней длительности обслуживания заявки:
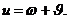 (10)
(10)
Важно отметить, что в системе М/М/ 1 времена ожидания и реакции, а
также периоды между моментами ухода следующих друг за другом заявок
распределены по экспоненциальному закону. Для других систем при аналитическом
моделировании не всегда представляется возможным определить законы
распределения выходных характеристик.
При ρ > 1 в системе не устанавливается стационарный режим. В пределе
длина очереди, а значит, и времена ожидания и реакции стремятся к
бесконечности.
. Характеристики вычислительных систем как сложных систем
массового обслуживания
Многомерный
поток. На вход обслуживающего прибора
может поступать многомерный поток заявок, состоящий из заявок типов 1, ..., М,
у которых интенсивности равны 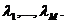 Предположим,
что каждый из потоков заявок одного типа является простейшим. Загрузка прибора
потоком заявок типа i будет составлять
Предположим,
что каждый из потоков заявок одного типа является простейшим. Загрузка прибора
потоком заявок типа i будет составлять
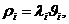
где
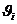 - средняя
длительность обслуживания заявок типа i. Суммарная загрузка прибора со
стороны всех потоков
- средняя
длительность обслуживания заявок типа i. Суммарная загрузка прибора со
стороны всех потоков
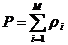 (11)
(11)
Рис. 4. Граф
состояний многоканальной СМО
моделирование
параметрическая идентификация вычислительная система
Условие
существования стационарного режима: Р < 1. Остальные характеристики
обслуживания ni, li, ui, 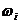 определяются
для каждого i-гo потока в отдельности по формулам (5)- (9).
определяются
для каждого i-гo потока в отдельности по формулам (5)- (9).
Средние
времена ожидания 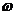 ср и реакции
uср по
одной заявке из суммарного потока в системе связаны со средними количествами
заявок в очереди и в системе следующими соотношениями:
ср и реакции
uср по
одной заявке из суммарного потока в системе связаны со средними количествами
заявок в очереди и в системе следующими соотношениями:
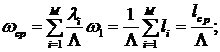 (12)
(12)
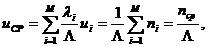 (13)
(13)
где
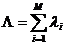 - суммарная интенсивность потоков;
- суммарная интенсивность потоков; 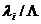 - вероятность того, что поступившая заявка является
заявкой i-гo типа;
- вероятность того, что поступившая заявка является
заявкой i-гo типа;
lcp -
средняя длина очереди заявок всех типов; n ср -
среднее число заявок всех типов в системе.
Многоканальная
СМО. Предположим, что система имеет т
обслуживающих каналов с одинаковой интенсивностью обслуживания 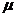 , при общем
простейшем потоке заявок с интенсивностью
, при общем
простейшем потоке заявок с интенсивностью 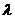 . Такая
система условно обозначается М/М/т. Граф состояний этой системы (рис. 4)
подобен графу одноканальной СМО. Интенсивности перехода в соседнее правое
состояние определяются, как и у одноканальной СМО, интенсивностью входного
потока : с приходом очередной заявки система переходит в следующее правое
состояние. Иначе обстоит дело с интенсивностями у нижних стрелок. Пусть система
находится в состоянии z1 -
работает один канал. Он производит
. Такая
система условно обозначается М/М/т. Граф состояний этой системы (рис. 4)
подобен графу одноканальной СМО. Интенсивности перехода в соседнее правое
состояние определяются, как и у одноканальной СМО, интенсивностью входного
потока : с приходом очередной заявки система переходит в следующее правое
состояние. Иначе обстоит дело с интенсивностями у нижних стрелок. Пусть система
находится в состоянии z1 -
работает один канал. Он производит 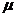 обслуживании
в единицу времени. Тогда
обслуживании
в единицу времени. Тогда 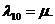 . Представим, что система находится в состоянии z2. Для перехода в состояние z1 надо, чтобы закончил обслуживание первый или второй
канал. Значит, суммарная интенсивность их обслуживания
. Представим, что система находится в состоянии z2. Для перехода в состояние z1 надо, чтобы закончил обслуживание первый или второй
канал. Значит, суммарная интенсивность их обслуживания 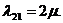 Суммарный поток обслуживания k
каналами имеет интенсивность k
Суммарный поток обслуживания k
каналами имеет интенсивность k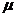 . При k
. При k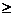 т интенсивность обслуживания сохраняется т
т интенсивность обслуживания сохраняется т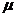 . Получается
модель размножения и гибели. Делая выкладки, как для одноканальной СМО, получим
. Получается
модель размножения и гибели. Делая выкладки, как для одноканальной СМО, получим
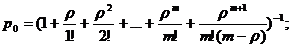
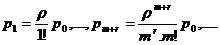
Средняя
длина очереди
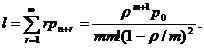 (14)
(14)
Прибавляя к ней среднее число заявок, находящихся под обслуживанием,
равное среднему числу занятых каналов
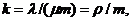
получим
среднее число заявок в системе:
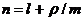 (15)
(15)
По формулам Литтла определяется среднее время пребывания заявки в
очереди:
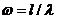 (16)
(16)
и в системе - время реакции:
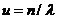 (17)
(17)
В теории массового обслуживания имеются аналитические формулы для
простейших СМО при одномерном и многомерном потоке заявок для одноканальных и
многоканальных систем без ограничений и с ограничениями длин очередей.
Потоки обслуживания. При моделировании конкретных ВС потоки заявок и обслуживания
могут отличаться от простейших. Потоки заявок могут быть, например,
пуассоновскими или эрланговскими. Длительности обслуживания можно представить в
общем случае гамма-распределением. Это распределение с плотностью вероятности
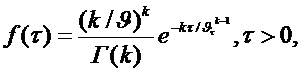 (18)
(18)
где
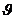 -
математическое ожидание длительности обслуживания М [
-
математическое ожидание длительности обслуживания М [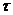 ]; k - параметр
распределения (k
]; k - параметр
распределения (k 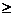 1); Г (k)
- гамма-функция.
1); Г (k)
- гамма-функция.
Дисперсия
гамма-распределения
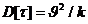 (19)
(19)
При
k = 1 гамма-распределение вырождается в экспоненциальное. В пределе при k
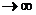 это распределение становится детерминированным с
постоянной длительностью обслуживания
это распределение становится детерминированным с
постоянной длительностью обслуживания 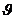 .
Параметр распределения k может быть определен по математическому
ожиданию и дисперсии:
.
Параметр распределения k может быть определен по математическому
ожиданию и дисперсии:
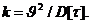 (20)
(20)
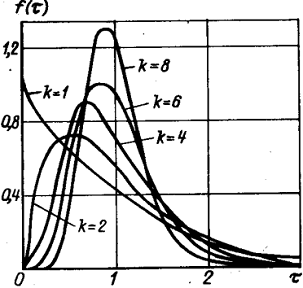
Рис. 5. Нормированное распределение Эрланга
При целочисленном k Г (k) = (k-1)!. Тогда из уравнения (18) имеем
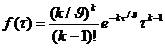 ,
,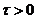 (21)
(21)
Это
плотность нормированного распределения Эрланга k-го порядка. Вид
распределения изображен на рис. 5. В данном распределении в отличие от потока
Эрланга математическое ожидание не зависит от k и при k 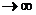 это распределение стремится к детерминированному, а
не к нормальному.
это распределение стремится к детерминированному, а
не к нормальному.
В
частных случаях длительности обслуживания могут быть распределены по
экспоненциальному, равномерному, нормальному и другим законам. Для некоторых
сочетаний законов распределений потоков заявок и обслуживании получены
аналитические зависимости характеристик от параметров системы.
Системы
с произвольным распределением длительности обслуживания. Представим, что моделью ВС является одноканальная СМО
с неограниченной очередью. В эту систему поступает простейший поток заявок с
интенсивностью 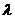 . Заявки
обслуживаются в порядке поступления. Длительность обслуживания имеет
произвольное распределение с математическим ожиданием
. Заявки
обслуживаются в порядке поступления. Длительность обслуживания имеет
произвольное распределение с математическим ожиданием 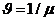 и коэффициентом вариации
и коэффициентом вариации 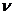 . Такая система обозначается M/G/1. В этой
системе в установившемся режиме среднее число заявок в очереди
. Такая система обозначается M/G/1. В этой
системе в установившемся режиме среднее число заявок в очереди
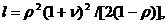 (26)
(26)
среднее
число заявок в системе
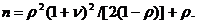 (27)
(27)
Последние два выражения называются формулами Поллачека-Хинчина. Средние
времена пребывания заявок в очереди и в системе определяются по формулам
Литтла.
Для системы M/G/1 могут быть аналитически определены дисперсии
выходных характеристик. Подобные формулы известны также для случая многомерного
простейшего потока заявок.
Системы с отказами. Предположим, что на ВС, представленную как m-канальная СМО, поступает простейший
поток заявок с интенсивностью К. Поток обслуживания имеет произвольный
закон распределения с интенсивностью р. Это система M/G/m. При этом очередная заявка, поступившая в систему,
когда все каналы заняты, покидает ее без обслуживания. Это означает, что
очереди в системе отсутствуют. Характеристиками такой системы могут служить
пропускная способность, вероятность обслуживания и среднее число занятых
каналов. Данная система соответствует модели размножения и гибели. На основании
формул (13) и (14) (лекция 9) можно вывести вероятность того, что в СМО
находится т заявок, т. е. все каналы заняты:
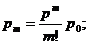
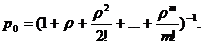 (28)
(28)
Вероятность того, что очередная заявка будет обслужена,
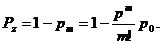 (29)
(29)
Пропускная способность системы определяется как среднее число
заявок, обслуживаемых в единицу времени;
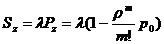 (30)
(30)
а среднее число занятых каналов определяется по формуле
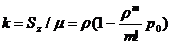 (31)
(31)
Системы с приоритетными дисциплинами диспетчеризации.
В теории вычислительных систем детально изложены и исследованы
аналитические зависимости характеристик от параметров ВС, представленных
моделями СМО с ординарными и неординарными, одномерными и многомерными потоками
заявок, обслуживаемых одноканальными и многоканальными приборами с
произвольными законами распределения длительности обслуживания и различными
дисциплинами диспетчеризации, включая системы с относительным, абсолютным,
смешанным и динамическим приоритетами.
Например,
допустим, что в СМО поступает М типов простейших потоков с
интенсивностями 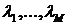 и длительности обслуживания заявок каждого потока
имеют математические ожидания
и длительности обслуживания заявок каждого потока
имеют математические ожидания 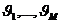 и
дисперсии
и
дисперсии 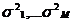 . В системе используется смешанная дисциплина
диспетчеризации с тремя классами: 1) заявкам типов 1,..., M1 присвоены абсолютные приоритеты по отношению к
заявкам второго и третьего классов; 2) заявкам типов M1+1,..., M1+M2 - относительные приоритеты по отношению к заявкам
третьего класса; 3) заявки типов M1+M2+1,..., M
обслуживаются в порядке поступления. Среднее время ожидания заявок различных
типов определяется из выражения:
. В системе используется смешанная дисциплина
диспетчеризации с тремя классами: 1) заявкам типов 1,..., M1 присвоены абсолютные приоритеты по отношению к
заявкам второго и третьего классов; 2) заявкам типов M1+1,..., M1+M2 - относительные приоритеты по отношению к заявкам
третьего класса; 3) заявки типов M1+M2+1,..., M
обслуживаются в порядке поступления. Среднее время ожидания заявок различных
типов определяется из выражения:
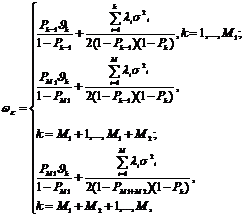 (22)
(22)
где
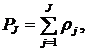
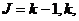
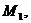
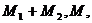
Из
формулы (22) могут быть получены как частные случаи
характеристики
систем с абсолютными (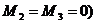 , относительными (М1 = M3 = 0) и смешанными приоритетами с двумя классами заявок:
с абсолютными и относительными приоритетами (М3 = 0), с
абсолютными приоритетами и без приоритетов (М2 = 0), с
относительными приоритетами и без приоритетов (M1 = 0).
, относительными (М1 = M3 = 0) и смешанными приоритетами с двумя классами заявок:
с абсолютными и относительными приоритетами (М3 = 0), с
абсолютными приоритетами и без приоритетов (М2 = 0), с
относительными приоритетами и без приоритетов (M1 = 0).
3.
Методы приближённой оценки характеристик вычислительных систем
Оценка при большой нагрузке. Аналитические зависимости,
позволяющие определить параметры распределений выходных характеристик, имеются
только для ограниченного круга систем. У более широкого круга систем могут быть
вычислены средние значения в стационарном установившемся режиме. Однако остается
ряд систем и режимов, для которых отсутствуют точные формулы даже по
определению средних значений. К таким системам относятся, в первую очередь,
системы с произвольными распределениями периодов поступления и длительностей
обслуживания заявок. Это системы G/G/1 и G/G/m. При отсутствии точных зависимостей приходится
довольствоваться приближенными оценками.
Одним из методов приближений является оценка характеристик при близких к
единице значениях коэффициента загрузки, как наиболее важных с практических
позиций. В частности, для системы G/G/1 время ожидания заявки в очереди
распределено по экспоненциальному закону и среднее время ожидания можно
определить по следующей формуле:
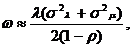
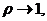 (33)
(33)
где
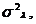
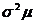 - дисперсия периодов поступления и длительностей
обслуживания заявок соответственно.
- дисперсия периодов поступления и длительностей
обслуживания заявок соответственно.
Используя
зависимость (10) и формулы Литтла, можно вычислить средние значения других
характеристик.
Определение
границ. При значениях 0 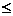 ρ < 1 для оценки характеристик используется несколько
различных подходов определения верхней и нижней границ, в пределах которых
находится истинное значение той или иной характеристики. Например, для системы G/G/1
приводятся следующие формулы расчета границ среднего времени ожидания заявки в
очереди:
ρ < 1 для оценки характеристик используется несколько
различных подходов определения верхней и нижней границ, в пределах которых
находится истинное значение той или иной характеристики. Например, для системы G/G/1
приводятся следующие формулы расчета границ среднего времени ожидания заявки в
очереди:
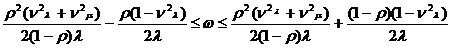 (24)
(24)
где
v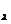 ,
, 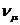 -
коэффициенты вариации периодов поступления и длительностей обслуживания заявок
соответственно.
-
коэффициенты вариации периодов поступления и длительностей обслуживания заявок
соответственно.
Средняя
длина очереди 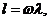 , и среднее число заявок в системе
, и среднее число заявок в системе 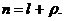 .
.
Дискретное
и непрерывное приближения. Другие
методы оценки ориентированы не на поиск приближенного решения исходной задачи,
а на точное решение упрощенно сформулированной задачи. Уравнения, описывающие
работу системы G/G/1, преднамеренно преобразуются к такому виду, при котором
полученная система уравнений может быть решена.
В
теории массового обслуживания показано, что если исходные величины являются
дискретными, можно определить точное распределение времени ожидания. На этом
основывается метод дискретного приближения, при котором промежутки времени
между моментами поступления заявок и длительности обслуживания аппроксимируются
дискретными распределениями.
Для
исследования нестационарных систем и режимов перегрузки оказывается полезным
метод непрерывного приближения. Процессы поступления и ухода заявок - это
ступенчатые вероятностные процессы (рис. 3). Но когда длины очередей
значительно больше единицы, а времена ожидания существенно больше среднего
времени обслуживания, становится разумной замена этих ступенчатых процессов
сглаженными непрерывными функциями времени, поскольку величины отдельных
ступенек малы по сравнению со средними значениями (рис. 6).
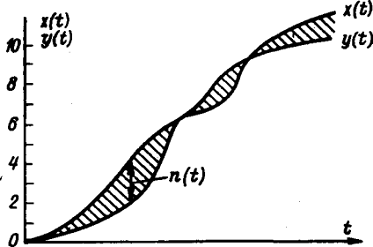
Рис.
6. Временная диаграмма процессов поступления и ухода заявок с
непрерывной аппроксимацией зависимостей количества заявок от времени М [х(t)]= На этом
основывается приближение первого порядка, которое заключается в замене
вероятностного процесса его средним значением, зависящим от времени, т. е.
детерминированным процессом
На этом
основывается приближение первого порядка, которое заключается в замене
вероятностного процесса его средним значением, зависящим от времени, т. е.
детерминированным процессом 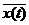 . Это
относится и к процессу ухода заявок
. Это
относится и к процессу ухода заявок 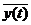 . Тогда число заявок в системе тоже представляет собой
детерминированную непрерывную функцию времени:
. Тогда число заявок в системе тоже представляет собой
детерминированную непрерывную функцию времени:
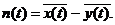 (23)
(23)
Функции
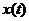 и
и 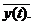 определяются
из зависимостей:
определяются
из зависимостей:
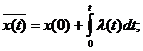 (36)
(36)
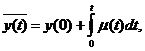 (37)
(37)
-число поступивших и покинувших систему заявок к нулевому моменту
времени.
Диффузионная аппроксимация. Непрерывное приближение является довольно грубым,
поскольку не учитывает случайный характер процессов поступления и ухода заявок.
По методу диффузионной аппроксимации непрерывное приближение усовершенствуется
путем учета флуктуаций относительно среднего значения. С этой целью случайный
процесс (23) заменяется марковским процессом диффузионного типа χ
(t) с непрерывным временем и
непрерывным множеством состояний. Диффузионный процесс определяется
коэффициентом сноса
и коэффициентом диффузии
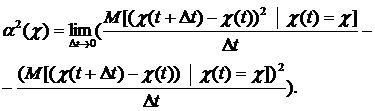
Эти
коэффициенты выражаются через параметры исходной модели. Для системы G/G/1
считается, что при больших t распределение Х (t) является
приближенно нормальным с математическим ожиданием 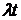 и дисперсией
и дисперсией 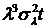 и
распределение Y(t) тоже приближенно нормальное с математическим
ожиданием
и
распределение Y(t) тоже приближенно нормальное с математическим
ожиданием 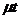 и дисперсией
и дисперсией 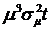 . Тогда коэффициент сноса
. Тогда коэффициент сноса
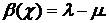 (38)
(38)
и коэффициент диффузии
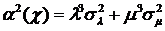 (39)
(39)
В связи с тем, что процесс п (t) не может принимать отрицательных значений, для
аппроксимирующего процесса χ(t) задается граничное условие, удерживающее его траекторию на
неотрицательной полуоси. Например, при достижении χ(t) =0 совершается скачок в
целочисленные точки положительной полуоси, выполняемый с заданным
распределением вероятностей после экспоненциальной задержки в нуле.
Применение диффузионной аппроксимации дает возможность получения оценок
различных характеристик СМО. В частности, для системы G/G/1 средняя
длина очереди в стационарном режиме определяется по формуле
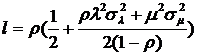 (40)
(40)
при постоянных коэффициентах сноса и диффузии, соответствующих случаю
независимых от длины очереди вероятностных характеристик поступления и
обслуживания заявок.
Контрольные вопросы
1. Одноканальная СМО для описания ВС.
2. Как определяется коэффициент загрузки
ВС?
3. Как определяется число заявок в СМО?
4. Как определяется длина очереди в СМО?
5. Как определяется время реакции в СМО?
6. Формулы Литтла.
7. Многоканальная СМО для описания ВС.
8. Основные характеристики
многоканальной СМО.
9. Для каких систем используются методы
приближенной оценки характеристик?
Литература
1. Альянах И.Н. Моделирование вычислительных систем, Л.: Машиностроение, 1988
г. - 223 стр.
2. Вентцель Е.С. Исследование операций: задачи, принципы, методология. М.:
Наука, 1980 г. - 208 стр.
3. Зобов Б.И., Сурков А.В. Основы моделирования вычислительных
систем. М.: МЛТИ, 1982 г. -32 стр.
4. Масков А.И. моделирование вычислительных систем. Пермь: ПГУ, 1982 г. - 95
стр.
Лекция 11. НЕСТАЦИОНАРНЫЕ РЕЖИМЫ
ФУНКЦИОНИРОВАНИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ (2 часа)
План
1.
Нестационарные режимы функционирования вычислительных систем
.
Характеристики вычислительных систем как стохастических сетей
. Нестационарные режимы функционирования вычислительных
систем
Переходные
процессы. До сих пор рассматривались
характеристики ВС в стационарном установившемся режиме. Однако на практике не
менее важным является анализ нестационарных режимов. Значения выходных
характеристик в нестационарных режимах функционирования ВС можно определить для
одних систем путем численного решения уравнений Колмогорова задавая в них
интенсивности как функции времени 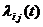 для
других систем - в результате непрерывной или диффузионной аппроксимации
процессов.
для
других систем - в результате непрерывной или диффузионной аппроксимации
процессов.
Частным
случаем нестационарных режимов является переходный процесс, когда, например, в
начальный момент времени в системе отсутствуют очереди и начинают поступать
заявки с постоянной интенсивностью λ. Важно уметь определять, когда установится стационарный режим.
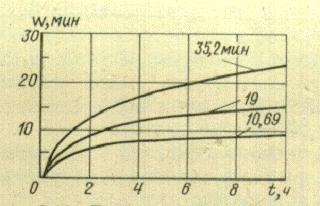
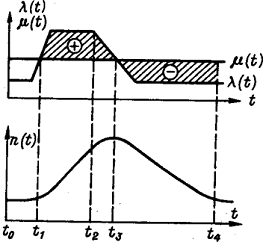
В
работе приводятся результаты анализа переходных процессов для системы M/G/1. Интенсивность входящего пуассоновского потока 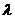 принималась равной 0,95 заявок в минуту, а среднее
время обслуживания v =1 мин. Коэффициент загрузки ρ = 0,95. Рассматривались следующие распределения длительности
обслуживания:
принималась равной 0,95 заявок в минуту, а среднее
время обслуживания v =1 мин. Коэффициент загрузки ρ = 0,95. Рассматривались следующие распределения длительности
обслуживания:
)
экспоненциальное распределение
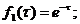
)
нормированное распределение Эрланга 8-го порядка со средним, равным восьми,
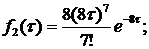
)
комбинация экспоненциального распределения со средним значением 4 и
распределения Эрланга 4-го порядка со средним значением 2/3
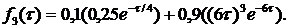
Зависимости
среднего времени ожидания заявок в очереди в течение переходного процесса для
этих случаев показаны на рис. 1. Установившиеся значения соответственно равны
19; 10,69 и 35,2 мин. Если принять длительность переходного процесса равной
бремени, в течение которого среднее время ожидания достигает 0,8 от
установившегося значения, то для этих случаев она соответственно составит 15,2;
8,55 и 28,2 ч. За эти времена система успевает обслужить 867, 487 или 1605
заявок. Можно утверждать, что ВС с суточным циклом никогда не работают
практически в установившемся режиме при большой загрузке. Этот вывод можно
распространить на ВС с большей длительностью цикла, если они имеют
соответственно меньшие интенсивности поступления и обслуживания заявок.
Режимы
перегрузок. Методы непрерывной и
диффузионной аппроксимации дают возможность проанализировать поведение системы
при изменяющихся во времени интенсивностях прихода и обслуживания заявок. С
практических позиций наибольшую важность представляет анализ режима перегрузок,
когда в течение некоторого интервала времени коэффициент загрузки ρ > 1.
Рассмотрим
этот режим на упрощенном примере (рис. 2). Предположим, что в одноканальную
систему поступает одномерный поток заявок с интенсивностью 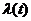 . Заявки обслуживаются в порядке поступления с
постоянной интенсивностью
. Заявки обслуживаются в порядке поступления с
постоянной интенсивностью 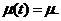
В
начальный момент t0
коэффициент загрузки ρ
< 1. В системе. имеются заявки,
накопление которых обусловлено случайным характером их поступления и
обслуживания.
Затем
интенсивность поступления заявок начинает расти, достигая максимального
значения. С момента t1
становится ρ > 1 и увеличивается число заявок в системе. При
максимальном 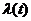 число
заявок n(t) растет линейно, стремясь к бесконечности. Но в связи
с тем, что в момент t2
интенсивность поступления начинает уменьшаться, рост n(t)
замедляется и достигает максимума в момент t3 при р = 1.
число
заявок n(t) растет линейно, стремясь к бесконечности. Но в связи
с тем, что в момент t2
интенсивность поступления начинает уменьшаться, рост n(t)
замедляется и достигает максимума в момент t3 при р = 1.
В
режиме перегрузки накопление заявок в системе определяется в основном не
случайными факторами, а превышением средней интенсивности поступления над
интенсивностью обслуживания. С момента t3 число заявок уменьшается до момента t4 принимая
установившееся значение. Длительность рассасывания числа заявок может быть
приближенно оценена по равенству заштрихованных на рисунке площадей, обозначенных
плюсом и минусом.
Важно
подчеркнуть, что такая система может быть вполне работоспособна, если
максимальное число заявок в системе, а соответственно и время реакции не
превысят допустимых значений. При правильном задании стохастических
ограничений, систему можно считать работоспособной даже при кратковременном
превышении допустимых значений математическим ожиданием времени реакции. Этот
подход дает возможность выбрать производительность ВС не по максимальной
интенсивности поступления заявок, обеспечивая ρ < 1, а на существенно более низком уровне. Отдельные
вопросы анализа нестационарных ВС рассматриваются в работах.
2. Характеристики вычислительных систем как стохастических
сетей
Описание стохастической сети. Обычно ВС представляется не
отдельной СМО, а стохастической сетью. Для описания ВС в виде стохастической
сети определяются следующие параметры:
) число СМО, образующих сеть (S1, S2, ..., Sn);
) число каналов каждой СМО (т1 ..., mn);
) матрица вероятностей передач Р = [pij], где рij - вероятность того, что заявка, покидающая систему Si, поступает в систему Sj (i, j=0,1,...n);
4)
интенсивность 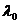 источника заявок S0 в
разомкнутой сети или число М заявок в замкнутой сети;
источника заявок S0 в
разомкнутой сети или число М заявок в замкнутой сети;
)
средние длительности обслуживания заявок 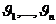 в
системах S1,...Sn.
в
системах S1,...Sn.
Рассмотрим
характеристики экспоненциальных сетей. Экспоненциальная стохастическая сеть
имеет простейшие входные потоки и распределенные по экспоненциальному закону
длительности обслуживания заявок в различных системах сети. В установившемся
режиме вероятность передачи заявки из системы Si; в систему Sj равна доле потока, поступающего из системы Si; в систему Sj. Если система без потерь, то на входе системы Si; имеется поток с интенсивностью
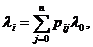
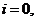 1, ..., n. (1)
1, ..., n. (1)
Из
этой системы уравнений находятся соотношения интенсивностей потоков 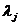 и
и 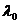 в виде
в виде
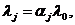
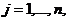 (2)
(2)
где
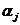 -
коэффициент передачи, который определяет среднее число этапов обслуживания
одной заявки в системе Sj.
-
коэффициент передачи, который определяет среднее число этапов обслуживания
одной заявки в системе Sj.
Для
замкнутой сети принимается 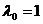 .
.
Определение
вероятности состояний. В стационарном
установившемся режиме вероятность того, что в системе Sj
находится Мj заявок,
определяется из выражения
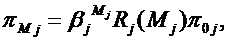 (3)
(3)
где
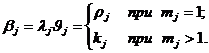 (4)
(4)
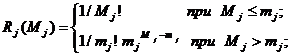 (5)
(5)
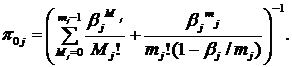 (6)
(6)
Вероятность состояния замкнутой сети Р (M1, ..., Mn), характеризующая вероятность того, что в системе S1 находится М1заявок,
и т. д., вычисляется по формуле
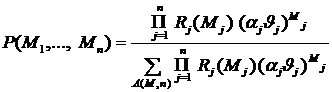 (7)
(7)
где
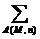 - символ суммирования по всем возможным
состояниям, для которых
- символ суммирования по всем возможным
состояниям, для которых
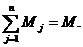 (8)
(8)
По вероятностям состояний определяются характеристики сети.
Вычисление характеристик разомкнутой сети. В разомкнутой экспоненциальной
сети в стационарном режиме согласно теореме Джексона можно считать, что сеть
состоит из совокупности независимых СМО с простейшими входными потоками. Для
каждой СМО характеристики определяются отдельно. Для каждой Sj СМО сети средняя длина очереди
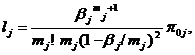 (9)
(9)
среднее число в системе
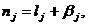 (10)
(10)
а
среднее время ожидания в очереди 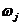 , и пребывания в системе uj определяется
по формулам Литтла из (9) и (10). Тогда характеристики сети в целом: среднее
число заявок во всех очередях
, и пребывания в системе uj определяется
по формулам Литтла из (9) и (10). Тогда характеристики сети в целом: среднее
число заявок во всех очередях
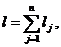 (11)
(11)
среднее число заявок в сети
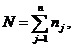 (12)
(12)
среднее время ожидания в очередях
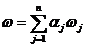 (13)
(13)
среднее время реакции сети
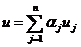 (14)
(14)
Вычисление характеристик замкнутой сети. Для любой Sj СМО сети средняя длина очереди
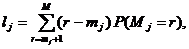 (15)
(15)
среднее число заявок в СМО
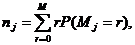 (16)
(16)
средние
времена ожидания 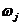 и пребывания uj
вычисляются по формулам Литтла. Среднее время цикла сети, т. е. интервал
времени между двумя последовательными выходами одной и той же заявки из СМО Si составляет Uj = M/
и пребывания uj
вычисляются по формулам Литтла. Среднее время цикла сети, т. е. интервал
времени между двумя последовательными выходами одной и той же заявки из СМО Si составляет Uj = M/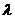 j.
j.
В
заключение отметим, что простые аналитические выражения для определения
характеристик ВС как сетевых моделей имеются лишь для узкого круга систем. В
ряде случаев приходится прибегать к численным моделям.
Существенный
недостаток сетевых моделей - трудность учета таких ситуаций, когда заявке
требуется одновременно несколько ресурсов. В теории массового обслуживания
слабо учитывается использование накопителей, неоднородность потока заявок.
Считается, что заявка обслуженная одной СМО, поступает на другую, в то время
как в ВС в передаче одновременно участвуют передающее устройство, коммуникатор
и принимающее устройство. Применение аналитического моделирования целесообразно
для предварительной оценки характеристик ВС.
Контрольные вопросы
1. Основные подходы исследования
характеристик ВС в нестационарном режиме.
2. Исследование характеристик в режиме
перегрузок.
3. Описание стохастической сети
применительно к ВС.
4. Определение вероятности состояний.
5. Определение характеристик разомкнутой
и замкнутой сети.
Литература
1. Альянах
И.Н. Моделирование
вычислительных систем, Л.: Машиностроение, 1988 г. - 223 стр.
2. Вентцель
Е.С. Исследование
операций: задачи, принципы, методология. М.: Наука, 1980 г. - 208 стр.
3. Зобов
Б.И., Сурков А.В. Основы
моделирования вычислительных систем. М.: МЛТИ, 1982 г. -32 стр.
4. Масков
А.И. моделирование
вычислительных систем. Пермь: ПГУ, 1982 г. - 95 стр.
Лекция 12. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ
ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ (2 часа)
План
1.
Процедура имитационного моделирования
.
Обобщенные алгоритмы имитационного моделирования
1. Процедура имитационного моделирования
Метод имитационного моделирования заключается в создании
логико-аналитической (математической) модели системы и внешних воздействий, в
имитации функционирования системы, т. е. в определении временных изменений
состояния системы под влиянием внешних воздействий, и в получении выборок
значений выходных параметров, по которым определяются их основные вероятностные
характеристики. Данное
определение справедливо для стохастических систем. При исследовании
детерминированных систем отпадает необходимость в получении выборок значений
выходных параметров.
Модель системы со структурным принципом управления представляет собой
совокупность моделей элементов и их функциональные взаимосвязи. Модель элемента
(агрегата, обслуживающего прибора) - это, в первую очередь, набор правил
(алгоритмов) поведения устройства по отношению к входным воздействиям (заявкам)
и правил изменения состояний элемента. При моделировании ВС на системном уровне
элемент отображает функциональное устройство на том или ином уровне
детализации.
В простейшем случае устройство может находиться в работоспособном
состоянии или в состоянии отказа. В работоспособном состоянии устройство может
быть занято, например, выполнением операции по обслуживанию заявки или
свободно. К правилам поведения устройства относятся правила выборки заявок из
очереди; реакция устройства на поступление заявки, когда устройство занято или
к нему имеется очередь заявок; реакция устройства на возникновение отказа в
процессе обслуживания заявки и некоторые другие.
Функциональные взаимосвязи устройств определяют возможные пути
продвижения заявок по системе от входных устройств к выходным. Они формируют
функциональную структуру ВС.
Модель внешних воздействий - это правила определения моментов поступления
входных сигналов (заявок) в систему, маршрута заявок в системе по каждому из
потоков в соответствии с алгоритмами обработки, приоритетов обслуживания заявок
одних потоков по отношению к другим, трудоемкости обслуживания заявок
устройствами, допустимого времени пребывания заявок в системе и др.
В процессе имитации функционирования системы измеряются те выходные
характеристики, которые интересуют исследователя. При изучении стохастических
систем измерения производятся многократно с тем, чтобы можно было с достаточной
точностью определить вероятностные характеристики системы.
Модель системы с программным принципом управления представляет собой, в
основном, формализованное описание параллельно протекающих процессов с
указанием используемых ресурсов и алгоритмов управления процессами.
Имитационное моделирование - это метод исследования, который
основан на том, что анализируемая динамическая система заменяется имитатором и
с ним проводятся эксперименты для получения информации об изучаемой системе. Роль имитатора зачастую выполняет
специальная программа ВС.
Основная идея метода имитационного моделирования
стохастических систем во многом исследована методом вычисления случайных
величин, который называется методом статистических испытаний или методом
Монте-Карло. Заключается
он в следующем. Пусть необходимо определить функцию распределения случайной
величины у. Допустим, что искомая величина у может быть представлена
в виде зависимости
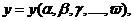
где
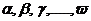 - случайные величины с известными функциями
распределения.
- случайные величины с известными функциями
распределения.
Для
решения задач такого вида применяется следующий алгоритм:
)
по каждой из величин 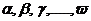 производится случайное испытание, в результате
которого определяется некоторое конкретное значение случайной величины
производится случайное испытание, в результате
которого определяется некоторое конкретное значение случайной величины 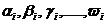 (способы проведения случайного испытания описаны
ниже);
(способы проведения случайного испытания описаны
ниже);
)
используя найденные величины, определяется одно частное значение yi по вышеприведенной зависимости;
)
предыдущие операции повторяются N раз, в результате чего определяется N
значений случайной величины у;
)
на основании N значений величины у находится ее эмпирическая
функция распределения.
Имитация
функционирования системы.
Предположим, что ВС состоит из процессора 1 с основной памятью,
устройства ввода 4, печатающего устройства 2 и монитора 3.
Через устройство ввода поступает поток заданий X1. Процессор
обрабатывает задания и результаты обработки выдает на печатающее устройство
(принтер). Одновременно с этим ВС используется, например, как информационно-справочная
система. Оператор-пользователь, работающий за монитором, посылает в систему
запросы X2, которые обрабатываются процессором, и ответы
выводятся на монитор. Процессор работает в двух программном режиме: в одном
разделе обрабатываются задания X1, в
другом, с более высоким относительным приоритетом, - запросы Х2.
Представим
данную ВС в упрощенном варианте в виде стохастической сети из четырех СМО.
Потоки заданий и запросов будем называть потоками заявок. Считаем потоки X1 и X2
независимыми. Известны функции распределения периодов следования заявок 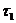 и
и 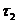 и
длительностей обслуживания Т1k и Т2k
заявок k-м устройством. Требуется определить времена загрузки каждого
устройства и времена реакции по каждому из потоков.
и
длительностей обслуживания Т1k и Т2k
заявок k-м устройством. Требуется определить времена загрузки каждого
устройства и времена реакции по каждому из потоков.
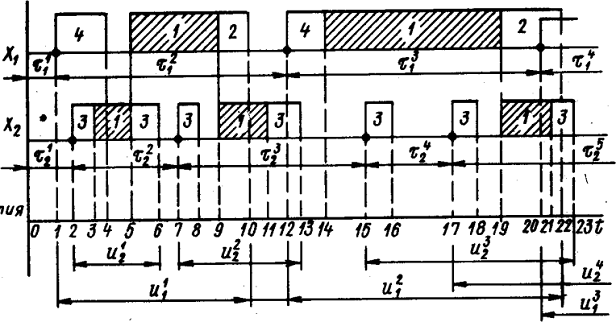
Рис. 1. Временная диаграмма функционирования ВС
В
начале определяется момент поступления в систему первой заявки потока Х1
по результатам случайного испытания в соответствии с функцией распределения
периода следования заявок. На рис. 1 это момент времени 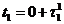 (здесь и далее верхний индекс обозначает порядковый
номер заявки данного потока). То же самое делается для потока Х2.
На рис. 1. момент поступления первой заявки потока
(здесь и далее верхний индекс обозначает порядковый
номер заявки данного потока). То же самое делается для потока Х2.
На рис. 1. момент поступления первой заявки потока 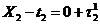 . Затем находится минимальное время, т.е. наиболее
раннее событие. В примере- это время t1. Для первой
заявки потока X1
определяется путем случайного испытания время обслуживания устройством ввода T114 и
отмечается момент окончания обслуживания
. Затем находится минимальное время, т.е. наиболее
раннее событие. В примере- это время t1. Для первой
заявки потока X1
определяется путем случайного испытания время обслуживания устройством ввода T114 и
отмечается момент окончания обслуживания 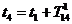 На
рисунке показан ступенькой переход устройства 4 в состояние «занято».
Одновременно определяется момент поступления следующей заявки потока
На
рисунке показан ступенькой переход устройства 4 в состояние «занято».
Одновременно определяется момент поступления следующей заявки потока 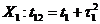 .
.
Следующее
минимальное время - это момент поступления заявки потока X2-t2. Для
этой заявки находится время обслуживания на мониторе T123 и
отмечается время окончания обслуживания 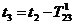 . Определяется момент поступления второй заявки потока
. Определяется момент поступления второй заявки потока 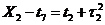 . Снова выбирается минимальное время- это tз. В этот момент заявка потока Х2 начинает
обрабатываться процессором. По результату случайного испытания определяется
время ее обслуживания T123 и отмечается момент
. Снова выбирается минимальное время- это tз. В этот момент заявка потока Х2 начинает
обрабатываться процессором. По результату случайного испытания определяется
время ее обслуживания T123 и отмечается момент 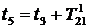 окончания обслуживания. Следующее минимальное время t4 - момент
завершения обслуживания заявки потока X1 устройством 4. С этого момента заявка может
начать обрабатываться процессором, но он занят обслуживанием заявки потока Х2.
Тогда заявка потока X1
переходит в состояние ожидания, становится в очередь.
окончания обслуживания. Следующее минимальное время t4 - момент
завершения обслуживания заявки потока X1 устройством 4. С этого момента заявка может
начать обрабатываться процессором, но он занят обслуживанием заявки потока Х2.
Тогда заявка потока X1
переходит в состояние ожидания, становится в очередь.
В
следующий минимальный момент времени t5 освобождается процессор. С этого момента процессор
начинает обрабатывать заявку потока X1, а заявка потока X2 переходит на обслуживание монитором, т. е. ответ на
запрос пользователя передается из основной памяти в буферный накопитель
монитора. Далее определяются соответствующие времена обслуживания 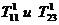 и отмечаются моменты времени
и отмечаются моменты времени 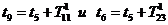 . В момент t6 полностью завершается обработка первой заявки потока
Х2. По разности времен t6 и t2
вычисляется время реакции по этой заявке:
. В момент t6 полностью завершается обработка первой заявки потока
Х2. По разности времен t6 и t2
вычисляется время реакции по этой заявке:
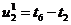
Следующий
минимальный момент времени t7 - это поступление второй заявки
потока Х2. Определяется время поступления очередной заявки
этого потока 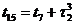 . Затем вычисляется время обслуживания второй заявки
на мониторе Т223 и отмечается момент
. Затем вычисляется время обслуживания второй заявки
на мониторе Т223 и отмечается момент 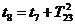 после чего заявка становится в очередь, так как
процессор занят. Эта заявка поступает на обслуживание в процессор только после
его освобождения в момент времени t9. В этот же
момент заявка потока Х1 начинает обслуживаться принтер. Определяются
времена обслуживания Т221 и T112 по
результатам случайных испытаний и отмечаются моменты окончания обслуживания
после чего заявка становится в очередь, так как
процессор занят. Эта заявка поступает на обслуживание в процессор только после
его освобождения в момент времени t9. В этот же
момент заявка потока Х1 начинает обслуживаться принтер. Определяются
времена обслуживания Т221 и T112 по
результатам случайных испытаний и отмечаются моменты окончания обслуживания 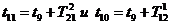 . В момент времени t10 завершается полное обслуживание первой заявки потока X1. Разность между этим моментом и моментом времени t1 дает первое
значение времени реакции по потоку
. В момент времени t10 завершается полное обслуживание первой заявки потока X1. Разность между этим моментом и моментом времени t1 дает первое
значение времени реакции по потоку 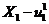 .
.
Вторая
заявка потока Х2 в момент t11 поступает с процессора на- монитор и обслуживается им
в течение времени Т223, которое завершается в
момент 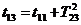 Снова определяется очередное минимальное время. Это
время - t12 когда в
систему поступает вторая заявка из потока Х1. Тогда
вычисляется время поступления третьей заявки потока
Снова определяется очередное минимальное время. Это
время - t12 когда в
систему поступает вторая заявка из потока Х1. Тогда
вычисляется время поступления третьей заявки потока 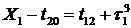 . Вторая заявка обслуживается устройством ввода в
течение времени Т214 (момент завершения -
. Вторая заявка обслуживается устройством ввода в
течение времени Т214 (момент завершения -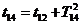 ) и процессором - T211 (момент
завершения -
) и процессором - T211 (момент
завершения - 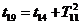 ). В момент t13 состояние
системы не изменяется, но вычисляется второе значение времени реакции по потоку
Х2:
). В момент t13 состояние
системы не изменяется, но вычисляется второе значение времени реакции по потоку
Х2:
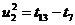
В
момент времени t15 систему
поступает третья заявка потока Х2. Определяется момент
поступления четвертой заявки потока 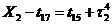 (предполагается,
что пользователь может посылать запросы, не дожидаясь ответов на предыдущие запросы).
Третья заявка обслуживается монитором в течение времени T323, но с
момента окончания обслуживания (
(предполагается,
что пользователь может посылать запросы, не дожидаясь ответов на предыдущие запросы).
Третья заявка обслуживается монитором в течение времени T323, но с
момента окончания обслуживания (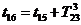 ) переходит в состояние ожидания, так как занят
процессор.
) переходит в состояние ожидания, так как занят
процессор.
Следующее
минимальное время t17, - это время поступления четвертой заявки потока Х2.
После ее обслуживания монитором (момент завершения 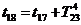 ) она также переходит в ожидание, т. е. образуется
очередь из двух заявок. После освобождения процессора в момент t19 начнется обслуживание процессором третьей заявки
потока X2, а затем с момента
) она также переходит в ожидание, т. е. образуется
очередь из двух заявок. После освобождения процессора в момент t19 начнется обслуживание процессором третьей заявки
потока X2, а затем с момента 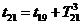 -
монитором. По завершении этого обслуживания (
-
монитором. По завершении этого обслуживания (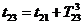 ) можно
будет вычислить третье значение времени реакции по потоку X2:
) можно
будет вычислить третье значение времени реакции по потоку X2:
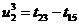
С
момента времени t19 принтер
начнет обслуживание второй заявки потока X1 и завершит его к моменту
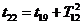 , после чего определяется второе значение времени
реакции по потоку X1:
, после чего определяется второе значение времени
реакции по потоку X1:
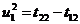
Указанные
процедуры выполняются до истечения времени моделирования. В результате
получается некоторое количество (выборка) случайных значений времен реакции {u1} и {u2} по
первому и второму потокам. По этим значениям могут быть определены эмпирические
функции распределения и вычислены количественные вероятностные характеристики
времен реакции. В процессе моделирования можно суммировать продолжительности
занятости каждого устройства обслуживанием всех потоков. Например, на рис. 1
занятость процессора 1 выделена заштрихованными ступеньками. Если результаты
суммирования разделить на время моделирования, то получатся коэффициенты
загрузки устройств.
Одновременно
появляется возможность определения таких характеристик системы, как время
ожидания заявок в очереди, число заявок, обслуженных системой, средняя и
максимальная длина очереди заявок к каждому из устройств, требуемая емкость
памяти и некоторые другие характеристики.
Имитационное
моделирование дает возможность учесть надежностные характеристики ВС. В
частности, если известны времена наработки на отказ и восстановления всех
входящих в систему устройств, определяются моменты возникновения отказов
устройств в период моделирования и моменты восстановления. Если в моменты
возникновения отказа устройство занято обслуживанием заявки, то может приниматься
разное решение в зависимости от типа устройства и режима его работы: заявка
снимается и больше не обслуживается (выбывает из системы) или заявка помещается
в очередь, а после восстановления устройства дообслуживается или поступает на
повторное обслуживание.
2. Обобщенные алгоритмы имитационного моделирования
Алгоритм моделирования по принципу особых состояний. В изложенном выше примере
моделирование проводилось по принципу особых состояний (событий). В качестве
особых событий выделены поступление заявки в систему, освобождение элемента
после обслуживания заявки, завершение моделирования. В общем случае в системе
могут быть выделены события и других типов, например возникновение отказа
устройства в процессе обслуживания заявки и завершение восстановления
устройства после отказа.
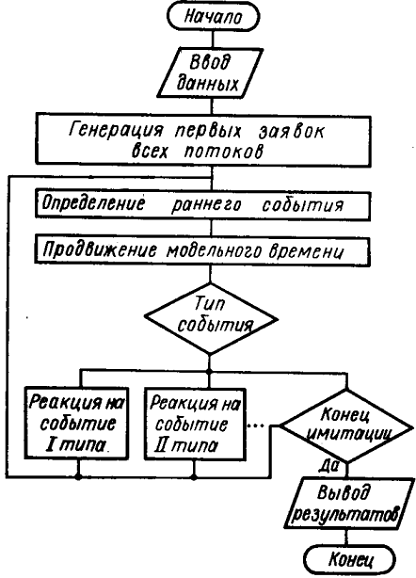
Рис. 2. Алгоритм моделирования по принципу особых состояний
Процесс
имитации функционирования системы развивался во времени с использованием
управляющих последовательностей, определяемых по функциям распределения
вероятностей исходных данных путем проведения случайных испытаний. В качестве
управляющих последовательностей использовались в примере последовательности
значений периодов следования заявок по каждому i-му потоку
{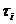 } и длительностей обслуживания заявок i-го
потока k-м устройством {Tik}. Моменты наступления будущих событий определялись по
простым рекуррентным соотношениям. Эта особенность дает возможность построить простой
циклический алгоритм моделирования, который сводится к следующим действиям:
} и длительностей обслуживания заявок i-го
потока k-м устройством {Tik}. Моменты наступления будущих событий определялись по
простым рекуррентным соотношениям. Эта особенность дает возможность построить простой
циклический алгоритм моделирования, который сводится к следующим действиям:
)
определяется событие с минимальным временем - наиболее раннее событие;
)
модельному времени присваивается значение времени наступления наиболее раннего
события;
)
определяется тип события;
)
в зависимости от типа события предпринимаются действия, направленные на
загрузку устройств и продвижение заявок в соответствии с алгоритмами их
обработки, и вычисляются моменты наступления будущих событий; эти действия
называют реакцией модели на события;
)
перечисленные действия повторяются до истечения времени моделирования.
В
процессе моделирования производится измерение и статистическая обработка
значений выходных характеристик. Обобщенная схема алгоритма моделирования по
принципу особых состояний (принцип 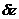 )
изображена на рис. 2. Вначале производится инициализация моделирующей программы
- подготавливаются массивы, вводятся и размещаются в оперативной памяти входные
данные, настраиваются датчики случайных чисел. Затем генерируются первые заявки
по каждому потоку - определяются моменты их поступления в систему и
конкретизируются другие параметры.
)
изображена на рис. 2. Вначале производится инициализация моделирующей программы
- подготавливаются массивы, вводятся и размещаются в оперативной памяти входные
данные, настраиваются датчики случайных чисел. Затем генерируются первые заявки
по каждому потоку - определяются моменты их поступления в систему и
конкретизируются другие параметры.
Остальные
операции выполняются в цикле. Определяется момент наступления наиболее раннего
события и до этого момента смещается модельное время. После определения типа
события реализуется соответствующая реакция на событие. В процессе этих
действий могут возникать те или иные события в будущем, что фиксируется в
массиве событий. Реакция на определенное событие, кроме всего прочего,
приводит, как правило, к исключению его из массива событий. Кончается каждая
реакция возвратом к определению события с минимальным временем.
Такой
цикл повторяется до достижения конца моделирования, после чего завершается
обработка статистики и выводятся результаты. На этом заканчивается модельный
эксперимент.
В системе-оригинале могут протекать одновременно несколько процессов. Это
приводит к тому, что в один и тот же момент времени в системе может возникнуть
несколько особых событий. При моделировании на однопроцессорной ВС эти ситуации
разрешаются таким образом: последовательно в установленном порядке реализуются
реакции на все одновременно возникшие ситуации без продвижения модельного
времени. Это называется псевдопараллельной имитацией нескольких процессов.
Рис. 3. Алгоритм моделирования по принципу временных приращений
Алгоритм
моделирования по принципу 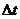 . Укрупненная схема моделирующего алгоритма,
который реализует принцип постоянного приращения модельного времени (принцип
. Укрупненная схема моделирующего алгоритма,
который реализует принцип постоянного приращения модельного времени (принцип 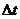 ), представлена на рис. 3. Как и в предыдущем
алгоритме, вначале инициализируется программа, в частности, вводятся значения zi(t0), i= 1,
...,n, которые характеризуют состояние системы в n-мерном фазовом пространстве состояний в начальный момент времени t0. Модельное время
устанавливается t = t0 = 0.
), представлена на рис. 3. Как и в предыдущем
алгоритме, вначале инициализируется программа, в частности, вводятся значения zi(t0), i= 1,
...,n, которые характеризуют состояние системы в n-мерном фазовом пространстве состояний в начальный момент времени t0. Модельное время
устанавливается t = t0 = 0.
Основные
операции, с помощью которых имитируется функционирование системы, выполняются в
цикле. Функционирование системы отслеживается по последовательной смене
состояний Zi (t). Для этого модельному времени дается некоторое
приращение 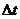 . Затем по вектору текущих состояний определяются
новые состояния zi (t
+
. Затем по вектору текущих состояний определяются
новые состояния zi (t
+ 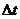 ), которые становятся текущими. Для определения новых
состояний по текущим в формализованном описании системы должны существовать
необходимые математические зависимости. Такой цикл продолжается до тех пор,
пока текущее модельное время меньше заданного времени моделирования Тm.
), которые становятся текущими. Для определения новых
состояний по текущим в формализованном описании системы должны существовать
необходимые математические зависимости. Такой цикл продолжается до тех пор,
пока текущее модельное время меньше заданного времени моделирования Тm.
По
ходу имитации измеряются, фиксируются и обрабатываются требуемые выходные
характеристики. При t 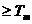 завершается
обработка измерений и выводятся результаты моделирования.
завершается
обработка измерений и выводятся результаты моделирования.
При
моделировании стохастических систем вместо новых состояний вычисляются
распределения вероятностей для возможных состояний. Конкретные значения вектора
текущего состояния определяются по результатам случайных испытаний. В
результате проведения имитационного эксперимента получается одна из возможных
реализации случайного многомерного процесса в заданном интервале времени (to, Tт).
Моделирующий
алгоритм, основанный на принципе 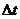 , применим для более широкого круга систем, чем
алгоритм, построенный по принципу особых состояний. Однако при его реализации
возникают проблемы с определением величины
, применим для более широкого круга систем, чем
алгоритм, построенный по принципу особых состояний. Однако при его реализации
возникают проблемы с определением величины 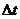 . Для
моделирования ВС на системном уровне в основном применяется принцип особых
состояний.
. Для
моделирования ВС на системном уровне в основном применяется принцип особых
состояний.
Контрольные вопросы
1. Общее определение имитационного
моделирования.
2. Имитация функционирования ВС.
3. Алгоритм моделирование по принципу
особых состояний.
4. Алгоритм моделирования по принципу
временных приращений.
Литература
1. Альянах И.Н. Моделирование вычислительных систем, Л.: Машиностроение, 1988
г. - 223 стр.
2. Вентцель Е.С. Исследование операций: задачи, принципы, методология. М.:
Наука, 1980 г. - 208 стр.
3. Зобов Б.И., Сурков А.В. Основы моделирования вычислительных
систем. М.: МЛТИ, 1982 г. -32 стр.
4. Масков А.И. моделирование вычислительных систем. Пермь: ПГУ, 1982 г. - 95
стр.
Лекция 13. МЕТОДЫ ИССЛЕДОВАНИЯ ВЫЧИСЛИТЕЛЬНЫХ СИСТЕМ (2 часа)
План
1.
Методы определения характеристик вычислительных систем
.
Метод повторных экспериментов
.
Методы генерации случайных величин и последовательностей
1. Методы определения характеристик вычислительных систем
Измеряемые характеристики ВС. При имитационном моделировании можно
измерять значения любых характеристик, интересующих исследователя. Обычно по
результатам измерений вычисляют характеристики всей системы, каждого потока и
устройства.
Для всей ВС производится подсчет поступивших в систему заявок, полностью
обслуженных и покинувших систему заявок без обслуживания по тем или иным
причинам. Соотношения этих величин характеризуют производительность ВС при
определенной рабочей нагрузке.
По каждому потоку заявок могут вычисляться времена реакции и ожидания,
количества обслуженных и потерянных заявок. По каждому устройству зачастую
определяются время загрузки при обслуживании одной заявки и число обслуженных
устройствам заявок, время простоя устройства в результате отказов и количество
отказов, возникших в процессе моделирования, длины очередей и занимаемые
емкости памяти.
При статистическом моделировании большая часть характеристик - это
случайные величины. По каждой такой характеристике у определяется N
значений, по которым строится гистограмма относительных частот, вычисляются
математическое ожидание, дисперсия и моменты более высокого порядка, определяются
средние по времени и максимальные значения. Коэффициенты загрузки устройств
вычисляются по формуле
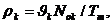 (1)
(1)
где
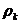 - коэффициент загрузки k-го устройства;
- коэффициент загрузки k-го устройства; 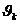 - среднее время обслуживания одной заявки k-м устройством; Nok- количество обслуженных
устройством заявок за время моделирования Тт
- среднее время обслуживания одной заявки k-м устройством; Nok- количество обслуженных
устройством заявок за время моделирования Тт
Определение
условий удовлетворения стохастических ограничений при имитационном
моделировании производится путем простого подсчета количеств измерений,
вышедших и не вышедших за допустимые пределы.
Расчет
математического ожидания и дисперсии выходной характеристики. В случае анализа стационарного эргодического процесса
функционирования системы вычисление математического ожидания и дисперсии
характеристики у производится усреднением не по времени, а по множеству N
значений, измеренных по одной реализации процесса достаточной продолжительности.
В целях экономии основной памяти ВС, на которой проводится моделирование,
математическое ожидание и дисперсия вычисляются в ходе моделирования путем
наращивания итогов при появлении очередного измерения случайной характеристики
по рекуррентным формулам. Математическое ожидание случайной величины у
для ее n-го измерения уn:
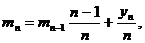 (2)
(2)
где mn-1 - математическое ожидание,
вычисленное по предыдущим п - 1 измерениям.
Дисперсия для n-го
измерения:
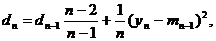 (3)
(3)
где
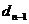 - дисперсия, вычисленная по предыдущим п - 1
измерениям. Вначале дисперсия принимается равной нулю.
- дисперсия, вычисленная по предыдущим п - 1
измерениям. Вначале дисперсия принимается равной нулю.
При
большом количестве измерений эти оценки являются состоятельными и несмещенными.
Расчет
среднего по времени значения выходной характеристики. В процессе моделирования постоянно ведется подсчет
длины очереди к каждому устройству и занимаемой емкости накопителей. При этом
отслеживается максимальное значение и вычисляется среднее по времени значение.
Например, средняя длина очереди вычисляется по формуле
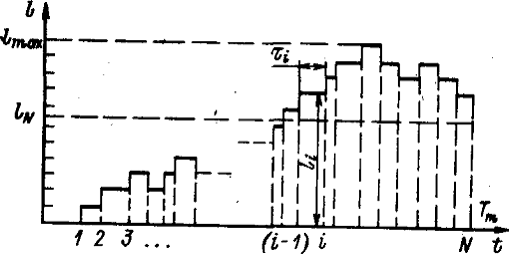
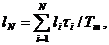 (4)
(4)
Рис. 1.
Временная диаграмма изменения длины очереди
где
i - номер очередного изменения состояния очереди
(занесения заявки в очередь или исключения из очереди) (рис. 1); N-количество
изменений состояния очереди; 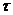 i; -
интервал времени от (i-1)-го до
1-го изменения состояния; li - число
заявок в очереди в интервале
i; -
интервал времени от (i-1)-го до
1-го изменения состояния; li - число
заявок в очереди в интервале 
По
аналогичной формуле вычисляется средняя по времени используемая емкость
накопителя:
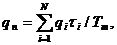 (5)
(5)
где qi - емкость накопителя, занятая в интервале времени между
двумя последовательными, обращениями к накопителю.
Формулы (4) и (5) приводят к виду, удобному для вычисления путем
наращивания итогов.
Построение гистограммы. Основное достоинство имитационного моделирования
заключается в том, что по любой выходной характеристике может быть построена
гистограмма относительных частот - эмпирическая плотность распределения
вероятностей, вне зависимости от сочетаний распределений параметров системы и
внешних воздействий. При исследовании стационарной системы гистограмма строится
по следующей методике.
Перед началом моделирования задаются предположительные границы изменения
интересующей выходной характеристики y, т. е. нижний
yH и верхний yB пределы, и указывается число
интервалов гистограммы Ng.
По этим данным вычисляется интервал
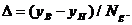

Затем
в процессе моделирования по мере появления измерений характеристики у,
определяется число попаданий этой случайной величины в i-й
интервал гистограммы Ri; и подсчитывается общее число измерений N. По
полученным данным вычисляется относительная частота по каждому интервалу:
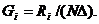
Этих
данных достаточно для построения гистограммы относительных частот: на оси
абсцисс откладываются пределы изменения анализируемой характеристики у;
весь диапазон изменения подразделяется на заданное число интервалов; над каждым
t-м интервалом проводится отрезок, параллельный оси абсцисс, на расстоянии,
равном Gi от оси абсцисс (рис. 2).
Отметим,
что площадь гистограммы относительных частот равна единице, так же, как
интеграл от плотности вероятности в пределах от минус до плюс бесконечности
равен единице. Площадь гистограммы равняется сумме площадей прямоугольников,
построенных на каждом i-ом интервале:
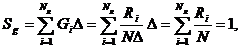
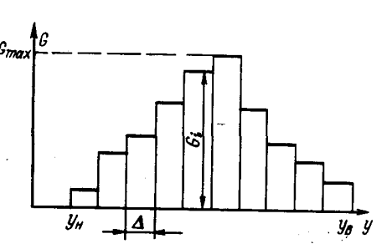
Рис.
2. Гистограмма относительных частот
поскольку
общее число измерений характеристики у равно сумме чисел попаданий в
каждый из интервалов:
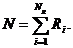
При
необходимости выдвигается гипотеза о том, что полученное эмпирическое
распределение согласуется с некоторым теоретическим распределением, имеющим
аналитическое выражение для функции или плотности распределения. Эта гипотеза
проверяется по тому или другому критерию. Например, при использовании критерия
хи-квадрат в качестве меры расхождения используется выражение
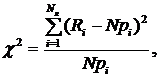 (6)
(6)
где pi - определенная из выбранного теоретического
распределения вероятность попадания случайной величины в i-й интервал.
Из
теоремы Пирсона следует, что для любой функции распределения F(у) случайной величины у при N  распределение величины
распределение величины 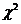 имеет
вид
имеет
вид
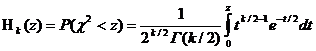 (7)
(7)
где
z - значение случайной величины 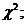 k = Ng -(r
+1) - число степеней свободы распределения хи-квадрат; r - количество
параметров теоретического закона распределения; Г (k/2)
- гамма-функция.
k = Ng -(r
+1) - число степеней свободы распределения хи-квадрат; r - количество
параметров теоретического закона распределения; Г (k/2)
- гамма-функция.
Функция
распределения хи-квадрат табулирована по вычисленному значению и числу степеней
свободы с помощью таблиц определяется вероятность (7). Если она превышает
заданный уровень значимости С, то выдвинутая гипотеза принимается.
2. Метод повторных экспериментов
Характеристики нестационарных процессов. Для системы, процесс
функционирования которой отличается от стационарного эргодического, нельзя
вычислять вероятностные характеристики по одной реализации процесса, поскольку
оценки могут получиться смещенными или несостоятельными. Следует ожидать, что
если на ВС поступает поток заявок, интенсивность которого изменяется во
времени, как это показано, например, на рис. 3. выходные характеристики такой
системы относятся к нестационарным случайным функциям (процессам).
Известно,
что в основе всех формальных методов лежит представление случайного процесса с
помощью ансамбля реализации и описание его посредством характеристик,
получаемых усреднением по ансамблю. Предположим, что случайный процесс Y(t)
задан ансамблем реализации 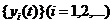 , а
интересующая исследователя вероятностная характеристика в
, а
интересующая исследователя вероятностная характеристика в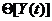 определяется предельным соотношением
определяется предельным соотношением
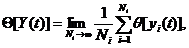 (8)
(8)
где
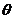 - оператор преобразования, лежащий в основе
определения характеристики
- оператор преобразования, лежащий в основе
определения характеристики 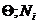 - количество реализации, по которым производится усреднение.
- количество реализации, по которым производится усреднение.
При
усреднении по ограниченной совокупности реализации прямые измерения значений
вероятностной характеристики в 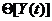 могут
быть выполнены в соответствии с формулой
могут
быть выполнены в соответствии с формулой
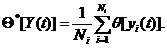 (9)
(9)
Полной
вероятностной характеристикой случайного процесса может служить многомерная
функция распределения вероятности мгновенных значений процесса. Случайный
процесс Y(t) считается исчерпывающе описанным в вероятностном
смысле на интервале 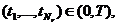 , если задана его Nr- мерная функция распределения:
, если задана его Nr- мерная функция распределения:
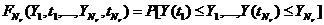 (10)
(10)
которая
соответствует любому сочетанию моментов времени tr на
интервале (О, Т) при произвольном Nr, в том числе при  . Исходя из этих предпосылок, при исследовании
стохастических систем необходимо получать для каждой выходной характеристики
совокупности Ni реализации, причем по каждой реализации следует
измерять значения no Nr сечениям
(отсчетам), как это показано на рис. 3. Таким способом могут быть получены
вероятностные оценки выходных характеристик, если они являются нестационарными
или стационарными неэргодическими процессами.
. Исходя из этих предпосылок, при исследовании
стохастических систем необходимо получать для каждой выходной характеристики
совокупности Ni реализации, причем по каждой реализации следует
измерять значения no Nr сечениям
(отсчетам), как это показано на рис. 3. Таким способом могут быть получены
вероятностные оценки выходных характеристик, если они являются нестационарными
или стационарными неэргодическими процессами.
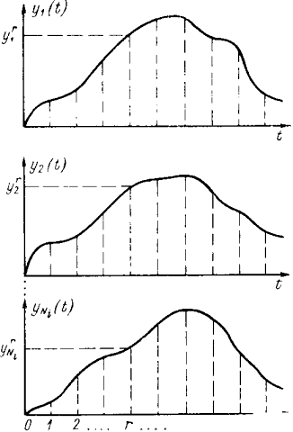
Рис. 3.
Реализации нестационарного случайного процесса
Алгоритм повторных экспериментов. При имитационном моделировании
нестационарного режима функционирования ВС требуется получить ni реализации случайных процессов по
всем выходным характеристикам. С этой целью необходимо проводить ni имитационных экспериментов в
интересующей исследователя области определения случайных процессов (О, Т).
Изменение характера сочетаний случайных событий в каждом последующем
эксперименте может быть достигнуто заменой начальных значений датчиков
случайных чисел, используемых в процессе моделирования, в частности, для
генерации управляющих последовательностей. Это можно реализовать, например,
так: при каждом последующем эксперименте в качестве начальных значений датчиков
случайных чисел используют последние значения предыдущего эксперимента.
Исследование систем с нестационарным режимом путем имитационного
моделирования с применением метода повторных экспериментов сводится к
следующему. Проводится Ni имитационных экспериментов. При каждом последующем эксперименте
параметры системы и нагрузки устанавливаются на исходные значения и в процессе
каждого эксперимента остаются неизменными или изменяются по одним и тем же
зависимостям. Датчики случайных чисел устанавливаются в начальное состояние
только один раз - перед моделированием и до конца моделирования вырабатывают
последовательности случайных чисел.
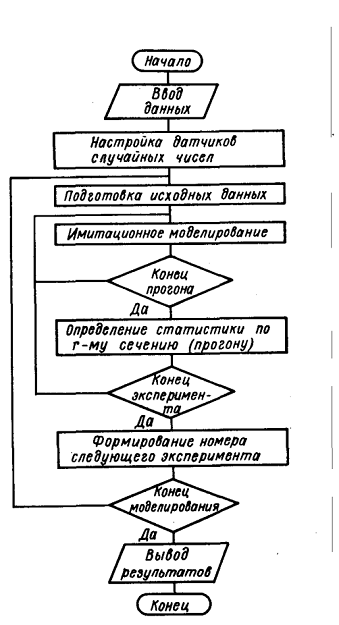
Рис. 4. Алгоритм моделирования по методу повторных экспериментов
Период
моделирования Тm по каждому эксперименту разделяется на Nr сечений.
Интервал времени моделирования между двумя соседними сечениями будем называть
прогоном. В каждом эксперименте для фиксированных моментов времени 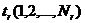 определяются численные значения выходных
характеристик.
определяются численные значения выходных
характеристик.
По
каждому i-му сечению для всех выходных характеристик может
определяться эмпирическая многомерная функция 
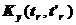 или
плотность распределения, оцениваться математическое ожидание my(tr), корреляционная функция
или
плотность распределения, оцениваться математическое ожидание my(tr), корреляционная функция  или
дисперсия Dy (tr) по всей совокупности Ni
реализации.
или
дисперсия Dy (tr) по всей совокупности Ni
реализации.
Для обеспечения статистической достоверности результатов обычно требуется
проведение нескольких сотен или тысяч экспериментов с измерением и обработкой
вектора выходных характеристик по нескольким десяткам сечений. Очевидно, что
выполнение этой работы «вручную» не представляется возможным в приемлемые
сроки. Это означает, что на ВС должно быть возложено не только проведение
имитации, но и реализация метода повторных экспериментов.
Машинный алгоритм повторных экспериментов представлен на рис. 4. В первом
блоке выполняется ввод данных о моделируемой системе и нагрузке, а также
производится инициализация программы. Отдельно выделен блок настройки датчиков
случайных чисел, чтобы подчеркнуть, что датчикам задаются начальные значения до
основных циклов моделирования. В дальнейшем датчики вырабатывают
неповторяющиеся последовательности случайных чисел. Затем вводятся и
размещаются в соответствующих массивах и переменных исходные данные. В
частности, задаются количества прогонов Nr, экспериментов Ni и период моделирования Тm.
В следующем блоке выполняется имитационное моделирование процесса
функционирования так, как это описано в п. 2, по тому или другому алгоритму. В
ходе имитации изменяются значения тех переменных параметров, которые заданы как
функции времени, и постоянно отслеживается достижение конца прогона, т. е.
событие, когда текущее модельное время станет равным tr. При
выполнении этого условия определяются, вычисляются и запоминаются
статистические данные по r-му
сечению, после чего имитация продолжается.
Если выполнено Nr прогонов, т. е. завершен очередной эксперимент, формируется номер
следующего эксперимента и управление передается блоку подготовки исходных
данных. После проведения Ni экспериментов завершается обработка и вывод результатов моделирования.
Расчет характеристик по методу повторных экспериментов. При анализе
систем с нестационарным процессом функционирования путем имитационного
моделирования с использованием метода повторных экспериментов для каждой
выходной характеристики, которая является случайным процессом, зачастую
оценивается математическое ожидание, корреляционная функция или дисперсия, а
также могут быть построены по каждому сечению гистограммы, чем определяется
многомерная плотность распределения вероятностей.
Математическое ожидание случайного процесса Y (t) - это неслучайная функция ту(t),
которая при каждом значении аргумента tr представляет собой математическое ожидание
соответствующего сечения случайной функции:
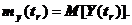
Корреляционная
функция случайного процесса - это тоже неслучайная функция двух аргументов Ку(t, t'),
которая при каждой паре значений аргументов t,t'
равна корреляционному моменту соответствующих сечений случайной функции:
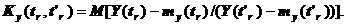
При
равенстве t=t' корреляционная функция превращается в дисперсию
случайной функции:
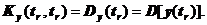
В
соответствии с формулой (9) Nr-мерная плотность распределения вероятностей
оценивается по формуле:
 (11)
(11)
где
значения функции 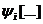 равны 1 при
равны 1 при 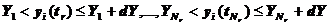 и равны
0, если хотя бы одно из этих неравенств для i-й реализации
не выполняется.
и равны
0, если хотя бы одно из этих неравенств для i-й реализации
не выполняется.
В
результате вычисления по формуле (11) получается многомерная плотность
распределения вероятностей, подобная той, которая изображена на рис. Важно
отметить, что для проверки выполнения стохастических ограничительных условий
нет необходимости вычислять плотность распределения по формуле (11), а
достаточно подсчитать общее количество Ny и
количество Np значений измерения случайной величины, попадающих
между ограничивающими пределами, по всей совокупности экспериментов, а затем
определить вероятность выполнения ограничительного условия:
Py=NP/Ny 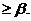 (12)
(12)
При моделировании вычисления результатов производятся в конце каждого
прогона путем наращивания итогов. В частности, количественные вероятностные
значения таких выходных характеристик, как длины очередей к каждому устройству,
времена реакции по каждому потоку заявок и времена загрузки каждого устройства,
определяются по r-му сечению для i-го эксперимента по следующим
формулам. Оценка математического ожидания длины очереди к устройству:
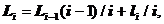 (13)
(13)
где Li-1 - математическое ожидание длины
очереди за предыдущие (i-1)
экспериментов; li -
длина очереди по r-му сечению для i-го эксперимента.
Дисперсия длины очереди
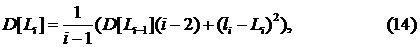
где D[Li-1] - дисперсия длины очереди за предыдущие
(i - 1) экспериментов; в первом
эксперименте дисперсия принимается равной нулю.
По временам реакции и загрузки при достаточно большом количестве сечений,
когда процесс можно считать стационарным на протяжении одного прогона, текущие
значения математических ожиданий и дисперсии вычисляются по формулам (2) и (3)
соответственно. Тогда в r-м
сечении i-го эксперимента оценка
математического ожидания времени загрузки каждого устройства при обслуживании
одной заявки:
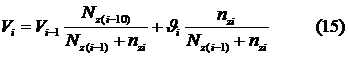
где
Vi-1 -
математическое ожидание времени загрузки за предыдущие (i- 1)
экспериментов; Nz(i-1) - число загрузок устройства на r-м
прогоне по предыдущим (i - 1) экспериментам; 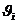 - математическое ожидание времени загрузки на r-м
прогоне в i-м эксперименте; nzi -
число загрузок устройства на r-м прогоне в i-м эксперименте.
- математическое ожидание времени загрузки на r-м
прогоне в i-м эксперименте; nzi -
число загрузок устройства на r-м прогоне в i-м эксперименте.
Дисперсия
времени загрузки каждого устройства на r-м прогоне
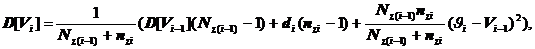
где
D [Vi-1] -
дисперсия, вычисленная по предыдущим (i - 1) экспериментам; di -дисперсия,
вычисленная в i-м эксперименте.
Коэффициенты
загрузки устройств вычисляются по формуле (1).
Оценки
математического ожидания и дисперсии времени реакции Ui по
каждому потоку в r-м сечении i-го эксперимента выполняются по
формулам, аналогичным (15) и (16). Для экономии места в памяти моделирующей ВС
обновленные статистические характеристики по r-му сечению записываются
на место прежних, вычисленных в (i - 1) эксперименте.
3. Методы генерации случайных величин и последовательностей
Датчики равномерно распределенных случайных чисел. При статистическом
моделировании стохастических систем возникает необходимость в определении
случайных событий, величин и последовательностей по заданным статистическим
характеристикам. В основе их определения лежит использование последовательности
чисел, равномерно распределенных в интервале (0,1). Программы ВС, формирующие
такие последовательности, называют датчиками или генераторами случайных чисел.
Для получения последовательности равномерно распределенных случайных
чисел с помощью ВС часто используется мультипликативный способ. Случайные числа
получаются из рекуррентного соотношения
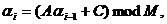 (17)
(17)
где А, С - константы; М - достаточно большое положительное
целое число.
При
соответствующем выборе констант и задании некоторого начального значения 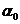 эта формула позволяет получать последовательность
целых чисел, равномерно распределенных в интервале (0, М - 1).
Последовательность имеет период повторения, равный М. Поэтому точнее
называть числа псевдослучайными. Случайные числа, равномерно распределенные в
интервале (0,1), находятся масштабным преобразованием полученных целых чисел.
эта формула позволяет получать последовательность
целых чисел, равномерно распределенных в интервале (0, М - 1).
Последовательность имеет период повторения, равный М. Поэтому точнее
называть числа псевдослучайными. Случайные числа, равномерно распределенные в
интервале (0,1), находятся масштабным преобразованием полученных целых чисел.
Моделирование
случайных событий и дискретных величин.
Для моделирования случайного события X, наступающего с вероятностью Р,
берется значение 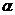 случайного числа, равномерно распределенного на
интервале (0,1), и сравнивается с Р. Если
случайного числа, равномерно распределенного на
интервале (0,1), и сравнивается с Р. Если 
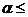 Р, то
считается, что произошло событие X.
Р, то
считается, что произошло событие X.
Предположим,
что дискретная случайная величина Y может принимать значения y1, …, yn вероятностями р1, ..., рп..
При этом
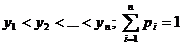 .
.
Тогда
берется значение 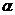 случайного числа, распределенного равномерно на
интервале (0, 1), и определяется такое k, принадлежащее совокупности (1, n),
при котором удовлетворяется неравенство
случайного числа, распределенного равномерно на
интервале (0, 1), и определяется такое k, принадлежащее совокупности (1, n),
при котором удовлетворяется неравенство
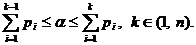
Тогда
случайная величина Y принимает значение уk..
Моделирование
случайных непрерывных величин. Пусть
непрерывная случайная величина Y имеет произвольный закон распределения.
Предположим, что она задается эмпирической плотностью распределения f*
(у) - гистограммой (рис. 5, а).
Из гистограммы определяется эмпирическая функция распределения F* (у) -
дискретная кумулятивная функция (рис. 5, б) для середин интервалов
группирования случайной величины в пределах (ymin, y max).
Для
определения одного конкретного значения случайной величины Y берется
значение α
случайного числа, равномерно
распределенного на интервале (0, 1). Затем находится такое k, при
котором
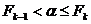
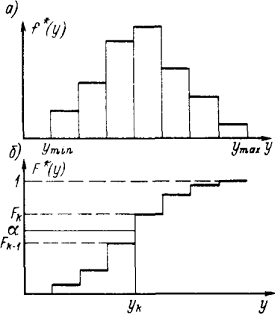
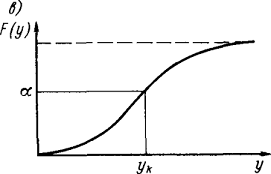
Рис.
5. Графики для определения значения случайного числа по дискретной и
интегральной функции распределения
Тогда
искомое случайное число равно yk (рис. 5, б). Это же правило применимо и при
задании случайной непрерывной величины интегральной функцией распределения F
(у), как показано на рис. 5, в. Оно вытекает из теоремы: если
случайная величина Y имеет плотность распределения F (у), то ее распределение
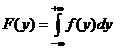 (18)
(18)
является равномерным на интервале (0, 1).
Для
некоторых законов распределения (экспоненциальный, Эрланга) имеются простые
аналитические зависимости у = Ф (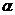 ).
Например, пусть требуется получить конкретное значение случайного числа Y
с экспоненциальным законом
распределения. Подставим в формулу (18) а и плотность распределения:
).
Например, пусть требуется получить конкретное значение случайного числа Y
с экспоненциальным законом
распределения. Подставим в формулу (18) а и плотность распределения:
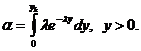
После
интегрирования получается
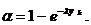
Разрешая
это уравнение относительно уk,, имеем
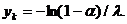
Учитывая,
что если случайная величина 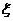 подчинена
равномерному закону распределения в интервале (0, 1), то случайная величина
подчинена
равномерному закону распределения в интервале (0, 1), то случайная величина 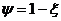 также имеет равномерный закон распределения в интервале
(0, 1), последнее соотношение можно заменить следующим:
также имеет равномерный закон распределения в интервале
(0, 1), последнее соотношение можно заменить следующим:
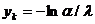 (19)
(19)
Процедура определения конкретного значения случайного числа с
заданным законом распределения называется случайным испытанием или «бросанием
жребия».
Моделирование
случайных процессов сводится на практике к определению последовательностей
случайных величин. Исходными данными являются функции распределения,
определенные в требуемые моменты времени, и последовательность случайных чисел 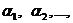 подчиняющаяся равномерному закону распределения в
интервале (0, 1). Конкретные значения случайных процессов в нужные моменты
времени находят по изложенным выше правилам.
подчиняющаяся равномерному закону распределения в
интервале (0, 1). Конкретные значения случайных процессов в нужные моменты
времени находят по изложенным выше правилам.
В
большом числе публикаций, рассматриваются вопросы алгоритмизации,
программирования и исследования качества датчиков случайных чисел.
В
процессе статистического моделирования существует необходимость в частом
обращении к датчикам случайных чисел. С их помощью формируются конкретные
значения случайных параметров каждой заявки, параметров обслуживания заявки
каждым устройством; определяются пути продвижения заявки по тому или иному
маршруту при вероятностной дисциплине маршрутизации и т. д. Имитационное
моделирование систем по принципу особых состояний проводится с постоянным
использованием датчиков случайных чисел для формирования всех управляющих
последовательностей.
Контрольные вопросы
1. Измеряемые характеристики ВС.
2. Основные формулы для расчета выходных
характеристик ВС.
3. Методика построения гистограммы и ее
использование для исследования ВС.
4. Основная идея метода повторных
экспериментов.
5. Что понимается под датчиком случайных
величин?
6. Какие методы (алгоритмы, программы)
генерации последовательностей случайных величин вы знаете?
7. Примеры использования датчиков
случайных чисел.
Литература
1. Альянах
И.Н. Моделирование
вычислительных систем, Л.: Машиностроение, 1988 г. - 223 стр.
2. Вентцель
Е.С. Исследование
операций: задачи, принципы, методология. М.: Наука, 1980 г. - 208 стр.
3. Зобов
Б.И., Сурков А.В. Основы
моделирования вычислительных систем. М.: МЛТИ, 1982 г. -32 стр.
4. Масков
А.И. моделирование
вычислительных систем. Пермь: ПГУ, 1982 г. - 95 стр.
Лекция 14. МОДЕЛИ ЛИНЕЙНОГО БУЛЕВА
ПРОГРАММИРОВАНИЯ (2 часа)
План
1.
Модели линейной дискретной оптимизации с булевыми переменными
.
Преобразование задачи с дискретными переменными к задаче с булевыми переменными
.
Преобразование задачи линейного булева программирования к задаче нелинейного
булева программирования
1. Модели линейной дискретной оптимизации с булевыми
переменными
Задача оптимизации линейной целевой функции с булевыми переменными и
линейными ограничениями является одной из самых распространенных моделей
дискретного программирования. Комбинаторные задачи с булевыми переменными,
принимающими значения 0 или 1, встречаются при решении многих практических
проблем из экономики, проектирования, управления и других областей.
Задача оптимизации (минимизации или максимизации) линейной целевой
функции с булевыми переменными и линейными ограничениями в общем виде
описывается с помощью одной из следующих моделей линейного булева
программирования: . Модель А - для задачи минимизации
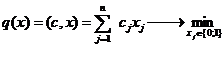 (1)
(1)
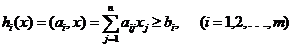 (2)
(2)
II. Модель В -
для задачи максимизации
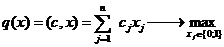 (3)
(3)
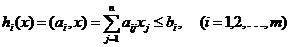 (4)
(4)
т.е. требуется минимизировать или максимизировать линейную целевую
функцию q(x) по булевым переменным xjÎ{0,1} при выполнении условия, задаваемого
системой линейных неравенств вида (2) или (4).
Проблема отыскания решения задачи (1), (2) или (3), (4) может в принципе
решаться с применением метода полного перебора, суть которого заключается в
переборе всех булевых векторов заданной длины, проверке для каждого вектора
выполнения линейных ограничений, вычислении значений целевой функции для
допустимых векторов и выборе из них минимального или максимального значения
целевой функции. Однако решение, полученное методом полного перебора, связано с
большим объемом вычислений, который неосуществим при больших размерностях
задачи даже на сверхпроизводительных ЭВМ. Так как каждая из n компонент
независимо от других может принимать два значения 0 или 1, поэтому общее число
булевых векторов длины n равно 2n.
Это величина и характеризует сложность алгоритма полного перебора. В
связи с тем, что для большинства задач дискретной оптимизации полный перебор
неосуществим, были разработаны различные методы неявного перебора, которые
обеспечивают нахождение точного решения без пересмотра всех булевых векторов.
Такими являются различные варианты метода отсечений, метода ветвей и границ,
метода динамического программирования. Но опыт применения этих методов при
решении реальных задач с достаточно большим числом переменных показал, что
многие задачи линейного программирования с булевыми переменными еще являются
нерешаемыми на ЭВМ из-за нехватки машинного времени. Следовательно, с ростом
размера задачи n она становится "труднорешаемой", т.е.
практически неразрешимой.
Задача (1), (2) или (3), (4) в числе многих задач комбинаторной
оптимизации отнесена к классу "труднорешаемых" или, NP (nо
polynomial) - полных задач. Причина заключается в том, что алгоритма, решающего
поставленную задачу за время, ограниченное полиномам от "размера
задачи", в настоящее время нет.
В связи с этим исследования, направленные на разработку новых эффективных
или полиномиальных методов решения задач линейного программирования с булевыми
переменными, являются, несомненно, актуальными.
Сначала рассмотрим широко распространенные практические задачи,
описываемые моделями линейного программирования с булевыми переменными.
2. Преобразование задачи с дискретными переменными к задаче с
булевыми переменными
Пусть x дискретная переменная, принимающая только целые значения 0,1,2,...,k.
Тогда эту переменную можно представить как линейную комбинацию (p+1)
булевых переменных y0, y1,...,yp, т.е.:
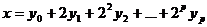 , (1)
, (1)
где
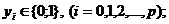 p-наименьшее целое число, удовлетворяющее условию
p-наименьшее целое число, удовлетворяющее условию
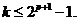 (2)
(2)
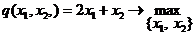
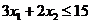
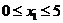
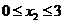
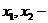 целые.
целые.
Переменная x1 принимает шесть целых значений: 0,1,2,3,4,5.
Для этой переменной k1=5. Возьмем для переменной x1
наименьшее целое число p1 , оно определяется из условия (2)
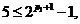 откуда
откуда 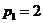
Исходя
из (1), можно произвести замену переменных:
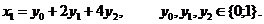
Переменная
x2 принимает четыре целых значения 0,1,2,3.
Следовательно,
для 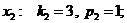

Исходная
задача дискретного программирования преобразована к следующей задаче булева
программирования :

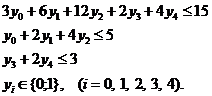
Если дискретная переменная x принимает произвольные целые
дискретные значения c1 , c2 , c3 ,..., ck
, то в этом случае соотношения (1) и (2) соответственно преобразуются в
следующие соотношения:
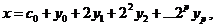
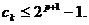
Таким образом, всегда можно ограничиться рассмотрением задачи булева
программирования вместо задачи дискретного программирования.
3. Преобразование задачи линейного булева программирования к
задаче нелинейного булева программирования
Задача вида
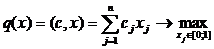 (1)
(1)
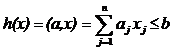 (2)
(2)
в числе многих задач комбинаторной оптимизации отнесена к классу
“труднорешаемых”. Следовательно, для эффективного решения на вычислительных
машинах задач большого размера нужно искать алгоритмические принципы,
позволяющие определять оптимальное решение без необходимости явно перечислять
элементы множества булева вектора x=(x1,x2, . . . , xn)
2n.
Именно эта идея неявного (в противоположность явному) перечисления
решений и лежит в основе методов, предлагаемых и исследуемых в данной книге.
Идейная основа последних заключается в преобразовании исходной задачи (1), (2)
к следующей задаче булева программирования:
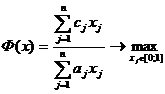 . (3)
. (3)
При переходе от задачи (1), (2) к задаче (3) возникает вопрос: не
теряется ли смысловое содержание исходной задачи при переходе к новой форме.
Оказывается, не теряется, это объясняется следующим образом: Максимизируя
функцию Ф(х) по булевым переменным x=(x1,x2,...,
xn ), практически мы , во-первых, максимизируем числитель
выражения (3), т.е. линейную функцию булевых переменных
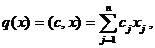
что
соответствует задаче (1). Во-вторых, при максимизации выражения (3),
минимизируется знаменатель этого выражения, т.е.
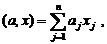
Следовательно,
минимизация выражения 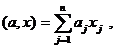 хотя это процедура не обеспечивает точного выполнения
условия (2), а способствует выполнению этого же условия.
хотя это процедура не обеспечивает точного выполнения
условия (2), а способствует выполнению этого же условия.
В
дальнейшем исследовании задачи о рюкзаке (см. п.п. 4.1)будет изложена
вычислительная схема получения решения задачи (3) в виде упорядоченного ряда
булевых переменных
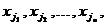 (4)
(4)
но этот ряд булевых переменных может не удовлетворять выполнению
ограничения вида (2). После получения упорядоченного ряда (4) каждый очередной
элемент этого ряда поочередно слева направо будет вставлен в выражения (2) и
таким образом проверено выполнение условия
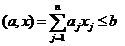
до
максимального числа первых n¢ переменных
упорядоченного ряда (4).
Таким образом, переход от исходной задачи линейного булева
программирования вида (1), (2) к новой задаче - максимизации фишерского типа
функционала вида (3) логичен.
Контрольные вопросы
1. Роль и место моделей булева
программирования в проблеме оптимизации.
2. Основные виды моделей линейного
булева программирования.
3. О полиномиальных и не полиномиальных
задачах в дискретной оптимизации.
4. Преобразование задачи с дискретными
переменными к задаче с булевыми переменными.
5. Преобразование задачи *** к задаче
нелинейного булева программирования.
6. Как записывается функционал
Фишерского типа.
Литература
1. Растригин
Л.А. Современные
принципы управления сложными объектами, М.: Советское радио, 1980 г. - 232 стр.
2. Хамдамов
Р.Х., Каюмов Ш. Моделирование
и оптимизация работы насосной станции // Материалы первой международной
научно-технической и практической конференции: Проблемы и перспективы
автоматизации производства и управления // Автоматизация-97. I часть. Ташкент,
1997. - С. 173-176.
3. Хамдамов
Р.Х., Эргашев А.К.
Решение задачи о рюкзаке методом обобщенных неравенств // Сб. научных трудов
ТашГТУ, 1993.
4. Хамдамов
Р.Х., Эргашев А.К. Решение
задачи булева программирования методом обобщенных неравенств// Вестник ТашГТУ. №: 1-2/98. - С. 6-12.
5. Hamdamov
R., Ergashev A., Kayumov Sh. Solution of the Task of Pumping Station Operation Automation
with linear Boolean Programming Usage// материалы конференции World Conference on
Intelligent Systems for Industrial Automation (WCIS 2000), Kaufering: b-Quadrat
Verlag, 2000, 30-33 стр.
Лекция 15. НОВЫЕ МОДЕЛИ ЗАДАЧ ЛИНЕЙНОГО БУЛЕВА
ПРОГРАММИРОВАНИЯ (2 часа)
План
1.
Задача и модель оптимизации работы насосной станции
.
Модель задачи автоматической классификации
.
Задача об оптимизации размещения букв алфавита на клавиатуре ЭВМ
. Задача и модель оптимизации работы насосной станции
Исследование и моделирование крупных насосных станций является одной из
ключевых задач в системе машинного водоподъема (СМВ). В настоящее время в СМВ в
основном используется диспетчерское управление, основанное на простых методах
принятия решений, исходя из личного опыта и интуиции лица, принимающего решения
(диспетчера) и решающего задачу управления для текущего момента времени. Такое
управление приводит к перерасходу электроэнергии на водоподъем,
непроизводительным сбросам и потерям воды, невыполнения графика водоподачи.
Поэтому задачи, связанные с исследованием, моделированием и разработкой
оптимальных алгоритмов управления работой насосной станции, особенно становятся
актуальными в связи с переходом к рыночным условиям хозяйствования.
Исследуем работу насосной станции и определим ее основные управляющие
параметры.
В крупных насосных станциях обычно устанавливается несколько насосных
агрегатов, предназначенных для подъема воды на высоту определенного диапазона.
В большинстве случаев насосная станция работает в режимах, при которых
недоиспользуются полные возможности, заложенные в насосных агрегатах.
Следовательно, возникает необходимость создания таких методов управления,
которые позволяют максимально использовать все потенциальные возможности
насосной станции и создать оптимальную систему управления по заданному
критерию.
В
насосных станциях используются крупные осевые насосные агрегаты типа
"Р" и "ОП", центробежные типа "В". Для подъема
воды на высоту до 25 м используются осевые насосные агрегаты, а на высоту более
25 м -центробежные. Для моделирования процесса водоподачи основными являются
гидроэнергетические и расходные характеристики. Гидроэнергетические
характеристики можно найти в каталогах. Расходная характеристика Q
насосного агрегата зависит от высоты подъема H и от угла 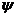 разворота лопасти насосного агрегата:
разворота лопасти насосного агрегата:
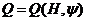 .
.
В каталогах насосных агрегатов расходная характеристика осевого насосного
агрегата задается в виде семейства кривых при различных углах разворота
лопастей:
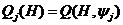 , (j=1,2,...,n),
, (j=1,2,...,n),
где
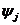 - угол разворота лопастей, соответствующий j-ой
кривой; n - количество кривых.
- угол разворота лопастей, соответствующий j-ой
кривой; n - количество кривых.
Таким
образом, расходная характеристика насосного агрегата полностью определяется
двойкой
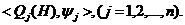
Состояние
насосной станции определяется количеством работающих насосных агрегатов mp
из общего числа насосных агрегатов m и последовательностью углов
разворота лопастей работающих насосных агрегатов
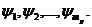
Например, i-й насосный агрегат может работать в n
положениях
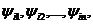 (i=1,2,...,m),
(i=1,2,...,m),
т.е.
положение насосного агрегата определяется положением угла разворота лопастей.
Для
работающих насосных агрегатов насосной системы введем следующие обозначения:
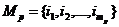 ,
,
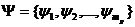 ,
,
где
MP - множество номеров работающих насосных агрегатов;
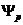
 -
множество углов разворота лопастей работающих насосных агрегатов.
-
множество углов разворота лопастей работающих насосных агрегатов.
Следовательно,
состояние насосной станции в каждый момент времени определяется тройкой 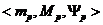 .
.
Общая
расходная характеристика насосной станции, соответствующая ее состоянию,
определяется как алгебраическая сумма расходов каждого работающего насосного
агрегата:
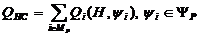 ,
,
где
Qi(H,yi) -
расходная характеристика i-го насосного агрегата;
H - высота подъема воды;
yi - угол разворота лопастей i-го насосного
агрегата.
Потребляемая
мощность насосной станции также определяется как алгебраическая сумма мощностей
каждого работающего насосного агрегата:
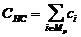 ,
,
где
 /кВт/ - мощность i-го насосного агрегата;
/кВт/ - мощность i-го насосного агрегата;
i -напор, м;
Qi -расход i-го насосного агрегата, м3
/с;
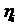 -КПД i-го
насосного агрегата.
-КПД i-го
насосного агрегата.
Оптимизация
управления заключается в определении количества и номеров работающих насосных
агрегатов, а также углов разворота их лопастей, обеспечивающих минимум
потребляемой насосной станцией мощности для реализации заданного графика
водоподачи.
Приводим
постановку задачи оптимизации, которая является общепринятой в СМВ.
Пусть
управляемый процесс в области
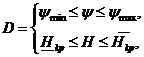
характеризуется
определением регулирующей тройки
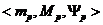 , (1)
, (1)
где ymin и ymax - минимальное и максимальное допустимые значения углов разворота
лопастей насосных агрегатов;
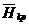 и
и  - критические значения уровней верхнего и нижнего
бьефов насосных станций, при которых требуется минимизировать функционал
- критические значения уровней верхнего и нижнего
бьефов насосных станций, при которых требуется минимизировать функционал
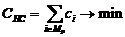 (2)
(2)
с выполнением ограничения следующего вида
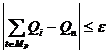 , (3)
, (3)
здесь e=0.05*Qn - допустимая погрешность управления.
Задача оптимизации (2), (3) с оптимизируемой тройкой параметров (1) не
подлежит эффективному решению существующими методами. В связи с этим возникшую
задачу сформулируем как задачу линейного булева программирования в обобщенной
постановке.
Предполагается, что в насосной станции имеются m насосных
агрегатов:
P1, P2,
... , Pm .
Насосный агрегат Pi может работать в ni
положениях
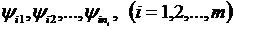 (4)
(4)
где ni -количество углов разворота лопастей i-го
насосного агрегата; причем рассматривается случай, когда количество углов
разворота лопастей для разных насосных агрегатов различно; кроме того, насосный
агрегат Pi может находиться только в одном из перечисленных
положений (4).
Известна производительность (производительность насосных агрегатов обычно
регулируется углом разворота лопастей рабочего колеса работающих насосных
агрегатов) каждого положения i-го насосного агрегата, т.е.
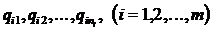
где
qij - расходная характеристика i-го насосного агрегата
при j-м положении угла разворота лопастей.
Также считаются известными значения следующих параметров
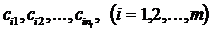 ,
,
где
cij - потребляемая мощность i-го насосного агрегата
при j-м положении угла разворота лопастей.
Введем
булевые переменные xij по следующему правилу: xij=1,
если i-й насосный агрегат работает в j-м положении; xij=0
-в противном случае.
Задача
оптимизации работы насосной станции может быть сформулирована как задача
линейного булева программирования следующего вида:
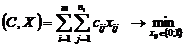 (5)
(5)
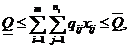 (6)
(6)
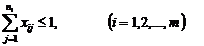 (7)
(7)
где
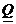 и
и 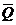 нижний и
верхний пределы общей расходной характеристики насосной станции.
нижний и
верхний пределы общей расходной характеристики насосной станции.
По
полученному решению задачи (5)-(7) можно устанавливать количество и номера
работающих насосных агрегатов. Количество работающих насосных агрегатов
определяется из соотношения
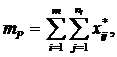
где
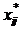 -(i=1,2,...,m; j=1,2,...,ni) - решение задачи (5)-(7). Номера работающих насосных
агрегатов определяются из следующего условия: если для произвольного значения i
-(i=1,2,...,m; j=1,2,...,ni) - решение задачи (5)-(7). Номера работающих насосных
агрегатов определяются из следующего условия: если для произвольного значения i
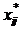 =1 (j=1,2,...,ni), то i-й насосный агрегат работает.
=1 (j=1,2,...,ni), то i-й насосный агрегат работает.
Здесь
путем минимизации целевой функции (5) уменьшается общая потребляемая мощность
насосной станции. Выполнения ограничения вида (6) обеспечивает подъем воды в
допустимых пределах [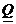 ,
,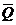 ]. Выполнением ограничения вида (7) обеспечивается
работа каждого насосного агрегата только в одном из возможных положений (4).
]. Выполнением ограничения вида (7) обеспечивается
работа каждого насосного агрегата только в одном из возможных положений (4).
2. Модель задачи автоматической классификации
Задача автоматической классификации возникает во многих прикладных
вопросах, когда требуется разбиение множества из конечного числа объектов на
определенное (может быть и заранее неопределенное) число классов таким образом,
чтобы минимизировать некоторый критерий их взаимной несогласованности. Вводим
необходимые обозначения и понятия.
Предполагается, что заданы п объектов, и для каждой пары объектов i
и j предполагается заданным число dij (dij³0), f называемое расстоянием между
объектами i и j (если эти объекты могут рассматриваться как
элементы п мерного евклидова пространства).
Задача состоит в разбиении множества всех объектов на р классов
(предполагается, что целое число р задано) и выборе в каждом классе
специального объекта, называемого представителем этого класса, так чтобы сумма
расстояний от объектов до их представителей была минимальна.
Вводится матрица булевых переменных по следующему правилу
1, если объект с номером i отнесен к классу, представителем
которого является объект с номером j;
0 - в противном случае.
Здесь для идентификации объектов через булевые переменные хij
использованы обозначения с двумя индексами, первый из которых i-указывает
номер объекта в исходной выборке; второй j-номер объекта, который
определен в качестве представителя одного из классов.
Приведенные обозначения и понятия разъясним на следующем примере. Пусть
задано 10 объектов и требуются их разбиения на 3 класса, т.е. п=10
и р=3.
Предположим, что в результате решения задачи автоматической классификации
получены следующие данные:
x17=1; x22=1; x32=1; x49=1;
x59=1;62=1; x77=1; x87=1;
x99=1; x102=1;
Остальные элементы матрицы булевых переменных Х равны нулю. В
качестве представителей классов определены следующие объекты:
x22=1 - представитель (условно первого) класса, куда входят
следующие объекты: x22, x32, x62 и x102,
;
x77=1 - представитель (условно второго) класса, куда входят
следующие объекты: x17, x77 и x87,
x99=1 - представитель (условно третьего) класса, куда входят
следующие объекты: x49, x59 и x99,.
Как стало ясно из примера, представителями классов могут быть определены
только диагональные элементы булевой матрицы X.
Теперь мы можем описать задачу автоматической классификации в виде
следующей модели линейного булева программирования:
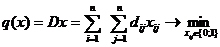 (8)
(8)
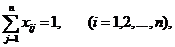 (9)
(9)
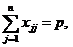 (10)
(10)
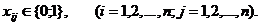
Задача минимизации суммы расстояний от объектов до их представителей
реализуется решением задачи (8). Ограничения (9) выражают тот факт, что каждый
объект должен быть привязан к одному и только одному классу. Ограничение (10)
обеспечивает определения р числа объектов, которые являются
представителями образованных р классов.
. Задача об оптимизации размещения букв алфавита на
клавиатуре ЭВМ
С момента появления пишущих машин, особенно средств вычислительной
техники, исследования, связанные с изучением проблемы оптимального размещения
букв любого алфавита на клавиатуре ЭВМ и пишущей машинки являются актуальными
по сей день и требует своего разрешения эффективными методами.
Из литературных источников известно, что также задача оптимального
размещения букв алфавита на клавиатуре ЭВМ как и любая задача размещения, относится
к задачам комбинаторной оптимизации.
В данной работе впервые предлагается новая модель для задачи оптимального
размещения букв алфавита любого языка на клавиатуре ЭВМ в виде линейной модели
булева программирования. Для формализации задачи вводится булева матрица
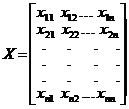
по
следующему правилу
xij
=
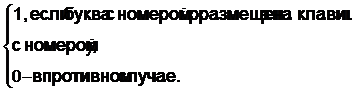
Первый
индекс i используется для определения порядкового номера буквы в
исходном алфавите, второй индекс j - для идентификации порядкового
номера клавиши на клавиатуре.
Вводятся
следующие понятия:
ai - частота появления буквы c порядковым номером i
в генеральной выборке слов рассматриваемого алфавита (в данном случае
необходимо исследовать достаточно большое число слов);
cj - расстояние от центра клавиатуры до клавиши с
порядковым номером j. После введения необходимых обозначений и понятий
задачу об оптимизации размещения букв алфавита на клавиатуре ЭВМ можно описать
с помощью следующей модели линейного булева программирования:
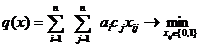 (11)
(11)
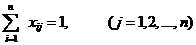 (12)
(12)
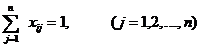 (13)
(13)
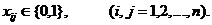
При
математической формулировке задачи основными критериями выступают суммарные
передвижения пальцев по клавиатуре ЭВМ. При минимизации этого критерия, как
известно, снижаются расходы пользователя по времени, что приводит к
естественному уменьшению утомляемости.
Ограничения видов (12) и (13) использованы для обеспечения закрепления
каждой буквы только за одной клавишей и обратно.
Относительно модели (11) - (13) можно сделать следующее замечание: в
модели рассматривается случай с исследованием частоты появления отдельных букв,
при котором и реализуется общий случай, когда исследуется комбинация букв в
тексте. Потому что комбинация (сочетание) букв в тексте состоит из отдельных
букв.
Для решения задачи (11) - (13) можно использовать эффективные методы
линейного булева программирования.
Контрольные вопросы
1. Общее описание работы насосной
станции.
2. Линейная булевая модель работы
насосной станции.
3. Что понимается под задачей
автоматической классификации?
4. Модель задачи оптимального размещения
букв алфавита на клавиатуре ЭВМ.
Литература
1. Хамдамов Р.Х., Каюмов Ш. Моделирование и оптимизация работы
насосной станции // Материалы первой международной научно-технической и
практической конференции: Проблемы и перспективы автоматизации производства и
управления // Автоматизация-97. I часть. Ташкент, 1997. - С. 173-176.
2. Хамдамов Р.Х., Эргашев А.К. Об одной модели задачи автоматической
классификации // Научно- теоретическая и техническая конференция Истиклол-5
посвящённая 5-летию независимости Республики Узбекистан. Навои, 1996.
3. Hamdamov R., Ergashev A.,
Kayumov Sh. Solution of the Task of Pumping Station Operation Automation with linear
Boolean Programming Usage// материалы конференции World Conference on Intelligent
Systems for Industrial Automation (WCIS 2000), Kaufering: b-Quadrat Verlag,
2000, 30-33 стр.
Лекция 16. РЕШЕНИЯ ПРАКТИЧЕСКИХ ЗАДАЧ ЛИНЕЙНОГО БУЛЕВА
ПРОГРАММИРОВАНИЯ (2 часа)
План
1.
Моделирование и оптимизация работы насосной станции
.
Проверка адекватности математической модели
.
Алгоритм оптимального управления работы насосной станции
. Моделирование и оптимизация работы насосной станции
Эффективное управление внутристанционным режимом работы насосной станции
предполагает определение количества и номеров работающих насосных агрегатов, а
также положения углов разворота лопастей, которые обеспечивают минимум
потребляемой мощности энергии для реализации заданного графика водоподачи. В
настоящее время на многих магистральных каналах с каскадом насосных станций
управление процессом водоподачи осуществляется центральной диспетчерской службой,
то есть диспетчер осуществляет управление водозабором, транспортированием и
распределением воды. Процесс принятия решения диспетчером сводится к сравнению
фактического состояния процесса водоподачи с запланированным и исходя из этого,
выработки приемлемых в данный момент времени мероприятий на основе личного
опыта и интуиции.
При реализации стратегии управления диспетчер опрашивает дежурных
инженеров о параметрах гидравлических режимов участков канала и насосных
станций, состоянии основного технологического процесса. Стратегия управления,
выработанная диспетчером, реализуется на каждой насосной станции и
гидротехническом сооружении дежурными инженерами. При нормальной эксплуатации
диспетчер получает информацию от насосных станций о значениях технологических
параметров через каждые шесть часов, а о параметрах потребителей через каждый
час. Диспетчер, проведя анализ обстановки в каскаде, принимает решение для
управления процессом водоподачи, которое по диспетчерской связи сообщается
дежурным инженерам насосных станций. По этим распоряжениям они осуществляют
пуск или остановку насосных агрегатов, изменяют производительность насосных
станций разворотом лопастей на определенный градус, включая или выключая
насосные агрегаты. То есть управление процессом водоподачи производится в
режиме ручного диспетчерского управления.
Диспетчер, управляя системой, полагается на свой личный опыт и интуицию,
основанные на простых методах принятия решений. Управление оборудованием и
объектами осуществляется вручную, а для связи между диспетчером и объектами
управления используется телефон или факс. Как уже говорилось такое управление
приводит к перерасходу электроэнергии на водоподъем, непроизводительным сбросам
и потерям воды, невыполнению графика водоподачи.
Целью разработки является минимизация расхода электроэнергии и
относительная погрешность уровня водоподачи заданного графика насосной станции
путём исследования различных режимов работы насосной станции.
Считается, что известны плановый объём водоподачи, количество насосных
агрегатов, количество положений каждого насосного агрегата в насосной станции,
а также гидротехнические и расходные характеристики в каждом положении.
Требуется определить номера работающих насосных агрегатов и их положения, при
которых обеспечивается требуемый объём водоподачи с минимальными потерями и
расходом электроэнергии.
Пусть управляемый процесс в области
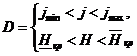
где
jmin и jmax - минимально и максимально
допустимые значения углов разворота лопастей насосных агрегатов;
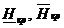 -
критические значения уровня верхнего и нижнего бьефов насосных станций;
-
критические значения уровня верхнего и нижнего бьефов насосных станций;
при
которой требуется минимизировать функционал
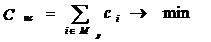 ,
,
здесь
Снс- общий расход электроэнергии насосной станцией;
сi - расходная характеристика i-го насосного
агрегата с выполнением ограничения следующего вида
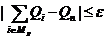 ,
,
здесь
Qi- расход i-го
насосного агрегата;
ε= 0.05*Q n - допустимая погрешность управления.
В
приведенной постановке задача о насосной станции относится к классу
"трудно решаемых задач", и для ее решения не существует эффективного
метода.
Но,
переходя от исходной постановки к другой (5-7), задача становится разрешимой с
применением эффективного метода.
Здесь
также была поставлена и реализована проблема минимизации относительной
погрешности уровня водоподачи. Погрешность (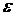 )
обозначим как разницу между плановым объёмом водоподачи (
)
обозначим как разницу между плановым объёмом водоподачи (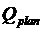 ) и реальным объемом водоподачи
) и реальным объемом водоподачи 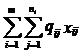 .
.
Тогда
задача оптимизации работы насосной станции может быть сформулирована как задача
линейного булева программирования следующего вида:
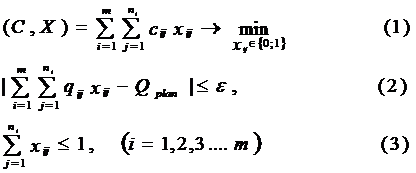
Для
решения поставленной задачи можно использовать эффективный алгоритм метода
обобщенных неравенств, для чего переходим к другой форме задачи булева
программирования:
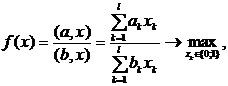 (4)
(4)
где матрицы qij ,cij ,xij (i=1,2,...,m;
j=1,2,...,ni ), используемые в (1)-(3)
преобразованы в вектора ak, bk, xk (k=1,2,...,l),
соответственно, построчно.
Как известно, при решении задачи (1)-(3) методом обобщенных неравенств
сначала получим решение задачи (4), для которой проверяется выполнение условия
(3) в первую очередь, а затем условия (2).
При нарушении условия (3.) сразу же переходят к очередному насосному
агрегату путем наращивания на единицу индексной переменной i в формуле
(3), не проверяя работы остальных положений текущего насосного агрегата, так
как насосный агрегат может работать только в одном положении. Решением задачи
(1)-(3.) будет такое решение задачи (4.) с минимальной мощностью, при котором
выполняются условия (2) и (3.) одновременно.
2. Проверка адекватности математической модели
С целью проверки адекватности предложенных в этой работе математической
модели и алгоритма управления процессом водоподъема насосной станции было
проведено тестирование написанного программного обеспечения. В качестве
тестовых данных были использованы данные насосных станций, расположенных на
территориях Бухарской и Кашкадарьинской областей. Технические характеристики
насосных агрегатов одной из насосных станций приведены в табл. 1.
Результаты численного моделирования с использованием метода обобщенных
неравенств для оптимального управления работой насосной станции проведены в
табл. 2.
Полученные результаты показывают адекватность математической модели и
алгоритма оптимизации работы насосной станции. Отклонение от заданного графика
водоподачи не превышает 4%, при этом затрачиваемая электроэнергия минимальна.
Проведен трехэтапный вычислительный эксперимент с использованием данных о
насосной станции. На первом этапе мы получили результаты в виде булевых переменных,
дающие оптимальные решения о режиме работы насосной станции. На втором этапе
были получены данные в виде таблиц, в которых отражены номера положений
лопастей, число работающих насосных агрегатов, данные о потребляемой мощности и
относительной погрешности водаподачи. На третьем этапе была минимизирована
относительная погрешность уровня водаподачи.
Таблица 1. Технические характеристики насосных агрегатов одной из
насосных станций, расположенных на территориях Бухарской и Кашкадарьинской
областей.
|
Марка насоса
|
Подача, Q, м3/ч
|
Подача, Q, м3/с
|
Напор, Н, м
|
КПД h , %
|
Мощность на валу насоса N,
кВт
|
Угол установки лопастей V,
град
|
|
ОП5-87
|
8784 9288 10080 12060 14220
|
2,44 2,58 2,8 3,35 3,95
|
8,8 7,8 11,7 11 7,15
|
80 80 80 85,5 80
|
263 246 400 423 345
|
-6030' -3020'
0 +2030' +6030'
|
|
ОП3-110
|
14400 17982 19152 20062
22500
|
4 4,98 5,32 5,57 6,25
|
22 15,4 22,8 21,5 14,6
|
80 83 87 87,5 77
|
1080 905 1368 1350 1160
|
-70 -40
-20 -00 +1030'
|
|
ОП5-145
|
24120 26820 27720 36360
41040
|
6.7 7.45 7.7 10.1 11.4
|
10.4 8.3 12.8 11 7.7
|
78 80 78 85.5 80
|
886 747 1380 1275 1075
|
-6030' -6030'
-3020' 0 +2030'
|
|
ОП11-185
|
52920 54900 61200 69840
79920
|
14.7 15.25 17.0 19.4 22.2
|
15.5 14.3 20.4 18 12.7
|
80 80 82 88 84
|
2785 2680 4040 3890 3290
|
-80 -60 -40
-20 -00
|
|
ОП10-260
|
102240 105840 129240 136800
152640
|
28.4 29.4 35.9 38 42.4
|
23.1 22.4 27.8 26 21
|
80 81 87 87.5 84.5
|
8050 7960 11250 11130 10330
|
-90 -60 -30
-10 -00
|
|
ОП10-145
|
25920 27720 32400 34920
39960
|
7,2 7,7 9 9,7 11,1
|
15,3 14,1 18 17 12,9
|
80 82 87 87,5 83
|
1350 1300 1985 1855 1680
|
-90 -60
-30 -10 0
|
где: V, град - углы разворота лопастей рабочего
колеса;
Q, м3/с - водоподача;
N, кВт - затрачиваемая энергия;
h, % - КПД насосного агрегата.
Таблица 2. Результаты численного моделирования
|
Насосные агрегаты №
экспе- римента
|
1-й насосный агрегат
|
2- й насосный агрегат
|
3- й насосный агрегат
|
4- й насосный агрегат
|
5- й насосный агрегат
|
6- й насосный агрегат
|
Плановый объем
водоподачи Q, м3/с
|
Плановый объем
водоподачи Q, м3/с
|
Потребляемая
электро-энергия С, кВт
|
Откло-нения от графика
DQ, %
|
Число работающих насосных
агрегатов N
|
|
4пол
|
2пол
|
1пол
|
-
|
-
|
-
|
15.000
|
15.030
|
2214.00
|
0.200
|
3
|
|
-
|
2пол
|
-
|
-
|
-
|
5пол
|
16.000
|
16.080
|
2585.00
|
0.500
|
2
|
|
-
|
-
|
-
|
3пол
|
-
|
-
|
17.000
|
17.000
|
4040.00
|
0.000
|
1
|
|
-
|
5пол
|
-
|
-
|
-
|
5пол
|
18.000
|
17.350
|
2840.00
|
3.611
|
2
|
|
2пол
|
2пол
|
5пол
|
-
|
-
|
-
|
19.000
|
18.960
|
2226.00
|
0.211
|
3
|
|
-
|
3пол
|
-
|
1пол
|
-
|
-
|
20.000
|
20.020
|
4153.00
|
0.100
|
2
|
|
5пол
|
2пол
|
5пол
|
-
|
-
|
21.000
|
20.330
|
2325.00
|
3.190
|
3
|
|
-
|
-
|
-
|
5пол
|
-
|
-
|
22.000
|
22.200
|
3290.00
|
0.909
|
1
|
|
-
|
2пол
|
1пол
|
-
|
-
|
5пол
|
23.000
|
22.780
|
3471.00
|
0.957
|
3
|
|
-
|
-
|
-
|
2пол
|
-
|
4пол
|
24.000
|
24.950
|
4535.00
|
3.958
|
2
|
|
-
|
-
|
-
|
2пол
|
-
|
4пол
|
25.000
|
24.950
|
4535.00
|
0.200
|
2
|
|
1пол
|
2пол
|
2пол
|
-
|
-
|
5пол
|
26.000
|
25.970
|
3595.00
|
0.115
|
4
|
|
4пол
|
2пол
|
2пол
|
-
|
-
|
5пол
|
27.000
|
26.880
|
3755.00
|
0.444
|
4
|
|
-
|
1пол
|
-
|
2пол
|
-
|
3пол
|
28.000
|
28.250
|
5745.00
|
0.893
|
3
|
|
-
|
3пол
|
-
|
1пол
|
-
|
3пол
|
29.000
|
29.020
|
6138.00
|
0.069
|
3
|
|
2пол
|
2пол
|
5пол
|
-
|
-
|
5пол
|
30.000
|
30.060
|
3906.00
|
0.200
|
4
|
|
5пол
|
2пол
|
5пол
|
-
|
-
|
5пол
|
31.000
|
31.430
|
4005.00
|
1.387
|
4
|
|
5пол
|
2пол
|
5пол
|
-
|
-
|
5пол
|
32.000
|
31.430
|
4005.00
|
1.781
|
4
|
|
-
|
3пол
|
-
|
4пол
|
-
|
3пол
|
33.000
|
33.200
|
7131.30
|
0.602
|
3
|
|
-
|
1пол
|
3пол
|
2пол
|
-
|
1пол
|
34.000
|
34.150
|
6490.00
|
0.441
|
4
|
|
-
|
1пол
|
3пол
|
2пол
|
-
|
1пол
|
35.000
|
34.150
|
6490.00
|
2.429
|
4
|
|
-
|
5пол
|
-
|
5пол
|
-
|
2пол
|
36.000
|
36.150
|
5750.00
|
0.417
|
3
|
|
-
|
-
|
3пол
|
5пол
|
-
|
1пол
|
37.000
|
37.100
|
6020.00
|
0.270
|
3
|
|
-
|
-
|
-
|
-
|
4пол
|
-
|
38.000
|
38.000
|
11130.0
|
0.000
|
1
|
Результаты вычислительного эксперимента показали адекватность
математической модели и алгоритма оптимизации работы насосной станции.
3. Алгоритм оптимального управления работы насосной станции
Ниже приведен алгоритм оптимального управления работой насосной станции с
применением метода обобщенных неравенств.
1.
Ввести m,
ni, cij, qij, Qplan .
2.
Перевести cij и qij в одномерные массивы аk
и bk (k=1,2,…,l; 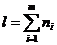 ) .
) .
.
Вычисление значений функции
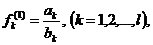 для
каждой переменной хk и определение первого решения
для
каждой переменной хk и определение первого решения 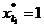 (при этом xk=0, k=1,2,...,l;
k¹k1), которому соответствует максимальное значение
функций среди вычисленных значений функции.
(при этом xk=0, k=1,2,...,l;
k¹k1), которому соответствует максимальное значение
функций среди вычисленных значений функции.
.
Вычисление значений функции последовательным присоединением новых элементов,
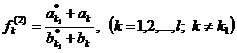 и
определение второго решения,
и
определение второго решения, 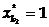 ,
которому соответствует максимальное значение функции среди вычисленных значений
функции.
,
которому соответствует максимальное значение функции среди вычисленных значений
функции.
.
Вычисление значений функции последовательным присоединением новых
элементов, т.е.
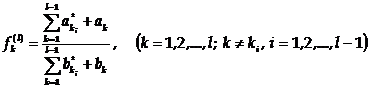 .
.
6.
Последовательно повторяя этот процесс и присоединяя остальные элементы,
получаем упорядоченный ряд х*1, х*2,…,
х*l .
.
Возвращаемся от одномерных массивов aк и bk
(k=1,2,…l) к двухмерным cij, qij
массивам (i=1,2,…,m; j=1,2,…,ni).
.
Решению задачи будет соответствовать минимальное число n' первых
элементов полученного упорядоченного ряда, которое будет удовлетворять условиям
(2) и (3).
.
Результаты вывести на экран, в файл или на принтер.
На рис.1 приведена блок - схема алгоритма оптимального управления работой
насосной станции.
Рис. 1. Блок-схема алгоритма оптимального управления работой насосной
станции с применением метода обобщенных неравенств
Контрольные вопросы
1. Почему задача оптимизации работы
насосной станции преобразовалась к задаче линейного булева программирования?
2. Для чего ведется проверка
адекватности полученной модели оптимизации работы насосной станции?
3. Какая сложность использованного
алгоритма оптимального управления работы насосной станции.
4. Обоснование выбора языка
программирования для реализации постановленной задачи.
Литература
1. Хамдамов Р.Х., Каюмов Ш. Моделирование и оптимизация работы
насосной станции // Материалы первой международной научно-технической и практической
конференции: Проблемы и перспективы автоматизации производства и управления //
Автоматизация-97. I часть. Ташкент, 1997. - С. 173-176.
2. Hamdamov R., Ergashev A.,
Kayumov Sh. Solution of the Task of Pumping Station Operation Automation with linear
Boolean Programming Usage// материалы конференции World Conference on Intelligent
Systems for Industrial Automation (WCIS 2000), Kaufering: b-Quadrat Verlag,
2000, 30-33 стр.
ЛИТЕРАТУРА
1. Горелик А.А., Скрипкин В.А. Методы распознавания. М.: Высшая школа.
1984. -208 с.
2. Хамдамов Р.Х. Сложность метода обобщенных неравенств решения одного класса
задач нелинейного булева программирования// Проблемы информатики и энергетики.
№2 .1994.
3. Хамдамов Р.Х., Эргашев А.К. К исследованию на максимум одного
класса функционалов // Узбекский математический журнал. 1992. №: 1. С.61-66.
ЛИТЕРАТУРА
1. Адлер Ю.П., Маркова Е.В., Грановский Ю.В. - Планирование эксперимента при
поиске оптимальных условий, М.: Наука, 1976 г. -278 стр.
2. Альянах И.Н. Моделирование вычислительных систем, Л.: Машиностроение,
1988 г. - 223 стр.
3. Вентцель Е.С. Исследование операций: задачи, принципы, методология. М.:
Наука, 1980 г. - 208 стр.
4. Горелик А.А., Скрипкин В.А. Методы распознавания. М.: Высшая
школа. 1984. -208 с.
5. Зобов Б.И., Сурков А.В. Основы моделирования вычислительных
систем. М.: МЛТИ, 1982 г. -32 стр.
6. Масков А.И. моделирование вычислительных систем. Пермь: ПГУ, 1982 г. - 95
стр.
7. Растригин Л.А. Современные принципы управления сложными объектами,
М.: Советское радио, 1980 г. - 232 стр.
8. Растригин Л.А., Маджаров Н.Е. Введение в идентификацию объектов
управления, М.: Энергия, 1977 г. - 216 стр.
9. Рузиев У.Т. Оптимальное управление объектами системы машинного
водоподъема. Модели и алгоритмы. Диссертация на соискание ученной степени
кандидата технических наук. Ташкент, 1995. -187 с.
10. Хамдамов Р.Х. Сложность метода обобщенных неравенств решения одного класса
задач нелинейного булева программирования// Проблемы информатики и энергетики.
№2 .1994.
11. Хамдамов Р.Х., Каюмов Ш. Моделирование и оптимизация работы
насосной станции // Материалы первой международной научно-технической и
практической конференции: Проблемы и перспективы автоматизации производства и
управления // Автоматизация-97. I часть. Ташкент, 1997. - С. 173-176.
12. Хамдамов Р.Х., Эргашев А.К. Решение задачи о рюкзаке методом
обобщенных неравенств // Сб. научных трудов ТашГТУ, 1993.
13. Хамдамов Р.Х., Эргашев А.К. К исследованию на максимум одного
класса функционалов // Узбекский математический журнал. 1992. №: 1. С.61-66.
14. Хамдамов Р.Х., Эргашев А.К. Об одной модели задачи автоматической
классификации // Научно- теоретическая и техническая конференция Истиклол-5
посвящённая 5-летию независимости Республики Узбекистан. Навои, 1996.
15. Хамдамов Р.Х., Эргашев А.К. Решение задачи булева
программирования методом обобщенных неравенств// Вестник ТашГТУ. №: 1-2/98. - С. 6-12.
16. Hamdamov R., Ergashev A.,
Kayumov Sh. Solution of the Task of Pumping Station Operation Automation with linear
Boolean Programming Usage// материалы конференции World Conference on Intelligent
Systems for Industrial Automation (WCIS 2000), Kaufering: b-Quadrat Verlag,
2000, 30-33 стр.