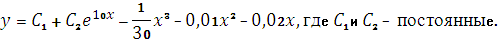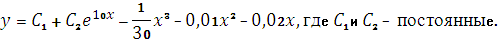Вычисление интеграла уравнения
Контрольная
работа
по
дисциплине "Математика"
Выполнила: студентка 1 курса
Специальность "Финансы и кредит
банковского дела"
Кокоева Т.Ю.
г. Нальчик,
2011
Задание 1. Найти
интеграл: 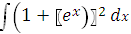
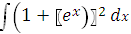 .
.
Решение:
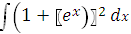
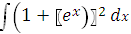 =
=
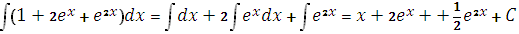
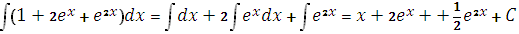 .
.
Ответ: 
 .
.
Задание 2. Найти
интеграл: 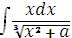
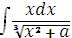 .
.
Решение:

Пусть 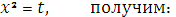
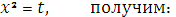
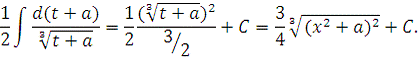
Ответ: 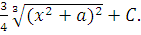
Задание 3. Найти
интеграл: 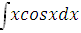
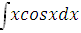 .
.
Решение:
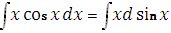
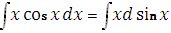 .
.
Пусть 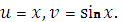
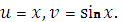 По формуле
По формуле 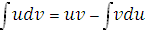
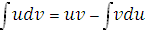 получим:
получим:

Ответ: 

Задание 4. Найти
интеграл: 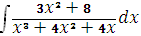
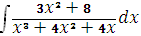 .
.
Решение:
Применим метод
неопределенных коэффициентов.
Пусть
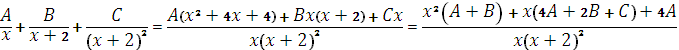
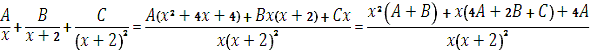 .
.
Приравнивая коэффициенты
при 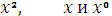
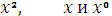 , получим систему:
, получим систему:
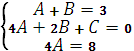
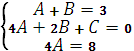 откуда
откуда 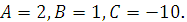
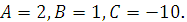
Тогда 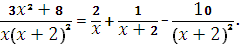
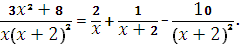
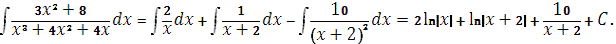
Ответ: 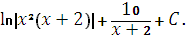
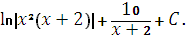
Задание 5. Найти
интеграл: 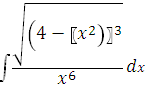
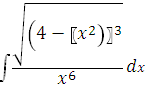 .
.
Решение:
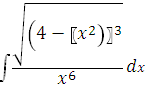
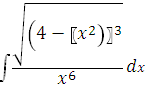 .
.
Сделаем замену
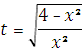
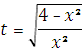 , тогда
, тогда 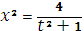
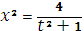 ,
, 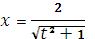
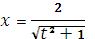 ,
,
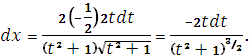
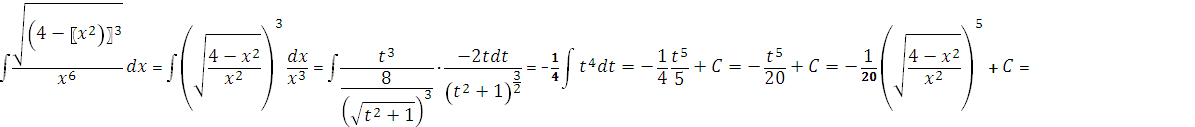
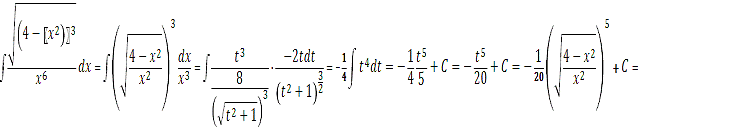 .
.
Ответ: 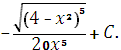
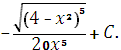
Задание 6. Вычислить
интеграл: 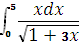
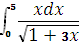 .
.
Решение:
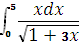
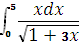 . Пусть
. Пусть 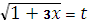
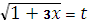 , тогда
, тогда 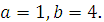
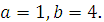
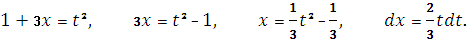
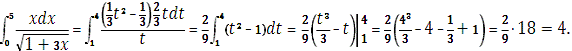
Ответ: 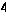
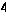 .
.
Задание 7. Найти
решение уравнения: 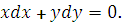
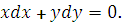
Решение:
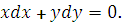
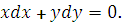 Разделяя переменные,
получим:
Разделяя переменные,
получим: 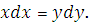
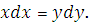
Интегрируя, получим: 

Ответ: 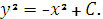
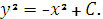
Задание 8. Найти
решение уравнения: 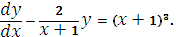
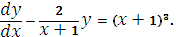
Решение:
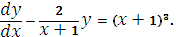
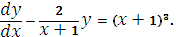
Пусть 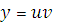
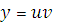 , тогда
, тогда 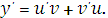
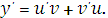
Получим

 или
или 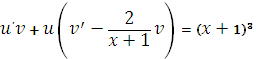
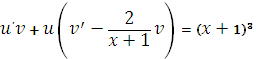 .
.
Пусть 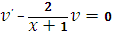
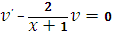 , тогда
, тогда 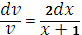
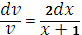 , значит
, значит 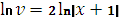
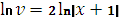 , т.е.
, т.е.
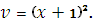
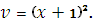 Следовательно,,
Следовательно,, 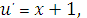
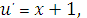
интеграл уравнение переменная система
Ответ: 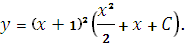
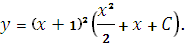
Задание 9. Найти
интеграл уравнения: 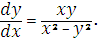
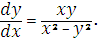
Решение:
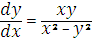
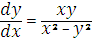 - уравнение однородное.
- уравнение однородное.
Введем вспомогательную
функцию: 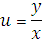
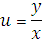 или
или 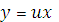
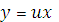 , тогда
, тогда 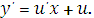
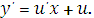
Уравнение примет вид:
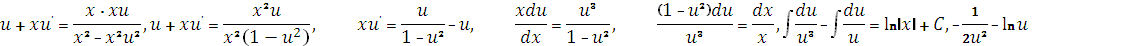
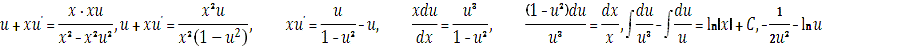
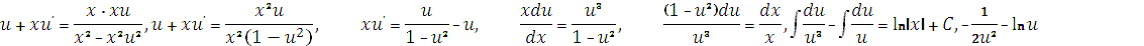
Возвращаясь к переменной
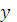
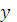 , находим общее решение:
, находим общее решение:
 Ответ:
Ответ: 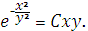
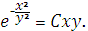
Задание 10. Найти
общее решение уравнения: 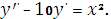
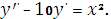
Решение:
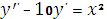
Составим
характеристическое уравнение: 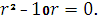
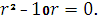
Его корни 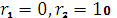
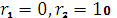 - действительные и
различные, значит, решение ищем в виде:
- действительные и
различные, значит, решение ищем в виде: 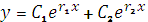
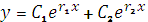 . Оно имеет вид
. Оно имеет вид 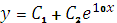
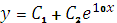 , т.к. правая часть
исходного уравнения равна
, т.к. правая часть
исходного уравнения равна 
 , т.е. имеет вид
, т.е. имеет вид 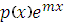
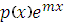 , где m = 0, то частное решение имеет вид
, где m = 0, то частное решение имеет вид 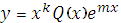
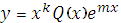 , т.к.
, т.к. 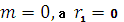
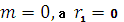 - корень
характеристического уравнения, то
- корень
характеристического уравнения, то 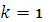
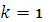 (плотность корня).
(плотность корня).
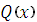
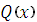 - многочлен второй
степени, т.е. имеет вид
- многочлен второй
степени, т.е. имеет вид 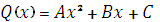
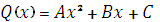 , следовательно, частное
решение имеет вид
, следовательно, частное
решение имеет вид 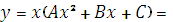
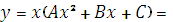
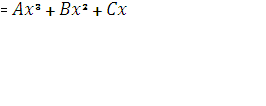
 . Значит,
. Значит, 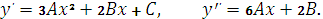
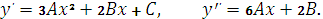
Подставим 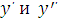
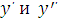 в исходное уравнение
Приравнивая коэффициенты при
в исходное уравнение
Приравнивая коэффициенты при 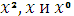
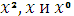 , получим систему:
, получим систему:

 отсюда
отсюда 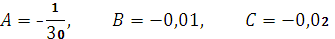
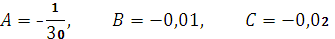 .
.
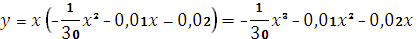
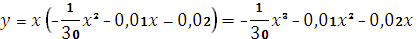 ,
,
а общим решением -
функция 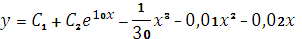
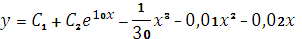 .
.
Ответ: