Геодезические работы в землеустройстве и земельном кадастре
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ОМСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ»
Землеустроительный
факультет
Кафедра
геодезии
Курсовой
проект
Геодезические
работы в землеустройстве и земельном кадастре
Выполнил:
Гринченко Г.А.
Проверил:
Купреева Е.Н.
Омск - 2011
РЕФЕРАТ
геодезическое измерение земельный межевой граница
Курсовой проект является важным звеном в изучении дисциплины «Геодезические
работы в землеустройстве и земельном кадастре» студентами четвертого курса.
Поскольку она дает возможность ознакомиться с различными способами решения
геодезических задач, возникающих при производстве работ в сфере межевания.
Данная курсовая работа составлена в объеме 59 страниц, она включает в
себя 20 таблиц, 7 рисунков, 88 формул и 8 приложений.
Цель курсового проекта: заключается в геодезической подготовке данных для
восстановления утраченных межевых знаков различными способами, установлении
необходимой точности линейных и угловых измерений, производстве выбора приборов
и методик измерений, выполнении проектирования границ земельных участков
различными способами, подготовке геодезических данных для перенесения проектных
границ земельных участков в натуру.
Курсовая работа состоит из трех основных задач:
1. Подготовка геодезических данных для восстановления
утраченных межевых знаков.
. Геодезическое проектирование границ земельных участков при
межевании.
. Геодезическая подготовка перенесения проектных границ
земельных участков в натуру.
СОДЕРЖАНИЕ
Реферат
Введение
. Подготовка
геодезических данных для восстановления утраченных межевых знаков
1.1 Подготовка
геодезических данных для восстановления утраченного межевого знака способом
полярных координат
1.2 Подготовка
геодезических данных для восстановления утраченного межевого знака способом
прямой угловой засечки
.3 Подготовка
геодезических данных для восстановления утраченного знака с использованием
вспомогательной точки, определенной обратной засечкой
1.4 Подготовка
геодезических данных для восстановления утраченного межевого знака 5 c вспомогательного пункта p способом полярных координат
2. Определение
площадей земельных участков
2.1 Определение
общей площади земельного участка комбинированным способом
.2 Определение
общей площади земельного участка способом Савича А.Н
3. Проектирование
границ земельных участков аналитическими способами
.1 Проектирование
границ земельного участка способом трапеции
3.2 Проектирование
границ земельного участка приемом треугольника
.3 Проектирование
границ земельного участка комбинированным способом
4. Проектирование
границ земельного участка графическим способом
.1 Проектирование
границ земельного участка графическим способом
. Проектирование
границ земельных участков графомеханическим способом
.1 Проектирование
границ земельных участков графомеханическим способом
. Геодезическая
подготовка перенесения проектных границ земельных участков в натуру
6.1 Подготовка
геодезических данных для разбивки на местности углов межевого участка (точек M и N) способом полярных координат
6.1.1 Подготовка
геодезических данных для разбивки на местности точки M с пункта 3 способом полярных координат
.1.2 Подготовка
геодезических данных для разбивки на местности точки N с пункта 4 способом полярных координат
.2 Подготовка
геодезических данных для построения на местности межевого знака способом прямой
угловой засечки
6.3 Подготовка
геодезических данных для построения на местности межевого знака способом
промеров по створу между существующими пунктами
6.4 Геодезическая
подготовка данных для выноса межевых знаков а,б,в,г в натуру способом
проектного теодолитного хода
Заключение
Список
использованной литературы
ВВЕДЕНИЕ
Реализация земельной реформы в России расширила сферу деятельности
геодезистов в области землеустройства и кадастров. Значительные объемы
геодезических работ выполняются при установлении, восстановлении границ
земельных участков, при инвентаризации земель поселений.
В данном курсовом проекте рассматриваются:
· подготовка геодезических данных для восстановления утраченных
межевых знаков: на данном этапе курсового проекта необходимо подготовить
геодезические данные для построения утраченных пунктов ОМС, способами полярных
координат, линейной засечки, прямой угловой засечки, для каждого способа
рассчитывается необходимая точность построения, выбираются приборы для каждого
вида работ.
· определение площадей участков аналитическим, комбинированным
и Савича А.Н. способами.
· проектирование границ земельных участков и подготовка данных
для выноса в натуру их границ. Проектирование границ земельных участков
выполняется как аналитически способами трапеции, треугольника, так и
графическим и графомеханическим. Также рассматривается вынос в натуру их границ
различными способами, такими как: способ полярных координат, способ прямой
угловой засечки, способом проложения теодолитного хода, выбираются приборы для
каждого вида работ.
1.
ПОДГОТОВКА ГЕОДЕЗИЧЕСКИХ ДАННЫХ ДЛЯ ВОССТАНОВЛЕНИЯ УТРАЧЕННЫХ МЕЖЕВЫХ ЗНАКОВ
Данный раздел предусматривает применение различных способов
восстановления отдельных утраченных межевых знаков:
· восстановление способом полярных координат;
· способом прямой угловой засечки;
· с использованием вспомогательной точки, определенной обратной
засечкой.
В каждой задаче выполняется вычисление геодезических данных, составление
разбивочного чертежа, установление необходимой точности угловых и линейных
измерений, выбор приборов и методики измерения, вычисление ожидаемой точности
положения восстановленного знака. Вычисления выполняются на микрокалькуляторах,
используя известные программы, или в ручном режиме с приведением промежуточных
результатов в соответствующих схемах.
Исходные данные:
Схема расположения пунктов ОМС представлена на рисунке 1, координаты
пунктов ОМС приведены в таблице 1.
Таблица 1. Координаты межевых знаков
|
Название межевого знака
|
Координаты, м
|
Примечания
|
|
X
|
Y
|
|
|
А
|
3604,80
|
2686,71
|
Утрачен
|
|
В
|
3490,00
|
3540,00
|
В сохранности
|
|
С
|
2662,16
|
3442,23
|
В сохранности
|
В данной таблице приведены координаты исходных пунктов ОМС.
1.1 ПОДГОТОВКА ГЕОДЕЗИЧЕСКИХ ДАННЫХ ДЛЯ ВОССТАНОВЛЕНИЯ
УТРАЧЕННОГО МЕЖЕВОГО ЗНАКА СПОСОБОМ ПОЛЯРНЫХ КООРДИНАТ
. Последовательность работ (рисунок 1): в точке А
откладывают проектный угол b, а на полученном направлении АМ откладывают проектное расстояние d и получают плановое положение
проектной точки М.
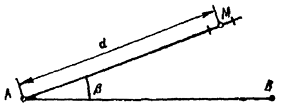
Рисунок 1. Принцип восстановления утраченного межевого знака способом
полярных координат
2. Определяют
дирекционные углы линий 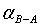 ,
, 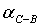 ,
, 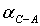 , и длину линии
, и длину линии 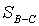 , решив
для этого обратные геодезические задачи по координатам знаков А, В, С.
, решив
для этого обратные геодезические задачи по координатам знаков А, В, С.
. Вычисляют
угол построения 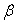 и для контроля работ по восстановлению получают угол
и для контроля работ по восстановлению получают угол 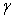 .
.
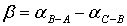 (1)
(1)
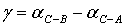 (2),
(2),
где
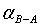 ,
, 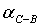 ,
, 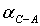 дирекционные направления линий,
дирекционные направления линий, 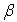 угол построения
угол построения 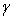 угол при
точке C.
угол при
точке C.
Таблица 2. Данные для восстановления утраченного пункта ОМС C способом полярных координат
|
Пункт
|
Гор. угол
|
Дир. угол
|
Гор. проложение, м
|
|
A
|
|
97°39'45"
|
847,45
|
|
B
|
269°04'23"
|
186°44'08"
|
833,59
|
|
C
|
|
|
|
В
данной таблице представлено значение угла 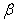 откладываемого
от направления с пункта B на пункт A.
откладываемого
от направления с пункта B на пункт A.
Данный
отчет подготовлен в программном комплексе CREDO_DAT.
Таблица
3. Вычисление угла 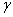 находящегося при точке C
находящегося при точке C
|
Пункт
|
Гор. угол
|
Дир. угол
|
Гор. проложение, м
|
|
A
|
|
141°17'17"
|
1208,05
|
|
C
|
45°26'51"
|
6°44'08"
|
833,59
|
|
B
|
|
|
|
Данный отчет подготовлен в программном комплексе CREDO_DAT.
4. Затем
устанавливается ожидаемая точность построения пункта и необходимая точность
угловых и линейных построений, задаваясь допустимой ошибкой восстановления
пункта ОМС на местности 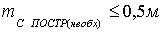 :
:
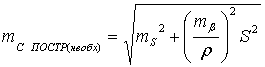 (3),
(3),
где
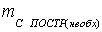 необходимая точность построения,
необходимая точность построения, 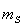 необходимая точность выноса расстояния,
необходимая точность выноса расстояния, 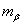 необходимая точность построения угла,
необходимая точность построения угла, 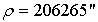 ,
, 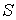 выносимое
расстояние.
выносимое
расстояние.
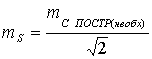 (4),
(4),
где
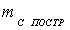 допустимая величина ошибки закрепления точки на
местности,
допустимая величина ошибки закрепления точки на
местности, 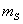 необходимая точность выноса расстояния.
необходимая точность выноса расстояния.
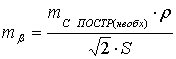 (5),
(5),
где
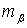 необходимая точность построения угла,
необходимая точность построения угла, 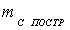 допустимая величина закрепления точки на местности,
допустимая величина закрепления точки на местности, 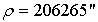 ,
, 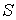 выносимое
расстояние.
выносимое
расстояние.
Например:
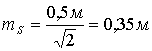
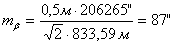
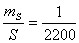
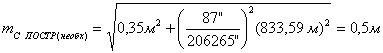
5.
Исходя из установленной необходимой точности угловых и линейных построений, для
восстановления точки C
способом полярных координат можно применить следующие приборы: прибор для
линейно-угловых измерений соответствующий угловой точности в 30” и прибор
соответствующий линейной точности 1/2000. Например: теодолит Т-30 для угловых
измерений и мерная лента для линейных измерений.
. После чего с учетом выбранных приборов, находят ожидаемую
точность построений.
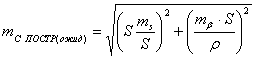 (6),
(6),
где
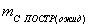 ожидаемая точность построений,
ожидаемая точность построений, 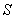 выносимое расстояние,
выносимое расстояние, 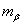 фактическое
значение ошибки выноса угла данным прибором,
фактическое
значение ошибки выноса угла данным прибором, 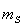 фактическое
значение ошибки выноса расстояния данным прибором.
фактическое
значение ошибки выноса расстояния данным прибором.
Например:
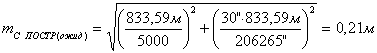
7. После чего сравнивают ожидаемую точность построений выбранным
прибором и допустимую, должно соблюдаться условие:
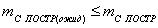 (7),
(7),
где
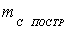 допустимая точность построения точки,
допустимая точность построения точки, 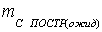 ожидаемая точность построений.
ожидаемая точность построений.
Например:
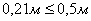
8. Составляют разбивочный чертеж.
Например:
Приложение А
Вывод: условие 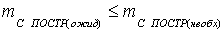 соблюдается
соблюдается
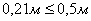 , следовательно, можно применить следующие приборы:
прибор для линейно-угловых измерений соответствующий угловой точности в 30” и
прибор соответствующий линейной точности 1/2000. Например: теодолит Т-30 для
угловых измерений и мерная лента для линейных измерений.
, следовательно, можно применить следующие приборы:
прибор для линейно-угловых измерений соответствующий угловой точности в 30” и
прибор соответствующий линейной точности 1/2000. Например: теодолит Т-30 для
угловых измерений и мерная лента для линейных измерений.
1.2 ПОДГОТОВКА ГЕОДЕЗИЧЕСКИХ ДАННЫХ ДЛЯ ВОССТАНОВЛЕНИЯ
УТРАЧЕННОГО МЕЖЕВОГО ЗНАКА СПОСОБОМ ПРЯМОЙ УГЛОВОЙ ЗАСЕЧКИ
1. Положение
проектной точки С (рисунок 2) определяется построением в пунктах
сети А и В проектных углов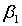 и
и 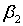 . Точкой С является точка пересечения
направлений АС и ВС.
. Точкой С является точка пересечения
направлений АС и ВС.
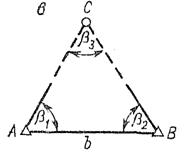
Рисунок 2. Схема для определения планового положения точки способом
прямой угловой засечки
2. Для
того чтобы произвести вынос точки, по координатам решая обратные геодезические
задачи находят проектные углы 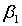 и
и 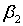 откладываемые от направлений на ориентируемые пункты.
откладываемые от направлений на ориентируемые пункты.
Например:
Таблица 4. Данные для восстановления утраченного пункта ОМС C методом прямой угловой засечки с
пункта B
|
Пункт
|
Гор. угол
|
Дир. угол
|
Гор. проложение, м
|
|
A
|
|
97°39'45"
|
847,45
|
|
B
|
269°04'23"
|
186°44'08"
|
833,59
|
|
C
|
|
|
|
В
данной таблице представлено значение угла 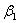 откладываемого
от направления с пункта B на пункт A.
откладываемого
от направления с пункта B на пункт A.
Данный
отчет подготовлен в программном комплексе CREDO_DAT.
Таблица 5. Данные для восстановления утраченного пункта ОМС C методом прямой угловой засечки с
пункта А
|
ПунктГор. уголДир. уголГор. проложение, м
|
|
|
|
|
B
|
|
277°39'45"
|
860,98
|
|
A
|
43°37'32"
|
141°17'17"
|
1208,05
|
|
C
|
|
|
|
В
данной таблице представлено значение угла 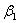 откладываемого
от направления с пункта A на пункт B.
откладываемого
от направления с пункта A на пункт B.
Данный
отчет подготовлен в программном комплексе CREDO_DAT.
. Угол
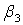 вычисляется из условия треугольника:
вычисляется из условия треугольника:
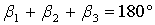 (8),
(8),
где 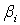 угол треугольника.
угол треугольника.
Например:
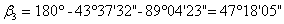
4. После
чего задаваясь допустимой величиной ошибки закрепления точки на местности 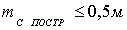 , определяют необходимую точность построений:
, определяют необходимую точность построений:
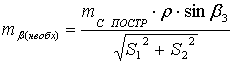 (9),
(9),
где
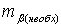 необходимая точность построения угла,
необходимая точность построения угла, 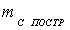 допустимая величина ошибки закрепления точки на
местности,
допустимая величина ошибки закрепления точки на
местности, 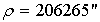
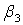 угол
треугольника,
угол
треугольника, 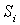 расстояние от точки стояния до выносимой точки.
расстояние от точки стояния до выносимой точки.
Например:
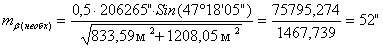
5. Исходя из установленной необходимой точности угловых построений,
для восстановления точки C
способом прямой угловой засечки можно применить следующие приборы: теодолит Т30
или ему равноточные.
. После чего, с учетом выбранных приборов, находят ожидаемую
точность построений.
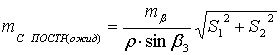 (10),
(10),
где
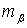 фактическое значение ошибки выноса угла данным
прибором,
фактическое значение ошибки выноса угла данным
прибором, 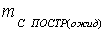 ожидаемая точность построений,
ожидаемая точность построений, 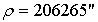
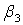 угол
треугольника,
угол
треугольника, 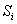 расстояние от точки стояния до выносимой точки.
расстояние от точки стояния до выносимой точки.
Например:
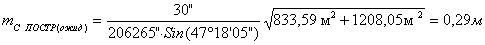
7. После чего сравнивают ожидаемую точность построений выбранным
прибором и допустимую, должно соблюдаться условие:
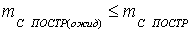 (11),
(11),
где
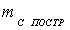 допустимая величина ошибки закрепления точки на
местности,
допустимая величина ошибки закрепления точки на
местности, 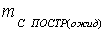 ожидаемая точность построений.
ожидаемая точность построений.
Например:
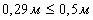
8. Составляют разбивочный чертеж.
Например:
Приложение Б
Вывод: условие 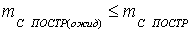 соблюдается
соблюдается
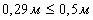 , следовательно, можно применить следующие приборы:
теодолит Т30 или ему равноточные.
, следовательно, можно применить следующие приборы:
теодолит Т30 или ему равноточные.
1.3 ПОДГОТОВКА ГЕОДЕЗИЧЕСКИХ ДАННЫХ ДЛЯ ВОССТАНОВЛЕНИЯ
УТРАЧЕННОГО ЗНАКА С ИСПОЛЬЗОВАНИЕМ ВСПОМОГАТЕЛЬНОЙ ТОЧКИ, ОПРЕДЕЛЕННОЙ ОБРАТНОЙ
ЗАСЕЧКОЙ
Таблица 6. Исходные данные для восстановления межевого знака способом
обратной засечки
|
Номер МЗ
|
Направления, измеренные с вспомогательной точки Р на МЗ ° ¢ ²
|
Координаты, м
|
Примечание
|
|
|
Х
|
Y
|
|
|
1
|
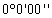 1387,252937,89В сохранности 1387,252937,89В сохранности
|
|
|
|
|
2
|
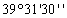 1088,722411,60В сохранности 1088,722411,60В сохранности
|
|
|
|
|
3
|
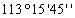 1968,152427,26В сохранности 1968,152427,26В сохранности
|
|
|
|
|
4
|
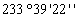 2216,773191,77В сохранности 2216,773191,77В сохранности
|
|
|
|
|
5
|
|
1885,25
|
2845,15
|
Утрачен
|
В данной таблице представлены исходные данные для восстановления межевого
знака способом обратной засечки.
1. Составляют схему расположения исходных пунктов по их известным
координатам.
2. По способу Болотова наносят точку P.
Например:
Приложение В
. Находят длины инверсионных сторон по формуле:
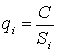 (12),
(12),
где
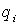 длина инверсионной стороны,
длина инверсионной стороны, 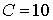
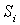 длина
стороны между пунктом P и данным пунктом.
длина
стороны между пунктом P и данным пунктом.
Например:
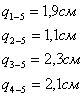
4. После чего вершины инверсионных сторон соединяют между собой,
образуя инверсионные треугольники. Большие по площади треугольники образуют
наилучшие варианты решения обратной засечки.
Например:
Треугольник: 1-3-4
Треугольник: 2-3-4
. После чего переходят к решению обратной засечки. Для удобства
составляют таблицы:
Например:
Таблица 7. Решение обратной засечки (треугольник 1(С)-3(A)-4(B))
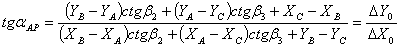
|
-4,185444163
|
|
|
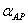 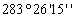
|
|
|
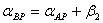 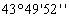
|
|
|
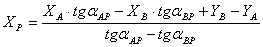 1865,96 1865,96
|
|
|
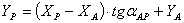 2854,99 2854,99
|
|
|
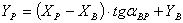 2854,99 2854,99
|
|
|
|
|
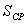 485,83 485,83
|
|
|
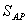 439,77 439,77
|
|
|
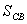 867,50 867,50
|
|
|
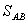 803,92 803,92
|
|
|
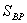 486,31 486,31
|
|
|
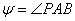 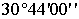
|
|
|
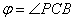 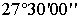
|
|
|
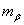 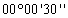
|
|
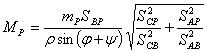 0,07
0,07
В данной таблице представлен пример решения обратной засечки (треугольник
1(С)-3(A)-4(B)).
Таблица 8. Решение обратной засечки (треугольник 2(С)-3(A)-4(B))
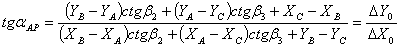
|
-4,184811175
|
|
|
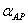 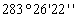
|
|
|
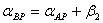 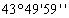
|
|
|
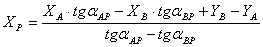 1865,95 1865,95
|
|
|
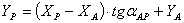 2854,96 2854,96
|
|
|
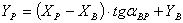 2854,96 2854,96
|
|
|
|
|
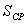 894,79 894,79
|
|
|
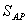 439,74 439,74
|
|
|
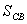 1371,55 1371,55
|
|
|
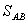 803,92 803,92
|
|
|
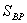 486,33 486,33
|
|
|
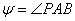 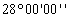
|
|
|
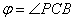 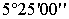
|
|
|
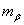 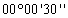
|
|
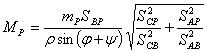 0,11
0,11
В данной таблице представлен пример решения обратной засечки (треугольник
2(С)-3(A)-4(B)).
. Находят абсолютную ошибку полученных координат точки P:
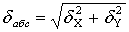 (13),
(13),
где
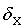 расхождение координат точки P по оси, X
расхождение координат точки P по оси, X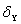 расхождение координат точки P по оси Y.
расхождение координат точки P по оси Y.
Например:
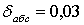
7. Вычисляют допустимое значение абсолютного расхождения координат:
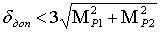 (14),
(14),
где
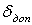 допустимое значение абсолютного расхождения
координат,
допустимое значение абсолютного расхождения
координат, 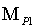
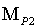 значения
средних квадратических погрешностей положения вспомогательной точки Р
полученных из разных треугольников.
значения
средних квадратических погрешностей положения вспомогательной точки Р
полученных из разных треугольников.
Например:
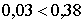
8. При соблюдении допуска находят средние значения координат:
Например:
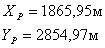
9. После чего производят оценку точности окончательных координат
точки P:
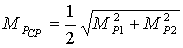 (15),
(15),
где
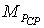 значение средней квадратической погрешности положения
вспомогательной точки P,
значение средней квадратической погрешности положения
вспомогательной точки P, 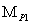
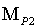 значения
средних квадратических погрешностей положения вспомогательной точки Р
полученных из разных треугольников.
значения
средних квадратических погрешностей положения вспомогательной точки Р
полученных из разных треугольников.
Например:
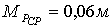
Вывод:
на данном этапе курсового проекта
были получены координаты вспомогательной точки P путем решения
обратной засечки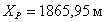
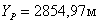 для восстановления утраченного межевого знака 5.
для восстановления утраченного межевого знака 5.
1.4 ПОДГОТОВКА ГЕОДЕЗИЧЕСКИХ ДАННЫХ ДЛЯ ВОССТАНОВЛЕНИЯ УТРАЧЕННОГО
МЕЖЕВОГО ЗНАКА 5 C ВСПОМОГАТЕЛЬНОГО
ПУНКТА P СПОСОБОМ ПОЛЯРНЫХ КООРДИНАТ
1.
Определяют дирекционные углы линий 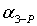 ,
, 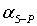 ,
, 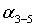 , и длину
линии
, и длину
линии 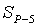 , решив для этого обратные геодезические задачи по
координатам знаков 3, 5, P.
, решив для этого обратные геодезические задачи по
координатам знаков 3, 5, P.
. Вычисляют
угол построения 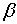 и для контроля работ по восстановлению получают угол
и для контроля работ по восстановлению получают угол 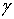 .
.
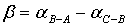 (16)
(16)
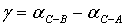 (17),
(17),
где
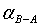 ,
, 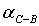 ,
, 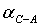 дирекционные направления линий,
дирекционные направления линий, 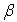 угол построения
угол построения 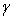 угол при
точке 5.
угол при
точке 5.
Таблица 9. Данные для восстановления утраченного пункта ОМС 5 способом
полярных координат
|
Пункт
|
Гор. угол
|
Дир. угол
|
Гор. проложение, м
|
|
3
|
|
103°26'19"
|
439,75
|
|
P
|
49°35'38"
|
333°01'57"
|
21,66
|
|
5
|
|
|
|
В
данной таблице представлено значение угла 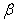 откладываемого
от направления с пункта P на пункт 3.
откладываемого
от направления с пункта P на пункт 3.
Данный
отчет подготовлен в программном комплексе CREDO_DAT.
Таблица
10. Вычисление угла 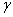 находящегося при точке 5
находящегося при точке 5
|
ПунктГор. уголДир. уголГор. проложение, м
|
|
|
|
|
P
|
|
333°01'57"
|
21,66
|
|
5
|
128°11'16"
|
281°13'13,88"
|
426,03
|
|
3
|
|
|
|
Данный отчет подготовлен в программном комплексе CREDO_DAT.
3. Затем
устанавливается ожидаемая точность построения пункта и необходимая точность
угловых и линейных построений, задаваясь допустимой ошибкой восстановления
пункта ОМС на местности 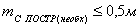 :
:
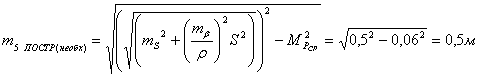 (18),
(18),
где
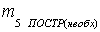 необходимая точность построения пункта,
необходимая точность построения пункта, 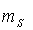 необходимая точность выноса расстояния,
необходимая точность выноса расстояния, 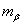 необходимая точность построения угла,
необходимая точность построения угла, 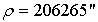 ,
, 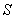 выносимое
расстояние.
выносимое
расстояние.
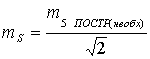 (19),
(19),
где
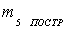 допустимая величина ошибки закрепления точки на
местности,
допустимая величина ошибки закрепления точки на
местности, 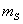 необходимая точность выноса расстояния.
необходимая точность выноса расстояния.
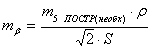 (20),
(20),
где
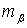 необходимая точность построения угла,
необходимая точность построения угла, 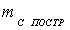 допустимая величина закрепления точки на местности,
допустимая величина закрепления точки на местности, 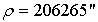 ,
, 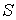 выносимое
расстояние.
выносимое
расстояние.
Например:
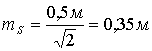
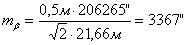
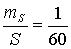

4. Исходя из установленной необходимой точности угловых и линейных
построений, для восстановления точки C способом полярных координат можно применить следующие приборы: прибор
для линейно-угловых измерений соответствующий угловой точности в 30” и прибор
соответствующий линейной точности 1/2000. Например: теодолит Т-30 для угловых
измерений и мерная лента для линейных измерений.
. После чего с учетом выбранных приборов, находят ожидаемую
точность построений.
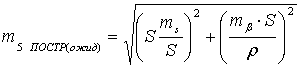 (21),
(21),
где
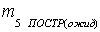 ожидаемая точность построений,
ожидаемая точность построений, 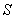 выносимое расстояние,
выносимое расстояние, 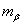 фактическое
значение ошибки выноса угла данным прибором,
фактическое
значение ошибки выноса угла данным прибором, 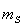 фактическое
значение ошибки выноса расстояния данным прибором.
фактическое
значение ошибки выноса расстояния данным прибором.
Например:
6. После чего сравнивают ожидаемую точность построений выбранным
прибором и допустимую, должно соблюдаться условие:
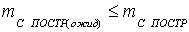 (22),
(22),
где
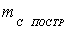 допустимая точность построения точки,
допустимая точность построения точки, 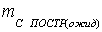 ожидаемая точность построений.
ожидаемая точность построений.
Например:
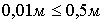
9. Составляют разбивочный чертеж.
Например:
Приложение Г
Вывод: условие 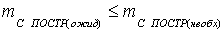 соблюдается
соблюдается
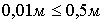 , следовательно, можно применить следующие приборы:
прибор для линейно-угловых измерений соответствующий угловой точности в 30” и
прибор соответствующий линейной точности 1/2000. Например: теодолит Т-30 для угловых
измерений и мерная лента для линейных измерений.
, следовательно, можно применить следующие приборы:
прибор для линейно-угловых измерений соответствующий угловой точности в 30” и
прибор соответствующий линейной точности 1/2000. Например: теодолит Т-30 для угловых
измерений и мерная лента для линейных измерений.
2.
ОПРЕДЕЛЕНИЕ ПЛОЩАДЕЙ ЗЕМЕЛЬНЫХ УЧАСТКОВ
2.1 ОПРЕДЕЛЕНИЕ ОБЩЕЙ ПЛОЩАДИ ЗЕМЕЛЬНОГО УЧАСТКА КОМБИНИРОВАННЫМ СПОСОБОМ
Таблица 11. Исходные данные для определения площадей земельного участка
|
Координаты, м _______________________ Х У
|
|
81620,25
|
6942,12
|
|
83595,00
|
6695,00
|
|
85253,44
|
7201,10
|
|
85160,25
|
9482,55
|
|
83250,00
|
10000,00
|
|
81692,10
|
9038,20
|
В данной таблице представлены исходные данные для определения площадей
земельного участка.
1. Общую площадь полигона вычисляют по
координатам:
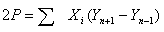
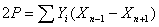
где
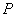 площадь полигона,
площадь полигона, 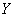
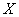 координаты
точек полигона.
координаты
точек полигона.
Например:
Пример вычисления площади указан в Приложении Л
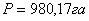
2. Затем графически находят площади участков
примыкающих к полигону, но находящихся за его границами.
Например:
Схема расположения сегментов примыкающих к полигону,
но находящихся за его границами представлена в Приложении И.
Площади участков были определены в программе AutoCAD 2007.
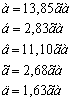
3. После чего определяют общую площадь
землепользования, руководствуясь схемой расположения сегментов примыкающих к
полигону, но находящихся за его границами.
Например:
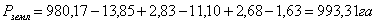
Вывод:
При решении задачи
комбинированным способом общая площадь землепользования составила 959,10 га.
2.2 ОПРЕДЕЛЕНИЕ ОБЩЕЙ ПЛОЩАДИ ЗЕМЕЛЬНОГО УЧАСТКА
СПОСОБОМ САВИЧА А.Н.
. Делят полигон на две части (А-2-3-4-5-B) (1-A-B-6), таким
образом, чтобы точки A и B лежали по оси абсцисс на линии
координатной сетки, как можно ближе к сегментам, примыкающим к полигону, но
находящихся за его границами, но чтобы линия A-B не пересекала
какие либо из сегментов.
Например:
Схема положения линии A-B представлена в
Приложении И
. Площадь полигона А-2-3-4-5-B получают аналитически.
Например:
Пример вычисления площади указан в Приложении М
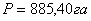
3. Площадь остальной части земельного участка -
второй фигуры, расположенную южнее линии А-В, определяют, используя способ А.Н.
Савича.
4. Намечают
секции с известными площадями 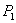 ,
, 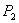 используют при этом целые квадраты координатной
сетки. И сегменты площади, которых необходимо определить.
используют при этом целые квадраты координатной
сетки. И сегменты площади, которых необходимо определить. 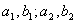 .
.
Например:
Схема расположения сегментов представлена в Приложении
И.
Площади участков были определены в программе AutoCAD 2007.
. После чего по способу Савича А.Н. находят
окончательные значения площадей сегментов.
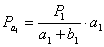 (23),
(23),
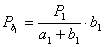 (24),
(24),
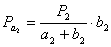 (25),
(25),
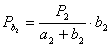 (26),
(26),
где
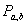 окончательная площадь сегмента, которую необходимо
определить,
окончательная площадь сегмента, которую необходимо
определить, 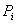 площадь сегмента образованного из квадратов
координатной сетки,
площадь сегмента образованного из квадратов
координатной сетки, 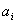
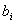 площадь сегмента полученная графически.
площадь сегмента полученная графически.
Например:
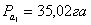
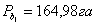
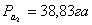
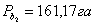
6. Затем производят контроль полученных
значений.
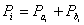 (27),
(27),
где
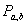 окончательная площадь сегмента, полученная по формуле
Савича А.Н.,
окончательная площадь сегмента, полученная по формуле
Савича А.Н., 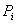 площадь сегмента образованного из квадратов
координатной сетки.
площадь сегмента образованного из квадратов
координатной сетки.
Например:
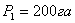
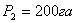
7. После чего находят окончательную площадь
землепользования.
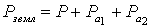 (28),
(28),
где
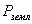 общая площадь землепользования,
общая площадь землепользования, 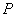 площадь полигона А-2-3-4-5-B
площадь полигона А-2-3-4-5-B 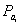 площадь сегмента, полученная по формуле Савича А.Н.
площадь сегмента, полученная по формуле Савича А.Н.
Например:
Вывод:
При решении задачи данным способом
общая площадь землепользования составила 993,20 га, что отличается от
предыдущего способа на 0,15 га.
3.
ПРОЕКТИРОВАНИЕ ГРАНИЦ ЗЕМЕЛЬНЫХ УЧАСТКОВ АНАЛИТИЧЕСКИМИ СПОСОБАМИ
3.1 ПРОЕКТИРОВАНИЕ ГРАНИЦ ЗЕМЕЛЬНОГО УЧАСТКА СПОСОБОМ ТРАПЕЦИИ
1. Проектная линия M-N параллельна стороне 3-4 (рисунок 3).
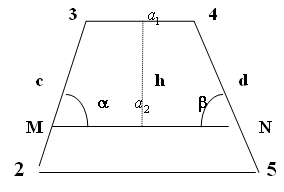
Рисунок 3.Проектирование границ земельного участка способом трапеции.
2. Определяют
дирекционные углы сторон 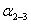 ,
, 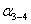 ,
, 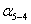 и длину стороны 3-4 (
и длину стороны 3-4 (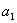 ,
согласно Рисунку 3) из решения обратных геодезических задач.
,
согласно Рисунку 3) из решения обратных геодезических задач.
Например:
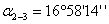
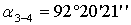
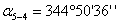
. Вычисляют
углы 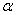 и
и 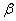 по
разности дирекционных углов.
по
разности дирекционных углов.
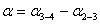 (29),
(29),
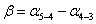 (30),
(30),
где
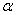 угол в точке М,
угол в точке М, 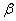 угол в
точке N,
угол в
точке N, 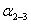
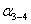
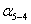 дирекционные
углы сторон.
дирекционные
углы сторон.
Например:
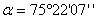
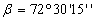
4. Находят значение нижнего основания трапеции.
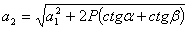 (31),
(31),
где
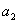 нижнее основание трапеции,
нижнее основание трапеции, 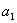 верхнее основание трапеции или длина линии 3-4,
верхнее основание трапеции или длина линии 3-4, 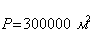 площадь выделяемого участка, выраженная в квадратных
метрах,
площадь выделяемого участка, выраженная в квадратных
метрах, 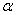 угол в точке М,
угол в точке М, 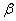 угол в
точке N.
угол в
точке N.
Например:
. После чего находят значение высоты трапеции:
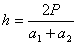 (32),
(32),
где
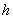 высота трапеции,
высота трапеции, 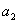 нижнее
основание трапеции,
нижнее
основание трапеции, 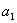 верхнее основание трапеции или длина линии 3-4,
верхнее основание трапеции или длина линии 3-4, 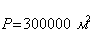 площадь выделяемого участка, выраженная в квадратных
метрах.
площадь выделяемого участка, выраженная в квадратных
метрах.
Например:
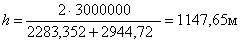
6. Находят значения боковых сторон трапеции:
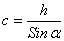 (33),
(33),
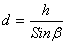 (34),
(34),
где
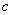
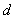 значения
боковых сторон трапеции,
значения
боковых сторон трапеции, 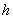 высота трапеции,
высота трапеции, 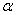 угол в
точке М,
угол в
точке М, 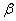 угол в точке N.
угол в точке N.
Например:
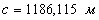
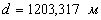
7. Далее находят координаты проектных точек:
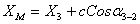 ,
,
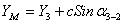 .
.
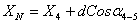
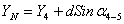
где
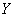
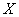 координаты
точек полигона,
координаты
точек полигона, 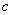
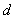 значения
боковых сторон трапеции,
значения
боковых сторон трапеции, 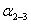 ,
, 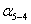 дирекционные
углы сторон.
дирекционные
углы сторон.
Например:
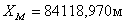
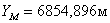
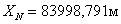
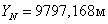
8. Для контроля используя координаты точек 3, 4, M, N находят площадь полигона.
Например:
Пример вычисления площади указан в Приложении Н.
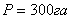
9. На кадастровом плане отмечают данный участок.
Например:
Приложение К
Вывод:
площадь полигона, вычисленная по
координатам запроектированных границ участка способом трапеции 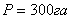 , что равно проектируемой площади.
, что равно проектируемой площади.
.2 ПРОЕКТИРОВАНИЕ ГРАНИЦ ЗЕМЕЛЬНОГО УЧАСТКА ПРИЕМОМ ТРЕУГОЛЬНИКА
1. Проектная линия 2-К проходит через точку 2 (рисунок 4).
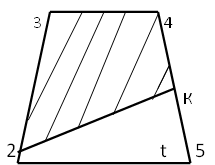
Рисунок 4. Проектирование границ земельного участка приемом
треугольника
2. Решая
обратные геодезические задачи, находят дирекционные углы всех сторон полигона, 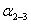
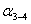
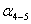
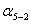 и длину
линии
и длину
линии 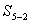 .
.
Например:
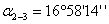
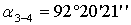
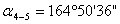
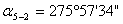
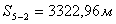
3. По координатам находят площадь полигона 2-3-4-5.
Например:
Пример вычисления площади указан в Приложении О.
. Определяют площадь треугольника 2-К-5 .
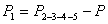 (35),
(35),
где
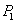 площадь треугольника 2-К-5,
площадь треугольника 2-К-5, 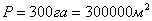 ,
, 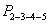 вычисленная
по координатам площадь полигона.
вычисленная
по координатам площадь полигона.
Например:
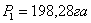
. В
треугольнике 2-К-5 вычисляют угол 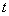 при
точке 5.
при
точке 5.
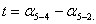 (36),
(36),
где
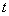 угол при точке 5,
угол при точке 5, 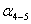
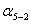 дирекционные
углы линий.
дирекционные
углы линий.
Например:
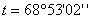
. Определяют
длину отрезка 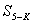 .
.
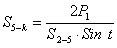 (37),
(37),
где
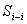 длины линий,
длины линий, 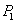 площадь
треугольника 2-К-5,
площадь
треугольника 2-К-5, 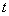 угол при точке 5.
угол при точке 5.
Например:
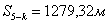
7. Далее находят координаты запроектированной
точки.
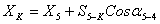 (38),
(38),
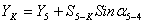 (39),
(39),
где
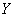
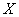 координаты
точек,
координаты
точек, 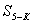 длина отрезка 5-К,
длина отрезка 5-К, 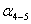 дирекционные
углы линий.
дирекционные
углы линий.
Например:
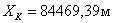
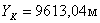
10. Для контроля используя координаты точек 2, 3, 4, К находят
площадь полигона.
Например:
Пример вычисления площади указан в Приложении П.
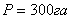
11. На кадастровом плане отмечают данный участок.
Например:
Приложение К.
Вывод:
площадь полигона, вычисленная по
координатам запроектированных границ участка способом треугольника 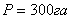 , что равно проектируемой площади.
, что равно проектируемой площади.
3.3 ПРОЕКТИРОВАНИЕ ГРАНИЦ ЗЕМЕЛЬНОГО УЧАСТКА КОМБИНИРОВАННЫМ СПОСОБОМ
. Проектная линия перпендикулярна стороне 2-3 (рисунок 5).
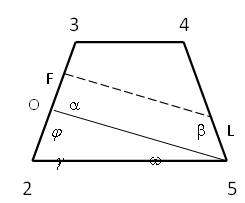
Рисунок 5. Проектирование границ земельного участка комбинированным
способом.
2. Решая
обратные геодезические задачи, находят дирекционные углы всех сторон полигона, 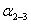
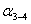
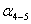
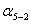 и длину
линии
и длину
линии 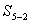 .
.
Например:
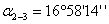
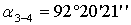
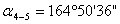
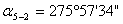
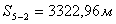
3. Из точки 5 на сторону 2-3 опускают перпендикуляр.
4. По
теореме синусов находят значение длин линий 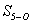
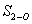
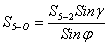 (40),
(40),
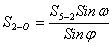 (41),
(41),
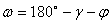 (42),
(42),
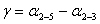 (43),
(43),
где
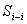 длины линий,
длины линий, 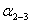
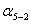 дирекционные
углы линий,
дирекционные
углы линий, 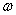 угол при точке 5 в треугольнике 2-О-5,
угол при точке 5 в треугольнике 2-О-5, 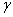 угол при точке 2 в треугольнике 2-О-5,
угол при точке 2 в треугольнике 2-О-5, 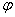 угол при точке О в треугольнике 2-О-5.
угол при точке О в треугольнике 2-О-5.
Например:
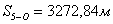
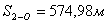
5. Находят площадь полученного треугольника 2-О-5.
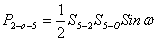 (44),
(44),
где
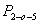 площадь треугольника 2-О-5,
площадь треугольника 2-О-5, 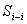 длины линий,
длины линий, 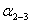
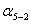 дирекционные
углы линий,
дирекционные
углы линий, 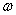 угол при точке 5 в треугольнике 2-О-5.
угол при точке 5 в треугольнике 2-О-5.
Например:
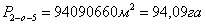
6. Вычисляют площадь четырехугольника О-3-4-5.
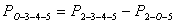 (45),
(45),
где
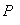 площади фигур соответственно нижним индексам, площадь
полигона 2-3-4-5 вычислялось ранее в п.п. 3.2 (приложение О).
площади фигур соответственно нижним индексам, площадь
полигона 2-3-4-5 вычислялось ранее в п.п. 3.2 (приложение О).
Например:
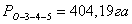
7. Если площадь полученного четырехугольника отличается от
проектной, то находят избыточную площадь.
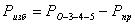 (46),
(46),
где
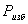 избыточная площадь,
избыточная площадь, 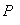 площадь
фигуры соответственно нижним индексам,
площадь
фигуры соответственно нижним индексам, 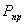 площадь
проектная.
площадь
проектная.
Например:
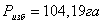
8. Проектируют избыточную площадь методом трапеции, рассмотренным
ранее, учитывая следующие значения:
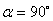
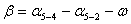 (47),
(47),
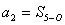 (48),
(48),
где
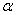 угол трапеции O-F-L-5 в
точке О,
угол трапеции O-F-L-5 в
точке О, 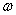 угол при точке 5 в треугольнике 2-О-5,
угол при точке 5 в треугольнике 2-О-5, 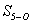 основание трапеции
основание трапеции 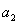 ,
, 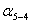
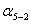 дирекционные
углы линий,
дирекционные
углы линий, 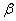 угол трапеции O-F-L-5 в
точке 5.
угол трапеции O-F-L-5 в
точке 5.
Например:
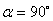
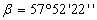
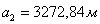
. Находят
значение основания трапеции 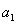
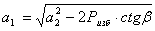 (49),
(49),
где
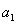 основание трапеции,
основание трапеции, 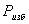 избыточная
площадь,
избыточная
площадь, 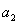 основание трапеции равное длине линии
основание трапеции равное длине линии 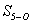 ,
, 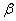 угол
трапеции O-F-L-5 в точке 5.
угол
трапеции O-F-L-5 в точке 5.
Например:
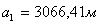
10. Вычисляют значение высоты трапеции, так как трапеция
прямоугольная, то значение высоты равно одной из сторон:
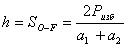 (50),
(50),
где
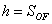 высота трапеции,
высота трапеции, 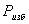 избыточная
площадь,
избыточная
площадь, 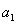
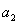 основания
трапеции
основания
трапеции
Например:
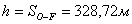
11. Находят значение второй боковой стороны:
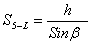 (51),
(51),
где
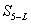 длина боковой стороны трапеции,
длина боковой стороны трапеции, 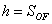 высота трапеции,
высота трапеции, 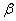 угол
трапеции O-F-L-5 в точке 5.
угол
трапеции O-F-L-5 в точке 5.
Например:
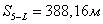
12. Далее находят координаты запроектированных точек:
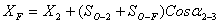 (52),
(52),
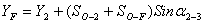 (53),
(53),
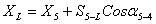 (54),
(54),
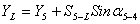 (55),
(55),
где
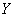
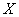 координаты
точек,
координаты
точек, 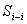 длины линий,
длины линий, 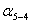
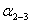 дирекционные
углы линий.
дирекционные
углы линий.
Например:
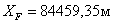
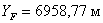
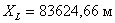
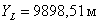
12. Для контроля используя координаты точек F, 3, 4, L
находят площадь полигона.
Например:
Пример вычисления площади указан в Приложении Р.
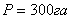
13. На кадастровом плане отмечают данный участок.
Например:
Приложение К
Вывод:
площадь полигона, вычисленная по
координатам запроектированных границ участка комбинированным способом 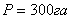 , что равно проектируемой площади.
, что равно проектируемой площади.
4.
ПРОЕКТИРОВАНИЕ ГРАНИЦ ЗЕМЕЛЬНОГО УЧАСТКА ГРАФИЧЕСКИМ СПОСОБОМ
.1 ПРОЕКТИРОВАНИЕ ГРАНИЦ ЗЕМЕЛЬНОГО УЧАСТКА
ГРАФИЧЕСКИМ СПОСОБОМ
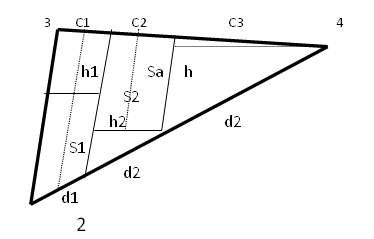
Рисунок 6. Проектирование границ земельного
участка графическим способом.
. По координатам межевых знаков 2, 3, 4
вычисляют общую площадь размежевываемого участка.
Например:
Пример вычисления площади указан в Приложении С
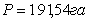
2. Вычисляют площадь выделяемого участка, как
1/3 от площади участка, подлежащего межеванию.
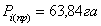
. На
плане приближенно намечают границу первого выделяемого участка (первой
трапеции). Проводят на глаз среднюю линию трапеции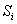 и измеряют ее.
и измеряют ее.
. Вычисляют
высоту трапеции:
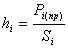 (56),
(56),
где
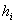 высота трапеции,
высота трапеции, 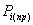 площадь
выделяемого участка,
площадь
выделяемого участка, 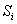 длина средней линии трапеции.
длина средней линии трапеции.
5. Откладывают половину значения высоты по
перпендикуляру от основания трапеции и получают 1…n-е уточненное положение средней линии трапеции.
. После чего измеряют 1…n-е уточненное положение средней линии
трапеции.
. И заново вычисляют высоту трапеции (1…n-я уточненная высота трапеции).
. Сравнивают новое значение высоты трапеции с
предыдущим.
9. Если
разность значений не превышает допуска, равного 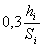 в мм в
масштабе плана, то откладывают значение последней вычисленной высоты трапеции
по перпендикуляру от основания трапеции и проводят второе основание трапеции
в мм в
масштабе плана, то откладывают значение последней вычисленной высоты трапеции
по перпендикуляру от основания трапеции и проводят второе основание трапеции 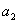 - границу участка.
- границу участка.
. Если
разность значений превышает допуск, то повторяют действия.
. Для
проектирования второго участка пользуются пунктами 3-10.
. Таким
образом, данный способ является способом приближений.
. Для
удобства выполнения данного задания строят таблицы:
Например:
Таблица 12. Определение значений элементов
проектируемой трапеции 1
|
|
1
|
2
|
3
|
4
|
|
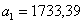 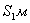 1330,391420,711466,991509,04 1330,391420,711466,991509,04
|
|
|
|
|
|
|
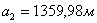 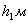 479,9094449,3997435,2222423,0946 479,9094449,3997435,2222423,0946
|
|
|
|
|
|
|
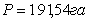 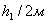 239,9547224,6999217,6111211,5473 239,9547224,6999217,6111211,5473
|
|
|
|
|
|
|
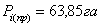 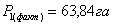 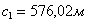 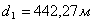 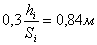
|
|
|
|
|
|
Таблица 13. Определение значений элементов
проектируемой трапеции 2
|
|
1
|
2
|
3
|
4
|
5
|
|
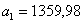 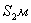 810,131129,091140,241187,301202,76 810,131129,091140,241187,301202,76
|
|
|
|
|
|
|
|
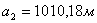 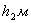 788,104565,4701559,9406537,7467530,8346 788,104565,4701559,9406537,7467530,8346
|
|
|
|
|
|
|
|
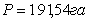 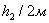 394,052282,7351279,9703268,8734265,4173 394,052282,7351279,9703268,8734265,4173
|
|
|
|
|
|
|
|
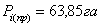 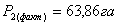 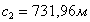 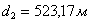 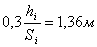
|
|
|
|
|
|
|
В данных таблицах приведены примеры определения
значений элементов проектируемых трапеций.
. Боковые стороны трапеций измеряют графически,
и записывают в таблицы.
. После проектирования второго земельного
участка на плане образуется третий участок треугольной формы. Его площадь
вычисляют по двум независимым основаниям и высотам, которые получают
графически. Для удобства составляют таблицы.
Например:
Таблица 14. Определение площади проектируемого треугольника 1 случай
В данной таблице приведен пример определения площади проектируемого
треугольника в 1 случае.
Таблица 15. Определение площади проектируемого треугольника 2 случай
В данной таблице приведен пример определения площади проектируемого
треугольника в 2 случае.
16. Расхождения
между двумя значениями площади треугольника, определенными графически не должно
превышать 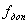 .
.
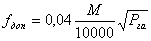 (57),
(57),
где
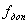 допустимое значение расхождения площади, определенной
дважды,
допустимое значение расхождения площади, определенной
дважды, 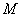 знаменатель масштаба плана,
знаменатель масштаба плана, 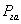 площадь участка.
площадь участка.
Например:
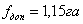
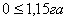
17.
Находят среднее арифметическое значение площади участка.
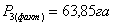
18. Находят общую площадь всех участков.
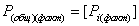 (58),
(58),
где
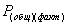 общая полученная площадь размежевываемого участка,
общая полученная площадь размежевываемого участка, 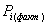 фактические площади запроектированных участков.
фактические площади запроектированных участков.
Например:

19. Находят разность между теоретическим значением площади
размежевываемого участка и фактическим значением.
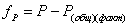 (59),
(59),
где
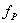 значение невязки между площадями,
значение невязки между площадями, 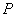 общая теоретическая площадь размежевываемого участка,
общая теоретическая площадь размежевываемого участка,
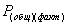 общая полученная площадь размежевываемого участка.
общая полученная площадь размежевываемого участка.
Например:
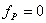
20. Распределяют полученную невязку, и получают окончательные
значения площадей участков.
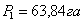
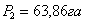
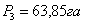
21. На кадастровом плане отмечают данный участок.
Например:
Приложение И
Вывод: площадь полигона, путем графического проектирования
составила 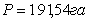 , что равно проектируемой площади.
, что равно проектируемой площади.
5.
ПРОЕКТИРОВАНИЕ ГРАНИЦ ЗЕМЕЛЬНЫХ УЧАСТКОВ
ГРАФОМЕХАНИЧЕСКИМ СПОСОБОМ
5.1 ПРОЕКТИРОВАНИЕ ГРАНИЦ ЗЕМЕЛЬНЫХ УЧАСТКОВ ГРАФОМЕХАНИЧЕСКИМ
СПОСОБОМ
. Участок проектируется таким образом, чтобы
одна из границ участка проходила через межевые знаки 1 и 6, а другая - была
параллельна линии 1-6.
. Проектируют предварительную границу участка
«на глаз» линией параллельной стороне 1-6.
. Измеряют площадь предварительно
запроектированного участка.
. Сравнивают измеренную площадь с проектной.
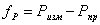 (60),
(60),
где
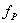 значение невязки между площадями,
значение невязки между площадями, 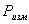 измеренная площадь запроектированного участка,
измеренная площадь запроектированного участка, 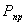 проектное значение площади проектируемого участка.
проектное значение площади проектируемого участка.
5. Если полученная разность не превышает
величины:
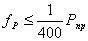 (61),
(61),
. То
участок считается запроектированным, в противном случае необходимо
запроектировать недостающую или избыточную площадь. Знак плюс - у значения 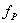 указывает избыточную площадь, знак минус - на
недостающую.
указывает избыточную площадь, знак минус - на
недостающую.
Например:
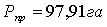
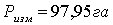
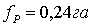
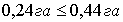
7. На кадастровом плане отмечают данный участок.
Например:
Приложение И
Вывод: площадь полигона, путем графомеханического
проектирования составила 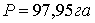 , что отличается от проектного значения на 0,04га
, что отличается от проектного значения на 0,04га 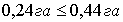 , что не превышает допустимой величины.
, что не превышает допустимой величины.
6.
ГЕОДЕЗИЧЕСКАЯ ПОДГОТОВКА ПЕРЕНЕСЕНИЯ ПРОЕКТНЫХ ГРАНИЦ ЗЕМЕЛЬНЫХ УЧАСТКОВ В
НАТУРУ
6.1 ПОДГОТОВКА ГЕОДЕЗИЧЕСКИХ ДАННЫХ ДЛЯ РАЗБИВКИ НА МЕСТНОСТИ УГЛОВ
МЕЖЕВОГО УЧАСТКА (ТОЧЕК M и N) СПОСОБОМ ПОЛЯРНЫХ КООРДИНАТ
. При подготовке геодезических данных для выноса в натуру точек M и N, используют полученные в ходе проектирования участка длины
выносимых сторон (длины сторон трапеции при проектировании), и дирекционные
углы линий. Или при использовании ПО Credo DAT 3.0 удобнее
использовать полученные координаты точек M и N.
6.1.1 Подготовка геодезических данных для разбивки на местности
точки M с пункта 3 способом полярных
координат
2. Определяют
дирекционные углы линий 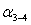 ,
, 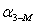 ,
, 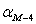 , и длину линии
, и длину линии 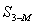 , решив
для этого обратные геодезические задачи по координатам знаков 3, 4, M.
, решив
для этого обратные геодезические задачи по координатам знаков 3, 4, M.
. Вычисляют
угол построения 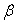 и для контроля работ по восстановлению получают угол
и для контроля работ по восстановлению получают угол 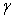 .
.
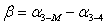 (62),
(62),
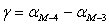 (63),
(63),
где
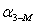 ,
, 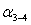 ,
, 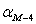 дирекционные направления линий,
дирекционные направления линий, 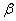 угол построения
угол построения 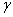 угол при
точке М.
угол при
точке М.
Таблица 16. Данные для разбивки на местности пункта М способом полярных
координат
|
Пункт
|
Гор. угол
|
Дир. угол
|
Гор. проложение, м
|
|
4
|
|
272°20'21"
|
2283,35
|
|
3
|
104°37'53"
|
196°58'14"
|
1186,12
|
|
M
|
|
|
|
В
данной таблице представлено значение угла 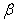 откладываемого
от направления с пункта 3 на пункт 4.
откладываемого
от направления с пункта 3 на пункт 4.
Данный
отчет подготовлен в программном комплексе CREDO_DAT.
Таблица
17. Вычисление угла 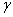 находящегося при точке М
находящегося при точке М
|
Пункт
|
Гор. угол
|
Дир. угол
|
Гор. проложение, м
|
|
3
|
|
196°58'14"
|
1186,12
|
|
M
|
51°24'44"
|
68°22'58"
|
2826,45
|
|
4
|
|
|
|
Данный отчет подготовлен в программном комплексе CREDO_DAT.
4. Затем
устанавливается ожидаемая точность построения пункта и необходимая точность
угловых и линейных построений, задаваясь допустимой ошибкой восстановления
пункта ОМС на местности 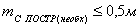 :
:
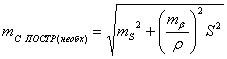 (64),
(64),
где
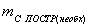 необходимая точность построения,
необходимая точность построения, 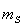 необходимая точность выноса расстояния,
необходимая точность выноса расстояния, 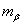 необходимая точность построения угла,
необходимая точность построения угла, 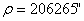 ,
, 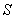 выносимое
расстояние.
выносимое
расстояние.
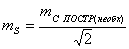 (65),
(65),
где
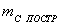 допустимая величина ошибки закрепления точки на
местности,
допустимая величина ошибки закрепления точки на
местности, 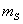 необходимая точность выноса расстояния.
необходимая точность выноса расстояния.
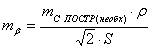 (66),
(66),
где
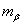 необходимая точность построения угла,
необходимая точность построения угла, 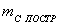 допустимая величина закрепления точки на местности,
допустимая величина закрепления точки на местности, 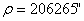 ,
, 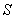 выносимое
расстояние.
выносимое
расстояние.
Например:
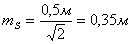
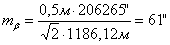
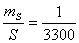
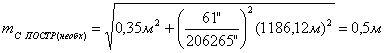
5. Исходя из установленной необходимой точности угловых и линейных
построений, для построения точки M
способом полярных координат можно применить следующие приборы: прибор для
линейно-угловых измерений соответствующий угловой точности в 30” и прибор
соответствующий линейной точности 1/50000. Например: электронный тахеометр Nikon 352W, Trimble
M3 для угловых измерений и линейных
измерений.
. После чего с учетом выбранных приборов, находят ожидаемую
точность построений.
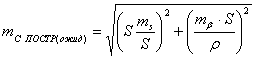 (67),
(67),
где
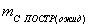 ожидаемая точность построений,
ожидаемая точность построений, 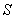 выносимое расстояние,
выносимое расстояние, 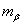 фактическое
значение ошибки выноса угла данным прибором,
фактическое
значение ошибки выноса угла данным прибором, 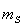 фактическое
значение ошибки выноса расстояния данным прибором.
фактическое
значение ошибки выноса расстояния данным прибором.
Например:
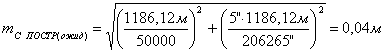
7. После чего сравнивают ожидаемую точность построений выбранным
прибором и допустимую, должно соблюдаться условие:
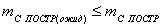 (68),
(68),
где
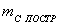 допустимая точность построения точки,
допустимая точность построения точки, 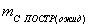 ожидаемая точность построений.
ожидаемая точность построений.
Например:
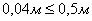
10. Составляют разбивочный чертеж.
Например:
Приложение Д
Вывод: условие 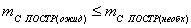 соблюдается
соблюдается
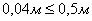 , следовательно, можно применить следующие приборы:
прибор для линейно-угловых измерений соответствующий угловой точности в 30” и
прибор соответствующий линейной точности 1/50000. Например: электронный
тахеометр Nikon 352W, Trimble M3 для угловых измерений и
линейных измерений.
, следовательно, можно применить следующие приборы:
прибор для линейно-угловых измерений соответствующий угловой точности в 30” и
прибор соответствующий линейной точности 1/50000. Например: электронный
тахеометр Nikon 352W, Trimble M3 для угловых измерений и
линейных измерений.
6.1.2
Подготовка геодезических данных для разбивки на местности точки N
с пункта 4 способом полярных координат
. Определяют
дирекционные углы линий 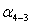 ,
, 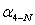 ,
, 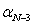 , и длину линии
, и длину линии 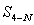 , решив
для этого обратные геодезические задачи по координатам знаков 3, 4, N.
, решив
для этого обратные геодезические задачи по координатам знаков 3, 4, N.
. Вычисляют
угол построения 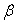 и для контроля работ по восстановлению получают угол
и для контроля работ по восстановлению получают угол 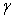 .
.
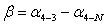 (69),
(69),
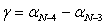 (70),
(70),
где
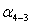 ,
, 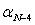 ,
, 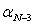 дирекционные направления линий,
дирекционные направления линий, 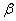 угол построения
угол построения 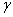 угол при
точке N.
угол при
точке N.
Таблица 16. Данные для разбивки на местности пункта N способом полярных координат.
|
Пункт
|
Гор. угол
|
Дир. угол
|
Гор. проложение, м
|
|
3
|
|
|
|
|
4
|
107°29'45"
|
344°50'36"
|
1203,32
|
|
N
|
|
272°20'21"
|
2283,35
|
В
данной таблице представлено значение угла 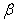 откладываемого
от направления с пункта 4 на пункт 3.
откладываемого
от направления с пункта 4 на пункт 3.
Данный
отчет подготовлен в программном комплексе CREDO_DAT.
Таблица
17. Вычисление угла 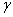 находящегося при точке N
находящегося при точке N
|
ПунктГор. уголДир. уголГор. проложение, м
|
|
|
|
|
3
|
|
115°47'38"
|
2883,35
|
|
N
|
49°02'58"
|
344°50'36"
|
1203,32
|
|
4
|
|
|
|
Данный отчет подготовлен в программном комплексе CREDO_DAT.
10. Затем
устанавливается ожидаемая точность построения пункта и необходимая точность
угловых и линейных построений, задаваясь допустимой ошибкой восстановления
пункта ОМС на местности 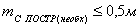 :
:
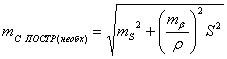 (71),
(71),
где
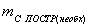 необходимая точность построения,
необходимая точность построения, 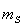 необходимая точность выноса расстояния,
необходимая точность выноса расстояния, 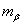 необходимая точность построения угла,
необходимая точность построения угла, 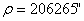 ,
, 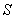 выносимое
расстояние.
выносимое
расстояние.
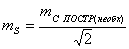 (72),
(72),
где
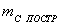 допустимая величина ошибки закрепления точки на
местности,
допустимая величина ошибки закрепления точки на
местности, 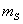 необходимая точность выноса расстояния.
необходимая точность выноса расстояния.
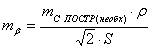 (73),
(73),
где
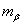 необходимая точность построения угла,
необходимая точность построения угла, 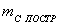 допустимая величина закрепления точки на местности,
допустимая величина закрепления точки на местности, 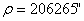 ,
, 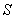 выносимое
расстояние.
выносимое
расстояние.
Например:
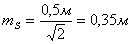
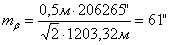
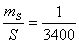
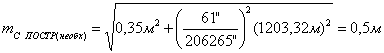
11. Исходя из установленной необходимой точности угловых и линейных
построений, для построения точки M
способом полярных координат можно применить следующие приборы: прибор для
линейно-угловых измерений соответствующий угловой точности в 30” и прибор
соответствующий линейной точности 1/50000. Например: электронный тахеометр Nikon 352W, Trimble
M3 для угловых измерений и линейных
измерений.
. После чего с учетом выбранных приборов, находят ожидаемую
точность построений.
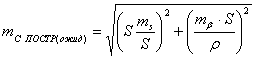 (74),
(74),
где
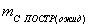 ожидаемая точность построений,
ожидаемая точность построений, 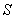 выносимое расстояние,
выносимое расстояние, 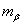 фактическое
значение ошибки выноса угла данным прибором,
фактическое
значение ошибки выноса угла данным прибором, 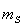 фактическое
значение ошибки выноса расстояния данным прибором.
фактическое
значение ошибки выноса расстояния данным прибором.
Например:
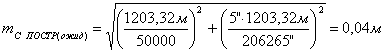
13. После чего сравнивают ожидаемую точность построений выбранным
прибором и допустимую, должно соблюдаться условие:
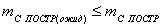 (75),
(75),
где
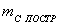 допустимая точность построения точки,
допустимая точность построения точки, 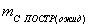 ожидаемая точность построений.
ожидаемая точность построений.
Например:
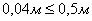
14. Составляют разбивочный чертеж.
Например:
Приложение Е.
Вывод: условие 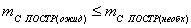 соблюдается
соблюдается
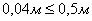 , следовательно, можно применить следующие приборы:
прибор для линейно-угловых измерений соответствующий угловой точности в 30” и
прибор соответствующий линейной точности 1/50000. Например: электронный тахеометр
Nikon 352W, Trimble M3 для угловых измерений и
линейных измерений.
, следовательно, можно применить следующие приборы:
прибор для линейно-угловых измерений соответствующий угловой точности в 30” и
прибор соответствующий линейной точности 1/50000. Например: электронный тахеометр
Nikon 352W, Trimble M3 для угловых измерений и
линейных измерений.
6.2 ПОДГОТОВКА ГЕОДЕЗИЧЕСКИХ
ДАННЫХ ДЛЯ ПОСТРОЕНИЯ НА МЕСТНОСТИ МЕЖЕВОГО ЗНАКА СПОСОБОМ ПРЯМОЙ УГЛОВОЙ
ЗАСЕЧКИ
1. Для
того чтобы произвести вынос точки, по координатам решая обратные геодезические
задачи находят проектные углы 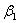 и
и 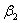 откладываемые от направлений на ориентируемые пункты.
откладываемые от направлений на ориентируемые пункты.
Например:
Таблица 18. Данные для построения пункта ОМС K методом прямой угловой засечки с
пункта 4
|
ПунктГор. уголДир. уголГор. проложение, м
|
|
|
|
|
3
|
|
92°20'21"
|
2283,35
|
|
4
|
256°57'54"
|
164°18'14"
|
703,08
|
|
K
|
|
|
|
В
данной таблице представлено значение угла 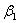 откладываемого
от направления с пункта 4 на пункт 3.
откладываемого
от направления с пункта 4 на пункт 3.
Данный
отчет подготовлен в программном комплексе CREDO_DAT.
Таблица 19. Данные для восстановления утраченного
пункта ОМС K методом прямой угловой засечки с
пункта 2
|
Пункт
|
Гор. угол
|
Дир. угол
|
Гор. проложение, м
|
|
3
|
|
196°58'14"
|
1733,94
|
|
2
|
56°20'55"
|
73°19'09"
|
3046,23
|
|
K
|
|
|
|
В
данной таблице представлено значение угла 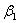 откладываемого
от направления с пункта 2 на пункт 3.
откладываемого
от направления с пункта 2 на пункт 3.
Данный
отчет подготовлен в программном комплексе CREDO_DAT.
. Угол
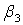 вычисляется из полученных дирекционных направлений
линий 4-K и 2-K:
вычисляется из полученных дирекционных направлений
линий 4-K и 2-K:
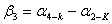 (76),
(76),
где
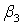 угол в точке K,
угол в точке K, 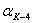
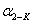 дирекционные углы линий
дирекционные углы линий
Например:
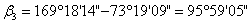
3. После
чего задаваясь допустимой величиной ошибки закрепления точки на местности 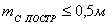 , определяют необходимую точность построений:
, определяют необходимую точность построений:
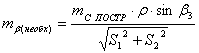 (77),
(77),
где
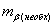 необходимая точность построения угла,
необходимая точность построения угла, 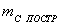 допустимая величина ошибки закрепления точки на
местности,
допустимая величина ошибки закрепления точки на
местности, 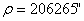
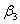 угол
треугольника,
угол
треугольника, 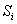 расстояние от точки стояния до выносимой точки.
расстояние от точки стояния до выносимой точки.
Например:
4. Исходя из установленной необходимой точности угловых построений,
для построения точки K
способом прямой угловой засечки можно применить следующие приборы: теодолит Т30
или ему равноточные.
. После чего, с учетом выбранных приборов, находят ожидаемую
точность построений.
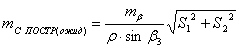 (78),
(78),
где
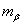 фактическое значение ошибки выноса угла данным
прибором,
фактическое значение ошибки выноса угла данным
прибором, 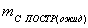 ожидаемая точность построений,
ожидаемая точность построений, 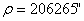
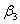 угол
треугольника,
угол
треугольника, 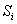 расстояние от точки стояния до выносимой точки.
расстояние от точки стояния до выносимой точки.
Например:
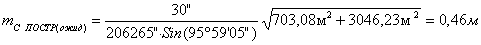
6.
После чего сравнивают ожидаемую точность построений выбранным прибором и
допустимую, должно соблюдаться условие:
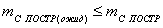 (79),
(79),
где
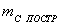 допустимая величина ошибки закрепления точки на
местности,
допустимая величина ошибки закрепления точки на
местности, 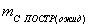 ожидаемая точность построений.
ожидаемая точность построений.
Например:
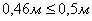
15. Составляют разбивочный чертеж.
Например:
Приложение Ж.
Вывод: условие 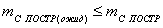 соблюдается
соблюдается
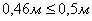 , следовательно, можно применить следующие приборы:
теодолит Т30 или ему равноточные.
, следовательно, можно применить следующие приборы:
теодолит Т30 или ему равноточные.
6.3 ПОДГОТОВКА ГЕОДЕЗИЧЕСКИХ ДАННЫХ ДЛЯ ПОСТРОЕНИЯ НА
МЕСТНОСТИ МЕЖЕВЫХ ЗНАКОВ СПОСОБОМ ПРОМЕРОВ ПО СТВОРУ МЕЖДУ СУЩЕСТВУЮЩИМИ
ПУНКТАМИ
. В этом способе положение точки F находят на местности путём отложения расстояния S1 в створе линии между межевыми знаками
2 и 3, аналогично находят положение точки L в створе линии 4-5.
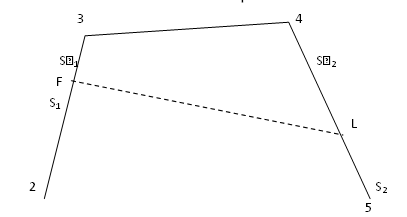
Рисунок 7. Принцип построения точек способом промеров по створу между
существующими пунктами.
. Необходимыми геодезическими данными для выноса точек F и L являются расстояния S1 и S2. Значения этих расстояний получены
при проектировании границ участка.
Например:
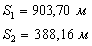
. Для
контроля находят стороны 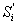 .
.
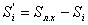 (80),
(80),
где
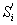 выносимая сторона для контроля,
выносимая сторона для контроля, 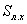 длина стороны линии между знаками с известными
координатами,
длина стороны линии между знаками с известными
координатами, 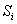 длина линии до выносимой в натуру точки от известного
пункта.
длина линии до выносимой в натуру точки от известного
пункта.
Например:
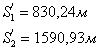
. После
чего задаваясь допустимой величиной ошибки закрепления точки на местности 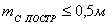 , определяют необходимую точность построений. Так как
вынос проектных точек будет производиться при помощи линейных построений, то на
ошибку закрепления точки на местности будет влиять только погрешность отложения
расстояний.
, определяют необходимую точность построений. Так как
вынос проектных точек будет производиться при помощи линейных построений, то на
ошибку закрепления точки на местности будет влиять только погрешность отложения
расстояний.
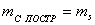 (81),
(81),
где
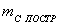 ошибка закрепления точки на местности,
ошибка закрепления точки на местности, 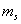 погрешность линейных построений.
погрешность линейных построений.
5. Для выбора прибора пользуются относительной линейной
погрешностью.
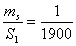
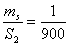
6. Исходя из установленной необходимой точности линейных
построений, для построения точек F и L способом промеров по створу можно
применить следующие приборы: мерная лента.
. После чего вычисляют ожидаемую точность построения межевых
знаков.
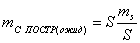 (82),
(82),
где
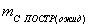 ожидаемая точность построений,
ожидаемая точность построений, 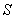 выносимое расстояние,
выносимое расстояние, 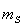 фактическое
значение ошибки выноса расстояния данным прибором.
фактическое
значение ошибки выноса расстояния данным прибором.
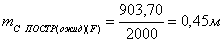
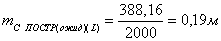
8. После чего сравнивают ожидаемую точность построений выбранным
прибором и допустимую, должно соблюдаться условие:
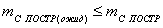 (83),
(83),
где
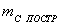 допустимая величина ошибки закрепления точки на
местности,
допустимая величина ошибки закрепления точки на
местности, 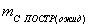 ожидаемая точность построений
ожидаемая точность построений
Например:
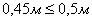
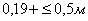
9. Составляют разбивочный чертеж.
Например:
Приложение З.
Вывод: условие 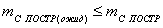 соблюдается
соблюдается
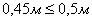
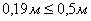 ,
следовательно, можно применить следующие приборы: мерная лента.
,
следовательно, можно применить следующие приборы: мерная лента.
6.4
ГЕОДЕЗИЧЕСКАЯ ПОДГОТОВКА ДАННЫХ ДЛЯ ВЫНОСА МЕЖЕВЫХ ЗНАКОВ А,Б,В,Г В НАТУРУ
СПОСОБОМ ПРОЕКТНОГО ТЕОДОЛИТНОГО ХОДА.
1. Графически проектируют пункты а, б, в, г, а затем снимают с
плана их координаты.
. После чего путем решения обратных геодезических задач, находят
проектные углы хода и расстояния.
Таблица 20. Данные для построения пунктов ОМС методом проложения
проектного теодолитного хода
|
Пункт
|
Гор. угол
|
Дир. угол
|
Гор. проложение, м
|
|
2
|
|
60°45'54"
|
608,54
|
|
a
|
136°28'54"
|
17°14'49"
|
1406,44
|
|
б
|
254°55'29"
|
92°10'18"
|
523,98
|
|
в
|
285°21'14"
|
197°31'32"
|
1007,19
|
|
г
|
43°16'10"
|
60°47'42"
|
1855,04
|
|
4
|
31°32'39"
|
272°20'21"
|
2283,35
|
|
3
|
104°37'53"
|
196°58'14"
|
1733,94
|
В данной таблице представлены значения углов и расстояний проектного
теодолитного хода.
Данный отчет подготовлен в программном комплексе CREDO_DAT
3. Приняв
погрешность положения конечной точки вытянутого теодолитного хода 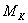 равной ошибке положения точек ближайших пунктов ОМС
или ГГС (0,1 мм в масштабе кадастрового плана, т.е. 0,5 м для масштаба 1:5000),
рассчитывают необходимую точность построений линий и углов проектного хода.
равной ошибке положения точек ближайших пунктов ОМС
или ГГС (0,1 мм в масштабе кадастрового плана, т.е. 0,5 м для масштаба 1:5000),
рассчитывают необходимую точность построений линий и углов проектного хода.
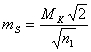 (84),
(84),
где
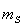 необходимая точность линейных построений,
необходимая точность линейных построений, 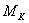 ошибка положения пункта вытянутого теодолитного хода,
ошибка положения пункта вытянутого теодолитного хода,
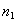 число сторон в ходе.
число сторон в ходе.
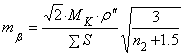 (85),
(85),
где
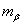 необходимая точность построений углов,
необходимая точность построений углов, 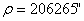 ,
, 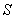 проектные
расстояния,
проектные
расстояния, 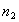 число измеренных углов в ходе,
число измеренных углов в ходе, 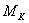 ошибка положения пункта вытянутого теодолитного хода.
ошибка положения пункта вытянутого теодолитного хода.
Например:
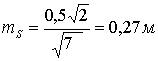
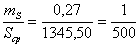
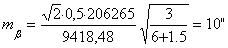
4. Преобразовав формулу профессора А.В. Гордеева для погрешности
продолжения конечной точки вытянутого теодолитного хода с примерно равными
сторонами для оценки положения точки расположенной в наиболее слабом месте хода
- его середине, находят необходимую точность построения пункта в слабом месте
теодолитного хода:
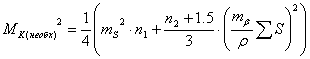 (86),
(86),
где
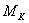 необходимая точность построения пункта в слабом месте
теодолитного хода,
необходимая точность построения пункта в слабом месте
теодолитного хода, 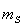 необходимая точность линейных построений,
необходимая точность линейных построений, 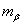 необходимая точность построений углов,
необходимая точность построений углов, 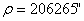 ,
, 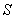 проектные
расстояния,
проектные
расстояния, 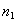 число сторон в ходе,
число сторон в ходе, 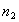 число
измеренных углов в ходе.
число
измеренных углов в ходе.
Например:
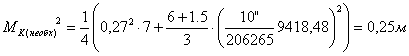
5. Исходя из установленной необходимой точности угловых и линейных
построений, для построения теодолитного хода можно применить следующие приборы:
прибор для линейно-угловых измерений соответствующий угловой точности в 5” и
прибор соответствующий линейной точности 1/50000. Например: электронный
тахеометр Nikon 352W, Trimble
M3 для угловых измерений и линейных
измерений.
. Устанавливается ожидаемая точность построения пункта в слабом
месте теодолитного хода.
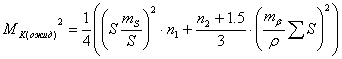 (87),
(87),
где
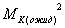 ожидаемая ошибка положения пункта в слабом месте
теодолитного хода,
ожидаемая ошибка положения пункта в слабом месте
теодолитного хода, 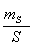 относительная линейная погрешность прибора,
относительная линейная погрешность прибора, 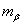 погрешность построения углов,
погрешность построения углов, 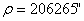 ,
, 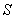 проектные
расстояния,
проектные
расстояния, 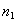 число сторон в ходе,
число сторон в ходе, 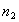 число
измеренных углов в ходе.
число
измеренных углов в ходе.
Например:
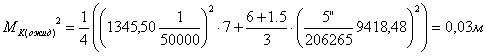
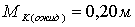
7. После чего сравнивают ожидаемую точность построений выбранным
прибором и допустимую, должно соблюдаться условие:
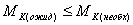 (88),
(88),
где
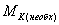 допустимая величина ошибки закрепления точек
теодолитного хода на местности,
допустимая величина ошибки закрепления точек
теодолитного хода на местности, 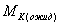 ожидаемая
точность построений.
ожидаемая
точность построений.
Например:
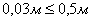
8. Составляют разбивочный чертеж.
Например:
Приложение И.
Вывод: условие 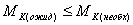 соблюдается
соблюдается
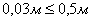 , следовательно, можно применить следующие приборы:
прибор для линейно-угловых измерений соответствующий угловой точности в 5” и
прибор соответствующий линейной точности 1/50000. Например: электронный
тахеометр Nikon 352W, Trimble M3 для угловых измерений и
линейных измерений.
, следовательно, можно применить следующие приборы:
прибор для линейно-угловых измерений соответствующий угловой точности в 5” и
прибор соответствующий линейной точности 1/50000. Например: электронный
тахеометр Nikon 352W, Trimble M3 для угловых измерений и
линейных измерений.
ЗАКЛЮЧЕНИЕ
В
заключении следует отметить, что:
· Для восстановления ОМС и других пунктов удобно применять как
способ полярных координат, так и линейную засечку. В определенных случаях
применять обратную засечку, наиболее целесообразно. Все зависит от обстановки,
имеющихся приборов, местности и густоты ОМС.
· Способы прямой угловой засечки и способ полярных координат
дают примерно одинаковую точность.
· Если необходимо вынести пункты ОМС на довольно длинном
расстоянии между известными пунктами, то целесообразно применять способ
проложения теодолитного хода.
· В связи с возможностями применения ПК при проектировании
границ участков, самым быстрым является графомеханический способ, недостатком
его является, то, что он не дает абсолютную точность.
· Для получения абсолютной точности проектирования границ
участков целесообразно применять аналитические способы проектирования, такие
как: способ трапеции, способ треугольника, комбинированный способ.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Маслов,
А.В. Геодезические работы при землеустройстве: учебник, А.В. Маслов, А.Г.
Юнусов, Г.И. Горохов.- М.: Недра, 1990.-215 с.
2. Методические
указания к выполнению курсового проекта по дисциплине "Геодезические
работы в землеустройстве и земельном кадастре", доценты Уваров А.И.,
Седышев М.Е., ст. преподаватели Васяева Е.Н., Хлынцева Е.О.
. Инструкция
по межеванию земельных участков. - М.: Росземкадастр, 2002. - 29с.