Основы теории электрических цепей
Еще
Министерство Образования Российской Федерации
Хабаровский
Государственный Технический Университет
Курсовая работа
по
дисциплине: Основы теории электрических цепей
Хабаровск,
2004
Часть I. Анализ цепи во временной области методом переменных состояния при
постоянных воздействиях
.1 Составить уравнения состояния цепи для t 0
.2 Найти точные решения уравнений состояния
.3 Найти решения уравнений состояния, используя по выбору студента один
из численных методов. Вид решаемых уравнений:

.4 Построить точные и численные решения уравнений состояния, совместив их
попарно на одном графике для каждой из переменных состояния
Схема соответствующая варианту 23, имеет вид:
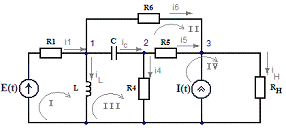
Рис.
1.1
(t) = const = E = 5 В.(t) = I*1(t) =
1*1(t) А.
1.1 Составить уравнения состояния цепи для t 0
Для составления уравнений воспользуемся 1-м и 2-м законом Кирхгофа.
Произвольным образом выберем и обозначим на схеме (рис. 1.1.) направления токов
и направления обхода контуров.
Определим количество уравнений, которое необходимо составить по 1-му и
2-му законам Кирхгофа:
· Количество уравнений по 1-му закону Кирхгофа:
Количество узлов в схеме минус один
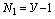
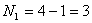
· Количество
уравнений по 2-му закону Кирхгофа:
Количество ветвей в схеме минус количество уравнений, составленных по
1-му закону Кирхгофа минус один
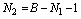
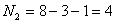
Составим уравнения по 1-му закону Кирхгофа для узлов 1, 2, 3 (обозначены
на рис. 1.1):
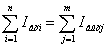
алгебраическая
сумма токов, входящих в узел равна алгебраической сумме токов, выходящих из
данного узла.
Для
узла 1:
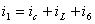
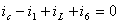
Для
узла 2:
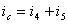
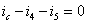
Для
узла 3:
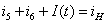
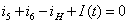
Составим
уравнения по 2-му закону Кирхгофа для контуров I, II, III, IV
(обозначены на рис. 1.1):
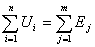
алгебраическая
сумма напряжений в контуре равна сумме ЭДС в данном контуре.
Для
контура I:
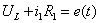
Для
контура II:
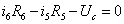
Для
контура III:
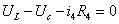
Для
контура IV:
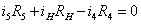
Таким
образом, получаем систему из 7 уравнений:
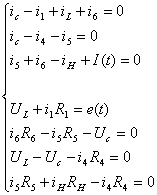
1.2 Найти точные решения уравнений состояния
Определим независимые начальные условия для исследуемой электрической
цепи.
Моменту времени до коммутации (отсутствует источник тока, катушка
вырождается в провод, на месте конденсатора - обрыв соединения, так как
протекает постоянный ток; источник тока играет роль ключа: I(t)=1*1(t) )
соответствует схема:
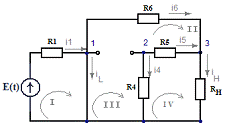
Используя 1-ый и 2-ой законы Кирхгофа, составим систему уравнений для
вышеуказанной схемы (направление обхода контура выберем в соответствии c движением часовой стрелки):
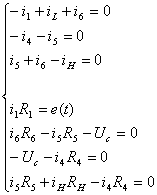
Все
токи, напряжения соответствуют моменту времени до коммутации.
Найдем
iL(0), UC(0):
Выразим
из 1-го уравнения 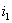 :
:
.
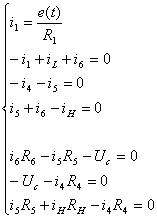
Подставим
полученное выражение для 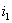 в другие уравнения системы:
в другие уравнения системы:
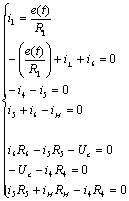
Выразим
из 2-го уравнения 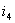 :
:
.
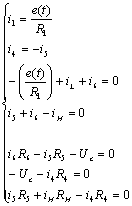
Подставим
полученное выражение для 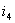 в другие уравнения системы:
в другие уравнения системы:
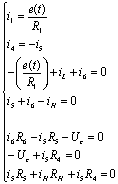
Выразим
из 3-го уравнения 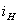 :
:
.
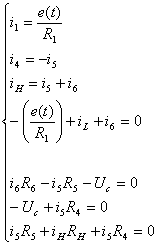
Подставим
полученное выражение для 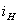 в другие уравнения системы:
в другие уравнения системы:
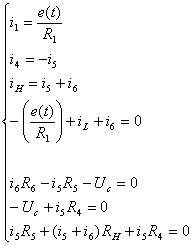
.
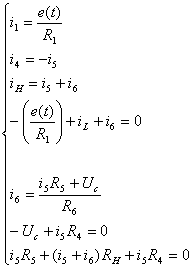
Подставим
полученное выражение для 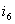 в другие уравнения системы:
в другие уравнения системы:
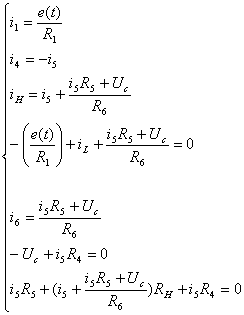
Выразим
из 6-го уравнения 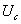 :
:
.
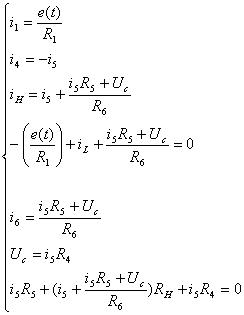
Подставим
полученное выражение для 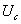 в другие уравнения системы:
в другие уравнения системы:
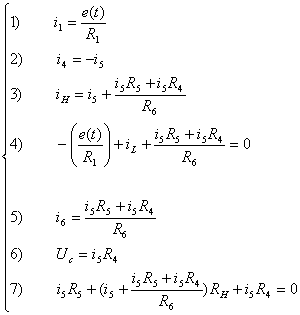
Из
последнего уравнения в системе находим, что 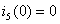 (А).
(А).
Используя
6-ое уравнение из полученной системы, найдем 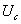 :
:
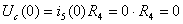 (В).
(В).
Используя
4-ое уравнение, найдем 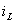 :
:
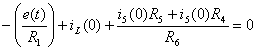
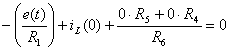
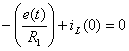 , Þ
, Þ 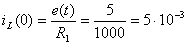 (А).
(А).
Откуда
находим:
iL(0) = e(t)/R1=E/R1=5/1000=5*10-3
А.
UC(0) = 0 В.
Таким
образом, получаем матрицу независимых начальных условий:
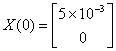
Составим уравнения состояния.
Используем ранее составленную систему уравнений (радел 1.1. данной
курсовой работы):
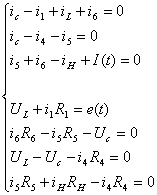
Следуя
методу переменных состояния, перепишем систему в дифференциальном виде. Для C
элемента запишем ЗТК (закон токов Кирхгофа - 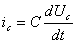 ), для L
элемента ЗНК (закон напряжений Кирхгофа -
), для L
элемента ЗНК (закон напряжений Кирхгофа - 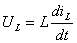 ).
).
Полученная система имеет вид:
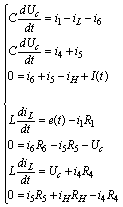
Получим
из данной системы дифференциальные уравнения (относительно дифференциалов 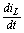 и
и 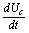 )
сведенные к нормальной форме Коши:
)
сведенные к нормальной форме Коши:
Запишем
систему в виде, в котором она была записана изначально, что позволит более
наглядно производить подстановки:
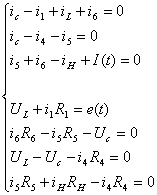
Фактически,
требуется выразить все переменные величины данной системы (за исключением
переменных состояния) через переменные состояния.
.
2.
.
4.
5.
|
Выразим 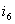
|
|
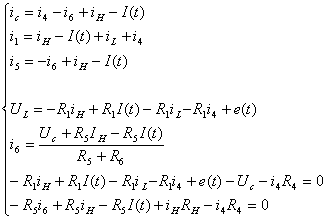
|
|
Подставим 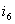 в остальные уравнения в остальные уравнения
|
6.
|
Выразим 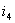
|
|
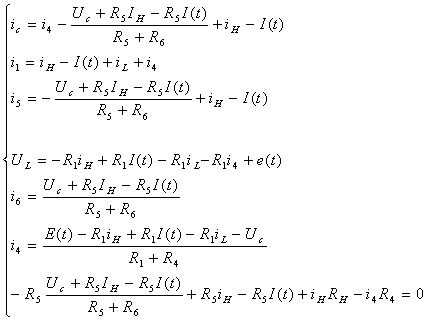
|
|
Подставим 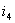 в остальные уравнения в остальные уравнения
|
|
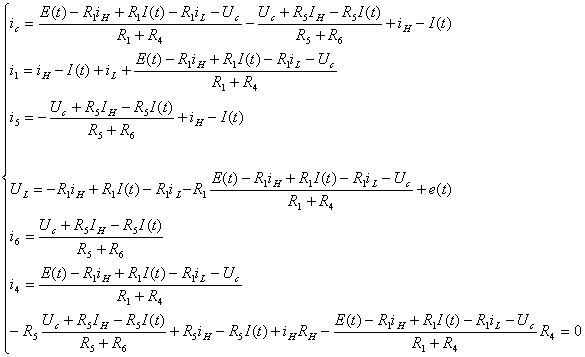
|
7.
|
Выразим 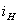
|
|
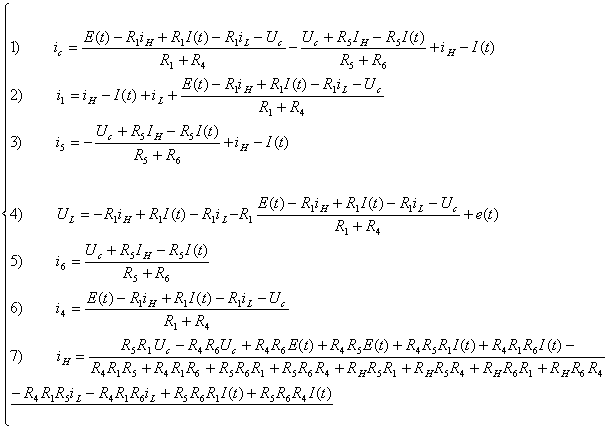
|
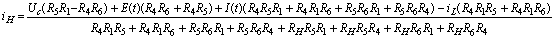
Подставим
полученное выражение для 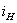 в уравнения 1 и 4. Таким образом, выразим
в уравнения 1 и 4. Таким образом, выразим 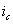 и
и 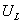 через
через 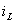 и
и 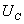 :
:
.
Выразим 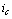 :
:
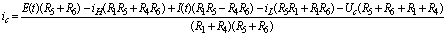
После
подстановки в данное выражение 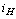 и
упрощения, получаем:
и
упрощения, получаем:
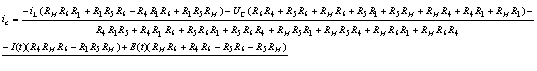

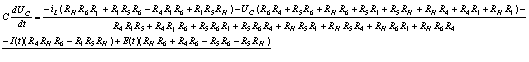
Подставим
численные значения сопротивлений:
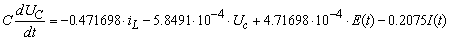
.
Выразим 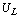 :
:
UL=
После
подстановки в данное выражение 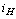 и
упрощения, получаем:
и
упрощения, получаем:
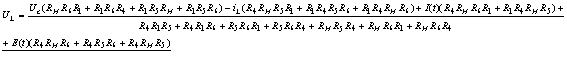
Подставим
численные значения сопротивлений:
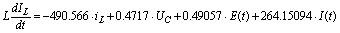
Таким
образом, получим 2 уравнения:
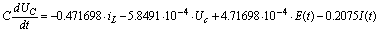
Откуда
получаем уравнения состояния:
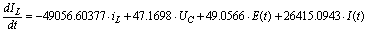
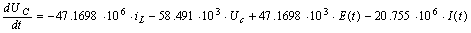
Запишем
полученные уравнения в матричной форме вида:
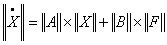
Где
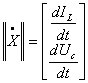 (Заметим,
что число элементов данной матрицы равно числу реактивных элементов в
исследуемой электрической цепи),
(Заметим,
что число элементов данной матрицы равно числу реактивных элементов в
исследуемой электрической цепи),
матрица соединений, которая содержит элементы, связывающие iL, UC,
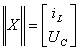 ,
,
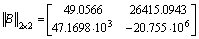 ,
,
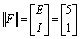 (из
условия)
(из
условия)
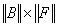 -
матрица, учитывающая внешние источники.
-
матрица, учитывающая внешние источники.
Таким
образом, получаем:
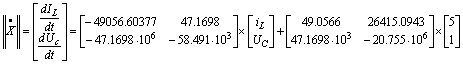
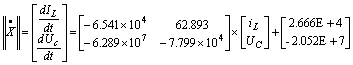
Записываем
решение для переменных состояния через экспоненциальную матричную функцию:
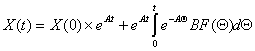
Так
как, в нашем случае, матрица F = const, то вид уравнения упрощается:
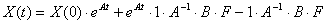
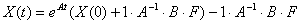
Найдем
собственные значения матрицы A:
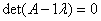
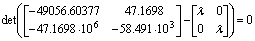
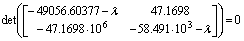
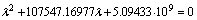
Откуда
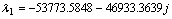
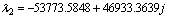
Разложим
экспоненциальную матричную функцию в ряд Тейлора:
Число
элементов разложения равно числу переменных состояния (=2).
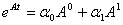
Находим
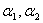 через найденные выше собственные значения:
через найденные выше собственные значения:
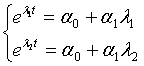
Откуда
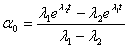
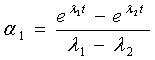
С
учетом 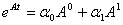 , получим:
, получим:
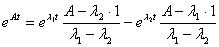 ;
;
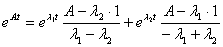
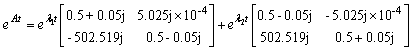
Получаем
функции состояния:
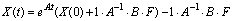
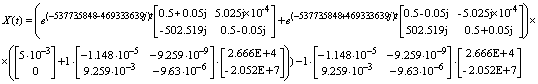
В
результате перемножения матриц и упрощения полученных зависимостей получим:

1.3
Найти решения уравнений состояния, используя по выбору студента один из численных
методов
Вид
решаемых уравнений:

Для
решения этих дифференциальных уравнений воспользуемся методом Эйлера с числом
шагов 15. Алгоритм расчета по этому методу для данного случая выглядит
следующим образом:
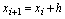 ;
;
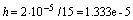
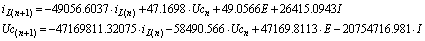
Первые
значения можем рассчитать, используя независимы начальные условия:
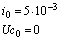
Таким
образом, найдем численное решение:
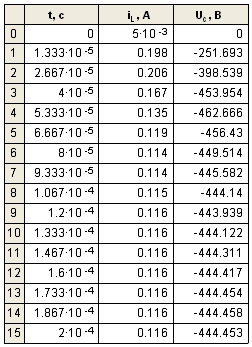
1.4 Построить точные и численные решения уравнений состояния,
совместив их попарно на одном графике для каждой из переменных состояния
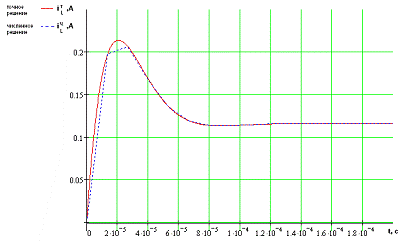
Рис. 1.1 Графики зависимости тока на катушке от времени.
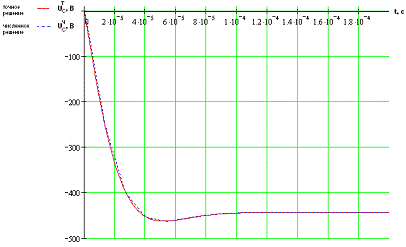
Рис. 1.2 Графики зависимости напряжения на конденсаторе от времени.
2. Анализ цепи операторным методом при апериодическом
воздействии
Требуется:
.1 Определить функцию передачи:
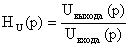
Символом
p обозначен оператор Лапласа.
.2
Найти нули и полюсы функции передачи и нанести их на плоскость комплексной
частоты.
.3
Найти переходную и импульсную характеристики для выходного напряжения.
.4
Определить изображение по Лапласу входного импульса.
.5
Найти напряжение на выходе цепи, используя HU(p).
.6
Построить на графике переходную и импульсную характеристики цепи, входной и
выходной сигналы.
Исследуемая
схема имеет вид:
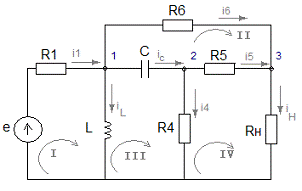
2.1
Определить функцию передачи
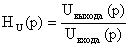
В
соответствии с законами Кирхгофа, составим уравнения для данной схемы:
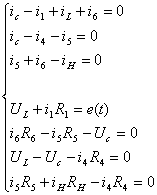
Запишем
систему в операторном виде, произведя следующие замены:
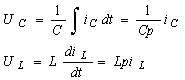
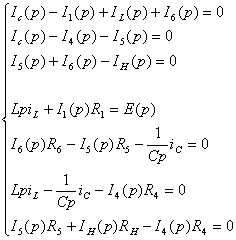
Определим
функцию передачи.
Передаточные
(системные) функции цепи могут быть определены как отношение выходной величины
ко входной. В зависимости от того какие величины входят в определение
передаточной функции различают: передаточные функции по напряжению, по току,
передаточные сопротивления и проводимости. Функция передачи по току может быть
представлена в виде: HU (p) = UН (p)/Uвх(p), где UН (p) и Uвх(p)
операторные изображения выходного и входного сигналов, соответственно.
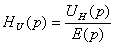 , где
, где 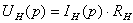
Из
составленной выше системы найдем ток 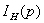 :
:
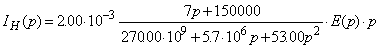
Тогда:
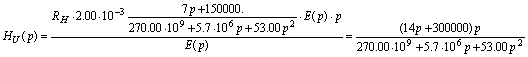
2.2
Найти нули и полюсы функции передачи и нанести их на плоскость комплексной
частоты
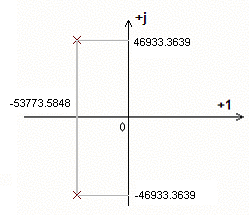
Нули:
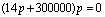
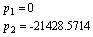
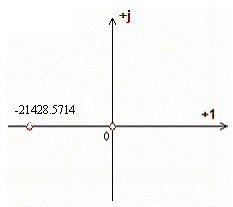
Полюса:
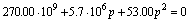
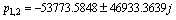
|
нули функции передачи
|
полюса функции передачи
|
|
|
|
Нетрудно заметить, что полюсы передаточной функции p1,2 совпадают с
собственными значениями, 2матрицы A. Это может быть дополнительным способом
проверки правильности нахождения передаточной функции цепи. Наиболее наглядным
способом охарактеризовать передаточную функцию является графическое
расположение ее полюсов и нулей на комплексной плоскости, называемое диаграммой
полюсов-нулей. Тип используемых элементов, а также структура цепи ограничивают
области комплексной плоскости в которых могут располагаться нули и полюсы. В
линейной пассивной цепи с потерями (с резистивными элементами) полюсы
передаточной функции лежат в левой полуплоскости. Только при этом условии
свободные составляющие токов и напряжений затухают. При отсутствии потерь
(резистивных элементов) все корни знаменателя будут чисто мнимыми. Нули
передаточной функции, корни числителя, при учете потерь могут располагаться в
любой части комплексной плоскости. Их положение не связано с характером изменения
во времени свободных составляющих токов и напряжений. Отсутствие нулей
передаточной функции на мнимой оси физически означает, что при любой частоте
гармонического напряжения на входе цепи на выходе будет какое-то напряжение.
При отсутствии резистивных элементов все корни числителя передаточной функции
(так же как и знаменателя) находятся на мнимой оси. Передаточные функции,
полюса которых не лежат в правой полуплоскости комплексной плоскости,
называются устойчивыми.
Знание передаточной функции цепи HU (p) позволяет определить переходную h1(t) и импульсную
h(t)характеристики цепи.
2.3 Найти переходную и импульсную характеристики для
выходного напряжения
Переходная характеристика цепи представляет собой реакцию цепи на
воздействие единичной ступенчатой функции (функции Хэвисайда 1(t), функции
включения) и может быть найдена как обратное преобразование Лапласа от HU (p)/p:
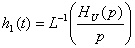
Переходная
характеристика введена в основном по двум причинам:
1. Если определена данная характеристика, то возможно определить
реакцию системы при любой форме внешнего воздействия (посредством интеграла
Дюамеля).
2. Единичное ступенчатое воздействие скачкообразное, и поэтому
является “тяжелым” для любой системы. Следовательно знать реакцию системы
именно при таком воздействии. Иные, более плавные, воздействия будут для
системы “легче”.
Обратное преобразование Лапласа проводим, используя теорему о разложении:
Если изображение функции представляет собой правильную дробь, числитель и
знаменатель которой представлены в полиномиальном виде, то переход к функции
времени производится по формуле:
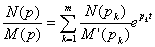 ,
,
где
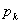 - корни уравнения M(p)=0
- корни уравнения M(p)=0
Обратное
преобразование Лапласа в результате дает следующую зависимость:
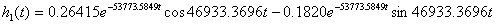
(Данное
выражение легко может быть проверено на крайних точках временного интервала
(при 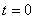 и
и 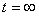 ):
):
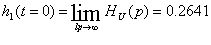 )
)
Импульсная
характеристика:
Импульсная
характеристика цепи h(t)представляет собой реакцию цепи на
воздействие единичной импульсной функции t) и может быть
найдена как обратное преобразование Лапласа от передаточной функции:

Дельта
функция (или функция Дирака) определяется как 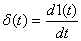 и
представляет собой предельный случай импульса очень большого значения и очень
малой продолжительности, когда его длительность стремится к нулю, но площадь
остается равной единице:
и
представляет собой предельный случай импульса очень большого значения и очень
малой продолжительности, когда его длительность стремится к нулю, но площадь
остается равной единице:
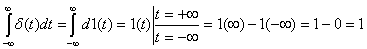
Обратное
преобразование Лапласа в результате дает следующую зависимость:
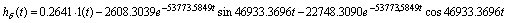
2.4
Определить изображение по Лапласу входного импульса
Запишем
зависимость входного напряжения от времени для указанной в условии формы
сигнала:
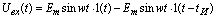
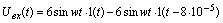
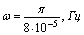
Или
в операторном виде:
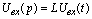
Преобразование
Лапласа для 1-ой части выражения табличное:
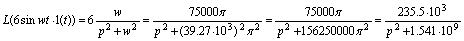
для
второй части распишем:
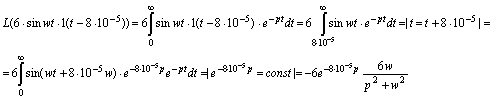
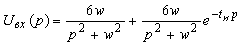
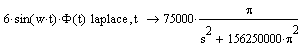
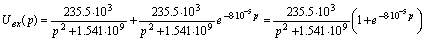
Найденная
зависимость потребуется при нахождении напряжения на выходе цепи.
2.5
Найти напряжение на выходе цепи, используя HU(p)
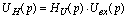
Так
как нас интересует временная зависимость напряжения на выходе цепи, используем
для ее нахождения обратное преобразование Лапласа:
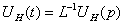
Обратное
преобразование Лапласа в результате дает следующую зависимость:


2.6
Построить на графике переходную и импульсную характеристики цепи, входной и
выходной сигналы
цепь уравнение импульс воздействие
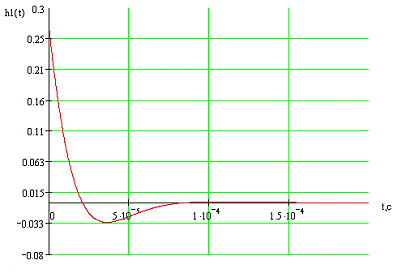
Рис.
2.1 Переходная характеристика
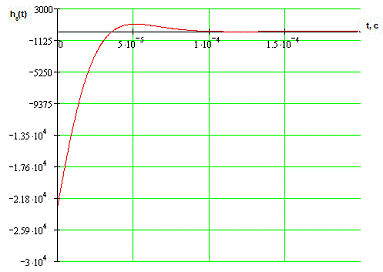
Рис.
2.2 Импульсная характеристика
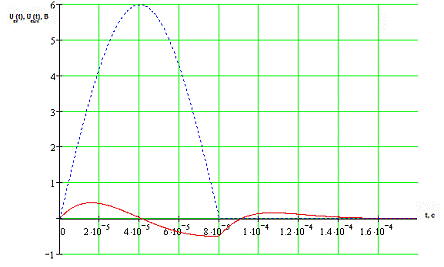
Рис.
2.3 Входное и выходное напряжения
Часть 3.
Анализ цепи частотным методом при апериодическом воздействии
Требуется:
3.1 Найти
и построить амплитудно-фазовую (АФХ), амплитудно-частотную (АЧХ) и фазо-частотную
(ФЧХ) характеристики функции передачи HU(jww).
.2 Определить
полосу пропускания цепи по уровню 0,707 |H(jww)|макс.
.3 Найти
и построить амплитудный и фазовый спектры входного сигнала. Определить ширину
спектра входного сигнала по уровню 0,1|U(jww)|макс.
.4 Сопоставляя
спектры входного сигнала с частотными характеристиками цепи, дать
предварительные заключения об ожидаемых искажениях сигнала на выходе цепи.
Сверить эти качественные оценки с сигналом на выходе, полученным в п. 2.5.
.5 Найти
и построить амплитудный и фазовый спектры выходного сигнала.
Определить выходной сигнал по вещественной или мнимой частотной
характеристике, используя приближённый метод Гиллемина.
Параметры для данного варианта:
3.1 Найти
и построить амплитудно-фазовую (АФХ), амплитудно-частотную (АЧХ) и
фазо-частотную (ФЧХ) характеристики функции передачи HU(jww)
Для анализа цепи используем ранее полученную функцию передачи
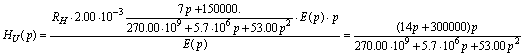
Для
исследования частотных характеристик воспользуемся тем фактом, что необходимое
нам преобразование Фурье есть частный случай преобразования Лапласа, когда
действительная часть оператора Лапласа 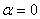 , т.е.
, т.е. 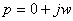 . Таким образом, необходимо произвести подстановку в
функцию передачи p=jw:
. Таким образом, необходимо произвести подстановку в
функцию передачи p=jw:
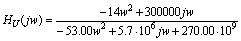
Амплитудно-частотная
характеристика (АЧХ) является одной из самых важных характеристик любой цепи и
позволяет исследовать искажения вносимые цепью в спектр входного сигнала.
Наличие частотно - зависимых элементов (L и C) в исследуемой цепи приводит к
неравномерному изменению составляющих спектра входного сигнала. Наиболее простой
способ получения АЧХ цепи - это замена в выражении для HU (p)
операторной переменной p на мнимую частоту jw и нахождение модуля полученной
комплексной функции частоты: |HU(jw)|.
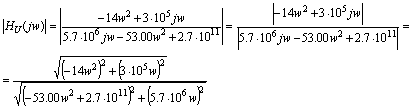
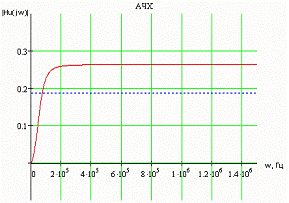
Рис.
3.1 АЧХ схемы
ФЧХ
схемы определяется как аргумент передаточной функции при w=0..∞
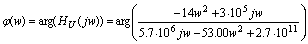
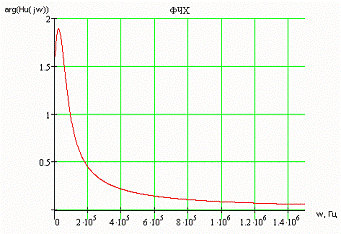
Рис.
3.2 ФЧХ схемы
Амплитуднофазочастотная
характеристика цепи (годограф) связывает воедино изменение коэффициента
передачи (в нашем случае, по напряжению - |HU(jw)| и
фазового сдвига между выходным и входным напряжением во всем диапазоне частот.
Годограф включает сведения которые содержатся как в АЧХ, так и в ФЧХ.
Годограф
является параметрической кривой, параметром которой является частота w.
Длина вектора, проведенного из начала координат к какой- либо точке годографа
соответствует абсолютному значению передаточной функции на этой частоте |HU(jw)|,
а угол между ним и положительным направлением вещественной оси - аргументу
передаточной функции arg(HU(jw)). На рис. 3.3. представлен годограф для
рассматриваемой цепи. Нулевой частоте соответствует точка с координатой 0 на
вещественной оси, очень большой (в пределе бесконечной) частоте соответствует
точка с координатой 0.2641 на вещественной оси. На этих граничных частотах
влияние реактивных элементов на фазовый сдвиг отсутствует.
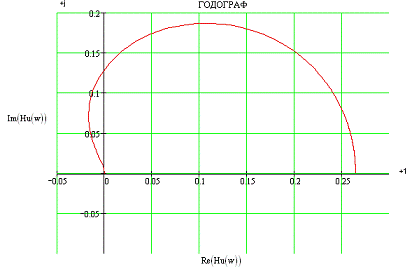
Рис.
3.3 АФХ цепи
3.2
Определить полосу пропускания цепи по уровню 0,707 |H(jw)|макс
По
построенной характеристике может быть определена полоса пропускания. Полосой
пропускания цепи называют диапазон частот для которых коэффициент передачи не
более чем в 2 отличается от его максимального значения. Это же соответствует
снижению уровня сигнала на 3 дБ. Для рассматриваемой цепи максимальное значение
передаточной функции составляет |HU(jw)|max = 0.2641.
Границе полосы пропускания соответствует значение передаточной функции |HU(jw)|max/2
= 0.707|HU(jw)|max =0.187. Это значение достигается на частоте w=73097.7126
Гц. Таким образом полоса пропускания равна w=[73097.7126,∞].Если
основные гармоники сигнала лежат в этой полосе частот, то не происходит
искажения формы сигнала.
3.3
Найти и построить амплитудный и фазовый спектры входного сигнала. Определить
ширину спектра входного сигнала по уровню 0,1|U(jw)|макс
АЧХ
входного сигнала находится как модуль от спектральной характеристики U(jw),
которую получаем на основе ранее найденного изображения сигнала.
Для
исследования частотных характеристик воспользуемся тем фактом, что необходимое
нам преобразование Фурье есть частный случай преобразования Лапласа, когда
действительная часть оператора Лапласа 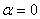 , т.е.
, т.е. 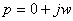 .
.
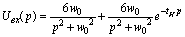 ;
;
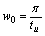
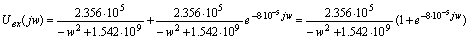
Построим
амплитудно-частотную характеристику входного сигнала 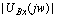 .
.
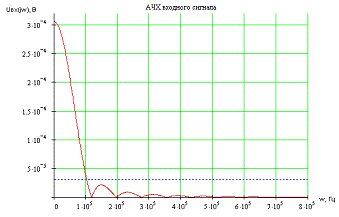
Рис.
3.4 АЧХ входного сигнала
Определяя
по уровню 0,1|U(jw)|макс. ширину спектра, получим w=1.056*105
с-1
Ограничивая
спектр сигнала определенной по уровню 0,1|U(jw)|макс.
шириной спектра w, мы учитываем Ww/Wt) · 100%
96от полной энергии Wt сигнала. Это следует из использования
теоремы Рейли для расчета данного отношения(
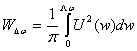
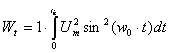 ) ).
) ).
Эта
информация может быть полезной, например, для выбора полосы пропускания
фильтра.
ФЧХ
входного сигнала определяется как аргумент от спектральной характеристики:
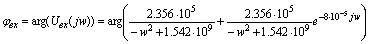
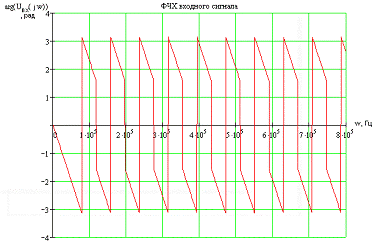
Рис.
3.5 ФЧХ входного сигнала.
3.4
Найти и построить амплитудный и фазовый спектры выходного сигнала
Используя
известную функцию передачи можем найти АЧХ и ФЧХ выходного сигнала.
АЧХ
входного сигнала находится как модуль от спектральной характеристики U(jw),
умноженный на модуль функции передачи
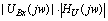
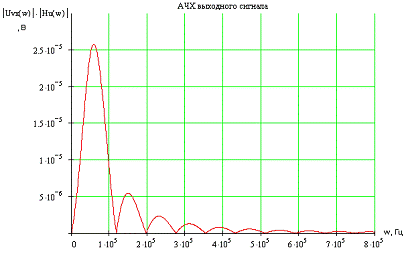
Рис.
3.6 АЧХ выходного сигнала.
ФЧХ
входного сигнала находится как сумма аргументов спектральной характеристики U(jw),
и функции передачи 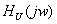 .
.
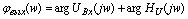
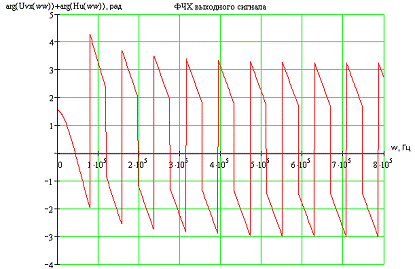
Рис.
3.7 ФЧХ выходного сигнала
3.5
Определить выходной сигнал по вещественной или мнимой частотной характеристике,
используя приближённый метод Гиллемина
Метод
Гиллемина является одним из методов позволяющих восстановить функцию времени
(какой - либо сигнал) по известной вещественной (или мнимой) частотной
характеристике. Метод основан на такой аппроксимации, когда аппроксимирующая
частотную характеристику функция либо ее производные состоят из
последовательности бесконечно коротких импульсов. Последовательность бесконечно
коротких импульсов представляет собой заданную функцию в так называемой
квантованной форме. Погрешность метода преимущественно связана со ступенчатым
характером аппроксимирующей функции. Уменьшение этой погрешности требует
увеличения общего числа членов в аппроксимации. Исходная частотная
характеристика аппроксимируется кусочнолинейным образом, после чего два
последовательных дифференцирования позволяют свести аппроксимирующую функцию к
последовательности бесконечно коротких импульсов. Окончательное выражение для
искомой функции времени f(t) полученной по мнимой частотной характеристике имеет
вид:
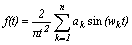
Здесь
ak - величины бесконечно коротких импульсов, wk -
координаты импульсов на частотной оси.
Мнимая
частотная характеристика Gн(w) может быть определена как:
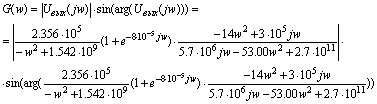
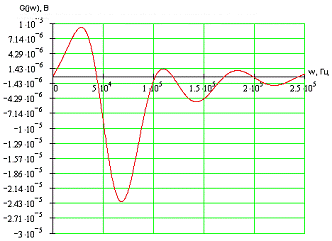
Интерполируем
полученную зависимость, взяв количество разбиений равным 20.
Диапазон
частот ограничим величиной примерно равной ширине спектра - 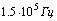 .
.
Тогда
интервал разбиений равен 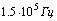 /20 =
/20 = 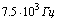
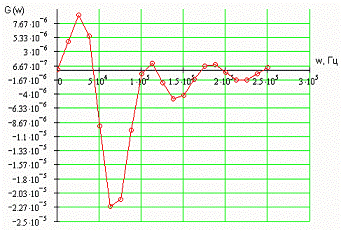
Рис.
3.8 Интерполированная зависимость
Найдем
производные первого порядка в точках разбиения и построим полученную
зависимость на графике.
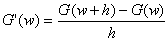
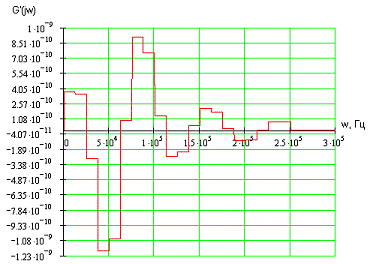
Рис.
3.8 График первой производной
Найдем
производные первого порядка в точках разбиения и построим полученную
зависимость на графике.
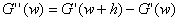
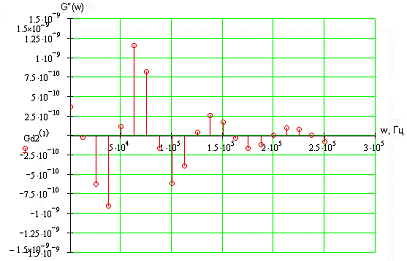
Рис.
3.8 График второй производной
Для
определения выходной зависимости напряжения от времени, на основе полученных
данных, воспользуемся формулой
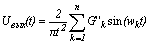
Здесь
G’’k - величины бесконечно коротких импульсов, wk -
координаты импульсов на частотной оси.
Восстановленная
временная зависимость имеет вид:
4.
Анализ цепи частотным методом при периодическом воздействии
Требуется:
.1
Разложить в ряд Фурье заданную периодическую последовательность импульсов и
построить её амплитудный и фазовый спектры.
4.2 Построить на одном графике заданную периодическую последовательность
импульсов и её аппроксимацию отрезком ряда Фурье, число гармоник которого
определяется шириной амплитудного спектра входного сигнала, найденной в п.
2.3.3.
.3 Используя рассчитанные в п. 2.3.1 АЧХ и ФЧХ функции передачи цепи,
определить напряжение или ток на выходе цепи в виде отрезка ряда Фурье.
.4 Построить напряжение или ток на выходе цепи в виде суммы гармоник
найденного отрезка ряда Фурье. Графики по пп. 2.4.2 и 2.4.4 построить на одном
масштабе времени и разместить их на одном листе один под другим.
Данные задачи: Um = 6
В, tи = 8×10-5 c, T = 12×10-5 c.
4.1 Разложить в ряд Фурье заданную периодическую
последовательность импульсов и построить её амплитудный и фазовый спектры
Ряд Фурье периодической функции можно представить в виде:
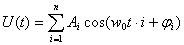
где
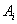 - амплитуда i-ой гармоники,
- амплитуда i-ой гармоники, 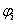 - начальная фаза.
- начальная фаза.
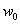 -
основная (главная) частота рассчитывается по формуле:
-
основная (главная) частота рассчитывается по формуле:
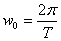 ,
,
T - период
сигнала;
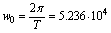 рад/с
рад/с
Далее,
в задании необходимо аппроксимировать входную и выходную зависимость,
количество гармоник, необходимых для аппроксимации выбираем исходя из того,
чтобы частоты этих гармоник помещались в ширину спектра, определенную в 3-ей
части.
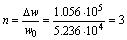 (с
учетом округления в большую сторону)
(с
учетом округления в большую сторону)
Для
нахождения амплитудных составляющих воспользуемся спектральной плотностью
сигнала, найденной в 3-ей части курсовой работы.
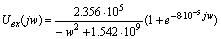
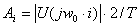
Для
нахождения фазы также воспользуемся ею:
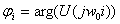
4.2 Построить на одном графике заданную периодическую
последовательность импульсов и её аппроксимацию отрезком ряда Фурье, число
гармоник которого определяется шириной амплитудного спектра входного сигнала,
найденной в п. 2.3.3
|
n
|
Ai
|
fi
|
|
0
|
2.546
|
0
|
|
1
|
 -2.0944 -2.0944
|
|
|
2
|
0.417
|
2.0944
|
|
3
|
0.34
|
3.1416
|
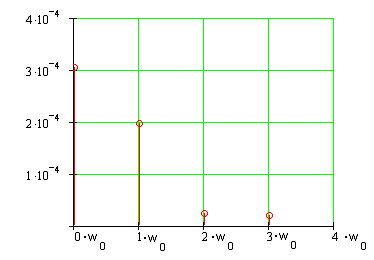
Рис. 4.1 Амплитудный спектр входного сигнала
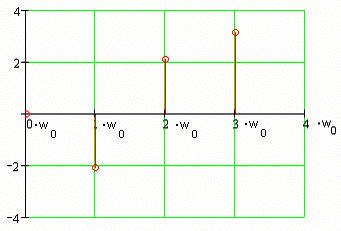
Рис. 4.2 Фазовый спектр входного сигнала
4.3 Используя рассчитанные в п. 2.3.1 АЧХ и ФЧХ функции
передачи цепи, определить напряжение или ток на выходе цепи в виде отрезка ряда
Фурье
Для определения амплитуд и фаз необходимых для аппроксимации выходного
сигнала отрезком ряда Фурье, используем функцию передачи, определенную во 2-ой
части курсовой работы.
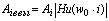
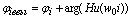
4.4
Построить напряжение или ток на выходе цепи в виде суммы гармоник найденного
отрезка ряда Фурье
Графики
по пп. 2.4.2 и 2.4.4 построить на одном масштабе времени и разместить их на
одном листе один под другим
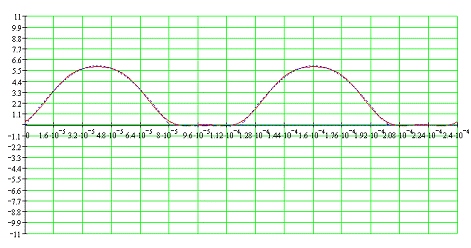
Рис
4.3 Входной сигнал и его аппроксимация рядом Фурье
Таким
образом по найденным коэффициентам и значениям начальных фаз, строим функцию
зависимости сигнала от времени:
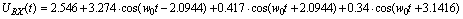
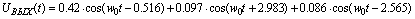
Вывод
В результате
выполнения курсовой работы были изучены и применены на практики некоторые
методы расчета электрических цепей. Методы, рассматриваемые в курсовой работе,
представляют собой 3 принципиально разных подхода к анализу электрических
цепей.
В первой
части курсовой работы был рассмотрен метод переменных состояния. В отличие от
классического метода расчета переходных процессов, метод переменных состояния
более формализован и больше подходит для программной реализации. Это связано с
тем, что, фактически, решение сводится к решению системы из N дифференциальных уравнений первого
порядка, где N - число реактивных элементов в цепи.
В классическом же методе приходится иметь дело с дифференциальными уравнениями
более высоких порядков (зависит от количества реактивных элементов в цепи), а
это увеличивает трудоемкость расчетов. Также следует отметить, что в методе
переменных состояния основные математические операции производятся в матричном
виде, что удобно при программной реализации данного метода, так как матричная
форма идеальна в плане представления данных на ЭВМ.
Вторая часть
курсовой представляет собой анализ цепи операторным методом при апериодическом
воздействии. Операторный метод наиболее прост в плане математических расчетов:
все операции дифференцирования и интегрирования заменяются на более простые
операции умножения и делении. Основная трудность заключается в нахождении
изображения и оригинала функции.
Третья часть
курсовой работы представляет собой анализ цепи частотным методом при
апериодическом воздействии. Данный метод широко распространен и почти всегда
используется при разработке реальных устройств. Это связано с тем, что он
позволяет проанализировать реакцию цепи на различные входные воздействия,
рассчитать или подобрать АЧХ и ФЧХ анализируемой цепи, что всегда необходимо
при разработке устройств с определенными параметрами.
В четвертой части
курсовой работы также используется частотный метод при периодическом
воздействии. Также в данной части работы рассмотрено использование ряда Фурье
для аппроксимации входного и выходного сигналов. Аппроксимация такого вида
часто встречается в реальных расчетах, связанных с анализом электрических
цепей. Также следует отметить, что представление ряда Фурье на ЭВМ при
программной реализации достаточно просто организовать.
Таким
образом, в курсовой работе были использованы основные современные методы расчета
и анализа электрических цепей.
Список
использованной литературы
1. Бессонов Л.А. Теоретические основы электротехники. - М.:
Высш. шк., 1996.
2. Кирьянов Д.В. Mathcad 11. - С.- П.: БХВ-Питербуг, 2003 г.
. Методические указания к выполнению курсовой работы
по курсу “Теоретическая электротехника”