|
C, В×с
|
wн, рад/c
|
w0, рад/c
|
Dwн, рад/c
|
Мн,
А×В×с
|
Кд1,
А×В×с2
|
Кд2,
1/А×В×c2
|
Тм,
с
|
Тэ,
с
|
Ком,
1/А×c
|
Кос,
В×c
|
|
0,643
|
314
|
342
|
55,989
|
5,787
|
0,103
|
9,675
|
0,406
|
0,102
|
0,864
|
0,032
|
3. Определение передаточных функций системы
При определении передаточной функции по управляющему
(задающему) воздействию, не учитывается возмущающее воздействие. Кроме того,
считаем, что фильтры и регуляторы отсутствуют, т.е.
ф1=Wф2=1 (3.1)
и
рп=Wрс=Wрм=1. (3.2)
Структурная схема системы при этом примет вид как на рисунке
3.
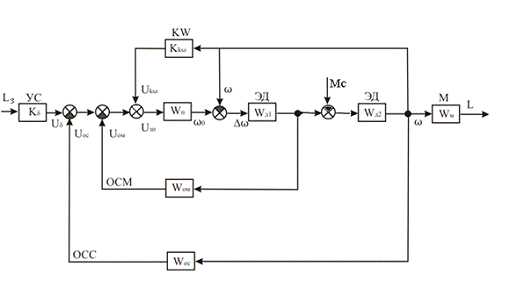
Рисунок 3 - Упрощенная структурная схема
Избавляемся от перекрестных связей и преобразуем схему к виду
более удобному для вычисления передаточной функции. Переносим узел справа через
звено Wd2 против хода сигнала. В результате приходим к схеме на рисунке 4.
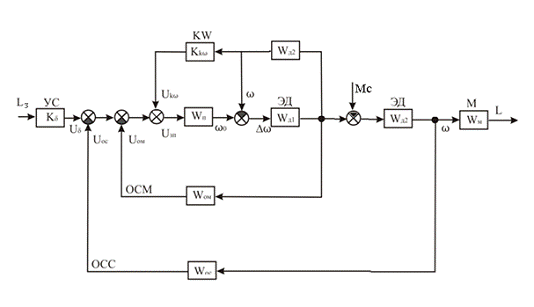
Рисунок 4 - Первое преобразование исходной схемы
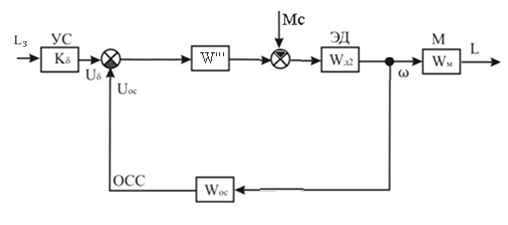
Избавляемся от обратных связей, упрощая схему, как
представлено на рисунке 5.
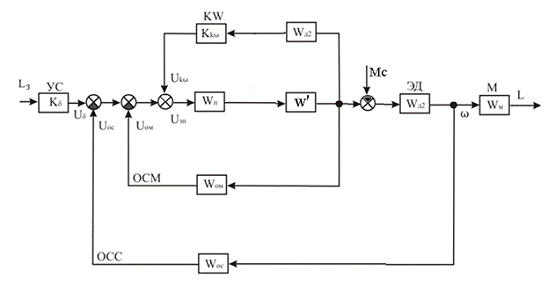
Рисунок 5 - Второе преобразование исходной схемы
Передаточная функция W’ будет равна
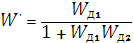
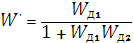 . (3.3)
. (3.3)
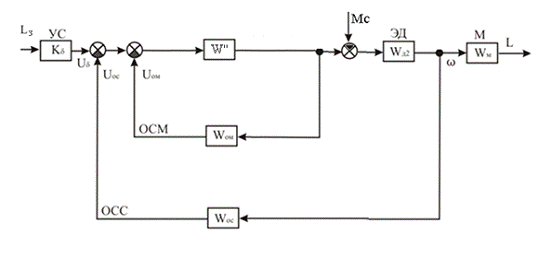
Рисунок 6 - Третье преобразование исходной схемы
Избавляемся от обратной связи ОСМ, как показано на рисунке 7.
4. Анализ системы на устойчивость
4.1 Проверка устойчивости системы методом Гурвица
Запишем характеристическое уравнение системы, приравняв нулю
полином знаменателя передаточной функции замкнутой системы по задающему
воздействию (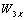 ):
): 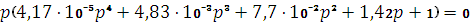
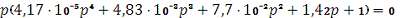 .
.
Один из корней уравнения p=0, следовательно, система находится на
границе устойчивости. Такое состояние системы называется критическим и
необходим дополнительный анализ.
Проверим устойчивость системы по критерию Гурвица.
Обозначим коэффициенты характеристического уравнения:0=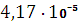
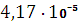 ;1=
;1=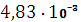
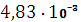 ;2=
;2=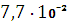
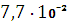 ;3=
;3=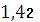
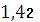 ;4=1.
;4=1.
Из уравнения видно, что все коэффициенты характеристического
уравнения положительны, а следовательно, выполняется необходимое условие
устойчивости системы.
Достаточным условием устойчивости системы является положительность
всех определителей Гурвица. Вычислим эти определители.
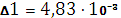
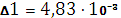 ;
;
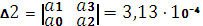
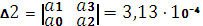 ;
;
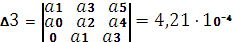
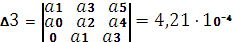 ;
;
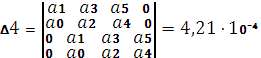
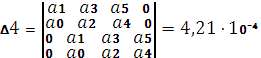 ;
;
Так как все определители Гурвица положительны, система устойчива.
4.2 Проверка устойчивости системы методом ЛАЧХ-ЛФЧХ
Наряду с алгебраическими критериями устойчивости систем используются
частотные критерии. К частотным критериям относятся критерии Михайлова и
Найквиста.
Исследуем устойчивость системы с помощью критерия Найквиста. Этот
критерий позволяет судить об устойчивости замкнутой системы по частотным
характеристикам разомкнутой системы. Так анализ можно провести с помощью ЛАЧХ и
ЛФЧХ характеристик.
Подставим в данное выражение формулы для передаточных функций
соответствующих блоков системы и окончательно получим
Построим ЛАЧХ и ЛФЧХ характеристики для полученной передаточной функции.
Полученные графики представлены на рисунке 8.
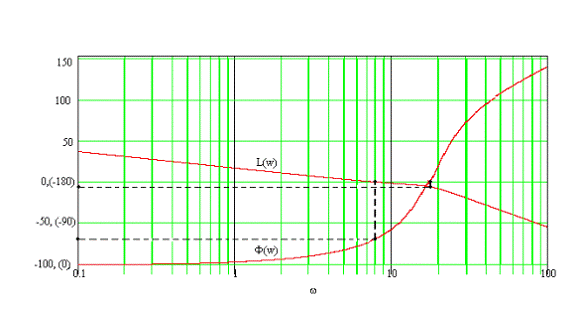
Рисунок 8 - ЛАЧХ и ЛФЧХ передаточной системы
ЛФЧХ пересекает линию j =00 при отрицательных
значениях асимптотической ЛАЧХ. Следовательно, замкнутая система устойчива.
Снимем с графиков величины запаса устойчивости по амплитуде и
по фазе:
запас по фазе составляет = 120 °,
запас по амплитуде = 10 Дб.
Определим быстродействие системы. Быстродействие системы равно
обратной величине частоты среза (частоты, на которой ЛАЧХ пересекает ось
нулевого усиления в децибелах): 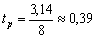 , tПП = 0,15 с; tp > tПП.
, tПП = 0,15 с; tp > tПП.
Т.к. tp > tПП, система требует
синтеза корректирующих устройств.
5. Оценка быстродействия системы. Граничный коэффициент усиления
5.1 Оценка быстродействия системы относительно заданного значения
Оценить соответствие переходных процессов заданным требованиям
можно по кривым переходных процессов, полученным экспериментально или
расчетном. Воспользуемся методом частотных характеристик. При этом время
переходных процессов в системе приближенно оцениваем с помощью выражения
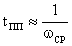 , (5.1)
, (5.1)
где 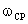 - частота среза ЛАЧХ.
- частота среза ЛАЧХ.
Частоту среза 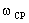 можно определить по графику ЛАЧХ, или, более точно, решая
уравнение
можно определить по графику ЛАЧХ, или, более точно, решая
уравнение
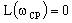 , (5.2)
, (5.2)
Получаем 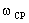 = 8 с-1, тогда время
переходных процессов
= 8 с-1, тогда время
переходных процессов
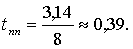 (5.3)
(5.3)
По заданию 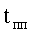 должно быть равным 0,15 с. Значит,
система не удовлетворяет этому условию.
должно быть равным 0,15 с. Значит,
система не удовлетворяет этому условию.
5.2 Определение граничного коэффициента усиления
Граничный коэффициент усиления вычисляется по формуле
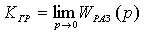 . (5.4)
. (5.4)
6. Синтез автоматизированной системы
6.1 Основные приемы оптимального синтеза структур систем автоматического
управления
В конечном итоге оптимизация систем автоматического управления
путем синтеза должна обеспечить наилучшие по качеству переходные процессы,
требуемое быстродействие и требуемые статические характеристики. Эта цель
всегда достигается при любой сложности оптимизируемой структуры, при любых
параметрах и показателях. Доказано, что динамика системы автоматического
управления будет наилучшей с требуемыми показателями качества и быстродействия
переходных процессов, если передаточную функцию синтезированной системы удается
привести к виду, описываемому выражениями:
для технического оптимума (ТО)
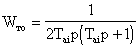 , (6.1)
, (6.1)
для симметричного оптимума (СО)
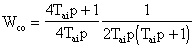 , (6.2)
, (6.2)
где
 ,
(6.3)
,
(6.3)
- номер синтезируемого контура;
Таi - эквивалентная постоянная времени синтезируемого
контура, не подлежащая компенсации (коррекции);
Та1 - расчетная эквивалентная постоянная времени внутреннего
(первого) контура системы автоматического управления, определяемая по заданному
быстродействию системы tпп:
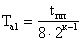 ,
(6.4)
,
(6.4)
где к - число синтезируемых контуров.
Обеспечить оптимальные передаточные функции (6.1) и (6.2) можно,
если в синтезируемом разомкнутом контуре убрать все постоянные времени,
превышающие в сумме значение Таi, и величину общего коэффициента
передачи контура заменить параметром 1/2Таi. Такая задача решается
включением в главный тракт контура специального звена последовательной
коррекции с необходимой передаточной функцией. Синтезируемая структура должна
быть одноконтурной с отрицательной единичной обратной связью, чтобы
передаточные функции с интегральными составляющими были для замкнутого контура
апериодическими. Если такой связи нет, то ее следует ввести. Например, при
указанной связи передаточная функция типа (6.1) станет равной
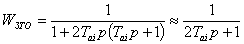 . (6.5)
. (6.5)
Кроме указанных главных принципов синтеза структуры с помощью
передаточных функций (6.1), (6.2) необходимо соблюдать дополнительные правила:
. В многоконтурной системе синтез ведется поконтурно от
внутреннего к последующему за ним внешнему (поочередно).
. Контур не должен содержать много звеньев интегрирующего и
дифференцирующего типов. Иначе это усложнит исполнение корректирующих звеньев.
Для упрощения многозвенного контура целесообразно выделять в нем дополнительные
внутренние контура за счет введения отрицательных связей, не предусмотренных в
системе по ее функциональному назначению.
. Корректирующие звенья (их называют регуляторами) должны иметь
стандартное исполнение из группы разработанного класса П, И, ПИ, Д, ПД, ПИД.
. Синтезируемый контур должен быть однолинейным.
. Эквивалентная некомпенсируемая постоянная времени Таi
внешнего синтезированного контура по отношению к такой же постоянной
внутреннего контура должна быть большей не менее чем в 2 раза по правилу (6.3).
Только в этом случае переходные процессы внутреннего контура заканчиваются до
начала переходных процессов во внешнем (динамически контура становятся
независимыми). Для быстродействующих систем нецелесообразно выполнять системы
автоматического управления с более, чем 4 контуров регулирования, так как
быстродействие его подчиняется правилу
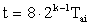 . (6.6)
. (6.6)
6.2 Синтез системы
Как было сказано выше, синтез ведётся поконтурно от внутреннего к
последующему за ним внешнему. Внутренний контур системы для данного варианта
имеет перекрестные связи, а согласно четвертому вышеназванному правилу
синтезируемый контур должен быть однолинейным. Для того чтобы исчезли
перекрестные связи произведем преобразования внутреннего контура и приведем его
к виду, показанному на рисунке 9.
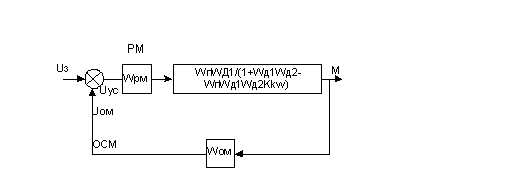
Рисунок 9 - Внутренний контур системы
Преобразуем контур к виду с единичной отрицательной обратной
связью как показано на рисунке 10.
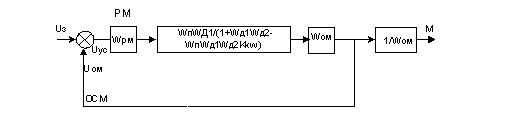
Рисунок 10 - Преобразованный внутренний контур системы
Чтобы контур был полезен системе, нужно наибольшую постоянную
времени свести до значения
Принимаем
а1=
Том, (6.8)
Для обеспечения контуру технического оптимума надлежит убрать из
его структуры все коэффициенты передачи, постоянные времени Тэ, Тп,
Том и ввести составляющую 1/2Та1p. Эта задача решается
вводом последовательного звена. Найдём передаточную функцию последовательного
корректирующего звена Wрм:
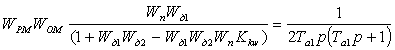 , (6.9)
, (6.9)
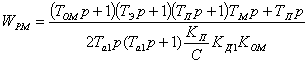 . (6.10)
. (6.10)
При Та1 равном Том получим
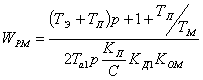 , (6.11)
, (6.11)
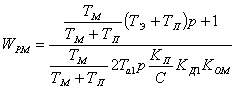 . (6.12)
. (6.12)
Такую передаточную функцию может обеспечить операционный усилитель
класса ПИ.
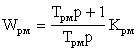 , (6.13)
, (6.13)
где
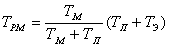 , (6.14)
, (6.14)
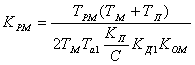 . (6.15)
. (6.15)
Внутренний контур синтезирован и представлен звеном Wk1.
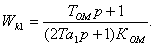 (6.16)
(6.16)
Для обеспечения контуру технического оптимума оставим составляющую
1/(2Та1p+1) и введём интегрирующую составляющую 1/4Та1.
Всё остальное убираем с помощью корректирующего последовательного звена,
передаточную функцию которого найдём так:
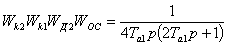 . (6.17)
. (6.17)
Отсюда
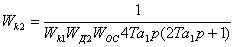 , (6.18)
, (6.18)
Выражение для Wк2 можно представить в виде
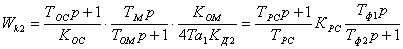 , (6.19)
, (6.19)
где
Трс=Тос;
(6.20)ф1=Тм;
(6.21)
Тф2=Том;
(6.22)
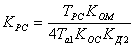 .
(6.23)
.
(6.23)
Таким образом, корректирующий блок Wк1 будет состоять
из последовательно включённых регулятора Wрс класса ПИ и фильтра 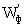 .
.
На рисунке 13 показано, что последние, внешние звенья не образуют
контур (нет цепи обратной связи), однако корректирующее звено необходимо, так
как действие звена Wм приводит к неустойчивости системы.
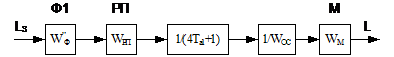
Рисунок 13 - Последнее преобразование
Так как цепь обратной связи отсутствует, передаточная функция
технического оптимума будет иметь вид: 1/(4Та1+1). Таким образом,
передаточную функцию корректирующего последовательного звена находим из
соотношения
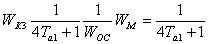 . (6.24)
. (6.24)
Отсюда
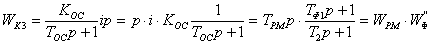 , (6.25)
, (6.25)
где
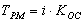 ; (6.26)ф1=0, (6.27)
; (6.26)ф1=0, (6.27)
Tф2= Tос.
Таким образом, корректирующий блок Wк2 будет состоять
из последовательно включённых регулятора Wрп класса Д и R-C фильтра 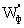 .
.
7. Расчет и построение динамических характеристик синтезированной
системы
После приведения системы к техническому оптимуму её передаточная
функция будет иметь вид:
синтез устойчивость
быстродействие гурвиц
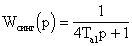 . (7.1)
. (7.1)
Как уже отмечалось выше, одним из способов построения переходных
процессов является аналитический вывод их функции. Воспользуемся этим методом.
Для этого достаточно взять обратное преобразование Лапласа от выражения
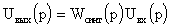 , (7.2)
, (7.2)
где Uвх(p) - отображение функции Хевисайда
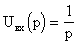 . (7.3)
. (7.3)
Получим
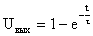 , (7.4)
, (7.4)
где t равно 0,035 -
постоянная времени системы.
Оценим качество переходных процессов представленных на рисунке
10.1. Как видно из графика система стала устойчивой, в ней нет перерегулирований.
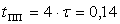 . (7.5)
. (7.5)
По заданию tпп должно быть равным 0,15 с. Видно, что
наша система удовлетворяет этому условию.
Таким образом, синтезированная система удовлетворяет всем
необходимым условиям и является конечным продуктом данной работы.
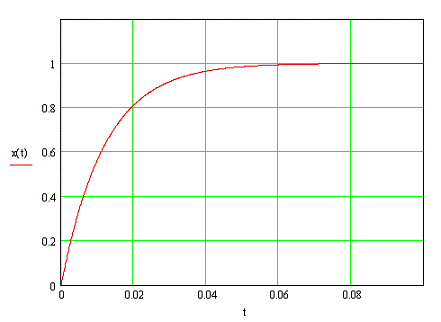
Рисунок 13 - Переходный процесс синтезированной системы
Заключение
В ходе выполнения курсового проекта был проведен анализ
автоматизированной электромеханической системы и выявлена устойчивость. Для
обеспечения требуемых динамических режимов была проведена оптимизация структуры
путем синтеза. В конечном итоге была получена автоматизированная
электромеханическая система, обеспечивающая требуемые динамические
характеристики.
Список
литературы
1. Бесекерский,
В.А. Теория систем автоматического управления [Текст] / В.А. Бесекерский; Е.П.
Попов, М.: Наука. 1975. - 767 с.
2. Ширабакина
Т.А. Основы автоматизации и системы автоматического управления: Учебное пособие
/В.С. Титов, В.И. Вахания: КурскГТУ. Курск, 2004. - 248 с.
3. Ширабакина
Т.А. Основы автоматики и системы автоматического управления [Текст]: практикум
/ Т.А. Ширабакина: КурскГТУ. Курск, 2004. - 101 с.