Биномиальные коэффициенты

Биномиальные коэффициенты

Содержание

Введение

. Сочетания

.1 Число C^k_n

.2 Свойства

.3 Упражнения

. Бином Ньютона

.1 Треугольник Паскаля

.2 Свойства

.3 Алгоритм вычисления биномиальных коэффициентов

.4 Упражнения

3. Комбинаторные тождества

Заключение

Список литературы

Введение

Как известно, биномиальные коэффициенты изучаются в разделе комбинаторика.

Комбинаторика возникла в XVI веке. В жизни привилегированных слоёв тогдашнего общества большое место занимали азартные игры. В карты и кости выигрывались и проигрывались золото и бриллианты, дворцы и имения, породистые кони и дорогие украшения. Широко были распространены всевозможные лотереи. Понятно, что первоначально комбинаторные задачи касались в основном азартных игр - вопросов, сколькими способами можно выбросить данное число очков, бросая две или три кости, или сколькими способами можно получить двух королей в данной карточной игре. Эти и другие проблемы азартных игр явились движущей силой в развитии комбинаторики и развивавшейся одновременно с теорией вероятностей.

Целью моей работы является проектирование содержания темы "Биномиальные коэффициенты" как элемента стохастической линии в курсе школьной математики.

Задачи при достижении этой цели ставятся следующие:

разработать содержание темы "Сочетания и число сочетаний";

разработать содержание темы "Бином Ньютона и свойства биномиальных коэффициентов" .

1. Сочетания

1.1 Числа С^k_n

Пусть X - множество, состоящее из n элементов. Любое подмножество Y множества X, содержащее k элементов, называется сочетанием k элементов из n; при этом, разумеется, k ≤ n.

Число различных сочетаний k элементов из n обозначается С_n^k . Одной из важнейших формул комбинаторики является следующая формула для числа С_n^k :

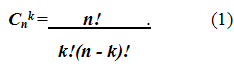
Её можно записать после очевидных сокращений следующим образом:

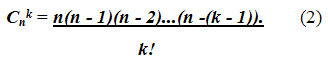
В частности,

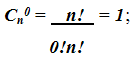
Это вполне согласуется с тем, что в множестве X имеется только одно подмножество из 0 элементов - пустое подмножество.

Приведём доказательство формулы (2). Пусть Y - какое-либо подмножество множества X , содержащее k элементов. Составив всевозможные перестановки из этих элементов, получим k! различных строк длинной k. Если указанную операцию проделать с каждым подмножеством Y, содержащим k элементов, то получим всего C_n^k · k! различных строк длинной k . Но очевидно, что таким путём должны получиться все без исключения строки длиной k без повторений, которые можно составить из элементов множества X. поскольку число таких строк равно A_n^k , то имеем соотношение C_n^k · k! = A_n , из которого следует C_n^k =A^k_n, т.е. формула (2).

1.2 Свойства

Числа C_n^k обладают рядом замечательных свойств. Эти свойства в конечном счёте выражают различные соотношения между подмножествами данного множества X. Их можно доказывать непосредственно, исходя из формулы (1), но более содержательными являются доказательства, опирающиеся на теоретико-множественные рассуждения.

1.   Справедлива формула

С_n^k = С^n-k_n , (3)

Вытекающая из (1) очевидным образом. Смысл формулы (3) состоит в том, что имеется взаимно-однозначное соответствие между множеством всех k-членных подмножеств из X и множеством всех (n - k)-членных подмножеств из X: чтобы установить это соответствие, достаточно каждому k-членному подмножеству Y сопоставить его дополнение в множестве X.

2.   Справедлива формула

С⁰_n + С¹_n + С²_n + … + Сⁿ_n = 2ⁿ . (4)

Поскольку сумма, стоящая в левой части, выражает собой число всех подмножеств множества X (C⁰_n есть число 0-членных подмножеств, C¹_n - число 1-членных подмножеств и т.д.), то для доказательства формулы (4) достаточно сослаться на уже известный читателю факт: число различных подмножеств n-членного множества X равно 2ⁿ.

3.   При любом k, 1≤ k≤ n , справедливо равенство

C^k_n = C_n-1^k + C_n-1^k-1. (5)

Это равенство нетрудно получить с помощью формулы (1). В самом деле,

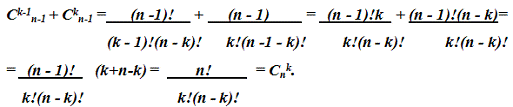
Вывод формулы (5), основанный на теоретико-множественных соображениях. Укажем, что для этого следует выделить какой-то определённый элемент а є X и все k-членные подмножества разбить на две группы: подмножества, содержащие а , и подмножества, не содержащие а.

4.   Арифметический треугольник Паскаля.

Равенство (5) позволяет вычислять значения C_n^k, если известны С_n-1^k и С^k-1_n-1 . Иными словами, с помощью этого равенства можно последовательно вычислять С_n^k сначала при n = 1, затем при n = 2, n = 3 и т.д. Вычисления удобно записывать в виде треугольной таблицы:

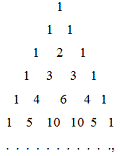
в (n + 1) строке которой по порядку стоят числа С⁰_n, С¹_n, …, Сⁿ_n . При этом крайние числа строки, т.е. С⁰_n и Сⁿ_n , равны 1, а остальные числа находяться по формуле (5). Поскольку С^k-1_n-1 и С^k_n-1 распологаются в этой таблице строкой выше, чем число С^k_n , и находяться в этой строке слева и справа от него, то для получения числа С^k_n надо сложить находящиеся слева и справа от него числа предыдущей строки. Например, число 10 в шестой строке мы получаем, сложив числа 4 и 6 пятой строки. Указанная таблица и есть как раз "арифметический треугольник Паскаля".

. Задача. Пусть n и k - два целых числа, при чём n > 0, k ≥0. сколько существует различных строк длиной n, состоящих из букв а и b , с условием, что в каждой из этих строк буква а встречается k раз .(и, следовательно, b-n-k раз)?

Решение. Пусть (x₁, x₂, ..., x_n) - одна из строк указанного вида. Рассмотрим все номера i , такие, что x_i = а. Совокупность таких номеров является подмножеством множества М = {1, 2, …, n}, состоящим из k элементов. Обратно, если Y - любое подмножество множества М, состоящее из k элементов, то, положив x_i = а для всех i є Y и x_i = b для всех i є Ŷ, получим строку (x₁, x₂, ..., x_n) требуемого вида. Значит, число указанных в задаче строк равно числу k-элементных подмножеств в n-элементном множестве М, т.е. равно числу С_n^k .

1.3 Упражнения

. Вычислите C₈³.

Решение.

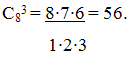
Ответ: 56.

II. Вычислите С₉⁴.

Решение.

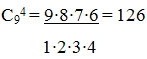
Ответ: 126.

III.

a) По какой формуле вычисляется С_n²?

b) Вычислите С₁₇² - С₁₅².

c) По какой формуле вычисляется С_n^k?

d) Вычислите С₁₇³ - С₁₅⁴.

Решение.

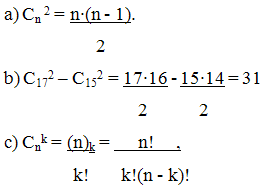
где (n)_k - убывающий k-факториал от n, т.е. произведение k убывающих натуральных чисел, начиная с n:

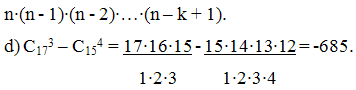
Ответ: b) 31; d) -685.

а) C_x³ = 2∙C_x²;

b) C_x^x-2 = 15;

c) C_x² + C_x+1² = 49;

d) C₈^x = 70.

Решение.

а) С_x³ = 2∙C_x²;

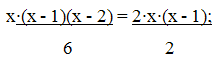- 2 = 6;= 8.) C_x^x-2 = 15;_x^x-2 = C_x^x-x+2 = C_x²;∙(x - 1) = 30 = 6∙5;= 6.) C_x² + C_x+1² = 49;∙(x - 1) + (x + 1)∙x = 98;x = 98;² = 49; x € N;= 7.) C₈^x = 70;= 1; C₈¹ = 8 ≠ 70;

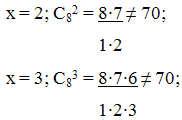 = 4; C₈⁴ = 8∙7∙6∙5 = 2∙7∙5 = 70.

Искомое значение x = 4.

Ответ: а) 8; b) 6; c) 7 d) 4.

2. Бином Ньютона

Из школьного курса читателю известны формулы:

(а + b)² = a² + 2ab + b²,

(a + b)³ = a³ +3a²b + 3ab² + b³.

Обобщением этих формул является следующая формула, называемая обычно формулой бинома Ньютона:

(a + b)ⁿ = C⁰_n a⁰bⁿ + C¹_n ab^n-1 + C²_n a²b^n-2 + ... + C^n-1_n a^n-1b + Cⁿ_n aⁿb⁰. (6)

В этой формуле может быть любым натуральным числом.

Вывод формулы (6) несложен. Прежде всего запишем:

(a + b)ⁿ = (a + b)(a + b) ... (a + b), (7)

где число перемножаемых скобок равно n. Из обычного правила умножения суммы на сумму вытекает, что выражение (7) равно сумме всевозможных произведений, которые можно составить следующим образом: любое слагаемое первой из сумм а + b умножается на любое слагаемое второй суммы a +b, на любое слагаемое третьей суммы и т.д. Hапример, при n = 3 имеем:

(a +b)(a + b)(a + b) = aaa + aab + aba + abb + baa + bab + bba + bbb.

Из сказанного ясно, что слагаемым в выражении для (a + b)ⁿ соответствуют (взаимно-однозначно) строки длиной n, составленные из букв а и b. Среди слагаемых будут встречаться подобные члены; очевидно, что таким членам соответствуют строки, содержащие одинаковое количество букв а. Но число строк, содержащих ровно k раз букву а, равно С^k_n . Значит, сумма всех членов, содержащих букву а множителем ровно k раз, равна С_n^k a^kb^n-k. Поскольку k может принимать значения 0, 1, 2, …, n-1, n, то из нашего рассуждения следует формула (6).

Заметим, что (6) можно записать короче: (a + b)ⁿ = ∑C^k_n a^kb^n-k. (8)

Хотя формулу (6) называют именем Ньютона, в действительности она была открыта ещё до Ньютона (например, её знал Паскаль). Заслуга Ньютона состоит в том, что он нашёл обобщение этой формулы на случай не целых показателей.

Числа С⁰_n, C¹_n, ..., Cⁿ_n, входящие в формулу (6), принято называть биномиальными коэффициентами, которые определяются так:

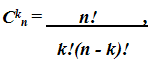
Из формулы (6) можно получить целый ряд свойств этих коэффициентов. Например, полагая а =1, b = 1, получим:

ⁿ = C⁰_n - C¹_n + C²_n - C³_n + ... +Cⁿ_n,

т.е. формулу (4). Если положить а = 1, b = -1, то будем иметь:

= С⁰_n - C¹_n + C²_n - C³_n + ... + (-1)ⁿCⁿ_n или С⁰_n + C²_n + C⁴_n + ... = C¹_n + C³_n + + C⁵_n + ... .

Докажем формулу (8). Рассмотрим функцию f(x) = (1 + x)ⁿ. Это многочлен n-ой степени, то есть

(1 + x)ⁿ = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀.

Найдём коэффициенты a_n, a_n-1, ..., a₁, a₀, вычислив значения функции и всех её производных от 1-го до n-го порядка при x = 0. Получим, что производная k-го порядка с одной стороны равна

f ^(k)(x) = (1 + x)^(k) = n(n - 1)· ... ·(n - k + 1)(1 + x)^(n-k).

С другой стороны, она равна

 ^(k)(x) = n( n - 1)· ... ·(n - k)a_nx^n-k + ... + k!a_k,

При x = 0 получим равенство

(n - 1)· ... ·(n - k + 1) = k!a_k

отсюда

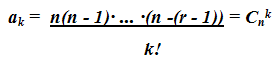
При всех k = 1, 2, …, n.

Тогда

(1 + x)ⁿ = C⁰ _nxⁿ + C¹_n x^n-1 + ... + C^k_n x^n-k + ... + Cⁿ_n x⁰

или короче

(1 + x)ⁿ = ∑C^k_n x^n-k,

Отсюда

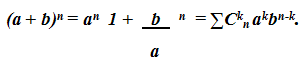
.1 Треугольник Паскаля

Коэффициент в разложении (a + b)ⁿ при a^n-kb^k обозначается k. Это обозначение в 1778 г. Ввёл Л. Эйлер. Таким образом, можно записать разложение бинома так:

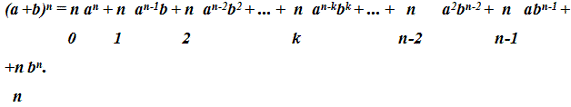
Соответственно,

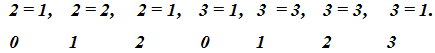
Разумеется, можно вычислить все биномиальные коэффициенты для любого n путём непосредственного перемножения n множителей (a + b), раскрытия скобок и приведения подобных членов. Правда, математикам древности и среднековья сделать это мешало отсутствие алгебраической символики. Например, в одном средневековом математическом тексте, имевшем хождение в Западной Европе в XV в. и, по-видимому, восходящем к арабам, биномиальные коэффициенты вычисляются очень наглядно путём возведения в степени числа 10001 и приводятся в виде таблицы.

Таблица 1. степень числа 1001 воспроизводит биномиальные коэффициенты.

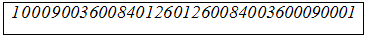
Ат-Тутси (XIII в.) располагал таблицей биномиальных коэффициентов до n = 2 и, что важнее, привёл общее правило для их получения, которое в современных обозначениях может быть выражено так:

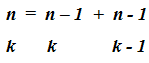
Доказательство:

Благодаря данному правилу можно вычислять биномиальные коэффициенты последовательно для всех больших степеней n: а именно, k-й коэффициент бинома степени n равен сумме k-го и (k-1)-го коэффициентов степени (n-1). К этому следует добавить, что в биноме степени n первый (точнее, нулевой, k = 0) и последний (k = n) коэффициенты - т.е. коэффициенты при aⁿ и при bⁿ - оба равны 1(при перемножении n множителей (a + b) член aⁿ получается единожды, а именно, при перемножении n раз чисел a; то же верно и для члена bⁿ).

Если записать биномиальные коэффициенты n в виде таблицы со строками n и столбцами k, то каждая строка будет начинаться и заканчиваться единицей, а каждое промежуточное число строки будет равняться сумме двух чисел предыдущей строки - того, что стоит непосредственно над ним, и то, что стоит левее:

Таблица 2. Биномиальные коэффициенты.

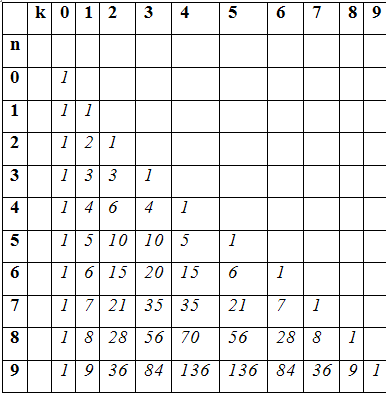
Не трудно видеть, что каждая строка данной таблицы симметрична: n = n , т.к. коэффициенты при a^kb^n-k и a^n-kb^k в разложении бинома совпадают. Полученный числовой треугольник называется треугольником Паскаля. Таблицы биномиальных коэффициентов были известны и предшествующим математикам - китайским, арабским и европейским (П. Аппиан, 1527 г.; М. Штифель, 1544 г.; Н. Тарталья, 1556 г.). Однако именно благодаря работе Паскаля "Тракт о арифметическом треугольнике", опубликованной уже после смерти автора (в 1665 г.), свойства биномиальных коэффициентов получили широкую известность. Правда сам Паскаль (и многие его предшественники) рисовали этот треугольник несколько иначе, с "повышенными" столбцами и прямым углом при вершине:

Таблица 3. Треугольник Паскаля.

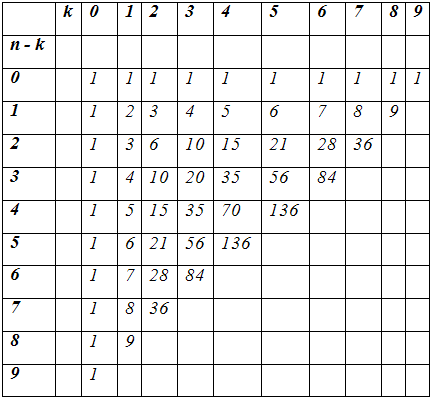
В такой таблице числа, соответствующие разложению бинома степени n, стоят не вдоль одной и той же строки, а вдоль одной и той же восходящей диагонали. Все восходящие диагонали, а значит, и вся таблица симметрична относительно главной нисходящей диагонали - "биссектрисы прямого угла". Каждое число в таблице (кроме единиц, находящихся на верхнем и левом краях), равняется сумме двух чисел, стоящих от него сверху и слева.

Вот ещё несколько свойств таблицы 3, доказанных Паскалем:

Интересно свойство делимости чисел, составляющих треугольник Паскаля. Если обозначить одним цветом числа, делящиеся нацело на какое-нибудь натуральное число, а другим - делящиеся с остатком, получается неожиданные узоры. Некоторые из них составлены из равных разноцветных треугольников - это результат деления на простые числа. Другие же похожи на фракталы. Почему? Числа, стоящие вдоль одной и той же строки (столбца) на таблице, так же интересны. То, что в нулевой строке и нулевом столбце стоят единицы, очевидно. Очевидно и то, что на первой строке и первом столбце стоят подряд все натуральные числа: 1, 2, 3, 4 и т.д.

А вот что за числа стоят на второй строке (столбце)? Оказывается, эти числа имеют своё название, причём носят его с глубокой древности - это треугольные числа. А числа на третьей строке (столбце) - пирамидальные числа, равные сумме треугольных.

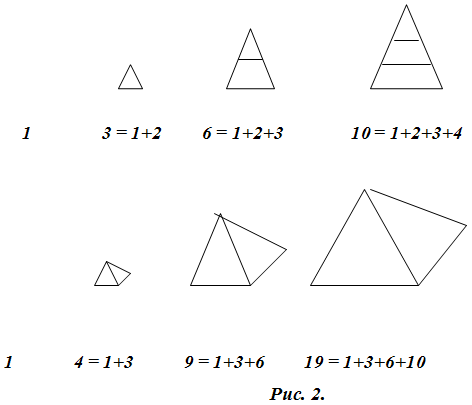
Если обратиться к форме треугольник Паскаля, представленный в таблице 2, и рассмотреть её столбцы и нисходящие диагонали, то это рассмотрение ничего не даст: фактически, столбцы у таблиц 2 и 3 одни и те же, а нисходящие диагонали таблицы 2 совпадают со строками таблицы 3. Строки же таблицы 2 совпадают с восходящими диагоналями таблицы 3. Последовательность (1, 1, 2, 3, 5, 8, …), полученная при разборе восходящих диагоналей: 1; 1; 1+1 = 2; 1+2 = 3; 1+3 = 5, 1+3+1 = 5; 1+4+3 = 8 и т.д., обладает тем свойством, что каждое число в ней равно сумме двух предыдущих. Эти числа носят название чисел Фибоначчи и обладают многими интересными математическими свойствами, возникая в самых неожиданных задачах.

Гораздо проще вопрос о том, чему равны суммы чисел, стоящих на каждой из строк таблицы 2 ( и ли на каждой из восходящих диагоналей таблицы 3).

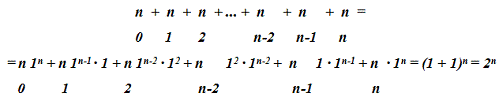
Ещё один вопрос - чему равна сумма:

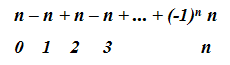
в которой все биномиальные коэффициенты степени n>0 c нечётными номерами взяты со знаком плюс, а с чётными - со знаком минус?

Ответ:

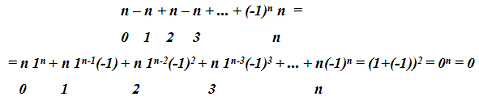
Чрезвычайно важное свойство биномиального разложения связано с тем, что его коэффициенты n , оказывается, представляют собой не что иное, как числа сочетаний по k элементов из множества с n элементами.

Приведём одно из свойств, связанных с делимостью биномиальных коэффициентов. Рассмотрим таблицу 2. Легко видеть, что все числа её 5-й строки, кроме крайних единиц, делятся на 5; все числа 7-й строки, кроме крайних единиц, делятся на 7. Очевидно, у 2-й и 3-й строки есть такое же свойство. А у остальных, легко видеть, такого свойства нет. Что объединяет числа 2, 3, 5 и 7 и отличает их от других чисел первого десятка? Верно, все они простые. Можно доказать, что, действительно, все числа n-ой строки треугольника Паскаля (в форме таблицы 2), кроме крайних единиц, делятся на n тогда и только тогда, когда n простое.

Еще одно красивое свойство треугольника Паскаля (в форме таблицы 2) связано с вопросом, сколько нечётных чисел содержит n-я строка. Оказывается, число этих нечётных чисел всегда равно 2^k, где k - число единиц в двоичной записи числа n.

И наконец приведём сравнительно недавно, в общем, то, случайно обнаруженное свойство треугольника Паскаля, связывающее его с простыми числами (Г.В. Манн, Д. Шенкс, 1972г.). запишем строки треугольника Паскаля (в форме таблицы 2), каждый раз сдвигая строки в право на две позиции.

Таблица 4. Связь ряда простых чисел и треугольника Паскаля.

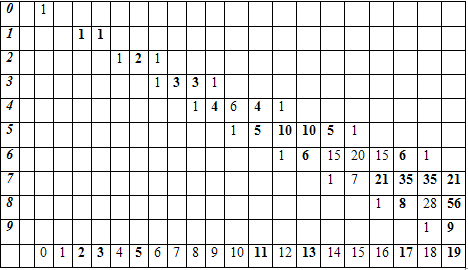
Числа, стоящие в таблице, выделены, если они делятся на номер строки. Числа в нижней строке, нумерующие столбцы, выделены, если в этом столбце все числа выделены. Выходит, что выделенные номера столбцов в точнсти соответствуют простым числам.

.2 Свойства

1. Сумма коэффициентов разложения (a + b)ⁿ равна 2ⁿ.

Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома мы будем иметь сумму биномиальных коэффициентов, а слева: (1 + 1)ⁿ = 2ⁿ.

.Коэффициенты членов, равноудалённых от концов разложения, равны. Это свойства следует из соотношения: C^k = C^n-k.

.Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна 2^n-1.

Для доказательства воспользуемся биномом: (1 - 1)ⁿ = 0ⁿ = 0. здесь чётные члены имеют знак "+", а нечётные - "-". Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов равны между собой, поэтому каждая из них равна: 2ⁿ : 2 = 2^n-1, что и требовалось доказать.

2.3 Алгоритмы вычисления биномиальных коэффициентов

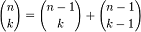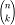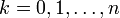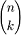·        Биномиальные коэффициенты могут быть вычислены с помощью формулы , если на каждом шаге хранить значения при . Этот алгоритм особенно эффективен, если нужно получить все значения при фиксированном n. Алгоритм требует O(n) памяти (O(n²) при вычислении всей таблицы биномиальных коэффициентов) и O(n²) времени (в предположении, что каждое число занимает единицу памяти и операции с числами выполняются за единицу времени).

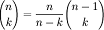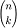·        Второй способ основан на тождестве . Он позволяет вычислить значения при фиксированном k. Алгоритм требует O(1) памяти (O(l) если нужно посчитать l последовательных коэффициентов с фиксированным k) и O(k) времени.

2.4 Упражнения

.

a)   Проверьте, что (а + b)² = C₂⁰a²b⁰ + C¹₂a¹b¹ + C²₂a⁰b².

b)      Проверьте, что (а + b)³ = C⁰₃a³b⁰ + C¹₃a²b¹ + C²₃a¹b² + C³₃a⁰b³.

c) Используя равенство (а + b)⁴ = (a + b)³·(a + b), выведите формулу сокращённого умножения для суммы двух чисел в четвёртой степени.

d) Проверте, что (a + b)⁴ = C⁰₄a⁴b⁰ + C¹₄a³b¹ + C²₄a²b² + C³₄a¹b³ + C⁴₄a⁰b⁴.

Решение:

a)   (a +b)² = a² + 2ab + b² = C⁰₂a²b⁰ + C ¹₂a¹b¹ + C²₂a⁰b².

b)      (a + b)³ = a³ + 3a²b + 3ab² + b³ = C⁰₃a³b⁰ + C¹₃a²b¹ + C²₃a¹b² + C³₃a⁰b³.)  (a + b)⁴ = (a + d)³·(a + b) = (a³ + 3a²b + 3ab² b³)·(a + b) = a⁴+4a³b + + 6a²b²+ 4ab³+ b⁴.) (a +b)⁴ =a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴ = C⁰₄a⁴b⁰ + C¹₄a³b¹ + C²₄a²b² + C³₄a¹b³ + C⁴₄a⁰b⁴.

Решённые примеры являются частными случаями бинома Ньютона.

II.

a) Составьте таблицу из двух строк, расположив в первой строке k от 0 до 5, во второй строке - числа C^k₅.

b) При каком значении числа k получится наибольшее значение числа C^k₅?

c) Найдите сумму чисел во второй строке составленной таблицы.

d) Отметьтье на координатной плоскости точки (k, C^k₅).

Решение.

а) Вторая строка в таблице будет пятой строкой в треугольнике Паскаля:

) Наибольшее значение С^k₅ получается при двух значениях k =2 и k = 3, т.е. при [5/2] и при [5/2]+1 (в квадратных скобках записываем целую часть числа, т.е. наибольшее целое, не превосходящее 5/2). В данном случае n = 5 - нечётное число.

c)   Сумма чисел во второй строке составленной таблицы равна 32 = 2⁵ (свойство биномиальных коэффициентов ∑С^k_n = 2ⁿ).

d)      Точки (k, C^k₅) на координатной плоскости:

Ответ: c)2; 3; d) 32.

III. Решите уравнения:

а) 14 C_n^n-2= 15A²_n-3;) 6C_n^n-3= 11A²_n-1;) 13C_2nⁿ⁺¹= 7_2n+1^n-1;) 21C_2nⁿ⁺¹= 11C_2n+1^n-1.

Решение:

а) 14С_n^n-2= 15Aⁿ_n-3; n є N.

Поскольку С_n^n-2= C_n^n-n+2= C_n ², то

C_n²= 15A²_n-3;

·n·(n -1) = 15·(n -3)·(n -4);

n² - 49n + 90 = 0;) 6C_n^n-3 = 11A²_n-1; n є N

C³_n = 11A²_n-1·(n - 1)·(n -2) = 11·(n - 1)·(n -2);= 11.) 13C_2nⁿ⁺¹ = 7C^n-1_2n+1; n є N.

13C_2n^n-1 = 7C_2n+1^n-1

Сокращая получаем:

отсюда n = 19.

d) 21C_2nⁿ⁺¹ = 11C^n-1_2n+1;

сокращая, получаем:

21·(n + 2) = 11·(2n + 1),

Отсюда n = 31.

Ответ: а) 10; b) 11; c) 19 d) 31.

Замечание. Расписывая факториалы, мы воспользовались формулой:

Поэтому С_2n+1^n-1 преобразуется аналогично.

IV. Вычислите.

C₂₇² - C₂₆²;

a)   C₁₁⁵ + C₁₁⁶;

b)      C₅² + C₇² + C₉²;

c)      Числа C_n^k при n = 1, 2,3,4 и 0 < k < n.

Решение:

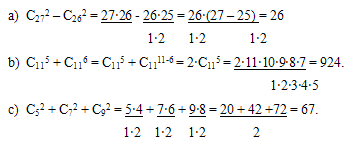
Числа С_n^k при заданных n и k удобнее всего записать в виде треугольника Паскаля:

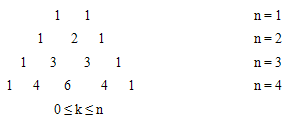
Ответ: a) 26; b) 9;2;4; c) 67; d) 14 чисел в треугольнике Паскаля.

Замечание. В условие варианта d) должно быть 0 ≤ k ≤ n, т.к. при

< n < k и n = 1 нет значений k (k€N).

3. Комбинаторные тождества.

Рассмотрим некоторые тождества, связанные с биноминальными коэффициентами.

арифметический биномиальный комбинаторный тождество

·             

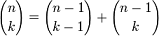
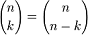·              (правило симметрии)

·             

·             

·             

·             

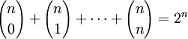
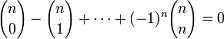
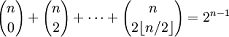
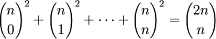
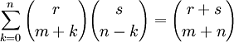·              (свёртка Вандермонда)

·              Мультисекция ряда <#"511008.files/image042.gif">в виде замкнутой суммы из s слагаемых:

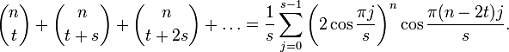
Применим последовательно формулу сложения:

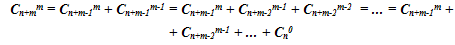
получили тождество

∑C_n+k^m = C_n+m^m,

C_n⁰ + C_n+1¹ + C_n+2² + … + C_n+m-1^m-1 = C_n+m^m

Применим формулу сложения иначе (пусть m ≤ n):

C_n+m^m+1 = C_n+m-1^m + C_n+m-1^m+1 = C_n+m-1^m + C_n+m-2^m + C_n+m-2^m+1 = C_n+m-1^m + C_n+m-2^m-1 + C_n+m-3^m + C_n+m-3^m+1 = ... = C_n+m-1^m + C_n+m-2^m-1 + ... + C_n^m

получили тождество ∑C_n+k^m = C_n+m^m,

C_n^m ₊ C_n+1^m + C_n+2^m + ... + C_n+m-1^m = C_n+m^m

в частности,

₁¹ + C₂¹ + C₃¹ + ... + C_n¹ = C_n+1²

то есть,

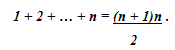
Заключение

При создании специальных программ для осуществления факультативов можно использовать данную тему моей работы как одну из тем изучения комбинаторики, так как она в современной школе выделяется отдельным разделом.

Список литературы

1.     Комбинаторика / автор - составитель Н.Я. Виленкин. - М., 1969 г.

2.       Комбинаторика / автор - составитель Н.Я. Виленвин. - изд. "Наука". - М., 1969 г.

.        Решение задач по статистике, комбинаторике и теории вероятностей. 7-9 кл./ автор - составитель В.Н. Студенецкая. - изд. 2-е., испр., - Волгоград: Учитель, 2009 г.