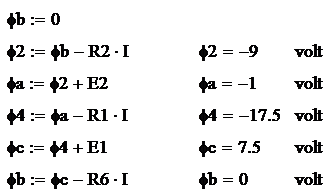|
R1(Ом)
|
R2(Ом)
|
R3(Ом)
|
R4(Ом)
|
R5(Ом)
|
R6(Ом)
|
Е1(В)
|
Е2(В)
|
|
110
|
60
|
45
|
150
|
80
|
50
|
25
|
8
|
Задание №1
Составить на основании
законов Кирхгофа систему уравнений для расчета токов во всех ветвях схемы
Приведенная
на чертеже схема электрической цепи имеет шесть ветвей, а значит и число
неизвестных токов равно шести (следовательно, система должна содержать шесть
уравнений); число узлов равно четырем.
Расставим на схеме
предполагаемое направление токов в ветвях. Так как число уравнений,
составленных по первому закону Кирхгофа, должно быть на единицу меньше числа узлов,
значит, составим три уравнения. Первое правило Кирхгофа гласит, что
алгебраическая сумма токов, сходящихся в узле равна 0.
узел а: I1-I2-I3=0
узел d: I3+-I4-I5=0
узел b: I2+I4-I6=0
Выберем направление
обхода в трех внутренних контурах по часовой стрелке и составим еще три
недостающих уравнения согласно второму закону Кирхгофа (В любом замкнутом
контуре, произвольно выбранном в разветвленной электрической цепи,
алгебраическая сумма напряжений на всех участках этого контура равна сумме
Э.Д.С. всех источников электрической энергии, включенных в контур.):
Контур acda: I1R1+I3R3+I5R5= -E1
Контур abda: I2R2-I3R3-I4R4= -E2
Контур cbdc: I4R4-I5R5+I6R6= 0
Тогда, получим следующую
систему для нахождения токов:
I1-I2-I3=0
I3+-I4-I5=0
I2+I4-I6=0
I1R1+I3R3+I5R5=
-E1
I2R2-I3R3-I4R4=
-E2
I4R4-I5R5+I6R6=
0
Задание №2
Определить токи во всех
ветвях системы методом контурных токов
Допустим, что в каждом
независимом контуре протекает свой независимый ток. Тогда пронумеруем контуры и
выберем направление контурных токов. Тогда на основе законов Ома и Кирхгофа,
можно составить следующую расчетную систему уравнений:
R11I11+R12I22+R13I33=E11
R21I11+R22I22+R23I33=E22
R31I11+R32I22+R33I33=E33,
где:
I11, I22, I33 –
независимые контурные токи,
R11, R22, R33 –
собственные сопротивления контуров, равные сумме сопротивлений, входящих в
данный контур,
R12, R13, R21, R23, R31, R32 –
взаимные сопротивления контуров, равные сумме сопротивлений, соединяющих данные
контура,
E11, E22, E33 –
суммарные э.д.с. контуров, равные сумме э.д.с., входящих в данный контур.
Тогда согласно
приведенной выше схеме
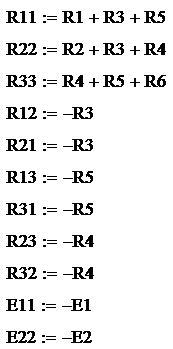
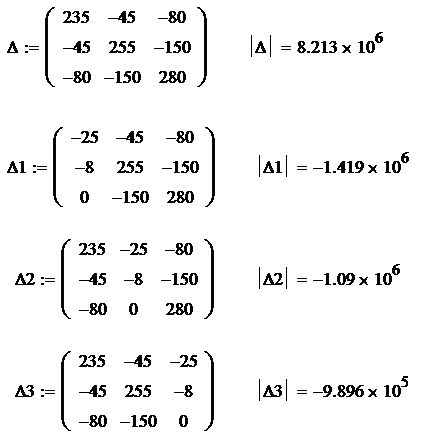
Соблюдая направление
контурных токов и направление токов в ветвях схемы, найдем значение всех токов.
При этом значение токов,
полученных со знаком “-“ означает лишь то, что ток имеет противоположное
направление.
Задание №3
Определить токи во всех
ветвях схемы методом узловых потенциалов
Составим
расчетную систему:
G11
1+G122+G133=I11
G211+G222+G233=I22
G311+G322+G333=I33,
где
gnn -
сумма проводимостей всех ветвей, сходящихся в соответствующем узле
gnm -
сумма проводимостей всех ветвей, соединяющих соответствующие узлы, и проводимость
типа gnm=gmn=-1/R.
- потенциал соответственного узла.
Inn -
узловой ток, равный алгебраической сумме токов, полученных от деления ЭДС всех
ветвей, подходящих к n узлу, на сопротивление данных ветвей.
Согласно определениям
рассчитаем проводимости и узловые токи.
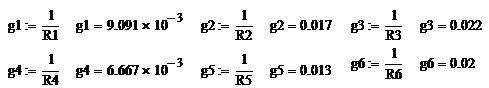
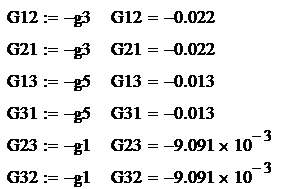
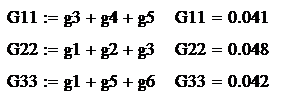
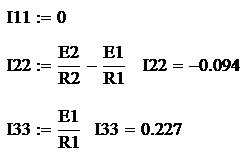
Подставляя полученные
значения в систему, и решая ее, найдем значения узловых напряжений,
предварительно заземлив точку 4 (.
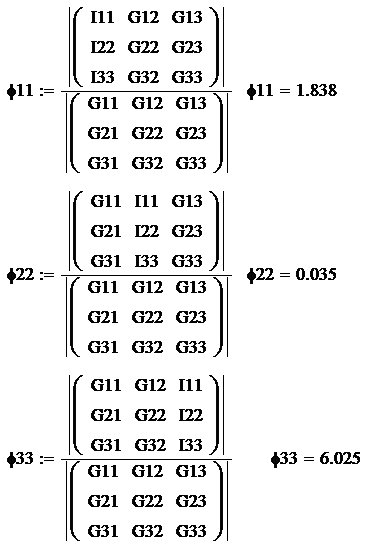
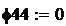
Используя закон Ома
найдем ток, протекающий через каждый из резисторов:
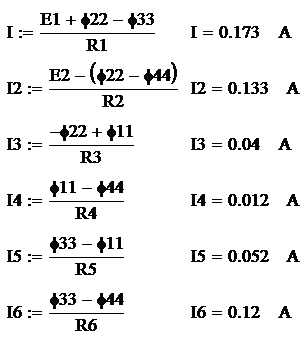
При этом значение токов,
полученных со знаком “-“ означает лишь то, что ток имеет противоположное
направление.
Задание №4
Результаты расчета токов,
проведенного двумя методами, свести в таблицу и сравнить между собой.
|
I1, А
|
I2, А
|
I3, А
|
I4, А
|
I5, А
|
I6, А
|
|
Метод контурных токов
|
0,173
|
0,133
|
0,04
|
0,012
|
0,052
|
0,12
|
|
Метод узловых потенциалов
|
0,173
|
0,133
|
0,04
|
0,012
|
0,052
|
0,12
|
Т.к. значения в обоих
методах совпадают, значит, погрешность при расчетах равна 0.
Задание №5
Составить баланс
мощностей в исходной схеме, вычислив суммарную мощность и суммарную мощность
нагрузок (сопротивлений)
Составим баланс мощностей
для данной цепи. Так как в цепи при постоянном токе не может происходить
накопление электромагнитной энергии, поэтому сумма мощностей, расходуемых в
пассивных двухполюсниках, и мощностей, теряемых внутри генераторов должна быть
равна алгебраической сумме мощностей, развиваемых всеми генераторами, то есть
сумме произведений EkIk всех генераторов, действующих в цепи:
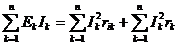
Так как в данном задании
сопротивление источника Э.Д.С. равно нулю, то
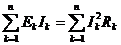
Найдем суммарную
мощность, вырабатываемую источниками Э.Д.С.
Так как в данной схеме
только два источника, вырабатывающих энергию, то мощность, развиваемая всеми
генераторами, будет равна:
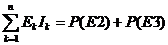
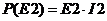(т.к.
через второй источник э.д.с. протекает ток I2)
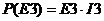( т.к. через второй источник э.д.с.
протекает ток I3)
Найдем суммарную
мощность, поглощаемую резисторами. Так как в данной схеме 6 сопротивлений, то
суммарная поглощаемая мощность будет равна:
,
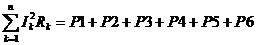где P1, P2, P3, P4, P5, P6 –
мощности, расходуемые на соответствующих резисторах.
Тогда, подставляя
исходные данные (R1=110 Ом, R2=60 Ом, R3=45 Ом, R4=150
Ом, R5=80 Ом, R6=50 Ом, E1=25
В, E=8 В) и полученные при предыдущих
расчетах токи, при расчете берем следующие значения токов, (I1=0,173 А, I2=0,133 А, I3=0,04
А, I4=0,012 А, I5=0,052 А, I6=0,12
А), получим соответствующие значения мощности:
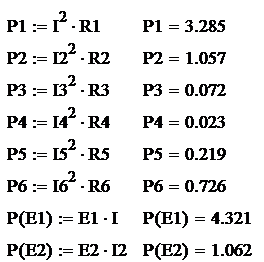
В схеме потребляется
мощность:
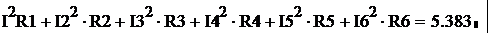
Источники ЭДС доставляют
мощность:
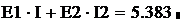
Задание №6
Определить ток I1 в заданной по условию схеме,
используя теорему об активном двухполюснике и эквивалентном генераторе
Представим всю схему в
виде активного двухполюсника, у которого Е=Uadxx, а внутреннее сопротивление генератора равно входному
сопротивлению двухполюсника. Для этого выделим сопротивление R1 и выберем путь от точки a к точке c и применяя закон Ома найдем разность потенциалов (напряжение)
между точками a и c.
Перечертим данную схему,
убрав сопротивление R1:
Так как было исключено
сопротивление R1, то в схеме появились новые
(частичные) токи. Значения которых можно найти, используя метод контурных
токов:
R11I11+R12I22=E11
R21I11+R22I22=E22,
где
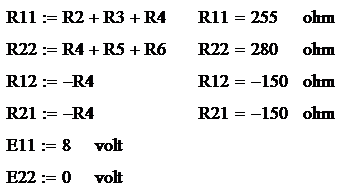
Тогда подставляя
полученные значения в систему и решая ее получим следующие значения контурных
токов:
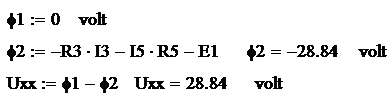
С помощью прямого
преобразования (треугольника в звезду) найдем входное сопротивление
двухполюсника.
Согласно расчетным
формулам преобразования:
Перечертив схему согласно
предыдущим преобразованиям, получим:
Согласно данному чертежу
имеем смешанное соединение проводников, где резисторы R54 и R3, R64 и R2 соединены последовательно, между собой параллельно, а с
резистором R56 последовательно, и их общее
сопротивление равно эквивалентному и входному сопротивлению схемы относительно
точек a и с. Рассчитаем входное сопротивление
относительно точек a и с.
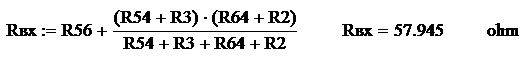
Тогда согласно расчетной
формуле, ток, протекающий через первый резистор, будет равен:
Задание №7
Начертить потенциальную
диаграмму для любого замкнутого контура, включающего обе э.д.с.
Для
того чтобы начертить потенциальную диаграмму для любого замкнутого контура,
включающего обе э.д.с.:
1)
выберем замкнутый контур acba и
заземлим точку b
2) выберем направление
тока в этом контуре и найдем его значение как:
Iобщ. = I =Eобщ./Rобщ. , где
Eобщ.=E=E1+E2
Rобщ.=R=R1+R2+R6
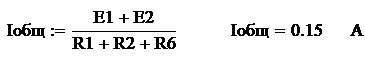
Так как в данном контуре
проводники R1, R2, R6
соединены последовательно, то ток, протекающий через каждый из проводников,
будет равен общему току контура, тогда:
I1=I2=I6= I =0.15 А
Согласно этому найдем
падение напряжения на каждом из участков цепи
