Методи вирішення проблем дискретного логарифмування
Методи вирішення
проблем дискретного логарифмування
1. Метод Поліга-Хелмана
Метод Поліга-Хелмана запропонований в 1978 році для визначення
дискретного логарифма в мультиплікативній групі поля 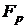 .
.
Він заснований на відомій для
групи факторизації порядку 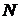 групи за ступенями простих чисел
групи за ступенями простих чисел 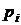
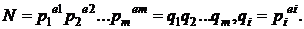
Стосовно до адитивної групи точок
з генератором 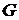 порядку
порядку 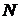 маємо
маємо 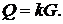 Відповідно до відомої китайської
теореми про залишки існує єдине натуральне число
Відповідно до відомої китайської
теореми про залишки існує єдине натуральне число  , таке що
, таке що
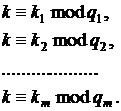
Після визначення значення 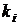 дискретний логарифм
дискретний логарифм 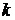 здобувають за допомогою
розширеного алгоритму Евкліда. Наведемо приклад.
здобувають за допомогою
розширеного алгоритму Евкліда. Наведемо приклад.
Приклад 1
Нехай порядок циклічної групи 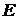 дорівнює
дорівнює 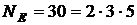 , а точка
, а точка  , тобто
, тобто  . Це значення має бути визначене в підсумку
рішення ECDLP.
. Це значення має бути визначене в підсумку
рішення ECDLP.
Тут 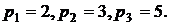 На першому етапі визначаємо точку
На першому етапі визначаємо точку 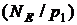
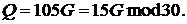 Отримуємо точку
Отримуємо точку  другого порядку з відомими координатами
другого порядку з відомими координатами 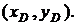 Оскільки
Оскільки 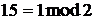 , маємо перше порівняння
, маємо перше порівняння
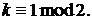
На наступному етапі знаходимо одну
із точок третього порядку 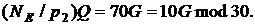 Ці точки також відомі, тому з
Ці точки також відомі, тому з 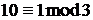 отримуємо наступне порівняння
отримуємо наступне порівняння
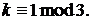
Нарешті, визначаємо точку 5-го
порядку 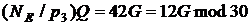 й отримуємо
й отримуємо
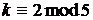 .
.
Наведені три порівняння дають
єдине розв’язання 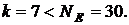 В загальному
випадку необхідно знати координати
В загальному
випадку необхідно знати координати 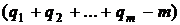 точок із загальної кількості
точок із загальної кількості 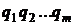 .
.
Задача ускладнюється із зростанням переважно простого
співмножника в розкладанні порядку 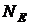 групи. У цьому зв'язку для захисту від атаки
Поліга-Хелмана порядок
групи. У цьому зв'язку для захисту від атаки
Поліга-Хелмана порядок 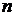 криптосистеми
обирають рівним великому простому числу, при цьому порядок кривої
криптосистеми
обирають рівним великому простому числу, при цьому порядок кривої 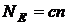 називають ²
майже простим ² (з малим множником
називають ²
майже простим ² (з малим множником 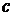 ).
).
2. Метод ділення точок на два
Метод ділення точок на два. Для кривих над полем 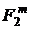 запропонований метод
розв’язання
запропонований метод
розв’язання 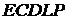 ,
заснований на процедурі, зворотної обчисленню точки
,
заснований на процедурі, зворотної обчисленню точки 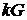 шляхом послідовних подвоєнь і додавань при
двійковому поданні числа
шляхом послідовних подвоєнь і додавань при
двійковому поданні числа 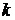 .
.
У звичайній
арифметиці двійкове подання цілого числа починається з визначення молодшого
біта: при непарних 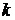 з
з 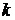 віднімається 1 (це молодший
біт двійкового подання
віднімається 1 (це молодший
біт двійкового подання 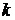 )
і результат ділиться на 2.
)
і результат ділиться на 2.
Якщо частка парна,
ділення триває, у протилежному випадку виконується віднімання 1 і ділення на 2
(отримуємо наступний розряд числа рівний відповідно 0 або 1). Процедура триває
до одержання частки, рівної 1. Якщо точка 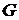 – генератор простого порядку
– генератор простого порядку 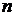 , то при знанні відповіді на питання
про парність (непарність) множника
, то при знанні відповіді на питання
про парність (непарність) множника 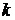 точки
точки 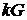
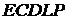 легко вирішується ( у поліноміальному часі )
описаною вище послідовною процедурою віднімання-ділення на два.
легко вирішується ( у поліноміальному часі )
описаною вище послідовною процедурою віднімання-ділення на два.
У простому полі 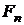 ділення на два тотожно
множення на елемент
ділення на два тотожно
множення на елемент
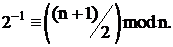
Виявляється
замість багаторазового додавання ділення точки на два виконується набагато
ефективніше й швидше.
Визначимо порядок кривої як
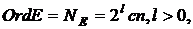
де 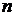 - велике
просте число (в існуючих криптографічних стандартах
- велике
просте число (в існуючих криптографічних стандартах 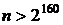 ),
), 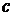 - непарне
число.
- непарне
число.
Нехай 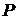 - точка
порядку
- точка
порядку 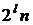 , тоді
генератор криптосистеми може бути визначений як точка
, тоді
генератор криптосистеми може бути визначений як точка 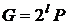 порядку
порядку 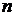 .
.
Введемо операцію ділення точки
несуперсингулярної кривої
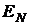 :
: 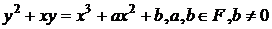 (1)
(1)
на два як зворотну подвоєнню.
Нехай маємо точку 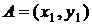 та
точку
та
точку 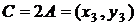 з координатами
з координатами
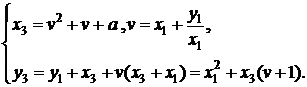 (2)
(2)
Інакше кажучи, визначення 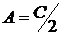 означає знаходження
координат точки
означає знаходження
координат точки 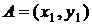 з
відомої точки
з
відомої точки 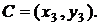 Відповідно
до (2) для цього необхідно вирішувати квадратне рівняння
Відповідно
до (2) для цього необхідно вирішувати квадратне рівняння
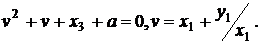 (3)
(3)
У загальному випадку це рівняння
має два розв'язки 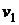 й
й 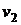 при наслідку
при наслідку
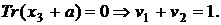 (4)
(4)
Якщо слід 
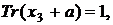 то точка
то точка 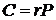 - непарна
точка
- непарна
точка 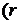 - непарне). Під час виконання (4) отримуємо дві точки:
- непарне). Під час виконання (4) отримуємо дві точки: 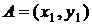 і
і 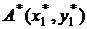 ділення точки
ділення точки 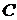 на два з координатами
на два з координатами
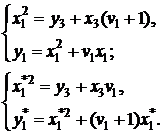 (5)
(5)
З (1) і (5) неважко отримати
співвідношення між координатами точок ділення
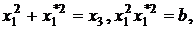
які можуть бути корисні при
криптоаналізі. Відзначимо дві властивості точок ділення.
Точки ділення пов'язані як 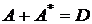 , де
, де  - точка другого порядку, дорівнює
- точка другого порядку, дорівнює 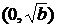 . Дійсно,
. Дійсно,
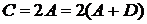 ,
,
тому що 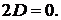
Якщо 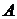 - точка
непарного порядку
- точка
непарного порядку 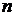 ,
тобто
,
тобто 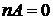 , то точка
, то точка
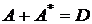
ає порядок 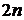 , тому що
, тому що
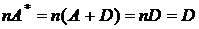 й
й 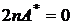 .
.
У порівнянні з подвоєнням точки
(2), яке вимагає обчислення двох множень й інверсії елемента 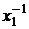 (найбільш трудомістка обчислювальна
операція), ділення (5) не вимагає інверсії елемента й може бути реалізоване набагато
швидше.
(найбільш трудомістка обчислювальна
операція), ділення (5) не вимагає інверсії елемента й може бути реалізоване набагато
швидше.
Найбільш ефективне розв’язання
рівняння (3) і операцій (4), (5) виконуються в НБ (нормальному базисі)
мінімальної складності, зокрема, в ОНБ (оптимальному нормальному базисі).
Розв’язання квадратного рівняння в
НБ здійснюється за допомогою простої 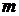 -бітової рекурентної послідовності. Слід (4)
елементів парної ваги дорівнює 0, а непарної ваги - 1.
-бітової рекурентної послідовності. Слід (4)
елементів парної ваги дорівнює 0, а непарної ваги - 1.
Піднесення у квадрат (добування
кореня квадратного) у нормальному базисі зводиться до циклічного зсуву вправо
(вліво) 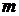 -бітового
елемента поля.
-бітового
елемента поля.
Поряд з додаванням елементів за
модулем 2 перераховані операції часто називають ²безкоштовними² і
не враховують у наближених розрахунках обчислювальної складності. Ділення
відповідно до (5) вимагає лише двох множень у нормальному базисі 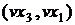 як найбільш складних операцій. Це
приблизно на порядок збільшує швидкість виконання операцій ділення на два в
порівнянні з операцією подвоєння точки.
як найбільш складних операцій. Це
приблизно на порядок збільшує швидкість виконання операцій ділення на два в
порівнянні з операцією подвоєння точки.
Розглянемо можливі підходи до
розв’язання задач дискретного логарифма. Найбільш проста ситуація виникає для
кривої
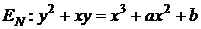 ,
,
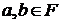 ,
, 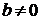
з коефіцієнтом 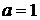 , порядок якої
, порядок якої 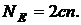
Максимальний простий порядок 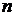 досягається при
досягається при 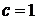 . Покладемо, що
. Покладемо, що 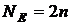 , а генератор
, а генератор 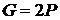 має порядок
має порядок 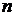 . У циклічній групі
. У циклічній групі 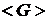 всі точки є точками подільності на два,
відповідно до (4) їх
всі точки є точками подільності на два,
відповідно до (4) їх 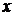 -координати
мають слід
-координати
мають слід 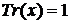 й, отже,
непарну вагу при поданні в НБ. При діленні на два отримуємо дві точки, одна з
яких належить групі
й, отже,
непарну вагу при поданні в НБ. При діленні на два отримуємо дві точки, одна з
яких належить групі 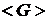 й
має порядок
й
має порядок 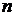 , а інша
максимальний порядок
, а інша
максимальний порядок 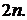
Вони мають відповідно непарну й
парну вагу 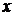 -координат і
легко розрізнюються без множення на
-координат і
легко розрізнюються без множення на 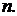 Вибір однієї із точок (5) порядку
Вибір однієї із точок (5) порядку 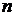 здійснюється досить просто.
Оскільки в групі
здійснюється досить просто.
Оскільки в групі 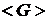 випливає,
що
випливає,
що
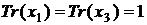
то після множення 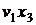 визначається вага елемента
визначається вага елемента  або його слід.
або його слід.
При 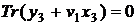 (парна вага елемента) користуються другою
формулою (5), у протилежному випадку - першою
формулою (5). Таким чином, ділення на два з вибором точки порядку
(парна вага елемента) користуються другою
формулою (5), у протилежному випадку - першою
формулою (5). Таким чином, ділення на два з вибором точки порядку 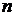 практично зводиться до двох
множень у поле.
практично зводиться до двох
множень у поле.
Відзначимо, що при послідовному
діленні на два для половини всіх кривих (з коефіцієнтом 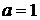 і порядком
і порядком 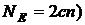 достатнім виявляється лише одне множення в
поле.
достатнім виявляється лише одне множення в
поле.
Для цього при кожному діленні
обчислюється лише розв'язання 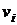 квадратного рівняння (4) і
квадратного рівняння (4) і 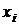 координата точки ділення. Нехай
координата точки ділення. Нехай 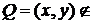
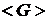 , і при послідовному діленні на два з вибором
точки із групи
, і при послідовному діленні на два з вибором
точки із групи 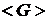 одержуємо
одержуємо
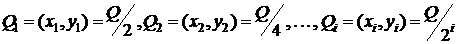 .
.
Згідно з (5) (перша формула) 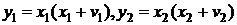 , . . . ,
, . . . , 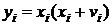 , тому підсумовуючи рівності
, тому підсумовуючи рівності
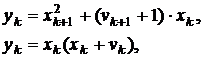
отримуємо з урахуванням першого
ділення
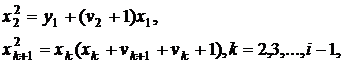 (6)
(6)
де кожне з рішень 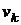 вибирається так, щоб виконувалася
умова
вибирається так, щоб виконувалася
умова 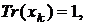 тобто в НБ вагу
вектора
тобто в НБ вагу
вектора 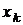 була непарним.
була непарним.
Як видно, рекурентне обчислення за
формулою (6) не вимагає обчислення 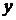 координати на кожному кроці ділення, замість
неї слід лише запам'ятати параметри
координати на кожному кроці ділення, замість
неї слід лише запам'ятати параметри 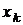 й
й 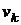 . За необхідності
. За необхідності 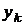 – координата обчислюється як
– координата обчислюється як 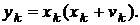
Таким чином, відповідно до (6)
алгоритм послідовного ділення на дві точки із групи 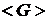 вимагає лише одного множення елементів у поле
вимагає лише одного множення елементів у поле 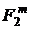 . Це чудова властивість
операції ділення на два можна використати з метою збільшення продуктивності
обчислень як при криптоаналізі, так і при швидкому експоненціюванні
. Це чудова властивість
операції ділення на два можна використати з метою збільшення продуктивності
обчислень як при криптоаналізі, так і при швидкому експоненціюванні 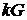 будь-якої точки із групи
будь-якої точки із групи 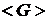 .
.
Якщо припустити, що для будь-якої
точки 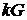 ми знайшли
спосіб визначення парності (непарності)
ми знайшли
спосіб визначення парності (непарності) 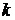 , то послідовна процедура віднімання й ділення
на два з вибором точки із групи
, то послідовна процедура віднімання й ділення
на два з вибором точки із групи 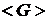 за поліноміальний час приведе нас до відомої
точки
за поліноміальний час приведе нас до відомої
точки 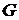 .
.
Значення 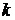 у двійковому поданні визначається самою
процедурою віднімання-ділення. Зрозуміло, що така функція вже не однобічна. Це
питання поки залишається відкритим і
у двійковому поданні визначається самою
процедурою віднімання-ділення. Зрозуміло, що така функція вже не однобічна. Це
питання поки залишається відкритим і 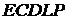 доводиться вирішувати відомими методами з
експонентною складністю.
доводиться вирішувати відомими методами з
експонентною складністю.
Визначити, яка з них має порядок 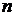 , можна шляхом множення
кожної з них на
, можна шляхом множення
кожної з них на 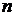 , але
це вимагає більших обчислювальних витрат. Більш раціональне дворазове ділення
на два, яке в одній з галузей дасть дві точки порядку
, але
це вимагає більших обчислювальних витрат. Більш раціональне дворазове ділення
на два, яке в одній з галузей дасть дві точки порядку 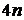 , вони не діляться на два й мають координати
непарної ваги. Ця галузь відбраковується й залишається точка із групи
, вони не діляться на два й мають координати
непарної ваги. Ця галузь відбраковується й залишається точка із групи 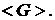
Приклад 1. Розглянемо криву Коблиця 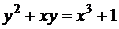 над полем
над полем 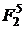 , яка має порядок
, яка має порядок  . Всі точки
. Всі точки 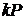 з генератором
з генератором 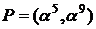 наведено в таблиці 1
наведено в таблиці 1
Таблиця 1- Координати точок 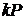 кривої
кривої 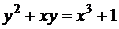 над полем
над полем 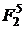
|
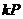
|
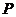
|
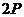
|

|
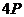
|

|
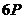
|
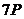
|
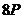
|
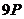
|
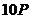
|
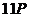
|
|
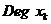
|
5
|
29
|
13
|
16
|
20
|
30
|
10
|
4
|
9
|
23
|
0
|
|
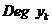
|
9
|
7
|
22
|
7
|
5
|
19
|
30
|
29
|
10
|
28
|
_
|
|
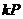
|
12P
|
13P
|
14P
|
15P
|
16P
|
17p
|
18P
|
19P
|
20P
|
21P
|
22P
|
|
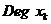
|
8
|
22
|
27
|
21
|
1
|
11
|
15
|
18
|
2
|
26
|
_
|
|
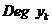
|
19
|
30
|
28
|
26
|
14
|
15
|
23
|
28
|
27
|
0
|
|
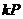
|
23P
|
24P
|
25P
|
26P
|
27P
|
28P
|
29P
|
30P
|
31P
|
32P
|
33P
|
|
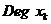
|
26
|
2
|
18
|
15
|
11
|
1
|
21
|
27
|
22
|
8
|
0
|
|
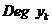
|
13
|
30
|
20
|
19
|
21
|
15
|
23
|
14
|
11
|
27
|
0
|
|
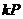
|
34P
|
35P
|
36P
|
37P
|
38P
|
39P
|
40P
|
41P
|
42P
|
43P
|
44P
|
|
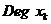
|
23
|
9
|
4
|
10
|
30
|
20
|
16
|
13
|
29
|
5
|
*
|
|
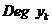
|
25
|
27
|
25
|
18
|
7
|
23
|
29
|
14
|
15
|
*
|
Приймемо
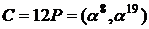 .
.
При діленні
точки 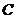 на два отримаємо дві точки
на два отримаємо дві точки
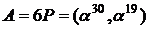 й
й 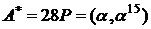 .
.
Розглянемо
всі операції при діленні точки
відповідно до (3), (5) (друга з формул) в ОНБ із ізоморфізмом, тобто
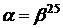 ,
, 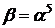 .
.
У нормальному базисі маємо  . Розв’язуємо рівняння (3)
. Розв’язуємо рівняння (3)
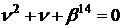 .
.
Відповідно до таблиці 2 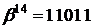 , тоді одне з розв’язань для
, тоді одне з розв’язань для
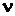 легко отримати,
задаючи перший біт, скажімо, рівним 0.
легко отримати,
задаючи перший біт, скажімо, рівним 0.
Таблиця 2 - Елементи поля 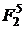 як степені елемента
як степені елемента  в ОНБ
в ОНБ
|
0
|
00000
|
1
|
11111
|
-
|
-
|
|
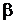
|
10000
|
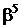
|
00011
|
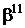
|
01101
|
|
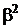
|
01000
|

|
10001
|
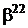
|
10110
|
|
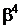
|
00100
|
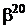
|
11000
|
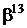
|
01011
|
|
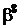
|
00010
|
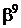
|
01100
|
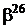
|
10101
|
|
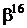
|
00001
|
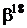
|
00110
|
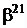
|
11010
|
|
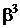
|
10010
|
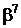
|
10111
|
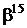
|
10011
|
|
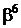
|
01001
|
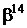
|
11011
|
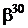
|
11001
|
|
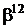
|
10100
|
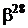
|
11101
|
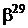
|
11100
|
|
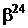
|
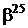
|
11110
|
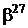
|
01110
|
|
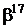
|
00101
|
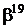
|
01111
|
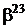
|
00111
|
При цьому інші біти визначаються
із суми
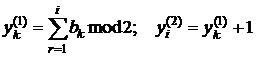 , тобто
, тобто
 .
.
Друге розв’язання, мабуть,
дорівнює 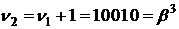 . Легко перевірити,
що отримані розв’язання задовольняють рівняння
. Легко перевірити,
що отримані розв’язання задовольняють рівняння
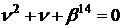 .
.
Згідно з (5) (перша з формул) і
даних таблиці 2 маємо
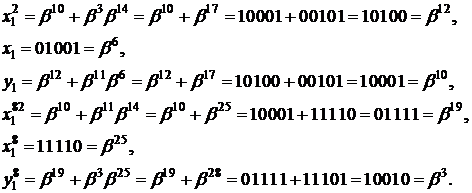
Отримано дві точки:
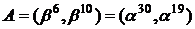 і
і 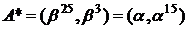 .
.
Для визначення кожної необхідно
виконати по два множення елементів поля. Неважко перевірити виконання умови
дискретне
логарифмування метод
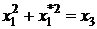 ,
, 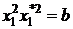 ,
,
зокрема,
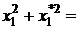
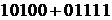
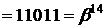 .
.
Обидві точки мають сліди
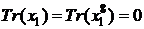 ,
,
і, отже, діляться на два, але
мають різні порядки. Точка 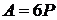 має порядок 22, а точка
має порядок 22, а точка 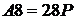 - порядок Для визначення порядку достатньо виконати ще
одне ділення на два. Якщо поділити точку
- порядок Для визначення порядку достатньо виконати ще
одне ділення на два. Якщо поділити точку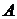 , то отримаємо дві точки порядку 44, що не
діляться на два (з непарною вагою x координат). При діленні точки
, то отримаємо дві точки порядку 44, що не
діляться на два (з непарною вагою x координат). При діленні точки 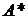 отримаємо дві точки з
порядками 22 й 11 (з парною вагою x координат).
отримаємо дві точки з
порядками 22 й 11 (з парною вагою x координат).
/