Степенные ряды
ВЫСШАЯ МАТЕМАТИКА
Степенные ряды
Содержание
1. Определение степенного ряда.
Теорема Абеля
2. Свойства степенных рядов
3. Ряды Тейлора, Маклорена для
функций
4. Разложение некоторых элементарных
функций в ряд Маклорена
5. Приложения степенных рядов
1. Определение степенного ряда.
Теорема Абеля
Степенные ряды являются частным
случаем функциональных рядов.
Определение 1.1. Степенным рядом называется
функциональный ряд вида 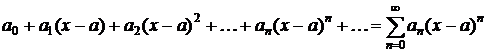 .(1.1)
.(1.1)
Здесь 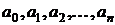 –
постоянные вещественные числа, называемые коэффициентами степенного ряда;
а – некоторое постоянное число, х – переменная, принимающая
значения из множества действительных чисел.
–
постоянные вещественные числа, называемые коэффициентами степенного ряда;
а – некоторое постоянное число, х – переменная, принимающая
значения из множества действительных чисел.
При 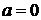 степенной
ряд (1.1) принимает вид
степенной
ряд (1.1) принимает вид
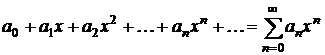 .
(1.2)
.
(1.2)
Степенной ряд (1.1) называют рядом
по степеням разности 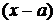 , ряд (1.2) –
рядом по степеням х.
, ряд (1.2) –
рядом по степеням х.
Если переменной х придать
какое-либо значение, то степенной ряд (1.1) (или (1.2)) превращается в числовой
ряд, который может сходиться или расходиться.
Определение 1.2. Областью сходимости
степенного ряда называется множество тех значений х, при которых
степенной ряд сходится.
Ряд (1.1) с помощью подстановки 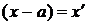 приводится к более простому виду (1.2),
поэтому вначале будем рассматривать степенные ряды вида (1.2).
приводится к более простому виду (1.2),
поэтому вначале будем рассматривать степенные ряды вида (1.2).
Для нахождения области сходимости
степенного ряда важную роль играет следующая теорема.
Теорема 1.1 (Теорема Абеля):
если степенной ряд (1.2) сходится при
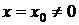 , то он абсолютно сходится при всех
значениях х, удовлетворяющих неравенству
, то он абсолютно сходится при всех
значениях х, удовлетворяющих неравенству 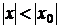 ; если
же ряд (1.2) расходится при
; если
же ряд (1.2) расходится при 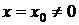 , то он расходится
при всех значениях х, удовлетворяющих неравенству
, то он расходится
при всех значениях х, удовлетворяющих неравенству 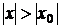 .
.
Теорема Абеля дает ясное
представление о структуре области сходимости степенного ряда.
Теорема 1.2:
область сходимости степенного ряда
(1.2) совпадает с одним из следующих интервалов:
1) 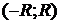 ; 2)
; 2) 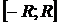 ; 3)
; 3) 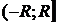 ; 4)
; 4) 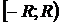 ,
,
где R – некоторое неотрицательное
действительное число или 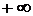 .
.
Число R называется радиусом сходимости,
интервал 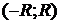 – интервалом сходимости
степенного ряда (1.2).
– интервалом сходимости
степенного ряда (1.2).
Если 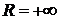 , то
интервал сходимости представляет собой всю числовую ось
, то
интервал сходимости представляет собой всю числовую ось 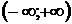 .
.
Если 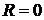 , то
интервал сходимости вырождается в точку
, то
интервал сходимости вырождается в точку 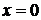 .
.
Замечание: если 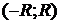 –
интервал сходимости для степенного ряда (1.2), то
–
интервал сходимости для степенного ряда (1.2), то 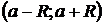 –
интервал сходимости для степенного ряда (1.1).
–
интервал сходимости для степенного ряда (1.1).
Из теоремы 1.2 следует, что для
практического нахождения области сходимости степенного ряда (1.2) достаточно
найти его радиус сходимости R
и выяснить вопрос о сходимости этого ряда на концах интервала сходимости 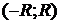 , т. е. при
, т. е. при 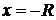 и
и 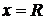 .
.
Радиус сходимости R степенного ряда можно найти по одной
из следующих формул:
формула Даламбера:
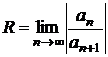 ;(1.3)
;(1.3)
формула Коши:
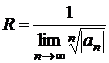 .(1.4)
.(1.4)
Если в формуле Коши 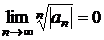 , то полагают
, то полагают 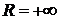 ,
если
,
если 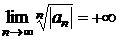 , то полагают
, то полагают 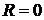 .
.
Пример 1.1. Найти радиус сходимости, интервал
сходимости и область сходимости степенного ряда 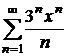 .
.
Решение
Найдем радиус сходимости данного ряда
по формуле
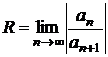
В нашем случае
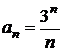 ,
, 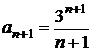 .
.
Тогда 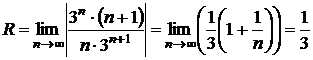 .
.
Следовательно, интервал сходимости
данного ряда имеет вид 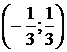 .
.
Исследуем сходимость ряда на концах
интервала сходимости.
При 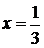 степенной
ряд превращается в числовой ряд
степенной
ряд превращается в числовой ряд
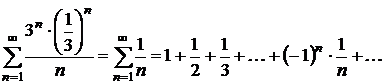 .
.
который расходится как гармонический
ряд.
При 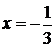 степенной
ряд превращается в числовой ряд
степенной
ряд превращается в числовой ряд
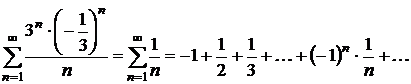 .
.
Это – знакочередующийся ряд, члены
которого убывают по абсолютной величине и 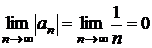 .
Следовательно, по признаку Лейбница этот числовой ряд сходится.
.
Следовательно, по признаку Лейбница этот числовой ряд сходится.
Таким образом, промежуток 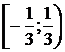 – область сходимости данного степенного
ряда.
– область сходимости данного степенного
ряда.
2. Свойства степенных рядов
Степенной ряд (1.2) представляет
собой функцию 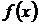 , определенную в интервале
сходимости
, определенную в интервале
сходимости 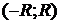 , т. е.
, т. е.
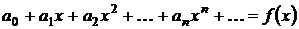 .
.
Приведем несколько свойств функции 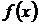 .
.
Свойство 1. Функция 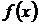 является
непрерывной на любом отрезке
является
непрерывной на любом отрезке 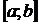 , принадлежащем
интервалу сходимости
, принадлежащем
интервалу сходимости 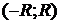 .
.
Свойство 2. Функция 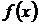 дифференцируема
на интервале
дифференцируема
на интервале 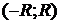 , и ее производная
, и ее производная 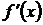 может быть найдена почленным
дифференцированием ряда (1.2), т. е.
может быть найдена почленным
дифференцированием ряда (1.2), т. е.
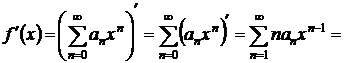
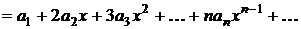 ,
,
для всех 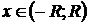 .
.
Свойство 3. Неопределенный интеграл от
функции 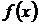 для всех
для всех 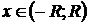 может быть получен почленным
интегрированием ряда (1.2), т. е.
может быть получен почленным
интегрированием ряда (1.2), т. е.
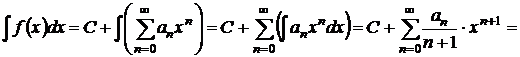
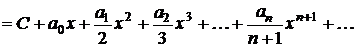
для всех 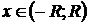 .
.
Приведенные свойства справедливы
также и для степенных рядов (1.1).
Пример 2.1. Рассмотрим степенной ряд
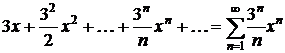 .
.
Область сходимости этого ряда, как
показано в примере 1.1, есть промежуток 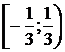 .
.
Почленно продифференцируем этот ряд:
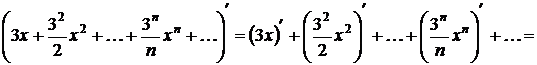
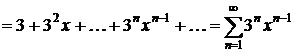 .(2.1)
.(2.1)
По свойству 2 интервал сходимости
полученного степенного ряда (2.1) есть интервал 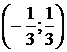 .
.
Исследуем поведение этого ряда на
концах интервала сходимости, т. е. при 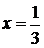 и
при
и
при 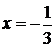 .
.
При 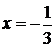 степенной
ряд (2.1) превращается в числовой ряд
степенной
ряд (2.1) превращается в числовой ряд
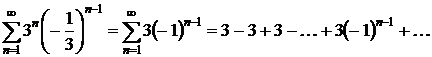 .
.
Этот числовой ряд расходится, так как
не выполняется необходимый признак сходимости 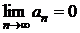 :
: 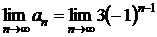 , который не существует.
, который не существует.
При 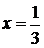 степенной
ряд (2.1) превращается в числовой ряд
степенной
ряд (2.1) превращается в числовой ряд
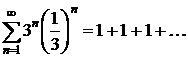 ,
,
который также расходится, так как не
выполняется необходимый признак сходимости.
Следовательно, область сходимости
степенного ряда, полученного при почленном дифференцировании исходного
степенного ряда, изменилась и совпадает с интервалом 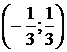 .
.
3. Ряды Тейлора, Маклорена для
функций
Пусть 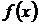 –
дифференцируемая бесконечное число раз функция в окрестности точки
–
дифференцируемая бесконечное число раз функция в окрестности точки 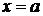 , т. е. имеет производные любых порядков.
, т. е. имеет производные любых порядков.
Определение 3.1. Рядом Тейлора
функции 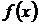 в точке
в точке 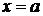 называется
степенной ряд
называется
степенной ряд
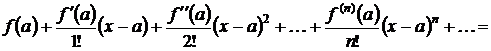
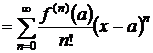 . (3.1)
. (3.1)
В частном случае при 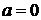 ряд (3.1) называется рядом
Маклорена:
ряд (3.1) называется рядом
Маклорена:
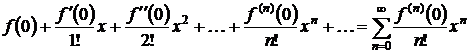 . (3.2)
. (3.2)
Возникает вопрос: в каких случаях ряд
Тейлора для дифференцированной бесконечное число раз функции 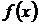 в окрестности точки
в окрестности точки 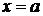 совпадает с функцией
совпадает с функцией 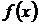 ?
?
Возможны случаи, когда ряд Тейлора
функции 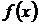 сходится, однако его сумма не равна
сходится, однако его сумма не равна
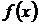 .
.
Приведем достаточное условие
сходимости ряда Тейлора функции 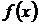 к этой функции.
к этой функции.
Теорема 3.1:
если в интервале 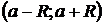 функция
функция 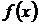 имеет
производные любого порядка и все они по абсолютной величине ограничены одним и
тем же числом, т. е.
имеет
производные любого порядка и все они по абсолютной величине ограничены одним и
тем же числом, т. е. 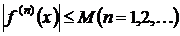 , то ряд Тейлора этой функции
сходится к
, то ряд Тейлора этой функции
сходится к 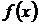 для любого х из этого интервала
для любого х из этого интервала 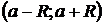 , т. е. имеет место равенство
, т. е. имеет место равенство
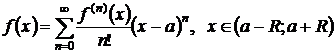 .
.
Для выяснения выполнения этого
равенства на концах интервала сходимости требуются отдельные исследования.
Следует отметить, что если функция
разлагается в степенной ряд, то этот ряд является рядом Тейлора (Маклорена)
этой функции, причем это разложение единственно.
4. Разложение некоторых элементарных
функций в ряд Маклорена
1. 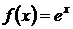 . Для
этой функции
. Для
этой функции 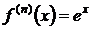 ,
, 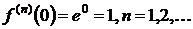 .
.
По формуле (3.2) составим ряд
Маклорена данной функции:
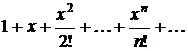 . (3.3)
. (3.3)
Найдем радиус сходимости ряда (3.3)
по формуле (1.3):
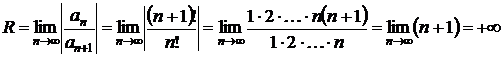 .
.
Следовательно, ряд (3.3) сходится при
любом значении 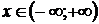 .
.
Все производные функции 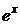 на любом отрезке
на любом отрезке 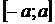 ограничены, т. е.
ограничены, т. е.
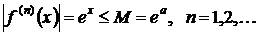 .
.
Поэтому, согласно теореме 3.1, имеет
место разложение
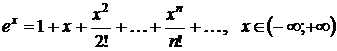 .
(3.4)
.
(3.4)
2. 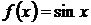 . Для
этой функции
. Для
этой функции 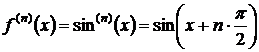 ,
, 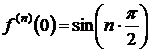 ,
, 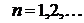 .
.
Отсюда следует, что при 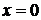 производные четного порядка равны нулю,
а производные нечетного порядка чередуют знак с плюса на минус.
производные четного порядка равны нулю,
а производные нечетного порядка чередуют знак с плюса на минус.
По формуле (3.2) составим ряд
Маклорена:
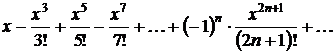 .
.
При любом фиксированном значении этот
ряд сходится как знакочередующийся по признаку Лейбница. При этом
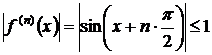
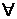
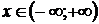 .
.
Поэтому, согласно теореме 3.1, имеет
место разложение
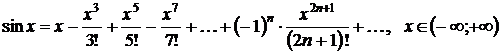 . (3.5)
. (3.5)
3. 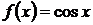 .
Воспользуемся разложением (3.5) в ряд Маклорена функции
.
Воспользуемся разложением (3.5) в ряд Маклорена функции 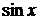 и
свойством 2 о дифференцировании степенного ряда. Имеем
и
свойством 2 о дифференцировании степенного ряда. Имеем
Поскольку при почленном
дифференцировании интервал сходимости степенного ряда не изменяется, то
разложение (3.6) имеет место при любом 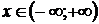 .
.
Приведем без доказательства
разложения других элементарных функций в ряды Маклорена.
4. 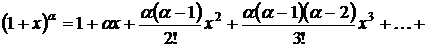
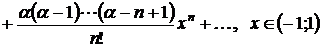 – биномиальный
ряд (
– биномиальный
ряд (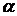 – любое действительное число).
– любое действительное число).
Если 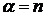 –
положительное целое число, то получаем бином Ньютона:
–
положительное целое число, то получаем бином Ньютона:
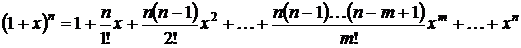 .
.
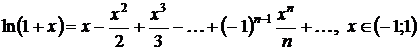 – логарифмический
ряд.
– логарифмический
ряд.
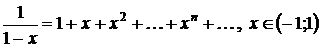 .
.
5. Приложения степенных рядов
Степенные ряды находят применение в
таких задачах, как приближенное вычисление функций с заданной степенью
точности, определенных интегралов, решение дифференциальных уравнений и др.
Приведем приближенные формулы для
вычисления некоторых наиболее часто встречающихся функций при достаточно малых
значениях х:
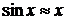 ;
; 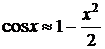 ;
; 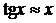 ;
; 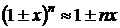 ;
;
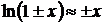 ;
; 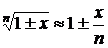 .
.
Литература
1. Высшая математика: Общий курс:
Учебник – 2-е изд., перераб. / А.И. Яблонский, А.В. Кузнецов, Е.И. Шилкина и
др.; Под общ. ред. С.А. Самаля. – Мн.: Выш. шк., 2000.– 351 с.
2. Марков Л.Н., Размыслович Г.П.
Высшая математика. Ч. 2. Основы математического анализа и элементы
дифференциальных уравнений. – Мн.: Амалфея, 2003. – 352 с.