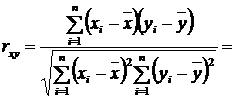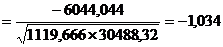Вариационные ряды
Задание № 1.
По данной выборке:
а) Найти вариационный ряд;
б) Построить функцию распределения;
в) Построить полигон частот;
г) Вычислить среднее значение СВ, дисперсию,
среднеквадратичное отклонение.
№=42. Элементы выборки:
1 5 1 8 1 3 9 4 7 3 7 8 7 3 2 3 5 3 8 3 5 2 8 3
7 9 5 8 8 1 2 2 5 1 6 1 7 6 7 7 6 2
Решение.
а) построение ранжированного вариационного ряда:
1 1 1 1 1 1 2 2 2 2 2 3 3 3 3 3 3 3 4 5 5 5 5 5
6 6 6 7 7 7 7 7 7 7 8 8 8 8 8 8 9 9
б) построение дискретного вариационного ряда.
Вычислим число групп в вариационном ряду
пользуясь формулой Стерджесса:
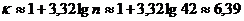
Примем число групп равным 7.
Зная число групп, рассчитаем величину интервала:
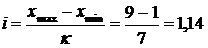
Для удобства построения таблицы примем число
групп равным 8, интервал составит 1.
Таблица 2
|
xj
|
1-2 (+)
|
2-3
|
3-4
|
4-5
|
5-6
|
6-7
|
7-8
|
8-9
|
Итого
|
|
fj
|
11
|
7
|
1
|
5
|
3
|
7
|
6
|
2
|
42
|
|
Середина интервала xj’
|
1,5
|
2,5
|
3,5
|
4,5
|
5,5
|
6,5
|
7,5
|
8,5
|
|
|
xj’fj
|
16,5
|
17,5
|
3,5
|
22,5
|
16,5
|
45,5
|
45
|
17
|
184
|
|
Накопленная частота fj’
|
11
|
18
|
19
|
24
|
27
|
34
|
40
|
42
|
|
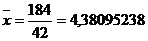
в) построение функции распределения:
С помощью ряда накопленных частот построим
кумулятивную кривую распределения.
Диаграмма 1
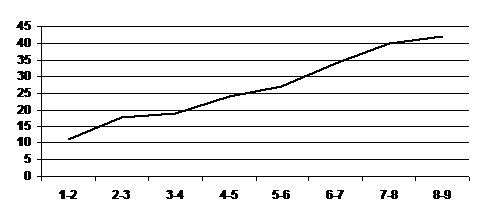
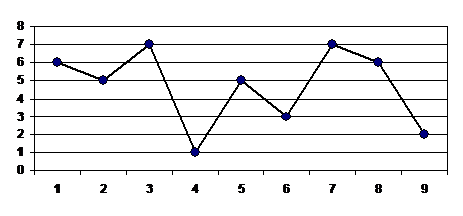
в) построение полигона частот:
Диаграмма 2
г) вычисление среднего значения СВ, дисперсии,
среднеквадратичного отклонения:
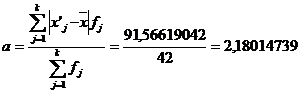
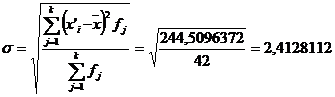
Задание № 2.
По заданной выборке проверить гипотезу о
нормальном распределении СВ по критерию согласия Пирсона. Произвести
интервальную оценку выборочного среднего значения с доверительной вероятностью
0,98
Таблица 1.
|
78
|
80
|
83
|
84
|
84
|
86
|
88
|
88
|
89
|
89
|
91
|
91
|
92
|
92
|
94
|
94
|
96
|
96
|
96
|
97
|
97
|
99
|
99
|
101
|
102
|
|
102
|
104
|
104
|
105
|
105
|
107
|
109
|
110
|
110
|
115
|
120
|
76
|
78
|
81
|
83
|
84
|
86
|
86
|
88
|
88
|
89
|
89
|
91
|
92
|
92
|
|
92
|
94
|
94
|
96
|
96
|
97
|
97
|
99
|
99
|
99
|
101
|
102
|
104
|
104
|
105
|
105
|
107
|
107
|
110
|
110
|
112
|
115
|
75
|
78
|
80
|
|
83
|
84
|
86
|
86
|
88
|
88
|
89
|
91
|
91
|
91
|
92
|
92
|
94
|
94
|
96
|
96
|
97
|
97
|
99
|
99
|
101
|
101
|
102
|
102
|
104
|
|
104
|
105
|
107
|
109
|
109
|
112
|
115
|
117
|
73
|
81
|
84
|
84
|
86
|
88
|
89
|
91
|
91
|
92
|
94
|
96
|
96
|
97
|
99
|
101
|
101
|
|
104
|
105
|
105
|
107
|
107
|
110
|
117
|
123
|
67
|
78
|
81
|
81
|
83
|
84
|
84
|
86
|
86
|
88
|
88
|
88
|
89
|
89
|
91
|
91
|
91
|
|
92
|
92
|
92
|
94
|
94
|
94
|
96
|
96
|
97
|
97
|
97
|
99
|
99
|
99
|
101
|
101
|
102
|
102
|
104
|
104
|
104
|
105
|
105
|
107
|
107
|
|
109
|
109
|
110
|
110
|
113
|
118
|
121
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№=182
Решение.
Вычислим число групп в вариационном ряду
пользуясь формулой Стерджесса:
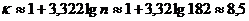
Определим величины интервала:
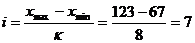
Примем число групп равным 8, а число интервалов
7.
Таблица 2.
|
Номер интервала
|
xj
|
fj
|
x’j
|
x’jfj
|
f’j
|
|
1
|
2
|
3
|
4
|
5
|
6
|
|
1
|
67-74 (+)
|
2
|
70,5
|
141
|
2
|
|
2
|
74-81
|
12
|
77,5
|
930
|
14
|
|
3
|
81-88
|
30
|
84,5
|
2535
|
44
|
|
4
|
88-95
|
40
|
91,5
|
3660
|
84
|
|
5
|
95-102
|
47
|
98,5
|
4629,5
|
131
|
|
6
|
102-109
|
32
|
105,5
|
3376
|
163
|
|
7
|
109-116
|
13
|
112,5
|
1462,5
|
176
|
|
8
|
116-123
|
6
|
119,5
|
717
|
182
|
|
Итого
|
|
182
|
|
17451
|
|
Условные обозначения в таблице: xj
- установленные интервалы; fj
- частота событий; x’j
- середина интервала; f’j
- накопленная частота.
На основании полученных данных построим таблицу
2.
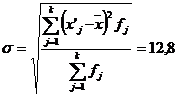
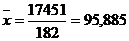
Значения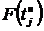 
и
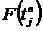находим
по таблице значений функции Лапласа.
Pj
определяется разностью 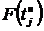и ,
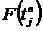а f’j
= Pj * n.
Таблица 3.
|
Номер интервала
|
Границы интервала
|
|
|
|
|
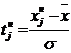
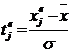
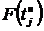
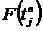
Pj
|
f’j
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
1
|
67-74
|
-2,26
|
-1,70
|
-0,4881
|
-0,4554
|
0,0327
|
5,9514
|
|
2
|
74-81
|
-1,70
|
-1,16
|
-0,4554
|
-0,3770
|
0,0784
|
14,2688
|
|
3
|
81-88
|
-1,16
|
-0,61
|
-0,3770
|
-0,2291
|
0,1479
|
26,9178
|
|
4
|
88-95
|
-0,61
|
-0,06
|
-0,2291
|
-0,0279
|
0, 2012
|
38,0268
|
|
5
|
95-102
|
-0,07
|
0,47
|
-0,0279
|
0,1808
|
0, 2087
|
37,9834
|
|
6
|
102-109
|
0,47
|
1,02
|
0,1808
|
0,3461
|
0,1653
|
30,0846
|
|
7
|
109-116
|
1,02
|
1,57
|
0,3461
|
0,4418
|
0,0957
|
17,4174
|
|
8
|
116-123
|
1,57
|
2,12
|
0,4418
|
0,4830
|
0,0412
|
7,4984
|
|
Итого
|
|
|
|
|
|
|
|
Условные обозначения в таблице:
xнj
- нижняя граница интервала;
xвj
- верхняя граница интервала;
tнj
и
tвj
- нормированные отклонения для нижней и верхней границ интервала;
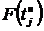и -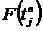
значение интегральной функции Лапласа для tнj
и
tвj;
Pj
- оценка вероятности попадания в интервал;
f’j
- частота теоретического распределения.
Итак, воспользуемся данными таблицы 1 и 2 для
расчета критерия "хи-квадрат", предварительно округлив теоретические
частоты в графе 8 табл.2, а также объединив частоты двух последних интервалов,
выполняя требование f’j
³ 5.
Таблица 4.
|
Номер интервала
|
Эмпирические частоты
|
Теоретические частоты
|
|
|
|
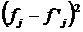
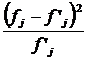
1
|
2
|
6
|
16
|
2,67
|
|
2
|
12
|
14
|
4
|
0,29
|
|
3
|
30
|
27
|
9
|
0,33
|
|
4
|
40
|
38
|
4
|
0,1
|
|
5
|
47
|
38
|
81
|
2,13
|
|
6
|
32
|
30
|
4
|
0,13
|
|
7
|
16
|
25
|
81
|
3,24
|
|
Итого
|
182
|
178
|
|
8,89
|
X2расч
= 8,89
Таким образом, проведенный расчет дает право не
отвергать гипотезу о нормальном характере эмпирического распределения.
Произведем интервальную оценку выборочного
среднего значения с доверительной вероятностью 0,98.
На основе имеющейся выборки получим точечную
оценку математического ожидания в виде выборочной средней:
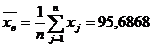
Среднеквадратичное отклонение составляет: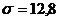 
.
Уровень надежности 
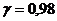. Определяем
значение функции Лапласса:
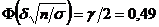
По таблице значений функции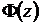 
находим
соответствующее значение z.
В данном случае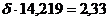 
. Тогда 
.
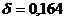Доверительный интервал] 95,6868 - 0,164, 95,6868
+ 0,164 [=
=] 95,5228, 95,8508 [.
Следовательно, 95,5228 < Mx
< 95,8508 с вероятностью 0,98.
Задание № 4.
По заданной выборке (x,y)
найти коэффициент корреляции и уравнения линейной регрессии y=a+b*x,
№=45
Таблица 5
|
x…... y
|
x…... y
|
x…... y
|
x…... y
|
x…... y
|
x…... y
|
x…... y
|
x…... y
|
x…... y
|
x…... y
|
x…... y
|
|
23
|
-115
|
18
|
-90
|
10
|
-48
|
19
|
-91
|
18
|
-84
|
9
|
-44
|
12
|
-55
|
24
|
-115
|
6
|
-26
|
22
|
-107
|
18
|
-84
|
|
18
|
-83
|
11
|
-54
|
15
|
-71
|
13
|
-64
|
8
|
-51
|
14
|
-64
|
22
|
-109
|
8
|
-38
|
14
|
-64
|
22
|
-106
|
9
|
-43
|
|
16
|
-74
|
17
|
-85
|
15
|
-71
|
13
|
-60
|
11
|
-37
|
24
|
-118
|
18
|
-87
|
6
|
-28
|
7
|
-31
|
22
|
-109
|
13
|
-64
|
|
8
|
-35
|
8
|
-35
|
12
|
-56
|
12
|
-54
|
14
|
-67
|
14
|
-68
|
21
|
-102
|
10
|
-46
|
16
|
-79
|
17
|
-80
|
18
|
-87
|
|
22
|
-105
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение:
На основании исходных данных найдем суммы и
средние значения x
и y:
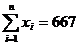
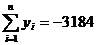
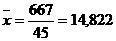
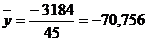
Вычислим параметр парной линейной корреляции:
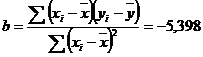
Свободный член уравнение регрессии вычислим по
формуле:
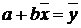, откуда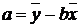 
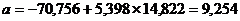
Уравнение регрессии в целом имеет вид:
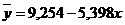
Коэффициент корреляции, рассчитанный на основе
полученных данных:
