Поиск с возвращением

Поиск с возвращением

Чувашский Государственный университет имени И.Н. Ульянова

Кафедра вычислительной техники

Курсовая работа на тему:

«Поиск с возвращением»

Выполнил студент

группы ИВТ 41-10

Петров Н.И.

Проверил: Павлов Л.А.

Чебоксары 2012

Содержание

1. Индивидуальное задание

. Уточнение задания

. Теоретические сведения (Метод контурных токов)

. Расчет цепи «ручным методом»

. Расчет цепи с помощью программы

. Моделирование цепи в схемном эмуляторе

. Анализ результатов

Заключение

Список используемой литературы

Приложение

1. Индивидуальное задание

Рассчитать электрическую схему (рис. 1) тремя способами. Провести анализ полученных результатов.

Расчёт необходимо произвести следующими способами:

1.    Вручную: расчёт осуществляется по приведенным формулам выбранной методики расчёта.

2.      Программно: расчёт цепи осуществляет программа, в которой реализованы необходимые методы вычислительной математики .

.        С помощью схемного эмулятора MicroCap: выбранная схема «собирается» в MicroCap и расчёт осуществляется с его помощью.

рис. 1

№ метода решения системы уравнений  =12 mod 5+1=3(Крамера)

№ метода вычисления определителя      =12 mod 2+1=1(Компактная схема Гаусса)

2. Уточнение задания

Для расчета цепи я выбрал метод непосредственного применения законов Кирхгофа. Этот метод довольно прост для вычисления токов в цепи(рис. 1). Однако в силу того, что в цепи присутствуют емкостные и индуктивные элементы расчет, а значит, цепь является цепью переменного тока, метод, основывающийся только на непосредственном применении законов Кирхгофа, не даст нам корректных результатов. Поэтому нам необходимо использовать комплексный метод расчета электрических цепей, который включает в себя применение законов Кирхгофа. Зададимся следующими величинами, характеризующими каждый элемент цепи.

=R5=R6=R8=R10=R11=200 Ом=C7= С5=С11=5 мкФ=L9=2*10^-7 Гн

 град/c=100 В    E3=200 В=150 В          =1 А

Ниже приведены теоретические сведения по данному методу.

. Теоретические сведения

Вычисление непосредственно по первому закону Кирхгофа некоторого тока по другим уже найденным токам, сходящимся к данному узлу цепи, или вычисление по второму закону Кирхгофа падения напряжения на некотором участке контура цепи по уже найденным падениям напряжения на других участках контура и э.д.с. Однако эта операция связана с громоздкими и трудоемкими вычислениями. Громоздкость подобных вычислений является следствием того, что синусоидальная величина - ток, напряжение, э.д.с. - при заданной частоте  определяется двумя величинами - амплитудой и начальной фазой.

Существенное упрощение достигается изображением синусоидальных функций времени комплексными числами , так как каждое комплексное число содержит в себе две величины - модуль A и аргумент  при показательной форме записи , или вещественную  и мнимую  при алгебраической и тригонометрической формах записи

.

Вычисления проводятся по приведенным ниже формулам в данной последовательности:

1)      вычисляем емкостное

=1/c

и индуктивное

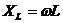
сопротивления для каждого конденсатора и катушки цепи соответственно;

2)      находим  по формуле

3)      E=(Em/)*;

находим  по формуле

=(Jm/)*;

4)      по первому и второму законам Кирхгофа составляем систему уравнений,в которой  заменяем на , а 1/ заменяем на -.

5) решая данную СЛАУ любым методом получим решение представленное комплексным числом.

6)      для всех найденных i получим

Imax= и (Im(i)/Re(i))

Далее остается только записать

i(t)=Imax*sin()

Далее приводятся теоретические сведения по методу применения законов Кирхгофа.

На рисунке 2 изображена схема разветвленной электрической цепи. Известны величины сопротивлений и ЭДС, необходимо определить токи.

ток контур цепной электрический

В схеме имеются семь узлов, можно составить семь уравнения по первому закону Кирхгофа. Укажем произвольно направления токов. Запишем уравнения:

) I₁ - I₂ - I₁₁ = 0

) I₂ - I₃ - I₄ = 0

) I₄ - I₅ - I₆ = J

) I₆ + I₇ - I₉ = 0

) I₁ + I₇ + I₈ = J

) I₅ + I₈ + I₉ - I₁₀ = 0

) I₃ + I₁₀ + I₁₁ = 0

Выберем контуры и для каждого из них запишем узлы в порядке их обхода по нему:

: 3 - 4 - 6;

: 2 - 3 - 6 - 7;

: 1 - 7 - 6 - 5;

По второму закону Кирхгофа:

1)

)

)

)

Решив совместно системы уравнений , определим токи в схеме.
Ток в ветви может иметь отрицательное значение. Это означает, что действительное направление тока противоположно выбранному нами.

. Расчет цепи «ручным методом»

В данном пункте будет приведен расчет цепи ручным методом по формулам, описанным мною выше. При расчете будут использованы значения параметров, установленные в пункте (3) данной пояснительной записки.

Вычислим емкостное сопротивление для каждого конденсатора:

Вычислим индуктивное сопротивление для катушек:

Найдем

=

Используя первый и второй закон Кирхгофа, получим следующую систему уравнений:

.0100 -0.0100 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 -0.0100 0.0000

.0000 0.0100 -0.0100 -0.0100 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000

.0000 0.0000 0.0100 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0100 0.0100 0.0000

.0000 0.0000 0.0000 0.0100 -0.0100 -0.0100 0.0000 0.0000 0.0000 0.0000 0.0000 0.7071

.0000 0.0000 0.0000 0.0000 0.0100 0.0000 0.0000 0.0100 0.0100 -0.0100 0.0000 | 0.0000

.0000 0.0000 0.0000 0.0000 0.0000 0.0100 0.0100 0.0000 -0.0100 0.0000 0.0000 0.7071

.0100 0.0000 0.0000 0.0000 0.0000 0.0000 0.0100 0.0100 0.0000 0.0000 0.0000 0.0000

.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0 + 0.0003i -2.0000 0 + 0.0126i 0.0000 0.0000 0.0000

.0000 0.0000 0.0000 0.0000 -2.0000 - 0.0003i 2.0000 0.0000 0.0000 0 + 0.0126i 0.0000 0.0000 0.0000

.0000 0.0000 0.0000 2.0000 2.0000 + 0.0003i 0.0000 0.0000 0.0000 0.0000 2.0000 0.0000 -141.4214

.0000 0.0000 0.0000 0.0000 0.0000 0.0000 0.0000 2.0000 0.0000 2.0000 -2.0000 - 0.0003i 70.7107

Решая данную СЛАУ любым методом получим решение представленное комплексным числом.

для всех найденных i получим

Imax=и (Im(i)/Re(i))

Далее остается только записать

i(t)=Imax*sin()

. Расчет цепи с помощью программы

Алгоритм расчёта цепи

Нахождение детерминанта для решения СЛАУ расчета токов с помощью компактной схемы Гаусса

LU-разложение - представление матрицы <#"551066.files/image034.gif">;

причем диагональные элементы матрицы L: l_ii = 1, .

Тогда, если известно LU-разложение матрицы, её определитель можно вычислить по формуле det(A) = det(LU) = det(L)det(U) = det(U)

Найти матрицы L и U можно следующим образом(выполнять шаги следует строго по порядку, т.к. следующие элементы находятся с использованием предыдущих):

Для

В итоге мы получим матрицы - L и U. В программной реализации данного метода (компактная схема Гаусса) для представления матриц L и U можно обойтись всего одним массивом, в котором совмещаются матрицы L и U. Например вот так(для матрицы размером

Решение СЛАУ методом Крамера

Рассмотрим систему из n уравнений с n неизвестными:

Вычислим определитель основной матрицы системы:

Обозначим через Δ_i определитель, получающийся из определителя Δ основной матрицы системы уравнений заменой его i-го столбца столбцом из свободных членов b₁,b₂,...,b_n (с сохранением без изменения всех остальных столбцов).

Квадратная система линейных уравнений с определителем основной матрицы, отличным от нуля, имеет и притом единственное решение, определяемое следующей формулой:

Далее находим токи по теоретическим сведениям

Результаты работы программы

. Моделирование цепи в схемном эмуляторе

Произведем моделирование схемы в пакете Micro-Cap (параметры цепи такие же, как в программном и ручном расчетах):

Результаты работы программы

7. Анализ результатов

Произведем сравнительный анализ результатов, полученных тремя различными способами, для чего сведем все полученные данные в одну таблицу:

Как видно из таблицы, результаты, полученные в Micro-Cap, немного отличаются от результатов, полученных с помощью программы и ручного расчета. Это объясняется тем, что в схемном эмуляторе используются элементы, близкие по своим параметрам к реальным, а в программе и при ручном расчете элементы принимались идеальными.

Заключение

В результате проделанной работы разработана программа, которая позволяет автоматизировать процесс расчета цепи постоянного тока.

Был произведен расчет заданной цепи тремя различными способами: вручную, с помощью программы и в схемном эмуляторе.

Результаты ручного расчета и работы программы совпадают, т.к. в программе реализован алгоритм ручного расчета законами Кирхгофа. Данные, полученные в схемном эмуляторе ненамного отличаются от результатов работы программы, т.к. в эмуляторе используются элементы, близкие к реальным, а в программном растете элементы идеальные.

Тем не менее, программная реализация расчета цепи значительно ускорит процесс расчета, повысит эффективность работы и упростит анализ результатов.

Список используемой литературы

1. Теоретические основы электротехники: Учебник для вузов. Том 1. - 4-е изд. /К. С. Демирчан, Л. Р. Нейман. СПб.:Питер,2004. - 463с.:ил.

. Джон Г. Мэтьюз, Куртис Д. Финк. Численные методы. Использование Matlab. - М.: Издательский дом «Вильямс», 2001. - 720 с.

Приложение

Модуль данных - файл data.m:

%модуль данных

%данные цепи

%время=0.25^10-3

%источник тока=1

%резисторы=200=200=200=200=200=200

%циклическая частота=2*3.14*10^6

%емкость конденсатора=5*10^-6=5*10^-6=5*10^-6=5*10^-6

%индуктивность катушки=2*10^-7=2*10^-7

%напряжение=100=150=200

Модуль подготовки данных для расчета - файл rasch.m:

n=11=zeros(n,n);q=1:nw=1:n(q,w)=0.000000000001;=[1 -1 0.000000001 0.000000001 0.000000001 0.000000001 0.000000001 0.000000001 0.000000001 0.000000001 -1;%1

.0000000001 1 -1 -1 0.000000001 0.000000001 0.000000001 0.000000001 0.000000001 0.000000001 0.000000001;%2

.000000001 0.000000001 1 0.000000001 0.000000001 0.000000001 0.000000001 0.000000001 0.00001 1 1%7

.000000001 0.000000001 0.000000001 1 -1 -1 0.000000001 0.000000001 0.000000001 0.000000001 0.000000001;%3

.000000001 0.000000001 0.000000001 0.000000001 1 0.000000001 0.000000001 1 1 -1 0.000000001;%6

.000000001 0.000000001 0.000000001 0.000000001 0.000000001 1 1 0.000000001 -1 0.000000001 0.000000001;%4

0.000000001 0.000000001 0.000000001 0.000000001 0.000000001 1 1 0.000000001 0.000000001 0.000000001;%5

];k=1:nj=1:7(j,k)=AK1(j,k);qw=1:n(qw,1)=0.000000001;(4,1)=J/(2^(1/2));(7,1)=J/(2^(1/2));(9,5)=-(i/(am*C5)+R5);(9,6)=R6;(9,9)=am*L9*i;(10,4)=R4;(10,5)=i/(am*C5)+R5;(10,10)=R10;(10,1)=-E3/(2^(1/2));(8,7)=i/(am*C7);(8,9)=am*L9*i;(8,8)=-R8;(11,8)=R8;(11,10)=R10;(11,11)=-(i/(am*C11)+R11);(11,1)=E1/(2^(1/2)) ;

Модуль расчета детерминанта компактной схемой Гаусса - determinant.m:

function D=determinant(A,n)

%определение определителя

=zeros(n,n);Al=zeros(n,n);

(1,:)=A(1,:);k=2:n,

Al(k,1)=A(k,1)/Y(1,1);l=2:n,=0;j=l:n,=0;k=1:l-1,=sum+(Al(l,k)*Y(k,j));(l,j)=A(l,j)-sum;j=l+1:n=0;k=1:l-1=sum+(Al(j,k)*Y(k,l));(j,l)=1/Y(l,l)*(A(j,l)-sum);l=1:nj=l:n(l,j)=Y(l,j);l=2:nj=l+1:n(j,l)=Al(j,l);=AA(1,1);l=2:n,=D*AA(l,l);;

Главный модуль - файл main.m

data

%Проверим невырожденность системы(A);

%По правилу Крамера=zeros(1,n);=determinant(A,n);i=1:n= A;(:,i)=B;=determinant(A1,n);=D1/D;(1,i)=sqrt(imag(x1)^2+real(x1)^2);=atan(imag(x1)/real(x1));(i)=x(1,i)*sqrt(2)*sin(am*t+fi);