Вычитание сил инерции и тяготения
Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное
образовательное
учреждение высшего профессионального
образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ
И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра радиотехнических систем (РТС)
СТАТИСТИЧЕСКОЕ ИССЛЕДОВАНИЕ СИСТЕМЫ ДВУХ СЛУЧАЙНЫХ
ВЕЛИЧИН
Пояснительная записка к курсовой работе по дисциплине
«Теория вероятностей и математическая статистика»
Вариант 13
Студент гр.1А2
___________Леконцев Д.Р.
Руководитель
Ассистент каф. РТС, к.т.н.
 ____________Аникин А.С.
____________Аникин А.С.
«___»____________2014 г.
Томск 2014
РЕФЕРАТ
Курсовая работа, 18 с.,
3 рис., 4 источника, 1 прилож.
СЛУЧАЙНЫЕ
ВЕЛИЧИНЫ, ПОЛЕ РАССЕЯНИЯ, МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ, ДИСПЕРСИЯ, КОЭФФИЦИЕНТ
КОРРЕЛЯЦИИ, ПЛОТНОСТЬ РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ, ЛИНЕЙНАЯ РЕГРЕССИЯ.
Объектом
исследования являются два массива чисел X и Y.
Цель
работы – статистическое исследование системы двух случайных величин X и Y и разработка программы, соответствующей техническому
заданию.
В
результате работы был построен график поля рассеяния пар чисел X и Y. Вычислены
оценки числовых характеристик и оценка коэффициента корреляции для X и Y. Рассчитана и
построена графически оценка плотности распределения вероятностей для X и Y. Оценены
параметры оптимальной линейной регрессии и изображено поле рассеяния и линия
регрессии Y на X.
Все
необходимые вычисления были выполнены с помощью программного пакета MathCAD 14.
Оглавление
Введение. 6
1 Поле рассеяния исходных случайных величин. 7
2 Оценка числовых характеристик для исходных
случайных величин. 8
3 Расчёт оценки плотности распределения
вероятностей для исходных случайных величин. 10
4 Расчёт оптимальной линейной регрессии для
исходных случайных величин 13
Выводы.. 15
Список использованных источников. 16
Приложение А.. 17
“В практических применениях теории вероятностей
очень часто приходится сталкиваться с задачами, в которых результат опыта
описывается не одной случайной величиной, а двумя или более случайными
величинами, образующими комплекс или систему”[1,стр.155].
В нашей курсовой работе
мы исследуем эти две случайные величины на предмет зависимости друг от друга. Исследовать
эти случайные величины будем с помощью статистического исследования.
“Статистика - отрасль
знаний, в которой излагаются общие вопросы сбора, измерения и анализа массовых
статистических (количественных или качественных) данных;
изучение количественной стороны массовых общественных явлений в числовой форме”[2].
Данную курсовую работу
можно условно разделить на две части. Первая часть заключает в себе вычисления
и оценку характеристик X и Y. Вторая же часть содержит в себе оценку и построение
зависимости этих случайных величин.
Исходные данные,
представленные в файлах Xi.xls и Yi.xls, представляют
собой два массива чисел. При построении графика зависимости Y от X эти
массивы будут являться координатами точек. Совокупность всех этих точек,
представленных в декартовых координатах, является полем рассеяния исходных
случайных величин. Поле рассеяния двух случайных исходных величин представлено
на рисунке 1.1.
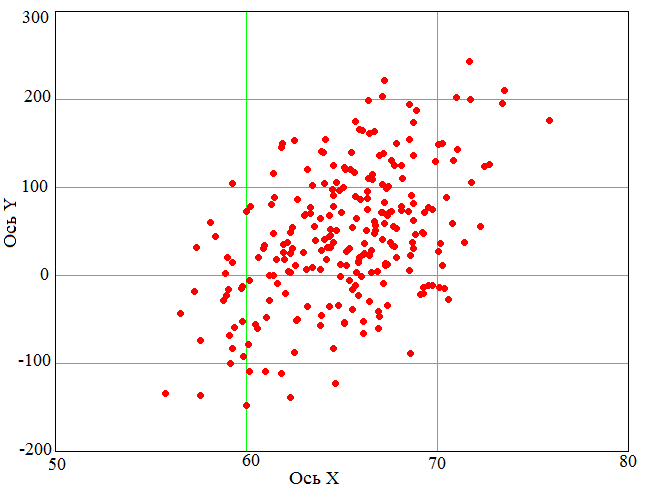
Рисунок 1.1 - Поле рассеяния двух исходных случайных
величин
Вероятностью случайного
события X называется численная
мера возможности появления этого события в результате данного опыта. Численная
мера возможности появления данного события в результате проводимого опыта
описывается отношением числа несовместных равновероятных событий, составляющих
событие X, к числу всех возможных элементарных событий
[3].
В данном случае для
каждой нашей выборки событием X является
появления любого числа из данной выборки. То есть число несовместных
равновероятных событий, составляющих событие X, будет
равно единице, так как появление любого из членов выборки равновероятно и
несовместно, из-за того что выборка образует полную группу событий и члены
одной выборки не зависят друг от друга. А числом всех возможных элементарных
событий выборки, будет являться количество элементов рассматриваемой выборки,
что в нашем случае составляет 247 элементов.
Из всего вышесказанного
получим формулу вероятности случайного события X и Y(1.1).
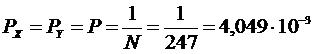 (1.1)
(1.1)
Для того чтобы
охарактеризовать исходные случайные величины, необходимо оценить их числовые
характеристики. Делается это главным образом, для того чтобы проследить
зависимость между данными случайными величинами. Основными характеристиками
случайных величин являются математическое ожидание, дисперсия и коэффициент
корреляции между двумя случайными величинами. Мы не можем определить значения
этих числовых характеристик, мы можем дать только оценку этих числовых
характеристик, потому что нашими исходными данными являются выборки из
генеральной совокупности, а не сама генеральная совокупность.
Из характеристик
положения в теории вероятностей важнейшую роль играет математическое ожидание
случайной величины, которое иногда называют средним значением случайной величины.
Математическим ожиданием случайной величины называется сумма произведений
значений случайной величины на вероятность появления значения случайной
величины [1,стр.80]. Математическое ожидание представлено формулой (2.1).
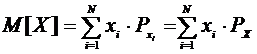 ,
(2.1)
,
(2.1)
где
N- количество всех возможных элементарных событий;
 - значения случайной величины;
- значения случайной величины;
 - вероятность появления значения
случайной величины.
- вероятность появления значения
случайной величины.
Применяя формулу (2.1) к нашим выборкам получим:
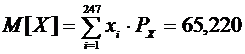
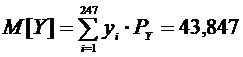
Для того чтобы дать
определения понятию “дисперсия”, необходимо для начала дать определение понятию
“центрированной случайной величине”. Центрированной случайной величиной
называется отклонение случайной величины от ее математического ожидания. Итак,
дисперсией случайной величины называется математическое ожидание квадрата
соответствующей центрированной величины[1,стр.89]. Дисперсия представлена формулой
(2.2).
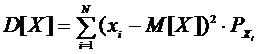 ,
(2.2)
,
(2.2)
где N- количество всех
возможных элементарных событий;
 - значения
случайной величины;
- значения
случайной величины;
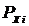 - вероятность
появления значения случайной величины;
- вероятность
появления значения случайной величины;
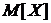 -
математическое ожидание.
-
математическое ожидание.
Применяя
формулу (2.2) к нашим выборкам, получим и учтя что для нашего случая 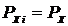 и
и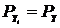 :
:
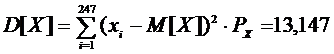

Для
того, чтобы показать насколько зависят друг от друга исходные случайные
величины вычислим оценку коэффициента корреляции. Корреляционным моментом
случайных величин X и Y
называется математическое ожидание произведения отклонений этих случайных
величин. Так как наши величины являются дискретными, то формула (2.3) является
формулой корреляционного момента для исходных случайных величин [1,стр.173].
 , (2.3)
, (2.3)
где  - значения случайных величин;
- значения случайных величин;
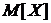 ,
,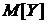 -
математические ожидания;
-
математические ожидания;
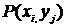 - вероятность выбора точки с координатами
- вероятность выбора точки с координатами и
и 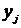 .
.
Применяя
формулу (2.3) к нашим выборкам и учитывая, что  , получим:
, получим:
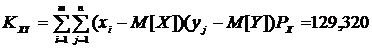
Проверим правильность формулы с помощью встроенной
в MathCAD функции нахождения оценки
корреляционного момента:
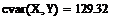
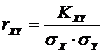 , (2.4)
, (2.4)
где 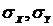 -среднеквадратичные
отклонения по X и Y;
-среднеквадратичные
отклонения по X и Y;
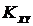 -
корреляционный момент.
-
корреляционный момент.
Теперь найдем
среднеквадратичные отклонения по X и
Y [1,стр.90]:

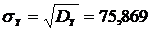
Используя формулу (2.4)
найдём корреляционный момент:

Проверим правильность
формулы с помощью встроенной в MathCAD
функции нахождения оценки коэффициента корреляции:
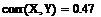
Исходя из проведённых
проверок, делаем вывод о том, что используемые формулы являются верными для
исходных случайных величин и коэффициент корреляции найден верно.
Для того чтобы
охарактеризовать случайную величину графически необходимо прибегнуть к понятию
плотность распределения вероятностей. Плотность распределения показывает, как
часто появляется случайная величина X в
некоторой окрестности точки x при
повторении опытов[1,стр.74].
Для того чтобы графически
представить плотность распределения вероятностей необходимо разделить ось Y на M интервалов.
Количество интервалов рассчитывается с помощью эмпирического правила Стёрджеса,
представленного формулой (3.1) [4].
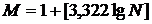 , (3.1)
, (3.1)
где N- количество всех
возможных элементарных событий.
Подставив исходное
количество всех возможных элементарных событий в формулу (3.1) и округлив до целого,
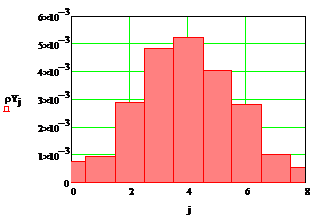
получим, что количество интервалов M=9. Графическое
представление плотности распределения вероятностей представлено на рисунке 3.1.
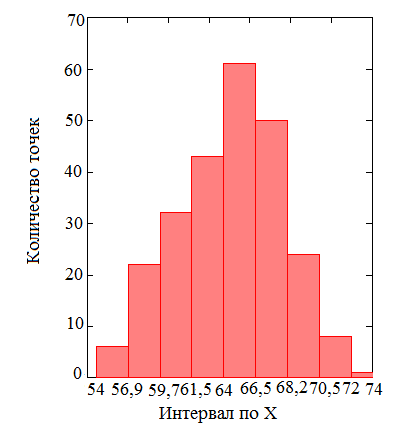
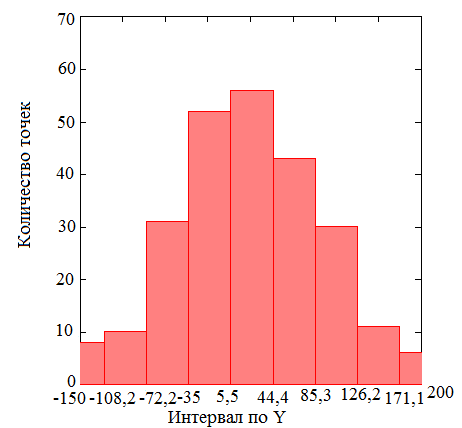
Рисунок 3.1 – Оценка
плотности распределения вероятности для X(первый) и для
Y(второй)
Произведём проверку
правильности графического построения плотности распределения вероятностей, при
помощи формулы (3.2) [1,стр.75].
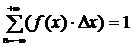 .
(3.2)
.
(3.2)
Формула (3.2)
подходит только для дискретной случайной величины, т.е. подходит для нашего
случая. Тогда применяя данную формулу, с ограничением интервала по X и по Y от 0
до M, получим:
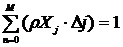 ,
,
 .
.
Данная проверка показала
правильность графического построения плотностей распределения вероятностей.
Для того чтобы
продемонстрировать зависимость одной случайной величины от другой существует
понятие линейная регрессия. Оно помогает графически представить зависимость одной
случайной величины от другой.
Если одна случайная
величина зависит от другой случайной величины, то тогда можно графически
построить их зависимость друг от друга, с помощью линейной регрессии. В данном
случае в пункте 2, с помощью коэффициента корреляции было показано, что
исходные случайные величины зависят друг от друга. Теперь определим линейную
регрессию, чтобы графически продемонстрировать эту зависимость. Определим
линейную регрессию по формуле (4.1)[1,стр.188].
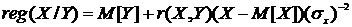 , (4.1)
, (4.1)
где 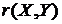 - коэффициент
корреляции, найденный в пункте 2;
- коэффициент
корреляции, найденный в пункте 2;
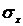 - среднеквадратичное
отклонение.
- среднеквадратичное
отклонение.
Линейная регрессия X на Y представлена на рисунке 4.1.
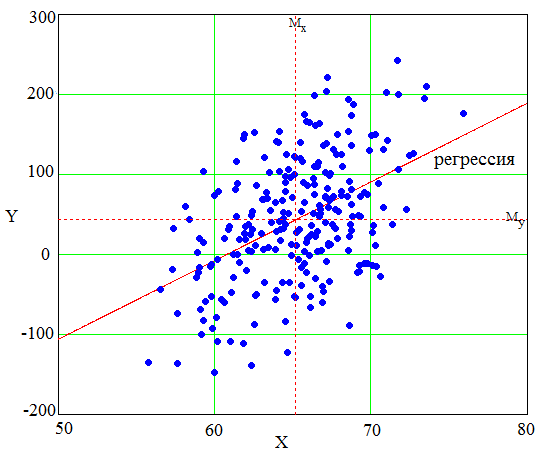
Рисунок 4.1 – Поле
рассеяния исходных случайных величин, с нанесением линии регрессии
В результате проведения
курсовой работы было произведено статистическое исследование системы двух
случайных величин.
Были получены оценки
числовых характеристик, таких как математическое ожидание, дисперсия и
коэффициент корреляции. Они равны:
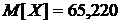
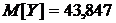



Также было получено и проверено графическое представление
плотности распределения вероятности для каждой случайной величины. Была оценена
оптимальная линейная регрессия, которая графически показала, что исходные
случайные величины обладают линейной корреляцией, а значит, зависят друг от
друга.
Если
данная работа была для Вас полезна, то вы можете поблагодарить автора!
Реквизиты
Сбербанк:4276 6400 1230 1216
Для связи
VK: https://vk.com/red_de
1)
Вентцель Е.С. Теория вероятностей: Учеб. для вузов. — 10-е изд.
стер. — М.: Издательский центр “Академия”, 2005.— 576 cтр.
2)
Статистика - Википедия [Электронный ресурс]. – URL:
Приложение А
(обязательное)
Листинг программы
Поле рассеяния
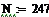
Нахождение вероятности
Математическое ожидание и дисперсия
Оценка корреляции
Оценка плотности распределения

Оптимальная регрессия