Профессия клинического психолога
Министерство образования и науки
Российской Федерации
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра телекоммуникаций и основ
радиотехники (ТОР)
СПЕКТРАЛЬНЫЙ АНАЛИЗ АНАЛОГОВЫХ
СИГНАЛОВ И РАСЧЕТ ОТКЛИКОВ НА ВЫХОДЕ ЛИНЕЙНОЙ ЦЕПИ
Пояснительная
записка к курсовой работе по дисциплине
«Теория
радиотехнических сигналов»
Вариант 79
Студент гр.
1А2
__________Леконцев
Д. Р.
Руководитель
Профессор
каф. ТОР, к.т.н.
____________Каратаева
Н.А.
2014
Министерство образования и науки
Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ
УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра телекоммуникаций и основ радиотехники (ТОР)
«УТВЕРЖДАЮ»
Зав.
кафедрой ТОР
_________ Демидов А.Я..
«___» ______________2014
г.
ЗАДАНИЕ
К КУРСОВОЙ РАБОТЕ
по
дисциплине «Теория радиотехнических сигналов»
Студенту группы 1А2
Леконцеву Д.Р.
1. Тема работы: Спектральный
анализ аналоговых сигналов и расчет откликов на выходе линейной цепи
2. Срок сдачи работы на
кафедру: «8-14»_апреля_ 2014г.
3. Цель: практическое
освоение методов анализа аналоговых периодических и непериодических сигналов
во временной и частотной областях, а также расчет прохождения этих сигналов
через линейную цепь на примере решения конкретной задачи.
4. Рекомендуемая
литература:
1. Баскаков С.И.
Радиотехнические цепи и сигналы. М.: Высш. школа, 2005.-462с.(304 экз.) ISBN:
5-06-003843-2
2. Каратаева Н.А.
Радиотехнические цепи и сигналы. Теория сигналов и линейные цепи. Учебное
пособие. Томск: ТУСУР, 2012.-261с Режим доступа:#"9368.files/image001.png">
6.2.2. Рассчитать и построить модуль
(АЧХ) и аргумент (ФЧХ) комплексной передаточной функции 
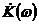
6.2.3 Рассчитать и построить переходную 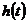 и импульсную
и импульсную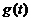 характеристики
заданной аналоговой линейной электрической цепи.
характеристики
заданной аналоговой линейной электрической цепи.
6.1.4. Рассчитать прохождение
периодического сигнала через аналоговую линейную электрическую цепь (методом
комплексных амплитуд). Построить отклик.
6.1.5. Рассчитать прохождение непериодического
сигнала через заданную цепь (операторным или временным методом). Построить
отклик.
7. Состав пояснительной
записки:
7.1.
Титульный лист.
7.2. Лист
задания с подписью руководителя.
7.3.
Содержание.
7.4.
Введение. Постановка задачи.
7.5. Расчет.
7.6.
Выводы по проделанной работе.
7.7.
Список использованных источников.
8. Отчетность по работе:
8.1.
Пояснительная записка, в обязательном порядке со всеми разделами п. 7.
8.2.
После оформления пояснительной записки – защита на кафедре.
Дата выдачи задания: «17»
февраля 2014 г.
Подпись руководителя_____________/Каратаева
Н.А./
Подпись студента___________/Леконцев
Д.Р./
Оглавление
Введение. 5
1. Спектральный анализ аналоговых
периодического и непериодического сигналов. 6
1.1. Исходные данные. 6
1.2. Нахождение спектральной
плотности аналогового сигнала. 6
1.2.1. Моделирование одиночного
видеоимпульса. 6
1.2.2. Нахождение спектральной
плотности нечётного симметричного сигнала прямоугольной формы 7
1.3. Построение частотных
характеристик аналогового сигнала. 9
1.4. Нахождение коэффициентов
комплексного ряда Фурье. 11
1.5. Построение таблицы коэффициентов
комплексного ряда Фурье. 12
1.6. Построение спектра коэффициентов
комплексного ряда Фурье. 13
1.7. Спектр фаз коэффициентов комплексного
ряда Фурье. 13
1.8. Нахождение ширины спектра
сигнала. 14
1.8.1 Ширина спектра по пороговому
критерию 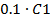 . 14
. 14
1.8.2 Ширина спектра по
пороговому критерию 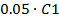 . 14
. 14
1.8.3 Ширина спектра по
энергетическому критерию.. 15
1.9. Восстановление сигнала
усеченным рядом Фурье. 16
1.9.1. Восстановление сигнала
по 16 гармоникам.. 16
1.9.2. Восстановление сигнала
по 36 гармоникам.. 16
1.9.3. Восстановление сигнала
по 6 гармоникам.. 17
1.10. Выводы.. 18
2.1. Нахождение передаточной
функции аналогового фильтра. 19
2.2. Построение частотных
характеристик аналогового фильтра. 19
2.3. Нахождение временных
характеристик аналогового фильтра-прототипа. 20
2.4. Построение отклика
аналогового фильтра на сигнал. 23
2.4.1. Построение отклика с
помощью переходной характеристики. 23
2.4.2. Построение отклика
методом комплексных амплитуд. 24
2.5 Выводы.. 25
Список использованной
литературы.. 26
Радиотехнические цепи и сигналы (РТЦиС) является
базовым курсом в системе подготовки современного инженера в области
радиотехники и радиоэлектроники. Его целью является изучение фундаментальных
закономерностей связанных с получением сигналов, их передачей по каналам связи,
обработкой и преобразованием в радиотехнических цепях.
Данная курсовая работа состоит из двух частей
первая– спектральный анализ аналогового периодического и непериодического
сигналов, вторая- анализ аналоговой линейной электрической цепи.
Целью первой части
данной курсовой работы является изучение спектра аналогового сигнала, путём
нахождения его спектральной плотности, коэффициентов комплексного ряда Фурье и
восстановления сигнала с помощью этих коэффициентов.
Целью второй части
данной курсовой работы является нахождения отклика ЛЭЦ на прохождение заданного
аналогового нечётного симметричного сигнала.
В качестве
начальных данных, задан нечётный симметричный аналоговый сигнал, с амплитудой 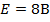 , периодом описания сигнала
, периодом описания сигнала 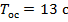 ,
циклической частотой
,
циклической частотой 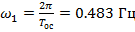 и
длительностью каждого импульса
и
длительностью каждого импульса 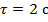 .
.
Заданный сигнал представлен на рисунке 1.1.
Рисунок 1.1- Временное представление
аналогового сигнала
Но данный сигнал
является лишь моделью идеального сигнала прямоугольной формы и не отражает
реального расчётного сигнала в системе передачи, именно по этой причине
необходимо найти сигнал восстановленный усечённым рядом Фурье.
Исходя из цели поставленной выше найдём
спектральную плотность аналогового сигнала. Но нельзя найти спектральную
плотность аналогового сигнала, просто посмотрев на его временное представление.
Исходя из этих соображений произведём нахождение спектральной плотности
поэтапно, начиная от нахождения спектральной плотности одиночного видеоимпульса
и постепенно усложняя, данный видеоимпульс мы найдем спектральную плотность
нечётного симметричного сигнала прямоугольной формы.
Для
упрощения нахождения спектральной плотности с помощью преобразования Лапласа, и
для последующего использования полученных в данном пункте формул, рассмотрим
одиночный видеоимпульс, он будет задаваться следующей формулой.
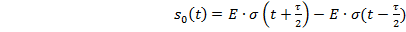 (1.1)
(1.1)
Рисунок 1.2- Временное представление одиночного
видеоимпульса
Для
того чтобы получить формулу для спектральной плотности одиночного
видеоимпульса, применим прямое преобразование Фурье к временному описанию
сигнала.
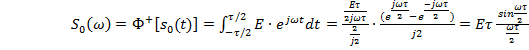 (1.2)
(1.2)
Используем
формулу (1.2) и получим графическое представление спектральной плотности
одиночного видеоимпульса, рисунок 1.3.
Рисунок 1.3- Спектральная плотность одиночного
видеоимпульса
Для
нахождения спектральной плотности симметричного сигнала прямоугольной
формы одиночного видеоимпульса недостаточно,
поэтому смоделируем нечетный сигнал путем смещение сигнала, данный сигнал
описывается формулой 1.3.
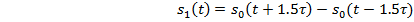 (1.3)
(1.3)
Использовав
формулу (1.3) получим временное представление смещённого аналогового сигнала,
которое представлено на рисунке 1.4.
Рисунок 1.4- Временное представление смещённого
аналогового сигнала.
Применив
прямого преобразования Фурье, к смещённому аналоговому сигналу получим формулу (1.4).
 (1.4)
(1.4)
Теперь
зная формулу смещённого аналогового сигнала (формула 1.4), найдём формулу для
нечётного симметричного сигнала прямоугольной формы, путём внесения смещения, в
данном случае 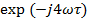 , в формулу
в качестве члена произведения. Произведя описанную операцию получим формулу
(1.5).
, в формулу
в качестве члена произведения. Произведя описанную операцию получим формулу
(1.5).
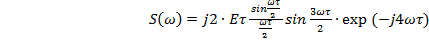 (1.5)
(1.5)
Формула (1.5)
является формулой спектральной плотности аналогового сигнала, следовательно
цель поставленная в пункте 1.2 выполнена.
Для более подробного понимания понятия
спектральной плотности, построим её графические характеристики. Вообще,
спектральная плотность является комплексной величиной. Следовательно модуль
спектральной плотности аналогового сигнала является её АЧХ, а аргумент
спектральной плотности аналогового сигнала – ёё ФЧХ.
АЧХ спектральной плотности представлена на
рисунке 1.5, при этом частотная ось нормирована относительно циклической
частоты 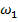 .
.
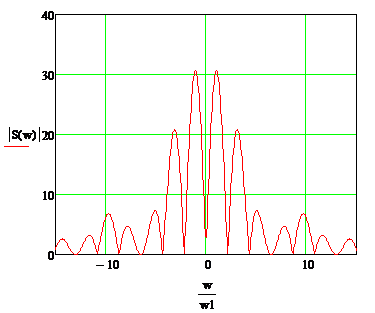
Рисунок 1.5- АЧХ аналогового сигнала
Из
рисунка 1.5 видно, что АЧХ как бы “пульсирует”. Данный эффект обусловлен, тем что
сигнал имеет ограниченный интервал описания во временной области.
ФЧХ
спектральной плотности представлена на рисунке 1.6, при этом частотная ось
нормирована относительно циклической частоты 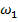 .
.
Рисунок 1.6- ФЧХ аналогового сигнала
Из
рисунка 1.6 видно, что ФЧХ изменяется слишком часто и очень трудно уловить,
почему происходят изменения. Такое явление происходит по причине того что ФЧХ
имеет большую линейную составляющую. Уберем задержку домножив 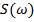 на
на 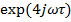 под знаком
аргумента, получим рисунок 1.7. Фактически полученная ФЧХ будет являться ФЧХ
смещённого сигнала из пункта 1.2.2.
под знаком
аргумента, получим рисунок 1.7. Фактически полученная ФЧХ будет являться ФЧХ
смещённого сигнала из пункта 1.2.2.
Рисунок 1.7- ФЧХ аналогового сигнала с
компенсированной линейной составляющей
Из рисунка видно,
что ФЧХ изменяется в пределах от 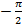 до
до 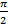 , причем
эти изменения происходят скачкообразно, что говорит что любой частоте будет
соответствовать ФЧХ либо
, причем
эти изменения происходят скачкообразно, что говорит что любой частоте будет
соответствовать ФЧХ либо 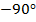 , либо
, либо 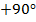 .
.
Для
того чтобы восстановить аналоговый сигнал с помощью комплексного ряда Фурье
необходимо найти его комплексные коэффициенты. Коэффициенты комплексного ряда
Фурье, это по существу продискретизированная спектральная плотность аналогового
сигнала. Формула (1.6) является формулой дискретизации спектральной плотности,
т.е. формулой коэффициентов комплексного ряда Фурье.
 (1.6)
(1.6)
Раскрывая
формулу(1.6), получим формулу (1.7).
 (1.7)
(1.7)
Произведя
замену 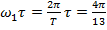 , в
формуле (1.7), получим формулу (1.8).
, в
формуле (1.7), получим формулу (1.8).
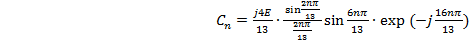 (1.8)
(1.8)
Формула (1.8)
является окончательной формулой, полностью описывающей коэффициенты
комплексного ряда Фурье.
Для проверки правильности графиков, приведённых
в пунктах 1.7 и 1.8 построим таблицу, в которой рассчитаны значения АЧХ, ФЧХ и
комплексное значение коэффициентов комплексного ряда Фурье. Все значения
рассчитаны по формуле (1.8)
Таблица
1- Модуль и аргумент коэффициентов комплексного ряда Фурье.
|
Гармоника
|
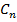
|

|
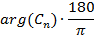
|
|
1
|
-2.197-0.833i
|
2.35
|
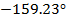
|
|
2
|
0.333-0.375i
|
0.502
|
|
3
|
-0.732-1.395i
|
1.576
|
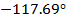
|
|
4
|
0.549-0.067i
|
0.553
|
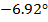
|
|
5
|
0.133-0.54i
|
0.556
|
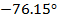
|
|
6
|
0.111+0.077i
|
0.135
|
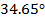
|
|
7
|
-0.095+0.066i
|
0.115
|
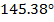
|
|
8
|
-0.083-0.337i
|
0.347
|
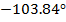
|
|
9
|
-0.244-0.03i
|
0.246
|
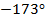
|
|
10
|
0.22-0.419i
|
0.473
|
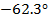
|
|
11
|
-0.06-0.068i
|
0.091
|
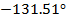
|
|
12
|
0.183-0.069i
|
0.196
|
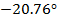
|
|
13
|
-1.392e-15
|
1.392e-15
|
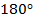
|
|
14
|
-0.157-0.06i
|
0.168
|
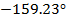
|
|
15
|
0.044-0.05i
|
0.067
|
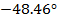
|
|
16
|
-0.137-0.262i
|
0.295
|
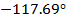
|
|
17
|
0.129-0.016i
|
0.13
|
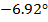
|
|
18
|
0.037-0.15i
|
0.154
|
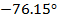
|
|
19
|
0.035+0.024i
|
0.043
|
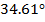
|
|
20
|
-0.033+0.023i
|
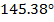
|
|
21
|
-0.032-0.129i
|
0.132
|
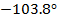
|
|
22
|
-0.1-0.012i
|
0.101
|
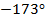
|
|
23
|
0.096-0.182i
|
0.206
|
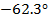
|
|
24
|
-0.028-0.031i
|
0.042
|
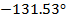
|
|
25
|
0.088-0.033i
|
0.094
|
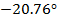
|
|
26
|
-1.392e-15
|
1.392e-15
|
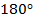
|
|
27
|
-0.081-0.031i
|
0.087
|
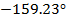
|
Опираясь на формулу (1.8) построим графическое
представление коэффициентов комплексного ряда Фурье.
На рисунке 1.8 представлен спектр коэффициентов
комплексного ряда Фурье.
Рисунок 1.8 Спектр коэффициентов комплексного ряда
Фурье
Для
сравнения с комплексными коэффициентами ряда, постоянную составляющую исходного
аналогового сигнала определим отдельно. Она определяется по формуле (1.9).
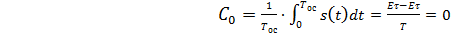 (1.9)
(1.9)
По
рисунку 1.8 и таблице 1 видно, что наибольшей энергией обладает первая
гармоника. Исходя из этого факта пороговый критерий для нахождения ширины
спектра сигнала будет определяться по первой гармоники.
Построим спектр фаз коэффициентов комплексного
ряда Фурье, опираясь на формулу(1.8). Данная характеристика графически
представлена на рисунке 1.9.
Рисунок 1.9- Спектр фаз коэффициентов комплексного
ряда Фурье
Из рисунка 1.9 видно, что коэффициенты
симметричные относительно начала координат являются комплексно-сопряженными.
Восстановление аналогового сигнала будем
производить по трём разным количествам гармоник. Следовательно ширину спектра
сигнала будем находить по трём критериям: пороговым критерием по уровню 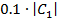 ; пороговым
критерием по уровню
; пороговым
критерием по уровню  и энергетическим
критерием.
и энергетическим
критерием.
На рисунке 1.10 представлен спектр
коэффициентов комплексного ряда Фурье. Прямая линия параллельная частотной оси это
пороговый критерий 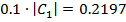 .
.
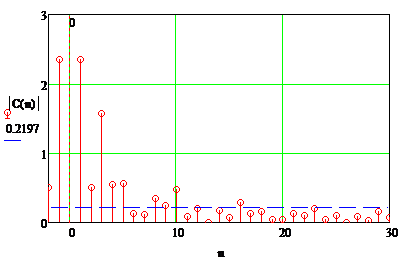
Рисунок 1.10- Определение ширины спектра аналогового
сигнала по уровню 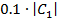
Использовав
рисунок 1.10 найдём ту гармонику, амплитуда которой является последней,
превышающей пороговый уровень в 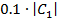 .
По порядковому номеру данной гармоники будем производить восстановление, т.е.
.
По порядковому номеру данной гармоники будем производить восстановление, т.е. 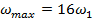 .
.
Второе восстановление будем производить, взяв пороговый
критерий по уровню 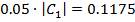 .
.
Рисунок 1.11- Определение ширины спектра по уровню 
Из рисунка 1.11 видно, что тридцать шестой–это
последний коэффициент с амплитудой, превышающей порог, очевидно, сигнал будем
восстанавливать по тридцати шести гармоникам, т.е. 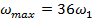 .
.
Для того, чтобы найти ширину спектра по
энергетическому критерию, необходимо произвести серию дополнительных расчётов. Формула
для расчета погрешности представлена ниже, это формула (1.10).
 (1.10)
(1.10)
Как видно в формуле (1.10) неизвестными являются
мощности 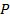 и
и 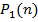 . Они находятся по формулам (1.11) и
(1.12).
. Они находятся по формулам (1.11) и
(1.12).
 (1.11)
(1.11)
 (1.12)
(1.12)
Как видим теперь в формуле (1.12) неизвестным
является ряд значений 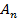 . Найдём этот ряд, использовав формулу
(1.13).
. Найдём этот ряд, использовав формулу
(1.13).
 (1.13)
(1.13)
Итак, произведя операции описанные выше и
подставив полученные значения из формул (1.11) и (1.12) в формулу (1.10)
получим графическое представление выражения (1.10), представленное на рисунке
1.12.
Рисунок 1.12- Определение ширины спектра по энергетическому
критерию.
Определять ширину спектра по энергетическому
критерию будем по уровню  , так как
гармоники выше
, так как
гармоники выше  содержат
основную часть энергии. Следовательно, гармониками лежащими ниже уровня
содержат
основную часть энергии. Следовательно, гармониками лежащими ниже уровня  можно пренебречь.
можно пренебречь.
Исходя из рисунка 1.12, делаем вывод, что
третье восстановление будем производить по шести гармоникам- 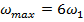 .
.
Восстановление сигнала усечённым рядом Фурье по N количеству гармоник задаётся
формулой (1.14).
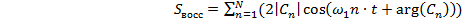 (1.14)
(1.14)
1.9.1. Восстановление сигнала по 16
гармоникам
Применяя формулу (1.14) к восстановлению
сигнала по 16 гармоникам получим формулу (1.15).
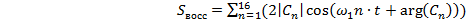 (1.15)
(1.15)
Использовав
формулу (1.15) получим временное представление восстановленного сигнала,
представленного на рисунке 1.14.
Рисунок 1.14- Восстановление сигнала усеченным рядом Фурье
по 16 гармоникам
Проанализировав рисунок 1.14 можно заметить
следующее: восстановленный сигнал имеет периодический характер, а периодизация
сигнала произошла из-за того что спектральная плотность была
продискретезирована в частотной области; из-за того что восстановленный сигнал
ограничен шестнадцатью гармониками ширины спектра он имеет пульсирующий
характер.
Применяя формулу (1.14) к восстановлению
сигнала по 36 гармоникам получим формулу (1.16).
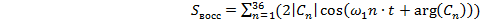 (1.16)
(1.16)
Использовав
формулу (1.16) получим временное представление восстановленного сигнала,
представленного на рисунке 1.15.
Рисунок 1.15- Восстановление сигнала усеченным рядом Фурье
по 36 гармоникам
1.9.3. Восстановление сигнала по 6
гармоникам
Применяя формулу (1.14) к восстановлению сигнала по 36
гармоникам получим формулу (1.17).
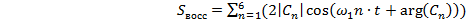 (1.17)
(1.17)
Использовав
формулу (1.17) получим временное представление восстановленного сигнала,
представленного на рисунке 1.16.
Рисунок 1.16- Восстановление сигнала усеченным рядом Фурье по
6 гармоникам
Проанализировав
графики 1.14, 1.15, 1.16 можно сделать следующие выводы. Наиболее точное
восстановление показано на графике 1.15, а следовательно пороговый критерий по
уровню более жёсткий и
более точный, чем по уровню
более жёсткий и
более точный, чем по уровню 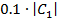 , т.е. исходя из
этого можно сделать вывод что чем жёстче будет пороговый критерий, тем точнее
будет восстановление. Встаёт вопрос, нужна ли такая высокая точность в данной
курсовой работе? Я считаю, что не нужна так как восстановление по большому
количеству гармоник приводит к большим затратам времени и ресурсов. Следовательно,
восстановление по пороговому критерию
, т.е. исходя из
этого можно сделать вывод что чем жёстче будет пороговый критерий, тем точнее
будет восстановление. Встаёт вопрос, нужна ли такая высокая точность в данной
курсовой работе? Я считаю, что не нужна так как восстановление по большому
количеству гармоник приводит к большим затратам времени и ресурсов. Следовательно,
восстановление по пороговому критерию 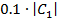 можно считать
оптимальным для данной курсовой работы, так как восстановление по энергетическому
критерию даёт очень “размазанное” восстановление с очень небольшой точностью.
можно считать
оптимальным для данной курсовой работы, так как восстановление по энергетическому
критерию даёт очень “размазанное” восстановление с очень небольшой точностью.
2 Анализ аналоговой линейной электрической цепи
Основной целью второй части курсовой работы
является нахождение отклика аналоговой линейной электрической цепи на
прохождение исходного аналогового сигнала.
Аналоговая
линейная электрическая цепь задана, как показано на рисунке 2.1.
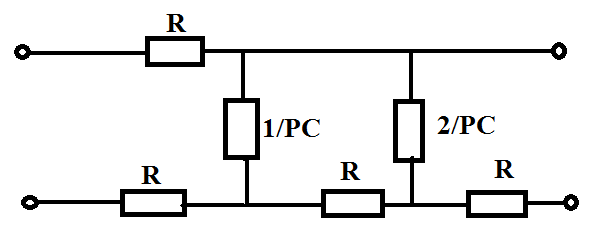
Рисунок 2.1 - Схема исходного аналогового
фильтра-прототипа
Также известно,
что 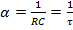 .
.
Передаточную функцию в операторной форме записи
цепи находим
методами ОТЦ:
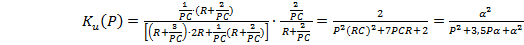 (2.1)
(2.1)
Путем замены 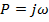 перейдём от передаточной функции в операторной форме
записи к частотным характеристикам. Используя знания ОТЦ найдём
выражение для АЧХ и ФЧХ, которые представлены формулами (2.2) и (2.3).
перейдём от передаточной функции в операторной форме
записи к частотным характеристикам. Используя знания ОТЦ найдём
выражение для АЧХ и ФЧХ, которые представлены формулами (2.2) и (2.3).
 (2.2)
(2.2)
 (2.3)
(2.3)
Графическое
представление выражений (2.3) и (2.4), изображено на рисунках 2.2 и 2.3
соответственно.
Рисунок 2.2- АЧХ аналогового фильтра-прототипа
Анализируя
рисунок 2.2, т.е. АЧХ аналогового фильтра прототипа, можно сделать вывод, что
цепь представленная на рисунке 2.1 является ФНЧ. Следовательно схема заданная
на рисунке 2.1 является интегратором.
Рисунок 2.3- ФЧХ аналогового фильтра-прототипа
Анализируя рисунок 2.3, т.е. ФЧХ аналогового
фильтра прототипа, можно сказать что падение фазы до уровня 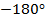 обусловлено,
наличием в цепи, представленной на рисунке 2.1, двух емкостей.
обусловлено,
наличием в цепи, представленной на рисунке 2.1, двух емкостей.
Для того чтобы найти отклик цепи на сигнал, необходимо
определить переходную и импульсную характеристики аналогового фильтра
прототипа, которые будут применяться к типовым составляющим сигнала.
Прежде чем приступить к нахождению переходной и импульсной
характеристики аналогового фильтра прототипа, необходимо найти корни
знаменателя выражения (2.1).
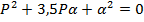
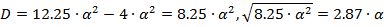
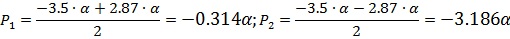
Переходную
характеристику найдем, взяв обратное преобразование Лапласа от передаточной
функции, поделенной на 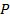 , при этом
появится ещё один корень
, при этом
появится ещё один корень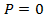 .
Нахождение переходной характеристики представлено формулой (2.4).
.
Нахождение переходной характеристики представлено формулой (2.4).

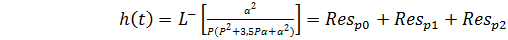 (2.4)
(2.4)

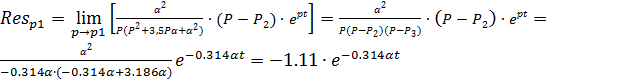
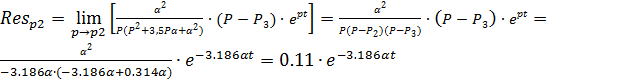
С учётом найденных вычетов формула (2.4), преобразуется в
выражение (2.5).
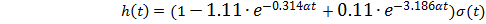 (2.5)
(2.5)
Графическое
представление выражения (2.5), изображено на рисунке 2.4.
Рисунок 2.4- Переходная
характеристика аналогового фильтра прототипа
Для того чтобы понять
правильно ли найдена переходная характеристика, произведем проверку на крайних
частотах:
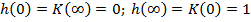
Импульсную характеристику найдем,
взяв обратное преобразование Лапласа от передаточной функции. Выражение для
нахождения импульсной характеристики представлено формулой (2.6).
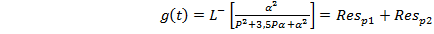 (2.6)
(2.6)
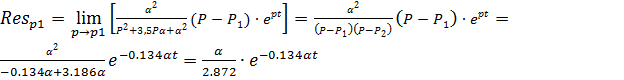
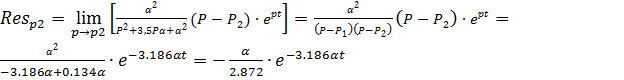
С учётом найденных
вычетов формула (2.6) преобразуется в формулу (2.7).
 (2.7)
(2.7)
Графическое
представление выражения (2.7), изображено на рисунке 2.5.
Рисунок 2.5- Импульсная характеристика
аналогового фильтра прототипа
Импульсную
характеристику можно проверить следующим образом: график производной от
переходной характеристики, должен совпадать с графиком импульсной
характеристики.
Рисунок 2.6 – Проверка импульсной
характеристики
Как видим рисунки 2.5
и 2.6 совпадают, а следовательно импульсная характеристика найдена правильно.
Зная выражения для
коэффициента передачи и переходной характеристики можно построить отклик
аналогового фильтра на сигнал двумя способами. Первый с помощью разложения
сигнала на элементарные составляющие и умножением на переходную характеристику.
Второй методом комплексных амплитуд.
Для того чтобы
получить отклик аналогового фильтра-прототипа на исходный аналоговый сигнал,
необходимо разложить исходный аналоговый сигнал на элементарные составляющие и
умножить на переходную функцию. Эта процедура представлена в формуле (2.8)
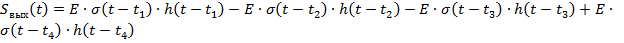 ,
(2.8)
,
(2.8)
где 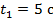 ;
; 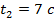 ;
; 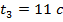 ;
;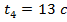 .
.
Использовав формулу
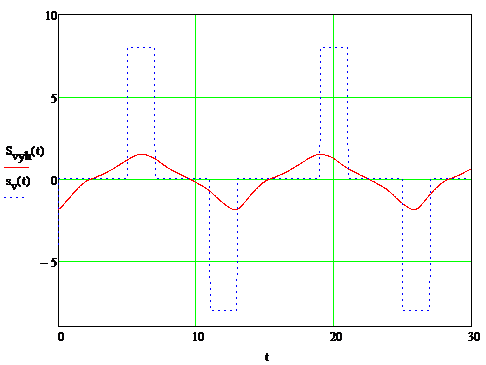
(2.8) получим отклик
аналогового фильтра-прототипа на исходный аналоговый сигнал, который
представлен на рисунке 2.7.
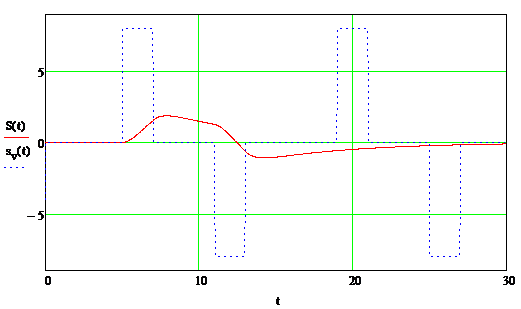
Рисунок 2.7 - Отклик аналогового
фильтра-прототипа на исходный аналоговый сигнал
Получим отклик
аналогового фильтра-прототипа на исходный аналоговый сигнал методом комплексных
амплитуд, для этого воспользуемся формулой (2.9).
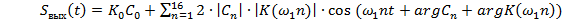 (2.9)
(2.9)
|
В ходе выполнения
второй части данной курсовой работы была выполнена поставленная цель, был
найден отклик аналогового фильтра прототипа на исходный аналоговый сигнал.
Отклик был найден двумя способами, один из которых это нахождение отклика с
помощью переходной функции, а другой это нахождения отклика по методу
комплексных амплитуд.
Проанализировав
данные методы были сделаны следующие выводы. Для того чтобы найти отклик с
помощью переходной характеристики, естественно необходимо находить переходную
характеристику, что бывает иногда сложно сделать. Чтобы задать отклик с помощью
переходной характеристики необходимо раскладывать аналоговый сигнал на типовые
составляющие, а если необходимо задать отклик на большом интервале времени, то
формула становится слишком громоздкой. Отклик по методу комплексных амплитуд
задаётся одной формулой, которая не изменяется и с помощью неё легко построить
отклик на большом временном интервале. Но для нахождения отклика по методу
комплексных амплитуд требуется находить коэффициенты комплексного ряда Фурье, в
отличие от первого метода, где этого не требуется.
Оба метода имеют свои
достоинства и недостатки, применять эти методы необходимо в зависимости от
известных данных. Если мы не можем найти коэффициенты комплексного ряда Фуре,
то применим метод отыскания отклика с помощью переходной характеристики. Если
же мы не можем найти переходную характеристику, но можем найти коэффициенты
комплексного ряда Фуре, то тогда применим метод комплексных амплитуд.
В данной курсовой
работе применимы оба метода, но лучше подходит метод комплексных амплитуд, так
как он задаёт отклик на всем временном интервале, что делает представление
отклика более наглядным и экономит время вычисления отклика в MathCAD, при задании одинаковых
временных интервалов в обоих методах.
Если данная работа была для Вас
полезна, то вы можете поблагодарить автора!
Реквизиты Сбербанк:4276 6400 1230 1216
Для связи VK: https://vk.com/red_de
1)
Радиотехнические
цепи и сигналы. . Часть 1 Теория сигналов и линейные цепи: Учебное пособие /
Каратаева Н. А. – 2012. 261 с.
2)
Радиотехнические
цепи и сигналы. Методические указания по выполнению курсовой работы «Дискретная
обработка сигналов и цифровая фильтрация» Каратаева Н.А. 2012. -70 с.
3) Радиотехнические цепи и сигналы
Часть 1 Теория сигналов и линейные цепи Учебно-методическое пособие / Каратаева
Н.А., Киселев П. С. 2012. 34 с.
Похожие работы на - Профессия клинического психолога
|