История комплексных чисел и основные открытия комплексного числа учеными

История комплексных чисел и основные открытия комплексного числа учеными

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ Государственное Бюджетное образовательное учреждение

высшего профессионального образования

«ТЮМЕНСКИЙ ГОСУДАРСТВЕННЫЙ НЕФТЕГАЗОВЫЙ УНИВЕРСИТЕТ»

Институт менеджмента и бизнеса

Кафедра Экономики, организации и управления производством

КОНТРОЛЬНАЯ РАБОТА

по дисциплине: «Математика»

на тему «История комплексных чисели основные открытия комплексного числа учеными»

                                                                  Выполнил студент группы:

                                                         _______________________________

(наименование группы, Ф.И.О.)

                                                                  Проверил  ______Шевелев А.В.______

____________________доцент, к.м.н _________

(Ф.И.О. преподавателя, ученая степень, должность)

Тюмень 2018

Содержание

Введение

Актуальность темы. Решение множества задач по физике и техники ввергает к квадратным уравнениям с отрицательным дискриминантом. Такие уравнения не обладают решениями в сфере реальных чисел. Но решение множества подобных задач обладает совершенно определенным физическим смыслом. Значение количеств в результате решения этих уравнений, назвали комплексными числами.

Комплексные числа являются вещественными числами и мнимой единицей, точнее число, для которого выполняется определенное равенство.

Комплексные числа являются математической концепцией чисел, а именно сумм вещественного и совершенно мнимого числа, точнее вещественного множителя абстрактной квази-величины, где мнимая единица инверсивно устанавливается через утверждение, что ее квадрат равен минус единице.

Комплексные числа были внедрены в математику, чтобы выполнить допустимым действие по извлечению квадратного корня из любого действительного числа. Данное, тем не менее, не является полным основанием для включения новых чисел в математике. Оказалось, что если выполнять вычисления по обычным правилам на выражениях, которые обладают квадратным корнем отрицательного числа, то имеется возможность прийти к результату, который больше не содержит квадратный корень отрицательного числа.

Процесс расширения представлений чисел от натурального к действительному был связан как с потребностями практики, так и с потребностями самой математики. Вначале, для подсчета предметов применялись натуральные числа, а именно:

- необходимость произведения деления повергла к понятию дробных положительных чисел;

- необходимость произведения вычитания к понятиям нуля и отрицательных чисел;

- необходимость извлечения корней из положительных чисел к понятию иррациональных чисел.

Все вышеуказанные операции выполнимы на множестве действительных чисел. Тем не менее существуют также операции, которые невозможны в этом наборе, например, извлечение квадратного корня из отрицательного числа. Следовательно, существует потребность в дальнейшем расширении понятия числа, в возникновении новых чисел, отличающиеся от действительных.

Геометрически действительные числа представляются точками на координатной прямой: каждому числу соответствует одна точка прямой («образ» действительного числа). Координатная линия полностью заполнена изображениями действительных чисел, точнее «нет места новым числам». Предполагалось, что геометрические изображения новых чисел следует искать не на прямой, а на плоскости.

Целью и объектом изучения является история комплексных чисел.

Для решения задач, необходимо:

а) рассмотреть историю комплексных чисел;

б) определить комплексные числа и их свойства;

в) разобрать действия с комплексными числами.

1 История комплексных чисел

1.1 Формирование понятия о числе

Древнегреческие математики считали «настоящими» только натуральные числа. Потихоньку возникало воззрение о бесконечности большинства натуральных чисел.

В III веке Архимед создал систему выражения близко к такому громадному как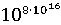.Вместе с натуральными числами использовались дробные числа, состоящие из целой доли единицы. В практических расчетах дроби использовались за две тысячи лет до нашей эры в Древнем Египте и древнем Вавилоне. [7, с.29]

Длительное время считалось, что результат измерения постоянно проявляется или в виде натурального числа, либо в виде отношения этих чисел, точнее дробей.

Древнегреческий философ и математик Пифагор поучал, что «компоненты чисел считаются компонентами всех вещей и весь мир есть гармония и число». Серьезный удар по этой точке зрения нанесло открытие, сделанное одним из Пифагорейцев. Он обосновал, что диагональ квадрата несоизмерима со стороной. Из этого места следует, что натуральных чисел и дробей недостаточно, чтобы сформулировать длину диагонали квадрата со стороной. Существуют основные положения ратифицировать, что собственно с данного открытия наступает эпоха теоретической математики: невозможно было обнаружить присутствие несоизмеримых величин при помощи опыта, не прибегая к абстрактным рассуждениям. [1, с.34]

Совершенные гражданские права мнимым числам дал Гаусс, который назвал их комплексными числами, выдал геометрическую интерпретацию и обосновал главную теорему алгебры о том, что каждый многочлен обладает хотя бы одним действительным корнем. [7, с.41]

Следующим значительным шагом в формировании определения числа было основание отрицательных чисел, а именно было выполнено китайскими математиками за два века до н.э.

Отрицательные числа использовались в III веке древнегреческий математик Диофант, который знал правила операций над ними, а в VII веке данные числа уже со всеми подробностями проанализировали индийские ученые, которые ассоциировали эти числа с долгом. При помощи отрицательных чисел имеется возможность одним видом показывать изменения величин. [1, с.55]

Уже в VIII веке было поставлено, что квадратный корень положительного числа обладает двумя значениями, а именно положительным и отрицательным, а из отрицательных чисел квадратный корень извлечь невозможно: нет такого числа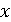, чтобы 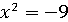. [4, с.40]

1.2 На пути к комплексным числам

В XVI веке из-за изучения кубических уравнений обнаружилось важным извлекать квадратные корни из отрицательных чисел. В Формуле с целью решения кубических уравнений вида кубические и квадратные корни обладают видом: [4, с.46]

.

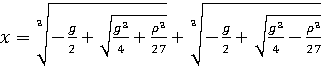Эта формула хорошо работает, когда уравнение обладает одним действительным корнем, то выглядит (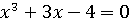), а если оно обладает тремя действительными корнями (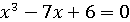), то под знаком квадратного корня было отрицательное число. Оказалось, что путь к этим корням проходит через невыполнимую операцию извлечения квадратного корня из отрицательного числа. После того, как были решены уравнения 4-й степени, математики интенсивно выискивали формулу с целью решения уравнения 5-й степени. [1, с.72]

Но Руффини (Италия) на рубеже XVIII и XIX веков обосновал, что буквенное уравнение пятой степени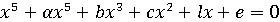невозможно решить алгебраически, а именно невозможно сформулировать корень через буквенные значения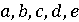используя шесть алгебраических действий (сложение, вычитание, умножение, деление, возведение в степень, извлечение корня). [7, с.52]

В 1830 году Галуа (Франция) доказал, что никакое общее уравнение, степень которого больше чем четыре могут быть решены алгебраически. Тем не менее, любое уравнение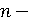й степени обладает (если анализировать и комплексные числа) 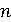 корнями (среди которых могут быть и равные).

В этом математики были убеждены еще в XVII веке (опираясь на рассмотрении многочисленных частных случаев), но только на рубеже XVIII и XIX веков упомянутая теорема была доказана Гауссом. [5, с.39]

Итальянский алгебраист Дж. математика. Кардано в 1545 внес предложение установить числа новой природы. Он представил, что система уравнений обладает видом: [4, с.55]

,

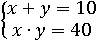Не имея решений во множестве вещественных чисел, существует решение такого вида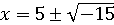, , 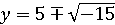необходимо только согласиться действовать по таким выражениям согласно правилам обычной алгебры и предположить, что.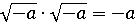

1.3 Утверждение комплексных чисел в математике

Кардано назвал их «чисто негативными» и даже «софистически негативными», сказал, что они бесполезны и пытался не использовать их. В действительности, при помощи данных чисел невозможно сформулировать результат измерения ни величиной, ни изменением какой-нибудь величины. Но уже в 1572 году была издана книга итальянского алгебраиста Р. Бомбелли, в которой были введены первые правила арифметических операций над этими числами, вплотную до извлечения из них кубических корней. [1, с.88]

Название «мнимые числа» ввел в 1637 году французский математик и философ Р. Декарт, а в 1777 году один из общепризнанных математиков XVIII века - Л. Эйлер внес предложение применять первую букву французского слова мнимого указать количество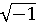(мнимой единицы). Этот символ уложился во всеобщее использование из-за К. Гаусса. [7, с.63]

Термин «комплексные числа» был введен Гауссом в 1831 году. Слово комплекс средств связи, сочетание, комплекс понятий, предметов, явлений и т.д. - образуя единое целое. [4, с.61]

В XVII веке продолжалось обсуждение арифметического характера мнимых чисел и способности предоставить им геометрическое обоснование. 

Понемногу формировалась техническое оснащение по процедурам над мнимыми числами. На этапе XVII и XVIII веков была выстроена общая теория корней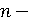ых степеней вначале из отрицательных, а вслед за этим из любых комплексных чисел, которая основана на такой формуле английского математика А. Муавра (1707), как: [5, с.47]

.

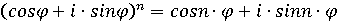При помощиданной формулы, имеется возможность создать формулу для косинусов и синусов кратных дуг. Л. Эйлер вывел в 1748 году примечательную формулу: 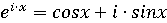,которая связала экспоненциальную функцию с тригонометрической.

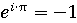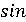С помощью формул Эйлера удалось построить число e любой комплексной степени. Любопытно, например, что. Имеется возможность находить  и 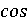от комплексных чисел, вычислять логарифмы таких чисел, точнеевыстроить теорию функций комплексных переменных. [1, с.104]

В конце восемнадцатого века французский математик Дж. Лагранж сумел огласить, что математическое исследование не представляет труда чисто мнимых значений. При помощи мнимых чисел обучились демонстрировать решения линейных дифференциальных уравнений с постоянными коэффициентами. Эти уравнения можно встретить, например, в теории колебаний материальной точки в сопротивляющейся среде. Немного ранее Швейцарский математик Дж. Бернулли использовал комплексные числа для решения интегралов. [7, с.74]

Хотя в XVIII веке многие вопросы решались при помощи комплексных чисел, в том числе прикладных, связанных с картографией, гидродинамикой и другие, но не было построенного логического объяснения теории данных чисел. Вследствие этого французский ученый Лаплас полагал, что результаты, приобретенные при помощи и мнимых чисел,которые являются только наведением, приобретающие характером истинных достоверностей только после доказательства прямыми подтверждениями. [4, с.79]

Ни один человек не сомневался в верности результатов, которые получены при вычислениях с мнимыми количествами, хотя они играют роль лишь алгебраической формы иероглифов нелепого количества.

После формирования теории комплексных чисел появился вопрос о присутствии «гиперкомплексных» чисел являются числами с несколькими «мнимыми» единицами. Такая система формы обладает видом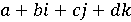, где 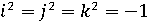, выстроил в 1843 году ирландский математик У. Гамильтон, который назвал их «кватернионами». [5, с.60]

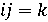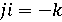Правила действий над кватернионами напоминают правила обычной алгебры, однако их умножение не обладает свойством коммутативности (смещение): например, , а . [1, с.112]

Наибольшее достижение в формирование теории функций комплексного переменного внесли русские, и советские ученые Мусхелишвили занимался ее приложениями к упругости, Келдыш и Лаврентьев занимались аэро- и гидродинамикой, Богомолов и Владимиров занимались проблемами квантовой теории поля.

Комплексные числа обширно применял отец русской авиации Жуковский (1847 – 1921) при создании теории крыла, автором которой он является. Комплексные числа и функции комплексных переменных используются во многих областях науки и техники. [7, с.85]

В конце XVIII века, в начале XIX века была получена Геометрическая интерпретация комплексных чисел. Датчанин Вессель, француз Арган и немец Гаусс независимо друг от друга рекомендовали воспроизвести комплексное число в виде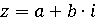 точкой  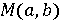на координатной плоскости. [4, с.88]

Позже оказалось, что еще удобнее представлять число не самой точкой 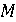, а вектором 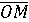, который проходит в данную точку из начала координат. При подобном толковании сложение и вычитание комплексных чисел отвечают этим же операциям над векторами.

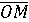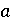Вектор имеется возможность задавать не только его координатами  и 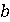, но в свою очередь длиной 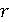 и углом 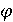, который он создает с положительным направлением оси абсцисс. При этом 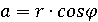, , 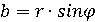и число  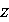принимает вид 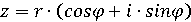, который называется тригонометрической формой комплексного числа. Число 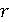 называют модулем комплексного числа 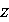 и обозначают 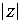. [5, с.75]

Число 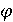 называют аргументом 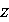 и обозначают 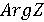. Отметим, что если 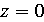, значение  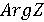не установлено, а при 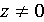 оно установлено с точностью до кратного .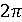

Упомянутая ранее формула Эйлера дозволяет записать число 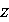 в виде 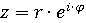(показательная форма комплексного числа). [1, с.119]

Геометрическое объяснение комплексных чисел разрешило предназначить многочисленные определения, которые связаны с функцией комплексного переменного, увеличило сферу их использования.

Из чего можно заключить, что комплексные числа могут быть полезны во многих вопросах, где они имеют дело с величинами, которые представлены векторами на плоскости, а именно: при исследовании течения жидкости, задач теории упругости.

Долгое время не получалось отыскать таких физических величин, над которыми можно было бы совершать действия, подчиненные тем же правилам, что и действия над комплексными числами - в частности правилу. Отсюда и названия: «мнимая единица», «мнимое число» и другие в настоящее время известен множеством таких физических величин, и комплексные числа обширно используются не только в математике, но и в физике и технике. [7, с.96]

Можно оставить в стороне вопрос о геометрическом или физическом смысле числа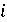, так как в разных сферах науки такой смысл разнообразен.

Правило каждого действия над комплексными числами выводится из установления данного действия. Но установления действий над комплексными числами не выдуманы безосновательно, а введены таким образом, чтобы они согласовывались с правилами действий над вещественными числами. Ведь сложные числа следует рассматривать не в отрыве от реальных, а вместе с ними. [4, с.97]

2 Основные открытия комплексного числаученых

2.1Вклад Декарта в развитие математики как науки

Рене Декарт является французским философом, математиком, механиком, физиком и физиологом. В том числе, создателем аналитической геометрии и современной алгебраической символики, автором метода радикального сомнения в философии, механики в физике, предтеча рефлексологии. [2, с.41]

Декарт является одним из авторов теории уравнений: им сформулировано правило знаков для определения числа положительных и отрицательных корней, поставил вопрос о границах действительных корней и выдвинул проблему приводимости, точнее представления целого числа рациональной функции с рациональными коэффициентами в виде произведения двух функций этого рода.

Декарт указал, что уравнение 3-й степени разрешимо в квадратных радикалах (а также указал решение с помощью циркуля и линейки, если это уравнение приводимо).

Декарт является одним из создателей аналитической геометрии (которую он разработал одновременно с Ферма), что позволило алгебраизировать эту науку при помощи координатного метода. Предложенная им система координат названа в его честь.

Занятия по математике привели Декарта к открытию новой науки, а именно аналитической геометрии. Сначала он нашел способ записать любую строку, применяя числовое уравнение.

Итак, он как бы комбинировал алгебру и геометрию.

В Голландии в 1618 году Декарт встретился с выдающимся физиком и философом природы Исааком Бекманом, оказавшим значительное влияние на его развитие как ученого. [2, с.56]

В 1637 году Декарт опубликовал основную философско-математическую работу под названием «рассуждение о методе» (полное название: «рассуждение о методе, позволяющем направить свой ум и найти истину в науках»).

В данной книге представлена аналитическая геометрия, а в приложениях представлены многочисленные результаты по алгебре, геометрии, оптике (а также правильная формулировка закона преломления света) и т.п.

Особенное вниманиенеобходимовыделить переработанной им математическую символику Виета, с этого момента близкую к современной. Коэффициенты он обозначал 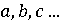, а неизвестные - .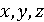

Натуральный показатель принял современный вид (дробный и отрицательный, установленный Ньютоном). Появилась черта над радикалами. Уравнения даны в каноническом виде (в правой части представлен ноль).

Символическая алгебра Декарта называлась «общей математикой» и она должна объяснить «все, что связано с порядком и мерой».

Создание аналитической геометрии позволило перевести исследование геометрических свойств кривых и тел на алгебраический язык, точнее анализировать уравнение кривой в некоторой системе координат. Создание аналитической геометрии обладает и недостатком, так как необходимо точно определить истинные геометрические свойства, не зависящие от системы координат (инварианты). [2, с.72]

Тем не менее, достоинства нового метода были весьма высоки, и Декарт продемонстрировал их в той же книге, открыв множество положений, неизвестных древним и современным математикам.

В приложении «Геометрия» были даны методы решения алгебраических уравнений (в том числе геометрические и механические), классификация алгебраических кривых.

Новый способ задания кривой является помощью уравнения, который был решающим шагом к понятию функции. Декарт формулирует точное «правило знаков» для установления числа положительных корней уравнения, хотя ему не докажешь.

Декарт изучал алгебраические функции (многочлены), в том числе множество «механических» функций (спирали, циклоиды). Для трансцендентных функций, по мнению Декарта, общего метода исследования не существует.

Комплексные числа еще не были рассмотрены Декартом на равных условиях с вещественными, но он сформулировал (хотя и не доказал) основную теорему алгебры: общее число вещественных и комплексных корней многочлена равно его степени. [2, с.84]

Отрицательные корни Декарт по традиции называют ложной, но в сочетании их с положительными термином действительные числа, отделяя от мнимых (комплексных). Этот термин вошел в математику. Однако Декарт показал некоторую несогласованность: коэффициенты 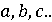. он был признан положительным, и случай неизвестного знака был специально отмечен многоточием слева.

Все неотрицательные вещественные числа, в том числе иррациональные, рассматриваются Декартом как равные, они определяются как отношение длины отрезка к длине отсчета. Позже Ньютон и Эйлер приняли аналогичное определение числа.

Декарт еще не отделяет алгебру от геометрии, хотя и меняет их приоритеты, он понимает решение уравнения как построение отрезка с длиной, равной корню уравнения. От этого анахронизма вскоре отказались его ученики, прежде всего они, являются англичанами, для которых геометрические конструкции являются чисто вспомогательной техникой.

Книга «метод» сразу сделала Декарта признанным авторитетом в математике и оптике. Примечательно, что она была издана на французском языке, а не на латыни.

Приложение «Геометрия», однако, сразу же было переведено на латинский язык и неоднократно публиковалось отдельно, вырастая из комментариев и становясь справочником европейских ученых. Труды математиков второй половины XVII века отражают сильнейшее влияние Декарта.

В работе «Геометрия» (1637), которая открыла взаимопроникновение алгебры и геометрии, Декарт впервые ввел понятия переменной и функции. В Декартовой системе координат получили реальное истолкование отрицательные числа. [2, с.89]

2.2Гауссовы целые комплексные числа

В 1820-х годах Карл Фридрих Гаусс исследовал биквадратичный закон взаимности и результатом стала монография «Теория биквадратичных вычетов» (1828-1832). Именно в этой работе целые числа доказали свою полезность для решения задач теории чисел, хотя формулировка этих задач не связана с комплексными числами.

Гауссовы целые числа комплексные числа (Гауссовы числа, целые комплексные числа) являются комплексными числами, в которых материальные и мнимую часть чисел.

Множество гауссовых целых комплексных чисел принято обозначать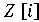, отражая тем самым тот факт, что оно получается из множества целых комплексных чисел 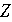 добавлением в него мнимой единицы 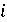 и комбинаций ее с целыми числами.

Гаусс писал, что «естественный источник общей теории следует искать в расширении области арифметики».

В книге Гаусса было показано, что новые числа по своим свойствам во многом напоминают обычные целые числа. Он описал четыре делителя одного, а именно: [2, с.95]

- определено отношение ассоциативности и понятие простого комплексного числа;

- дал критерии простоты и доказанные аналоги основной теоремы арифметики и малой теоремы Ферма;

- подробно рассмотрены вычеты для комплексного модуля;

- подробно рассмотрены индексы и первичные корни.

Главным достижением построенной теории был биквадратный закон взаимности.

Гаусс также использовал числа, которые он ввел в других своих работах, таких как «об алгебраических уравнениях».

Например, кольцо целых чисел Гаусса было одним из первых примеров алгебраической структуры с необычными свойствами.

По аналогии с множеством вещественных чисел делимость в кольце Гауссовых чисел можно отличить по подмножеству целых чисел.  Множество чисел вида 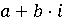 , где 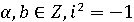 назовем целыми комплексными числами или гауссовыми числами. Нетрудно проверить, что для этого множества выполняются аксиомы кольца.

Таким образом, это множество комплексных чисел  является кольцом и называется кольцом целых чисел Гаусса. Обозначим его как 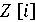 , так как оно является расширением кольца 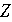 элементом, а именно.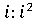

Поскольку кольцо гауссовых чисел является подмножеством комплексных чисел, то для него справедливы некоторые определения и свойства комплексных чисел. Так, например, каждому гауссовому числу   соответствует вектор с началом в точке 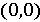 и с концом в 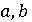(рис.1). [1, с.140]

Следовательно, модуль гауссова числа 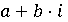есть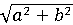. Заметим, что в рассматриваемом множестве, подмодульное выражение всегда есть число неотрицательное целое. Поэтому в некоторых случаях удобнее пользоваться нормой, то есть квадратом модуля.

Таким образом,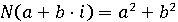, где 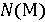  является множеством натуральных чисел, то есть целых положительных чисел Можно выделить следующие свойства нормы.

Так, например, В прямоугольной системе координат комплексное число 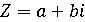 играет роль точки в плоскости с координатами (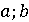), и эта точка помечается той же буквой 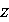 (рис. 1). [1, с.148]

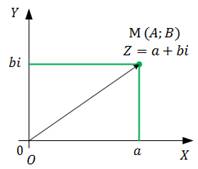
Рисунок 1 - Прямоугольная система координат интерпретации комплексного числа

Кольцо гауссовых чисел - это коммутативное кольцо без делителей 0, так как оно является подкольцом поля комплексных чисел. Отсюда следует мультипликативная сократимость кольца 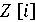, то есть:

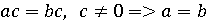
Простое гауссово число является ненулевым числом, не имеющее других делителей, кроме тривиальных. Число, не являющееся простым, называется составным. При этом делители единицы‚ подобно натуральной единице‚ не считаются ни простыми, ни составными числами.

Перечислим некоторые свойства простых гауссовых комплексных чисел: [2, с.106]

- если 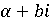 простое гауссово число, то и сопряженное к нему гауссово число 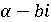 тоже является простым;

- если простое гауссово число является делителем произведения гауссовых чисел, то оно является делителем, по крайней мере, одного из сомножителей;

- норма любого простого гауссова числа, кроме ассоциированных с 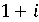, всегда нечетна и поэтому имеет вид .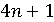

Натуральное простое комплексное число может не быть гауссовым простым числом.Например‚ числа 2 и 5 в 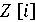 уже не простые, а именно:

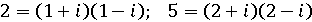
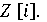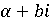Гаусс указал определяющие признаки простого комплексного числа в Гауссово число  является простым тогда и только тогда, когда:

- либо одно из чисел 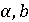 нулевое, а другое целое простое число;

- либо, 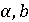 оба не нулевые и норма 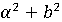 простое натуральное число.

Со временем было открыто большое количество структур такого типа‚ а в конце ХІХ века появилась абстрактная алгебра, которая изучает алгебраические свойства отдельно от объектов-носителей этих свойств.

2.3Новые глубинные математические закономерностиГалуа

Эварист Галуа (26.10.1811, Бур-ля-Рен, О-де-Сен – 31.05.1832, Париж) – гениальный французский мыслитель и математик, основатель современной высшей алгебры. [3, с.19]

Э. Галуа входит в десятку величайших математиков всех времен. Он открыл новую эпоху мировой научной мысли, кардинальным образом преобразовал динамику математических наук.

Эварист Галуа первым осознал, что математические вопросы можно решить путем перенесения их в область более абстрактных рассуждений.

Великий французский ученый привнес в математику совершенно новый подход, новую точку зрения, сделав важнейший и необходимый шаг в сторону абстракции.

В трудах Э. Галуа «математика перестает быть наукой о числах и формах – арифметикой, геометрией и набором связанных с ними идей, таких, как алгебра и тригонометрия.

Значение трудов Э. Галуа состоит в том, что в них в полной мере раскрытысовершенно новые глубинные математические закономерности: возникла новаяматематическая парадигма – теория полей, концепция группы, теория Галуа.

Появившаясяна свет целая ветвь математики – исчисление симметрий, называемое теорией групп,проникла в каждый уголок математики, во многие области современного научного познания.

В центре внимания Галуа оказалась основная проблема – разрешимость в радикалах общих алгебраических уравнений. Причем не только в случае уравнений пятой степени. Цель Галуа заключалась в том, чтобы найти критерий, способ разрешимости для всех алгебраических уравнений.

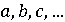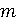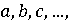Затем Галуа вводит свое ключевое понятие «группы уравнения» (комплексные числа), а именно: пусть дано уравнение и  суть  его корней. Существует всегда группа перестановок букв  обладающая следующими свойствами: [3, с.28]

- всякая функция от корней, инвариантная относительно подстановок этой группы, рационально известна;

- обратно, всякая рационально определяемая функция от корней инвариантна относительно этих подстановок.

Эварист Галуа совершил революцию в математике. Он является автором, изобретателем языка, который позволил описывать симметрии в математических структурах и выводить их следствия.

В настоящее время этот язык называется теорией групп. Он имеет весьма широкое распространение в чистой и прикладной математике, а также используется для выражения закономерностей в физическом мире.

Симметрия играет центральную роль в современной физике – в бесконечно малом квантовом мире и бесконечном мире Вселенной. Есть основания утверждать, что симметрия может проложить путь к будущей так называемой «теории всего», то есть математическому объединению двух главных направлений в современной физике – квантовой теории и теории относительности.

С точки зрения Э. Галуа, разрешимость некоторого уравнения перестала быть абсолютной проблемой, требующей готового ответа. Ученый рассматривает ее как связь между определенным алгебраическим объектом – уравнением и его «средой» – полем, или областью рациональности, к которой оно относится. [3, с.38]

Как только изменяется область рациональности уравнения, изменяется и его группа Галуа.

Понятие группы объединило аналитическую и проективную геометрии в комплексные числа. Цели и результаты программы объединили алгебру и геометрию. Так, «теория бинарных форм и проективная геометрия плоскости, которую изучаем, полагая в основу некоторое коническое сечение, эквивалентны между собой», или же «теория бинарных форм и общая проективная метрическая геометрия на плоскости – одно и то же».

Идея относительности группы – это личное изобретение Галуа. Она проникла затем во все математические и физические теории, ведущие свое происхождение от теории групп, которые в основном относятся к комплексным числам.

В современной математизированной теории понятие группы, развитой на основе идей Галуа, служит средством теоретизации различных областей знания в силу того, что в ней в абстрактной форме выражен принцип инвариантности как методологический императив.

Роль Галуа проявляется в процессе построения математических и физических теорий и служит важнейшим условием эффективности и плодотворности математических идей в современном естественнонаучном познании. Так, например, наиболее четко и ярко это проявляется в комплексных числах и неевклидовых геометриях.

Сейчас имя Галуа – одно из самых популярных в математике. Оно содержится в таких фундаментальных понятиях, как группа Галуа, поле Галуа, теория Галуа, соответствие Галуа и другие. [3, с.46]

Идеи Галуа оказали решающее влияние на развитие алгебры в течение столетия и проникли в другие области математики. Классическая теория Галуа обобщалась и развивалась во многих направлениях.

Заключение

Древнегреческие математики считали «настоящими» только натуральные числа. Потихоньку возникало воззрение о бесконечности большинства натуральных чисел.

Древнегреческий философ и математик Пифагор поучал, что «компоненты чисел считаются компонентами всех вещей и весь мир есть гармония и число».

В шестнадцатом веке Кардано обнаружил формулу для решения кубического уравнения.

Отрицательные числа использовались в III веке древнегреческий математик Диофант, который знал правила операций над ними, а в VII веке данные числа уже со всеми подробностями проанализировали индийские ученые, которые ассоциировали эти числа с долгом.

В XVII веке продолжалось обсуждение арифметического характера мнимых чисел и способности предоставить им геометрическое обоснование. 

С помощью формул Эйлера удалось построить число e любой комплексной степени.

Комплексные числа обширно применял отец русской авиации Жуковский (1847 – 1921) при создании теории крыла, автором которой он является.

Долгое время не получалось отыскать таких физических величин, над которыми можно было бы совершать действия, подчиненные тем же правилам, что и действия над комплексными числами - в частности правилу.

Рене Декарт является французским философом, математиком, механиком, физиком и физиологом. В том числе, создателем аналитической геометрии и современной алгебраической символики, автором метода радикального сомнения в философии, механики в физике, предтеча рефлексологии.

Декарт является одним из создателей аналитической геометрии (которую он разработал одновременно с Ферма), что позволило алгебраизировать эту науку при помощи координатного метода. Предложенная им система координат названа в его честь.

Комплексные числа еще не были рассмотрены Декартом на равных условиях с вещественными, но он сформулировал (хотя и не доказал) основную теорему алгебры: общее число вещественных и комплексных корней многочлена равно его степени.

Гауссовы целые числа комплексные числа (Гауссовы числа, целые комплексные числа) являются комплексными числами, в которых материальные и мнимую часть чисел.

Свойства гауссовских комплексных чисел аналогичны свойствам обычных целых чисел, но есть и существенные различия.

Кольцо гауссовых чисел - это коммутативное кольцо без делителей 0, так как оно является подкольцом поля комплексных чисел.

Э. Галуа входит в десятку величайших математиков всех времен. Он открыл новую эпоху мировой научной мысли, кардинальным образом преобразовал динамику математических наук.

Значение трудов Э. Галуа состоит в том, что в них в полной мере раскрыты совершенно новые глубинные математические закономерности

В современной математизированной теории понятие группы, развитой на основе идей Галуа, служит средством теоретизации различных областей знания в силу того, что в ней в абстрактной форме выражен принцип инвариантности как методологический императив.

Роль Галуа проявляется в процессе построения математических и физических теорий и служит важнейшим условием эффективности и плодотворности математических идей в современном естественнонаучном познании.

Идеи Галуа оказали решающее влияние на развитие алгебры в течение столетия и проникли в другие области математики. Классическая теория Галуа обобщалась и развивалась во многих направлениях.

Список использованных источников

1. Глазков Ю. А., Варшавский И. К., Гаиашвили М. Я. Комплексные числа. 9-11 классы; Экзамен - Москва, 2013. - 160 c.

2. Деменева Н.В. Комплексные числа: учебное пособие / Н. В. Деменева; М-во с.-х. РФ, федеральное гос. бюджетное образов. учреждение высшего образования «Пермская гос. с.-х. акад. им. акад. Д. Н. Прянишникова». – Пермь: ИПЦ «Прокростъ», 2017. – 112 с.

3. Фролов С.В. Простейшие функции комплексного переменного. Учебно-методическое пособие. – СПб.: ИТМО, 2013. – 66 с.

4. Шахмейстер А. Х. Комплексные числа; МЦНМО, Петроглиф, Виктория плюс - Москва, 2018. - 196 c.

5. Шахмейстер А. Х. Комплексные числа; МЦНМО, Петроглиф, Виктория плюс - Москва, 2017. - 176 c.

6. Шахмейстер А.Х. Комплексные числа; Книга по Требованию - Москва, 2016. - 176 c.

7. Яглом И. М. Комплексные числа и их применение в геометрии; Либроком - Москва, 2018. - 192 c.