Поведение частицы в поле Кулона-Дирака
Содержание
Введение
. Квантовое
усреднение
. Когерентное
преобразование
. Построение
ВКБ-асимптотики
. Решение
многоточечной спектральной задачи. Вычисление поправки в спектральной серии
. Вычисление
нормы. Формулировка итоговой теоремы
Заключение
Список литературы
Введение
В данной работе рассматривается поведение
частицы в поле Кулона-Дирака, возмущенном однородными магнитными и
неоднородными электрическими полями. Необходимо исследовать задачу на
собственные значения в гильбертовом пространстве  для
следующего гамильтониана частицы:
для
следующего гамильтониана частицы:
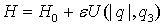 , (1)
, (1)
где гамильтониан 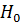 задается
соотношением
задается
соотношением 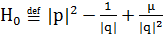 ,
, 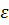 -
малый параметр, характеризующий напряженность поля и заряд частицы; функция
-
малый параметр, характеризующий напряженность поля и заряд частицы; функция 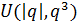 определяет
аксиальное возмущение данного поля Кулона-Дирака, причем
определяет
аксиальное возмущение данного поля Кулона-Дирака, причем 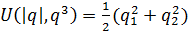 .
На магнитный заряд
.
На магнитный заряд 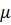 накладывается
условие квантования
накладывается
условие квантования 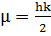 , где
, где 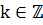 ,
,
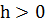 .
.
Известно [1], что алгебра, возникающая при
рассмотрении данной задачи, является алгеброй с квадратичными коммутационными
соотношениями. Каждому представлению полученной алгебры можно поставить в
соответствие спектральный кластер около уровня энергии невозмущенной частицы.
Состояния системы (1) вблизи границ спектральных кластеров требуют
дополнительного исследования, так как к ним невозможно применить стандартные
интегральные представления.
Метод нахождения асимптотики спектра вблизи
границ спектральных кластеров был предложен в работах [2], [3], где
рассматривалась спектральная задача для двумерного возмущенного осциллятора [4]
и задача о спектре атома водорода [5]. Этот метод был применен в данной работе
для нахождения асимптотики спектра вблизи нижних границ спектральных кластеров
для задачи (1) . Кроме того, формула, полученная для асимптотики собственной
функции, будет глобальной.
Цель данной работы - найти асимптотику решения
спектральной задачи
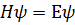 ,
, 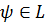 (2)
(2)
в области отрицательных энергий 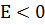 .
.
Введя предположение, что 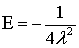 ,
и произведя регуляризацию задача (2) сводится к спектральной задаче
,
и произведя регуляризацию задача (2) сводится к спектральной задаче
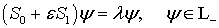 (3)
(3)
в гильбертовом пространстве 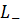 ,
в котором скалярное произведение определяется следующим равенством:
,
в котором скалярное произведение определяется следующим равенством:
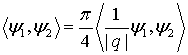 (4)
(4)
где 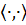 -
скалярное произведение в
-
скалярное произведение в  . Для
. Для 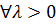 определяется
оператор «действие»
определяется
оператор «действие» 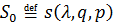 , где
, где 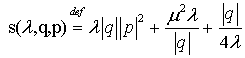 .
.
Оператор 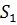 задается
формулой
задается
формулой 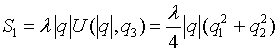 .
.
Спектр оператора 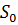 в
гильбертовом пространстве
в
гильбертовом пространстве 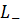 составлен из чисел
составлен из чисел
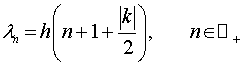
где собственные значения 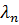 кратны
кратны
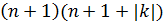 .
.
Так как собственные числа оператора 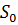 -
арифметическая прогрессия, то его название оператор «действия» является
корректным.
-
арифметическая прогрессия, то его название оператор «действия» является
корректным.
. Квантовое усреднение
В работах [1], [6]
описана схема квантового усреднения. Следуя ей, находим обратимый оператор 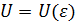 и
операторы
и
операторы 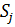 с точностью
с точностью 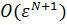 ,
которые задаются следующими формулами:
,
которые задаются следующими формулами:
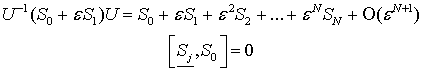
Получившийся оператор 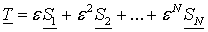 называется
усредненным оператором. Так как оператор
называется
усредненным оператором. Так как оператор 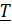 коммутативен
старшей части
коммутативен
старшей части 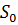 , то решение
спектральной задачи для оператора
, то решение
спектральной задачи для оператора 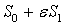 с
точностью
с
точностью 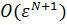 можно свести к
решению спектральной задачи для оператора
можно свести к
решению спектральной задачи для оператора 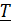 на
собственных подпространствах оператора
на
собственных подпространствах оператора 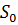 .
.
Для первого приближения по 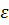 справедливо:
справедливо:
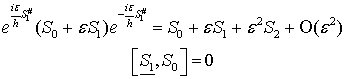
где 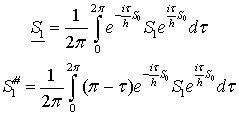
В итоге спектральная задача (3) с точностью 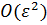 приводится
к новой спектральной задаче
приводится
к новой спектральной задаче 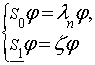
Причем, 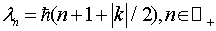 .
Собственные значения задачи (3) удовлетворяют следующему равенству
.
Собственные значения задачи (3) удовлетворяют следующему равенству 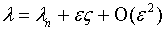 ,
а связь между ее собственными функциями
,
а связь между ее собственными функциями 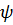 и
собственными функциями
и
собственными функциями 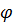 задачи (4)
определяется как
задачи (4)
определяется как 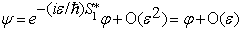 . Здесь операторы
. Здесь операторы 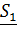 ,
,
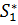 задаются
явными формулами.
задаются
явными формулами.
Следует отметить, что по построению операторы 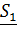 и
и
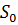 коммутируют.
Операторы
коммутируют.
Операторы 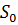 и
и 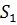 оба
коммутируют с оператором момента
оба
коммутируют с оператором момента 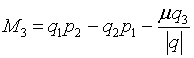 ,
откуда вытекает, что
,
откуда вытекает, что 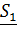 коммутирует с
коммутирует с 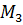 .
В итоге, в задаче возникает операторная алгебра Карасева-Новиковой
.
В итоге, в задаче возникает операторная алгебра Карасева-Новиковой 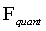 [1],
в которой находятся все операторы, коммутирующие с
[1],
в которой находятся все операторы, коммутирующие с 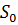 и
и
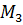 .
Образующие
.
Образующие 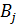 этой алгебры
подчиняются следующим коммутационным соотношениям:
этой алгебры
подчиняются следующим коммутационным соотношениям:
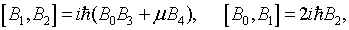
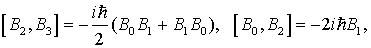

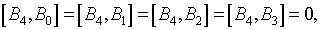
Запишем усредненный оператор 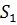 ,
как функцию, зависящую от образующих
,
как функцию, зависящую от образующих 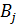 операторной
алгебры
операторной
алгебры 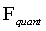 :
:
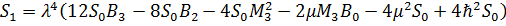 ,
,
при условии, что 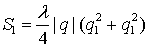 .
.
Задачу (4) можно рассматривать отдельно на
каждом собственном подпространстве 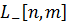 операторов
операторов
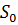 и
и
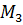 .
Тогда все сводится к задаче
.
Тогда все сводится к задаче
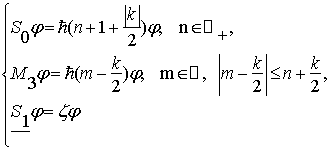 (5)
(5)
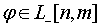 , где n,m
- квантовые числа.
, где n,m
- квантовые числа.
2. Когерентное преобразование
Для решения полученной задачи (5) необходимо
использовать когерентное преобразование
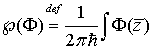
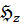
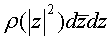 ,(6)
,(6)
где 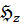 -
это гипергеометрическое когерентное состояние, которое определяется следующим
образом
-
это гипергеометрическое когерентное состояние, которое определяется следующим
образом 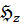
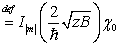 .
. 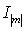 -
функция Бесселя [7], а весовая функция
-
функция Бесселя [7], а весовая функция 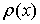 выражается
через гипергеометрическую функцию определенным образом.
выражается
через гипергеометрическую функцию определенным образом.
Пусть k,m,n
- целые числа, 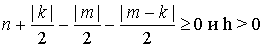 . Введена функция
. Введена функция
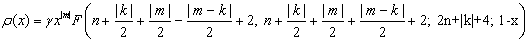
Где F-гипергеометрический
ряд [7]
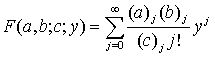
Операция 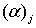 определяется
формулой
определяется
формулой 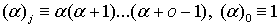 ,
а
,
а 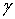 -
нормировочная константа:
-
нормировочная константа:
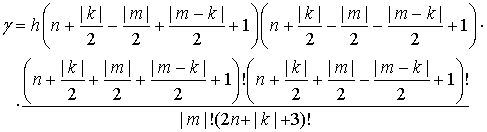
А именно, весовая функция 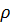 -
это решение следующего гипергеометрического уравнения:
-
это решение следующего гипергеометрического уравнения:
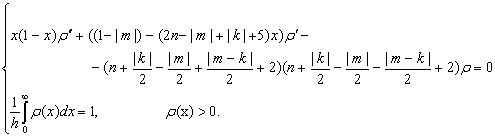
Когерентное преобразование взаимно-однозначно
отображает пространство 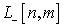 на пространство 𝒫
на пространство 𝒫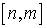 антиголоморфных полиномов над ℂ степени не
выше
антиголоморфных полиномов над ℂ степени не
выше 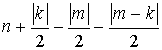 с
нормой
с
нормой 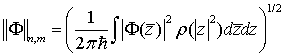 .
.
Таким образом, после когерентного преобразования
образующие 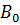 ,
, 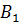 ,
,
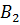 ,
,
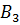 ,
,
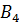 становятся
дифференциальными операторами первого и второго порядка, которые удовлетворяю
следующим соотношениям:
становятся
дифференциальными операторами первого и второго порядка, которые удовлетворяю
следующим соотношениям:
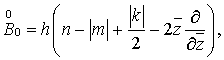
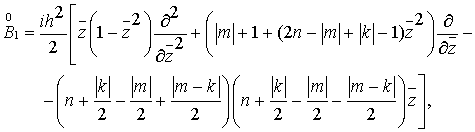
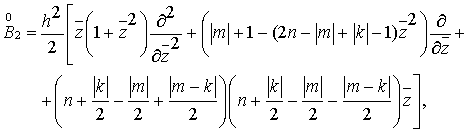
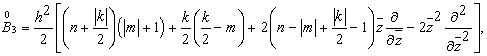
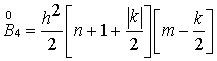
Также необходимо, чтобы соблюдалось условие
Формула когерентного преобразования ( 6)
позволяет точно найти решения первых двух уравнений (5) при любых амплитудах Φ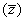 .
Таким образом, достаточно решить лишь третье уравнение системы (5), которое
после когерентного преобразования в пространстве 𝒫
.
Таким образом, достаточно решить лишь третье уравнение системы (5), которое
после когерентного преобразования в пространстве 𝒫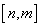 имеет вид:
имеет вид:
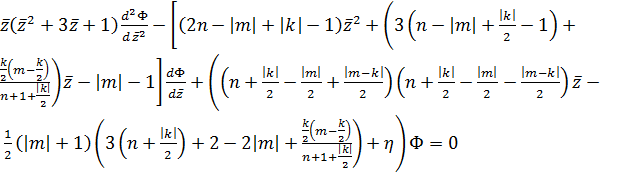 (8)
(8)
Здесь 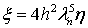
3. Построение ВКБ-асимптотики
Полученное уравнение (8) является уравнением
Гойна. Оно принадлежит классу уравнений Фукса [8], и все его особые точки
являются регулярными особыми точками. В рассматриваемой задаче четыре особые
точки, три из них конечные особые точки и бесконечность: 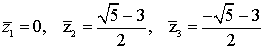 ,
,
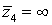 .
.
Предположим, что : 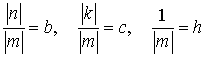 ,
,
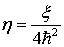 .
.
При 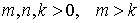 эти
параметры удовлетворяют неравенствам
эти
параметры удовлетворяют неравенствам 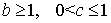 .
Пусть
.
Пусть 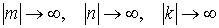 .
Тогда числа b,c
имеют порядок 1,а
.
Тогда числа b,c
имеют порядок 1,а 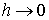
Будем искать решение уравнения (8) в виде
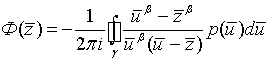 , (9)
, (9)
где 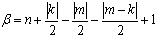 ,
,
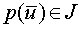 ,
где
,
где 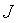 -
множество антиголоморфных в окрестности нуля функций.
-
множество антиголоморфных в окрестности нуля функций.
Заданный оператор на множестве 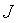 является
проектором на пространстве 𝒫
является
проектором на пространстве 𝒫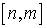 .
В правую часть формулы (9) подставляется асимптотическое решение уравнения (8),
а не асимптотическое решение уравнения
.
В правую часть формулы (9) подставляется асимптотическое решение уравнения (8),
а не асимптотическое решение уравнения 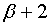 -ого
порядка, в которое преобразуется (8) под действием преобразования (9). Такая
замена возможна, потому что аналогично [3] доказывается, что возникающие
дополнительные слагаемые в уравнении вносят экспоненциально малый вклад в
невязку.
-ого
порядка, в которое преобразуется (8) под действием преобразования (9). Такая
замена возможна, потому что аналогично [3] доказывается, что возникающие
дополнительные слагаемые в уравнении вносят экспоненциально малый вклад в
невязку.
При построении асимптотических решений уравнения
(8) существенную роль играет их поведение вблизи особых точек. Исследуем
многоточечную спектральную задачу вместе со спектральной задачей (8), (7). Ее
суть заключается в поиске собственных значений 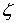 ,
при которых у уравнения (8) существуют ненулевые антиголоморфные решения,
характеристические показатели которых в особых точках равны нулю, а в особой
точке
,
при которых у уравнения (8) существуют ненулевые антиголоморфные решения,
характеристические показатели которых в особых точках равны нулю, а в особой
точке 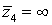 показатель
равен
показатель
равен 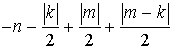 .
.
Предположив, что собственные значения - это
число 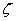 ,
а функция
,
а функция 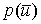 - асимптотическое
решение такой многоточечной спектральной задачи, то при подстановке
- асимптотическое
решение такой многоточечной спектральной задачи, то при подстановке 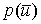 в
правую часть формулы (9) получаем многочлен
в
правую часть формулы (9) получаем многочлен 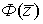 -
асимптотическое решение уравнения (8) из пространства 𝒫
-
асимптотическое решение уравнения (8) из пространства 𝒫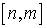 .
Из условия нормировки (7) для
.
Из условия нормировки (7) для 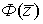 можно найти
константу, содержащуюся в
можно найти
константу, содержащуюся в 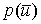 . Таким образом,
число
. Таким образом,
число 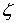 и
многочлен
и
многочлен 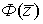 являются
асимптотическим решением исходной спектральной задачи (8), (7).
являются
асимптотическим решением исходной спектральной задачи (8), (7).
Запишем уравнение (8) в виде: 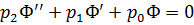 .
.
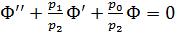 ,
,
Теперь будем строить асимптотическое решение
уравнения (8). Представим решение Ф в виде  (10)
и найдем его производные первого и второго порядка.
(10)
и найдем его производные первого и второго порядка.
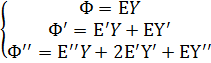 ,
,
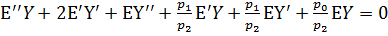 ,
,
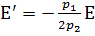 ,
,
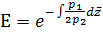 , (10)
, (10)
Найдем 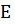 :
для этого посчитаем интеграл
:
для этого посчитаем интеграл 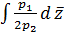 с помощью метода
неопределенных коэффициентов.
с помощью метода
неопределенных коэффициентов.
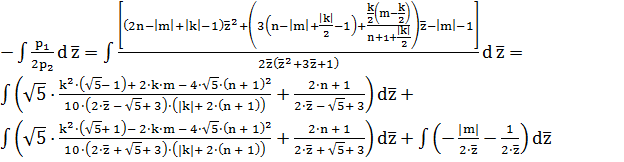 ,
,
c учетом замен и
разложения в ряд Тейлора:
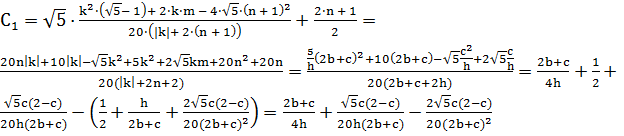 ,
,
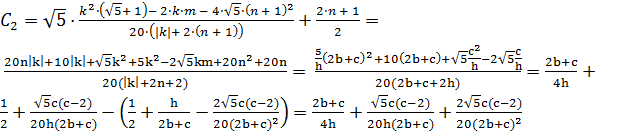 ,
,
В итоге, нашли Е:
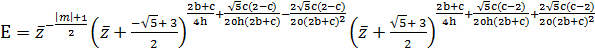 (11)
(11)
Уравнение (8) можно представить в виде: 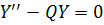 (12)
, исключив из него первую производную.
(12)
, исключив из него первую производную.
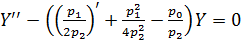 ,
,
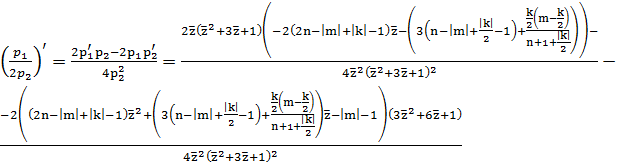 ,
,
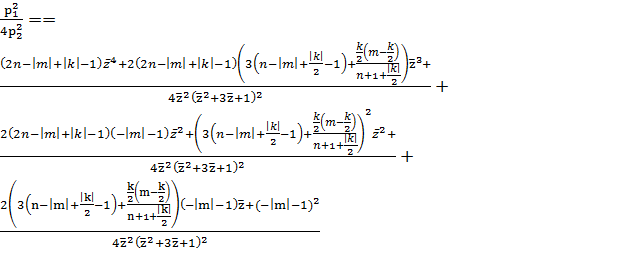 ,
,
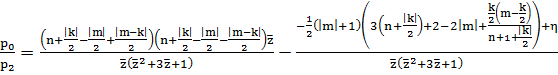 ,
,
Сделаем замену:
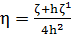 ,
,
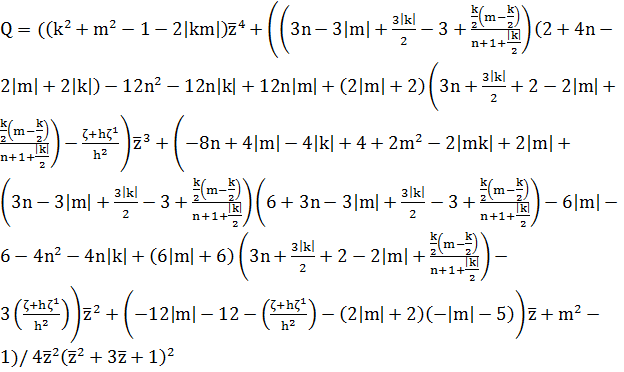 , (12)
, (12)
Сделаем замены 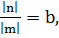
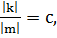
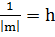
Лемма 1. Справедливо равенство:
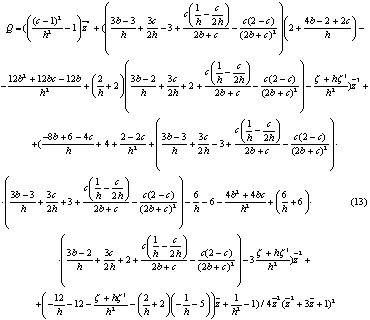
Выделяем слагаемые порядка 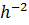
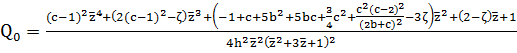 (14)
(14)
Выделяем слагаемые порядка 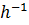
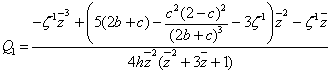 (15)
(15)
Затем решаем систему: 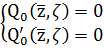 ,
чтобы найти кратные точки поворота и главный член разложения
,
чтобы найти кратные точки поворота и главный член разложения 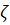 вблизи
этой точки.
вблизи
этой точки.
Представим 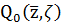 в
виде:
в
виде: 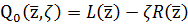 .
Тогда
.
Тогда 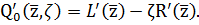
Получаем новую систему:
 ,
,
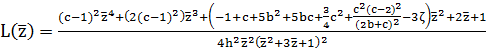 ,
,
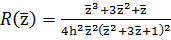 ,
,
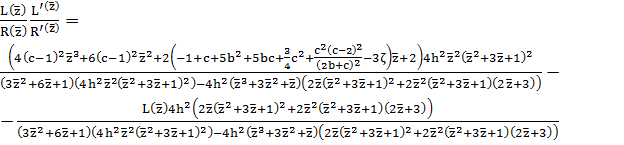 ,
,
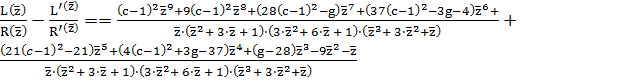 ,
,
где 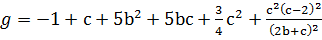
В рассматриваемой задаче 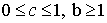 .
Тогда точка
.
Тогда точка 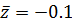 будет точкой
поворота кратности два.
будет точкой
поворота кратности два.
Сначала, устанавливаем связь между
коэффициентами c и b:
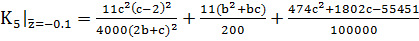 ,
,
Отсюда получаем, что
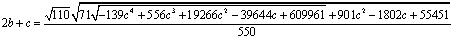 (16)
(16)
Замечание: данное условие (16) носит технический
характер и требуется затем, чтобы кратная точка поворота, расположенная в точке
-0.1 имела простой вид. Иначе, эта точка является корнем уравнения четвертого
порядка.
Далее ищем 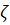
 ,
,
Получаем выражение для 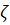
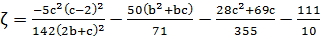 (17)
(17)
Числитель 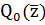 (обозначим
его
(обозначим
его 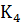 )-
многочлен четвертой степени, с точкой поворота
)-
многочлен четвертой степени, с точкой поворота 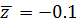 кратности
два, а также простыми точками поворота
кратности
два, а также простыми точками поворота 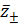 Тогда
его можно представить в виде
Тогда
его можно представить в виде 
Найдем коэффициенты D,
A, B
разложения.
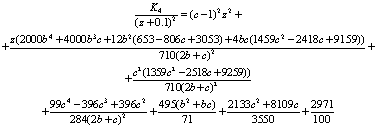
Учитывая найденную ранее связь между
коэффициентами a и b,
искомые коэффициенты квадратного многочлена принимают вид:
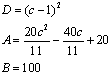 (18)
(18)
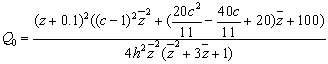 (19)
(19)
Теперь будем строить ВКБ-приближение для решения
уравнения (12) или 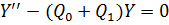 . Они верны около
малых окрестностей точек поворота и вычисляются по следующей формуле [9],[10]:
. Они верны около
малых окрестностей точек поворота и вычисляются по следующей формуле [9],[10]:
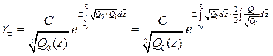 (20),
(20),
где С-константа Необходимо посчитать,
возникающие в (20) интегралы. Их вычисление проводим с помощью табличных
интегралов [11] и метода неопределенных коэффициентов.
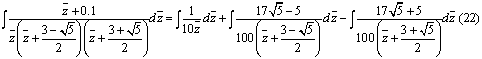
Вычислим первый интеграл из формулы (22):
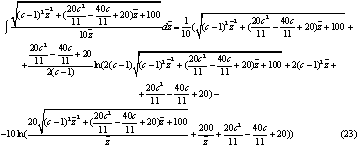
Вычислим второй интеграл из формулы (22):
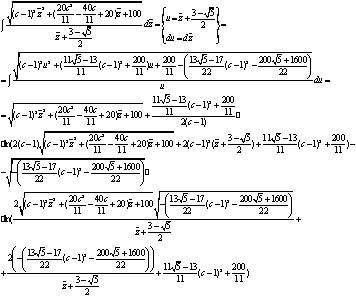 (24)
(24)
Вычислим третий интеграл из формулы (22):

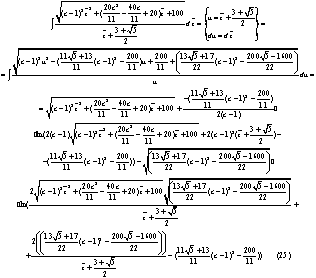
Таким образом, можем посчитать общий интеграл
(21), используя (22)-(25):
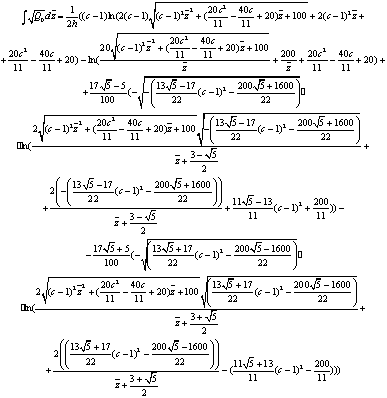 (26)
(26)
Теперь посчитаем следующий интеграл из формулы
(20):
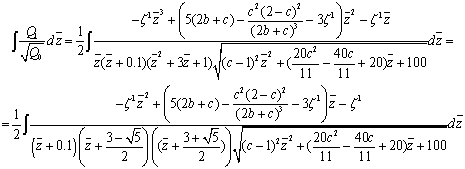 (27)
(27)
Решаем интеграл (27) с помощью метода
неопределенных коэффициентов:
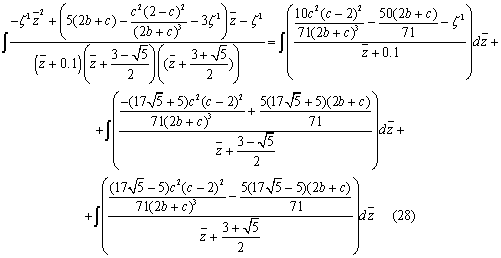
С помощью замены сведем интеграл к табличному
[11] и вычислим его:
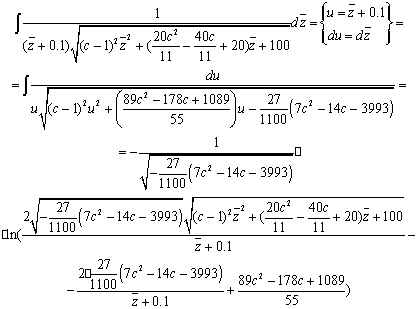 (29)
(29)
Вычислим второй интеграл из формулы (28):
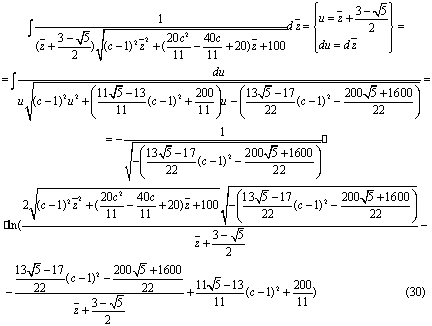
Вычислим третий интеграл из формулы (28):
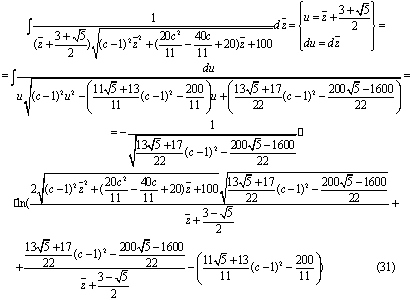
Находим общий интеграл с помощью формул (28),
(29)- (31):
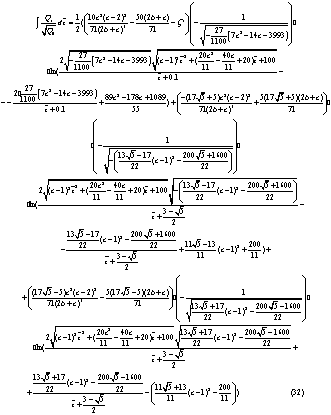
Итак, найдем ВКБ-приближение решений уравнения
(8) 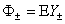
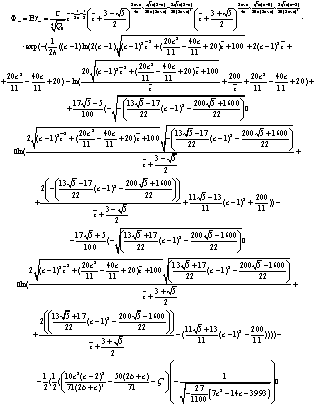
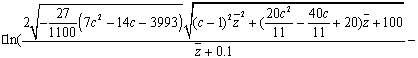
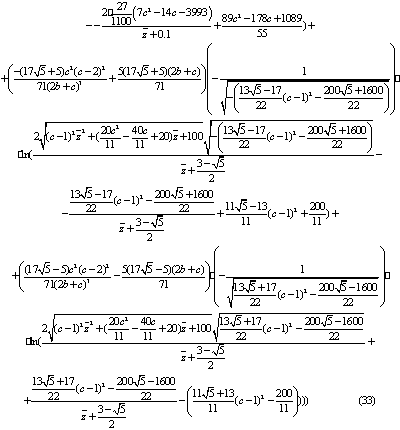
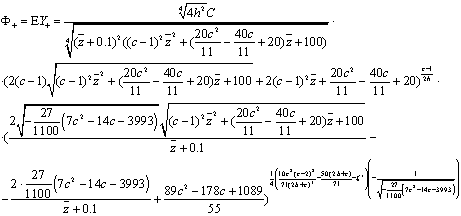 (34)
(34)
Итак, мы нашли асимптотику решения
рассматриваемой задачи во всей комплексной плоскости вне малых окрестностей
точек 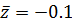 ,
,
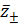 .
.
Теорема 1:
ВКБ-приближение для уравнения (8) имеет вид
(33), (34).
4. Решение многоточечной спектральной задачи.
Вычисление поправки в спектральной серии
Следующим этапом является построение
асимптотического решения вблизи точек поворота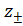 .
.
Найдем точки поворота 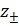 ,
как корни квадратного многочлена с коэффициентами, заданными формулой (18).
,
как корни квадратного многочлена с коэффициентами, заданными формулой (18).
 (35)
(35)
 (36)
(36)
Из уравнения (12) следует, что около точек
поворота 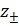
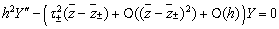 (37)
(37)
Из этого вытекает, что главные члены
асимптотических разложений вблизи (35),(36) записываются через функции Эйри
[12]:
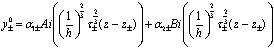 , (38)
, (38)
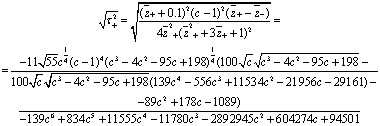
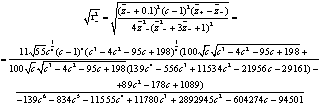
А 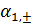 ,
,
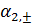 -
константы.
-
константы.
Лемма 1 .
Вблизи точек 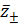 асимптотическое
решения уравнения (12) имеют вид (38). Следовательно, решение задачи (8) вблизи
точек поворота будет иметь вид:
асимптотическое
решения уравнения (12) имеют вид (38). Следовательно, решение задачи (8) вблизи
точек поворота будет иметь вид:
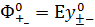 ,
,
Затем необходимо построить решение уравнения
(12) вблизи точки поворота 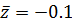 и найти
спектральную поправку
и найти
спектральную поправку 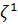 .
.
Пусть 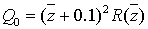 .
Разложим в ряд Тейлора
.
Разложим в ряд Тейлора 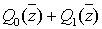 в окрестности
в окрестности 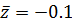 .
.
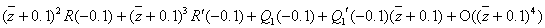
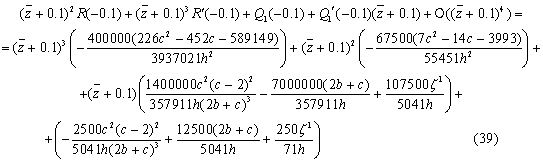
Сделав замены, уравнение (39) можно представить
в следующем виде:
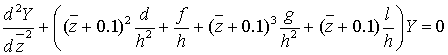 (40)
(40)
Асимптотическое решение уравнения (40) будем
искать в виде:
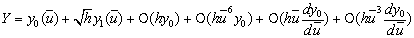 (41)
(41)
Сделаем замену
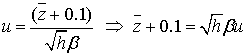 . (42)
. (42)
Тогда уравнение(40) принимает вид :
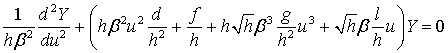 (43)
(43)
Главный член асимптотики находится из следующего
уравнения:
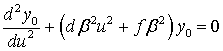 (44)
(44)
Задаем коэффициент 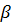 так,
чтобы уравнение (44) приняло вид Вебера [7]:
так,
чтобы уравнение (44) приняло вид Вебера [7]:
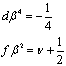 . (45)
. (45)
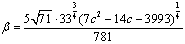 (46)
(46)
Теперь ищем 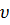 .
.
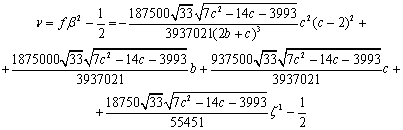 (47)
(47)
В итоге, получаем уравнение Вебера для главных
членов асимптотики
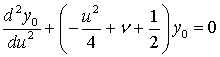 (48)
(48)
Известно [7], что его общее решение выражается
через функции параболического цилиндра
 (49)
(49)
Линии Стокса [9],[10] для уравнения (12) имеют
следующий вид
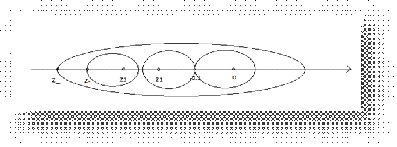
Поскольку линии Стокса для для уравнения (12)
имеют такой вид, то после согласования найденной асимптотики разложения,
которые призводятся аналогично работе [3], приходим к условию:
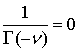 (50)
(50)
Кроме того, получаем, что из (49)
α2=0 и из (38) α2±=0.
Известно [12], что гамма-функция имеет полюсы
только при 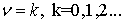
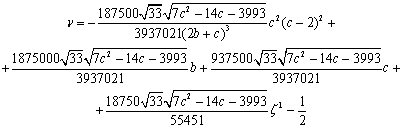 (51)
(51)
Лемма 2. Спектральная поправка 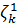 удовлетворяют
следующему равенству
удовлетворяют
следующему равенству
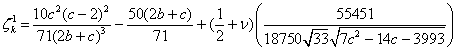 (52)
(52)
Из формул (49), (50) следует, что
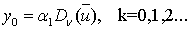 (53)
(53)
Функции параболического цилиндра можно выразить
через многочлены Эрмита [7]:
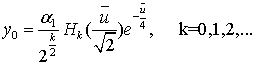 (54)
(54)
Теперь необходимо найти второй член в разложении
(41). Из (40), (50),(53) следует, что 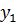 удовлетворяет
уравнению:
удовлетворяет
уравнению:
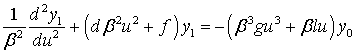 (55)
(55)
Предположим, что частное решение этого уравнения
можно представить в следующем виде:
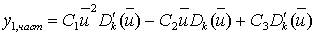 (56)
(56)
Тогда общее решение уравнения (55) имеет вид:
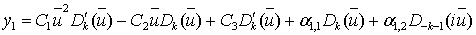 ,(57)
,(57)
где 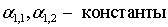 .
.
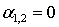 из-за
условия согласования функции с ВКБ-приближением. Пусть
из-за
условия согласования функции с ВКБ-приближением. Пусть 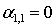 ,
при условии, что поправка порядка
,
при условии, что поправка порядка 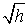 входит
входит
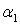 .
.
Найдем частное решение путем непосредственного
дифференцирования.
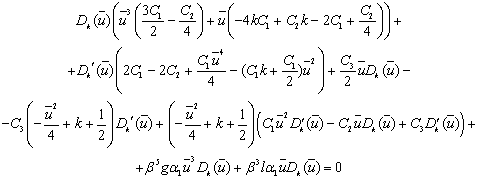
Получили систему уравнений для коэффициентов
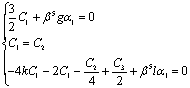
Таким образом, общее решение 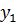 принимает
следующий вид:
принимает
следующий вид:
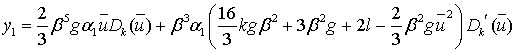 (58)
(58)
Или решение можно выразить посредством полиномов
Эрмита:
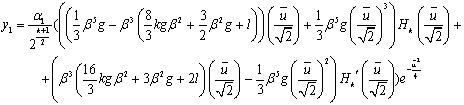 (59)
(59)
Лемма 2.
Асимптотическое решение вблизи 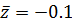 имеет
вид (41), где
имеет
вид (41), где 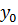 задается формулой
(54), а
задается формулой
(54), а 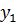 задается
формулой (59).
задается
формулой (59).
Следующим шагом вычисляется норма решения. Для
этого необходимо разложить функцию 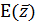 по
степеням
по
степеням 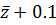 ,
с учетом замены (42) из-за справедливости равенства (10).
,
с учетом замены (42) из-за справедливости равенства (10). 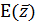 определено
формулой (11), для удобства проведём такие замены, что
определено
формулой (11), для удобства проведём такие замены, что
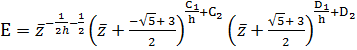 (60)
(60)
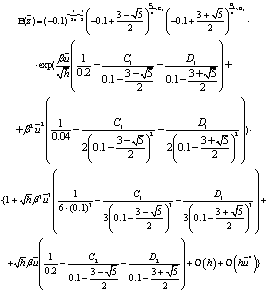 (61)
(61)
Далее ищем разложение 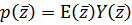 ,
где
,
где 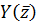 определено
соотношением (41), а
определено
соотношением (41), а 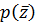 - это решение (8)
вблизи -0.1, и получаем:
- это решение (8)
вблизи -0.1, и получаем:
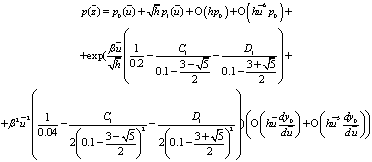 , (62)
, (62)
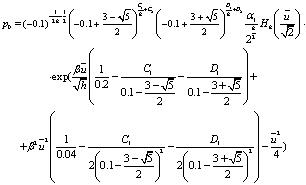 (63)
(63)
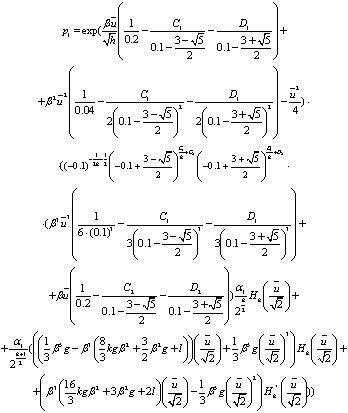 (64)
(64)
Лемма 3.
Асимптотическое решение многоточечной
спектральной задачи вблизи точки поворота 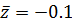 имеет
вид (62).
имеет
вид (62).
. Вычисление нормы. Формулировка итоговой
теоремы
Весовая функция 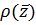 задает
меру в формуле скалярного произведения (4).
задает
меру в формуле скалярного произведения (4).
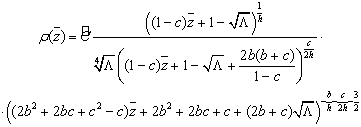 (65)
(65)
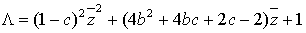 (66)
(66)
Коэффициент 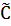 находится
из условия нормировки
находится
из условия нормировки 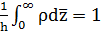 по следующей
формуле (67):
по следующей
формуле (67):
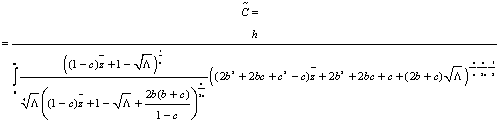 (67)
(67)
Разложим функцию 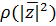 по
степеням
по
степеням 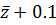
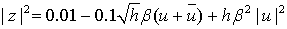 (68)
(68)
Введем следующие замены:
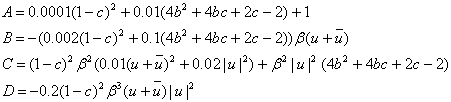 (69)
(69)
Через эти замены (69) выразим следующие
переменные:
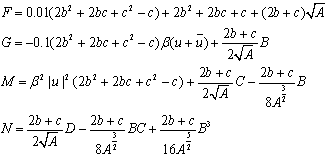 (70)
(70)
Тогда весовая функция удовлетворяет равенству
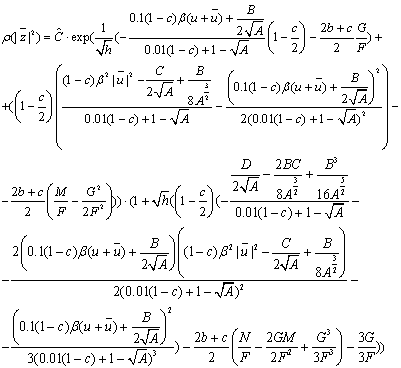 (71)
(71)
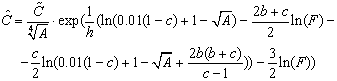 (72)
(72)
Теперь вычислим 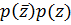 :
:
 (73)
(73)
Затем ищем норму по формуле 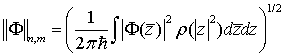 :
:
 (74)
(74)
где 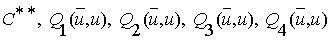 определяются
из формул(73), (72).
определяются
из формул(73), (72).
Введем вещественные переменные 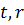 такие,
что
такие,
что
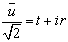 (75)
(75)
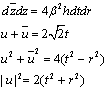 (76)
(76)
и норма (74) принимает следующий вид:
 (77)
(77)
где константа 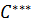 определяется
из формул (74), (76).
определяется
из формул (74), (76).
В формуле (77) слагаемые порядка 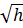 являются
интегралами от нечетных функций в симметричных пределах. Следовательно, они
равны нулю. спектральный многочлен
когерентный
являются
интегралами от нечетных функций в симметричных пределах. Следовательно, они
равны нулю. спектральный многочлен
когерентный
Таким образом, находим 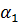 .
.
 (78)
(78)
Таким образом, приходим к основной теореме.
Теорема 2: Пусть 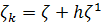 ,
,
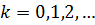 определено
формулами (17), (52), а многочлен
определено
формулами (17), (52), а многочлен 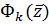 определен
формулой (9), где
определен
формулой (9), где 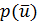 - решение
многоточечной спектральной задачи, такое что
- решение
многоточечной спектральной задачи, такое что 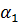 имеет
вид (78). Тогда
имеет
вид (78). Тогда 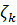 и
и 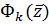 являются
асимптотическим собственным значением и асимптотической собственной функцией
задачи (8), (7) при
являются
асимптотическим собственным значением и асимптотической собственной функцией
задачи (8), (7) при 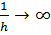 в пространстве
в пространстве 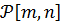 .
Более точно, если
.
Более точно, если 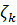 определено (17),
(52), то многочлен
определено (17),
(52), то многочлен 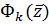 удовлетворяет
уравнению (8) с точностью
удовлетворяет
уравнению (8) с точностью 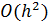 с оценкой невязки
в норме
с оценкой невязки
в норме 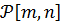 ,
а также условию нормировки (7) с точностью
,
а также условию нормировки (7) с точностью 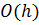 .
.
Заключение
В итоге, найдена квазиклассическая асимптотика
спектра вблизи нижних границ спектральных кластеров для задачи, описывающей
частицу в аксиально-симметричном поле Кулона-Дирака. В работе была найдена
асимптотика собственных значений Е исходной задачи (2) с точностью до членов
четвертого порядка малости по магнитному полю. Найденные формулы описывают
расщепление спектра, то есть эффект Зеемана для данной задачи.
При построении асимптотических собственных
функций было использовано интегральное представление (9), предложенное в работе
[2]. Полученные в выпускной работе результаты могут быть использованы в
квантовой теории при изучении атомов и молекул.
Список литературы
1. Карасев М. В., Новикова Е.
М. Алгебра с квадратичными коммутационными соотношениями для
аксиально-возмущенного поля Кулона-Дирака // ТМФ, 2004, Т. 141, №3, С. 424-454
2. Перескоков А. В.
Асимптотика спектра и квантовых средних вблизи границ спектральных кластеров
для возмущенного двумерного осциллятора // Мат. заметки, 2012, Т. 92, №4, С.
583-596
. Шифф Л. Квантовая механика.
М., ИЛ, 1959.
. Лисица В. С. Новое в
эффектах Штарка и Зеемана для атома водорода // УФН. 1987. Т. 153,№3. С.
379-421. (атом водорода)
6. Карасев М. В., Новикова Е.
М. Представление точных и квазиклассических собственных функций через
когерентные состояния. Атом водорода в магнитном поле // ТМФ. 1996.Т. 108, №3.
С. 339-387.
7. Бейтмен Г., Эрдейи А.
Высшие трансцендентные функции. В 2-x т. М., Наука, 1973, 1974.
. Голубев В. В. Лекции по
аналитической теории дифференциальных уравнений. М., Л., Гостехиздат, 1950.
9. Олвер Ф. Асимптотика и
специальные функции. М., Наука, 1990.
. Федорюк М. В.
Асимптотические методы для линейных обыкновенных дифференциальных уравнений.
М., Наука, 1983.
11. Градштейн И. С., Рыжик И. М.
Таблицы интегралов, сумм, рядов и произведений. М., Наука, 1975.
. Справочник по специальным функциям
с формулами, графиками и математическими таблицами / Под ред. М. Абрамовиц, И.
Стиган. М., Наука, 1979.