Характеристики интерференции двух пересекающихся широкополосных диспергированных пучков
ФЕДЕРАЛЬНОЕ
ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ имени М.В.ЛОМОНОСОВА»
Характеристики
интерференции двух пересекающихся широкополосных диспергированных пучков
Введение
Явление обращения волнового фронта оптического
излучения имеет широкие перспективы применения как в науке, так и в современных
наукоемких технологиях. Обращение волнового фронта позволяет создавать лазерные
системы с высоким качеством излучения и возможностью его самонаведения на
объект исследования или воздействия.
Для широкополосных лазеров обращение волнового
фронта излучения может быть получено в схемах четырехволнового взаимодействия с
пересекающимися световыми пучками. Наряду с "классической" схемой
четырехволнового взаимодействия с встречными плоскими опорными волнами [1],
могут быть использованы и разработанные на нашей кафедре схемы с петлей
обратной связи, не требующие создания опорных волн. Однако, при большой ширине
спектра
Δλ поле светового пучка когерентно лишь в пределах
узкого слоя когерентности толщиной 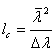 ,
ориентированного обычно перпендикулярно оси пучка. Непараллельность тонких
слоев когерентности пересекающихся световых пучков ограничивает область их
когерентного взаимодействия, которая для мощных многомодовых пучков оказывается
много меньше диаметра пучка. Указанное ограничение можно снять при
использовании диспергированных световых пучков, в которых слои когерентности
наклонены по отношению к фазовым фронтам и не перпендикулярны к оси пучка. Это
позволяет при соответствующей установке угла между осями пересекающихся пучков
сделать слои обоих пучков параллельными друг другу, распространяя тем самым
область когерентного взаимодействия на все поперечное сечение пересекающихся
пучков независимо от ширины спектра излучения. Когерентный режим обращения
волнового фронта, характеризующийся высокой степенью обращения и отсутствием
«зашумления» обращенной волны, реализуется при наличии пространственной когерентности
обращаемого лазерного пучка.
,
ориентированного обычно перпендикулярно оси пучка. Непараллельность тонких
слоев когерентности пересекающихся световых пучков ограничивает область их
когерентного взаимодействия, которая для мощных многомодовых пучков оказывается
много меньше диаметра пучка. Указанное ограничение можно снять при
использовании диспергированных световых пучков, в которых слои когерентности
наклонены по отношению к фазовым фронтам и не перпендикулярны к оси пучка. Это
позволяет при соответствующей установке угла между осями пересекающихся пучков
сделать слои обоих пучков параллельными друг другу, распространяя тем самым
область когерентного взаимодействия на все поперечное сечение пересекающихся
пучков независимо от ширины спектра излучения. Когерентный режим обращения
волнового фронта, характеризующийся высокой степенью обращения и отсутствием
«зашумления» обращенной волны, реализуется при наличии пространственной когерентности
обращаемого лазерного пучка.
Для расчета и практического применения устройств
с наклонными слоями когерентности необходимо знать, как влияет внесение
дисперсии на пространственную когерентность широкополосного лазерного пучка. В
этом направлении уже выполнен ряд работ. Теоретически изучены статистические
характеристики пространственных флуктуаций интенсивности диспергированных
лазерных пучков. Методом численного моделирования получены двумерные
распределения случайной интенсивности, дающие наглядную картину трансформации
спекл-структуры при распространении лазерного пучка. когерентность
диспергированный лазерный спектр
Результаты, полученные при исследовании
пространственной когерентности диспергированного лазерного пучков, также
необходимы при проектировании устройств обращения волнового фронта для
широкополосных лазеров. Так, было показано, что с ростом продольной координаты
степень когерентности уменьшается, а толщина слоя когерентности возрастает.
Установлены зависимости степени когерентности диспергированного пучка от угла
между слоями когерентности и направлением распространения, ширины спектра
излучения. Методом численного моделирования изучена геометрия спеклов
пространственной когерентности.
Однако, на эффективность нелинейного
взаимодействия в устройствах с пересекающимися диспергированными лазерными
пучками влияет не только пространственная когерентность каждого из пучков, но и
их взаимная когерентность. Ее исследованию посвящено очень небольшое число
работ. В частности, остался не рассмотренным такой аспект проблемы, как
зависимость характеристик взаимной пространственной когерентности от ширины
спектра интерферирующих пучков. В данной бакалаврской работе путем численного
моделирования рассчитывается зависимость степени взаимной когерентности от
продольной координаты при различной ширине спектра излучения. Проводится
сравнение с теоретическими зависимостями, полученными ранее на основе
приближенного аналитического расчета.
Глава
1. РАСШИРЕНИЕ ОБЛАСТИ ВЗАИМОДЕЙСТВИЯ ШИРОКОПОЛОСНЫХ ПУЧКОВ. ОБЗОР ЛИТЕРАТУРЫ
.1 Метод наклона слоев когерентности
Впервые теоретически и экспериментально
возможность кардинального расширения области когерентного взаимодействия
пересекающихся световых пучков была показана в работе [2]. Для решения этой
задачи был предложен и реализован метод, основанный на наклоне слоев
когерентности взаимодействующих пучков относительно их направлений
распространения. Такой наклон может быть создан при пропускании пучков через
диспергирующие элементы. Рассмотрим этот метод, следуя работе [2], на примере
использования призмы.
Для несфокусированных лазерных пучков область, в
которой степень пространственной когерентности излучения велика, обычно имеет
вид слоя, перпендикулярного направлению распространения. Его толщина в
направлении оси пучка приблизительно равна длине когерентности излучения
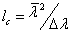 ,
,
где 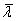 -
средняя длина волны частотного спектра,
-
средняя длина волны частотного спектра, 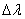 -
его ширина. Если поле представляет собой суперпозицию неограниченных по
поперечным координатам x,y
плоских волн с различными частотами
-
его ширина. Если поле представляет собой суперпозицию неограниченных по
поперечным координатам x,y
плоских волн с различными частотами 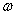 ,
распространяющихся вдоль оси z,
то его слои когерентности будут плоскими и перпендикулярными к оси z.
В диспергирующей среде плоский слой когерентности пучка распространяется с
групповой скоростью
,
распространяющихся вдоль оси z,
то его слои когерентности будут плоскими и перпендикулярными к оси z.
В диспергирующей среде плоский слой когерентности пучка распространяется с
групповой скоростью 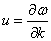 , а его фазовый
фронт - с фазовой скоростью
, а его фазовый
фронт - с фазовой скоростью
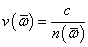
где  -
средняя частота спектрального распределения. При прохождении пучком такого
диспергирующего элемента, как призма, при определенном выборе ее дисперсии
можно добиться того, что поле после призмы останется пространственно
когерентным, а его слои когерентности будут не перпендикулярны к оси пучка,
которая задается направлением волнового вектора
-
средняя частота спектрального распределения. При прохождении пучком такого
диспергирующего элемента, как призма, при определенном выборе ее дисперсии
можно добиться того, что поле после призмы останется пространственно
когерентным, а его слои когерентности будут не перпендикулярны к оси пучка,
которая задается направлением волнового вектора 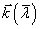 .
Выбор дисперсии призмы диктуется параметрами спектрального состава пучка:
средней длиной волны
.
Выбор дисперсии призмы диктуется параметрами спектрального состава пучка:
средней длиной волны 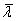 и шириной спектра.
и шириной спектра.
Рисунок 1 поясняет ход лучей в призме,
обеспечивающий наклон слоев когерентности. До призмы слои когерентности
перпендикулярны оси 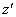 и оси пучка. После
призмы слой когерентности распространяется перпендикулярно оси z
и под углом
и оси пучка. После
призмы слой когерентности распространяется перпендикулярно оси z
и под углом 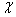 к оси пучка. Угол
к оси пучка. Угол 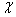 между
осевым вектором
между
осевым вектором 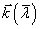 и нормалью к слоям
когерентности (ось z)
определяется дисперсией призмы. Его также можно определить, исходя из различия
между групповой скоростью u,
с которой движется огибающая поля в призме, и скоростью распространения
фазового фронта
и нормалью к слоям
когерентности (ось z)
определяется дисперсией призмы. Его также можно определить, исходя из различия
между групповой скоростью u,
с которой движется огибающая поля в призме, и скоростью распространения
фазового фронта 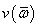 . Подробное
рассмотрение прохождения широкополосной плоской волны через призму дано в [2].
Возникающая при спектральном разложении угловая расходимость пучка
. Подробное
рассмотрение прохождения широкополосной плоской волны через призму дано в [2].
Возникающая при спектральном разложении угловая расходимость пучка 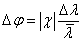 очень
мала (значительно меньше
очень
мала (значительно меньше 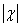 ) и в дальнейшем
рассмотрении ею можно пренебречь. Следует заметить, что подобный эффект наклона
слоев когерентности будет иметь место и при прохождении тонкой дифракционной
решетки с треугольным профилем штриха, работающей в первом порядке дифракции.
) и в дальнейшем
рассмотрении ею можно пренебречь. Следует заметить, что подобный эффект наклона
слоев когерентности будет иметь место и при прохождении тонкой дифракционной
решетки с треугольным профилем штриха, работающей в первом порядке дифракции.
Рис.1. Ход лучей в оптической схеме,
обеспечивающей наклон слоев когерентности
Достигнутая таким образом неперпендикулярность
слоев когерентности к направлению распространения позволяет обеспечить
параллельность слоев когерентности пересекающихся широкополосных пучков во всей
области их наложения. Для этого необходимо, чтобы угол 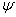 между
взаимодействующими пучками удовлетворял условию
между
взаимодействующими пучками удовлетворял условию 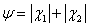 ,
где
,
где 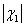 ,
,
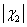 -
углы наклона слоев когерентности, которые должны иметь разные знаки. Рисунок 2
поясняет оптическую схему, в которой может быть реализовано когерентное
взаимодействие пучков с широким частотным спектром.
-
углы наклона слоев когерентности, которые должны иметь разные знаки. Рисунок 2
поясняет оптическую схему, в которой может быть реализовано когерентное
взаимодействие пучков с широким частотным спектром.
При параллельности слоев когерентности периоды
интерференционных картин, даваемых отдельными спектральными компонентами,
равны. Интерференционная картина в этом случае может наблюдаться на всем
поперечном размере перекрывающихся пучков.
Описанный метод расширения области когерентного
взаимодействия с помощью наклона слоев когерентности в работе [2] был
реализован экспериментально. При использовании модифицированного интерферометра
Майкельсона, призм с преломляющими углами до 10° и установке угла между
пересекающимися пучками 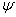 ~3∙10-2
рад интерференционные полосы наблюдались во всем поперечном сечении, имевшем
диаметр ~ 20 мм.
~3∙10-2
рад интерференционные полосы наблюдались во всем поперечном сечении, имевшем
диаметр ~ 20 мм.
Рис.2. Схема когерентного взаимодействия
широкополосных пучков
Ширина спектра излучения от теплового источника
варьировалась от 50 нм до 370 нм. В белом свете интерференционные полосы были
видны в области диаметром ~ 8 мм. При сдвиге слоев когерентности относительно
друг друга на толщину слоя 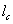 интерференционные
полосы исчезали.
интерференционные
полосы исчезали.
Дальнейшее теоретическое и экспериментальное
развитие метода внесения дисперсии для случая пространственно некогерентного
излучения было проведено в работе [3]. В теории это потребовало усреднения по
пространственно-временным реализациям поля, а в эксперименте угловая
расходимость пучка, в отличие от [2], бралась много больше дифракционной.
Полученные теоретически условия высокого контраста интерференционной картины
при интерференции диспергированных световых пучков были подробно исследованы и
подтверждены экспериментально. Подобные условия можно реализовать, если пучок с
плоским слоем когерентности направить на тонкий амплитудно-фазовый транспарант
со случайной структурой, комплексное пропускание которого не зависит от
частоты. Его слои когерентности при условии 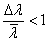 окажутся
приблизительно плоскими, оставаясь перпендикулярными к оси z.
окажутся
приблизительно плоскими, оставаясь перпендикулярными к оси z.
Рис.3. Наклонные слои когерентности пересекающихся
пространственно некогерентных пучков
Поле такого исходного пучка можно представить в
виде суммы полей 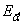 , представляющих
собой суперпозицию плоских волн с перпендикулярными к оси
, представляющих
собой суперпозицию плоских волн с перпендикулярными к оси 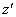 составляющими
волновых векторов
составляющими
волновых векторов 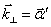 . После прохождения
через призму поле
. После прохождения
через призму поле 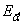
 преобразуется в
поле
преобразуется в
поле  ,
для которого фиксированы составляющие волновых векторов, перпендикулярные к оси
z. Огибающие полей
,
для которого фиксированы составляющие волновых векторов, перпендикулярные к оси
z. Огибающие полей  перемещаются
вдоль оси z со скоростями,
зависящими от
перемещаются
вдоль оси z со скоростями,
зависящими от 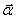 , что приводит к
ухудшению пространственной когерентности суммарного поля
, что приводит к
ухудшению пространственной когерентности суммарного поля 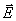 .
В то же время для эффективного действия схем четырехволнового взаимодействия и
петлевых схем обращения волнового фронта необходима высокая пространственная
когерентность каждого из взаимодействующих пучков. Поэтому, для использования в
этих схемах метода наклона слоев когерентности необходимо знать, как изменяется
степень когерентности излучения при распространении диспергированного пучка.
.
В то же время для эффективного действия схем четырехволнового взаимодействия и
петлевых схем обращения волнового фронта необходима высокая пространственная
когерентность каждого из взаимодействующих пучков. Поэтому, для использования в
этих схемах метода наклона слоев когерентности необходимо знать, как изменяется
степень когерентности излучения при распространении диспергированного пучка.
.2 Пространственная когерентность
диспергированных пучков
Исследованию пространственной когерентности
диспергированного пучка был посвящен ряд работ [4-7].
Теоретическое рассмотрение пространственной
когерентности диспергированных широкополосных пучков было выполнено в работе
[4]. В ней на основе приближенного подхода были получены аналитические
выражения, описывающие изменение степени когерентности и толщины слоев
когерентности в процессе распространения пучков. Установлено, что нарушение
пространственной когерентности с расстоянием происходит тем быстрее, чем больше
угол наклона 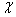 слоев
когерентности по отношению к фазовым фронтам.
слоев
когерентности по отношению к фазовым фронтам.
Методом численного моделирования
пространственное распределение комплексной степени когерентности исследовалось
в [5]. Был проведен численный расчет одномерных и двумерных реализаций
пространственного распределения комплексной степени когерентности
диспергированных широкополосных пучков. Изучалась геометрия пространственных
неоднородностей (спеклов) степени когерентности при различной степени дисперсии
пучка, характеризуемой отношением угла 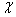 к
полуширине угловой расходимости пучка
к
полуширине угловой расходимости пучка 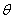 ,
она варьировалась от 0 - недиспергированный пучок до 10 - сильно
диспергированный пучок. Полученные данные свидетельствуют, что при внесении
дисперсии уменьшение степени когерентности с ростом z
значительно ускоряется. Результаты численного моделирования, проведенного в
[4], хорошо согласуются с аналитическим расчетом в [4].
,
она варьировалась от 0 - недиспергированный пучок до 10 - сильно
диспергированный пучок. Полученные данные свидетельствуют, что при внесении
дисперсии уменьшение степени когерентности с ростом z
значительно ускоряется. Результаты численного моделирования, проведенного в
[4], хорошо согласуются с аналитическим расчетом в [4].
Кроме пространственной когерентности каждого из
взаимодействующих пучков на эффективность их взаимодействия оказывает влияние
степень их взаимной когерентности. Взаимную когерентность пересекающихся
диспергированных лазерных пучков можно характеризовать комплексной функцией
взаимной когерентности 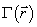 , впервые введенной
в работе [4]. Эта функция определяет усредненную по времени корреляцию двух
световых полей в конкретной точке
, впервые введенной
в работе [4]. Эта функция определяет усредненную по времени корреляцию двух
световых полей в конкретной точке 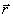 .
От значений функции взаимной когерентности зависит контраст интерференционной
картины, возникающей в области наложения пересекающихся пучков. В [4]
теоретически было установлено, что для свободно распространяющихся пучков
модуль функции взаимной когерентности по мере их распространения убывает.
.
От значений функции взаимной когерентности зависит контраст интерференционной
картины, возникающей в области наложения пересекающихся пучков. В [4]
теоретически было установлено, что для свободно распространяющихся пучков
модуль функции взаимной когерентности по мере их распространения убывает.
Путем численного моделирования интерференция
диспергированных широкополосных пучков различных реализаций была впервые
изучена в работе [7]. Объектами исследования были комплексная функция взаимной
когерентности и интенсивность интерференционной картины. Были получены
двумерные распределения модуля и фазы функции 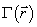 .
Эти распределения, в частности, показали, что в окрестности нуля модуля функции
.
Эти распределения, в частности, показали, что в окрестности нуля модуля функции
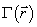 изменение
ее аргумента в поперечном сечении пучков носит характер винтовой дислокации.
Однако, исследования степени взаимной когерентности и ее зависимости от
продольной координаты не проводилось. Кроме того, все численные расчеты были
проведены при одном значении ширины спектра пересекающихся пучков, равной 1000
см-1. В то же время ясно, что поскольку толщина слоя когерентности
широкополосного излучения определяется шириной спектра, то степень взаимной
когерентности должна зависеть от ширины спектра. В настоящей бакалаврской
работе поставлена задача восполнить этот пробел. Целью данной работы является
исследование функции взаимной когерентности от ширины спектра пересекающихся
диспергированных лазерных пучков. Это исследование включает в себя решение
нескольких задач.
изменение
ее аргумента в поперечном сечении пучков носит характер винтовой дислокации.
Однако, исследования степени взаимной когерентности и ее зависимости от
продольной координаты не проводилось. Кроме того, все численные расчеты были
проведены при одном значении ширины спектра пересекающихся пучков, равной 1000
см-1. В то же время ясно, что поскольку толщина слоя когерентности
широкополосного излучения определяется шириной спектра, то степень взаимной
когерентности должна зависеть от ширины спектра. В настоящей бакалаврской
работе поставлена задача восполнить этот пробел. Целью данной работы является
исследование функции взаимной когерентности от ширины спектра пересекающихся
диспергированных лазерных пучков. Это исследование включает в себя решение
нескольких задач.
.Изучение 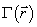 проводится
с использованием двумерных распределений ее параметров, а именно: ее модуля,
фазы, действительной и мнимой частей. Такие двумерные распределения
представляют собой большие матричные массивы, получаемые при численном расчете
в пакете программ Mathcad.
В связи с этим актуальной является модернизация уже используемых программ
расчета с тем, чтобы получаемые массивы могли формироваться автоматически.
проводится
с использованием двумерных распределений ее параметров, а именно: ее модуля,
фазы, действительной и мнимой частей. Такие двумерные распределения
представляют собой большие матричные массивы, получаемые при численном расчете
в пакете программ Mathcad.
В связи с этим актуальной является модернизация уже используемых программ
расчета с тем, чтобы получаемые массивы могли формироваться автоматически.
.Выполнение численного расчета (с использованием
модернизированных программ) двумерных распределений параметров комплексной
функции 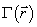 в
поперечной плоскости x,y
в зависимости от продольной координаты z
для различной ширины спектра излучения.
в
поперечной плоскости x,y
в зависимости от продольной координаты z
для различной ширины спектра излучения.
.Расчет по полученным численным данным степени
взаимной когерентности пересекающихся диспергированных пучков в зависимости z
от при различной ширине спектра, а также сравнение результатов, полученных при
численном моделировании, с аналитическими зависимостями рассчитанными на основе
приближенного подхода.
ГЛАВА 2. РАСЧЕТ ФУНКЦИИ ВЗАИМНОЙ КОГЕРЕНТНОСТИ
ПЕРЕСЕКАЮЩИХСЯ ДИСПЕРГИРОВАННЫХ ПУЧКОВ
.1 Основные уравнения и параметры расчета
Функция взаимной когерентности широкополосных
полей 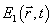 и
и
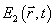 определяется
выражением [4]:
определяется
выражением [4]:
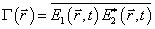 , (1)
, (1)
где черта означает усреднение во времени. Она
определяет интенсивность излучения в области наложения двух широкополосных
полей
 , (2)
, (2)
где 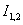 -
интенсивность каждого из полей. Принимается, что в исходной плоскости
-
интенсивность каждого из полей. Принимается, что в исходной плоскости 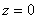 оба
интерферирующих пучка пространственно-когерентны и коррелированно изменяются во
времени, а параллельность слоев когерентности пересекающихся под небольшим
углом пучков, расширяющая область их когерентного взаимодействия, достигается
методом внесения дисперсии [1]. В качестве диспергирующих элементов могут быть
использованы стеклянные призмы с малым углом преломления или дифракционные
решетки с треугольным профилем штриха, работающие в одном порядке дифракции.
оба
интерферирующих пучка пространственно-когерентны и коррелированно изменяются во
времени, а параллельность слоев когерентности пересекающихся под небольшим
углом пучков, расширяющая область их когерентного взаимодействия, достигается
методом внесения дисперсии [1]. В качестве диспергирующих элементов могут быть
использованы стеклянные призмы с малым углом преломления или дифракционные
решетки с треугольным профилем штриха, работающие в одном порядке дифракции.
Оптическая схема на основе интерферометра
Маха-Цендера с дифракционными решетками, в которой может быть осуществлена
интерференция таких световых пучков, приведена на рис.4. Широкополосная плоская
световая волна L падает на полупрозрачное делительное зеркало 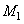 .
Показан слой когерентности толщиной
.
Показан слой когерентности толщиной  ,
ориентированный перпендикулярно направлению падающей волны. Разделенные
световые пучки
,
ориентированный перпендикулярно направлению падающей волны. Разделенные
световые пучки 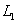 и
и 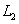 проходят
через тонкие амплитудно-фазовые транспаранты
проходят
через тонкие амплитудно-фазовые транспаранты 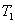 и
и
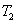 ,
установленные непосредственно перед дифракционными решетками
,
установленные непосредственно перед дифракционными решетками 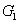 и
и
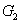 с
ориентацией штрихов перпендикулярно плоскости рисунка. Дифракционные решетки
работают в противоположных порядках дифракции. Направления падающих и
дифрагированных световых пучков указаны стрелками. Наложение друг на друга
световых пучков D1
и D2,
выходящих из двух плеч интерферометра, осуществляется с помощью поворотного
зеркала M3
и полупрозрачного зеркала M4.
Наклонная стеклянная пластина P служит для выравнивания оптических длин плеч
интерферометра, что позволяет совместить параллельные коррелированные слои
когерентности в интерферирующих световых пучках D1 и D2.
с
ориентацией штрихов перпендикулярно плоскости рисунка. Дифракционные решетки
работают в противоположных порядках дифракции. Направления падающих и
дифрагированных световых пучков указаны стрелками. Наложение друг на друга
световых пучков D1
и D2,
выходящих из двух плеч интерферометра, осуществляется с помощью поворотного
зеркала M3
и полупрозрачного зеркала M4.
Наклонная стеклянная пластина P служит для выравнивания оптических длин плеч
интерферометра, что позволяет совместить параллельные коррелированные слои
когерентности в интерферирующих световых пучках D1 и D2.

Рис.2. Схема интерференции диспергированных
световых пучков. L - падающий световой пучок, L1, L2 -
пучки в плечах интерферометра, D1, D2 - диспергированные
пучки, M1, M4 - полупрозрачные зеркала, M2, M3
- поворотные зеркала, T1, T2 - амплитудно-фазовые
транспаранты, G1, G2 - дифракционные решетки, lc
- слои когерентности падающего и двух диспергированных пучков, P -
плоскопараллельная стеклянная пластина.
Дифракционные решетки G1,2,
работающие в одном порядке дифракции и установленные перпендикулярно оси 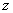 ,
преобразуют падающие на них монохроматические плоские волны с волновым вектором
,
преобразуют падающие на них монохроматические плоские волны с волновым вектором
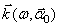 (
(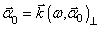 - перпендикулярная к оси составляющая волнового вектора
- перпендикулярная к оси составляющая волнового вектора 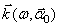 )
в плоские волны с волновым вектором
)
в плоские волны с волновым вектором 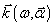 ,
где
,
где 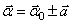 ,
вектор
,
вектор 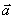 перпендикулярен
к оси z и к направлению штрихов решетки,
перпендикулярен
к оси z и к направлению штрихов решетки, 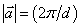 ,
,
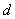 -
период решетки. Осевые направление широкополосных диспергированных световых
пучков после решеток задаются векторами
-
период решетки. Осевые направление широкополосных диспергированных световых
пучков после решеток задаются векторами 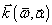 .
Они образуют с осью z углы
.
Они образуют с осью z углы 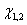 , противоположные
по знаку и равные углу отклонения дифракционной решетки для частоты
, противоположные
по знаку и равные углу отклонения дифракционной решетки для частоты  .
.
Что касается слоев когерентности, то после
прохождения через дифракционные решетки их ориентация не изменяется - в
дифрагированных пучках, как и в падающих, они перпендикулярны оси z. Таким
образом, осевые направления диспергированных световых пучков отклонены от
нормали к слоям когерентности на углы 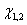 .
При этом слои когерентности интерферирующих световых пучков D1 и D2
параллельны друг другу, а угол пересечения пучков равен
.
При этом слои когерентности интерферирующих световых пучков D1 и D2
параллельны друг другу, а угол пересечения пучков равен 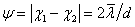 .
.
Поля 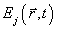 (j=1,2)
интерферирующих световых пучков можно представить в виде суперпозиции
монохроматических составляющих:
(j=1,2)
интерферирующих световых пучков можно представить в виде суперпозиции
монохроматических составляющих:
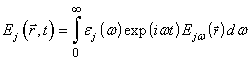 , (3)
, (3)
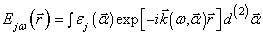 . (4)
. (4)
При совмещении коррелированных слоев
когерентности обоих пучков в (3) можно положить
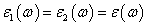 . (5)
. (5)
Представляя временное изменение поля, падающего
на делительное зеркало M1, как стационарный случайный процесс, а
поперечное пространственное распределение поля после каждого из транспарантов
как однородный гауссов случайный процесс, можно ввести нормированные на 1
спектральные плотности 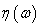 и
и 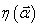 соотношениями
[8]
соотношениями
[8]
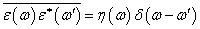 , (6)
, (6)
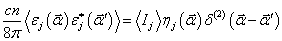 , (7)
, (7)
где черта означает усреднение по временным
реализациям поля, а угловые скобки - усреднение по реализациям поперечного
пространственного распределения поля, возникающим при установке различных
статистически однородных транспарантов Т1,2, 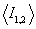 -
средние по сечению интенсивности световых пучков.
-
средние по сечению интенсивности световых пучков.
Вследствие отклонения диспергированного пучка  ,
где
,
где 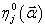 -
спектральная плотность светового пучка, падающего на дифракционную решетку Gj
. В дальнейшем принимается
-
спектральная плотность светового пучка, падающего на дифракционную решетку Gj
. В дальнейшем принимается 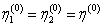 .
.
Функцию взаимной когерентности можно представить
в виде
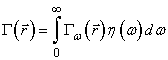 , (8)
, (8)
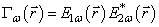 . (9)
. (9)
По известным значениям 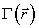 рассчитывается
усредненная по пространственным реализациям пучков степень взаимной
когерентности,
рассчитывается
усредненная по пространственным реализациям пучков степень взаимной
когерентности, 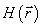 , определяемая
выражением [4]:
, определяемая
выражением [4]:
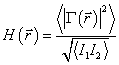 . (10)
. (10)
При численном моделировании расчет начинался с
вычисления полей 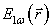 ,
, 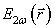 в
соответствии с (4). На дискретном множестве значений
в
соответствии с (4). На дискретном множестве значений 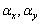 с
помощью генератора случайных чисел задавались действительная и мнимая части
комплексных амплитуд
с
помощью генератора случайных чисел задавались действительная и мнимая части
комплексных амплитуд 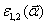 , распределенные по
закону Гаусса. Полученные таким образом два независимых набора комплексных
амплитуд
, распределенные по
закону Гаусса. Полученные таким образом два независимых набора комплексных
амплитуд 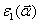 ,
,
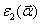 использовались
в (4) для расчета полей
использовались
в (4) для расчета полей 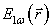 ,
, 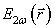 и
далее в соответствии с (9) для определения
и
далее в соответствии с (9) для определения 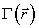 .
.
Расчеты были проведены при средней длине волны 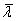 =
10-4 см(
=
10-4 см(  = 10 000см-1)
, и угловой расходимости 2
= 10 000см-1)
, и угловой расходимости 2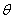 исходного пучка 4∙10-3рад.
Параметр
исходного пучка 4∙10-3рад.
Параметр 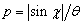 ,
характеризующий величину дисперсии пучка, брался равным 10. Форма частотного
спектра принималась гауссовой. Ширина спектра
,
характеризующий величину дисперсии пучка, брался равным 10. Форма частотного
спектра принималась гауссовой. Ширина спектра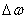 варьировалась, принимая значения 500 см-1, 1000 см-1 и
1500 см-1. При этом параметр
варьировалась, принимая значения 500 см-1, 1000 см-1 и
1500 см-1. При этом параметр 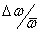 составлял
соответственно 0.05, 0.1 и 0.15. При выбранной средней длине волны 1000 нм
такие значения соответствуют широким диапазонам длин волн 70 нм, 100 нм и 150
нм соответственно.
составлял
соответственно 0.05, 0.1 и 0.15. При выбранной средней длине волны 1000 нм
такие значения соответствуют широким диапазонам длин волн 70 нм, 100 нм и 150
нм соответственно.
.2 Модернизация программы расчета
Чтобы получить двумерные распределения
действительной и мнимой частей, модуля и фазы функции 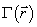 при
различных z, необходимо было
рассчитать матрицы комплексных значений
при
различных z, необходимо было
рассчитать матрицы комплексных значений 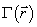 в
каждой точке (x,y)
при заданном значении z
= const, начиная с
начальной плоскости z = 0 и
проследить их эволюцию вдоль направления распространения. Координата z
изменялась в интервале [0,50 см]. Шаг изменения по z
изменялся в зависимости от поставленной задачи. В интервале[0,10 см] он
составлял 0.5 см, далее 5 см и 10 см.
в
каждой точке (x,y)
при заданном значении z
= const, начиная с
начальной плоскости z = 0 и
проследить их эволюцию вдоль направления распространения. Координата z
изменялась в интервале [0,50 см]. Шаг изменения по z
изменялся в зависимости от поставленной задачи. В интервале[0,10 см] он
составлял 0.5 см, далее 5 см и 10 см.
Уже созданные программы позволяли посчитать
только один столбец матрицы 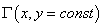 при каждом
конкретном значении координаты y.
Далее он вручную заносился в отдельный файл, созданный для двумерного
распределения
при каждом
конкретном значении координаты y.
Далее он вручную заносился в отдельный файл, созданный для двумерного
распределения 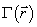 , соответствующего
выбранному значению продольной координаты z.
Это значительно осложняло вычисления, так как приходилось отслеживать момент
завершения расчета столбца и далее вручную формировать матрицу двумерного
распределения. Поэтому программа была модернизирована таким образом, чтобы
координата y автоматически
изменяла свое значение. При этом, в среде Mathcad удалось получить все значения
, соответствующего
выбранному значению продольной координаты z.
Это значительно осложняло вычисления, так как приходилось отслеживать момент
завершения расчета столбца и далее вручную формировать матрицу двумерного
распределения. Поэтому программа была модернизирована таким образом, чтобы
координата y автоматически
изменяла свое значение. При этом, в среде Mathcad удалось получить все значения
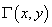 ,
но не в виде матрицы, а в виде столбца, где столбцы
,
но не в виде матрицы, а в виде столбца, где столбцы 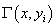 с
последовательно изменяющимися значениями yi
записывались друг за другом. Ввиду того, что матрица имеет пятьдесят тысяч
элементов, Mathcad не позволял оперировать такими большими массивами данных, в
том числе, отображать их.
с
последовательно изменяющимися значениями yi
записывались друг за другом. Ввиду того, что матрица имеет пятьдесят тысяч
элементов, Mathcad не позволял оперировать такими большими массивами данных, в
том числе, отображать их.
Для решения этой проблемы был использован
программный пакет Microsoft Excel. Столбец, состоящий из 50000 значений
копировался из Mathcad в Excel и, с помощью записанного макроса, компоновался в
искомую матрицу значений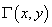 . Она включала
значения действительной и мнимой частей функции
. Она включала
значения действительной и мнимой частей функции 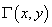 .
По этим значениям рассчитывались модуль и фаза функции взаимной когерентности.
Всего было создано три макроса. Первый позволяет компоновать столбец из 50000
элементов в матрицу 500x100 элементов. Второй макрос позволяет из двух столбцов
значений
.
По этим значениям рассчитывались модуль и фаза функции взаимной когерентности.
Всего было создано три макроса. Первый позволяет компоновать столбец из 50000
элементов в матрицу 500x100 элементов. Второй макрос позволяет из двух столбцов
значений 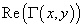 и
и
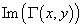 вычислять
значения модуля и фазы функции взаимной когерентности по соответствующим
формулам.
вычислять
значения модуля и фазы функции взаимной когерентности по соответствующим
формулам.
Третий макрос позволяет получить из столбца
значений модуля функции 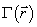 значение его
квадрата, что было необходимо при расчете степени взаимной когерентности
значение его
квадрата, что было необходимо при расчете степени взаимной когерентности 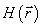 .
Таким образом, появилась возможность значительно упростить процедуру
формирования матриц
.
Таким образом, появилась возможность значительно упростить процедуру
формирования матриц 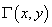 и существенно
ускорить расчет данных для последующего анализа и обработки.
и существенно
ускорить расчет данных для последующего анализа и обработки.
ГЛАВА 3. РЕЗУЛЬТАТЫ РАСЧЕТА И ИХ ОБСУЖДЕНИЕ
При расчете двумерных распределений функции 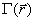 координаты
точки
координаты
точки 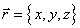 изменялись
в поперечной плоскости x,y
при различных значениях продольной координаты z.
Шаг изменения поперечной координаты x
составлял 0.0005 см. Эта величина была выбрана путем расчета функции с шагом по
изменялись
в поперечной плоскости x,y
при различных значениях продольной координаты z.
Шаг изменения поперечной координаты x
составлял 0.0005 см. Эта величина была выбрана путем расчета функции с шагом по
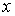 ,
последовательно убывающим до тех пор, пока его дальнейшее уменьшение не
переставало приводить к уточнению хода функции. Шаг изменения поперечной
координаты y определялся таким
же образом и составлял 0.0025 см. Диапазон изменения поперечных координат
составлял 0.25 см. При его выборе учитывалось, что характерный размер изменения
интенсивности в поперечной плоскости размер
,
последовательно убывающим до тех пор, пока его дальнейшее уменьшение не
переставало приводить к уточнению хода функции. Шаг изменения поперечной
координаты y определялся таким
же образом и составлял 0.0025 см. Диапазон изменения поперечных координат
составлял 0.25 см. При его выборе учитывалось, что характерный размер изменения
интенсивности в поперечной плоскости размер 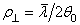 составляет
величину 0.025 см, таким образом выбранный размер области расчета по каждой из
линейных координат
составляет
величину 0.025 см, таким образом выбранный размер области расчета по каждой из
линейных координат 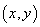 превышал
превышал 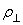 на
порядок.
на
порядок.
Рис.5. Распределение модуля функции 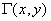 при
z = 2 см, по оси
абсцисс отложены значения x,
по оси ординат - y
при
z = 2 см, по оси
абсцисс отложены значения x,
по оси ординат - y
На рисунке 5 представлено типичное распределение
модуля функции 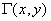 , (более светлые
участки соответствуют большим значениям модуля) в области значений 0.25 см
, (более светлые
участки соответствуют большим значениям модуля) в области значений 0.25 см 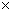 0.25
см . Ширина спектра взята равной 1000 см-1.
0.25
см . Ширина спектра взята равной 1000 см-1.
Характерный масштаб изменения 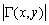 по
по
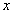 и
и
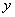 составляет
~
составляет
~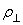 .
Обращают на себя внимание воронкообразные углубления, в которых модуль функции
обращается в нуль. Как видно из следующего рисунка 6, на котором дано
пространственное распределение фазы
.
Обращают на себя внимание воронкообразные углубления, в которых модуль функции
обращается в нуль. Как видно из следующего рисунка 6, на котором дано
пространственное распределение фазы 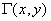 в
той же области, этим точкам соответствуют характерные раздвоения фазовых линий
-"вилки".
в
той же области, этим точкам соответствуют характерные раздвоения фазовых линий
-"вилки".
Рис.6. Распределение фазы функции 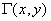 при
z = 2 см; область
расчета совпадает с областью расчета
при
z = 2 см; область
расчета совпадает с областью расчета 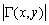
Фазовые линии (линии, на которой фаза одинакова)
вдали от точек сингулярности, где модуль функции 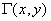 обращается
в нуль, имеют вид прямолинейных полос, повторяющихся с периодом
интерференционной картины, равным
обращается
в нуль, имеют вид прямолинейных полос, повторяющихся с периодом
интерференционной картины, равным 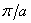 .
Пространственная неоднородность амплитуд интерферирующих пучков нарушает
регулярную структуру полос. Изменения амплитуд полей, происходящие на длине ~
.
Пространственная неоднородность амплитуд интерферирующих пучков нарушает
регулярную структуру полос. Изменения амплитуд полей, происходящие на длине ~ 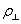 ,
приводят к плавному хаотическому искажению полос и нарушению их
пространственной периодичности.
,
приводят к плавному хаотическому искажению полос и нарушению их
пространственной периодичности.
Аналогичные вилки около точек фазовой
сингулярности возникают и при интерференции монохроматических световых пучков,
впервые наблюдавшиеся [9].
Фазовая сингулярность проявляется и в двумерном
распределении действительной части функции взаимной когерентности, определяющей
контраст интерференционной картины. Это распределение в той же области расчета 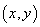 приведено
на рисунке 7. Дислокациям волнового фронта соответствует характерное
“раздвоение” интерференционных полос действительной части функции
приведено
на рисунке 7. Дислокациям волнового фронта соответствует характерное
“раздвоение” интерференционных полос действительной части функции 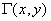 .
.
Представленные двумерные распределения
рассчитаны вблизи начальной плоскости z
= 0, где оба интерферирующих пучка взяты пространственно-когерентными и
коррелированно изменяющимися во времени. Аналогичные расчеты, выполненные на
больших расстояниях от начальной плоскости, показывают, что при сохранении
общего вида распределения функции взаимной когерентности, они становятся менее
контрастными, что связано с уменьшением степени взаимной когерентности.
Влияние ширины частотного спектра
интерферирующих пучков проявляется в том, что уменьшение контраста двумерных
распределений модуля и действительной части 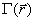 с
ростом продольной координаты происходит тем быстрее, чем шире спектр излучения.
Это также связано с уменьшением степени взаимной когерентности, подробное
рассмотрение которой проведено в следующем разделе.
с
ростом продольной координаты происходит тем быстрее, чем шире спектр излучения.
Это также связано с уменьшением степени взаимной когерентности, подробное
рассмотрение которой проведено в следующем разделе.
.2 Зависимость степени взаимной когерентности
пересекающихся широкополосных лазерных пучков от ширины спектра
Как следует из выражения (10), величина 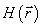 -
степень взаимной когерентности, усредненная по пространственным реализациям
пучков, зависит от среднего значения квадрата модуля
-
степень взаимной когерентности, усредненная по пространственным реализациям
пучков, зависит от среднего значения квадрата модуля 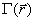 и
средних значений интенсивности интерферирующих пучков. Для
и
средних значений интенсивности интерферирующих пучков. Для 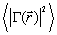 в
[4] получено приближенное аналитическое выражение:
в
[4] получено приближенное аналитическое выражение:
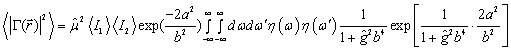 , (11)
, (11)
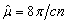 ,
, 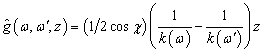 ,
,
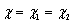 ,
,
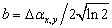
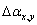 - ширина углового
спектра диспергированных пучков. Подставляя в него данные, выбранные для
выполнения настоящих расчетов и полагая для простоты величину
- ширина углового
спектра диспергированных пучков. Подставляя в него данные, выбранные для
выполнения настоящих расчетов и полагая для простоты величину 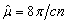 равной
1, можно рассчитать ход теоретических зависимостей
равной
1, можно рассчитать ход теоретических зависимостей 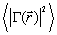 от
z при различной
ширине спектра излучения.
от
z при различной
ширине спектра излучения.
На рисунке представлены расчетные кривые 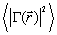 ,
отнесенные к
,
отнесенные к 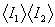 , при различной
ширине спектра.
, при различной
ширине спектра.
Расчетные кривые показывают, насколько быстро
убывает средняя степень взаимной когерентности с увеличением ширины спектра.
Так, при ширине спектра 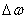 = 500 см-1
степень взаимной когерентности уменьшается вдвое на длине взаимодействия,
равной 20 см. В то же время, при ширине спектра 1500 см-1 такое же
падение происходит на длине 6.5 см.
= 500 см-1
степень взаимной когерентности уменьшается вдвое на длине взаимодействия,
равной 20 см. В то же время, при ширине спектра 1500 см-1 такое же
падение происходит на длине 6.5 см.
Для сравнения теоретических кривых с данными
численного моделирования был выполнен численный расчет величины 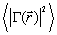 при
тех же значениях ширины углового и частотного спектров. Значения средних
интенсивностей были взяты из работы. Ниже представлены соответствующие графики
теоретических кривых(сплошные линии) с нанесенными данными численного
моделирования(точки). Результаты численного моделирования хорошо согласуются с
теоретическими кривыми, рассчитанными на основе приближенного аналитического
подхода [4].
при
тех же значениях ширины углового и частотного спектров. Значения средних
интенсивностей были взяты из работы. Ниже представлены соответствующие графики
теоретических кривых(сплошные линии) с нанесенными данными численного
моделирования(точки). Результаты численного моделирования хорошо согласуются с
теоретическими кривыми, рассчитанными на основе приближенного аналитического
подхода [4].
1.Путем
численного моделирования исследованы характеристики функции взаимной
когерентности пересекающихся диспергированных пучков с широким спектром.
.Модернизированы ранее созданные программы
расчета характеристик интерференции пересекающихся диспергированных пучков, что
позволило значительно уменьшить время, необходимое для получения больших
матричных массивов.
.Выполнен численный расчет двумерных
распределений параметров комплексной функции взаимной когерентности в
поперечной плоскости в зависимости от продольной координаты при трех различных
значениях ширины спектра.
.Показано, что в окрестности нулевых значений
модуля функции взаимной когерентности изменение ее аргумента носит характер
винтовой дислокации, что проявляется в наличии около нулевых точек характерного
раздвоения полос - "вилок" - в пространственном распределении фазы.
.Полученные численные массивы данных открывают
возможность дальнейшего исследования статистических характеристик винтовых
дислокаций функции взаимной когерентности при различной ширине спектра.
.С использованием аналитических соотношений,
взятых из литературных данных, рассчитан ход теоретических зависимостей степени
взаимной когерентности от продольной координаты при различной ширине спектра.
.Выполнен численный расчет степени взаимной
когерентности пересекающихся диспергированных пучков в зависимости
)от продольной координаты; 2)ширины спектра.
.Проведено сравнение зависимостей, полученных
путем численного моделирования, с ходом теоретических кривых. Установлено
хорошее согласие численных и аналитических результатов.
ЗАКЛЮЧЕНИЕ
Для обеспечения когерентного взаимодействия лазерных
пучков с широким спектром в нелинейно-оптической среде важно знать, какова
степень их взаимной когерентности. Численное моделирование интерференционной
картины, выполненное в данной бакалаврской работе позволяет исследовать
пространственную когерентность и возможности эффективного взаимодействия
широкополосных пространственно-неоднородных лазерных полей.
Проведена модернизация программ расчета
параметров комплексной функции взаимной когерентности. Получены двумерные
распределения модуля, фазы действительной и мнимой частей этой функции в
поперечном сечении пересекающихся световых пучков при разной ширине их спектра.
Показано существование фазовых сингулярностей функции взаимной когерентности в
точках, где ее модуль обращается в нуль. Рассчитанные матричные массивы данных
позволяют в дальнейшем провести рассмотрение статистических характеристик
фазовых сингулярностей при разной ширине спектра излучения.
Изучены статистические характеристики степени
взаимной когерентности в зависимости от продольной координаты и ширины спектра.
Показано, что убывание степени взаимной когерентности с расстоянием происходит
тем быстрее, чем шире спектр интерферирующих пучков.
Полученные результаты могут быть использованы
при изучении эффектов фазовой сингулярности в схемах четырехволнового смешения
с пересекающимися световыми пучками, а также при осуществлении обращения
волнового фронта излучения широкополосных лазеров.
Список использованных
источников
1.С.Г.Одулов, М.С.Соскин, А.И.Хижняк. Лазеры на
динамических решетках. М., "Наука". 1990.
. В.И.Одинцов, Е.Ю.Соколова.
Расширение области когерентного взаимодействия пересекающихся световых пучков с
широким спектром // Квантовая электроника, Т. 21. № 8, С.778. 1994.
.В.И.Одинцов, Е.Ю.Соколова.
Получение протяженной интерференционной картины в пересекающихся световых
пучках с большой шириной спектра // Оптика и спектроскопия, Т. 85, №2, С.273.
1998.
.В.И. Одинцов, Е.Ю.Соколова.
Пространственная когерентность и когерентное взаимодействие диспергированных
лазерных пучков с широким спектром // Оптика и спектроскопия, Т.101. №3. С.505.
2006.
.О.М.Вохник, В.И.Одинцов.
Пространственная структура степени когерентности широкополосных
диспергированных лазерных пучков // Оптика и спектроскопия, Т.114, № 3, С.175.
2013.
.А.Н.Бушмелева, О.М.Вохник.
Пространственное распределение интенсивности диспергированных лазерных пучков с
различной шириной спектра // Сборник трудов XIV Школы молодых ученых
"Актуальные проблемы физики", Москва, ФИАН, 2012. С.63.
.О.М.Вохник, В.И.Одинцов. Винтовые
дислокации при интерференции широкополосных лазерных полей // Сборник трудов VIII-й
Международной конференции "Фундаментальные проблемы оптики", 20-24
октября 2014 года, Санкт-Петербург, стр.201-203.
.С.А.Ахманов, Ю.Е.Дьяков,
А.С.Чиркин. Введение в статистическую радиофизику и оптику. М.,
"Наука", 1981.
.Н.Б.Баранова, Б.Я.Зельдович,
А.В.Мамаев, Н.Ф.Пилипецкий, В.В.Шкунов. Исследование плотности дислокаций
волнового фронта световых полей со спекл-структурой // ЖЭТФ, Т.83, №5, С.1702.
1982.