Моделирование автотранспортного потока
САНКТ-ПЕТЕРБУРГСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПЕТРА ВЕЛИКОГО
ИНСТИТУТ
КОМПЬЮТЕРНЫХ НАУК И ТЕХНОЛОГИЙ
Кафедра
«Системный анализ и управление»
ДИССЕРТАЦИЯ
на
соискание степени МАГИСТРА
на
тему: «Моделирование автотранспортного потока»
Выполнил
Пинто Д.А.
Руководитель
Фирсов А.Н.
Санкт-Петербург
2017
Реферат
Ключевые слова:
Модель транспортных потоков, клеточный автомат, C++, Qt, микромоделирование,
гидродинамические модели транспортных потоков.
В работе решен ряд задач, включающий в себя
разработку информационной системы для имитации транспортных потоков, обхода
препятствий во время движения автомобиля, регулировку автотранспортного
траффика с использованием светофора, принятие решения об изменении траектории
движения автомобиля после светофора. Представлен алгоритм решения перечисленных
задач в рамках клеточного автомата, проанализированы возможные погрешности при
решении такого класса задач и выявлены методы их устранения.
Содержание
Введение
.
Постановка задача
.1
Общая постановка задачи
.2
Конкретная постановка задачи
.
Обзор литературы
.1
Обзор моделей транспортных потоков
.2
Гидродинамические модели транспортного потока
.3
Стохастические модели
.4
Микроскопические модели
.
Описание разработанной математической модели
.
Описание информационной системы и результаты моделирования
Заключение
Список
литературы
Приложение
Введение
Так как количество транспортных средств и
транспортные потребности растут, города в мире показывают серьезные заторы на
дорогах. Затраты включают потерю времени, увеличение потребления топлива,
загрязнение окружающей среды, проблемы со здоровьем, стрессом и дискомфортом.
Кроме того, перегрузка замедляет движение товаров и услуг, так что,
увеличивается стоимость продукции и снижается конкурентоспособность бизнеса.
Если проблема не решается правильно, может даже парализоваться экономический
рост и развитие наших городов и в значительной мере способствовать
нежелательному парниковому эффекту и изменению климата. Даже когда
перенасыщение транспортными средствами продолжается недолго и происходит в
небольшой области, негативное влияние на трафик может продолжаться довольно
долго. Перенасыщение будет определяться как ситуация, при которой автомобили не
могут двигаться свободно из-за количества автомобилей, которые находятся на
перекрестке, или из-за заторов, которые образовались на улицах, по которым
можно покинуть перекресток. С другой стороны, когда нет заторов, мы хотим
также, чтобы транспортные средства пересекали различные районы города, или
двигались по основными направлениями достаточно быстро. Таким образом,
необходимо получить эффективную транспортную систему, которая будет
способствовать мобильности людей и товаров.
Мы можем утверждать, что такая мобильность
является важным фактором, который способствует устойчивому экономическому росту
и созданию рабочих мест. Для этого не только необходимо формировать адекватную
физическую инфраструктуру, а также свести к минимуму последствия для окружающей
среды, которые городской транспорт и другие факторы оказывают на окружающую
среду. В самом деле, мобильность порождает ряд экологических затрат, из-за
отрицательного влияния на изменение климата (в настоящее время выбросы CO2
превышают 30% производимых в 1990), и транспортные средства всех видов - это
"единственный сектор экономики, в котором прогнозируется рост числа
выбросов" [1]. Несмотря на некоторое улучшение энергоэффективности
легковых автомобилей, с помощью применения новых технологий, и их вес
уменьшился, что повлияло на низкий расход топлива, количество автомобилей
выросло. Но, кроме того, шум, пробки, чье "сокращение, будет значительно
способствовать сокращению выбросов СО2" [2].
Начиная с 80-х годов прошлого века, руководители
отделов трафика решили, что традиционные решения, которые применялись не смогут
решить эту проблему. Эти решения, как правило, приводили к строительству новых
объектов инфраструктуры или к расширению уже существующих, но во многих случаях
не были жизнеспособные решения, главным образом из-за высоких затраты, из-за
недостатка свободного пространства и неизбежного воздействия на окружающую
среду.
По этому, отделы трафика со всего мира очень
заинтересованы в оптимизации существующей инфраструктуры, с целью максимального
улучшения их функционирования.
Основная функция светофоров в контроле перекрестка
- это разрешать проезд поочередно различным группам транспортных средств,
пешеходов, велосипедистов и т.д., таким образом, чтобы они пересекать
перекресток с минимумом проблем, рисков и задержек. Целями проектирования
регулируемого светофором перекрестка являются:
· Уменьшение и предотвращение
определенного типа происшествиях на перекрестках.
· Сокращение задержек, которые
испытывают пешеходы и транспортные средства при пересечении перекрёстка, и в то
же время избежать препятствий на ближайших перекрестках, вызванных длинными
пробками.
· Снижение расхода топлива автомобилей
на пересечении.
· Уменьшение выбросов загрязняющих
веществ в атмосферу (СО2), что положительно повлияет на парниковый эффект, а
также снижение шума.
· Повышение качества жизни граждан и
их здоровья.
Для выполнения этих целей, основной элемент -
это синхронизировать и оптимизировать цикл светофора, то есть, синхронизировать
и оптимизировать последовательность состояний (красный, зеленый и т. д.), через
которые проходит светофор и которые повторяются циклично. Каждый цикл связан с
одним перекрестком, то есть, может регулироваться несколько светофоров.
Каждая фаза цикла (или stage) состоит из
состояний, в которых находятся все светофоры перекрестка в течение
определенного времени, и которые позволяют одно или несколько синхронных
движений через перекресток.
Этот цикл светофора следует рассмотреть с трех
разных точек зрения:
• Продолжительность полного цикла работы
светофоров, то есть, времени необходимого, чтобы обеспечить полную последовательность
состояний светофоров, подключенных к одному регулятору. Независимо от
результатов расчетов, продолжительность цикла должна быть обязательно в
пределах психологической границы водителя.
• Доля времени, отведенного для каждой фазы.
• Последовательные переходы светофоров. Типичным
примером этого обстоятельства является наличие двух светофоров подряд на улице.
В этом случае определяется время перехода (offset time), как время с того
момента, когда светофор переходит на зеленый свет, до того момента, когда
следующий светофор на проспекте переходит также на зеленый.
Цель работы - разработка
информационной системы для имитации транспортных потоков.
Задачи работы:
. Анализ существующих
моделей автотранспортных потоков.
2. составление алгоритма обхода транспортных
средств во время движения по дорожному полотну.
. разработка алгоритма регулирования
светофора.
. составление алгоритма имитации выбора
пути водителем.
1. Постановка задача
1.1 Общая постановка задачи
Задача, поставленная в этой работе, охватывает
небольшой круг подзадач, каждая из которых решается по отдельности. Основная
задача состоит в том, чтобы создать модель (систему), которая позволит наглядно
продемонстрировать работу различных алгоритмов, применяемых в рамках теории
моделирования транспортного потока. Теория моделирования транспортного потока
позволяет получить сведения о возможной перегруженности транспортного пути или
аварийных ситуациях, которые могут быть результатом как неаккуратности вождения
транспортных средств, так и самой перегруженности транспортного пути.
Обход транспортных средств во время движения по
дорожному полотну является важной составляющей корректной работы системы,
поскольку процесс моделирования должен соответствовать реальной задаче, в
которой каждый водитель должен принимать решение о том, каким образом безопасно
обойти другое транспортное средство во время движения по дорожному полотну при
условии, что скорость движения этого транспортного средства меньше. Для обхода
таких ситуаций в моделировании общим решением является поиск на каждом цикле
всех автомобилей, которые находятся рядом с перемещаемым автомобилем и в
случае, если транспортное средство на следующем шаге может спровоцировать
столкновение, просто уменьшить скорость до безопасной, если обход невозможен,
или обойти транспортное средство. Для подобных алгоритмов всегда существует ряд
критериев сравнения, благодаря которым возможно построить шаблоны.
Алгоритм
регулирования светофором, как правило, дополняет подобные задачи и не всегда
нужен. Такой алгоритм должен создать определенные условия, при которых
транспортное средство не должно пересекать ограниченную светофором зону до тех
пор пока состояние светофора не поменяется. Очень часто этот алгоритм
комбинируют с моделированием пешеходного перехода. В таком случае задача
усложняется еще и тем, что необходимо моделировать поведение пешеходов в
очереди как перед переходом дороги, так и при переходе. Алгоритм движения
пешеходов через дорогу является частным случаем алгоритма обхода препятствий
или других транспортных средств во время движения по дороге, поэтому его можно
не рассматривать. Кроме регулирования движения светофор так же создаст условия
для проверки корректности алгоритма обхода транспортных средств и накопления
автомобилей перед светофором.
Алгоритм имитации выбора пути является наиболее
простым в реализации и не всегда должен иметь множество входных параметров. Во
время движения по дороге водитель самостоятельно принимает решение о том в
какую сторону ехать исходя из заданных правил дорожного движения и исходя из
собственных нужд. Водитель может выбрать самостоятельно даже другой путь но все
равно выбор стороны поворота он будет делать только исходя из разрешенных на
данном участие. Исходя из этих рассуждений моделирования самостоятельного выбора
можно выполнить с помощью генератора псевдо случайных величин который позволит
получить псевдо случайную величину и в зависимости от этой величины выполнить
поворот в определенную сторону или продолжать ехать прямо.
.2 Конкретная постановка задачи
Необходимо разработать алгоритмы обхода
транспортных средств во время движения по дорожному полотну, алгоритм
регулирования движения с использованием светофора и алгоритм имитации выбора
пути водителем.
Для выполнения работы были рассмотрены различные
модели, среди которых гидродинамическая модель, модель Лайтхилла-Уизема,
Гриншилдса и Гринберга и модель клеточного автомата. Для реализации наиболее
подходящей оказалась модель клеточного автомата, поскольку с ее помощью можно
легко визуализировать результаты работы алгоритмов. В основе клеточного
автомата будет взята матрица размером NxM элементов, где каждый элемент
представляет собой символ. Каждый такой символ в матрице будет представлен в
виде квадратной области определенного цвета. Таким образом, матрица
 ,
,
будет представлять из себя в рамках клеточного
автомата дорожное полотно, которое обозначено числом 1, и пространство, которое
не относится к дорожному полотну, обозначаемое значение в качестве автомобиля
будет выступать значение 4.
Каждая позиция будет проверена алгоритмом
визуализации и в ответ в зависимости от значения в этой позиции будет нарисован
квадрат определенного цвета. Таким образом, применяя алгоритмы обхода
препятствий в рамках такой матрицы, можно будет получить программу визуализации
перемещения как автомобилей по дорожному полотну, так и алгоритм регулирования
с использованием светофора. Регулировка светофора может происходить за счет
ввода в матрицу специальных значений, которые будут рассматриваться алгоритмом
обхода автомобилей как красный или зеленый сигнал светофора.
2. Обзор литературы
2.1 Обзор моделей транспортных
потоков
В моделировании дорожного движения исторически
сложилось два основных подхода - детерминистический и вероятностный (стохастический).
В основе детерминированных моделей лежит
функциональная зависимость между отдельными показателями, например, скоростью и
дистанцией между автомобилями в потоке. В стохастических моделях транспортный
поток рассматривается как вероятностный процесс.
Все модели транспортных потоков можно разбить на
три класса: модели-аналоги, модели следования за лидером и вероятностные
модели.
В моделях-аналогах движение транспортного
средства уподобляется какому-либо физическому потоку (гидро- и газодинамические
модели). Этот класс моделей принято называть макроскопическими.
В моделях следования за лидером существенно
предположение о наличии связи между перемещением ведомого и головного
автомобиля. По мере развития теории в моделях этой группы учитывалось
время реакции водителей, исследовалось движение на многополосных дорогах,
изучалась устойчивость движения. Этот класс моделей называют
микроскопическими. К микроскопическим моделям также относят модели, построенные
на клеточных автоматах. В модели клеточных автоматов дорога разделена на
клетки, каждая клетка может либо содержать автомобиль, либо быть пустой.
Вышеописанные модели представлены на рисунке 1.
В вероятностных моделях транспортный поток
рассматривается как результат взаимодействия транспортных средств на
элементах транспортной сети. В связи с жестким характером ограничений
сети и массовым характером движения в транс- портном потоке складываются
отчетливые закономерности формирования очередей, интервалов, загрузок по
полосам дороги и т. п. Эти закономерности носят существенно стохастический
характер.
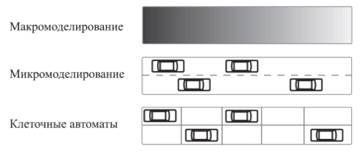
Рис 1. Методы моделирования транспортных потоков
2.2 Гидродинамические модели
транспортного потока
Транспортный̆ поток можно рассматривать как
поток одномерной сжимаемой жидкости, допуская, что поток
сохраняется и существует взаимнооднозначная зависимость между скоростью и
плотностью транспортного потока.
Первое допущение выражается уравнением
неразрывности. Второе - функциональной зависимостью между скоростью и плотностью
для учета уменьшения скорости движения автомобилей с ростом плотности
потока. Это интуитивно верное допущение теоретически может привести к
отрицательной величине плотности или скорости. Очевидно, одному значению
плотности может соответствовать несколько значений скорости. Поэтому для
второго допущения средняя скорость потока в каждый момент времени должна
соответствовать равновесному значению при данной плотности автомобилей
на дороге. Равновесная ситуация - чисто теоретическое допущение и может
наблюдаться только на участках дорог без пересечений. Поэтому часть
исследователей отказались от непрерывных моделей, часть
рассматривает их как слишком грубые.
Среди гидродинамических моделей различают
модели с учетом и без учета эффекта инерции. Последние могут быть получены из
уравнения неразрывности, если скорость рассматривать как функцию плотности.
Модели, учитывающие инерцию, представляются уравнениями Навье-Стокса со
специфическим членом, описывающим стремление водителей ехать с комфортной
скоростью.
Закон сохранения транспортного
потока
Рассмотрим поток транспорта на однополюсной
дороге, т.е. при движении без обгонов. Плотность автомобилей (количество
автомобилей на единицу длины дороги) ρ(x,t),
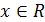 ,
в момент времени t ≥ 0. Число автомобилей в интервале
,
в момент времени t ≥ 0. Число автомобилей в интервале 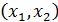 в
момент времени t равно
в
момент времени t равно
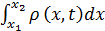 ,
,
Пусть v(x, t) - скорость автомобилей в
точке x в момент t. Число проходящих через x (единицу
длины) автомобилей в момент t, есть 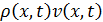 Найдём
уравнение изменения плотности. Число автомобилей в интервале
Найдём
уравнение изменения плотности. Число автомобилей в интервале 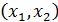 за
время t изменяется в соответствии с числом въезжающих и выезжающих машин:
за
время t изменяется в соответствии с числом въезжающих и выезжающих машин:
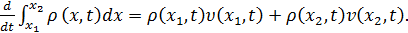 ,
,
Интегрируя по времени и полагая, что ρ
и v - непрерывные функции, получим.
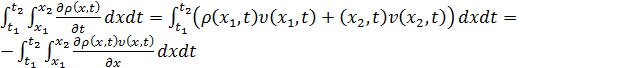 ,
,
Поскольку 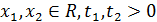 произвольны,
произвольны,
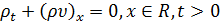 ,
,
Дополним это уравнение начальными условиями
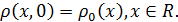
Найдём уравнение для скорости v. Положим,
что v зависит только от плотности ρ.
Если дорога пуста (ρ = 0),
автомобили едут с максимальной скоростью 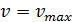 При
наполнении дороги, скорость падает вплоть до полной остановки
При
наполнении дороги, скорость падает вплоть до полной остановки 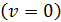 ,
когда машины расположены “бампер-к-бамперу"
,
когда машины расположены “бампер-к-бамперу" 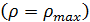 .
Эта простейшая модель выражается следующим линейным соотношением (рис. 1)
.
Эта простейшая модель выражается следующим линейным соотношением (рис. 1)
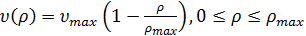 ,
,
Тогда уравнение (4) примет вид
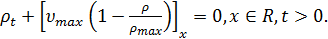 ,
,
Очевидно, это закон сохранения количества
автомобилей. В самом деле, интегрируя (7) по 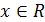 ,
получим
,
получим
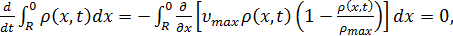 ,
,
и, следовательно, количество автомобилей в 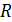 постоянно
для любых значений t ≥ 0.
постоянно
для любых значений t ≥ 0.
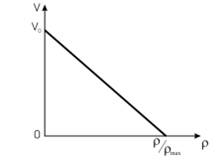
Рис. 2. Линейная аппроксимация Гриншилдса
Модели Гриншилдса и Гринберга
Можно построить макроскопическую модель, в
которой уравнение Гриншилдса является частным случаем. Рассмотрим связь между
скоростью v и плотностью ρ
автомобилей на дороге. В общем случае, когда плотность ρ
повышается, водители снижают скорость и наоборот, поэтому
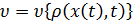 .
.
где x(t) - координата движения элемента
потока.
Проследим изменение скорости для некоторого
передвигающегося элемента потока во времени, которое определяется как полная
производная по времени
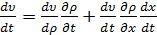 ,
,
Из (4) следует соотношение
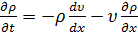 ,
,
которое после подстановки (10) принимает вид
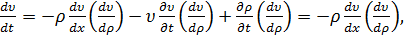
Так как согласно (9)
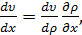
соотношение (12) можно переписать в виде
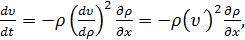
где v′
= dv/dρ, а отрицательный коэффициент
пропорциональности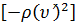 можно
интерпретировать как вязкость в жидкости. Для классической сжимаемой жидкости
уравнение (14) называется уравнением Эйлера, в этом случае:
можно
интерпретировать как вязкость в жидкости. Для классической сжимаемой жидкости
уравнение (14) называется уравнением Эйлера, в этом случае:
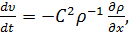
где C - неотрицательная константа с размерностью
скорости.
Принято рассматривать более общий класс моделей,
в которых
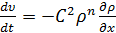 ,
,
Уравнение (15) соответствует случаю 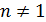 ,
следовательно, из уравнений (14) и (15)
,
следовательно, из уравнений (14) и (15)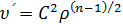 .
Решением этого уравнения будет
.
Решением этого уравнения будет
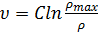 ,
,
при n = −1, и
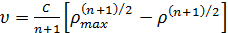 ,
,
при 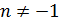 .
.
Модель (17) была впервые получена Гринбергом.
Обозначив за 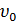 - скорость при
ρ = 0, для значений n ≤ 0, можно
записать
- скорость при
ρ = 0, для значений n ≤ 0, можно
записать
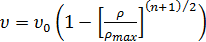 .
.
Уравнение (6), впервые полученное Гриншилдсом,
является частным случаем уравнения (19) при n = 1.
Модель Лайтхилла-Уизема.
Кинематические волны.
При построении модели были приняты следующие
допущения:
· транспортный поток непрерывен, его плотность
ρ(x,
t)
есть число машин занимающих единицу длины дороги;
· величина потока q(x,t) равна
числу машин пересекающих черту x за единицу времени, определяется
локальной плотностью ρ:
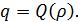
· скорость потока равна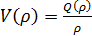 ,т.е.
средняя скорость является функцией плотности
,т.е.
средняя скорость является функцией плотности 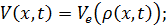
· на участке дороги без
съездов-въездов количество машин сохраняется (7).
Уравнения (20) и (7) образуют полную систему.
После подстановки получим,
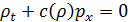 ,
,
где 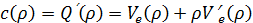 -
скорость распространения возмущений. Соотношение
-
скорость распространения возмущений. Соотношение 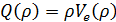 играет
важную роль в теории транспортных потоков и называется фундаментальной диаграммой
(рис.3). В модели Лайтхилла-Уизема эта зависимость непрерывна,
следовательно, предельная пропускная способность участка дороги определяется
плотностью потока.
играет
важную роль в теории транспортных потоков и называется фундаментальной диаграммой
(рис.3). В модели Лайтхилла-Уизема эта зависимость непрерывна,
следовательно, предельная пропускная способность участка дороги определяется
плотностью потока.
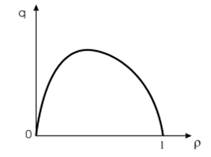
Рис 3. Фундаментальная диаграмма транспортного потока
Общий вид решения нелинейного уравнения (21):
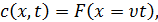
где F - произвольная функция. Соотношение (22)
описывает бегущую волну, рассматриваемую как волну уплотнения в среде. Волны
типа (22) называют кинематическими волнами, что подчеркивает их кинематическое
происхождение в противоположность динамической природе акустических и упругих
волн.
Ударные волны в транспортном потоке
Анализ рассмотренных моделей показал
существование области неустойчивости на кривых q(v). Рассмотрим модель
Гриншилдса (6) (случай n=1). Пусть скорость 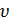 лежит
в пределах
лежит
в пределах
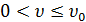 ,
,
так что 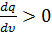 .
Если по какой-либо причине скорость некоторой части потока понизится на
.
Если по какой-либо причине скорость некоторой части потока понизится на 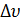 ,
интенсивность движения понизится на
,
интенсивность движения понизится на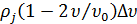 .
Плотность этой части потока ρ
повысится, и скорость будет далее снижаться. Возмущение скорости является
незатухающим, что и демонстрирует неустойчивость поведения транспортного
потока. В этих случаях автомобили в потоке вынуждены неоднократно трогаться с
места и останавливаться. Это явление носит название ударной волны.
.
Плотность этой части потока ρ
повысится, и скорость будет далее снижаться. Возмущение скорости является
незатухающим, что и демонстрирует неустойчивость поведения транспортного
потока. В этих случаях автомобили в потоке вынуждены неоднократно трогаться с
места и останавливаться. Это явление носит название ударной волны.
Уравнение (4) также демонстрирует наличие
ударных волн. Его решение было впервые предложено Лайтхиллом и Уиземом
(1955) и независимо Ричардсом (1956). Аналитическое решение уравнения (4) в
общем случае сложно и в практических расчетах не используется. Для частного
случая, на участке дороге без съездов-въездов можно положить 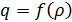 или
или
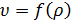 (равновесный
поток), то есть
(равновесный
поток), то есть
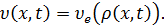
Перепишем теперь уравнение (4) в виде:
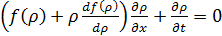 ,
,
Функция f (ρ),
вообще говоря, произвольна. Если положить связь скорость-плотность линейной
(Гриншилдс, 1934), то уравнение (25) примет вид
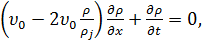
Уравнение (25) решается методом характеристик.
Анализ решения уравнения (26) приводит к
следующим выводам:
· плотность ρ
постоянна
вдоль семейства характеристик;
· наклон характеристик
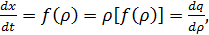
равен тангенсу наклона кривой плотности потока в
точке, представляющей состояние потока на границе, с которой выходят эти
характеристики;
· плотность в любой точке фазовой
области (x,t) находится проведением собственных характеристик через эту
точку.
Пересечение характеристик объясняется
существованием ударных волн, так как в точке пересечения плотность имеет два
значения, что физически невозможно. Математически ударная - разрыв ρ,
q или
v. Скорость ударной волны определяется наклоном линии, соединяющей два
состояния потока (восходящий и нисходящий)
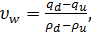
где 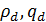 представляют
течение потока вниз, а
представляют
течение потока вниз, а 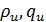 - вверх. Когда
- вверх. Когда 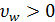 ,
ударная волна движется вниз относительно дороги, если
,
ударная волна движется вниз относительно дороги, если 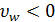 -
вверх.
-
вверх.
Гидродинамические модели второго
порядка-1
Рассмотренные модели выше имеют следующие
ограничения:
• стационарность соотношения скорость-плотность
(средняя скорость движения при определённой плотности устанавливается
мгновенно);
• колебательные решения, описывающие
возникновение неустойчивости в виде регулярных старт-стоп волн с зависящим от
амплитуды временем колебания не могут быть выведены из уравнений
кинематических волн;
• не позволяют описать явление гистерезиса -
возврат потока в устойчивое состояние при меньших значениях плотности.
В реальном потоке плотность не меняется
скачками. Водители обычно снижают скорость при увеличении плотности машин
впереди, и наоборот. Поэтому q зависит еще и от градиента плотности 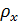 .
.
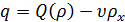 ,
,
где ν - некоторая
положительная постоянная величина.
В силу (21) и (29) имеем
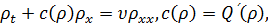
Умножив (30) на c′(ρ),
перепишем его в виде
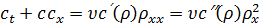 ,
,
При аппроксимации Q(ρ)
квадратичной функцией, c(ρ)
будет линейна по ρ, а c′′(ρ)
= 0.
Таким образом, уравнение (31) принимает вид уравнения Бюргерса.
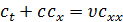
где член 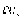 описывает
образование “пробок” - быстрые машины догоняют медленные, возникает скачок
плотности. Член
описывает
образование “пробок” - быстрые машины догоняют медленные, возникает скачок
плотности. Член 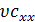 задает конечную
ширину этого скачка. Уравнение Бюргерса (32) можно рассматривать как одномерное
уравнение Навье-Стокса для сжимаемой жидкости с единичной плотностью.
Нелинейное уравнение (32) сводится к линейному уравнению теплопроводности
заменой Коула-Хопфа.
задает конечную
ширину этого скачка. Уравнение Бюргерса (32) можно рассматривать как одномерное
уравнение Навье-Стокса для сжимаемой жидкости с единичной плотностью.
Нелинейное уравнение (32) сводится к линейному уравнению теплопроводности
заменой Коула-Хопфа.
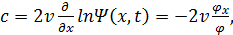
При изучении свойств транспортного потока
представляют интерес также и другие версии уравнения Бюргерса.
Гидродинамические модели второго
порядка-2
Недостатком модели Лайтхилла-Уизема
является допущение о равновесном значении скорости 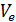 при
данной плотности автомобилей. Это не позволяет адекватно описывать
ситуаций вблизи неоднородностей дороги (въезды, съезды и сужения).
при
данной плотности автомобилей. Это не позволяет адекватно описывать
ситуаций вблизи неоднородностей дороги (въезды, съезды и сужения).
Для описания неравновенных ситуаций вместо
детерминированного уравнения 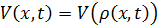 было предложено
использовать дифференциальное уравнение для моделирования динамики средней
скорости. Впервые предложенное Пэйном (Payne) в 1971 году уравнение
скорости имело вид.
было предложено
использовать дифференциальное уравнение для моделирования динамики средней
скорости. Впервые предложенное Пэйном (Payne) в 1971 году уравнение
скорости имело вид.
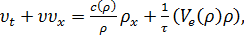
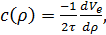
Уравнение (34) было выведено из микроскопического
описания движения отдельных автомобилей в соответствии с моделью следования за
лидером. Слагаемое 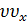 называется
конвекционным и описывает изменение скорости в данном месте дороги за счет
кинематического переноса автомобилей из предшествующего сегмента дороги
со средней скоростью потока. Первое слагаемое в правой части называется
упреждающим и описывает тенденцию к сокращению скорости при возрастании
плотности. Наиболее общая форма упреждающего члена имеет вид:
называется
конвекционным и описывает изменение скорости в данном месте дороги за счет
кинематического переноса автомобилей из предшествующего сегмента дороги
со средней скоростью потока. Первое слагаемое в правой части называется
упреждающим и описывает тенденцию к сокращению скорости при возрастании
плотности. Наиболее общая форма упреждающего члена имеет вид:
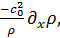
Второе слагаемое в правой части называется
релаксационным и описывает тенденцию приближения средней скорости 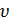 к
равновесному при данной плотности значению
к
равновесному при данной плотности значению 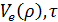 -
характерное время релаксации.
-
характерное время релаксации.
Анализ эмпирических данных показывает, что при
высоких значениях плотности ламинарное движение транспортного потока становится
неустойчивым, и малые возмущения приводят к возникновению старт-стоп волн.
Именно устойчивость в линейном приближении к малым возмущениям при всех
значениях плотности стационарного однородного решения 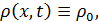
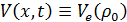 уравнения
Пэйна является его существенным недостатком. Этот недостаток можно
устранить следующим изменением в упреждающем члене уравнения
уравнения
Пэйна является его существенным недостатком. Этот недостаток можно
устранить следующим изменением в упреждающем члене уравнения
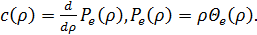
Здесь P - внутреннее давление
транспортного потока, выраженное через вариацию скоростей в потоке Θ.
Тогда
уравнение скорости при такой замене приобретает вид.
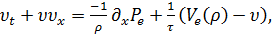
Уравнение (38) описывает поведение водителей в
зависимости от давления потока впереди - торможение при его возрастании и
ускорение в противном случае. Для оценки вариации Θ
как
функции плотности, применяются различные приближения, полученные при анализе
эмпирических данных. Например, в моделях Кюне (Kühne) и
Кернера-Конхойзера (Kerner-Konhauser) в качестве первого приближения
используется положительная константа: 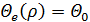 .
.
Уравнение (38) также предсказывает возникновение
ударных волн. Для предотвращения разрывов в правую часть добавляется
диффузионный член 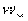 , аналог вязкости в
уравнениях гидродинамики
, аналог вязкости в
уравнениях гидродинамики
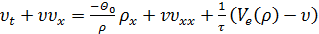 ,
,
Анализ устойчивости стационарного однородного
решения показывает, что при значениях плотности, превышающих критическое
значение, решение становится неустойчивым к малым возмущениям. Это свойство
позволяет моделировать возникновение фантомных заторов - режимов старт-стоп
волн в однородном потоке, возникающих в результате малых случайных возмущений.
Известная модель этого класса - модель Кернера- Конхойзера. Стандартная
модель предполагает уравнение в форме
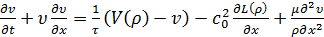 ,
,
Правая часть (40) содержит три коэффициента,
касающихся скорости транспортного потока. Первый член отражает тенденцию потока
на заданной плотности ρ
к понижению средней скорости V (ρ)
до некоторой естественной величины. При малых плотностях эта
скорость определяется дорожными условиями и ограничениями по скорости движения
и слабо зависит от ρ.
При высоких плотностях, V (ρ) приближается
к нулю и слабо зависит от ρ.
При средних плотностях она быстро падает и сильно обусловлена тем фактом, что
при высокой плотности потока водителям сложно совершить обгон. Таким
образом мы предполагаем, что V (ρ)
будет убывающей функцией с малой производной при
больших и малых ρ. Второй
- фактор упреждения, означает, что водители снижают скорость, если впереди
поток транспорта имеет более высокую плотность. Безразмерная функция
L(ρ) должна в таком случае быть монотонно
возрастающей. Ее обычно полагают равной 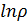 ,
а величина
,
а величина 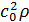 играет роль
давления. Последний член - “вязкость” или “диффузия”, отражает тенденцию
согласования скорости движения со скоростью окружающих автомобилей в
потоке.
играет роль
давления. Последний член - “вязкость” или “диффузия”, отражает тенденцию
согласования скорости движения со скоростью окружающих автомобилей в
потоке.
.3 Стохастические модели
Одной из важнейших характеристик перекрестка
является длина очереди автомобилей, ожидающих проезда. Построим простую модель
образования очереди на перекрестке со светофорным регулированием. Рассмотрим
пересечение двух дорог с односторонним движением. Пусть τ+
- длительность горения зеленого света, а τ
- длительность всего цикла светофора. Предположим, что когда для одной
полосы загорелся красный свет, зеленый свет для второй полосы
загорается спустя некоторое время, чтобы “проскочившие” автомобили успели
проехать.
Пусть поток автомобилей, проходящих через точку
А (некоторую точку на участке дороги перед перекрестком), есть простейший
поток с параметром λ, λ > 0.
При накоплении автомобилей в системе точка А сдвигается влево (рис. 4).
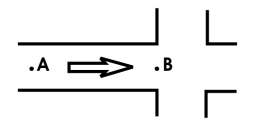
Рис. 4. Модель очереди на перекрестке
Автомобили, поступающие в систему, либо
пересекают перекресток (получают обслуживание как запросы), если проезд
свободен и горит зелёный свет, либо становятся в очередь у перекрестка.
Предположим, что водители не едут на красный свет, даже если на пересекающей
полосе пусто.
Обслуживание одного автомобиля в рамках данной
модели представляет собой проезд через точку В - начало
перекрестка. Примем время проезда через точку В одинаковым для всех
автомобилей и равным T, T > 0. За это время следующий
автомобиль подъезжает к перекрестку (точке В) и ждет своего облуживания.
Таким образом, поведение перекрестка будет описывается с помощью однолинейной
системы массового обслуживания (СМО) с ожиданием и буфером размера M
(максимальное число автомобилей, способных поместиться на дороге), 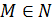 .
.
Будем искать среднюю длину очереди. Допустим,
что перед перекрестком может стоять не более M автомобилей, M ≥
1. Каждый автомобиль занимает одну ячейку (одинаковой длины для всех
автомобилей). Когда первый автомобиль проезжает через перекресток, остальные,
стоящие в очереди, подвигаются на одну ячейку вперед.
Подсчитаем, сколько автомобилей могут проехать
перекресток за период горения зеленого света. За единицу времени через
перекресток могут проехать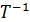 автомобилей.
Значит, на зеленый свет через перекресток могут проехать
автомобилей.
Значит, на зеленый свет через перекресток могут проехать 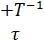 автомобилей.
Таким образом, величина
автомобилей.
Таким образом, величина
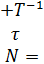 ,
,
представляет собой пропускную способность
перекрестка за время горения зеленого света, где [·] есть целая часть числа.
Рассмотрим накопление автомобилей в системе за
время одного цикла светофора. Будем исследовать поведение системы в моменты
времени 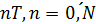 ,
то есть моменты начала периода зеленого света и моменты окончания обслуживания
запросов (автомобилей̆). Обозначим через
,
то есть моменты начала периода зеленого света и моменты окончания обслуживания
запросов (автомобилей̆). Обозначим через 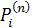 вероятности
того, что в момент времени
вероятности
того, что в момент времени 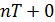 (непосредственно
сразу после ухода автомобиля из очереди) длина очереди составляет i
автомобилей,
(непосредственно
сразу после ухода автомобиля из очереди) длина очереди составляет i
автомобилей, 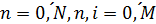 Обозначим также
через
Обозначим также
через 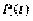 вероятность
того, что за время t в систему приедут i автомобилей, i ≥
0. Выражение для
вероятность
того, что за время t в систему приедут i автомобилей, i ≥
0. Выражение для  имеет вид
имеет вид
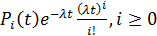 ,
,
Уравнения для вероятностей 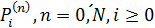 имеют
вид
имеют
вид
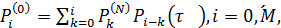 ,
,
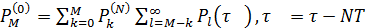 ,
,
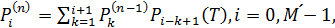 ,
,
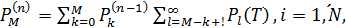
причем каждая группа вероятностей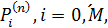 удовлетворяет
условиям нормировки
удовлетворяет
условиям нормировки
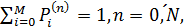
Обозначим через 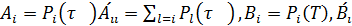 .
и распишем систему (41) более подробно:
.
и распишем систему (41) более подробно:
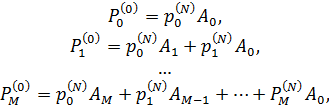
где 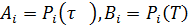
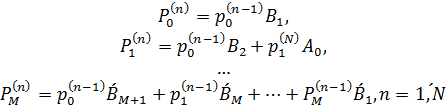
Запишем системы (43) и (44) в матричном виде
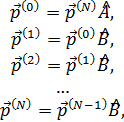
где
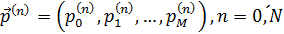 ,
,
 ,
,
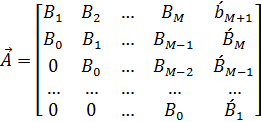 .
.
Из системы (45) и условия нормировки (42) при
n = 0 находим значение для вектора 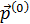
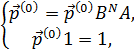 ,
,
где 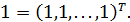
Остальные векторы вероятностей находим с помощью
равенств
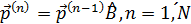 ,
,
Тогда средняя длина очереди на перекрестке к
моменту начала периода зеленого света равна
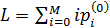 .
.
2.4 Микроскопические модели
Модели следования за лидером
Кроме случая очень малых интенсивностей движение
любого автомобиля ограничено впереди идущим автомобилем.
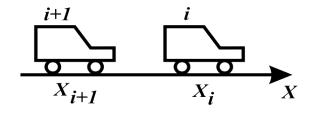
Рис. 5. Порядок следования автомобилей
Первоначально предполагалось, что каждый
водитель согласует свою скорость со скоростью впереди идущего автомобиля.
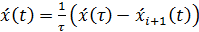 ,
,
где τ
- время согласования скоростей (рис. 5).
Данная модель не описывает свойств
неустойчивости, возникновения ударных волн и заторов. Позднее был предложен ряд
модификаций. Например, в [3] в левую часть уравнения (46) добавляют
задержку 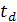 ≈
1, 3с, описывающую время реакции водителя на изменение скорости лидирующего
автомобиля. Множитель 1/τ
в [5] интерпретируется как коэффициент чувствительности α,
характеризующий
скорость реакции водителя. Тогда (46) можно записать в виде
дифференциально-разностного уравнения
≈
1, 3с, описывающую время реакции водителя на изменение скорости лидирующего
автомобиля. Множитель 1/τ
в [5] интерпретируется как коэффициент чувствительности α,
характеризующий
скорость реакции водителя. Тогда (46) можно записать в виде
дифференциально-разностного уравнения
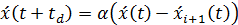 ,
,
При α = const
условие неустойчивости уравнения (47) имеет вид 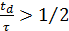 .
Наличие неустойчивости позволяет моделировать ударные волны и заторы, но
предположение о неизменности чувствительности не позволяет воспроизвести фундаментальную
диаграмму. Более адекватная модель получается при учете возрастания
чувствительности с уменьшением дистанции до лидирующего автомобиля. С этой
точки зрения Газис и др. [4] преобразовали уравнение (47)
.
Наличие неустойчивости позволяет моделировать ударные волны и заторы, но
предположение о неизменности чувствительности не позволяет воспроизвести фундаментальную
диаграмму. Более адекватная модель получается при учете возрастания
чувствительности с уменьшением дистанции до лидирующего автомобиля. С этой
точки зрения Газис и др. [4] преобразовали уравнение (47)
 ,
,
и выполнили оценку коэффициентов 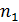 и
и
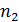 по
экспериментальным данным, было найдено, что коэффициент корреляции между
по
экспериментальным данным, было найдено, что коэффициент корреляции между 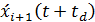 и
и
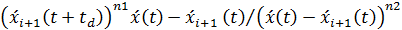 равен
0,87; 0,78 и 0,73 для
равен
0,87; 0,78 и 0,73 для 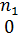 ,
, 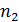 (1,2);
(0, 1) и (0, 2) соответственно и принимает меньшие значения порядка 0,2 - 0,5
для других целочисленных комбинаций параметров
(1,2);
(0, 1) и (0, 2) соответственно и принимает меньшие значения порядка 0,2 - 0,5
для других целочисленных комбинаций параметров 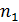 и
и
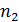 простейший
случай
простейший
случай 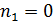 и
и 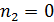 ,
,
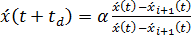 ,
,
часто используется для моделирования и
теоретического анализа.
После интегрирования выражения (49), получаем.
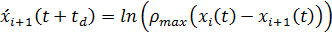 ,
,
где  -
константа, описывающая движение автомобилей̆ в плотном потоке на очень
близком расстоянии - “бампер-к-бамперу”.
-
константа, описывающая движение автомобилей̆ в плотном потоке на очень
близком расстоянии - “бампер-к-бамперу”.
Когда транспортный поток является стационарным,
плотность ρ выражается формулой
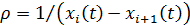 ,
а так как скорость в стационарном режиме постоянна, то
,
а так как скорость в стационарном режиме постоянна, то
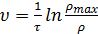 ,
,
Выражение (51) идентично уравнению (17), и мы из
микроскопической модели следования за лидером получаем макроскопическую модель
Гринберга.
Клеточные автоматы
В настоящее время имеется обширный набор
публикаций по клеточным автоматам (см.[5]). Применение концепции
клеточного автомата фон Неймана для моделирования транспортных потоков
впервые было предложено в работе [6]. Активные разработки начались с работ
Нагеля и Шрекенберга [7].
Формулировка исходной модели Нагеля-Шрекенберга
заключается в следующем [8]. Пусть 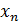 и
и
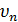 координата
и скорость n-го автомобиля,
координата
и скорость n-го автомобиля, 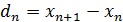 -
дистанция до лидирующего автомобиля. Скорость может принимать одно из
-
дистанция до лидирующего автомобиля. Скорость может принимать одно из 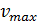 +
1 допустимых целочисленных значений
+
1 допустимых целочисленных значений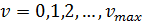 .
На каждом шаге
.
На каждом шаге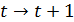 состояние всех
автомобилей в системе обновляется в соответствии со следующими правилами:
состояние всех
автомобилей в системе обновляется в соответствии со следующими правилами:
. Ускорение. Если 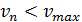 ,
то скорость n-го автомобиля увеличивается на единицу, если
,
то скорость n-го автомобиля увеличивается на единицу, если 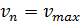 ,,
то скорость не изменяется:
,,
то скорость не изменяется:
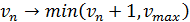 ,
,
2. Торможение. Если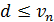 , то скорость n-го автомобиля уменьшается до
, то скорость n-го автомобиля уменьшается до 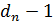
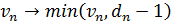 ,
,
3. Случайные возмущения. Если 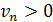 ,
то скорость n-го автомобиля может быть уменьшена на единицу с
вероятностью p; скорость не изменяется, если
,
то скорость n-го автомобиля может быть уменьшена на единицу с
вероятностью p; скорость не изменяется, если 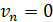 :
:
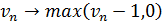 ,
,
4. Движение. Каждый автомобиль продвигается
вперед на количество ячеек, соответствующее его новой скорости после выполнения
шагов 1-3:
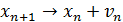 .
.
Первый шаг (52) отражает общее стремление всех
водителей ехать как возможно быстрее. Второй (53) гарантирует отсутствие
столкновений с впереди идущими автомобилями. Элемент стохастичности,
учитывающий случайности в поведении водителей вносится на третьем шаге (54).
3. Описание разработанной
математической модели
Задача реализована с
использованием модели клеточного автомата поэтому всю систему можно
рассматривать как матрицу NxM клеток. Каждая клетка имеет свое определенное
значение что равноценно матричному представлению когда матрица имеет элементы
определенного веса. Каждый элемент будет рассматриваться системой как элемент с
определенными характеристиками.
В качестве элементов системы
будут выступать:
- границы которые нельзя
пересекать, 1 - дорога по которой можно перемещаться автомобилям, 2 - красный
светофор, 3 - желтый светофор, 4 - зеленый светофор, 5 - автомобиль Таким
образом участок дороги можно рассмотреть как матрицу следующего вида:
 ,
,
В качестве модели можно выбрать систему с
ограниченной очередью, тогда количество мест в очереди n равно количеству
автомобилей, которые поместятся по полосе движения на протяжении данного
квартала. Таким образом,
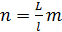
где L - длина квартала, l - длина автомашины
вместе с динамическими габаритами. Обычные значения количества мест в очереди
10,20,30 автомобилей. При таком подходе предполагается, что машина, подъехавшая
в момент, когда весь квартал заполнен, покидает систему.
Можно также рассмотреть в качестве модели
систему с неограниченной очередью. Для упрощения модели считается, что
поступающий поток автомашин является простейшим, с интенсивностью λ
автомобилей
в секунду.
Задача заключается в исследовании зависимости
длины очереди от интенсивности входного потока, а также нахождении оптимального
режима работы светофора при заданных интенсивностях входного потока автомашин.
В качестве критериев оптимальности могут быть
выбраны: средняя длина очереди (или среднее время ожидания в очереди),
вероятность того, что количество машин в очереди превысит заданное значение.
Для расчета характеристик системы при движении
автомобилей в одну сторону по одной полосе можно использовать одноканальную
модель системы массового обслуживания с ограниченной очередью. Пусть T - длина
полного цикла светофора, а зеленая фаза, например, составляет половину длины
цикла 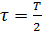 .
.
Интенсивность обслуживания μ(t)
можно задать периодической функцией с периодом T:
ᶙ(t)=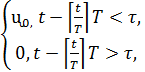
где [x] - целая часть числа; μ0
- интенсивность
проезда перекрестка при разрешающем сигнале светофора (сколько, в среднем,
автомашин может проехать перекресток в данном направлении за 1 минуту при
включенном разрешающем сигнале).Таким образом, основные параметры описанной
системы: T - длина полного цикла светофора; λ - интенсивность
входного потока; μ0 -
интенсивность потока обслуживания в «зеленой» фазе; n - максимальная длина
очереди.
В процессе моделирования также необходимо
создать случайный временной интервал возникающий между двумя следующими друг за
другом автомобилями в очереди.
Для моделирования случайного временного
интервала - экспоненциально распределенной случайной величины воспользуемся
методом обратной функции, также известным как метод инверсии. Чтобы найти
возможное значение 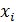 непрерывной
случайной величины X, зная ее функцию распределения F(x),
надо выбрать случайное число
непрерывной
случайной величины X, зная ее функцию распределения F(x),
надо выбрать случайное число 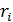 , приравнять его
функции распределения и решить относительно
, приравнять его
функции распределения и решить относительно 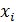 полученное
уравнение, то есть найти функцию, обратную к функции распределения F(
полученное
уравнение, то есть найти функцию, обратную к функции распределения F(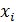 )=
)=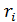 .
Применим этот метод для генерации случайной величины по показательному закону.
Функция показательного распределения.
.
Применим этот метод для генерации случайной величины по показательному закону.
Функция показательного распределения.
(x)=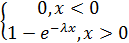
Рассмотрим случай x≥0 и приравняем
случайное число 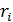 функции
показательного распределения
функции
показательного распределения 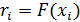 , получим
, получим 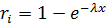 .
Решение уравнения относительно
.
Решение уравнения относительно 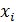 :
: 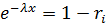 следовательно
следовательно
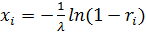
Случайное число 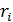 заключено
в интервале (0, 1), следовательно, число 1−
заключено
в интервале (0, 1), следовательно, число 1−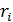 также является случайным и принадлежит интервалу (0, 1) или иначе, величины R и
1 - R распределены одинаково. Поэтому для отыскания
также является случайным и принадлежит интервалу (0, 1) или иначе, величины R и
1 - R распределены одинаково. Поэтому для отыскания 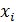 можно
воспользоваться более простой формулой:
можно
воспользоваться более простой формулой:
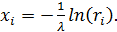
где 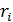 -
случайная величина, равномерно распределенная на отрезке (0, 1);
-
случайная величина, равномерно распределенная на отрезке (0, 1); 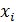 случайная
величина, имеющая показательное распределение с параметром λ.
случайная
величина, имеющая показательное распределение с параметром λ.
Таким образом, с помощью формулы (4.10)
моделируется выборочная совокупность, составленная из временных интервалов
между созданием автомобилей и имеющая показательное распределение. В
разработанной программе значение параметра 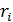 генерируется
с помощью встроенной функции генератора случайных чисел - rand(),
которая возвращает непрерывную случайную величину, равномерно распределенную на
отрезке (0, 1).
генерируется
с помощью встроенной функции генератора случайных чисел - rand(),
которая возвращает непрерывную случайную величину, равномерно распределенную на
отрезке (0, 1).
С помощью параметра λ
задается
интенсивность входного потока автомобилей. В программе интенсивность можно
задать указав количество автомобилей которое должно быть сгенерировано для
определенной дороги за определённое время.
Для того чтобы в результате работы имитационной
модели основанной на принципе клеточного автомата получить определенные данные
и затем их обработать необходимо выполнить дополнительные шаги для их
получения.
Введем обозначения: T - продолжительность цикла
светофора, 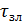 -
продолжительность зеленого сигнала для первого направления движения,
-
продолжительность зеленого сигнала для первого направления движения, 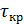 .-
продолжительность красного сигнала. Продолжительность желтого сигнала
.-
продолжительность красного сигнала. Продолжительность желтого сигнала 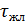 равно
3с. Таким образом, продолжительность цикла светофора равна:
равно
3с. Таким образом, продолжительность цикла светофора равна:
= (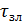 +
+ 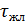 )
+ (
)
+ (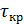 +
+ 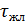 )
=
)
= 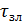 +
+
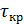 +
2
+
2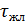 .
.
Для того чтобы автомобиль мог
перемещаться ему необходимо задавать определенные координаты и направление, для
чего используется следующие параметры: x,y - координаты автомобиля в системе,
speed - текущая скорость автомобиля, turn -поле определяющее направление
поворота автомобиля после светофора, direction - направление движения
автомобиля которое может получать параметры UP, DOWN, LEFT, RIGHT (вверх, вниз,
лево, право), speedVector - вектор содержащий скорость автомобиля в течении
всех временных промежутков lightVector - вектор содержащий параметры светофора
в течении всех временных промежутков, moveVector - вектор содержащий параметры
перемещения автомобиля в течение всех временных промежутков.
Используя такую структуру можно создать функцию
устанавливающую автоматически автомобили на выбранных участках дорожного
полотна. Каждый созданный автомобиль будет занесен в список после чего система
сможет получать каждый автомобиль из этого списка.
В процессе вывода матрицы на экран будет
происходить проверка всех автомобилей на значение поля direction, которое
отвечает за направление движения по дорожному полотну и в зависимости от
значения этого поля будет происходить изменение только определенных координат
автомобиля.
Например если задано два автомобиля car1 и car2
расположенных в списке под номерами 1 и 2 тогда в упрощенном виде алгоритм
выбора направления будет иметь вид конечного множества значений среди которых
будет выбрано только одно. Выбранное значение при условии, что это единица
будет обозначать поворот, во всех иных случаях движение автомобиля будет
происходить в установленном изначально направлении.
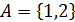 .
.
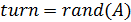 .
.
где rand - функция генерации случайного
числового значения, turn - поворот i-того автомобиля.
Такой подход даст возможность опрашивать весь
список автомобилей и в зависимости от состояния turn
изменять направление движения.
В процессе перемещения автомобиля по дороге
необходимо проверять возможен ли обход других автомобилей которые едут с более
медленной скоростью.
Для решения этой задачи был так же применен
матричный подход позволяющий сравнить заданный участок дороги с шаблоном и в
случае если шаблон соответствует такому участку дороге запретить обгон другого
транспортного средства. Для реализации были взяты следующие шаблоны:
{"141"},
{"XXX"},
{"X4X"},
{"1X1"},
{"X4X"},
{"XX1"},
{"X4X"},
{"1XX"},
{"X4X"},
{"XXX"},
где X - это значение которое принимает один из
следующих вариантов 0 - область не являющаяся дорогой, 2 - красный сигнал
светофора, 5 - автомобиль с которым возможно столкновение.
Оставшиеся значения каждого шаблона это 1 -
дорога по которой возможно перемещение, 4 - выбранный автомобиль.
Таким образом, шаблоны описывают возможные
дорожные ситуации при которых автомобиль должен сбавить ход или не перемещается
вообще в заданном направлении
Рассмотрим ситуацию, при которой
автомобиль A должен обойти другой автомобиль B перед тем, как подъехать к
красному светофору. Для этого можно использовать небольшую часть дороги
представленной в виде матрицы
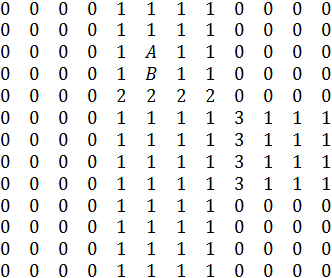 ,
,
Автомобиль А будет считан
вместе со значениями находящимися вокруг него что в результате будет
представлено в виде матрицы
{1A1}
{1B1}
Такая матрица будет проверена
по шаблонам
{141} {X4X} {X4X} {X4X} {X4X}
{XXX} {1X1} {XX1} {1XX} {XXX}
при этом для универсальной
проверки в ней автомобиль A будет заменен на 4, а все остальные значения
матрицы кроме единиц на X, в результате получим матрицу:
{141}
{1x1}
Поученная матрица не
соответствует н одному из шаблонов, поэтому будет принято решение объехать
автомобиль B с одной из сторон.
Если рассмотреть автомобиль B,
который находится радом с красным сигналом светофора, то можно получить матрицу
{1B1}
{222},
которая будет представлена как:
{141}
{XXX},
что соответствует одному из
шаблонов. В результате автомобиль B не будет перемещаться вниз по дороге до тех
пор, пока не будет включен зеленый сигнал светофора.
В случае, если автомобиль
движется в другом направлении, например, слева на право, то рассмотренные
шаблоны просто не подходят в том виде, в котором они представлены, поэтому
матрица участка дороги будет повернута, чтобы соответствовать шаблону и затем
произойдет проверка. Таким образом, имея только один набор шаблонов, можно
использовать его для различных дорожных ситуаций, на рис. 6 приставлены разные
варианты перестроения автомобилей в зависимости от конкретной ситуации.
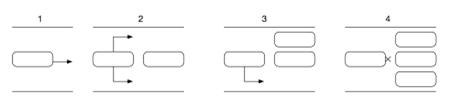
Рис. 6. Правила перестроения
автомобилей
Регулировка скорости движения
автомобиля происходит за счет проверки заполнения счетчика задержки. Каждому
автомобилю при создании присваивается скорость генерируемая псевдо случайной
величиной через функцию rand() в пределах 10, однако система клеточного автомата была бы
слишком сложна, если бы у каждого автомобиля был собственный таймер, поэтому в
системе используется только один таймер, который отсчитывает время перед каждым
циклом проверки списка автомобилей. Во время такой проверки из структуры
автомобиля будет извлечено значение delay и увеличено на единицу. Этот цикл
увеличения будет повторяться до тех пор, пока значения delay и speed не будут
равны и только после этого автомобиль будет перемещен на новую клетку. Алгоритм
можно представить следующим выражением
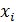 =speed+1
=speed+1
где 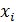 -
автомобиль в очереди, speed - текущая скорость.
-
автомобиль в очереди, speed - текущая скорость.
В процессе работы система будет принимать
решение для того, чтобы выполнить поворот автомобиля в определенную сторону или
продолжить движение в установленном направлении. В реальной ситуации на дороге
водитель принимает решение об изменении курса следования в соответствии с
правилами дорожного движения. Изменение курса следования происходит после того,
как водитель пересечет линию светофора. Для того, чтобы имитировать подобную
ситуацию изменения курса наиболее всего подходит принятие решения на основе
псевдо случайного значения. Применение такого подхода обусловлено тем, что
никаких других параметров в системе для принятия решения на их основе не
существует.
Решение о выполнении поворота система принимает
при появлении автомобиля на карте.
Алгоритм работы поворота можно представить в виде
функции генерации псевдо случайного значения rand(2) которая сгенерирует одно
из двух значений и в зависимости от того что это за значение произвести
изменение состояния turn выбранного автомобиля. Проще говоря, автомобиль может
ехать прямо или повернуть.
 =random(direction)
=random(direction)
Такой алгоритм можно так же настраивать для
того, чтобы решения о повороте принимались не слишком часто в списке
автомобилей, для этого достаточно будет увеличить порог генерации псевдо
случайных значений.
Таким образом, на базе клеточного автомата можно
построить модель транспортного потока, которая может быть легко расширена за
счет увеличения самой матрицы и при этом в такой модели возможно
визуализировать состояние дорожного полотна, что является немаловажной деталью
при анализе работы алгоритма. Принимая во внимание все положительны стороны
модели клеточного автомата необходимо обратить внимание и на отрицательные
стороны. Минусом клеточного автомата является то, что очень сложно реализовать
плавное перемещение или инерцию при невысоком разрешении матрицы клеточного
автомата, при этом используя высокое разрешение обработка такой матрицы, займет
значительное время, что отрицательно скажется на скорости моделирования.
4. Описание информационной системы и
результаты моделирования
В данной работе смоделирован перекресток двух
дорог с двумя направлениями движения, в которой соединяются четыре полосы L1,
L2, L3 и L4, и в котором на каждом углу установлен светофор (T1, T2, T3и T4)
(рис. 7). автомобильный
дорожный светофор водитель
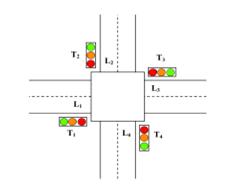
Рис. 7. Простой перекрёсток.
Для каждого светофора и в каждом цикле есть три
последовательных состояния: зеленый, желтый и красный. Доля подъехавших
автомобилей на полосе движения Li в момент времени t - λi(t),
i=1,2,3,4.
Когда на светофоре зажегся зеленый (соответственно, желтый) доля выехавших
автомобилей на полосе движения Li в момент времени t µi(t) (соответственно,
ki(t)), i=1,2,3,4. Предполагается, что желтый свет горит в течение
фиксированного времени и равна δжелт
(это время определяется на основе установленных стандартов, существуют
различные виды стандарта: американские, европейские и т. д; в целом колеблется
между 3 и 4 секундами).
Зеленый свет горит в течение определенного
переменного периода времени, который рассчитывается в зависимости от:
поддержанной скорости на дорогах, количества полос движения, потока транспортных
средств и т. д.; оно колеблется между 20 и 30 секундами. Считается, что красный
свет светофора горит в течение времени, равного сумме времен, в течение которых
включены зеленый и желтый свет светофоров, расположенных на полосах,
противоположных направлений (См. табл.1).
Табл.1. Схема переключений сигналов светофора
|
Цикл
|
T1
|
T2
|
T3
|
T4
|
|
[t0, t1 − δжел)
|
Красный
|
Зеленый
|
Красный
|
Зеленый
|
|
[t1 − δжел, t1)
|
красный
|
Жёлтый
|
Красный
|
Желтый
|
|
[t1, t2 − δжел)
|
Зеленый
|
Красный
|
Зеленый
|
Красный
|
|
[t2 − δжел, t2)
|
Желтый
|
Красный
|
Желтый
|
Красный
|
|
[t2, t3 − δжел)
|
Красный
|
Зеленый
|
Красный
|
Зеленый
|
|
[t3 − δжел, t3)
|
красный
|
Жёлтый
|
Красный
|
Желтый
|
|
…
|
…
|
…
|
…
|
…
|
В этой работе также представляем модель для
задачи контроля движения на простом перекрестке. Есть перекресток, на котором сходятся
две улицы, обе с двумя полосами движения в одном направлении и в которых не
возможно повернуть влево. На каждом углу перекрестка есть светофор. Нужно найти
периоды, в которых должны остаться зеленымисветофоры T1 и T3, (красный T2 и
T4), и в течение которых T1 и T3 показывают красный свет (зеленый T2 и T4),
чтобы избежать заторов на дорогах, описанных количеством транспортных средств в
ожидания (длина очереди) на каждой из полос.
Это исследование также используется для оценки
перегрузки полос движения, учитывая различные критерии: сумма средней длины
очередей на каждой полосе, среднее время ожидания, длина самой длинной очереди
или их сочетание. Так что, цель - это вычислить временную последовательность,
оптимальную для светофоров, которая сводит к минимуму все вышеперечисленные
критерии. Это позволяет нам моделировать и решать проблему, которая в каждом
цикле имеет две фазы: рис.8 и рис. 9.
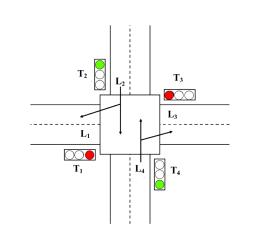
Рис. 8. Первая фаза
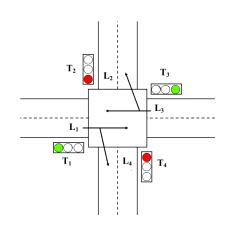
Рис. 9. Вторая фаза
На основе поставленной задачи была разработана
информационная система имитационного моделирования. Система позволяет
имитировать перемещение автомобиля по дорожному полотну, анализировать
необходимость въезда на перекресток автомобилей в процессе движения, т.е., при
красном свете автомобиль остановится и не въедет на перекресток, а при зеленом
- въедет. В системе возможно изменить необходимую скорость работы для
обеспечения более качественного наблюдения за процессом имитации. Для настройки
задержки светофоров установлены специальные элементы управления которые
позволяют указать задержку между переключение сигнала светофора. Для закуска
системы необходимо установить требуемое количество автомобилей для каждой
дороги или для хотя-бы одной дороги и нажать на кнопку "пуск"
(рис.10). Параметр «количество автомобилей» позволяет имитировать разные
степени загруженности дорог, прилегающих к перекрестку.
После чего система будет запущена с той
скоростью имитации, которая была выбрана. Для более детального наблюдения за
процессом имитации можно открыть таблицы нажав на кнопку "график"
(см. Таб. 2) в результате чего для каждого направления можно будет увидеть
результаты. Таблицы реализованы так чтобы отобразить текущее данные автомобиля
исходя из его скорости передвижения и времени заданного на это передвижение.
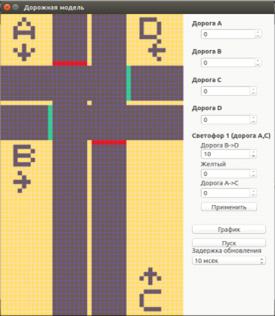
Рис. 10. Интерфейс программы
Используя исходные данные, программа моделирует
поведения транспортных средств на перекрестке. В результате этого моделирования
мы получаем данные (в виде HTML-кода) В них содержится: время ожидания
автомобилей на светофоре, направления движений, среднее время в пути для
каждого автомобиля, принимаемые решения для движения (см. Табл. 2).
Табл.2. Выходные программ
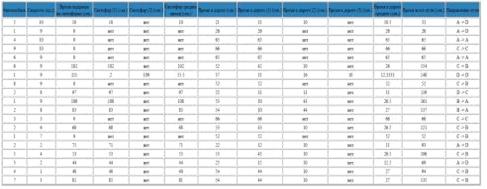
Полученные результаты моделирования движения
транспортных средств на регулируемых перекрестках используются для решения
проблем заторов. На следующем примере, увидеть значения задержек. Светофоры
настроены таким образом, что красный света горит 100 с, зеленый - 60 с, желтый
может быть проигнорирован, так как может быть включен в цикл зеленого или
красного. Транспортные средствами подъезжают к светофору в среднем, каждые 4 с,
и когда включается зеленый свет, они начинают движением через перекресток с
разницей в 1 с. Также считается, что-то сумма циклов зеленого и красного света
равна 160 с, и возьмем значение количества транспортных средств, равное 40.
Таким образом, ожидается, что-то всегда транспортные средства проедут через
перекресток во время цикла горения зеленого света.
Программа может быть настроена так, чтобы
транспортные средствами подъезжали к светофору каждые 4 с. Когда параметры
настроены, полученные результаты показывают, что, 33й транспортное средство
въедет в перекресток на 132й секунде, и следующие семь не будут останавливаться
передвигающегося перекрестком.
Табл. 3. Временных параметров

Используя данные таблицы, можно засчитать
среднее значение задержки транспортных средств.
среднее значение задержки = 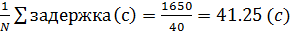
Мы можем считать, что предыдущее уравнение с
общими значениями параметров:
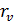 -
продолжительность цикла красного света (секунды).
-
продолжительность цикла красного света (секунды).
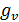 -
продолжительность цикла зеленого света (секунды).
-
продолжительность цикла зеленого света (секунды).
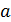 - интервал времени
прибытия между двумя идущими друг за другом транспортными средствами (секунды).
- интервал времени
прибытия между двумя идущими друг за другом транспортными средствами (секунды).
d - интервал
времени начала движения между идущими друг за другом транспортными средствами
(секунды).
Мы можем написать уравнение, которое содержит
параметры 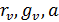 и d
среднее
значение задержки=
и d
среднее
значение задержки=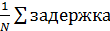 .
.
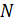 количество
транспортных средств
количество
транспортных средств 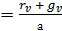 .
.
где 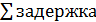 ,
может быть выражена как сумма арифметической прогрессии:
,
может быть выражена как сумма арифметической прогрессии:
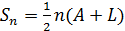 .
.
где A=
a - d и
L= 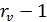 .=
.=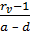 ,
,
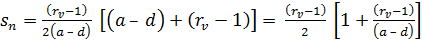 .
.
среднее значение задержки=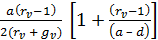 .
.
Диаграмма ниже показывает вымышленное
расположение светофоров в определённой зоне, каждый перекресток обозначен
буквой (А, Б, В, Г, Д, Е, Ж, З), как показано на рис. 11. Светофор Г расположен
в центре дорожной сети, следовательно можно ожидать очень большой трафик на
этом перекрёстке (Г), так как все потоки сходятся на этом перекрестке, трафик
может быть перераспределён путем применения уравнения (64), таким образом в
основном уменьшается трафик на перекрестке (Г), стратегически создавая
однородное распределение потоков во всей дорожной сети.
Данные, полученные с помощью моделирования
движения автотранспортных потоков и используемые совместно с данными других
дорожных сетей, позволяют уменьшать количества заторов в городе. В процессе
моделирования движения автотранспортных потоков на перекрёстках также
рассчитывается время прохождения через светофоры от момента подъезда к нему до
полого выезда из него.
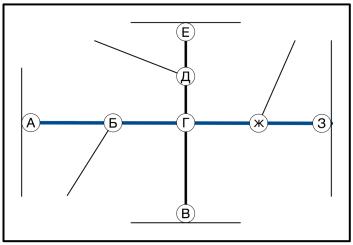
Рис. 11. Диаграмма расположения светофоров
Заключение
Обобщая представленные классификацию и обзор
моделей, стоит отметить большое разнообразие методов и моделей, разработанных
для решения задач, связанных с проблемами автомобильного движения.
Однако до сих пор не существует идеальной
модели, позволяющей решить все проблемы, связанные с транспортными потоками,
как не существует и всеохватывающей классификации этих моделей, учитывающей все
их аспекты. Выбор метода моделирования определяется как поставленной задачей,
так и техническими возможностями и предпочтениями исполнителей.
Выполненные в диссертации исследования позволяют
анализировать движение транспортных средств, в местах их большого скопления,
особенно на регулируемых перекрестах. Они являются очень важными инструментом,
такая как получение параметров как время ожидания транспортных средства на
перекрестках, дает достаточно определенное представление потерь, которые
провоцируют заторы в экономическом плане, влияние выбросов СО2 на окружающую
среду среди других.
Хочется особенно упомянуть город Каракас,
который занимает четвертое место в мире по количеству пробок на дорогах. В
настоящее время в некоторых районах города применяются современные технологии,
но всегда программное обеспечение приобретается в других странах, и это делает
нашу страну уязвимой и зависимой, поэтому наше правительство уделяет особое
внимание подготовке кадров за рубежом, с целью создания собственного
программного обеспечения и обеспечения национальной безопасности и
независимости от иностранных технологии.
В будущем эти системы смогут работать на
перекрестках с фактическими данными потока транспортных средств, полученными с
помощью различных средств, такие как сенсоры и спутниковые снимки. Данные с
разных перекрёстков и дорог будут обрабатываться в едином центре, что даст
возможность улучшать дорожную ситуацию в целом городе или районе.
Целью разработки данной программы является
положить начало целого ряда разработок, которые будут учитывать больше
параметров, такие как, данные с сенсоров, статистики, совместная работа с
другими светофорами с применением интеллектуальных технологий, как нейронные
сети.
Список литературы
1. D.S.
Johnson, C.R. Aragon, L.A. McGeoch, and C. Schevon. Optimization by simulated
annealing: An experimental evaluation; part i, graph coloring and number
partitioning. Operations research, 37:865-892, 1989.
2. E.
Taniguchi and H. Shimamoto. Intelligent transportation system based
dynamicvehicle routing and scheduling with variable travel times.
Transportation Research Part C: Emerging Technologies, 12(3-4):235-250, 2004.
3. Chandler
R.E. at al. Traffic dynamics: Studies in car following - Opreations Research. -
1958. - Vol. 6. - P. 165-185.
. Gasis
D.C. et al. Car following theory of steady state flow - Operations Research. -
1959. - Vol. 7. - P. 499-505.
2. Krug
J., Spohn H. // Phys. Rev. A. - Vol. 83. - P. 4271.
3. Cremer
M., Ludwig J. A fast simulation model for traffic flow on the basis of Boolean
operations // Math. Comp Simul. - 1986. - V. 28. - P.
297-303.
4. Nagel
K., Schreckenberg M. A cellular automation model for freeway traffic // J.
Phys. I
France. - 1992. - Vol. 2. - P. 2221- 2229.
. Швецов
В.И. Математическое моделирование транспортных потоков // Автоматика и
телемеханика. - 2003. - No11.Chandler R.E. at al. Traffic
dynamics: Studies in car following // Opreations Research. - 1958. - Vol. 6. -
P. 165-185.
6. Comisión
de las Comunidades Europeas. Comunicación de la Comisión al
Consejo y al Parlamento Europeo. Hacia un transporte
más ecológico, p. 2. COM(2008) 433, 2008.
7. Q.
Yang. A simulation laboratory for evaluation of dynamic traffic management
systems. PhD Thesis, Massachusetts Institute of
Technology, 1997.
8. D.W.
Huang and W.N. Huang. Optimization of traffic lights at crossroads.
International Journal of Modern Physics C, Physics and Computer, 14(5):539-548,
2003.
Приложение
Представлена основная функция для программы
включающая в себя вызов операций рисования объектов на карте и алгоритм выбора
траектории движения. Эта функция вызывается по таймеру и на каждой итерации
проходит весь список автомобилей, затем определяет направление движения
выбранного из списка автомобиля после чего проверяет возможно ли его движение и
если это возможно и при этом присутствует светофор установленный в зеленый цвет
позволяет принять решение на основе случайной величины.
#include "mainwindow.h"
#include "ui_mainwindow.h"
#include<QPainter>::MainWindow(QWidget
*parent) :
QMainWindow(parent),
ui(new Ui::MainWindow){
ui->setupUi(this);
tm=new
QTimer(this);
// включение таймера
tm->connect(tm,SIGNAL(timeout()),this,SLOT(updateModel()));//
функция updatemodel
вызывается после задержки
tm->start(10);
// установка задержки таймеру в милисекундах. таймер нужен для обновления
клеточного автомата
srand(time(NULL));
setFixedSize(640,700);
//установка размеров окна
for(int
i=0;i<4;i++)
carThreadSize[i]=0;
clearMapFlag=false;
work=false;
graphics=NULL;
}::~MainWindow(){
delete tm;
delete ui;
}
//функция обновления всего клеточного автомата.
она вызывается таймером
void
MainWindow::updateModel(){
update();
}
// функция рисования одного квадрата клеточного
автомата
void MainWindow::drawRect(int x,int
y,int w,int h,int color){
paint->setRenderHint(QPainter::Antialiasing,
true);
paint->setPen(QPen(QColor(color+100),
0, Qt::SolidLine, Qt::RoundCap));
paint->setBrush(QBrush(QColor(color),Qt::SolidPattern));
paint->drawRect(x,y,w,h);
//рисование самого квадрата
}
/*
* функция задержки автомобиля. эта функция будет
устанавливать задержку автомобилю в зависимости от скорости
* например скорость автомобиля speed=8
значит до тех пор пока значение delay
не станет равно speed
* автомобиль не будет перемещатся на новую
клетку
*/MainWindow::calulateSpeedDelay(Car
*car){
if(car->speed<=car->defaultSpeed){
car->speed++;
return true;
}
car->speed=0;
return false;
}MainWindow::calculateDifference(Car
*car,int position){
bool flag=false;
if(car->difference>0){
car->difference--;
flag=true;
}
carList.removeAt(position);
carList.insert(position,car);
return
flag;
}
/*
* функция рисования автомобилей и карты
* эта функция проходит по списку атомобилей и
узнает напрвление (direction).
Направление может быть
* DOWN,
UP, LEFT,
RIGHT и для каждого
напрвления увеличивает нужную координату
* например для того чтобы двигатся вниз нужно
увеличивать координату Y
автомобиля и проверять
* не выходит ли она за пределы клеточного
автомата
*/MainWindow::drawSystem(){
Car *car=new Car;
for(int i=0;i<carList.size();i++){
car=carList.at(i);
RoadMatrix[car->y][car->x]='1';
//удаление старого автомобиля с карты
if(calulateSpeedDelay(car)==false
&& calculateDifference(car,i)==false && car->end==false){
switch(car->direction){
case ROAD_A:
switch(RoadMatrix[car->y+1][car->x]){
case '1':
if(car->lightBuf>0){
car->lightVector.append(car->lightBuf);
car->lightBuf=0;
}
car->y++;
car->speedVector.append(11-car->defaultSpeed);
car->moveBuf++;
break;
case '2':
if(car->moveBuf>0){
car->moveVector.append(car->moveBuf);
car->moveBuf=0;
}
car->lightBuf++;
car->speedVector.append(0);
break;
case '4':
car->y+=2;
car->direction=car->turn;
break;
}
if(RoadMatrix[car->y+1][car->x]=='5'
&& (RoadMatrix[car->y][car->x-1]=='1' && RoadMatrix[car->y][car->x+1]=='1'))car->x++;
if(car->y==N-2){
car->y++;
car->end=true;
car->moveVector.append(car->moveBuf);
}
break;
case ROAD_B:
switch(RoadMatrix[car->y][car->x+1]){
case '1':
if(car->lightBuf>0){
car->lightVector.append(car->lightBuf);
car->lightBuf=0;
}
car->x++;
car->speedVector.append(11-car->defaultSpeed);
car->moveBuf++;
break;
case '2':
if(car->moveBuf>0){
car->moveVector.append(car->moveBuf);
car->moveBuf=0;
}
car->lightBuf++;
car->speedVector.append(0);
break;
case '4':
car->x+=2;
car->direction=car->turn;
break;
}
if(RoadMatrix[car->y][car->x+1]=='5'
&& (RoadMatrix[car->y-1][car->x]=='1' &&
RoadMatrix[car->y+1][car->x]=='1'))car->y++;
if(car->x==M-2){
car->x+=2;
car->end=true;
car->moveVector.append(car->moveBuf);
}
break;
case ROAD_C:
switch(RoadMatrix[car->y-1][car->x]){
case '1':
if(car->lightBuf>0){
car->lightVector.append(car->lightBuf);
car->lightBuf=0;
}
car->y--;
car->speedVector.append(11-car->defaultSpeed);
car->moveBuf++;
break;
case '2':
if(car->moveBuf>0){
car->moveVector.append(car->moveBuf);
car->moveBuf=0;
}
car->lightBuf++;
car->speedVector.append(0);
break;
case '4':
car->y-=2;
car->direction=car->turn;
break;
}
if(RoadMatrix[car->y-1][car->x]=='5'
&& (RoadMatrix[car->y][car->x-1]=='1' &&
RoadMatrix[car->y][car->x+1]=='1'))car->x++;
if(car->y==0){
car->y--;
car->end=true;
car->moveVector.append(car->moveBuf);
}
break;
case ROAD_D:
switch(RoadMatrix[car->y][car->x-1]){
case '1':
if(car->lightBuf>0){
car->lightVector.append(car->lightBuf);
car->lightBuf=0;
}
car->x--;
car->speedVector.append(11-car->defaultSpeed);
car->moveBuf++;
break;
case '2':
if(car->moveBuf>0){
car->moveVector.append(car->moveBuf);
car->moveBuf=0;
}
car->lightBuf++;
car->speedVector.append(0);
break;
case '4':
car->x-=2;
car->direction=car->turn;
break;
}
if(RoadMatrix[car->y][car->x-1]=='5'
&& (RoadMatrix[car->y-1][car->x]=='1' &&
RoadMatrix[car->y+1][car->x]=='1'))car->y++;
if(car->x==0){
car->x-=2;
car->end=true;
car->moveVector.append(car->moveBuf);
}
break;
}
}
carList.removeAt(i);
//удаляем из списка старый автомобиль
carList.insert(i,car);//
на место старого автомобиля устанавливается автомобиль с измененными
координатами
switch(car->direction){
case ROAD_A:
if(car->y>0&&car->end==false)
RoadMatrix[car->y][car->x]='5';
// рисование автомобиля на карте
break;
case ROAD_B:
if(car->x>0&&car->end==false)
RoadMatrix[car->y][car->x]='5';
// рисование автомобиля на карте
break;
case ROAD_C:
if(car->y<N&&car->end==false)
RoadMatrix[car->y][car->x]='5';
// рисование автомобиля на карте
break;
case ROAD_D:
if(car->x<M-2&&car->end==false)
RoadMatrix[car->y][car->x]='5';
// рисование автомобиля на карте
break;
}
}
TrafficLight();
}MainWindow::TrafficLightSwitcher(char
VerticalRoadLight,char HorizontalRoadLight){
for(int i=12;i<12+8;i++){
RoadMatrix[11][i]=VerticalRoadLight;
RoadMatrix[11][i+9]=VerticalRoadLight;
RoadMatrix[29][i]=VerticalRoadLight;
RoadMatrix[29][i+9]=VerticalRoadLight;
RoadMatrix[i][11]=HorizontalRoadLight;
RoadMatrix[i][29]=HorizontalRoadLight;
RoadMatrix[i+9][11]=HorizontalRoadLight;
RoadMatrix[i+9][29]=HorizontalRoadLight;
}
}MainWindow::TrafficLight(){
if(trafficlighttimer>500)trafficlighttimer=0;((trafficlighttimer*10)==trafficlightdelay[0]*10)TrafficLightSwitcher('2','4');((trafficlighttimer*10)==trafficlightdelay[1]*10)TrafficLightSwitcher('3','3');((trafficlighttimer*10)==trafficlightdelay[2]*10)TrafficLightSwitcher('4','2');
/*
switch(trafficlighttimer){
case 0:
//красный сигнал на вертикальных дорогах и зеленый на горизонтальных
TrafficLightSwitcher('2','4');
break;
case 50://
оранжевый сигнал на всех дорогах
TrafficLightSwitcher('3','3');
break;
case
60://зеленый сигнал на вертикальных дорогах и красный на горизонтальных
TrafficLightSwitcher('4','2');
break;
case 110:
TrafficLightSwitcher('3','3');
break;
case 120:
trafficlighttimer=-1;
break;
}
*/
trafficlighttimer++;
}MainWindow::drawMap(){
int color;
for(int i=0;i<N;i++)
if(clearMapFlag==true)
if(RoadMatrix[i][j]=='5')RoadMatrix[i][j]='1';
switch (RoadMatrix[i][j])
{
case '0': //
цвет границ дорог который нельяза пересекать
color=0xf5d76e;
break;
case '1':// цвет
самой дороги
color=0xa6a5950;
break;
case '2'://цвет
красного светофора
color=0xd91e18;
break;
case '3'://цвет
желтый светофора
color=0xfff7ca18;
break;
case '4'://цвет
зеленый светофора
color=0x3fc380;
break;
case '5'://цвет автомобиля
color=0xffff00;
break;
}
drawRect(j*ITEMSIZE,i*ITEMSIZE,ITEMSIZE,ITEMSIZE,color);
//нарисовать
}
clearMapFlag=false;
}
// функция автоматически вызывается когда
перерисовка окна
void
MainWindow::paintEvent(QPaintEvent *){
paint=new QPainter(this);
drawMap();
drawSystem();
}
/*
* функция создания одного автомобиля
* принимает roadNumber
это номер дороги на которой нужно установить автомобиль
* потом устанавливает по координатам и к каждому
автомобилю добавляет direction
* это направление движения
*
*/* MainWindow::generateCar(int
roadNumber){
Car *car=new Car;
switch(roadNumber){
case ROAD_A:
car->y=0; // координата Y
car->x=(rand()%6)+13;
// координа X устанавливается
случайно чтобы автомобили не пересекались во время создания
car->direction=ROAD_A; //
направление движения
car->defaultDirection=ROAD_A;
car->turn=ROAD_A;
car->path[0]="A";
car->path[1]="A";
if((rand()%2)==1){
car->turn=ROAD_D;
car->path[1]="D";
}
break;
case ROAD_B:
car->y=(rand()%6)+22;
car->x=0;
car->direction=ROAD_B;
car->defaultDirection=ROAD_B;
car->turn=ROAD_B;
car->path[0]="B";
car->path[1]="B";
if((rand()%2)==1){
car->turn=ROAD_A;
car->path[1]="A";
}
break;
case ROAD_C:
car->y=N-1;
car->x=(rand()%6)+22;
car->direction=ROAD_C;
car->defaultDirection=ROAD_C;
car->turn=ROAD_C;
car->path[0]="C";
car->path[1]="C";
if((rand()%2)==1){
car->turn=ROAD_B;
car->path[1]="B";
}
break;
case ROAD_D:
car->y=(rand()%6)+13;
car->x=M-1;
car->direction=ROAD_D;
car->defaultDirection=ROAD_D;
car->turn=ROAD_D;
car->path[0]="D";
car->path[1]="D";
if((rand()%2)==1){
car->turn=ROAD_C;
car->path[1]="C";
}
break;
}
car->defaultSpeed=(rand()%10)+1;
//установка случайной скорости
car->speed=0;
car->end=false;
car->difference=(rand()%50)+10;
car->lightBuf=0;
car->moveBuf=0;
car->enable=true;
return car;
}MainWindow::on_pushButton_4_clicked()
{
graphics=new Dialog;
graphics->setCarT(&carList);
graphics->setModal(true);
graphics->show();
}MainWindow::on_comboBox_activated(int
index)
{
switch(index){
case 0:
tm->setInterval(10);
break;
case 1:
tm->setInterval(20);
break;
case 2:
tm->setInterval(50);
break;
case 3:
tm->setInterval(80);
break;
case 4:
tm->setInterval(100);
break;
case 5:
tm->setInterval(200);
break;
case 6:
tm->setInterval(300);
break;
}
}MainWindow::on_pushButton_6_clicked()
{
if(work==true){
work=false;
clearMapFlag=true;
}
else {
work=true;
clearMapFlag=false;
}
for(int
i=0;i<carList.length();i++)
delete carList.at(i);
carList.clear();
for(int i=0;i<4;i++)
for(int
j=0;j<carThreadSize[i];j++)
carList.append(generateCar(i));
}MainWindow::on_spinBox_valueChanged(int
arg1)
{
carThreadSize[0]=arg1;
}MainWindow::on_spinBox_2_valueChanged(int
arg1)
{
carThreadSize[1]=arg1;
}MainWindow::on_spinBox_3_valueChanged(int
arg1)
{
carThreadSize[2]=arg1;
}MainWindow::on_spinBox_4_valueChanged(int
arg1)
{
carThreadSize[3]=arg1;
}MainWindow::on_spinBox_5_valueChanged(int
arg1)
{
trafficlightdelay[0]=arg1;
}MainWindow::on_spinBox_6_valueChanged(int
arg1)
{
trafficlightdelay[1]=arg1;
}MainWindow::on_spinBox_7_valueChanged(int
arg1)
{
trafficlightdelay[2]=arg1;
}