|
№
|
Фізична величина
|
Визначальне рівняння
|
Розмірність величини
|
|
|
1
|
Площа
|
|
|
|
|
2
|
Об’єм
|
|
|
|
|
3
|
Швидкість
|
|
|
|
|
4
|
Момент інерції
|
|
|
|
|
5
|
Густина
|
|
|
|
|
6
|
Питомий об’єм
|
|
|
|
|
7
|
Прискорення
|
|
|
|
|
8
|
Імпульс тіла
|
|
|
|
|
9
|
Момент імпульсу
|
|
|
|
|
10
|
Сила
|
|
|
|
|
11
|
Момент сили
|
|
|
|
|
12
|
Тиск
|
|
|
|
13
|
Робота, енергія
|
|
|
|
14
|
Потужність
|
|
|
|
|
|
|
|
|
|
|
Послідовність величин, які приведені у таблиці, не є єдиною,
що задовольняє вказаним вище умовам. Наприклад, густина (рядок 5) і момент
інерції (рядок 4) або момент сили (рядок 11) і тиск (рядок 12) можна поміняти
місцями, оскільки розмірності цих величин визначаються незалежно один від
одного.
Але густину в цій послідовності не можна поставити раніше
об’єму (рядок 2), так як густина виражається через об’єм і для визначення її
розмірності необхідно знати розмірність об'єму. Момент сили, тиск і робота
(рядок 13) не можуть бути поставлені раніше сили, оскільки для визначення їх
розмірності треба знати розмірність сили [9, c. 12].
З наведеної таблиці випливає, що розмірність будь-якої
фізичної величини в системі в загальному вигляді може бути виражена рівністю:
де цілі числа.
В системі величин механіки розмірність величини виразиться в
загальному вигляді формулою:
Тоді відповідно формули розмірності в системі та
відповідно:
навчання фізика школа
де кількість основних величин більше трьох.
З формул випливає, що розмірність величини являє собою
добуток розмірностей основних величин, зведених у відповідні степені.
Показник степені до якої зведена розмірність основної
величини, що входить до розмірність похідною величини, називається показником
розмірності фізичної величини. Як правило, показники розмірності є цілими
числами.
Деякі показники розмірності можуть виявитися рівними нулю.
Наприклад розмірності швидкості і моменту інерції в системі матимуть
відповідно вигляд:
тобто, у швидкості дорівнює нулю показник розмірності , у
моменту інерції рівний нулю показник розмірності .
Може виявитися, що всі показники розмірності деякої величини
дорівнюють нулю. Така величина називається безрозмірною. Безрозмірними
величинами є, наприклад, відносна деформація, відносна діелектрична проникність,
коефіцієнт тертя-ковзання.
Величина називається розмірною, якщо в її розмірності хоча б
одна з основних величин зведена в степінь, не рівну нулю [9, c. 13].
Поділ величин на розмірні та безрозмірні є в деякій мірі
умовним. Наприклад, кути нами було віднесено до безрозмірних величин. Проте
відомо, що кути можна вимірювати як у радіанах, відносячи довжину відповідної
дуги кола до його радіуса, так і в градусах або граданах - рівних частинах
прямого кута. Але оскільки в усіх системах виміру (системах одиниць виміру)
використовують в якості основної одиниці виміру кутів радіани, то кути дійсно
можна вважати безрозмірною величиною. Так само, якщо б в усіх системах виміру
була вибрана одна й та ж одиниця виміру довжини, то довжина теж була б
безрозмірною величиною. Проте в різних системах існують різні одиниці для
виміру довжини, що пояснюється тим фактом, що подібні фігури мають рівні кути,
але не завжди рівні розміри сторін. Отже довжина є розмірною величиною.
Тиск звичайно розглядають як розмірну величину і вимірюють його в
паскалях (1Па=1Н/м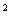 ) або в кг/см
) або в кг/см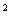 .
З іншого боку, в багатьох задачах зустрічається у вигляді параметру атмосферний
тиск, тобто тиск стовпа повітря на рівні поверхні моря (10
.
З іншого боку, в багатьох задачах зустрічається у вигляді параметру атмосферний
тиск, тобто тиск стовпа повітря на рівні поверхні моря (10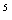 Па). Цей параметр можна використати у якості еталона і
вимірювати тиск у частинах від атмосферного тиску, тобто в атмосферах (ат).
Тиск виміряний у атмосферах є безрозмірною величиною, бо його значення не
залежить від системи одиниць виміру.
Па). Цей параметр можна використати у якості еталона і
вимірювати тиск у частинах від атмосферного тиску, тобто в атмосферах (ат).
Тиск виміряний у атмосферах є безрозмірною величиною, бо його значення не
залежить від системи одиниць виміру.
Таким чином, поняття розмірних та безрозмірних величин є відносними.
При побудові системи виміру вводиться деякий запас одиниць виміру. Тоді
величини, для яких одиниці виміру однакові в усіх системах виміру, будуть
безрозмірними. Відповідно всі інші величини будуть розмірними [4, c. 81-82].
Однак це не заважає використовувати розмірність як ефективний засіб
дослідження ряду питань метричного характеру. Зупинимося коротко на деяких з
них.
. Розмірність дозволяє визначити, як змінюється розмір похідної
величини при зміні розмірів основних величин. Якщо розмірність величини
дорівнює і довжина змінюється від до маса - від 𝑚 до і час - від до , то новий розмір
величини буде більшим від попереднього в раз, тобто
. Користуючись розмірностями фізичних величин, можна визначити, як
зміниться розмір похідною одиниці із зміною розмірів основних одиниць, через
які вона виражається, а також встановити співвідношення одиниць в різних
системах.
. Розмірності фізичних величин дозволяють виявити помилки при
розв’язуванні фізичних задач. Для розрахункової формули, яку отримали в
результаті розв’язання даної задачі слід перевірити, чи збігаються розмірності
лівої і правої частин формули. Розбіжність цих розмірностей свідчить про те, що
в ході розв’язання задачі була допущена помилка. Звичайно, збіг розмірностей ще
не означає, що задача розв’язана правильно
[9 c. 14].
. Теорія розмірностей дозволяє швидко і досить точно отримати
аналітичну залежність будь-якого процесу від основних його параметрів. Оскільки
зазвичай інтуїтивно відомо від чого залежить основна характеристика процесу і
залишається лише визначити міри впливу кожного параметра на цю характеристику.
РОЗДІЛ ІІ. МЕТОД АНАЛІЗУ РОЗМІРНОСТЕЙ ТА ЙОГО
ЗАСТОСУВАННЯ
2.1 Історія застосування аналізу
розмірностей
Аналіз розмірностей виник як результат природного поширення
на фізичні явища понять геометричної подібності, відношення і пропорції, які
були відомі ще грекам. Так, Дж. Фур'є згадував, що греки знали розмірності
площі та об'єму. Сам Фур'є вперше встановив, що існують певні основні одиниці
виміру, відносно яких кожна фізична величина має визначені розмірності, які
треба записувати як показники степенів основних одиниць виміру [7, c. 82].
Ще Галілео Галілей за допомогою аналізу розмірностей вперше
прийшов до висновку, що величина безпечного навантаження на одиницю об'єму
обернено пропорційна довжині, і передбачив багато інших класичних результатів в
механіці. Потім аналіз розмірностей застосовували Е.Д. Маріотт та І. Ньютон. До
речі саме в системі Ньютона вперше було чітко виділено три фізичні категорії:
довжина, інерція (маса) і час, які розглядалися як основні і незалежні. Вони
досі вважаються первинними поняттями, і ніякими філософськими міркуваннями не
вдалося довести, що одне з них залежить від будь-якого з двох інших. Пізніше
аналіз розмірностей з успіхом використовували в різних галузях науки [8, c. 35].
Ідеї, що лежать в основі аналізу розмірностей, по суті
очевидні і прості та пов’язані з фізичними законами (зв'язком між фізичними величинами),
вони не залежать від вибору основних одиниць виміру. З цієї ідеї на основі
простих міркувань і застосування простого математичного апарату можна отримати
важливий наслідок: функції, що виражають фізичні закономірності, повинні
володіти деякою фундаментальною властивістю, яка у математиці називається
узагальненою однорідністю або симетрією. Ця властивість дозволяє записати
шукані закономірності в безрозмірному вигляді, інваріантному відносно вибору
систем одиниць виміру, з меншим числом аргументів (вже безрозмірних) і тим
самим спростити їх знаходження [7, c. 82].
2.2 Метод аналізу розмірностей у
шкільному курсі фізики
Метод аналізу розмірностей - це метод розв’язання таких
задач, в яких точні розрахунки або вимірювання зробити важко, а часом просто
неможливо. Цей метод є суто якісним i не дає змоги зробити остаточні висновки
щодо точного вигляду рівнянь фізики. Основою даного методу є пошук показників
степенів у формулі розмірностей і на основі цього запис функціональної
залежності між ними. А, отже, при його використанні безрозмірні сталі величини
(тобто просто числа) не розглядаються. Таким чином, усі результати, одержані за
допомогою аналізу розмiрностей, є справедливими з точністю до числового
множника.
Він привабливий для учнів, оскільки дозволяє майже «з нічого»
отримувати правильні оцінки масштабів досліджуваних явищ або створювати
«портрет» експериментальної установки. Витончений і потужний інструмент, що
дозволяє вивчати непрості фізичні закономірності [3, c. 48].
При цьому принципове значення мають два моменти: вибір
системи розмірностей та перелік суттєвих величин. Обидві проблеми вирішуються
тільки на основі достатньо глибокого розуміння фізичного механізму
досліджуваного процесу. Тому для успішного застосування аналізу розмірностей необхідно
володіти певним рівнем фізичних уявлень та інтуїцією дослідника. Остаточно
вирішити, які розмірніснi сталі слід або не слід включати в рівняння, що описує
даний процес, можна лише після ретельного аналізу i значною мірою, інтуїтивно.
При цьому слід пам’ятати, що збільшення числа основних величин на одиницю
приводить до появи нової розмірної сталої.
Характерною особливістю аналізу розмірностей є те, що він не
вимагає залучення основних рівнянь задачі. Крім того, часто виникає ситуація,
коли рівняння відомі, проте аналітичне їх дослідження наштовхується на
непереборні математичні труднощі. У таких випадках головну роль відіграють
експериментальні методи дослідження, які дозволяють встановити найпростіші
факти і записати їх у вигляді деяких математичних співвідношень. Для правильної
постановки експериментів і узагальнення одержаних результатів на випадки, коли
експеримент безпосередньо не проводився, необхідно вміти складати безрозмірні
комплекси із величин, які суттєві для процесу і які для подібних явищ
залишаються незмінними. Можливість такого попереднього теоретичного аналізу
якраз і забезпечує теорія розмірностей [4, c.
78-79].
Оскільки розв’язування задач цим методом є невеликим
самостійним дослідженням. Учень на початковому етапі повинен, опираючись на
власну інтуїцію та досвід, сам проаналізувати фізичну ситуацію і вибрати
потрібні фізичні величини. Отже, цей початковий етап можна віднести до
дослідницького типу творчого завдання, оскільки під час його виконання учень
повинен дати собі відповідь на запитання: чому певна фізична величина повинна
залежати від тієї чи іншої? Окрім цього, він мусить висловити припущення
стосовно імовірної залежності шуканої фізичної величини від інших, висунути
гіпотезу для якісного пояснення цієї залежності та перевірити її. Оскільки така
послідовність дій повністю відповідає стадіям методу гіпотез у наукових
дослідженнях, то, безумовно, вона сприяє формуванню вмінь застосовувати даний
метод на практиці. Окрім цього метод розмірностей фізичних величин дає
можливість орієнтуватися у складних фізичних ситуаціях, надійно оцінювати
масштабність досліджуваних явищ, відновлювати в пам’яті забуті формули,
перевіряти правильність проміжних і кінцевих результатів при розв’язуванні
задач [5, c. 120].
Зупинимося на методичній стороні використання методу
розмірностей в шкільному курсі фізики. Так як у учнів 7-х та 8-х класів ще
немає достатньої фізичної та математичної бази для успішного застосування
методу, то на цьому етапі навчання можна лише займатися пропедевтичною роботою,
тобто систематично тренуватися у визначенні одиниць вимірювання фізичних
величин, їх найменувань, та поступово переходити до запису їх розмірностей.
Спочатку цей метод доцільно застосовувати на заняттях під час розв’язання задач
(перевіряючи кожного разу, коли в цьому є потреба, розмірність результату або
проміжних виразів), при проведенні лабораторного практикуму і лише потім
використовувати його під час пояснення нового матеріал. Якщо систематично
проводити таку пропедевтичну роботу в 7-х і 8-х класах, то подальше
застосування методу не повинно викликати в учнів серйозних труднощів, а у
вчителя - додаткових витрат часу.
Для учнів старших класів (9-11) можна запропонувати інший
шлях ознайомлення з основами обговорюваного методу та подальшого впровадження
його в навчальну практику. Цей шлях йде через гурткову роботу. Роботу такого
гуртка можна організувати наступним чином:
Заняття 1. Фізичні величини та їх характеристики. Системи
одиниць. Мета заняття - узагальнити знання учнів про системах одиниць, про
вимір фізичних величин, познайомити їх з історією введення систем одиниць
фізичних величин, показати на конкретних прикладах значення систем одиниць в
практичній діяльності людини.
Заняття 2. Розмірність похідних фізичних величин.
Однорідність фізичних формул. Заняття проводиться у формі розв’язання ряду
кількісних і якісних завдань, за допомогою яких ілюструється введення похідних
фізичних величин і визначення їх розмірностей.
Заняття 3. Метод аналізу розмірностей. Мета заняття -
ознайомити учнів з елементами методу розмірностей, показати на ряді прикладів
його можливості.
Заняття 4. Розв’язання задач методом розмірностей. Мета
заняття - закріпити вивчений матеріал, підібравши задачі з різних розділів
шкільного курсу фізики.
Заняття 5 є підсумковим, проводиться, як і попереднє у формі
заняття розв’язання задач, але з більшою самостійністю учнів, розглядаються
задачі підвищеного типу, наприклад, такі, які пропонуються на фізичних
олімпіадах.
Засвоєння учнями ідей методу розмірностей на факультативних
заняттях дозволить потім, спираючись на знання учнів, що ходять на факультатив,
ознайомити і решту учнів на звичайних уроках з можливостями цього методу.
2.3 Застосування методу розмірностей до
розв’язування задач
Для розв’язання задач методом розмірностей потрібно спиратися
на такі твердження:
. Розмірність фізичної величини може бути лише добутком
степенів розмірностей основних величин.
. Розмірності обох частин рівності, яка відображає певну
фізичну закономірність, мають бути тотожними.
. Розмірність фізичної величини співпадає з розмірністю її
одиниці [3, c. 50].
Для засвоєння методу аналізу розмірностей застосуємо його
безпосередньо при розв’язуванні задач.
Задача 1. Знайти період коливань математичного маятника.
Під математичним маятником будемо розуміти важку матеріальну
точку, яка підвішена на невагомому та недеформованому стержні, який закріплений
іншим своїм кінцем так, що може вільно обертатися в деякій вертикальній площині
навколо точки підвісу [4,
c. 93].
Рис. 2.1
Спочатку виберемо систему одиниць в якій будемо працювати. В
загальному випадку будемо користуватися міжнародна система одиниць СІ, хоча
інколи використання інших систем одиниць фізичних величин може полегшити
розв’язання задачі, що ми покажемо далі.
Наступним кроком складемо перелік фізичних величин, від яких
може залежати відповідь. Очевидно, що період коливання може залежати від
довжини маятника, його маси, прискорення вільного падіння і кутової амплітуди
коливань. Випишемо розмірності цих величин, застосовуючи основну систему
величин, тобто масу, довжину і час: - безрозмірна величина.
Оскільки одна з величин безрозмірна (кут ), то період
коливань можна представити у вигляді:
де - парна функція, яка залежить від кутової амплітуди
коливання і вигляд якої є невизначеною в рамках методу розмірностей, -
невідомі показники степенів відповідних фізичних величин.
У рівняння (2.1) замість фізичних величин підставимо їх
розмірності.
Прирівняємо степені однорідних одиниць величин:
Розв’язуючи систему рівнянь, одержимо:
Остаточна формула для знаходження періоду коливань
математичного маятника матиме вигляд:
Отже, період коливань маятника не залежить від його маси, а
залежить лише від довжини маятника, та географічної широти.
Подальші дослідження не пов`язані з аналізом розмірностей,
тому лише зауважимо, що для малих значень амплітуди може бути покладеним
рівним . Як відомо, кожен методичний прийом не є ідеальним, це відноситься і до
методу розмірностей. Разом з тим, він поєднує необхідність аналізу фізичної
залежності шуканої величини від інших величин або в теоретичному плані, або
експериментально.
Задача 2. Вивести формулу шляху рівноприскореного руху без початкової
швидкості.
Будемо шукати формулу у вигляді степеневої функції виду:
або
На підставі правила про однорідність фізичних формул можемо
написати:
або
звідки одержимо такі значення коефіцієнтів: Отже, шукана
формула має вигляд:
Постійний множник методом розмірностей не може бути
визначений, про це йшлося вище.
Задача 3. Довести, що друга космічна швидкість залежить від розмірів
планети - , прискорення вільного падіння - і не залежить від маси ракети .
Представимо функціональну залежність між даними величинами у
вигляді:
Розмірність цього співвідношення запишеться так:
де використані розмірності швидкості, прискорення, маси і
відстані.
Очевидно, що показник ступеня і тоді повинні виконуватися
наступні рівності для показників степенів:
Отже, маємо, що Таким чином, формула для другої космічної
швидкості має вигляд:
Задача 4. Оцініть гравітаційний тиск у центрі Землі.
Зрозуміло, що безпосередньо виміряти цю величину неможливо.
Розв’яжемо задачу методом розмірностей. Проаналізуємо умову й укладемо повний
перелік фізичних величин, які відбивають істотні, на нашу думку, грані
виникнення гравітаційного тиску: - тиск, який необхідно оцінити, - маса, -
радіус Землі й гравітаційна стала . Розмірності даних фізичних величин мають наступний вигляд: ,
Розв’язок задачі шукатимемо у вигляді рівності:
або
Запишемо рівність розмірностей одиниць фізичних величин:
Прирівняємо степені однорідних одиниць величин:
Розв’язуючи систему рівнянь, одержимо: . Остаточна формула
матиме вигляд:
Для оцінки тиску покладемо . Тоді:
При підстановці
відповідних величин отримаємо, що тиск у центрі Землі Па. Цікаво, що геофізики
в ході спеціальних досліджень оцінюють цей тиск як Па, як бачимо ці величини
одного порядку [3, c. 48].
Задача 5. Визначити напруженість магнітного поля нескінченно довгого соленоїда,
якщо радіус витка - , число витків на одиницю довжини - .
Природно припустити, що напруженість магнітного поля
всередині соленоїда (поза соленоїдом магнітного поля не буде, тому що силові
лінії магнітного поля, що йдуть всередині соленоїда, не виходять з нього, а
замикаються в нескінченності, де знаходяться кінці нескінченно довгого
соленоїда) буде пропорційна числу витків, що припадають на одиницю довжини і,
крім того, буде функціонально залежати від сили струму і радіуса витка. Тому
можна написати наступний вираз для напруженості магнітного поля даного
соленоїда:
Далі поступаємо за загальним правилом. Запишемо рівність
розмірностей одиниць фізичних величин:
звідки, прирівнюючи відповідні показники ступеня, отримуємо:
.
І, отже, шукана формула має наступний вигляд:
Напруженість магнітного поля всередині нескінченно довгого
соленоїда не залежить від радіуса витка R.
Задача 6. Дослідити залежність напруженості електричного поля зарядженої
нескінченної площини від густини електричного заряду і відстані від площини до
точки спостереження.
В силу нескінченної протяжності зарядженої площини, вона є
площиною симетрії, тому досить досліджувати поле по одну сторону від неї. Для
розв’язання даної задачі скористаємось системою одиниць Гауса (у цій системі а
діелектрична стала - число), включимо діелектричну сталу в сталий множник ,
будемо шукати вираз для напруженості як функцію густини зарядів - і
найкоротшої відстані від площини до точки спостереження - (із симетрії задачі
і відсутності струму уздовж поверхні випливає, що вектор напруженості
направлений перпендикулярно до цієї поверхні):
Запишемо розмірності даних величин в системі одиниць Гауса:
Запишемо рівність розмірностей одиниць фізичних величин:
Після того, як прирівняємо показники степенів відповідних
величин, отримаємо: Таким чином, напруженість поля однорідно зарядженої
нескінченної площини пропорційна густині заряду і не залежить від відстані до
площини, тобто поле однорідне і визначається за формулою:
Задача 7. Встановити залежність періоду коливань в коливальному
контурі від його індуктивності і ємності (формула Томсона).
Аналізуючи фізичний зміст завдання, припустимо, що шукана
величина може залежати від ємності - , індуктивності - і, можливо, від початкового
заряду на пластинах конденсатора - . Останнє припущення, взагалі кажучи, зайве, тому що період коливань
повинен бути характеристикою самого коливального контуру. Але це ми покажемо в
процесі розв’язання.
Функціональну залежність періоду коливань від ємності,
індуктивності і заряду запишемо так:
На підставі однорідності обох сторін цієї рівності маємо:
де
Таким чином, отримуємо наступну рівність:
Прирівнюючи показники степеня відповідних величин, отримаємо
систему чотирьох рівнянь:
Розв’язок даної системи:
Тоді шукана формула має вигляд:
Задача 8. Оцінити інтервал часу, протягом якого в озері розтане шматок
льоду у вигляді кульки з радіусом . Температура води в озері . Коефіцієнт
теплопровідності води
Аналітичний розв’язок цієї задачі (задача була запропонована
учасникам обласного турніру юних фізиків, Рівне, 2006 р.) виходить за межі
навчальної програми з математики загальноосвітньої школи. Оскільки у задачі
мова йде про оцінку інтервалу часу танення шматка льоду, її доцільно розв’язати
методом розмірностей [2,
c. 74].
Є очевидним, що час танення льоду залежить від питомої
теплоти плавлення льоду, його маси та кількості теплоти, яка надходить від
навколишнього середовища. Оскільки маса льоду визначається густиною і об’ємом,
а кількість теплоти - теплопровідністю, температурою середовища та площею
поверхні дотику, включимо у перелік величини, які визначають час танення льоду,
питому теплоту плавлення і густину льоду , радіус кульки , коефіцієнт
теплопровідності і температуру води . Розмірності даних величин мають наступний вигляд:,
Вважаючи показник степеня при рівним одиниці, розв’язок
задачі шукатимемо у вигляді рівності:
або:
де - числовий коефіцієнт, значення якого в межах методу розмірностей
є невизначеним, - невідомі показники степенів відповідних фізичних величин.
Запишемо рівність розмірностей одиниць фізичних величин:
Прирівняємо степені однорідних одиниць величин:
Розв’язуючи систему рівнянь, одержимо: . Остаточна формула
для знаходження часу танення матиме вигляд:
Для оцінки часу покладемо . Тоді:
Аналітичний шлях розв’язання цієї задачі може бути таким.
Вважатимемо, що вся кулька знаходиться у воді, температура
льоду , а процес танення льоду відбувається повільно. За цих умов миттєвий
розподіл температури у воді навколо кульки льоду буде таким, як і у
стаціонарному випадку, тобто з незмінним значенням температур на кінцях
розглядуваної ділянки (на поверхні льоду , а на значній відстані від кульки ).
Для визначення розподілу температури у просторі навколо
кульки охопимо її сферами двох радіусів і (рис. 2.2).
Рис. 2.2
Для теплового потоку, що проходить через сферу радіуса ,
можна записати:
де - радіус сфери, на поверхні якої температура води .
Температура води на поверхні сфери радіуса становить . Оскільки температури
середовищ, що відповідають положенню цих двох сфер, незмінні, то тепловий
потік, який надходить до льодяної кульки від води через сферу радіуса , є
величиною сталою. Тобто:
Останнє рівняння можна записати так:
де- деяка стала величина.
Інтегруючи диференціальне рівняння (2.11), можна записати:
де - стала інтегрування. Сталі і можна визначити,
використовуючи граничні умови: якщо , то , якщо , то . За цих умов система
рівнянь запишеться так:
Розв’язуючи систему рівнянь, одержимо:
Підставляючи ці вирази у рівняння (2.12), одержимо
співвідношення, яке описує розподіл температури у воді навколо кульки:
За умови останнє рівняння набуде вигляду:
Диференціюючи дане рівняння, визначимо градієнт температури у
воді навколо льоду:
З урахуванням останньої рівності рівняння (2.10) для
визначення кількості теплоти, яку одержує кулька від оточуючої води за інтервал
часу можна записати так:
Внаслідок поглинання цієї кількості теплоти розтане маса
льоду:
Враховуючи, що , можна записати:
де - питома теплота плавлення, - товщина шару льоду, який
розплавився. Прирівнюючи праві частини рівнянь (2.13) і (2.14), одержимо:
Звідси:
Інтегруючи останній вираз, одержимо:
Як бачимо, одержане нами співвідношення (2.15) з точністю до
числового коефіцієнта збігається з формулою (2.9), одержаною методом аналізу
розмірностей [2, c.
76-78].
Підставляючи в останню формулу значення фізичних величин, оцінимо час танення
такої кульки льоду у воді:
Задача 9. Куля випущена з початковою швидкістю в горизонтальному
напрямку на висоті від земної поверхні. Визначити дальність горизонтального
польоту кулі.
Дальність польоту кулі у цьому випадку може залежати від початкової швидкості початкової
висоти , та прискорення вільного падіння . Тоді можемо записати наступний
вираз:
Розмірність цього співвідношення запишеться так:
Оскільки маємо систему лише двох рівнянь з трьома невідомими
показниками, то два з них повинні бути виражені через третій:
Звідки:
В даній задачі чотири фізичні величини виражені через дві
основні величини, а отже повний розв’язок отримати неможливо. Кількість
фізичних змінних не можна зменшити. Але чи можливо збільшити кількість основних
одиниць виміру?
Для цього використаємо доповнення Хантлі, тобто «розкладемо»
розмірність довжини по трьох взаємно перпендикулярних напрямках. Ці основні
величини можна назвати векторними одиницями довжини, які розрізняються
індексами, тобто , , . Первісну розмірність для відмінності
будемо називати скалярною одиницею довжини і позначати як У тих випадках, коли
необхідно підкреслити векторні властивості розмірності довжини, в той час як
напрямок вектору не має значення, можна використовувати позначення . Векторна
одиниця довжини утворюється при додаванні векторів , і .
Додатковою перевагою при використанні векторних довжин в
якості основних одиниць виміру є та обставина, що замість трьох тепер маємо
п'ять основних одиниць. Отже, якщо всі вони незалежні, в загальному випадку ми
отримаємо систему з п'яти незалежних рівнянь замість звичайних трьох, що
зв'язують невідомі показники формули розмірності. Таким чином, стає можливим
виводити шляхом лише аналізу розмірностей формули фізики, які містять більше
число змінних величин і розмірних постійних величин, ніж раніше. Використовуючи
, , і, можна отримати систему з п'яти рівнянь, хоча часто лише чотири з цих
рівнянь є незалежними [8, с. 83-86].
Розглянемо знову задачу про політ кулі, яка раніше була
вирішена лише частково. І нами був отриманий наступний розв’язок:
Неважко зрозуміти, що оцінка значення залежить від
експериментально знайденої залежності, наприклад, від . Спробуємо знайти цю
залежність не виконуючи експеримент. Запишемо розмірності даних фізичних
величин з використанням векторних довжин:
Звідси:
Таким чином за допомогою нових векторних основних одиниць
аналіз розмірностей дозволяє отримати повний розв’язок даної задачі.
Задача 10. Куля випущена з початковою швидкістю і під кутом до
горизонтальної площини. Знайти дальність польоту.
Якщо не вводити векторні позначення, то розмірності таких
фізичних величин запишемо наступним чином:
Функцію запишемо у вигляді:
тоді рівняння розмірності матиме вигляд:
Кут , який є безрозмірною величиною, відсутній в цьому
рівнянні, і ми отримаємо формулу виду:
Такий результат нічого не говорить про залежність від кута .
Повторимо ті ж обчислення але використаємо векторні
властивості одиниць довжини. Як і раніше, позначимо горизонтальне і вертикальне
переміщення індексами і Замість запишемо і . Запишем функцию у вигляді:
Тоді:
Звідси:
Тому:
Якщо замість підставити 2, то одержимо повний розв’язок
задачі
Висновки
Розв’язання фізичних задач полягає у встановленні
співвідношень між початковими даними, фізичними константами й табличними
величинами, а з отриманого співвідношення шляхом математичних обчислень
отримуємо відповідь. Для розв’язання задач традиційного типу розмірність
фізичної величини використовується тільки для перевірки правильності формули
отриманого виразу. Проте розмірність фізичної величини дозволяє учням
розв’язувати задачі, зробити ще один упевнений крок у світ фізичних явищ. Метод
аналізу розмірностей дає можливість здійснювати оцінку фізичних величин:
оцінити розміри Всесвіту, осягнути світ атомів, молекул і зірок, встановити
нові співвідношення між фізичними величинами.
Метод розмірностей не є універсальним, але він практично
незамінний у тих галузях фізики, де строгий аналітичний розв’язок задач
пов'язаний із значними труднощами, а кількість параметрів, що визначають
фізичне явище, велика. У випадку, якщо виникають сумніви щодо доцільності
врахування певної величини, її можна включити до розгляду у задачі і за
виглядом кінцевої формули судити про її необхідність.
Також не слід забувати, що початковий етап застосування
методу аналізу розмірностей є фактично творчим завданням дослідницького типу,
яке сприяє формуванню логічного та творчого мислення, а також дослідницьких
навичок учня.
Отже, метод розмірностей має ряд переваг як на уроках
вивчення нового матеріалу, так і на уроках розв’язування задач, якими слід
користуватися при кожній зручній нагоді.
Список використаних джерел
1. Бриджмен П. Анализ размерностей: Пер. с англ./под
ред. акад. С.И. Вавилова. - Ижевск: НИЦ «Регулярная и хаотическая динамика»,
2001. - 148 с.
2. Галатюк Ю. М. та інші. Методи розв’язування
фізичних задач - Х.: Вид. група «Основа», 2010.- 224 с.
3. Касьяненко В. В. Деякі методи розв’язування
фізичних задач // Фізика в школах України. - Х.: Вид. група «Основа», 2011р. -
№ 15-16 (187-188). - С. 48-51.
. Основи теорії подібності та аналізу
розмірностей та їх застосування в задачах механіки: Навчальний посібник /
Упорядники: Т.Ю.Кепич та О.Г.Куценко — К.:Вища школа, 2004. - 101 с.
5. Рибалко А. В., Рибалко О. С. Класифікація методів розв’язування
навчальних фізичних задач за основними методами теоретичного пізнання у фізиці
// Фізика для фізиків. -
Рівне: РОІППО, 2011. - № 1(13). - С. 119-121.
6. Седов Л.И. Методы подобия и размерности в механике.
М.: Наука, 1987. - 221 с.
7. Тирский Г.А. Анализ размерностей //
Соросовский образовательный журнал. - М.: ISSEP, 2001г. - том 7, № 6. - С. 82-87.
8. Хантли Г. Анализ размерностей: Пер. с англ./под ред.
И.Т. Аладьева, К.В. Воскресенского. - М.: Мир, 1970. - 177 с.
9. Чертов А.Г. Единици физических величин. Учеб.
Пособие для вузов. М.: Высш. школа, 1977. - 287 с.