Математическое моделирование расчета напряжений в упругом полупространстве
Министерство образования Республики
Беларусь
Учреждение образования
"Гомельский государственный
университет имени Франциска Скорины"
Математический факультет
Кафедра вычислительной математики и
программирования
Курсовой проект
Математическое моделирование расчета
напряжений в упругом полупространстве
Исполнитель: студент группы ПМ-32
Гарягдыев А.А.
Научный руководитель: д.т.н, профессор
Можаровский В.В.
г. Гомель 2015
Реферат
Курсовой проект: 32 страниц, 1 таблица, 9 рисунков, 9 источников.
Ключевые слова: математическое моделирование, аналитические функции, упругие
градиентные материалы, деформация, напряжения.
Объект исследования: математическое моделирование методов расчета
напряжение полупространстве.
Методы исследования: деформация твердых тел под действием напряжений
Цель курсового проекта: изучить теорию, постановку задачи,
научиться владеть материалом, применять теорию на практике, и научится
составлять программу для нахождения напряжений в деформируемых твердых телах.
Содержание
Введение
. Определение напряженно-деформированного состояния упругого
ортотропного покрытия на упругом основании
. Распределение напряжений и перемещений в ортотропной полосе
на жестком основании
. Напряженно-деформированного состояния ортотропной полуплоскости
. Приближенный расчет напряженного состояния покрытия из
композиционного материала
Вывод
Список использованных источников
Приложения
Введение
Целью излагаемой работы является изучение основных теоретических
положений математического моделирования расчета напряжений в упругом
полупространстве, определение деформации твердых тел под действием силы,
изучение основных уравнений.
Раздел механики, в котором изучаются перемещения, деформации и
напряжения, возникающие в покоящихся или движущихся упругих телах под действием
нагрузки - теоретическая основа расчётов на прочность, деформируемость и устойчивость в строительном деле,
авиа и ракетостроении, машиностроении, горном деле и др. областях техники и
промышленности, а так же в физике, сейсмологии, биомеханике и др. науках.
Объектами исследования методами, являются разнообразные тела (машины,
сооружения, конструкции и их элементы, горные массивы, плотины, геологические
структуры, части живого организма и т.п.), находящиеся под действием сил,
температурных полей, радиоактивных облучений и др. воздействий. В результате
расчётов методами. Определяются допустимые нагрузки, при которых в
рассчитываемом объекте не возникают напряжения или перемещения, опасные с точки
зрения прочности или недопустимые по условиям функционирования; наиболее
целесообразные конфигурации и размеры сооружений, конструкций и их деталей;
перегрузки, возникающие при динамическом воздействии, например при прохождении
упругих волн, амплитуды и частоты колебаний конструкций или их частей и возникающие
в них динамические напряжения; усилия, при которых рассчитываемый объект теряет
устойчивость. Этими расчётами определяются так же материалы, наиболее
подходящие для изготовления проектируемого объекта, или материалы, которыми
можно заменить части организма. Методы Эффективно используются и для решения
некоторых классов задач теории пластичности (в методе последовательных
приближений).
1.
Определение напряженно-деформированного состояния упругого ортотропного
покрытия на упругом основании
Пусть на верхней границе полосы действует произвольно распределенная
нагрузка. Рассмотрим две граничные задачи.
Задача а). Ортотропная полоса жестко скреплена с упругой плоскостью.
Задача б). Ортотропная полоса свободно без трения лежит на упругой
полуплоскости.
Необходимо определить напряженно-деформированное состояние как в
ортотропной полосе, так и в упругой полуплоскости. В дальнейшем введем
следующие обозначения: индекс "I" - для полосы, "II" - для
упругой полуплоскости.
Известно, что при отсутствии массовых сил для плоских задач механики
анизотропного тела напряжения для полосы можно выразить через функцию
напряжений Эри:
 ;
; 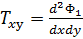 ;
; 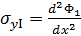 (1.1)
(1.1)
где функция напряжений 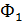 для полосы удовлетворяет бигармоническому уравнению
для полосы удовлетворяет бигармоническому уравнению
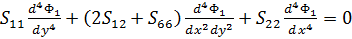 (1.2)
(1.2)
Коэффициенты Sij в уравнении (1.2) в случае плоской деформации:
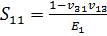 ;
; 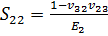 ;
;
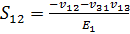 ;
; 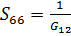 ; (1.3)
; (1.3)
плоского напряженного состояния: 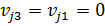 , j= 1, 2;
, j= 1, 2;
Ех =E1, Еy =E2; 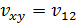
Здесь Еj, , v
__ технические постоянные материала.
, v
__ технические постоянные материала.
Примем физические соотношения для плоского ортотропного композита:
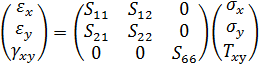 ; (1.4)
; (1.4)
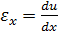 ;
; 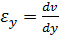 ;
; 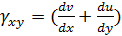
где σx, σy, Txy,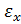 ,
,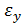 ,
,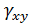 - компоненты тензора напряжений н деформаций.
- компоненты тензора напряжений н деформаций.
Соответственно для упругой полуплоскости функция напряжений 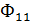 должна удовлетворять уравнению
должна удовлетворять уравнению
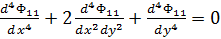 (1.5)
(1.5)
Решения уравнений (1.2) и (1.5) для слоистого композита представим
соответственно в виде
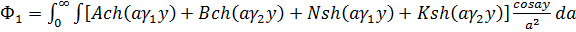 (1.6)
(1.6)
 (1.7)
(1.7)
Здесь 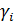 , i= 1, 2 -
действительные корни характеристического
, i= 1, 2 -
действительные корни характеристического 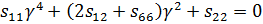 определяются по формулам
определяются по формулам
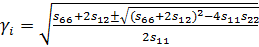 (1.8)
(1.8)
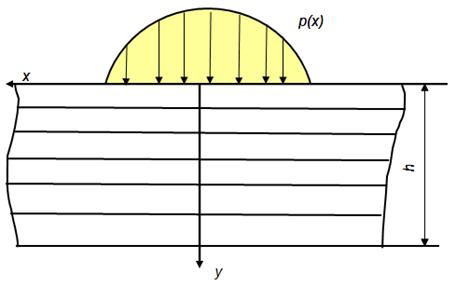
Рисунок 1.1 схема ортотропной полосы из слоистого композита
Обозначив 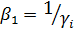 , на основании свойств корней характеристического уравнения
имеем
, на основании свойств корней характеристического уравнения
имеем
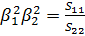 ;
; 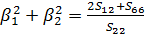
Для изотропной полосы 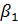 =
=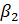 = 1- Неизвестные коэффициенты А, В, N, К, С и D определяются из граничных условий. Подставим функцию
= 1- Неизвестные коэффициенты А, В, N, К, С и D определяются из граничных условий. Подставим функцию 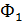 из (1.6) в (1.1) и, учитывая (1.3),
находим компоненты напряжений и перемещений для полосы:
из (1.6) в (1.1) и, учитывая (1.3),
находим компоненты напряжений и перемещений для полосы:
 ;
;
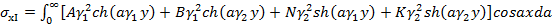
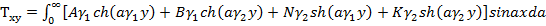
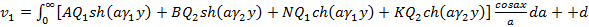 ;
;
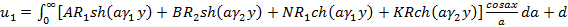 ;
;
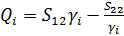 ;
; 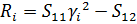 ; i=1,2; (1.9)
; i=1,2; (1.9)
- произвольная константа.
Соответственно, принимая
функцию 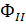 (1.7) по зависимости (1.1), а также учитывая закон
Гука, определяем компоненты напряжений и перемещений:
(1.7) по зависимости (1.1), а также учитывая закон
Гука, определяем компоненты напряжений и перемещений:
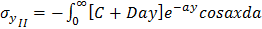 ;
;
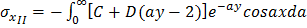 ;
;
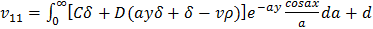 ;
;
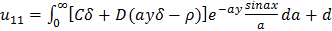
При плоской деформации
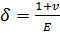 ;
; 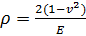 ;
;
при плоском напряженном
состоянии
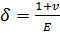 ;
; 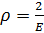 .
.
Примем граничные условия на
верхней границе полосы:
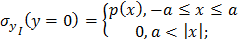 (1.11)
(1.11)
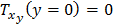
Определим граничные условия
на нижней границе у = h для задачи а):
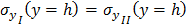 ;
; 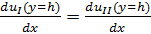 ;
;
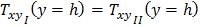 ;
; 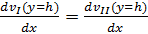 ; (1.12)
; (1.12)
для задачи б):
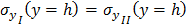 ;
; 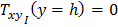 ;
; 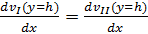 (1.13)
(1.13)
Функцию р(х), задающую
закон нагружения, представим интегралом Фурье, считая, что она четная по х,
и, используя зависимости (1.9) и (1.10), с учетом граничных условий (1.11) -
(1.13) получаем систему шести уравнений с шестью неизвестными коэффициентами.
Для задачи а):
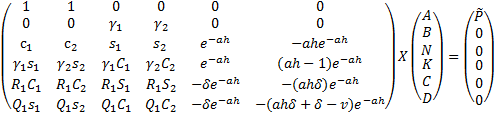 (1.14)
(1.14)
Аналогично запишем систему уравнений для задачи б):
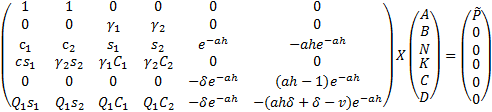 (1.15)
(1.15)
Здесь и далее введены следующие обозначения:
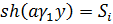 ; c
; c ;
;
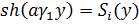 ; c
; c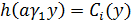 ;
;
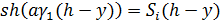 ; c
; c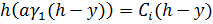 ;
;
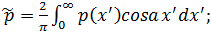 (1.16)
(1.16)
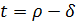 ;
; 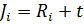 ;
; 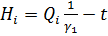 , i=1,2
, i=1,2
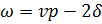
Решая систему уравнений (1.14), получаем для задачи а):
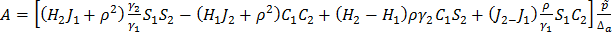 ;
; 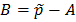 ;
;
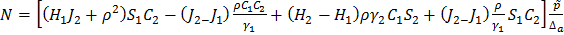 ;
;
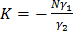 (1.17)
(1.17)
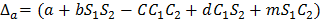 ;
;
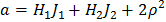 ;
; 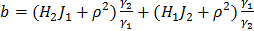 ; (1.18)
; (1.18)
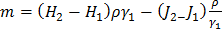
Решаем систему (1.15) для задачи б):
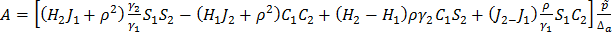 ;
; 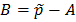 ;
; 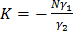
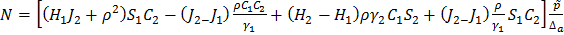
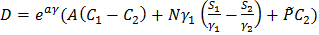 ;
;
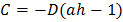 .
.
Здесь
 .
.
.
Распределение напряжений и перемещений в ортотропной полосе на жестком
основании
Рассмотрим упрощенную задачу об ортотропной полосе на жестком основании,
приняв
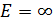 ;
; 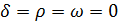 ;
; 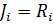 ;
; 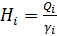 ; i = l, 2.
; i = l, 2.
Тогда системы уравнений (1.14), (1.15) значительно упрощаются.
Так, из уравнения (1.13) определяем систему коэффициентов, с помощью
которых легко находим, используя зависимости (1.9)
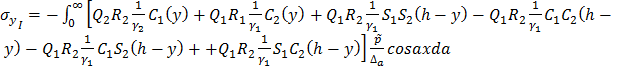 ; (2.1)
; (2.1)

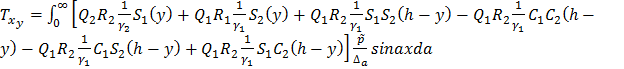
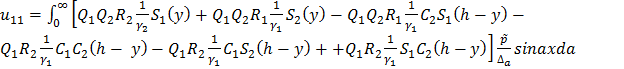 (2.2)
(2.2)
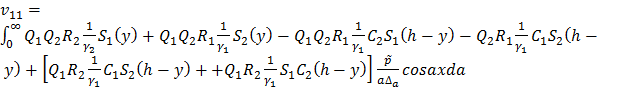 ;
;
где
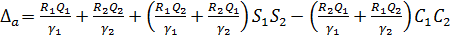
Для задачи б):
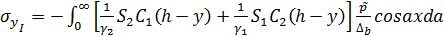 ;
;
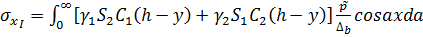 ; (2.3)
; (2.3)
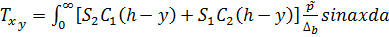 ;
;
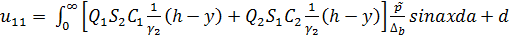 ; (2.4)
; (2.4)
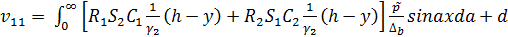 ;
;
где
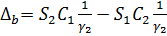
Приняв 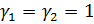 и
и 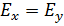 исключив неопределенность по правилу Лопиталя в зависимостях
(2.1) - (2.2), получим известные формулы для изотропной полосы на жестком
основании. Если нормальная нагрузка равномерно распределена
исключив неопределенность по правилу Лопиталя в зависимостях
(2.1) - (2.2), получим известные формулы для изотропной полосы на жестком
основании. Если нормальная нагрузка равномерно распределена
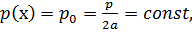 то напряжения и перемещения определяются по зависимостям
(2.1)-(2.2) при подстановке
то напряжения и перемещения определяются по зависимостям
(2.1)-(2.2) при подстановке
p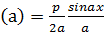 ,
,
а при действии сосредоточенной силы.
При использовании тонких композиционных покрытии необходимо знать
напряжения, возникающие на границе раздела покрытие - основание.
Определяем напряжения 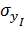 ,
,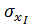 ,
, 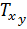 на границе раздела при p=const:
на границе раздела при p=const:
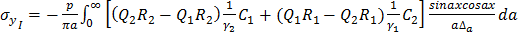 ;
;
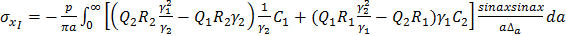 ;
;
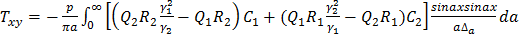
Рассмотрим конкретный пример. Задана композитная среда, представляющая
собой полосу из ортотропного углепластика с техническими постоянными E1= 11.95-104 МПа, E2 = 0,95-104 МПа, G12=0,46-104 МПа, v12=0,3, на которую на отрезке [-a, а] действует постоянная нагрузка p=const. Для упрощения распета принимаем, что основание
жесткое, выполняются граничные условия задачи а).
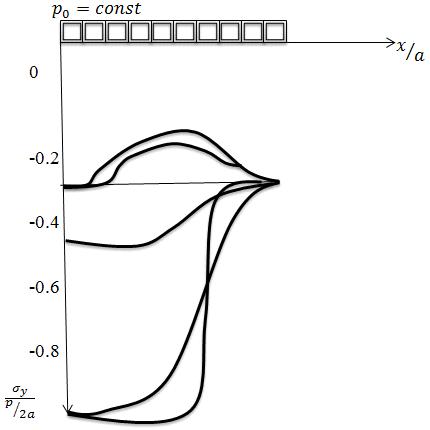
Последуем влияние направления анизотропии на распределения напряжений н
полосе. Рассмотрим изменение напряжений на границе раздела ортотропная полоса
жесткое основание. Напряжения вычисляется. по зависимости (2.3). Распределение
напряжений и этом случае показано на рисунке. 2.1 . Eсли расположить композитное покрытие на ортотропного
углепластика таким образом, чтобы ось OX совпадала с направлением, соответствующим меньшому модулю упругости, то
напряженное состояние на границе раздела сред значительно изменится.
На рисунке 3.3 также показано изменение напряжений 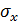 ,
, 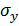 ,
, 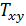 на границе раздела сред дли
изотропной полосы при E1=E2 и v
=0,3. Здесь рассмотрено плоское напряженное состояние. Анализ кривых
распределении напряжений на рисунок 2.1 позволяет сделать вывод, что
напряженное состояние существенно зависит от материала, в частности от
параметров ортотропно.
на границе раздела сред дли
изотропной полосы при E1=E2 и v
=0,3. Здесь рассмотрено плоское напряженное состояние. Анализ кривых
распределении напряжений на рисунок 2.1 позволяет сделать вывод, что
напряженное состояние существенно зависит от материала, в частности от
параметров ортотропно.
Рассмотрим влияние ширины полосы на распределение напряжений. На рисунке
показано изменение касательных напряжений на границе раздела ортотропная полоса
- основание н зависимости от a/h. Характер кривых свидетельствует о том, что существует
значительная зависимость напряжений от ширины полосы. Там же показано изменение
напряжений 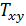 на границе при y=h
для случая изотропной полосы. Расчет по формулам (3.23) при E1=E2, v =0,3 и
на границе при y=h
для случая изотропной полосы. Расчет по формулам (3.23) при E1=E2, v =0,3 и 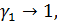 .
. 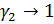 l дает идентичные результаты.
l дает идентичные результаты.
При решении контактных задач для многослойных композиционных конструкций
необходимо использовать перемещения верхней границы композита:
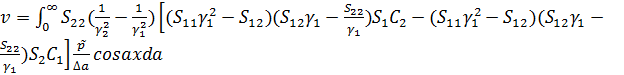 (2.5)
(2.5)
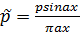
Изменение осадки поверхности для разных отношений a/h при постоянной нагрузке р0=Р/2а для
ортотропного углепластика показано. Рассмотрим некоторые асимптотические
зависимости. Если покрытие очень тонкое (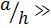 1), то формулы для перемещений (2.2)
и (2.3) легко можно преобразовать в более простые:
1), то формулы для перемещений (2.2)
и (2.3) легко можно преобразовать в более простые: 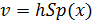 .
.
Здесь
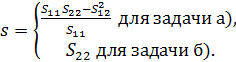
Как видно из формулы (2.3) для тонких ортотропных покрытий, выполняется
гипотеза основания Винклера. Так, если нагрузка
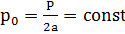
равномерно распределена па отрезке (-а, а), то для ортотропной
полосы на жестком основании имеем
 (2.6)
(2.6)
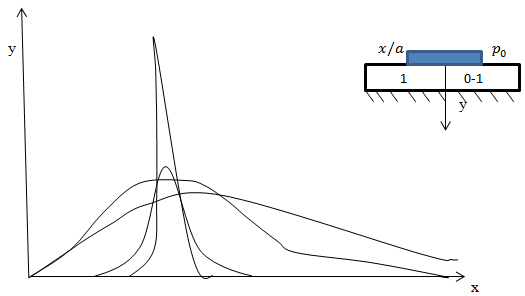
Рисунок 2.2. Изменение касательных напряжений  на границе раздела полоса - основание
в зависимости от х/а: 1 - a/h=0,75; 2-1,5; 3-5; 4 - a/h =5 (штриховая линия - для случая изотропной полосы)
на границе раздела полоса - основание
в зависимости от х/а: 1 - a/h=0,75; 2-1,5; 3-5; 4 - a/h =5 (штриховая линия - для случая изотропной полосы)
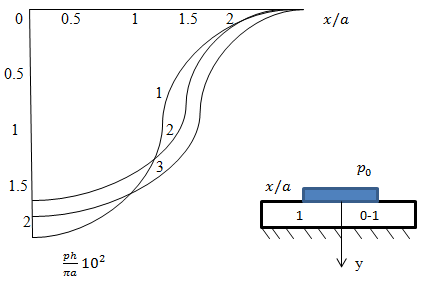
Рисунок 2.3 Изменение осадки поверхности ортотропного покрытия при личных
отношениях: 
Для углепластика с указанными выше модулями упругости определим
перемещение поверхности, которое при a/h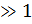 хорошо соответствует вычисленным ранее результатам,
представленным на рисунке 2.3
хорошо соответствует вычисленным ранее результатам,
представленным на рисунке 2.3
Асимптотические зависимости для определения НДС ортотропной полосы. Как и
для изотропной полосы, находим асимптотические зависимости для определения
перемещений v(x, 0) и и(х, 0) ортотропной полосы на жестком
основании при действии нормальной р(х) и касательной q(x) нагрузок на границе -а<х<а. Рассмотрим
случай h<a. После преобразований, формул, пренебрегая членами
высших порядков, получаем
задача а):
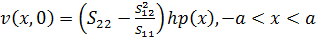
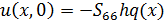 (2.7)
(2.7)
задача б):
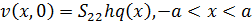
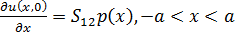
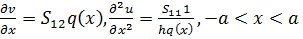 (2.8)
(2.8)
Случай h>a. Для симметричной нормальной нагрузки р (х) рассчитаем
перемещения (осадку поверхности):
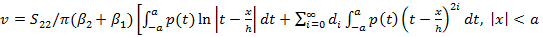 (2.9)
(2.9)
Коэффициенты di определяются численным
интегрированием, как в случае изотропной полосы:
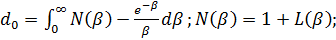 (2.10)
(2.10)
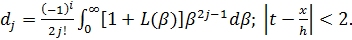
Здесь 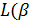 ) -подынтегральная функция, входящая в формулы для
перемещения v. Так, к
примеру, для задачи б)
) -подынтегральная функция, входящая в формулы для
перемещения v. Так, к
примеру, для задачи б)
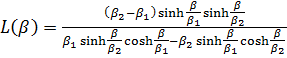
Приведем некоторые значения коэффициентов. Если ортотропная полоса
изготовлена из стеклопластика с эпоксидным связующим и координатные оси для
полосы х, у (см. рис. 3.2) совпадают с основными направлениями материала
1, 2, а модули упругости равны, Мпа: 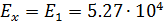 ;
; 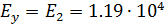 ;
; 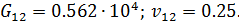 Тогда, по уравнению,
Тогда, по уравнению, 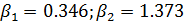 . Находим некоторые значения
коэффициентов dr. так, d0=0,236; d1=-0,471;
d2=0,136.
. Находим некоторые значения
коэффициентов dr. так, d0=0,236; d1=-0,471;
d2=0,136.
Таблица 2.1. Упругие постоянные однонаправленных композиционных
материалов
|
Материалы
|
Плотность, г/см3
|
Модули упругости,ГПа
|
Коэффициент Пуассона
|
|
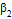
|
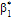
|
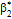
|
|
|
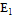
|
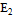
|
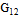
|
|
|
|
|
|
|
Эпоксидное связующее:
|
1,99
|
52,7
|
11,9
|
5,62
|
0,25
|
0,34
|
1,37
|
0,33
|
1,46
|
|
Стеклянные волокна
|
1,385
|
80,8
|
4,21
|
2,1
|
0,30
|
0,16
|
1,4
|
0,23
|
1,42
|
|
Высокопрочные углеродные
волокна
|
1,55
|
10,5
|
5,62
|
0,27
|
0,22
|
1,33
|
0,16
|
1,36
|
|
Высокомодульные углеродные
волокна
|
1,63
|
194
|
7,72
|
4,21
|
0,30
|
0,15
|
1,34
|
0,15
|
1,35
|
|
Сверхвысокомодульные
углеродные волокна
|
1,61
|
316
|
6,32
|
4,21
|
0,26
|
0,11
|
1,21
|
0,12
|
1,22
|
|
Борные волокна
|
2,08
|
210,5
|
21
|
4,92
|
0,21
|
0,16
|
2,0
|
0,15
|
2,06
|
|
Борные волокна-алюминий
|
2,71
|
232
|
147,5
|
49,2
|
0,23
|
0,14
|
5,45
|
0,14
|
5,47
|
Примечания. Модули упругости взяты иэ работы [174]. Приближенные
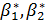 вычислялись по формулам
вычислялись по формулам

Приведенные данные упругих постоянных соответствуют 60%-ному объемному
содержанию волокон.
Принимаем модули упругости, МПа, для ортотропного материала с углеродным
волокном: 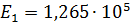 ;
; 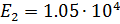 ;
; 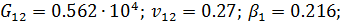
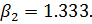 Тогда
Тогда
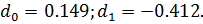 . Для некоторых ортотропных пластиков значения рь р 2
приведены в табл. 2.1.
. Для некоторых ортотропных пластиков значения рь р 2
приведены в табл. 2.1.
3.
Напряженно-деформированного состояния ортотропной полуплоскости
Рассмотрим некоторые частные случаи. Используя формулы, можно найти
напряжения и перемещения ортотропной полуплоскости при 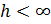 . Вычислим перемещение, определенное
по зависимости при
. Вычислим перемещение, определенное
по зависимости при 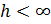 . для единичной сосредоточенной силы
. для единичной сосредоточенной силы 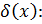
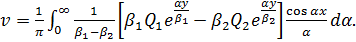
Вычислив определенные интегралы, входящие в выражения dv/dx:
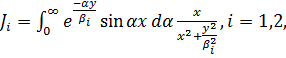
Получаем
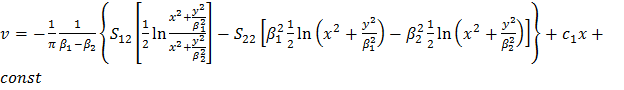 (3.1)
(3.1)
Определив предел v(x, у) при 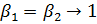 , предварительно сделав замену
упругих постоянных
, предварительно сделав замену
упругих постоянных
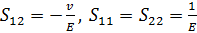 ,
,
найдем перемещение упругой изотропной полуплоскости для плоского
напряженного состояния:
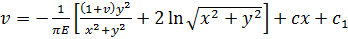 (3.2)
(3.2)
Для плоской деформации в зависимостях для перемещений нужно заменить v и Е соответственно на  и
и 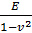 . Для определения напряжения ау
для ортотропной плоскости из при
. Для определения напряжения ау
для ортотропной плоскости из при 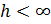 . необходимо вычислить интегралы вида
. необходимо вычислить интегралы вида
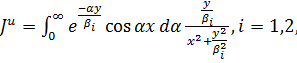
Тогда легко определить напряжение аа для ортотропной
полуплоскости:
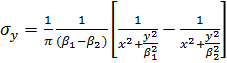 (3.3)
(3.3)
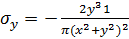
Найдем остальные компоненты тензора напряжений для ортотропной
полуплоскости:
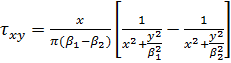
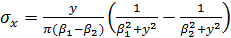
определим перемещение:
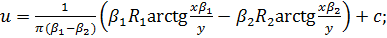
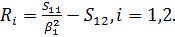
В пределе при 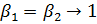 для изотропной полуплоскости имеем
для изотропной полуплоскости имеем

 (3.4)
(3.4)
В частном случае, когда модули упругости в направлении осей х и у
равны, т. е. 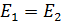 ,
из свойств корней характеристического уравнения имеем
,
из свойств корней характеристического уравнения имеем
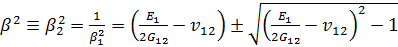
Определим составляющие тензора напряжений в точке х, у для единичной
сосредоточенной силы:
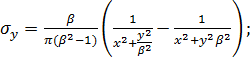
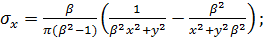
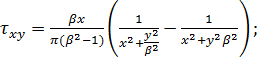
Эти зависимости совпадают с формулами, полученными В. Вайскопфом для
среды с модулем G, намного меньшим модуля сдвига
изотропной среды.
Построим функции Грина для задачи об ортотропной полуплоскости,
нагруженной силами, перпендикулярными к границе L1
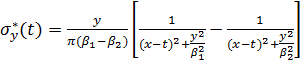
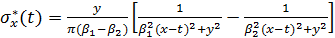
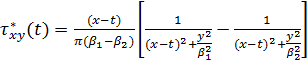 . (3.5)
. (3.5)
Например, если на границе y=0
действует нагрузка на отрезке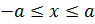 , то
, то
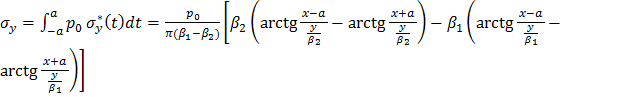 .
.
Для остальных напряжений имеем
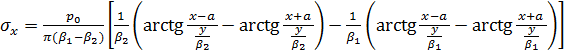
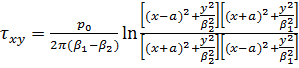 (3.6)
(3.6)
4.
Приближенный расчет напряженного состояния покрытия из композиционного
материала
упругий ортотропный покрытие напряжение
Исследования слоистого композита, представляющего собой высокомодульные
параллельные волокна в податливой полимерной матрице, показали, что материал
обладает достаточно большой жесткостью в одном направлении. Расчет композитов
из такого материала был рассмотрен Спенсером и приведен в работе для
полуплоскости при использовании так называемой концепции пограничных слоев.
Направление действия внешнего усилия совпадало с расположением параллельного
волокна композита. В соответствии с этим модуль упругости в направлении волокна
значительно превышал модули упругости в других направлениях. Использование
данной концепции для такой анизотропной среды, как композит, упрощается
решением плоских задач, так как упругие составляющие перемещений описываются
гармонической функцией нахождение которой не представляет трудностей.
Применительно к слоистым средам примем, что направление наибольшей жесткости
соответствует координате у Рассмотрим использование зависимостей общей теории
анизотропного тела в случае 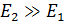 Из свойств корней ш р характеристического уравнения следует,
что если значение
Из свойств корней ш р характеристического уравнения следует,
что если значение 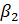 достаточно мало, можно принять его равным пулю (
достаточно мало, можно принять его равным пулю (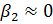 ), при этом
), при этом
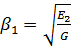
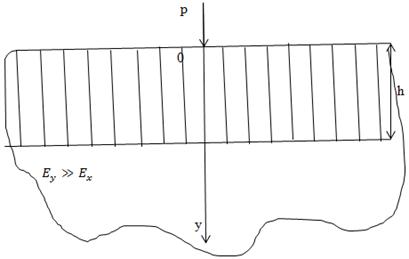
Рисунок 4.1 Действие сосредоточенной силы на ортотропную полосу
Исследуем напряженное состояние полосы из композитного материала,
свободно лежащей на жестком основании, при действии сосредоточенной силы 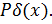 Армирующие жесткие волокна материала
параллельны и совпадают с направлением у. Компоненты тензора напряжений находим
с помощью выражения как предельный случай при
Армирующие жесткие волокна материала
параллельны и совпадают с направлением у. Компоненты тензора напряжений находим
с помощью выражения как предельный случай при 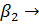 0. После несложных преобразований
получаем достаточно простые формулы, не содержащие интегралов:
0. После несложных преобразований
получаем достаточно простые формулы, не содержащие интегралов:
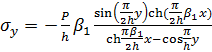 (4.1)
(4.1)
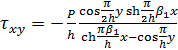 (4.2)
(4.2)
Найдем нормальное перемещение
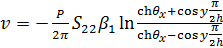 (4.3)
(4.3)
где 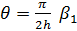 .
.
Определим изменение напряженного состояния полосы в предельном случае при
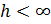 :
:
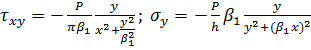
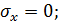 (4.4)
(4.4)
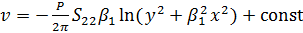 ;
;
Напряжения совпадают с зависимостями, приведенными в работе для
полуплоскости. Зависимости можно получить по формулам. Таким образом, для
слоистой среды рассматриваемого вида при произвольном нагруженные нормальными
усилиями на границе формулы, представляют собой функции Грина, и напряженное
состояние описывается выражениями
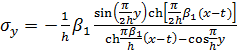
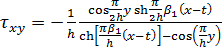 (4.5)
(4.5)
Рассмотрим следующий пример: полоса из углепластика лежит на жестком
основании. Волокна расположены по нормали к нему, а модуль упругости,
относящийся к оси у, совпадающей с направлением волокна, имеет следующее
значение: 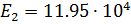 МПа; соответственно модуль упругости, относящийся к оси х,
ортогональной направлению волокна:
МПа; соответственно модуль упругости, относящийся к оси х,
ортогональной направлению волокна: 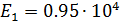 МПа; модуль сдвига G=0,46-104 МПа; v12=0,3. На границе полосы действует
сосредоточенная сила Р. Определим напряженно-деформированное состояние полосы.
Так как
МПа; модуль сдвига G=0,46-104 МПа; v12=0,3. На границе полосы действует
сосредоточенная сила Р. Определим напряженно-деформированное состояние полосы.
Так как 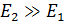 то, применяя теорию пограничных
слоев, записываем:
то, применяя теорию пограничных
слоев, записываем:
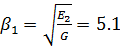
Найдем распределение нормальных напряжений 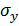 на границе раздела полоса из
композита - жесткое основание. При y=h имеем
на границе раздела полоса из
композита - жесткое основание. При y=h имеем
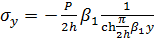
Определим максимальную величину 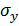 при х =0:
при х =0:
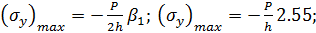
Так как изменение напряжений ау на границе раздела полоса -
основание описывается аналитической зависимостью, то, естественно, параметр 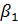 можно подобрать таким образов, что
максимальное напряжение изотропной и ортотропной полос совпадает. Из этого
условия имеем
можно подобрать таким образов, что
максимальное напряжение изотропной и ортотропной полос совпадает. Из этого
условия имеем 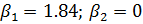 . Тогда для приближенного вычисления напряжений в изотропной
полосе имеем
. Тогда для приближенного вычисления напряжений в изотропной
полосе имеем
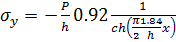 (4.6)
(4.6)
Выполнение условия равновесия 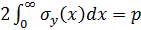 легко проверяется при использовании значения
интеграла
легко проверяется при использовании значения
интеграла
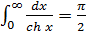
Вывод
В процессе написания курсовой работы мною была изучена теория упругости,
основные уравнения упругости, решения задач, и основные теоретические выкладки
по определению напряжений применять теорию на практике, и научится составлять
программу для нахождения напряжений в деформируемых твердых телах. Были
разработаны программы на С++ в среде Embarcadero.
Список
использованных источников
1. Лехницкий С.Г. "Теория упругости анизотропного тела".
- М.: Наука, 1977. - 416 с.
2. Галин Н.А. "Контактные задачи теории упругости
и вязкоупругости". - М.: Наука, 1980.
. Горячева И.Г. "Механика контактного
взаимодействия". - М.: Наука, 2001.
. Уфлянд Я.С. "Интегральные преобразования в
задачах теории упругости". - Л., 1967.
. Лурье А.И. "Теория упругости". - М., 1970.
. Ворович И.И., Александров В.М., Бабешко В.А.
"Неклассические смешанные задачитеории упругости". - М., 1974.
. Джонсон "Механика контактного
взаимодействия". 1989.
. Александров А.В. "Основы теории
упругости". - М., 1990.
. Можаровский В.В. и Старжинский "прикладная
механика слоистых тел из композитов", 1988
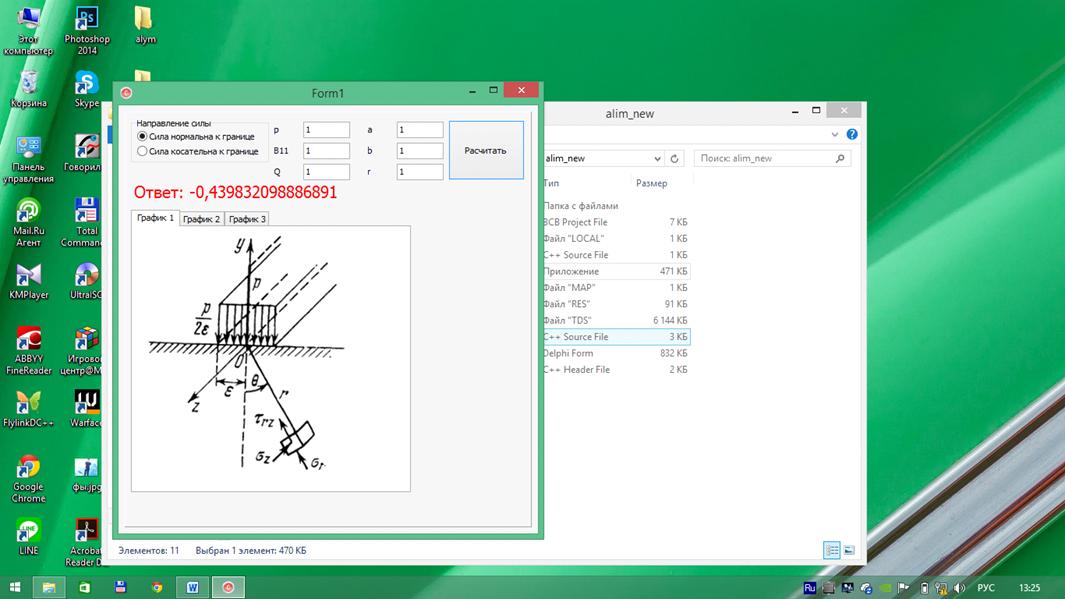
Приложение 1
//---------------------------------------------------------------------------
#include <vcl.h>
#pragma hdrstop
#include <Math.h>
#include <iostream>
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"= 1, B11 = 2, B12=1, a=1,
x=2, r=1,y=2;F(double q){q; }get_answer(int type){answer = 1;(type == 0) {
answer =
p/(M_PI*(B11-B12))*((1/B12*(1/(tan((x-a)/y/B12))-1/(tan((x+a)/y/B12))))-(1/B11*(1/(tan((x-a)/y/B11))-1/(tan((x+a)/y/B11)))));
} else {
answer =
p/(2*M_PI*(B11-B12))*log((pow((x-a),2)+pow(y,2)/pow(B12,2))*(pow((x+a),2)+pow(y,2)/pow(B11,2))/((pow((x+a),2)+pow(y,2)/pow(B12,2))*(pow((x-a),2)+pow(y,2)/pow(B11,2))));
}answer;
}*Form1;
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
: TForm(Owner){->Edit2->Text = 2;->Edit5->Text =
1;->Edit3->Text = 1;->Edit4->Text = 2;->Edit6->Text =
2;->Edit1->Text = 1; }
//---------------------------------------------------------------------------__fastcall
TForm1::Button1Click(TObject *Sender){power_type = Form1->RadioGroup1->ItemIndex;=
Form1->Edit1->Text.ToDouble();= Form1->Edit2->Text.ToDouble();=
Form1->Edit5->Text.ToDouble();= Form1->Edit3->Text.ToDouble();=
Form1->Edit4->Text.ToDouble();= Form1->Edit6->Text.ToDouble();s = "Ответ:
";(power_type==0){= "Ответ: ";+= get_answer(power_type);->Label7->Caption
= s;->Label7->Visible = true;
}else {->Label7->Caption = get_answer(power_type);=
"Ответ: ";+= get_answer(power_type);->Label7->Caption =
s;->Label7->Visible = true;
} }
//---------------------------------------------------------------------------__fastcall
TForm1::RadioGroup1Click(TObject *Sender){power_type =
Form1->RadioGroup1->ItemIndex;(power_type==1){->Label1->Caption =
"P";->Label4->Caption = "B";
}else {->Label1->Caption =
"p";->Label4->Caption = "b";
} }
//---------------------------------------------------------------------------

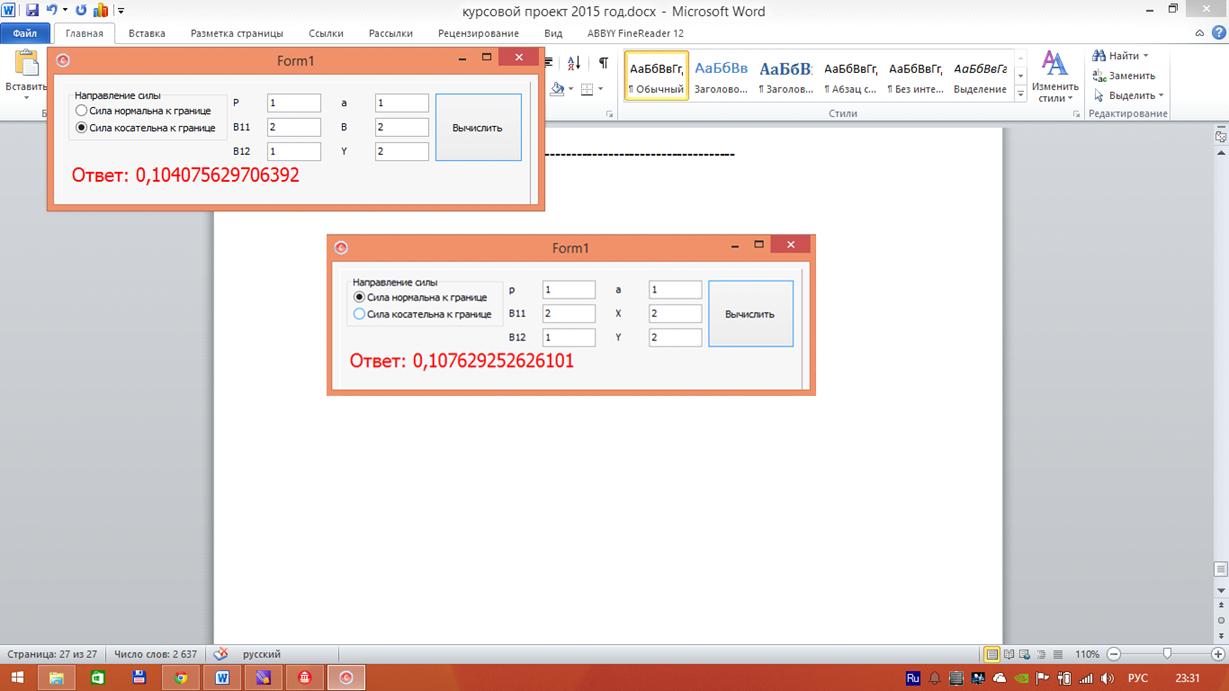
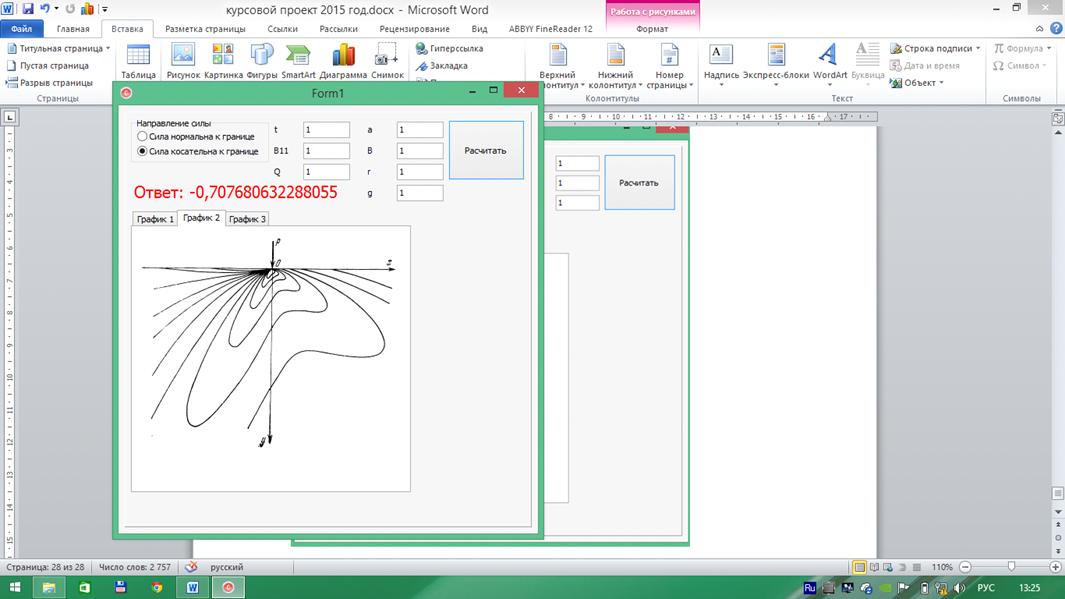
Приложение 2
//---------------------------------------------------------------------------
#include <vcl.h>
#pragma hdrstop
#include <Math.h>
#include <iostream>
#include "Unit1.h"
//---------------------------------------------------------------------------
#pragma package(smart_init)
#pragma resource "*.dfm"= 1, B11 = 1, Q=1, a=1,
b=1, r=1,, g, B_t;F(double q){q;
}get_answer(int type){answer = 1;(type == 0) {= -
(p*B11/M_PI)*(a*sin(Q)+b*cos(Q))/(r*F(Q));
} else {= - (t*B11/M_PI)*((B_t+g)*sin(Q)+a*cos(Q))/(r*F(Q));
}answer;
}*Form1;
//---------------------------------------------------------------------------
__fastcall TForm1::TForm1(TComponent* Owner)
: TForm(Owner){->Edit2->Text = 1;->Edit5->Text =
1;->Edit3->Text = 1;->Edit4->Text = 1;->Edit6->Text =
1;->Edit1->Text = 1;->Edit7->Text = 1;
}
//---------------------------------------------------------------------------__fastcall
TForm1::Button1Click(TObject *Sender){power_type =
Form1->RadioGroup1->ItemIndex;= Form1->Edit1->Text.ToDouble();=
Form1->Edit2->Text.ToDouble();= Form1->Edit5->Text.ToDouble();=
Form1->Edit3->Text.ToDouble();= Form1->Edit4->Text.ToDouble();=
Form1->Edit6->Text.ToDouble();= Form1->Edit1->Text.ToDouble();_t =
Form1->Edit4->Text.ToDouble();= Form1->Edit7->Text.ToDouble();s =
"Ответ: ";(power_type==0){=
"Ответ: ";+=
get_answer(power_type);->Label7->Caption = s;->Label7->Visible =
true;
}else {->Label7->Caption = get_answer(power_type);=
"Ответ: ";+=
get_answer(power_type);->Label7->Caption = s;->Label7->Visible =
true;
}->PageControl1->Visible = true;
}
//---------------------------------------------------------------------------__fastcall
TForm1::RadioGroup1Click(TObject *Sender){power_type =
Form1->RadioGroup1->ItemIndex;(power_type==1){->Label1->Caption =
"t";->Label4->Caption = "B";->Label8->Visible =
true;->Edit7->Visible = true;
}else {->Label1->Caption = "p";->Label4->Caption
= "b";->Label8->Visible = false;->Edit7->Visible = false;
}
}
//---------------------------------------------------------------------------