Система автоматического регулирования температуры сушильного шкафа
Федеральное агентство по образованию
ГОУВПО « Тульский государственный
университет»
Кафедра автоматики и телемеханики
Пояснительная записка к курсовому
проекту
по курсу «Моделирование систем
управления»
Система автоматического регулирования
температуры сушильного шкафа
Выполнил студент группы 220171 Медведев А.П.
Проверил ассистент кафедры АТМ Ермаков А.С.
Тула 2010 г.
Содержание
Введение
. Принцип действия САР температуры сушильного шкафа
. Сигнальный граф САР температуры сушильного шкафа
. Система дифференциальных уравнений
. Линеаризация системы уравнений
. Операторная форма записи системы линейных дифференциальных
уравнений. Передаточные функции связей
. Взвешенный сигнальный граф и структурная схема линейной
математической модели САУ
. Передаточные функции САР
Заключение
Список используемых источников
Введение
Нормальный ход различных технологических и производственных процессов
может быть обеспечен лишь тогда, когда те или иные величины, характеризующие
эти процессы, удовлетворяют определенным условиям. Необходимость поддержания
постоянства той или иной величины или изменения ее в соответствии с каким-либо
законом возникает в самых разнообразных отраслях техники. Сами по себе объекты,
в которых протекают те или иные рабочие процессы, часто не обеспечивают их
нормального хода, иначе говоря, сами по себе объекты не могут устранить
отклонения режима от заданного, вызываемого различными причинами. Поэтому такие
объекты снабжаются управляющим или регулирующим органом, воздействием на который
можно изменить режим их работы, а значит, нужным образом управлять процессом.
Создание условий, обеспечивающих требуемое протекание процесса, т.е.
подержание необходимого режима работы, называется управлением.
Управление может быть ручным и автоматическим. При ручном управлении
воздействие на управляющий орган осуществляет человек, наблюдающий за ходом
процесса или, точнее, за отклонением процесса от требуемого, и воздействующий в
зависимости от этого отклонения на управляющий орган так, чтобы процесс
удовлетворял заданным требованиям.
При автоматическом управлении воздействие на управляющий орган
осуществляет специальное управляющее устройство. В частности, в простейшем
случае задача управления может состоять в поддержании постоянства тех или иных
величин, характеризующих рабочий процесс. В этом случае процесс управления
называют регулированием, а управляющее устройство - автоматическим регулятором.
Данная САР представляет собой систему по поддержанию на заданном уровне
температуры воздуха внутри шкафа.
1.
Принцип действия САР температуры сушильного шкафа
Рассмотрим принципиальную схему САР температуры сушильного шкафа (рис.
1).
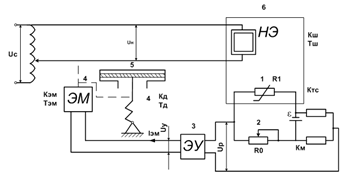
Рисунок 1 - Принципиальная схема САР температуры сушильного шкафа
Заметим, что системы автоматического управления отличаются друг от друга
объектами управления, физической природой управляемых и регулируемых величин,
конструкциями элементов управляющих устройств, но, тем не менее, можно выделить
несколько типов элементов, каждый из которых характеризуется определенной
функцией в составе системы, а взаимосвязь этих элементов отражает
функциональная схема системы, общий вид которой приведен на рис.2.
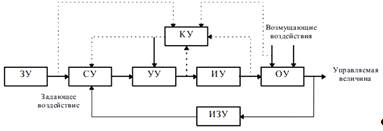
Рисунок 2 - Общий вид функциональной схемы САР
Рассмотрим назначение и особенности элементов функциональной схемы и
найдем соответствия с принципиальной схемой исследуемой САР напряжения генератора
постоянного тока.
1) Объект
управления (ОУ). Вследствие большого разнообразия объектов управления
природа управляемых величин различна, поэтому для осуществления автоматического
управления необходимо хорошо знать свойства и особенности объекта, для
определения которых следует использовать знания из специальных дисциплин
соответствующих отраслей техники. В нашем случае управляемой величиной является
температура воздуха 
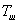 в шкафу,
а объектом управления - сушильный шкаф.
в шкафу,
а объектом управления - сушильный шкаф.
) Измерительное
устройство (ИЗУ). Его назначением является измерение действительного
значения управляемой величины. Всякое измерительное устройство является
преобразователем управляющей величины в величину, вообще говоря, иной
физической природы, удобную для дальнейшего использования. Для нашей САР
измерительным устройством является терморезистор 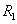 ,
сопротивление которого зависит от температуры воздуха в шкафу.
,
сопротивление которого зависит от температуры воздуха в шкафу.
) Задающее
устройство (ЗУ). Оно предназначено для установления необходимого значения
управляемой величины и как и измерительное устройство является
преобразователем. Величина на выходе задающего устройства должна быть
одинаковой природы с величиной на выходе измерительного устройства. Задающим
устройством в системе является реостат 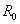 ,
который, как и терморезистор, включен в одно из плеч моста сопротивлений.
,
который, как и терморезистор, включен в одно из плеч моста сопротивлений.
) Сравнивающее
устройство (СУ). Оно служит для сопоставления значения управляемой величины
с ее заданным значением и, следовательно, для выявления отклонения управляемой
величины от заданного значения. Сравнивающим устройством в САР температуры
сушильного шкафа является мост сопротивлений, который выдает ошибку
рассогласования между реостатом и терморезистором в виде напряжения
рассогласования 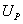 .
.
) Усилительное
устройство (УУ). Данный элемент функциональной схемы предназначен для
усиления мощности сигналов ошибки. Оно управляет энергией, поступающей от
постороннего источника. В данной системе электронный усилитель (ЭУ) играет роль
усилительного устройства, на выходе которого получаем 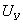 .
.
) Исполнительное
устройство (ИУ). Назначением исполнительного устройства является
воздействие на управляющий орган объекта. В системе регулирования температуры,
коей является наша система, исполнительное устройство представляет собой
электромагнит и демпфер.
) Корректирующее
устройство (КУ). Оно применяется для изменения свойств САУ в нужном направлении.
Часто корректирующие устройства используются для формирования управляющих
воздействий, зависящих от задающих и возмущающих воздействий. В нашей системе
такое устройство отсутствует.
Рассмотрев
назначение и особенности элементов функциональной схемы и найдя соответствия с
принципиальной схемой исследуемой САР температуры сушильного шкафа, также
определим все возмущающие воздействия, связывающие систему с вешней средой и не
зависящие от процессов в системе. К ним можно отнести ε - напряжение питания моста сопротивлений, 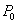 - давление воздуха, окружающего демпфер,
- давление воздуха, окружающего демпфер, 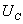 - напряжение питания системы,
- напряжение питания системы, 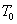 - температура окружающей среды.
- температура окружающей среды.
Рассмотрим
принцип действия САР температуры сушильного шкафа. От температуры 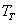 терморезистора
терморезистора
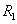 зависит его сопротивление. Терморезистор
зависит его сопротивление. Терморезистор 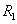 включен в одно из плеч измерительного моста. В другое
плечо включен переменный резистор
включен в одно из плеч измерительного моста. В другое
плечо включен переменный резистор 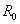 , с
помощью которого задается требуемая температура воздуха в шкафу. Измерительный
мост сравнивает величину сопротивления датчика
, с
помощью которого задается требуемая температура воздуха в шкафу. Измерительный
мост сравнивает величину сопротивления датчика 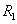 со
значением сопротивлений других плеч и выдает сигнал ошибки в виде напряжения
разбаланса моста
со
значением сопротивлений других плеч и выдает сигнал ошибки в виде напряжения
разбаланса моста 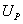 , которое подается на электронный усилитель (ЭУ). На
выходе усилителя образуется напряжение
, которое подается на электронный усилитель (ЭУ). На
выходе усилителя образуется напряжение 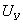 , которое
создает ток возбуждения электромагнита
, которое
создает ток возбуждения электромагнита 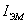 . Ток
приводит к появлению магнитного потока
. Ток
приводит к появлению магнитного потока 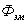 ,
который, в свою очередь, создает усилие
,
который, в свою очередь, создает усилие 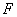 ,
втягивающее стержень внутрь. Перемещение X рычага и поршня демпфера зависит
только от разности входной силы F и силы сопротивления F1 сжимаемого в цилиндре
воздуха. Связь между перемещением и разностью этих сил определяется свойствами
пружины. Сила сопротивления воздуха над поршнем зависит от разности давления в
цилиндре
,
втягивающее стержень внутрь. Перемещение X рычага и поршня демпфера зависит
только от разности входной силы F и силы сопротивления F1 сжимаемого в цилиндре
воздуха. Связь между перемещением и разностью этих сил определяется свойствами
пружины. Сила сопротивления воздуха над поршнем зависит от разности давления в
цилиндре 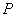 и давления окружающего демпфер воздуха
и давления окружающего демпфер воздуха 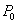 . Это давление будем рассматривать как внешнее
возмущение. Давление в цилиндре P определяется двумя факторами: массой воздуха
в цилиндре
. Это давление будем рассматривать как внешнее
возмущение. Давление в цилиндре P определяется двумя факторами: массой воздуха
в цилиндре 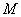 и объемом цилиндра
и объемом цилиндра 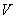 при
данном положении поршня. Масса воздуха в цилиндре
при
данном положении поршня. Масса воздуха в цилиндре 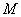 не является постоянной величиной, поскольку приток и
отток воздуха через отверстие поршня зависит от разности давлений в цилиндре
не является постоянной величиной, поскольку приток и
отток воздуха через отверстие поршня зависит от разности давлений в цилиндре 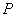 и вне его
и вне его 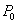 . Объем
цилиндра
. Объем
цилиндра 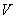 определяется текущим положением поршня, т.е.
перемещением
определяется текущим положением поршня, т.е.
перемещением 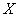 , которое влияет на напряжение на нагревательном
элементе
, которое влияет на напряжение на нагревательном
элементе 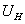 . Это напряжение создается также напряжением сети
. Это напряжение создается также напряжением сети 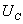 . От величины напряжения на нагревательном элементе
. От величины напряжения на нагревательном элементе 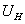 будет зависеть электрическая мощность
будет зависеть электрическая мощность 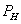 , выделяемая на нагревательном элементе. В свою
очередь, эта мощность в виде теплового потока Qн идёт на изменение температуры
, выделяемая на нагревательном элементе. В свою
очередь, эта мощность в виде теплового потока Qн идёт на изменение температуры 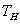 нагревательного
элемента. Скорость перехода тепла от нагревательного элемента к воздуху
определяется разностью текущих температур нагревательного элемента и
температуры воздуха - тепловой поток
нагревательного
элемента. Скорость перехода тепла от нагревательного элемента к воздуху
определяется разностью текущих температур нагревательного элемента и
температуры воздуха - тепловой поток 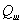 .
Тепловой поток
.
Тепловой поток 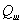 расходуется на изменение температуры воздуха в шкафу
расходуется на изменение температуры воздуха в шкафу 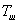 . Эта температура будет одинаковая во всех точках в
силу идеализации (будем считать, что воздух в шкафу идеально перемешивается и
его температура во всех точках одинакова) и зависит от разности тепловых
потоков
. Эта температура будет одинаковая во всех точках в
силу идеализации (будем считать, что воздух в шкафу идеально перемешивается и
его температура во всех точках одинакова) и зависит от разности тепловых
потоков 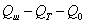 , где
, где 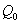 -
тепловой поток, который выделяется через стенки шкафа в окружающую среду, а
-
тепловой поток, который выделяется через стенки шкафа в окружающую среду, а 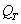 - тепловой поток, который расходуется на нагревание
терморезистора. В свою очередь, скорость рассеивания тепла в окружающую среды
зависит от разности температур в шкафу
- тепловой поток, который расходуется на нагревание
терморезистора. В свою очередь, скорость рассеивания тепла в окружающую среды
зависит от разности температур в шкафу 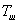 и окружающей
среды
и окружающей
среды 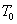 . Аналогично скорость перехода тепла от воздуха внутри
шкафа к терморезистору
. Аналогично скорость перехода тепла от воздуха внутри
шкафа к терморезистору 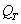 определяется разностью температур воздуха внутри
шкафа
определяется разностью температур воздуха внутри
шкафа 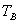 и терморезистора
и терморезистора 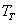 .
Наконец, температура терморезистора
.
Наконец, температура терморезистора 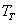 зависит
от величины теплового потока
зависит
от величины теплового потока 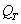 .
.
Таким
образом, осуществляется регулирование температуры сушильного шкафа. Данная
система является статической, т.к. теплота из шкафа непрерывно рассеивается в
окружающее пространство. Следовательно, нагревательный элемент даже в
установившемся режиме должен выделять теплоту, компенсирующую это рассеивание.
Рассмотрев
принцип действия САР температуры сушильного шкафа и определив элементы
функциональной схемы, можно непосредственно построить функциональную схему
нашей системы (рис. 3).
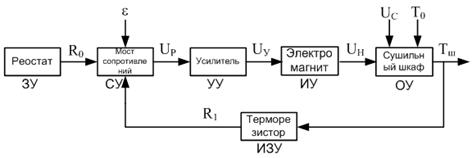
Рисунок
3 - Функциональная схема САР температуры сушильного шкафа
2.
Сигнальный граф САР температуры сушильного шкафа
Построение исходного сигнального графа является первым этапом анализа САР
с целью разработки её математической модели. Сигнальный граф определяет
структуру создаваемой математической модели САР.
Вид математической модели САР (системы её дифференциальных уравнений)
зависит, прежде всего, от того, совместное изменение во времени каких
переменных отражает данная модель и какова качественная структура взаимосвязи
этих переменных. Структуру взаимосвязи переменных в системе отражает сигнальный
граф САР.
Сигнальный граф является направленным графом и как таковой представляет
собой совокупность некоторого множества элементов (множество вершин) и некоторого
множества упорядоченных пар этих элементов (множества направленных рёбер). В
сигнальном графе роль множества вершин играет множество сигналов в САР,
совместное изменение которых во времени описывается данной математической
моделью.
Рёбра сигнального графа, входящие в некоторую вершину, указывают
совокупность значений или законов изменения во времени каких сигналов полностью
определяют значение или закон изменения во времени данного сигнала,
соответствующего данной вершине.
Сигнальный граф полностью определяет структуру системы дифференциальных
уравнений, входящих в математическую модель САР. Множество вершин сигнального
графа задаёт множество переменных, совместное изменение которых описывается
данной моделью. Вершины, имеющие только исходящие рёбра и не имеющие входящих
рёбер, соответствуют переменным, через которые передаётся влияние внешней среды
на поведение САР, т. е. задающему и возмущающему воздействиям (входам модели).
Такие вершины сигнального графа называются внешними вершинами. Вершины сигнального
графа, имеющие хотя бы по одному входящему ребру, называются внутренними
вершинами сигнального графа.
Таким образом, перед построением сигнального графа необходимо определить
принадлежность сигналов к внешним и внутренним вершинам.
Внешние вершины:
· 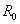 [Ом] -
сопротивление реостата;
[Ом] -
сопротивление реостата;
· ε[В] -
напряжение питания моста сопротивления;
· 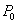 [Па] -
разность давлений вне цилиндра;
[Па] -
разность давлений вне цилиндра;
· 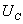 [В] -
напряжение питания системы;
[В] -
напряжение питания системы;
· 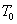 [°С] -
температура окружающей среды.
[°С] -
температура окружающей среды.
Внутренние вершины:
· 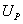 [В] -
напряжение на выходе моста сопротивлений;
[В] -
напряжение на выходе моста сопротивлений;
· 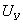 [В] -
напряжение на выходе усилителя;
[В] -
напряжение на выходе усилителя;
· 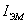 [А] - ток
на электромагните;
[А] - ток
на электромагните;
· 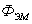 [Вб] -
магнитный поток ЭМ;
[Вб] -
магнитный поток ЭМ;
· 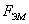 [Н] -
сила; создаваемая электромагнитом;
[Н] -
сила; создаваемая электромагнитом;
· 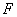 [Н] -
сила, действующая на рычаг демпфера;
[Н] -
сила, действующая на рычаг демпфера;
· 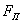 [Н] -
сила, действующая со стороны пружины;
[Н] -
сила, действующая со стороны пружины;
· 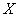 [м] -
перемещение рычага демпфера;
[м] -
перемещение рычага демпфера;
· 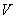 [м3] -
объем цилиндра поршня демпфера;
[м3] -
объем цилиндра поршня демпфера;
· 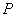 [Па]
-давление в цилиндре демпфера;
[Па]
-давление в цилиндре демпфера;
· 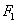 [Н] -
сила сопротивления сжимаемого в демпфере воздуха;
[Н] -
сила сопротивления сжимаемого в демпфере воздуха;
· 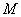 [кг] -
масса воздуха в цилиндре;
[кг] -
масса воздуха в цилиндре;
· 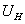 [В] -
напряжение на нагревательном элементе;
[В] -
напряжение на нагревательном элементе;
· 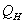 [ккал/c]
- тепловой поток, выделяемый нагревательным элементом;
[ккал/c]
- тепловой поток, выделяемый нагревательным элементом;
· 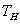 [°С] -
температура нагревательного элемента;
[°С] -
температура нагревательного элемента;
· 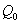 [ккал/с]
- тепловой поток, выделяемый в окружающую среду;
[ккал/с]
- тепловой поток, выделяемый в окружающую среду;
· 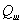 [ккал/с]
- тепловой поток, расходуемый на нагревания воздуха в шкафу;
[ккал/с]
- тепловой поток, расходуемый на нагревания воздуха в шкафу;
· 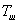 [°С] -
температура воздуха в шкафу;
[°С] -
температура воздуха в шкафу;
· 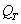 [ккал/с]
- тепловой поток, расходуемый на нагревания терморезистора;
[ккал/с]
- тепловой поток, расходуемый на нагревания терморезистора;
· 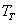 [°С] -
температура терморезистора;
[°С] -
температура терморезистора;
· 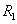 [Ом] -
сопротивление терморезистора.
[Ом] -
сопротивление терморезистора.
Сигнальный граф изображен на рис.4. Рассмотрим связь между приведенными
выше вершинами графа.
Реостатом
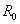 задается необходимое значение моста сопротивлений.
При разбалансировке моста на его выходе появляется напряжение разбаланса
задается необходимое значение моста сопротивлений.
При разбалансировке моста на его выходе появляется напряжение разбаланса 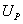 . Это напряжение усиливается и подается на обмотку
электромагнита, в котором протекает ток
. Это напряжение усиливается и подается на обмотку
электромагнита, в котором протекает ток 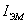 . Ток
приводит к появлению магнитного потока Фэм, который, в свою очередь, создает
силу F. Это усилие прикладывается к стержню демпфера, в результате чего
преобразуется в перемещение
. Ток
приводит к появлению магнитного потока Фэм, который, в свою очередь, создает
силу F. Это усилие прикладывается к стержню демпфера, в результате чего
преобразуется в перемещение 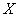 движка
трансформатора. С движка трансформатора подается напряжение
движка
трансформатора. С движка трансформатора подается напряжение 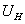 на нагревательный элемент. Мощность, выделяемая
нагревательным элементом в виде теплового потока
на нагревательный элемент. Мощность, выделяемая
нагревательным элементом в виде теплового потока 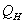 ,
поглощается воздухом шкафа
,
поглощается воздухом шкафа 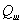 . От
разности
. От
разности 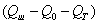 будет зависеть температура воздуха в шкафу
будет зависеть температура воздуха в шкафу 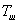 . От теплового потока
. От теплового потока 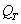 зависит
температура
зависит
температура 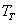 терморезистора, которая влияет на его сопротивление.
Изменение напряжения на терморезисторе R1 влияет на напряжение разбаланса моста
Uр.
терморезистора, которая влияет на его сопротивление.
Изменение напряжения на терморезисторе R1 влияет на напряжение разбаланса моста
Uр.
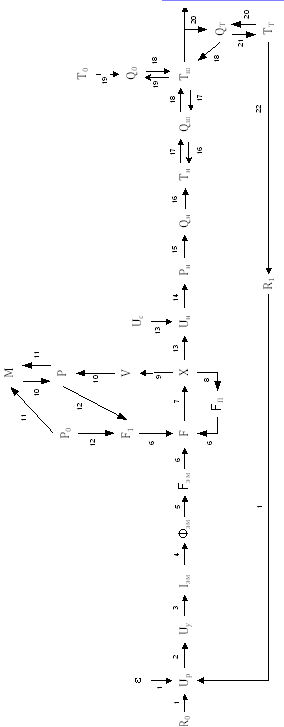
Рисунок 4 - Сигнальный граф САР температуры сушильного шкафа
3.
Система дифференциальных уравнений
Система дифференциальных уравнений САР полностью определяется ее
сигнальным графом. Под структурой системы дифференциальных уравнений
понимается, во-первых, множество функций времени, задаваемых извне, во-вторых,
множество искомых функций времени, относительно которых составляется система
дифференциальных уравнений и, в-третьих, список дифференциальных уравнений с
указанием для каждого уравнения, какие функции времени являются для него
заданными, а какая функция - искомой.
Множество сигналов, задаваемых извне, полностью определяется множеством
внешних вершин сигнального графа, а множество искомых сигналов - множеством
внутренних вершин. Каждой внутренней вершине соответствует одно уравнение,
причем сигнал, соответствующий этой вершине является для данного уравнения
искомым. Ребра, входящие в данную вершину, указывают, какие сигналы являются
заданными для данного уравнения. Таким образом, общее число уравнений равно
общему числу внутренних вершин сигнального графа.
Уравнение, соответствующее некоторой вершине сигнального графа, должно
определять значение или закон изменения физической величины, символически
обозначаемой этой вершиной, если заданы значения или законы изменения во
времени физических величин, соответствующих вершинам, из которых исходят ребра,
ведущие в данную вершину. При составлении каждого уравнения необходимо отдавать
себе отчет, насколько это уравнение идеализирует связь реальных переменных.
Руководствуясь вышеизложенными принципами, составим систему уравнений,
определяющих работу САР температуры сушильного шкафа, используя ее сигнальный
граф, приведенный на рис. 4. Согласно методическим указаниям, для простоты
записи аргумент t переменных величин будем опускать.
1) Напряжение разбаланса моста:
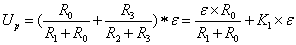 , где
, где
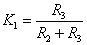 = [1]
= [1]
2) Напряжение на выходе усилителя:
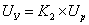 , где
, где
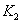 = [1]
= [1]
3) Ток в обмотке электромагнита:
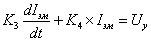 , где
, где
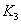 = [
Гн],
= [
Гн], 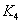 = [ Ом]
= [ Ом]
4) Магнитный поток возбуждения ЭМ (рис. 5):
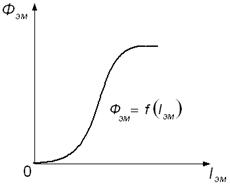
Рисунок 5 - Кривая намагничивания ЭМ
5) Сила, создаваемая электромагнитом:
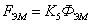 , где
, где
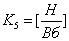
6) Сила, действующая на рычаг демпфера:
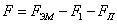
7) Сила, действующая на рычаг демпфера:
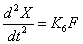 , где
, где
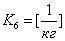
8) Сила, действующая со стороны пружины:
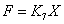 , где
, где
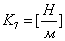
9) Объем воздуха в цилиндре поршня демпфера:
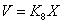 , где
, где
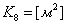
10) Давление в цилиндре демпфера:
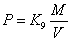 , где
, где
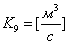 .
.
11) Масса воздуха в цилиндре:
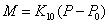 , где
, где
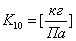
12) Сила сопротивления сжимаемого в цилиндре демпфера воздуха:
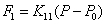 , где
, где
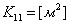 ;
;
13) Напряжение на нагревательном элементе сушильного шкафа:
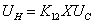 , где
, где
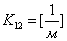
14) Электрическая мощность, выделяемая на нагревательном элементе
сушильного шкафа:
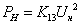 , где
, где
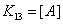
15) Тепловой поток, выделяемый нагревательным элементом:
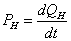
16) Температура на нагревательном элементе:
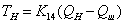 , где
, где
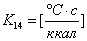
17) Тепловой поток, идущий на обогрев воздуха в шкафу:
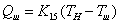 , где
, где
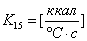
18) Температура воздуха в шкафу:
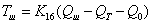 , где
, где
19) Тепловой поток, испускаемый в окружающую среду:
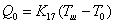 , где
, где
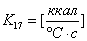
20) Тепловой поток, идущий на нагревание терморезистора:
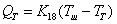 , где
, где
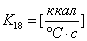
21) Температура на терморезисторе:
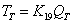 , где
, где
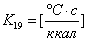
22) Сопротивление терморезистора:
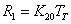 , где
, где 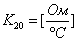 .
.
4. Линеаризация
системы уравнений
Линеаризация системы дифференциальных уравнений
основана на двух предположениях:
Во-первых, предполагается, что при номинальной работе
системы отклонения внешних воздействий от их постоянных номинальных значений
малы, следовательно малы и отклонения всех переменных в системе.
Во-вторых, линеаризация некоторого дифференциального
уравнения предполагает, что все функции, входящие в данное уравнение, не имеют
разрывов и являются гладкими при номинальном значении аргументов. Другими
словами, предполагается, что для каждой функции существуют первые производные
по всем аргументам в точке, соответствующей номинальному режиму.
Дифференциальные уравнения и функции, удовлетворяющие этому условию, называются
линеаризуемыми уравнениями или функциями. В противном случае они называются
существенно-нелинейными. Линеаризация существенно-нелинейных функций и
уравнений невозможна.
Определим теперь, какие из дифференциальных уравнений
САР являются нелинейными и требуют линеаризации. Линейным является уравнение
вида:
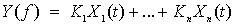 ,
,
где
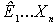 - некоторые коэффициенты,
- некоторые коэффициенты, 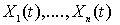 - независимые переменные, т.е. входные воздействия.
- независимые переменные, т.е. входные воздействия.
Система дифференциальных уравнений:
1. Линеаризуем
уравнение 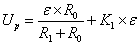 :
:
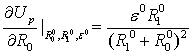 ;
;
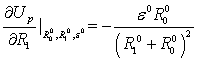 ;
;
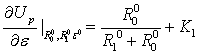
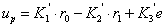 , где
, где
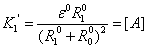 ,
, 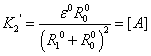 ,
, 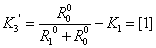 ;
;
. Уравнение
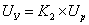 является линейным:
является линейным:
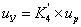 , где
, где
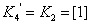 ;
;
. Уравнение
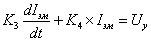 является линейным
является линейным
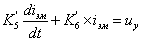 , где
, где
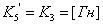 ,
, 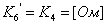 ;
;
4. Проведем касательную к кривой в точке номинального режима
Зависимость
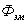 от
от 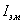 представляется
графически (рис. 6).
представляется
графически (рис. 6).
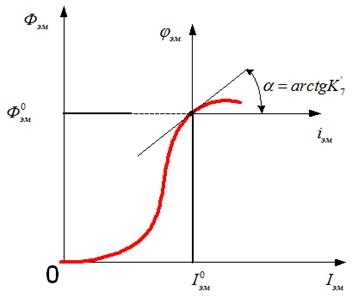
Рисунок 6 - График линеаризации Ф от I
Получим линеаризованную зависимость:
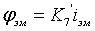 , где
, где
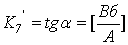 ;
;
. Уравнение
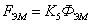 является линейным:
является линейным:
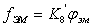 , где
, где
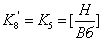 ;
;
6. Уравнение
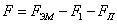 является линейным:
является линейным:
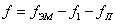 ;
;
. Уравнение
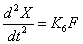 является линейным:
является линейным:
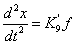 , где
, где
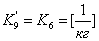 ;
;
. Уравнение
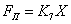 является линейным:
является линейным:
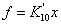 , где
, где
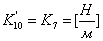 ;
;
. Уравнение
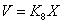 является линейным:
является линейным:
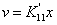 , где
, где
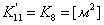 ;
;
. Линеаризуем
уравнение 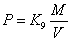 :
:
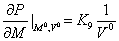
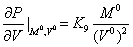
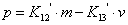 , где
, где
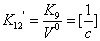 ,
, 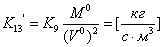 ;
;
. Уравнение
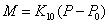 является линейным:
является линейным:
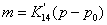 , где
, где
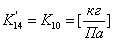 ;
;
. Уравнение
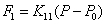 является линейным:
является линейным:
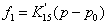 , где
, где
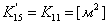 ;
;
. Линеаризуем
уравнение 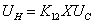 :
:
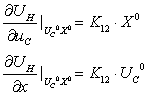
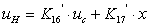 , где
, где
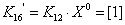 ,
, 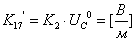 ;
;
. Линеаризуем
уравнение 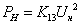 :
:
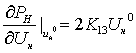
температура сушильный шкаф автоматический регулирование
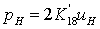 , где
, где
. Уравнение
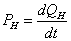 является линейным:
является линейным:
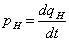 ;
;
. Уравнение
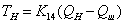 является линейным:
является линейным:
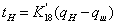 , где
, где
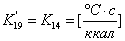 ;
;
. Уравнение
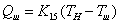 является линейным:
является линейным:
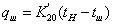 , где
, где
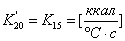 ;
;
. Уравнение
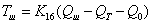 является линейным:
является линейным:
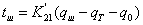 , где
, где
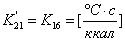 ;
;
. Уравнение
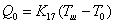 является линейным:
является линейным:
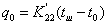 , где
, где
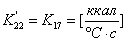 ;
;
. Уравнение
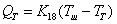 является линейным:
является линейным:
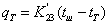 , где
, где
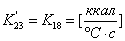 ;
;
. Уравнение
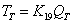 является линейным:
является линейным:
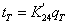 , где
, где
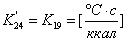 ;
;
. Уравнение
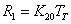 является линейным:
является линейным:
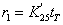 , где
, где
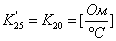 .
.
5. Операторная
форма записи системы лнейных дифференциальных уравнений. Передаточные функции
связей
Запишем
в операторной форме систему линеаризованных дифференциальных уравнений САР
температуры сушильного шкафа. Коэффициенты, возникающие при переходе к
операторной форме записи, будем нумеровать по порядку 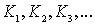 , не связывая с этими обозначениями тот смысл, который
был вложен в них ранее при составлении исходной системы дифференциальных
уравнений( размерность коэффициентов приведена лишь для удобства дальнейшей
проверки). Постоянные времени также будем нумеровать по порядку их
возникновения:
, не связывая с этими обозначениями тот смысл, который
был вложен в них ранее при составлении исходной системы дифференциальных
уравнений( размерность коэффициентов приведена лишь для удобства дальнейшей
проверки). Постоянные времени также будем нумеровать по порядку их
возникновения: 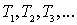 .
.
Система
дифференциальных уравнений в операторной форме записи для САР температуры
сушильного шкафа будет иметь следующий вид:
. Уравнение
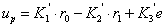 не является дифференциальным и поэтому его вид не
изменяется:
не является дифференциальным и поэтому его вид не
изменяется:
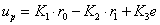 , где
, где
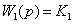 ,
, 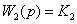 ,
, 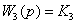 ,
,
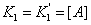 ,
, 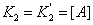 ,
, 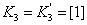 ;
;
. Уравнение
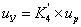 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
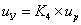 , где
, где
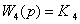 ,
, 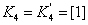
. Уравнение
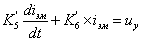 - дифференциальное. Разделим обе части уравнения на
- дифференциальное. Разделим обе части уравнения на 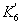 и введём обозначения
и введём обозначения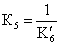 и
и 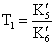 . Заменим оператор дифференцирования в левой части
сомножителем р и вынесем за скобки переменную
. Заменим оператор дифференцирования в левой части
сомножителем р и вынесем за скобки переменную 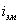 .
Разрешим полученное уравнение относительно
.
Разрешим полученное уравнение относительно 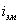 и
получим запись дифференциального уравнения в виде передаточной функции:
и
получим запись дифференциального уравнения в виде передаточной функции:
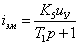 , где
, где
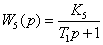 ,
, 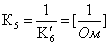 ,
, 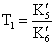 ;
;
. Уравнение
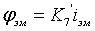 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
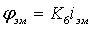 , где
, где
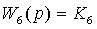 ,
, 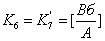 ;
;
. Уравнение
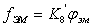 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
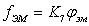 , где
, где
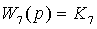 ,
, 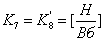 ;
;
. Уравнение
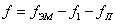 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
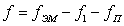 ;
;
. Уравнение
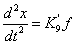 - дифференциальное. Заменим оператор
дифференцирования в левой части сомножителем р. Разрешим полученное уравнение
относительно
- дифференциальное. Заменим оператор
дифференцирования в левой части сомножителем р. Разрешим полученное уравнение
относительно 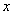 и получим запись дифференциального уравнения в виде
передаточной функции:
и получим запись дифференциального уравнения в виде
передаточной функции:
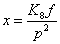 , где
, где
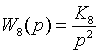 ,
, 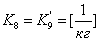 ;
;
. Уравнение
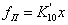 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
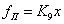 , где
, где
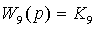 ,
, 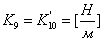 ;
;
. Уравнение
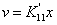 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
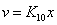 , где
, где
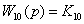 ,
, 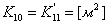 ;
;
. Уравнение
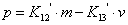 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
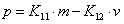 , где
, где
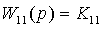 ,
, 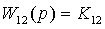
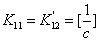 ,
, 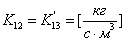 ;
;
. Уравнение
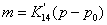 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
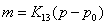 , где
, где
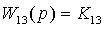 ,
, 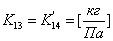 ;
;
. Уравнение
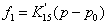 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
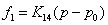 , где
, где
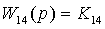 ,
, 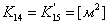 ;
;
. Уравнение
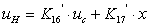 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
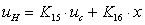 , где
, где
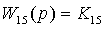 ,
, 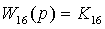
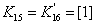 ,
, 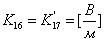 ;
;
. Уравнение
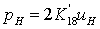 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
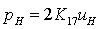 , где
, где
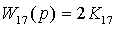 ,
, 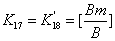 ;
;
. Уравнение
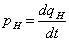 - дифференциальное. Разрешим полученное уравнение
относительно
- дифференциальное. Разрешим полученное уравнение
относительно 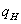 и получим запись дифференциального уравнения в виде
передаточной функции:
и получим запись дифференциального уравнения в виде
передаточной функции:
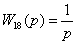 ;
;
. Уравнение
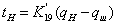 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
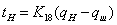 , где
, где
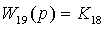 ,
, 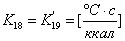 ;
;
. Уравнение
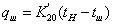 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
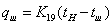 , где
, где
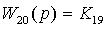 ,
, 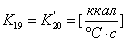 ;
;
. Уравнение
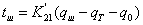 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
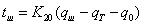 , где
, где
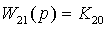 ,
, 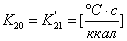 ;
;
. Уравнение
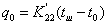 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
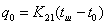 , где
, где
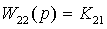 ,
, 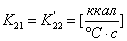 ;
;
. Уравнение
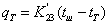 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
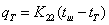 , где
, где
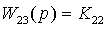 ,
, 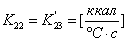 ;
;
. Уравнение
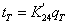 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
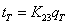 , где
, где
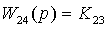 ,
, 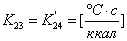 ;
;
. Уравнение
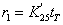 не является дифференциальным и поэтому его вид не
изменится:
не является дифференциальным и поэтому его вид не
изменится:
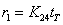 , где
, где
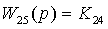 ,
, 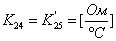 ;
;
6. Взвешенный
сигнальный граф и структурная схема линейной математической модели САУ
Взвешенный сигнальный граф представлен на рис. 7, а структурная схема,
приведена на рис. 8. Все они являются эквивалентными формами наглядного
графического представления системы линейных дифференциальных уравнений САУ. Как
взвешенный сигнальный граф, так и структурная схема используют запись
дифференциальных уравнений связей в виде передаточных функций. Взвешенный
сигнальный граф по своей структуре почти полностью совпадает с исходным
сигнальным графом, рассмотренным ранее, а каждому его ребру приписан вес,
имеющий вид некоторой передаточной функции. Вершины взвешенного сигнального
графа, соответствуют отклонениям соответствующих переменных от их номинальных
значений.
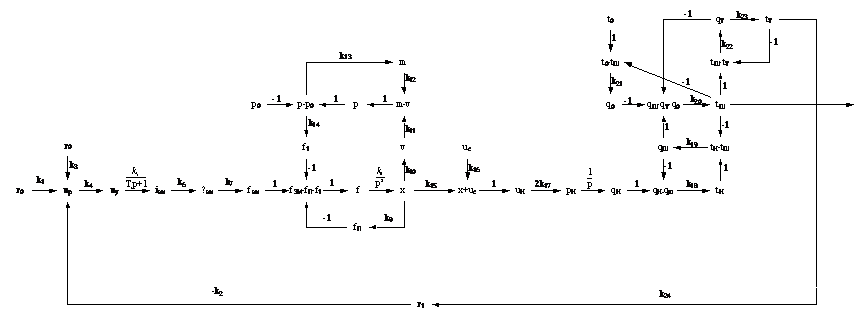
Рисунок
7 - Взвешенный сигнальный граф САР температуры сушильного шкафа
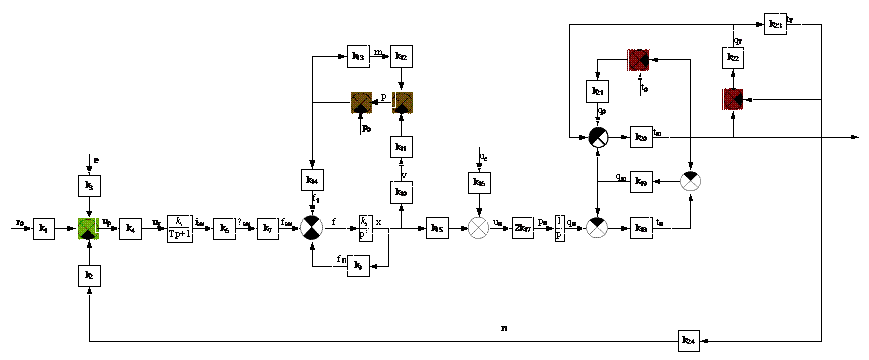
Рисунок
8 - Структурная схема САР температуры сушильного шкафа
В заключении заметим, что фундаментальное отличие взвешенного сигнального
графа от исходного состоит в том, что внутренняя вершина с несколькими
входящими ребрами интерпретируется как линейная зависимость переменной х от
переменных у1,. . . ,уq:
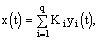
в
то время как в исходном графе такая вершина соответствовала зависимости x(t) от
у1(t), ..., уq(t) произвольного вида.
Кроме
того, вершины взвешенного сигнального графа, соответствуют отклонениям
соответствующих переменных от их номинальных значений, поэтому они обозначаются
маленькими буквами. В исходном сигнальном графе фигурировали полные переменные,
обозначавшиеся большими буквами.
7. Передаточные
функции САР
Завершающим этапом данной курсовой работы является определение передаточных
функций САР. Сквозные и контурные передаточные функции САУ можно найти, полагая
равными нулю “лишние” входные сигналы и приводя полную структурную схему к
нужному простейшему виду с помощью эквивалентных преобразований.
1.Определение сквозной передаточной функции САР от задающего
воздействия к выходу модели (главный оператор). Для определения передаточных функций
автоматических систем по их структурным схемам необходимо уметь определять
передаточные функции групп соединенных определенным образом элементов по
передаточным функциям отдельных элементов. Можно выделить три характерных
соединения - последовательное, параллельное, и обратное (в виде отрицательной
либо положительной обратной связи). Правила, позволяющие определять
передаточные функции системы в целом по передаточным функциям отдельных
элементов, составляют алгебру передаточных функций.
Перед преобразованиями необходимо обнулить все внешние воздействия, кроме
входного, после чего структурная схема САР примет вид, изображенный на рисунке
9.

Рисунок 9 - Структурная схема САР при определении главного оператора
Объединим группы последовательно соединенных звеньев, применив правило
умножения передаточных функций.
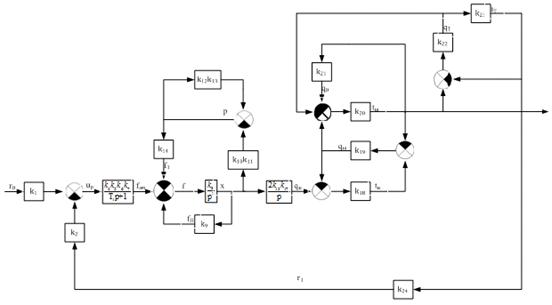
Рисунок 10 - Первый этап преобразования структурной схемы при определении
главного оператора
Для лучшего восприятия и наглядности преобразуем структурную схему
демпфера. Перенесем точку разветвления, после чего будет четко прослеживаться
ПОС. После проведенных преобразований имеем следующую структурную схему,
которая представлена на рисунке 11.
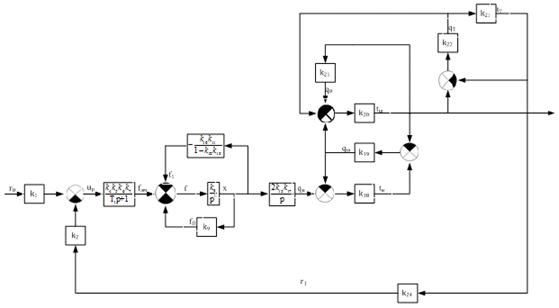
Рисунок 11 - Второй этап преобразования структурной схемы при определении
главного оператора
Упростим полученную схему, заменив элементы, соединенные обратной связью,
на одиночные. После чего объединим последовательно соединенные элементы (рис.
12).
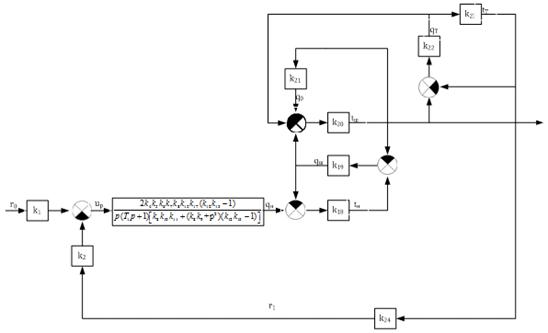
Рисунок 12 - Третий этап преобразования структурной схемы при определении
главного оператора
Для наглядности представим структурную схему теплообмена в следующем виде
(рис.13):
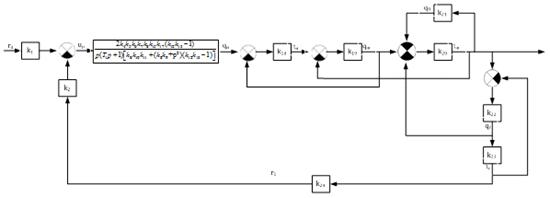
Рисунок 13 - Четвертый этап преобразования структурной схемы при
определении главного оператора
Преобразуем полученную структурную схему и получим (рис.14):

Рисунок 14 - Пятый этап преобразования структурной схемы при определении
главного оператора
Упростим полученную схему, заменив элементы, соединенные обратной связью,
на одиночные. После чего объединим последовательно соединенные элементы (рис.
15).

Рисунок 15 - Шестой этап преобразования структурной схемы при определении
главного оператора
Введем
обозначения К для общего коэффициента передачи, 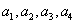 для
коэффициентов при
для
коэффициентов при 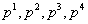 в знаменателе.
в знаменателе.
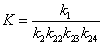 ;
;
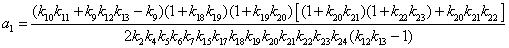 ;
;
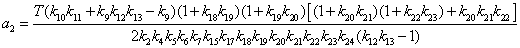 ;
;
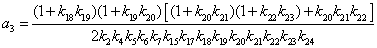 ;
;
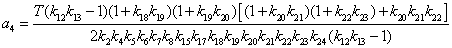
Сквозная
передаточная функция примет вид:
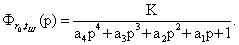
Проверим
правильность вычислений, сопоставляя единицы измерения символьного
коэффициента, выражаемого данной передаточной функцией, с единицами измерения
входной и выходной величин:
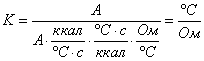 ;
;
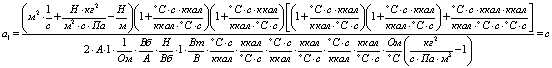 ;
;
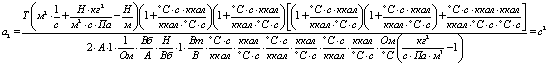 ;
;
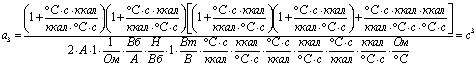 ;
;
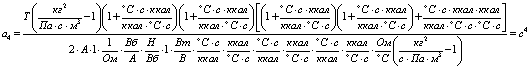 ;
;
В
результате получаем, что размерность сквозной передаточной функции (главного
оператора)-[ ], что полностью совпадает с ее физическим смыслом.
], что полностью совпадает с ее физическим смыслом.
2.Определение
контурной передаточной функции САР. Разорвём
цепь обратной связи и, используя правила преобразования структурных схем,
найдем контурную передаточную функцию САР температуры сушильного шкафа (рис.
16).
Рисунок
16 - Структурная схема САР при определении контурной передаточной функции
Объединим
группы последовательно соединенных звеньев, применив правило умножения
передаточных функций.
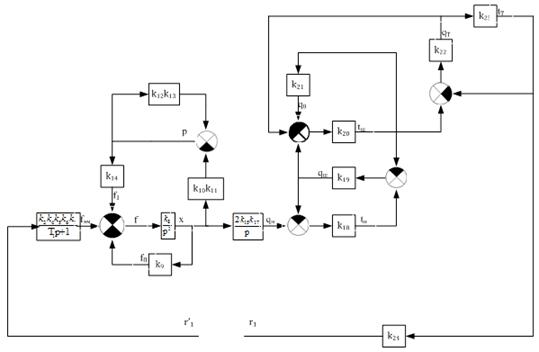
Рисунок
17 - Первый этап преобразования структурной схемы при определении контурной
передаточной функции
Для
лучшего восприятия и наглядности преобразуем структурную схему демпфера.
Перенесем точку разветвления, после чего будет четко прослеживаться ПОС. После
проведенных преобразований имеем следующую структурную схему, которая
представлена на рисунке 18.
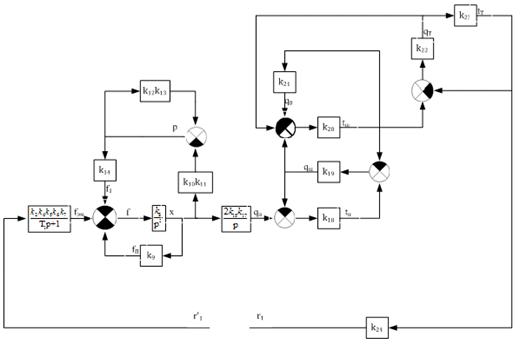
Рисунок
18 - Второй этап преобразования структурной схемы при определении контурной
передаточной функции
Упростим
полученную схему, заменив элементы, соединенные обратной связью, одиночными.
После чего объединим последовательно соединенные элементы (рис. 19).
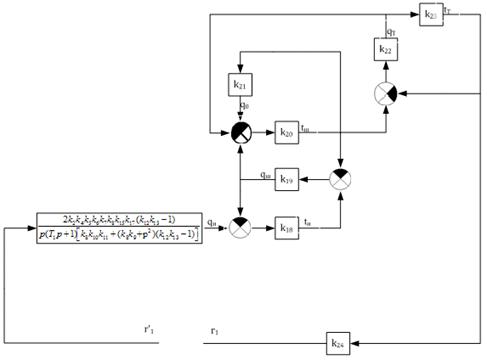
Рисунок
19 - Третий этап преобразования структурной схемы при определении контурной
передаточной функции
Для
наглядности представим структурную схему теплообмена в следующем виде (рис.
20):
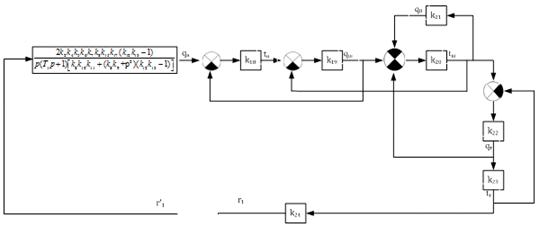
Рисунок
20 - Четвертый этап преобразования структурной схемы при определении контурной
передаточной функции
Преобразуем
полученную структурную схему и получим (рис.21):

Рисунок
21 - Пятый этап преобразования структурной схемы при определении контурной
передаточной функции
Упростим
полученную схему, объединив последовательно соединенные элементы.

Рисунок
22 - Шестой этап преобразования структурной схемы при определении контурной
передаточной функции
Введем
обозначения К для общего коэффициента передачи, 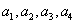 для
коэффициентов при
для
коэффициентов при 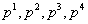 в знаменателе.
в знаменателе.
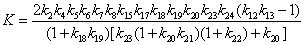 ;
;
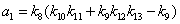 ;
;
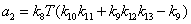 ;
;
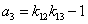 ;
;
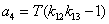 ;
;
Сквозная
передаточная функция примет вид:

Проверим
правильность проведения выкладок, сопоставляя единицы измерения символьного
коэффициента, выражаемого данной передаточной функцией, с единицами измерения
входной и выходной величин:
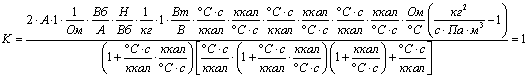 ;
;
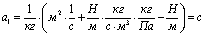 ;
;
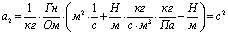 ;
;
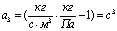 ;
;
 ;
;
В
результате получаем, что размерность сквозной передаточной функции (главного
оператора)-[1], что полностью совпадает с ее физическим смыслом.
3.Определение
сквозной передаточной функции САР от возмущающего воздействия к выходу модели. Главным (основным) возмущающим воздействием данной
САР является напряжение сети UC. Определим эту передаточную функцию,
используя правила преобразования структурных схем. Для этого изобразим
структурную схему в следующем виде (рис.23):
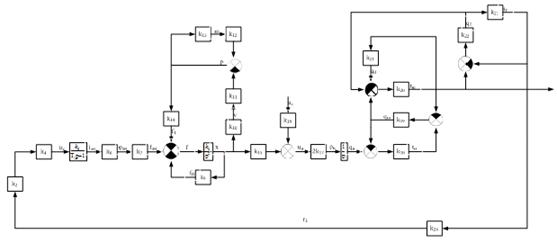
Рисунок
23 - Структурная схема САР при определении сквозной передаточной функции
Объединим
группы последовательно соединенных звеньев, применив правило умножения
передаточных функций.
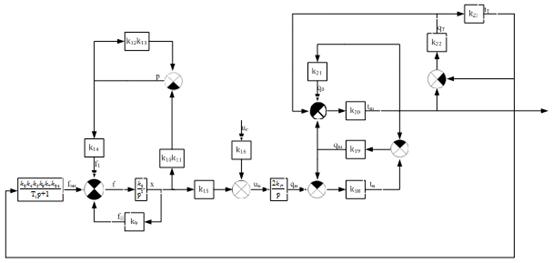
Рисунок
24 - Первый этап преобразования структурной схемы при определении сквозной
передаточной функции
Для
лучшего восприятия и наглядности преобразуем структурную схему демпфера. После
проведенных преобразований имеем следующую структурную схему, которая
представлена на рисунке 25.
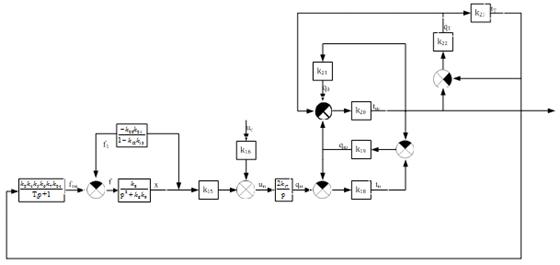
Рисунок
25 - Второй этап преобразования структурной схемы при определении сквозной
передаточной функции
Упростим
полученную схему, заменив элементы, соединенные обратной связью, одиночными.
После чего объединим последовательно соединенные элементы (рис. 26).
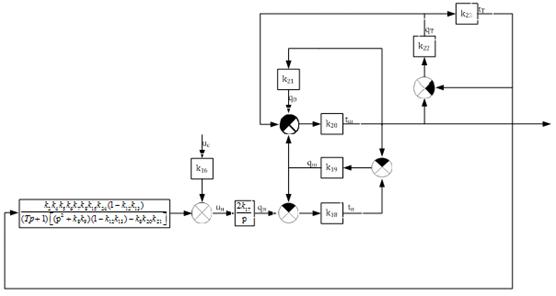
Рисунок
26 - Третий этап преобразования структурной схемы при определении сквозной
передаточной функции
Для
наглядности представим структурную схему теплообмена в следующем виде (рис.
27):
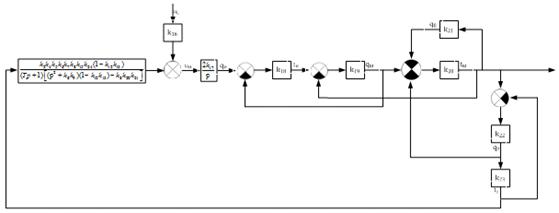
Рисунок
27 - Четвертый этап преобразования структурной схемы при определении сквозной
передаточной функции
Преобразуем
полученную структурную схему и получим (рис.28):

Рисунок
28 - Пятый этап преобразования структурной схемы при определении сквозной
передаточной функции
Упростим
полученную схему, заменив элементы, соединенные обратной связью, одиночными. После
чего объединим последовательно соединенные элементы (рис. 29).
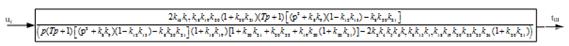
Рисунок
29 - Шестой этап преобразования структурной схемы при определении сквозной
передаточной функции
Раскроем
скобки в числителе и знаменателе и введем обозначения К для общего
коэффициента передачи, 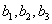 для коэффициентов при
для коэффициентов при 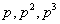 в
числителе,
в
числителе, 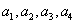 для коэффициентов при
для коэффициентов при 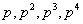 в
знаменателе:
в
знаменателе:
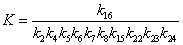 ;
;
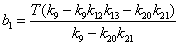 ;
;
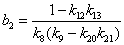 ;
;
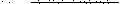 ;
;
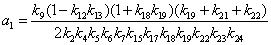 ;
;
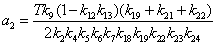 ;
;
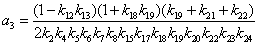 ;
;
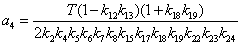 ;
;
Сквозная
передаточная функция примет вид:
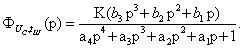
Проверим
правильность проведения выкладок, сопоставляя единицы измерения символьного
коэффициента, выражаемого данной передаточной функцией, с единицами измерения
входной и выходной величин:
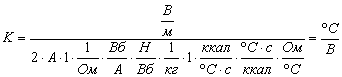 ;
;
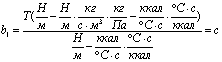 ;
;
 ;
;
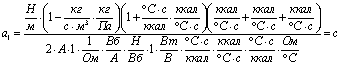 ;
;
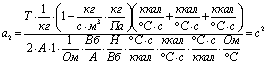 ;
;
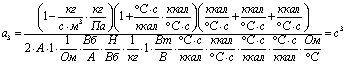 ;
;
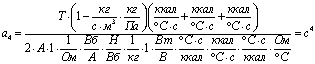 ;
;
В
результате получаем, что размерность сквозной передаточной функции (главного
оператора)-[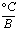 ], что полностью совпадает с ее физическим смыслом.
], что полностью совпадает с ее физическим смыслом.
Заключение
В данной работе было проведено исследование принципа
работы САР температуры сушильного шкафа, изучены протекающие в ней физические
процессы. Процессы и взаимодействия, происходящие между различными внутренними
и внешними величинами, влияющими на состояние системы, были описаны при помощи
различных физических законов в виде системы дифференциальных уравнений а затем
приведены к линейному виду. Таким образом была получена а затем и линеаризована
математическая модель исследуемой САР. При помощи системы дифференциальных
уравнений были получены взвешенный сигнальный граф и структурная схема системы,
из которых были получены зависимости выходной величины - температуры воздуха в
шкафу от задающего воздействия - перемещения движка потенциометра и
возмущающего воздействия - напряжения сети; была построена контурная
передаточная функция.
Метод преобразования структурных схем достаточно прост для реализации и
поэтому может часто использоваться при практических расчетах.
Список
используемых источников
1. Воронов А.А. «Основы теории автоматического
управления» - Москва: Энергия, 1980 г.
2. Иващенко Н.И. «Автоматическое регулирование» -
Машиностроение 1978 г.
. Макаров И.М., Менский Б.М. «Линейные автоматические
системы. “Машиностроение” 1982 г.
. Моттль В.В. «Конспект лекций по курсу Моделирование
систем правления» - Тула, 1999 г.
. Савельев И.В. «Курс физики. T1-T2» -Москва: Наука,
1989 г.
. Чиликин М.Г., Сандлер А.С. «Общий курс
электропривода». Москва 1981 г.