Множественное заполнение пропусков как метод борьбы с пропущенными данными
Введение
статистический агрегатирование пропуск данные
Одной из неизбежных проблем, сопутствующих любому социологическому
исследованию, являются пропуски в данных, приводящие к невозможности применения
изначального дизайна исследования, потере данных и смещению результатов.
Некоторые виды пропусков - систематические, или неигнорируемые - возможно
избежать или устранить только на этапе сбора информации, например, при помощи
внесения изменений в анкету, дополнительного инструктажа интервьюеров или
многократного обращения к одному и тому же респонденту. Однако существуют
методы, позволяющие бороться с игнорируемыми (случайными и полностью
случайными) пропусками уже на этапе анализа данных, когда информация собрана и
вернуться к этапу опроса нет возможности. На сегодняшний день таких методов
разработано достаточно много, от наиболее простых (например, исключение
неполных наблюдений) до сложных, в основе которых лежат сложные алгоритмы
подбора пропущенных значений в зависимости от характера пропусков, имеющихся в массиве
данных и предположений исследователя.
Один из таких сложных способов борьбы с пропущенными данными -
разработанный Дональдом Рубином в 1987 году и активно развивающийся метод
множественного заполнения пропусков - предполагает подстановку на место каждого
пропуска не одного значения, как в случае более простых способов, а нескольких
(в среднем, от 3 до 5). В результате исследователь получает три-пять полных
массивов, затем анализирует каждый из них и агрегирует результаты, полученные
одним и тем же методом на каждом из заполненных массивов, с применением
специфических формул, называемых правилом Рубина. Многократная подстановка
пропущенных значений позволяет ввести поправку на неопределенность пропуска, то
есть не рассматривать подставленное значение как фиксированное и точное
отражение того ответа, который на самом деле мог бы дать респондент на данный
вопрос.
Очевидно, что проводить один и тот же анализ несколько раз на каждом
массиве, а затем объединять их - задача достаточно трудоемкая. Этот процесс
отчасти автоматизирован в статистических пакетах, поддерживающих процедуру
множественного заполнения пропусков, однако нередко исследователь все же
сталкивается с необходимостью подсчитывать параметры вручную с использованием
правила Рубина (к примеру, если дизайн исследования предполагает использование
процедуры бутстреп для верификации результатов, а используемым статистическим
пакетом является SPSS, который не
производит процедуру бутстреп на массиве, созданном в результате применения
множественного заполнения пропусков). В связи с этим исследователями
неоднократно производились попытки упростить алгоритм множественного заполнения
пропусков, однако до сих пор они ограничивались каким-либо специфическим видом
анализа (к примеру, отбором подобного по вероятности - propensity score estimation [18]) или не слишком
распространенной исследовательской ситуацией (например, когда есть возможность
опросить всю генеральную совокупность и, в результате, отпадает необходимость в
учете выборочной дисперсии [22]). Таким образом, не существует теоретических
или эмпирических доказательств того, что эффективные альтернативы применению
правила Рубина для всех прочих исследовательских ситуаций действительно
существуют.
В данном исследовании предпринята попытка сравнения эффективности двух
подходов к агрегированию результатов множественного заполнения пропусков.
Первый - классический - предполагает проведение анализа на каждом из
восстановленных при помощи множественного заполнения пропусков массивов и
агрегирование результатов этого анализа при помощи правила Рубина. Этот метод
используется практически во всех исследованиях, где для борьбы с пропусками
применяется множественное заполнение. Второй возможный подход - поменять шаги
классического алгоритма местами для упрощения работы с ним, то есть сначала
произвести агрегирование заполненных значений так, чтобы несколько массивов
снова объединить в один (в данной работе - при помощи «усреднения»
подставленных вместо пропусков значений для каждого наблюдения, то есть
подстановки на место пропуска в единичном массиве подходящей меры центральной
тенденции значений, полученных для этого пропуска в результате множественного
заполнения), и уже на нем проводить интересующие исследователя тесты. Очевидно,
что использование классического, теоретически и методически хорошо
разработанного и неоднократно протестированного алгоритма - путь более
надежный, однако второй подход существенно ускоряет и облегчает работу с
методом множественного заполнения пропусков и, согласно нашим предположениям, в
определенных исследовательских ситуациях может служить эффективной заменой
классическому алгоритму. Сравнить эффективность того или иного подхода
теоретически достаточно трудно, поэтому для первичного тестирования
предположений, на который направлена данное исследование, мы будем использовать
статистический эксперимент.
Таким образом, данное исследование призвано установить, существуют ли
исследовательские ситуации, в которых агрегирование результатов множественного
заполнения пропусков при помощи усреднения подставленных значений и проведение
анализа на единственном массиве будет более эффективно, чем агрегирование
результатов анализа с применением правила Рубина. Мы предполагаем, что
эффективность применения того или иного подхода зависит от конкретной
исследовательской ситуации, под которой в данной работе мы подразумеваем
комбинацию типа шкалы изучаемой переменной с пропусками, доли пропусков в
массиве и метода анализа данных, который будет применяться к изучаемой
переменной. В данном исследовании будут рассмотрены три типа шкал (номинальная,
порядковая и интервальная), случаи 10, 30 и 50% пропусков в массиве и такие
распространенные в социологических исследованиях методы анализа данных, как
описательная статистика, поиск связи между переменными и линейная регрессия.
Таким образом, проблема исследования заключается в недостаточной
изученности эффективности применения правила Рубина и усреднения значений,
подставленных на место каждого пропуска как подходов к агрегированию
результатов множественного заполнения пропусков в зависимости от
исследовательской ситуации.
Цель исследования - оценить эффективность подходов к агрегированию
результатов множественного заполнения пропусков (применение правила Рубина и
усреднение заполненных значений) в зависимости от исследовательской ситуации.
Достижение указанной цели предполагает последовательное решение следующих
задач:
. Описать суть алгоритма множественного заполнения пропусков и
проанализировать основные подходы к агрегированию результатов множественного
заполнения пропусков.
. Предложить методику эксперимента для сравнения эффективности применения
правила Рубина и усреднения подставленных значений в зависимости от
исследовательской ситуации.
. Сравнить эффективность применения правила Рубина и агрегирования при
помощи усреднения подставленных значений в зависимости от исследовательской
ситуации.
. Выявить наиболее эффективный подход к агрегированию результатов
множественного заполнения пропусков для каждой из рассматриваемых
исследовательских ситуаций.
. Составить рекомендации по выбору подхода к агрегированию результатов
заполнения пропусков в каждой исследовательской ситуации.
В связи с повсеместным применением классического подхода к агрегированию
результатов множественного заполнения пропусков (то есть агрегированию
результатов статистических тестов при помощи правила Рубина, заложенного в
инструменты анализа результатов множественного заполнения пропусков в тех
статистических пакетах, которые поддерживают эту процедуру), на данный момент
не существует достаточных теоретических или эмпирических оснований, на которых
можно было бы строить гипотезы. Соответственно, рамках данного исследования
гипотез выдвинуто не будет.
Теоретическим объектом исследования являются подходы к агрегированию
результатов множественного заполнения пропусков.
Предмет исследования - эффективность подходов к агрегированию результатов
множественного заполнения пропусков в зависимости от исследовательской
ситуации.
В качестве эмпирического объекта в исследовании выступают жители России,
принявшие участие в шестой волне Европейского социального исследования,
проведенного в 2012 году. Мы используем вторичные данные, поскольку не ставим
перед собой никаких содержательных задач, а значит особенности эмпирического
объекта не играют роли для целей исследования.
В качестве метода исследования выступает статистический эксперимент.
Таким образом, результатом данного исследования должен стать набор
рекомендаций относительно выбора наиболее эффективного подхода к агрегированию
результатов множественного заполнения пропусков - правила Рубина или усреднения
подставленных значений - для некоторых исследовательских ситуаций.
Глава 1. Множественное заполнение пропусков как метод борьбы
с пропущенными данными
Проблема пропусков в социологических данных
Пропущенные данные - проблема, практически неизбежно возникающая при
проведении количественного научного исследования и влекущая за собой негативные
последствия для его результатов. Хортон и Липшиц [14, p. 244] выделяют три типа затруднений, возникающих по причине
наличия пропусков в собранных данных. Во-первых, таким затруднением является
существенная потеря отдачи от информации, собранной на полевом этапе, поскольку
итоговое количество полных наблюдений не соответствует дизайну исследования.
Далее, стандартные статистические пакеты по умолчанию исключают наблюдения с
пропусками из анализа тем или иным образом, что не только ставит под вопрос
достоверность результатов анализа, но и ограничивает круг применимых к данным
статистических инструментов; именно такие ограничения Хортон и Липшиц относят
ко второму типу затруднений. Наконец, третий тип касается возможных смещений в
результатах исследования по причине различий между наблюдаемыми и пропущенными
данными [Ibid.]. Необходимо заметить, что коррекции на этапе анализа данных
поддаются не все виды пропусков, поэтому существенным моментом является
определение области применимости нашего исследования, а именно типов пропусков,
представляющих интерес для данного исследования, которые мы рассмотрим далее.
Классификация пропусков
В процессе сбора социологической информации может возникнуть несколько
ситуаций, относящихся к пропускам в данных. Если респондент оказался достижим
для исследователя и ему предложили пройти опрос, он может отказаться отвечать
вообще (в результате чего мы будем иметь случай отсутствия наблюдения - unit nonresponse), либо ответить на все вопросы (в
этом случае мы получим full response - полный
ответ), а также отказаться отвечать только на некоторые вопросы анкеты или не
суметь на них ответить, в этом случае возникает ситуация неполных наблюдений,
то есть отсутствия некоторого набора значений переменных - item nonresponse, борьба с которой происходит уже на
этапе обработки полученных данных [2, с. 29]. В фокус нашего исследования
находятся именно пропуски типа item nonresponse, для
борьбы с которыми применяются статистические методы борьбы с пропусками, в
частности, множественное импутирование.
Наиболее принципиальной для выбора способа борьбы с пропусками является
природа пропусков, характеризующаяся их случайностью или систематичностью,
впервые систематизированная Рубином и Литтлом [6] и подробно описанная в [2,
10, 11, 23].
Пусть имеется некоторая база данных, в которой для каждого респондента k имеется набор из n ответов: k = (k1, …, kn). Тогда в ситуации item nonresponse некоторые из этих ответов, скорее
всего, отсутствуют, и все ответы респондента можно разделить на наблюдаемые kobs и пропущенные kmis. Кенвард и Карпентер вводят для
каждого ki коэффициент r, который Рубин и Литтл называют индикатором присутствия: он
равен единице, если ответ присутствует, и нулю, если ответ пропущен [6, с. 18],
и является так называемой случайной величиной второго типа: если обозначить
распределение всех возможных значений переменной с пропусками как случайную величину
первого типа, то случайная величина второго типа будет указывать на
распределение для нее дихотомии «ответ-неответ» [3, с. 149]. В свою очередь,
механизм порождения пропуска (missing data mechanism) - это вероятностное распределение r при условии k: P (r | k). Наше знание или незнание о механизме порождения пропусков
определяет, каким методом анализа необходимо воспользоваться в каждом
конкретном случае, причем если механизм неясен, то выбор производится в
соответствии с предположениями исследователя об этом механизме. Анализ не
всегда включает в себя механизм порождения пропусков в явном виде, но, если это
необходимо, механизм вводится в модель посредством индикатора присутствия [6,
с. 18]. Структура пропусков называется монотонной в том случае, если пропуск ki означает, что kj также пропущен для всех i > j [10, p.
200].
Перейдем к самой классификации. Рубин и Литтл выделяют три типа пропусков
в зависимости от степени случайности их возникновения. Первый тип - полностью
случайные пропуски или MCAR (missing completely at random), механизм порождения которых заключается в том, что
вероятность пропуска не зависит от k: P(r | k) = P(r). Кроме того, пропуски называют полностью случайными, если
их возникновение обусловлено дизайном исследования, не подразумевающим
зависимость от k [10, p. 201].
Случайная величина второго типа в этом случае является определенной, то есть
выборочная доля неответов может быть адекватно перенесена на генеральную
совокупность [3, с. 152]. Зависимость между вероятностью пропуска, ответами на
другие вопросы анкеты или потенциальными ответами на пропущенный вопрос для
полностью случайных пропусков отсутствует, и уточнить предсказание о
пропущенных значениях при помощи имеющейся информации мы не сможем [13, p. 50]. Те наблюдения, для которых
ответ присутствует, образуют простую случайную подвыборку, а значит, являются
несмещенной выборкой из генеральной совокупности. К ней можно применять те же
статистические критерии, что и к оригинальной выборке, однако их мощность
снижается из-за уменьшения ее объема. [2, с. 35].
Пропуск называют случайным или MAR (missing at random) если распределение r не зависит от пропущенных значений интересующей нас
переменной: P (r | k) = P (r | kobs). Проще говоря, значения случайных пропусков можно предсказать
при помощи других переменных в базе, для которых ответы присутствуют [13, с.
51]. В этом случае мы не можем утверждать, что наблюдения без пропусков
образуют случайную подвыборку из оригинальной выборки, однако случайной
подвыборкой является совокупность наблюдений с пропуском интересующей нас
переменной в каждой подгруппе, выделенной в соответствии со значением
определенной полной переменной [6, с. 23]. Таким образом, в данном случае
отсутствует зависимость между распределением пропусков в ответах на вопрос и
теми ответами, которые потенциально могли дать не ответившие респонденты,
однако их неответы связаны со значениями других признаков. Распределение
случайной величины для таких пропусков имеет смысл только в подвыборках, но не
на всей генеральной совокупности [3, с. 152]. Как для MCAR, так и для MAR функцию f(r | k) можно не вводить в модель, поэтому эти виды пропусков
называют игнорируемыми [10, p.
201].
Наконец, третий тип подразумевает, что распределение пропусков зависит
как от пропущенных значений, так и от наблюдаемых признаков. В этом случае
пропуски называют систематическими или MNAR (missing not at random) и относят к неигнорируемым. Можно сказать, что для
систематических пропусков случайная величина второго типа вообще не существует
[3, с. 153]. Такая ситуация требует обязательного включения в модель механизма
порождения пропусков для устранения систематической ошибки в результатах,
причем этот механизм, скорее всего, будет неизвестен исследователю [10, p. 202], поэтому стандартные методы борьбы
со смещениями в неполных базах данных - взвешивание, анализ полных наблюдений
или заполнение пропусков - не будут корректно выполнять свою задачу [12, p.
984]. Основная рекомендация по устранению систематических пропусков заключается
в доработке инструментария до или во время этапа сбора данных, однако Р Глинн,
Н. Лэрд и Д. Рубин [12] предлагают метод, позволяющий пользоваться уже
имеющимся опросником. Суть их метода заключается в повторной попытке опроса
респондентов, в ответах которых возникли неигнорируемые пропуски, получения
случайной подвыборки тех, кто ответил при повторном опросе и использования этих
наблюдений в смешанной модели с применением множественного заполнения
пропусков.
Несмотря на четкое определение механизма порождения пропусков для каждого
из рассмотренных случаев, на практике точно сказать, в какую категорию попадают
имеющиеся пропуски, не представляется возможным. Однако существует несколько
способов установить, являются ли имеющиеся пропуски не полностью случайными или
MNCAR (missing not completely at random). Один из них - показатель DRSS, оценивающий различия сумм квадратов остатков в
регрессионных уравнениях, построенных на массивах, к которым были применены
несколько разных методов заполнения пропусков. В случае, если различия значимы,
пропуски являются не полностью случайными. Другой показатель - DXX - использует оценку изменения
матрицы Х’Х, где Х - ковариационная матрица для независимых переменных. На не
полную случайность пропусков в этом случае указывает значимое изменение
ковариационной матрицы признаков [2, с. 37].
Эти способы, как мы видим, позволяют с уверенностью различать полную (MCAR) и не полную (MAR и MNAR) случайность пропусков; различение же MAR и MNAR может базироваться только на исследовательских
допущениях, но полностью исключить присутствие в базе данных систематических
пропусков на основании анализа наблюдаемых значений нельзя [13, p. 51]. Кроме того, необходимо
помнить, что определить степень случайности пропусков возможно исключительно с
точностью до имеющихся в массиве переменных: в случае отсутствия в нем
переменной, от которой может зависеть распределение пропусков, исследователь
может ошибочно определить их как полностью случайные.
Таким образом, областью применимости данного исследования являются только
случаи игнорируемых пропусков, поскольку с ними есть возможность эффективно
бороться уже после этапа сбора информации с помощью различных способов
устранения пропущенных данных, о которых пойдет речь далее.
Методы борьбы с пропущенными данными
На сегодняшний день для устранения пропусков в данных разработано
множество методов, от самых простых (например, исключение неполных наблюдений)
до комплексных, в основе которых лежат сложные алгоритмы подбора пропущенных
значений в зависимости от характера пропусков, имеющихся в массиве данных и
предположений исследователя. Кратко обратимся к наиболее распространенным из
них.
В первую очередь, обратимся к простым, или, как их называют Литтл и
Рубин, быстрым методам борьбы с пропусками: анализу полных наблюдений, анализу
доступных наблюдений и взвешиванию данных. Необходимо заметить, что эти подходы
подразумевают полную случайность имеющихся пропусков и не подходят для случаев,
когда пропуски являются случайными. Рассмотрим каждый из них в отдельности.
При использовании метода анализа полных наблюдений пропуски из базы
удаляются построчно, в SPSS,
где быстрые методы борьбы с пропусками являются установленными по умолчанию,
этот метод обозначен как listwise deletion.
Очевидно, что в этом случае потеря информации окажется, как минимум,
существенной. Как уже было сказано выше, данный метод применим исключительно к
полностью случайным неответам и только в этом случае не приведет к смещению
результатов анализа данных. Несмотря на очевидные недостатки в виде жестких
требований к пропускам и высокой потере данных, данный способ является простым
и позволяет сравнивать между собой одномерные статистики [6, с. 49], что и
обеспечивает ему популярность в академической среде. К примеру, исследование
Кинга и его коллег показало, что в период с 1993 по 1997 год (то есть спустя
15-20 лет после того, как Дональд Рубин разработал и представил научному
сообществу метод множественного заполнения пропусков) около 94% исследователей
использовали метод анализа полных наблюдений с потерей до трети собранных
данных [13, p. 49].
Метод анализа доступных наблюдений (pairwise deletion) в некоторой степени избавлен от
недостатков метода полных наблюдений и подразумевает использование в анализе
всех наблюдений, содержащих интересующую исследователя переменную. В этом
случае одномерные статистики приобретают смысл сами по себе, однако теряют
преимущество сравнимости, поскольку вычисляются на различных подвыборках в
зависимости от распределения пропусков. К примеру, если на вопрос о доверии
политикам ответы не дали одни респонденты, а на вопрос о доверии полиции -
другие, сравнивать уровни доверия политикам и полиции нельзя, поскольку на
первый вопрос давала ответ одна подвыборка, а на второй - другая. В случае,
если метод анализа данных требует использования более чем одной переменной, в
рамках данного способа необходимо рассматривать только наблюдения, для которых
присутствуют значения каждой из интересующих исследователя переменных.
Взвешивание данных позволяет исследователю применить к базе метод удаления
неполных наблюдений, но сохранить при этом запланированный объем выборки. Для
этого полные наблюдения в очищенной базе «взвешивают», то есть назначают
каждому наблюдению некоторый вес при расчетах в соответствии с коэффициентом,
заданным исследователем. Коэффициент определяется переменной (или переменными),
для которых необходимо сохранить структуру выборки. Например, необходимо
провести сравнение средних значений индекса счастья в десяти странах, и
исследователь хочет применить для этого параметрический метод, однако в двух из
десяти стран количество полных наблюдений меньше тридцати, и, следовательно,
параметрические методы к таким выборкам неприменимы. В этом случае
исследователь при помощи специальных процедур, предусмотренных статистическими
пакетами, может увеличить вес каждого наблюдения в двух малых выборках
относительно всей совокупности так, что в процессе анализа данных с поправкой
на весовой коэффициент выборки для двух интересующих нас стран окажутся
достаточными для параметрических тестов. Альтернативный способ применения
взвешивания в данном случае - увеличение веса случайно отобранных наблюдений из
малых выборок, пока их не окажется достаточно для проведения параметрического
анализа. Метод взвешивания полных наблюдений, однако, не лишен тех же
недостатков, что и прочие рассмотренные нами быстрые способы борьбы с
пропусками: увеличение веса случайных наблюдений может создать или усугубить
смещения, имевшиеся в выборке полных наблюдений [2, с. 41], причем не только
для выборок с пропусками, но и для полных переменных.
Рассмотрев простые методы борьбы с пропусками и их недостатки, обратимся
к более эффективному и современному способу - заполнению пропусков, целью
которого является восстановление исходной структуры информации на основании
имеющихся в массиве данных. Таким образом исследователь ни в коем случае не
производит ответы, которые респондент не давал, но делает предположения о
возможном ответе.
Существует несколько методов заполнения пропусков в данных, которые Р.
Литтл разделил на простые и сложные, локальные и глобальные. К простым методам
относятся заполнение пропусков мерами центральной тенденции, регрессионное
моделирование (метод Бака) и Hot Deck. Сложные
методы, в свою очередь, подразделяются на локальные (множественное заполнение
пропусков) и глобальные (EM-алгоритм).
«Глобальность» алгоритма указывает на то, что для заполнения пропуска
используются все остальные значения переменных в базе данных, а «локальность» -
на использование только близких к пропуску полных наблюдений [2, с. 52-54].
Рассмотрим подробно каждый из этих методов.
Наиболее простые методы заполнения пропусков - заполнение безусловными
мерами средней тенденции и заполнение условными средними. В первом случае
пропуски заполняются модой для номинальных переменных, медианой для порядковых
и средним для интервальных, вычисленными на имеющихся значениях переменной,
однако простота данного метода нивелируется тем, что оценки дисперсии и
ковариации в этом случае занижаются из-за увеличения количества срединных
значений в распределении. Второй случай - метод Бака или регрессионное
моделирование - более комплексный и подразумевает «подстановку средних,
условных по присутствующим в наблюдении переменным» [6, с. 55]. Он подходит для
двух коррелирующих между собой переменных и предполагает построение линейной
регрессии зависимости переменной с пропусками от полной переменной на основе
наблюдаемых пар ответов. В случае подстановки условных средних дисперсия и
ковариация также занижаются, но не так выраженно, как в случае подстановки безусловных
мер [1, с. 74].
Hot Deck (метод
ближайшего соседа, метод заполнения выборочными значениями) - это метод
заполнения пропусков, основанный на расстояниях между объектами, вычисленных
исходя из значений известных признаков. Для подстановки можно использовать как
значение признака, соответствующее наблюдению, наиболее близкого к неполному
[2, с. 44], так и усредненное значение признака в некотором кластере близких
объектов либо случайно выбранное в этом кластере значение [1, с. 74]. Способ
вычисления расстояний между объектами может варьироваться в зависимости от
специфики данных и целей исследования.
Метод максимального правдоподобия, или EM (Expectation-Maximization) -алгоритм - это итеративная
процедура, применимая только к интервальным шкалам для решения задач
взвешивания оценок наименьших квадратов, оценивания компонент дисперсии и
заполнения пропусков в данных. Алгоритм состоит из двух шагов, условно
обозначенных Е от Expectation и M от Maximization. На шаге E, основываясь на ковариационных матрицах, мерах центральной
тенденции и корреляции между переменной с пропусками и другими переменными в
базе предсказывается значение пропуска. На шаге М итеративно максимизируется
соответствие между ковариационными матрицами [4, с. 46]. Этот метод является достаточно
медленным в условиях большого количества пропусков, поскольку оптимизация
потребует большого количества итераций [1, с. 74].
Множественное заполнение пропусков (Multiple Imputation) отличается от всех предыдущих
методов тем, что каждое пропущенное значение заменяется рассчитанным значением
не однократно, как в методах, рассмотренных выше, а несколько раз, в результате
чего исследователь получает несколько полных массивов. В случае применения
классического алгоритма с применением правила Рубина процедура происходит
следующим образом: на каждом из полученных в результате множественного
заполнения пропусков исследователь должен провести интересующий его
статистический тест, а затем агрегировать результаты тестов при помощи набора
формул, называемых правилом Рубина. В случае же применения метода, который
будет протестирован против правила Рубина в данном исследовании, подставленные
значения из полученных в результате множественного заполнения пропусков
массивов сначала агрегируются (усредняются), результатом чего становится
единственный массив с усредненными результатами множественного импутирования, и
уже на нем производится интересующий исследователя статистический тест.
Применение метода множественного заполнения пропусков позволяет рассматривать
подставленное значение не как фиксированное и однозначно известное, но внести
поправку на его неопределенность. Поскольку именно множественное заполнение
пропусков находится в фокусе данного исследования, рассмотрим смысл этого
подхода более подробно и обратим внимание на каждый из шагов алгоритма в том
виде, который был разработан Рубином и используется в большинстве случаев до
сих пор, затем рассмотрим альтернативы классическому способу агрегирования
результатов множественного заполнения пропусков, а также опишем реализацию
множественного заполнения пропусков в пакете SPSS, который будет использован в рамках данного
исследования.
Множественное заполнение пропусков
При подстановке значений на место пропущенных данных исследователь должен
помнить, что результаты импутирования не являются реальными ответами
респондентов, и при анализе необходимо учитывать неопределенность, порождаемую
совместным распределением интересующей нас переменной с пропусками и
соответствующего ей индикатора присутствия, а также самой моделью заполнения
(модели заполнения будут подробно рассмотрены ниже) [23, p. 581]. Для снижения этой
неопределенности Рубином и Литтлом был разработан метод множественного
заполнения пропусков, подразумевающий, что пропуски в исходном массиве
заполняются несколько раз с использованием одной и той же модели заполнения
пропусков. Тот факт, что в каждом из полученных массивов подставленные значения
существенно различаются, эмпирически доказывает существование упомянутой нами
неопределенности [2, с. 46].
Достоинства этого метода перед прочими заключаются, во-первых, в том, что
множественное импутирование вводит случайную ошибку в процесс заполнения
пропусков, что позволяет получить относительно несмещенные оценки
статистических параметров; во-вторых, он вносит поправку на дополнительную
ошибку, возникающую в процессе импутирования; в-третьих, разнообразие моделей
заполнения пропусков и вариабельность позволяют применять этот метод к любому
типу данных без использования специальных программ [9, p. 304]. Разберем подробнее, что конкретно здесь
подразумевается под «поправкой на дополнительную ошибку». В том случае, если на
вопрос ответили все респонденты, в распределении их ответов будет наблюдаться
некоторая дисперсия, которую мы можем оценить с точностью до имеющейся выборки
и которая является одним из основных показателей искомого закона распределения
интересующей нас величины. В том случае, если на вопрос ответили не все
респонденты, оценка дисперсии по имеющимся наблюдениям будет гораздо менее
точной, чем предполагал изначальный дизайн исследования. Если же мы заполняем
эти пропуски только один раз, мы рассматриваем полученные значения как реальные
ответы и можем учесть их искусственную природу только условно, а не
статистически. В случае применения множественного заполнения пропусков к
выборочной («внутримассивной») дисперсии добавляется «межмассивная» дисперсия,
которая и позволяет брать в расчет тот факт, что подставленные значения не
являются реальными ответами респондентов, иными словами, рассматривать набор подставленных
вместо конкретного пропуска значений как выборку, позволяющую установить не
истинный ответ респондента, а интервал, в котором этот ответ лежит с некоторой
вероятностью.
Сам алгоритм состоит из четырех последовательных шагов:
. Обследование пропусков.
. Определение модели заполнения.
. Подстановка значений.
. Анализ данных и агрегирование результатов.
Рассмотрим принципы и особенности работы с алгоритмом множественного
заполнения пропусков по порядку производимых для его осуществления действий.
Шаг 1: оценка количества и характера пропусков в массиве
На данном шаге исследователь должен, во-первых, определить, к какой шкале
относится переменная, содержащая пропуски, во-вторых, проверить пропуски на
монотонность и, в-третьих, установить, присутствуют ли в массиве переменные,
которые можно использовать для расчета значений, подставляемых на место
пропуска. Тип шкалы (дискретная или непрерывная) и структура пропусков
(монотонная или немонотонная) определяет, какую модель импутирования нужно
будет применить на следующем шаге. Если тип шкалы исследователь может
определить самостоятельно, то для оценки на монотонность в статистических
пакетах, поддерживающих процедуру множественного заполнения пропусков,
существуют специальные инструменты (к примеру, в пакете SPSS для этого используется команда Analyze patterns).
Не существует строгих принципов выбора переменных, используемых для
расчета подставляемых значений, в этом вопросе исследователю следует полагаться
на собственные предположения и ограниченный набор рекомендаций. К примеру,
одним из способов, позволяющих установить наиболее подходящие в смысле расчета
значений для заполнения переменные, является моделирование пропусков.
Моделирование пропусков предполагает оценку связи между индикатором присутствия
интересующей нас переменной с пропусками и переменными, потенциально
подходящими для внесения в модель, рассчитывающую значения, которые будут
подставлены не место пропусков. Например, так можно установить, что наиболее
часто волны панельного исследования пропускали люди с низкой субъективной
оценкой здоровья.
Таким образом, для того, чтобы перейти к следующему шагу - выбору и
построению модели множественного заполнения пропусков - необходимо:
· установить тип шкалы переменной, содержащей пропуски - дискретный
или непрерывный;
· определить структуру пропусков - монотонная или немонотонная;
· отобрать переменные-предикторы, наиболее тесно связанные с
переменными, требующими множественной импутации, для внесения в модель
множественного заполнения.
Шаг 2: определение модели множественного заполнения
В соответствии с информацией, полученной на предыдущем шаге,
исследователю необходимо выбрать модель, наиболее подходящую для заполнения
пропусков в интересующей его переменной, и включить в нее отобранные переменные-предикторы.
Предназначение модели импутирования заключается в том, чтобы создать на
основании наблюдаемых значений переменной с пропусками и ее связей с
переменными-предикторами распределение, из которого затем в случайном порядке
будут извлекаться значения для подстановки на место пропусков. В литературе
описываются три таких модели - предиктивная, степени предрасположенности и
дискриминантная. Рассмотрим их основные принципы.
Предиктивная модель множественного заполнения пропусков предназначена для
работы с непрерывными переменными. Ее суть заключается в подстановке на место
пропуска «ближайшего к спрогнозированному значению реальное значение
переменной, принадлежащее полному наблюдению» [2, с. 47]. Прогнозирование
производится при помощи построения на полных наблюдениях линейного
регрессионного уравнения вида:
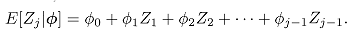 ,
,
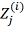
где Z1…Zj-1 - известные значения наблюдаемой переменной, содержащей пропуски. На
основании полученных коэффициентов регрессии рассчитывается прогнозируемое
значение :
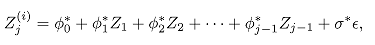 .
.
где ϭ* - значение дисперсии, а ε - случайная величина, которое и
подставляется на место пропуска.
Применение модели степени предрасположенности также является обоснованным
в том случае, если переменные, содержащие пропуски, - непрерывные, а структура
пропусков - монотонная. Она базируется на оценках предрасположенности
респондента, то есть вероятности получения его ответа на вопрос [2, с. 47].
Применение модели степени предрасположенности реализуется следующим образом. На
основании индикатора присутствия рассчитывается предрасположенность респондента
sij ответить или не ответить на вопрос:
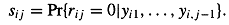
После этого с помощью уравнения логистической регрессии рассчитывается
итоговая оценка предрасположенности sij:
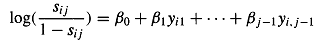
На следующем шаге наблюдаемые значения распределяются по квинтилям в
зависимости от оценок предрасположенности. Квинтиль содержит r полных наблюдений и m неполных наблюдений. После этого из r полных наблюдений создается выборка
с возвращением объемом r
наблюдений, из которой случайно отбирается m наблюдений, которые заменяют пропуски в переменной [9,
p. 304].
Дискриминантная модель, в отличие от первых двух, призвана заполнять
пропуски в дискретных переменных. В ее основе лежит теорема Байеса, в
соответствии с которой определяется вероятность того, что вместо пропуска
стояло бы то или иное значение в случае, если респондент ответил на вопрос [2,
с. 48]. На практике это означает, что на место каждого пропуска подставляется
значение (или, другими словами, наблюдение с пропуском относится к некоторой
категории, поскольку переменная является категориальной) с наибольшей условной
вероятностью, вычисляемой на основании ковариат, отобранных на основании наличия
и выраженности связи с переменной, содержащей пропуски, и распределения
наблюдаемых значений переменной с пропусками [21, p. 58].
Шаг 3: подстановка значений на место каждого пропуска
Этот шаг включает в себя сам алгоритм множественного заполнения пропусков.
Из апостериорного вероятностного распределения, построенного при помощи
выбранной на предыдущем шаге модели заполнения, случайным образом извлекаются m наборов значений интересующей нас
переменной, которые подставляются в неполный массив, в результате чего мы
получаем m полных массивов. Их количество
обычно составляет от 3 до 10, согласно рекомендации Рубина, поскольку большое
количество подстановок не дает существенного увеличения эффективности оценки ε,
вычисляемой по формуле
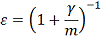 ,
,
где γ - доля пропусков, а m - количество массивов. К примеру, эффективность оценки для 10 массивов и
50% пропусков составляет 95%, а для 5 массивов и 10% пропусков - 99%.
Шаг 4: анализ данных и агрегирование результатов
Классический алгоритм множественного заполнения пропусков предполагает
проведение анализа данных на каждом из сформированных на предыдущем шаге
массивов и агрегирование результатов анализа данных при помощи набора формул -
правила Рубина, - который позволяет вычислить оценки статистических параметров:
точечную оценку, стандартное отклонение, доверительный интервал и значение t-статистики [11, p. 66].
Агрегированная оценка параметра Ǭ (например, выборочная оценка
коэффициента корреляции) будет равна:
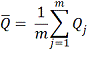
где j - набор данных (j=1,2,...,m), а Uj - стандартная ошибка параметра Qj.
Для оценки агрегированной дисперсии необходимо вычислить внутригрупповую
дисперсию:

и межгрупповую дисперсию:
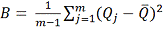 .
.
Тогда общая дисперсия будет равна:
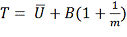 .
.
Доверительные интервалы вычисляются при помощи значения распределения
Стьюдента с df степенями свободы, вычисляемыми по формуле:
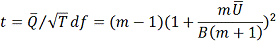
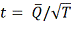
Проверка нулевой гипотезы выполняется при помощи сравнения соотношения с
соответствующим значением распределения Стьюдента [5, с. 205-206].
Как мы видим, метод множественного заполнения пропусков является достаточно
комплексным и трудоемким при условии того, что исследователь (как это обычно и
происходит) придерживается классического алгоритма, то есть анализирует
пропуски, заполняет их, в среднем, три-пять раз, анализирует каждый из
трех-пяти полных массивов, а затем агрегирует результаты. Поэтому для упрощения
работы с этим методом были предприняты неоднократные попытки упрощения
алгоритма в зависимости от исследовательской ситуации.
К примеру, в статье «Pooling multiple
imputations when the sample happens to be the population» [22] рассматривалась ситуация,
когда выборка исследования представляет собой всю генеральную совокупность: в
пример авторы привели ситуацию исследования редких медицинских состояний. В
этом случае классический алгоритм переоценивает дисперсию переменной с
пропусками ввиду использования при агрегировании результатов предположения о
бесконечном объеме генеральной совокупности, из которой отобраны имеющиеся
наблюдения. В результате доверительные интервалы оказываются шире, чем
требуется, что ведет к снижению точности оценки. Для подобных случаев авторы
предлагают упрощенную формулу агрегирования результатов анализа каждого из
полных массивов, которая принимает во внимание дисперсию пропущенных значений,
обусловленную механизмом возникновения пропуска, и игнорирует выборочную
дисперсию.
В исследовании Робина Митры и Джерома Рейтера [18], посвященном
применению метода отбора подобного по вероятности с использованием
множественного заполнения пропусков, сравнивались два метода агрегирования
применительно к задаче измерения эффектов обработки. В первом случае
агрегирование производилось по правилу Рубина, то есть статистический анализ
производился на каждом из m
заполненных массивов, а затем его результаты объединялись. Во втором случае
заполненные значения для всех m
массивов усреднялись и анализ производился на одном полном массиве с
усредненными заполненными значениями. Митра и Рейтер аргументируют легитимность
применения предлагаемого способа агрегирования результатов множественного
заполнения пропусков «интуитивной адекватностью» [18, p. 189]. Контраргументом к этому утверждению может служить
вопрос: не сводится ли множественное заполнение пропусков к заполнению условным
средним в случае применения альтернативного способа агрегирования?
Простой ответ на него можно получить, рассуждая следующим образом.
Основное отличие множественного заполнения пропусков от заполнения условным
средним заключается во введении поправки на неопределенность пропуска:
единичное заполнение предполагает рассмотрение заполненного значения как
фиксированного и известного, а множественное, напротив, берет во внимание
неопределенность, задаваемую вероятностным распределением возможных значений
пропуска в зависимости от наблюдаемых переменных [11, p. 44]. Исходя из этой принципиальной особенности метода,
агрегирование результатов множественного заполнения пропусков при помощи
усреднения подставленных значений не сводится к единичному заполнению и все еще
принимает во внимание данный тип неопределенности. Следовательно, подобный
метод призван упростить работу с алгоритмом без потери комплексного подхода к
анализу и заполнению пропусков. Тем не менее, рассматриваемый исследователями
метод анализа - отбор подобного по вероятности - является достаточно
специфическим и применяется только в случае необходимости оценки эффектов
обработки, а исследований, посвященных сравнению эффективности разных подходов
к агрегированию результатов множественного заполнения пропусков применительно к
более распространенным исследовательским ситуациям, насколько нам известно, не
существует. В связи с этим данное исследование направлено на первичное
сравнение эффективности агрегирования результатов множественного заполнения
пропусков при помощи усреднения подставленных значений с эффективностью
применения правила Рубина для набора исследовательских ситуаций, описываемых
долей пропусков в массиве, шкалой, в которой измерена переменная, содержащая
пропуски, и несколькими распространенными в социологических исследованиях
инструментами анализа данных.
Реализация множественного заполнения пропусков в пакете SPSS
Статистический пакет SPSS
предусматривает две процедуры для работы с пропущенными данными: анализ
пропущенных переменных, включающий инструменты анализа и единичного заполнения
пропусков, и множественное заполнение пропусков, содержащий инструменты для
анализа пропусков, непосредственно направленные на последующую множественную
импутацию, а также сам алгоритм множественного заполнения пропусков. Рассмотрим
вторую процедуру подробнее.
Задача изучения структуры пропущенных данных реализуется при помощи
инструмента Analyze Patterns, который позволяет определить,
является ли она монотонной или немонотонной, выявить переменные с наибольшим
числом пропусков, долю пропущенных данных в массиве и т. д. Инструмент импутирования
Impute Missing Data Values работает следующим образом: после выбора как минимум
двух переменных с пропусками и определения количества импутирований (по
умолчанию их 5) SPSS создает новый
файл, содержащий исходные наблюдения с пропусками и все наборы наблюдений с
импутированиями, то есть если мы, к примеру, имеем 10 неполных наблюдений и 5
импутирований, то результирующий файл будет содержать 60 наблюдений. Кроме
того, создается дополнительные переменные Imputation_, которые по сути являются индикаторами
присутствия по числу импутирований для каждого наблюдения.
По умолчанию алгоритм автоматически оценивает пропуски на монотонность и
выбирает между монотонной моделью и методом Монте-Карло с цепями Маркова, если
пропуски оказываются немонотонными. Кроме того, можно запросить вручную
применение метода Монте-Карло или предиктивную модель, а также назначить
максимальное число итераций. В качестве результата пакет SPSS выдает спецификации метода,
информацию об использованной модели и описательные статистики для переменных с
импутированными значениями в каждом из массивов. Для дальнейшего анализа
переменная, содержащая индикаторы присутствия, используется в качестве
группирующей.
Итак, основные выводы первой главы, посвященной теоретическим основаниям
исследования, заключаются в следующих тезисах:
· сфера применимости исследования ограничивается игнорируемыми
пропусками, поскольку направлено на устранение пропусков в данных уже после
окончания этапа сбора информации;
· исследование направлено на оптимизацию алгоритма
множественного заполнения пропусков - наиболее комплексного и наименее
«жесткого» из распространенных на сегодняшний день методов борьбы с
пропущенными данными - при помощи альтернативного подхода к агрегированию
результатов множественного заполнения пропусков;
· необходимость поиска оптимизированного метода агрегирования
обусловлена тем, что заложенное в классическом алгоритме агрегирование при
помощи правила Рубина является трудоемким и длительным, а исследований,
посвященных альтернативным способам агрегирования в распространенных
исследовательских ситуациях, на данный момент не существует.
Рассмотрев проблему пропусков в социологических исследованиях, основные
методы борьбы с пропусками и специфику такого метода, как множественное
заполнение пропусков, мы можем перейти к описанию методологии проведенного нами
статистического эксперимента.
Глава 2. Методика статистического эксперимента для сравнения
подходов к агрегированию результатов множественного заполнения пропусков
Данная глава посвящена описанию методики статистического эксперимента,
проведенного нами с целью сравнения эффективности применения правила Рубина и
усреднения подставленных значений как подходов к агрегированию результатов
множественного заполнения пропусков.
Этапы эксперимента
Наш эксперимент состоит из 8 последовательных этапов:
. Отбор переменных, позволяющих провести интересующие нас виды анализа:
описательную статистику для переменных, измеренных в номинальной, порядковой и
интервальной шкале, множественную линейную регрессию и поиск связи между двумя
переменными.
. Искусственное формирование эталонного массива из полных наблюдений:
отбор только наблюдений, не содержащих пропусков по всем переменным, отобранным
нами на предыдущем этапе.
. Фиксация эталонных результатов анализа данных: реализация методов
описательной статистики, поиска связи между переменными и множественной
линейной регрессии на эталонном массиве с применением процедуры бутстреп.
. Искусственное внесение в эталонной массив разного количества полностью
случайных пропусков.
. Заполнение пропусков в каждом из сформированных на предыдущем этапе
массивов при помощи множественного заполнения пропусков.
. Реализация методов описательной статистики, поиска связи между
переменными и множественной линейной регрессии на полученных массивах с
применением процедуры бутстреп и агрегирование результатов по правилу Рубина.
. Агрегирование результатов множественного заполнения пропусков через
усреднение подставленных значений для каждого пропуска, реализация методов
описательной статистики, поиска связи между переменными и множественной
линейной регрессии на единичных массивах с усредненными подставленными
значениями с применением процедуры бутстреп.
. Сравнение результатов анализа данных, полученных на шагах 6 и 7, с
эталонными результатами для определения для каждой рассмотренной
исследовательской ситуации наиболее эффективного подхода к агрегированию
результатов множественного заполнения пропусков.
Использование процедуры бутстреп необходимо в рамках статистического
эксперимента для того, чтобы верифицировать полученные выводы об эффективности
каждого подхода к агрегированию результатов множественного заполнения
пропусков. Процедура бутстреп предполагает интервальное оценивание параметров
при помощи извлечения большого количества псевдовыборок с возвращением из
эталонного массива полных наблюдений, то есть каждый объект может попасть в
одну и ту же псевдовыборку несколько раз.
Используя распределение значений параметра, полученных на каждой из
извлеченных выборок, бутстреп позволяет рассчитать стандартную ошибку параметра
и построить доверительный интервал.
По итогам процедуры бутстреп рассчитывается стандартная ошибка
оцениваемого параметра с использованием формулы:
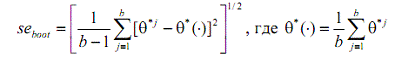 ,
,
где b - количество искусственно созданных
выборок, а θ*j - разброс значений изучаемого параметра на b выборках.
Доверительный интервал строится по следующей формуле:
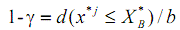 ,
,
где 1-γ - выбранный исследователем уровень значимости, b - количество извлеченных
бутстреп-выборок, х*j - количество оценок среднего на b выборок, принявших значение меньшее,
чем Х*В, Х*В - верхний предел
доверительного интервала.
В соответствии с одной из основных предпосылок статистики - о том, что с
увеличением объема выборки выборочные значения будут приближаться к реальным -
кажется рациональным предположение о том, что с увеличением количества
псевдовыборок оценки параметров будут приближаться к реальным. Тем не менее,
извлечение сотен тысяч псевдовыборок даже на современных компьютерах занимает
значительное время, поэтому для данного исследования мы ограничимся тремя
наборами - 1000, 10 000 и 50 000 выборок - поскольку такое количество выборок
считается достаточным и используется в большинстве публикаций, в которых описываются
результаты, полученные с применением процедуры бутстреп.
Теперь обратимся к подробному описанию реализации каждого этапа
эксперимента.
Отбор переменных для сравнительного анализа эффективности
подходов к агрегированию результатов множественного заполнения пропусков
Переменные, которые использовались нами для демонстрации рассматриваемых
методов анализа данных:
. Описательная статистика: по одной переменной, измеряемой в номинальной,
порядковой и интервальной шкале.
. Поиск связи между признаками:
· две номинальные переменные, между которыми существует
немонотонная статистическая связь, и две номинальные переменные, между которыми
немонотонной связи нет;
· две порядковые переменные, между которыми существует
монотонная статистическая связь, и две порядковые переменные, между которыми
монотонная связь отсутствует;
· две интервальные переменные, между которыми существует
линейная статистическая связь, и две интервальные переменные, между которыми
линейная связь отсутствует.
. Для построения модели множественной линейной регрессии: одна
интервальная переменная на роль зависимой, две интервальные переменные на роль
предикторов с незначимыми регрессионными коэффициентами и две интервальные
переменные на роль предикторов со значимыми регрессионными коэффициентами.
Таким образом, в сумме необходимо отобрать по три или четыре переменных,
измеренных в порядковой и номинальной шкале, а также от пяти до девяти
интервальных переменных, в зависимости от возможности многократного
использования одной и той же переменной для разных исследовательских ситуаций.
В итоге нами были отобраны 13 переменных:
Таблица 1. Переменные, отобранные для эксперимента
|
№
|
Переменная
|
Смысл переменной
|
Шкала
|
Вид анализа
|
|
1
|
gndr
|
Пол респондента
|
номинальная
|
Поиск связи (наличие,
отсутствие)
|
|
2
|
domicil
|
Тип населенного пункта
|
номинальная
|
Описательная статистика,
поиск связи (отсутствие)
|
|
3
|
emplrel
|
Трудовые отношения, в
которых состоит респондент
|
номинальная
|
Поиск связи (наличие)
|
|
4
|
polintr
|
Заинтересованность в
политике
|
порядковая
|
Описательная статистика,
поиск связи (наличие)
|
|
5
|
tvpol
|
Время просмотра новостей по
телевизору в рабочий день
|
порядковая
|
Поиск связи (наличие)
|
|
6
|
prtdgcl
|
Степень близости к
определенной партии
|
порядковая
|
Поиск связи (отсутствие)
|
|
7
|
health
|
Субъективная общая оценка
здоровья
|
порядковая
|
Поиск связи (отсутствие)
|
|
8
|
lrscale
|
Положение на шкале «левое
крыло - правое крыло»
|
интервальная
|
Поиск связи (отсутствие)
|
|
9
|
eduyrs
|
Количество лет полученного
очного образования
|
интервальная
|
Описательная статистика,
поиск связи (отсутствие), регрессия (незначимый предиктор)
|
|
10
|
plinsoc
|
Положение в обществе
|
интервальная
|
Поиск связи (наличие),
регрессия (зависимая переменная)
|
|
11
|
happy
|
Субъективная оценка уровня
счастья
|
интервальная
|
Поиск связи (наличие),
регрессия (значимый предиктор)
|
|
12
|
stfedu
|
Уровень удовлетворенности
системой образования
|
интервальная
|
Регрессия (незначимый
предиктор)
|
|
13
|
agea
|
Возраст респондента
|
интервальная
|
Регрессия (значимый
предиктор)
|
Необходимо заметить, что значимые и незначимые предикторы для
множественной линейной регрессии мы отобрали двух типов: один значимый и один
незначимый предиктор измерены в истинной интервальной шкале («длительность
очного образования» и «возраст респондента»), а еще один значимый и один
незначимый («уровень счастья» и «удовлетворенность системой образования») - в
11-балльной шкале, которую, тем не менее, рассматривают как интервальную в
исследовательской практике в большинстве случаев, поскольку, учитывая такое
большое количество градаций, респондент едва ли способен дифференцировать расстояния
между градациями 1 и 2 или 7 и 8, а именно равенство и порядок не только для
объектов, но и для расстояний между ними является основным признаком
интервальной шкалы. Тем не менее, подобный отбор в случае обнаружения отличий
может позволить сделать определенные выводы относительно более эффективного
метода агрегирования результатов заполнения пропусков и наметить дальнейшие
направления для исследований в этой области.
Формирование эталонного массива
В качестве основы для статистического эксперимента мы использовали массив
респондентов из России, принявших участие в шестой волне Европейского
социального исследования, проведенного в 2012 году. Кроме того, для получения
эталонного массива нами отобраны только полные наблюдения, то есть те, которые
не имеют ни одного пропуска в отобранных нами на предыдущем шаге переменных. Из
промежуточного массива, содержащего 2484 наблюдения, были удалены все
наблюдения, содержащие хотя бы один пропуск, при помощи команды вида:
Select if (not missing(Var1) … and not missing(Var13).,
где Var1 … Var13 - оставленные в массиве переменные.
В результате были отобраны 613 полных наблюдений. Отсеиванию подверглось
более 75% наблюдений, поэтому содержательный смысл результатов анализа не
следует считать надежным, однако для экспериментальных целей данного
исследования подобная ситуация ущерба не несет.
Фиксация эталонных результатов анализа данных
На полученном в предыдущем шаге эталонном массиве без пропусков
реализуются все запланированные нами виды анализа и с использованием процедуры
бутстреп фиксируются следующие параметры:
· для описательной статистики: выборочные доли, стандартные
ошибки и доверительные интервалы для долей людей, проживающих в населенных
пунктах разного типа (номинальная переменная), долей людей с разной степенью
заинтересованности в политике (порядковая переменная) и среднего
арифметического и дисперсии среднего количества лет очного образования
(интервальная переменная);
· для поиска связи между двумя признаками: выборочное значение,
значимость, стандартная ошибка и доверительный интервал для а) коэффициента V Крамера в случаях наличия
(переменные «пол» и «трудовые отношения») и отсутствия (переменные «пол» и «тип
населенного пункта проживания») немонотонной связи; б) для коэффициента
ранговой корреляции Спирмена в случаях наличия (переменные «заинтересованность
в политике» и «длительность просмотра новостей по телевизору в будний день») и
отсутствия (переменные «близость к партии» и «субъективная оценка здоровья»)
монотонной связи, и в) для коэффициента корреляции Пирсона в случаях наличия
(переменные «уровень счастья» и «положение в обществе») и отсутствия
(переменные «положение на шкале левое-правое крыло» и «количество лет очного
образования») линейной связи;
· для множественной линейной регрессии: выборочные значения,
значимость, стандартные ошибки и доверительные интервалы для константы
(переменная «положение в обществе») и значимых (при переменных «уровень
счастья», «возраст») и незначимых (при переменных «количество лет очного
образования», «удовлетворенность системой образования») регрессионных
коэффициентов.
Результаты вычисления эталонных параметров приведены в Приложении 1.
Внесение в массив искусственных пропусков
Для охвата большего количества возможных исследовательских ситуаций было
принято решение создать три экспериментальных массива: с 10%, 30% и 50%
пропусков. Выбор таких долей был обусловлен следующими рассуждениями: 10%
пропусков - это та доля, которой, с одной стороны, зачастую легче пренебречь, а
с другой - достаточно существенная потеря информации; 50% пропусков - это тот
максимум, после которого странным представляется восстановление бóльшей части отсутствующей информации
за счет меньшей; 30% пропусков представляют середину между условной минимальной
(10%) и максимальной (50%) долей пропусков.
В силу ограниченности временных ресурсов в данном эксперименте не
моделируется случай частично случайных пропусков.
Полностью случайные пропуски вносились в эталонный массив следующим
образом:
. Эталонный массив был перенесен в приложение Excel и каждому наблюдению был присвоен идентификационный
номер.
. При помощи команды СЛЧИС к базе была добавлена новая переменная,
присваивающая каждому наблюдению случайное число от 1 до 613. Наблюдения были
отсортированы по новой переменной, после чего из столбца, содержащего значения
первой экспериментальной переменной были удалены первые 10% значений (расчет
количества наблюдений, которые необходимо удалить для создания необходимой доли
пропусков, см. в таблице 12). Далее была создана еще одна переменная, случайным
образом присваивающая наблюдениям числа от 1 до 613, наблюдения снова
сортировались по этой переменной, и из второй экспериментальной переменной
удалялись первые 10% значений. Этот шаг был повторен 13 раз (по числу
экспериментальных переменных). Создание случайной нумерации для внесения
пропусков в каждую экспериментальную переменную необходимо для того, чтобы
пропуски содержались не в одних и тех же наблюдениях, поскольку в этом случае
наблюдения, оказавшиеся в начале списка обратились бы в полные неответы, к
которым неприменим метод множественного заполнения пропусков.
. Полученный экспериментальный массив с 10% искусственных пропусков был
отсортирован по идентификационному номеру респондента и перенесен обратно в SPSS. Вся процедура повторялась еще два
раза для создания массивов с 30% и 50% искусственных пропусков.
Таблица 2. Расчет количества подлежащих удалению из эталонного массива
значений каждой переменной для создания экспериментальных массивов с 10%, 30% и
50% искусственных пропусков
|
Массив
|
Исходное количество
значений
|
Количество значений каждой
переменной, подлежащих удалению
|
|
С 10% пропусков
|
613
|
61
|
|
С 30% пропусков
|
613
|
184
|
|
С 50% пропусков
|
613
|
306
|
Таким образом, внесенные нами в каждый массив пропуски являются полностью
случайными. Поскольку в полученных массивах на каждую переменную приходится как
минимум одна переменная, с которой у первой наблюдается статистическая связь
(ввиду характера тестируемых методов анализа данных) внесение дополнительных
переменных, позволяющих более точно рассчитать подставляемые на следующем шаге
значения не является обязательным - они уже присутствуют в массиве.
По итогам данного этапа нами были поучены три массива данных с 10, 30 и
50% полностью случайных пропусков.
Заполнение пропусков в экспериментальных массивах
Искусственные пропуски в созданных на предыдущем шаге экспериментальных
массивах заполняются при помощи алгоритма множественного заполнения пропусков с
созданием пяти заполненных массивов на каждый экспериментальный с пропусками.
В модель заполнения, автоматически выбираемую SPSS, мы ввели все имеющиеся в массиве переменные.
Поскольку на каждую из этих переменных в массиве имеется как минимум одна
другая переменная, с которой наблюдается статистическая связь, введение в
массив и модель дополнительных переменных для повышения точности расчетов
импутируемых значений не требуется.
В связи с тем, что модели импутации для номинальных переменных «тип
населенного пункта» и «трудовые отношения», строящиеся при использовании
настроек по умолчанию, включали слишком много параметров, в модель были внесены
следующие корректировки:
. максимальное число разрешенных параметров для модели импутации было
увеличено со 100 до 500 при помощи внесения в подкоманду IMPUTE строчки MAXMODELPARAM=500; данная коррекция не влияет на
качество заполнения, а лишь увеличивает время выполнения команды.
. Интервальные переменные «положение на шкале левое-правое крыло»,
«количество лет очного образования» и «удовлетворенность системой образования»,
были только импутированы, но не использовались в качестве предикторов для
других моделей импутации, поскольку эти переменные создавали большое количество
категорий для логистической регрессии, рассчитывающей значения для заполнения
пропусков в дискретных переменных, но сами по себе ввиду их слабых или
отсутствующих связей со многими переменными в модели не несли особой пользы для
расчетов значений для заполнения прочих переменных.
В качестве метода импутации нами была выбрана полностью условная
спецификация, поскольку структура пропущенных данных в экспериментальных
массивах немонотонная, в качестве модели для импутации количественных
переменных - линейная регрессия, для дискретных переменных SPSS по умолчанию применяет логистическую
регрессию. Итогом данного шага стали 15 массивов, состоящих из полных
наблюдений с импутированными значениями, по 5 для каждой из трех возможных
долей искусственных пропусков.
Анализ данных на отдельных массивах с заполненными пропусками
и агрегирование с применением правила Рубина
На каждом из 15 полученных массивов реализуются те же операции, что
проводились на эталонном массиве, после чего результаты анализа данных
агрегируются с применением правила Рубина и процедуры бутстреп для каждого из
экспериментальных массивов с разными долями заполненных значений. В используемом
нами пакете SPSS не автоматизирована процедура
бутстреп для импутированных данных, поэтому агрегирование показателей
производилась вручную с использованием приложения Excel на основании результатов бутстрепа в каждом из
подмассивов (интересующего нас показателя и его стандартной ошибки) с
применением уже описанных нами формул:
1. Для рассчета показателя:
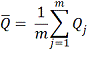
: Для оценки агрегированной стандартной ошибки - внутригрупповая
дисперсия:

и межгрупповая дисперсия:
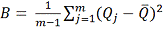 ,
,
при помощи которых вычислялась общая дисперсия:
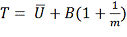 .
.
. Для проверки гипотез - критическое значение t-статистики со степенями свободы, рассчитанными по формуле:
 ,
,
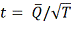
И t-эмпирическим, равным .
Результаты расчета агрегированных при помощи правила Рубина результатов
анализа данных приведены в Приложении 2.
Агрегирование при помощи усреднения пропущенных значений и
анализ данных на усредненных массивах
На этом этапе используются 15 массивов, полученные на шаге 5 в результате
множественного заполнения пропусков в трех массивах разными долями пропущенных
значений.
Для пяти массивов, содержащих по 10% заполненных данных, мы производим
усреднение заполненных значений по следующей схеме:
· подставленные значения в переменных, измеренных по
номинальной шкале, «усредняются» при помощи моды:
· подставленные значения в переменных, измеренных по порядковой
шкале, «усредняются» при помощи медианы;
· подставленные значения в переменных, измеренных по
интервальной шкале, усредняются при помощи среднего арифметического.
Эти же операции мы производим для пяти массивов с 30% пропусков и для
пяти массивов с 50% пропусков, получая в результате три массива с усредненными
подставленными значениями. Для того, чтобы усреднить результаты множественного
заполнения пропусков и снова получить единый массив, нами были предприняты
следующие практические действия.
В приложении Excel для каждого
наблюдения были сопоставлены пять значений каждой переменной и усреднены при
помощи соответствующей меры центральной тенденции. Мы не дифференцировали
значения, подставленные в результате множественного заполнения, и значения, не
подвергшиеся удалению на шаге внесения искусственных пропусков («изначальные»
ответы респондентов), поскольку последние не изменяются от массива к массиву, а
мерой центральной тенденции для пяти одинаковых чисел, очевидно, будет само это
число. Усредненные таким образом значения были снова отсортированы по столбцу ID и благодаря этому мы смогли
перенести их в новую базу данных SPSS в
том же порядке, в котором они располагались в изначальном массиве с пропусками.
Результатом этой процедуры стали три массива из полных наблюдений, в
которых было восстановлено 10%, 30% и 50% пропусков, на которых мы произвели
анализ данных по той же схеме, что и на эталонном массиве, получая тот же набор
доверительных интервалов для статистик с применением процедуры бутстреп.
Сравнение результатов анализа данных с применением разных
подходов к агрегированию результатов множественного заполнения пропусков с
эталонными
Для того, чтобы сравнить эффективность подходов к агрегированию
результатов множественного заполнения пропусков, мы используем два основных
критерия, введенных для схожих целей в [4].
Первым критерием эффективности подхода к агрегированию результатов
множественного заполнения пропусков будет служить пересечение эталонного
доверительного интервала для оценки параметра с доверительным интервалом
оценки, полученной на каждом из заполненных массивов, образованных на этапах 7
и 8, в рамках конкретной исследовательской ситуации, которое мы будем оценивать
при помощи степени отклонения доверительных интервалов (Δ):
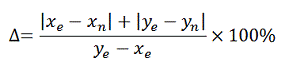 ,
,
гдеe - нижняя граница эталонного доверительного интервалаn
- нижняя граница доверительного интервала, полученная после заполнения
пропусков e - верхняя граница эталонного доверительного интервалаn - верхняя граница доверительного
интервала, полученная после заполнения пропусков.
Формула, таким образом, выражает отношение абсолютного отклонения
доверительного интервала, полученного после заполнения пропусков, от эталонного
доверительного интервала, к длине эталонного доверительного интервала. Критерий
принимает значения от нуля (в том случае, когда доверительный интервал после
заполнения пропусков совпадает с эталонным доверительным интервалом) до
бесконечности, следовательно, чем меньше значение показателя, тем эффективнее
подход к агрегированию результатов множественного заполнения пропусков.
Второй критерий заключается в оценке устойчивости доверительных
интервалов при изменении количества выборок, создаваемых при помощи процедуры
бутстреп. Под устойчивостью в данном случае подразумевается неизменность
доверительных интервалов при разном количестве извлекаемых бутстрепом выборок.
В следующей главе мы сравним результаты, полученные с помощью каждого
подхода к агрегированию результатов множественного заполнения пропусков. На
основе результатов этого сравнения мы сможем составить набор рекомендаций по
выбору подхода для описанных нами выше исследовательских ситуаций.
Глава 3. Сравнительный анализ подходов к агрегированию
результатов множественного заполнения пропусков
В данной главе мы рассмотрим результаты сравнения эффективности подходов
к агрегированию результатов множественного заполнения пропусков. Как говорилось
выше, сравнение будет производиться на основании двух критериев - степени
пересечения доверительных интервалов с эталоном и устойчивости результатов при
увеличении количества извлекаемых с помощью бутстрепа выборок - для каждой из смоделированных
нами исследовательских ситуаций.
Описательная статистика
Рассмотрим степени отклонения доверительных интервалов в ситуации 10%
пропущенных значений в массиве и вычисления доверительных интервалов для долей
применительно к интервальной шкале.
Таблица 3. Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки долей значений номинальной переменной в
массиве с 10% импутированных значений
|
Количество извлеченных
выборок
|
Значение признака
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
1000
|
Мегаполис
|
Правило Рубина
|
40,8
|
36,9
|
44,7
|
39%
|
|
|
Усреднение
|
41,6
|
37,8
|
45,7
|
16%
|
|
Пригород
|
Правило Рубина
|
6,4
|
4,5
|
8,3
|
203%
|
|
|
Усреднение
|
6,7
|
4,7
|
8,6
|
221%
|
|
Маленький город
|
Правило Рубина
|
33
|
29,3
|
36,7
|
27%
|
|
|
Усреднение
|
29,2
|
25,3
|
33,1
|
130%
|
|
Деревня
|
Правило Рубина
|
16,3
|
13,2
|
19,3
|
127%
|
|
|
Усреднение
|
19,6
|
16,6
|
23
|
16%
|
|
10 000
|
Мегаполис
|
Правило Рубина
|
40,8
|
36,9
|
44,7
|
37%
|
|
|
Усреднение
|
41,6
|
37,7
|
45,5
|
16%
|
|
Пригород
|
Правило Рубина
|
6,4
|
4,5
|
8,3
|
207%
|
|
|
Усреднение
|
6,7
|
4,7
|
8,6
|
225%
|
|
Маленький город
|
Правило Рубина
|
33
|
29,3
|
36,7
|
28%
|
|
|
Усреднение
|
32,1
|
28,5
|
35,9
|
49%
|
Правило Рубина
|
19,8
|
16,6
|
23
|
16%
|
|
|
Усреднение
|
19,6
|
16,5
|
22,8
|
20%
|
|
Количество извлеченных
выборок
|
Значение признака
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
50 000
|
Мегаполис
|
Правило Рубина
|
40,8
|
36,9
|
44,7
|
37%
|
|
|
Усреднение
|
41,6
|
37,7
|
45,5
|
16%
|
|
Пригород
|
Правило Рубина
|
6,4
|
4,5
|
8,3
|
207%
|
|
|
Усреднение
|
6,7
|
4,7
|
8,6
|
225%
|
|
Маленький город
|
Правило Рубина
|
33
|
29,3
|
36,7
|
28%
|
|
|
Усреднение
|
32,1
|
28,5
|
35,9
|
49%
|
|
Деревня
|
Правило Рубина
|
19,8
|
16,6
|
23
|
16%
|
|
|
Усреднение
|
19,6
|
16,5
|
22,7
|
22%
|
Только для самой большой выборочной доли признака усреднение
подставленных значений показало большую эффективность, чем правило Рубина. Если
рассматривать все четыре доли, то правило Рубина оказалось эффективнее (то есть
дало результаты, которые оказались ближе к эталонным) или настолько же
эффективно, как усреднение подставленных значений (к примеру, для доли людей,
проживающих в деревне, при извлечении 10 000 выборок разница в долях составила
всего 4%, что можно списать на статистическую погрешность), в трех случаях из
четырех, и этот результат оставался неизменным при увеличении количества
выборок, извлекаемых процедурой бутстреп.
Таблица 4. Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки долей номинальной переменной в массиве с 30%
импутированных значений
|
Количество извлеченных
выборок
|
Значение признака
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
1000
|
Мегаполис
|
Правило Рубина
|
39,9
|
36
|
43,7
|
62%
|
|
|
Усреднение
|
39,5
|
35,6
|
43,2
|
73%
|
|
Пригород
|
Правило Рубина
|
11,7
|
9,1
|
14,3
|
569%
|
|
|
Усреднение
|
13,9
|
11,3
|
16,6
|
724%
|
|
Маленький город
|
Правило Рубина
|
30,3
|
26,7
|
34
|
99%
|
|
|
Усреднение
|
29,2
|
25,3
|
33,1
|
130%
|
|
Деревня
|
Правило Рубина
|
18,1
|
15,1
|
21,2
|
67%
|
|
|
Усреднение
|
17,5
|
14,5
|
20,6
|
86%
|
|
Количество извлеченных
выборок
|
Значение признака
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
10 000
|
Мегаполис
|
Правило Рубина
|
39,9
|
36
|
43,7
|
61%
|
|
|
Усреднение
|
39,5
|
35,7
|
43,4
|
68%
|
|
Пригород
|
Правило Рубина
|
11,7
|
9,1
|
14,3
|
586%
|
|
|
Усреднение
|
13,9
|
11,1
|
16,6
|
739%
|
|
Маленький город
|
Правило Рубина
|
30,3
|
26,7
|
34
|
99%
|
|
|
Усреднение
|
29,2
|
25,6
|
32,8
|
129%
|
|
Деревня
|
Правило Рубина
|
18,1
|
15,1
|
21,2
|
67%
|
|
|
Усреднение
|
17,5
|
14,5
|
20,6
|
86%
|
|
50 000
|
Мегаполис
|
Правило Рубина
|
39,9
|
36
|
43,7
|
61%
|
|
|
Усреднение
|
39,5
|
35,7
|
43,4
|
68%
|
|
Пригород
|
Правило Рубина
|
11,7
|
9,1
|
14,3
|
586%
|
|
|
Усреднение
|
13,9
|
11,3
|
16,6
|
746%
|
|
Маленький город
|
Правило Рубина
|
30,3
|
26,7
|
34
|
99%
|
|
|
Усреднение
|
29,2
|
25,6
|
32,8
|
129%
|
|
Деревня
|
Правило Рубина
|
18,1
|
15,1
|
21,2
|
67%
|
|
|
Усреднение
|
17,5
|
14,5
|
20,6
|
86%
|
В массивах с 30% подставленных значений в каждом случае доверительный
интервал, рассчитанный при помощи правила Рубина, оказывался ближе к
эталонному, чем вычисленный на аналогичном усредненном массиве. Минимальная
разница в степени отклонения составила 7%, максимальная - 178%, причем
результаты демонстрируют высокую устойчивость при увеличении количества извлекаемых
выборок. Для массивов с 30% пропусков, таким образом, более эффективным
оказалось правило Рубина.
Таблица 5 Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки долей номинальной переменной в массиве с 50%
импутированных значений
|
Количество извлеченных
выборок
|
Значение признака
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
1000
|
Мегаполис
|
Правило Рубина
|
35,4
|
31,6
|
39,2
|
171%
|
|
|
Усреднение
|
35,9
|
32,1
|
39,5
|
161%
|
|
Пригород
|
Правило Рубина
|
17,1
|
14,1
|
20,1
|
941%
|
|
|
Усреднение
|
19,7
|
16,6
|
23
|
1128%
|
|
Маленький город
|
Правило Рубина
|
29,5
|
25,9
|
33,2
|
120%
|
|
|
Усреднение
|
27,6
|
24
|
31
|
176%
|
|
Деревня
|
Правило Рубина
|
17,9
|
14,8
|
21
|
75%
|
|
|
Усреднение
|
16,8
|
13,9
|
19,7
|
109%
|
|
Количество извлеченных
выборок
|
Значение признака
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
10 000
|
Мегаполис
|
Правило Рубина
|
35,4
|
31,6
|
39,2
|
173%
|
|
|
Усреднение
|
35,9
|
32,1
|
39,6
|
162%
|
|
Пригород
|
Правило Рубина
|
17,1
|
14,1
|
20,1
|
971%
|
|
|
Усреднение
|
19,7
|
16,6
|
23
|
1164%
|
|
Маленький город
|
Правило Рубина
|
29,5
|
25,9
|
33,2
|
120%
|
|
|
Усреднение
|
27,6
|
24
|
31,2
|
172%
|
|
Деревня
|
Правило Рубина
|
17,9
|
14,8
|
21
|
75%
|
|
|
Усреднение
|
16,8
|
13,9
|
19,7
|
109%
|
|
50 000
|
Мегаполис
|
Правило Рубина
|
35,4
|
31,6
|
39,2
|
173%
|
|
|
Усреднение
|
35,9
|
32,1
|
39,6
|
162%
|
|
Пригород
|
Правило Рубина
|
17,1
|
14,1
|
20,1
|
971%
|
|
|
Усреднение
|
19,7
|
16,6
|
23
|
1164%
|
|
Маленький город
|
Правило Рубина
|
29,5
|
25,9
|
33,2
|
120%
|
|
|
Усреднение
|
27,6
|
31,2
|
172%
|
|
Деревня
|
Правило Рубина
|
17,9
|
14,8
|
21
|
75%
|
|
|
Усреднение
|
16,8
|
13,9
|
19,7
|
109%
|
Ожидаемо, на массивах с 50% пропусков оба подхода показали достаточно
низкую эффективность: для самой маленькой выборочной доли из четырех степень
отклонения доверительного интервала достигает 1164%, в остальном же результаты
повторяют полученные на массиве с 10% подставленных значений: доверительный
интервал для самой большой выборочной доли оказывается ближе к эталонному при
использовании усреднения подставленных значений, а для всех остальных - при
использовании правила Рубина.
Таким образом, при любом количестве пропусков в массиве для описания
номинальной переменной более эффективным подходом оказывается применение
правила Рубина.
Далее рассмотрим результаты сравнения эффективности подходов
применительно к описательной статистике для порядковых переменных, где мы также
использовали доли значений признака для описания переменной.
Таблица 6. Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки долей порядковой переменной в массиве с 10%
импутированных значений
|
Количество извлеченных
выборок
|
Значение признака
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
1000
|
Очень заинтересован
|
Правило Рубина
|
17,5
|
14,5
|
20,6
|
25%
|
|
|
Усреднение
|
17,1
|
14,4
|
20,1
|
14%
|
|
Довольно заинтересован
|
Правило Рубина
|
42,4
|
38,5
|
46,3
|
0%
|
|
|
Усреднение
|
44
|
40,5
|
48
|
47%
|
|
Едва ли заинтересован
|
Правило Рубина
|
29,8
|
26,2
|
33,4
|
25%
|
|
|
Усреднение
|
29,4
|
25,9
|
32,8
|
38%
|
|
Совершенно не заинтересован
|
Правило Рубина
|
10,3
|
7,9
|
12,7
|
6%
|
|
|
Усреднение
|
9,5
|
7,2
|
11,7
|
29%
|
|
10 000
|
Очень заинтересован
|
Правило Рубина
|
17,5
|
14,5
|
20,6
|
26%
|
|
|
Усреднение
|
17,1
|
14,2
|
20,2
|
14%
|
|
Довольно заинтересован
|
Правило Рубина
|
42,6
|
38,7
|
46,5
|
0%
|
|
|
Усреднение
|
44
|
40,1
|
48,1
|
38%
|
|
Едва ли заинтересован
|
Правило Рубина
|
29,8
|
26,2
|
33,4
|
26%
|
|
|
Усреднение
|
29,4
|
25,8
|
33
|
37%
|
|
Совершенно не заинтересован
|
Правило Рубина
|
10,3
|
7,9
|
12,7
|
11%
|
|
|
Усреднение
|
9,5
|
7,2
|
11,9
|
21%
|
|
50 000
|
Очень заинтересован
|
Правило Рубина
|
17,5
|
14,5
|
20,6
|
26%
|
|
|
Усреднение
|
17,1
|
14,2
|
20,2
|
14%
|
|
Довольно заинтересован
|
Правило Рубина
|
42,6
|
38,7
|
46,5
|
0%
|
|
|
Усреднение
|
44
|
40,1
|
48,1
|
38%
|
|
Едва ли заинтересован
|
Правило Рубина
|
29,8
|
26,2
|
33,4
|
26%
|
|
|
Усреднение
|
29,4
|
25,8
|
33
|
37%
|
|
Совершенно не заинтересован
|
Правило Рубина
|
10,3
|
7,9
|
12,7
|
11%
|
|
|
Усреднение
|
9,5
|
7,2
|
11,9
|
21%
|
Для массива с 10% подставленных значений ситуация аналогична той, которую
мы наблюдали в результатах анализа номинальной переменной: при любом количестве
извлеченных выборок наиболее близкие к эталонным результаты, а значит и более
высокую эффективность, показывает применение правила Рубина для всех долей,
кроме доли значения «Очень заинтересован». Отклонение в пользу усреднения для
этого значения признака составило 11-12%, а в пользу правила Рубина для всех
остальных долей - от 10% до 47%. Для данной исследовательской ситуации, таким
образом, более эффективным подходом к агрегированию результатов множественного
заполнения пропусков можно назвать применение правила Рубина.
Таблица 7. Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки долей порядковой переменной в массиве с 30%
импутированных значений
|
Количество извлеченных
выборок
|
Значение признака
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
1000
|
Очень заинтересован
|
Правило Рубина
|
39,5
|
35,7
|
43,4
|
796%
|
|
|
Усреднение
|
15,7
|
12,7
|
18,8
|
39%
|
|
Довольно заинтересован
|
Правило Рубина
|
39,5
|
35,7
|
43,4
|
73%
|
|
|
Усреднение
|
44,9
|
40,8
|
48,6
|
59%
|
|
Едва ли заинтересован
|
Правило Рубина
|
27,8
|
24,3
|
31,4
|
79%
|
|
|
Усреднение
|
30,3
|
26,6
|
34,1
|
10%
|
|
Совершенно не заинтересован
|
Правило Рубина
|
15,7
|
12,8
|
18,6
|
227%
|
|
|
Усреднение
|
9,1
|
7
|
11,3
|
41%
|
|
10 000
|
Очень заинтересован
|
Правило Рубина
|
39,5
|
35,7
|
43,4
|
784%
|
|
|
Усреднение
|
15,7
|
12,9
|
18,6
|
36%
|
|
Довольно заинтересован
|
Правило Рубина
|
39,5
|
35,7
|
43,4
|
78%
|
|
|
Усреднение
|
44,9
|
40,9
|
48,8
|
58%
|
|
Едва ли заинтересован
|
Правило Рубина
|
27,8
|
24,3
|
31,4
|
79%
|
|
|
Усреднение
|
30,3
|
26,8
|
34,1
|
8%
|
|
Совершенно не заинтересован
|
Правило Рубина
|
15,7
|
12,8
|
18,6
|
240%
|
|
|
Усреднение
|
9,1
|
6,9
|
11,4
|
38%
|
|
50 000
|
Очень заинтересован
|
Правило Рубина
|
39,5
|
35,7
|
43,4
|
784%
|
|
|
Усреднение
|
15,7
|
12,9
|
18,6
|
36%
|
|
Довольно заинтересован
|
Правило Рубина
|
39,5
|
35,7
|
43,4
|
78%
|
|
|
Усреднение
|
44,9
|
40,9
|
48,8
|
58%
|
|
Едва ли заинтересован
|
Правило Рубина
|
27,8
|
24,3
|
31,4
|
79%
|
|
|
Усреднение
|
30,3
|
26,8
|
34
|
10%
|
|
Совершенно не заинтересован
|
Правило Рубина
|
15,7
|
12,8
|
18,6
|
240%
|
|
|
Усреднение
|
9,1
|
6,9
|
11,4
|
38%
|
Для массива с 30% пропусков ситуация обстоит иначе: доверительные
интервалы для всех четырех долей при любом количестве извлеченных выборок более
точно (ближе к эталонному результату) оценивались в том случае, если
агрегирование производилось при помощи усреднения подставленных значений.
Результат, таким образом, можно назвать устойчивым, а отклонение доверительных
интервалов в пользу усреднения подставленных значений составило от 14% до 748%.
Таблица 8. Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки долей порядковой переменной в массиве с 50%
импутированных значений
|
Количество извлеченных
выборок
|
Значение признака
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
1000
|
Очень заинтересован
|
Правило Рубина
|
19,1
|
16
|
22,2
|
79%
|
|
|
Усреднение
|
17,1
|
14,2
|
20,1
|
11%
|
|
Довольно заинтересован
|
Правило Рубина
|
38,7
|
34,8
|
42,5
|
96%
|
|
|
Усреднение
|
51,4
|
47
|
55,1
|
222%
|
|
Едва ли заинтересован
|
Правило Рубина
|
25,9
|
22,4
|
29,3
|
135%
|
|
|
Усреднение
|
25,4
|
22,2
|
29,2
|
139%
|
|
Совершенно не заинтересован
|
Правило Рубина
|
16,4
|
13,5
|
255%
|
|
|
Усреднение
|
6
|
4,2
|
8
|
165%
|
|
10 000
|
Очень заинтересован
|
Правило Рубина
|
19,1
|
16
|
22,2
|
79%
|
|
|
Усреднение
|
17,1
|
14,2
|
20,1
|
12%
|
|
Довольно заинтересован
|
Правило Рубина
|
38,7
|
34,8
|
42,5
|
101%
|
|
|
Усреднение
|
38,7
|
34,8
|
42,5
|
101%
|
|
Едва ли заинтересован
|
Правило Рубина
|
25,9
|
22,4
|
29,3
|
134%
|
|
|
Усреднение
|
25,4
|
22
|
28,9
|
145%
|
|
Совершенно не заинтересован
|
Правило Рубина
|
16,4
|
13,5
|
19,3
|
270%
|
|
|
Усреднение
|
6
|
4,2
|
8
|
168%
|
|
50 000
|
Очень заинтересован
|
Правило Рубина
|
19,1
|
16
|
22,2
|
79%
|
|
|
Усреднение
|
17,1
|
14,2
|
20,1
|
12%
|
|
Довольно заинтересован
|
Правило Рубина
|
38,7
|
34,8
|
42,5
|
101%
|
|
|
Усреднение
|
38,7
|
34,8
|
42,5
|
101%
|
|
Едва ли заинтересован
|
Правило Рубина
|
25,9
|
22,4
|
29,3
|
134%
|
|
|
Усреднение
|
25,4
|
22
|
28,9
|
145%
|
|
Совершенно не заинтересован
|
Правило Рубина
|
16,4
|
13,5
|
19,3
|
270%
|
|
|
Усреднение
|
6
|
4,2
|
8
|
168%
|
Применительно к массиву с 50% пропусков оба подхода имеют одинаковую
эффективность при любом количестве извлеченных выборок: для 1 000 выборок
правило Рубина и усреднение оказались эффективнее по два раза из четырех, для
10 000 и 50 000 выборок в двух случаях эффективнее оказывалось усреднение, в
одном - правило Рубина, и еще в одном оба подхода были эффективны в равной
степени. Мы можем сделать общий для описания порядковой переменной вывод, что в
ситуации этой ситуации подход к агрегированию следует выбирать в зависимости от
доли пропусков в массиве: для 10% пропусков более эффективным оказывается
применение правила Рубина, для 30% - усреднение подставленных значений до
проведения анализа данных, а для 50% пропусков оба подхода имеют одинаковую
эффективность.
Таблица 9. Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки среднего и дисперсии количества лет очного
образования
|
Доля пропусв
|
Кол-тво извлеч выбок
|
Параметр
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
10%
|
1000
|
Среднее
|
Правило Рубина
|
13,07
|
13,04
|
13,10
|
87%
|
|
|
|
Усреднение
|
13,07
|
12,85
|
13,30
|
21%
|
|
|
Дисперсия
|
Правило Рубина
|
8,61
|
8,55
|
8,67
|
95%
|
|
|
|
Усреднение
|
8,077
|
6,966
|
9,293
|
28%
|
|
10 000
|
Среднее
|
Правило Рубина
|
13,07
|
13,04
|
13,10
|
87%
|
|
|
|
Усреднение
|
13,07
|
12,85
|
13,29
|
26%
|
|
|
Дисперсия
|
Правило Рубина
|
8,61
|
8,55
|
8,67
|
95%
|
|
|
|
Усреднение
|
8,077
|
7,004
|
9,242
|
27%
|
|
50 000
|
Среднее
|
Правило Рубина
|
13,07
|
13,04
|
13,10
|
87%
|
|
|
|
Усреднение
|
13,07
|
12,85
|
13,29
|
26%
|
|
|
Дисперсия
|
Правило Рубина
|
8,61
|
8,55
|
8,67
|
95%
|
|
|
|
Усреднение
|
8,077
|
7,009
|
9,245
|
27%
|
|
30%
|
1000
|
Среднее
|
Правило Рубина
|
13,06
|
13,03
|
13,09
|
87%
|
|
|
|
Усреднение
|
13,05
|
12,87
|
13,25
|
28%
|
|
|
Дисперсия
|
Правило Рубина
|
0,08
|
8,02
|
8,14
|
95%
|
|
|
|
Усреднение
|
6,150
|
5,327
|
6,920
|
204%
|
|
10 000
|
Среднее
|
Правило Рубина
|
13,06
|
13,03
|
13,09
|
87%
|
|
|
|
Усреднение
|
13,05
|
12,86
|
13,25
|
33%
|
|
|
Дисперсия
|
Правило Рубина
|
0,08
|
8,02
|
8,14
|
95%
|
|
|
|
Усреднение
|
6,150
|
5,387
|
6,954
|
197%
|
|
50 000
|
Среднее
|
Правило Рубина
|
13,06
|
13,03
|
13,09
|
87%
|
|
|
|
Усреднение
|
13,05
|
12,86
|
13,25
|
33%
|
|
|
Дисперсия
|
Правило Рубина
|
0,08
|
8,02
|
8,14
|
95%
|
|
|
|
Усреднение
|
6,150
|
5,367
|
6,966
|
197%
|
|
50%
|
1000
|
Среднее
|
Правило Рубина
|
13,05
|
13,02
|
13,08
|
87%
|
|
|
|
Усреднение
|
13,05
|
12,88
|
13,23
|
30%
|
|
|
Дисперсия
|
Правило Рубина
|
8,85
|
8,78
|
8,92
|
94%
|
|
|
|
Усреднение
|
4,894
|
4,276
|
5,546
|
311%
|
|
10 000
|
Среднее
|
Правило Рубина
|
13,05
|
13,02
|
13,08
|
87%
|
|
|
|
Усреднение
|
13,05
|
12,88
|
13,23
|
33%
|
|
|
Дисперсия
|
Правило Рубина
|
8,85
|
8,78
|
8,92
|
94%
|
|
|
|
Усреднение
|
4,894
|
4,249
|
5,552
|
308%
|
|
50 000
|
Среднее
|
Правило Рубина
|
13,05
|
13,02
|
13,08
|
87%
|
|
|
|
Усреднение
|
13,05
|
12,88
|
13,23
|
33%
|
|
|
Дисперсия
|
Правило Рубина
|
8,85
|
8,78
|
8,92
|
94%
|
|
|
|
Усреднение
|
4,894
|
4,258
|
5,568
|
306%
|
Для вычисления среднего и дисперсии интервальной переменной результаты
моделирования демонстрируют следующие тенденции:
· В случае, когда анализ осуществлялся на массивах с 10%
заполненных значений, как для среднего, так и для дисперсии более эффективным
подходом к агрегированию оказалось усреднение пропущенных значений при любом
количестве извлекаемых бутстрепом выборок.
· В случае, когда анализ осуществлялся на массивах с 30%
пропущенных значений для вычисления среднего более эффективным подходом к
агрегированию оказалось усреднение подставленных значений, а для дисперсии -
применение правила Рубина.
· В случае, когда анализ осуществлялся на массиве с 50%
заполненных значений, для вычисления среднего более эффективным оказалось также
усреднение пропущенных значений, а для дисперсии - правило Рубина вне
зависимости от количества извлекаемых бутстрепом выборок. Перейдем к
рассмотрению результатов анализа данных с применением коэффициентов,
предназначенных для поиска связи между двумя признаками. Поиск связи между
двумя признаками
Перейдем к сравнению эффективности подходов к агрегированию применительно
к методам поиска связи между признаками, начиная с коэффициента V Крамера, предназначенного для поиска
немонотонной связи между признаками.
Таблица 10. Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки коэффициента V Крамера в ситуации отсутствия связи (переменные «пол» и «тип
населенного пункта»)
|
Доля пропусков
|
Количество извлеченных
выборок
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
10%
|
1000
|
Правило Рубина
|
0,08
|
0,07
|
0,1
|
77%
|
|
|
Усреднение
|
0,094
|
0,043
|
0,182
|
20%
|
|
10 000
|
Правило Рубина
|
0,08
|
0,07
|
0,1
|
78%
|
|
|
Усреднение
|
0,094
|
0,044
|
24%
|
|
50 000
|
Правило Рубина
|
0,08
|
0,07
|
0,1
|
78%
|
|
|
Усреднение
|
0,094
|
0,044
|
0,186
|
24%
|
|
30%
|
1000
|
Правило Рубина
|
0,09
|
0,07
|
0,1
|
77%
|
|
|
Усреднение
|
0,098
|
0,042
|
0,195
|
29%
|
|
10 000
|
Правило Рубина
|
0,09
|
0,07
|
0,1
|
78%
|
|
|
Усреднение
|
0,098
|
0,044
|
0,193
|
29%
|
|
50 000
|
Правило Рубина
|
0,09
|
0,07
|
0,1
|
78%
|
|
|
Усреднение
|
0,098
|
0,044
|
0,193
|
29%
|
|
50%
|
1000
|
Правило Рубина
|
0,12
|
0,1
|
0,13
|
77%
|
|
|
Усреднение
|
0,141
|
0,08
|
0,224
|
79%
|
|
10 000
|
Правило Рубина
|
0,12
|
0,1
|
0,13
|
78%
|
|
|
Усреднение
|
0,141
|
0,079
|
0,226
|
79%
|
|
50 000
|
Правило Рубина
|
0,12
|
0,1
|
0,13
|
78%
|
|
|
Усреднение
|
0,141
|
0,08
|
0,228
|
81%
|
В ситуации отсутствия немонотонной связи между признаками более эффективным
подходом оказывается усреднение подставленных значений для небольшого
количества пропусков (10-30%), но в случае, если доля пропусков высока (50%)
разница между степенью отклонения для двух подходов составила меньше 5%, что
можно списать на статистическую погрешность, а значит, в этой исследовательской
ситуации можно говорить об одинаковой эффективности обоих подходов. При
увеличении количества извлекаемых бутстрепом выборок данные результаты
оказались устойчивыми.
Таблица 11Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки коэффициента V Крамера в ситуации наличия связи (переменные «пол» и
«трудовые отношения»)
|
Доля пропусков
|
Количество извлеченных
выборок
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
10%
|
1000
|
Правило Рубина
|
0,16
|
0,14
|
0,18
|
91%
|
|
|
Усреднение
|
0,156
|
0,075
|
0,236
|
84%
|
|
10 000
|
Правило Рубина
|
0,16
|
0,14
|
0,18
|
90%
|
|
|
Усреднение
|
0,156
|
0,074
|
0,230
|
78%
|
|
50 000
|
Правило Рубина
|
0,16
|
0,14
|
0,18
|
90%
|
|
|
Усреднение
|
0,156
|
0,074
|
0,230
|
78%
|
|
30%
|
1000
|
Правило Рубина
|
0,163
|
0,159
|
0,167
|
95%
|
|
|
Усреднение
|
0,162
|
0,078
|
0,247
|
95%
|
|
10 000
|
Правило Рубина
|
0,163
|
0,159
|
0,167
|
94%
|
|
|
Усреднение
|
0,162
|
0,078
|
0,243
|
90%
|
|
50 000
|
Правило Рубина
|
0,163
|
0,159
|
0,167
|
94%
|
|
|
Усреднение
|
0,162
|
0,078
|
0,242
|
90%
|
|
50%
|
1000
|
Правило Рубина
|
0,07
|
0,05
|
0,09
|
70%
|
|
|
Усреднение
|
0,099
|
0,021
|
0,181
|
20%
|
|
10 000
|
Правило Рубина
|
0,07
|
0,05
|
0,09
|
71%
|
|
|
Усреднение
|
0,099
|
0,020
|
0,180
|
18%
|
|
50 000
|
Правило Рубина
|
0,07
|
0,05
|
0,09
|
71%
|
|
|
Усреднение
|
0,099
|
0,020
|
0,180
|
18%
|
В ситуации же наличия связи между признаками усреднение подставленных
значений является более эффективным подходом к агрегированию результатов
заполнения для самой большой и самой маленькой долей пропусков при любом
количестве извлекаемых бутстрепом выборок, разница степени отклонения в пользу
усреднения составила 7-53%. Для 30%-й доли пропусков при любом количестве
выборок разница между степенями отклонения для того или иного подхода составила
от 0% до 4%, что мы можем списать на статистическую погрешность, поэтому в
данной исследовательской ситуации оба подхода демонстрируют одинаковую
эффективность. Таким образом, при вычислении коэффициента V Крамера усреднение подставленных
значений предпочтительнее во всех исследовательских ситуациях, за исключением
ситуации отсутствия немонотонной связи между признаками и большого количества
пропусков в массиве, а также 30% пропусков и наличия немонотонной связи между
признаками: в этих случаях оба подхода одинаково эффективны.
Перейдем к сравнению результатов применительно к поиску связи между
порядковыми признаками с использованием рангового коэффициента корреляции
Спирмена.
Таблица 12 Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки коэффициента корреляции Спирмена в ситуации
отсутствия связи (переменные «близость к партии» и «субъективная оценка
здоровья»)
|
Доля пропусков
|
Количество извлеченных
выборок
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
10%
|
1000
|
Правило Рубина
|
-0,01
|
-0,02
|
0,01
|
81%
|
|
|
Усреднение
|
0,026
|
-0,062
|
0,105
|
37%
|
|
10 000
|
Правило Рубина
|
-0,01
|
-0,02
|
0,01
|
80%
|
|
|
Усреднение
|
0,026
|
-0,054
|
0,105
|
41%
|
|
50 000
|
Правило Рубина
|
-0,01
|
-0,02
|
0,01
|
81%
|
|
|
Усреднение
|
0,026
|
-0,051
|
0,107
|
43%
|
|
30%
|
1000
|
Правило Рубина
|
-0,06
|
-0,08
|
0,04
|
25%
|
|
|
Усреднение
|
-0,091
|
-0,168
|
0,01
|
89%
|
|
10 000
|
Правило Рубина
|
-0,06
|
-0,08
|
0,04
|
22%
|
|
|
Усреднение
|
-0,091
|
-0,167
|
0,012
|
94%
|
|
50 000
|
Правило Рубина
|
-0,06
|
-0,08
|
0,04
|
23%
|
|
|
Усреднение
|
-0,091
|
-0,167
|
0,012
|
93%
|
|
50%
|
1000
|
Правило Рубина
|
-0,04
|
-0,05
|
-0,02
|
81%
|
|
|
Усреднение
|
-0,059
|
-0,138
|
0,016
|
66%
|
|
10 000
|
Правило Рубина
|
-0,04
|
-0,05
|
-0,02
|
80%
|
|
|
Усреднение
|
-0,059
|
-0,137
|
0,017
|
71%
|
|
50 000
|
Правило Рубина
|
-0,04
|
-0,05
|
-0,02
|
81%
|
|
|
Усреднение
|
-0,059
|
-0,137
|
0,017
|
70%
|
Применительно к раноговому коэффициенту Спирмена правило Рубина является
более эффективным подходом к агрегированию в том случае, если исследовательская
ситуация характеризуется отсутствием монотонной связи между признаками и
средним количеством пропусков в массиве (разница степени отклонения в пользу
правила Рубина составила от 64% до 72%). В случаях отсутствия связи и очень
большого или очень маленького количества пропусков, усреднение подставленных
значений оказывается более эффективным (разница составила от 11% до 44%). В
данном случае также наблюдается устойчивость результатов вне зависимости от
количества извлекаемых бутстрепом выборок.
Таблица 13. Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки коэффициента корреляции Спирмена в ситуации
наличия связи («интерес к политике» и «длительность просмотра новостей в будний
день»)
|
Доля пропусков
|
Количество извлеченных
выборок
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
10%
|
1000
|
Правило Рубина
|
-0,33
|
-0,35
|
-0,31
|
87%
|
|
|
Усреднение
|
-0,346
|
-0,423
|
-0,270
|
63%
|
|
10 000
|
Правило Рубина
|
-0,33
|
-0,35
|
-0,31
|
86%
|
|
|
Усреднение
|
-0,346
|
-0,421
|
-0,269
|
64%
|
|
50 000
|
Правило Рубина
|
-0,33
|
-0,35
|
-0,31
|
86%
|
|
|
Усреднение
|
-0,346
|
-0,419
|
-0,269
|
66%
|
|
30%
|
1000
|
Правило Рубина
|
-0,16
|
-0,14
|
335%
|
|
|
Усреднение
|
-0,141
|
-0,224
|
-0,056
|
364%
|
|
10 000
|
Правило Рубина
|
-0,16
|
-0,18
|
-0,14
|
329%
|
|
|
Усреднение
|
-0,141
|
-0,224
|
-0,056
|
357%
|
|
50 000
|
Правило Рубина
|
-0,16
|
-0,18
|
-0,14
|
329%
|
|
|
Усреднение
|
-0,141
|
-0,224
|
-0,056
|
357%
|
|
50%
|
1000
|
Правило Рубина
|
-0,04
|
-0,05
|
-0,02
|
518%
|
|
|
Усреднение
|
-0,151
|
-0,229
|
-0,069
|
351%
|
|
10 000
|
Правило Рубина
|
-0,04
|
-0,05
|
-0,02
|
507%
|
|
|
Усреднение
|
-0,151
|
-0,228
|
-0,074
|
341%
|
|
50 000
|
Правило Рубина
|
-0,04
|
-0,05
|
-0,02
|
507%
|
|
|
Усреднение
|
-0,151
|
-0,228
|
-0,075
|
341%
|
В случае наличия монотонной связи между признаками ситуация является
идентичной: более эффективным устойчиво для любого количества выборок
оказывается правило Рубина для среднего количества пропусков в массиве (разница
степеней отклонения в пользу правила Рубина составляет 28-29%) и усреднение подставленных
значений для очень большого и маленького количества пропусков (разница
составляет степеней отклонения составляет 20-167%).
Таблица 14 Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки коэффициента корреляции Пирсона в ситуации
отсутствия связи (переменные «количество лет очного образования» и «положение
на шкале левое-правое крыло»)
|
Доля пропусков
|
Количество извлеченных
выборок
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
10%
|
1000
|
Правило Рубина
|
-0,04
|
-0,05
|
-0,02
|
81%
|
|
|
Усреднение
|
-0,047
|
-0,128
|
-0,030
|
38%
|
|
10 000
|
Правило Рубина
|
-0,04
|
-0,05
|
-0,02
|
81%
|
|
|
Усреднение
|
-0,047
|
-0,125
|
-0,032
|
43%
|
|
50 000
|
Правило Рубина
|
-0,04
|
-0,05
|
-0,02
|
81%
|
|
|
Усреднение
|
-0,047
|
-0,125
|
-0,032
|
42%
|
|
30%
|
1000
|
Правило Рубина
|
-0,05
|
-0,07
|
-0,03
|
75%
|
|
|
Усреднение
|
-0,084
|
-0,160
|
-0,005
|
3%
|
|
10 000
|
Правило Рубина
|
-0,05
|
-0,07
|
-0,03
|
75%
|
|
|
Усреднение
|
-0,084
|
-0,160
|
-0,007
|
9%
|
|
50 000
|
Правило Рубина
|
-0,05
|
-0,07
|
-0,03
|
75%
|
|
|
Усреднение
|
-0,084
|
-0,160
|
-0,007
|
10%
|
|
50%
|
1000
|
Правило Рубина
|
-0,05
|
-0,06
|
-0,03
|
81%
|
|
|
Усреднение
|
-0,106
|
-0,181
|
-0,029
|
31%
|
|
10 000
|
Правило Рубина
|
-0,05
|
-0,06
|
-0,03
|
81%
|
|
|
Усреднение
|
-0,106
|
-0,182
|
-0,029
|
36%
|
|
50 000
|
Правило Рубина
|
-0,05
|
-0,06
|
-0,03
|
81%
|
|
|
Усреднение
|
-0,106
|
-0,182
|
-0,029
|
37%
|
Применительно к коэффициенту корреляции Пирсона при любом из трех
вариантов количества извлекаемых бутстрепом выборок более эффективным оказалось
усреднение подставленных значений при всех рассмотренных долях пропусков в
массиве как в случае наличия, так и в случае отсутствия линейной связи между
признаками (таблицы 14 и 15). Разница степеней отклонения в пользу правила
Рубина в случае отсутствия линейной связи составила от 38% до 72%, а в ситуации
наличия линейной связи - от 53% до 191%.
Таблица 15. Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки коэффициента корреляции Пирсона в ситуации
наличия связи (переменные «уровень счастья» и «положение в обществе»)
|
Доля пропусков
|
Количество извлеченных
выборок
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
10%
|
1000
|
Правило Рубина
|
0,2
|
0,19
|
0,22
|
201%
|
|
|
Усреднение
|
0,244
|
0,175
|
0,318
|
142%
|
|
10 000
|
Правило Рубина
|
0,2
|
0,19
|
0,22
|
196%
|
|
|
Усреднение
|
0,244
|
0,168
|
0,317
|
143%
|
|
50 000
|
Правило Рубина
|
0,2
|
0,19
|
0,22
|
196%
|
|
|
Усреднение
|
0,244
|
0,167
|
0,317
|
144%
|
|
30%
|
1000
|
Правило Рубина
|
0,12
|
0,1
|
0,13
|
328%
|
|
|
Усреднение
|
0,166
|
0,090
|
0,239
|
258%
|
|
10 000
|
Правило Рубина
|
0,12
|
0,1
|
0,13
|
323%
|
|
|
Усреднение
|
0,166
|
0,092
|
0,239
|
251%
|
|
50 000
|
Правило Рубина
|
0,12
|
0,1
|
0,13
|
323%
|
|
|
Усреднение
|
0,166
|
0,092
|
0,239
|
251%
|
|
50%
|
1000
|
Правило Рубина
|
0,03
|
0,02
|
0,05
|
442%
|
|
|
Усреднение
|
0,110
|
0,036
|
0,178
|
340%
|
|
10 000
|
Правило Рубина
|
0,03
|
0,02
|
0,05
|
435%
|
|
|
Усреднение
|
0,110
|
0,037
|
0,184
|
329%
|
|
50 000
|
Правило Рубина
|
0,03
|
0,02
|
0,05
|
435%
|
|
|
Усреднение
|
0,110
|
0,037
|
0,184
|
329%
|
Таким образом, моделирование позволило выявить следующие тенденции в
отношении подходов к агрегированию результатов множественного заполнения
пропусков для поиска связи между признаками:
· для поиска связи между двумя номинальными переменными с
использованием коэффициента V
Крамера более эффективным оказался метод усреднения подставленных значений для
любой доли пропусков в случае наличия связи между признаками и для небольшого и
среднего количества пропусков в массиве в случае отсутствия связи. В случае
большой (50%) доли пропусков и отсутствия немонотонной связи, а также в случае
наличия связи и средней доли пропусков (30%) оба подхода одинаково эффективны.
· для поиска связи между двумя порядковыми переменными с
использованием коэффициента Спирмена усреднение подставленных значений
оказалось эффективнее в ситуации очень большого и очень маленького количества
пропусков в массиве; если же количество пропусков являлось средним (30%), то
более эффективным подходом оказывалось правило Рубина как для ситуации
отсутствия, так и для ситуации наличия связи между признаками;
· для поиска связи между двумя интервальными переменными с
использованием коэффициента Пирсона в любой исследовательской ситуации
усреднение подставленных значений оказывалось более эффективным подходом.
Далее рассмотрим результаты, полученные нами при моделировании
множественной линейной регрессии.
Множественная линейная регрессия
Перейдем к сравнению эффективности подходов к агрегированию результатов
множественного заполнения пропусков применительно к множественной линейной
регрессии, рассматривая поочередно доверительные интервалы, вычисленные на
массивах с разными долями заполненных значений.
· В случае, если в массиве присутствует небольшое число
пропусков, мы можем наблюдать следующие тенденции:
· для константы границы доверительного интервала сильно
колебались при изменении количества извлекаемых бутстрепом выборок для обоих
подходов, однако в случаях 1 000 и 50 000 выборок этот интервал оказывался
ближе к эталонному в том случае, если вычислялся на массиве с усредненными
подставленными значениями;
· для всех четырех коэффициентов регрессии при значимых и
незначимых предикторах более эффективным оказывалось применение правила Рубина.
Таблица 16 Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки линейных регрессионных коэффициентов на
массиве с 10% пропусков (зависимая переменная «положение в обществе»)
|
Член уравнения
|
Количество извлеченных
выборок
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
Константа
|
1000
|
Правило Рубина
|
4,05
|
4,00
|
4,11
|
225%
|
|
|
Усреднение
|
4,887
|
3,731
|
6,029
|
210%
|
|
10 000
|
Правило Рубина
|
4,05
|
3,98
|
4,13
|
223%
|
|
|
Усреднение
|
4,887
|
3,771
|
5,971
|
306%
|
|
50 000
|
Правило Рубина
|
4,05
|
3,98
|
4,13
|
318%
|
|
|
Усреднение
|
4,887
|
3,747
|
5,996
|
305%
|
|
Длительность очного
образования
|
1000
|
Правило Рубина
|
0,03
|
0,02
|
0,04
|
85%
|
|
|
Усреднение
|
-0,037
|
-0,095
|
0,022
|
107%
|
|
10 000
|
Правило Рубина
|
0,02
|
0,04
|
87%
|
|
|
Усреднение
|
-0,037
|
-0,092
|
0,019
|
128%
|
|
50 000
|
Правило Рубина
|
0,03
|
0,02
|
0,04
|
109%
|
|
|
Усреднение
|
-0,037
|
-0,092
|
0,020
|
123%
|
|
Удовлетворенность системой
образования
|
1000
|
Правило Рубина
|
0,04
|
0,02
|
0,05
|
79%
|
|
|
Усреднение
|
0,142
|
0,075
|
0,204
|
132%
|
|
10 000
|
Правило Рубина
|
0,04
|
0,02
|
0,05
|
77%
|
|
|
Усреднение
|
0,142
|
0,076
|
0,207
|
156%
|
|
50 000
|
Правило Рубина
|
0,04
|
0,02
|
0,05
|
101%
|
|
|
Усреднение
|
0,142
|
0,08
|
0,205
|
159%
|
|
Уровень счастья
|
1000
|
Правило Рубина
|
0,17
|
0,16
|
0,19
|
197%
|
|
|
Усреднение
|
0,022
|
-0,051
|
0,092
|
363%
|
|
10 000
|
Правило Рубина
|
0,17
|
0,16
|
0,19
|
198%
|
|
|
Усреднение
|
0,022
|
-0,049
|
0,092
|
450%
|
|
50 000
|
Правило Рубина
|
0,17
|
0,16
|
0,19
|
286%
|
|
|
Усреднение
|
0,022
|
-0,051
|
0,093
|
452%
|
|
Возраст
|
1000
|
Правило Рубина
|
-0,02
|
-0,02
|
-0,01
|
138%
|
|
|
Усреднение
|
-0,007
|
-0,017
|
0,003
|
156%
|
|
10 000
|
Правило Рубина
|
-0,02
|
-0,02
|
-0,01
|
138%
|
|
|
Усреднение
|
-0,007
|
-0,017
|
0,002
|
56%
|
|
50 000
|
Правило Рубина
|
-0,02
|
-0,02
|
-0,01
|
38%
|
|
|
Усреднение
|
-0,007
|
-0,017
|
0,003
|
56%
|
Таблица 17 Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки линейных регрессионных коэффициентов на
массиве с 30% пропусков (зависимая переменная «положение в обществе»)
|
Член уравнения
|
Количество извлеченных
выборок
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
Константа
|
1000
|
Правило Рубина
|
5,76
|
5,54
|
5,8
|
313%
|
|
|
Усреднение
|
6,153
|
4,802
|
7,551
|
271%
|
|
10 000
|
Правило Рубина
|
5,76
|
5,54
|
5,8
|
310%
|
|
|
Усреднение
|
6,153
|
4,740
|
7,592
|
360%
|
|
50 000
|
Правило Рубина
|
5,76
|
5,54
|
5,8
|
405%
|
|
|
Усреднение
|
6,153
|
4,729
|
7,575
|
360%
|
|
Длительность очного
образования
|
1000
|
Правило Рубина
|
0
|
-0,01
|
0,02
|
51%
|
|
|
Усреднение
|
-0,081
|
-0,158
|
-0,007
|
178%
|
|
10 000
|
Правило Рубина
|
0
|
-0,01
|
0,02
|
53%
|
|
|
Усреднение
|
-0,081
|
-0,154
|
-0,008
|
199%
|
|
50 000
|
Правило Рубина
|
0
|
-0,01
|
0,02
|
75%
|
|
|
Усреднение
|
-0,081
|
-0,154
|
-0,008
|
194%
|
|
Удовлетворенность системой
образования
|
1000
|
Правило Рубина
|
-0,03
|
-0,04
|
-0,01
|
34%
|
|
|
Усреднение
|
0,057
|
-0,009
|
0,123
|
53%
|
|
10 000
|
Правило Рубина
|
-0,03
|
-0,04
|
-0,01
|
40%
|
|
|
Усреднение
|
0,057
|
-0,009
|
0,123
|
73%
|
|
50 000
|
Правило Рубина
|
-0,03
|
-0,04
|
-0,01
|
62%
|
|
|
Усреднение
|
0,057
|
-0,009
|
0,124
|
73%
|
|
Уровень счастья
|
1000
|
Правило Рубина
|
0,11
|
0,09
|
0,12
|
252%
|
|
|
Усреднение
|
0,007
|
-0,069
|
0,083
|
377%
|
|
10 000
|
Правило Рубина
|
0,11
|
0,09
|
0,12
|
254%
|
|
|
Усреднение
|
0,007
|
-0,066
|
0,081
|
464%
|
|
50 000
|
Правило Рубина
|
0,11
|
0,09
|
0,12
|
341%
|
|
|
Усреднение
|
0,007
|
-0,069
|
0,081
|
466%
|
|
Возраст
|
1000
|
Правило Рубина
|
-0,02
|
-0,03
|
-0,01
|
188%
|
|
|
Усреднение
|
-0,07
|
-0,028
|
0,004
|
175%
|
|
10 000
|
Правило Рубина
|
-0,02
|
-0,03
|
-0,01
|
188%
|
|
|
Усреднение
|
-0,07
|
-0,028
|
0,004
|
75%
|
|
50 000
|
Правило Рубина
|
-0,02
|
-0,03
|
-0,01
|
88%
|
|
|
Усреднение
|
-0,07
|
-0,019
|
0,004
|
44%
|
Результаты анализа данных, проведенные на массивах с 30% подставленных
значений, в целом, демонстрируют те же тенденции, что и для массивов с 10%
подставленных значений, за одним исключением: для предиктора «Возраст
респондента» со значимым регрессионным коэффициентом для любого количества
извлекаемых бустрепом выборок более эффективных подходом оказалось усреднение
подставленных значений. Учитывая первичный, пробный характер нашего
исследования, мы не можем дать какой-либо теоретически подкрепленной
интерпретации отличий именно для этого предиктора, однако можем отметить, что
этот предиктор отличается от трех других, во-первых, тем, что он является
значимым, и, во-вторых, тем, что измерен он в истинной интервальной шкале.
Таблица 18 Сравнение эффективности правила Рубина и усреднения
подставленных значений для оценки линейных регрессионных коэффициентов на
массиве с 50% пропусков (зависимая переменная «положение в обществе»)
|
Член уравнения
|
Количество извлеченных
выборок
|
Способ агрегирования
|
Точечная оценка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
Степень отклонения
|
|
Константа
|
1000
|
Правило Рубина
|
4,60
|
4,50
|
4,71
|
254%
|
|
|
Усреднение
|
6,754
|
5,248
|
8,180
|
296%
|
|
10 000
|
Правило Рубина
|
4,60
|
4,50
|
4,71
|
252%
|
|
|
Усреднение
|
6,754
|
5,386
|
8,142
|
396%
|
|
50 000
|
Правило Рубина
|
4,60
|
4,50
|
4,71
|
347%
|
|
|
Усреднение
|
6,754
|
5,367
|
8,166
|
396%
|
|
Длительность очного
образования
|
1000
|
Правило Рубина
|
0,02
|
0,00
|
0,04
|
63%
|
|
|
Усреднение
|
-0,191
|
-0,032
|
216%
|
|
10 000
|
Правило Рубина
|
0,02
|
0,00
|
0,04
|
64%
|
|
|
Усреднение
|
-0,112
|
-0,191
|
-0,035
|
241%
|
|
50 000
|
Правило Рубина
|
0,02
|
0,00
|
0,04
|
86%
|
|
|
Усреднение
|
-0,112
|
-0,190
|
-0,036
|
236%
|
|
Удовлетворенность системой
образования
|
1000
|
Правило Рубина
|
-0,04
|
-0,06
|
-0,03
|
53%
|
|
|
Усреднение
|
-0,008
|
-0,063
|
0,051
|
57%
|
|
10 000
|
Правило Рубина
|
-0,04
|
-0,06
|
-0,03
|
60%
|
|
|
Усреднение
|
-0,008
|
-0,067
|
0,050
|
90%
|
|
50 000
|
Правило Рубина
|
-0,04
|
-0,06
|
-0,03
|
82%
|
|
|
Усреднение
|
-0,008
|
-0,065
|
0,049
|
86%
|
|
Уровень счастья
|
1000
|
Правило Рубина
|
0,04
|
0,03
|
0,06
|
299%
|
|
|
Усреднение
|
-0,011
|
-0,099
|
0,077
|
401%
|
|
10 000
|
Правило Рубина
|
0,04
|
0,03
|
0,06
|
301%
|
|
|
Усреднение
|
-0,011
|
-0,102
|
0,079
|
492%
|
|
50 000
|
Правило Рубина
|
0,04
|
0,03
|
0,06
|
388%
|
|
|
Усреднение
|
-0,011
|
-0,098
|
0,080
|
489%
|
|
Возраст
|
1000
|
Правило Рубина
|
0,00
|
0,00
|
0,01
|
263%
|
|
|
Усреднение
|
-0,006
|
-0,018
|
0,006
|
150%
|
|
10 000
|
Правило Рубина
|
0,00
|
0,00
|
0,01
|
263%
|
|
|
Усреднение
|
-0,006
|
-0,019
|
0,006
|
44%
|
|
50 000
|
Правило Рубина
|
0,00
|
0,00
|
0,01
|
163%
|
|
|
Усреднение
|
-0,006
|
-0,019
|
0,006
|
44%
|
Результаты, полученные на массивах с 50% заполненных значений, в целом,
повторяют результаты, полученные на массивах с меньшими долями пропусков, кроме
того, что для константы при любом количестве извлеченных бутстрепом выборок
более эффективным подходом оказалось правило Рубина. При этом для трех
коэффициентов, доверительные интервалы для которых оказались ближе к эталону в
случае применения усреднения подставленных значений, разница в степенях
отклонения составила от 4% до 191%, а для коэффициента, который был точнее
(ближе к эталону) оценен при использовании правила Рубина - от 113% до 219%,
следовательно, во втором случае результаты оказались в среднем более
чувствительными к изменению подхода к агрегированию. Поэтому с точки зрения
частоты преобладания эффективности в данном случае более эффективным можно
назвать усреднение пропущенных значений, а с точки зрения чувствительности
результатов к изменению подхода - правило Рубина. Однако верхний предел разницы
сопоставим в обоих случаях, поэтому, на наш взгляд, ориентироваться стоит все
же на частоту.
Таким образом, применительно к множественной линейной регрессии мы можем
отметить следующие тенденции:
· эффективный подход к вычислению константы изменялся в
зависимости от количества извлекаемых бутстрепом выборок на массивах с 10% и
30% подставленных значений, однако для 50% пропусков более эффективным подходом
оказалось применение правила Рубина при извлечении любого количества выборок;
· для вычисления регрессионных коэффициентов для всех четырех
предикторов на массивах с 10% подставленных значений более эффективным подходом
к агрегированию оказалось правило Рубина;
· для вычисления одного значимого коэффициента регрессии при
предикторе, измеренной в 11-балльной шкале и двух незначимых при истинном и
11-балльном предикторах на массивах с 30% и 50% подставленных значений более
эффективным подходом к агрегированию оказалось также правило Рубина;
· усреднение подставленных значений показало большую
эффективность только в одном случае: для вычисления коэффициента регрессии при
значимом предикторе, измеренном в «истинной» интервальной шкале.
Описав полученные нами результаты анализа данных, мы можем перейти к
решению последней задачи данного исследования, а именно составлению
рекомендаций по выбору подхода к агрегированию в зависимости от
исследовательской ситуации.
Рекомендации по выбору подхода к агрегированию результатов множественного
заполнения пропусков
Обобщим результаты проведенного нами эксперимента в виде набора
рекомендаций по выбору подхода к агрегированию результатов множественного
заполнения пропусков в рассмотренных нами исследовательских ситуаций.
. Описательная статистика.
· Для описания номинальной переменной при помощи долей значений
признака в ситуации большого (до 50%), маленького (до 10%) и умеренного (30%)
количества пропусков в массиве для агрегирования результатов множественного
заполнения пропусков предпочтительно выбирать правило Рубина.
· Для описания порядковой переменной при помощи долей значений
признака для агрегирования результатов множественного заполнения пропусков
предпочтительно выбирать:) в ситуации маленького (10%) количества пропусков в
массиве - правило Рубина;) в ситуации умеренного (30%) количества пропусков
в массиве - усреднение подставленных значений;) в ситуации большого (50%)
количества пропусков в массиве оба подхода имеют одинаковую эффективность.
· Для описания интервальной переменной при помощи среднего
арифметического и дисперсии для агрегирования результатов множественного
заполнения пропусков предпочтительно выбирать:) в ситуации небольшого
(10%) количества пропусков в массиве - усреднение подставленных значений;) в
ситуации умеренного (30%) количества пропусков в массиве - правило Рубина для
среднего арифметического и усреднение подставленных значений для дисперсии;) в
ситуации большого (50%) количества пропусков в массиве - усреднение
подставленных значений для среднего арифметического и правило Рубина для
дисперсии.
. Поиск связи между двумя признаками.
· для поиска немонотонной связи между двумя номинальными
переменными с использованием коэффициента V Крамера для агрегирования результатов множественного
заполнения пропусков предпочтительно выбирать:) в случае предположения
о наличии немонотонной связи между признаками и любого (10-50%) количества
пропусков в массиве - усреднение подставленных значений;) в случае
предположения об отсутствии немонотонной связи между признаками и большого
(50%) количества пропусков в массиве, а также в случае предположения об
отсутствии немонотонной связи между признаками и небольшого (10%) или
умеренного (30%) количества пропусков в массиве оба подхода одинаково
эффективны.
· для поиска монотонной связи между двумя порядковыми
переменными с использованием коэффициента Спирмена для агрегирования
результатов множественного заполнения пропусков предпочтительно выбирать:) в
случае предположения о наличии или отсутствии монотонной связи между двумя признаками
и небольшого (10%) или большого (50%) количества пропусков в массиве -
усреднение подставленных значений;) в случае предположения о наличии или
отсутствии монотонной связи между двумя признаками и умеренного (30%)
количества пропусков в массиве - правило Рубина.
· для поиска линейной связи между двумя интервальными
переменными с использованием коэффициента Пирсона для агрегирования результатов
множественного заполнения пропусков в случае предположения о наличии или
отсутствии линейной связи и любого (10-50%) количества пропусков в массиве
предпочтительно выбирать усреднение подставленных значений.
3. Множественная линейная регрессия.
· Для оценки константы и предположениях о значимости или
незначимости регрессионных коэффициентов во множественной линейной регрессии в
ситуации любого (10-50%) количества пропусков в массиве
Заключение
Пропущенные значения являются проблемой, с которой приходится
сталкиваться в любом социологическом исследовании и приводят к ряду
затруднений, таких как невозможность применения изначального дизайна
исследования, потеря данных и смещение результатов. На сегодняшний день
разработано много методов борьбы с пропусками, которые не удалось устранить на
этапе сбора информации, но возможно скорректировать уже на этапе анализа данных
(такие пропуски называют игнорируемыми). Одним из наиболее современных и
активно развивающихся методов борьбы с пропусками после завершения полевого
этапа является разработанное Дональдом Рубином множественное заполнение
пропусков, которое, однако, является методом достаточно долгим и трудоемким. По
этой причине одним из направлений развития метода является его оптимизация, то
есть поиск способов упрощения работы с алгоритмом множественного заполнения
пропусков без потери эффективности, отличающей его от прочих методов борьбы с
пропущенными данными. В качестве такого способа оптимизации в противовес
классическому алгоритму мы предложили «усреднение» подставленных значений, то
есть замена пропусков в массиве соответствующей мерой центральной тенденции,
рассчитанной на наборе подставленных в ходе множественного заполнения пропусков
значений.
В данном исследовании нами был проведен сравнительный анализ
эффективности применения правила Рубина и усреднения подставленных значений как
подходов к агрегированию результатов множественного заполнения пропусков в
зависимости от исследовательской ситуации. При помощи реализованного нами
статистического эксперимента мы оценили эффективность подходов применительно к
исследовательским ситуациям, характеризующимся разными долями пропусков в
массиве, разными шкалами переменных, и тремя распространенными в
социологических исследованиях методами анализа данных - описательная
статистика, поиск связи между двумя признаками и множественная линейная
регрессия. На основании сравнения оценок эффективности подходов мы составили
следующие рекомендации по выбору подхода к агрегированию результатов
множественного заполнения пропусков для перечисленных исследовательских
ситуаций:
. Описательная статистика: для описания номинальных переменных следует
выбирать правило Рубина, а для описания порядковых и интервальных выбор подхода
зависит от количества пропусков в массиве.
. Поиск связи между признаками: для поиска связи между номинальными
признаками с помощью коэффициента V Крамера и между порядковыми признаками с помощью коэффициента Спирмена
выбор подхода также зависит от доли пропусков в массиве, а для поиска связи
между интервальными переменными при помощи коэффициента Пирсона при любом
количестве пропусков в массиве предпочтительно выбирать усреднение
подставленных значений.
. Множественная линейная регрессия: вычисление как константы, так и
регрессионных коэффициентов при значимых и незначимых предикторах
предпочтительно производить с применением правила Рубина для агрегирования
результатов заполнения.
Сфера применения результатов данного исследования ограничивается только
случаями игнорируемых (случайных и полностью случайных) пропусков, поскольку
только игнорируемые пропуски поддаются корректировке на этапе анализа данных,
когда вернуться к этапу сбора информации уже невозможно. Кроме того, в данном
исследовании был рассмотрен только очень узкий круг исследовательских ситуаций:
мы рассмотрели всего три инструмента анализа данных из очень широкого круга
статистических методов, применяемых в социологии. В связи с этим делать широкие
теоретические или методические обобщения на основании данного исследования
нельзя, однако одним из наиболее общих результатов исследования стало
экспериментальное доказательство того, что для определенных исследовательских
ситуаций более простой в осуществлении подход к агрегированию результатов
множественного заполнения пропусков - усреднение подставленных значений при
помощи соответствующей меры центральной тенденции для шкалы переменной,
содержащей пропуски -оказывается эффективнее классического теоретически
обоснованного правила Рубина.
Таким образом, данное исследование проложило новое направление для
оптимизации применения множественного заполнения пропусков в зависимости от
исследовательской ситуации. Дальнейшие исследования в данной области могут
касаться следующих проблем:
· теоретическое обоснование адекватности применения усреднения
подставленных значений для агрегирования результатов множественного заполнения
пропусков;
· расширение круга экспериментально обоснованных рекомендаций
по выбору подхода к агрегированию результатов множественного заполнения
пропусков в различных исследовательских ситуациях;
· теоретическое обоснование эффективности усреднения
пропущенных значений или применения правила Рубина в конкретных
исследовательских ситуациях.
Список использованной литературы
1. Дударев В.А. Подход к заполнению пропусков в
обучающих выборках для компьютерного конструирования неорганических соединений
// Вестник МИТХТ. 2014. Т. 9. № 1. С. 73-75.
. Зангиева И.К. Проблема пропусков в социологических
данных: смысл и подходы к решению // Социология: Методология, методы,
математическое моделирование. 2011. Т. 33. С. 28-56.
. Зангиева И.К., Толстова Ю.Н. Понятие случайности и
проблема пропусков данных в социологии // В кн.: Математическое моделирование
социальных процессов / Науч. ред.: А. Михайлов. Вып. 14. М. : Социологический
факультет МГУ, 2012. Гл. 14. С. 146-165.
. Зангиева И.К., Тимонина Е.С. Сравнение эффективности
алгоритмов заполнения пропусков в данных в зависимости от используемого метода
анализа // Мониторинг общественного мнения, №1 (119). 2014. сс. 41-55.
. Кутлалиев А. Х. Метод множественного восстановления
данных // В кн.: Социологические методы в современной исследовательской
практике: Сборник статей, посвященный памяти первого декана факультета
социологии НИУ ВШЭ А.О. Крыштановского [Электронный ресурс] / Отв. ред.: О. А.
Оберемко. М.: Издательский дом НИУ ВШЭ, 2011. С. 201-208.
. Литтл Р., Рубин Д. Статистический анализ данных с
пропусками / пер. с англ. - М.: Финансы и статистика, 1990. - 336 с.
. Толстова Ю.Н. Математико-статистические модели в
социологии (математическая статистика для социологов): учебное пособие. М.:
Изд. дом ГУ-ВШЭ, 2008.
. Шитиков В.К., Розенберг Г.С. Рандомизация и бутстреп:
статистический анализ в биологии и экологии с использованием R. Тольятти: Кассандра, 2013. - 314 с.
9. Allison P. Multiple imputation for missing
data: A cautionary tale // Sociological Methods and Research. 2000. No. 28.
301-309.
. Carpenter J., Kenward M. Multiple imputation:
current perspectives // Statistical Methods in Medical Research. 2007. Vol. 16,
no. 3. 199-218.
. Brand J.P.L. Development, Implementation and
Evaluation of Multiple Imputation Strategies for the Statistical Analysis of
Incomplete Data Sets. Thesis Erasmus University Rotterdam, 1999.
. Glynn R., Laird N., Rubin D. Multiple
imputation in Mixture models for Nonignorable Nonresponse with Follow-ups //
Journal of the American Statistical Association. Vol. 88, No. 423. 1993. 984-993.
. Honaker J., Joseph A., King G., Scheve K.
Analyzing Incomplete Political Science Data: An Alternative Algorithm for
Multiple Imputation // The American Political Science Review. 2001. Vol. 95,
No. 1. 49-69.
. Horton N., Lipsitz S. Multiple Imputation in
Practice: Comparison of Software Packages for Regression Models With Missing
Variables // The American Statistician. 2001. Vol. 55, No. 3. 244-254.
. Hutchenson G., Pampaka M., Williams J.
Handling missing data: analysis of a challenging data set using multiple
imputation // International Journal of Recearch & Method in Education.
2016. Vol. 29, No. 1. 19-37.
. IBM SPSS Missing Values 22 [on-line]. URL:
http://www.sussex.ac.uk/its/pdfs/SPSS_Missing_Values_22.pdf (accessed: May 15,
2016).
. Lee K., Simpson J. Introduction to multiple
imputation for dealing with missing data // Respirology. 2014. No 19. 162-167.
. Mitra R., Reiter J.P. A comparison of two
methods of estimating propensity scores after multiple imputation //
Statistical Methods in Medical Research. 2016. Vol. 25, Issue 1. 188-204.
. Rubin D. Multiple Imputation for Nonresponse
in Surveys. John Wiley & Sons, 2009.
. Rubin D. Multiple imputation in sample
surveys - a phenomenological Bayesian approach to nonresponse / ASA Proc
Section on Survey Res Methods. 1978. 20-34.
. SOLAS Version 4.0: manual [on-line]. URL:
http://www.statsols.com/wp-content/uploads/2013/12/Solas-4-Manual1.pdf
(accessed: April 27, 2016).
. Vink G., van Buuren S. Pooling multiple
imputations when the sample happens to be the population [online source] //
Cornell University Library. 2014. URL: http://arxiv.org/abs/1409.8542
(accessed: May 3, 2016).
. Zhang P. Multiple imputation: theory and
method // International Statistical Review. 2003. Vol. 71, no. 3. 581-592.
Приложение
Таблица 1. Эталонные параметры бутстрепа для долей людей, проживающих в
населенных пунктах разного типа
|
Значение переменной
|
Число выборок
|
Выборочная доля, %
|
Стд. Ошибка, %
|
Нижняя граница ДИ, %
|
Верхняя граница ДИ, %
|
|
Мегаполис
|
1000
|
42,3
|
2,1
|
38,3
|
46,5
|
|
10 000
|
42,3
|
2,0
|
38,3
|
46,2
|
|
50 000
|
42,3
|
2,0
|
38,3
|
46,2
|
|
Пригород мегаполиса
|
1000
|
3,4
|
0,7
|
2,0
|
4,9
|
|
10 000
|
3,4
|
0,7
|
2,1
|
4,9
|
|
50 000
|
3,4
|
0,7
|
2,1
|
4,9
|
|
Небольшой город
|
1000
|
34,1
|
1,9
|
30,3
|
37,7
|
|
10 000
|
34,1
|
1,9
|
30,3
|
37,8
|
|
50 000
|
34,1
|
1,9
|
30,3
|
37,8
|
|
Деревня
|
1000
|
20,2
|
1,6
|
17,1
|
23,5
|
|
10 000
|
20,2
|
1,6
|
17,1
|
23,5
|
|
50 000
|
20,2
|
1,6
|
17,1
|
23,5
|
Таблица 2. Эталонные параметры бутстрепа для долей людей с разным уровнем
заинтересованности в политике
|
Значение переменной
|
Число выборок
|
Выборочная доля, %
|
Стд. Ошибка, %
|
Нижняя граница ДИ, %
|
Верхняя граница ДИ, %
|
|
Очень заинтересован
|
1000
|
16,8
|
1,5
|
14,0
|
19,7
|
|
10 000
|
16,8
|
1,5
|
13,9
|
19,7
|
|
50 000
|
16,8
|
1,5
|
13,9
|
19,7
|
|
Довольно заинтересован
|
1000
|
42,6
|
2,0
|
38,5
|
46,3
|
|
10 000
|
42,6
|
2,0
|
38,7
|
46,5
|
|
50 000
|
42,6
|
2,0
|
38,7
|
46,5
|
|
Едва ли заинтересован
|
1000
|
30,7
|
1,9
|
27,1
|
34,3
|
|
10 000
|
30,7
|
1,9
|
27,1
|
34,4
|
|
50 000
|
30,7
|
1,9
|
27,1
|
34,4
|
|
Совершенно не заинтересован
|
1000
|
10,0
|
1,2
|
7,7
|
12,6
|
|
10 000
|
10,0
|
1,2
|
7,7
|
12,4
|
|
50 000
|
10,0
|
1,2
|
7,7
|
12,4
|
Таблица 3. Параметры бутстрепа для среднего количества лет очного
образования и дисперсии на эталонном массиве
|
Число выборок
|
Выборочное среднее
|
Стд. Ошибка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
|
Среднее
|
1000
|
13,13
|
0,12
|
12,89
|
13,36
|
|
10 000
|
13,13
|
0,12
|
12,90
|
13,36
|
|
50 000
|
13,13
|
0,12
|
12,90
|
13,36
|
|
Дисперсия
|
1000
|
8,389
|
0,591
|
7,306
|
9,581
|
|
10 000
|
0,587
|
7,286
|
9,580
|
|
50 000
|
8,389
|
0,588
|
7,286
|
9,592
|
Таблица 4. Параметры бутстрепа для коэффициента V Крамера на эталонном массиве в ситуации отсутствия связи,
переменные «пол» и «тип населенного пункта»
|
Число выборок
|
Выборочное значение
|
Значимость
|
Стд. Ошибка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
|
1000
|
0,074
|
0,343
|
0,035
|
0,033
|
0,166
|
|
10 000
|
0,074
|
0,343
|
0,035
|
0,031
|
0,167
|
|
50 000
|
0,074
|
0,343
|
0,035
|
0,031
|
0,167
|
Таблица 5. Параметры бутстрепа для коэффициента V Крамера на эталонном массиве в ситуации наличия связи,
переменные «пол» и «трудовые отношения»
|
Число выборокВыборочное
значениеЗначимостьСтд. ОшибкаНижняя граница ДИВерхняя граница ДИ
|
|
|
|
|
|
|
1000
|
0,141
|
0,000
|
0,04
|
0,056
|
0,215
|
|
10 000
|
0,141
|
0,000
|
0,04
|
0,060
|
0,216
|
|
50 000
|
0,141
|
0,000
|
0,04
|
0,061
|
0,216
|
Таблица 6.Параметры бутстрепа для коэффициента ранговой корреляции
Спирмена на эталонном массиве в ситуации наличия связи, переменные «интерес к
политике» и «продолжительность просмотра новостей»
|
Число выборокВыборочное
значениеЗначимостьСтд. ОшибкаНижняя граница ДИВерхняя граница ДИ
|
|
|
|
|
|
|
1000
|
-0,006
|
0,890
|
0,041
|
-0,088
|
0,072
|
|
10 000
|
-0,006
|
0,890
|
0,039
|
-0,082
|
0,071
|
|
50 000
|
-0,006
|
0,890
|
0,39
|
-0,083
|
0,072
|
Таблица 7. Параметры бутстрепа для коэффициента ранговой корреляции
Спирмена на эталонном массиве в ситуации отсутствия связи, переменные «близость
к партии» и «субъективная оценка здоровья»
|
Число выборокВыборочное
значениеЗначимостьСтд. ОшибкаНижняя граница ДИВерхняя граница ДИ
|
|
|
|
|
|
|
1000
|
-0,392
|
0,000
|
0,035
|
-0,458
|
-0,321
|
|
10 000
|
-0,392
|
0,000
|
0,036
|
-0,460
|
-0,320
|
|
50 000
|
-0,392
|
0,000
|
0,036
|
-0,460
|
-0,320
|
Таблица 8. Параметры бутстрепа для коэффициента корреляции Пирсона на
эталонном массиве в ситуации отсутствия связи, переменные «количество лет
очного образования» и «положение на шкале левое крыло-правое крыло»
|
Число выборокВыборочное
значениеЗначимостьСтд. ОшибкаНижняя граница ДИВерхняя граница ДИ
|
|
|
|
|
|
|
1000
|
-0,076
|
0,060
|
0,041
|
-0,160
|
-0,001
|
|
10 000
|
-0,076
|
0,060
|
0,041
|
-0,157
|
0,005
|
|
50 000
|
-0,076
|
0,060
|
0,041
|
-0,156
|
0,005
|
Таблица 9. Параметры бутстрепа для коэффициента корреляции Пирсона на
эталонном массиве в ситуации наличия связи, переменные «уровень счастья» и
«положение в обществе»
|
Число выборокВыборочное
значениеЗначимостьСтд. ОшибкаНижняя граница ДИВерхняя граница ДИ
|
|
|
|
|
|
|
1000
|
0,346
|
0,000
|
0,036
|
0,276
|
0,417
|
|
10 000
|
0,346
|
0,000
|
0,036
|
0,273
|
0,415
|
|
50 000
|
0,346
|
0,000
|
0,036
|
0,273
|
0,415
|
Таблица 11. Параметры бутстрепа для регрессионных коэффициентов на
эталонном массиве, зависимая переменная - «положение в обществе»
|
Переменная
|
Число выборок
|
Значение B
|
Значимость
|
Стд. Ошибка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
|
Константа
|
1000
|
3,278
|
0,001
|
0,460
|
2,434
|
4,197
|
|
10 000
|
3,278
|
0,000
|
0,457
|
2,377
|
4,167
|
|
50 000
|
3,278
|
0,000
|
0,457
|
2,379
|
4,164
|
|
Количество лет очного
образования
|
1000
|
0,015
|
0,488
|
0,023
|
-0,028
|
0,060
|
|
10 000
|
0,015
|
0,488
|
0,022
|
-0,028
|
0,059
|
|
50 000
|
0,015
|
0,493
|
0,022
|
-0,028
|
0,059
|
|
Удовлетворенность системой
образования
|
1000
|
0,021
|
0,416
|
0,27
|
-0,034
|
0,072
|
|
10 000
|
0,021
|
0,410
|
0,26
|
-0,029
|
0,073
|
|
50 000
|
0,021
|
0,408
|
0,26
|
-0,030
|
0,073
|
|
Уровень счастья
|
100
|
0,269
|
0,001
|
0,032
|
0,205
|
0,332
|
|
10 000
|
0,269
|
0,000
|
0,032
|
0,206
|
0,333
|
|
50 000
|
0,269
|
0,000
|
0,032
|
0,206
|
0,333
|
|
Возраст
|
1000
|
-0,013
|
0,002
|
0,004
|
-0,021
|
-0,005
|
|
10 000
|
-0,013
|
0,001
|
0,004
|
-0,021
|
-0,005
|
|
50 000
|
-0,013
|
0,001
|
0,004
|
-0,021
|
-0,005
|
Результаты анализа данных, агрегированные при помощи правила
Рубина
Таблица 1. Параметры бутстрепа для долей людей, проживающих в населенных
пунктах разного типа, агрегированные при помощи правила Рубина
|
Значение переменной
|
Доля пропущенных значений
|
Число выборок
|
Выборочная доля, %
|
Стд. Ошибка, %
|
Нижняя граница ДИ, %
|
Верхняя граница ДИ, %
|
|
Мегаполис
|
10%
|
1000
|
40,8
|
2
|
36,9
|
44,7
|
|
|
10 000
|
40,8
|
2
|
36,9
|
44,7
|
|
|
50 000
|
40,8
|
2
|
36,9
|
44,7
|
|
30%
|
1000
|
39,9
|
2
|
36
|
43,7
|
|
|
10 000
|
39,9
|
2
|
36
|
43,7
|
|
|
50 000
|
39,9
|
2
|
36
|
43,7
|
|
50%
|
1000
|
35,4
|
1,9
|
31,6
|
39,2
|
|
|
10 000
|
35,4
|
1,9
|
31,6
|
39,2
|
|
|
50 000
|
35,4
|
1,9
|
31,6
|
39,2
|
|
Пригород мегаполиса
|
10%
|
1000
|
6,4
|
1
|
4,5
|
8,3
|
|
|
10 000
|
6,4
|
1
|
4,5
|
8,3
|
|
|
50 000
|
6,4
|
1
|
4,5
|
8,3
|
|
30%
|
1000
|
11,7
|
1,3
|
9,1
|
14,3
|
|
|
10 000
|
11,7
|
1,3
|
9,1
|
14,3
|
|
|
50 000
|
11,7
|
1,3
|
9,1
|
14,3
|
|
50%
|
1000
|
17,1
|
1,5
|
14,1
|
20,1
|
|
|
10 000
|
17,1
|
1,5
|
14,1
|
20,1
|
|
|
50 000
|
17,1
|
1,5
|
14,1
|
20,1
|
|
Небольшой город
|
10%
|
1000
|
33
|
1,9
|
29,3
|
36,7
|
|
|
10 000
|
1,9
|
29,3
|
36,7
|
|
|
50 000
|
33
|
1,9
|
29,3
|
36,7
|
|
30%
|
1000
|
30,3
|
1,9
|
26,7
|
34
|
|
|
10 000
|
30,3
|
1,9
|
26,7
|
34
|
|
|
50 000
|
30,3
|
1,9
|
26,7
|
34
|
|
50%
|
1000
|
29,5
|
1,8
|
25,9
|
33,2
|
|
|
10 000
|
29,5
|
1,8
|
25,9
|
33,2
|
|
|
50 000
|
29,5
|
1,8
|
25,9
|
33,2
|
|
Деревня
|
10%
|
1000
|
16,3
|
1,5
|
13,2
|
19,3
|
|
|
10 000
|
19,8
|
1,6
|
16,6
|
23
|
|
|
50 000
|
19,8
|
1,6
|
16,6
|
23
|
|
30%
|
1000
|
18,1
|
1,6
|
15,1
|
21,2
|
|
|
10 000
|
18,1
|
1,6
|
15,1
|
21,2
|
|
|
50 000
|
18,1
|
1,6
|
15,1
|
21,2
|
|
50%
|
1000
|
17,9
|
1,5
|
14,8
|
21
|
|
|
10 000
|
17,9
|
1,5
|
14,8
|
21
|
|
|
50 000
|
17,9
|
1,5
|
14,8
|
21
|
Таблица 2. Параметры бутстрепа для долей людей, в разной степени
заинтересованных в политике, агрегированные при помощи правила Рубина
|
Значение переменной
|
Доля пропущенных значений
|
Число выборок
|
Выборочная доля, %
|
Стд. ошибка, %
|
Нижняя граница ДИ, %
|
Верхняя граница ДИ, %
|
|
Очень заинтересован
|
10%
|
1000
|
17,5
|
1,5
|
14,5
|
20,6
|
|
|
10 000
|
17,5
|
1,5
|
14,5
|
20,6
|
|
|
50 000
|
17,5
|
1,5
|
14,5
|
20,6
|
|
30%
|
1000
|
16,9
|
1,5
|
14
|
19,9
|
|
|
10 000
|
16,9
|
1,5
|
14
|
19,9
|
|
|
50 000
|
16,9
|
1,5
|
14
|
19,9
|
|
50%
|
1000
|
19,1
|
1,6
|
16
|
22,2
|
|
|
10 000
|
19,1
|
1,6
|
16
|
22,2
|
|
|
50 000
|
19,1
|
1,6
|
16
|
22,2
|
|
Довольно заинтересован
|
10%
|
1000
|
42,4
|
2
|
38,5
|
46,3
|
|
|
10 000
|
42,6
|
2
|
38,7
|
46,5
|
|
|
50 000
|
42,6
|
2
|
38,7
|
46,5
|
|
30%
|
1000
|
39,5
|
2
|
35,7
|
43,4
|
|
|
10 000
|
39,5
|
2
|
35,7
|
43,4
|
|
|
50 000
|
39,5
|
2
|
35,7
|
43,4
|
|
50%
|
1000
|
38,7
|
2
|
34,8
|
42,5
|
|
|
10 000
|
38,7
|
2
|
34,8
|
42,5
|
|
|
50 000
|
38,7
|
2
|
34,8
|
42,5
|
|
Едва ли заинтересован
|
10%
|
1000
|
29,8
|
1,8
|
26,2
|
33,4
|
|
|
10 000
|
29,8
|
1,8
|
26,2
|
33,4
|
|
|
50 000
|
29,8
|
1,8
|
26,2
|
33,4
|
|
30%
|
1000
|
27,8
|
1,8
|
24,3
|
31,4
|
|
|
10 000
|
27,8
|
1,8
|
24,3
|
31,4
|
|
|
50 000
|
27,8
|
1,8
|
24,3
|
31,4
|
|
50%
|
1000
|
25,9
|
1,8
|
22,4
|
29,3
|
|
|
10 000
|
25,9
|
1,8
|
22,4
|
29,3
|
|
|
50 000
|
25,9
|
1,8
|
22,4
|
29,3
|
|
Совершенно не заинтересован
|
10%
|
1000
|
10,3
|
1,2
|
7,9
|
12,7
|
|
|
10 000
|
10,3
|
1,2
|
7,9
|
12,7
|
|
|
50 000
|
10,3
|
1,2
|
7,9
|
12,7
|
|
30%
|
1000
|
15,7
|
1,5
|
12,8
|
18,6
|
|
|
10 000
|
15,7
|
1,5
|
12,8
|
18,6
|
|
|
50 000
|
15,7
|
1,5
|
12,8
|
18,6
|
|
50%
|
1000
|
16,4
|
1,5
|
13,5
|
19,3
|
|
|
10 000
|
16,4
|
1,5
|
13,5
|
19,3
|
|
|
50 000
|
16,4
|
1,5
|
13,5
|
19,3
|
Таблица 3. Параметры бутстрепа для среднего и дисперсии количества лет
очного образования, агрегированные при помощи правила Рубина
|
Доля пропусков
|
Показатель
|
Число выборок
|
Выборочное среднее
|
Стд. Ошибка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
|
10%
|
Среднее
|
1000
|
13,07
|
0,01
|
13,04
|
13,10
|
|
|
10 000
|
13,07
|
0,01
|
13,04
|
13,10
|
|
|
50 000
|
13,07
|
0,01
|
13,04
|
13,10
|
|
Дисперсия
|
1000
|
8,61
|
0,03
|
8,55
|
8,67
|
|
|
10 000
|
8,61
|
0,03
|
8,55
|
8,67
|
|
|
50 000
|
8,61
|
0,03
|
8,55
|
8,67
|
|
30%
|
Среднее
|
1000
|
13,06
|
0,01
|
13,03
|
13,09
|
|
|
10 000
|
13,06
|
0,01
|
13,03
|
13,09
|
|
|
50 000
|
13,06
|
0,01
|
13,03
|
|
Дисперсия
|
1000
|
0,08
|
0,03
|
8,02
|
8,14
|
|
|
10 000
|
0,08
|
0,03
|
8,02
|
8,14
|
|
|
50 000
|
0,08
|
0,03
|
8,02
|
8,14
|
|
50%
|
Среднее
|
1000
|
13,05
|
0,01
|
13,02
|
13,08
|
|
|
10 000
|
13,05
|
0,01
|
13,02
|
13,08
|
|
|
50 000
|
13,05
|
0,01
|
13,02
|
13,08
|
|
Дисперсия
|
1000
|
8,85
|
0,03
|
8,78
|
8,92
|
|
|
10 000
|
8,85
|
0,03
|
8,78
|
8,92
|
|
|
50 000
|
8,85
|
0,03
|
8,78
|
8,92
|
Таблица 4. Параметры бутстрепа для V Крамера, агрегированные при помощи правила Рубина в ситуации
отсутствия связи, переменные «пол» и «тип населенного пункта»
|
Доля пропусков
|
Число выборок
|
Выборочное значение
|
Стд. Ошибка
|
Низ ДИ
|
Верх ДИ
|
|
10%
|
1000
|
0,08
|
0,01
|
0,07
|
0,1
|
|
10 000
|
0,08
|
0,01
|
0,07
|
0,1
|
|
50 000
|
0,08
|
0,01
|
0,07
|
0,1
|
|
30%
|
1000
|
0,09
|
0,01
|
0,07
|
0,1
|
|
10 000
|
0,09
|
0,01
|
0,07
|
0,1
|
|
50 000
|
0,09
|
0,01
|
0,07
|
0,1
|
|
50%
|
1000
|
0,12
|
0,01
|
0,1
|
0,13
|
|
10 000
|
0,12
|
0,01
|
0,1
|
0,13
|
|
50 000
|
0,12
|
0,01
|
0,1
|
0,13
|
Таблица 5. Параметры бутстрепа для V Крамера, агрегированные при помощи правила Рубина в ситуации
наличия связи, переменные «пол» и «трудовые отношения»
|
Доля пропусков
|
Число выборок
|
Выборочное значение
|
Стд. Ошибка
|
Низ ДИ
|
Верх ДИ
|
|
10%
|
1000
|
0,16
|
0,01
|
0,14
|
0,18
|
|
10 000
|
0,16
|
0,01
|
0,14
|
0,18
|
|
50 000
|
0,16
|
0,01
|
0,14
|
0,18
|
|
30%
|
1000
|
0,63
|
0,02
|
0,59
|
0,67
|
|
10 000
|
0,63
|
0,02
|
0,59
|
0,67
|
|
50 000
|
0,63
|
0,02
|
0,59
|
0,67
|
|
50%
|
1000
|
0,07
|
0,01
|
0,05
|
0,09
|
|
10 000
|
0,07
|
0,01
|
0,05
|
0,09
|
|
50 000
|
0,07
|
0,01
|
0,05
|
0,09
|
Таблица 17. Параметры бутстрепа для коэффициента Спирмена агрегированные
при помощи правила Рубина в ситуации отсутствия связи, переменные «близость к
партии» и «субъективная оценка здоровья»
|
Доля пропусков
|
Число выборок
|
Выборочное значение
|
Стд. Ошибка
|
Низ ДИ
|
Верх ДИ
|
|
10%
|
1000
|
-0,01
|
0,01
|
-0,02
|
0,01
|
|
10 000
|
-0,01
|
0,01
|
-0,02
|
0,01
|
|
50 000
|
-0,01
|
0,01
|
-0,02
|
0,01
|
|
30%
|
1000
|
-0,06
|
0,01
|
-0,08
|
0,04
|
|
10 000
|
-0,06
|
0,01
|
-0,08
|
0,04
|
|
50 000
|
-0,06
|
0,01
|
-0,08
|
0,04
|
|
50%
|
1000
|
-0,04
|
0,01
|
-0,05
|
-0,02
|
|
10 000
|
-0,04
|
0,01
|
-0,05
|
-0,02
|
|
50 000
|
-0,04
|
0,01
|
-0,05
|
-0,02
|
Таблица 18. Параметры бутстрепа для коэффициента Спирмена, агрегированные
при помощи правила Рубина в ситуации наличия связи, переменные «интерес к политике»
и «продолжительность просмотра новостей»
|
Доля пропусков
|
Число выборок
|
Выборочное значение
|
Стд. Ошибка
|
Низ ДИ
|
Верх ДИ
|
|
10%
|
1000
|
-0,33
|
0,01
|
-0,35
|
-0,31
|
|
10 000
|
-0,33
|
0,01
|
-0,35
|
-0,31
|
|
50 000
|
-0,33
|
0,01
|
-0,35
|
-0,31
|
|
30%
|
1000
|
-0,16
|
0,01
|
-0,18
|
-0,14
|
|
10 000
|
-0,16
|
0,01
|
-0,18
|
-0,14
|
|
50 000
|
-0,16
|
0,01
|
-0,18
|
-0,14
|
|
50%
|
1000
|
-0,04
|
0,01
|
-0,05
|
-0,02
|
|
10 000
|
-0,04
|
0,01
|
-0,05
|
-0,02
|
|
50 000
|
-0,04
|
0,01
|
-0,05
|
-0,02
|
Таблица 19. Параметры бутстрепа для коэффициента Пирсона, агрегированные
при помощи правила Рубина в ситуации отсутствия связи, переменные «количество
лет очного образования» и «положение на шкале левое крыло-правое крыло»
|
Доля пропусков
|
Число выборок
|
Выборочное значение
|
Стд. Ошибка
|
Низ ДИ
|
Верх ДИ
|
|
10%
|
1000
|
-0,04
|
0,01
|
-0,05
|
-0,02
|
|
10 000
|
-0,04
|
0,01
|
-0,05
|
-0,02
|
|
50 000
|
-0,04
|
0,01
|
-0,05
|
-0,02
|
|
30%
|
1000
|
-0,05
|
0,01
|
-0,07
|
-0,03
|
|
10 000
|
-0,05
|
0,01
|
-0,07
|
-0,03
|
|
50 000
|
-0,05
|
0,01
|
-0,07
|
-0,03
|
|
50%
|
1000
|
-0,05
|
0,01
|
-0,06
|
-0,03
|
|
10 000
|
-0,05
|
0,01
|
-0,06
|
-0,03
|
|
50 000
|
-0,05
|
0,01
|
-0,06
|
-0,03
|
Таблица 20. Параметры бутстрепа для коэффициента Пирсона, агрегированные
при помощи правила Рубина в ситуации наличия связи, переменные «уровень
счастья» и «положение в обществе»
|
Доля пропусков
|
Число выборок
|
Выборочное значение
|
Стд. Ошибка
|
Низ ДИ
|
Верх ДИ
|
|
10%
|
1000
|
0,2
|
0,01
|
0,19
|
0,22
|
|
10 000
|
0,2
|
0,01
|
0,19
|
0,22
|
|
50 000
|
0,2
|
0,01
|
0,19
|
0,22
|
|
30%
|
1000
|
0,12
|
0,1
|
0,13
|
|
10 000
|
0,12
|
0,01
|
0,1
|
0,13
|
|
50 000
|
0,12
|
0,01
|
0,1
|
0,13
|
|
50%
|
1000
|
0,03
|
0,01
|
0,02
|
0,05
|
|
10 000
|
0,03
|
0,01
|
0,02
|
0,05
|
|
50 000
|
0,03
|
0,01
|
0,02
|
0,05
|
Таблица 14. Параметры бутстрепа для линейной регрессии с зависимой
переменной «положение в обществе», агрегированные при помощи правила Рубина
|
Член регр. уравнения
|
Доля пропущенных значений
|
Число выборок
|
Точечная оценка корр.
коэффициента
|
Стд. Ошибка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
|
Константа
|
10%
|
1000
|
4,05
|
0,03
|
4,00
|
4,11
|
|
|
10 000
|
4,05
|
0,04
|
3,98
|
4,13
|
|
|
50 000
|
4,05
|
0,04
|
3,98
|
4,13
|
|
30%
|
1000
|
5,76
|
0,07
|
5,54
|
5,8
|
|
|
10 000
|
5,67
|
0,07
|
5,54
|
5,8
|
|
|
50 000
|
5,67
|
0,07
|
5,54
|
5,8
|
|
50%
|
1000
|
4,60
|
0,05
|
4,50
|
4,71
|
|
|
10 000
|
4,60
|
0,05
|
4,50
|
4,71
|
|
|
50 000
|
4,60
|
0,05
|
4,50
|
4,71
|
|
Длительность очного
образования
|
10%
|
1000
|
0,03
|
0,01
|
0,02
|
0,04
|
|
|
10 000
|
0,03
|
0,01
|
0,02
|
0,04
|
|
|
50 000
|
0,03
|
0,01
|
0,02
|
0,04
|
|
30%
|
1000
|
0
|
0,01
|
-0,01
|
0,02
|
|
|
10 000
|
0
|
0,01
|
-0,01
|
0,02
|
|
|
50 000
|
0
|
0,01
|
-0,01
|
0,02
|
|
50%
|
1000
|
0,02
|
0,01
|
0,00
|
0,04
|
|
|
10 000
|
0,02
|
0,01
|
0,00
|
0,04
|
|
|
50 000
|
0,02
|
0,01
|
0,00
|
0,04
|
|
Удовлетворенность системой
образования
|
10%
|
1000
|
0,04
|
0,01
|
0,02
|
0,05
|
|
|
10 000
|
0,04
|
0,01
|
0,02
|
0,05
|
|
|
50 000
|
0,04
|
0,01
|
0,02
|
0,05
|
|
30%
|
1000
|
-0,03
|
0,01
|
-0,04
|
-0,01
|
|
|
10 000
|
-0,03
|
0,01
|
-0,04
|
-0,01
|
|
|
50 000
|
-0,03
|
0,01
|
-0,04
|
-0,01
|
|
50%
|
1000
|
-0,04
|
0,01
|
-0,06
|
-0,03
|
|
|
10 000
|
-0,04
|
0,01
|
-0,06
|
-0,03
|
|
|
50 000
|
-0,04
|
0,01
|
-0,06
|
-0,03
|
|
Уровень счастья
|
10%
|
1000
|
0,17
|
0,01
|
0,16
|
0,19
|
|
|
10 000
|
0,17
|
0,01
|
0,16
|
0,19
|
|
|
50 000
|
0,17
|
0,01
|
0,16
|
0,19
|
|
30%
|
1000
|
0,11
|
0,01
|
0,09
|
0,12
|
|
|
10 000
|
0,11
|
0,01
|
0,09
|
0,12
|
|
|
50 000
|
0,11
|
0,01
|
0,09
|
0,12
|
|
50%
|
1000
|
0,04
|
0,01
|
0,03
|
0,06
|
|
|
10 000
|
0,04
|
0,01
|
0,03
|
0,06
|
|
|
50 000
|
0,04
|
0,01
|
0,03
|
0,06
|
|
Член регр. уравнения
|
Доля пропущенных значений
|
Число выборок
|
Точечная оценка корр.
коэффициента
|
Стд. Ошибка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
|
Возраст
|
10%
|
1000
|
-0,02
|
0,00
|
-0,02
|
-0,01
|
|
|
10 000
|
-0,02
|
0,00
|
-0,02
|
-0,01
|
|
|
50 000
|
-0,02
|
0,00
|
-0,02
|
-0,01
|
|
30%
|
1000
|
-0,02
|
0,00
|
-0,03
|
-0,01
|
|
|
10 000
|
-0,02
|
0,00
|
-0,03
|
-0,01
|
|
|
50 000
|
-0,02
|
0,00
|
-0,03
|
-0,01
|
|
50%
|
1000
|
0,00
|
0,00
|
0,00
|
0,01
|
|
|
10 000
|
0,00
|
0,00
|
0,00
|
0,01
|
|
|
50 000
|
0,00
|
0,00
|
0,00
|
0,01
|
|
|
|
|
|
|
|
|
|
|
|
|
Результаты анализа данных, агрегированные при помощи
усреднения подставленных значений
Таблица 1. Параметры бутстрепа для долей людей, проживающих в населенных
пунктах разного типа, агрегированные при помощи усреднения пропущенных значений
|
Значение переменной
|
Доля пропущенных значений
|
Число выборок
|
Выборочная доля, %
|
Стд. Ошибка, %
|
Нижняя граница ДИ, %
|
Верхняя граница ДИ, %
|
|
Мегаполис
|
10%
|
1000
|
41,6
|
2
|
37,8
|
45,7
|
|
|
10 000
|
41,6
|
2
|
37,7
|
45,5
|
|
|
50 000
|
41,6
|
2
|
37,7
|
45,5
|
|
30%
|
1000
|
39,5
|
2
|
35,6
|
43,2
|
|
|
10 000
|
39,5
|
2
|
35,7
|
43,4
|
|
|
50 000
|
39,5
|
2
|
35,7
|
43,4
|
|
50%
|
1000
|
35,9
|
1,9
|
32,1
|
39,5
|
|
|
10 000
|
35,9
|
1,9
|
32,1
|
39,6
|
|
|
50 000
|
35,9
|
1,9
|
32,1
|
39,6
|
|
Пригород мегаполиса
|
10%
|
1000
|
6,7
|
1
|
8,6
|
|
|
10 000
|
6,7
|
1
|
4,7
|
8,6
|
|
|
50 000
|
6,7
|
1
|
4,7
|
8,6
|
|
30%
|
1000
|
13,9
|
1,4
|
11,3
|
16,6
|
|
|
10 000
|
13,9
|
1,4
|
11,1
|
16,6
|
|
|
50 000
|
13,9
|
1,4
|
11,3
|
16,6
|
|
50%
|
1000
|
19,7
|
1,6
|
16,6
|
23
|
|
|
10 000
|
19,7
|
1,6
|
16,6
|
23
|
|
|
50 000
|
19,7
|
1,6
|
16,6
|
23
|
|
Небольшой город
|
10%
|
1000
|
32,1
|
1,9
|
28,5
|
35,9
|
|
|
10 000
|
32,1
|
1,9
|
28,5
|
35,9
|
|
|
50 000
|
32,1
|
1,9
|
28,5
|
35,9
|
|
30%
|
1000
|
29,2
|
1,9
|
25,3
|
33,1
|
|
|
10 000
|
29,2
|
1,8
|
25,6
|
32,8
|
|
|
50 000
|
29,2
|
1,8
|
25,6
|
32,8
|
|
50%
|
1000
|
27,6
|
1,8
|
24
|
31
|
|
|
10 000
|
27,6
|
1,8
|
24
|
31,2
|
|
|
50 000
|
27,6
|
1,8
|
24
|
31,2
|
|
Деревня
|
10%
|
1000
|
19,6
|
1,6
|
16,6
|
23
|
|
|
10 000
|
19,6
|
1,6
|
16,5
|
22,8
|
|
|
50 000
|
19,6
|
1,6
|
16,5
|
22,7
|
|
30%
|
1000
|
17,5
|
1,5
|
14,5
|
20,6
|
|
|
10 000
|
17,5
|
1,5
|
14,5
|
20,6
|
|
|
50 000
|
17,5
|
1,5
|
14,5
|
20,6
|
|
50%
|
1000
|
16,8
|
1,5
|
13,9
|
19,7
|
|
|
10 000
|
16,8
|
1,5
|
13,9
|
19,7
|
|
|
50 000
|
16,8
|
1,5
|
13,9
|
19,7
|
Таблица 2. Параметры бутстрепа для долей людей, в разной степени
заинтересованных в политике, агрегированные при помощи усреднения пропущенных
значений
|
Значение переменной
|
Доля пропущенных значений
|
Число выборок
|
Выборочная доля, %
|
Стд. Ошибка, %
|
Нижняя граница ДИ, %
|
Верхняя граница ДИ, %
|
|
Очень заинтересован
|
10%
|
1000
|
17,1
|
1,5
|
14,4
|
20,1
|
|
|
10 000
|
17,1
|
1,5
|
14,2
|
20,2
|
|
|
50 000
|
17,1
|
1,5
|
14,2
|
20,2
|
|
30%
|
1000
|
15,7
|
1,5
|
12,7
|
18,8
|
|
|
10 000
|
15,7
|
1,5
|
12,9
|
18,6
|
|
|
50 000
|
15,7
|
1,5
|
12,9
|
18,6
|
|
50%
|
1000
|
17,1
|
1,5
|
14,2
|
20,1
|
|
|
10 000
|
17,1
|
1,5
|
14,2
|
20,1
|
|
|
50 000
|
17,1
|
1,5
|
14,2
|
20,1
|
|
Довольно заинтересован
|
10%
|
1000
|
44
|
2
|
40,5
|
48
|
|
|
10 000
|
44
|
2
|
40,1
|
48,1
|
|
|
50 000
|
44
|
2
|
40,1
|
48,1
|
|
30%
|
1000
|
44,9
|
2
|
40,8
|
48,6
|
|
|
10 000
|
44,9
|
2
|
40,9
|
48,8
|
|
|
50 000
|
44,9
|
2
|
40,9
|
48,8
|
|
50%
|
1000
|
51,4
|
2
|
47
|
55,1
|
|
|
10 000
|
51,4
|
2
|
47,5
|
55,5
|
|
|
50 000
|
51,4
|
2
|
47,6
|
55,7
|
|
Едва ли заинтересован
|
10%
|
1000
|
29,4
|
1,8
|
25,9
|
32,8
|
|
|
10 000
|
29,4
|
1,8
|
25,8
|
33
|
|
|
50 000
|
29,4
|
1,8
|
25,8
|
33
|
|
30%
|
1000
|
30,3
|
1,8
|
26,6
|
34,1
|
|
|
10 000
|
30,3
|
1,9
|
26,8
|
34,1
|
|
|
50 000
|
30,3
|
1,9
|
26,8
|
34
|
|
50%
|
1000
|
25,4
|
1,8
|
22,2
|
29,2
|
|
|
10 000
|
25,4
|
1,8
|
22
|
28,9
|
|
|
50 000
|
25,4
|
1,8
|
22
|
28,9
|
|
Совершенно не заинтересован
|
10%
|
1000
|
9,5
|
1,2
|
7,2
|
11,7
|
|
|
10 000
|
9,5
|
1,2
|
7,2
|
11,9
|
|
|
50 000
|
9,5
|
1,2
|
7,2
|
11,9
|
|
30%
|
1000
|
9,1
|
1,1
|
7
|
11,3
|
|
|
10 000
|
9,1
|
1,2
|
6,9
|
11,4
|
|
|
50 000
|
9,1
|
1,2
|
6,9
|
11,4
|
|
50%
|
1000
|
6
|
1
|
4,2
|
8
|
|
|
10 000
|
6
|
1
|
4,2
|
8
|
|
|
50 000
|
6
|
1
|
4,2
|
8
|
Таблица 3. Параметры бутстрепа для среднего количества лет очного
образования и дисперсии, агрегированные при помощи усреднения пропущенных
значений
|
Доля пропущенных значений
|
Показатель
|
Число выборок
|
Выборочное среднее
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
|
10%
|
Среднее
|
1000
|
13,07
|
0,119
|
12,85
|
13,30
|
|
|
10 000
|
13,07
|
0,113
|
12,85
|
13,29
|
|
|
50 000
|
13,07
|
0,114
|
12,85
|
13,29
|
|
Дисперсия
|
1000
|
8,077
|
0,589
|
6,966
|
9,293
|
|
|
10 000
|
8,077
|
0,570
|
7,004
|
9,242
|
|
|
50 000
|
8,077
|
0,571
|
7,009
|
9,245
|
|
30%
|
Среднее
|
1000
|
13,05
|
0,1
|
12,87
|
13,25
|
|
|
10 000
|
13,05
|
0,1
|
12,86
|
13,25
|
|
|
50 000
|
13,05
|
0,1
|
12,86
|
13,25
|
|
Дисперсия
|
1000
|
6,150
|
0,399
|
5,327
|
6,920
|
|
|
10 000
|
6,150
|
0,404
|
5,387
|
6,954
|
|
|
50 000
|
6,150
|
0,407
|
5,367
|
6,966
|
|
50%
|
Среднее
|
1000
|
13,05
|
0,09
|
12,88
|
13,23
|
|
|
10 000
|
13,05
|
0,09
|
12,88
|
13,23
|
|
|
50 000
|
13,05
|
0,09
|
12,88
|
13,23
|
|
Дисперсия
|
1000
|
4,894
|
0,329
|
4,276
|
5,546
|
|
|
10 000
|
4,894
|
0,335
|
4,249
|
5,552
|
|
|
50 000
|
4,894
|
0,334
|
4,258
|
5,568
|
Таблица 4. Параметры бутстрепа для V Крамера, агрегированные при помощи усреднения пропущенных
значений в ситуации отсутствия связи, переменные «пол» и «тип населенного
пункта»
|
Доля пропущенных значений
|
Число выборок
|
Выборочное значение
|
Стд. Ошибка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
|
10%
|
1000
|
0,094
|
0,037
|
0,043
|
0,182
|
|
10 000
|
0,094
|
0,037
|
0,044
|
0,186
|
|
50 000
|
0,094
|
0,037
|
0,044
|
0,186
|
|
30%
|
1000
|
0,098
|
0,038
|
0,042
|
0,195
|
|
10 000
|
0,098
|
0,038
|
0,044
|
0,193
|
|
50 000
|
0,098
|
0,038
|
0,043
|
0,193
|
|
50%
|
1000
|
0,141
|
0,037
|
0,08
|
0,224
|
|
10 000
|
0,141
|
0,037
|
0,079
|
0,226
|
|
50 000
|
0,141
|
0,037
|
0,08
|
0,228
|
Таблица 5. Параметры бутстрепа для V Крамера, агрегированные при помощи усреднения пропущенных
значений в ситуации отсутствия связи, переменные «пол» и «трудовые отношения»
|
Доля пропущенных значений
|
Число выборок
|
Выборочное значение
|
Стд. Ошибка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
|
10%
|
1000
|
0,156
|
0,04
|
0,075
|
0,236
|
|
10 000
|
0,156
|
0,04
|
0,074
|
0,230
|
|
50 000
|
0,156
|
0,04
|
0,074
|
0,230
|
|
30%
|
1000
|
0,162
|
0,043
|
0,078
|
0,247
|
|
10 000
|
0,162
|
0,043
|
0,077
|
0,243
|
|
50 000
|
0,162
|
0,043
|
0,077
|
0,242
|
|
50%
|
1000
|
0,099
|
0,041
|
0,021
|
0,181
|
|
10 000
|
0,099
|
0,041
|
0,020
|
0,180
|
|
50 000
|
0,099
|
0,041
|
0,020
|
0,180
|
Таблица 6. Параметры бутстрепа для коэффициента Спирмена агрегированные
при помощи усреднения пропущенных значений в ситуации отсутствия связи,
переменные «близость к партии» и «субъективная оценка здоровья»
|
Доля пропусков
|
Число выборок
|
Выборочное значение
|
Стд. Ошибка
|
Низ ДИ
|
Верх ДИ
|
|
10%
|
1000
|
0,026
|
0,042
|
-0,062
|
0,105
|
|
10 000
|
0,026
|
0,040
|
-0,054
|
0,105
|
|
50 000
|
0,026
|
0,040
|
-0,051
|
0,107
|
|
30%
|
1000
|
-0,091
|
0,040
|
-0,168
|
0,01
|
|
10 000
|
-0,091
|
0,039
|
-0,167
|
0,012
|
|
50 000
|
-0,091
|
0,039
|
-0,167
|
0,012
|
|
50%
|
1000
|
-0,059
|
0,039
|
-0,138
|
0,016
|
|
10 000
|
-0,059
|
0,039
|
-0,137
|
0,017
|
|
50 000
|
-0,059
|
0,039
|
-0,137
|
0,017
|
Таблица 7. Параметры бутстрепа для коэффициента Спирмена, агрегированные
при помощи усреднения пропущенных значений в ситуации наличия связи, переменные
«интерес к политике» и «продолжительность просмотра новостей»
|
Доля пропусков
|
Число выборок
|
Выборочное значение
|
Стд. Ошибка
|
Низ ДИ
|
Верх ДИ
|
|
10%
|
1000
|
-0,346
|
0,038
|
-0,423
|
-0,270
|
|
10 000
|
-0,346
|
0,038
|
-0,421
|
-0,269
|
|
50 000
|
-0,346
|
0,038
|
-0,419
|
-0,269
|
|
30%
|
1000
|
-0,141
|
0,043
|
-0,224
|
-0,056
|
|
10 000
|
-0,141
|
0,043
|
-0,223
|
-0,056
|
|
50 000
|
-0,141
|
0,043
|
-0,223
|
-0,056
|
|
50%
|
1000
|
-0,151
|
0,040
|
-0,229
|
-0,069
|
|
10 000
|
-0,151
|
0,039
|
-0,228
|
-0,074
|
|
50 000
|
-0,151
|
0,039
|
-0,228
|
-0,075
|
Таблица 8. Параметры бутстрепа для коэффициента Пирсона, агрегированные
при помощи усреднения пропущенных значений в ситуации отсутствия связи,
переменные «количество лет очного образования» и «положение на шкале левое
крыло-правое крыло»
|
Доля пропусков
|
Число выборок
|
Выборочное значение
|
Стд. Ошибка
|
Низ ДИ
|
Верх ДИ
|
|
10%
|
1000
|
-0,047
|
0,041
|
-0,128
|
-0,030
|
|
10 000
|
-0,047
|
0,040
|
-0,125
|
-0,032
|
|
50 000
|
-0,047
|
0,040
|
-0,125
|
-0,031
|
|
30%
|
1000
|
-0,084
|
0,039
|
-0,160
|
-0,005
|
-0,084
|
0,039
|
-0,160
|
-0,007
|
|
50 000
|
-0,084
|
0,039
|
-0,160
|
-0,007
|
|
50%
|
1000
|
-0,106
|
0,039
|
-0,181
|
-0,029
|
|
10 000
|
-0,106
|
0,039
|
-0,182
|
-0,029
|
|
50 000
|
-0,106
|
0,039
|
-0,182
|
-0,029
|
Таблица 9. Параметры бутстрепа для коэффициента Пирсона, агрегированные
при помощи усреднения пропущенных значений в ситуации наличия связи, переменные
«уровень счастья» и «положение в обществе»
|
Доля пропусков
|
Число выборок
|
Выборочное значение
|
Стд. Ошибка
|
Низ ДИ
|
Верх ДИ
|
|
10%
|
1000
|
0,244
|
0,037
|
0,175
|
0,318
|
|
10 000
|
0,244
|
0,037
|
0,168
|
0,317
|
|
50 000
|
0,244
|
0,037
|
0,167
|
0,317
|
|
30%
|
1000
|
0,166
|
0,039
|
0,090
|
0,239
|
|
10 000
|
0,166
|
0,039
|
0,092
|
0,239
|
|
50 000
|
0,166
|
0,039
|
0,092
|
0,239
|
|
50%
|
1000
|
0,110
|
0,036
|
0,036
|
0,178
|
|
10 000
|
0,110
|
0,037
|
0,037
|
0,184
|
|
50 000
|
0,110
|
0,037
|
0,037
|
0,184
|
Таблица 10. Параметры бутстрепа для линейной регрессии с зависимой
переменной «положение в обществе», агрегированные при помощи усреднения
пропущенных значений
|
Член регр. уравнения
|
Доля пропущенных значений
|
Число выборок
|
Точечная оценка корр.
коэффициента
|
Стд. Ошибка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
|
Константа
|
10%
|
1000
|
4,887
|
0,571
|
3,731
|
6,029
|
|
|
10 000
|
4,887
|
0,567
|
3,771
|
5,971
|
|
|
50 000
|
4,887
|
0,571
|
3,747
|
5,996
|
|
30%
|
1000
|
6,153
|
0,700
|
4,802
|
7,551
|
|
|
10 000
|
6,153
|
0,719
|
4,740
|
7,592
|
|
|
50 000
|
6,153
|
0,726
|
4,729
|
7,575
|
|
50%
|
1000
|
6,754
|
0,726
|
5,248
|
8,180
|
|
|
10 000
|
6,754
|
0,712
|
5,386
|
8,142
|
|
|
50 000
|
6,754
|
0,713
|
5,367
|
8,166
|
|
Длительность очного
образования
|
10%
|
1000
|
-0,037
|
0,029
|
-0,095
|
0,022
|
|
|
10 000
|
-0,037
|
0,028
|
-0,092
|
0,019
|
|
|
50 000
|
-0,037
|
0,029
|
-0,092
|
0,020
|
|
30%
|
1000
|
-0,081
|
0,037
|
-0,158
|
-0,007
|
|
|
10 000
|
-0,081
|
0,037
|
-0,154
|
-0,008
|
|
|
50 000
|
-0,081
|
0,037
|
-0,154
|
-0,008
|
|
50%
|
1000
|
-0,112
|
0,041
|
-0,191
|
-0,032
|
|
|
10 000
|
-0,112
|
0,039
|
-0,191
|
-0,035
|
|
|
50 000
|
-0,112
|
0,039
|
-0,190
|
-0,036
|
|
Удовлетворенность системой
образования
|
10%
|
1000
|
0,142
|
0,033
|
0,075
|
0,204
|
|
|
10 000
|
0,142
|
0,033
|
0,076
|
0,207
|
|
|
50 000
|
0,142
|
0,032
|
0,080
|
0,205
|
|
30%
|
1000
|
0,057
|
0,034
|
-0,009
|
0,123
|
|
|
10 000
|
0,057
|
0,034
|
-0,009
|
0,123
|
|
|
50 000
|
0,057
|
0,034
|
-0,011
|
0,124
|
|
50%
|
1000
|
-0,008
|
0,029
|
-0,063
|
0,051
|
|
|
10 000
|
-0,008
|
0,030
|
-0,067
|
0,050
|
|
|
50 000
|
-0,008
|
0,029
|
-0,065
|
0,049
|
|
Уровень счастья
|
10%
|
1000
|
0,022
|
0,036
|
-0,051
|
0,092
|
|
|
10 000
|
0,022
|
0,036
|
-0,049
|
0,092
|
|
|
50 000
|
0,022
|
0,037
|
-0,051
|
0,093
|
|
30%
|
1000
|
0,007
|
0,038
|
-0,069
|
0,083
|
|
|
10 000
|
0,007
|
0,037
|
-0,066
|
0,081
|
|
|
50 000
|
0,007
|
0,038
|
-0,069
|
0,081
|
|
50%
|
1000
|
-0,011
|
0,045
|
-0,099
|
0,077
|
|
|
10 000
|
-0,011
|
0,046
|
-0,102
|
0,079
|
|
|
50 000
|
-0,011
|
0,045
|
-0,098
|
0,080
|
|
Член регр. уравнения
|
Доля пропущенных значений
|
Число выборок
|
Точечная оценка корр.
коэффициента
|
Стд. Ошибка
|
Нижняя граница ДИ
|
Верхняя граница ДИ
|
|
Возраст
|
10%
|
1000
|
-0,007
|
0,005
|
-0,017
|
0,003
|
|
|
10 000
|
-0,007
|
0,005
|
-0,017
|
0,002
|
|
|
50 000
|
-0,007
|
0,005
|
-0,017
|
0,003
|
|
30%
|
1000
|
-0,07
|
0,006
|
-0,028
|
0,004
|
|
|
10 000
|
-0,07
|
0,006
|
-0,028
|
0,004
|
|
|
50 000
|
-0,07
|
0,006
|
-0,019
|
0,004
|
|
50%
|
1000
|
-0,006
|
0,006
|
-0,018
|
0,006
|
|
|
10 000
|
-0,006
|
0,006
|
-0,019
|
0,006
|
|
|
50 000
|
-0,006
|
0,006
|
-0,019
|
0,006
|