Обработка результатов многократных измерений
МИнОБРнауки россии
ФГБОУ ВО Пензенский государственный технологичесий Университет
(пензгту)
Кафедра
«Техническое управление качеством»
Дисциплина
«Метрология, стандартизация и сертификация»
Отчет
по лабораторной работе №1
«Обработка
результатов многократных измерений»
Выполнила: студентка группы 14ЗТ1бп
Кондрашова А.О.
Проверил: К.т.н., доцент Баклин А.А.
Пенза
г.
Прямые - это измерения, при которых искомое
значение физической величины находят непосредственно из опытных данных. Прямые
измерения можно выразить формулой
= X,
где Q - искомое значение измеряемой величины, а
X - значение, непосредственно получаемое из опытных данных. Примерами таких
измерений являются: измерение длины линейкой или рулеткой, измерение диаметра
штангенциркулем или микрометром, измерение угла угломером, измерение
температуры термометром и т.п.
Абсолютная погрешность измерения 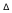 -
разность между результатом измерения Х и истинным значением Хo измеряемой
величины:
-
разность между результатом измерения Х и истинным значением Хo измеряемой
величины:
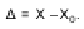
Абсолютная погрешность выражается в единицах
измеряемой величины.
Относительная погрешность измерения 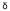 -
отношение абсолютной погрешности измерения
-
отношение абсолютной погрешности измерения 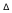 к
истинному значению измеряемой величины Хo:
к
истинному значению измеряемой величины Хo:
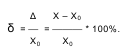
Проверить наличие грубых
погрешностей - нет ли значений 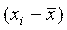 ,
которые выходят за пределы ±3S. При нормальном законе распределений с
вероятностью, практически равной 1 (0,997), ни одно из значений этой разности
не должно выйти за указанные пределы. Если они имеются, то следует исключить из
рассмотрения соответствующие значения
,
которые выходят за пределы ±3S. При нормальном законе распределений с
вероятностью, практически равной 1 (0,997), ни одно из значений этой разности
не должно выйти за указанные пределы. Если они имеются, то следует исключить из
рассмотрения соответствующие значения 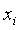 и заново повторить вычисления
и заново повторить вычисления 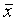 и оценку S.
и оценку S.
Систематические погрешности обычно оцениваются
либо путем теоретического анализа условий измерения, основываясь на известных
свойствах средств измерений, либо использованием более точных средств
измерений. Как правило, систематические погрешности стараются исключить с
помощью поправок. Поправка представляет собой значение величины, вводимое в
неисправленный результата измерения с целью исключения систематической
погрешности. Знак поправки противоположен знаку величины.
Коэффициент Стьюдента, зависящий от числа
наблюдений n и выбранной доверительной вероятности Р. Он определяется с помощью
таблицы q-процентных точек распределения Стьюдента, которая имеет два
параметра: k = n - 1 и q= 1 - P; - оценка среднего квадратического отклонения
среднего арифметического.
Исходные данные
|
Номер
измерения
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
|
Полученное
значение, мм
|
71,012
|
71,042
|
71,018
|
71,048
|
71,024
|
71,066
|
71,036
|
71,060
|
71,030
|
погрешность
коэффициент стьюдент
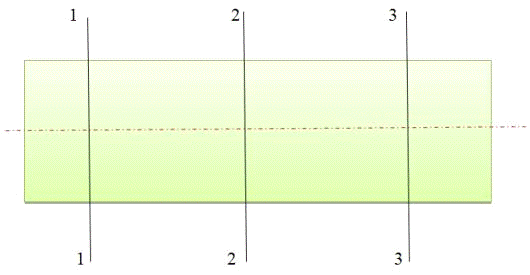
Схема измерения
Доверительная вероятность Р=0,95
Коэффициент Стьюдента tp=2,26
Табл.1
«Обработка результатов многократных измерений»
|
Среднее
арифметическое значение
|
|
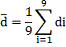
|
71,037
|
Табл.2
|
di
|
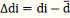
|
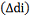 2 2
|
|
1.
|
0,025333333
|
0,000641778
|
|
2.
|
-0,004666667
|
2,17778E-05
|
|
3.
|
0,019333333
|
0,000373778
|
|
4.
|
-0,010666667
|
0,000113778
|
|
5.
|
0,000177778
|
|
6.
|
-0,028666667
|
0,000821778
|
|
7.
|
0,001333333
|
1,77778E-06
|
|
8.
|
-0,022666667
|
0,000513778
|
|
9.
|
0,007333333
|
5,37778E-05
|
|
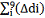 2 2
|
0,00272
|
Табл.3
|
Параметр
|
Формула
|
Значение
|
|
σ
|
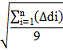
|
0,017
|
|
Sx
|
Sx=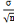
|
0,0058
|
|
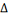
|
±tp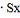
|
±0,013
|
|
δ
|
δ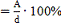
|
0,018 %
|
|
d
|
d= 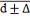
|
71,037±
0,013
|
Обработка результатов в программе Microsoft
Excel
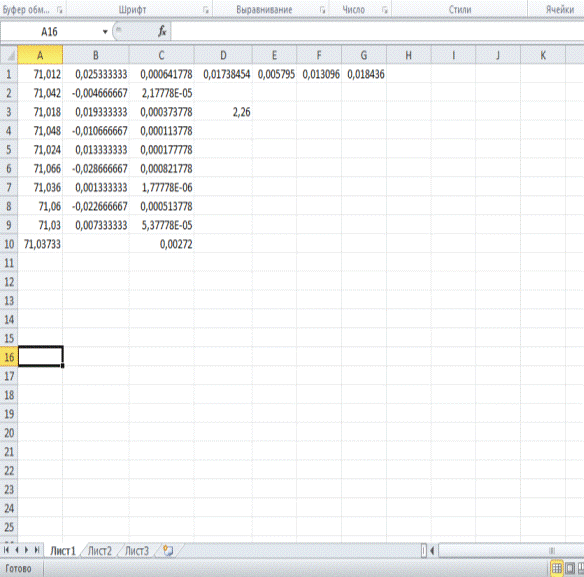
Выводы:
Пределы действительного значения 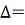 ±0,013
±0,013
Относительная погрешность измерения δ
= 0,018%
Результат измерения d=71,037±
0,013; Р=0, 95