Синтез, структурный и кинематический анализ кривошипно-кулисного механизма поперечно-строгального станка
Содержание
Введение
. Синтез, структурный и кинематический анализ рычажного
механизма
.1 Синтез механизма
.2 Структурный анализ механизма
.3 Кинематический анализ механизма
.3.1 Построение планов положений механизма
.3.2 Построение кинематических диаграмм для точки Е выходного
звена
.3.3 Определение линейных скоростей характерных точек и
угловых скоростей звеньев механизма методом планов
.3.4 Определение линейных ускорений характерных точек и
угловых ускорений звеньев механизма методом планов
. Силовое исследование рычажного механизма
. Синтез зубчатого механизма
. Синтез кулачкового механизма
Заключение
Список литературы
Введение
Развитие современной науки и техники неразрывно связано с созданием новых
машин, повышающих производительность и облегчающих труд человека на
производстве. Главная задача, стоящая перед современным машиностроением -
подготовка высококвалифицированных инженеров. Инженер-конструктор должен
владеть совершенными методами. Рационально спроектированная машина должна
удовлетворять современным экологическим, техническим и производственным
требованиям. Эти требования представляют собой комплекс задач, которые должны
быть решены в процессе проектирования новой машины.
1. Синтез, структурный и кинематический анализ рычажного механизма
Задано: структурная схема механизма, размеры звеньев (или их
соотношения), закон движения ведущего звена и другие параметры.
Требуется: определить недостающие размеры звеньев механизма и произвести
структурный и кинематический анализ механизма графическим способом.
.1 Синтез механизма
Рассмотрим кривошипно-кулисный механизм поперечно-строгального станка
(рис.1.1).
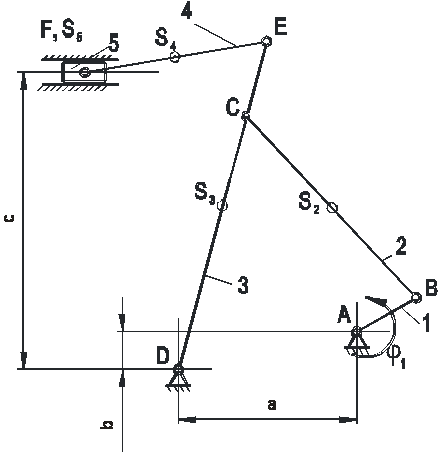
Рис.1.1
Структурная схема механизма: 1- кривошип; 2- шатун; 3- коромысло; 4- шатун; 5-
ползун; 6- стойка
Исходные данные:
Длина
кривошипа 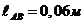 ,
,
Длина
шатуна 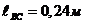 ,
,
Длина
коромысла 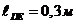 ,
,
Длина
звена 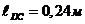 ,
,
Длина
шатуна 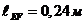 ,
,
Координаты
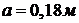
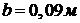 ,
,
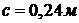 ,
,
Угловая
скорость кривошипа 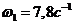 ,
,
Решение
Определяем
расстояния до центров тяжести 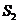 и
и 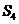 звеньев 3 и 4:
звеньев 3 и 4:
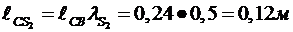 ;
;
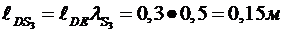 ;
;
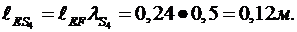
1.2 Структурный анализ механизма
При структурном анализе нужно решить следующие задачи: подсчитать число
степеней свободы механизма и определить количество начальных звеньев; разложить
механизм на структурные группы с нулевой степенью свободы (группы Ассура) и
начальный механизм (начальные механизмы); определить класс и порядок каждой
группы; определить класс механизма; написать формулу строения механизма.
Структурный анализ механизма представлен в таблицах 1.1 и 1.2,
Структурный анализ механизма
Таблица 1.1
|
Звенья
|
Кинематические пары (КП)
|
|
Условные обозначения
|
Название
|
Cхема
|
Вид относи-тельного
движения
|
Cимвол
|
Обознач КП
|
Класс
|
|
|
|
|
|
|
|
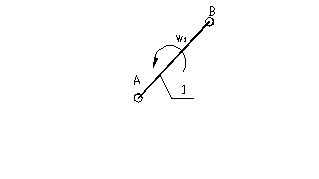 Кривошип
Кривошип Вращ.
Вращ.
Определяем степень подвижности механизма по формуле П.Л.Чебышева для
плоских механизмов:
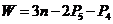 ,
,
где
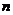 -число подвижных звеньев;
-число подвижных звеньев;
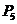 -число
кинематических пар 5 класса;
-число
кинематических пар 5 класса;
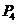 -число
кинематических пар 4 класса;
-число
кинематических пар 4 класса;
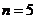 ;
; 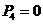 ;
; 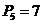 ;
;
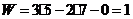
рычажный зубчатый кулачковый механизм
Группы
Ассура и начальный механизм
Таблица
1.2
|
Схемы групп Ассура и
начального механизма
|
Название, класс, порядок
|
Число звеньев
|
Число кинематических пар
|
Формула строения группы
|
|
|
|
всего
|
поводков
|
|
|
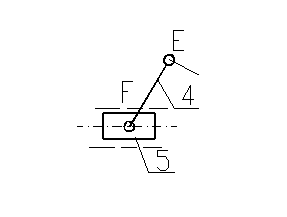 Двухповодковая группа Ассура 2-го класса,2-го
порядка232 Двухповодковая группа Ассура 2-го класса,2-го
порядка232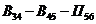
|
|
|
|
|
|
|
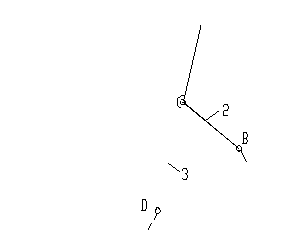 Двухповодковая группа Ассура 2-го класса, 2-го
порядка.232 Двухповодковая группа Ассура 2-го класса, 2-го
порядка.232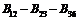
|
|
|
|
|
|
|
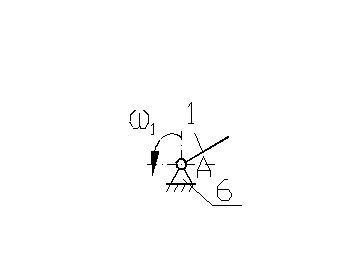 Начальный механизм 1-го класса Начальный механизм 1-го класса
|
2
|
1
|
-
|
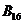
|
|
|
Формула строения механизма:
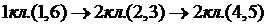
|
Исследуемый механизм состоит из двух групп Ассура второго класса, и групп
более высокого класса в этом механизме нет, следовательно, механизм в целом относится
к механизмам второго класса.
.3 Кинематический анализ механизма
Кинематический анализ механизма заключается в исследовании движения его
звеньев независимо от сил, вызывающих это движение. При этом решаются следующие
задачи: определяются положения звеньев и траектории движения характерных точек
в зависимости от обобщенной координаты (угловой или линейной), линейные
скорости и ускорения этих точек, угловые скорости и ускорения звеньев.
Существуют различные методы кинематического анализа, позволяющие
установить функциональную зависимость между кинематическими и метрическими
параметрами механизма: аналитический, графоаналитический, графический и
экспериментальный.
В курсовом проекте предлагается использовать графоаналитический (метод
планов) и графический (построение кинематических диаграмм) методы.
.3.1 Построение планов положений механизма
Чертим
кривошип  в одном из положений произвольной длины. В данном
примере мы взяли
в одном из положений произвольной длины. В данном
примере мы взяли 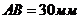 .
.
Определяем
масштабный коэффициент длины:
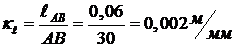 .
.
Траекторию
точки 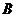 , принадлежащей кривошипу 1 (окружность радиусом
, принадлежащей кривошипу 1 (окружность радиусом 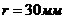 ) разбиваем на 12 равных частей и методом засечек
определяем соответствующие положения точек
) разбиваем на 12 равных частей и методом засечек
определяем соответствующие положения точек 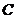 ,
, 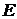 и
и 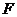 .
Получаем 12 планов положений механизма на одном чертеже.
.
Получаем 12 планов положений механизма на одном чертеже.
Первое
положение кривошипа  соответствует крайнему правому положению точки
соответствует крайнему правому положению точки 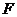 ползуна 5 (точка
ползуна 5 (точка 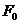 ). Далее
нумеруем все положения в соответствии с направлением угловой скорости
). Далее
нумеруем все положения в соответствии с направлением угловой скорости 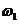 (против часовой стрелки).
(против часовой стрелки).
Положения
центров тяжести 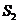 ,
, 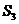 и
и 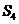 звеньев 2, 3 и 4 отмечаем на соответствующих звеньях
звеньев 2, 3 и 4 отмечаем на соответствующих звеньях 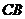 ,
, 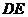 и
и 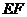 во всех двенадцати положениях механизма, принимая
во всех двенадцати положениях механизма, принимая 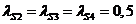 .
.
.3.2
Построение кинематических диаграмм для точки F выходного
звена 5
Обозначим
расстояние от 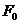 до
до  через
через 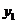 ,от
,от 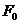 до
до 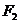 через
через 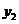 , от
, от 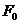 до
до 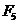 через
через 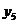 , от
, от 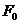 до
до 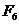 через
через 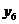 и так
далее..
и так
далее..
Строим
диаграмму перемещения  точки
точки 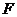 ползуна
5 в зависимости от угла поворота кривошипа
ползуна
5 в зависимости от угла поворота кривошипа 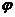 . На оси
абсцисс откладываем отрезок
. На оси
абсцисс откладываем отрезок 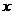 , который
изображает полный угол поворота кривошипа
, который
изображает полный угол поворота кривошипа 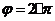 . Длину
отрезка выбираем произвольно (в данном случае
. Длину
отрезка выбираем произвольно (в данном случае 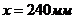 ), а
затем определяем масштабный коэффициент
), а
затем определяем масштабный коэффициент 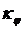 :
:
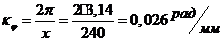
Отрезок
(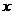 ) делим на 12 равных частей и в точках 1, 2, 3, 4, 5,
6, 7, 8, 9, 10, 11 откладываем ординаты
) делим на 12 равных частей и в точках 1, 2, 3, 4, 5,
6, 7, 8, 9, 10, 11 откладываем ординаты 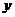 , равные
соответственно
, равные
соответственно 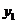 ,
, 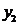 ,
, 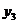 ,
, 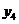 ,
, 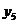 ,
, 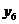 ,
,  ,
, 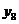 ,
, 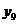 ,
, 
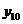 ,
, 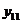 . Соединяем концы ординат плавной кривой и получаем
диаграмму
. Соединяем концы ординат плавной кривой и получаем
диаграмму  перемещений точки
перемещений точки 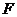 в
зависимости от угла поворота кривошипа.
в
зависимости от угла поворота кривошипа.
Диаграмму
аналогов скоростей точки 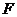 строим методом графического дифференцирования кривой
строим методом графического дифференцирования кривой  . Намечаем систему координат
. Намечаем систему координат 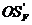 и
и 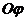 ниже
кривой
ниже
кривой  . На продолжении оси
. На продолжении оси 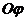 влево от
начала координат откладываем полюсное расстояние
влево от
начала координат откладываем полюсное расстояние 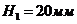 . Из
точки
. Из
точки 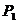 проводим лучи параллельно хордам кривой перемещений
проводим лучи параллельно хордам кривой перемещений  . Эти лучи отсекут на оси
. Эти лучи отсекут на оси 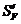 отрезки, пропорциональные средним значениям аналогов
скоростей
отрезки, пропорциональные средним значениям аналогов
скоростей 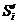 на соответствующих участках диаграммы. Отложим эти
отрезки на средних ординатах соответствующих участков и соединим полученные
точки плавной кривой. Эта кривая будет диаграммой аналогов скоростей
на соответствующих участках диаграммы. Отложим эти
отрезки на средних ординатах соответствующих участков и соединим полученные
точки плавной кривой. Эта кривая будет диаграммой аналогов скоростей 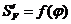 .
.
После
построения диаграммы аналогов скоростей аналогично строим диаграмму аналогов
ускорений 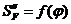 .
.
При
построении диаграмм 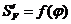 и
и 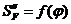 описанным
методом нельзя получить те участки диаграмм, которые соответствуют половине
крайних участков оси абсцисс. Чтобы закончить построение диаграмм, нужно
дополнительно построить средние значения
описанным
методом нельзя получить те участки диаграмм, которые соответствуют половине
крайних участков оси абсцисс. Чтобы закончить построение диаграмм, нужно
дополнительно построить средние значения 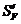 и
и 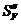 для одного- двух участков следующего цикла.
для одного- двух участков следующего цикла.
Масштабные
коэффициенты 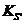 и
и 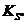 диаграмм
аналогов скоростей и ускорений
диаграмм
аналогов скоростей и ускорений 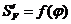 и
и 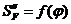 определяем по следующим зависимостям:
определяем по следующим зависимостям:
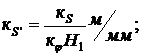
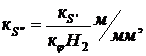
где 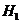 и
и 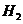 -полюсные
расстояния (приняли произвольно);
-полюсные
расстояния (приняли произвольно);
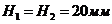 ;
;

.3.3
Определение линейных скоростей характерных точек и угловых скоростей звеньев
механизма методом планов
При реальном проектировании планы строят чаще всего для 12 равноотстоящих
положений механизма. В учебном курсовом проекте нужно построить планы скоростей
и ускорений всего для двух положений механизма (в рабочем и холостом ходе). По
планам скоростей и ускорений нужно определить линейные скорости и ускорения
всех характерных точек механизма, включая центры тяжести звеньев, угловые
скорости и ускорения звеньев, а также их направления.
Исследуем механизм в первом и восьмом положениях.
Положение 1
Рассматриваем
начальный механизм (1,6) и определяем скорость центра шарнира 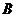 :
:
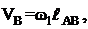
где
ω1-угловая скорость кривошипа;
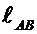 -длина
звена AB;
-длина
звена AB;
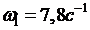 ;
;
 =0,06 м;
=0,06 м;
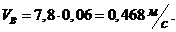
Вектор
скорости 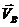 перпендикулярен звену
перпендикулярен звену  и
направлен в сторону его вращения. Вектор скорости
и
направлен в сторону его вращения. Вектор скорости 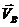 изображаем на плане скоростей отрезком произвольной
длины
изображаем на плане скоростей отрезком произвольной
длины 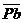 . Принимаем
. Принимаем 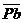 =46 мм.
=46 мм.
После
этого определяем масштабный коэффициент скорости

Известны
скорости точек 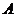 и
и 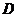 (
(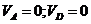 ). Нужно определить скорость точки
). Нужно определить скорость точки 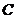 , принадлежащей шатуну 2 и коромыслу 3.
, принадлежащей шатуну 2 и коромыслу 3.
Рассматривая
движение точки 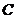 сначала по отношению к звену
сначала по отношению к звену 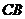 , а затем по отношению к звену
, а затем по отношению к звену 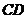 , записываем соответственно два векторных уравнения:
, записываем соответственно два векторных уравнения:
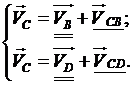 ;
;
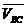 направлен
перпендикулярно
направлен
перпендикулярно 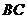 , а вектор относительной скорости
, а вектор относительной скорости  во вращательном движении звена 3 вокруг точки
во вращательном движении звена 3 вокруг точки 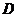 - перпендикулярно к
- перпендикулярно к 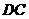 .
.
Решаем
эту систему уравнений графически. Через точку b на плане скоростей проводим
прямую, перпендикулярную 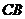 , а через полюс Р, (так как точка
, а через полюс Р, (так как точка 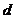 лежит в полюсе)- прямую, перпендикулярную к
лежит в полюсе)- прямую, перпендикулярную к 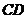 . Точка пересечения этих прямых линий определит
положение точки
. Точка пересечения этих прямых линий определит
положение точки 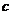 вектора
вектора 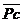 абсолютной
скорости точки
абсолютной
скорости точки 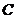 коромысла..
коромысла..
Положение
точек 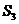 и
и 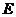 находим
по теореме подобия, используя соотношения:
находим
по теореме подобия, используя соотношения:
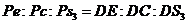 .
.
Зная
длины звеньев 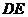 и
и 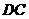 и
измерив на плане скоростей
и
измерив на плане скоростей 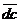 , найдем
длину отрезков
, найдем
длину отрезков 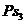 и
и 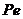 . Точка
. Точка 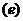 в соответствии с теоремой подобия будет находиться на
продолжении отрезка
в соответствии с теоремой подобия будет находиться на
продолжении отрезка 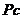 , а точка
, а точка 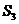 - на
отрезке
- на
отрезке 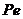 плана скоростей:
плана скоростей:
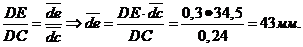
Рассматриваем
группу Ассура (4,5). В этой группе определяем скорость точки 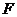 . Рассматривая движение точки
. Рассматривая движение точки 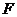 сначала по отношению к точке
сначала по отношению к точке 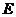 , а затем по отношению к направляющей ползуна 5,
запишем векторные уравнения:
, а затем по отношению к направляющей ползуна 5,
запишем векторные уравнения:
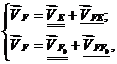
где
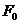 -точка на оси движения ползуна 5;
-точка на оси движения ползуна 5;
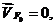 так как
направляющая неподвижна;
так как
направляющая неподвижна;
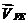 перпендикулярен
шатуну
перпендикулярен
шатуну 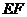 и
и 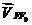 параллелен
оси движения ползуна.
параллелен
оси движения ползуна.
Решаем
эти уравнения графически. Через точку 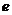 плана
скоростей проводим прямую, перпендикулярно к звену
плана
скоростей проводим прямую, перпендикулярно к звену 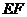 , а через полюс
, а через полюс 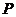 (так как
(так как
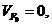 и точка
и точка 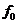 находится
в полюсе)- прямую, параллельную траектории движения ползуна 5 (горизонтальная
линия).
находится
в полюсе)- прямую, параллельную траектории движения ползуна 5 (горизонтальная
линия).
После
определения положений точек 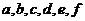 наносим
на соответствующих отрезках плана скоростей точки центров тяжести звеньев
наносим
на соответствующих отрезках плана скоростей точки центров тяжести звеньев 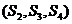 в соответствии с заданными координатами, используя
теорему подобия.
в соответствии с заданными координатами, используя
теорему подобия.
Пользуясь
построенным планом скоростей и с учетом 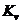 , находим
величины скоростей:
, находим
величины скоростей:
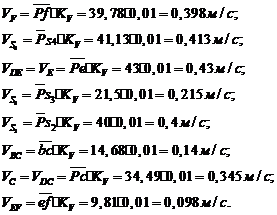
Направление
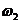 определяем по направлению вектора
определяем по направлению вектора 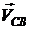 ,
, 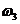 определяем
по направлению вектора
определяем
по направлению вектора 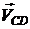 , а направление
, а направление 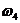 по
направлению вектора
по
направлению вектора 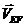 . В данном положении механизма
. В данном положении механизма 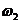 направлена против часовой стрелки,
направлена против часовой стрелки, 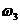 - по часовой стрелки и
- по часовой стрелки и 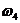 - против
часовой стрелке.
- против
часовой стрелке.
Определяем
угловые скорости 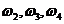 звеньев 2, 3 и 4:
звеньев 2, 3 и 4:
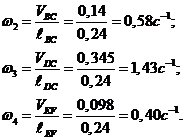
Исследование
механизма в восьмом положении проводим аналогично и результаты заносим в
таблицу 1.3.
Таблица 1.3
Таблица скоростей
|
Положения
|
Линейные скорости, м/c
|
Угловые скорости, с-1
|
|
VB
|
VBС
|
VS2
|
VS3
|
VDC
|
VEF
|
VS4
|
VE
|
VF
|
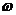 2 2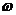 3 3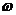 4 4
|
|
|
|
1
|
0,468
|
0,14
|
0,4
|
0,215
|
0,345
|
0,098
|
0,413
|
0,43
|
0,398
|
0,58
|
1,43
|
0,40
|
.3.4 Определение линейных ускорений характерных точек и угловых ускорений
звеньев механизма методом планов
Для
механизма первого класса (1,6) определяем ускорение точки 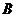 , принадлежащей кривошипу 1 и совпадающей с центром
шарнира
, принадлежащей кривошипу 1 и совпадающей с центром
шарнира 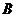 :
:
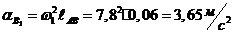 .
.
Намечаем
на чертеже полюс плана ускорений (точка 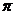 ). Из
полюса (
). Из
полюса (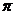 ) проводим вектор (
) проводим вектор (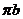 )
ускорения
)
ускорения 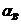 параллельно звену
параллельно звену  в
направлении от точки
в
направлении от точки 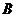 к точке
к точке 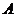 . Длину
отрезка
. Длину
отрезка 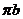 приняли произвольно
приняли произвольно 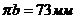 . После
этого определяем масштабный коэффициент ускорения:
. После
этого определяем масштабный коэффициент ускорения:
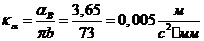 .
.
Переходим
к рассмотрению группы Ассура (2,3). В этой группе определяем вначале ускорение 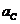 точки
точки 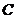 .
Рассматриваем движение точки
.
Рассматриваем движение точки 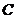 сначала
по отношению к шатуну 2, а затем по отношению к точке
сначала
по отношению к шатуну 2, а затем по отношению к точке 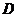 , принадлежащей коромыслу 3. Записываем два векторных
уравнения:
, принадлежащей коромыслу 3. Записываем два векторных
уравнения:
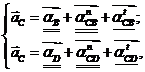
где 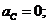
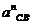 -
нормальное ускорение, возникающее при вращении шатуна 2 относительно точки В.
Величина этого ускорения равна:
-
нормальное ускорение, возникающее при вращении шатуна 2 относительно точки В.
Величина этого ускорения равна:
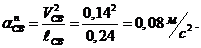
Вектор
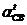 тангенциального ускорения звена 2 в его движении
относительно точки
тангенциального ускорения звена 2 в его движении
относительно точки 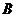 направлен перпендикулярно звену
направлен перпендикулярно звену 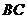 .
.
Вектор
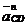 нормального ускорения звена 3, возникающего при
вращении коромысла 3 относительно точки
нормального ускорения звена 3, возникающего при
вращении коромысла 3 относительно точки 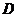 ,
направлен параллельно
,
направлен параллельно 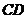 в направлении от точки
в направлении от точки 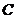 к точке
к точке 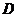 . Величина этого ускорения равна:
. Величина этого ускорения равна:
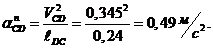
Вектор
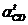 тангенциального ускорения звена 3 в его движении
относительно точки
тангенциального ускорения звена 3 в его движении
относительно точки 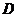 направлен перпендикулярно звену
направлен перпендикулярно звену 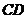 .
.
Чтобы
решить графически векторные уравнения ускорений, нужно из точки 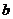 отложить отрезок
отложить отрезок 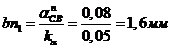 и через
точку
и через
точку 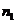 провести прямую, параллельную
провести прямую, параллельную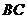 , а из полюса
, а из полюса 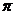 (так как
(так как
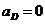 , и точка
, и точка 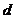 лежит в
полюсе) отложить отрезок
лежит в
полюсе) отложить отрезок 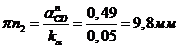 и через точку
и через точку 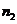 провести
прямую перпендикулярную звену
провести
прямую перпендикулярную звену 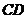 . На
пересечении получим точку
. На
пересечении получим точку 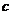 . Соединив точку
. Соединив точку 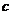 с
полюсом, получаем отрезок
с
полюсом, получаем отрезок 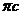 , изображающий абсолютное ускорение
, изображающий абсолютное ускорение 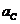 точки
точки 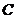 коромысла.
В соответствии с теоремой подобия точка
коромысла.
В соответствии с теоремой подобия точка 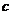 на плане
ускорений должна находиться на продолжении отрезка
на плане
ускорений должна находиться на продолжении отрезка 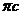 , а точка
, а точка 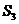 будет
лежать на линии
будет
лежать на линии 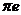 в такой же пропорции, в какой она находится на звене
в такой же пропорции, в какой она находится на звене 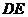 плана механизма. Положение точек
плана механизма. Положение точек 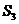 и
и 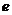 находится
из соотношения:
находится
из соотношения:
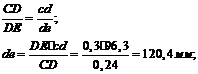
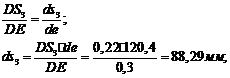
Переходим
к рассмотрению группы Ассура (4,5). В этой группе известны ускорения точки 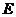 звена 3 и неподвижной точки
звена 3 и неподвижной точки 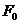 на направляющей.
на направляющей.
Нужно
определить ускорение 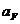 точки
точки 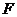 ползуна
5.
ползуна
5.
Рассматривая
движения точки 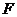 сначала по отношению к точке
сначала по отношению к точке 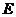 , а затем по отношению к точке
, а затем по отношению к точке 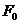 , составляем два векторных уравнения:
, составляем два векторных уравнения:
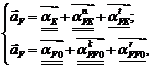
где 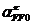 - поворотное (кориолисово) ускорение;
- поворотное (кориолисово) ускорение;
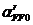 -
ускорение скольжения (релятивное) точки Е относительно
-
ускорение скольжения (релятивное) точки Е относительно 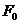 .
.
В
приведенных уравнениях вектор 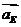 известен,
известен,
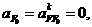 так как направляющая ползуна неподвижна. Величину
нормального ускорения
так как направляющая ползуна неподвижна. Величину
нормального ускорения 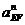 определим:
определим:
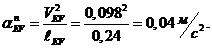
У
векторов тангенциального ускорения 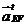 и
релятивного
и
релятивного 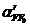 известны только направления:
известны только направления:
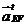 перпендикулярен
перпендикулярен
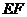 ,
, 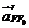 параллелен
направляющей ползуна 5.
параллелен
направляющей ползуна 5.
Решаем
векторные уравнения графически. В соответствии с первым уравнением из точки (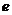 ) плана ускорений откладываем отрезок
) плана ускорений откладываем отрезок 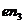 , изображающий ускорение
, изображающий ускорение 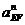 :
:
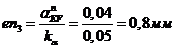 .
.
Отрезок
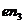 проводим параллельно звену
проводим параллельно звену 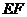 в направлении от точки
в направлении от точки 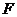 к точке
к точке 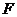 . Через точку
. Через точку 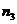 проводим
перпендикулярно к
проводим
перпендикулярно к 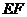 направление вектора
направление вектора 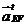 . В
соответствии со вторым уравнением через точку
. В
соответствии со вторым уравнением через точку 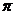 (так как
(так как
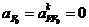 ) проводим параллельно направляющей ползуна 5
направление вектора
) проводим параллельно направляющей ползуна 5
направление вектора 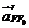 .
.
Линии
действия 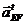 и
и 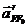 пересекутся
в точке
пересекутся
в точке  . Положения центров тяжести звеньев (точек
. Положения центров тяжести звеньев (точек 
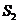 и
и 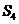 ) определяем по теореме подобия в соответствии с их
расположением на плане механизма.
) определяем по теореме подобия в соответствии с их
расположением на плане механизма.
Из
построенного плана ускорений определяем величины ускорений:
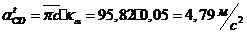 ;
;
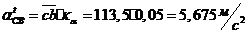 ;
;
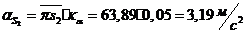 ;
;
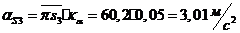 ;
;
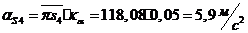 ;
;
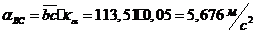 ;
;
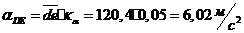 ;
;
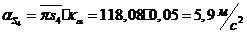 ;
;
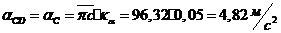 ;
;
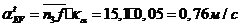 ,
,
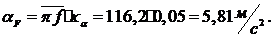
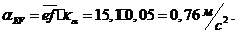
Определяем
угловые ускорения 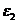 ,
, 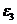 и
и 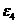 звеньев 2, 3 и 4:
звеньев 2, 3 и 4:
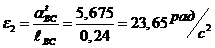
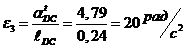 ;
;
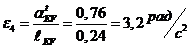 .
.
Направления
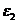 ,
, 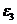 и
и 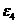 определяем по направлениям тангенциальных ускорений
определяем по направлениям тангенциальных ускорений 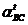 ,
, 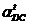 и
и 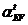 . В данном положении механизма
. В данном положении механизма 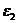 направлено против часовой стрелки,
направлено против часовой стрелки, 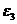 - против часовой стрелки и
- против часовой стрелки и 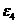 направлены по часовой стрелке.
направлены по часовой стрелке.
Аналогично строим план ускорения для положения 8:
Результаты исследования представлены в таблице 1.4.
Таблица 1.4
Таблица ускорений
|
Поло-жения
|
Линейные ускорения точек
(м/c2)
|
Угловые ускорения звеньев
(с-2)
|
|
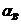 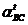 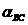 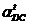 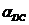 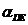 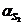 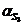 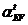 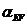 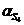 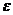 2 2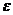 3 3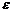 4 4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
3,65
|
5,675
|
5,676
|
4,79
|
4,82
|
6,02
|
3,19
|
3,01
|
0,76
|
0,76
|
5,9
|
23,65
|
20
|
3,2
|
2. Силовое исследование рычажного механизма
Силовой анализ механизма предлагает решение первой задачи динамики -по
заданному закону движения определить действующие силы. Так как законы движения
начальных звеньев и внешние силы, действующие на звенья механизмов, заданы, то
силовой расчет сводится, в основном, к определению реакций в кинематических
парах. Результаты силового анализа необходимы для дальнейших расчетов деталей
на прочность, жесткость, износостойкость, надежность, для выбора типов и
размеров подшипников, определения коэффициента полезного действия механизма.
Чертим кинематическую схему механизма (лист 2) для положения 8, в
масштабе
Чертим в этом же масштабе группу Асcура 4-5.
Обозначаем векторами все силы, действующие на звенья группы, включая силы
инерции и моменты сил инерции.
Определяем
массы 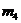 и
и 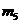 звеньев
4 и 5 по приближенным формулам
звеньев
4 и 5 по приближенным формулам 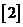 :
:
Массу
шатуна 4 определяем по формуле:
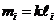 ,
,
где
k=8…12 кг/м ;
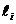 -длина
звена, м;
-длина
звена, м;
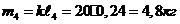 .
.
Массу
ползуна 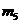 определяем по формуле:
определяем по формуле:
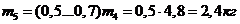 .
.
Определяем силы тяжести звеньев по формуле:
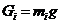 ,
,
где 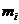 - масса звена
- масса звена 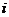 ,
кг;ускорение свободного падения;
,
кг;ускорение свободного падения;
g=9,81 м/с2;
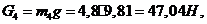
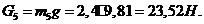
Определяем
силы инерции звеньев по формуле:
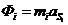 ,
,
где
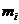 - масса звена
- масса звена 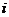 , кг;
, кг;
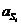 -
ускорение центра тяжести звена
-
ускорение центра тяжести звена 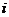 ;
;
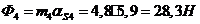 ;
;
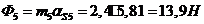 .
.
Векторы
сил инерции направляем противоположно векторам ускорений центров масс.
Определяем
главный момент силы инерции 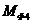 звена 4:
звена 4:
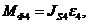
где 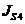 - осевой момент сил инерции звена 4;
- осевой момент сил инерции звена 4;
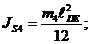
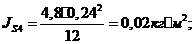
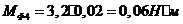
Момент
МФ4 направляем противоположно направлению 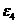 (в данном
положении по часовой стрелке). На звене 5 момента нет, так как это звено не
вращается, а совершает возвратно-поступательное движение.
(в данном
положении по часовой стрелке). На звене 5 момента нет, так как это звено не
вращается, а совершает возвратно-поступательное движение.
Определяем
движущую силу 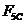 . Так как силовой расчет проводим на холостом ходу, то
по диаграмме полезного сопротивления
. Так как силовой расчет проводим на холостом ходу, то
по диаграмме полезного сопротивления 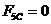 .
.
Определяем
реакции в кинематических парах группы Ассура 4-5.
Находим
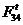 из уравнения моментов сил звена 2 относительно точки
С:
из уравнения моментов сил звена 2 относительно точки
С:
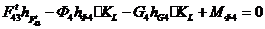
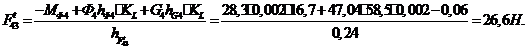
Находим
неизвестные по величине, но известные по направлению силы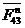 и
и 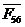 из
векторного уравнения сил звеньев 4 и 5:
из
векторного уравнения сил звеньев 4 и 5:
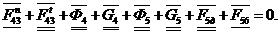
Строим
план сил, выбрав масштабный коэффициент сил 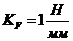 и
определив отрезки, которыми будем изображать известные силы на плане:
и
определив отрезки, которыми будем изображать известные силы на плане:
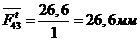 ;
; 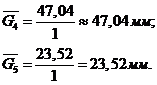
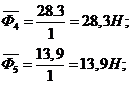
Из
плана сил находим силы 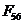 и
и 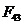 , умножая
длины соответствующих векторов на масштабный коэффициент сил:
, умножая
длины соответствующих векторов на масштабный коэффициент сил:
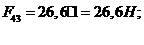
Находим
реакцию 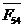 во внутренней кинематической паре (5-4В).
во внутренней кинематической паре (5-4В).
Исследуем
группу Ассура 2-3, которая состоит из коромысла 3 и шатуна 2.
Чертим
схему группы в масштабе и показываем векторами направления всех действующих на
звенья этой группы сил.
Определяем
массы 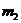 и
и 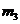 звеньев
2 и 3 по приближенной формуле
звеньев
2 и 3 по приближенной формуле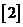 :
:
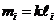
где
k=8…12 кг/м для шатуна;=10…20 кг/м для коромысла;
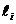 -длина
звена, м;
-длина
звена, м;
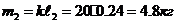 .
.
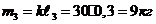
Определяем
силу тяжести звенев по формуле:
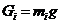 ,
,
где g-ускорение
свободного падения;
g=9,81м/с2;
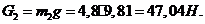
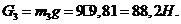
Определяем
силы инерции звеньев:
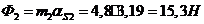
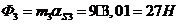 .
.
Вектор
силы инерции направляем противоположно вектору ускорения центра масс.
Определяем
главный момент силы инерции звена 2:
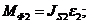
где 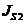 - осевой момент звена 2;
- осевой момент звена 2;
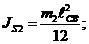
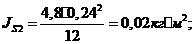
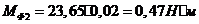 .
.
Определяем
главный момент силы инерции звена 3:
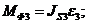
где 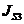 - осевой момент звена 3;
- осевой момент звена 3;
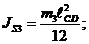
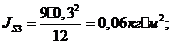
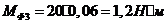 .
.
Момент
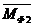 направляем противоположно направлению
направляем противоположно направлению 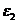 , то есть против часовой стрелки. Момент
, то есть против часовой стрелки. Момент 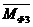 направляем противоположно направлению
направляем противоположно направлению 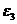 , то есть по часовой стрелке.
, то есть по часовой стрелке.
Рассматриваем
равновесие звена 2 и определяем силу 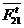 , для
чего составляем уравнение моментов сил звена 2 относительно точки
, для
чего составляем уравнение моментов сил звена 2 относительно точки 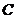 :
:
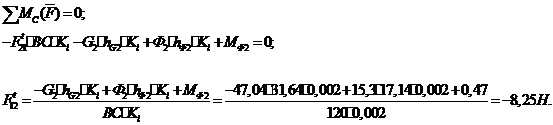
Плечи
определяем непосредственными измерениями на чертеже с учетом 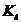 . Если сила
. Если сила 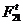 получится
со знаком минус, то при дальнейших расчетах нужно изменить ее направление.
получится
со знаком минус, то при дальнейших расчетах нужно изменить ее направление.
Рассматриваем
равновесие звена 3 и определяем силу 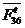 , для
чего составляем уравнение моментов сил звена 3 относительно точки
, для
чего составляем уравнение моментов сил звена 3 относительно точки 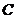 :
:
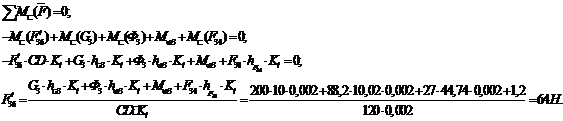
Рассматриваем
равновесие всей группы в целом и определяем силы 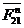 и
и 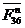 . Поскольку группа находится в равновесии, то
геометрическая сумма всех сил, действующих на ее звенья, равна нулю:
. Поскольку группа находится в равновесии, то
геометрическая сумма всех сил, действующих на ее звенья, равна нулю:
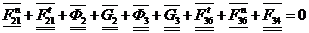
Строим план сил согласно записанному векторному уравнению в масштабе
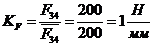 .
.
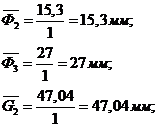
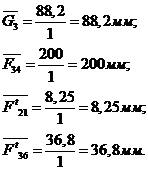
Находим
вектора неизвестных сил 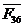 и
и 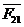 .
.
Действительная
величина сил:
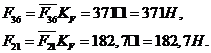 .
.
Рассматриваем
начальный механизм, который состоит из начального звена 1 и стойки 6.
Из
уравнения моментов сил относительно точки А находим уравновешивающую силу 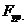 , приложенную в точке В перпендикулярно звену АВ:
, приложенную в точке В перпендикулярно звену АВ:
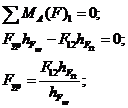
где 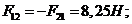
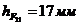 (измерили
на чертеже);
(измерили
на чертеже);
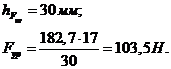
Определяем
реакцию 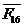 из векторного уравнения сил звена 1:
из векторного уравнения сил звена 1:
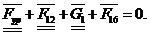
Силой
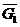 пренебрегаем, так как она мала по сравнению с другими
силами.
пренебрегаем, так как она мала по сравнению с другими
силами.
Строим
план сил, предварительно выбрав масштабный коэффициент сил 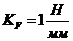 и определив длины векторов известных сил:
и определив длины векторов известных сил:
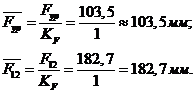
Из
плана сил находим величину и направление силы 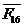 :
:
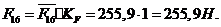
В соответствующих точках прикладываем векторы всех активных сил (тяжести
звеньев, производственного сопротивления), а также векторы сил инерции, главных
моментов сил инерции и уравновешивающей силы.
Главные
моменты 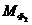 ,
, 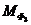 и
и  сил инерции заменяем парами сил:
сил инерции заменяем парами сил:
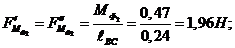
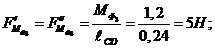
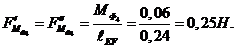
Определяем плечи всех сил относительно полюса ( Р ) плана скоростей
непосредственным измерением на чертеже (кратчайшее расстояние от полюса до векторов
сил или их продолжения).
Составляем
уравнение моментов всех сил относительно полюса ( Р ) плана скоростей, из
которого затем определяем величину уравновешивающей силы 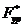 :
:
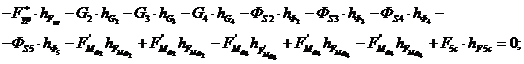
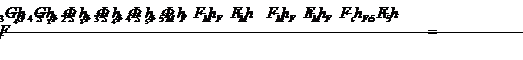
Сравниваем
значения 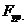 и
и 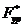 :
:
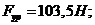
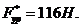
Разница
( ) составляет:
) составляет:
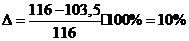 (допускается
(допускается
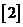 до 10%).
до 10%).
3. Синтез зубчатого механизма
Схема многоступенчатого редуктора, состоящего из планетарной ступени и
внешней пары колес 4 и 5.
Передаточное отношение всего редуктора i15=7,16.
Числа зубьев z4 и z5 колес 4 и 5:
z4=20;
z5=31.
Модули колес планетарной ступени и внешней пары:
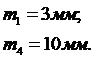
Частота
вращения колеса 1: 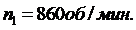
Решение.
Проектируем планетарную ступень зубчатого механизма.
Определяем передаточное отношение планетарной ступени:
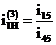 ,
,
где 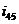 - передаточное отношение внешней пары колес 4 и 5;
- передаточное отношение внешней пары колес 4 и 5;
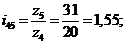
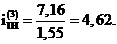
Задаемся
числом зубьев z1 центрального колеса 1 из условия, что все колеса в
планетарном редукторе нулевые, а редуктор должен быть минимальных габаритов:
z1=19.
Определяем
число зубьев z3 центрального колеса 3 из формулы для определения
передаточного отношения однорядного планетарного редуктора:
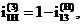
где
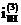 - передаточное отношение механизма, когда движение
передается от колеса 1 к водилу Н при неподвижном колесе 3;
- передаточное отношение механизма, когда движение
передается от колеса 1 к водилу Н при неподвижном колесе 3;
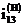 -
передаточное отношение механизма в обращенном движении (от колеса 1 к колесу 3
при остановленном водиле и освобожденном колесе 3)
-
передаточное отношение механизма в обращенном движении (от колеса 1 к колесу 3
при остановленном водиле и освобожденном колесе 3)
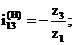
тогда
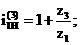
отсюда
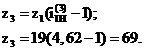
Определяем
число зубьев колеса 2 (сателлита) из условия соосности механизма:
1+2r2=r3,
где r1,r2,r3 - радиусы
делительных (начальных) окружностей колес, мм
или z1+2z2=z3;
отсюда
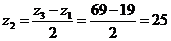 .
.
Так
как 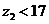 , находим общий множитель:
, находим общий множитель: 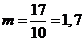 и помножаем на него числа зубьев:
и помножаем на него числа зубьев: 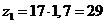 ,
, 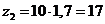 ,
, 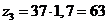 .
.
Определяем количество сателлитов (k), удовлетворяющее условию сборки:
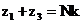 ,
,
где
N-целое число;
k-число
сателлитов (k рекомендуется проверять в пределах от 2 до 6).
При
k=6 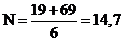 -дробное
число;
-дробное
число;
при
k=5 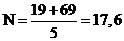 -дробное
число;
-дробное
число;
при
k=4 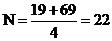 -целое
число;
-целое
число;
при
k=3 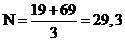 -дробное
число;
-дробное
число;
при
k=2 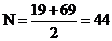 -целое
число.
-целое
число.
Таким образом, k
можно принять равным четырем и двум. При k=4 нагрузка на зубья колес равномернее распределяется. С
другой стороны, легче и экономичнее изготовить и собрать механизм с двумя
сателлитами.
Принимаем k=4 из соображений
экономичности и простоты конструкции.
Проверяем условие соседства для внешнего зацепления (зацепление колес 1 и
2):
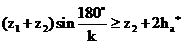 ,
,
где
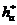 -коэффициент высоты головки зуба;
-коэффициент высоты головки зуба;
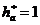 для зуба
нормальной высоты;
для зуба
нормальной высоты;
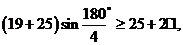

 (sin
90
(sin
90 =1),
=1),
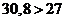 .
.
Условие
соседства для внешнего зацепления колес 1 и 2 выполняется.
Проверяем условие соседства для внутреннего зацепления (зацепление колес
2 и 3):
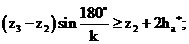
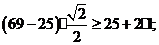
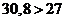 .
.
Условие
соседства выполняется и для внутреннего зацепления.
Таким
образом, принимаем: 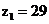 ,
, 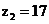 ,
, 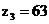 ,
, 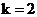 .
.
Определяем диаметры делительных (начальных) окружностей колес 1, 2 и 3
планетарной ступени механизма:
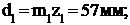
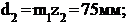
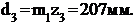
Чертим схему планетарного редуктора в двух проекциях и проводим
кинематическое исследование планетарного механизма графическим методом.
Графический
метод кинематического исследования сводится к построению треугольников линейных
скоростей каждого колеса механизма и нахождению из них угловых скоростей 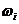 (или чисел оборотов в минуту
(или чисел оборотов в минуту 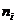 ), а также передаточных отношений.
), а также передаточных отношений.
Определяем
линейную скорость точки А, являющейся общей для колес 1 и 2:
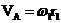 ,
,
где
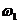 - угловая скорость колеса 1;
- угловая скорость колеса 1;
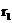 - радиус
делительной окружности колеса 1;
- радиус
делительной окружности колеса 1;
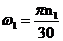 ;
;
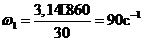 ;
;
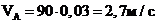 .
.
Проводим
прямую 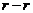 , параллельную линии центров
, параллельную линии центров 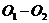 , и спроектируем на нее точки
, и спроектируем на нее точки 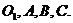 Из точки
Из точки 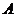 перпендикулярно
к прямой
перпендикулярно
к прямой 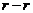 проводим отрезок
проводим отрезок 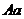 ,
изображающий в масштабе
,
изображающий в масштабе 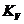 скорость точки
скорость точки 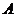 :
:
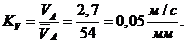
С
другой стороны, колесо 2 находится в зацеплении с неподвижным колесом 3,
поэтому скорость точки С колеса 2 равна нулю. Этих данных достаточно, чтобы
построить закон распределения скоростей колеса 2 в виде прямой 2, проходящей
через С и а. При помощи этой прямой находим скорость  центра колеса 2 в виде отрезка
центра колеса 2 в виде отрезка 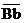 . Эту скорость будет иметь и центр подвижного
подшипника водила H. Так как водило H вращается
вокруг центра О1, то закон распределения скоростей будет представлен прямой
линией О1-Н, проходящей через точку в. При этом отрезок
. Эту скорость будет иметь и центр подвижного
подшипника водила H. Так как водило H вращается
вокруг центра О1, то закон распределения скоростей будет представлен прямой
линией О1-Н, проходящей через точку в. При этом отрезок 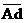 представляет скорость точки D водила H,
удаленной от центра О на расстояние
представляет скорость точки D водила H,
удаленной от центра О на расстояние 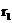 .
.
Числовую
величину скорости точки 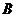 определяем:
определяем:
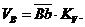
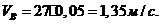
Для
построения картины угловых скоростей перпендикулярно к линии центров проведем
линию 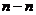 . Выберем на этой линии произвольную точку
. Выберем на этой линии произвольную точку 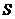 . Проведем через эту точку параллель к линии центров и
отложим вниз от точки
. Проведем через эту точку параллель к линии центров и
отложим вниз от точки 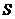 произвольный отрезок
произвольный отрезок 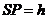 . Из
точки
. Из
точки 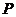 проведем лучи, параллельные линиям
проведем лучи, параллельные линиям 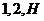 до пересечения их с прямой
до пересечения их с прямой 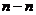 . Эти лучи пересекут прямую
. Эти лучи пересекут прямую 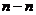 в точках 1, 2 и H. Рассмотрим треугольник
в точках 1, 2 и H. Рассмотрим треугольник 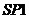 :
:
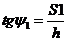 .
.
Определим
угловую скорость колеса 1:
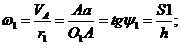
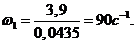
Определяем
масштабный коэффициент угловой скорости:
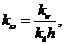 ,
,
где
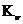 - масштабный коэффициент линейной скорости;
- масштабный коэффициент линейной скорости;
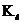 -
масштабный коэффициент длины;
-
масштабный коэффициент длины;
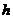 -
полюсное расстояние,
-
полюсное расстояние,
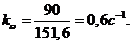
 С учетом
масштаба:
С учетом
масштаба:
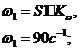
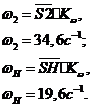
Определяем основные геометрические параметры эвольвентных прямозубых
цилиндрических зубчатых колес 4 и 5.
Так как z4<17, то колеса нарезаются со
смещением режущего инструмента.
Определяем
минимальный коэффициент смещения 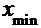 для
шестерни 4, при котором не происходит подрезание ножек зубьев:
для
шестерни 4, при котором не происходит подрезание ножек зубьев:
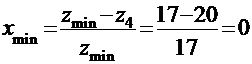
Проектируем
равносмещенную передачу, приняв x4=0 и x5=0.
Определяем
диаметры делительных окружностей:
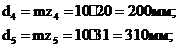
соответственно
г4=100мм;
г5=155
мм.
Определяем
диаметры основных окружностей:
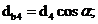
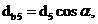
где
a- угол наклона зуба исходного профиля инструмента;
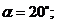
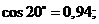
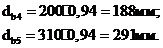
Определяем
диаметры окружностей ножек зубьев:
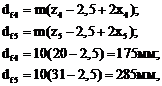
соответственно,
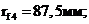
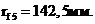
Определяем
межосевое расстояние:
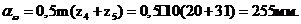
Определяем
радиусы окружностей вершин зубьев:

соответственно,
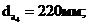
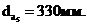
Определяем
шаг зацепления:
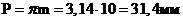
Определяем
высоту зуба:
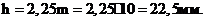
Определяем
толщину зубьев по делительным окружностям:
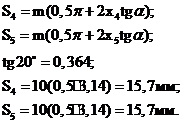
Определяем
коэффициент перекрытия:
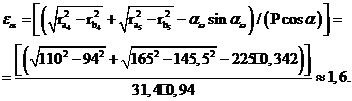
Требуемое
условие 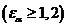 выполняется:
выполняется:
,6>1,2.
4. Синтез кулачкового механизма
Задано:
Схема кулачкового механизма с роликовым толкателем.
Cинусоидальный
закон движения толкателя в виде диаграммы аналогов ускорений.
Фазовые углы:
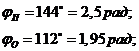
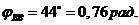
Требуется
определить основные размеры кулачкового механизма и кулачка. Построить профиль
кулачка, который будет обеспечивать заданный закон движения толкателя.
Строим
кинематические диаграммы для выходного звена кулачкового механизма расчетным
методом.
Вначале
строим заданную диаграмму аналогов ускорений 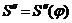 ,
предварительно определив максимальное значение аналогов
,
предварительно определив максимальное значение аналогов 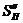 и
и 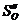 на фазах
подъема и опускания для синусоидального закона по формуле:
на фазах
подъема и опускания для синусоидального закона по формуле:
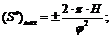
где
H-максимальный ход толкателя, мм;
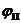 и
и 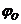 -фазовые углы подъема и опускания, рад;
-фазовые углы подъема и опускания, рад;
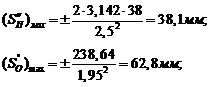
Откладываем
ось абсцисс длиной  - ось
- ось 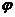 . Считаем
масштабный коэффициент оси
. Считаем
масштабный коэффициент оси 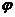 :
:
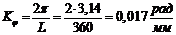 .
.
На
отложенной оси отмечаем заданные фазовые углы с учетом масштаба:

Далее
по оси ординат откладываем максимальное значение аналога ускорения, равное 100
мм. Считаем масштабный коэффициент оси 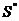 :
:
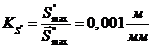 .
.
Затем
делим угол подъема и опускания на шесть равных частей. Далее находим аналоги
ускорений во всех фазах угла подъема и опускания.
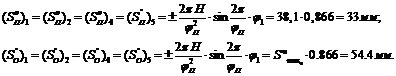
где
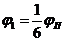 .
.
Затем
строим кинематическую диаграмму аналогов скоростей 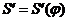 , предварительно определив максимальное значение
, предварительно определив максимальное значение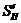 и
и 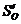 на фазах
подъема и опускания по формуле:
на фазах
подъема и опускания по формуле:
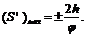
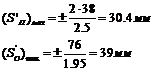
По
оси ординат откладываем максимальное значение аналога скорости, равное 64мм.
Считаем масштабный коэффициент оси 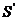 :
: 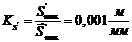 , по оси ординат масштабный коэффициент оставляем
прежним.
, по оси ординат масштабный коэффициент оставляем
прежним.
Также
делим угол подъема и опускания на шесть равных частей. Далее находим аналоги
скоростей во всех фазах угла подъема и опускания.
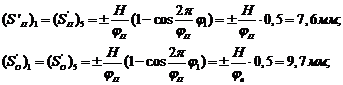
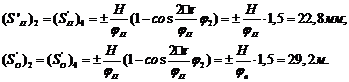
где
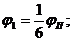
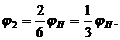
Последней
строим диаграмму перемещения толкателя 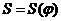 , при
этом:
, при
этом: 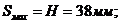 .
.
По
оси ординат откладываем максимальное значение перемещения, равное 64 мм.
Считаем масштабный коэффициент оси 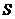 :
: 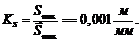 , по оси ординат масштабный коэффициент оставляем
прежним.
, по оси ординат масштабный коэффициент оставляем
прежним.
Также
делим угол подъема и опускания на шесть равных частей. Далее находим
перемещение во всех фазах угла подъема и опускания.
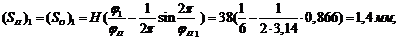
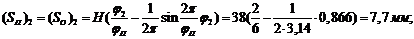
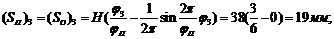
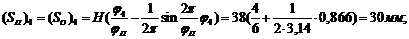
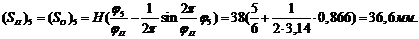
где
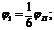
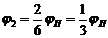 ,
, 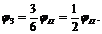 и так
далее.
и так
далее.
Находим
значение фазового угла нижнего выстоя 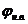 толкателя:
толкателя:
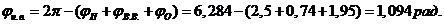
Определяем
минимальный начальный радиус кулачка Ro из условия выпуклости профиля
упрощенным графическим способом, предварительно определив максимальное значение
аналога отрицательной скорости. Построение выполняем, используя масштабный
коэффициент 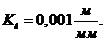 .
.
Из
построения находим: 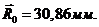 Определяем действительный размер минимального радиуса:
Определяем действительный размер минимального радиуса:
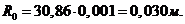
Строим
профиль кулачка методом обращенного движения, используя масштабный коэффициент 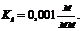 .
.
Определяем
радиус ролика:
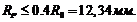
Принимаем
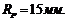
Заключение
Данный курсовой проект помог мне обобщить и закрепить знания и методы
исследования механизмов и машин. На всех четырёх листах были применены все
методы, которые изучались в течение всего курса теории машин и механизмов.
Особенно это касается метода графического дифференцирования для построения
диаграмм, построения планов сил, скоростей и ускорений. При выполнении задач
были применены общие методы кинематического и динамического анализа и синтеза.
Кроме того, приведены кинематическая цепь редуктора и выполнены графические
построения плана скоростей и плана ускорений.
Таким образом, выполненный курсовой проект отражает уровень знаний,
которые студент получил при изучении курса теории машин и механизмов.
Список литературы
1. Артоболевский
И.И. Теория механизмов и машин.- М.: Наука, 1988.-640с.
2. Кореняко
А.С. Теория механизмов и машин.- Киев: Виша школа, 1976.-443с.
. Силовой
анализ рычажных механизмов. Методические указания к курсовому проекту по теории
механизмов и машин В.Ф.Филиппов: Изд.филиала ТПУ.-2002.- 26с.
. Геометрический
синтез планетарных зубчатых механизмов с помощью ЭВМ. Методические указания к
курсовому проекту по теории механизмов и машин. В.Ф.Филиппов: Изд.филиала
ТПУ.-2000.- 27с.
. Синтез
плоских кулачковых механизмов с использованием ЭВМ. Методические указания к
курсовому проекту по теории механизмов и машин. В.Ф.Филиппов: Изд.филиала
ТПУ.-2000.- 22.
. Теория
механизмов и механика машин. Методические указания к курсовому проекту по
теории механизмов и машин. В.Ф.Филиппов: Изд.филиала ТПУ.-2000.- 17с.
. Синтез
и анализ зубчатого механизма. Методические указания к курсовому проекту по
теории механизмов и машин Н.А.Сапрыкина, В.В.Седнев: Изд.филиала ТПУ.-2003.-
14с.