Решение уравнения теплопередачи методом конечных разностей

Решение уравнения теплопередачи методом конечных разностей

Содержание

Введение

. Теоретические основы исследования

.1 Численные методы решения

.2 Метод конечных разностей

.2.1 Основное содержание метода

.2.2 Метод формальной замены производной конечно-разностными отношениями

.2.3 Метод неопределенных коэффициентов

.2.4 Метод интегральных тождеств

.3 Метод конечных элементов

.4 Преимущества и недостатки численных методов

. Практическая часть исследования

.1 Исследование методов повышения точности аппроксимации

.2 Вычисление температур в узлах ограждающей конструкции и нахождение сопротивления теплопередачи

.3 Расчет температур наружного угла и нахождение сопротивления теплопередачи

.4 Расчет температур наружного угла с теплопроводной вставкой и нахождение сопротивления теплопередачи

.5 Исследование методов оптимизации теплопотерь и способов утепления наружных углов

. Экологическое влияние ЭВМ на человека

.1 Влияние электромагнитного излучения на человека

. Технико-экономический расчет трудозатрат

.1 Определение состава исполнителей, их функций и фондов времени работы

.2 Технико-экономическое обоснование проекта

. Безопасность жизнедеятельности при эксплуатации ЭВМ

.1 Общие положения и область применения

.2 Требования к ПЭВМ

.3 Требования к помещениям для работы с ПЭВМ

.4 Требования к микроклимату, содержанию аэроионов и вредных химических веществ в воздухе на рабочих местах, оборудованных ПЭВМ

.5 Требования к уровням шума и вибрации на рабочих местах, оборудованных ПЭВМ

.6 Требования к освещению на рабочих местах, оборудованных ПЭВМ

Заключение

Список использованных источников

Введение

Только ясное представление о процессах, происходящих в ограждениях при теплопередаче, и умение пользоваться соответствующими расчетами дают возможность проектировщику обеспечить требуемые теплотехнические качества наружных ограждающих конструкций.

Поэтому целью данной работы является адаптация метода конечных разностей для решения сложных задач (нахождение сопротивления теплопередаче ограждающих конструкции) студентами специальностей ТГВ и ПТЭ. численный сопротивление теплопередача

Основные задачи выпускной квалификационной работы:

1. Изучение теории и практики метода конечных разностей.

2.      Особенности обучения специальностей ТГВ и ПТЭ:

•  Определение температурных полей;

•        Определение тепловых потоков;

•        Определение термосопротивления;

•        Изучение теплопередачи в сложных конструкциях.

3. Исследование методов повышения точности аппроксимации

4.      Разработка методики расчета ограждающих конструкции методом конечных разностей.

.        Исследование оптимизации теплопотерь и способов утепления наружных углов.

1. Теоретические основы исследования

.1 Численные методы решения

Применение вычислительной техник и численных методов значительно расширяет классы исследуемых полевых задач теплообмена, позволяя получать приближенные решения многомерных, нелинейных, нестационарных задач, для которых использование точных и приближенных аналитических методов не представляется возможным. При выборе математических моделей, описывающих процессы теплообмена в реальных объектах, границы их допустимой сложности в настоящее время часто определяются не столько возможностями численных методов и ресурсами ЭВМ, сколько недостатком достоверной входной информации для этих моделей.

При определении различных пространственно-временных полей необходимо находить решения краевых задач для дифференциальных уравнений в частных производных в заданных областях изменения пространственных переменных и временных интервалах. Отличительной особенностью применения численных методов является дискретизация пространственной и временной областей на первом же этапе решения задачи.

На втором этапе составляется система алгебраических уравнений относительно значений искомых функций в этих узловых точках. На третьем - проводится решение системы, и находятся значения исследуемых величин в узловых точках. Отметим, что дискретизация области часто делается и при расчете на основе аналитических решений, однако в этих случаях она проводится на заключительных этапах, реализуемых уже после получения аналитического решения.

Существуют два основных численных метода решения уравнений в частных производных: метод конечных разностей и метод конечных элементов. Они отличаются способами получения системы уравнений для значений искомых функций в узловых точках. Метод конечных разностей базируется непосредственно на дифференциальном уравнении и граничных условиях, а метод конечных элементов - на эквивалентной вариационной постановке задачи.

1.2 Метод конечных разностей

Численный метод анализа, называемый методом конечных разностей, имеет длительную историю развития. Первоначально он использовался при ручном счете. Однако из-за малой производительности расчетчиков этот метод еще относительно недавно применялся лишь для ориентировочных расчетов, когда аналитические методы решения оказывались совершенно неприемлемыми. Появление ЭВМ с большим быстродействием и значительным объемом оперативной памяти вывело конечно-разностные методы в первые ряды современных методов решения теплофизических задач.

Идея метода конечных разностей (МКР) состоит в следующем. Область непрерывного изменения аргументов заменяется расчетной сеткой - дискретным множеством точек (узлов). Вместо функции непрерывных аргументов вводятся функции дискретных аргументов - сеточные функции, определяемые в узлах сетки. Частные производные, входящие в дифференциальное уравнение и граничные условия, заменяются (аппроксимируются) разностными соотношениями.

В результате такой замены краевая задача в частных производных сводится к системе разностных (алгебраических) уравнений, называемых разностной схемой. Если решение системы разностных уравнений существует и при измельчении сетки стремится к решению поставленной задачи (т.е. сходится), то оно и является искомым численным решением краевой задачи.

При разработке конечно-разностного аналога конкретной задачи тепломассопереноса необходимо рассмотреть, как выбрать сетку и построить разностную схему, определить точность аппроксимации исходной задачи разностной схемой, проверить устойчивость разностной схемы и выяснить скорость сходимости решения разностной задачи к решению исходной задачи тепло-, массопереноса.

1.2.1 Основное содержание метода

Основное содержание МКР рассмотрим на примере одномерного уравнения теплопроводности; распространение полученных результатов на другие задачи тепло-, массопереноса не вызывает принципиальных затруднений.

Заменим область непрерывного изменения аргументов искомой функции t некоторым конечным множеством точек в этой области. Это множество назовем разностной сеткой, сами точки - узлами сетки, а функции, определенные тем или иным способом на этой сетке, - сеточными функциями.

Расположение узлов сетки в области может быть произвольным, оно определяется спецификой решаемой задачи. Поэтому можно выделить равномерные и неравномерные сетки. В сетках первого типа все узлы по одной координате расположены на равном расстоянии один от другого, называемым шагом сетки. Пример такой сетки для уравнения

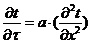
показан на рисунке 1.1. Здесь координаты любой точки на плоскости рисунка 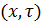 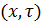определяются соотношениями:

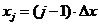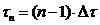,, где ,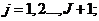

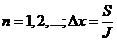J - число шагов по толщине пластины. Равномерные сетки используются в тех случаях, когда все элементарные объемы исследуемой области Ω равноценны в физическом плане, и не ожидается каких-либо особенностей в изменениях переменных процесса.

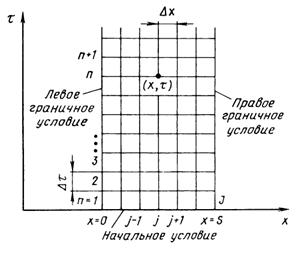
Рисунок 1.1. Разностная сетка для уравнения теплопроводности

При численном анализе закономерностей конвективного тепло- массопереноса целесообразно применение неравномерных сеток, поскольку в этом случае основное изменение параметров задачи происходит в пределах пограничного слоя. Здесь сетку строят таким образом, чтобы непосредственно у омываемой газами поверхности шаг сетки по перпендикулярной к поверхности координате был минимальным, а затем нарастал по тому или иному закону по мере приближения узла к ядру потока. Вообще неравномерная сетка используется при решении задач, относительно которых априори известно, что в некоторых элементарных объемах исследуемой области имеют место (или невозможны) особенности искомой функции.

Решение исходной краевой задачи сводится к нахождению таблицы числовых значений функции t в узлах сетки. Для приближенного вычисления этой таблицы необходимо дифференциальный оператор краевой задачи (дифференциальное уравнение и краевые условия), заданный в классе непрерывных аргументов, аппроксимировать разностным оператором, заданным на множестве сеточных функций. Такая замена - операция неоднозначная. Среди множества конструктивных подходов к построению разностных аналогов для дифференциальных операторов в МКР можно выделить следующие методы: формальной замены производных конечно-разностными выражениями; неопределенных коэффициентов; интегральных тождеств (интегрально-интерполяционный).

1.2.2 Метод формальной замены производной конечно-разностными отношениями

Метод формальной замены производной конечно-разностными отношениями основан на разложении в ряд Тейлора достаточно гладких функций. Запишем, например, следующее разложение по формуле Тейлора:

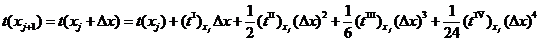.    (1.1)

Используя нижний индекс j для значения сеточной функции t в точке: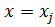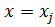, можно переписать это соотношение в виде:

.

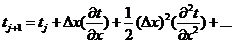и, следовательно:

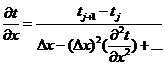.    (1.2)

Это ведет к так называемой аппроксимации разностью вперед (правой

разности) для первой производной функции, тогда:

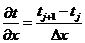. (1.3)

Из сопоставления (1.3) с (1.2) нетрудно определить погрешность

такой аппроксимации:

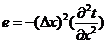.     (1.4)

где 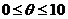, и так как е пропорциональна ∆x, то записывают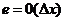 - так указывается порядок погрешности. Отметим, что некоторый разностный оператор аппроксимирует производную с порядком m > 0 в точке; если разность между ними не превышает .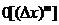

Из (1.4) нельзя получить точную величину погрешности, так как фактическое значение 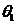 неизвестно, однако:

.

Аналогичным образом, пользуясь разложением по формуле Тейлора, получим:

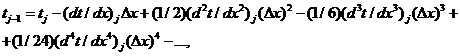. (1.5)

откуда:

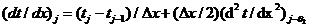.где 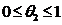, и приходим к аппроксимации разностью назад (левой разностью):

.    (1.6)

Погрешность е этой аппроксимации снова имеет порядок 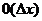 и

.

Необходимо подчеркнуть следующее. Аппроксимации (1.3) и (1.6) основаны на разложении функции t в ряде Тейлора с точностью до линейных слагаемых, поэтому они будут строго справедливы для линейных функций.

Вычитая (1.5) из (1.1), находим:

.

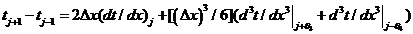Что позволяет ввести аппроксимацию центральной разностью:

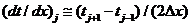.        (1.7)

Погрешность аппроксимации:

.

Так как порядок погрешности 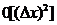, то данное представление должно быть лучше, чем аппроксимации правой и левой разностями. Это утверждение становится понятным, если отметить, что аппроксимация центральной разностью предполагает квадратичное изменение функции t между узлам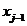и  и 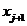. В общем случае может возникнуть необходимость обеспечения достаточно гладкой стыковки отрезков параболы в процессе численного решения.

Складывая разложения в ряд Тейлора (1.1) и (1.5), обнаруживаем, что слагаемые с первой и третьей производными взаимно уничтожаются. В результате имеем:

.

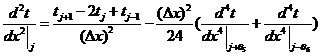Таким образом, вторую производную можно аппроксимировать выражением:

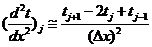.      (1.8)

Погрешность е этой аппроксимации имеет порядок 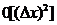, причем

.

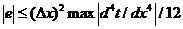Эти аппроксимации первой и второй производных достаточны для наших последующих целей. Аппроксимации (возрастающей сложности) производных более высоких порядков, если они потребуются, можно получить аналогично.

Перейдем к одномерному уравнению теплопроводности. Чтобы написать для него разностную аппроксимацию, необходимо прежде всего определить шаблон, т.е. совокупность узлов сетки, на которых конструируется разностный аналог дифференциального уравнения. Так как уравнение теплопроводности содержит первую производную во времени и вторую по координате, а первую производную можно тремя способами заменить конечными разностями, то набор возможных шаблонов весьма обширен.

Остановимся сначала на простейших аппроксимациях. Пусть шаблон состоит из четырех точек (рисунке 1.2, а). Тогда можно записать:

.

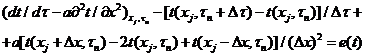Используя индексные обозначения и пренебрегая е(t):

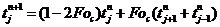.  (1.9)

где

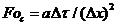- так называемое сеточное число Фурье.

Для момента 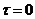 (n=1) распределение температур по сечению нагреваемого тела известно из начальных условий. Поэтому расчет температур на следующем временном слое (при n=2) не вызывает затруднений. Повторяя теперь процедуру вычислений для n = 3, 4, . . . и т.д. находим изменение поля температур во времени.

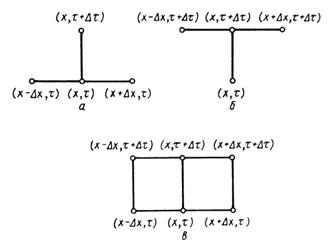
Рисунок 1.2 - Типичные шаблоны конечно-разностной схемы

Так как новые температуры определяются из (1.9) явным образом, то данная разностная схема называется явной.

Используя шаблон (рисунок 1.2, б), можно записать:

.

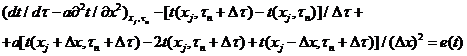Пренебрегая e(t),:

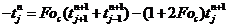. (1.10)

Нетрудно заметить, что в этом случае температуры нового временного слоя явным образом не определяются. Здесь необходимо записать уравнение (1.10) для каждого узла сетки и затем решать совместно получившуюся систему уравнений. По этой причине разностная схема (1.10) называется неявной.

Взяв линейную комбинацию (1.9) и (1.10), получим однопараметрическое уравнение конечно-разностных уравнений, определяемых на шеститочечном шаблоне, указанном на рисунке 1.2, в:

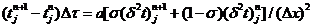.  (1.11)

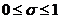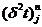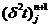где ; через  и  обозначены числители разностных аппроксимаций второй производной

.

Если производную по времени заменить центральной разностью, то можно записать:

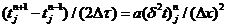. (1.12)

Этими формулами мы далеко не исчерпали возможных схем для решения уравнения теплопроводности. Однако большинство из них можно получить из (1.11), варьируя параметр σ.

Для оценки порядка разностной аппроксимации воспользуемся соотношением (10.1) и формулами

.

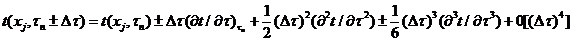
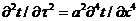Подставляя эти выражения в (1.9), (1.10) - (1.12), находим, что во всех случаях аппроксимация по х имеет второй порядок. Формулы (1.9) и (1.10) обеспечивают первый порядок аппроксимации во времени, а уравнение (1.12) - второй, т.е. с учетом порядка аппроксимации формула (1.12) более точна. Погрешность аппроксимации (1.11) можно записать в виде:

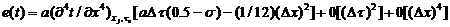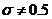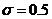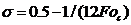.Видно, что при формула (1.11) аппроксимирует уравнение теплопроводности с тем же порядком, что и явная схема. При порядок аппроксимации по времени увеличивается до двух, а для порядок аппроксимации по х равен четырем. В частном случае, когда 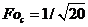0, погрешность аппроксимации уменьшается до .

Таким образом, метод формальной замены производных конечно-разностными отношениями прост и шаблонен. Полученный им разностный аналог дифференциального уравнения аппроксимирует это уравнение в узле сетки, т.е., строго говоря, не вполне справедлив в межузловом пространстве. Недостатком данного метода является отсутствие наглядности и физического содержания.

1.2.3 Метод неопределенных коэффициентов

Суть его в том, что для аппроксимации производной записывают линейную комбинацию значений сеточной функции в узлах наперед заданного шаблона. Неопределенные постоянные коэффициенты этой комбинации определяют из условия получения необходимого порядка аппроксимации в данном узле.

Рассмотрим использование метода неопределенных коэффициентов на следующем примере. Пусть нам требуется аппроксимировать первую производную dt/dx на левой границе тела (см. рис. 87), со вторым порядком. Поскольку для этого необходимы три узла сетки, то запишем:

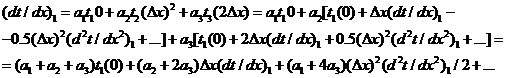. (1.13)

Так как требуется второй порядок аппроксимации, то в правой части (10.13) должно остаться лишь слагаемое с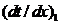 Отсюда приходим для отыскания неизвестных  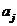к системе уравнений:

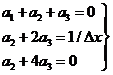.     (1.14)

Решения системы таковы:

, , .

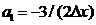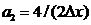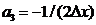Следовательно, с порядком 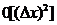 имеем:

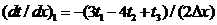.   (1.15)

Таким образом, как можно заметить, метод неопределенных коэффициентов отличается от предыдущего метода лишь порядком действий. И здесь используется разложение в ряд Тейлора, однако в отличие от метода формальной замены производных конечными разностями, порядок аппроксимации является исходной (заданной) величиной, а не следствием преобразований. Он особенно удобен для конструирования разностных аналогов граничных условий требуемой точности.

1.2.4 Метод интегральных тождеств

Уравнение теплопроводности является частным случаем закона сохранения энергии. Оно получено из уравнения баланса теплоты при стягивании элемента объема к нулю в предположении существования непрерывных производных, входящих в уравнение. Естественно потребовать, чтобы при переходе к конечно-разностным аналогам дифференциальных уравнений основные свойства описываемого ими физического процесса сохранялись. Такими свойствами, прежде всего, являются законы сохранения. Разностные схемы, выражающие на сетке законы сохранения, называют консервативными (или дивергентными). Законы сохранения для всей сеточной области ("интегральные законы сохранения'*) для консервативных схем должны быть алгебраическим следствием разностных уравнений.

При получении консервативных разностных схем исходят из уравнений баланса, записанных для элементарных объемов (ячеек) сеточной области (напомним, что при использовании рядов Тейлора разностный аналог удовлетворяет исходному уравнению лишь в узле сетки). Входящие в эти уравнения баланса интегралы и производные следует заменить приближенными разностными выражениями. Поскольку разностные отношения могут быть взяты не единственным образом, то можно получить разные разностные схемы.

Проиллюстрируем особенности этого метода, называемого также интегро-интерполяционным методом, на примере уравнения нестационарной теплопроводности с переменной теплопроводностью

.

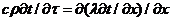Проинтегрируем это уравнение по площади элементарной ячейки сетки, показанной на рисунке 1.3.

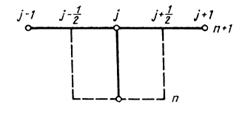
Рисунок 1.3. К построению консервативной схемы

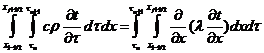.   (1.16)

Правую часть выражения (1.16) можно один раз проинтегрировать по координате. Левую часть можно было бы проинтегрировать повремени, если бы не объемная теплоемкость пластины ср, которая, в общем случае, зависит от температуры, а, следовательно, косвенно, от времени и координаты; возможна и непосредственная зависимость ср от координаты (для составных тел). Предположим поэтому, что объемная теплоемкость вычисляется в момент времени 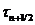 далее не зависит от времени. Тогда после одного интегрирования в (1.16) получаем:

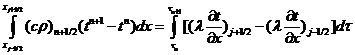.   (1.17)

Будем считать, что все слагаемые левой части (1.17) - для сечения 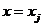. В этом случае они не зависят от х, тогда:

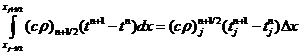.     (1.18)

По определению плотности теплового потока:

.

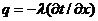Отсюда видим, что в подынтегральном выражении правой части (1.17) величина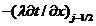 характеризует количество теплоты, втекающее через сечение 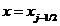 в элементарный объем штриховой ячейки, а  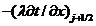- количество вытекающей через сечение 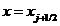теплоты. Естественно, эти количества изменяются во времени, т.е. вдоль левой и правой сторон элементарного объема. Вычисляя интеграл правой части (1.17) методом трапеций и заменяя производные конечными разностями, окончательно получим следующую разностную аппроксимацию нестационарного уравнения теплопроводности:

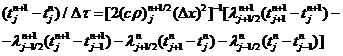.      (1.19)

Есл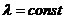и и 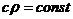, то эта схема совпадает с (10.11) для случая .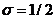

Интегро-интерполяционный метод особенно целесообразен при уравнениях с негладкими или разрывными коэффициентами, поскольку именно интегральная запись законов сохранения выделяет из всех математически допустимых решений таких уравнений физически правильное обобщенное решение.

Какими должны быть шаги сетк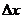и  и 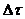? При выборе шага разбиения 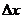 будем руководствоваться следующими соображениями. При малых 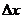 требуются большие затраты рабочего времени и оперативной памяти ЭВМ, при больших возникают значительные погрешности решения, поэтому должны существовать некоторые оптимальные шаги 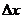, обеспечивающие нужную точность при минимуме затрат. Величина 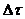 в ряде случаев ограничена определенными условиями, о чем подробно мы будем говорить ниже.

1.3 Метод конечных элементов

Системы алгебраических уравнений для определения численного решения мы получали путем замены производных в дифференциальном уравнении и в граничных условиях или в уравнениях теплового баланса для элементарных ячеек конечными разностями. Таким образом, в методе конечных разностей отправной точкой для получения приближенного решения является дифференциальная краевая задача. Однако искомое поле можно находить и из решения соответствующей вариационной задачи. На ее численном решении основан получивший широкое распространение метод конечных элементов (МКЭ) [7,27].

Сущность МКЭ рассмотрим на примере решения двумерной стационарной задачи теплопроводности в области D произвольной формы (рисунок 1.4):

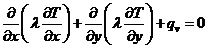.     (1.20)

При граничных условиях третьего рода:

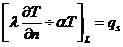,   (1.21)

где λ - теплопроводность; α - коэффициент теплоотдачи на границе; qv, qs - объемная и поверхностная плотности мощности источников теплоты.

Величины λ, α, qv, qs могут быть заданы в виде произвольных функций координат х, у, в том числе и кусочно-исправных функций.

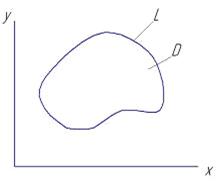
Рисунок.1.4 Двумерная стационарная задача теплопроводности в области D

Метод конечных элементов основан на определении температурного поля путем приближенного решения соответствующей вариационной задачи. Для формулировки этой задачи напомним понятие функционала. Оператор I[f(x)] называется функционалом, заданным на некотором множестве функций, если каждой функции f(x) из этого множества по некоторому правилу ставится в соответствие числовое значение I[f(x)]. Иными словами, функционал является как бы "функцией от функции". В практических приложениях обычно встречаются функционалы, заданные в виде некоторых интегралов, в подынтегральные выражения которых входят функции f(x).

Многие краевые дифференциальные задачи теплопроводности и конвективного теплообмена эквивалентны задачам отыскания функций, доставляющих минимум некоторым специально сконструированным функционалам. Задача на отыскание функции, минимизирующей функционал, называется вариационной. На основе перехода от краевых дифференциальнах задач к вариационным развиты многие приближенные аналитические методы решения задач теплопроводности. Отметим, что возможность вариационной формулировки задачи определения температурного поля (1.20), (1.21) обусловлена свойствами дифференциального оператора уравнения теплопроводности. Мы приведем вариационную формулировку рассматриваемой краевой дифференциальной задачи (1.1), (1.2) без доказательства. Задача решения уравнения (1.21) с граничными условиями (1.2) эквивалентна задаче определения функции Т(х, у), минимизирующей функционал I[Т(x,у)] вида

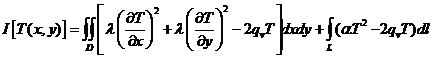.      (1.22)

Наиболее широко распространенный прием получения приближенного решения вариационных задач состоит в следующем. Приближение для искомой функции Т(x,у) разыскивается в виде:

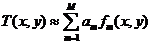,      (1.23)

где am - неизвестные постоянные коэффициенты, а fm(x,y)- известные функции пространственных координат. Если подставить (1.23) в функционал (1.22), то можно провести интегрирование по пространственным переменным и получить величину I, зависящую уже не от неизвестной функции, а от неизвестных коэффициентов разложения (1.23):

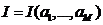.       (1.24)

Очевидно, что для определения приближенного решения вариационной задачи в виде (1.23) следует найти значения a1…,aM, обеспечивающие минимум функций (1.24), т.е. задача сводится к отысканию точки минимума "обычной" функции нескольких переменных. Как известно, значения a1…,aM, обеспечивающие минимум функции I, находятся из решения системы уравнений:

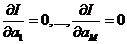.  (1.25)

Решив систему (1.25), можно найти значения a1…,aM, и подставив их в (1.23), определить приближенное решение вариационной задачи.

Центральным местом в изложенном методе является назначение координатных функций разложения (1.23) I1…,IM. Метод конечных элементов основан на использовании описанной схемы приближенного решения при специфическом выборе вида координатных функций f1…,fM. Благодаря этому выбору неизвестные коэффициенты в разложении (1.23) приобретают ясный физический смысл.

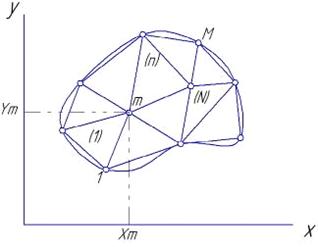
Рисунок 1.5 Разбиения области определения искомой непрерывной величины

Построение координатных функций проводится в МКЭ после разбиения области определения искомой непрерывной величины на N подобластей, называемых элементами, и фиксации в них М узловых точек, выбираемых на границах элементов (рисунок 1.5). Отметим, что число членов в разложении равно числу узловых точек. Каждая из функций fm(x,y) обладает следующими свойствами. Значение функции fm(x,y) в m-ой узловой точке с координатами х=хm, y=ym равно единице, а в остальных узловых точках - нулю. Кроме того, функция Im(x,y) может быть отлична от нуля только в элементах, содержащих m-й узел. В остальной части области D она считается равной нулю.

При таком выборе координатных функций fm(x,y)любой неизвестный коэффициент am в разложении равен приближенному значению температуры am в m-й узловой точке. Действительно при постановке в аппроксимацию координат m-ого узла (х=хm, y=ym) значение всех координатных функций, кроме m-й функции, будут равны нулю, а значит m-й функции - единице, и следовательно:

.

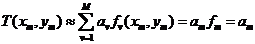При использовании разложения в каждой точке области D "работают" только те координатные функции, у которых коэффициенты равны приближенным значениям температур узловых точек конечного элемента, содержащего данную точку.

Отметим два важных факта вытекающих из рассмотренных свойств координатных функций.

Во-первых, функция I(a1…,aM), получающаяся при подстановке разложения в функционал, будет функцией от неизвестных приближенных значений температуры в узловых точках u1…,uM 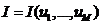, а уравнении, вытекающие из условия минимума (1.25),

.

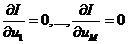Будут алгебраическими уравнениями разностной схемы метода конечных элементов относительно искомых температур в узлах.

Во-вторых, пространственное распределение температуры внутри любого элемента аппроксимируется суммой произведений координатных функций на коэффициенты, равные приближенным значениям температуры в узловых точках, принадлежащих данному элементу.

Координатные функции fm(x,y), m=1, M строятся на основе так называемых функций формы элементов. Каждая из функций формы конкретного элемента равна единице в одной "своей" узловой точке, принадлежащей данному элементу, и нулю в остальных узлах этого элемента, т.е. для элемента вводится столько функций формы, сколько в нем содержится узлов. Вне элемента все его функции формы считаются равными нулю. Таким образом, функция формы n-ого элемента, равна единице в принадлежащей ему m-й точке, является "представителем" координатной функции fm(x,y) в этом n-м элементе. Поэтому температурное поле в n-м элементе аппроксимируется суммой произведений его функций формы на приближенные значения температур в его узловых точках. Очевидно, что для каждого элемента получается своя аппроксимация, но на границах элементов должна сохраняться непрерывность температурного поля.

1.4 Преимущества и недостатки численных методов

На практике часто возникает вопрос, какой из вышеописанных методов больше подходит для решения конкретной задачи. Аналитические и различные численные методы различаются как по объему вычислений, так и по точности и качеству получаемых результатов.

Аппроксимация реального процесса производится за счет подходящей суперпозиции одномерных моделей. Преимущества аналитических методов заключаются в следующем:

• поскольку желаемые параметры связаны с заданными граничными условиями простыми уравнениями, аналитические методы являются быстрыми и простыми в использовании. Вычисления с их помощью могут проводиться даже на карманном калькуляторе. Расчет на персональном компьютере еще более эффективен, поскольку желаемые ответы будут получены еще быстрее;

• основным преимуществом простых расчетных методов на основе аналитических решений является то, что уравнения, используемые в них, обратимы. За счет этого такие уравнения можно дифференцировать, интегрировать, а также решать относительно любого параметра. Можно, например, за один шаг рассчитать геометрию коллектора на основании требования равномерного распределения скорости на выходе.

С другой стороны, простые методы обладают рядом существенных недостатков:

• область их применения ограничивается экструзионными головками, которые аппроксимируются основными геометрическими формами, легко определяемыми путем несложного анализа;

• простые вычислительные методы на основе аналитических решений не позволяют получить полного описания эффектов взаимодействия и переходных процессов;

• зачастую результаты (например, потери давления, объемный расход, время охлаждения) могут быть получены только в интегральной форме (т. е. по всему поперечному сечению канала).

При расчете более сложной геометрической формы или когда требуется более точное моделирование следует использовать численные методы решения дифференциальных уравнений, например, такие как МКР и МКЭ.

При использовании разностных методов дифференциальные уравнения заменяются их аналогами, выраженными в конечных разностях, составленных для узлов прямоугольной сетки.

Вывод уравнений в конечных разностях, последующее решение полученной системы уравнений, а зачастую и построение сетки осуществляются самой компьютерной программой. По сравнению с простыми вычислительными методами, МКР обладает следующими преимуществами

• МКР позволяет рассчитывать геометрические конфигурации, к которым неприменимы простые расчетные методы на основе аналитических решений;

• МКР позволяет получить расчетные значения во всех точках сетки, а не только интегральные значения по поперечному сечению канала;

• точность получаемых результатов повышается за счет того, что в систему дифференциальных уравнений можно включить практически любой закон течения материала;

• возможность учета взаимосвязи дифференциальных уравнений (например, уравнений движения и энергии, зависимостей температуры и скорости сдвига от вязкости);

• так как система уравнений решается одновременно во всей расчетной области, результаты отражают все эффекты взаимодействия (это утверждение не является справедливым для явных разностных схем).

Однако наряду с перечисленными преимуществами разностных методов по сравнению с простыми аналитическими методами МКР обладает рядом внутренне присущих недостатков

• определение геометрии или рабочей точки возможно только методом итераций, поскольку уравнения необратимы;

• расчеты невозможно выполнить вручную или на карманном калькуляторе; для их осуществления необходим, как минимум, персональный компьютер;

• для выполнения расчетов требуется существенно большее время по сравнению с простыми аналитическими методами.

Метод конечных элементов, как и метод конечных разностей, по сравнению с простыми аналитическими методами имеет как преимущества, так и недостатки.

Сравнение МКР и МКЭ представляет собой действительно сложную задачу, так как получаемые результаты существенно зависят от конкретного случая и от используемых методов. При использовании прямоугольных областей и квадратных расчетных сеток или конечных элементов решение задач для некоторых частных случаев показало, что неявные схемы МКР и МКЭ (при использовании линейных функций формы) дают одинаковые результаты, а потому являются практически идентичными

При расчете криволинейных областей неправильной формы МКЭ предоставляют некоторые преимущества за счет возможности построения конечных элементов с границами, которые могут быть криволинейными и не обязательно должны быть перпендикулярны друг другу. Как уже упоминалось ранее, функции формы представляют собой основу МКЭ: они служат не только для интерполяции формы, но и для получения желаемых величин (скорости, давления, температуры) в каждом узле. Таким образом, они оказывают непосредственное влияние на результат. Введение функций формы представляет собой основное различие между МКР и МКЭ. В отличие от МКР, где известны только значения в узловых точках, МКЭ позволяют точно определить значения желаемых параметров в каждой точке рассматриваемой области путем интерполяции с помощью функций формы. За счет того, что этот факт учитывается при выводе уравнений МКЭ, данный метод, по определению, более точен, чем МКР. Кроме более точной аппроксимации геометрии и более точного описания изменения расчетных величин, МКЭ предоставляет следующие преимущества по сравнению с МКР:

• рассматриваемая геометрия может быть любой, поскольку она определяется независимо от компьютерной программы. Это означает, что программы, реализующие МКЭ, работают независимо от геометрии;

• возможность определения расчетных параметров в любой точке рассматриваемой области;

• поскольку уравнения МКЭ решаются одновременно, существует возможность учесть все взаимодействия, имеющие место в системе, с высокой степенью гибкости и точности.

Тем не менее МКЭ тоже не свободен от недостатков:

• время, необходимое для расчетов, а также требования к аппаратным средствам компьютера и объему носителей информации в несколько раз превышают аналогичные требования для МКР. Для решения задач этим методом требуется как минимум высокопроизводительный 16- или 32-разрядный ПК. За редким исключением, применение программ, реализующих МКЭ, ограничивается плоскими задачами;

• поскольку геометрия канала, а также начальные и граничные условия задаются пользователем самостоятельно, время, необходимое для расчета, существенно больше, чем для МКР, где эти параметры более или менее фиксированы;

• большая гибкость МКЭ, касающаяся выбора геометрии, плотности сетки, выбора типов элементов и граничных условий требует от пользователя более глубокого понимания сущности данного метода, иначе получение надежных результатов становится проблематичным.

Сравнительный анализ аналитических и численных методов позволяет сделать следующие выводы: методы, более требовательные к аппаратным средствам и квалификации пользователя, дают преимущества только в том случае, если более простые методы не позволяют добиться требуемого результата вследствие присущих им ограничений. Если расчетные области имеют правильную форму и позволяют построить разностную сетку, то на первый план выходят преимущества МКР. Однако если геометрические формы сильно отличаются, преимуществом будет обладать МКЭ как метод, независимый от геометрии.

2. Практическая часть исследования

.1 Исследование методов повышения точности аппроксимации

Как известно, полное аналитическое описание процесса теплопроводности включает в себя дифференциальное уравнение и краевые условия, которые задаются в виде начальных и граничных условий. В численном методе конечных разностей дифференциальные операторы уравнения теплопроводности заменяются (аппроксимируются) разностным оператором, заданным на множестве сеточных функций. Разностные аналоги могут быть построены следующими методами: формальная замена производных конечно-разностными выражениями, методом неопределенных коэффициентов, интегро-интерполяционный методом и при использовании вариационного метода. При замене дифференциальных операторов все эти аналоги аппроксимируют производные дифференциального уравнения приближенно, т.е. с каким-то порядком погрешности. И поэтому задача представления начальных и граничных условий в конечно-разностной форме состоит в том, чтобы порядок аппроксимации граничных условий был бы не ниже порядка аппроксимации самого уравнения теплопроводности. Эти требования полностью выполняются для условий первого рода, т.к. в данном случае эти параметры задаются точно. Для решения задач теплопроводности при граничных условиях второго и третьего родов требуется повышение порядка погрешности аппроксимации из-за их низкого порядка.

Вначале рассмотрим граничные условия II рода для уравнения теплопроводности с постоянными коэффициентами в виде:

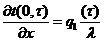,      (2.1)

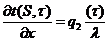,      (2.2)

где 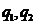- плотности теплового потока на границе рассматриваемого тела (из-за одинаковости задания граничных условий рассмотрим только левую границу тела),

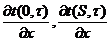- градиенты температуры на границах тела,

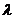- коэффициент теплопроводности тела.

Чтобы найти невязку граничных условий (погрешность аппроксимации) заменим производную 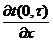, например, разностью вперед (правой разностью)

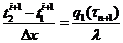.   (2.3)

Далее используя разложение функции по формуле Тейлора в граничной точке :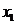

.

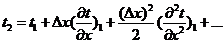Находим первую производную в точке 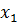 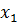на границе тела:

.

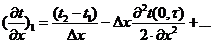Отсюда невязка этого разностного уравнения получится в виде:

,

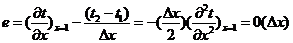имеет только первый порядок аппроксимации.

Для получения невязки во внутренних (регулярных) узлах тела используются простые шаблоны из четырех точек при явной, неявной и центральной разностях. Тогда искомые формулы температур получаются в виде:

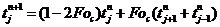 для явных схем;

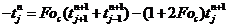 для неявных схем;

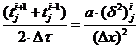 для центрально разности.

где

= -

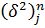
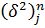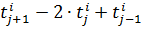
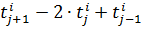числитель разностных аппроксимаций второй производной

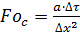
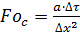 - это сеточное число Фурье.

Для оценки порядка аппроксимаций этих разностных функций разложим их также по формуле Тейлора и найдем вторую производную, например, для центральной аппроксимации:

.

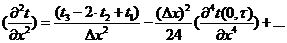Обозначая вторую производную как:

.

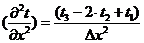Выражаем погрешность аппроксимации:

,  (2.4)

которая имеет второй порядок аппроксимации.

Во всех этих случаях аппроксимации уравнения теплопроводности погрешность по x имеет второй порядок аппроксимации. Это приводит к понижению общей точности расчета. Следовательно, необходимо повысить точность граничного, например, хотя бы второго порядка 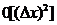, как и в случае для внутренних точек тела. Существует несколько способов повышения точности аппроксимации на границе тела. Расчеты проведем на примере явной схемы.

Вначале рассмотрим способ фиктивных узлов, который очень нагляден. В данном способе вводится вне тела 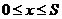 фиктивный узел  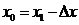и считается, что уравнение теплопроводности справедливо для точек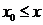. Тогда разностное уравнение для явной схемы

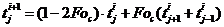 можно написать при j=1:

.

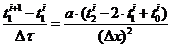Например, для левого граничного условия (2.1) заменим производную центральной разностью, включая фиктивный узел

.

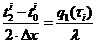Решая два последних уравнения относительно температуры на границе тела (исключив значение температуры в фиктивном узле), получим разностный аналог граничного условия:

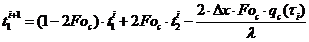.   (2.5)

Как видим, это уравнение содержит только одно значение температуры нового слоя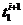, т.е. оно явное и имеет второй порядок аппроксимации.

Второй способ увеличения порядка аппроксимации граничных условий решается использованием метода уменьшения невязки, который менее нагляден, но более универсален.

Выразим 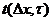 при помощи формулы Тейлора:

.

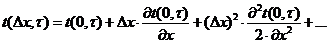На основании граничного условия (1) положим

,

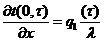а из уравнения теплопроводности найдем

.

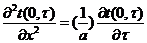Подставляя эти выражения в формулу Тейлора, находим:

.

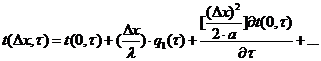Заменяя производную по времени на границе

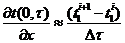
и переходя к индексным обозначениям, снова получаем формулу:

.

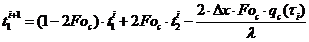В последнем способе если учесть большее число слагаемых ряда Тейлора, то можно получить граничные условия не только нормальной, но и повышенной точности.

Теперь покажем, как можно получить разностный аналог граничных условий III рода, например, на правой поверхности пластины:

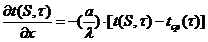,    (2.6)

где 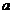 - коэффициент теплоотдачи;

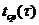 - температура среды.

Покажем формулу получения температуры последующего узла (по координате и времени). Используя разложение по формуле Тейлора к аппроксимации назад, получим:

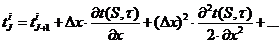.Перепишем данное уравнение используя индексы узлов:

.

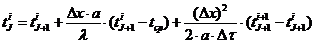Обозначив

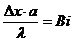(число Био),

Использование метода уменьшения невязки приводит к выражению:

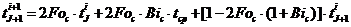.  (2.7)

Можно показать, что порядок аппроксимации выражений (2.5) и (2.7) составляет .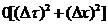

Однако применение этих формул в расчетах ограничивает выбор сеточного числа Фурье. Приемлемая точность численного решения будет достигнута при:

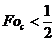,       (2.8)

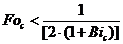.   (2.9)

Снятие отмеченных ограничений на 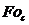 возможно при использовании для аппроксимации граничных условий метода неопределенных коэффициентов. Если, например, в граничное условие третьего порядка:

.

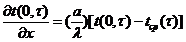И если подставить разложение:

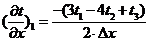.       (2.10)

То после решения получившегося выражения относительно температуры поверхности (стенки) найдем:

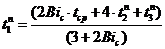.    (2.11)

В этом случае 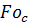 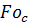определяется исключительно условиями, налагаемыми разностным аналогом уравнения теплопроводности.

Далее рассмотрим построение разностных схем повышенной точности. Путем повышения порядка невязки. Разложим функции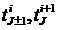, которые входят в дифференциальное уравнение теплопроводности

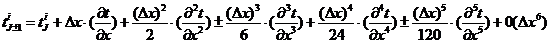,  (2.12)

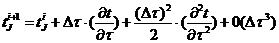.         (2.13)

Если рассматриваемая функция гладкая, то из уравнения теплопроводности следует:

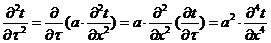. (2.14)

Из уравнения (2.13) получим

.

Отсюда невязка .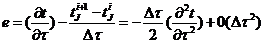

Из уравнения (2.12) получим:

,

.

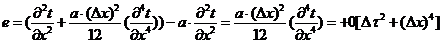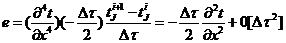C учетом (2.14) получим:

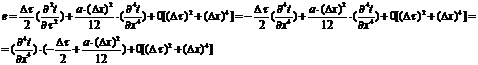
В последнем уравнении главный член приравняем нулю, тогда невязка равна

.

Отсюда получим

.

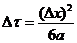Если сетку построить по этому соотношению, то точность шага в явной сетке увеличивается на порядок по времени и на два порядка по переменной х.

2.2 Вычисление температур в узлах ограждающей конструкции и нахождение сопротивления теплопередачи

Ограждающая конструкция представленна на рисунке 2.1.

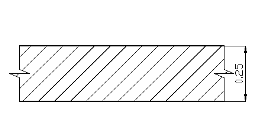
Рисунок 2.1 Ограждающая конструкция (стена).

) Исходные данные:

- наружная температура воздуха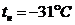

наружная температура воздуха

коэффициенты теплоотдачи ,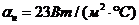

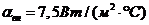
коэффициент теплопроводности материала (пенобетон)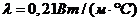

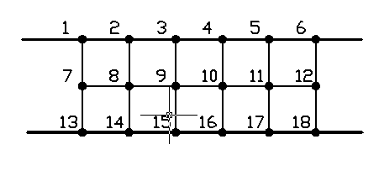
Рисунок 2.2 Пример наложения сетки (стена).

3) Нахождение температур на поверхности стены (для примера узел 1)

Запишем уравнение теплопроводности:

.

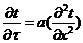Раскладываем в ряд Тейлора:

.

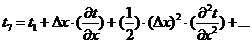Выражаем

:

.

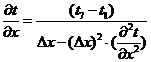Это ведет к аппроксимации для первой производной функции:

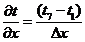.Берем граничные условия для уравнения теплопроводности:

.

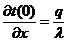Тепловой поток, проходящий через тело везде одинаковый :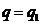

,

.

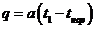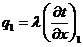Следовательно, получаем следующее уравнение:

.

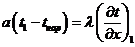Из этого уравнения выражаем

:

.

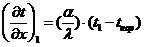Приравниваем получившиеся выражения:

.

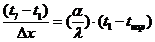Выражаем:

.

Так как

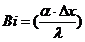
заменяем:

.

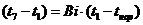Вычисляем нужную нам температуру:

.

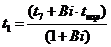Аналогично находим температуры на всей поверхности стены.

) Нахождение температуры во внутренней части стены.

Для нахождения температур во внутренней части стены нам потребуется двухмерное уравнение теплопроводности:

.

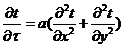Берем вторую производную от этого дифференциального уравнения и получаем:

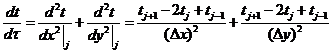.Для примера возьмем узел 8:

.

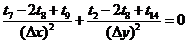Для крайних внутренних узлов (7 и 12) принимаем Bi=0, так как тепло туда не идет и получаем:

,

,

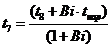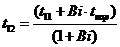Составляем систему уравнений и находим температуры во всех узлах ограждающей конструкции (рисунок 2.3):

Рисунок 2.3 Температуры в узлах ограждающей конструкции

) Нахождение сопротивления теплопередаче

Для нахождения сопротивления теплопередаче нам потребуется найти среднюю температуру на внутренней поверхности стены:

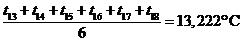.Сопротивление теплопередаче находим по следующему уравнению:

.

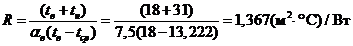2.3 Расчет температур наружного угла и нахождение сопротивления теплопередачи

Ограждающая конструкция представленна на рисунке 2.4.

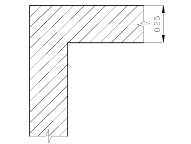
Рисунок 2.4 Ограждающая конструкция (наружный угол).

1) Исходные данные:

наружная температура воздуха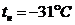

наружная температура воздуха

коэффициенты теплоотдачи ,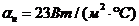

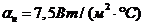
коэффициент теплопроводности материала (пенобетон)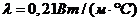

) На исследуемую поверхность накладываем сетку с множеством узлов, по которым будем проводить расчет (рисунок 2.5).

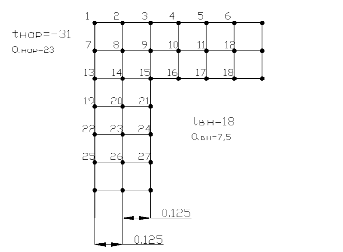
Рисунок 2.5 Примера наложения сетки (наружный угол).

3) Нахождение температуры во внутренней части стены.

Вычисление температуры в узлах лежащих внутри ограждающей конструкции производится идентично узлам, находящимся в внутри прямой стены.

Для нахождения температур во внутренней части наружного угла нам потребуется двухмерное уравнение теплопроводности:

.

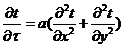Далее берем вторую производную от этого дифференциального уравнения и получаем

.

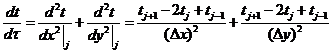Для примера возьмем узел 8

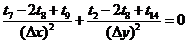.Аналогично находим температуры во всех внутренних узлах ограждающей конструкции

) Вычисление температур на поверхности ограждающей конструкции.

Расчет на поверхности производим другим способом потому, что разные теплопроводности материалов (ограждающая конструкция и окружающая среда).

Рассмотрим узел 2 для примера. Этот узел получает или отдает тепло в 4 направлениях, к узлу 1, 3, 8 и в направление к наружному воздуху.

Количество тепла, передаваемое от узла 2 к узлу 1 равно:

.

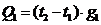Количество тепла, передаваемое от узла 2 к узлу 3 равно:

.

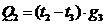Количество тепла, передаваемое от узла 2 к узлу 8 равно:

.

Количество тепла, передаваемое от узла 2 в направление окружающей среды:

.

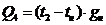Из условия теплового баланса мы получаем

.

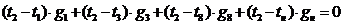Решая это уравнение относительно 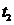, получим

,

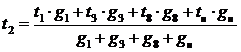где g - коэффициент теплопроводимости,

;

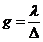λ - коэффициент теплопроводности;

∆ - расстояние между узлами сетки

Если узел лежит в плоскости, граничащей с воздушной средой, то коэффициент теплопроводимости к воздуху будут равен соответсвующей величине теплоотдачи.

И с учетом всех вводных получаем уравнение:

.

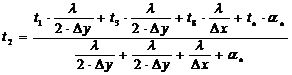Аналогичным образом вычисляем уравнения температур для оставшихся узлов на поверхности ограждающей конструкции.

) Вычисление температуры в наружном и внутреннем углу ограждающей конструкции (узел 1 и 15)

Нахождение температур в этих узлах отличается от нахождения температур на поверхности, т.к. эти узлы граничат с окружающей средой в двух плоскостях.

Сначала рассмотрим узел 1. Этот узел получает или отдает тепло в 4 направлениях, к узлу 2, 7 и в направление к наружному воздуху.

Количество тепла, передаваемое от узла 1 к узлу 2 равно:

.

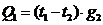Количество тепла, передаваемое от узла 1 к узлу 7 равно:

.

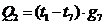Количество тепла, передаваемое от узла 1 в направление окружающей среды:

.

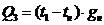Количество тепла, передаваемое от узла 2 в направление окружающей среды:

.

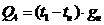Из условия теплового баланса получаем:

.

Решая это уравнение относительно узла 1, получаем:

.

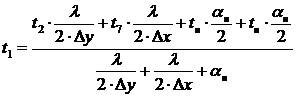Для узла 15 количество теплоты находим точно также только учитываем, что теплота идет к 4 узлам (9, 14, 16 и 21) и также в направлении к окружающей среде. Решая это уравнение относительно данного узла получаем:

.

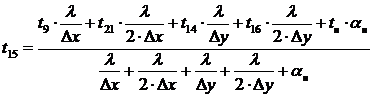После проведения расчетов в MathCad получились следующие температуры (рисунок 2.6):

Рисунок 2.6 Температуры в узлах ограждающей конструкции

) Вычисление сопротивления теплопередаче

Для нахождения сопротивления теплопередаче нам потребуется найти среднюю температуру на внутренней поверхности стены:

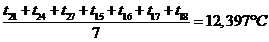
Сопротивление теплопередаче находим по следующему уравнению:

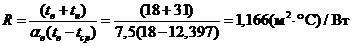
2.4 Расчет температур наружного угла с теплопроводной вставкой и нахождение сопротивления теплопередачи

Ограждающая конструкция представленна на рисунке 2.7.

Рисунок 2.7 Ограждающая конструкция (наружный угол с теплопроводной вставкой).

Расчет похож с расчетом обычного наружного угла, за исключением того, что в этой ограждающей конструкции есть теплопроводная вставка которая усложняет расчет.

) Исходные данные:

наружная температура воздуха ,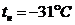

наружная температура воздуха ,

коэффициенты теплоотдачи , ,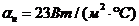

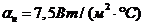коэффициент теплопроводности материала (пенобетон),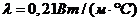

(железобетон) .

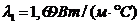) На исследуемую поверхность накладываем сетку с множеством узлов, по которым будем проводить расчет (рисунок 2.8).

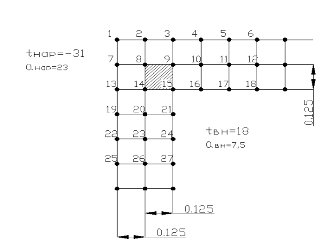
Рисунок 2.8 Пример наложения сетки (наружный угол с теплопроводной вставкой).

3) Вычисления температур на поверхности наружного угла с консолью производится, так же как и расчет обычного наружного угла (для примера возьмем узел 2.)

Этот узел получает или отдает тепло в 4 направлениях, к узлу 1, 3, 8 и в направление к наружному воздуху.

Количество тепла, передаваемое от узла 2 к узлу 1 равно:

.

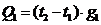Количество тепла, передаваемое от узла 2 к узлу 1 равно:

.

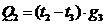Количество тепла, передаваемое от узла 2 к узлу 1 равно:

.

Количество тепла, передаваемое от узла 2 к узлу 1 равно:

.

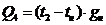Из условия теплового баланса мы получаем

.

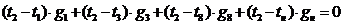Решая это уравнение относительно 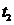, получим

,

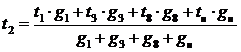где g - коэффициент теплопроводимости,

;

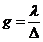λ - коэффициент теплопроводности;

∆ - расстояние между узлами сетки

Если узел лежит в плоскости, граничащей с воздушной средой, то коэффициент теплопроводимости к воздуху будут равен соответствующей величине теплоотдачи.

И с учетом всех вводных получаем уравнение:

.

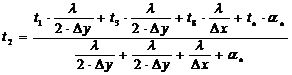Аналогичным образом вычисляем уравнения температур для оставшихся узлов на поверхности ограждающей конструкции.

) Расчет температур в узлах граничащей с теплопроводной вставкой.

На примере узла 9 рассмотрим, как это делается.

Так как теплота проводится по 2 материалам и учитывая приближенные вычисления считаем, что теплота проводится только через половину шага стенки

Этот узел получает или отдает тепло в 4 направлениях, к узлу 8, 3, 10 и 15.

Количество тепла, передаваемое от узла 9 к узлу 8 равно:

.

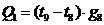Количество тепла, передаваемое от узла 9 к узлу 10 равно:

.

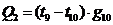Количество тепла, передаваемое от узла 9 к узлу 15 равно:

.

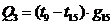Количество тепла, передаваемое от узла 9 к узлу 3 равно:

.

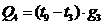Из условия теплового баланса мы получаем:

.

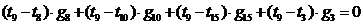Решая это уравнение относительно 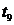, получим:

,

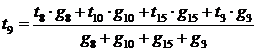где g - коэффициент теплопроводимости,

;

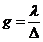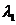λ - коэффициент теплопроводности;

 - коэффициент теплопроводности;

∆ - расстояние между узлами сетки.

Так как этот узел проводит тепло по двум материалам коэффициент g будет выглядеть:

К узлу 8 (два материала):

.

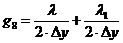К узлу 10 (один материал):

.

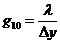К узлу 15 (два материала):

.

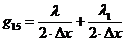К узлу 3 (один материал):

.

В итоге получаем уравнение:

.

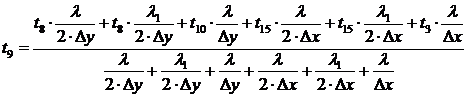) Расчет температуры в узле 1 наружного угла с теплопроводной вставкой выполняется точно так же как и расчет температуры для обычного наружного угла.

) Расчет температуры во внутреннем углу ограждающей конструкции (узел 15)

Этот узел получает или отдает тепло в 4 направлениях по двум материалам, к узлу 9, 16, 14 и 21, а так же граничит с окружающей средой.

Количество тепла, передаваемое от узла 15 к узлу 9 равно:

.

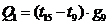Количество тепла, передаваемое от узла 15 к узлу 16 равно:

.

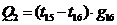Количество тепла, передаваемое от узла 15 к узлу 14 равно:

.

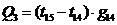Количество тепла, передаваемое от узла 15 к узлу 21 равно:

.

Количество тепла, передаваемое от узла 15 к окружающей среде:

.

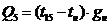И находим температуру в нужном узле:

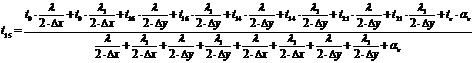
) Нахождение сопротивление теплопередаче

Сопротивление теплопередаче находим исходя из средней температуры на внутренней поверхности ограждающей конструкции:

.

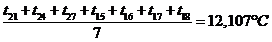Сопротивление теплопередаче вычисляем по следующему уравнению:

.

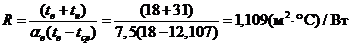После проведения расчетов в MathCad получились следующие температуры (рисунок 2.9):

Рисунок 2.9 Температуры в узлах ограждающей конструкции

2.5 Исследование методов оптимизации теплопотерь и способов утепления наружных углов

При конструировании наружных углов необходимо принимать меры к повышению температуры на их внутренней поверхности, т.е. утеплять углы, что можно делать следующими способами:

.Скашиванием внутренних поверхностей (рисунок 2.10) наружного угла вертикальной плоскостью. При этом с внутренней стороны прямой угол разбивается на два тупых угла. Ширина скашивающей плоскости должна быть не менее 25 см. Это скашивание можно делать или тем же материалом, из которого состоит стена, или другим материалом с несколько меньшим коэффициентом теплопроводности. В последнем случае утепление углов можно делать независимо от возведения стен. Эта мера рекомендуется для утепления углов уже существующих зданий, если теплотехнический режим этих углов оказывается неудовлетворительным (отсыревание или промерзание).

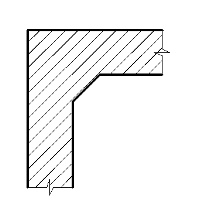
Рисунок 2.10 Скашивание внутренней поверхности

Скашивание угла при ширине скашивающей плоскости 25 см снижает разность температур между гладью стены и наружным углом, по данным опытов, примерно на 30%

.Скруглением наружного угла (рисунок 2.11). Внутренний радиус скругления должен быть не менее 50 см. Скругление угла можно делать как по обеим поверхностям угла, так и по одной его внутренней поверхности (рис.г). В последнем случае утепление аналогично скашиванию угла и радиус скругления может быть уменьшен до 30 см. В гигиеническом отношении скругление угла дает еще более благоприятный результат, поэтому в первую очередь рекомендуется для лечебных и других зданий, к чистоте которых предъявляются повышенные требования.

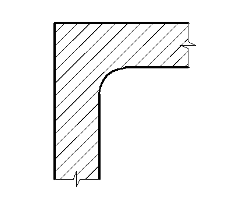
Рисунок 2.11 Скруглением наружного угла

Скругление угла при радиусе 50см снижает разность температур между гладью стен

. Установкой в наружных углах стояков разводящего трубопровода центрального отопления (рисунок 2.12). Эта мера наиболее эффективна, т.к. при этом температура внутренней поверхности наружного угла может стать даже выше температуры на глади стены. Поэтому при проектировании систем центрального отопления стояки разводящего трубопровода, как правило, прокладываются во всех наружных углах здания. Стояк отопления повышает температуру в углу примерно на шесть градусов, при расчетной температуре наружного воздуха и наружным углом примерно на 25%.

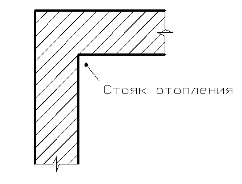
Рисунок 2.12 Установка в наружных углах стояков разводящего трубопровода центрального отопления

Температурные поля в данных конструкциях распределяются следующим образом (рисунок 2.13).

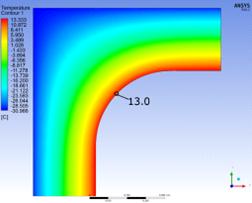
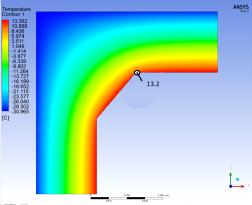
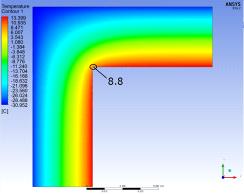
Рисунок 2.13 Распределение температурных полей

3. Экологическое влияние ЭВМ на человека

.1 Влияние электромагнитного излучения на человека

Так как большая часть дипломного проектирования была разработана и оформлена на персональном компьютере, необходимо было выполнять ряд правил по технике безопасности, при работе с персональными электронно-вычислительными машинами (ПЭВМ).

При работе с компьютером человек подвергается воздействию электромагнитного излучения.

Энергетическое воздействие электромагнитного излучения может иметь разную степень и силу. От человека, незаметного до теплового ощущения в случае мощного излучения. Тяжелые электромагнитные воздействия могут повредить оборудование и электрооборудование. Из-за серьезности эффекта электромагнитное излучение не может восприниматься человеком вообще или привести к полному истощению с функциональным изменением активности мозга и смерти. Исследования показали, что долгосрочный эффект электромагнитного излучения, даже на относительно слабом уровне, может вызвать рак, потерю памяти и многие другие.

Для того чтобы предотвратить последствия рентгеновского излучения, необходимо также не превышать норму этого излучения. Этого можно добиться, ограничивая количество часов работы за компьютером и соблюдая необходимое расстояние до монитора, являющегося источником рентгеновского излучения. Для человека, не живущего рядом источником излучения и не работающего непосредственно с источником, норма излучения составляет 0,1 бэр/год.

Рассмотрим, какую дозу рентгеновского излучения за год получит пользователь при работе за компьютером ежедневно в течение 4 часов.

Полученная доза рассчитывается по формуле (3.1)

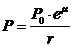; мкР/час,       (3.1)

где ;

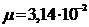P0 = 100 мкР/час

r - Расстояние от источника излучения до человека.

Ниже в Таблице 3.1 приведены значения полученных пользователем доз в зависимости от расстояния до источника.

Таблица 3.1. Зависимость дозы рентгеновского излучения, получаемой пользователем, от расстояния от пользователя до монитора.

По требованиям СанПиН 2.2.2/2.4.1340-03, гигиенические требования к персональным электронно-вычислительным машинам и организации работы. Пользователь должен находиться от монитора на расстоянии 60 см.

На основе данных, приведённых в таблице, рассчитаем дозу рентгеновского излучения, полученную пользователем за год, если он находится во время работы за монитором на расстоянии 60 см от него. Учитывая, что пользователь работает по 4 часа в день 5 дней в неделю 45 недель в году, доза за год рассчитывается по формуле (3.2):

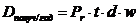; мкР/час,    (3.2)

где Pr - доза рентгеновского излучения на расстоянии r от источника, мкР/час;

t - количество часов работы за компьютеров в сутки, ч;

d - количество рабочих дней в неделю;

w - количество недель в году.

По формуле 6.2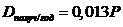

Доза излучения, полученная пользователем, не должна превышать нормированного значения дозы: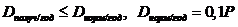

Выводы к главе:

В нашем случае соблюдается требование нормирования, и пользователю рекомендуется находиться на расстоянии 60 см от монитора во время работы.

В качестве защитных мер мы можем называть регулярные прогулки на открытом воздухе, проветривать комнату, заниматься спортом, работать с хорошим оборудованием, которое соответствует всем стандартам безопасности и здоровья.

4. Технико-экономический расчет трудозатрат

При разработке программного изделия необходимо распределить трудовые ресурсы таким образом, чтобы достичь нужных целей проекта и его завершения.

Для этого должны быть определены трудозатраты и назначены исполнители, а ресурсы должны перераспределяться таким образом, чтобы план работ при этом постоянно выполнялся

Можно выделить следующие этапы разработки:

- вводный (подготовительный) этап;

- сбор необходимых данных;

программирование;

обработка данных;

- анализ полученных результатов

4.1 Определение состава исполнителей, их функций и фондов времени работы

Число человек, работающих над проектом - 2 чел., а именно:

-руководитель проекта;

исполнитель (он же разработчик) проекта.

Функции исполнителей работ:

руководитель проекта: руководит проектом, определяет общие требования к решению необходимых задач, выявляет ошибки;

-исполнитель: реализует требования руководителя, выявляет и исправляет ошибки.

Распределение объемов работы между исполнителем и руководителем приведено в таблице 4.1

Таблица 4.1 - Распределение фонда времени

Таким образом, объем всех выполняемых работ равен 101 чел. дней.

4.2 Технико-экономическое обоснование проекта

Рассчитаем сметную стоимость разработки.

Для исчисления амортизационных отчислений на оборудование необходимо определить стоимость всего оборудования и программного обеспечения для выполнения проекта. Полная стоимость всех необходимых затрат представлена в табл. 4.2.

Таблица 4.2. - Стоимость оборудования и программного обеспечения

Поскольку предполагается, что ЭВМ уже есть, ее стоимость не входит в затраты, считается только размер амортизационных отчислений на оборудование, который определяется по формуле (4.1):

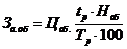,  (4.1)

где Цоб - стоимость оборудования (43500 руб.);

tp- время работы оборудования, дней (101 день, так как все работы проводятся на ПК);

Тр - число рабочих дней в году (251 день);

- норма отчисления на амортизацию оборудования(10% в год).

В итоге получим:

.

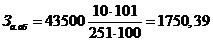Затраты на основную заработную плату исполнителей определяются исходя из оклада и трудоемкости исполняемых ими работ, формула (4.2).

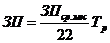,     (4.1)

где ЗПср.мес - среднемесячная заработная плата;

- среднее число рабочих дней в месяце.

Возьмем следующие размеры зарплат для участников: руководитель - 6000 руб., исполнитель - 4000 руб. Расчет фонда заработной платы приведен в таблице 4.3.

Таблица 4.3 Расчет заработной платы

Отчисления по ЕСН составляют 26,2% от общего фонда ЗП:

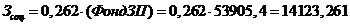руб.

Единый социальный налог делится на следующие части:

·   20% - отчисления в пенсионный федеральный фонд;

·   2.9% - фонд социального налога (остается у предприятия);

·   3.1% - фонд обязательного медицинского страхования;

·   0.2% - фонд страхования от несчастных случаев. Накладные расходы берутся в процентах от заработной платы (60%):

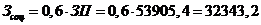руб.

Расчет затрат на прочие расходы определяется в процентном соотношении от суммы предыдущих статей затрат (5%).

.

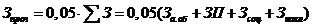Подставляя численные значения, получим:

.

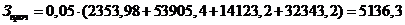Смета затрат на разработку представлена в таблице 4.4

Таблица 4.4. Смета затрат на разработку

Таким образом, сметная стоимость разработки системы составит 107862,12 руб.

5. Безопасность жизнедеятельности при эксплуатации ЭВМ

5.1 Общие положения и область применения

Так как большая часть дипломного проектирования была разработана и оформлена на персональном компьютере, необходимо было выполнять ряд правил по технике безопасности, при работе с персональными электронно-вычислительными машинами. Эти правила прописаны в законодательстве и представлены ниже.

Настоящие государственные санитарно-эпидемиологические правила и нормативы (далее Санитарные правила) разработаны в соответствии с Федеральным законом" О санитарно-эпидемиологическом благополучии населения от 30 марта 1999 года № 52 - ФЗ (Собрание законодательства Российской Федерации, 1999, № 14, ст. 1650) и Положением о государственном санитарно - эпидемиологическом нормировании, утвержденным Постановлением Правительства Российской Федерации от 24 июля 2000 года № 554 (Собрание законодательства Российской Федерации, 2000, № 31, ст. 3295).

Санитарные правила действуют на всей территории Российской Федерации и устанавливают санитарно-эпидемиологические требования к персональным электронно-вычислительным машинам (ПЭВМ) и условиям труда.

Требования Санитарных правил направлены на предотвращение неблагоприятного влияния, на здоровье человека вредных факторов производственной среды и трудового процесса при работе с ПЭВМ.

Настоящие Санитарные правила определяют санитарно-эпидемиологические требования к:

· проектированию, изготовлению и эксплуатации отечественных ПЭВМ, используемых на производстве, в обучении, в быту, в игровых автоматах на базе ПЭВМ;

· эксплуатации импортных ПЭВМ, используемых на производстве, в обучении, в быту и в игровых комплексах (автоматах) на базе ПЭВМ;

· проектированию, строительству и реконструкции помещений, предназначенных для эксплуатации всех типов ПЭВМ, производственного оборудования и игровых комплексов (автоматов) на базе ПЭВМ;

• организации рабочих мест с ПЭВМ, производственным оборудованием и игровыми комплексами (автоматами) на базе ПЭВМ.

Требования Санитарных правил распространяются:

· на условия и организацию работы с ПЭВМ;

· на вычислительные электронные цифровые машины персональные, портативные; периферийные устройства вычислительных комплексов (принтеры, сканеры, клавиатура, модемы внешние, электрические компьютерные сетевые устройства, устройства хранения информации, блоки бесперебойного питания и пр.), устройства отображения информации (видео дисплейные терминалы (ВДТ) всех типов) и игровые комплексы на базе ПЭВМ.

Требования Санитарных правил не распространяются на проектирование, изготовление и эксплуатацию:

· бытовых телевизоров и телевизионных игровых приставок;

· средств визуального отображения информации микроконтроллеров, встроенных в технологическое оборудование;

· ПЭВМ транспортных средств;

· ПЭВМ, перемещающихся в процессе работы.

Ответственность за выполнение настоящих Санитарных правил возлагается на юридических лиц и индивидуальных предпринимателей, осуществляющих:

· разработку, производство и эксплуатацию ПЭВМ, производственное оборудование и игровые комплексы на базе ПЭВМ;

· проектирование, строительство и реконструкцию помещений, предназначенных для эксплуатации ПЭВМ в промышленных, административных общественных зданиях, а также в образовательных и культурно - развлекательных учреждениях.

Индивидуальными предпринимателями и юридическими лицами в процессе производства и эксплуатации ПЭВМ должен осуществляться производственный контроль над соблюдением настоящих Санитарных правил.

Рабочие места с использованием ПЭВМ должны соответствовать требованиям настоящих Санитарных правил.

5.2 Требования к ПЭВМ

ПЭВМ должны соответствовать требованиям настоящих Санитарных правил, и каждый их тип подлежит санитарно-эпидемиологической экспертизе с оценкой в испытательных лабораториях, аккредитованных в установленном порядке.

Перечень продукции и контролируемых гигиенических параметров вредных и опасных факторов.

Допустимые визуальные параметры устройств отображения информации представлены в приложении

Концентрации вредных веществ, выделяемых ПЭВМ в воздух помещений, не должны превышать предельно допустимых концентраций (ПДК), установленных для атмосферного воздуха.

Мощность экспозиционной дозы мягкого рентгеновского излучения в любой точке на расстоянии 0,05 м от экрана и корпуса ВДТ (на электронно-лучевой трубке) при любых положениях регулировочных устройств не должна превышать 1 мкЗв/час (100 мкР/час).

Конструкция ПЭВМ должна обеспечивать возможность поворота корпуса в горизонтальной и вертикальной плоскости с фиксацией в заданном положении для обеспечения фронтального наблюдения экрана ВДТ. Дизайн ПЭВМ должен предусматривать окраску корпуса в спокойные мягкие тона с диффузным рассеиванием света. Корпус ПЭВМ, клавиатура и другие блоки и устройства ПЭВМ должны иметь матовую поверхность с коэффициентом отражения 0,4 - 0,6 и не иметь блестящих деталей, способных создавать блики.

Конструкция ВДТ должна предусматривать регулирование яркости и контрастности.

Документация на проектирование, изготовление и эксплуатацию ПЭВМ не должна противоречить требованиям настоящих санитарных правил.

5.3 Требования к помещениям для работы с ПЭВМ

Помещения для эксплуатации ПЭВМ должны иметь естественное и искусственное освещение. Эксплуатация ПЭВМ в помещениях без естественного освещения допускается только при соответствующем обосновании и наличии положительного санитарно - эпидемиологического заключения, выданного в установленном порядке.

Естественное и искусственное освещение должно соответствовать требованиям действующей нормативной документации. Окна в помещениях, где эксплуатируется вычислительная техника, преимущественно должны быть ориентированы на север и северо-восток. Оконные проемы должны быть оборудованы регулируемыми устройствами типа: жалюзи, занавесей, внешних козырьков и др.

Не допускается размещение мест пользователей ПЭВМ во всех образовательных и культурно - развлекательных учреждениях для детей и подростков в цокольных и подвальных помещениях.

Площадь на одно рабочее место пользователей ПЭВМ с ВДТ на базе электронно-лучевой трубки (ЭЛТ) должна составлять не менее 6 м 2, в помещениях культурно - развлекательных учреждений и с ВДТ на базе плоских дискретных экранов (жидкокристаллические, плазменные) - 4,5 м 2.

При использовании ПВЭМ с ВДТ на базе ЭЛТ (без вспомогательных устройств - принтер, сканер и др.), отвечающих требованиям международных стандартов безопасности компьютеров, с продолжительностью работы менее 4-х часов в день допускается минимальная площадь 4,5 м 2 на одно рабочее место пользователя (взрослого и учащегося высшего профессионального образования).

Для внутренней отделки интерьера помещений, где расположены ПЭВМ, должны использоваться диффузно отражающие материалы с коэффициентом отражения для потолка - 0,7 - 0,8; для стен-0,5 - 0,6; для пола - 0,3 - 0,5.

Полимерные материалы используются для внутренней отделки интерьера помещений с ПЭВМ при наличии санитарно-эпидемиологического заключения.

Помещения, где размещаются рабочие места с ПЭВМ, должны быть оборудованы защитным заземлением (занулением) в соответствии с техническими требованиями по эксплуатации.

Не следует размещать рабочие места с ПЭВМ вблизи силовых кабелей и вводов, высоковольтных трансформаторов, технологического оборудования, создающего помехи в работе ПЭВМ.

5.4 Требования к микроклимату, содержанию аэроионов и вредных химических веществ в воздухе на рабочих местах, оборудованных ПЭВМ

В производственных помещениях, в которых работа с использованием ПЭВМ является вспомогательной, температура, относительная влажность и скорость движения воздуха на рабочих местах должны соответствовать действующим санитарным нормам микроклимата производственных помещений.

В производственных помещениях, в которых работа с использованием ПЭВМ является основной (диспетчерские, операторские, расчетные, кабины и посты управления, залы вычислительной техники и др.) и связана с нервно - эмоциональным напряжением, должны обеспечиваться оптимальные параметры микроклимата для категории работ 1а и 16 в соответствии с действующими санитарно-эпидемиологическими нормативами микроклимата производственных помещений. На других рабочих местах следует поддерживать параметры микроклимата на допустимом уровне, соответствующем требованиям указанных выше нормативов.

В помещениях всех типов образовательных и культурно - развлекательных учреждений для детей и подростков, где расположены ПЭВМ, должны обеспечиваться оптимальные параметры микроклимата

В помещениях, оборудованных ПЭВМ, проводится ежедневная влажная уборка и систематическое проветривание после каждого часа работы на ПЭВМ.

Уровни положительных и отрицательных аэро ионов в воздухе помещений, где расположены ПЭВМ, должны соответствовать действующим санитарно-эпидемиологическим нормативам.

Содержание вредных химических веществ в воздухе производственных помещений, в которых работа с использованием ПЭВМ является вспомогательной, не должно превышать предельно допустимых концентраций вредных веществ в воздухе рабочей зоны в соответствии с действующими гигиеническими нормативами.

Содержание вредных химических веществ в производственных помещениях, в которых работа с использованием ПЭВМ является основной (диспетчерские, операторские, расчетные, кабины и посты управления, залы вычислительной техники и др.), не должно превышать предельно допустимых концентраций загрязняющих веществ в атмосферном воздухе населенных мест в соответствии с действующими гигиеническими нормативами.

Содержание вредных химических веществ в воздухе помещений, предназначенных для использования ПЭВМ во всех типах образовательных учреждений, не должно превышать предельно допустимых среднесуточных концентраций для атмосферного воздуха в соответствии с действующими санитарно - эпидемиологическими нормативами.

5.5 Требования к уровням шума и вибрации на рабочих местах, оборудованных ПЭВМ

В производственных помещениях при выполнении основных или вспомогательных работ с использованием ПЭВМ уровни шума на рабочих местах не должны превышать предельно допустимых значений, установленных для данных видов работ в соответствии с действующими санитарно-эпидемиологическими нормативами.

В помещениях всех образовательных и культурно-развлекательных учреждений для детей и подростков, где расположены ПЭВМ, уровни шума не должны превышать допустимых значений, установленных для жилых и общественных зданий.

При выполнении работ с использованием ПЭВМ в производственных помещениях уровень вибрации не должен превышать допустимых значений вибрации для рабочих мест (категория 3,тип "в") в соответствии с действующими санитарно-эпидемиологическими нормативами. В помещениях всех типов образовательных и культурно-развлекательных учреждений, в которых эксплуатируются ПЭВМ, уровень вибрации не должен превышать допустимых значений для жилых и общественных зданий в соответствии с действующими санитарно-эпидемиологическими нормативами.

Шумящее оборудование (печатающие устройства, серверы и т.п.), уровни шума которого превышают нормативные, должно размещаться вне помещений с ПЭВМ.

5.6 Требования к освещению на рабочих местах, оборудованных ПЭВМ

Рабочие столы следует размещать таким образом, чтобы видеодисплейные терминалы были ориентированы боковой стороной к световым проемам, чтобы естественный свет падал преимущественно слева.

Искусственное освещение в помещениях для эксплуатации ПЭВМ должно осуществляться системой общего равномерного освещения.

В производственных и административно - общественных помещениях, в случаях преимущественной работы с документами, следует применять системы комбинированного освещения (к общему освещению дополнительно устанавливаются светильники местного освещения, предназначенные для освещения зоны расположения документов).

Освещенность на поверхности стола в зоне размещения рабочего документа должна быть 300 - 500 лк. Освещение не должно создавать бликов на поверхности экрана. Освещенность поверхности экрана не должна быть более 300 лк.

Следует ограничивать прямую блесткость от источников освещения, при этом яркость светящихся поверхностей (окна, светильники и др.), находящихся в поле зрения, должна быть не более 200 кд/м 2.

Следует ограничивать отраженную блесткость на рабочих поверхностях (экран, стол, клавиатура и др.) за счет правильного выбора типов светильников и расположения рабочих мест по отношению к источникам естественного и искусственного освещения, при этом яркость бликов на экране ПЭВМ не должна превышать 40 кд/м 2 и яркость потолка не должна превышать 200 кд/м 2.

Показатель ослепленности для источников общего искусственного освещения в производственных помещениях должен быть не более 20. Показатель дискомфорта в административно-общественных помещениях не более 40, в дошкольных и учебных помещениях не более 15.

Яркость светильников общего освещения в зоне углов излучения от 50 до 90 градусов с вертикалью в продольной и поперечной плоскостях должна составлять не более 200 кд/м, защитный угол светильников должен быть не менее 40 градусов.

Светильники местного освещения должны иметь не просвечивающий отражатель с защитным углом не менее 40 градусов.

Следует ограничивать неравномерность распределения яркости в поле зрения пользователя ПЭВМ, при этом соотношение яркости между рабочими поверхностями не должно превышать 3:1 - 5:1, а между рабочими поверхностями и поверхностями стен и оборудования - 10:1.

В качестве источников света при искусственном освещении следует применять преимущественно люминесцентные лампы типа ЛБ и компактные люминесцентные лампы (КЛЛ). При устройстве отраженного освещения в производственных и административно - общественных помещениях допускается применение металлогалогенных ламп. В светильниках местного освещения допускается применение ламп накаливания, в том числе галогенных.

Для освещения помещений с ПЭВМ следует применять светильники с зеркальными параболическими решетками, укомплектованными электронными пускорегулирующими аппаратами (ЭПРА). Допускается использование многоламповых светильников с электромагнитными пускорегулирующими аппаратами (ЭПРА), состоящими из равного числа опережающих и отстающих ветвей. Применение светильников без рассеявателей и экранирующих решеток не допускается.

При отсутствии светильников с ЭПРА лампы многоламповых светильников или рядом расположенные светильники общего освещения следует включать на разные фазы трехфазной сети.

Общее освещение при использовании люминесцентных светильников следует выполнять в виде сплошных или прерывистых линий светильников, расположенных сбоку от рабочих мест, параллельно линии зрения пользователя при рядном расположении видеодисплейных терминалов. При периметральном расположении компьютеров линии светильников должны располагаться локализовано над рабочим столом ближе к его переднему краю, обращенному к оператору.

Коэффициент запаса (Кз) для осветительных установок общего освещения должен приниматься равным 1,4.

Коэффициент пульсации не должен превышать 5%.

Заключение

В магистерской диссертации была проведена работа по адаптации метода конечных разностей для решения сложных задач (нахождение сопротивления теплопередаче ограждающих конструкции) студентами специальностей ТГВ и ПТЭ.

В магистерской диссертации решены следующие задачи:

. Изучена теория метода конечных разностей;

. Изучены особенности обучения студентов кафедры ТГВ;

. Исследованы методы повышения точности аппроксимации;

. Разработана методика расчета ограждающих конструкций;

.Исследованы способы оптимизации тепловых потерь и способы утепления наружных углов зданий.

Список использованных источников

1.        Фокин, К.Ф. Строительная теплотехника ограждающих частей здания / К.Ф. Фокин. - Москва: АВОК-ПРЕСС, 2006. - 256 с.

2.        Телегин, А.С. Тепломассоперенос: учебник для вузов / А.С. Телегин, В.С. Швыдкий, Ю.Г. Ярошенко - Москва.:"Металлургия", 1995, 400с

3.      Применение ЭВМ для решения задач теплообмена: учеб. пособие для теплофизических и теплоэнергетических вузов / Г.Н. Дульнев, В.Г. Парфенов, А.В. Сигалов. - Москва: Высшая школа, 1990.-207 с.

4.        Турчак, Л.И. Основы численных методов: учеб. пособие. - Москва: Наука. Главная редакция физико-математической литературы, 1987. - 320 с.

5.      СП 131.13330.2012. Свод правил. Строительная климатология: актуализированная редакция СНиП 23-02-99*: утв. Минрегионом России от 30.06.2012 №275. - Введ. 01.01.2013. - Москва: ФАУ "ФЦС", 2015. - 120 с

6.      СанПиН 2.2.2/2.4.1340-03. Санитарно-эпидемиологические правила и нормативы: Утверждено постановлением Главного государственного санитарного врача России от 03.06.03: Срок введения в действие. 30.0.03.- Москва., 2003.-42 с.