Аппроксимационные методы измерений периодических сигналов
Введение
Имеется целый ряд задач при
проведении операций измерения, испытаний и контроля, в которых вид сигналов
характеризуется физическими законами исследуемых процессов, а погрешности
результатов измерений очень малы. К таким сигналам, в частности, относятся
периодические сигналы.
Среди периодических сигналов,
которые очень часто используются как в теории, так и в практических целях,
выделяются гармонические сигналы. Это связано с тем, что такие сигналы
независимы к преобразованиям, которые производятся линейными системами. При
подаче на вход подобной системы гармонического сигнала, выходной сигнал
останется гармоническим и будет иметь такую же частоту, а будет отличаться от
входного только амплитудным значением и фазой.
Выполненные в работе исследования
состава высших гармоник сигналов в цепях ряда энергообъектов и электрического
оборудования показали, что: в электрических сетях с номинальным напряжением 110
кВ и более высокими номинальными напряжениями действующие сигналы имеют форму,
которая близка к синусоидальной; коэффициенты искажения синусоидальности,
которые являются комплексной величиной и характеризуют в целом соотношение
между высшими гармониками и первой гармоникой сигналов, меньше 2 %. Кроме того,
коэффициенты отдельных гармоник в сигналах, имеют наибольшую амплитуду, меньше
1,5 %. Достаточно близки к гармоническим моделям сигналы, которые имеют место в
силовых цепях разных электромеханических систем.
Для того, чтобы проводить измерение
параметров данных сигналов можно эффективно использовать аппроксимационный
подход (АП).
АП - это соединение принципов, а
также методов, и реализующих их систем, которые направлены на разработку таких
аналитических моделей, параметры которых находятся на основе заранее известной
информации и определенного экспериментального материала. Всё это должно быть в
непосредственной связи с целями исследований.
Применение такого АП к определению
параметров гармонических сигналов обеспечивает возможность значительного
сокращения времени измерения, а также использования арифметических операций с
мгновенными значениями сигналов вместо достаточно сложных интегральных
преобразований.
Основными параметрами периодических
сигналов служат следующие: среднеквадратические значения напряжения (СЗН) и
тока (СЗТ), активная (АКМ) и реактивная (РЕМ) мощности. Данные параметры обычно
называют интегральными характеристиками периодических сигналов (ИПС).
Кроме необходимости обеспечения
высокой точности измерения ИПС, другой проблемой является достижение высокого
быстродействия процедур измерения, которое определяется требованиями к
оперативности выполнению операций контроля и испытаний.
В магистерской диссертации решается
задача уменьшения времени определения ИПС при обеспечении высокой точности
измерения, что является важной и актуальной задачей.
Разработка и исследование аналоговых
методов определения ИПС и, реализующих их приборов и систем, проводились
научными коллективами, возглавляемыми Алиевым Т.М., Волгиным В.Л., Зыкиным
Ф.А., Кизиловым В.У., Поповым В.С. и многими другими учеными. Важнейшими
недостатками, которые присуще таким аналоговым методам и средствам измерения
являются невысокое быстродействие и низкая универсальность.
В середине двадцатого века начали
распространяться цифровые методы измерения ИПС. При этом вначале многие
цифровые приборы и системы представляли собой некоторое сочетание какого-либо
аналогового измерительного преобразователя отдельной интегральной
характеристики и аналого-цифрового преобразователя аналоговой выходной
величины. Этим вопросам посвящены труды Лаппе Р., Фишера Ф., Безиковича А.Я.,
Шапиро Е.З. и ряда других ученых.
В более позднее время начали
создаваться, так называемые, комбинированные средства измерения ИПС. Они
характеризовались неполным аналоговым преобразованием измеряемых сигналов,
добавленным определенными преобразованиями входных сигналов, производимыми в
цифровой форме. Подобные исследования проводились Наконечным А.И., Чайковским
О.И., Тузом Ю.М., Шаховым Э.К., Шляндиным В.М., Мазеттой Л.A., Гермером Г. и
рядом других ученых.
С конца прошлого века широкое
распространение для измерения ИПС получили цифровые методы, в основе которых
лежит аналого-цифровое преобразование мгновенных значений входных сигналов
(МЗС) при их равномерном распределении на периоде, с дальнейшим выполнением
обработки кодов. Такие вопросы затрагивались в трудах Клисторина И.Ф.,
Коршевера И.И., Кларка Ф.Дж.Дж., Стоктона Дж.Р., Янга A.Г., Стейденто П.M. и
многих других специалистов.
В этих методах первоначально
считается, что мгновенные значения сигналов взяты по периоду равномерным
образом. В практических случаях данное предположение не исполняется, что
вызывает дополнительную погрешность. Данная разновидность погрешности вызвана
изменением частоты входного сигнала и, кроме того, неточным разделением
длительности периода на требуемое число временных интервалов дискретизации. Для
уменьшения влияния этих факторов и, следовательно, для повышения точности
измерения ИПС используются, в основном, только увеличение числа разрядов
аналого-цифровых преобразователей и количества точек дискретизации, а также
введение процесса автоподстройки частоты дискретизации. Всё это приводит к
увеличению времени измерения.
Необходимо отметить ученых, которые
в настоящее время занимаются вопросами разработки новых методов и средств
определения ИПС, имеющих улучшенные метрологические характеристики, это: Сo
Г.К., Хосеини Г., Mусеик A.К., Дуган Р.К., Агалиалов Ю.Р., Желбаков И.Н. и
другие.
Однако проводимые ими исследования
посвящены, в основном, попыткам увеличить точность определения отдельных ИПС с
помощью соответствующей обработки полученных результатов измерений. В работах
этих ученых нет системного подхода к измерению комплекса интегральных
характеристик. Задача уменьшения времени измерения ими не ставится.
В.С. Мелентьев предложил применять
аппроксимационный подход для оперативного измерения ИПС, основанный на
определении интегральных характеристик по функциональной связи с параметрами
гармонической модели, обоснованный выбор которой возможен только на основе
априорной информации о реальном сигнале. При этом он предлагает производить
оценку методической погрешности, которая обусловлена отклонением реального
сигнала от гармонического.
Но вопросы создания
аппроксимационных методов и систем определения ИПС, основанных на формировании
одного или нескольких дополнительных сигналов, которые сдвинуты по фазе
относительно входных, решены не в полной мере.
Задачей магистерской диссертации
является разработка и исследование новых аппроксимационных методов и систем
измерения параметров гармонических сигналов, отличающихся высокой точностью и
малым временем определения параметров.
Для того, чтобы достичь поставленной
цели, в работе были определены и решены следующие задачи:
классификация известных
аппроксимационных методов и систем измерения интегральных параметров гармонических
сигналов (ИПГРС), которые основаны на формировании ортогональных составляющих
(ОС) сигналов;
анализ известных аппроксимационных
методов и систем измерения ИПГРС, основанных на формировании ОС сигналов;
разработка новых аппроксимационных
методов и систем определения ИПГРС с улучшенными метрологическими
характеристиками;
анализ новых аппроксимационных
методов и систем измерения ИПГРС.
Объектом исследования служат сами
аппроксимационные методы измерения ИПГРС.
Предметом исследования является
метрологический анализ известных методов и систем определения ИПГРС, которые
основаны на создании ОС сигналов, а также новых методов.
Научная новизна состоит в следующем:
. Разработан новый метод измерения
ИПГРС с коррекцией погрешности, обусловленных формированием дополнительного
сигнала, который позволяет избавиться от частотной, угловой погрешности,
возникающей при создании дополнительного сигнала, и погрешности по модулю
фазосдвигающего блока (ФСДВБ).
. Разработан новый метод измерения
ИПГРС на основе сравнения мгновенных значений гармонических сигналов, которые
имеют пространственное разделение, который не осуществляет выявление точек
перехода сигналов через ноль, что позволяет сократить время определения ИПГРС
особенно при больших значениях угла сдвига фаз между напряжением и током
. Проведено исследование
метрологических характеристик новых методов и систем определения ИПГРС,
основанных на применении дополнительных сигналов, сдвинутых по сравнению с
входными на произвольный угол, которое позволило определить их возможности с
точки зрения метрологических характеристик.
. Проведено исследование
метрологических характеристик известных методов и систем определения ИПГРС,
основанных на применении ОС сигналов, которое позволило определить возможные
области применения методов.
Научная и практическая ценность
работы.
. Разработаны новые методы и
системы, которые позволяют повысить точность и сократить время определения
ИПГРС.
. Результаты анализа метрологических
характеристик известных методов и систем, основанных на применении ОС сигналов,
а также вновь разработанных методов и средств определения ИПГРС позволили
определить области их возможного применения при известных спектрах реальных
сигналов и предъявляемых требованиях к точности и времени измерения.
При написании магистерской
диссертации были использованы отдельные разделы теории измерений и численного
анализа, положения теории электрических цепей и сигналов, а также методы
цифровой обработки сигналов. Для подтверждения основных теоретических выводов
использовались методы аналитического и имитационного моделирования.
На защиту магистерской диссертации
выносятся следующие основные положения и результаты:
. Методы и системы определения
ИПГРС, использующие формирование дополнительных сигналов и нахождение
информативных параметров по МЗС с коррекцией и при отсутствии коррекции.
. Полученные результаты анализа
погрешностей известных и новых методов и систем определения ИПГРС.
Достоверность результатов
проведенного исследования обеспечивается за счет правомерного и корректного
использования в магистерской диссертации известных теоретических положений, а
также методов аналитического и компьютерного моделирования.
По результатам выполненных в
магистерской диссертации исследований опубликовано 4 научных работы. Полученные
в работе результаты были опробированы на 3 международных конференциях.
1. Оценка возможности использования
аппроксимационного подхода для измерения параметров периодических сигналов
Существуют задачи измерения,
испытаний и контроля, в которых вид сигналов строго обусловлен физическими
законами исследуемых явлений, а погрешности измерений невероятно малы. Такими,
к примеру, очень часто бывают перепериодические сигналы. На основе измерения их
характеристик производиться контроль разного вида электронных и электрических
генераторов, оценивается качество электрической энергии, испытываются колебания
механических систем.
Использование аппроксимационного
метода к данным измерительным задачам, с одной стороны, повышает эффективность
их решения, с другой стороны, обеспечивает общеметодологическую платформу для
унификации средств измерений и их метрологического анализа.
В математической модели
детерминированного сигнала известны все параметры и используется они для
описания образцовых сигналов.
Для характеристики неслучайных
измерительных сигналов используют квазидетерминированные модели, в которых
значение одного или нескольких параметров неизвестны и в большинстве своем
считаются случайными величинами с малой случайной компонентой, влияние которой
можно не учитывать
Для решения подобных задач
используют следующий аппроксимационный подход. Если измерительный сигнал 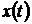 аппроксимируется моделью
аппроксимируется моделью 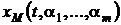 , то, измеряя m значений сигнала при различных, в общем случае
произвольных, значениях аргумента t, возможно скомпоновать систему m уравнений:
, то, измеряя m значений сигнала при различных, в общем случае
произвольных, значениях аргумента t, возможно скомпоновать систему m уравнений:
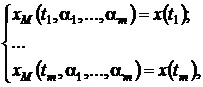 (1.1)
(1.1)
которая решена относительно этих
параметров  .
.
В случае, когда модель 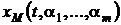 считается нелинейной относительно параметров
считается нелинейной относительно параметров  функцией и значения
функцией и значения 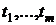 выбраны произвольно, система (1.4) может оказаться сложной для
аналитического или явного численного решения. В связи с этим в тех случаях,
когда есть альтернатива, следует выбрать модели, линейные относительно
параметров. Если это невозможно, упрощение решения системы (1.4) может быть
обеспечено соответствующим выбором значений
выбраны произвольно, система (1.4) может оказаться сложной для
аналитического или явного численного решения. В связи с этим в тех случаях,
когда есть альтернатива, следует выбрать модели, линейные относительно
параметров. Если это невозможно, упрощение решения системы (1.4) может быть
обеспечено соответствующим выбором значений 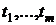 .
.
Таким образом, привлечение априорной
информации о характере сигнала позволяет заменить интегральные преобразования
арифметическими операциями с точечными оценками. Рассмотренный подход помогает
обобщать известные методы, алгоритмы и средства измерения интегральных
характеристик сигналов и изобретать новые.
Одной из основных проблем
рассматриваемого здесь метода является анализ точности измерения. Если модель и
реальный сигнал совпадают, то методически точный результат неизбежен. При
несоответствии модели моделируемуемого сигнала характеристики параметров могут
значительно отличаться от оптимальных.
В соответствии с общей методологией
метрологического анализа аппроксимационных методов и алгоритмов характеристики
результирующей погрешности будут определятся целями обработки и измерений
результатов. В общем случае, качество решения аппроксимационных задач
оценивается некой результирующей погрешностью, включающей в себя все части,
определяющие несоответствие модели и моделируемой зависимости. При случайных
сигналах это интегральные, как правило, среднеквадратические характеристики.
При квазидетерминированных сигналах могут быть получены более грубые
характеристики равномерного приближения. Однако для выявления таких оценок
необходимо знать реальную аппроксимирующую зависимость.
Для выявления аналитических оценок
погрешностей предлагается использовать модель более обобщенного вида,
включающие используемую интерпретационную модель как исключительный случай.
Такими общими примерными моделями
могут быть функциональные ряды:
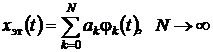 (1.2)
(1.2)
В таком случае наиболее значимое
отклонение модели от соответствующих значений сигналов определяется так:
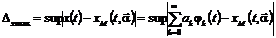 . (1.3)
. (1.3)
Для характеристики отклонения модели
от реального сигнала используют среднеквадратическую погрешность:
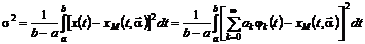 . (1.4)
. (1.4)
При наличии случайных погрешностей в
исходных значениях корректнее использовать усредненные характеристики
погрешностей.
Относительная взвешенная среднеквадратическая
погрешность аппроксимации сигнала 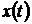 равна:
равна:
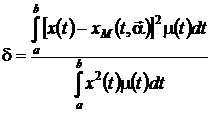 . (1.5)
. (1.5)
Погрешность (1.7) является
несоответствием модели виду сигнала и свойствам оценок параметра.
Метрологическая аттестация выводов
по суммарной погрешности аппроксимации сигнала моделью в практических задачах
используется редко. В большинстве случаев конечной стадией измерений и
обработки является числовые, как правило, интегральные характеристики сигналов.
В этом случае цель сводится к анализу влияния отдельных переменных на
погрешности определения характеристик. В случае детерминированных задач такими
влияющими факторами служыт несоответствие модели виду сигнала, нестабильность
параметров сигнала. Закон трансформации составляющие погрешность в
результирующую определяется последовательностью преобразования результатов
отдельных измерений в нужную оценку, что делает задачи специфичными для каждой
области приложения.
В общем случае для характеристики
влияния составляющих погрешности, обусловленных несоответствием моделей виду
сигналов, на погрешность результата измерения той или иной интегральной
характеристикой сигнала  ,
определяемой в соответствии с (1.4), можно использовать следующую методологию.
,
определяемой в соответствии с (1.4), можно использовать следующую методологию.
. С помощью рассчитанного значения
интегральной характеристики реального сигнала и определения относительной
погрешности:
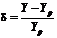 , (1.6)
, (1.6)
где 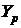 - рассчитанное значение интегральной характеристики,
определеляемое для реального сигнала.
- рассчитанное значение интегральной характеристики,
определеляемое для реального сигнала.
Такой метод используют для
прогнозирования погрешности и выявления области применяемости методологии
определения интегральной характеристики в соответствии (1.4) исходя из
требования по точности при известных спектрах реального сигнала.
. С помощью вычислений погрешности
определения интегральных характеристик как функций, аргументы которой заданы
приближенно с погрешностью, соответствующей отклонению модели от реального
сигнала.
Как известно, погрешность вычисления
значения какой-либо функции, аргументы которой заданы приближенно, может
служить оценка с помощью которой дифференциала этой функции. Погрешности
функции есть не что иное как возможное приращение функций, которое она получит,
если ее аргументам дать приращения, равные их погрешностям. Так как погрешности
бывают обыкновенно достаточно не значительны, то практически вполне допустима
замена приращений дифференциалами. В случае если известны только предельные
абсолютные погрешности аргументов, то при расчете дифференциалов необходимо для
всех производных брать их абсолютные значения.
В зависимости от того как
оцениваются отклонения модели от реального сигнала, возможны три варианта к
определения погрешности.
Считая, что предельная абсолютная
погрешность аргументов соответствует наибольшему отклонению, определяемому в
соответствии (1.5), то для интегральной характеристики 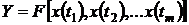 абсолютная погрешность будет равна:
абсолютная погрешность будет равна:
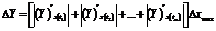 . (1.7)
. (1.7)
Если думать, что значение абсолютных
погрешностей аргументов определяется через среднеквадратическую погрешность 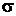 в
соответствии с (1.6), то
в
соответствии с (1.6), то
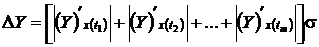 . (1.8)
. (1.8)
Если абсолютные погрешности
аргументов соответствуют действительным разностям между мгновенными значениями
реального сигнала и модели в точках 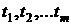 :
:
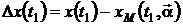 ; …
; … 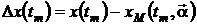 ,
,
то:
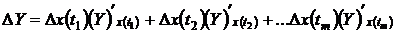 . (1.9)
. (1.9)
При использовании этого метода
относительная погрешность равняется
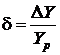 .
(1.10)
.
(1.10)
. Третий метод предусматривает
экспериментальное определение погрешности. Для этого измеряется интегральная
характеристика 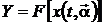 образцовыми
средствами измерения с метрологическими характеристиками, обеспечивающим
возможности его использования в условиях реального сигнала, и сравнение с
результатом измерения Y прибором, использующим аппроксимационный метод (1.4).
образцовыми
средствами измерения с метрологическими характеристиками, обеспечивающим
возможности его использования в условиях реального сигнала, и сравнение с
результатом измерения Y прибором, использующим аппроксимационный метод (1.4).
Практическое использование
рассматриваемой методологии характеристики влияния составляющих погрешности,
обусловленных несоответствием модели виду сигнала, на результат измерения будет
рассмотрено ниже.
Все эти особенности использования
аппроксимационного подхода к определению параметров квазидетерминированных
сигналов и метрологическому анализу результатов позволяют нам обобщить принцип,
метод и средства определения информативных параметров сигналов, основанные на
определении этих параметров по функциональной связи с параметрами модели,
выбираемой на основе той информации об объекте исследования, и метрологическом
анализе результатов измерения из-за несоответствия модели реальному сигналу.
2. Исследование методов измерения
параметров гармонических сигналов, основанных на формировании дополнительных
сигналов
.1 Классификация методов измерения
параметров гармонических сигналов, основанных на формировании дополнительных
сигналов
Уменьшением времени измерения могут
служить методы, основанные на выявлении дополнительных сигналов, сдвигаемых по
фазе относительно входных, и определении ИПГРС по мгновенным значениям главных
и дополнительных сигналов.
При характеристике методов измерения
ИПГРС, основанных на формировании определенных сигналов, в качестве
классификационных признаков используются: род дополнительных сигналов
(формирование ортогональных составляющих сигналов или сигнала, сдвинутого
относительно входных на произвольный угол); количество формируемого
дополнительного сигнала (один, два и более); связь с характерными точками
сигналов (переходы через ноль) и их количество; применение образцовых
интервалов времени (рис. 2.1).
Исключая разные друг к другу
операции, формирование одного или более дополнительных сигналов; связь или
отсутствие связи с характерными точками сигналов; использование или
игнорирование образцовых интервалов времени), можно условно отметить шесть
групп, характеризующих принципы синтеза методов.
Первая группа состоит из методов,
основанных на формировании одного дополнительного сигнала, не использующая
характерные точки сигналов.
Для этой группы возможно
синтезировать и такие методы.
При использовании ортогональных
составляющих сигналов: I-AC-E; I-AC-G (формирование именно дополнительного
напряжения); I-BC-E; I-BC-G (формирование именно дополнительного тока);
I-AC-BC-E; I-AC-BC-G (формирование дополнительных сигналов как напряжения, так
и тока).
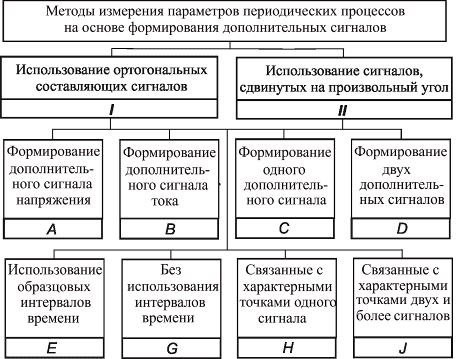
Рис. 2.1
среднеквадратический аппроксимационный сигнал
При использовании других сигналов,
сдвинутых на какой-то угол: II-AC-E; II-AC-G (формирование именно
дополнительного напряжения); II-BC-E; II-BC-G (формирование именно
дополнительного тока); II-AC-BC-E; II-AC-BC-G (формирование дополнительных
сигналов как напряжения, так и тока).
Ко второй группе относятся методы,
основанные на формировании одного дополнительного сигнала, связанное с
характерными точками одного из сигналов.
К этой группе можно отнести
следующие методы.
При использовании ортогональных
составляющих сигналов: I-AC-EH; I-AC-GH (формирование именно дополнительного
напряжения); I-BC-EH; I-BC-GH (формирование именно дополнительного тока.);
I-AC-BC-EH; I-AC-BC-GH (формирование дополнительных сигналов как напряжения,
так и тока.)
При использовании дополнительных
сигналов, сдвинутых на произвольный угол: II-AC-EH; II-AC-GH (формирование
именно дополнительного напряжения); II-BC-EH; II-BC-GH (формирование именно
дополнительного тока); II-AC-BC-EH; II-AC-BC-GH (формирование дополнительных
сигналов как напряжения, так и тока).
Третья группа состоит из методов,
основанных на формировании одного дополнительного сигнала, связанных с
характерными точками двух и более сигналов.
Для этой группы можно синтезировать
следующие методы.
При использовании ортогональных
составляющих сигналов: I-AC-EJ; I-AC-GJ (формирование именно дополнительного
напряжения); I-BC-EJ; I-BC-GJ (формирование именно дополнительного тока);
I-AC-BC-EJ; I-AC-BC-GJ (формирование дополнительных сигналов как напряжения,
так и тока).
При использовании дополнительных
сигналов, сдвинутых на произвольный угол: II-AC-EJ; II-AC-GJ (формирование
только дополнительного напряжения); II-BC-EJ; II-BC-GJ (формирование только
дополнительного тока); II-AC-BC-EJ; II-AC-BC-GJ (формирование дополнительного
сигнала как напряжения, так и тока).
К четвертой группе отнесены методы,
основанные на формировании двух дополнительных сигналов напряжения, либо тока,
либо как напряжения, так и тока, не использующие характерные точки сигналов.
С учетом того, что формирование двух
дополнительных ортогональных составляющих одного сигнала не возможно, то для
этой группы могут быть синтезированы только методы, использующие дополнительные
сигналы, сдвинутые на отличный от 90° угол: II-AD-E; II-AD-G (формирование двух
дополнительных сигналов напряжения); II-BD-E; II-BD-G (формирование двух
дополнительных сигналов тока); II-AD-BC-E; II-AD-BC-G (формирование двух
дополнительных сигналов напряжения и одного дополнительного сигнала тока);
II-AC-BD-E; II-AC-BD-G (формирование одного дополнительного напряжения и двух
дополнительных сигналов тока); II-AD-BD-E; II-AD-BD-G (формирование по два
дополнительных напряжения и тока).
Пятую группу составляют методы,
основанные на формировании двух дополнительных сигналов напряжения, либо тока,
либо как напряжения, так и тока, связанные с характерными точками одного из
сигналов.
Поскольку здесь также не могут быть
использованы ортогональные части сигналов, то возможно синтезировать следующие
методы: II-AD-EH; II-AD-GH (формирование двух дополнительных сигналов
напряжения); II-BD-EH; II-BD-GH (формирование двух дополнительных сигналов
тока); II-AD-BC-EH; II-AD-BC-GH (формирование двух дополнительных сигналов
напряжения и одного дополнительного сигнала тока); II-AC-BD-EH; II-AC-BD-GH
(формирование одного дополнительного напряжения и двух дополнительных сигналов
тока); II-AD-BD-EH; II-AD-BD-GH (формирование по два дополнительных напряжения
и тока).
К шестой группе относится метод,
основанный на формировании еще двух дополнительных сигналов напряжения, либо
тока, либо как напряжения, так и тока, связанное с характерными точками двух
или более сигналов.
Если не будут использованы
ортогональные части сигналов, то для этой группы могут быть синтезированы
другие методы: II-AD-EJ; II-AD-GJ (формирование двух дополнительных сигналов
напряжения); II-BD-EJ; II-BD-GJ (формирование двух дополнительных сигналов
тока); II-AD-BC-EJ; II-AD-BC-GJ (формирование двух дополнительных сигналов
напряжения и одного дополнительного сигнала тока); II-AC-BD-EJ; II-AC-BD-GJ
(формирование одного дополнительного напряжения и двух дополнительных сигналов
тока); II-AD-BD-EJ; II-AD-BD-GJ (формирование по два дополнительных напряжения
и тока).
Таким образом, если не использовать
структурную избыточность, то предоставленная классификация позволяет в частых
случаях синтезировать 66 методов.
Огромное количество различных
вариантов методов требует использования их дополнительной классификации.
Заметное упрощение реализации
обеспечивают методы измеряемые ИПГРС, в которых в качестве вспомогательных
используются ортогональные части входных сигналов.
Имеется возможность классифицировать
методы измерения интегральных характеристик с использованием ортогональных
составляющих сигналов по следующим некоторым признакам: сравнение главного и
дополнительного сигналов; связь с основными точками сигналов; сохранение
мгновенных значений сигналов для последующего сравнения; раздел мгновенных
значений сигналов во времени.
На рисунке 2.2 представлена
классификация методов измерения ИПГРС, основанных на формировании ортогональных
составляющих сигналов.

Рис. 2.2
Исключая противоположные друг к
другу связи (связь или отсутствие связи с характерными точками сигналов;
использование или отсутствие разделения во времени), а также, принимая во
внимание тот факт, что запоминание мгновенных значений сигналов производится
только с их последующим сравнением, можно условно разделить три группы,
характерные для синтеза методов.
Первая группа состоит из методов, не
использующие сравнение основного и дополнительного сигналов. Для этой группы
возможно синтезировать такие методы: CH; CJ; DH; DJ; EH; EJ.
Во вторую группу входят такие
методы, которые основанны на сравнении основного и дополнительного сигналов напряжения
или тока. Для этой группы можно синтезировать такие методы как: ACH; ACJ; ACFH;
ADGJ; AEFH; AEFJ; AEGH; AEGJ; АCFJ; ADH; ADJ; AEH; AEJ; ADFH; ADFJ; ADGH;.
Наконец, третья группа состоит из
методов, основанных на сравнении основного и дополнительного сигналов и
напряжения и тока. Для этой группы можно синтезировать такие методы как: ВCH;
ВCJ; ВCFH; ВCFJ; ВDH; ВDJ; ВEH; ВEJ; ВDFH; ВDFJ; ВDGH; ВDGJ; ВEFH; ВEFJ; ВEGH;
ВEGJ.
Так, представленная классификация
позволяет в общем случае синтезировать 38 методов.
2.2 Метод измерения интегральных
параметров на основе сравнения ортогональных составляющих напряжения
Первый метод основанный на том, что
формируют ОС напряжения и тока; в момент когда равенство основного и
дополнительного сигналов напряжения одновременно измеряет мгновенные значения
главного сигнала напряжения, главного и дополнительного сигналов тока и
определяют ИПГРС по измеренным значениям.
Временные диаграммы, поясняющие
метод, представлены на рисунке 2.3.
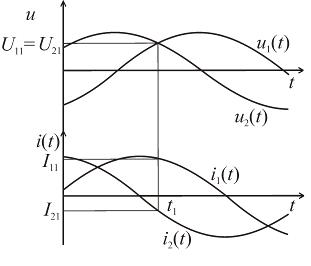
Рис. 2.3
Для входного напряжения 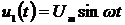 и тока
и тока 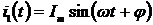 и
дополнительных сигналов напряжения
и
дополнительных сигналов напряжения 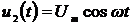 и тока
и тока 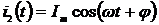 в
момент времени t1, когда главный и дополнительный сигналы напряжения будут
равны, выражения для мгновенных значений сигналов примут вид:
в
момент времени t1, когда главный и дополнительный сигналы напряжения будут
равны, выражения для мгновенных значений сигналов примут вид: 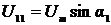 ;
; 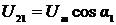 ;
; 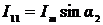 ;
; 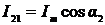 , где α1,
, где α1, 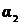 - фазы
сигналов напряжения и тока в момент времени t1;
- фазы
сигналов напряжения и тока в момент времени t1;  - угол сдвига фаз между сигналами напряжения и тока; ω - угловая частота
входного сигнала.
- угол сдвига фаз между сигналами напряжения и тока; ω - угловая частота
входного сигнала.
Мгновенные значения  и
и  будут
равны при угле
будут
равны при угле  , где
, где  .
.
В таком случае выражения для
определения основных ИПГРС примут вид:
СКЗ напряжения и тока:
 ;
(2.11)
;
(2.11)
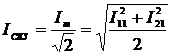 ;
(2.12)
;
(2.12)
АКТМ и РКМ
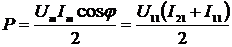 ;
(2.13)
;
(2.13)
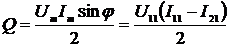 .
(2.14)
.
(2.14)
Информационно-измерительная система,
показывающая метод, предоставлена на рисунке 2.4.
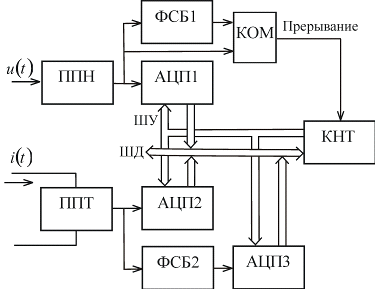
Рис. 2.4
В составе ИИС: первичные
преобразователи напряжения ППН и тока ППТ, аналого-цифровые преобразователи
АЦП1, АЦП2 и АЦП3, фазосдвигающие блоки ФСБ1 и ФСБ2, позволяющие сдвиг входных
сигналов напряжения и тока на 90°, компаратор КОМ, контроллер КНТ, шины
управления ШУ и данных ШД.
В КНТ производятся вычисления в
соответствии с выражениями (2.11) - (2.14).
В рассмотренном методе время
измерений не зависит от угла сдвига фаз между напряжением и током, а
определяется исключительно временным промежутком между моментом начала
измерения и моментом равенства текущих значений напряжений  и
и  .
.
Одним из главных недостатков ИИС,
реализующих скопление методов, основанных на формировании исключительных ОСС,
является погрешность фазосдвигающих блоков. В результате чего при изменении
частоты входного сигнала ФСБ сдвигают сигнал на угол, отличный от 90°.
Если принимать, что ФСБ1 (канал
напряжения) имеет угол сдвига фазы равный (90°+Δβ),
а ФСБ2 (канал тока) имеет угол сдвига фазы равный (90°+Δξ), то выражение для
мгновенных значений сигналов будет равно:
 (2.15)
(2.15)
Рассмотрим исключительный случай,
когда ФСБ1 и ФСБ2 имеют схожий угол сдвига фазы равный (90°+Δβ).
В соответствии с (2.14) и (2.15),
относительная погрешность определения СКЗ напряжения примет вид:
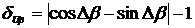 .
(2.16)
.
(2.16)
Согласно (2.13) и (2.15)
относительная погрешность измерения СКЗ тока выражаться в виде:
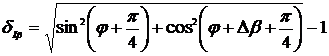 .
(2.17)
.
(2.17)
В соответствии с (2.13) - (2.15)
приведенные погрешности определения активной и реактивной мощности будут равны
выражениям:
 ;
(2.18)
;
(2.18)
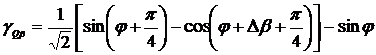 .
(2.19)
.
(2.19)
На рис. 2.5 представлены графики
зависимости относительной погрешности определения СКЗ напряжения от отклонения
угла сдвига фазы ФСБ от номинальных значений в соответствии с выражениями
(2.16).
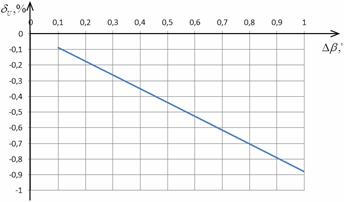
Рис. 2.5
Изучение рис. 2.5 показывает, что
относительность погрешности измерения СКЗ напряжения от отклонения угла сдвига
фазы ФСБ носит линейный характер и увеличиваеться прямо пропорционально Δβ.
На рис. 2.6 предоставлены графики
относительной зависимости погрешности определения СКЗ тока от угла сдвига фаз
между сигналами напряжения и тока в соответствии с выражением (2.17) при
различных значениях отклонения угла сдвига фазы ФСБ от нормального значения.
Анализ рис. 2.6 показывает, что при 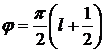 (где l=0,1,…) погрешность равна нулю, а при
(где l=0,1,…) погрешность равна нулю, а при 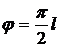 - принимает максимальные значения.
- принимает максимальные значения.
На рис. 2.7 и 2.8 предоставлены
графики зависимости приведенной погрешности определения АКМ и РЕМ от угла
сдвига фаз между сигналами напряжения и тока в соответствии с выражениями
(2.18) и (2.19) при различных значениях отклонения угла сдвига фазы ФСБ от
номинального значения.
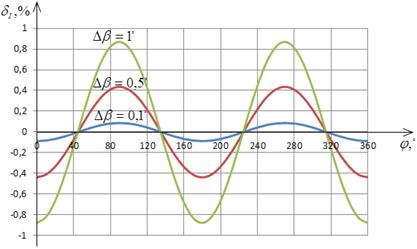
Рис. 2.6
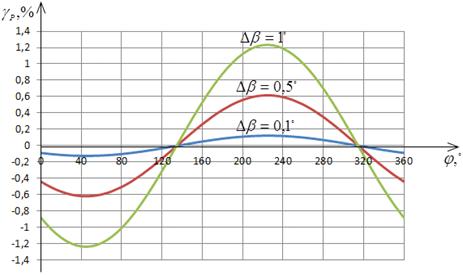
Рис. 2.7
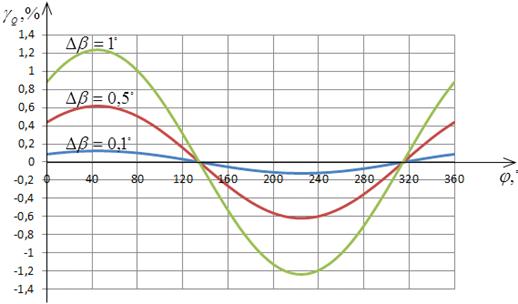
Рис. 2.8
Анализ рис. 2.7 и 2.8 указывает, что
при 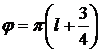 погрешность приравнивается к нулю, а при
погрешность приравнивается к нулю, а при 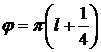 - погрешность принимает наибольшее значение.
- погрешность принимает наибольшее значение.
ФСБ также могут иметь погрешность по
напряжению (погрешность по модулю). Наличие этого вида погрешности приводит к
тому, что амплитудные параметры входного и дополнительного сигналов будут
отличаться.
Если амплитудное значение сигнала на
выходе ФСБ в канале напряжения отличается от входного на величину ΔUm, то мгновенное значение
дополнительного напряжения имеет вид 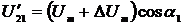 . Так же, при отличии дополнительного тока от входного на значение ΔIm, мгновенное значение
дополнительного сигнала будет равно
. Так же, при отличии дополнительного тока от входного на значение ΔIm, мгновенное значение
дополнительного сигнала будет равно 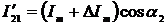 .
.
Оценим влияние этого вида
погрешности ФСБ на погрешность результатов измерений ИПГРС.
Поэтому воспользуемся алгоритмом
характеристики погрешностей результатов измерений интегральной характеристики
как функции, аргументы которых заданы приближенно с погрешностью, соотносящейся
к отклонению модели от основного сигнала.
Если абсолютные погрешности
аргументов соответствуют отклонению мгновенных значений дополнительного
напряжения и тока на величины ΔUm и ΔIm то, считая, что мгновенные значения входных сигналов напряжения и
тока измерены без погрешности, можно отметить предельные значения абсолютных
погрешностей измерения СКЗ тока, АКМ и РЕМ:
 ;
(2.20)
;
(2.20)
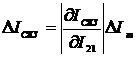 ;
(2.21)
;
(2.21)
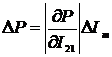 ;
(2.22)
;
(2.22)
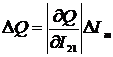 .
(2.23)
.
(2.23)
Используя (2.11) - (2.14), с учетом
этих погрешностей (2.20) - (2.23) можно определить главные погрешности
измерения СКЗ напряжения и тока и приведенные погрешности определения АКМ и
РЕМ:
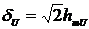 ;
(2.24)
;
(2.24)
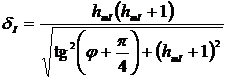 ;
(2.25)
;
(2.25)
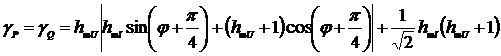 ,
(2.26)
,
(2.26)
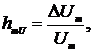
 .
.
Например, при hmU=0,05% δU=0,07%.
На рис. 2.9 и 2.10 представлены
графики зависимостей относительной погрешности измерения СКЗ тока и приведенных
погрешностей АКМ и РЕМ в соответствии с выражениями (2.25) и (2.26) для
hmI=0,05%.
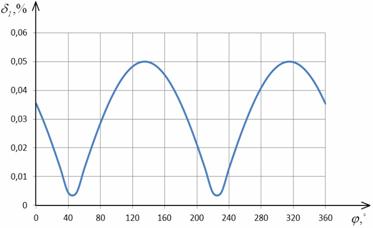
Рис. 2.9 Зависимость погрешности  от φ
от φ
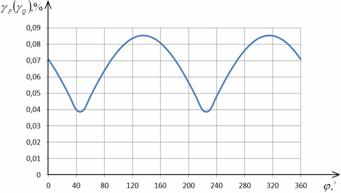
Рис. 2.10. Зависимость погрешности  от φ
от φ
Кроме того, при отличии реального
сигнала от гармонической модели возникают погрешности. В частности, при углах
сдвига фаз близких к нулю, погрешность измерения АКМ и РЕМ не превышает 1,25 %,
СКЗ тока - 0,5 % при коэффициентах пятой гармоники hu5=hi5=0,005. Погрешность
измерения СКЗ напряжения в зависимости только от спектра сигнала и при
hu5=0,005 составляет около 0,7%.
.3 Метод измерения интегральных
параметров на основе сравнения ортогональных составляющих и напряжения и тока
Второй метод основан на том, что
формируют ОС напряжения и тока; в момент равенства основного и дополнительного
сигналов напряжения одновременно измеряя мгновенные значения главных сигналов
напряжения и тока; в момент равенства основного и дополнительных сигналов тока
измеряют мгновенные значения основных сигналов тока и напряжения и определяют
ИПГРС по измеренным значениям.
Временные диаграммы, поясняющие
методы, представленые на рисунке 2.11.
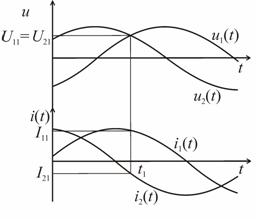
Рис. 2.11. Временные диаграммы,
поясняющие второй метод
В момент времени t1, когда главный и
дополнительные сигналы напряжения будут равны, выражения для мгновенных
значений сигналов будут иметь вид:
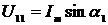 ;
; 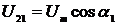 ;
; 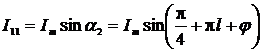 ,
,
где l=0,1.
В тот момент времени t2, когда будут
равны основной и дополнительный сигналы тока, выражения для мгновенных значений
сигналов будут иметь следующий вид:
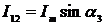 ;
; 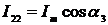 ;
; 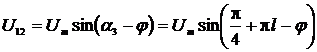 ,
,
где 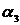 - фаза сигнала тока в момент времени t2.
- фаза сигнала тока в момент времени t2.
Мгновенные значения 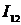 и
и 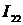 будут
равны, при угле
будут
равны, при угле 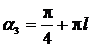 .
.
В этом случае выражения для
определения основных ИПГРС будут равны:
 ;
(2.27)
;
(2.27)
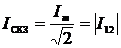 ;
(2.28)
;
(2.28)
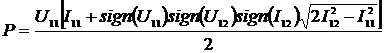 ;
(2.29)
;
(2.29)
 .
(2.30)
.
(2.30)
ИИС, реализующая второй метод,
представлена на рисунке 2.12.
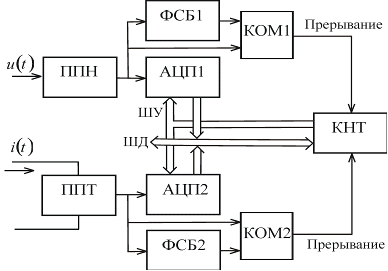
Рис. 2.12. Структурная схема ИИС,
реализующей второй метод
В данном случае время измерения
зависит от угла сдвига фаз между сигналами напряжения и тока.
Если считать, что ФСБ в каналах
напряжения и тока имеют углы сдвига фаз равные (90°+Δβ) и (90°+Δξ) соответственны, то
выражения для мгновенных значений сигналов в моменты времени t1 и t2 примут
вид:
 (2.31)
(2.31)
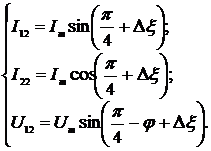 (2.32)
(2.32)
Посмотрим частный случай анализ погрешностей
определения интегральных характеристик вследствии нестабильности углов сдвига
фаз ФСБ, приняв Δβ=Δξ.
В соответствии с (2.27) - (2.32)
такие погрешности измерения СКЗ напряжения и тока и представленные погрешности
определения АКМ и РЕМ определяются в соответствии с выражениями:
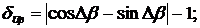 (2.33)
(2.33)
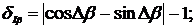 (2.34)
(2.34)

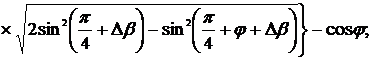 (2.35)
(2.35)
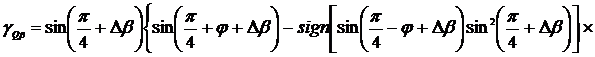
 (2.36)
(2.36)
Анализ выражений (2.33) - (2.36)
указывает, что погрешности измерения СКЗ напряжения и тока определены
непосредственно отклонением угла сдвига фаз ФСБ от 90°, а погрешность определения
АКМ и РЕМ также зависят и от угла сдвига фаз между напряжением и током.
Графики зависимостей относительных
погрешностей измерений СКЗ напряжения и тока аналогичны представленным на рис.
2.5.
На рис. 2.13 и 2.14 превидены
графики зависимостей приведенных погрешностей измерения АКМ и РЕМ в
соответствии с выражениями (2.35) и (2.36) для различных значений угла Δβ.
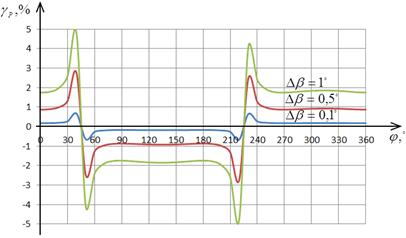
Рис. 2.13. Зависимость погрешности 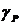 от φ
от φ
Если амплитуда значений выходных
сигналов ФСБ в канале напряжения и тока отличаются от входные на величины ΔUm и ΔIm, то мгновенные значения
дополнительных сигналов соответственно примут вид:
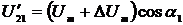 ,
, 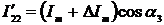 .
.
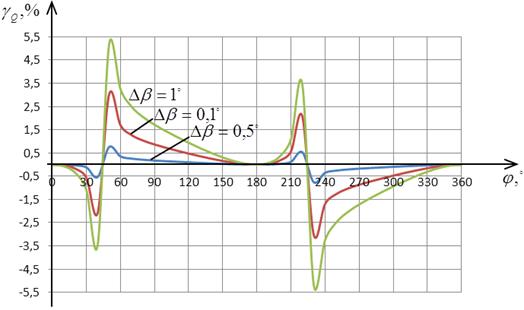
Рис. 2.14. Зависимость погрешности 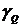 от φ
от φ
Предельные показатели абсолютных
погрешностей измерений СКЗ напряжения и тока, АКМ и РЕМ в соответствии с
выражениями (2.27) - (2.30) будут равняться:
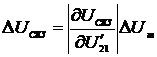 ;
(2.37)
;
(2.37)
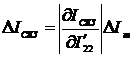 ;
(2.38)
;
(2.38)
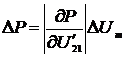 ;
(2.39)
;
(2.39)
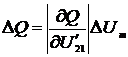 . (2.40)
. (2.40)
Используя (2.27) - (2.30), с учетом
абсолютных погрешностей (2.37) - (2.40) относительно погрешностей измерения СКЗ
напряжения и тока и приведенные погрешности измерения АКМ и РЕМ примет вид:
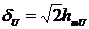 ;
(2.41)
;
(2.41)
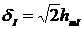 ;
(2.42)
;
(2.42)
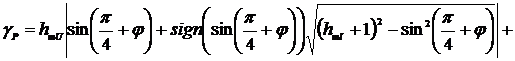
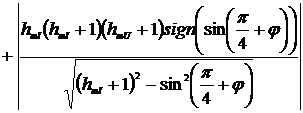 ;
(2.43)
;
(2.43)
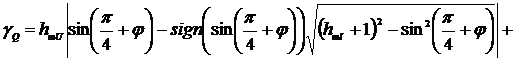
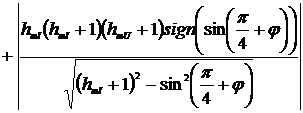 .
(2.44)
.
(2.44)
Например, при hmU=hmI=0,05 % δU=δI=0,07%.
Анализ выражений (2.43) и (2.44)
показывает, что погрешности определения АКМ и РЕМ зависит не только от
погрешности по модулю ФСБ, но и от угла сдвига фаз между сигналами напряжеия и
тока.
На рис. 2.15 и 2.16 представлены
графики зависимостей приведенных погрешностей измерения АКМ и РЕМ в
соответствии с (2.43) и (2.44) для hmI=0,05%.
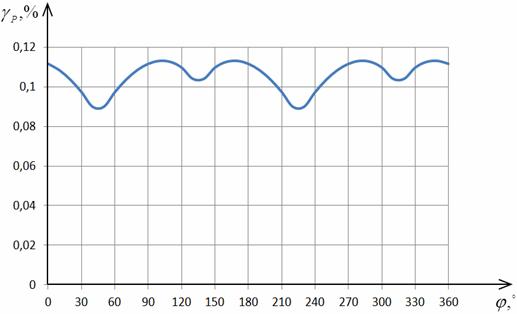
Рис. 2.15. Зависимость погрешности  от φ
от φ
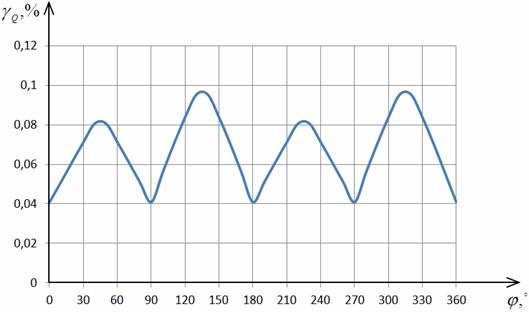
Рис. 2.16. Зависимость погрешности  от φ
от φ
Кроме того, при соответсвии в
сигналах напряжения и тока высших гармоник, появляется погрешность.
Относительная погрешность измерения СКЗ сигналов относительна только от наличий
высших гармоник, и при hu5=hi5=0,5% она составляет 0,7%. Приведенная
погрешность измерения АКМ и РЕМ еще зависит и от угла сдвига фазы между
сигналами напряжения и тока. При φ=0 она составляет порядка 1,5% и возрастает с увеличением φ.
.4 Метод измерения интегральных
параметров по мгновенным значениям ортогональных составляющих, связанным с
переходами через ноль дополнительных сигналов напряжения и тока
Третий метод основанный на том, что
в момент перехода дополнительного сигнала напряжения, сдвинутого относительно
входного на 90°, через ноль одновременно проверяют первые мгновенные значения
входного напряжения и тока; в момент перехода дополнительного сигнала тока,
сдвинутого относительно входного на 90°, через ноль измеряются вторые
мгновенные значения входного тока и определяются ИХГРС по измеренным значениям.
Временные диаграммы, объясняющие
метод, представлены на рисунке 2.17.
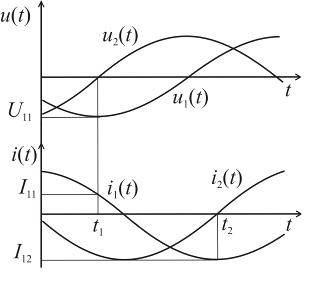
Рис. 2.17. Временные диаграммы,
поясняющие третий метод
Выражения для мгновенных значений
сигналов в моменты времени t1 и t2 имеют следующий вид:
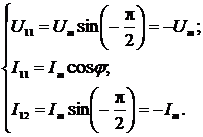 (2.45)
(2.45)
В этом случае выражения для
определения основных ИПГРС примут вид:
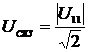 ;
(2.46)
;
(2.46)
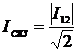 ;
(2.47)
;
(2.47)
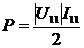 ;
(2.48)
;
(2.48)
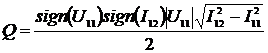 .
(2.49)
.
(2.49)
Информационно-измерительная система,
реализующая метод, представлена на рисунке 2.18.
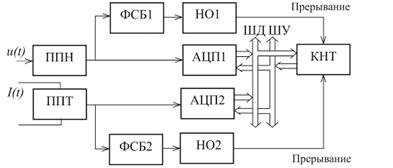
Рис. 2.18. Структурная схема ИИС,
реализующей третий метод
ИИС содержит те же блоки, что и
предшествущие схемы, дополнительно в каналы напряжения и тока добавлены
нуль-органы НО1 и НО2 для определения переходов сигналов через ноль.
В этом методе время измерений также
зависитят от угла сдвига фаз между сигнала напряжения и тока.
Если принимать, что ФСБ в каналах
напряжения и тока имеют угол сдвига фазы равный (90°+Δβ), то выражения для
мгновенных значений сигналов равны:
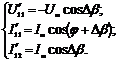 (2.50)
(2.50)
В соответствии с (2.46) - (2.50)
выражения для выявления относительных погрешностей измерения СКЗ напряжения и
тока и приведенных погрешностей измерения АКТМ и РКМ будут иметь вид:
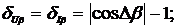 (2.51)
(2.51)
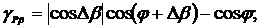 (2.52)
(2.52)
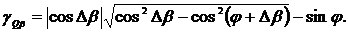 (2.53)
(2.53)
Анализ выражений (2.51) - (2.53)
показывает, что погрешности измерения интегральных характеристик соответсвенно
зависят от отклонения угла сдвига фаз ФСБ от 90°, кроме того, погрешности
измерений АКТМ и РКМ зависят от угла сдвига фаз между сигналами напряжения и
тока φ.
На рис. 2.19 - 2.21 приведены
графики зависимостей погрешностей измерения ИХГРС в соответствии с выражениями
(2.51) - (2.53).
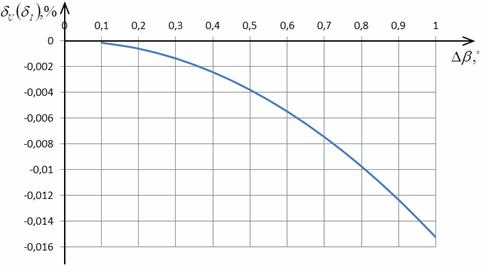
Рис. 2.19. Зависимость погрешности 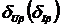 от Δ β
от Δ β
Рис. 2.20. Зависимость погрешности 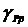 от φ
от φ
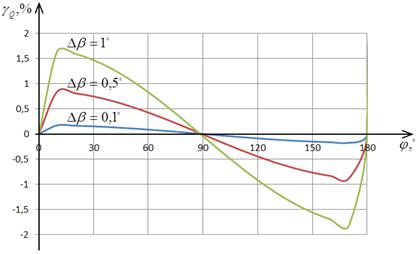
Рис. 2.21. Зависимость погрешности 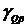 от φ
от φ
Погрешности по модулю ФСБ
отсутствует, так как дополнительные сигналы применяются только для выявления
переходов через ноль.
При отличии правдивого сигнала от
гармонической модели возникает погрешность. К примеру, при наличии пятых
гармоник в сигналах напряжения и тока с коэффициентами hu5=hi5=0,5%,
относительная погрешность измерений СКЗ составляет около 0,5%; приведенная
погрешность определения АКМ изменяется в диапазонах от 0,5 до 1%, принимая
минимальные значения при 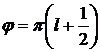 и
максимальные при
и
максимальные при 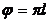 ;
приведенная погрешность измерения РЕМ имеет минимальное значение 1 % при
;
приведенная погрешность измерения РЕМ имеет минимальное значение 1 % при 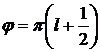 .
.
.5 Метод измерения интегральных
параметров по ортогональным составляющим, связанным с переходами через ноль
входных сигналов напряжения и тока
Четвертый метод построен на
определении ИПГРС по двум мгновенным значениям напряжения и одному мгновенному
значению тока. В данном методе мгновенные значения тока взяты в моменты
перехода через ноль сигнала напряжения, мгновенные значения напряжений взяты
одновременно в момент перехода сигнала тока через ноль, причем второе
мгновенное значение напряжения сдвинуто относительно первого на 90º.
Временные диаграммы, поясняющие
метод, представлены на рисунке 2.22.
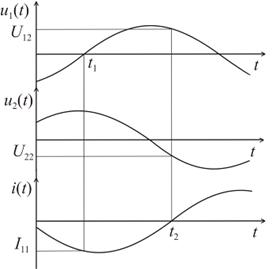
Рис. 2.22. Временные диаграммы,
поясняющие четвертый метод
Для данного метода мгновенные
значения сигналов имеют вид:
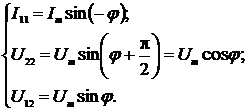 (2.54)
(2.54)
Для гармонических моделей напряжения
и тока примеры для определения интегральных характеристик сигналов имеют такой
вид:
- СКЗ напряжения и
тока:
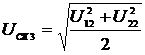 ;
(2.55)
;
(2.55)
 ;
(2.56)
;
(2.56)
АКМ и РЕМ:
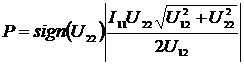 ;
(2.57)
;
(2.57)
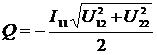 .
(2.58)
.
(2.58)
Рассмотренный метод заметно
сокращает время измерений при φ=0 или φ=π.
Если в моменты перехода сигнал
напряжения через ноль I1=0, то это означает, что угол сдвига фаз между
напряжением и током принимает одно из двух значений: φ1=0 или φ2= π, что соответствует
cosφ1=1 или cosφ2=-1.
В этом случае для определения ИПГРС
производится измерение мгновенных значений тока и напряжения u'(t) в момент
времени t2=t1+Δt.
Временные диаграммы при φ=0 представлены на рисунке
2.23.

Рис. 2.23. Временные диаграммы при φ=0
При этом РКМ приравнена нулю, а
остальные интегральные характеристики определяют в соответствии с выражениями:
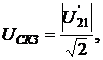 (2.59)
(2.59)
 (2.60)
(2.60)
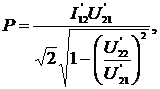 (2.61)
(2.61)
где 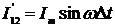 ,
, 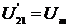 ,
, 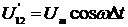 .
.
В данном методе время измерения
также зависит от угла сдвига фаз между сигналами напряжения и тока.
Структурная схема ИИС, реализующей,
метод представленна на рисунке 2.24.
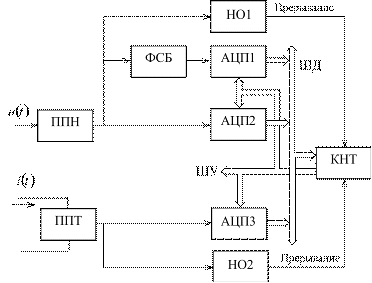
Рис. 2.24. Структурная схема ИИС,
реализующей четвертый метод
В состав ИИС входят так же блоки,
что и у предшествующих схем.
Если считать, что ФСБ в канале
напряжения имеет угол сдвига фазы равный (90°+Δβ),
то выражения для мгновенных значений сигналов равны:
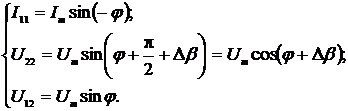 (2.62)
(2.62)
В соответствии с (2.55), (2.56) и
(2.62) относительные погрешности измерения СКЗ напряжения и тока определяется
соответственно выражениями:
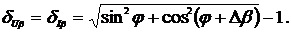 (2.63)
(2.63)
В соответствии с (2.57), (2.58) и
(2.62) приведенные погрешности измерения АКМ и РЕМ соответствуют выражениям:
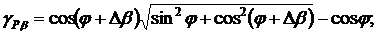 (2.64)
(2.64)
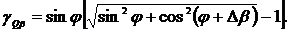 (2.65)
(2.65)
На рис. 2.25 представлены графики
зависимостей относительных погрешностей определения СКЗ напряжения и тока от
угла сдвига фаз между сигналами и отклонения угла сдвига фазы ФСБ от 90° в
соответствии с выражением (2.40).
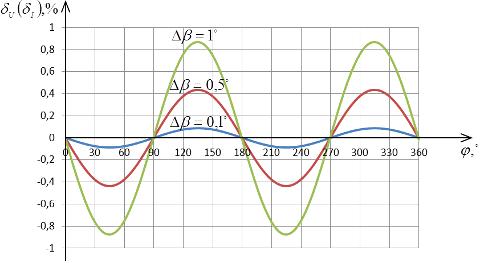
Рис. 2.25. Зависимости погрешностей 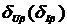 от φ
от φ
Анализируя рис. 2.25 кажется, что
при 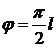 погрешность равна нулю, а при
погрешность равна нулю, а при 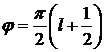 - принимает максимальные значения.
- принимает максимальные значения.
На рис. 2.26 и 2.27 представлены
графики зависимости приведенной погрешности определения АКМ и РЕМ от угла
сдвига фаз между сигналами напряжения и тока в соответствии с выражениями
(2.90) и (2.91) для различных значений угла Δβ.
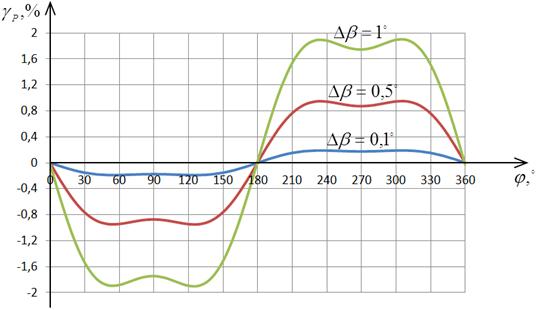
Рис. 2.26
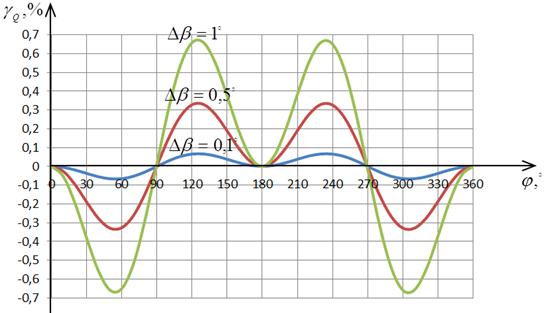
Рис. 2.27. Зависимости погрешностей 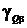 от φ
от φ
Анализ рис. 2.26 указывает, что при
значении 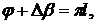 l=0,1,… погрешность имеет минимальные значения.
l=0,1,… погрешность имеет минимальные значения.
Анализ рис. 2.27 указывает, что при 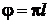 погрешность практически равна нулю, а при
погрешность практически равна нулю, а при 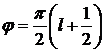 погрешность задает максимальные значения.
погрешность задает максимальные значения.
Когда амплитудное значение сигнала
на выходе ФСБ в канале напряжения отличаются от входного на величину ΔUm, то мгновенное значение
дополнительного напряжения будет иметь вид: 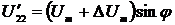 .
.
Предельные значения абсолютных
погрешностей измерения СКЗ напряжения и тока, АКМ и РЕМ имеют вид:
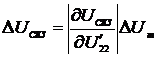 ;
(2.66)
;
(2.66)
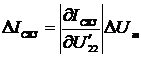 ;
(2.67)
;
(2.67)
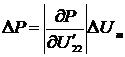 ;
(2.68)
;
(2.68)
 .
(2.69)
.
(2.69)
Используя (2.55) - (2.58), с учетом
абсолютных погрешностей (2.66) - (2.69) можно определить относительные
погрешности измерения СКЗ напряжения и тока и приведенные погрешности
определения АКМ и РЕМ (при φ≠πl):
 ;
(2.70)
;
(2.70)
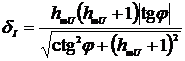 ;
(2.71)
;
(2.71)
 ;
(2.72)
;
(2.72)
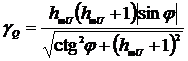 .
(2.73)
.
(2.73)
Анализ выражений (2.70) - (2.73)
указывает, что погрешности определения ИПГРС зависят не только от погрешности
по модулю ФСБ в канале напряжения, но и от угла сдвига фаз между сигналами
напряжения и тока φ.
На рис. 2.28 - 2.31 предоставлены
графики зависимостей относительного погрешностей определения СКЗ напряжении и
тока и приведенных погрешностей измерений АКМ и РЕМ от угла сдвига фаз между
сигналами φ при
hmU=hmI=0,05%.
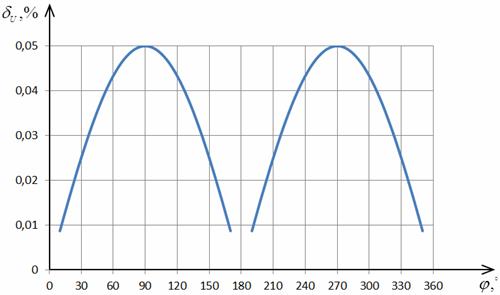
Рис. 2.28. Зависимость погрешности 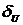 от φ
от φ
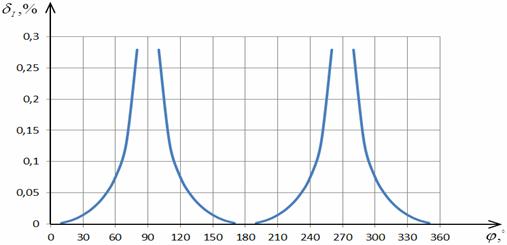
Рис. 2.29. Зависимость погрешности 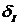 от φ
от φ
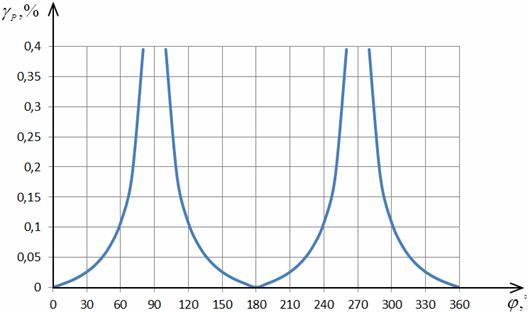
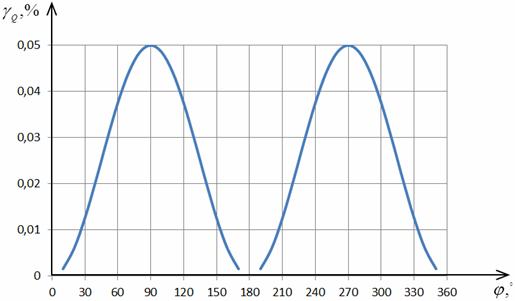
Рис. 2.31. Зависимость погрешности 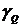 от φ
от φ
Анализ показывает прибыль
погрешностей при углах сдвига фаз между сигналом напряжения и тока в пределах φ=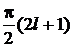 .
.
При наличии в сигналах высших
гармоник появляется погрешность. Например, при hu5=hi5=0,5% относительные
погрешности измерения СКЗ напряжения и тока имеют минимальные значения, равные
0,22% и 0,5% соответственно. Приведенные погрешности измерения АКМ и РЕМ при
тех же значениях коэффициенты пятых гармоник равно 0 и 1% соответственно.
.6 Метод измерения интегральных
параметров по мгновенным значениям ортогональных составляющих сигналов,
измеренным в произвольный момент времени
Пятый метод основан на определении
интегральных характеристик сигналов по двум мгновенным значениям напряжения и
тока, одновременно измеренным в произвольный момент времени, причем вторые
мгновенные значения напряжения и тока сдвинуты относительно первых на угол 90°
в сторону опережения.
Если сигналы напряжения и тока в
исследуемой цепи имеют гармонические модели, то их точные значения в
произвольный момент времени t1 равны:
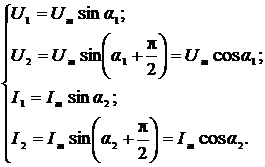 (2.74)
(2.74)
Выражения для определения ИПГРС
принимают следующий вид:
- СКЗ напряжения и
тока:
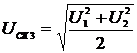 ;
(2.75)
;
(2.75)
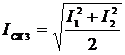 ;
(2.76)
;
(2.76)
АКМ и РЕМ:
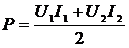 ;
(2.77)
;
(2.77)
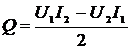 .
(2.78)
.
(2.78)
Временные диаграммы, поясняющие
метод, приведены на рисунке 2.32.
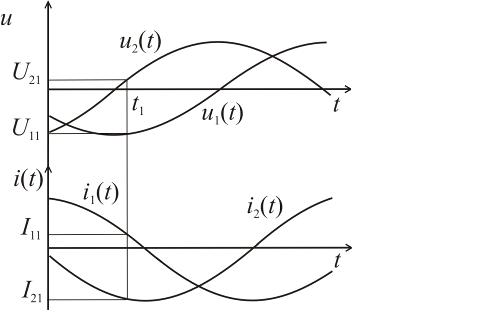
Рис. 2.32. Временные диаграммы,
поясняющие пятый метод ИИС, реализующая метод, представлена на рисунке 2.33
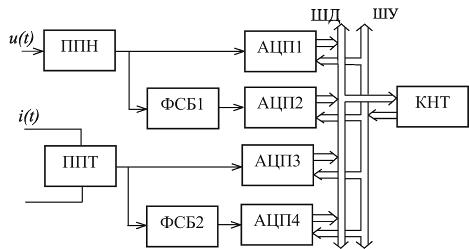
Рис. 2.33. ИИС, реализующая пятый
метод
Время измерений ИПГРС в данной ИИС
не зависит от момента начала измерения и угла сдвига фаз между током и
напряжением, а определяется только временем аналого-цифрового преобразования
мгновенных значений сигналов, ввода кодов в контроллер и выполнения
вычислительных операций.
В связи с наличием в составе схемы
ФСБ, методу свойственна угловая погрешность. Значения погрешностей измерения
ИПГРС похожи приведенным в разделе 2.3.
Если амплитудное значение сигнала на
выходе ФСБ в канале напряжения отличное от входного на величину ΔUm, то мгновенное значение
дополнительного напряжения примет вид: 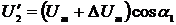 . Так же, при отличии дополнительного тока от входногых на величины ΔIm, мгновенные значения
дополнительного сигнала будут равны
. Так же, при отличии дополнительного тока от входногых на величины ΔIm, мгновенные значения
дополнительного сигнала будут равны 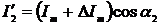 .
.
Предельные значения абсолютных
погрешностей измерения СКЗ напряжения тока, АКТМ и РКМ примут вид:
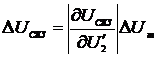 ;
(2.79)
;
(2.79)
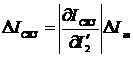 ;
(2.80)
;
(2.80)
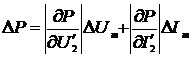 ;
(2.81)
;
(2.81)
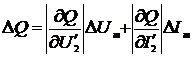 .
(2.82)
.
(2.82)
Используя (2.75) - (2.78), с учетом
абсолютных погрешностей (2.79) - (2.82) возможно определить относительные
погрешность измерений СКЗ напряжения и тока и приведенная погрешности
определения АКМ и РЕМ:
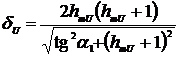 ;
(2.83)
;
(2.83)
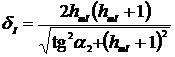 ;
(2.84)
;
(2.84)
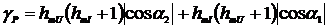 ;
(2.85)
;
(2.85)
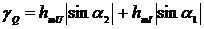 .
(2.86)
.
(2.86)
Графики зависимостей относительных
погрешностей измерений СКЗ напряжения и тока похожи представленным на рисунке
2.22.
На рис. 2.34 и 2.35 представлены
графики зависимостей приведенных погрешности определения АКМ и РЕМ от α1 и α2 при hmU= hmI =0,05%.
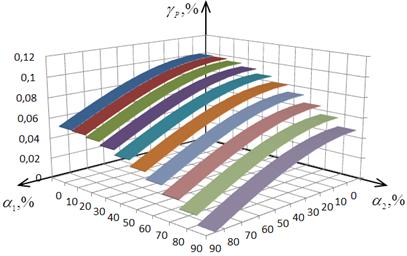
Рис. 2.34. Зависимость погрешности γP от α1 и α2
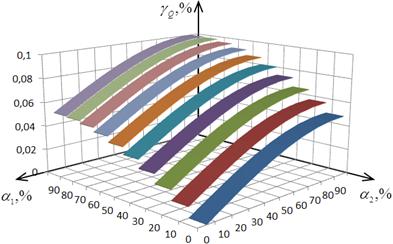
Рис. 2.35. Зависимость погрешности γQ от α1 и α2
Анализ графиков (рис. 2.34 и 2.35)
указывает на уменьшение погрешности измерения АКМ и увеличение погрешностей
определения РЕМ с ростом α1 и α2.
При разности реального сигнала от
гармонической модели появляется погрешность [56]. К примеру, при наличии пятой
гармоник в сигналах напряжения и тока с коэффициентами hu5=hi5=0,5%,
относительно погрешности измерения СКЗ принимает минимальное значение, равное
0,5% при 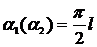 и максимальное 0,7% при
и максимальное 0,7% при 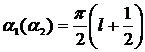 ; приведенная погрешность измерения АКМ и РЕМ зависит от начальнго
фаз сигнала и принимает минимальные значения, равные 1 % при
; приведенная погрешность измерения АКМ и РЕМ зависит от начальнго
фаз сигнала и принимает минимальные значения, равные 1 % при 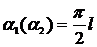 .
.
.7 Метод измерения интегральных
параметров по мгновенным значениям входных и дополнительных сигналов, сдвинутых
на произвольный угол
Метод основан на
том, что в любой момент времени одновременно измеряют три мгновенных значения
напряжения и тока, при том вторые мгновенные значения напряжения и тока
сдвинуты в отношении первых на угол Δα,
а третьи мгновенные значения напряжения и тока отличны
относительно вторых на угол Δα. ИПГРС определяют по измеренным мгновенным значениям сигналов.
Если сигналы
напряжения и тока в исследуемых цепях имеют гармонические модели, то их
мгновенные значения равняются:
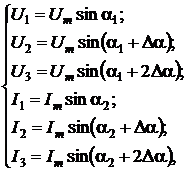 (2.87)
(2.87)
где 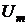 ,
,  -
амплитудные значения напряжения и тока;
-
амплитудные значения напряжения и тока; 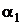 ,
, 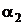 -
начальные фазы сигналов напряжения и тока.
-
начальные фазы сигналов напряжения и тока.
Временные диаграммы, поясняющие
метод, приведены на рисунке 2.36.
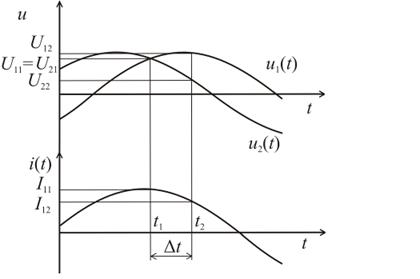
Рис. 2.36. Временные диаграммы,
поясняющие метод
ИПГРС в
соответствии с (2.87) определяются в соответствии выражениям:
среднеквадратические
значения СКЗ напряжения и тока:
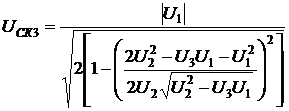 ;
(2.88)
;
(2.88)
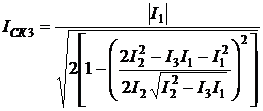 ;
(2.89)
;
(2.89)
активная (АКТМ) и
реактивная (РКМ) мощности:
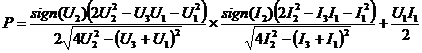 ;
(2.90)
;
(2.90)
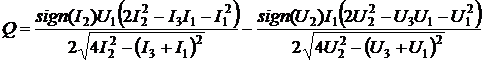 .
(2.91)
.
(2.91)
Для анализа погрешностей из-за
отклонений реальных сигналов от гармонической модели используют рассмотренную
выше методику. Тогда в соответствии с (2.87) - (2.90) относительные погрешности
определения СКЗ сигналов и приведенные погрешности измерения АКМ и РЕМ будут
равняться:
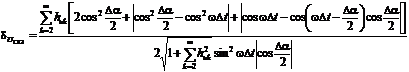 ;
;
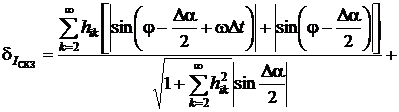
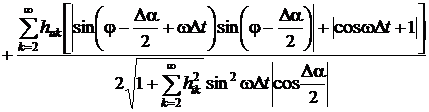 ;
;
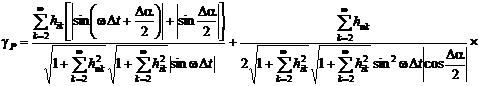
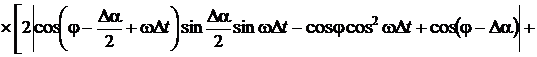
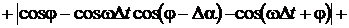
 ;
;
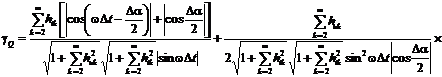
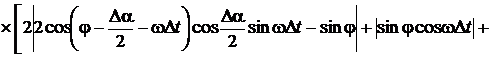
 .
.
Анализ данных выражений поясняет,
что относительная погрешность измерения СКЗ напряжения зависит только от
спектра сигнала, временного интервала Δt и угла сдвига фазы ФCБ Δα.
Погрешности определения остальных параметров зависит еще и от угла
сдвигов фазы между напряжениями и током φ.
При проветке метода
для формирования дополнительных сигналов напряжения и тока используют
фазосдвигающие блоки. Из-за не идеальности ФСБ возможно появление погрешности
по модулю блока, что может вести к большой потери точности измерений ИПГРС.
Если брать, что
погрешность по модулю ФСБ1 и ФСБ2 в канале напряжения, ФСБ3 и ФСБ4 в канале
тока все равны, то считается, что амплитудные значения сигналов на выходе ФСБ1
(ФСБ2) не похожи на амплитуду сигнала на их входе на величину ΔUm, а амплитудные значения
сигналов на выходе ФСБ3 (ФСБ4) отличаются от амплитуды сигнала на их входе на
значение ΔIm.
В таком случае
мгновенные значения дополнительных напряжений и токов будут иметь вид:
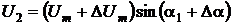 ;
; 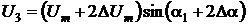 ;
;
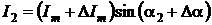 ;
; 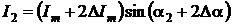 .
.
Одним из главных недостатков средств
измерений, реализующих данный метод и использующих мгновенные значения как
входного, так и дополнительного напряжений, будут погрешности по напряжению
(погрешность по модулю) ФСБ.
В том случае, если амплитудное
значение напряжения на выходе фазосдвигающего блока отличное от амплитуды
входного сигнала на величину 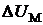 , то
мгновенные значения дополнительного сигнала будут иметь вид:
, то
мгновенные значения дополнительного сигнала будут иметь вид:
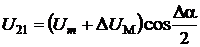 ,
, 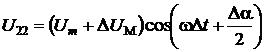 .
.
В том случае для характеристики
точности измерения ИХГРС можно рассматривать методику определения
результирующей погрешности, как погрешности вычисления значения функции,
аргументы которой заданы близко, с погрешностями, соответствующими разности
амплитудных значений сигнала на входе и выходе ФСБ.
Если думать, что мгновенные значения
входного напряжения измерены без погрешности, то возможно определить конечные
значения абсолютных погрешностей измерения СКЗ напряжения и тока, АКТМ и РКМ:
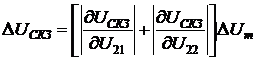 ;
(2.92)
;
(2.92)
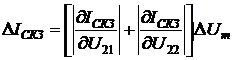 ;
(2.93)
;
(2.93)
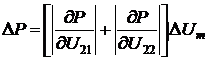 ;
(2.94)
;
(2.94)
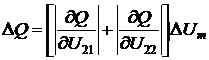 .
(2.95)
.
(2.95)
Используя (2.87) - (2.91) и
абсолютные погрешности (2.92) - (2.95), можно определить относительные
погрешности определения СКЗ напряжения и тока и АКМ и РЕМ:
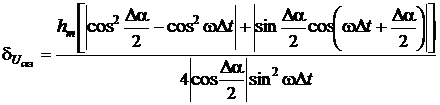 ;
(2.96)
;
(2.96)
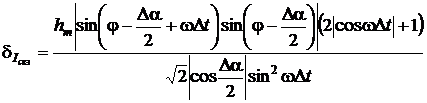 ;
(2.97)
;
(2.97)
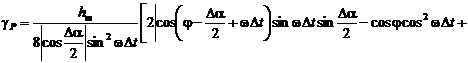
 ;
(2.98)
;
(2.98)
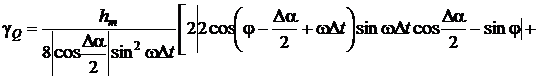
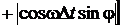 ,
(2.99)
,
(2.99)
где:
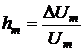 .
.
Характеристика выражения (2.96)
указывает, что погрешность измерения СКЗ напряжения зависит от погрешности по
модулю фазо-сдвигающего блока hm, угла сдвига ФСБ Δα и интервала времени
Δt.
Исходя из выражений (2.97) - (2.99)
следует, что погрешности определения СКЗ тока, АКТМ и РКМ зависят не только от
hm, Δα и Δt, но и угла сдвига фазы
между напряжением и током φ.
На рис. 2.37 видны графики
зависимости относительной погрешности определения СКЗ напряжения от Δα и ωΔt в соответствии с
(2.97) при hm=0,1%.
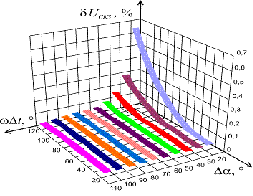
Рис. 2.37. Графики зависимости δUскз от Δα и ωΔt
На рис. 2.38 - 2.40 показаны графики
зависимостей относительной погрешности определения СКЗ тока и приведенных
погрешностей измерения АКТМ и РКМ от Δα
и ωΔt при hm=0,1% для φ=0°.
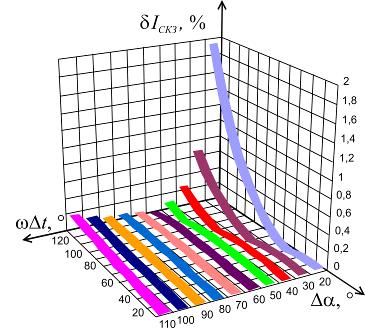
Рис. 2.38. Графики зависимости δIскз от Δα и ωΔt для φ=0°
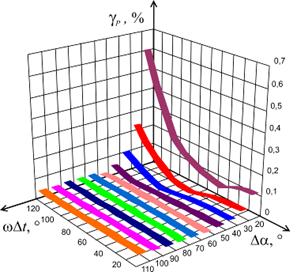
Рис. 2.39. Графики зависимости γP от Δα и ωΔt для φ=0°
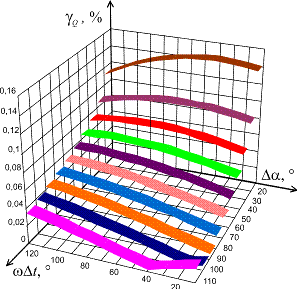
Рис. 2.40. Графики зависимости γQ от Δα и ωΔt для φ=0°
Анализ рис. 2.37 - 2.40 указывает на
существенную зависимость погрешностей определения ИХГРС от угла сдвига фазы ФСБ
Δα и соотношения между
интервалами времени Δt и периодами сигналов, то есть ωΔt.
При том меньшие значения погрешностей, в общем случае, имеют место
быть при ωΔt=60÷100º.
При малых значениях ωΔt погрешности
определения СКЗ сигналов и АКТМ в большей мере зависят от угла Δα.
.8 Основные результаты и выводы
. Рассмотренные в работе
исследования показывают, что для определения интегральных параметров
периодических сигналов может быть успешно адаптирован аппроксимационный подход,
который заключается в определении информативных параметров по отдельным
мгновенным значениям сигналов, не связанным с периодом сигнала, в предположении
их соответствия известным моделям с последующей оценкой погрешностей,
обусловленных отклонением принятых моделей от реальных сигналов
. Анализ методов измерения
интегральных параметров на основе использования мгновенных значений ортогональных
составляющих сигналов показал, что всем методам присуща существенная
погрешность, обусловленная отклонением реального сигнала от гармонической
модели.
При этом наименьшие значения
погрешностей обеспечивает метод, основанный на определении интегральных характеристик
по двум мгновенным значениям напряжения и одному мгновенному значению тока.
. При реализации рассмотренных
методов могут возникнуть погрешности, обусловленные не идеальностью
фазосдвигающих блоков, осуществляющих формирование дополнительных сигналов.
. Наименьшее время измерения
обеспечивает пятый метод определения ИПГРС по мгновенным значениям
ортогональных составляющих сигналов, измеренным в произвольный момент времени.
. Исключение частотной погрешности,
приводящей к отклонению угла сдвига фазы дополнительного сигнала от 90º, обеспечивают методы,
основанные на формирование дополнительных сигналов, сдвинутых относительно
входных на произвольный угол.
. Проведенный анализ показал, что
для повышения точности измерения необходимо разработать новые аппроксимационные
методы и системы определения интегральных параметров при сохранении высокого
быстродействия.
3. Разработка и исследование методов
и систем измерения параметров гармонических сигналов с улучшенными
метрологическими характеристиками
В третьей главе рассматриваются и
исследуются новые методы и средства решения ИПГРС, реализация которых
гарантирует повышение точности измерения. Как было замечено выше, значительным
недостатком информационно-измерительных систем, реализующих методы, использующие
формирование дополнительных ортогональных сигналов, является частотная
погрешность фазосдвигающих блоков. Погрешность заключается в отклонении угла
сдвига дополнительного сигнала от 90° при изменении частоты входного сигнала.
3.1 Метод измерения интегральных
параметров на основе сравнения мгновенных значений гармонических сигналов,
распределенных в пространстве
Значительное сокращение времени
измерений обеспечивает методы, основанные на формировании дополнительных
сигналов, сдвинутых по фазе на любой, в общем случае, угол относительно
входного сигнала, и определении интегральные характеристики по мгновенным
значениям входного и дополнительного сигнала. При этом проиходит
пространственное разделение мгновенных значений сигналов.
Новый метод
измерений ИПГРС исключает влияние частотной погрешности на конечный результат
определения интегральных параметров. В методе используется формирование двух
дополнительных сигналов, сдвинутых на одинаковые произвольные (в общем случае)
углы, и сравнение их мгновенных значений.
Метод основан на
формировании двух дополнительных сигналов напряжения и тока, сдвинутых по фазе
на углы Δα и 2Δα относительно
входных, и сравнении основного и дополнительных сигналов напряжения и тока.
Притом, в момент равенства мгновенных значений основных и, сдвинутых
относительно него на 2Δα, дополнительного сигнала напряжения измеряют мгновенное значение
напряжений, сдвинутых относительно основного сигнала на какой то угол Δα. В этот же момент
времени измеряется мгновенное значение дополнительных сигналов тока, сдвинутых
относительно основного сигнала на Δα.
В момент равенства мгновенных значений основного и, сдвинутого
относительно него на 2Δα, дополнительного тока измеряют точное значение сигнала тока,
сдвинутого относительно главного сигнала на угол Δα.
ИПГРС определяют по измеренным мгновенным значениям сигналов
напряжения и тока.
Временные
диаграммы, поясняющие метод, приведены на рисунке 3.1.
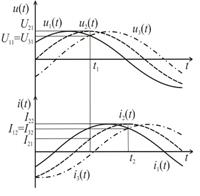
Рис. 3.1. Временные диаграммы,
поясняющие метод
В момент времени 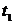 , когда
, когда 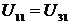 ,
мгновенное значение главного сигнала напряжения
,
мгновенное значение главного сигнала напряжения 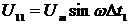 (где
(где 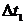 -
интервал времени, пропорциональный начальной фазе сигнала), а мгновенные
значения первого и второго дополнительных сигналов будут равнятся:
-
интервал времени, пропорциональный начальной фазе сигнала), а мгновенные
значения первого и второго дополнительных сигналов будут равнятся: 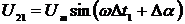 и
и 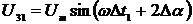 .
.
Равенство мгновенных значений
сигналов 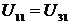 выполняется в том случае, если
выполняется в том случае, если 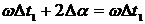 (
(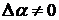 ), то
есть, когда
), то
есть, когда 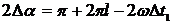 или
или 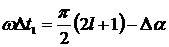 , где l=0, 1. Отсюда
, где l=0, 1. Отсюда 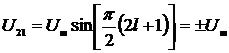 .
.
Среднеквадратическое значение
напряжения равняется:
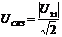 . (3.1)
. (3.1)
В момент времени 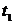 мгновенное значение дополнительного сигнала тока
мгновенное значение дополнительного сигнала тока 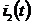 будет равняться:
будет равняться:
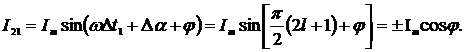
В момент времени 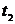 , когда
, когда 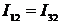 , по
принципу с напряжением, мгновенные значения основногых и дополнительных
сигналов будут равны:
, по
принципу с напряжением, мгновенные значения основногых и дополнительных
сигналов будут равны: 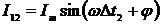 ;
; 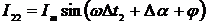 и
и 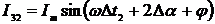 (где
(где 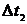 - интервал времени между переходом сигнала
- интервал времени между переходом сигнала 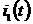 через ноль до момента времени
через ноль до момента времени 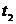 ).
).
Равенство мгновенных значений
сигналов 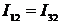 выполняется в том случае, когда
выполняется в том случае, когда 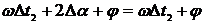 , то есть, когда
, то есть, когда 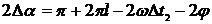 или
или 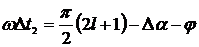 . Отсюда
. Отсюда 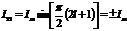 .
.
Среднеквадратическое значение тока
равняется:
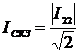 . (3.2)
. (3.2)
Активная и реактивная мощности
определяются следующими выражениями:
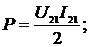 (3.3)
(3.3)
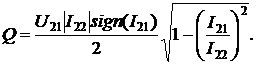 (3.4)
(3.4)
Если в момент времени 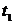 мгновенное значение тока
мгновенное значение тока 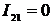 , то это означает, что
, то это означает, что 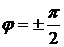 .
.
В этом случае определение угла сдвига
фаз производится таким образом.
Если измерение мгновенного значения
напряжения 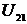 вышло
раньше, чем мгновенного значения тока
вышло
раньше, чем мгновенного значения тока 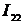 и знаки равны, т.е.
и знаки равны, т.е. 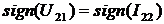 , то
, то 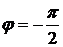 . Если
измерение
. Если
измерение 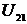 произошло
прежде, чем
произошло
прежде, чем 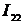 и
знаки отличны, то
и
знаки отличны, то 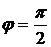 , т.е.
, т.е. 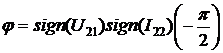 .
.
Если измерение мгновенного значения
тока 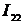 произошло прежде, чем мгновенного значения напряжения
произошло прежде, чем мгновенного значения напряжения 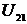 и знаки равны, то
и знаки равны, то 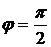 . Если
измерение
. Если
измерение 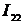 произошло
прежде, чем
произошло
прежде, чем 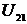 и
знаки отличны, то
и
знаки отличны, то 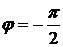 , т.е.
, т.е. 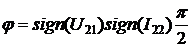 .
.
При углах сдвига фаз между сигналами
напряжения и тока φ>Δα рассмотренный метод обеспечивает время измерения 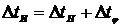 , где
, где 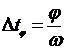 ;
; 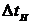 - промежуток времени с момента начала измерений до момента
равенства основного и, сдвинутого по отношению его на 2Dα, дополнительного сигнала
напряжения.
- промежуток времени с момента начала измерений до момента
равенства основного и, сдвинутого по отношению его на 2Dα, дополнительного сигнала
напряжения.
Схема ИИС, реализирующий метод,
показана на рисунке 3.2.

Рис. 3.2. ИИС, реализующая метод
ИИС содержит: первые преобразователи
напряжения ППН и тока ППТ, четыре фазосдвигающих блока ФСБ1 - ФСБ4,
осуществляющие сдвиг сигналов на угол Dα, два сравнивающих
устройства СУ1 и СУ2, два аналого-цифровых преобразователя АЦП1 и АЦП2,
контроллер КНТ, шины управления ШУ и данных ШД.
В моменты времени 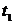 (рис. 3.1), когда сигнал напряжения
(рис. 3.1), когда сигнал напряжения 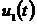 и
и 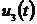 будут
равны, задействовано сравнивающее устройство СУ1, на выходе которого образкется
импульс, поступающий на вход прерывания КНТ. Контроллер пускает АЦП1, на входе
которого в этот промежуток времени действует сигнал напряжения
будут
равны, задействовано сравнивающее устройство СУ1, на выходе которого образкется
импульс, поступающий на вход прерывания КНТ. Контроллер пускает АЦП1, на входе
которого в этот промежуток времени действует сигнал напряжения 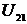 , равный амплитудному значению входного напряжения.
Аналого-цифровой преобразователь образует этот сигнал в код, который
сохраняется в оперативную память КНТ. В тот же момент с помощью АЦП2
производится трансформация в код мгновенного значений сигнала, пропорциональных
мгновенному значений тока
, равный амплитудному значению входного напряжения.
Аналого-цифровой преобразователь образует этот сигнал в код, который
сохраняется в оперативную память КНТ. В тот же момент с помощью АЦП2
производится трансформация в код мгновенного значений сигнала, пропорциональных
мгновенному значений тока 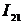 .
.
В момент времени 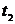 (рис. 3.1), когда сигналы напряжения, пропорциональные сигналу
тока
(рис. 3.1), когда сигналы напряжения, пропорциональные сигналу
тока 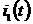 и
и 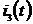 будут
равны, срабатывают сравнивающие устройства СУ2, на выходе которых формируется
импульс, поступающий на вход прерывания КНТ. Контроллер пускает АЦП2, на входе
котортого в это промежуток времени срабатывает сигнал напряжения,
пропорциональный мгновенному значению
будут
равны, срабатывают сравнивающие устройства СУ2, на выходе которых формируется
импульс, поступающий на вход прерывания КНТ. Контроллер пускает АЦП2, на входе
котортого в это промежуток времени срабатывает сигнал напряжения,
пропорциональный мгновенному значению 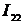 , т.е. амплитудному значению входного сигнала тока.
Аналого-цифровой преобразователь образует этот сигнал в код, который
сохраняется в оперативную память КНТ.
, т.е. амплитудному значению входного сигнала тока.
Аналого-цифровой преобразователь образует этот сигнал в код, который
сохраняется в оперативную память КНТ.
В КНТ вычисляются в соответствии с
выражениями (3.1) - (3.4).
.2 Метод измерения интегральных
характеристик гармонических сигналов с коррекцией погрешности формирования
дополнительного сигнала
Рассмотренный выше метод
обеспечивает исключение влияния частотной погрешности ФСБ. Однако при
реализации подобных методов неизбежно возникает погрешность по модулю
фазосдвигающих блоков, обусловленная отличием амплитуд входного и
дополнительных сигналов.
Разработан новый метод к определению
ИПГРС, исключающийся данный вид погрешности и основанный на использовании
коррекции мгновенных значений сигналов.
Метод заключается в том, что когда
будет переход входного тока через ноль измеряют первое мгновенное значение
входного напряжения; во время перехода дополнительного сигнала напряжения,
сдвинутого по фазе относительно входного на любой (в общем случае) угол Δα, через ноль
одновременно измеряется второе мгновенное значение входного напряжения и первое
мгновенное значение тока; в момент перехода входного сигнала напряжения через
ноль измеряется второе мгновенное значение тока. ИПГРС определяют по измеренным
мгновенным значениям сигналов.
Временные диаграммы, поясняют метод,
представлены они на рисунке 3.3.
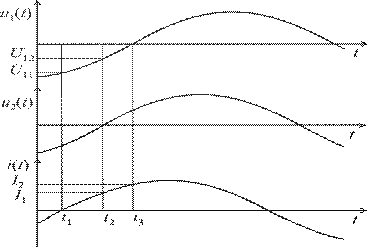
Рис. 3.3. Временные
диаграммы, поясняющие второй метод
При гармонических моделях входной и
дополнительный сигналы напряжения и тока равны следующим выражениям:
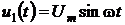 ;
;  ;
; 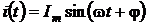 ,
,
где 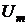 ,
, 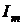 -
амплитудные коэфициенты напряжения и тока; ω - угловая частота входного сигнала; φ
- угол сдвига фаз между входными сигналами напряжения и тока.
-
амплитудные коэфициенты напряжения и тока; ω - угловая частота входного сигнала; φ
- угол сдвига фаз между входными сигналами напряжения и тока.
В момент времени t1 перехода сигнала
тока через ноль, мгновенное значение входного напряжения 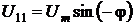 .
.
В момент времени t2 перехода
дополнительного напряжения через ноль, мгновенные значения входного напряжения
и тока равны:
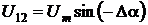 ;
;  .
.
В момент времени t3 перехода
входного напряжения через ноль, мгновенное значение тока 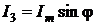 .
.
Определим следующий коэффициент 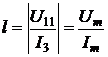 , выражающий соотношение между амплитудой значения, напряжения и
тока.
, выражающий соотношение между амплитудой значения, напряжения и
тока.
С помощью этого коэффициента
возможно вычислить значение напряжения 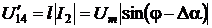 .
.
Использовать мгновенные значения
сигнала и выбирать угол сдвига фазы дополнительного сигнала Δα<90°,
возможно получить соотношения для определения основных ИПГРС:
среднеквадратические значения СКЗ
напряжения и тока:
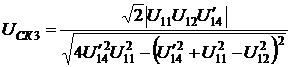 ; (3.5)
; (3.5)
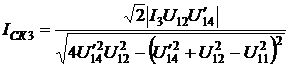 ; (3.6)
; (3.6)
активная и реактивная мощности:
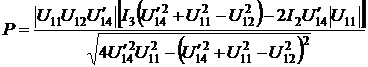 ; (3.7)
; (3.7)
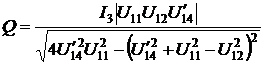 . (3.8)
. (3.8)
Определение ИПГРС в соответствии с
(3.5) - (3.7) справедливо только в том случае, если 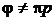 , где p=0; 1.
, где p=0; 1.
В случае, если 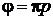 , измерение параметров производится следующим образом.
, измерение параметров производится следующим образом.
Временные диаграммы для угла сдвига
фаз между напряжением и током φ=0 приведены на рисунке 3.4.
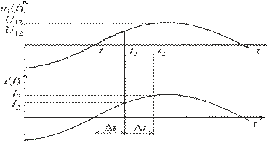
Рис. 3.4. Временные диаграммы, поясняющие
метод при φ=0
Когда в момент времени  входные сигналы напряжения и тока одновременно становятся больше
чем ноль, то измеряется мгновенное значение сигнала через произвольный (в общем
случае) интервал времени Δt.
входные сигналы напряжения и тока одновременно становятся больше
чем ноль, то измеряется мгновенное значение сигнала через произвольный (в общем
случае) интервал времени Δt.
Через интервал времени Δt (в момент времени 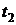 ) мгновенные значения входного напряжения и тока будут равны:
) мгновенные значения входного напряжения и тока будут равны:
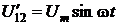 ;
; 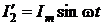 .
.
Через интервалы времени 2Δt (в момент времени 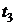 ) мгновенные значения сигнала примет вид:
) мгновенные значения сигнала примет вид:
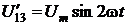 ;
; 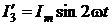 .
.
Использовать мгновенные значения
сигналов, можно определив СКЗ напряжения и тока:
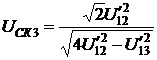 ;
; 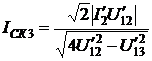 .
.
Если знаки вторых мгновенных
значений входного сигнала напряжения и тока совпадают (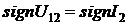 ), то φ=0. При этом активная мощность
), то φ=0. При этом активная мощность 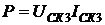 , а реактивная мощность Q=0.
, а реактивная мощность Q=0.
Если вторые мгновенные значения
входных сигналов напряжения и тока имеют противоположные знаки (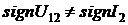 ), то φ=π. При том АКТМ
), то φ=π. При том АКТМ 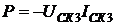 , а РКМ
Q=0.
, а РКМ
Q=0.
Схема ИИС, использующего метод,
приведена на рисунке 3.5.
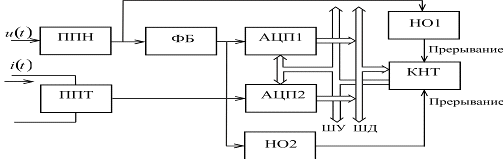
Рис. 3.5. ИИС, реализующая второй
метод
ИИС содержит: первые преобразователи
напряжения ППН и тока ППТ, фазосдвигающий блок ФСБ, дающий сдвиг сигнала
напряжения на угол Dα, два нуль-органа НО1 и НО2, два аналого-цифровых преобразователя
АЦП1 и АЦП2, контроллер КНТ, шины управления ШУ и данных ШД.
В этом методе не используют
мгновенные значения дополнительного сигнала напряжения, а только его переход
через ноль, что исключает погрешность по модулю фазосдвигающего блока. Кроме
того, углы сдвига фазы ФБ Δα могут быть выбраны произвольными 0<Δα<90°, что не
приведет к угловой погрешности фазосдвигающего блока.
3.3 Основные результаты и выводы
. Разработан первый метод
определения ИПГРС на основе сравнения мгновенных знаков гармонических сигналов
не определяет выявление свойственных точек сигналов, что решает сократить время
измерений при больших значениях угла сдвига фаз между напряжением и током.
. Осуществление разработанного
метода измерения ИПГРС помогает исключить частотную погрешность фазосдвигающих
блоков, также уменьшить погрешность из-за отклонения метрологических
характеристик аналого-цифровых преобразователей, так как разумеет собой
использование только по одному АЦП в путях напряжения и тока.
. Второму разработанному методу
сопутствует полное исключение погрешности по модулю фазосдвигающего блока за
счет коррекции мгновенного значения напряжения.
. Реализация этого метода
обеспечивает сокращение других затрат, поскольку также возможно использование
только по одному АЦП в каналах напряжения и тока. Кроме того, в данном случае
используется только один фазосдвигающий блок.
4. Анализ погрешностей разработанных
методов и систем измерения параметров гармонических сигналов
.1 Анализ погрешностей методов
определения интегральных параметров из-за отклонения реального сигналов от
гармонической модели
Разработанные методы предназначены
для выявления интегральных характеристик в цепях с гармоническими напряжениями
и токами. Потому есть необходимость оценки погрешности метода из-за
несоответствия модели реальному сигналу.
Для анализа этого вида погрешности
есть смысл взять рассмотренную в первой главе методику свойства погрешности
результата измерения интегральной свойств как функции, аргументы которой заданы
приблизиткльно с погрешностью, соответствующей отклонению модели от реального
сигнала, с помощью дифференциала этой функции.
Для первого метода абсолютная
погрешность определения СКЗ напряжения и тока, АКТМ и РКМ в соответствии с
выражениями (3.1) - (3.4) равна:
 (4.1)
(4.1)
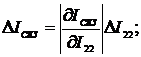 (4.2)
(4.2)
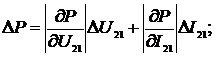 (4.3)
(4.3)
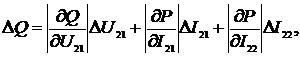 (4.4)
(4.4)
где DU21, DI21 и DI22 - отклонение мгновенного знаков реальных сигналов напряжения и
тока от гармонической модели в соответствующий момент времени.
Если считать, что абсолютная
погрешность аргументов соответствуюет наибольшему отклонению в момент времени
t1 и t2, то предельные абсолютные погрешности принимают вид:
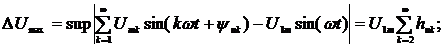 (4.5)
(4.5)
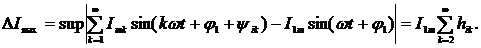 (4.6)
(4.6)
Используя (4.1) - (4.6), получим
значение для относительной погрешности определения СКЗ напряжения и тока и
значение для приведенной погрешности определения активной и реактивной
мощностей:
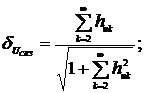 (4.7)
(4.7)
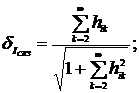 (4.8)
(4.8)
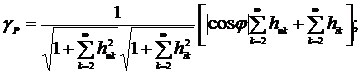 (4.9)
(4.9)
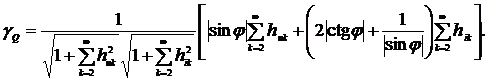 (4.10)
(4.10)
Анализ выражений (4.7) - (4.10)
показывает, что погрешность определений ИПС не зависит от угла сдвига дополнительных
сигнала напряжений и тока относительно выходных сигналов. Кроме того,
погрешность измерения СКЗ сигнала зависят только от спектра сигнала.
Зная спектры реального сигнала, с
помощью выражений (4.7) - (4.10) можно оценить предельное значение относительного
измерения СКЗ напряжения и тока.
На рис. 4.1 и 4.2 привидены графики
зависимостей γP и
γQ от угла сдвига фаз между
напряжением и током, при возникновении в сигналах 1-й и 5-й гармоник с
hu5=0,002 и hi5=0,004.
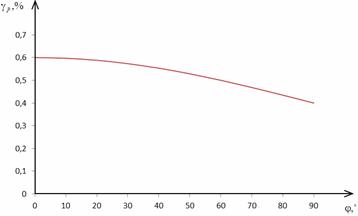
Рис. 4.1. График зависимости γP от φ при наличии в сигналах
1-й и 5-й гармоник с hu5=0,002 и hi5=0,004
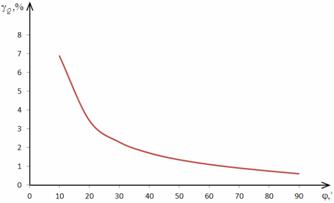
Рис. 4.2. График зависимости γQ от φ при наличии в сигналах
1-й и 5-й гармоник с hu5=0,002 и hi5=0,004
Анализ выражений (4.7) - (4.10) и
рис. 4.1 и 4.2 показывает, что при изменении формы сигнала возникает
погрешность определения интегральных характеристик сигналов, значений которых
значительно зависят от спектра сигнала и угла сдвига фаз между напряжением и
током (кроме СКЗ сигналов).
С увеличением угла сдвига фаз φ приведенные погрешности
измерения АКМ и РЕМ снижается и достигает минимального значения при φ=90°.
Если считать, что предельная
абсолютная погрешность аргументов соответствуюет отклонению модели от реального
сигнала, определяет через среднеквадратичную погрешность, то:
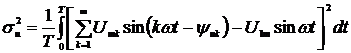 ;
(4.11)
;
(4.11)
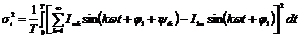 .
(4.12)
.
(4.12)
Если параметры первых гармоник
реального сигнала совпадут с параметрами сигнала, соответствующего гармонической
модели, то, в силу ортогональности тригонометрических функций, выражения (4.11)
и (4.12) приведутся к виду:
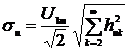 ;
(4.13)
;
(4.13)
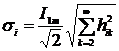 ,
(4.14)
,
(4.14)
т.е. (4.13) соответствует
среднеквадратическому значению высших гармоник сигнала напряжения UГ, а (4.14)
- СКЗ высших гармоник тока IГ.
Предельные значения абсолютной
погрешности определения интегральных характеристик сигнала будут равны:
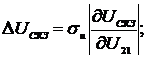 (4.15)
(4.15)
 (4.16)
(4.16)
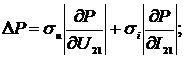 (4.17)
(4.17)
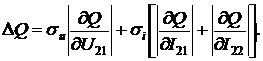 (4.18)
(4.18)
Используя (4.15) - (4.18), в
соответствии с (3.1) - (3.4) получим выражения для относительной погрешности
определения СКЗ напряжения и тока и выражения для приведенной погрешности
измерения активной и реактивной мощности:
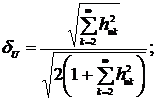 (4.19)
(4.19)
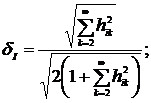 (4.20)
(4.20)
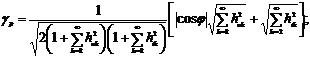 (4.21)
(4.21)
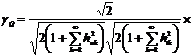
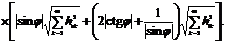 (4.22)
(4.22)
Анализ показывает, что погрешности,
определенные в соответствии (4.19) - (4.22), в 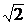 раз меньше аналогичных погрешностей, вычисленных в соответствии
выражениями (4.7) - (4.10).
раз меньше аналогичных погрешностей, вычисленных в соответствии
выражениями (4.7) - (4.10).
Если использовать второй метод
определения интегральных характеристик сигналов абсолютные погрешности
аргументов соответствуют наибольшему отклонению моделей от реальных сигналов,
то предельные значения абсолютных погрешностей определения параметров сигналов
будут равны:
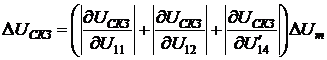 ; (4.23)
; (4.23)
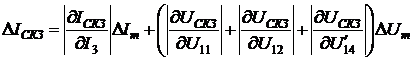 ;
(4.24)
;
(4.24)
 ;
(4.25)
;
(4.25)
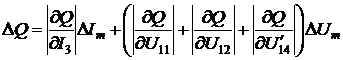 .
(4.26)
.
(4.26)
Используя предельные значения
абсолютных погрешностей (4.23) - (4.26), можно определить относительные
погрешности определения СКЗ напряжения и тока и приведенные погрешности
определения АКМ и РЕМ:

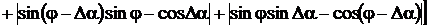 ;
(4.27)
;
(4.27)
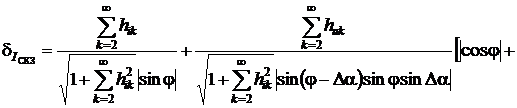
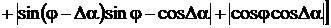 ;
(4.28)
;
(4.28)
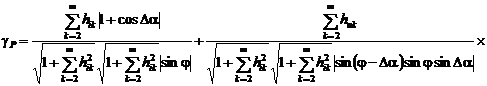
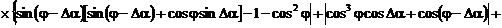
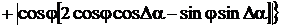 ;
(4.29)
;
(4.29)
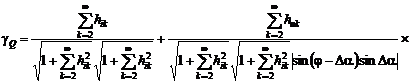
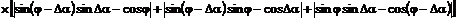 .
(4.30)
.
(4.30)
Из выражений (4.27) - (4.30)
следует, что погрешность определения параметров периодических сигналов зависит
не только от гармонического состава сигнала, но и от угла сдвига фаз между
напряжением и током φ и угла сдвига фазы ФСБ Δα.
Анализ указывает, что, выбирая
соответствующие значения угла Δα, можно значительно снизить погрешность, обусловленная отклонением
реальных сигнала от гармонической модели.
4.2 Анализ погрешностей реализации
методов определения интегральных параметров гармонических сигналов
Использование
аналого-цифрового преобразования мгновенных значений неизбежно приводет к
погрешности квантования. Для анализа влияния погрешности квантования
аналого-цифровых преобразователей на точность измерения ИПГРС может быть
использована, рассмотренная в первой главе, методика характеристики погрешности
результата измерения интегральной характеристики как функции, аргументы которой
заданы приближенно с погрешностью, соответствующей погрешности квантования.
Если принимать, что при реализации
первого метода определения ИПГРС при амплитудном значении напряжения Um
мгновенное значение напряжения, пропорционально U21, измеряет с погрешност
преобразования первого АЦП и наибольшая абсолютная погрешность измерений соответствует
ΔU21=ΔU=Um/2n (где n -
разрядность АЦП), то наибольшая абсолютная погрешность вычисления СКЗ
напряжения в соответствует (3.1) с учетом погрешности квантования изменяеться к
виду:
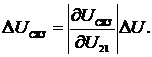 (4.31)
(4.31)
Относительная погрешность вычисления
UСКЗ равна:
 (4.32)
(4.32)
Если считать, что при амплитудном
значении тока Im мгновенные значения тока, пропорциональные I21 и I22
измеряются с погрешностью преобразования второго АЦП и предельные абсолютной
погрешности измерений соответствуют ΔI21=ΔI22=ΔI=Im/2n,
то в соответствии с (3.2) предельная абсолютная погрешность
вычисления СКЗ тока с учетом погрешности квантования АЦП:
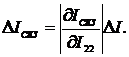 (4.33)
(4.33)
Относительная погрешность вычисления
IСКЗ равна
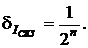 (4.34)
(4.34)
Например, для 12-разрядного АЦП
погрешность вычисления среднеквадратических значений напряжения и тока составит
0,024 %.
Так же, абсолютные погрешности
определения АКМ и РЕМ с учетом выражения (3.3) и (3.4) соответствуют виду:
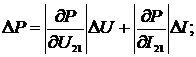 (4.35)
(4.35)
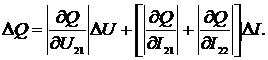 (4.36)
(4.36)
Используя такие же допущения о
погрешности преобразования мгновенных значений напряжения и тока, получим
выражения для приведенных погрешностей вычисления АКТМ и РКМ
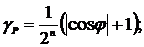 (4.37)
(4.37)
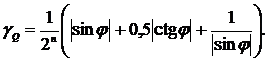 (4.38)
(4.38)
Анализ выражений (4.32) и (4.34)
показывает, что погрешность, обусловленная влиянием квантования на результаты
определения СКЗ напряжения и тока, не зависит от угла сдвига дополнительных
сигналов относительно входного напряжения и тока, а зависит только от
разрядности АЦП. Выражения (4.37) и (4.38) показывают, что влияние погрешностей
квантования при определении активной и реактивной мощности также не зависит от
угла сдвига дополнительных сигналов относительно входного напряжения и тока,
однако зависит от угла сдвига фаз между напряжением и током φ.
На рис. 4.4 и 4.5 приведены
соответственно графики зависимости приведенной погрешности АКМ и РЕМ от угла
сдвига фаз между напряжением и током φ для 12-разрядного АЦП.
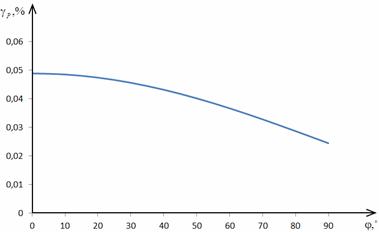
Рис. 4.4. Зависимость  от φ для 12-разрядного АЦП
от φ для 12-разрядного АЦП
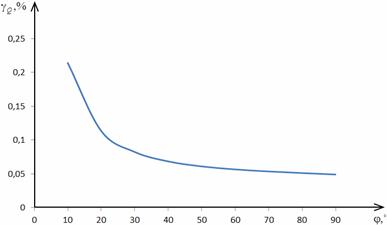
Рис. 4.5. Зависимость 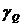 от φ для 12-разрядного АЦП
от φ для 12-разрядного АЦП
Анализируя выражения (4.32), (4.34),
(4.37) и (4.38), можно увидеть, что наиболее эффективным методом сокращения
данного вида погрешности является определение разрядности АЦП, однако это не всегда
можно и имеет предел.
Так же, если считать, что при
реализации второго метода определения ИПГРС при амплитудном значении напряжения
Um мгновенное значение напряжения измеряется с погрешностью преобразования
АЦП1, а при амплитудном значении тока Im мгновенные значения тока измеряются с
погрешностью преобразования АЦП2, то абсолютные погрешности вычисления ИПГРС
примут вид:
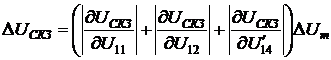 ;
(4.39)
;
(4.39)
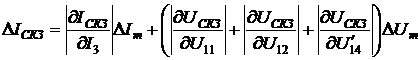 ;
(4.40)
;
(4.40)
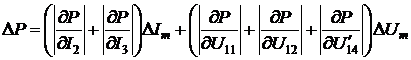 ;
(4.41)
;
(4.41)
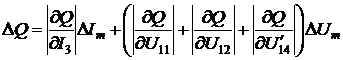 .
(4.42)
.
(4.42)
Используя выражения для абсолютных
погрешностей (4.39) - (4.42), можно сделать вывод что относительные погрешности
измерения СКЗ напряжения и тока и приведенны погрешность измерений АКМ и РЕМ:

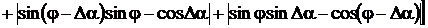 ;
(4.43)
;
(4.43)
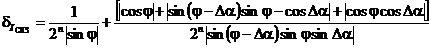 ;
(4.44)
;
(4.44)
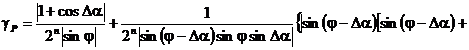
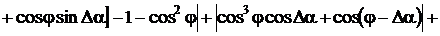
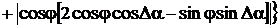 ;
(4.45)
;
(4.45)

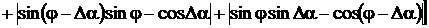 .
(4.46)
.
(4.46)
На рис. 4.6 и 4.7 представлен график
зависимостеи относительной погрешности определения СКЗ напряжения и приведенной
погрешности измерения АКМ в соответствии с выражениями (4.43) и (4.46).
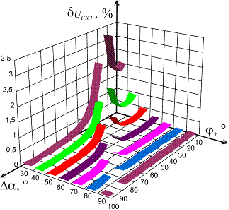
Рис. 4.6. Графики зависимости δUСКЗ от Δα и φ

Рис. 4.7. Графики зависимости γP от Δα и φ
Анализ рис. 4.6 и 4.7 дает нам
представление о зависимости погрешностей как от угла сдвига фаз между
напряжением и током φ, так и от угла сдвига фазы ФСБ.
При этом меньшее значение
погрешности имеет место быть для Δα,
соответствующих 70 - 90º (при 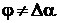 ). В
случае, если
). В
случае, если 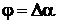 ,
знаменатели выражений (4.43) - (4.46) преврящаются в ноль, что соответствует
взрывам графиков на рис. 4.6 и 4.7.
,
знаменатели выражений (4.43) - (4.46) преврящаются в ноль, что соответствует
взрывам графиков на рис. 4.6 и 4.7.
Если считать, что при реализации
первого метода ФСБ1 (канал напряжения) и ФСБ3 (канал тока) имеют одинаковые
углы сдвига фаз равные Δα, а ФСБ2 (канал напряжения) и ФСБ4 (канал тока) имеют углы сдвига
фаз равные (Δα+Δβ) и (Δα+Δξ), где Δβ и Δξ - разность между углами сдвига фаз ФСБ1 и ФСБ2, ФСБ3 и ФСБ4
соответственно, то выражения для мгновенных значений сигналов будут равны:
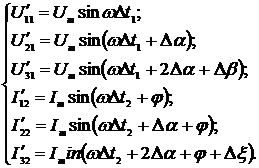 (4.47)
(4.47)
Рассмотрим частный случай анализа
погрешности ФСБ, приняв Δβ=Δξ.
Равенство мгновенных значений
сигналов  выполняется в том случае, если
выполняется в том случае, если 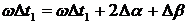
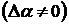 , то
есть когда
, то
есть когда 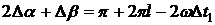 или
или 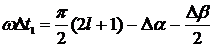 .
.
Отсюда:
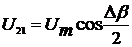 ;
(4.48)
;
(4.48)
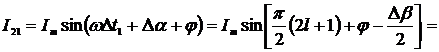
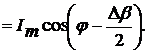 (4.49)
(4.49)
Согласно с (3.1) и (4.48)
относительная погрешность определения СКЗ напряжения определяет выражение:
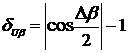 .
(4.50)
.
(4.50)
Соотношение мгновенных значений
сигналов 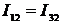 выполняется в том случае, если
выполняется в том случае, если 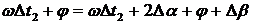 , то есть когда
, то есть когда 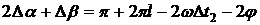 или
или 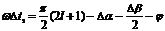 . Отсюда:
. Отсюда:
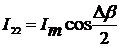 .
(4.51)
.
(4.51)
Согласно (3.2) и (4.49)
относительная погрешность определения СКЗ тока определяется выражением:
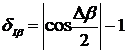 .
(4.52)
.
(4.52)
В соответствии с (3.3), (3.4),
(3.48), (3.49) и (4.51) приведенные погрешности определения АКМ и РЕМ будет
равна:
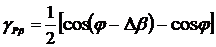 ;
(4.53)
;
(4.53)
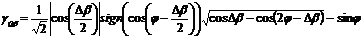 .
(4.54)
.
(4.54)
На рис. 4.8 виден график зависимости
погрешности определения СКЗ напряжения и тока от отклонения угла сдвига
номинальной фазы ФСБ на величину Δβ
в соответствии с выражениями (4.50) и (4.52).
Анализ рис. 4.8 показывает, что
погрешность измерения СКЗ напряжения и тока, обусловленна отклонением угла
сдвига фазы ФСБ от Δα, мала и в некоторых случаях ею можно пренебречь.
На рис. 4.9 и 4.10 видны графики
зависимостей приведенные погрешности определения АКТМ и РКМ, обусловленные
отклонения угла сдвига номинальной фазы ФСБ от Δβ
и угла сдвига фаз между сигналам напряжения и тока в
соответственно с выражениями (4.53) и (4.54).
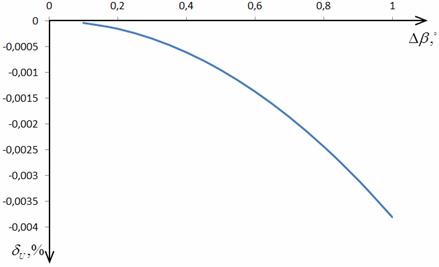
Рис. 4.8. Зависимость погрешности 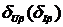 от Δβ
от Δβ
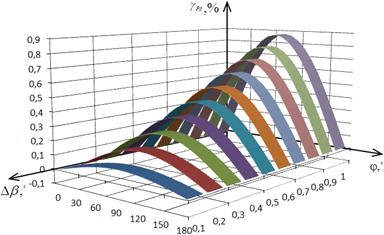
Рис. 4.9. Зависимость погрешности 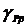 от Δβ и φ
от Δβ и φ
Анализируя рис. 4.9 и 4.10, увидим
прогрессирующий рост погрешности с увеличением Δβ.
Из недостатков
информационно-измерительной системы, реализующей этот метод, являеться
погрешности по модулю фазосдвигающихся блоков, которая может привести к
значительному потери точности измерения ИПГРС.
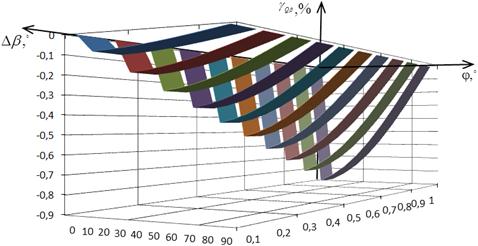
Рис. 4.10. Зависимость погрешности 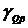 от Δβ и φ
от Δβ и φ
Если думать, что амплитудные
значения напряжений на выходах первого и второго фазосдвигающихся блоков,
используемого для формирования дополнительных сигналов, отличаются от амплитуды
входного сигнала на величину 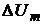 и
и 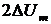 , то мгновенные значения дополнительных сигналов напряжения будут
иметь вид:
, то мгновенные значения дополнительных сигналов напряжения будут
иметь вид: 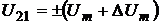 и
и 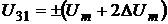 . Так же, при отличии амплитудных значений дополнительных сигналов
на выходах ФСБ в канале тока от амплитуды входного сигнала на величину
. Так же, при отличии амплитудных значений дополнительных сигналов
на выходах ФСБ в канале тока от амплитуды входного сигнала на величину 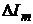 и
и 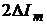 ,
мгновенные значения дополнительных сигналов будут равны:
,
мгновенные значения дополнительных сигналов будут равны:
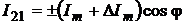 ,
, 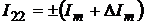 ,
, 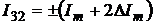 .
.
Оценивая влияние этого вида
погрешностей на погрешности измерений ИПГРС.
Поэтому воспользуемся рассмотренной
ранее методикой.
Если абсолютная погрешность
аргументов соответствует отклонений мгновенных значений дополнительной
напряжения и тока на величины 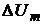 и
и 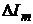 , то, считая, что мгновенные значения входных сигналов напряжения
и тока измерены без погрешности, возможно определить наибольшие значения
абсолютных погрешности измерения СКЗ напряжений и тока, АКМ и РЕМ:
, то, считая, что мгновенные значения входных сигналов напряжения
и тока измерены без погрешности, возможно определить наибольшие значения
абсолютных погрешности измерения СКЗ напряжений и тока, АКМ и РЕМ:
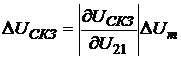 ;
(4.55)
;
(4.55)
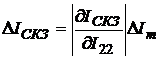 ;
(4.56)
;
(4.56)
 ;
(4.57)
;
(4.57)
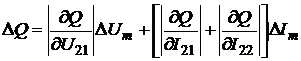 .
(4.58)
.
(4.58)
Используя (3.1) - (3.4), с учетом
абсолютных погрешности (4.55) - (4.58) возможно определить относительные
погрешности измерений СКЗ напряжения и тока и приведенные погрешностей
измерений АКМ и РЕМ:
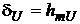 ;
(4.59)
;
(4.59)
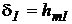 ;
(4.60)
;
(4.60)
 ;
(4.61)
;
(4.61)
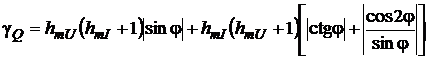 .
(4.62)
.
(4.62)
Анализ выражений (4.59) - (4.62)
показывают, что погрешность определения ИПГРС зависит не только от погрешности
по модулю фазосдвигающих блоков, но и от угла сдвигов фаз между сигналами
напряжения и тока (для АКМ и РЕМ)
На рис. 4.11 и 4.12 представлены
графики зависимостей приведенных погрешностей определениям АКМ и РЕМ от угла
сдвига фаз между сигналам напряжения и тока в соответствии с выражениями (4.61)
и (4.62).
Анализ указывает падение погрешности
с ростом угла сдвига фаз между сигналами напряжения и тока φ.
Недостатком метода и, реализующей
его ИИС, является возможность возникновений погрешностей, обусловленной
отличием от угла сдвига фаз в каналах напряжения и тока.
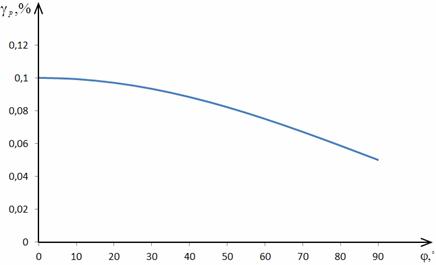
Рис. 4.11. Зависимость погрешности 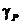 от φ при hmU=hmI=0,05%
от φ при hmU=hmI=0,05%
Рис. 4.12. Зависимость погрешности 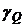 от φ при hmU=hmI=0,05%
от φ при hmU=hmI=0,05%
4.3 Основные результаты и выводы
. Анализы погрешностей измерений
интегральных характеристик из-за отклонения реальных сигналов от гармонической
модели показывают, что возникают существенные погрешности, значения которых
определяется, в первую очередь, спектром реальных сигналов.
В первом методе, использующем
пространственное разделение сигналов, данный вид погрешностей так же зависит от
угла сдвига фаз между первым и гармониками напряжения и тока (кроме СКЗ
напряжений и тока).
Во втором методе погрешность,
обусловленная отклонением реальных сигналов от гармонической модели, зависит от
угла сдвига фаз между первыми гармониками напряжениями и токами и углами сдвига
фазы ФСБ.
3. Проведенный
анализ погрешности позволяет определить область использования рассматриваемого
метода в зависимости от требований по точности измерения интегральной
характеристики периодического сигнала и спектра сигналов напряжения и тока.
4. При реализации методов степень
влияния погрешностей квантования АЦП на погрешности результата измерения
интегральных характеристик сигналов определятся, в первую очередь, разрядностью
АЦП.
В ИИС, реализующий первый метод,
данный вид погрешностеи зависит от угла сдвига фаз между первыми гармониками
напряжения и тока (кроме СКЗ напряжения и тока).
При реализации второго метода
погрешностей, обусловленная квантованием, мгновенных значений сигнала, зависит
от угла сдвига фаз между первыми гармониками напряжений и тока и угла сдвига
фазы ФСБ.
. Реализация первого метода может
привести к возникновению погрешностеи, обусловленных не идеальностью ФСБ
(погрешность по модулю). Наличие данных вида погрешностеи вызвано отличием
амплитудных значений входного и дополнительного напряжений.
Данный вид погрешностеи при
реализации первого метода зависят от угла сдвига фаз между первыми гармониками
напряжений и тока (кроме СКЗ напряжения и тока).
Погрешности, возникающие при
реализации второго метода, корректируются.
. При реализации первого метода
может возникнуть существенная дополнительная погрешность, в случае, если углы
сдвига фаз ФСБ отличается друг от друга.
Второй метод исключает данный вид
погрешности.
. Полученные результаты позволяет
выбрать параметр измерительного процесса для обеспечений оптимальных
соотношений по точности и времени измерения.
. В общем случае реализация второго
разработанного метода обеспечивает значительное повышение точности измерения
ИПГРС.
Заключение
Результаты, полученные в рамках
магистерской диссертации, направлены на разработку и исследование
аппроксимационных методов измерения интегральных параметров периодических сигналов
и создание на их основе быстродействующих информационно-измерительных систем.
В работе получены
следующие основные результаты:
1. Выявлено, что среди периодических
сигналов, которые очень часто используются как в теории, так и в практических
целях, выделяются гармонические сигналы. Это связано с тем, что такие сигналы
независимы к преобразованиям, которые производятся линейными системами.
. Выполненные в работе исследования
состава высших гармоник сигналов в цепях ряда энергообъектов и электрического
оборудования показали, что: в электрических сетях с номинальным напряжением 110
кВ и более высокими номинальными напряжениями действующие сигналы имеют форму,
которая близка к синусоидальной; коэффициенты искажения синусоидальности,
которые являются комплексной величиной и характеризуют в целом соотношение
между высшими гармониками и первой гармоникой сигналов, меньше 2 %.
Кроме того, коэффициенты отдельных
гармоник в сигналах, имеют наибольшую амплитуду, меньше 1,5 %. Достаточно
близки к гармоническим моделям сигналы, которые имеют место в силовых цепях
разных электромеханических систем.
3. Анализ существующих методов и
систем измерения ИПГРС, основанных на формировании ортогональных составляющих
сигналов, выявил наличие частотной погрешности фазосдвигающих блоков,
значительно снижающей точность измерения даже в узком диапазоне изменения
частоты.
. Разработанные новые методы
измерения ИПГРС позволяют устранить частотную погрешность фазосдвигающих
блоков, кроме того, второй метод позволяет устранить угловую погрешность,
возникающую из-за отличия углов сдвига фаз ФСБ.
Литература
1. Анашкин С.В., Карташов С.В., Любарский Ю.Я., Мирошкин
А.Г. Автоматизированный анализ нештатных ситуаций в электрических сетях //
Электрические станции. - 2013. - №9.- С. 49 - 53.
. Гореликов Н.И., Николайчук О.Л. Измерительные
преобразователи интегральных характеристик сигналов сложной формы // ЦНИИТЭИ
приборостроения. - 1981. - Вып. 3. - 32с.
. Лаппе Р., Фишер Ф. Измерения в энергетической
электронике. - М.: Энергоатомиздат, 1986. - 232с.
. Безикович А.Я., Шапиро Е.З. Измерение электрической
мощности в звуковом диапазоне частот. - Л.: Энергия, 1980. - 168с.
. Волгин Л.И. Измерительные преобразователи переменного
напряжения в постоянное. - М.: Сов. радио, 1979. - 240с.
. Кизилов В.У. Аналоговые измерительные преобразователи
мощности // Измерение, контроль, автоматизация. - 1976. - Вып. 1(5). - С.
55-63.
. Кизилов В.У. Методы и средства измерения активной и
реактивной мощности в трехфазных цепях // Приборы и системы управления. - 1985.
- №10. - С. 26-28.
. Попов В.С., Желбаков И.Н. Измерение
среднеквадратического значения напряжения. - М.: Энергоатомиздат, 1987. - 120с.
. Туз Ю.М., Синицкий О.П., Губарь В.И. Цифровой
малокосинусный ваттметр / Новые электронные приборы: Сб. науч. трудов. - Киев:
КПИ, 1972. - С. 3 - 6.
10. Marzetta Lois A. An evaluation of three-voltmeter method
for AC power measurement // IEEE Trans. On
Instrum. and Measur. - 1972. - V. 21. - №4. - P. 353 -357.
. Клисторин И.Ф. Цифровые вольтметры действующих значений
(обзор принципов построения и перспективы развития) // Автометрия. - 1966. - №
2. - С. 3-11.
. Кудряшов Э.А. Терморезонансные преобразователи //
Приборы и системы управления. - 1972. - № 2. - С. 33-35.
13. Germer H. Electronic method with direct time encoding for
precision measurement of electric power over a wide range of frequency // IEEE
Trans. On Instrum. and Measur. - 1972. - V. 21. - № 4. - P. 350-353.
. Кирьяков В.П. Об одном методе обработки результатов
прямых измерений для определения действующих значений периодических напряжений
произвольной формы // Автометрия. - 1967. - № 2. - С. 17-22.
. Клисторин И.Ф., Коршевер И.И. Методы определения
интегральных характеристик переменных напряжений путем обработки их мгновенных
значений // Автометрия. - 1967. - № 2. - С. 3-16.
. Клисторин И.Ф., Коршевер И.И. Определение интегральных
характеристик напряжений произвольной формы путем обработки результатов
измерения мгновенных значений // Автометрия. - 1966. - № 2. - С.28-40.
. Левин М.И., Семко Ю.И. Определение параметров
периодических сигналов путем измерения их мгновенных значений // Автометрия. -
1966. - № 1. - С. 33-40.
. Пат.
3959724 США. Rochester
Instrument Systems Inc. / R.L. Kraley, E.A. Hauptmann, B.M. Pressman. №490783; заявл. 22.07.74; опубл. 25.05.76. Бюл. №5.
19. Smith Y.R. Rapid detection and mesurement of 3-phase
reactive power, power and power-factor // Electron. Lett. - 1972. - V. 8. - №23. - P. 574, 575.
20. Clarke F.J.J., Stockton J.R. Principles and theory of
wattmeters operating on the base of regulary spaced sample pairs // J. Phys.
Ser. E. Sci. Instr. - 1982. - V. 15. - №6. - P.
645-652.