Дослідження двоконтурної автоматичної системи регулювання з динамічною корекцією
Зміст
Анотація
Вступ
.
Особливості технологічних об'єктів регулювання
.
Функціональна та структурна схеми двоконтурної АСР з динамічною корекцією
.1
Методи розрахунку каскадних АСР з динамічною корекцією
.1.1
Метод розрахунку по контурах
.1.2
Метод інформаційної моделі
.
Задачі дослідження
.
Параметричний синтез двоконтурної АСР з динамічною корекцією і аналіз
результатів
.1
Метод багатокритеріальної параметричної оптимізації
.1.1
Розрахунок параметрів настроювання неперервних ПІ-регуляторів з умов багатокритеріального
оптимуму
.1.2
Особливості розрахунку каскадної АСР з динамічною корекцією за методом
багатокритеріального оптимуму
.2
Програмна реалізація методу багатокритеріального оптимуму та моделювання
системи
.3
Результати дослідження АСР з динамічною корекцією та їх аналіз
.4
Порівняльна оцінка характеристик АСР з динамічною корекцією і одноконтурної
системи
Висновок
Література
Анотація
двоконтурний
автоматичний регулювання динамічний
У роботі розглянуті особливості
промислових об’єктів регулювання, обгрунтована необхідність застосування,
зокрема, двоконтурних автоматичних систем регулювання з динамічною корекцією
для покращання якості регулювання складних у динамічному відношенні об’єктів.
Описана функціональна схема та
проаналізована алгоритмічна структура каскадної АСР з динамічною корекцією,
показані можливості її трансформації в залежності від співвідношення
інерційності допоміжної та головної ділянок об’єкта. На підставі цього аналізу
зроблено висновок про можливі варіанти розрахунку такого типу АСР.
Наведений стислий огляд відомих
методів параметричного синтезу двоконтурних АСР, розглянуті особливості
застосування методу багатокритеріальної параметричної оптимізації при розробці
систем з динамічною корекцією. За цим методом з використанням спеціально
розробленої програми (у середовищі MAPLE V) для системи з заданим об’єктом
розраховані оптимальні параметри настроювання ПІ-регулятора та диференціатора.
За допомогою засобу імітаційного моделювання SIMULINK (MATLAB), досліджені
перехідні процеси в АСР по різних каналах та визначені їх основні показники
якості.
Проведений порівняльний аналіз
характеристик одноконтурної системи з різними типами регуляторів та каскадної
АСР з динамічною корекцією, що підтверджує її переваги і доцільність
практичного застосування.
Вступ
Практика автоматизації складних
технологічних об’єктів, які характеризуються значним запізненням по каналу
регулюючої дії , а також високими вимогами щодо точності підтримання
регульованої величини як в усталеному так і в перехідному режимах, показала,
що, використовуючи лише відхилення регульованої величини від завдання і
реалізуючи автоматичну систему регулювання (АСР) за одноконтурною структурою,
отримати задовільну якість регулювання здебільшого не вдається.
Підвищити якість регулювання у таких
об’єктах можна завдяки використанню додаткової інформації про хід
технологічного процесу і введенні її у контур регулювання. Такою інформацією
можуть бути випереджуючі сигнали по похідних від однієї або декількох проміжних
регульованих величин. Системи регулювання, які побудовані за таким принципом,
прийнято називати системами з динамічною корекцією. У найпростішому варіанті
подібної системи використовується сигнал по похідній лише від однієї проміжної
(допоміжної) регульованої величини, яка реагує на регулюючу дію значно швидше,
ніж основна регульована величина. В результаті цього система стає двоконтурною,
причому внутрішній контур діє тільки у перехідних режимах.
АСР з динамічною корекцією є досить
ефективним засобом підвищення якості функціонування складних у динамічному
відношенні об’єктів, проте методи параметричного синтезу таких систем
розроблені недостатньо і розповсюджуються, головним чином, на випадки, коли
підтверджується гіпотеза про незалежність процесів у контурах системи. Стосовно
ж цифрових систем, які вже стали домінуючими, можна зазначити, що ця проблема
взагалі ще практично не розв’язана.
Таким чином, вдосконалення та
дослідження методів параметричного синтезу АСР з динамічною корекцією є
важливим і актуальним.
1. Особливості технологічних
об'єктів регулювання
Аналіз промислових об'єктів
регулювання показує, що звичайно речовина в них або енергія накопичується в
багатьох ємностях (багатоємнісні об'єкти). Фізично ємність об'єкта проявляється
у вигляді теплоємності, геометричної ємності резервуара, інерційності рухомих
мас, тощо.
Речовина, або енергія, як правило,
накопичується в об'єктах сповільнено, що обумовлено наявністю опорів, які
перешкоджають їх надходженню і виходу. Тому в багатоємнісних об'єктах
спостерігається перехідне (ємнісне) запізнення tп
, що визначається з перехідної характеристики об'єкта як час з моменту початку
зміни регульованого параметра до перетину з віссю часу дотичної до кривої
перехідного процесу в точці її перегину. Крім цього, багатьом об'єктам властиве
чисте (транспортне) запізнення tт , яке е
наслідком процесів, що відбуваються всередині об'єкта. Одноємнісні і
багатоємнісні об'єкти можуть мати або не мати властивість самовирівнювання,
тобто можуть бути статичними або астатичними.
Перехідні процеси у багатоємнісних
регульованих об'єктах описуються диференціальними рівняннями, порядок яких
дорівнює числу ємностей об'єкта, розділених опорами. Складання таких рівнянь і
користування ними роблять процес дослідження регульованого об'єкта і АСР
загалом складним та громіздким.
Повільний характер протікання
перехідних процесів і монотонний вигляд динамічних характеристик більшості
промислових об'єктів обумовлюють можливість апроксимації цих характеристик
операторами виду:
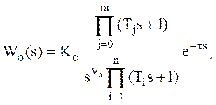
де Кo, 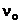 -
коефіцієнт підсилення та порядок астатизму об'єкта; Ti, Tj - сталі часу; t
- чаc запізнення; t = tn+tт
; m
-
коефіцієнт підсилення та порядок астатизму об'єкта; Ti, Tj - сталі часу; t
- чаc запізнення; t = tn+tт
; m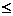 n
.
n
.
Передавальна функція (1.1) дає змогу
відобразити широкий клас об'єктів як з s-подібними перехідними
характеристиками, так і з перехідними характеристиками, що мають екстремум.
Найбільш поширеним є клас об'єктів,
які описуються передавальними функціями виду (1.1), але “без чисельника” і тому
їх перехідні характеристики мають монотонний характер. Проте у практиці
автоматизації зустрічаються, хоча й рідко, об'єкти з коливним характером
перехідного процесу, а також об'єкти, у яких відхилення регульованої величини
залежить не тільки від значень збурення чи регулюючої дії, але й від швидкості
їх зміни, тобто їх динаміка описується операторами виду (1.1). Прикладом такого
об'єкта може бути барабанний паровий котел, як об'єкт регулювання рівня води в
барабані при зміні витрати пари.
При параметричній оптимізації АСР,
особливо з використанням методів, орієнтованих на автоматичне підстроювання
параметрів регулятора, часто предавальну функцію багатоємнісного об’єкта
апроксимують моделлю у вигляді аперіодичної ланки першого порядку з запізненням
:
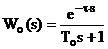
Таку модель об’єкта у літературі
прийнято називати як FOPDT-модель (first order plant with dead time ). При
апроксимації багатоємнісного об’єкта статичною (або астатичною) ланкою першого
порядку з запізненням важливим показником динамічних властивостей об’єкта є не
стільки абсолютне значення 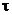 , скільки
відношення запізнення до сталої часу То , тобто
, скільки
відношення запізнення до сталої часу То , тобто 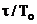 .
Відношення
.
Відношення 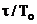 може розглядатися,
як деякий узагальнений показник інерційності об’єкта, при цьому, чим воно
більше, тим важче забезпечити необхідну якість регулювання.
може розглядатися,
як деякий узагальнений показник інерційності об’єкта, при цьому, чим воно
більше, тим важче забезпечити необхідну якість регулювання.
В технологічних об'єктах регулювання
набагато сильніше проявляється можливість дії не одного, а багатьох збурень,
які діють на об'єкт по різних каналах з різними динамічними властивостями, що
істотно відрізняє їх від інших об'єктів (наприклад, від об'єктів
електромеханічних слідкуючих систем). Серед цих збурень є неконтрольовані
випадкові з невідомими статистичними характеристиками.
Одним з найважливіших збурень є
збурення по навантаженню, і тому розрахунок АСР часто орієнтують саме на
збурення за навантаженням n. При цьому треба мати на увазі, що динамічні
властивості об'єкта по каналу дії цього збурення звичайно дуже відрізняються
від властивостей об'єкта по каналу регулюючої дії. Інерційність технологічних
об'єктів регулювання по каналу дії збурення за навантаженням менша від його
інерційності по каналу регулюючої дії і тому відхилення регульованої величини, викликане
збуренням f, що діє на вхід об'єкта по регулюючому каналу, буде меншим ніж
відхилення, яке виникне в об'єкті при аналогічному збуренні за навантаженням.
Збурення, яке діє по будь-якому
каналу, не може бути приведене до еквівалентного збурення, прикладеного зі
сторони регулюючого органу, яке могло б бути фізично реалізоване, оскільки
завдяки відмінностям динамічних властивостей каналів форма еквівалентного
збурення буде суттєво відрізнятися від форми дійсного збурення. Зокрема,
ступінчасте збурення, при якому виконуються розрахунки (оскільки воно
вважається для лінійних систем найважчим), і яке виникає при зміні
навантаження, повинне містити імпульси нескінченно великої амплітуди [1].
Фізично більша інерційність
регулюючих каналів технологічних об'єктів порівняно з інерційністю каналу дії
збурення, викликаного зміною навантаження споживача, пояснюється тим, що
найважливіші регульовані величини пов'язані з якістю продукції, яку одержує
споживач, і просторово розміщені в кінці технологічного процесу, ближче до
споживача. У той же час регулюючі дії на технологічний процес формуються на
його початку зміною подачі в об'єкт вихідних продуктів технології,
співвідношенням їх компонентів, енергії, тощо.
Крім контрольованих збурень на
кожний технологічний об'єкт діє більше чи менше число неконтрольованих збурень
(їх число та точки прикладання до об'єкта можуть бути невідомими).
Неконтрольовані збурення в технологічних об'єктах можуть складати основну масу
збурень, причому навіть збурення за навантаженням об'єкта може виявитися
неконтрольованим.
Розглянемо, як приклад
технологічного об'єкта регулювання, двоступеневий пароперегрівник (ПП) парового
котла (рис.1.1), тобто
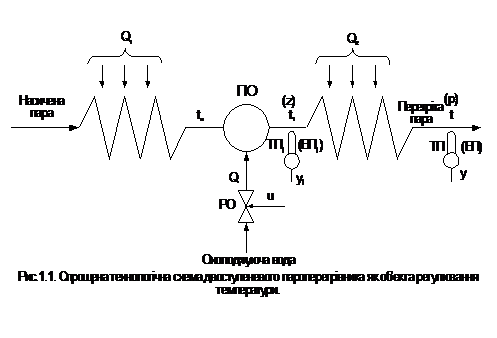
теплообмінник для перетворення
насиченої водяної пари в перегріту, яка подається в турбіну. Він складається з
двох секцій, до яких підводиться кількість тепла відповідно Q1 і Q2 . Для
точного регулювання температури (грубе регулювання здійснюється зміною подачі
палива в котел) між секціями встановлюєтся впорскуючий пароохолоджувач (ПО), у
який подається охолоджуюча вода, її кількість визначається відкриттям u
регулюючого клапану (РО). Регульованою величиною є температура перегрітої пари
t на виході ПП, що контролюється термопарою ТП (ВП). Температура пари t1 на виході
ПO вимірюється термопарою ТП1 (ВП1); вихідні сигнали термопар позначені через y
та y1 . Алгоритмічна структура такого об'єкта може бути відображена за
допомогою паралельно-послідовного (рис.1.2а, рис.1.2б) та послідовного
(рис.1.2в) з’єднання відповідних ланок.
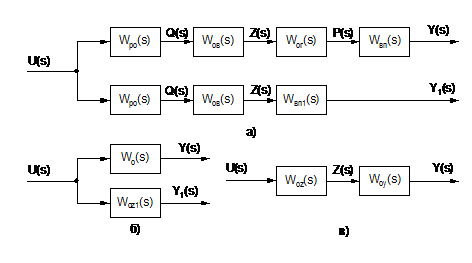

У відповідності з рис.1.2 динаміка
такого об'єкта в загальному вигляді описується передавальними функціями:
(s) = Wpo(s) Wов(s) Wвп1 (s), (s) =
Wpo(s) Wов(s) Wог(p) Wвп(s) ,(s) = Wpo(s) Wов(s), (s) = Woz(s) Woy(s) ,
де Wов(s) - передавальна функція
випереджуючої (малоінерційної) ділянки об'єкта (див. рис.1.2) від РО до точки
вимірювання допоміжної регульованої величини - температури t1 (у загальному
випадку - z); Wог(s) - передавальна функція головної (інерційної) ділянки
об'єкта регулювання, що визначається точками вимірювання t1 ,t; Wpo(s), Wвп(s),
Wвп1(s) - передавальні функції відповідно РО, ВП та ВП1.
Структуру, аналогічну розглянутій,
мають багато інших промислових об'єктів.
Внаслідок великої інерційності
об'єкта, що тут розглядається, проста одноконтурна АСР не може забезпечити
потрібної якості регулювання. Тому з метою її покращання необхідно забезпечити
регулятору можливість отримання більш своєчасної інформації про результат своєї
роботи (стан об'єкта).
Введення додаткових змінних стану
виявляється ефективним, коли сильні збурення діють у початкових за ходом
технологічного процесу ємностях об'єкта або впливають на нього по одному каналу
з регулюючою дією. В подібних випадках часто достатньо ввести в систему
регулювання лише одну додаткову змінну стану, вибираючи її відносно близько до
регулюючого органу. Відповідно об'єкт регулювання розбивається на дві ділянки:
головну (інерційну) і допоміжну (малоінерційну). Оскільки зміна допоміжної
змінної стану випереджує в часі зміну основної регульованої величини через те,
що термопара ТП1 (ВП1) розміщена значно ближче до ПО і РО, ніж термопара ТП
(ВП), допоміжну ділянку називають випереджуючою.
Ефективне регулювання об'єктів, подібних
описаному, можна забезпечити за допомогою двоконтурних (каскадних) АСР [1 - 6].
2. Функціональна та структурна схеми
двоконтурної АСР з динамічною корекцією
На практиці зустрічаються такі
промислові об’єкти, у яких регульована величина може інтенсивно змінюватися під
дією збурень, що виникають на певних ділянках технологічного об’єкта, при цьому
вона має істотне запізнення щодо регулюючої дії. Тому у таких випадках
застосування одноконтурних систем, навіть з оптимально настроєними регуляторами
не забезпечують, як правило, необхідної якості регулювання.
Ефективним способом зменшення
відхилень регульованої величини від заданого значення у подібних ситуаціях є
спосіб, який полягає у введенні в регулятор додаткового сигналу, швидко
реагуючого на збурення, які діють у проміжних точках об’єкта регулювання.
Цей сигнал повинен бути
випереджуючим відносно сигналу, що несе інформацію про регульовану величину, а,
крім того, повинен діяти тільки під час перехідних процесів і зникати в
усталених режимах , що дасть можливість ефективно компенсувати дію
дестабілізуючих факторів і отримувати близькі до оптимальних перехідні процеси.
Вказаний сигнал зручний ще й тим, що у статичному режимі він не викликає
додаткових відхилень регульованого технологічного параметра від його заданого
значення. Тому системи, у яких використовується сигнал похідної з проміжної
точки об’єкта, називають системами з динамічною корекцією (умовно будемо їх
позначати, як КАСР2н). Умовне позначення відображає той факт, що розглядається
неперервна система.
Характерним прикладом такої АСР з
динамічною корекцією є типова схема регулювання температури перегрітої пари в
котельному агрегаті (рис.2.1 ).
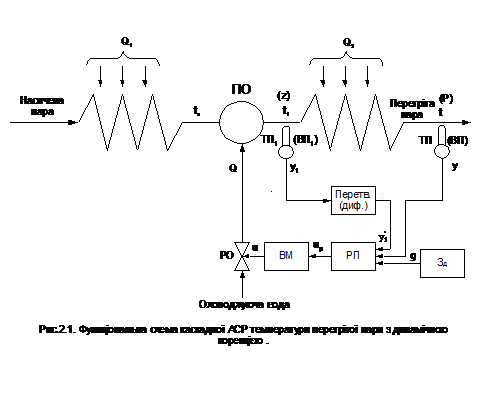
Головною ділянкою об'єкта
регулювання є друга секція пароперегрівника, а основною регульованою величиною
- температура перегрітої пари t, що вимірюється термопарою ТП (ВП), вихідний
сигнал якої y подається (інколи через нормуючий перетворювач) в регулюючий
пристрій (РП). У схемі використовується сигнал y1, пропорційний допоміжній
регульованій величині - температурі t1 (надалі в загальному z. ).
В результаті змін величини z , які
можуть викликатися змінами температури tн або самовільною зміною витрати
охолоджуючої води, тобто збуреннями, що йдуть з боку РО, відразу сприймаються
термопарою ТП1 (ВП1), вихідний сигнал якої через перетворювач подається на
регулюючий пристрій, який за допомогою виконавчого механізму та РО здійснює
необхідну зміну витрати охолоджуючої води ще до початку зміни температури t .
Оскільки в усталених режимах роботи
котла регулятор повинен контролювати тільки температуру пари на виході ПП,
зміни величини z повинні впливати на РП лише в перехідних режимах (інакше РП
буде підтримувати на заданому значенні не температуру пари на виході ПП, а суму
температур t1 і t). Тому перетворювач сигналу y1 вибирають у вигляді реальної
диференціюючої ланки, яка забезпечує форсування перехідних процесів у системі.
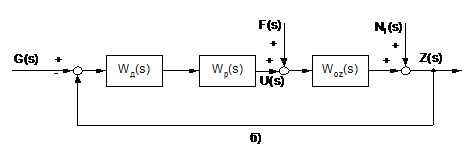
Узагальнюючи і враховуючи структуру
технологічного об'єкта регулювання, функціональну схему каскадної АСР цього
типу можна зобразити у вигляді, показаному на рис.2.2.
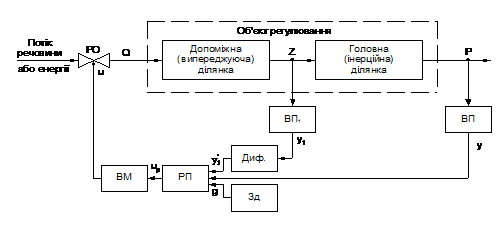

Замінюючи елементи схеми (рис. 2.2)
відповідними передавальними функціями, і беручи до уваги (1.3) - (1.6), а також
, враховуючи, що 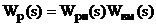 , одержимо
узагальнену структурну схему КАСР2н (рис.2.3а), де G(s) - завдання регулятору.
, одержимо
узагальнену структурну схему КАСР2н (рис.2.3а), де G(s) - завдання регулятору.
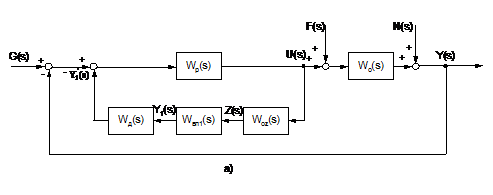
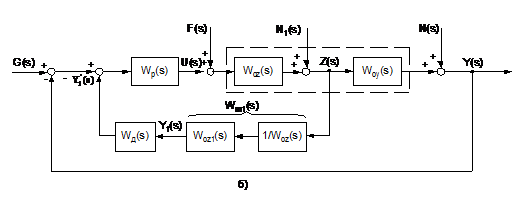

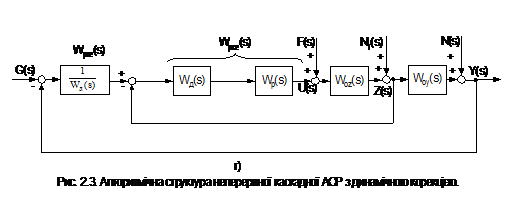
Рисунки 2.3б - 2.3г ілюструють етапи
структурних перетворень початкової схеми (рис.2.3а), в результаті яких схема
каскадної АСР з динамічною корекцією приводиться до вигляду, аналогічного
двоконтурній АСР з коректуючим та стабілізуючим регуляторами [1]. Передавальні
функції відповідних еквівалнтних регуляторів мають вигляд:
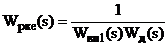 рсe(s) =
Wвп1(s)Wд(s)Wр(s).
рсe(s) =
Wвп1(s)Wд(s)Wр(s).
Зауважимо, що схема на рис.2.3г
отримана у припущенні, що інерційність вимірювального перетворювача (у цьому
випадку ВП1) є значно меншою від інерційності допоміжної ділянки об’єкта.
Звичайно диференціатор вибирають у
вигляді реальної диференціюючої ланки з оператором:
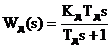
що дає змогу отримати в основному
контурі ефект ПІ-регулювання, оскільки у цьому випадку
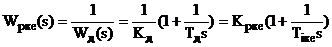
де Крке = 1/Кд; Tiке = Tд.
При цьому, якщо регулятор у
внутрішньому контурі функціонує за ПІ - алгоритмом, передавальна функція
еквівалентного стабілізуючого регулятора матиме вигляд:
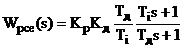
тобто у внутрішньому контурі буде
інтегро-дифереціююча ланка. Ця ланка є коректуючою стосовно допоміжної ділянки
об’єкта. Чисельник виразу (2.5) забезпечує випередження по фазі
arctg ωTi , а знаменник зумовлює відставання по
фазі, рівне arctg ωTд.
Випередження можливе, якщо Ті > Tд. При послідовному вмиканні такої ланки і
відповідному виборі її параметрів можна досягти підвищення коефіцієнта
підсилення і частоти зрізу системи без зменшення запасу стійкості, отже,
зменшити динамічну помилку і час регулювання [ 7-12 ].
При застосуванні у внутрішньому контурі
регулятора з реальним ПІД-алгоритмом функціонування (з урахуванням
передавальної функції виконавчого механізму)
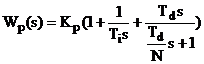
і реального диференціатора (2.3)
отримаємо еквіалентний коректуючий регулятор (2.1), а еквівалентний
стабілізуючиий регулятор матиме вигляд:
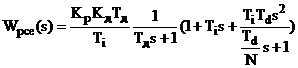
тобто у внутрішньому контурі
реалізується ПДД2 - алгоритм з фільтром на вході.
Якщо в основному контурі необхідно
отримати ефект ПІД-регулювання, то перетворювач повинен бути вибраний у вигляді
реальної диференціюючої ланки з інерційністю, а саме:
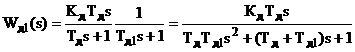
Тоді алгоритм функціонування
еквівалентного коректуючого регулятора є ідеалізованим ПІД - алгоритмом:
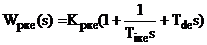
де 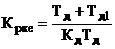 ;
;
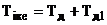 ;
;
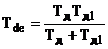 .
.
При цьому, якщо застосовується
ПІ-регулятор, то у внутрішньому контурі реалізується алгоритм
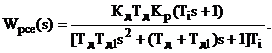
У процесі параметричної оптимізації
можна визначити Крке, Тіке, Тdе, а по них знайти значення параметрів
диференціатора - Кд, Тд, Тд1 з системи рівнянь
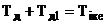
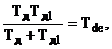
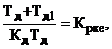
розв’язок якої зводиться до
розв’язку квадратного рівняння
Тд2 - Тіке Тд + ТікеТdе = 0.
Аналізуючи дискримінант рівняння
(2.12), знаходимо, що умовою додатності коефіцієнтів алгоритму (2.9) є
відношення (Тdе/Тіке) ≤ 0.25.
Враховуючи, що параметрична оптимізація
систем вимагає, як правило, значень (Тdе/Тіке) > 0.25, подібний спосіб
реалізації АСР з динамічною корекцією треба вважати доцільним лише в окремих
випадках.
На підставі рис.2.3г, приймаючи
гіпотезу про незалежність процесів у внутрішньому та зовнішньому контурах
каскадної АСР, можна записати передавальні функції контурів
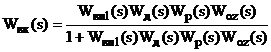
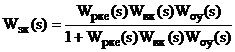
Підставляючи (2.13) у (2.14),
отримаємо передавальну функцію замкненої двоконтурної АСР:
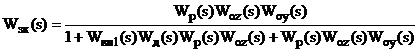
Поділимо чисельник і знаменник
останнього виразу на добуток Wвп1(s)Wp(s)Wд(s)Woz(s) i, спрямовуючи коефіцієнт
підсилення регулятора до нескінченності (тобто, приймаючи Wp(s) → ∞
), одержимо:

або, нехтуючи Wвп1(s),
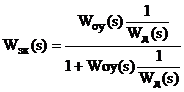
Структура формули (2.17) відповідає
передавальній функції одноконтурної АСР з об’єктом і регулятором, що описуються
виразами: Wo(s) = Woy(s); Wp(s) = 1/Wд(s). При цьому внутрішній контур має
передавальну функцію
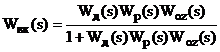
і структуру, зображену на рис.2.4б.

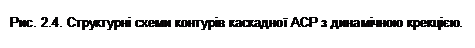
Як зазначалося, вищенаведені
міркування та висновки справедливі, коли інерційність допоміжної ділянки
об’єкта значно (приблизно у два і більше разів) менша, ніж головної його
ділянки. Коли ж така умова не виконується, необхідно аналізувати двоконтурну
систему, враховуючи взаємозв’язок і взаємовплив контурів системи (точніше,
параметрів регулятора і диференціатора).
На підставі рис.2.3а можна записати
передавальні функції еквівалентних об’єктів для регулятора та еквівалентного
коректуючого регулятора (2.1):
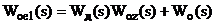
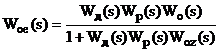
Використовуючи введені поняття
еквівалентних об’єктів, двоконтурну систему КАСР2н шляхом очевидних перетворень
можна подати у вигляді одноконтурної системи двома способами (рис.2.5).
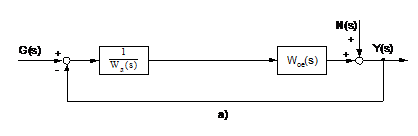
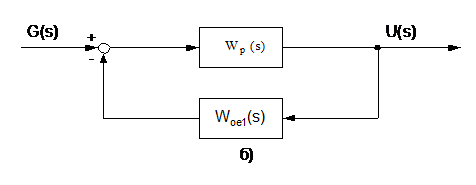
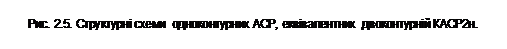
Схеми, зображені на рис.2.5, містять
одні й ті ж елементи, але згруповані по-різному, що дає змогу досліджувати
специфіку процесів, які відбуваються у контурах еквівалентного коректуючого і
стабілізуючого регуляторів.
При цьому передавальні функції
відповідних розімкнених контурів з урахуванням (2.19) і (2.20) мають вигляд:
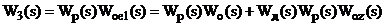
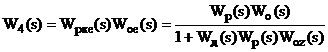
На підставі (2.21), (2.22) і (2.19),
(2.20) можна записати характеристичне рівняння замкненої двоконтурної АСР:
+W3(s) = 1+W4(s) = 1+Wp(s)Wo(s)+
Wд(s)Wp(s)Woz(s) = 0,
або з врахуванням Wвп1(s)
+Wp(s)Wo(s)+Wвп1(s)Wд(s)Wp(s)Woz(s)
= 0.
Оскільки, як було показано, у таких
системах можуть використовуватися різні типи диференціаторів і регуляторів,
характеристичне рівняння замкненої двоконтурної АСР доцільно записати у більш
загальному вигляді (див. рис.2.3г):
+Wpсe(s)Woz(s)+ Wpке(s)Wpcе(s)Wo(s)
= 0,
де Wрке(s), Wpce(s) описуються
виразами (2.4), (2.5), або (2.9), (2.10).
Основні динамічні характеристики
двоконтурної КАСР2н наведені у табл.2.1.
Таблиця 2.1 - Передавальні функції
неперервної двоконтурної системи КАСР2н.
|
Вхідні величини
|
Вихідні величини
|
|
G
|
Y
|
Z
|
|
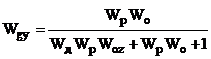
|
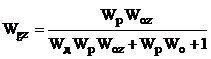
|
|
Uк
|
U
|
|
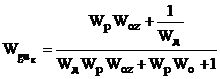
|
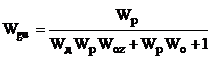
|
|
Ек
|
Е
|
|
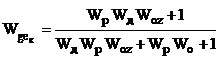
|
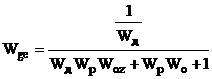
|
|
F
|
Z
|
U
|
|
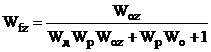
|
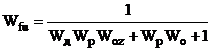
|
|
N1
|
Z
|
U
|
|
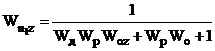
|
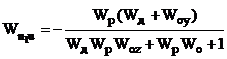
|
|
N
|
Y
|
Uк
|
|
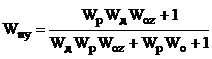
|
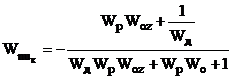
|
Передавальні функції (табл.2.1)
отримані за допомогою спеціальної програми (Додаток 1) шляхом аналітичного
розв’язку системи рівнянь, що описує усі зв’язки між вхідними та вихідними величинами
ланок КАСР2н, а з метою спрощення виразів комплексна змінна s в них опущена.
Рівняння (2.24) чи (2.25) можуть
бути використані в процесі параметричного синтезу каскадної АСР з динамічною
корекцією при різних співвідношеннях параметрів (у межах доцільності), що
характеризують інерційність допоміжної та головної ділянок об’єкта.
Як доведено в [ 4 ], застосування
додаткового інформаційного каналу дає змогу збільшити граничну ефективність
системи лише тоді, коли вибір місця вимірювання допоміжної регульованої
величини z(t) здійснюється за умовою 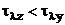 ,
тобто коли ця регульована величина реагує на довільне збурення λ
з
меншим запізненням, ніж основна регульована величина y(t). Крім того, далеко не
байдужими виявляються динамічні властивості каналу дії збурення на основну
регульовану величину. За відсутності запізнення у цьому каналі введення у
систему регулювання додаткової інформації про зміну допоміжної величини z(t), з
огляду на підвищення граничної динамічної точності, виявляється зайвим.
Натомість, при достатньо великому запізненні у цьому каналі, точніше за
виконання умови
,
тобто коли ця регульована величина реагує на довільне збурення λ
з
меншим запізненням, ніж основна регульована величина y(t). Крім того, далеко не
байдужими виявляються динамічні властивості каналу дії збурення на основну
регульовану величину. За відсутності запізнення у цьому каналі введення у
систему регулювання додаткової інформації про зміну допоміжної величини z(t), з
огляду на підвищення граничної динамічної точності, виявляється зайвим.
Натомість, при достатньо великому запізненні у цьому каналі, точніше за
виконання умови
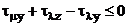
де 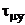 -
запізнення основної регульованої величини по каналу регулюючої дії, введення
додаткової регульованої величини дає можливість повністю усунути вплив збурення
на y(t), так що при будь-яких змінах цього збурення відхилення регульованої
величини y(t) будуть відсутні. Таким чином, стосовно збурення λ
система
стає інваріантною.
-
запізнення основної регульованої величини по каналу регулюючої дії, введення
додаткової регульованої величини дає можливість повністю усунути вплив збурення
на y(t), так що при будь-яких змінах цього збурення відхилення регульованої
величини y(t) будуть відсутні. Таким чином, стосовно збурення λ
система
стає інваріантною.
.1 Методи розрахунку каскадних АСР з
динамічною корекцією
Порівняно з одноконтурними системами
оптимальний розрахунок каскадних АСР ускладнюється завдяки двом причинам.
По-перше, при оптимізації КАСР2н, що досліджується в цій роботі, у два рази
зростає число параметрів, які підлягають визначенню. Зокрема, потрібно
визначати параметри настроювання регулятора - Кр, Ті та частоту власних
коливань Ω внурішнього
контуру, а також параметри настроювання диференціатора - Kд, Tд і власну
частоту зовнішнього контуру ω. По-друге,
ускладнюються умови забезпечення заданого запасу стійкості. На відміну від
одноконтурної системи, у якій для забезпечення заданого запасу стійкості цей
показник для будь-якої точки її структури не повинен перевищувати заданого
допустимого значення, для двоконтурної системи ця вимога повинна виконуватися у
двох точках, кожна з яких має відображати поведінку свого контуру.
Врахування двох показників
коливності у двоконтурній системі регулювання відображається також на якості
процесів регулювання при дії збурень. У таких системах далеко не байдужим є
характер зміни не тільки головної, але й допоміжної регульованих величин, а
обмеження лише на показник коливності головного контуру не виключає можливості
появи недопустимо великої коливності допоміжного. Треба зауважити, що
двоконтурна система загалом може бути стійкою і при нестійкому внутрішньому
контурі, однак, у зв’язку з тим, що зовнішній контур іноді переводять на ручне
керування, нестійкості внутрішнього контуру слід уникати [3].
У процесі розробки каскадної системи
потрібно намагатися також уникати нелінійностей, які можуть бути спричиненими
великими сигналами у внутрішньому контурі. При дуже великому коефіцієнті
підсилення регулятора може виникнути його перенасичення при дії якогось
збурення, що призводить до переміщення регулюючого органу в крайнє положення.
Іноді система при цьому залишається стійкою, але перехідні процеси в ній гірші,
ніж в одноконтурних АСР.
Розрахунок каскадної АСР з
динамічною корекцією може виконуватися різними методами [1- 4, 6].
.1.1 Метод розрахунку по контурах
регулювання
Цей метод є найбільш уживаним і може
бути застосований, якщо інерційність випереджуючого контуру значно (у два і
більше разів) менша від інерційності основного контуру регулювання.
У відповідності з цим методом
спочатку на підставі структурної схеми (рис.2.4а) за методом розширених КЧХ [6]
або за методом максисмуму АЧХ [1,2], враховуючи певний прийнятий критерій
оптимальності, наприклад, мінімум дисперсії помилки регулювання при
низькочастотних збуреннях (або мінімум лінійного інтегрального критерію)
визначаються параметри настроювання диференціатора - Кд, Тд .
Значення Кд, Тд, при цьому визначені
з умови, що коефіцієнт підсилення регулятора достатньо великий, але практично
його значення завжди обмежене. Тому розрахунок повинен бути доповнений
визначенням оптимальних параметрів настроювання регулятора і перевіркою
коректності заміни реальної двоконтурної АСР (рис.2.3а) одноконтурною
(рис.2.4а).
Як було показано вище, диференціатор
разом з об’єктом утворюють для регулятора деякий еквівалентний об’єкт, що
описується передавальною функцією (2.19), в результаті чого двоконтурна система
може бути зображена у вигляді одноконтурної (рис.2.5б). За характеристиками
еквівалентного об’єкта (2.19) на підставі схеми (рис.2.5б) будь-яким з методів
визначають параметри настроювання регулятора - Кр, Ті.
На завершення здійснюється перевірка
припущення про малу інерційність випереджуючого контуру. Один з можливих
способів такої перевірки полягає у наступному [4]:
Обчислюється вираз
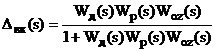
і за ним визначаються 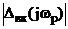 та
та
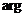
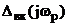 , де
, де 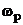 -
частота, при якій визначені оптимальні значення Кд, Тд.
-
частота, при якій визначені оптимальні значення Кд, Тд.
Якщо виконуються умови
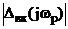 - 1 < 0.1;
- 1 < 0.1;
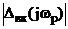 > -5º,
> -5º,
то припущення щодо малої
інерційності випереджуючого контуру допустиме.
У випадку, коли умови (2.28) не
виконуються, розрахунок оптимальних параметрів настроювання слід здійснювати
сумісно (відшукувати оптимум одночасно у просторі параметрів настроювання Кд,
Тд, Кр, Ті).
Головні недоліки описаного методу
полягають в тому, що, по-перше, тут лише частково враховується взаємозалежність
процесів у контурах системи, а, по-друге, він дає прийнятні результаті тільки
при великій різниці в інерційності допоміжної та головної ділянок об’єкта.
.1.2 Метод інформаційної моделі
Цей метод дає змогу розрахувати
каскадну АСР з урахуванням характеристик діючих збурень, не вводячи обмежуючих
припущень щодо різної інерційності контурів [ 6 ].
При застосуванні цього методу
замкнена АСР розглядається як еквівалентний розімкнений канал передачі
інформації. З інформаційних позицій точність системи тим вища, чим вища її
пропускна здатність (кількість інформації, яка може бути передана за одиницю
часу), оскільки вона визначає граничну динамічну точність усієї системи. За
критерій оптимальності приймається
ΔR = Rx - Rφ = макс,
де Rx
, Rφ - пропускна здатність системи для
сигналів завдання та збурення відповідно.
Для розповсюдженого у промислових
умовах випадку низькочастотних збурень цей доволі складний метод значно
спрощується і вибір оптимальних значень параметрів настроювання зводиться до
пошуку трьох величин С0 = Кр /Ті; С1 = Кр; С3 = 1/Кд з системи рівнянь
дС3/ дС1 = 0; дС0/ дС3 = 0; ψ(C0,
C1, C3) = 0
у такій послідовності.
. Значення Тд вибирається
максимально можливим для диференціатора, що застосовується у цій системі. У
такому випадку Wд(s) ≈ Кд.
Двоконтурна система перетворюється в
одноконтурну з еквівалентним об’єктом
(s) = Wo(s) + KдWoz(s) ≈
KдWoz(s).
Використовуючи передавальну функцію
еквівалентного об’єкта (2.31), при різних значеннях Кд (С3,1; C3,2…C3,n) ,
будують (за методом розширених КЧХ) у площині С0 - С1 границі області заданого
запасу стійкості С0 = f(C1) при C3,n = const.
Вздовж кривої, що з’єднує максимуми
границь областей заданого запасу стійкості для різних C3,n , з умови dC0
макс/dC3 визначають С0 опт, С1 опт, С3 опт, а по них - оптимальні значення Кд,
Кр, Ті.
Недоліки описаного методу пов’язані
з використанням спрощених передавальних функцій дифереціатора та еквівалентного
об’єкта, а також необхідністю побудови графіків.
Крім розглянутих вище методів,
беручи до уваги можливість зведення КАСР2н до структури, аналогічної системі з
коректуючим і стабілізуючим регуляторами (КАСР1н), вона може бути розрахована
за методами, розробленими для КАСР1н, що розглядаються, наприклад, в [13, 14].
3.
Задачі
дослідження
Для дослідження каскадної АСР з
динамічною корекцією прийняти об’єкт - пароперегрівник парового котла
енергетичного блоку потужністю 800 МВт з передавальними функціями [2]:
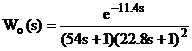
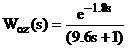
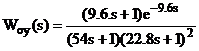
Сталі часу і запізнення у формулах
(3.1) - (3.3) виражені в секундах.
. Передавальні функції регулятора і
диференціатора:
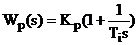
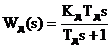
За методом багатокритеріального
оптимуму розрахувати оптимальні параметри настроювання регулятора і
диференціатора з урахуванням взаємозалежності контурів каскадної системи.
Дослідити перехідні процеси у двоконтурній
системі по основних вхідних-вихідних координатах при оптимальних параметрах
настроювання регулятора і диференціатора.
Виконати порівняльний аналіз
показників якості процесів регулювання в одноконтурній системі та в каскадній
АСР з динамічною корекцією.
4. Параметричний синтез двоконтурної
АСР з динамічною корекцією
.1 Метод багатокритеріальної
параметричної оптимізації АСР
При розв’язанні задач оптимізації
АСР необхідно орієнтуватися на технологічно і економічно обґрунтовані критерії
управління. Суперечливість різноманітних вимог, що ставляться до системи,
вимагає застосування багатьох критеріїв. Існують спроби звести їх до одного
узагальненого показника, суб’єктивно приписуючи кожному окремому критерію, що
входить в нього, деяку вагу. В кінцевому підсумку це призводить до такого ж
довільного “оптимального” рішення. Отже задача оптимального управління тим чи
іншим технологічним процесом повинна ставитися і розв’язуватися як
багатокритеріальна.
Внаслідок неконтрольованості
збурень, що діють на об’єкт, та їх статистичної невизначеності реальне
розв’язання задачі синтезу систем управління полягає у максимальному віддаленні
у лівій півплощині усіх полюсів передавальної функції замкненої системи від
уявної осі.
Надмірне наближення полюсів системи
до уявної осі не відповідає вимогам швидкого протікання і стійкості її вільного
руху. Віддалення від уявної осі навіть усіх полюсів ще не гарантує інтенсивного
згасання вільного руху системи. Тому в теорії і практиці автоматичного керування
використовуються відповідні обмеження
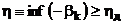
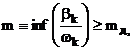
де 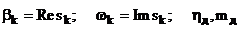 -
допустимі значення h і m;
-
допустимі значення h і m; 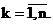
Вирази (4.1), (4.2) є частковими
критеріями модального керування, переваги та недоліки їх використання добре
відомі:
на відміну від безрозмірного
показника m, практично важливі значення якого знаходяться у порівняно вузьких
межах, величина h має розмірність і може
змінюватися в залежності від типу і призначення системи;
мінімум h
забезпечує повне згасання усіх компонент перехідного процесу протягом деякого
часу, однак, при цьому можлива присутність відносно слабо згасаючих
високочастотних коливань;
мінімум m забезпечує можливість
досягнення інтенсивного згасання усіх компонент незалежно від частоти (але у
цьому випадку не виключається наявність низькочастотних складових, які
затягують перехідний процес).
У зв’язку з цим доцільно
застосовувати обидва критерії, причому h
може слугувати в якості оцінки швидкодії системи, що підлягає оптимізації.
Існує й інший модальний критерій
швидкодії системи, а саме, середньогеометричний полюс
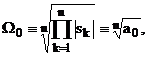
де а0 - вільний член
характеристичного рівняння замкненої АСР.
Для визначення границь областей
простору параметрів настроювання системи, у яких виконується (4.1), або (4.2),
широко використовується апарат розширених комплексних частотних характеристик
[1, 2, 6].
Розширена КЧХ, як і звичайна КЧХ, є
частковим випадком частотної передавальної функції і її можна одержати за
допомогою підстановок  або
або 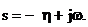
У випадку звичайної КЧХ W(jw)
системи в розімкненому стані вираз 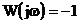 є
необхідною і достатньою умовою знаходження хоча б пари комплексно-спряжених
полюсів замкненої системи на уявній осі. Аналогічні рівняння для розширених
КЧХ:
є
необхідною і достатньою умовою знаходження хоча б пари комплексно-спряжених
полюсів замкненої системи на уявній осі. Аналогічні рівняння для розширених
КЧХ:
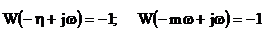
є умовами знаходження цієї пари
полюсів на вертикальній осі h і променях,
що виходять з початку координат у лівій півплощині під кутом arctg mд до
від’ємної та додатньої півосей .
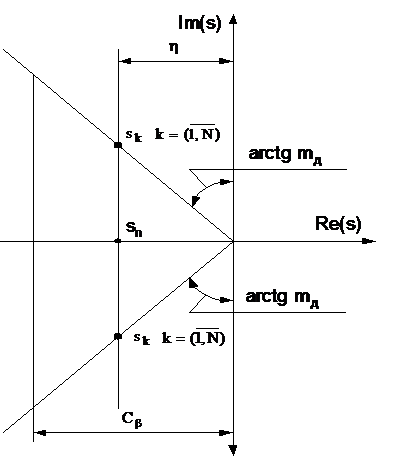
Рис.4.1. Область оптимального
розміщення полюсів системи (при n = 2N дійсний полюс sn відсутній).
Підставляючи h
= hд, і m = mд в умови (4.4), можна
визначити для кожного значення частоти w
точку поверхні, що обмежує область заданого гранично допустимого значення h
або m.
Як показано в [15], у цих областях
може бути досягнений одночасний оптимум (4.1), (4.3) та деяких інших функцій
управління. Вибір вказаних функцій базується на економічному обґрунтуванні
вимог, що ставляться до протікання того чи іншого технологічного процесу.
Таким чином, багатокритеріальність
модального управління може бути досягнута максимізацією (4.3) при обмеженні
(4.2), а також швидкості зміни та потужності керуючих дій.
У теорії автоматичного керування
відомо багато різних критеріїв якості, у тому числі так звані узагальнені критерії
якості [7-12], що використовуються при аналітичному конструюванні регуляторів.
Однак, незважаючи на зручності аналітичного використання, узагальнені критерії
не можуть бути рекомендовані, враховуючи неявне припущення, що нестача в одному
частковому показнику може бути компенсована за рахунок іншого. Крім цього,
проблема вибору відповідних вагових коефіцієнтів ускладнюється тим, що вони
залежать від значень часткових показників, які входять у цільову функцію і
обмежень на допустимі значення цих показників [16]. Тому найбільш правильною
при проектування АСР треба вважати вимогу щоб показники якості її
функціонування наближалися до оптимуму одночасно, в іншому випадку навіть
працездатна система виявиться неефективною.
Метод багатокритеріальної параметричної
оптимізації АСР найбільш повно обгрунтований у роботі [15]. Зокрема, у ній
вказується, що ефективність керування технологічним процесом не може бути
повністю охарактеризована за допомогою лише одного часткового критерію. Для
розв’язання задачі багатокритеріального керування важливо визначити з
врахуванням похибок математичного опису об’єкта полюси та нулі лінійної
системи, що забезпечують одночасний оптимум найважливіших характеристик
усталених і перехідних процесів. Задача багатокритеріальної оптимізації
розглядається у припущенні повної керованості багатовимірної системи, іншими
словами, можливості розміщення полюсів у будь-якому наперед заданому положенні.
Щоб гарантувати інтенсивне згасання
вільних складових вихідного сигналу, обмежується розміщення коренів
характеристичного рівняння
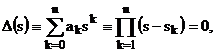
тобто полюсів системи sk:

де m, mд - показник коливності та
його допустиме значення.
Обмеження на потужність та швидкість
зміни керуючих дій записується у вигляді
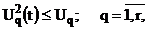
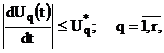
де 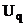 і
і
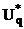 -
максимально допустимі потужність і швидкість керуючих дій, що подаються на q-й
вхід об’єкта.
-
максимально допустимі потужність і швидкість керуючих дій, що подаються на q-й
вхід об’єкта.
Умови (4.7), (4.8) доцільно
врахувати у вигляді обмежень на розміщення полюсів:
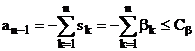
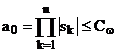
Нерівності (4.9), (4.10) ведуть до
додаткового обмеження на значення показника коливності:
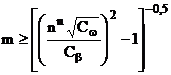
Для забезпечення максимуму запасу стійкості
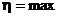
як одного з критеріїв швидкодії, з
врахуванням обмеження 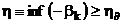 і (4.9) значення m
необхідно вибирати так, щоб виконувалася умова
і (4.9) значення m
необхідно вибирати так, щоб виконувалася умова
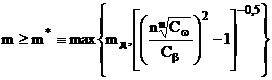
Вибір значення m у відповідності з
(4.13) гарантовано забезпечує виконання співвідношення (4.2). Крім того, при
виконанні (4.13) завдяки обмеженню (4.9) і нерівності (4.11) забезпечується
також виконання обмеження (4.10), тому в подальшому його окремо можна не
враховувати.
Таким чином, для лінійних автономних
систем в якості обмеження на розміщення полюсів застосовуються співвідношення
(4.1), (4.9) і (4.13). При вказаних обмеженнях вимога h
= max забезпечується тоді, коли полюси системи розміщені так, що
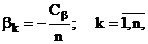
тобто їх дійсні частини є
однаковими.
Максимум середньогеометричного
полюса, як одного з критеріїв швидкодії системи, при обмеженнях (4.1), (4.9),
(4.13) і вимозі (4.14) досягається, якщо полюси 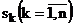 задовольняють
вимогам
задовольняють
вимогам
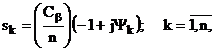
де 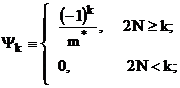
N - ціла частина від n/2.
У роботі [15] доведена теорема, за
якою замість (4.15) можна використовувати вимогу
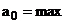
при обмеженнях таких самих, як і для
(4.15).
Одночасному наближенню до оптимальних
значень критеріїв економічної ефективності [15], сприяє також максимізація АЧХ
замкненої системи 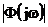 для будь-якого
значення
для будь-якого
значення 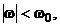 де
де
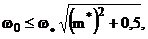
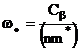 -
власна частота системи.
-
власна частота системи.
АЧХ |Ф(jw)|
характеризує фільтруючі властивості системи по відношенню до гармонічних
складових спектру збурень. Вимога оптимуму фільтруючих властивостей вступає у
протиріччя з вимогами забезпечення інтенсивності згасання вільного руху і
стійкості системи.
Розміщення полюсів системи у
відповідності з вимогами (4.15) забезпечує їй також і добрі фільтруючі
властивості, якщо основна вага спектральних густин збурень зосереджена в
області низьких частот, отже у багатьох випадках одночасно оптимізуються також
і критерії економічної ефективності.
У практиці автоматизації
технологічних процесів широко розповсюджені системи з об’єктами, що мають
запізнення. Характеристичне рівняння систем з запізнюючим аргументом є
трансцендентним і має нескінченне число коренів, які неможливо помістити у
будь-яке наперед задане положення за допомогою регулятора скінченної
розмірності.
У цьому випадку не лише умову
(4.15), але навіть обмеження (4.2) для усіх полюсів виконати не вдається.
Однак, і для систем з запізненням можна виділити домінуючі полюси і поставити
вимоги (4.15) з метою наближення до багатокритеріального оптимуму за умов
статистичної невизначеності.
Оскільки оптимізація системи
пов’язана із зміною h, а0, |Ф(jw)|,
то домінуючими є ті полюси, зміна розміщення яких найбільше впливає на зміну
вказаних критеріїв. В [15] показано, що у системах з запізнюючим аргументом
вказані критерії приймають значення, близькі до максимальних, при такому
розміщенні домінуючих полюсів:
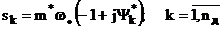
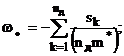
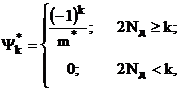
причому Nд - ціла частина від 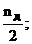
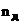 -
число домінуючих коренів.
-
число домінуючих коренів.
У такому випадку обмеження (4.1)
повинне виконуватися для усіх полюсів системи.
.1.1 Розрахунок параметрів
настроювання неперервних ПІ- регуляторів з умов багатокритеріального оптимуму
Застосування цього методу для
параметричної оптимізації систем з типовими регуляторами пов’язане з деякими
особливостями подібних АСР.
Системи з типовими регуляторами
відносяться до систем з неповним зворотним зв’язком за станом. Звичайно цей
зв’язок здійснюється лише по скалярному вихідному сигналу об’єкта , тобто по
доступній прямому контролю змінній стану - регульованій величині. Отже,
виконати вимоги (4.15), для усіх полюсів такої системи звичайно не вдається.
Крім того, для багатьох промислових об’єктів характерним є запізнення у
регулюючому каналі. Тому розрахунок параметрів настроювання типових регуляторів
зводиться до вибору їх параметрів на основі вимоги (4.17) лише для домінуючих
полюсів.
Двоконтурна АСР, що досліджується в
цій роботі, у відповідності з завданням містить ПІ-регулятор у внутрішньому
контурі та еквівалентний ПІ-регулятор у зовнішньому контурі. Тому необхідно
конкретизувати умови багатокритеріального оптимуму саме для систем з
ПІ-регуляторами.
Отже, в АСР з ПІ-регулятором і
об’єктом, що описується дробово-раціональною передавальною функцією 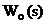 не
нижче другого порядку, або трансцендентною функцією від s, вимоги (4.17) можна
виконати для
не
нижче другого порядку, або трансцендентною функцією від s, вимоги (4.17) можна
виконати для 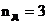 домінуючих полюсів
:
домінуючих полюсів
:

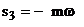
Дійсно, оскільки полюси 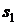 і
і
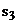 є
коренями характеристичного рівняння системи
є
коренями характеристичного рівняння системи
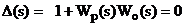
то повинні виконуватися рівності :
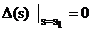
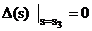
Прирівнюючи до нуля дійсні та уявні
частини рівняння (4.21), і враховуючи (4.22), можна отримати систему з трьох
дійсних рівнянь :
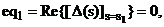
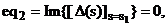

Розв’язок цієї системи за допомогою
будь-якого числового методу дає можливість знайти значення параметрів
настроювання ПІ-регулятора - 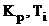 , а також власної
частоти
, а також власної
частоти 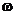 системи,
які відповідають вимогам (4.17).
системи,
які відповідають вимогам (4.17).
.1.2 Особливості розрахунку
каскадної АСР з динамічною корекцією за методом багатокритеріального оптимуму
На підставі структурних схем
(рис.2.4, рис.2.5) можна зробити висновок, що каскадна система може бути
розрахована за методом багатокритеріального оптимуму трьома способами:
Виходячи з припущення про повне
частотне розділення контурів системи, і, беручи до уваги рис.2.4 та вираз
(2.4), можна отримати характеристичні поліноми для зовнішнього та внутрішнього
контурів відповідно

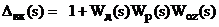
Підставляючи у (4.24), (4.25) вирази
для коренів (4.18), (4.19), одержимо дві системи з трьох рівнянь кожна,
аналогічних системі (4.23). Розв’язуючи ці системи одним з числових методів,
можна визначити параметри настроювання диференціатора - Кд, Тд і власну частоту
ω
зовнішнього
контуру, а також параметри регулятора - Кр, Ті і частоту власних коливань Ω
внутрішнього
контуру. Необхідно підкреслити, що першою потрібно розв’язувати систему
рівнянь, яка описує зовнішній контур, оскільки в систему рівнянь, яка описує
внутрішній контур, крім параметрів регулятора входять також і невідомі ще
параметри диференціатора.
При необхідності розрахунок можна
доповнити процедурою перевірки прийнятої гіпотези про незалежність процесів у
контурах системи за виразами (2.27), (2.28).
Другий спосіб розрахунку (подібно до
описаного у п.2.1.1) дає змогу частково врахувати взаємозалежність процесів у
контурах каскадної системи. При цьому для розрахунку за основу беруться
структури рис.2.4а і рис.2.5б, а також вирази (3.3), (2.19). Далі, як і в
попередньому випадку, формується та розв’язується система рівнянь, що описує
багатокритеріальний оптимум для зовнішнього контуру. В результаті знаходять
параметри диференціатора та частоту власних коливань зовнішнього контуру.
Наступним кроком є формування на
підставі рис.2.5б, а також виразів (2.19), (2.23), (4.21), (4.22) системи
рівнянь, аналогічної системі (4.23), яка описує умови багатокритеріального
оптимуму двоконтурної системи загалом. Розв’язок цієї системи рівнянь дає
значення параметрів регулятора і частоти Ω. В
разі необхідності розв’язок також можна доповнити перевіркою коректності
прийнятого припущення про частотну незалежність контурів.
Третій спосіб розрахунку грунтується
на використанні структур рис.2.5., що є одноконтурними еквівалентами
двоконтурної системи. Обидві ці системи, природньо, мають, як було показано
вище, одне й те ж характеристичне рівняння (2.23), яке містить чотири
параметри, що підлягають визначенню. Алгоритм розрахунку, який дає можливість
знайти розв’язок оптимізаційної задачі у просторі чотирьох параметрів
настроювання - Кд, Тд, Кр, Ті (а крім того ще й Ω
та
ω)
полягає
у наступному.
Задаються шість коренів
характеристичного рівняння (2.23) у вигляді:

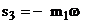
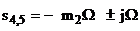

Підставляючи корені s1, s3, s4, s6 у
характеристичне рівняння (2.23), і виділяючи його дійсні та уявні частини,
отримуємо систему з шести нелінійних алгебраїчних рівнянь, яка й визначає умови
досягнення багатокритеріального оптимуму для двоконтурної системи з урахуванням
взаємозалежності її контурів:
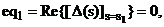
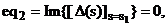
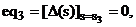
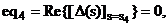
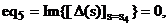

Розв’язавши цю систему рівнянь за
допомогою одного з числових методів, одночасно можна отримати значення
оптимальних параметрів настроювання диференціатора і регулятора, а також частот
ω
і
Ω.
При
цьому значення показників коливності m1, m2, які характеризують запаси
стійкості зовнішнього та внутрішнього контурів системи, в загальному випадку
можуть бути різними, однак, більш доцільно задавати для обох контурів деяке
однакове значення m, тобто m1 = m2 = m.
До цього треба додати, що рівняння,
які входять у систему (4.30), при складних передавальних функціях об’єкта,
наприклад, таких, як (3.1) - (3.3), є дуже громіздкими, так що навіть вивести
їх “ручним” способом практично неможливо. Очевидно, ще складнішою є задача
розв’язку системи таких рівнянь. Проте вказані труднощі досить легко обійти за
допомогою пакету символьної математики MAPLE V [17, 18]. Описаний алгоритм
оптимізації легко програмується і задача швидко розв’язується навіть за
допомогою комп’ютера з обмеженою пам’яттю та швидкодією.
.2 Програмна реалізація методу
багатокритеріального оптимуму та моделювання системи
З метою оптимального розрахунку
параметрів настроювання регулятора та диференціатора розроблена програма мовою
MAPLE V. Програма розрахунку каскадної АСР з динамічною корекцією (Додаток 2)
розрахована на роботу в діалоговому режимі. Вона, зокрема, передбачає :
- завдання передавальної функції
об’єкта та його параметрів;
- виведення передавальної
функції еквівалентного коректуючого регулятора;
- автоматичне виведення системи
з шести нелінійних алгебраїчних рівнянь, що описує умови досягнення
багатокритеріального оптимуму для двоконтурної системи;
- завдання значення показника
коливності m для внутрішнього та зовнішнього контурів;
- числовий розв’язок системи
рівнянь, в результаті якого визначаються оптимальні параметри регулятора - Кр,
Ті, диференціатора - Кд, Tд, а також власна частота внутрішнього контуру Ω
і
зовнішнього контуру - ω;
- можливість розв’язання задачі
оптимізації будь-яким з описаних у п.4.1.2 методів;
- обчислення деяких допоміжних
величин (Крк, Кік, Кіс, KдTд), необхідних для моделювання АСР.
З метою дослідження перехідних
процесів у каскадній АСР при різних значеннях параметрів настроювання
регулятора і диференціатора та різних вхідних величинах за допомогою засобів
імітаційного моделювання SIMULINK, що входить до популярного пакету МАТLAB
[19], розроблена відповідна модель (рис.4.2). Модель побудована так, що дає
можливість одночасно досліджувати перехідні процеси в АСР по різних каналах і
порівнювати процеси, що відбуваються у внутрішньому та зовнішньому контурах.
Регулятор та еквівалентний
коректуючий регулятор моделюються у вигляді передавальних функцій:
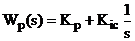
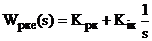
де 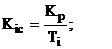
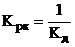 ;
; 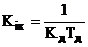 .
.
Модель передбачає також визначення
інтегрального квадратичного критерію якості процесів за формулою
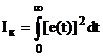
Числові значення цього критерію
відображаються на дисплеях, що дає змогу об'єктивно оцінювати і порівнювати
якість процесів регулювання у контурах системи.
Модель забезпечує також відображення
на графіках границь, наприклад, п’ятипроцентного відхилення від усталеного
значення, що дає змогу оцінювати тривалість перехідних процесів, тобто час
регулювання.
.3 Результати дослідження каскадної
АСР та їх аналіз
За допомогою програми (Додаток 2)
були розраховані оптимальні параметри настроювання диференціатора і регулятора
(табл.4.1) при різних значеннях показника коливності. Це пояснюється тим, що,
по-перше, важко обгрунтувати його допустиме значення mд, оскільки для систем
вище другого порядку не існує однозначної залежності між показником коливності
і досить наочним коефіцієнтом згасання коливань, а, по-друге, важко задати у
конкретному числовому вигляді обмеження на швидкість зміни та потужність
керуючих дій. Тому для вибору значення m , а, отже, і параметрів настроювання ,
треба брати до уваги деякі додаткові критерії, наприклад, інтегральну
квадратичну оцінку процесів регулювання.
Необхідно також вказати, що дані
табл.4.1 отримані в результаті розрахунку системи за третім з описаних вище
способів, тобто з урахуванням взаємозалежності контурів при однаковому значенні
показників їх коливності.
При знайдених параметрах
настроювання (для різних прийнятих значень m) за допомогою моделі (рис.4.2)
були досліджені перехідні процеси у двоконтурній системі при відпрацюванні
завдання регулятору, а також компенсації збурень f і n1, тобто саме тих збурень
для ліквідації яких, власне, й застосовуються системи з динамічною корекцією.
Аналізуючи дані табл.4.1, варто
звернути увагу на те, що коефіцієнт підсилення регулятора у три і більше разів
є більшим, ніж у еквівалентного коректуючого регулятора, а частота власних
коливань внутрішнього контуру більш ніж у двадцять разів перевищує власну
частоту зовнішнього контуру.
Таблиця 4.1 - Параметри настроювання
регулятора і диференціатора у двоконтурній КАСР2н.
|
m
|
Kp
|
Ti, c
|
Ω, c-1
|
Kд
|
Tд, c
|
ω, c-1
|
Kic
|
Kpk
|
Kik
|
KдTд
|
|
0.221
|
14.00
|
6.65
|
0.727
|
0.38
|
109.50
|
0.036
|
2.10
|
2.61
|
0.024
|
42.01
|
|
0.25
|
12.01
|
6.21
|
0.703
|
0.42
|
101.43
|
0.034
|
1.93
|
2.35
|
0.023
|
43.07
|
|
0.30
|
9.42
|
5.69
|
0.663
|
0.50
|
91.35
|
0.032
|
1.65
|
2.00
|
0.022
|
45.64
|
|
0.367
|
7.04
|
5.28
|
0.613
|
0.61
|
82.38
|
0.029
|
1.33
|
1.65
|
0.020
|
49.99
|
|
0.40
|
6.19
|
5.15
|
0.590
|
0.66
|
79.14
|
0.027
|
1.20
|
1.51
|
0.019
|
52.36
|
|
0.50
|
4.40
|
4.94
|
0.525
|
0.83
|
72.16
|
0.024
|
0.89
|
1.20
|
0.017
|
60.04
|
|
0.60
|
3.33
|
4.90
|
0.470
|
1.00
|
67.74
|
0.021
|
0.68
|
1.00
|
0.015
|
67.91
|
|
0.70
|
2.65
|
4.93
|
0.422
|
1.17
|
64.76
|
0.019
|
0.54
|
0.86
|
0.013
|
75.55
|
|
0.80
|
2.21
|
5.00
|
0.382
|
1.32
|
62.64
|
0.017
|
0.44
|
0.76
|
0.012
|
82.71
|
Основні характеристики перехідних
процесів наведені у табл. 4.2, а самі перехідні процеси відображені на рис.4.3
- рис.4.9.
При дослідженні перехідних процесів
фіксувалися максимальні значення допоміжної zm та основної ym регульованих
величин, максимальні значення вихідних сигналів регулятора ump і еквівалентного
коректуючого регулятора umкр, час регулювання tpz по допоміжній і tpy по
основній регульованих величинах, а також значення інтегральних квадратичних
критеріїв Ікz, Iкy відповідних процесів по помилці регулювання. При цьому для
процесів компенсації збурень час регулювання по основній регульованій величині
не визначався, оскільки її відхилення є значно меншими від загальноприйнятої
п’ятипрoцентної зони.
У табл. 4.2 наведена також сумарна
інтегральна квадратична оцінка IкΣ = Ікz
+ Ікy процесів відпрацювання завдання для внутрішнього та зовнішнього контурів
системи.
Таблиця 4.2 - Показники якості
перехідних процесів у двоконтурній КАСР2н.
|
m
|
Контур еквівалентного стабілізуючого
регулятора
|
Контур еквівалентного коректуючого регулятора
|
IkΣ
|
|
zm
|
umр
|
Iкz
|
tpz, c
|
ym
|
umкр
|
Iкy
|
tpy, c
|
|
|
По завданню
|
|
|
0.221
|
4.38
|
17.8
|
26.29
|
400
|
1.35
|
3.00
|
45.99
|
300
|
72.28
|
|
0.30
|
3.10
|
12.3
|
13.12
|
350
|
1.26
|
2.41
|
46.66
|
260
|
59.78
|
|
0.367
|
2.50
|
9.40
|
8.81
|
290
|
1.21
|
2.07
|
48.60
|
275
|
57.41
|
|
0.40
|
2.27
|
8.30
|
7.37
|
300
|
1.19
|
1.94
|
49.85
|
280
|
57.22
|
|
0.50
|
1.69
|
6.00
|
4.72
|
235
|
1.14
|
1.66
|
54.16
|
210
|
58.87
|
|
0.60
|
1.45
|
4.55
|
3.40
|
240
|
1.10
|
1.47
|
58.48
|
220
|
61.88
|
|
По збуренню f
|
|
|
0.221
|
0.21
|
-1.50
|
0.19
|
16.0
|
0.011
|
-0.037
|
0.005
|
-
|
-
|
|
0.30
|
0.30
|
-1.47
|
0.21
|
9.0
|
0.012
|
-0.032
|
0.006
|
-
|
-
|
|
0.367
|
0.23
|
-1.42
|
0.24
|
9.0
|
0.013
|
-0.030
|
0.008
|
-
|
-
|
|
0.40
|
0.23
|
-1.39
|
0.25
|
9.0
|
0.013
|
-0.030
|
0.009
|
-
|
-
|
|
0.50
|
0.24
|
-1.35
|
0.29
|
11.0
|
0.015
|
-0.030
|
0.012
|
-
|
-
|
|
0.60
|
0.25
|
-1.34
|
0.33
|
11.0
|
0.017
|
-0.030
|
0.016
|
-
|
-
|
|
По збуренню n1
|
|
|
0.221
|
-0.60
|
-6.3
|
3.21
|
18.0
|
0.012
|
-0.039
|
0.006
|
-
|
-
|
|
0.30
|
-0.57
|
-5.8
|
3.24
|
18.0
|
0.012
|
-0.034
|
0.007
|
-
|
-
|
|
0.367
|
-0.50
|
-5.4
|
3.18
|
14.0
|
0.013
|
-0.030
|
0.009
|
-
|
-
|
|
0.40
|
-0.46
|
-5.3
|
3.14
|
14.0
|
0.014
|
-0.030
|
0.010
|
-
|
-
|
|
0.50
|
-0.40
|
-4.8
|
3.14
|
15.0
|
0.015
|
-0.030
|
0.014
|
-
|
-
|
|
0.60
|
-0.34
|
-4.4
|
3.12
|
11.0
|
0.017
|
-0.030
|
0.017
|
-
|
-
|
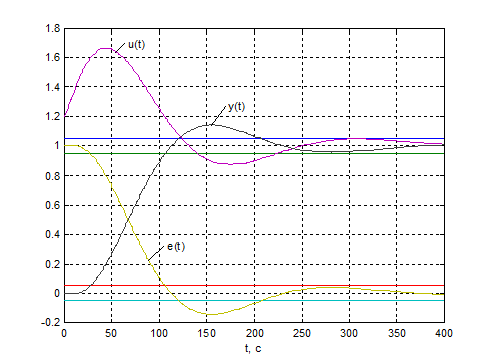
Рис.4.3. Перехідні процеси у
зовнішньому контурі КАСР2н при відпрацюванні сигналу завдання (m = 0.5).
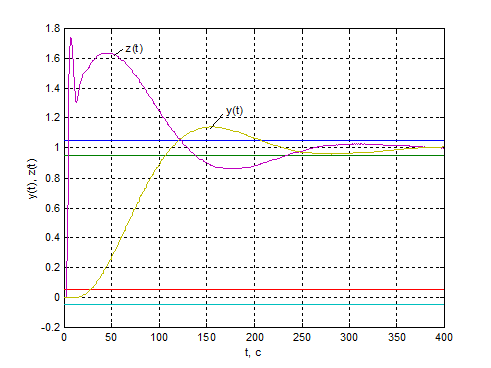
Рис.4.4. Перехідні процеси по
основній та допоміжній регульованих величинах у КАСР2н при відпрацюванні
сигналу завдання (m = 0.5).
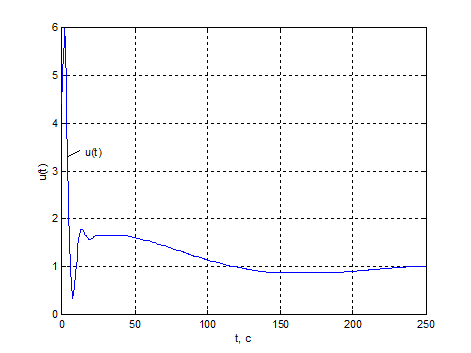
Рис.4.5. Регулююча змінна при
відпрацюванні сигналу завдання у двоконтурній КАСР2н.
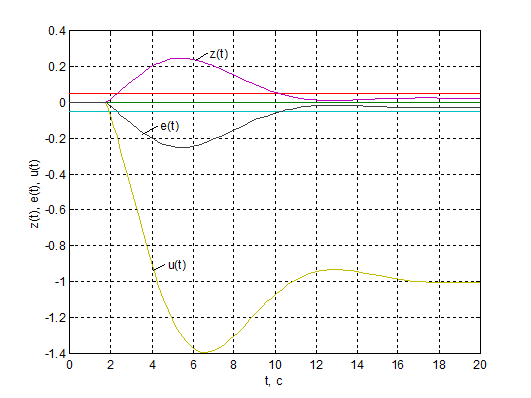
Рис.4.6. Перехідні процеси у
внутрішньому контурі КАСР2н при компенсації сигналу збурення f (m = 0.5).
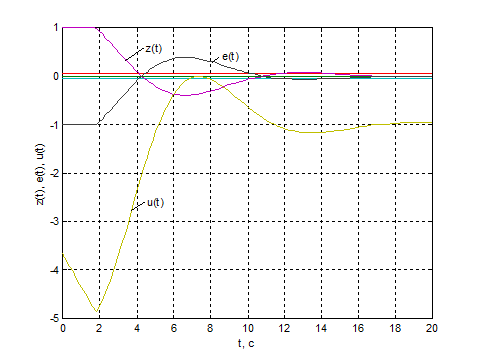
Рис.4.7. Перехідні процеси у КАСР2н
при компенсації збурення n1 ( m = 0.5).
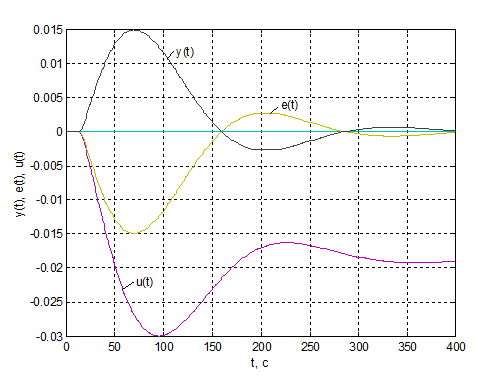
Рис.4.8. Перехідні процеси у
зовнішньому контурі КАСР2н при компенсації збурення f ( m = 0.5).
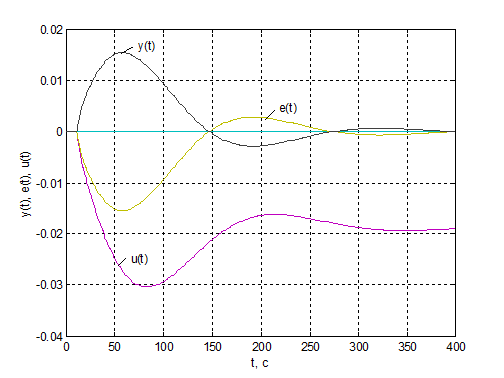
Рис.4.9. Перехідні процеси у
зовнішньому контурі КАСР2н при компенсації збурення n1 ( m = 0.5).
За результатами дослідження
перехідних процесів у каскадній системі з динамічною корекцією можна зробити
висновки:
Абсолютне значення відхилення
допоміжної регульованої величини z для процесів відпрацювання завдання та
компенсації збурення n1 із зростанням m зменшується, а для процесу по збуренню
f - збільшується.
Динамічне відхилення основної
регульованої величини y із зростанням m при відпрацюванні завдання зменшується,
а у процесах компенсації збурень f та n1 - зростає, причому, в останньому
випадку значення ym практично збігаються.
Абсолютне значення вихідних сигналів
регулятора та еквівалентного коректуючого регулятора в усіх процесах при
збільшенні m зменшується, при цьому найбільшими є значення ump для процесів по
завданню, а найменшими - при компенсації збурення f.
Інтегральна квадратична оцінка
процесів у внутрішньому контурі при зростанні m зменшується при відпрацюванні
завдання і зростає при компенсації збурення f.
Інтегральна квадратична оцінка
процесів у зовнішньому контурі в залежності від m при відпрацюванні завдання
має складний, немонотонний характер, а її значення для процесів компенсації
збурень настільки малі, що ними можна нехтувати.
Час регулювання при відпрацюванні
завдання в обох контурах системи при зростанні m спочатку зменшується, а потім
починає зростати. При цьому тривалість процесів по збуреннях у внутрішньому
контурі є у двадцять і більше разів меншою, ніж процесів по завданню.
Значення zm, ump,, Iкz, tpz для
внутрішнього контуру при компенсації збурення f набагато менші, ніж при дії
збурення n1 .
Загалом при виборі значень
параметрів настроювання у такій системі можна орієнтуватися на такі додаткові
критерії, як ІкΣ = мін,
мінімальне значення регулюючої дії, або мінімальний час регулювання. Саме
останній варіант і прийнятий для побудови графіків на рис.4.3 - рис.4.9.
.4. Порівняльна оцінка характеристик
АСР з динамічною корекцією і одноконтурної системи
Щоб зробити кінцевий висновок про
доцільність реалізації каскадної системи з динамічною корекцією для регулювання
заданого об’єкта необхідно виконати аналіз її основних характеристик у
порівнянні з одноконтурною системою, точніше, треба порівняти показники якості
процесів відпрацювання завдання і компенсації збурення, що діє на вхід об’єкта,
в одноконтурній системі і зовнішньому контурі каскадної системи.
Для порівняння візьмемо одноконтурну
систему з різними типами регуляторів, перехідні процеси у якій показані на
рис.4.10 і рис.4.11 [20, 21].
Таблиця 4.3 - Показники якості
перехідних процесів в одноконтурній системі і каскадній АСР з динамічною
корекцією.
|
Тип АСР
|
Тип регулятора
|
m
|
По завданню
|
По збуренню f
|
IkΣ
|
|
|
|
ygm
|
Ikg
|
tpg, c
|
yfm
|
ufm
|
Ikf
|
tpf, c
|
|
|
Одноконтурна АСР
|
ПІн
|
0.221
|
1.28
|
2.25
|
58.9
|
375
|
0.45
|
-1.26
|
17.5
|
380
|
76.46
|
|
ПІД1н
|
0.80
|
1.45
|
3.05
|
59.0
|
250
|
0.33
|
-1.34
|
7.39
|
170
|
66.40
|
|
ПІД2н
|
0.70
|
1.36
|
19.0
|
43.5
|
240
|
0.33
|
-1.38
|
7.45
|
240
|
50.94
|
|
ПІД3н
|
0.70
|
1.34
|
8.0
|
45.8
|
250
|
0.36
|
-1.34
|
9.07
|
260
|
54.85
|
|
КАСР2н
|
ПІн-ПІн
|
0.50
|
1.14
|
1.66
|
54.16
|
210
|
0.015
|
-0.03
|
0.012
|
-
|
58.9
|
З порівняння даних табл.4.3, а також
рис.4.3 і рис.4.10 та рис.4.8 і рис.4.11 видно, що при відпрацюванні сигналу
завдання каскадна АСР має значно кращі показники порівняно з будь-якою
одноконтурною системою щодо максимального відхилення основної регульованої
величини і часу регулювання, але дещо програє за інтегральною квадратичною
оцінкою.
У процесах компенсації збурення f,
яке діє на вхід об’єкта по каналу регулювання, а також зовнішнього по
відношенню до випереджуючої ділянки об’єкта збурення n1 переваги каскадної
системи незаперечні. Зокрема, відхилення основної регульованої величини у
процесах компенсації цих збурень у двадцять і більше разів менше, ніж в
одноконтурній системі, тобто система КАСР2н фактично є інваріантною відносно
збурень, які діють на допоміжну ділянку об’єкта. Це підтверджується і тим, що
значення інтегрального квадратичного критерію процесів компенсації вказаних збурень
в КАСР2н у сотні разів менші, ніж аналогічні оцінки для одноконтурної системи.
Таким чином, наведений порівняльний
аналіз показує високу ефективність застосування каскадної системи з динамічною
корекцією для регулювання складних у динамічному відношенні об’єктів.
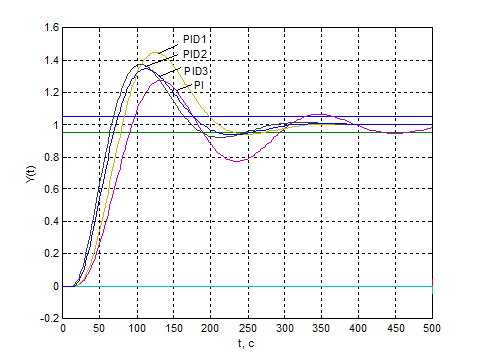
Рис.4.10. Перехідні процеси в
одноконтурній АСР з неперервними регуляторами при відпрацюванні сигналу
завдання.
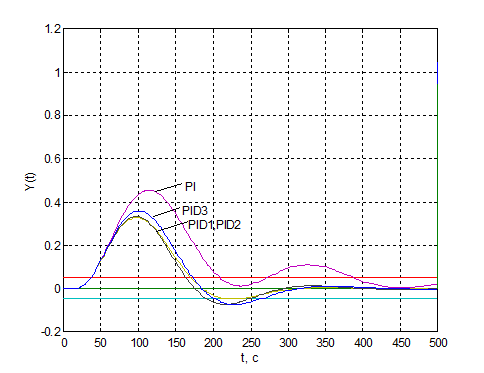
Рис.4.11. Перехідні процеси в
одноконтурній АСР з неперервними регуляторами при компенсації сигналу збурення,
що діє на вхід об’єкта.
Висновок
Дослідження двоконтурної
автоматичної системи регулювання з динамічною корекцією, виконані у цій роботі,
дають підстави для таких основних висновків:
Метод багатокритеріального оптимуму
може бути успішно застосований для параметричного синтезу двоконтурних АСР в
просторі усіх параметрів настроювання без введення обмежень щодо співвідношення
інерційності внутрішнього та зовнішнього контурів.
Прямі показники якості процесів
регулювання при відпрацюванні сигналу завдання у каскадній системі є кращими,
ніж в одноконтурній системі з будь-яким типовим регулятором.
Збурення, що діють на допоміжну
ділянку об’єкта, компенсуються у двоконтурній системі настільки ефективно, що
стосовно цих збурень вона може вважатися інваріантною,
Зважаючи на те, що параметричний
синтез двоконтурної системи за методом багатокритеріального оптимуму
здійснюється досить легко, забезпечуючи одночасно її великі переваги порівняно
з одноконтурною системою, а також те, що реалізація такої системи за допомогою
сучасних технічних засобів не викликає особливих труднощів, саме двоконтурна
АСР може бути рекомендована для регулювання складних у динамічному відношенні
об’єктів.
Література
1. Автоматизация
настройки систем управления/ Под ред. В.Я.Ротача. - М.: Энергоатомиздат, 1984.
- 272 с.
. Ротач
В.Я. Теория автоматического управления теплоэнергетическими процессами.- М.:
Энергоатомиздат. 1985.-296с.
. Эрриот
П. Регулирование производственных процессов.- М.: Энергия, 1967. - 480 с.
. Ротач
В.Я. Расчет динамики промышленных автоматических систем регулирования. М.:
Энергия, 1973.- 440 с.
. Изерман
Р. Цифровые системы управления: Пер.с англ. - М.: Мир, 1984.- 541 с.
. Клюев
А.С. и др. Наладка систем автоматического регулирования барабанных паровых
котлов/А.С. Клюев.-М.: Энергоатомиздат, 1985.- 280 с.
. Зайцев
Г.Ф. Теория автоматического управления и регулирования.- К.: Вища шк., 1989 -
431 с.
. Бесекерский
В.А., Попов Е.П. Теория систем автоматического регулирования. - М.: Наука ,
1966.- 992с.
. Воронов
А.А. и др. Основы теории автоматического регулирования и управления. - М.:
Высшая школа, 1977.- 519с.
. Воронов
А.А. Основы теории автоматического управления. - М.Энергия, 1980.-312с.
. Теория
линейных систем автоматического регулирования и управления.-М.:Наука,
1978.-256с.
. Макаров
Н.М. Линейные автоматические системы.-М.:Машиностроение, 1982.-504с.
. Биленко
В.А.,Давыдов Н.И. Метод расчета на ЭЦВМ оптимальных параметров настройки
двухконтурных систем регулирования //Теплоэнергетика. 1977. №1. с.32-36.
. Ротач
В.Я. Расчет каскадных систем автоматического регулирования //Теплоэнергетика.
1997. №10. с.16-23.
. Шавров
А.В. Многокритериальное управление в условиях статистической
неопределенности.-М.: Машиностроение.-1990.-160с.
. Вентцель
Е.С. Исследование операций: Задачи, принципы, методология. - М.: Наука, 1980.-
208 с.
. Maнзон
Б.M. Maple V Power Edition.- M.: ”Филин”, 1998.-240с.
. Дьяконов
В.П. Математическая система Maple V R3/R4/R5.- М.: Солон, 1998.-399с.
. Гультяев
А.К. MATLAB 5.2. Имитационное моделирование в среде Windows: - СПб.:
Коронапринт, 1999.-288с.
. Ковела
І.М. Багатокритеріальна параметрична оптимізаця неперервних АСР з типовими
лінійними регуляторами//Автоматика, вимірювання та керування. Львів, 1998.
№324. с.3-9.
. Дудикевич
В.Б., Ковела І.М., Мороз Л.В., Іванюк О.П. Багатокритеріальна параметрична
оптимізація автоматичних систем регулювання з реальними ПІД-регуляторами.
Автоматика-2000, ч.1, Львів, 2000, с. 158-163.