Модель эластичной компьютерной сети
Содержание
Введение
1. Теоретические основы
1.1 Сети, их архетипы
1.2 Эластичные сети и молекулярные машины
2. Методы исследования
2. Объекты исследования
4. Исследования и результаты
Выводы
Библиография
Приложения
Введение
Научное исследование таких моделей, как компьютерные сети,
биологические сети, и социальные сети - это междисциплинарная область, которая
сочетает в себе идеи из математики, физики, биологии, информатики, социальных
наук и многих других областей. Используя понятие эластичной сети можно провести
анализ характеристик для динамических молекулярных структур, которые называются
молекулярные машины [1].
Используя принципы работы с эластичной сетью можно провести
оценку поведения структуры молекулярной машины во время динамического цикла.
Данное исследование предполагает оценку топологических
характеристик для эластичной сети, построенной на основе исследуемой
молекулярной машины. На основе данных характеристик проводится анализ
распределений и гистограмм основных характеристик [1].
1. Теоретические
основы
1.1 Сети, их
архетипы
В общем случае случайная сеть представляет собой модель, в которой
некоторый набор параметров принимают фиксированные значения, а другие являются
случайными [2,3]. Один из простейших примеров такой случайной сети является
сеть с фиксированными числом ребер m и
числом вершин n. В этом случае берутся n узлов сети и между ними случайным образом образуются n связей. По другому, данную сеть можно обозначить как
модель, которая создается путем равномерного выбора случайных множеств всех
простых графов с числом вершин равным n и
числом ребер равным m. Другое полностью эквивалентное
определение модели состоит в том, чтобы сказать, что сеть создается путем
равномерного выбора случайных множеств всех простых графов с числом вершин n и
количеством ребер m. Строго говоря случайная модель сети не
определена в терминах единственной произвольно генерируемой сети, а
представляет собой совокупность сетей, то есть в котором каждая из сетей имеет
определенную вероятность реализации, что значит, что каждая сеть ансамбля имеет
свой собственный статистический вес. Самым простейшим примером случайной сети
является классический случайный граф Эрдеша-Реньи, где в статистическом
ансамбле все возможные графы с числом узлов n и количеством связей m имеют
одинаковый статистический вес реализации. Иными словами для таких сетей будет
одинакова вероятность существования связи между любыми двумя узлами [2].
Рассмотрим модель 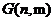 , для которой определено распределение вероятности
, для которой определено распределение вероятности 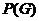 по всем графам
по всем графам 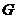 , где
, где 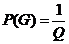 для простых графов с числом узлов n и числом ребер m, где
для простых графов с числом узлов n и числом ребер m, где 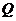 -общее количество таких простых графов.
Когда рассматривают свойства случайных сетей, то обычно это соответствует
средним свойствам ансамбля [2-4]. Например, диаметр
-общее количество таких простых графов.
Когда рассматривают свойства случайных сетей, то обычно это соответствует
средним свойствам ансамбля [2-4]. Например, диаметр 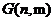 будет равен диаметру
будет равен диаметру 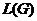 графа
графа 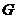 , усредненный по ансамблю
, усредненный по ансамблю
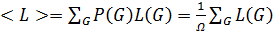
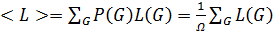 .
.
Множество таких средних свойств случайных графов могут быть
рассчитаны точно, по крайней мере, в пределе большого размера графика. Очень
часто нас интересуют характерные свойства сетей. Например, мы можем узнать
диаметр сети с заданным числом ребер. Конечно, существуют особые случаи сетей,
которые имеют существенно большие или существенно малые диаметры, но они не
показывают типовое поведение сети. Для расчета типового поведения, то средние
значения свойств по статистическому ансамблю может дать приближенное к точному
значение [2].
Для подробного описания сети необходимо дать понятия основных
характеристикам сети. Степень узла сети представляет собой число связей узла.
Данная характеристика является локальной характеристикой. Для задания
нелокальных характеристик используются понятия путь и цикл. Путь представляет
собой неповторяющуюся чередующуюся последовательность близлежащих узлов и
связей между ними. Цикл представляет из себя путь, при котором начальный узел
равен конечному узлу сети. Основной характеристикой сети является ее размер,
который представляет собой число узлов этой сети. Еще одной важной глобальной
характеристикой сети является кратчайшая длина пути. Если принимать длинны
связей сети между смежными узлами равными единице, то расстояние между узлами 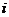 и
и 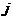 есть кратчайшее расстояние пути между ними. Диаметр сети
позволяет описать максимальное расстояние между узлами в исследуемой сети.
есть кратчайшее расстояние пути между ними. Диаметр сети
позволяет описать максимальное расстояние между узлами в исследуемой сети.
Существует несколько способов математического представления сети.
Лучшим представлением случайной сети для проведение математических и
статистических исследований является матрица смежности. Матрицей смежности A простого графа является матрица с элементами 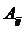 , такая, что
, такая, что

Необходимо учесть два замечания для матрицы смежности:
) Матрица смежности является симметричной, так как если
между узлами 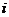 и
и 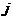 существует ребро, то и между
существует ребро, то и между 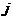 и
и 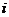 узлами существует ребро
узлами существует ребро
) Все диагональные матричные элементы все равны нулю, так
как связи у узла с самим собой нет
Еще одной важной характеристикой случайной сети является
распределение степеней 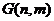 . Каждый узел в сети связан с некоторой
вероятностью
. Каждый узел в сети связан с некоторой
вероятностью 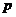 с каждой из
с каждой из 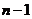 других узлов сети [3-5]. Таким образом
вероятность связи с
других узлов сети [3-5]. Таким образом
вероятность связи с 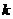 узлами будет определяться, как
узлами будет определяться, как
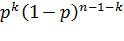
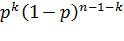 ,
,
Где 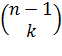
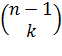 позволяет определить эти k узлов, а полная вероятность будет рассчитываться по следующей
формуле
позволяет определить эти k узлов, а полная вероятность будет рассчитываться по следующей
формуле
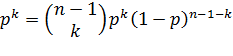
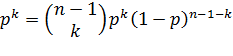 ,
,
которая представляет из себя биномиальное распределение. Другими
словами, 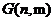 имеет биномиальное распределение
степеней. В большинстве случаев исследуются свойства больших сетей, поэтому
имеет биномиальное распределение
степеней. В большинстве случаев исследуются свойства больших сетей, поэтому  можно считать большим.
можно считать большим.
Средняя степень случайного графа обозначается как 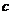 и вычисляется по формуле
и вычисляется по формуле
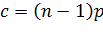
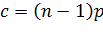 .
.
Так как n принимается
бесконечно большим, то p будет
бесконечно малым, что позволяет прийти к следующему
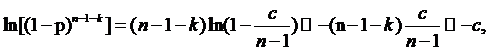
Данный логарифм представляется в виде ряда Тейлора, а при 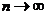 уравнение становится более точным [3].
Если рассматривать экспоненты по обе стороны уравнения, то
уравнение становится более точным [3].
Если рассматривать экспоненты по обе стороны уравнения, то 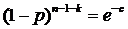 в пределах большого значения n что позволяет получить следующее равенство:
в пределах большого значения n что позволяет получить следующее равенство:
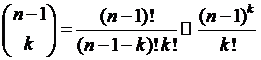
Если преобразовать данное уравнение, то получится следующее:
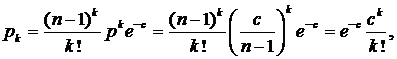
Данное уравнение в пределах большого значения n представляет собой распределение Пуассона, т.к.
распределение степеней для 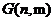 подчиняется распределению Пуассона. Данная модель представляется
эталонной для сравнения с другими исследуемыми моделями различных сетей.
подчиняется распределению Пуассона. Данная модель представляется
эталонной для сравнения с другими исследуемыми моделями различных сетей.
Для вычисление пуассоновского случайного графа используется
понятие коэффициента кластеризации, которая является мерой транзитивности в
сети и определяет вероятность того, что двое соседей узла являются соседями
друг друга [3-5].
В случайной сети график вероятности того, что любые две вершины
являются соседями, является точно тем же самым, что и для вероятности 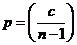 . Следовательно, коэффициент кластеризации
определяется следующей формулой
. Следовательно, коэффициент кластеризации
определяется следующей формулой
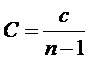
Это одна из нескольких характеристик, по которой случайный граф
резко отличается от большинства из реальных сетей, многие из которых имеют
довольно высокую степень кластеризации.
Еще одна важная характеристика при оценке графов является
центральность. Центральность-это мера, которая описывается числом кратчайших
путей, которое проходит через узел. Для каждой пары узлов в сети существует, по
крайней мере, хотя бы один такой кратчайший путь между вершинами, что, либо число
ребер, через которые проходит путь, либо сумма весов узлов сводится к минимуму.
Данная характеристика была описана Л. Фриманом в своей работе по описанию мер
центральностей узлов сети в 1977 году. Центральность позволяет описать степень
взаимодействия узлов соседей между собой. Например, в телекоммуникационной сети
узел с более высокой степенью центральности будет иметь больший контроль над
сетью, поскольку дополнительная информация будет проходить через этот узел [3].
Сети бывают направленными и ненаправленными. Направленная сеть или
ориентированный граф представляет собой сеть, в которой каждое ребро имеет
направление, указывающее от одной вершины к другой. Такие ребра сами называются
направленными ребрами. В данной дипломной работе исследуются ненаправленные
сети.
Помимо случайных сетей существуют сети других типов, например small-world
сеть и scale-free
сеть. Сеть small-world
представляет собой тип математического графа, в котором большинство узлов не
соседствуют друг с другом, но соседи любого заданного узла могут быть соседями
друг от друга, и большинство узлов могут иметь связь от каждого другого узла с
помощью небольшого количество шагов. В частности, сеть малого мира определяется
как сеть, где типичное расстояние L между двумя случайно выбранными узлами
(число требуемых шагов) растет пропорционально логарифму числа узлов N. Сеть scale-free или
безмасштабная сеть - это сеть, распределение которой по степенному закону, по
крайней мере, асимптотическое. То есть доля 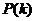 узлов в сети, имеющая k связей с другими узлами, при больших
значениях k принимает вид:
узлов в сети, имеющая k связей с другими узлами, при больших
значениях k принимает вид:
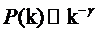 ,
,
где 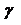 - это параметр, значение которого обычно
находится в диапазоне 2 <
- это параметр, значение которого обычно
находится в диапазоне 2 < 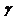 <3, хотя периодически он может оказаться за пределами этих
границ [2].
<3, хотя периодически он может оказаться за пределами этих
границ [2].
модель эластичная компьютерная сеть
1.2
Эластичные сети и молекулярные машины
Молекулярная машина представляет из себя отдельную молекулу
или комплекс молекул, который осуществляет квазимеханические движения, которые
направлены на выполнение полезной работы. Молекулярными машинами, как правило,
обозначаются те молекулярные структуры, которые имитируют определенные функции
на макроскопическом уровне. Молекулярные машины бывают двух видов:
синтетические и биологические.
Синтетические молекулярные машины бывают двух видов:
молекулярные переключатели и молекулярные двигатели. Основное различие между
этими двумя системами состоит в том, что переключатель влияет на систему как на
функцию состояния, тогда как двигатель влияет на систему как функцию
траектории. Переключатель, как может казаться, имитируют поступательное
движение, но возврат переключателя в исходное положение отменяет механический
эффект и высвобождает энергию для системы. Кроме того, переключатели не могут
использовать химическую энергию повторно и постепенно вытеснять систему из
равновесия, в то время как двигатель может. Куда более сложными молекулярными
машинами являются белки, обнаруженные в клетках. К ним относятся моторные
белки, такие как миозин, который отвечает за сокращение мышц, кинезин, который
перемещает груз внутри клеток от ядра вдоль микротрубочек. Эти белки и их
наномасштабная динамика намного сложнее, чем любые молекулярные машины, которые
были искусственно сконструированы. В последние годы были получены разработки и
составлены описания белковых структур основываясь на эластичных сетях.
При таком подходе структурные элементы белка описываются при
помощи тождественных узлов, которые соединяются между собой упругими связями,
если соответствующие узлы находятся по соседству друг с другом в первоначальном
состоянии белка. Таким образом структура белка представляет из себя упругую
эластичную сеть, где главным объектом исследований выступает динамика этой сети.
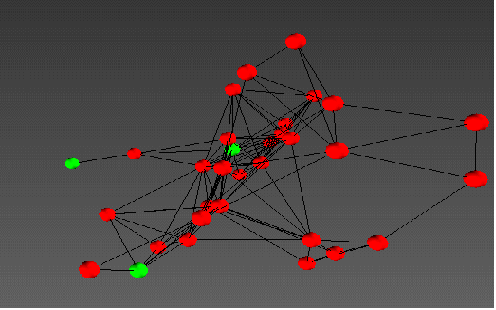
Рисунок 1 - Представление молекулярной структуры в виде
эластичной сети
В качестве узлов эластичной сети можно принимать различные
элементы структуры в зависимости от того, насколько точные данные необходимо
получить в ходе исследования. При наличии суперкомпьютерных вычислительных
машин можно принимать за узлы сети атомы молекулы, а при отсутствии подобных
вычислительных ресурсах за узлы эластичной сети принимаются целые атомные
звенья. Для формирования эластичных связей между узлами необходимо выбрать
правильный радиус обрезания, т.е. определить некоторую фиксированную величину,
сравнивая с которой можно формировать связи между узлами: если расстояние между
двумя элементами сети больше этого радиуса обрезания, то связь не
устанавливается, а если меньше-то связь образуется. Все полученные связи
упругие и подчиняются закону Гука, что позволяет проводить расчеты, опираясь на
законы упругости сжатия и растяжения связей.
При исследовании эластичных сетей рассматривается набор из N одинаковых узлов сети, которые соединены между собой
упругими нитями. Сеть определяется характеристиками состояния равновесия всех
узлов. Упругие силы между узлами, как уже было сказано ранее, подчиняются
закону Гука и зависят только от изменения расстояний между ними. В момент
предела сжатия скорость узла пропорциональная сумме упругих сил, которые
приложены к нему. Если принять, что 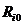 -равновесное состояние узла, а
-равновесное состояние узла, а 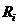 -фактические координаты, то динамика будет описываться следующим
образом [6-7]:
-фактические координаты, то динамика будет описываться следующим
образом [6-7]:
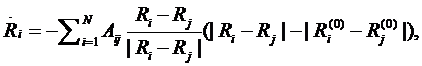
Где 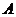 - матрица смежности, где
- матрица смежности, где 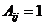 если
если 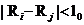 и
и 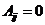 в противном случае. Зависимость от
коэффициентов жесткости и вязкого трения здесь опускается путем
соответствующего изменения масштаба по времени. Динамика упругих сетей
нелинейна, поскольку расстояния
в противном случае. Зависимость от
коэффициентов жесткости и вязкого трения здесь опускается путем
соответствующего изменения масштаба по времени. Динамика упругих сетей
нелинейна, поскольку расстояния 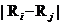 являются нелинейными функциями по координатам
являются нелинейными функциями по координатам 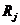 и
и 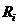 . Данные уравнения при необходимости можно линеризировать
. Данные уравнения при необходимости можно линеризировать
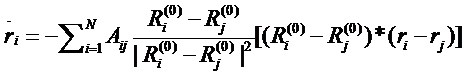
Для небольших отклонений 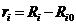 . Данные уравнения могут быть записаны в форме
. Данные уравнения могут быть записаны в форме 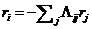 , где
, где 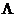 представляет из себя линеаризованную матрицу
представляет из себя линеаризованную матрицу  . Линейная апроксимация релаксационной
динамики описывается суммой независимых экспоненциально затухающих нормальных
мод [6]:
. Линейная апроксимация релаксационной
динамики описывается суммой независимых экспоненциально затухающих нормальных
мод [6]:
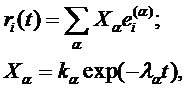
Где значения 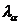 и
и 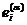 представляют из себя ненулевые значения собственных значений и
соответствующих собственных векторов матрицы. Следует отметить, что одни и те
же собственные значения характеризуют частоту колебаний эластичной сети
представляют из себя ненулевые значения собственных значений и
соответствующих собственных векторов матрицы. Следует отметить, что одни и те
же собственные значения характеризуют частоту колебаний эластичной сети 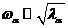 , а колебательные нормальные моды
одинаковые.
, а колебательные нормальные моды
одинаковые.
Рассмотрим результаты построения эластичной сети на примере
миозина-белковой молекулярной машины. В результате исследований эластичной сети
и динамики выяснилось, что самые медленные движения для миозиновой структуры
описываются двумя выделенными модами, которые отделены от основного спектра мод
спектральной щелью.
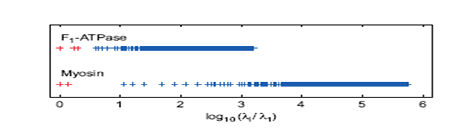
Рисунок 2 - Спектральная щель, отделяющая медленные релаксационные
моды от основного спектра для миозина
У биологических белковых молекулярных машин динамика отличная от
других молекулярных машин. После возмущения белок миозин в многомерном
динамическом пространстве движений миозиновой структуры быстро релаксирует на
некоторую плоскость, которая лежит в многомерном пространстве, а после этого
медленно начинает смещаться к состоянию равновесия по этой плоскости, но не
покидая ее. Это описывается медленными модами. Быстрые движения, которые
попадают в основной спектр, это стохастические движения атомов миозина. Если
сравнивать модели эластичной сети для молекулярной машины с микроскопическими
машинами, то можно найти сходства в функционировании этих моделей. Основное
отличие заключается в том, что молекулярная машина, которая описывает белок,
имеет сильные флуктуации структуры при передаче энергии от быстрых степеней
свободы к медленным. Исследования показывают, что у разных белков существует
немного выделенных мод, но они всегда есть [6].
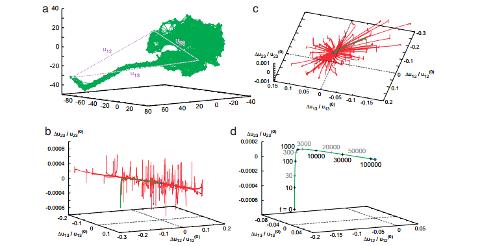
Рисунок 3 - Упругая сеть одиночной тяжелой цепи миозина (А) и
набор релаксационных траекторий для этой сети (B-D). B и C рассматриваются под разными
углами; Каждая из 100 траекторий начинается с другой исходной конформации. D
показывает траекторию (показана зеленой кривой в B и C) с метками времени
прохождения.
Рассмотрим для сравнения полимерную
глобулу, которая внешне похожа на свой белковый аналог (возьмем в пример миоглобин,
который является молекулярной машиной). Отличия данных глобул заключается в
структуре: в полимерной глобуле нить укладывается случайным образом. Поэтому
нельзя говорить о том, что полимерная глобула является молекулярной машиной.
Если представлять обе глобулы в виде эластичной сети, то у белковой глобулы
имеются выделенные медленные моды на спектре релаксационных мод, а у полимерной
глобулы будет отсутствовать спектральная щель. Динамика у биологической
молекулярной машины быстро релаксирует на определенную плоскость или кривую, то
есть на низкоразмерное многообразие, и то, что делает молекулярная машина, ее
функция, осуществляется при движении на этом низкоразмерном многообразии. У
полимерной глобулы такого не происходит. Динамические траектории притягиваются
к разным точкам-аттракторам, поэтому низкоразмерное многообразие, которое
присуще белковой глобуле будет отсутствовать [6-7].
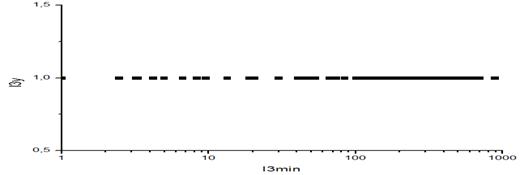
Рисунок 4 - Спектр релаксационных мод для полимерной глобулы
- миоглобин.
2. Методы
исследования
В данной дипломной работе проводится исследование
топологических характеристик молекулярной машины, основываясь на методе описания
структурных элементов при помощи ненаправленной эластичной сети в процессе
динамики молекулярной машины, а также проводится визуализация полученной
эластичной сети.
Первоначально сеть задается при помощи матрицы смежности,
матрицы координат узлов сети в пространстве. Основываясь на данных параметрах
составляется матрица связей узлов сети и разрабатывается программа для
получения основных топологических характеристик сети. В процессе эксперимента
по динамике молекулярной машины отслеживаются моменты, когда на спектре
релаксационных мод отчетливо выделяются одна или две медленные моды. Проводится
анализ данных состояний молекулярной машины, в ходе которого рассматриваются
следующие топологические характеристики сети: распределение степеней связности
узлов, распределение коэффициентов кластеризации узлов сети, а также
центральность узлов в эластичной сети.
Основываясь на полученных характеристиках эластичной сети
молекулярной машины производится сравнение распределения степеней связности и
распределения коэффициентов кластеризации с распределением Пуассона для
случайной сети Ёрдыша-Реньи, которая имеет аналогичное число узлов и степень
связности. Полученные данные по центральностям каждого состояния сети
анализируются на предмет обнаружения одной или двух выделенных значений,
которые определяют наличие двух связанных кликов в сети между собой. Кликами
(или кластерами) в сети называются полносвязные подграфы исследуемой сети.
Топологические свойства молекулярной машины хорошо отражают структуру сильно
связанных кликов, соединенных относительным числом связей. Произведение
расчетов топологических характеристик эластичной сети проводилось с помощью
программы, указанной в Приложении. Листинг программы был написан на языке Python.
2. Объекты
исследования
В качестве объекта исследования рассматривается объект,
полученный входе разработок на базе РАН, основываясь на метоах
блочнополимерного синтеза в расчтворе со встроенными функциональными звеньями.
Изображение модели молекулярной машины показано на Рисунке 5. В качестве
доказательства того, что в качестве исследования рассматривается именно
молекулярная машина говорит тот факт, что характерный спектр релаксационных мод
для данной структуры имеет одну или две медленные моды, которые образуют
спектральную щель. На рисунках 6 и 7 показаны характерные спектры
релаксационных мод для двух состояний, в которых спектр имеет одну и две
выделенные моды соответственно.
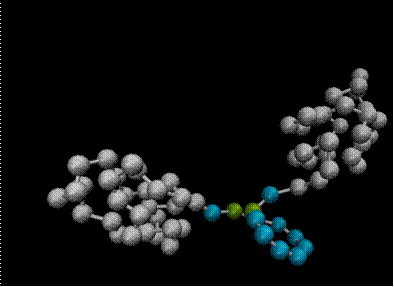
Рисунок 5 - Модель исследуемой молекулярной машины

Рисунок 6 - Характерный спектр релаксационных мод с одной
медленной модой

Рисунок 7 - Характерный спектр релаксационных мод с двумя
медленными модами
Исследование молекулярной машины заключается в исследования
изменения топологических характеристики эластичной сети во время ее динамики.
Полный цикл состоит из четырех этапов: (уточнить названия этапов динамики).
Весь цикл динамики молекулярной машины проиллюстрирован на рисунках 8-11.
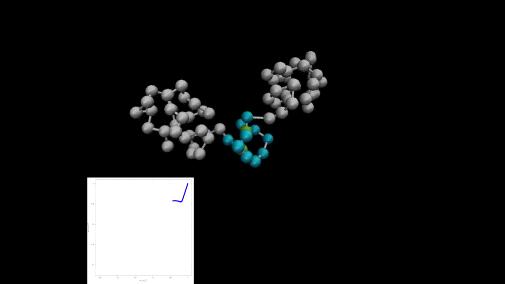
Рисунок 8 - Первый этап: Начало цикла динамики молекулярной
машины
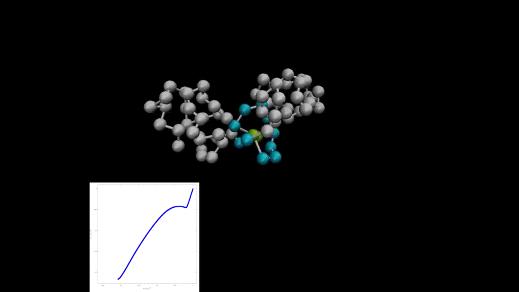
Рисунок 9 - Второй этап динамики молекулярной машины
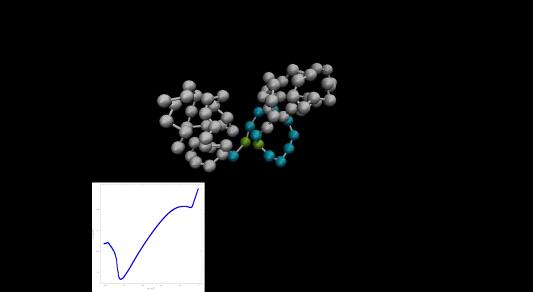
Рисунок 10 - Третий этап динамики молекулярной машины
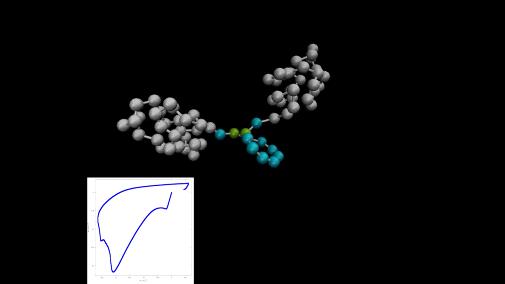
Рисунок 11 - Четвертый этап динамики молекулярной машины:
окончание цикла.
4.
Исследования и результаты
Исследуемая сеть состоит из N=128 узлов, соединенных
между собой упругими связями. Визуализированная эластичная сеть показана на
рисунках 12 и 13 - в развернутом и свернутом состояниях соответственно. Данные
состояния соответствуют различным этапам динамики молекулярной машины.
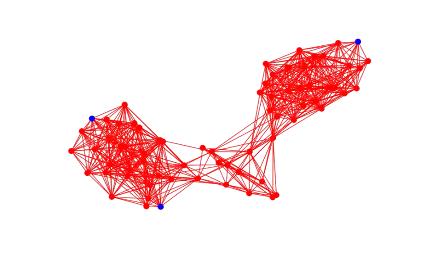
Рисунок 12 - Изображение эластичной сети исследуемой
молекулярной машины в состоянии релаксации
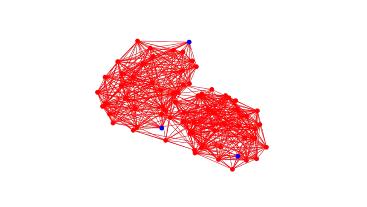
Рисунок 13 - Изображение эластичной сети исследуемой
молекулярной машины в возбужденном состоянии
Во время динамики молкулярная машина проходит цикл, в течение
котрого из свернутого состояния сеть переходит в свернутое состояние и обратно,
тем самым замыкая цикл. На этапе динамики было зафиксировано 24 состояния
молекулярной машины: 12 состояний с одной явновыраженной медленной модой и 12
состояний с двумя явновыраженными медленными модами. По каждой из этих групп,
основываясь на рассмотренных в предыдущем разделе методах, были проведены
исследования их топологических характеристик. В исследованиях для каждой из
двух групп были полученны топлогические характеристики: распределение степеней
связности, распределение коэффициентов кластеризации и гистограмма
распределения центральностей узлов.
Одна выделенная мода
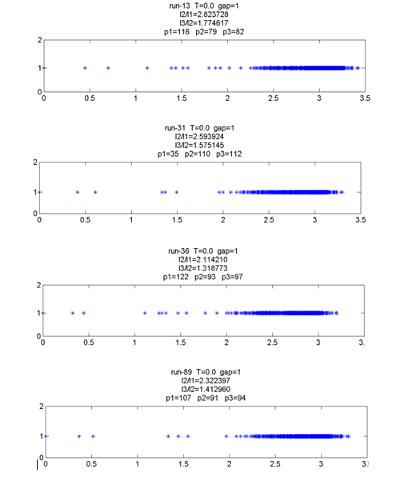
Рисунок 14 - Спектр релаксационных мод с одной выделенной
модой
На данных спектрах указаны отделенные от остального спектра
медленные моды. Для каждого из этих спектров характерна одна выделенная мода,
которая отделена от быстрых мод спектральной щелью. По этим спектрам
производится выборка моментов динамического цикла молекулярной машины для
дальнейших исследований топологических характеристик.
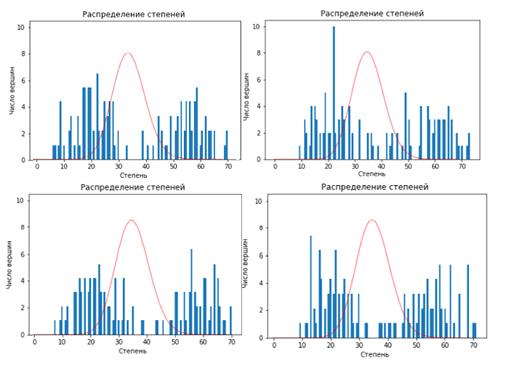
Рисунок 15 - Распределения степеней связности исследуемой
эластчной сети с наложенным поверх него распределением степеней связности для
случайной сети Ёрдыша-Реньи с одной выделенной модой
Распределение степеней связности узлов эластичной сети
отличается от характерного Пуассоновского распределения случайной сети
Ёрдыша-Реньи наличием провала между двумя максимальными значениями по числу
вершин. Данная характеристика является покзазательной для моделей с одной
выделенной модой и характеризует наличие узлов с очень высокой и очень низкой
степенью связности.
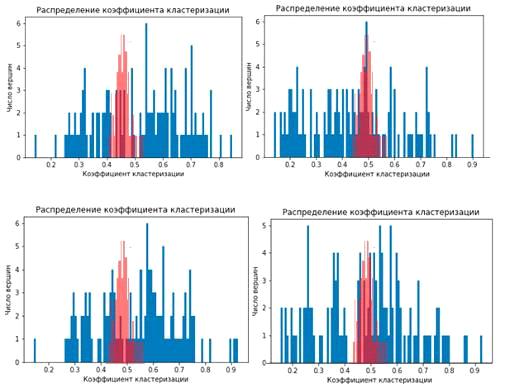
Рисунок 16 - Распределение коэффициентов кластеризации для
исследуемой эластичной сети с одной выделенной модой
Распределение коэффиицентов кластеризации для исследуемой
модели отличается от распределения случайной сети Ёрдыша-Реньи распывчатым
спектром распределения.
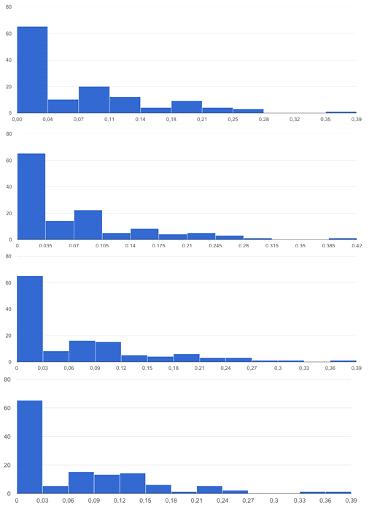
Рисунок 17 - Гистограмма распределения центральности узлов
эластичной сети с одной выделенной модой
Гистограмма распределения центральностей для сети с одной
выделенной модой характеризуется наличием выделенной модой с высоким
показателем центральности, в отличие от других мод, а также показывает наличие
большого числа мод с низким значением показателя центральности.
Данная характеристика говорит о наличии кластеров в сети, где
показатель центральности будет близок к минимальному значению или равняется нулю.
Помимо этого имеется мода с высоким показателем
центральности, находящаяся между двумя кластерами в сети.
Для показательности на координатной плоскости значения
центральностей взяты в масштабе 10: 1 для показательности данных.
Две выделенные моды
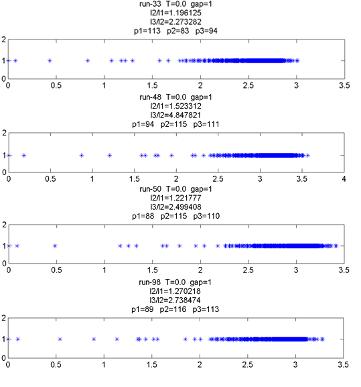
Рисунок 18 - Спектр релаксационных мод с двумя выделенными
модами
На данных спектрах указаны отделенные от остального спектра
медленные моды. Для каждого из этих спектров характерны две выделенные моды,
которые отделены от быстрых мод спектральной щелью. По этим спектрам
производится выборка моментов динамического цикла молекулярной машины для
дальнейших исследований топологических характеристик.
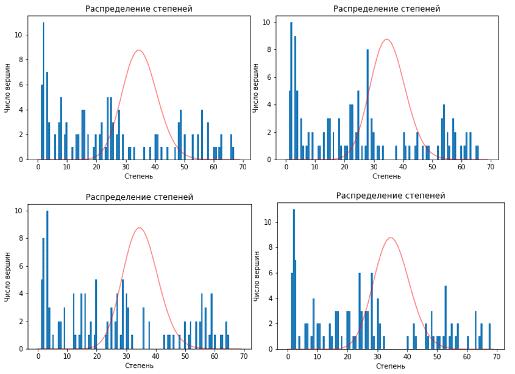
Рисунок 19 - Распределения степеней связности исследуемой
эластчной сети с наложенным поверх него распределением степеней связности для
случайной сети Ёрдыша-Реньи с двумя выделенными модами
Распределение степеней связности узлов эластичной сети
отличается от характерного Пуассоновского распределения случайной сети
Ёрдыша-Реньи наличием провала между двумя максимальными значениями по числу
вершин. Данная характеристика является покзазательной для моделей с одной
выделенной модой и характеризует наличие узлов с очень высокой и очень низкой
степенью связности. В отличие от графиков распределения с одной выделенной
модой для распределения с двумя выделенными модами харктерно большое
колличество узлов с низким показателем связности в сети.
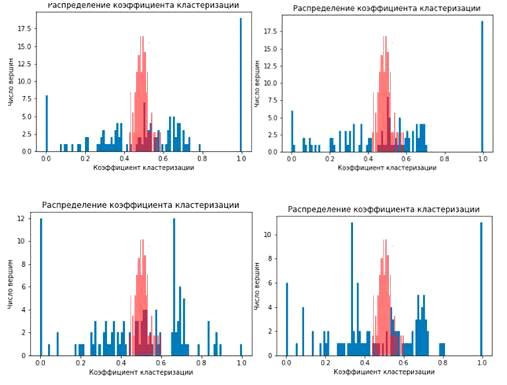
Рисунок 20 - Распределение коэффициентов кластеризации для
исследуемой эластичной сети с двумя выделенными модами
Распределение коэффиицентов кластеризации для исследуемой
модели отличается от распределения случайной сети Ёрдыша-Реньи распывчатым
спектром распределения.
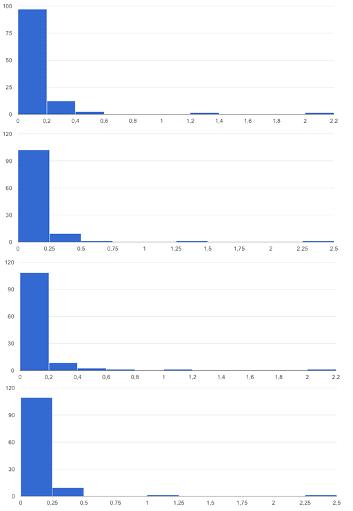
Рисунок 21 - Гистограммы распределения центральности узлов
эластичной сети с двумя выделенными модами
Гистограмма распределения центральностей для сети с двумя
выделенными медленными модами характеризуется наличием выделенных мод с высоким
показателем центральности, в отличие от других мод, а также показывает наличие
большого числа мод с низким значением показателя центральности. Данная
характеристика говорит о наличии кластеров в сети, где показатель центральности
будет близок к минимальному значению или равняется нулю. В отличие от
гистограммы распределения центральностей с одной выделенной модой, как и в
показателе распределения степеней связности, имеет место большое число узлов с
очень маленькой центральностью. Помимо этого для данной гистограммы характерно
наличие двух отдельных мод с показателем центральности намного выше, чем
максимальный показатель центральности для одной выделенной моды. Для
показательности на координатной плоскости значения центральностей взяты в
масштабе 10: 1 для показательности данных.
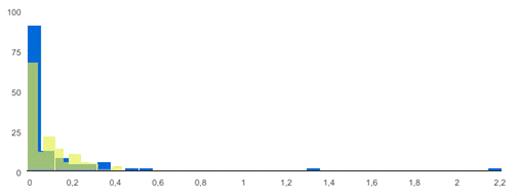
Рисунок 22 - Сравнение гистограмм центральностей для одной и
двух выделенных медленных мод (Желтым обозначена гистограмма для одной
выделенной моды, синим-для двух выделенных мод)
На рисунке 22 приведена сравнительная характеристика двух
гистограмм по значениям центральностей для одной и двух выдеенных мод. Исходя
из рисунка можно сделать вывод, что для двух выделенных мод характерны два
значения с очень большим значением центральности и очень большое число узлов,
для которых центральность будет близка к нулю. Для моментов динамики, где
отчтливо выделяется одна выделенная медленная мода центральность будет иметь
более сглаженный спектр и не содержит в себе узлов с очень большим значением
центральности, которые отделены такой же большой спектральной щелью, как и
график с двумя выделенными медленными модами.
Выводы
В результате исследовательской работы были получены данные топологических
характеристик для эластичной сети, полученные на основе молекулярной машины,
взятой в качестве объекта исследования. Топологические характеристики сети были
получены для моментов динамики, когда отчетливо проявляются одна и две
выделенные медленные моды. Данные исследования топологических характеристик
показывают, что топологические свойства молекулярной машины хорошо отражают
структуру сильносвязанных кликов, которые соединены относительным числом
связей. Характеристики данных сетей отличаются от аналогичных характеристик
сетей Ердыша-Реньи на всех проведенных сериях экспериментальных исследований.
Эластичная сеть представляет собой структурированный граф с
небольшим числом кликов и разряженными связями между ними. Представляет интерес
разработать алгоритмы синтеза структур, эластичные сети которых имеют такую
структуру.
Библиография
1. Milo
R., Itzkovitz S., Alon U. (2004) Superfamilies of Evolved and Designed
Networks; 14 July 2003; accepted 23 January 2004
2. Евин
И.А. Сложные сети: Введение в теорию; Институт машиноведения имени А.А.
Благонравова РАН.
. Newman
M.E.J. (2010) Networks An Introduction; Oxford University Press
. Newman,
M.E.J. and Girvan, M. 2004, Finding and evaluating community structure in
networks, Phys. Rev. E 69, 026113; cond-mat/0308217.
. Newman,
M. E. J. (2003), The structure and function of complex networks, SIAM Review;
cond-mat/0303516
. Togashi
Y., Mikhailov A. (2007) Nonlinear relaxation dynamics in elastic networks and
design principles of molecular machines; PNAS 2007; 104; 8697-8702;
. Albert,
R. and Barabasi, A. - L. (2002), Statistical mechanics of complex networks,
Rev. Mod. Phys.; cond-mat/0106096
Приложения
Листинг программы на языке Python
# - * - coding: utf-8 - *-networkx as nxpylab as
pltnumpy as np= []open ('C: \\Users\\Олег\\Анаконда\\2\\2. txt', encoding='ascii') as
fin:line in fin:. append (list (line. rstrip ('\n')))
#print (matr)open ("C: \\Users\\Олег\\Анаконда\\2\\2SR.
txt","w") as out:i in range (128):j in range (128):
#print (matr [i] [j], end=' ')matr [i] [j]
=='1':(i+1,' ',j+1,file=out)
#Выбор файла, построение графа
filename='C: \\Users\\Олег\\Анаконда\\7\\7SR.
txt'=nx. read_edgelist (filename, nodetype=int)= nx. spring_layout (G).
draw_networkx_nodes (G, pos, G. nodes (), node_size = 20). draw_networkx_edges
(G,pos, alpha=0.5). savefig ('7-граф. png')("\n")
#for random graph models
#G=nx. erdos_renyi_graph (1000,0.1)
#G=nx. random_regular_graph (10,100)
#G=nx. barabasi_albert_graph (1000,40)
#for graph plotting
#pos = nx. spring_layout (G)
#nx. draw_networkx_nodes (G, pos, G. nodes (),
node_size = 20)
#nx. draw_networkx_edges (G,pos, alpha=0.5)
#Число узлов в графе("Число узлов в графе", nx.
number_of_nodes (G))("\n")
#Количество связей в графе
print ("Число связей в графе", nx.
number_of_edges (G))
#Распределение степеней=sorted (nx. degree (G). values (),reverse=True).
figure (). hist (degree,100). xlabel ('Степень'). ylabel ('Число вершин')
plt. title ("Распределение вероятностей"). savefig
('7-распределение. png'). show ()
#Характеристики сети
#Радиус сети
print ("\n")("Радиус: %d" %
nx. radius (G))
#Диаметр сети("\n")("Диаметр: %d" %
nx. diameter (G))
#Плотность сети("\n")("Плотность: %s" %
nx. density (G))
#Число треугольников для каждого
узла("\n")("Число треугольников каждого узла: ")(nx.
triangles (G))
#Коэффициент кластеризации для каждого
узла("\n")("Коэффициент кластеризации каждого узла: ")(nx.
clustering (G))
#Отношение числа треугольников к числу триад
print ("\n")
#print ("Транзитивность Т=", nx. transitivity (G))
#Центральности
# Betweenness centrality, или посредничество
# Эта мера показывает, насколько узел связывает несколько
несвязанных сообществ,
# или занимает позицию "между"_centr = nx. betweenness_centrality
(G)("\n")('Betweenness centrality',bet_centr)
# Closeness centrality
# Эта мера показывает, насколько узел близок ко всем
остальным узлам в сети
clo_centr = nx. closeness_centrality
(G)("\n")('Closeness centrality',clo_centr)
# Eigenvector centrality
# Эта мера показывает, насколько узел связан с узлами,
# которые сами имеют большое количество связей
eig_centr = nx. eigenvector_centrality
(G)("\n")('Eigenvector centrality',eig_centr)
Распределение коэффициента кластеризации=sorted (nx.
clustering (G). values (),reverse=True). hist (clust,100). xlabel ('Коэффициент кластеризации')
plt. ylabel ('Число вершин'). title ("Распределение
коэффициента кластеризации"). savefig ('7-кластеризация. png')
plt. show ()(np. linalg. eig (matr))
### for graph communities
#partition = community. best_partition (G)
#print (float (len (set (partition. values ()))))
#plt. xscale ('log')
#plt. yscale ('log'). show ()