Исследование эффективности использования системы Maxima в курсе ТАУ

Содержание

 

Введение

1. Программные средства исследования систем автоматического управления

1.1 Обзор и анализ программных средств

1.2 Описание системы компьютерной математики Maxima

1.3 Постановка задачи

2. Анализ сау в компьютерной среде Maxima

2.1 Математическое описание САУ

2.2 Характеристики системы

2.2.1 Импульсная (весовая) функция

2.2.2 Переходная функция

2.2.3 Частотные характеристики

2.2.4 Характеристики систем в пространстве состояний

3. исследование устройчивости САУ

3.1 По корням характеристического полинома

3.2 По критериям устойчивости

3.2.1 Критерий Гурвица

3.2.2 Критерий Михайлова

3.2.3 Критерий Найквиста

4. Разработка методического обеспечения

4.1 Руководство пользователя

4.2 Реализация практикума по ТАУ

5. Maxima 5.38.1

6. Установка и запуск программы

7. Интерфейс wxMaxima

8. Ввод простейших команд в wxMaxima

9. Арифметические и логические операции и константы

9.1 Переменные

9.2 Математические функции

9.3 Решение задач элементарной математики

9.4 Нахождение корней уравнений и систем алгебраических уравнений

10. Графики функций

10.1 Построение графиков

10.2 Опции оформления графиков

11. Решение задач линейной алгебры

11.1 Операции с матрицами

11.2 Функции для работы с матрицами

12. Решение задач математического анализа

Заключение

Список использованных источников

Введение

Теория автоматического управления (ТАУ) - это дисциплина, которая сформировалась как самостоятельная наука сравнительно недавно, несмотря на то, что с древних времен известны отдельные устройства, которые работают без участия человека. С помощью методов ТАУ можно объяснить работу различных объектов везде, где можно предусмотреть обратную связь - в механике, радио и электротехнике, энергетике. Как любая теория, теория автоматического управления связана с моделями различных систем, а не их инженерными реальными конструкциями. Поэтому проблемы проектирования и составления математического описания управляющих систем являются актуальными.

С развитием вычислительных средств появилась возможность решать задачи по управлению в технических системах любой степени сложности. Создано много графических сред, которые дают возможность вводить описание системы моделирования в привычной для пользователя форме.

В представленной работе рассматривается и оценивается эффективность использования программного комплекса Maxima как инструмента для составления математического описания конкретной линейной системы, обработки частотных и алгебраических критериев оценки устойчивости, а также определения показателей качества ее регулирования.

программный комплекс maxima

1. Программные средства исследования систем автоматического управления

1.1 Обзор и анализ программных средств

В настоящее время невозможно представить эффективную работу инженера без персональных компьютеров и развитых телекоммуникационных средств. Существует немало графических сред, которые позволяют вводить описание моделируемой системы в привычной для пользователя форме. Затем это описание автоматически переводится в язык компьютера, и пользователь видит полученные результаты в виде диаграмм, таблиц, графиков. Для эффективности результата необходимо на ранней стадии решения задачи выбрать наиболее подходящий пакет программ, который будет использоваться.

На сегодняшний день наиболее известными пакетами, используемыми при инженерных расчетах, являются MathCad, Mathematica, Matlab, VisSim, Maxima.

Лидирующее положение по популярности для решения технических задач занимает мощный пакет программ MathCAD. Сокращение CAD от Computer Aided Design в названии системы указывает на то, что система принадлежит к автоматизированному проектированию. MathCAD предназначен для решения различных математических, физических, экономических, инженерных задач с возможностью программирования. Использование данной системы резко повысило скорость решения и уровень сложности прикладных задач. Основными особенностями MathCad являются: удобная справочная система, использование привычного способа математической записи, широкие графические возможности для анализа результатов, большое количество числовых алгоритмов и т.д. Главным недостатком является то, что здесь отсутствует возможность разрабатывать графические интерфейсы пользователя, которая имеется, например, в Matlab, Excel, Maxima. На практике, такой недостаток заключается в следующем. При наличии математической модели какого-либо процесса, начальные данные будут находиться в начале документа, а результаты, например, графики, в конце. MathCad следит за соблюдением данного правила. При появлении необходимости поменять исходные данные приходится возвращаться в начало документа, а затем снова в конец, чтобы проанализировать результаты. Если исходные данные - это массивы, у которых может меняться размер, то тратиться значительное время на то, чтобы ввести эти массивы. Еще одним не маловажным недостатком является то, что пакет не является свободно распространяемым и необходима покупка лицензии, а это не маленькие дополнительные затраты. [1]

Для исследования систем автоматического управления отличным средством является использование программного пакета Matlab корпорации MathWorks Inc. Это эффективное средство для реализации аналитического, имитационного, ситуационного и численного моделирования. Для расширения функциональности система имеет многочисленные пакеты. Например, для исследования линейных и нелинейных блочных динамических систем дополнительно подключается пакет визуального моделирования - Simulink. В пакет входит множество функциональных графических блоков, параметры которых задаются с помощью удобных панелей. Язык MatLab имеет преимущества и недостатки. Достоинства - язык обладает понятным и простым синтаксисом, легок для изучения, частые обновления, возможность преобразовывать в "быстрый" код на С++, С. Большим недостатком является дороговизна программного обеспечения (пакет не является свободно распространяемым). Также язык медленный и перегружен функциями, операторами, командами. [2]

Для моделирования с реальной аппаратурой наиболее удобна программа VisSim. Она имеет развитый графический интерфейс. Модель создается пользователем почти так, как если бы он строил реальную систему. Это позволяет исследовать модели разной степени сложности. Результаты решений технических задач выводятся в наглядной форме. Поэтому программу может использовать и тот, кто имеет не большие познания в области математики и программирования. В то же время, тот, кто владеет программированием, сможет создать собственные блоки, дополнив ими стандартную библиотеку VisSim'а. У данной программы также есть свои плюсы. Например, решение дифференциальных уравнений значительно эффективнее и быстрее в VisSim, чем в MathCad. А по сравнению с Matlab, VisSim занимает во много раз меньше места в оперативной памяти и на жестком диске. [3]

1.2 Описание системы компьютерной математики Maxima

Maxima - свободная система компьютерной математики, которая написана на языке Lisp. Среди аналогичных программ по части символьных вычислений обладает более широкими возможностями. Система идеально подходит как для студентов вузов, так и для профессиональных математиков в качестве инструмента для проведения исследований и выполнения сложных расчетов. Программа Maxima предоставляет похожий функционал как MathCad, Maple, Mathematica. Она имеет огромный набор средств для проведения численных и аналитических вычислений, построения графиков. Главное ее отличие в том, что она является открытой и не коммерческой. Использование свободного программного обеспечения более естественно для науки, так как модель, используемая в свободном программном обеспечении (ПО) - модель открытости и общедоступности. Результаты работ также могут распространяться и использоваться без ограничений, налагаемых лицензиями платного ПО. В случае коммерческого ПО есть много ограничений, начиная от невозможности законно передавать его вместе с результатами работы и заканчивая распространением самодельных библиотек к нему.

Основным направлением востребованности бесплатной программы является высшее образование. Это реальная возможность без существенных денежных затрат иметь легальные копии такого ПО.

Maxima - это консольная программа, которая отрисовывает все математические формулы обычными текстовыми символами. Ее можно использовать без каких-либо интерфейсных надстроек, она нетребовательна и может работать на старых компьютерах. Это может оказаться актуальным для научной лаборатории или вуза, у которых не хватает денег на обновление машин, но есть потребность в ПО для символьных вычислений. Также, Maxima может быть использована как ядро. Для этого поверх нее надстраиваются графические интерфейсы, два из которых наиболее интересны.

Первый представляет собой обособленное самостоятельное графическое программное обеспечение, носящее наименование wxMaxima. Эта программа, как и сама Maxima, существует в версиях и для Linux/*BSD, и для MS Windows. Ввод формул здесь осуществляется в текстовом виде, а вывод отображается графически, математическими символами. Помимо этого, большое внимание уделено здесь удобству ввода: реализовано отделение командной строки от окна ввода-вывода, а дополнительные кнопки и система меню позволяют вводить команды в диалоговом режиме. Клавишей "Tab" можно вызвать так называемое "автодополнение". Однако ведет оно себя только лишь как умная история команд, то есть вызывает ту команду из уже выполненных в этой сессии, которая начинается с набранных в командной строке символов, но не дополняет при этом до имен команд и их параметров. Данный интерфейс наиболее удобен тогда, когда необходимо производить много вычислений и выводить результаты на экране, а также, если пользователь не хочет вводить все команды с клавиатуры. Также стоит отметить удобство предоставляемого wxMaxima интерфейса к документации по системе. Но для этого можно использовать обычный браузер, так как документация поставляется в формате html.

Второй достаточно интересный интерфейс к Maxima - это дополнительный режим в редакторе TeXmacs. Данный редактор имеет общее прошлое с хорошо известным Emacs, как видно из названия, однако практического сходства между ними мало. TeXmacs используется для визуального редактирования текстов научной тематики, при котором на экране редактируемый текст отображается практически в том же виде, в котором он будет выведен на печать. Например, в редакторе имеется математический режим ввода, наиболее подходящий для работы с различными формулами, и позволяющий импортировать/экспортировать текст в LaTeX и XML/HTML. Именно возможностями по работе с формулами оперирует Maxima, вызванная из TeXmacs’а. Формулы показываются в обыкновенной математической нотации, но они поддаются редактированию и копированию в другие документы в виде обыкновенного текста. Меню для вызова сессии Maxima: "вставить → Сессия → Maxima", при этом возникает дополнительное меню с командами программы. После запуска сессии возможен переход в математический режим ввода (для этого нужно воспользоваться первой кнопкой на панели ввода), а также можно применить при вводе элементы математической нотации. Данный интерфейс наиболее подходящий для пользователей, желающих использовать результаты вычислений в текстах и ищущих возможность редактировать их в визуальном режиме. [4]

1.3 Постановка задачи

Цель данной работы - проанализировать принцип работы системы компьютерной алгебры Maxima и оценить эффективность ее использования в курсе ТАУ.

Задачи:

изучить систему Maxima как программное средство для исследования систем автоматического управления, определить задачи и функции;

проанализировать САУ в компьютерной среде Maxima: составить математической описание, определить импульсную и переходную функцию, частотные характеристики, а также характеристики системы в пространстве состояний;

исследовать устойчивость САУ по корням характеристического полинома и по критериям устойчивости;

на основе проведенного исследования разработать руководство пользователя по системе Maxima и реализовать практикум по предмету "Теория автоматического управления".

2. Анализ сау в компьютерной среде Maxima

2.1 Математическое описание САУ

Система управления - это совокупность элементов, взаимосвязанных между собой, которые участвуют в процессе управления. В некоторый период разработки и исследования системы автоматического управления (САУ) становится необходимым получить описание происходящих процессов в системе на математическом языке, то есть составить ее математическое описание. Оно может быть графическим - описание с помощью структурных схем, графиков и графов, аналитическим - в виде уравнений и табличным - представление в виде таблиц. Обычно сначала составляют уравнение для каждого элемента системы, совокупность которых представит математическую модель. В зависимости от цели, с которой проводится исследование, модели одной системы бывают разными. С одной стороны, модель должна быть простой и не усложнять исследование, а с другой быть - должна быть наиболее близка по свойствам к оригиналу. [5]

С помощью средств Maxima можно построить различные математические модели.

Рассмотрим простейшую САУ с обратной связью, структурная схема которой представлена на рисунке 2.1 Система состоит из объекта управления и датчика рассогласования.

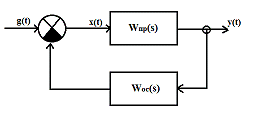
Рисунок 2.1 - Простейшая структурная схема САУ с обратной связью

На рисунке 2.1 показаны:

Wпр (s) и Wос (s) - передаточные функции объекта управления и обратной связи соответственно;

g (t) и y (t) - задающее воздействие и величина, которой управляем;

Сначала необходимо определить передаточные функции отдельных элементов системы, то есть найти отношения изображений Лапласа выходных величин к изображениям входных величин при нулевых начальных данных. Передаточные функции элементов представлены в формулах 2.1 и 2.2.

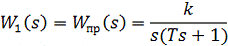, (2.1)

где k = 50 - коэффициент передачи объекта управления, с^-1;

T = 0,1 - постоянная времени датчика, c.

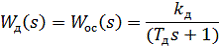, (2.2)

где K_д = 1 - коэффициент передачи датчика, с^-1;

T_д = 0,01 - постоянная времени объекта управления, c.

На основании структурной схемы составим передаточные функции замкнутой и разомкнутой систем с помощью Maxima.

Для ввода команд используется поле ВВОД, команды разделяются точкой с запятой. Для их обработки и вывода результата необходимо нажать Enter. Чтобы вычислить результат, не выводя его на экран, необходимо вместо точки с запятой поставить символ ‘$’. Если же выражение нужно просто отобразить не вычисляя, то перед ним нужно поставить символ одинарной кавычки "’".

Каждой введенной команде и ее вычисленному результату присваивается порядковый номер. Это позволяет избежать последующего повторения записи уже выполненных команд. [6]

Определим передаточные функции отдельных элементов, как показано на рисунке 2.2.

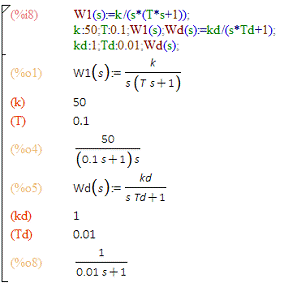
Рисунок 2.2 - Определение передаточных функций отдельных элементов

Так как звенья соединены последовательно, то передаточная функция замкнутой системы рассчитывается как произведение передаточных функций первого и второго элемента. Определим передаточные функции замкнутой и разомкнутой системы, как показано на рисунке 2.3.

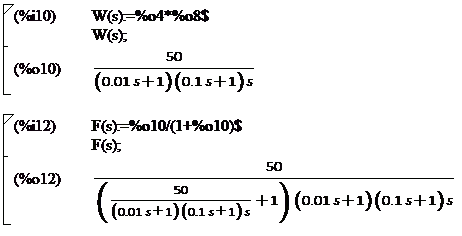
Рисунок 2.3 - Определение передаточных функций замкнутой и разомкнутой систем

Упростим передаточные функции с помощью команды ratsimp:

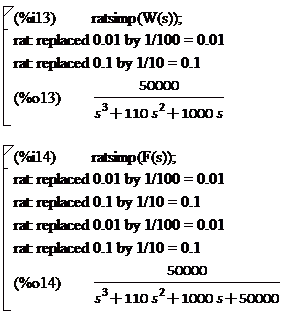
Рисунок 2.4 - Упрощение передаточных функций замкнутой и разомкнутой систем

Математическое описание получено. Далее можно перейти к получению характеристик систем.

2.2 Характеристики системы

По признаку учитывается ли зависимость объекта моделирования от времени или нет, разделяют динамические и статические характеристики систем.

Поведение системы в установившемся режиме определяют статические характеристики, т.е. они определяют статику системы. Такие характеристики позволяют определить степень нелинейности системы, коэффициент ее усиления, величину статизма.

Поведение системы в неустановившемся режиме (переходном) определяют динамические характеристики. Основными динамическими характеристиками являются:

передаточная функция;

частотные характеристики;

временные характеристики.

Временной характеристикой принято считать изменение выходной величины во времени при изменении по определенному закону входного воздействия при условии нахождения системы в покое до приложения внешнего воздействия. Другими словами можно сказать, что это реакция системы управления на типовые воздействия при начальных условиях равных нулю. Основными временными характеристиками являются переходная и импульсная функции.

2.2.1 Импульсная (весовая) функция

Импульсная (весовая) функция отображает реакцию системы при нулевых начальных условиях на единичный импульс. Единичный импульс представляет собой мгновенный импульс бесконечно малой продолжительностью, с бесконечно большой амплитудой и имеющий конечную единичную площадь. График зависимости весовой функции от времени принято называть импульсной характеристикой. Иначе говоря, весовая функция w (t) представляет собой переходный процесс на выходе звена (рисунок 2.5) при подаче на его вход единичного импульса.

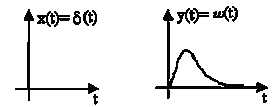
Рисунок 2.5 - Временные диаграммы входного и выходного сигналов звена

Для построения импульсной характеристики сначала найдем изображения по Лапласу для входного и выходного воздействий. В Maxima есть функции для совершения преобразования Лапласа - laplace и, соответственно, обратного преобразования Лапласа - ilt. Изображение выходной величины будет равно произведению изображения входного воздействия на передаточную функцию замкнутой системы. Изображения по Лапласу для входного воздействия и выходной величины показаны на рисунке 2.6.

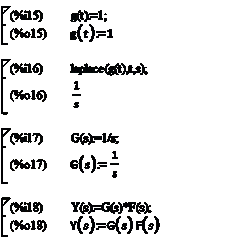
Рисунок 2.6 - Изображение по Лапласу входного воздействия и выходной величины

Обратное преобразование Лапласа для данной сложной функции не берется. Требуется разложить передаточную функцию замкнутой системы, которая представляет собой дробно-рациональную функцию, на элементарные дроби. Для начала определим характеристический полином и найдем его корни. Для вычисления численных приближений действительных и комплексных корней полинома используется команда allroots. Для удобства дальнейшего использования запишем найденные корни в список (рисунок 2.7). [7]

Рисунок 2.7 - Нахождение корней характеристического полинома

Разложим передаточную функцию замкнутой системы на элементарные дроби используя полученные корни характеристического полинома (рисунок 2.8).

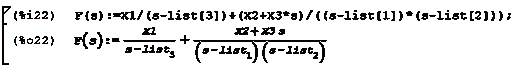
Рисунок 2.8 - Разложение функции на элементарные дроби

Далее найдем Х1, Х2 и Х3 методом неопределенных коэффициентов, решив матричное уравнение АХ=В. Раскроем скобки с помощью команды expand и упростим функцию с помощью команды ratsimp (рисунок 2.9).

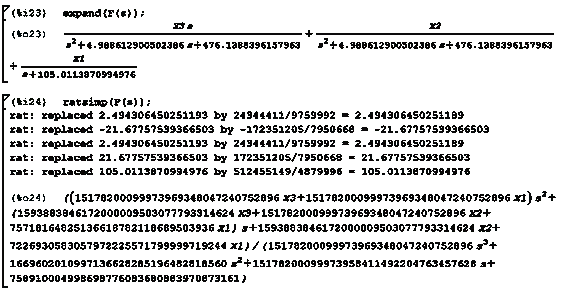
Рисунок 2.9 - Приведение передаточной функции к удобному виду

Определим матрицы A и B и найдем корни. Разделим каждый член функции на коэффициент, стоящий перед переменной наибольшей степени в знаменателе, чтобы он стал равным единице (рисунок 2.10). Для представления рациональных выражений в виде десятичных дробей используем функцию float.

Рисунок 2.10 - Нахождение корней

Выполним проверку на правильность нахождения корней и подставим корни в передаточную функцию (рисунок 2.11).

Рисунок 2.11 - Проверка корней и подстановка в передаточную функцию

После разложения функции на элементарные дроби мы можем найти обратное преобразование по Лапласу и построить импульсную функцию (рисунки 2.12 и 2.13).

Рисунок 2.12 - Обратное преобразование по Лапласу выходной величины

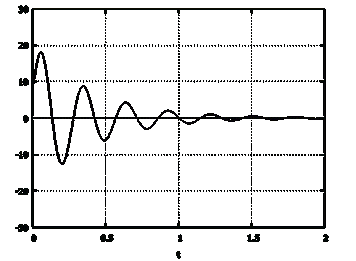
Рисунок 2.13 - Импульсная характеристика системы

2.2.2 Переходная функция

Переходная функция представляет собой реакцию звена на единичную ступенчатую функцию. Как видим (рисунок 2.14), переходная функция является переходным процессом на выходе звена при единичном скачке на его входе.

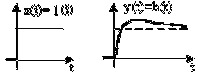
Рисунок 2.14 - Временные диаграммы входного и выходного сигналов звена

Найдем обратное преобразование Лапласа выходной величины и построим переходную функцию. Для этого выполним команды как на рисунке 2.15.

Рисунок 2.15 - Команды для построения переходной функции

Результаты показаны на рисунке 2.16.

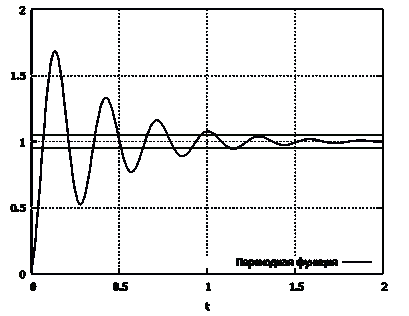
Рисунок 2.16 - График переходной функции

По графику определяем перерегулирование - 68%, время регулирования - 1,17 с.

2.2.3 Частотные характеристики

С помощью частотных характеристик описываются передаточные свойства САУ и её элементов в установившемся режиме гармонических колебаний, которые вызваны внешним гармоническим воздействием. Зная частотные характеристики системы, можно определить ее реакцию на гармонические воздействия различной частоты. Логарифмические амплитудно-фазовые частотные характеристики (ЛАФЧХ) в Maxima можно построить с помощью одной команды, для этого есть соответствующие две функции bode_gain и bode_phase. Они содержатся в пакете bode. Построим ЛАЧХ и ЛФЧХ. Ввод команд - рисунок 2.17. Полученные результаты на рисунках 2.18 и 2.19.

Рисунок 2.17 - Ввод команд для построения частотных характеристик

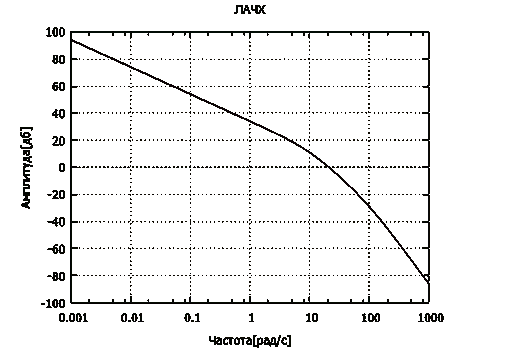
Рисунок 2.18 - Логарифмическая амплитудная частотная характеристика

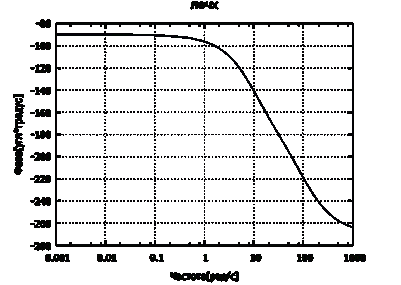
Рисунок 2.19 - Логарифмическая фазовая частотная характеристика

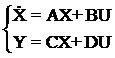, (2.3)

где X - вектор состояния системы;

Y - вектор выходных управляемых величин;

U - вектор внешних задающих и возмущающих воздействий;

A, B, C, D - матрицы системы, управления, наблюдения и связи.

Элементы матрицы системы A определяются значениями параметров элементов, определяемых структурной схемой. Данная матрица отражает свободное движение системы, её динамические свойства. Матрица управления B отражает как влияют внешние воздействия на переменные состояния системы. Матрица наблюдения C отражает связь вектора состояния системы с выходной величиной. Матрица связи D устанавливает связь выходной величины системы с внешним воздействием. Таким образом, матрицы A, B, C, D полностью определяют систему управления.

Выделим коэффициенты полиномов числителя и знаменателя передаточной функции системы и определим матрицы A, B, C, D в Maxima (рисунки 2.20 и 2.21). Основной способ создания матриц - использование функции matrix. Синтаксис вызова: matrix (row1,., rown). Каждая строка - список выражений, все строки одинаковой длины. На множестве матриц определены операции сложения, вычитания, умножения и деления. Эти операции выполняются поэлементно, если операнды - две матрицы, скаляр и матрица или матрица и скаляр. Возведение в степень возможно, если один из операндов - скаляр. Перемножение матриц (в общем случае некоммутативная операция) обозначается символом".". [8]

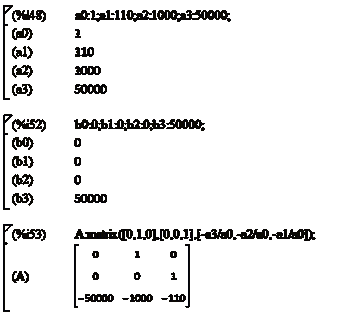
Рисунок 2.20 - Определение матрицы А

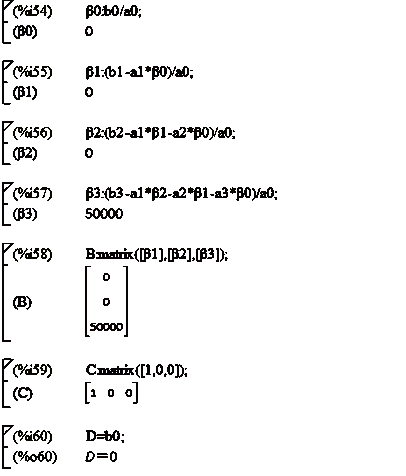
Рисунок 2.21 - Определение матриц B, C, D

Определим устойчивость системы по Ляпунову. Согласно теореме система будет устойчивой тогда и только тогда, когда вещественные части всех собственных чисел матрицы системы отрицательны. Найдем собственные числа матрицы с помощью функции eigenvalues (рисунок 2.22). Функция eigenvalues (M) находит характеристические числа матрицы. В качестве результата возвращается список, состоящий из двух подсписков. В первом из них содержатся характеристические числа, во втором - множители, в соответствующем порядке.

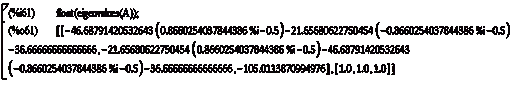
Рисунок 2.22 - Собственные числа матрицы A

Система устойчивая, так как вещественные части всех собственных чисел матрицы системы А отрицательны.

Используя матрицы системы, можно исследовать ее на управляемость и наблюдаемость. Управляемость - одно из важнейших свойств системы управления и объекта управления, описывающее возможность перевести систему из одного состояния в другое. Исследование системы управления на управляемость является одним из важных шагов в синтезе управляющих систем. Для линейных систем существует критерий управляемости в пространстве состояний. Для системы n-го порядка можно составить матрицу управляемости: [B AB A²B … A^n-1B]. Согласно критерию управляемости, система является полностью управляемой, если ранг невырожденной матрицы управляемости равен n. Определим матрицу управляемости K, найдем ее определитель и ранг (рисунок 2.23).

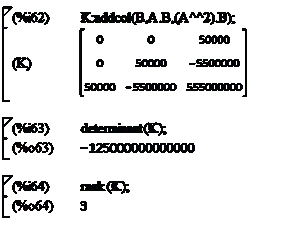
Рисунок 2.23 - Матрица управляемости

Для того чтобы определить матрицу K воспользуемся функцией addcol, которая добавляет один или несколько столбцов, заданных списками или матрицами к матрице. Таким образом получим необходимую матрицу. Для вычисления определителя используем функцию determinant, для определения ранга матрицы - функцию rank. Можно сделать вывод, что система полностью управляемая, так как при невырожденности матрицы К (определитель не равен нулю) ее ранг равен размерности матрицы А.

Наблюдаемость в теории управления - свойство системы, показывающее, можно ли по выходу полностью восстановить информацию о состояниях системы. Для линейных систем существует критерий наблюдаемости в пространстве состояний. Для системы n-го порядка можно составить матрицу управляемости: [C^T (CA) ^T (CA²) ^T … (CA^n-1) ^T]. Согласно критерию наблюдаемости, система является полностью наблюдаемой, если ранг невырожденной матрицы наблюдаемости равен n.

Определим матрицу наблюдаемости L, найдем ее определитель и ранг (рисунок 2.24).

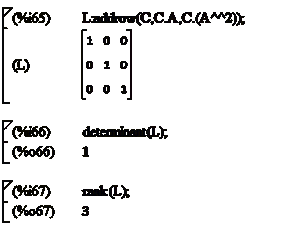
Рисунок 2.24 - Матрица наблюдаемости

Для того чтобы определить матрицу L воспользуемся функцией addrow, которая добавляет одну или несколько строк, заданных списками или матрицами к матрице. Таким образом получим необходимую матрицу. Для вычисления определителя также используем функцию determinant, для определения ранга матрицы - функцию rank. Можно сделать вывод, что система полностью наблюдаемая, так как при невырожденности матрицы L (определитель не равен нулю) ее ранг равен размерности матрицы А.

3. исследование устройчивости САУ

Понятие устойчивости является важнейшей качественной оценкой динамических свойств систем управления. Под устойчивостью понимают способность системы возвращаться в исходное состояние равновесия после снятия внешнего возмущения. Состояние системы можно назвать устойчивым, если отклонение от него остается очень мало при любом малом изменении входного сигнала. Все состояния линейной системы управления либо устойчивы, либо неустойчивы. Существуют различные методы, которые позволяют оценить может ли система нормально функционировать и противостоять различным неизбежным внешним воздействиям. Одним из возможных способов оценки является исследование системы по корням характеристического полинома.

3.1 По корням характеристического полинома

Для устойчивости стационарной линейной системы автоматического управления, описываемой обыкновенными дифференциальными уравнениями, необходимо и достаточно, чтобы все корни соответствующего характеристического уравнения имели отрицательные действительные части. Все случаи устойчивости зависят от вида корней характеристического уравнения: они могут быть действительными числами или комплексно-сопряженными числами. Если корни характеристического уравнения - действительные числа, то процесс будет апериодическим, а при комплексных числах - колебательным. Решение дифференциального уравнения состоит из двух составляющих - вынужденной и переходной. При времени, стремящемся к бесконечности система является устойчивой, если переходная составляющая решения дифференциального уравнения стремится к нулю. Если переходная составляющая стремится к бесконечности - система не устойчива, если остается постоянной - система находится на границе устойчивости, т.е. нейтральная. Возможные виды переходной составляющей показаны на рисунке 3.1.

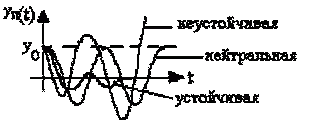
Рисунок 3.1 - Возможные виды переходной составляющей

Если действительные корни характеристического уравнения положительные, то переходная составляющая с ростом времени неограниченно возрастает, а если они отрицательны, то эта составляющая стремится к нулю. Если корни являются комплексными числами, то переходная составляющая с ростом времени стремится к нулю, если вещественные части корней отрицательны. В противном случае амплитуда колебаний переходной составляющей возрастает. Определение корней характеристического полинома было произведено и описано при нахождении импульсной функции и в пункте 2.2.1 Полученные корни представлены на рисунке 3.2.

Рисунок 3.2 - Корни характеристического полинома

Из полученного результата можно сделать вывод, что заданная система устойчива, так как все корни характеристического уравнения имеют отрицательные вещественные части.

Если характеристическое уравнение имеет высокий порядок, то нахождение его корней является затруднительным. Поэтому разработаны специальные критерии, позволяющие судить об устойчивости системы без расчета корней уравнения.

3.2 По критериям устойчивости

3.2.1 Критерий Гурвица

Одним из способов, применяемых для анализа устойчивости линейной системы, является критерий устойчивости Гурвица, который разработал Адольф Гурвиц. Основное достоинство - метод принципиально прост; основной недостаток - необходимо выполнять операции расчета определителя, в ходе которых может возникнуть вычислительная ошибка.

Для оценки устойчивости системы сначала строится матрица Гурвица по алгоритму: сначала на главной диагонали располагают слева направо все коэффициенты характеристического уравнения от a₁ {\displaystyle \ a_{1}} до a_n. Затем достраиваются строки и столбцы матрицы таким образом, чтобы индексы убывали. Если индекс больше, чем n (порядок характеристического уравнения) или меньше нуля, то на место таких коэффициентов ставятся нули. [9]

Составим матрицу Гурвица в Maxima, используя уже описанную функцию matrix (рисунок 3.3).

Рисунок 3.3 - Матрица Гурвица

Согласно критерию Гурвица, для того, чтобы линейная динамическая система являлась устойчивой, необходимо и достаточно, чтобы все n главные диагональные миноры определителя Гурвица были положительными, если a₀>0. Такие миноры были названы определителями Гурвица.

Вычислим все главные определители матрицы, которые получим, вычеркивая равное количество строк и столбцов от левого верхнего угла матрицы. Для получения матриц используем функцию submatrix, которая возвращает из заданной подматрицы новую матрицу. Подматрица строится путем удаления заданных строк и столбцов. Для нахождения определителей воспользуемся уже описанной ранее функцией determinant (рисунок 3.4).

Рисунок 3.4 - Определители Гурвица

Так как все определители положительны, можно сделать вывод, что система устойчива.

3.2.2 Критерий Михайлова

Так же, как и для критерия Гурвица, для исследования устойчивости по критерию Михайлова основной информацией является характеристическое уравнение. Данный критерий является частотным. Об устойчивости судят по геометрической иллюстрации траектории движения конца вектора Михайлова - годографу Михайлова. Основное достоинство - нет необходимости вычислять полюса передаточной функции для замкнутой системы, критерий базируется на принципе аргумента.

По годографу вектора определятся изменение аргумента характеристического уравнения, который можно записать в виде:

D (jw) = X (w) + jY (w) = D (w) e^{jy (w),} (3.1)

где X (w) - действительная часть характеристического вектора;

Y (w) - мнимая часть характеристического вектора;

D (w) - модуль характеристического вектора;

y (w) - аргумент характеристического вектора.

Линейную систему n-го порядка можно считать устойчивой, если при изменении частоты при изменении w от 0 до ¥ изменение аргумента D (jw) равняется n*π/2. Другими словами, необходимо, чтобы кривая Михайлова начиналась на положительной части действительной оси и обходила последовательно против часовой стрелки (в положительном направлении) столько квадрантов, каков порядок характеристического уравнения системы.

Для выделения действительной и мнимой части характеристического уравнения используем функции realpart и imagpart соответственно. Далее используя полученные действительную и мнимую части построим параметрический график - годограф. Синтаксис построения параметрического графика в Maxima:

plot2d ([parametric,X (t),Y (t)], [t,0,100], [nticks,1000]) $, (3.2)

где X (t) - действительная часть выражения;

Y (t) - мнимая часть выражения;

[t,0,100] - диапазон точек, в котором необходимо нарисовать годограф;

[nticks,1000] - параметр, задающий число точек для интерполяции графика. Чем больше точек, тем более гладким будет выглядеть график и больше времени потребуется на его построение.

Ввод команд показан на рисунке 3.5, полученный годограф - рисунок 3.6.

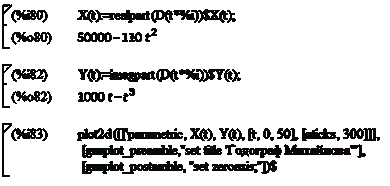
Рисунок 3.5 - Ввод команд для построения годографа

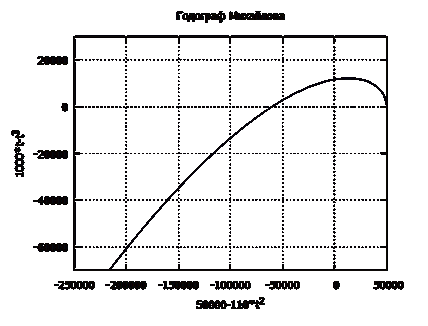
Рисунок 3.6 - Годограф Михайлова

По критерию Михайлова для того, чтобы система 3-го порядка была устойчива, кривая Михайлова должна последовательно проходить три квадранта. По рисунку 3.6 видно, что полученная кривая Михайлова соответствует данному условию, следовательно - система устойчива.

3.2.3 Критерий Найквиста

Для оценки устойчивости системы широко применяется логарифмический критерий Найквиста. Чтобы замкнутая система была устойчивой необходимо, чтобы в её разомкнутом состоянии фазовое запаздывание не достигло - 180° до частоты среза при амплитуде равной нулю или чтобы при таком запаздывании по фазе линейная частотная характеристика была меньше нуля. Для определения запасов устойчивости находят частоту среза ω_с и критическую частоту ω_кр., На критической частоте ФЧХ равна - π, на частоте среза АЧХ равна единице.

Чтобы избежать громоздких вычислений целесообразно оценивать устойчивость разомкнутых систем по логарифмическим частотным характеристикам (ЛЧХ). Замкнутую систему можно считать устойчивой, если ее ЛАХ в разомкнутом состоянии начинает принимать отрицательные значения раньше, чем ЛФХ примет значения фазы - 180⁰. Т.е. должно соблюдаться условие - ω_с < ω_кр. Если критическая частоты будет больше частоты среза, то замкнутая система неустойчивая. Если данные частоты равны - значит, система находится на границе устойчивости. [10]

Построить ЛАХ и ЛФХ в Maxima можно не только используя функции bode_gain и bode_phase, описанные в пункте 2.2.3, а также с помощью стандартной функции построения графиков plot2d. Для наглядной проверки условия устойчивости (ЛАХ принимает отрицательные значения позже, чем ЛФХ достигнет фазу - 180) построим ЛАЧХ и ЛФЧХ на одном графике. Для этого необходимо задать функции в виде списка. Также для удобства восприятия используем некоторые опции команды опции команды plot2d. Название графика задается командой gnuplot внутри опции gnuplot_postamble. Команды gnuplot пишутся внутри общих кавычек и отделяются друг от друга точкой с запятой. Опишем некоторые из них:

подпись названий осей - [xlabel, "имя для оси x"], [ylabel, "имя для оси у"];

задать имя графика - [gnuplot_postamble, "set title 'имя графика'; "];

задать подписи кривых - [legend, "кривая 1", "кривая 2", "и т.д. "].

Для изменения шкал и линий сетки можно использовать следующие команды:

указать шаг между основными линиями сетки (по x и y) - set xtics dx; set ytics dy;

убрать отражение оси х сверху - set xtics nomirror;

нарисовать ось y в m раз больше, чем размер оси х;

отобразить шкалы на оси координат в логарифмическом масштабе.

С помощью опции color можно менять цвет графиков:

[color, "цвет графика функции 1", "цвет графика функции 2", "и т.д. "].

Для графика ЛАХ по оси Y откладывается амплитуда, измеренная в децибелах, для графика ЛФХ - фаза, измеренная в углах, умноженных на градус. По оси X откладывается частота в логарифмическом масштабе (укажем с помощью опции [logx]). Модуль значения передаточной функции определим с помощью функции abs, аргумент комплексного выражения найдем с помощью функции carg. Введенные команды показаны на рисунке 3.7, где W (s) - передаточная функция разомкнутой системы, L (ω) - амплитуда [дб], ω - частота, s - оператор Лапласа, ψ (ω) - фаза [угл*град]. Полученные ЛАЧХ и ЛФЧХ представлены на рисунке 3.8.

Рисунок 3.7 - Ввод команд для построения ЛАЧХ и ЛФЧХ

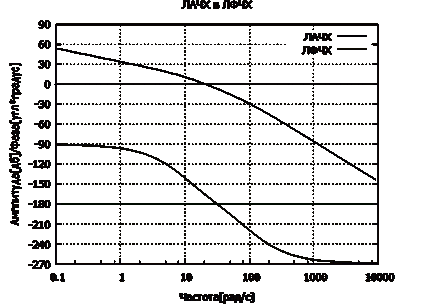
Рисунок 3.8 - ЛАЧХ и ЛФЧХ

Как видим на рисунке 3.8 ЛАХ принимает отрицательные значения раньше, чем ЛФХ достигнет фазу - 180 - получаем подтверждение, что заданная система устойчива. Определим по графику частоту среза и критическую частоту, а также определим запасы устойчивости. Частота среза ω_с = 20,54 с^-1, критическая частота ω_к = 30,8 с^-1. Запасы устойчивости: по фазе m = |-180 - (-165) | = 15 град., по амплитуде L_h = |0 - (-6,7) | = 6,7 дБ.

4. Разработка методического обеспечения

4.1 Руководство пользователя

Maxima является сложным прикладным продуктом. Для того, чтобы студенты могли самостоятельно работать с интерфейсом wxMaxima, решать все основные задачи составим руководство пользователя. В руководство пользователя включим:

назначение программы;

установку и запуск программы;

основные возможности;

арифметические и логические операции;

используемые переменные, математические функции и константы;

решение задач элементарной математики;

нахождений корней уравнений;

различные варианты построения графиков функций;

решение задач линейной алгебры и математического анализа;

список дополнительных источников для изучения Maxima.

Составленное руководство пользователя поможет сэкономить значительное количество времени на адаптацию пользователя к программе и изучение ее основ. Руководство представлено в приложении 1.

4.2 Реализация практикума по ТАУ

Используя полученные знания о возможностях программы реализуем практикум по теории автоматического управления на языке Maxima. Сначала составим математическое описание заданной системы, получим ее характеристики (временные, частотные и характеристики в пространстве состояний). Затем исследуем систему автоматического управления на устойчивость: по корням характеристического полинома и по критериям устойчивости.

Исходные данные:

структурная схема, представленная на рисунке 4.1;

заданные значения параметров системы, представленные в таблице 4.1.

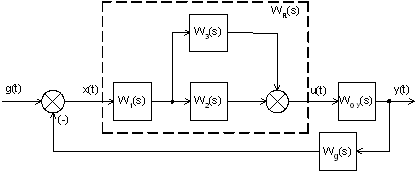
Рисунок 4.1 - Структурная схема исследуемой системы

На рисунке 4.1 обозначены:

W_oy (s) - передаточная функция объекта управления;

W_g (s) - передаточная функция датчика;

W_R (s) - передаточная функция регулятора;

W₁ (s) - передаточная функция усилителя;

W₂ (s) - передаточная функция безынерционного звена;

W₃ (s) - передаточная функция интегрирующего звена;

g (t) и u (t) - задающее и управляющее воздействия;

y (t) - управляемая (регулируемая) величина;

x (t) - рассогласование (ошибка).

Таблица 4.1 - Значения параметров системы

Коу	Т1	Т2	К1	KП	КИ
0,15	0,5	0,8	8	0,8	2

В таблице 4.1 обозначены:

К_{оу -} коэффициент передачи объекта управления;

Т₁ и Т₂ - постоянные времени;

К₁ - коэффициент передачи усилителя;

K_П и К_{И -} коэффициенты пропорциональной и интегральной составляющих закона управления.

Полученный программный код с комментариями представлен в приложении 2.

5. Maxima 5.38.1

Примечание: данное пособие разработано для В предыдущих версиях Maxima могут быть особенности записи выражений, отличные от указанных в данном пособии.

Maxima - система для работы с символьными и численными выражениями, включающая дифференцирование, интегрирование, разложение в ряд, преобразование Лапласа, обыкновенные дифференциальные уравнения, системы линейных уравнений, многочлены, множества, списки, векторы, матрицы и тензоры. Maxima производит численные расчеты высокой точности, используя точные дроби, целые числа и числа с плавающей точкой произвольной точности. Система позволяет строить графики функций и статистических данных в двух и трех измерениях.

Исходный код Maxima может компилироваться на многих системах, включая Windows, Linux и MacOS X. С каждой новой версией в Maxima появляются новые функциональные возможности и виды решаемых задач. Система аналитических вычислений Maxima идеально подходит для изучения студентами.

Основными преимуществами программы являются:

возможность свободного использования (Maxima относится к классу свободных программ и распространяется на основе лицензии GNU);

возможность функционирования под управлением различных ОС (в частности Linux и Windows);

небольшой размер программы (дистрибутив занимает порядка 23 мегабайт, в установленном виде со всеми расширениями потребуется около 80 мегабайт);

широкий класс решаемых задач;

возможность работы как в консольной версии программы, так и с использованием одного из графических интерфейсов (xMaxima,

wxMaxima или как плагин (plug-in) к редактору TexMacs);

расширение wxMaxima (входящее в комплект поставки) предоставляет пользователю удобный и понятный интерфейс, избавляет от необходимости изучать особенности ввода команд для решения

интерфейс программы на русском языке;

наличие справки и инструкций по работе с программой (русскоязычной версии справки нет, но в сети Интернет присутствует большое количество статей с примерами использования Maxima).

6. Установка и запуск программы

Скачать последнюю версию программы Вы можете с ее сайта в сети Интернет: #"896618.files/image037.gif">

В следующем окне жмем "далее", читаем лицензионное соглашение, выбираем "я принимаю условия соглашения" и снова жмем "далее".

В следующем окне снова жмем далее, на следующей форме выбираем путь установки программы:

Переходим к выбору устанавливаемых компонент. Из всего перечисленного

для нас "лишними" являются Пакеты поддержки языков Maxima, а также графическая оболочка XMaxima.

В следующих окнах нам будет предложено выбрать, куда помещать ярлыки для запуска программы (в меню "Пуск", на рабочий стол и т.д.). Завершающим этапом будет окно с предложением начать установку. По окончании установки жмем "далее" и "завершить".

7. Интерфейс wxMaxima

Рассмотрим рабочее окно программы. Сверху располагается текстовое меню программы - доступ к основным функциям и настройкам программы. В текстовом меню wxMaxima находятся функции для решения большого количества типовых математических задач, разделенные по группам: уравнения, алгебра, анализ, упростить, графики, численные вычисления. Ввод команд через диалоговые окна упрощает работу с программой для новичков. Ниже располагается графическое меню - наиболее часто используемые функции для работы с файлами: открыть / сохранить / печать данных, а также функции правки - копировать / удалить / вставить текст и другие, затем расположено окно вывода результатов расчетов и поле ввода команд.

8. Ввод простейших команд в wxMaxima

Все команды вводятся в поле ВВОД, разделителем команд является символ; (точка с запятой). После ввода команды необходимо нажать клавишу Enter для ее обработки и вывода результата. В случае, когда выражение надо отобразить, а не вычислить, перед ним необходимо поставить знак ‘ (одинарная кавычка). Но этот метод не работает, когда выражение имеет явное значение, например, выражение sin (π) заменяется на значение равное нулю.

Правила ввода чисел в Maxima точно такие, как и для многих других подобных программ. Целая и дробная часть десятичных дробей разделяются символом точка. Перед отрицательными числами ставится знак минус. Числитель и знаменатель обыкновенных дробей разделяется при помощи символа / (прямой слэш). Преобразование к форме с плавающей точкой осуществляет функция float.

При вводе каждой команде и результату присваивается порядковый номер. Используемый стиль обозначений позволяет при дальнейшей записи команд сослаться на ранее полученные результаты, например, таким образом (%o1) + (%o2) - результаты требуется сложить. Для последнего ответа в Maxima есть специальное обозначение %. А для последней команды _ (знак подчёркивания).

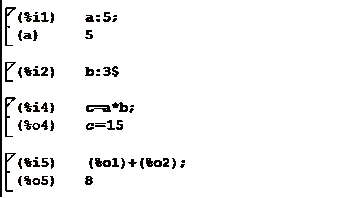
9. Арифметические и логические операции и константы

Обозначение арифметических операций в Maxima ничем не отличается от классического представления: +, - , *, /. Возведение в степень можно обозначать несколькими способами: ^, ^^, **. Извлечение корня степени n записываем, как степень 1/n. Нахождение факториала числа обозначается восклицательным знаком. Для увеличения приоритета операции, как и в математике, используются круглые скобки: ().

Основные арифметические операторы:

Основные логические операторы:

В Maxima для удобства вычислений есть ряд встроенных констант, самые распространенные из них:

9.1 Переменные

Для хранения результатов промежуточных расчетов применяются переменные. Заметим, что при вводе названий переменных, функций и констант важен регистр букв. Присваивание значения переменной осуществляется с использованием символа: (двоеточие). Если необходимо удалить значение переменной (очистить ее), то применяется метод kill (x) - удалить значение переменной x; kill (all) - удалить значения всех используемых ранее переменных.

Пример:

 

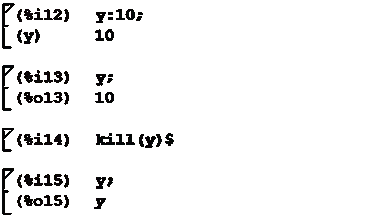
9.2 Математические функции

В Maxima имеется достаточно большой набор встроенных математических функций. Вот некоторые из них: тригонометрические функции: sin (синус), cos (косинус), tan (тангенс), cot (котангенс); обратные тригонометрические функции: asin (арксинус), acos (арккосинус), atan (арктангенс), acot (арккотангенс); sec (секонс, sec x = 1/cos x), csc (косеконс, csc x = 1/sin x); sinh (гиперболический синус), cosh (гиперболический косинус), tanh (гиперболический тангенс), coth (гиперболический котангенс), sech (гиперболический секанс), cosh (гиперболический косеканс); log (натуральный логарифм); sqrt (квадратный корень); mod (остаток от деления); abs (модуль); min (x1,…,xn) и max (x1,…,xn) - нахождение минимального и максимального значения в списке аргументов; sign (определяет знак аргумента: pos - положительный, neg - отрицательный, pnz - не определен, zero - значение равно нулю).

Для записи функции необходимо указать ее название, а затем, в круглых скобках записать через запятую значения аргументов. Если значением аргумента является список, то он заключается в квадратные скобки, а элементы списка также разделяются запятыми. Пользователь может задать собственные функции. Для этого сначала указывается название функции, в скобках перечисляются названия аргументов, после знаков: = (двоеточие и равно) следует описание функции. После задания пользовательская функция вызывается точно так, как и встроенные функции Maxima. Пример:

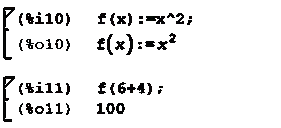
9.3 Решение задач элементарной математики

К таким задачам можно отнести вычисление и преобразование арифметических выражений, построение графиков функций, решение уравнений и систем алгебраических уравнений. Рассмотрим некоторые полезные функции:

sqrt - нахождение корня:

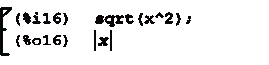
divide - нахождение частного и остатка от деления одного многочлена на другой:

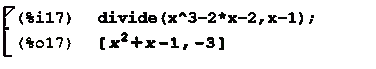
Первый элемент полученного массива - частное, второй - остаток от деления. factor - разложение на множители:

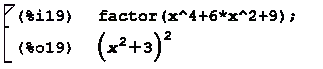
expand - раскрытие скобок:

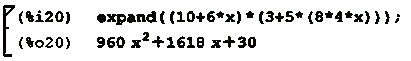
ratsimp - упрощение выражения:

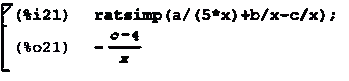
partfrac - преобразовать в простые дроби по заданной переменной:

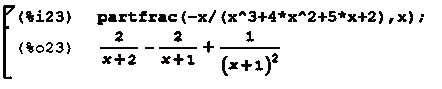
9.4 Нахождение корней уравнений и систем алгебраических уравнений

solve - решение алгебраических уравнений и их систем (в качестве параметров в первых квадратных скобках указывается список уравнений через запятую, во-вторых - список переменных, через запятую):

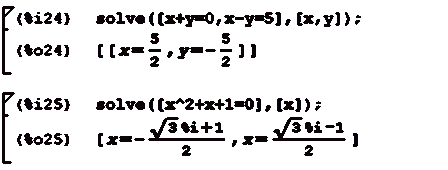
10. Графики функций

10.1 Построение графиков

В Maxima имеется несколько альтернативных библиотек для отображения графиков функций, наборов точек, трехмерных тел, градиентов и т.д. Рассмотрим несколько примеров построения графиков. По умолчанию используется библиотека Plot, которая и будет рассмотрена ниже. Также для решения некоторых задач рекомендуется ознакомиться с возможностями библиотеки Draw (см. справочную систему Maxima). Сразу стоит отметить, что при построении графика стоит обращать внимание на масштаб делений по осям. И, если, вместо ожидаемой окружности, мы увидим эллипс, то, скорее всего это произошло именно из-за несоответствия масштаба делений по осям. Пример 1.

Двумерный график. На графике показаны три зависимости. График построен с использованием функции plot2d. Первый аргумент - список функций, второй и третий - ограничения по осям координат. Третий аргумент является необязательным. Если его не указать - он будет подобран автоматически.

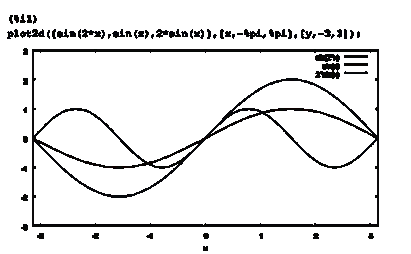
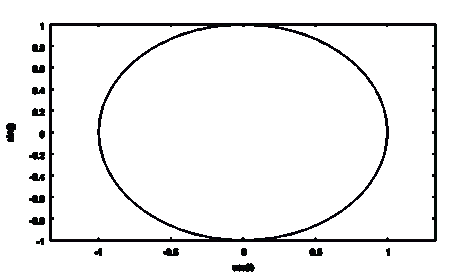
Пример 2.

Построение графиков функций, заданных параметрически. Приведем пример построения графика функции с зависимостью, заданной параметрически: (%i31) plot2d ([parametric, cos (t), sin (t), [t,-%pi,%pi], [nticks,80]], [x, - 4/3, 4/3]);

Параметр nticks,80 указывает сколько опорных точек используется для построения графика. В данном примере, при значении 4 получим треугольник, при значении 5 - четырехугольник и т.д.

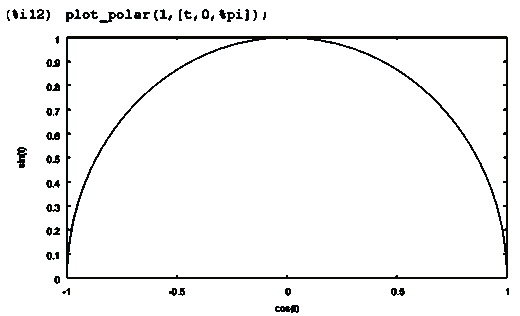
Пример 3.

Построение графиков функций в полярных координатах. На первом этапе необходимо задать функцию для построения графиков в полярных координатах.

(%i11) plot_polar (expr,range): =block ([theta_var: range [1]],plot2d (['parametric,cos (theta_var) *expr, sin (theta_var) *expr,range, [nticks,80]]))

Теперь для построения дуги необходимо ввести

Пример 4.

Построение трехмерных графиков.

Чтобы записать график в файл нужно указать тип графического терминала [gnuplot_term, тип] и имя выходного фала [gnuplot_out_file, " имя"]. Тип может быть либо ps (формат post script) либо один из графических форматов png, jpg и т.п. Если не указывать имя выходного файла, то будет применено стандартное имя maxplot.

10.2 Опции оформления графиков

Название графика задается командой gnuplot внутри опции gnupot_preamble. Команды gnuplot пишутся внутри общих кавычек и отделяются друг от друга точкой с запятой: [gnuplot_preamble, "set title 'имя графика'; "];

Названия осей: [xlabel, "имя для оси x"], [ylabel, "имя для оси у"];

Подписи кривых (легенда): [legend, "кривая 1", "кривая 2", "и т.д. "].

Легенда выводятся в правом верхнем углу, изменить её положение можно командой gnuplot set key:

set key bottom - внизу;

set key top left - вверху слева;

set key bottom center outside - внизу по центру за пределами графика.

Шкалы и линии сетки можно менять при помощи следующих команд gnuplot:

set grid polar df - задает радиальную сетку в полярной системе координат, df угол между ее линиями в радианах;

set xtics dx; set ytics dy - указание шага между основными линиями сетки (по x шаг=dx, по y шаг=dy);

set border 3; set xtics nomirror - убирает отражение оси х сверху;

set mxtics n - разбивает основные деления шкалы по оси х на n интервалов;

set size ratio m - рисует размер оси y в m раз больше размера оси х;

set log x; set log y - отображает шкалы на оси координат в логарифмическом масштабе.

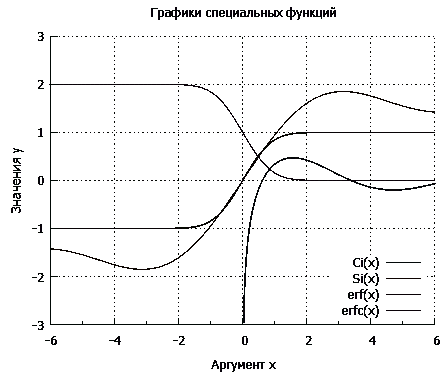
Например, построим графики с использование некоторых опций:

11. Решение задач линейной алгебры

В данном разделе будут рассмотрены основные операции с матрицами. Для задания матрицы используется функция matrix:

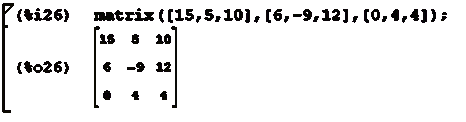
11.1 Операции с матрицами

Рассмотрим основные операции с матрицами на примере, для этого зададим две матрицы: x и y

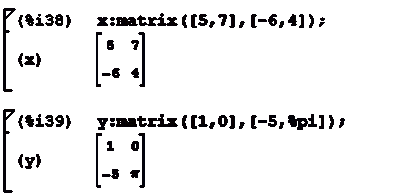
Поэлементное сложение, вычитание, умножение и деление матриц, возведение в степень:

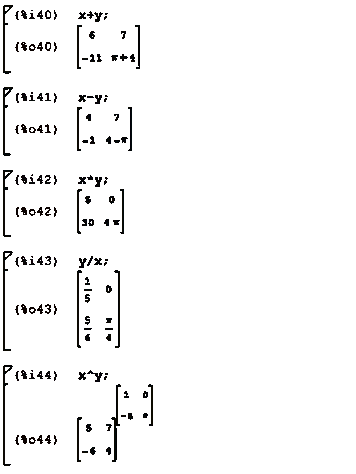
Пример применения функции к матрице:

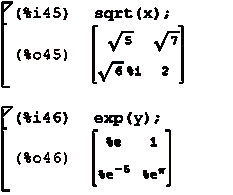
Умножение матриц:

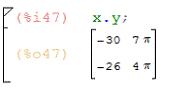
11.2 Функции для работы с матрицами

determinant - нахождение определителя матрицы:

eigenvalues - нахождение собственных значений матрицы:

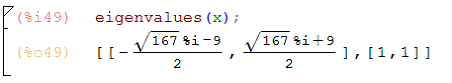
invert - получение обратной матрицы:

minor - определяет минор матрицы. Первый аргумент - матрица, второй и третий - индексы строки и столбца соответственно:

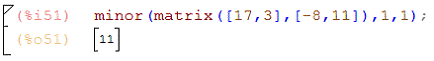
rank - ранг матрицы:

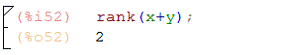
submatrix - возвращает матрицу, полученную из исходной удалением соответствующих строк и (или) столбцов. В качестве параметров следуют номера удаляемых строк, исходная матрица, номера удаляемых столбцов.

12. Решение задач математического анализа

Нахождение производной:

Функция diff позволяет найти производные, как первого, так и более высоких порядков. При наличии у функции нескольких переменных можно найти частную производную по одной из них.

Синтаксис: diff (функция, переменная, порядок производной);

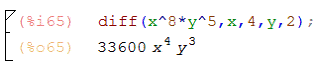
Интегрирование:

Для нахождения неопределенного интеграла в качестве аргументов указывается функция и переменная интегрирования.

Синтаксис: integrate (функция, переменная);

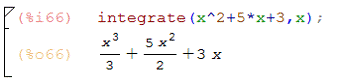
Разложение в ряд Тейлора:

Синтаксис: taylor (функция, x, a, n).

Параметр n определяет, до какой степени (x-a) находить решение.

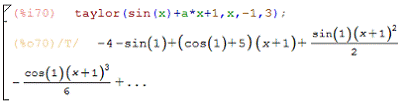
Прямое преобразование Лапласа: laplace (выражение, переменная, параметр)

Обратное преобразование Лапласа: ilt (выражение, переменная, параметр)3

Заключение

В выпускной квалификационной работе была рассмотрена система компьютерной алгебры, представленная в графическом интерфейсе wxMaxima.

Была поставлена задача изучить систему Maxima и исследовать эффективность ее использования в курсе теории автоматического управления в качестве инструмента для выполнения практикума. Использование данной системы в техническом государственном вузе является рациональным, так как программа является свободно распространяемой, в отличие от другого аналогичного программного обеспечения, а также она нетребовательна и может работать на старых компьютерах.

В ходе выполнения данной работы был реализован программный код для исследования конкретной системы автоматического управления. Получено математическое описание, построены временные (импульсная и переходная) и частотные (амплитудная и фазовая) характеристики, а также характеристики системы в пространстве состояний. Затем была выполнена оценка устойчивости заданной системы по корням характеристического полинома и по критериям устойчивости. Таким образом, используя систему компьютерной алгебры Maxima, можно решить все задачи практикума по курсу ТАУ.

В данной работе отражены все действия, которые необходимо воспроизвести для успешного выполнения практикума. Также для экономии времени на адаптацию студентов к программе и изучение ее основ на основе проведенного исследования разработано руководство пользователя по системе Maxima.

Список использованных источников

1.      PTC Mathcad [Электронный ресурс]: офиц. сайт. - Режим доступа: http://www.ptc.com/engineering-math-software/mathcad.

2.      MATLAB и Simulink центр компетенций компании Mathworks [Электронный ресурс] офиц. сайт. - Режим доступа: http://matlab.ru.

.        VisSim web site [Электронный ресурс]: офиц. сайт. - Режим доступа: http://vissim.com.

.        Система компьютерной алгебры Maxima [Электронный ресурс] офиц. сайт. - Режим доступа: http://maxima. sourceforge.net/ru/.

.        Тюкин, В.Н. Теория управления: Конспект лекций. Часть 1. Обыкновенные линейные системы управления - 2-е изд., испр. и доп. / В.Н. Тюкин. - Вологда: ВоГТУ, 2000. - 200 с.

.        Чичкарев, Е.А. Компьютерная математика с Maxima: Руководство для школьников и студентов / Е.А. Чичкарев, К.А. Семендяев. - М.: ALT Linux, 2009. - 233 с.

.        Бронштейн, И.Н. Справочник по математике для инженеров и учащихся втузов - 13-е изд., исправленное / И.Н. Бронштейн, К.А. Семендяев. - М.: Наука, Гл. ред. физ. - мат. лит., 1986. - 544 с.

8.      Maxima 5.40.0 Manual [Электронный ресурс]: документация по текущей версии пакета. - Режим доступа: http://maxima. sourceforge.net/docs/manual/en/maxima.html <http://maxima.sourceforge.net/docs/manual/en/maxima.html>.

.        Бесекерский, В.А. Теория систем автоматического управления: учебник / В.А. Бесекерский, Е.П. Попов. - СПб: Профессия, 2003. - 752 с.

.        Тюкин, В.Н. Основы теории управления: методические указания к лабораторному практикуму / Тюкин В.Н. - Вологда:, 2015. - 38 с.