Задача о наименьшем покрытии: решение, алгоритмы, применение (обзор с примерами программных реализаций)

Федеральное государственное автономное образовательное учреждение
 высшего образования

«Санкт-Петербургский политехнический университет Петра Великого»

Институт компьютерных наук и технологий

Кафедра «Компьютерные интеллектуальные технологии»

КУРСОВОЙ ПРОЕКТ

Задача о наименьшем покрытии: решение, алгоритмы, применение (обзор с примерами программных реализаций)

по дисциплине: «Структуры и алгоритмы компьютерной обработки данных»

Содержание

Введение

. Обзор алгоритмов решения задачи

.1 Точные методы

.2 Генетический алгоритм

.3 Жадный алгоритм

. Жадный алгоритм

.1 Описание алгоритма

.2 Анализ точности приближения

.3 Анализ вычислительной сложности

.4 Программная реализация

.5 Экспериментальная проверка корректности и быстродействия

Заключение

Список использованных источников

Приложение 1

Приложение 2

Введение

алгоритм жадный вычислительный быстродействие

Задача о наименьшем покрытии множества, рассматриваемая в данной работе, заключается в поиске минимального набора подмножеств, полностью покрывающих исходное множество. Она является классической задачей комбинаторики, информатики и теории вычислений, входит в список 21 NP-полной задачи Р. Карпа.

К задаче о покрытии сводятся многие известные задачи дискретной оптимизации: задачи стандартизации, упаковки и разбиения множества, задачао наибольшей клике, задача минимизации полинома от булевых переменных и др. Известна также и обратная сводимость задачи о покрытии к этим задачам.

На практике задачи о покрытии возникают при размещении пунктов обслуживания, в системах информационного поиска, при назначении экипажей на транспорте, проектировании интегральных схем и конвейерных линий и т. д. Задача о вершинном покрытии может использоваться при разработке систем контроля и наблюдения, в построении помехоустойчивых алгоритмов передачи информации, при диагностике оборудования и в других областях.

Цели работы

1.      Проанализировать задачу о покрытии, дать её формальную постановку;

.        Рассмотреть методы решения задачи и их применения на практике;

.        Для одного из методов - жадного алгоритма - привести анализ точности, быстродействия и программную реализацию;

.        Подтвердить полученные в предыдущем пункте теоретические данные экспериментально;

Постановка задачи

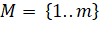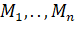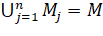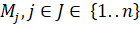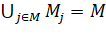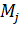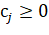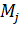Комбинаторная постановка задачи о покрытии множества состоит в следующем. Пусть даны множество, и его набор подмножеств таких, что . Совокупность подмножеств , называется покрытием множества M, если . Каждому  приписан вес . Требуется найти покрытие минимального суммарного веса. Задача называется невзвешенной, если все подмножества  имеют единичные веса.

В качестве простого примера предположим, что нам нужно собрать команду для работы над проектом; каждый человек из выборки обладает ограниченным набором навыков. Мы хотим подобрать наименьшую группу людей, обладающих в совокупности всеми нужными навыками.

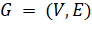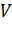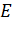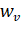Значительное внимание уделяется задачам о покрытиях в графе, в частности задаче о вершинном покрытии, которая может быть сформулирована следующим образом. Пусть - граф с множеством вершин  и множеством ребер . Для каждой вершины  определен вес > 0. Подмножество 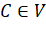называется вершинным покрытием, если каждое ребро из 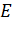 инцидентно хотя бы одной вершине из 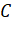. Требуется найти вершинное покрытие минимального веса.

1. Обзор алгоритмов решения задачи

.1 Точные методы

Для решения общей задачи о покрытии предложено большое число точных алгоритмов, основанных на методах ветвей и границ, отсечения, перебора L-классов и др.Верхние оценки временной сложности точных методов сопоставимы сосложностью переборных алгоритмов. В данной работе не приводятся в виду большой сложности анализа их работы

.2 Генетический алгоритм

Генетический алгоритм представляет собой эвристический метод случайного поиска, основанный на принципе имитации эволюции биологической популяции. Сначала выбирается семейство покрытий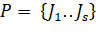,заданного объема s. Множество Pназывают популяцией, а его элементы - особями. Из популяции Pвыбираются две особи, например 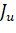и 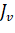, называемые родителями, и из покрытия 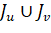, выделяется покрытие J, называемое их потомком. Потомок подвергается мутации (случайному изменению), после чего он замещает в Pнаихудшую особь. Этот цикл - выбор родителей, создание потомка, его мутация и обновление популяции - повторяется заданное число раз 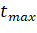. Результатом работы алгоритма является наилучшее из покрытий, возникших в ходе развития популяции.Обе существующие модификации генетического алгоритма намного превосходят жадный алгоритм по весовым показателям получившихся покрытий, но по параметру трудоемкости жадный алгоритмвыигрывает с огромным отрывом. Если важна скорость вычислений, то в задачах небольшой размерности можно использовать жадный алгоритм..

1.3 Жадный алгоритм

Для задач о покрытии разработано значительное число приближенных алгоритмов с априорными оценками точности получаемых решений. Одним из первых приближенных алгоритмов, предложенных для невзвешенной задачи о покрытии, является жадный алгоритм.

2. Жадный алгоритм

2.1 Описание алгоритма

Жадный метод работает путем выбора на каждом этапе множества S, покрывающего максимальное количество элементов, оставшихся непокрытыми.

Листинг 1 - Псевдокод жадного алгоритма

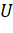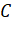Опишем принцип действия алгоритма [листинг 1]. На каждом этапе его работы множество содержит оставшиеся непокрытыми элементы. Множество  содержит покрытие, которое конструируется. Строка 4 - это этаппринятия решения в жадном методе. Выбирается подмножество 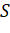, покрывающее максимально возможное количество еще непокрытых элементов (с произвольным разрывом связей). После выбора подмножества 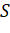 его элементы удаляются из множества 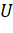, а подмножество 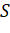помещается в семейство 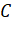. Когда алгоритм завершает свою работу, множество 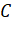 будет содержать подсемейство семейства 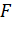, покрывающее множество 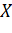. В примере, проиллюстрированном на рис1, алгоритм GREEDY_SET_COVERдобавляет в семейство 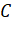 множества 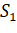, , 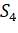 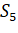и 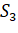 в порядке перечисления.

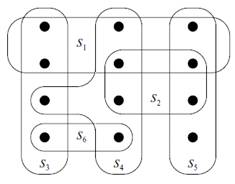
Рисунок 1 - Пример работы процедуры GreedySetCover [1]

2.2 Анализ точности приближения

В общем случае, если на каком-то шаге осталось 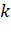 непокрытых элементов исходного множества 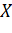 и если каждое данное подмножество множества  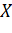имеет не более  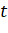этих элементов, то оптимальное решение будет содержать как минимум 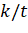множеств. При помощи этого наблюдения можно доказать, что жадный алгоритм имеет степень точности.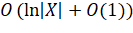

Присвоим каждому из выбранных алгоритмом множеств стоимость 1, распределим эту стоимость по всем элементам, покрытым за первый раз, а потом с помощьюэтих стоимостей получим нужное соотношение между размером оптимального покрытия множества 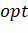 и размером покрытия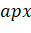, возвращенного алгоритмом. Обозначим через 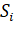i-е подмножество, выбранное алгоритмом GREEDY_SET_COVER; добавление подмножества 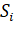 в множество 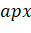приводит к увеличению стоимости на 1. Равномерно распределим стоимость, соответствующую выбору подмножества 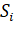, между элементами, которые впервые покрываются этим подмножеством. Пусть 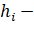число элементов, покрытых на том же шаге вместе с 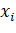.Обозначим через  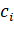стоимость, выделенную элементу 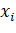∈X, 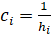Стоимость выделяется каждому элементу только один раз, когда этот элемент покрывается впервые.На каждом шаге алгоритма присваивается единичная стоимость, поэтому

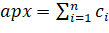
Теперь рассмотрим элементы 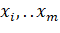. Каждое данное подмножество содержит не более чем 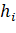 этих элементов (а всего их  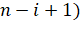и мы можем, используя оптимальное решение, покрыть все элементы, включая элементы 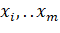, наименьшим возможным числом множеств. В этом случае

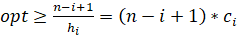
Откуда получаем

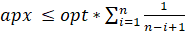
Число 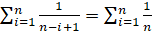 не превосходит 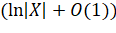, и, следовательно, 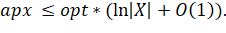[1] [2] [3]

2.3 Анализ вычислительной сложности

Поскольку количество итераций цикла в строках 3-6 (рис. 1) ограничено сверху величиной 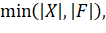 а тело цикла можно реализовать таким образом, чтобы его выполнение завершалось за время 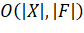, простая реализация алгоритма имеет время работы, равное 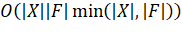. [1]

2.4 Программная реализация

Для реализации алгоритма был выбран язык Python (версия интерпретатора 3.6.1). Этот язык был выбран из-за наличия в нем максимально подходящих с точки зрения автора работы для данной задачи структур данных, позволяющих довольно просто воплотить в коде нужные математические объекты: множества и подмножества.

Набор подмножествS и набор соответствующих им весовw реализован структурой данных список (List). Исходное множество Uпредставлено структурой данных словарь (Dictionary, по принципу действия является ассоциативным массивом) и собирается путем объединения вводимых пользователем подмножеств и их весов. Фактически, Uпредставляет собой отображение элемента на индекс того подмножества из S, которому оно принадлежит[приложение 1].

Поиск наиболее дешевого множества на очередной итерации осуществляется при помощи очереди с приоритетом, реализация её методов представлена в приложении 2.

2.5 Экспериментальная проверка корректности и быстродействия

Для исследования работы алгоритма при помощи сторонних библиотек были созданы целочисленные множества вида 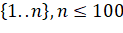0. В целом, анализ показал, что оценка, полученная в главе 2.3, выполняется приблизительно, некоторая неточность вызвана операцией поиска самого дешевого множества, использующей приоритетную очередь. Основываясь на полученных данных, более точной оценкой можно было бы назвать .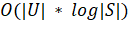

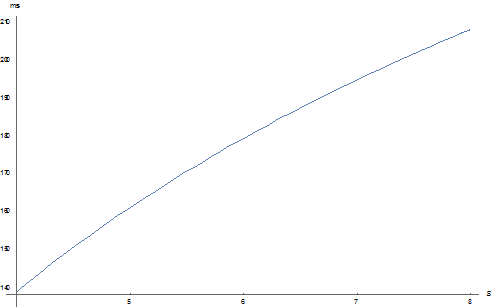
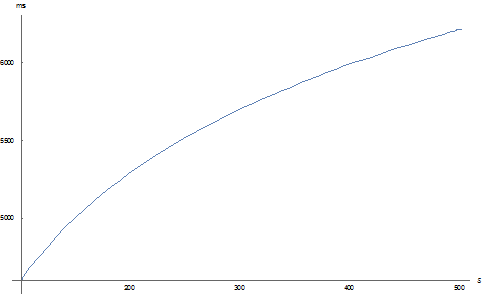
Рисунок 3 - График для U = 1000

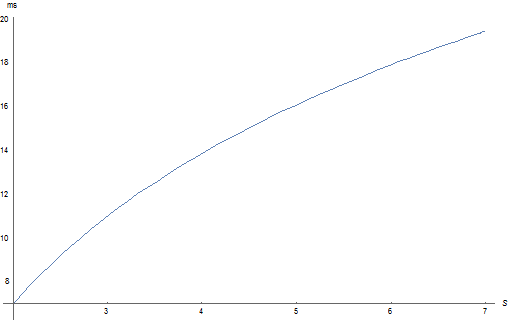
Рисунок 4 - График для U = 10

Для проверки корректности алгоритма при помощи сторонних библиотек были сгенерированы целочисленные множества вида [1..n]. Результаты тестирования приведены в таблице 1.12

Таблица 1 - Примеры входных и выходных данных

Заключение

Была рассмотрена задача о минимальном покрытии множества: постановка, практическая значимость,методы решения. Для жадного алгоритма получено теоретическое обоснование временной оценки и точности, его программная реализация. Кратко рассмотрены другие подходы к решению задачи.

Список использованных источников

1.      А. Ахо, Дж. Хопкрофт, Дж. Ульман Построение и анализ вычислительных алгоритмов - М.: Мир, 1979, - 536 с.

.        Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. Алгоритмы: Построение и анализ. - 2-е изд. - М.: Издательский дом «Вильямс», 2013. - 1227 с.

.        А. В. Еремеев, Л. А. Заозерская, А. А. Колоколов. Задача о покрытии множества: сложность, алгоритмы, экспериментальные исследования. Дискретный анализ и исследование операций. Сер. 2. 2000. Т. 7, N 2. С.22-46.

4.      Еремеев, А. В. Генетический алгоритм для задачи о покрытии / А. В. Еремеев // Дискретный анализ и исследование операций. - 2000. - Т. 7, № 1. - С. 47-60.

Приложение 1

Жадный алгоритм

importpriorityqueue= 999999(S, w):= {}

selected = list()= []

for index, item in enumerate(S):.append(set(item))

for j in item:

if j not in udict:[j] = set()[j].add(index)= priorityqueue.PriorityQueue()

cost = 0= 0

for index, item in enumerate(scopy):

if len(item) == 0:.addtask(index, MAXPRIORITY)

else:.addtask(index, float(w[index]) / len(item))

while coverednum<len(udict):

a = pq.poptask().append(a)

cost += w[a]+= len(scopy[a])m in scopy[a]:

for n in udict[m]:

if n != a:[n].discard(m)

if len(scopy[n]) == 0:.addtask(n, MAXPRIORITY)

else:.addtask(n, float(w[n]) / len(scopy[n]))[a].clear().addtask(a, MAXPRIORITY)

returnselected, cost

Приложение 2

Очередь с приоритетом

importitertoolsheapq import *PriorityQueue:__init__(self):

self._pq = []

self._entry_map = {}._counter = itertools.count()(self, task, priority = 0):

if task in self._entry_map:.removetask(task)

count = next(self._counter)

entry = [priority, count, task]

self._entry_map[task] = entry(self._pq, entry)(self, task):

entry = self._entry_map.pop(task)

entry[-1] = 'removed'(self):

while self._pq:

priority, count, task = heappop(self._pq)

if task is not 'removed':

del self._entry_map[task]

return task__len__(self):

return len(self._entry_map)