Использование дидактических игр для развития воображения при обучении математике в начальных классах
Содержание
Введение
Глава 1. Дидактические игры в
процессе обучения детей математикой
.1 Понятие игры. Понятие
дидактической игры. Виды дидактических игр
.2 Дидактические игры как ведущая
деятельность в обучении математики
.3 Влияние дидактических игр на изучение
математики
Глава 2. Использование дидактических
игр при обучении математике при помощи квеста. Экспериментальное исследование
.1 Подготовка учеников младшего
школьного возраста к прохождению квеста при помощи различных дидактических игр
.2 Разработка дидактических игр,
используемые в математическом квесте, для 1 класса
.3 Прохождение учениками квеста и
отношение учеников на подобный вид деятельности
Заключение
Список литературы
Приложения
Введение
Математика является стандартизированным языком, который известен всем на
свете и этот язык одинаков во всех странах. В современном мире такой школьный
предмет, как математика, играет огромную роль в развитии умственных
способностей детей. Математика присутствует в жизни людей различных профессий,
что показывает на истинную востребованность данного предмета. Математика с
раннего возраста способствует развитию воображения, восприятия мира. В
последнее время в учебной практике становится более популярным и актуальным
такой метод преподавания, как внедрение дидактических игр в классический подход
к обучению. Для детей младшего школьного возраста более близким является такой
вид деятельности, как игра. Так как ребенок только начинает приспосабливаться к
новому образу жизни, а школа и есть огромная перемена в жизни ребенка, то на
первых этапах более действенна и плодотворна является именно игра. Если
вспомнить слова Л.С. Выготского по поводу игры, то он делал акцент на
следующее, само понятие «игра», все время должно быть понято как воображаемое
иллюзорное исполнение нереализуемых желаний. Воображение и есть то
новообразование, отсутствующее в сознании ребенка младшего возраста; как все
функции сознания, воображение возникает вначале в действии. Понятие «детская
игра» - это воображение в действии, можно перевернуть и сказать, что
воображение у подростка и школьника есть игра без действия [15]. Проблема
дидактической игры является одной из самых актуальных проблем при обучении
математике. Проблема воображения в дидактических играх также является
актуальной, именно поэтому мы решили взять темой дипломной работы:
«Использование дидактических игр для развития воображения при обучении
математике в начальных классах».
Проблема исследования: как использовать дидактические игры для развития
воображения в познавательной деятельности младших школьников.
Согласно данной проблеме, мы ставим цель исследования: выявить
эффективность в использовании дидактических игр для развития воображения
младших школьников при обучении математике.
Объект исследования: процесс обучения младших школьников математике.
Гипотеза исследования: если использовать дидактические игры для развития
воображения при обучении математике, то это поможет развить: интерес к изучению
математики и к самой математики в целом; стремление у детей узнавать новый материал;
интерес к активно-игровой деятельности при обучении математике; активность при
обучении математике; способность к восприятию математического мира по средству
воображения.
Задачи исследования: изучение и анализ имеющейся литературы по проблеме;
сбор фактических данных; анализ полученных данных.
Теоретическая значимость исследования заключается в накоплении и
обобщении информации по использованию дидактических игр для развития
воображения при обучении математике.
Практическая значимость исследования заключается в возможности
использования полученных результатов и накопленного опыта в дальнейшей работе в
качестве учителя начальных классов.
Выпускная квалификационная работа (ВКР) состоит из введения, двух глав,
заключения, списка используемой литературы и электронных ресурсов, приложений.
В первой главе нами рассматривается суть понятия «дидактические игры», его
специфика и влияние на изучение математики в начальных классах. Во второй главе
описывается проведенное нами экспериментальное исследование. В заключении
обобщаются результаты эксперимента, подводятся итоги, формируются выводы и
практические рекомендации.
Глава 1.
Дидактические игры в процессе обучения детей математикой
.1 Понятие
игры. Понятие дидактической игры. Виды дидактических игр
Первой концепцией, рассматривающей игру, как вид деятельности, была
концепция, выдвинутая немецким философом и психологом К. Гросом в 1899 году. В
этой концепции он рассматривал игру животных как предварительное приспособление
инстинктов к условиям будущей жизни.
Игра - это вид непродуктивной деятельности, где мотив лежит не в
результате ее, а в самом процессе [17]. Игры переплетены с жизнью человечества
на протяжении всего его существования. На любом языке слово «игра» имеет
различные значения. Оно используется для описания веселья и развлечений,
театральных и музыкальных произведений. Мы также можем заметить, что разные
нации имеют различное понимание слова «игра». Как например, в древней Греции
слово «игра» описывало такой вид деятельности ребенка как шалость и озорство. В
то время как евреи понимали под словом «игра» шутку или смех. В санскрите
«Kliada» слово «игра» использовалось как выражение удовольствия. Это слово
вобрало в себя очень много понятий, начиная от детей, играющих в солдат до
представления героев на театральных сценах, от шахматной игры до
профессионализма скрипача. В современных европейских языках под «игрой»
понимают широкую сферу человеческой деятельности, которая не связана с тяжелой
работой, с одной стороны, и обеспечивает радость и удовлетворение людей, с
другой. В настоящее время роль игры в жизни человека очень велика, весь мир с
замиранием сердца следит за чемпионатами по футболу, олимпийскими играми. Но
мало кто догадывается, что человек знакомится с игрой с самого раннего детства.
Ребенок познает окружающий мир в игре, ошибаясь и начиная все сначала он
постоянно экспериментирует с разнообразными игрушками и материалами для
приобретения знания о том, как функционируют предметы, которые его окружают.
Обратимся к описанию понятия «Игры» [7]. Игра, как форма деятельности,
отличается от работы или учебы. Люди занимаются «играми» всю свою жизнь, но
игры занимают определенную роль в их дошкольном возрасте. Игра в дошкольном
возрасте является основным видом деятельности. Игра имеет множество различных
аспектов:
· познавательная;
· практическая;
· эмоциональная;
· мотивационная;
· творческая;
· фантастическая;
· социальная;
· рекреационная;
· диагностическая;
· терапевтическая;
В играх могут участвовать как один человек, так и пара людей, как небольшая,
так и большая группа людей. Существуют игры, требующие специальных пособий,
например, игрушки, игровые инструменты, спортивное снаряжение, инструменты,
приборы. Большинство игр имеют форму социального взаимодействия с четко
сформулированными правилами (дается по соглашению вовлеченных лиц). Большое
внимание уделяется ходу игры (игры с акцентом на сотрудничество, конкуренция).
Можно формализовать исходную ситуацию, ход и результаты некоторых игр, а также
детально изучить процесс принятия решений игроками. Специальная дисциплина
математики посвящена этим вопросам - теория игр.
Указанное выше определение отличает игры от работы или учебы. В основном
это связано с тем, что участие в игре не является обязательным, а отличие от
работы в том, что материальное вознаграждение не является целью игры. Участие в
игре в основном обусловлено положительными чувствами и радостью от участия в
ней. Важно отметить, что некоторые аспекты, которые также необходимы для работы
или учебы, могут быть развиты посредством игр. Опираясь на определение «игры»
данное Винфрид Бем (профессором по педагогике в университете Вюрцбурга) в 1988
[1], можно выделить краткие мнения о функции игры.
«Игра - это спонтанная деятельность, целью которой является сама игра.
Каждая человеческая деятельность может приобретать природу игры, если она
выполняется просто для удовольствия или для удовольствия, получаемого от ее
выполнения. Игры имеют связь со всеми видами деятельности человека и выступают
как детская форма познания искусства, общения, спорта и труда». Можно выделить
следующие виды игр:
· эмпирические;
· эмоциональные;
· творческие;
· имитирующие;
· языковые;
· социальные;
· любовные;
· умственные;
· и др.
Всегда есть попытки разделить многообразие игр и прояснить их в
соответствии с их функциями. Наиболее распространены следующие подходы к играм:
· игра как выражение избыточной энергии (Г. Спенсер [10]);
· понимание игры как возвращение к предыдущим этапам развития;
· релаксация;
· бессознательная подготовка к будущему (К. Грос [4]);
· форма познания.
По Ф. В. А. Фребелю (немецкий учитель и последователь Песталоцци) и Ф.
Шиллеру (немецкий поэт и философ) в дополнении к дидактической функциональности
и связанному с ней взаимодействию чувств, в отдельных играх есть глубокие
педагогико-антропологические рассуждения. К таким играм относятся
образовательные и дидактические игры. Фребель считает, что «игра - это
деятельность, ориентированная изнутри индивида наружу, при этом индивид
получает внешние стимулы внутрь». Данный вид деятельности превосходит односторонний
подход к исследованию и приводит к символическому познанию и представлению мира
[3]. Шиллер видит форму человеческой жизни в игре. Он думает, что в игре люди
не только выполняют свои инстинкты и желания, но также забывают об окружающих
условиях, обязательствах и правилах и имеют за счет этого более приятную жизнь
[9].
Отметим, что М. Монтессори использовала работы Ф. Фребеля, И. Песталоцци
и Ж. Ж. Руссо при построении своей теории образования. Она разработала
вспомогательную программу для помощи ученикам в написании и расстройстве
чтения, и она разработала систему воспитания и воспитания детей 3-6 лет. Она
отметила важность создания стимулирующей среды для детей, которая обеспечивает
мотивацию для развития учеников. В теории М. Монтессори одной из главных задач
учителя является создание и поддержание такой стимулирующей среды. В своей
системе образования Монтессори сосредоточилась на общем развитии детей:
развитии их сенсорно-моторных навыков, лексике, подготовке к письму, чтении и
простых математических операциях, а также об общем развитии поведения
дошкольников. Чтобы развить эти способности и навыки, Монтессори широко
использовала игры как естественную форму деятельности для детей. Она поддержала
мнение К. Гроса о важной роли игр для развития молодежи.
К функциям игр, непосредственно связанным с образованием, приписывают
подготовку к будущему, форму познания мира. Жан Пиаже и Барбель Инелдер
(швейцарские психологи) подробно рассмотрели функцию игр в развитии детской
психологии. Они приписывали биологическую функцию активного повторения и
экспериментирования игре, в которой мысленно обрабатываются и подготавливаются
новые ситуации и переживания [6]. Учитывая эти функции, игра кажется
естественным способом получения знаний и приобретения новых умственных
процессов. Исходя из этого, становится ясно почему игры стали частью школьного
обучения. Пиаже, и Инелдер признали общую функцию игр для развития детей.
Согласно их исследованиям, игры развивают сенсорно-моторные навыки,
эмоциональные и интеллектуальные области, а также воображение. Значимость игры
была также подтверждена в плане общения детей, развития их способности к
сотрудничеству, а также подготовки к конструктивной творческой деятельности и
способности решать проблемы, необходимые во взрослой жизни. Поэтому, исходя из
результатов их работы, игры являются необходимой и важной частью образования и
воспитания.
Целесообразно было бы уделить внимание Л. С. Выготскому, который детально
изучил детское когнитивное развитие. Он в основном изучал связь между языком и
мышлением. По его мнению, когнитивные способности и модели мышления не
определяются прежде всего врожденными факторами, а являются продуктом
деятельности, осуществляемой в социальных учреждениях культуры, где человек
растет. Игра, как деятельность, может создать подходящее условие для развития
навыков познания и мышления. В своей теории Выготский подчеркивает
социализирующую роль игр.
Перейдем к определению дидактической игры. Дидактическая игра - это
активная учебная деятельность по моделированию изучаемых систем, явлений,
процессов. Основными отличиями дидактической игры от спонтанной детской игры
являются:
· обязательное участие учащихся;
· использование игры для достижения определенных
образовательных целей;
· управление играми (часто с помощью правил).
Рассмотрим определение понятия «дидактическая игра» в различных
источниках. «Дидактическая игра - это аналогия спонтанной детской деятельности,
преследующая дидактические цели (не всегда очевидным образом для учеников). Это
может происходить в классной комнате, в тренажерном зале, на детской площадке
или на открытом воздухе. Такая игра имеет свои собственные правила и требует
постоянного наблюдения и окончательной оценки. Она предназначена как для
отдельных лиц, так и для групп учеников, а роль педагогического лидера имеет
широкий диапазон: от главного организатора до наблюдателя. Основная его задача
- это стимулирование интереса, усиление вовлеченности учеников в выполняемые
действия, стимулирование их творчества, спонтанности, сотрудничества и
конкуренции. Если педагог хорошо справляется со своей задачей, ученики начинают
использовать разные знания и способности и применять собственный жизненный
опыт. Некоторые дидактические игры имитируют реальные ситуации» [стр. 48, 7].
«Дидактическая игра - это деятельность не только для учеников, но и для
учителя, ориентированная на достижение определенных дидактических целей.
Учебный метод - это организация учебного материала и деятельность учителя и
учеников для достижения определенных дидактических целей» [16]. При сравнении
этого утверждения с определением учебного метода мы видим, что дидактическую
игру можно рассматривать как метод обучения. Данное определение ограничивает
определенную стандартную структуру дидактической игры. Наиболее важными частями
дидактической игры являются:
· игровая среда;
· игровые цели;
· сама игровая процедура, определяемая правилами;
· итоговая оценка игры.
Рассмотрим определение понятия «игровая среда». Игровая среда - это
материальная среда (необходимые средства и оборудование). Компонентом этой
среды является сама игра, ее правила, задачи, процедура и форма взаимодействия
между учениками и учителем. Самая важная часть игровой среды - это ученики и
учитель. Ученики применяют свой опыт, знания и навыки в математике для каждой
игры. Учитель обычно выполняет контрольную и организационную функции. Его
основная задача - это обеспечить плавный и успешный ход игры. Игровая среда
должна мотивировать учеников и побуждать их к активному участию в игре, для
совершения попыток достичь целей игры.
Разберем понятие «игровые цели». Дидактические цели игры определяются
образовательной целью, которую необходимо достичь в игре. На основе данной цели
выбирается подходящий тип и форма дидактической игры. Использование игры в
качестве метода обучения имеет смысл только тогда, когда она позволяет достичь
определенных целей обучения.
Перейдем к разбору значения понятия «игровая процедура». Процедура игры -
это проведение дидактической игры, основанной на деятельности учеников и
учителя. Необходимо, чтобы эта деятельность была интересна ученикам и побуждала
их быть активными. Игра должна соответствовать возрасту учеников, их навыкам и
удовлетворять их потребности. В то же время она должен быть ориентирована на
достижение образовательной цели.
Правила игры должны гарантировать, что успешное выполнение поставленных
задач приведет к достижению цели игры. Правила игры определяют характер и форму
деятельности учеников, организуют их. Элементы игры, такие как конкуренция или
стремление добиться лучших результатов, обычно скрыты в правилах.
Окончательная оценка игры предназначена для проверки достижения
образовательной цели. Ее задача заключается в вознаграждении учеников и
мотивировании их на другие виды деятельности.
В дидактической игре основным типом деятельности является учебная
деятельность, которая вплетается в игровую и соответственно приобретает черты
игровой учебной деятельности. Согласно статье Савченко А.А. [21] дидактические
игры различают по следующим аспектам:
· обучающему содержанию;
· познавательной деятельности детей;
· игровым действиям;
· правилам организации и
взаимоотношениям детей;
· по роли преподавателя.
Перечисленные аспекты можно отнести ко всем играм, но каждый признак в
отдельности преобладает только в определенных видах дидактических игр. Четкая
классификация игр по видам отсутствует, но обычно игры соотносятся с
содержанием обучения и воспитания. Выделяют следующие виды дидактических игр:
· игры по сенсорному воспитанию;
· словесные игры;
· игры по ознакомлению с природой;
· по формированию математических представлений и др. Приведем
еще одну классификацию дидактических игр:
· Игры-поручения;
· Игры-предположения;
· Игры-загадки;
· Игры-беседы;
· Настольно-печатные;
· Сюжетно-ролевые;
· Предметные;
· Игры-упражнения;
· Игры-соревнования;
· Познавательные;
· Коллективные дидактические игры.
В разных источниках указано более 500 дидактических игр, мы упомянули
лишь самые используемые дидактические игры в процессе обучения.
Основываясь на статье «Дидактические игры как метод обучения» [27] можно
выделить основные структурные элементы дидактических игр:
· моделируемый объект учебной деятельности;
· совместная деятельность участников игры;
· правила игры;
· принятие решения в изменяющихся условиях;
· эффективность применяемого решения.
Суммируя все вышеупомянутые определения, можно сказать, что дидактическая
игра - это средство обучения, в следствие этого она может применяться при
закреплении различного программного материала и проводиться на всевозможных
школьных занятиях. В дидактической игре формируются такие условия, в которых
каждый ребенок получает возможность самостоятельно действовать в определенной
ситуации или с определенными предметами, для получения собственного опыта.
Дидактическая игра позволяет обеспечить нужное количество повторений на разном
материале при сохранении эмоционально положительного отношения к заданию. Таким
образом, особая роль дидактической игры в обучающем процессе определяется тем,
что игра должна сделать сам процесс обучения эмоциональным, действенным,
позволить ребенку получить новый опыт.
В данном пункте мы подробно рассмотрели понятие «игра» и «дидактическая
игра», основываясь на работах выдающихся личностей. Также, мы рассмотрели,
какие существуют виды дидактических игр. В следующем пункте, мы рассмотрим роль
дидактических игр при обучении математике.
дидактический игра обучение математика
1.2
Дидактические игры как ведущая деятельность в обучении математики
Многие учителя все чаще используют дидактические игры в своей
педагогической практике. Педагоги и дидактические эксперты внедряют
дидактические игры для преподавания как теоретических, так и практических
заданий по математике.
Б. Онслоу в своей работе [5] исследовал положительные эффекты социального
взаимодействия учеников во время дидактических игр. Онслоу обнаружил, что
дискуссии между учениками и учителем необходимы во время игр, чтобы прояснить
концептуальные конфликты и объяснить новые термины и математические задачи.
Автор выдвинул следующие требования, которые необходимо выполнить, чтобы
повысить эффективность усвоения математического материала при использовании
дидактических игр в обучении:
· Дидактические игры должны быть внедрены в математическую
учебную программу, используя математические термины, материалы и символы;
· Участие учащихся должно быть активным на протяжении всей
игры;
· Вмешательства учителя в игру является очень важной
составляющей успешной дидактической игры, так как необходимо управлять игрой,
чтобы помочь ученикам узнать новые термины, математические задачи и развить
новые методы и способы решения примеров.
Следующие авторы такие, как J. Randel, B. Morris, C. Wetzel и B.
Whitehill в своей работе [22] считали, что использование дидактических игр в
обучении математике может быть полезно для мотивации учеников к работе во время
урока. По мнению упомянутых авторов, лучшее понимание и запоминание предмета в
играх обусловлено активным участием учеников в играх.
Роль дидактических игр в обучении также изучалась теоретическими и
практическими методами. С. Пулос и С. Снейдер в своей работе [8] описывают, что
дидактическая игра с правильной структурой помогает ученикам приобретать новые
математические термины и навыки. В результате этих исследований, авторы
предложили включать дидактические игры в учебную программу по математике в
качестве альтернативного вида образовательной деятельности. Они обнаружили, что
опыт, полученный в дидактической игре, которая проводится после того, как
ученики ознакомились с новыми математическими терминами или навыками решения
математических задач, помогает ученикам лучше понять и надолго запомнить
изученный на уроках материал.и H. Wiegel в своей работе [11] сосредоточили свое
внимание на том, как дидактические игры могут помочь ученикам в построении их
математической реальности, а также улучшить их интерес к математике. В
результате проведенного ими исследования, было выявлено, что дидактические игры
вызвали спонтанную активность учеников на уроках математики и развитие у них
математического мышления. Социальное взаимодействие учеников также было
воспринято позитивно.
Австралийский университетский педагог Г. Букер занимается активным
использованием дидактических игр в преподавании математики в начальных школах.
В своей работе «Математические игры» [2] он описывает свой опыт и наблюдения,
которые он получил при применении дидактических игр на уроках математики. В
своей работе он писал: «Ученики находят игры забавной деятельностью, которая не
только мотивирует их, но и полностью захватывает их, что так необходимо для
конструктивного обучения. Дети, которые не хотят учиться, как правило пытаются
угодить своим родителям или учителям. Другие дети учат предмет, потому что им
сказали, что математика будет необходима для их будущей жизни. Настоящий
интерес к предмету ученика возникает тогда, когда он обучается, взаимодействуя
с другими учениками. Этого можно добиться только в игре. По этим причинам игры
занимают важное место в математическом образовании. Они предлагают условия, при
которых могут быть построены и разработаны математические концепции. Игры
улучшают навыки решения проблем учеников благодаря их необходимости открывать и
использовать новые стратегии, и, как правило, они улучшают навыки других
учеников благодаря их использованию в мотивационной деятельности. Они
поддерживают социальные взаимодействия, ведущие к обучению».
Перейдем непосредственно к процессу обучения математике, рассмотрев
данную тему на примере работы Питера Ванкуса [12]. В своей работе П. Ванкус
уделяет внимание проведенным исследованиям, связанным с использованием
дидактических игр как неотъемлемой частью обучения, позволяющей приобретать
новые знания и развивать понимание новых математических понятий. Целью этих
исследований заключалось в том, чтобы найти механизм для конструктивного
отношения к преподаванию математики. В конструктивном отношении ученики учатся
на собственном опыте посредством специально отобранных видов деятельности.
Дидактические игры - одно из таких видов деятельности. В играх также был
разработан язык, необходимый для работы с математическими понятиями. Приведем
результаты исследования, упомянутые в работе Ванкуса: Дидактические игры:
1. предлагают реальный контекст ученикам, где они могут
полностью участвовать, и которые поддерживают конструктивное обучение;
2. увеличивают субъективную ценность математических знаний для
учеников, поскольку эти знания необходимы для участия в игре, которая является
желаемой деятельностью;
3. помогают ученикам строить математические концепции путем
манипулирования объектами как частью игры, вербализации их деятельности, мыслей
и установок;
4. требуют, чтобы ученики соблюдали правила игры, и это полезно
для математических дисциплин, основанных на правилах;
5. более эффективны, когда они построены на основе
математических идей, и для игры необходимо понимание определенных математических
понятий или овладение определенными математическими навыками;
6. поддерживают учеников творчески строить новые идеи, которые
они должны защищать перед другими игроками;
7. они дают стимулы проверять и проверять математические
процессы других игроков, в этих учениках проверки больше полагаются на
собственную проверку правильности этих процессов, вместо того, чтобы полагаться
на заявления внешнего авторитета (учителя, учебника и т. Д.);
8. улучшают самооценку и самосознание учеников, поскольку
случайные игровые элементы позволяют каждому ученику побеждать;
9. дают учителю возможность сосредоточиться на оценке истинной
картины способностей учеников, а не оценивать их результаты в искусственных
условиях.
Рассмотрим несколько точек зрения по поводу использования дидактических
игр на уроках математики. Акцент будет сделан на следующие темы: «Используют ли
данные учителя дидактические игры на своих уроках?», «Отношение учителей к
дидактическим играм», «Формируют ли какие-либо качества дидактические игры по мнению
учителей начальных классов». Для многих учеников в первые дни в школе самым
нелюбимым предметом становится математика, это можно объяснить тем, что у
младших школьников еще не до конца развиты функции мыслительной деятельности,
например, анализ; синтез; умение сравнивать, обобщать, классифицировать. Для
того, чтобы избежать подобных трудностей, нужно с 1 класса пробудить в учениках
интерес к занятиям математикой, увлечь и вовлечь в процесс обучения.
Как утверждает Анисимова Елена Владимировна учитель математики: «Для
развития познавательного интереса к математическим знаниям я использую
разнообразные методы и приемы обучения математике, привлекая красочный
наглядный и раздаточный материал, технические средства обучения…Игра ценна
только в том случае, когда она содействует лучшему пониманию математической
сущности вопроса, уточнению и формированию математических знаний учащихся.
Дидактические игры и игровые упражнения стимулируют общение между учениками и
преподавателем, отдельными учениками, поскольку в процессе проведения этих игр,
взаимоотношения между детьми начинают носить более непринужденный и
эмоциональный характер» [28].
Учитель Яхина Екатерина Сергеевна в своей статье утверждает, что: «Из
всего существующего многообразия различных видов игр именно дидактические игры
самым тесным образом связаны с учебно-воспитательным процессом. Они
используются в качестве одного из способов обучения различным предметам в
начальной школе, в том числе особое место данные игры занимают на уроках
математики…Основным типом дидактических игр, используемых при начальных этапах
урока, являются игры, формирующие устойчивый интерес к учению и снимающие
напряженность, которое возникает в период адаптации ребенка к школьному режиму.
Не следует приучать детей к тому, чтобы на каждом уроке они ждали новых игр или
сказочных героев. Необходим последовательный переход от уроков, насыщенных
игровыми ситуациями, к урокам, где игра является поощрением за работу на уроке
или используется для активизации внимания.» [30].
На примере этих мнений, мы видим, что отношение к дидактическим играм
среди учителей положительное, но с использованием дидактических игр нужно быть
аккуратными. В данном пункте мы рассмотрели роль дидактических игр в обучении
математики, отношение учителей к дидактическим играм и какую пользу
дидактические игры могут привнести в обучение математикой.
1.3 Влияние
дидактических игр на изучение математики
В данном пункте рассмотрим влияние дидактических игр на изучении
математики у учащихся в начальной школе.
В своей работе такие педагоги, как Э. Крейчова и М. Вольфова [18] высоко
ценят роль игры как важной части образования. По мнению авторов, использование
дидактических игр в обучении увеличивает интерес учеников к активной работе во
время математических занятий и математики в целом, и в целом улучшает ход
занятий. Авторы также считают, что ученики должны интегрировать знания из
разных областей математики, а также из разных предметов. Исходя из своего опыта
использования дидактических игр в преподавании математики, авторы
сформулировали следующие требования к подходящей интеграции игр в образовании:
· Игры должны быть привлекательными и запоминающимися для
учеников.
· Игры должны соответствовать возрастным особенностям и
индивидуальным возможностям детей. Младшие ученики в основном любят игры,
наполненные элементами тайны и безвестности. Ученики, которые имеют какие-либо
трудности по математике предпочитают командные игры. Одаренные и старшие
ученики, предпочитают индивидуальные игры.
· Каждая игра должна иметь четкие и понятные правила, которые
тщательно соблюдаются. Санкции должны быть определены для возможного нарушения
правил. Нецелесообразно менять правила без каких-либо целей.
· Хорошая организация и материальное оборудование для игры -
необходимость.
· Неправильно вводить новые игры слишком часто.
· Никогда нельзя использовать игры в обучении случайно. Каждая
игра должна служить определенной дидактической цели, которую мы хотим достичь в
преподавании математики.
· Мы должны стараться стимулировать как можно больше учеников с
игрой, в идеале - весь класс одновременно. Каждый ученик должен иметь шанс быть
успешным в игре, будь то индивидуально или как часть команды. Чтобы
дифференцировать учеников в зависимости от их способностей, целесообразно
подготовить менее или более требовательные варианты данной игры.
· При выборе дидактической игры нужно выбирать игру, которая
развивает их разнообразные навыки и знания.
Обратимся к работе П. Ванкуса [26], в которой он описывает положительные
эффекты игр по развитию учеников в классах 1-4 в начальных школах. Автор
отмечает потенциал дидактических игр в своих следующих функциях:
· они активируют учеников;
· они развивают память, воображение, внимание, мышление и речь;
· они развивают и культивируют эмоции учеников и поддерживают
эмоциональное обучение через опыт;
· они углубляют самопознание и укрепляют уверенность в себе;
· они обеспечивают социальное обучение и готовятся к различным
социальным ситуациям;
· они мотивируют, развивают интересы, удовлетворяют
потребности, приводят к независимости и творчеству;
· они являются поддержкой сенсорно-моторному обучению;
· они имеют значительный эффект релаксации.
Автор данной статьи [30] считает следующее: «Дидактическая игра учителем
может использоваться, и как форма обучения, и как самостоятельная игровая
деятельность и, как средство воспитания различных сторон личности. Ее
систематическое применение способствует повышению эффективности психолого -
педагогической работы по развитию внимания у детей младшего школьного
возраста…через дидактическую игру учитель может повысить у учащихся не только
внимание на уроке к слову и действию учителя, она приучает детей думать,
проникать в суть явлений, делает учащихся активными участниками
учебно-воспитательного процесса. А от того, насколько сознательно, творчески, с
желанием будут учиться дети в начальной школе, зависит их дальнейшая
самостоятельность, их мышление, умение связывать теоретический материал с
практикой».
Как считают многие современные исследователи, игровая деятельность влияет
на формирование произвольности всех психических процессов - от элементарных до
самых сложных. Так, в игре начинают развиваться произвольное поведение,
произвольное внимание и память. В условиях игры дети лучше сосредоточиваются и
больше запоминают, чем по прямому заданию взрослого. Сознательная цель -
сосредоточиться, запомнить что-то, сдержать импульсивное движение - раньше и
легче всего выделяется ребенком в игре (см. по этому поводу [24]).
В своих работах П. Ванкус (см. подробнее, [14], [13]) изучал влияние
использования дидактических игр в преподавании математики в классах 5-9, в
начальных школах. Основным результатом исследования было обнаружение автором
того, что интеграция дидактических игр положительно влияет на отношение
учеников к математике и ее учению. Одним из самых положительных качеств игр
является тот факт, что игры - это естественный способ обучения детей. Также
важно, чтобы дети находили игры в виде желаемой деятельности, которая им
нравится. У игр есть близкий контекст для детей, и поэтому они помогают им
преодолевать некоторые дидактические трудности в процессе преподавания
математики. Опишем упомянутые выше трудности более подробно: дидактические
трудности вызваны выбором образовательных методов и разработкой учебного
контента. Эти трудности могут быть преодолены путем выбора методов обучения и
учебного плана. Дидактические игры могут помочь ученикам преодолеть
дидактические трудности в учебном процессе математики. Как мы уже говорили,
подходящая дидактическая игра - это деятельность, соответствующая возрасту,
способностям и интересам учеников. Кроме того, игры являются естественным
способом обучения детей. Эти причины указывают на потенциал дидактической игры
как метода, ведущего к устранению дидактических трудностей.
Следует сделать акцент на том, что идеальная дидактическая игра подходит
для достижения определенной образовательной цели, соответствующей и интересной
для учеников. В этой игре одновременно задействован весь класс. Идеальная
дидактическая игра развивает широкий спектр знаний, способностей, навыков и
позитивных особенностей учащихся. Интеграция дидактической игры в учебный
процесс приведет к повышению эффективности учебного процесса по сравнению с
преподаванием без игры. Следовательно, внедрение дидактических игр в процесс
обучения положительно повлияет на отношение учеников к математике и будет
стимулировать их к дальнейшему образованию и развитию.
После анализа различных статей, книг, можно сказать, что исследователи,
которые занимаются дидактическими играми в математическом образовании, согласны
с тем, что игры имеют много положительных качеств и могут быть полезным методом
для работы учеников во время уроков математики.
В данной главе были рассмотрены различные виды дидактических игр, которые
чаще всего применяются на уроках математики и остальных общеобразовательных
предметах. Проанализировав научную литературу, мы выявили следующее, что
дидактические игры помогают ученикам лучше понять и надолго запомнить изученный
на уроках материал. Многие учителя математики применяют дидактические игры на
своих уроках и видят положительные аспекты в использовании дидактических игр в
процессе обучения.
Мы используем дидактические игры в обучении только после того, когда
убедимся в преимуществах данной дидактической игры по сравнению с преподаванием
без игры. Например, вместо обычной практики, мы можем достичь этой цели более
привлекательным образом для учеников - через подходящую дидактическую игру. Не
обязательно всегда использовать новый тип дидактической игры. Использование
известной игры имеет свое преимущество, например, то, что ученики знают правила
игры и ее организацию. Поэтому они могут сосредоточиться на самой игре, а не
запоминать новые правила. Экономия времени, которое, в противном случае, мы
потратили бы на объяснение новой игры ученикам, также является преимуществом.
Однако необходимо чередовать дидактические игры, чтобы сделать уроки более
интересными для учеников.
В заключении к первой главе хочется отметить, помимо всевозможных плюсов
в использовании дидактических игр, специалисты, занимающиеся данной проблемой,
утверждают, что не стоит постоянно полагаться только на игры. Постоянное
использование дидактических игр вызовет у учащихся младших классов привыкание к
такому виду деятельности, а, следовательно, у учеников пропадет интерес к данной
деятельности. Специалисты рекомендуют не только чередовать дидактические игры,
но и давать детям отдых от подобного вида деятельности.
Экспериментальное исследование проводилось во время государственной
педагогической практики, в феврале-марте 2017 года, в ГБОУ Школе №1392 им.
Д.В.Рябинкина г. Москвы в 1 классе «Б». Общее количество учащихся класса - 24
человек: 10 девочек и 14 мальчиков, но максимальное количество исследуемых - 20
человек. На разных этапах экспериментальной работы количество исследуемых
менялось в зависимости от целей и задач того или иного этапа, а также, в
зависимости от присутствия учащихся в школе. Возраст учеников - 6-8 лет.
Класс работает по образовательной программе «Начальная школа XXI века».
Гипотеза исследования: если при обучении математике использовать
дидактические игры для развития воображения в начальной школе уже с 1 класса (в
рамках уроков математики или на внеурочной деятельности, на постоянной
систематической основе), то это поможет лучшему усвоению знаний и увеличит у
детей интерес к данному общеобразовательному предмету.
2.1
Подготовка учеников младшего школьного возраста к прохождению квеста при помощи
различных дидактических игр
При прохождении государственной педагогической практики была проделана
следующая работа по подготовке учеников 1 класса «Б» к реализации
математического квеста. На уроках математики помимо традиционных заданий из
учебника [19, с. 75-82] и рабочей тетради [20, с. 53- 57] также был
предоставлен набор заданий в виде дидактических игр на развитие воображение,
памяти и внимания.
Перед тем как мы перейдем к разбору комплекта заданий, следует упомянуть,
что собой представляет математический квест. Для начала стоит упомянуть, что
собой представляет определение слова «квест». Данное слово пришло к нам из
английского языка ―quest, что в переводе значит «поиск,
приключение, разыскивать» (см. подробнее [23]). В наше время «квест», в
большинстве своем, относится к компьютерным играм, где подразумевает под собой
различные уровни с заданиями, которые должны пройти игроки, чтобы получить
главный «приз». Данный вид деятельности является игровым. Мы можем дать
следующее определение, квест - это процесс поиска чего-либо, при котором нужно
преодолевать различные трудности/уровни/этапы/станции, результат такого поиска
имеет некую ценность для участников данного процесса. Перейдем к определению
понятия «математический квест» - это игра- путешествие (странствие) по станциям
или этапам, на которых команде или командам предлагаются разнообразные математические
задания на смекалку, некоторые станции (этапы) направлены на практическое
выполнение заданий, набор этапов (станций) показывают практичность и
доступность математики [29].
Перейдем к разбору различных дидактических игр, проведенных на уроках математики
с целью подготовить учащихся к прохождению математического квеста.
В начале урока после проверки устного счета детям были даны следующие
задания («Домики и цветочки», «Найди и раскрась», «Кроссворд», «Пустые
окошки»), идеи для данных дидактических игр были взяты из электронного
источника (см. подробнее [25], [26]) и переработаны под уровень и особенности
класса. Стоит упомянуть, что в период преддипломной практики 1 класс «Б» по
математике проходил следующую тему «Прибавление и вычитание числа 6». Далее мы
рассмотрим:
· каждое задание отдельно;
· формат задания (в каком виде задание было продемонстрировано
ученикам);
· какие качества развивает то или иное задание у учеников;
· время, за которое ученики справились с заданием;
· какой результат мы получили;
· реакцию детей на введение дидактических игр на уроках
математики.
«Домики и цветочки». Данное задание дается ученикам на листочках, без
инструкции к выполнению задания, ученики сами поняли, что от них требуется.
Ученики подписывают свои листочки именем и первой буквой фамилии, кто-то пишет
фамилию целиком (от детей не требовалось подписывать свои работы фамилиями, но
мы в свою очередь не стали запрещать, если ученику было так удобнее). На
листочках изображены домики и цветочки, на каждом рисунке присутствуют числа и
пропуски, например, на листочках цветка есть числа 6 и 7, на голове цветка
пустое место. По такому примеру дети делают вывод, что нужно найти сумму чисел
и вписывают ответ в пустое место. В изображении домика присутствуют «окошки», в
которых также есть числа и пропуск, например, под крышей есть число 10 ниже
есть число 4, рядом в «окошке» пустое место, дети понимают, что нужно найти
слагаемое, в данном примере выполняют вычитание. Ученикам было предоставлено 2
варианта, дабы избежать того, чтобы ученики списывали или подглядывали друг у
друга. Данная дидактическая игра развивает у учеников личные качества, такие
как воображение, внимание и память. На выполнение задания не устанавливается
ограничения во времени, это сделано для того, чтобы ученики не чувствовали
давления со стороны учителя и задание для учеников было в радость. Задание было
выполнено через 5-7 минут всем классом, были такие ученики, которые спустя 2
минуты предоставили готовый вариант. Проверка правильности решения задания на
уроке не была проведена, что вызвало у учеников только положительные эмоции,
так как отсутствовал фактор «оглашения своих ошибок перед всем классом». Мы
хотели добиться от проведения этой дидактической игры того, чтобы ребенок не
чувствовал, что это задание является упражнением подобно упражнениям из
учебника, которые в итоге проверяются и отмечаются ошибки учеников.
Проанализировав ответы учеников, мы получили следующее, 14 учеников выполнили
задание без единой ошибки; 3 учеников выполнили задание с одной ошибкой; один
ученик выполнил задания, сделав две ошибки; один ученик не смог справиться с
выполнением задания, все ответы были не верны. Данная дидактическая игра была
проведена с 19 учениками. После урока математики дети подходили и спрашивали,
будут ли еще подобного типа заданий на уроках, данный вид деятельности, а
именно, задания в виде дидактической игры был принят учениками на высшем
уровне. Перейдем к следующему заданию.
«Найди и раскрась». Данное задание раздается ученикам на листочках, на
них присутствует таблица с примерами и квадрат с клеточками, в которых записаны
числа. Ученики подписывают свои листочки именем и первой буквой фамилии, кто-то
пишет фамилию целиком (от детей не требовалось подписывать свои работы
фамилиями, но мы не стали запрещать, если ученику было так удобнее). Ученики не
смогли самостоятельно разобраться с тем, что от них требуется в этой
дидактической игре. На объяснение задания было потрачено 5 минут. Ученикам
нужно было вначале решить примеры и записать ответы в предоставленную на
листочках таблицу, каждому числу соответствовал определенный цвет (голубой,
фиолетовый или желтый). После решения примеров и занесения ответов в таблицу,
ученикам предлагалось найти свои ответы в квадрате с числами и разукрасить
клеточки в соответствии с инструкцией. В результате у учеников должна была
получиться картинка «утка», что и является показателем правильного выполнения
дидактической игры «Найди и раскрась». На выполнение задания у всего класса
ушло 10 минут, пару учеников выполнили задание за 5 минут. В процессе
выполнения задания учеников не торопили и не подгоняли. Что вызвало у учеников
только положительные эмоции, все хотели, как можно быстрее «разгадать» тайну
зашифрованной картинки. Данная дидактическая игра развивает у учеников младшего
школьного возраста такие личные качества, как воображение, внимательность и
память. Проверка правильности выполнения задания на уроке не была проведена, но
в данной дидактической игре «Найди и раскрась» это не требуется, так как
результат деятельности учеников сразу же виден. Акцент на верное или неверное
выполнение задания каждого ученика в данной дидактической игре не был уделен.
Данная дидактическая игра «Найди и раскрась» должна была развить у детей
интерес к подобным видам заданиям, а не оттолкнуть из-за неправильного решения.
Проанализировав ответы учеников, мы получили следующее, 10 учеников выполнили
задание без единой ошибки; 6 учеников решили примеры верно, но видна путаница с
разукрашиванием клеточек в таблице, либо цвета были наложены друг на друга,
либо цвет не подходил к данному числу, что указывает на невнимательность
учеников при выполнении задания; один ученик сделал одну ошибку в примерах и не
до конца разукрасил клеточки. Дидактическая игра «Найди и раскрась» была
проведена с 17 учениками. После урока математики ученики подходили и узнавали,
будут ли еще подобного типа заданий на уроках, данный вид деятельности, а
именно, задания в виде дидактической игры был принят учениками на высшем
уровне. Ученик, который до конца не выполнил задание, был доволен заданием и
просил, повторить на следующем уроке. Что показывает нам, интерес к математике
проявляется не только у тех учеников, которые без проблем справляются с
поставленной задачей при выполнении тех или иных заданий, но и у тех, у кого имеются
различные сложности при выполнении заданий. Перейдем к следующему заданию.
«Кроссворд». Дидактическая игра дается ученикам на листочках, инструкция
к выполнению задания напечатана на листе «Разгадай кроссворд. Выпиши числа,
находящиеся в кружках, в порядке увеличения». Ученики подписывают свои листочки
именем и первой буквой фамилии. На раздаточном материале присутствует
математический кроссворд с пропусками, задача учеников заполнить пропуски
числами и выписать числа в порядке увеличения. Дидактическая игра «Кроссворд»
развивает у учеников младшего школьного возраста такие личные качества, как
воображение, внимательность и память. При выполнении задания у класса были
некоторые трудности с пониманием поставленной перед ними задачей, связанной с
порядком увеличения. Приходилось несколько раз объяснять ученикам, что означает
«порядок увеличения», хотя на предыдущих уроках с классом была проведена
соответствующая работа. Выполнение дидактической игры «Кроссворд» у класса
заняло 15 минут, но стоит отметить, что были ученики, которые справились с
поставленной задачей минут за 7. Стоит отметить, что данный тип задания у детей
вызвал смешанные чувства, некоторые ученики начинали волноваться и переживать,
что они не могут без помощи учителя справиться с заданием, но мы постарались
поддерживать учеников, не делая акцент на каких-либо ошибках, а только
подбадривая их. Проверка правильного ответа к заданию на уроке не была
проведена, что вызвало у учеников только позитивные эмоции, так как ученики
итак испытывали различные трудности в решении, мы решили лишний раз не
указывать на их ошибки. Проанализировав ответы учеников, мы получили следующее,
8 учеников справились с выполнением задания без единой ошибки; 3 учеников
справились с разгадыванием кроссворда, но у них возникли трудности с порядком
увеличения; один ученик справился с кроссвордом, но вместо порядка увеличения,
ученик предоставил ряд чисел в порядке убывания; один из учеников сделал одну
ошибку в решении примера, но числа в порядке увеличения построены верно; один
ученик не смог справиться с кроссвордом, а также, выстроить числа в порядке
увеличения. Дидактическая игра «Кроссворд» была проведена с 14 учениками. Не
смотря на возникшие трудности при выполнении задания, ученики положительно
отреагировали на данный вид деятельности, после урока у учеников отмечался
интерес к продолжению выполнения подобных заданий. Перейдем к следующему
заданию.
«Пустые окошки». Данная дидактическая игра раздается ученикам на
листочках, на них напечатаны три колонки примеров с пропусками (количество
примеров равняется 9), мы назвали их «окошками». Ученики не записывают свои
имена, задание намеренно выполняется анонимно. Класс сразу же приступает к
выполнению задания, данный формат близок к ученикам, так как в учебнике по
математике [2] присутствуют такого рода задания. Но в отличии от заданий из
учебника, мы не стремимся делать акцент на верность решения, мы хотим показать
ученикам, что выполнение подобных заданий не должно вызывать у них страх
сделать ошибку. Ученикам было предоставлено 2 варианта, дабы избежать
списывания или подглядывания друг к другу, а также, это сделано для того, чтобы
проверить на сколько каждый ученик владеет знаниями по теме урока «Прибавление
и вычитание числа 6». Интересно то, что дети не просили помощи у своих соседей
по парте, каждый самостоятельно справлялся с заданием. На выполнение данной
дидактической игры не устанавливается ограничения во времени, это сделано для
того, чтобы ученики не чувствовали давления со стороны учителя и задание для
учеников было в радость. На выполнение задания у всего класса ушло 10 минут,
пару учеников выполнили задание за 7 минут. Правильность полученных ответов на
уроке не проверялась, об этом мы говорили чуть раннее. Дидактическая игра
«Пустые окошки» развивает у учеников младшего школьного возраста такие личные
качества, как воображение, внимательность и память. Проанализировав ответы
учеников, мы получили следующее, 9 учеников выполнили задание без единой
ошибки; 3 учеников сделали только одну ошибку; 3 учеников допустили в своих
работах две ошибки. Дидактическая игра «Пустые окошки» была проведена с 15
учениками. Данная дидактическая игра была проведена на последнем уроке по
математике в период государственной педагогической практики, результаты задания
должны были послужить нам показателем усвоения темы «Прибавление и вычитание
числа 6».
В ходе преддипломной практики у данного класса было выявлено стремление к
решению трудных задач, получению новых знаний, также отмечается интерес к
различным творческим заданиям и заинтересованность в изучении математики при
помощи дидактических игр. Представленный нами набор дидактических игр должен
был послужить к подготовке учеников к прохождению математического квеста.
Задания были разработаны под определенную тему «Прибавление и вычитание числа
6», которую проходили на уроках. Дидактические игры хорошо влились в процесс
обучения математике у данного класса, но не стоит забывать, что дидактические
игры не являются всего лишь игрой с классом, это работа над получением знаний в
увлекательной для учеников форме.
После проведения данной работы с классом, а также, после проведения
анализа результатов, мы можем отметить, что использование дидактических игр для
развития воображения в начальной школе уже с 1 класса при обучении математике,
может благоприятно помочь лучшему усвоению знаний и увеличить у детей интерес к
данному общеобразовательному предмету. Работу над подготовкой детей к
прохождению математического квеста можно считать успешной. В следующем пункте,
мы подробно расскажем про наш математический квест, какие дидактические игры
были разработаны для данного класса, какой вид прохождения математического
квеста был выбран, какие дидактические игры были более и менее успешны в данном
классе, какие результаты были получены после проведения математического квеста.
2.2
Разработка дидактических игр, используемых в математическом квесте, для 1
класса
В данном пункте мы хотим уделить внимание набору дидактических игр,
который был задействован нами в математическом квесте на уроке математике. Каждая
дидактическая игра была разработана и продумана персонально под 1 класс «Б»
ГБОУ Школы №1392 им. Д.В.Рябинкина г. Москвы.
В нашем математическом квесте был использован следующий набор
дидактических игр для развития воображения у учащихся младшего школьного
возраста, который содержал в себе 4 различных дидактических игры:
1. Дидактическая игра «Собиралка».
2. Дидактическая игра «Цветник».
3. Дидактическая игра «Цепочка».
4. Дидактическая игра «Художники».
К каждой дидактической игре прилагалась инструкция, в которой было
подробно расписано, что требуется сделать ученикам, чтобы выполнить задание и
получить следующий «ключ», для того, чтобы перейти к следующему этапу
математического квеста. Кроме основных дидактических игр в математическом
квесте были использованы различные типы заданий, такие как: ребусы, загадки,
задания на смекалку, задание на внимательность. Данные задания служили
«связкой» между этапами в математическом квесте, то есть, для того, чтобы
понять к какому этапу нужно приступить, учащимся нужно было разгадать
«подсказку» и после этого переходить к тому или иному этапу.
Кроме дидактических игр, заданий, инструкций к играм и «ключей» в
математическом квесте присутствовали «секретные конверты». Каждый «секретный
конверт» находился на различных этапах и предназначался каждой команде,
участвующей в математическом квесте. Данные конверты содержали в себе
обрывочные фразы, которые после прохождения математического квеста должны были
сложиться в одно предложение «Мы самый дружный класс». Данную фразу можно
считать неким «призом» для учащихся за прохождение математического квеста. Выше
мы упоминали о том, что каждый квест должен заключать в себе не только
различные этапы и задания на этих этапах, но и по окончанию квеста участники
должны получить некий «приз» за свои старания и участие в квесте.
Перейдем к анализу разработанного нами набора дидактических игр,
используемых в математическом квесте. Далее мы подробно разберем следующие
пункты:
· название дидактической игры и заложенный смысл в названии;
· укажем на что нацелена та или иная дидактическая игра;
· отметим сложность дидактической игры;
· предполагаемое затраченное время на прохождение дидактической
игры;
· какие материалы необходимы для реализации той или иной
дидактической игры.
· акцент дидактической игры при обучении математике.
Анализ дидактических игр мы начнем с самой, на наш взгляд, сложной
дидактической игры и дальше будем переходить к менее трудным по уровни
сложности дидактическим играм.
Дидактическая игра «Собиралка». Мы назвали данную дидактическую игру
именно так, вследствие того, что в основе игры заложено составление цельной
фигуры из маленьких частей. Перед учениками располагалось «поле» с различными
фигурами, на которых были написаны числа. Ученики должны были найти фигуры только
с четными числами и составить из этих фигур геометрическую фигуру. Составление
геометрической фигуры начиналось с карточки, на которой было написано «0».
Также в инструкции была подсказка «выложите фигуры с четными числами в порядке
увеличения (от меньшего к большему)». Данная подсказка была заранее продумана и
отработана на уроках математики в период преддипломной практики, были выполнены
задания на соответствующую тему, об этом упоминалось в главе 2 пункте 2.1.
Дидактическая игра нацелена на развитие у младшего школьника воображения и
внимания, также данная дидактическая игра показывает готовность учеников
работать в команде и слушать своих одноклассников, анализировать полученные
ответы и выбирать верный вариант. Что касается уровня сложности дидактической
игры «Собиралка», то можно отметить, что данная дидактическая игра является
самой сложной, на наш взгляд, из представленных нами дидактических игр в данном
математическом квесте. В следующем пункте 2.3 мы рассмотрим подробнее, являлась
ли «Собиралка» самой сложной дидактической игрой для данного класса. На
прохождение этой дидактической игры подразумевалось отвести 15 минут (самое
большое по продолжительности время, отведенное на этап). Для реализации
дидактической игры «Собиралка» мы использовали следующие материалы: пошаговая
инструкция к дидактической игре (инструкция содержала в себе подсказку к
выполнению дидактической игры); «поле» с выложенными на нем фигурами, на
которых были написаны четные и нечетные числа; фигуры с нечетными числами (от 1
до 25); фигуры с четными числами (от 2 до 20); фигура с «0»; карточка с
названием «старт»; карточка с названием этапа «Собиралка». Дидактическая игра
«Собиралка» была придумана нами с целью развить у младших школьников
воображение при решении тех или иных математических задач, которые были
поставлены перед ними в процессе прохождения математического квеста.
«Собиралка» делает акцент на такие темы: четные и нечетные числа,
геометрические фигуры; данные темы были пройдены в классе на уроках математики.
Мы хотели привнести что-то новое и интересное для самих учащихся при получении
новых знаний (отработке полученных знаний) по математике. Не смотря на той или
иной уровень сложности дидактической игры, мы хотели заинтересовать учащихся и
постараться привлечь каждого в процесс нахождения верного варианта ответа.
Работа над поиском верного ответа, по нашему мнению, не только развивает
личностные качества учащегося, но и должна способствовать сближению класса и
взаимопониманию между одноклассниками.
Перейдем к следующей разработанной нами дидактической игре под названием
«Цветник».
Дидактическая игра «Цветник». Мы дали такое название дидактической игре
по причине того, что в самой игре присутствуют цветные карточки. В основе игры
заложена работа с цветом (красный, синий, желтый, зеленый, розовый, оранжевый).
Перед учениками располагалось «поле» с 12 клетками (на двух клетках уже
присутствовали цветные карточки, одна карточка обозначала «старт», другая
«финиш»), в середине «поля» был отдельный «центральный» кусок бумаги, который
переворачивался при завершении дидактической игры (о значимости этого шага мы
подробнее расскажем ниже). Ученикам предлагалось заполнить «поле» оставшимися
10 карточками. После заполнения «поля», ученики должны были увидеть загаданную
нами геометрическую фигуру. В инструкции (см. приложение 6), которая
прилагалась к дидактической игре, были подробно прописаны шаги, следуя которым
ученики смогут верно выполнить представленную перед ними задачу. Всего в
инструкции было прописано 3 шага: первый - «карточки нужно соединить так, чтобы
цвет был к нужному цвету (синий к синему, красный к красному и т.д.).
Присутствовал, также, пример выполнения. Второй - увидеть/распознать
зашифрованную геометрическую фигуру. Третий - позвать учителя. После того как
шаги были выполнены, мы проверили верное выполнение игры; на этом моменте, мы
перевернули тот самый кусочек бумаги и цвет на нем должен был подтвердить ответ
детей. Цвет должен был совпасть с тем цветом, который был выложен карточками.
Дидактическая игра нацелена на развитие у младшего школьника воображения, также
«Цветник» показывает готовность учеников слушать своих одноклассников, работать
в команде, анализировать полученные ответы и выбирать верный вариант.
Дидактическая игра «Цветник», по нашему мнению, имеет средний уровень
сложности, точны ли наши предположения, можно будет понять только после анализа
прохождения учащимися математического квеста. На прохождение дидактической игры
подразумевалось отвести 10 минут. Для реализации дидактической игры «Цветник» мы
использовали следующие материалы: пошаговая инструкция к дидактической игре
(инструкция содержала в себе пример к выполнению дидактической игры); «поле» с
расчерченными 12 клеточками для карточек; 12 цветных карточек; «центральный»
кусок бумаги (мы выбрали синий цвет на одной стороне); карточка с названием
этапа «Цветник». Дидактическая игра «Цветник» была придумана нами с целью
развить у младших школьников воображение при решении тех или иных
математических задач, которые были поставлены перед ними в процессе прохождения
математического квеста. «Цветник» делает акцент на такие темы: геометрические
фигуры и цвета; данные темы были пройдены в классе на уроках математики.
Разработав данную дидактическую игру, мы хотели привнести что-то занимательное
для самих учащихся при отработке полученных знаний по математике. Несмотря на
той или иной уровень сложности дидактической игры, мы хотели заинтересовать
учащихся и постараться привлечь каждого в процесс нахождения верного варианта
ответа. Работа над поиском верного ответа, по нашему мнению, не только
развивает личностные качества учащегося, но и должна способствовать сближению
класса и взаимопониманию между одноклассниками.
Перейдем к следующей разработанной нами дидактической игре под названием
«Цепочка».
Дидактическая игра «Цепочка». Мы дали такое название дидактической игре
именно потому, что в основе игры заложено выстроить цепочку (линию) из 9
карточек. Перед учениками лежала карточка с примером (11-2), это начальная
карточка, данная карточка являлась отправной точкой в выполнении игры. Рядом
лежали остальные 8 карточек с примерами, которые и должны были использовать
участники квеста при выполнении игры. На столе, также, лежала инструкция (см.
приложение 7) к выполнению дидактической игры «Цепочка». В инструкции было
написано следующее: «Вам нужно: 1) Решить пример на начальной карточке
(вычислить 11-2). 2) Найти карточку с примером, который начинается с ответа
предыдущей карточки. 3) Выложить цепочку из карточек. Заключительная карточка
должна быть той, где ответом является число, с которого начинается пример на
начальной карточке, то есть число 11. 4) Позвать учителя и показать выполнение
этапа. Также в инструкции была подсказка: Пример: «1+2 → 3+4 →
7-6».
Мы решили добавить подсказку в инструкцию для того, чтобы избежать
непонимания со стороны учащихся при выполнении задания. Дидактическая игра
«Цепочка» нацелена на развитие у младшего школьника воображения, также данная
дидактическая игра показывает готовность учеников работать в команде и слушать
своих одноклассников, анализировать полученные ответы. Если говорить про
уровень сложности представленной дидактической игры, то на наш взгляд, игра
имеет легкий уровень, подходящий под уровень и знания данного класса. В
следующем пункте 2.3, мы рассмотрим подробнее, являлась ли дидактическая игра
«Цепочка» легкой для данного класса. На прохождение этой дидактической игры
подразумевалось отвести 5 минут. Для реализации дидактической игры «Цепочка» мы
использовали следующие материалы: инструкция к дидактической игре (инструкция,
которая содержала в себе подсказку к выполнению дидактической игры); 9 карточек
с примерами; карточка с названием этапа «Цепочка». Дидактическая игра «Цепочка»
была придумана нами с целью развить у младших школьников воображение при
решении тех или иных математических задач, которые были поставлены перед ними в
процессе прохождения математического квеста. «Цепочка» делает акцент на такие
темы: сложение и вычитание; данные темы были пройдены в классе на уроках
математики. Данной разработанной нами дидактической игрой, мы хотели привнести
для самих учащихся интересный и увлекательный способ при отработке полученных
знаний по математике. Не смотря на уровень сложности дидактической игры, мы
хотели заинтересовать учащихся и постараться привлечь каждого в процесс
нахождения верного варианта ответа. Работа над поиском верного ответа в
команде, по нашему мнению, не только развивает личностные качества учащегося,
но и должна способствовать сближению класса и взаимопониманию между
одноклассниками.
Перейдем к следующей разработанной нами дидактической игре под названием
«Художники».
Дидактическая игра «Художники». Мы назвали разработанную нами
дидактическую игру именно так, потому, что в основе игры задействуются
художественные навыки учащихся, дети, непосредственно, рисуют изображения.
Перед учениками лежали пустые листы А4, карандаши, лист с символами и числами,
также на столе лежала инструкция к дидактической игре. Каждый из учеников
должен был нарисовать свою картину, следуя правилам, указанным в инструкции. В
дополнении к инструкции на листе А4 было написано следующее: «Перед вами
находятся числа и различные символы, такие как: ( 1 2 3 4 5 6 7 8 9 - + = ●
: ). Вам нужно нарисовать что- нибудь, где будут использованы от 3 до 5
символов или чисел (предлагаемые вам)». Данная дидактическая игра имеет
несколько сходств с другими дидактическими играми, известные многим учителям в
начальной школе, но следует отметить, что мы переработали игру под наш
математический квест. Различия заключаются в том, что в других дидактических
играх от ребенка требуется нарисовать изображение или составить композицию,
используя геометрические фигуры; в нашей игре «Художники», мы просим учеников
использовать символы и числа. Разработанная нами дидактическая игра нацелена на
развитие воображения у ученика младшего школьного возраста, эта дидактическая
игра наглядно показывает работу воображения при выполнении игры, результатом
является плоды воображения учащихся. Что касается уровня сложности
дидактической игры «Художники», то можно отметить, данная дидактическая игра,
на наш взгляд, имеет легкий уровень сложности. В следующем пункте 2.3 мы
подробнее рассмотрим, являлась ли дидактическая игра «Художники» легкой в
выполнении для данного класса. На прохождение этой дидактической игры подразумевалось
отвести 10 минут. Для реализации дидактической игры «Художники» мы использовали
следующие материалы: пошаговая инструкция к дидактической игре; листок бумаги
А4 с символами и числами; чистые листы бумаги А4; карандаши; карточка с
названием этапа «Художники». Дидактическая игра «Художники» была придумана нами
с целью развить воображение у младших школьников при решении математических
задач, которые были поставлены перед ними в процессе прохождения
математического квеста. Дидактическая игра «Художники» делает акцент на знание
таких тем, как числа и математические символы; данные темы были пройдены в
классе на уроках математики. Мы, представленной дидактической игрой, хотели
привнести в отработку полученных знаний по математике что-то интересное для самих
учащихся. Не смотря на той или иной уровень сложности дидактической игры, мы
хотели заинтересовать учащихся и постараться привлечь каждого в процесс
нахождения ответа. Работа над поиском ответа, по нашему мнению, не только
развивает личностные качества учащегося, но и должна способствовать сближению
класса и взаимопониманию между одноклассниками.
В данном пункте мы подробно разобрали все разработанные нами
дидактические игры, которые были включены в математический квест. Мы старались
придумать и использовать такие дидактические игры, которые способствовали бы
развитию воображения при обучении математике в начальных классах. В следующем
пункте, мы подробно расскажем о прохождение математического квеста в 1 классе
«Б» ГБОУ Школы №1392 им. Д.В.Рябинкина г. Москвы.
2.3
Прохождение учениками квеста и отношение учеников на подобный вид деятельности
В данном пункте мы хотим уделить внимание, непосредственно, тому, как
именно проходил наш математический квест в 1 классе «Б» ГБОУ Школы №1392 им.
Д.В.Рябинкина г. Москвы на уроке математики.
Уделим внимание следующим пунктам:
· тематике математического квеста;
· представлению математического квеста учащимся 1 класса «Б»;
· делению класса на группы (как именно это проходило);
· реакции учеников на математический квест;
· трудностям, возникшим при подготовке математического квеста и
при проведении данного вида деятельности, у учащихся младшего школьного
возраста, которым данный вид работы был в новизну;
· анализу полученных результатов;
· подтвердилась ли наша гипотеза, которую мы ставили в начале
нашего исследования. Наша гипотеза заключалась в следующем, если при обучении
математике использовать дидактические игры для развития воображения в начальной
школе уже с 1 класса (в рамках уроков математики или на внеурочной
деятельности, на постоянной систематической основе), то это поможет лучшему
усвоению знаний и увеличит у детей интерес к данному общеобразовательному
предмету.
В ходе математического квеста был проведен видеоотчет и фотоотчет, по
которым можно проследить за ходом проведения математического квеста. Также в
результате прохождения математического квеста мы имеем на руках работы,
выполненные учениками на последнем этапе «Художники». Данные работы не
подписаны, так как работа была выполнена коллективно. Перейдем к подробному
рассмотрению нашего математического квеста.
Рассмотрим тематику квеста. Для начала разберемся, что имеется ввиду под
понятием тематика квеста. Тематика квеста, в нашем понимании, это единая связь
для всех этапов, для всех деталей, присутствующих в квесте. В нашем
математическом квесте каждый этап и каждое задание было продумано и придумано
на развитие воображения у младших школьников. В квесте присутствовали такие
наименования, как «станция», «ключ», что могло натолкнуть на идею о том, что тема
(наименование) математического квеста, это «путешествие на поезде» или «страна
сокровищ», но это не было обговорено перед учениками, то есть, мы не давали
название математическому квесту. После приветствия, мы объяснили классу, что
сейчас будет не просто урок математики, а математический квест.
Квест был представлен ученикам следующим образом. Мы объяснили, что
сейчас перед ними стоит задача «пройти математический квест». Рассказали о том,
что их ожидает в квесте, а именно, предоставили алгоритм их действий. Алгоритм
действий учеников был следующим:
5. Класс должен быть поделен на три команды, у каждой команды
свой цвет (красный, желтый и зеленый);
6. В каждой группе должен быть выделен «капитан» команды;
7. «Капитаны» должны получить первую подсказку, мы называем это
«ключ», где написано станция, к которой должна перейти команда;
8. Ученикам было сказано, что на различных этапах они найдут
конверты (у каждой команды свой конверт), которые нужно будет использовать
после прохождения всех этапов (станций).
9. Также были сказаны слова напутствия, был сделан большой
акцент на том, чтобы каждая команда была дружной и сплоченной.
10. Ученикам было сказано, что математический квест будет
проходить в рамках одного урока математики, а также, было сказано, чтобы ученики
помнили о других командах и о том, что не следует слишком долго оставаться на
одном этапе (станции).
Подробнее разберем деление класса на команды. Перед проведением
математического квеста нами были подготовлены карточки различных цветов
(красные, желтые, зеленые), это было сделано для того, чтобы разделить класс на
команды. Мы выбрали данный вид разделения на команды, так как с классом были
проведены различные виды деятельности ранее на уроках, где использовалось такое
деление, это было сделано для удобства учеников. А также, для экономии времени,
то есть, не нужно было объяснять ученикам, каким именно способом будет
проходить деление. На парте лежали карточки, лицом (цветом) вниз, каждый ученик
подходил, брал карточку и после того, как у каждого на руках были карточки,
дети самостоятельно нашли «своих» по цвету. Можем сделать вывод, что выбор
именно такого деления на команды был сделан верно, так как ученикам не пришлось
объяснять, кто с кем в команде вместе, экономия времени на лицо.
Что касается реакции младших школьников на то, когда они узнали, что им
предстоит участвовать в прохождении математического квеста, можно сказать
следующее, ученики отреагировали на такую новость позитивно и радостно. Каждый
ученик хотел скорее приступить к прохождению, им был интересен каждый фрагмент
квеста. Квест считается развлекательным видом деятельности и предполагались
некоторые трудности с дисциплиной во время прохождения квеста, например, крики,
смех, бег по классу или вместо решения представленных задач, дети общались бы
друг с другом, что мешало бы другим ученикам, которые занимаются решением
задач, но на практике мы отметили идеальную дисциплину, не было трудностей,
которые предполагались. Следовательно, можно сказать, что данный вид
деятельности, а именно квест, является для младших школьников интересным и
занимательным. Несмотря на то, что с дисциплиной не было трудностей, трудности
возникли в другом. Далее мы будем вести речь о трудностях, которые возникли во
время проведения математического квеста.
Выше мы упоминали о том, что трудностей с дисциплиной на период
прохождения математического квеста не возникло, однако, трудности все же
возникли, но другого рода. Мы перечислим различные трудности, возникшие при
подготовке нами математического квеста. Также, отметим, какие возникли
трудности во время прохождения квеста у младших школьников, в связи с тем, что
математический квест в учебной деятельности был для учащихся нововведением.
Следует отметить, что такой вид деятельности, как квест, не был досконально
изучен и отработан данным классом, первое знакомство с квестом был у 1 класса
«Б» за неделю до прохождения нашего математического квеста (знакомство с данным
видом деятельности у класса произошло в период государственной педагогической
практики, в феврале - марте 2017 года). Классный руководитель класса знакомил
учащихся с таким видом деятельности (квест) на примере квеста, основанном на
межпредметных заданиях, в которых был сделан акцент на русском языке,
литературе и математике. Трудности, возникшие у нас при использовании
математического квеста в 1 классе «Б»:
1. Проведение квеста со всем классом. Следить за правильным
выполнением заданий при большом количестве участвующих было проблематично.
2. Разработка заданий, подходящих именно под данный 1 класс «Б»,
нужно было опираться именно на уровень учащихся.
3. Разработка маршрута для каждой команды, так, чтобы команды не
пересекались на этапах (станциях).
4. Распределение времени на прохождение каждого этапа (станции).
Трудности, возникшие у младших школьников:
1. Чтение инструкций к этапам (станциям), пропуски подсказок,
непонимание условий к заданиям.
3. При решении дидактических игр забывчивость о том, что они
находятся в команде. Каждый пытался самостоятельно справиться с заданием, не
слушая своих одноклассников.
Мы рассмотрели различные трудности, возникшие при математическом квесте.
Далее мы проанализируем полученные результаты.
По завершению математического квеста мы имеем следующие результаты.
Каждая команда показала себя с различных сторон. Для каждой команды нашелся
этап, который вызвал трудности при решении. Например, команда «желтых» имела
трудности при решении задания на этапе «Цветник», в то время как команда
«красных» и «зеленых» без каких-либо проблем справились с поставленной задачей.
В конце математического квеста был проведен разговор и по результату этого
разговора, мы поняли, что для команды «желтых» данный этап оказался трудным
только потому, что учащиеся не внимательно прочитали инструкцию. Для команды
«красных» наиболее трудным этапом (станцией) оказался «Собиралка», прохождение
данного этапа у них заняло больше всего времени по сравнению с другими
командами. Команда «красных» не поняла условие задания и приступила к
выполнению своего «вымышленного» задания, в последствии, команда пришла к
верному решению, так как один ученик из команды решил еще раз перечитать
инструкцию к дидактической игре. Команда «зеленых» не имела каких-либо
трудностей с решением дидактических игр, каждый этап прошел у них спокойно и
ответ был найден без каких-либо проблем. На итоговом этапе (станции)
«Художники» все команды объединяются за одни столом и выполняют поставленную
перед ними задачу. При завершении данного этапа, представитель от каждой
команды объясняет рисунки, объяснение должно быть построено верно и должно быть
доказано правильность выполнения задания. С данной дидактической игрой
справились все команды. После «речи доказательств» каждая команда должна была
передать конверты, которые они находили в период прохождения математического
квеста. В конвертах содержались кусочки фразы, ученики, выйдя к доске должны
были составить из этих кусков цельное предложение «Мы самый дружный класс».
После завершения математического квеста была проведена беседа с классом по
поводу квеста, были обговорены следующие темы: «Вызвали ли у вас какие- либо
этапы трудности при решении?», «Хотелось бы вам, чтобы такие квесты проходили
на уроках чаще?», «Были ли вы дружным классом? Слушали ли вы своих
одноклассников?». При полученных результатах, мы видим, что разработанный нами
математический квест, а именно, дидактические игры, успешно проявили себя в
данном 1 классе «Б». Наш математический квест на развитие воображения у младших
школьников проявил себя с лучшей стороны, дидактические игры были разработаны
верно. Воображение при прохождении квеста у учеников было задействовано на
первом месте. Далее мы уделим внимание нашей гипотезе, проверим подтвердилась
ли наша гипотеза.
Рассмотрим следующее, подтвердилась ли наша гипотеза, которую мы ставили
в начале нашего исследования. Наша гипотеза заключалась в следующем, если при
обучении математике использовать дидактические игры для развития воображения в
начальной школе уже с 1 класса (в рамках уроков математики или на внеурочной
деятельности, на постоянной систематической основе), то это поможет лучшему
усвоению знаний и увеличит у детей интерес к данному общеобразовательному
предмету. Мы можем отметить следующее, что наша гипотеза подтвердилась, так как
у учащихся 1 класса «Б» отмечается активный рост заинтересованности в данном
общеобразовательном предмете, даже у тех детей, которые имеют различные
трудности с математикой. С помощью дидактических игр, использованных на уроках
и в математическом квесте, мы можем отметить лучшее усвоение знаний по математике.
Задания были представлены ученикам не в классическом варианте, как в учебнике.
Были использованы различные творческие задумки, что привлекло внимание и
интерес у учащихся к выполнению заданий. Результаты были продемонстрированы на
более высоком уровне, нежели результаты при решении классических задач из
учебника. Также стоит вспомнить реакцию младших школьников на дидактические
игры, они были встречены с интересом и оживлением, в отличии от задач в
учебнике. После окончания математического квеста учащиеся 1 класс «Б»
интересовались, будут ли еще подобного вида квесты, как они сообщили, им бы
хотелось, чтобы такие квесты были почаще. Несмотря на явный интерес детей к
дидактическим играм, стоит помнить, что обучение не стоит строить только лишь
на дидактических играх, так как со временем и такой вид деятельности ученикам
может стать повседневным и не будет вызывать заинтересованности в обучении.
В данном пункте мы постарались подробно разобрать прохождение
математического квеста в 1 классе «Б» ГБОУ Школы №1392 им. Д.В.Рябинкина г.
Москвы.
Целью нашего эксперимента было следующее, проверить, действительно ли
следует использовать дидактические игры для развития воображения при обучении
математике. По полученным данным, можно сделать вывод, что использовать
дидактические игры для развития воображения при обучении математике
действительно следует, так как результаты, которые мы получили, были на высоком
уровне, что показывает продуктивность дидактических игр. Данную проблему мы
решили подробнее рассмотреть, так нами было составлено социологическое
исследование для молодых специалистов, работающих в школах и для будущих
учителей. Ниже мы предоставим вниманию данный социологический опрос, который
содержит в себе анкету, анализ и обработку результатов, вывод.
Тема: Нужны ли дидактические игры при обучении математике?
Проблема: роль дидактической игры в обучении младших школьников.
Цель: выявить степень положительного отношения учителей/будущих учителей
к дидактическим играм при обучении математике.
Задачи:
· определить отношение к дидактическим играм у учителей/будущих
учителей;
· определить степень использования дидактических игр в процессе
обучения;
· определить влияет ли дидактические игры по мнению будущих
учителей на качество усвоения математики.
Гипотеза: дидактические игры помогут улучшить знания при обучении
математике.
Целевая аудитория: молодежь в возрасте от 22-23 (молодые специалисты,
работающие в школах и будущие учителя).
Анкета на
тему «Нужны ли дидактические игры при обучении математике?»
Уважаемый участник опроса, просим вас ответить на представленные ниже
вопросы. Опрос имеет анонимный характер, и полученные данные будут использованы
только в обобщенном виде. Отвечая на каждый вопрос, выбирайте один вариант
ответа (если в формулировке вопроса не указано иное).
1. Знаете ли/Слышали ли Вы о дидактических играх, проводимых на
уроках?
○ Да ○ Нет
2. Являются ли дидактические игры на Ваш взгляд неотъемлемой
частью в процессе обучения?
○ Да ○ Иногда ○ Нет
3. Проводите ли/Планируете ли Вы дидактические игры на своих
уроках?
○ Да
○ Нет
При обучении математике Вы используете/будете использовать дидактические
игры?
○ Да ○ Нет
5. Как часто Вы используете/планируете использовать
дидактические игры при обучении математики?
○ Часто ○Два-три раза в неделю ○ Никогда
6. Каким видам дидактических игр при обучении математике Вы бы
отдали предпочтение?
○ игре-путешествию ○ игре-загадке ○ иной вид ○
никаким
7. Как вы считаете дидактические игры при обучении математике
увеличили/увеличат интерес детей к предмету?
○ Да, дети более заинтересованы предметом ○ Нет, детям
не нравится отвлекаться на дид.игры ○ Большой разницы не наблюдаю
8. После проведения дидактических игр при обучении математике
улучшился ли/улучшится ли уровень знаний учеников?
○ Да ○ Затрудняюсь ответить ○ Нет
9. С какими трудностями в организации и проведении дидактической
игры при обучении математике Вы сталкивались/столкнетесь?
○ отсутствие необходимых условий ○ безучастность детей
○ сложности во внедрении игры в учебный процесс ○
другие
10. С какого класса Вы считаете нужно использовать дидактические
игры в процессе обучения математике, дабы избежать всевозможные трудности?
○ С первого класса ○ Дидактические игры не следует
использовать в процессе обучения ○ В любом классе
Анализ и
обработка результатов:
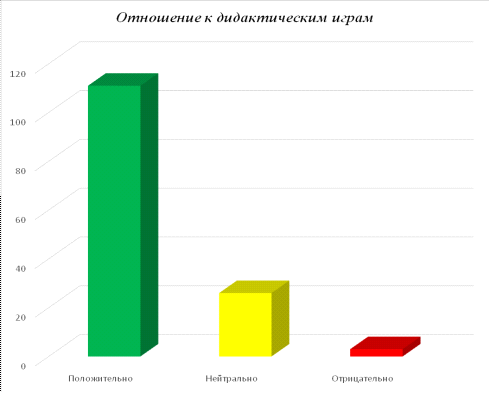
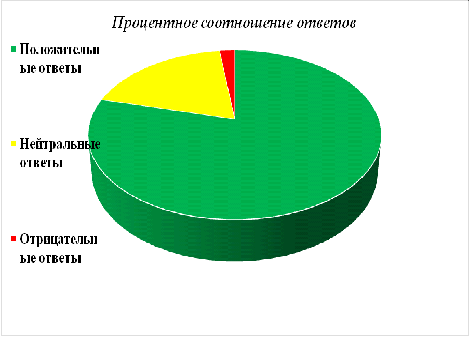
После обработки результатов мы можем сделать вывод, что среди молодых
специалистов/будущих учителей отношение к дидактическим играм в процессе
обучении математике отмечается как положительное. По полученным данным мы
видим, что положительное отношение к внедрению в процесс обучения дидактических
игр составляет 79%; нейтральное отношение составляет 19% и отрицательное
отношение составляет всего 2%. Нужно помнить, что опрос проводился анонимно и
что получение данных ответов зависит от различных обстоятельств, можно
допускать тот факт, что участники опроса были не совсем честными. По итогам
опроса мы смогли определить отношение к дидактическим играм у учителей/будущих
учителей - в большей мере, это положительное отношение. А также, смогли
определить степень использования дидактических игр в процессе обучения -
умеренное использование дидактических игр. Суммируя полученные ответы, мы
подтвердили нашу гипотезу, что дидактические игры помогут улучшить знания при
обучении математике.
Данное социологическое исследование, опирающееся на мнения молодых
специалистов и будущих учителей, наглядно доказывает пользу дидактических игр в
процессе обучении математике. Стоит помнить, что продуктивность дидактических
игр зависит от верной разработки игр, то есть, дидактическая игра должна быть
ориентирована специально на тот класс, в котором проводится игра.
Мы стремились доказать, если при обучении математике применять
дидактические игры для развития воображения в начальной школе начиная с 1
класса (в рамках уроков математики или на внеурочной деятельности, на
постоянной систематической основе), то это поможет лучшему усвоению знаний и
увеличит у детей интерес к данному общеобразовательному предмету.
Заключение
Математика присутствует в жизни каждого человека, что показывает на
истинную востребованность данного предмета. Математика с раннего возраста
способствует развитию воображения, а также, восприятия мира. В последнее время
в учебной практике стал популярным и актуальным такой вид деятельности, как
дидактические игры. Существуют различные мнения на тему использования
дидактических игр в процессе обучения математике. Многие исследователи по
данной проблеме считают, что использование дидактических игр на уроках
математики является полезным для процесса обучения. Также они отмечают, что
каждая дидактическая игра должна быть разработана специально под класс, в
котором она в последствии будет использована. Специалисты, занимающиеся
дидактическими играми, утверждают, что не стоит постоянно полагаться только на
игры в процессе обучения. Постоянное использование дидактических игр может
вызвать у учащихся младших классов привыкание к такому виду деятельности, а,
следовательно, у учеников пропадет интерес к данной деятельности. Специалисты
рекомендуют не только чередовать дидактические игры, но и давать детям отдых от
подобного вида деятельности. Дидактические игры развивают личностные качества
учащихся младших классов, а также, способствуют развитию внимания и воображения.
Дидактические игры, которые были специально разработаны для
математического квеста, на практике показали положительное влияние на развитие
воображения у младших школьников. Можно отметить, что стремление к обучению у
учеников повысился благодаря дидактическим играм. Применение дидактических игр
для развития воображения в начальной школе начиная с 1 класса (в рамках уроков
математики или на внеурочной деятельности, на постоянной систематической
основе), поможет лучшему усвоению знаний и увеличит у детей интерес к данному
общеобразовательному предмету. Используя математический квест в нашем
эксперименте, мы на практике доказали истинность вышеизложенного мнения, а
соответственно, наша гипотеза, которую мы выдвинули перед экспериментом,
подтвердилась.
Также следует отметить, что экспериментальное исследование проводилось
только с учениками первого класса общеобразовательной школы. Возможно, что
результаты эксперимента могли быть другими, если бы эксперимент проводился с
детьми, обучающимися со второго по четвертый класс, или в школах с углубленным
изучением математики. В дальнейшем можно провести эксперимент во втором,
третьем и четвертом классах с целью окончательного подтверждения выдвинутой
нами гипотезы.
Список
литературы
1. Böhm W.: Словарь педагогики. Stuttgart, Verlag
Alfred Kröner, 1988.
2. Booker G.
«Математические игры. Использование обучающих игр для обучения математике».
Wellington, 2000.
3. Fröbel F. W. A.: Человеческое образование. Leipzig,
Wienbrach, 1826.
4. Groos K.:
Игры животных, 1896
5. Onslow B.
«Преодоление концептуальных препятствий: квалифицированное использование игры».
Школьная наука и математика, 1990.
6. Piaget
J., Inhelder B. Детская психология. Братислава, 1997.
7. Průcha, Walterová and
Mareš Педагогический
словарь, игра 1998.
8. Pulos, S.
Sneider «Разработка и оценка эффективных игр для преподавания науки и
математики», C. Иллюстрация для геометрии в координатах. Сосредоточение на
проблемах обучения в математике, 1994.
9. Schiller F.: On the Aesthetic Education of Man. New York, Dover Publications, 2004.
10. Spencer H.:
Essays on Education and Kindred Subjects, London, 1911:
#"895473.files/image003.jpg">


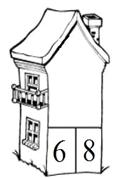



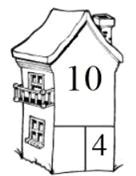

Приложение 2
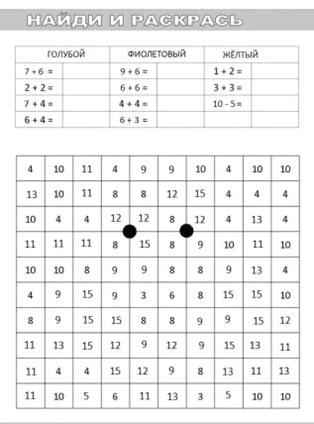
Приложение 3
Разгадай кроссворд. Выпиши числа, находящиеся в ○, в порядке
увеличения.
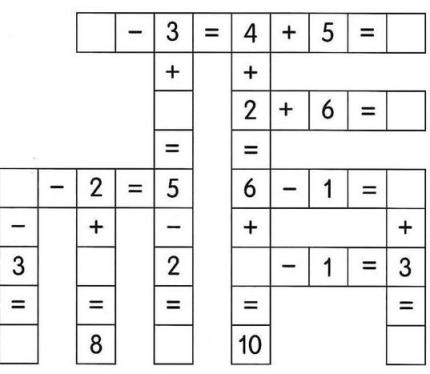
Приложение 4
Заполни пустые окошки
7 + =
13 + 5 = 11 10 - = 6
14 - = 6 15 - = 10 13 - =
7
+ 5 = 12 + 9 = 15 15 - =
9
6 + =
12 + 11 = 15 11 - = 3
15 - = 6 16 - = 10 13 - =
7
+ 2 = 12 + 4 = 9 15 - = 9
Приложение 5
Собиралка
Перед Вами поле с различными фигурами, на которых написаны числа. Вам
нужно:
1. Найти четные числа.
2. Составить из фигур, на которых написаны четные числа,
геометрическую фигуру.
Ø Подсказка: выкладывайте фигуры с четными числами в порядке
увеличения (от меньшего к большему).
3. Позвать учителя и показать выполнение этапа.
После
выполнения задания вы получите «ключ» к следующему этапу.
Приложение 6
Цветник
Перед Вами находится поле, на котором уже есть две разноцветные карточки.
Вы должны заполнить поле остальными карточками. После заполнения поля, вы
увидите геометрическую фигуру. Что это за фигура?
Ваши шаги:
1. Карточки нужно соединить так, чтобы был цвет к цвету (синий к
синему, красный к красному и тд).
Ø Пример:
2. Решить, какая геометрическая фигура получилась.
3. Позвать учителя и показать выполнение этапа.
После
выполнения задания вы получите «ключ» к следующему этапу.
Приложение 7
Цепочка
Перед Вами лежат карточки с примерами. Вам нужно составить цепочку из
примеров, начальная карточка Вам нужно:
1. Решить пример на начальной карточке (вычислить 11-2).
2. Найти карточку с примером, который начинается с ответа
предыдущей карточки.
3. Выложить цепочку из карточек. Заключительная карточка должна
быть той, где ответом является число, с которого начинается пример на начальной
карточки, т.е. число 11.
Ø Подсказка: Пример
4. Позвать учителя и показать выполнение этапа.
После
выполнения задания вы получите «ключ» к следующему этапу.
Приложение 8
Художники
Перед Вами находятся цифры и различные символы. Вам нужно нарисовать
что-то, где будут использованы от 3 до 5 символов/цифр.
Ваши шаги:
1. На листе А4 нарисовать картинку, следуя правилам
2. Позвать учителя и показать выполнение этапа.
Приложение 9

