Методика проведения курса по выбору 'Площади многоугольников' для учащихся 9 класса

Введение

Современная школа ориентирована на гуманизацию образования, усиление внимания к ученику, к его саморазвитию. Всё большее внимание уделяется развивающему обучению, где математика занимает одну из ведущих позиций, особенно геометрический материал позволяет обеспечить более гармоничную мыслительную деятельность школьников, что особенно важно на начальном этапе обучения математике. Поэтому многие отечественные ученые (А.Д.Александров, Г.Д. Глейзер, В.М. Тихомиров, И.Ф. Шарыгин и др.) стремились создать свои оригинальные концепции обучения геометрии в школе, которые учитывают не только специфику предмета и метода геометрии, но и содержат огромный развивающий эффект.

Исторически возникновение геометрии связано с потребностью сравнения земельных участков той или иной формы. Отцом науки-геометрии легенда считает Фалеса - ионийского купца, путешественника и философа. Фалеса причисляют к числу семи мудрецов древности, ему приписывают изречение «Познай самого себя», которое было высечено в храме Аполлона в Дельфах. Считается, что Фалес первым, анализируя геометрические истины, задался вопросом: почему? Затем наступила эра Пифагора, который превратил занятия геометрией в настоящую науку, рассматривая ее основы с высшей точки зрения и исследуя ее теории менее материальным и более умственным образом. А спустя два века греческие философы задумались над тем, как должна строиться научная теория. Итоги их размышлений были подытожены Аристотелем. Подведение итогов развития геометрии за четыре столетия и ее дедуктивное построение было осуществлено Евклидом. «Начала» Евклида считают одной из самых значительных книг в истории человечества.

Поиском новых моделей обучения геометрии в последнее время занимались многие исследователи, такие как В.А. Гусев, Г.А. Клековкин, В.А. Панчишина, Н.С. Подходова, И.М. Смирнова и В.А. Смирнов, Т.Г. Ходот, И.Ф. Шарыгин и др., в результате чего появились новые систематические и пропедевтические курсы геометрии.

Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности, достаточных для изучения смежных дисциплин и продолжения образования. И именно в геометрии заложены потенциальные возможности воспитывать интеллектуальные качества личности. Но чтобы реализовать эти возможности необходимо знать различные методические подходы в изучении элементов геометрии. Этими вопросами занимались Б.П. Белоцерковский, В.Г. Болтянский, В.А. Гусев, В.А. Жаров, Ю.М. Колягин, Ф.Ф. Нагибин, А.Д. Семушин, З.А. Скопец, Д. Пойа и др., в работах которых отражены проблемы обучения учащихся элементам геометрии и решению геометрических задач, формированию рациональных приемов учебной работы. Также отдельные вопросы методики затронуты в диссертационных исследованиях Э.Г. Готмана, Г.Б. Кузнецовой, М.С. Мацкиной, Л.М. Ноздрачевой, Е.В. Потоскуева, Ю.А. Розки, Г.И. Саранцева, Е.Е. Овчинниковой и др.

Тема «Площади многоугольников» является частью школьного курса геометрии. Образовательные возможности темы «Площадь» в средней школе используются далеко не полностью, хотя она является базовой, фундаментальной и изучается на протяжении всего курса математики, начиная с начальных и заканчивая старшими классами.

В процессе обучения математике важное место отводится организации повторения изученного материала. Повторение тем содействует интенсивному протеканию процесса запоминания и предусматривает формирование у учащихся устойчивого интереса к предмету, вырабатывание гибкости, подвижности ума, развитие их математических способностей, ориентацию на профессии, существенным образом связанных с математикой, подготовку к дальнейшему обучению. Однако на повторение темы отводится недостаточно времени.

Теоретическое обоснование вычисления площадей геометрических фигур и применение площади в качестве инструмента для решения задач в современной методической литературе исследовано достаточно полно. Э.Г. Готман, И.А. Кушнир, Н.Д. Новиков, В.В. Прасолов, И.Ф. Шарыгин рассматривают в своих работах методы вычисления площадей, однако в школе из-за недостаточного времени этим аспектам не уделяется должного внимания. И несмотря на достаточно серьезные исследования в области методики обучения математике усвоение школьниками темы «Площадь» вызывает определенные трудности. Об этом свидетельствуют опыт работы учителей и результаты экзаменов. Тем более, что в 9 классе у учащихся обязательный основной государственный экзамен, на котором ученики должны показать, что умеют выполнять действия с геометрическими фигурами. И каждый из них желает показать хороший результат для продолжения обучения или поступления в новое образовательное учреждение.

Всё вышесказанное говорит об актуальности проблемы исследования.

Проблема исследования состоит в разработке курса по выбору по теме «Площади многоугольников».

Объектом исследования является процесс обучения математике в основной школе.

Предметом исследования является методика проведения курса по выбору «Площади многоугольников» в 9 классах.

Целью исследования является разработка содержания и методики проведения занятий курса по выбору «Площади многоугольников» в 9 классах общеобразовательной школы.

Гипотеза исследования заключается в том, что разработанный курс способствует повышению уровня математической культуры, а также воспитания и развития учащихся, оказывает существенное воздействие на повышение качества их знаний по предмету.

Реализация поставленной цели исследования потребовала решения ряда конкретных задач:

1.   На основе анализа психолого-педагогической и методической литературы выявить особенности проведения курсов по выбору в основной школе.

2.       Разработать содержание и методику проведения курса по выбору «Площади многоугольников» для 9 класса.

3.       Провести опытно-экспериментальную проверку разработанного курса, дать необходимые методические рекомендации.

Решение поставленных задач осуществлялось методами исследования: анализ психолого-педагогической, методической и математической литературы, школьных программ; наблюдение; анализ самостоятельных и контрольных работ обучающихся.

1. Теоретические основы изучения площадей многоугольников

Особенности проведения курсов по выбору в основной школе в 9 классе.

Л.С. Выготский считал, что любой педагог должен строить свою работу с опорой на психологическую науку. Таким образом он доказал связь психологии с педагогикой [13]. Также проблемами возрастной психологии занимались А.Н. Леонтьев [29], В.А. Крутецкий [24, 25] и др.

Рассмотрим возрастные особенности учащихся основной школы. Девятиклассники находятся на переходном периоде от подросткового к раннему юношескому возрасту. Это один из самых сложных периодов в жизни ребёнка, это пик «подросткового кризиса». Особенность девятого класса, самого старшего из подростковых, заключается в переходности, в пересечении специфических возрастных черт - подростковых и юношеских.

Претендующие на роль взрослого человека подростки не терпят отношения к себе как к детям, они хотят полного равноправия со взрослыми.

С другой стороны, потребность быть взрослым постепенно заменяется необходимостью быть им: многие девятиклассники уже всерьез задумываются о своем профессиональном и личностном будущем.

Девятиклассники все чаще обращают взгляд на собственный внутренний мир и соотносят его с миром внешним: «Кто я? Какой я? Каково мое место среди других».

Стремление подростка углубленно понять себя, разобраться в своих чувствах, настроениях, мнениях, отношениях, что побуждает интерес к психологическим переживаниям других людей и к своим собственным. Это порождает у подростка стремление к самоутверждению, самовыражению (проявлению себя в тех качествах, которые он считает наиболее ценными) и самовоспитанию.

Подростки критично относятся к отрицательным чертам своего характера, переживают из-за тех черт, которые мешают им в дружбе и взаимоотношениях с другими людьми.

Межличностное общение девятиклассников может осложняться и другими проблемами, если класс находится на низкой ступени коллективного развития: старшие подростки в этом случае бывают более нетерпимы и даже агрессивны по отношению друг к другу, чем школьники других возрастов. Этому может способствовать тревожность по поводу предстоящих жизненных перемен и волнующих ребят вопросов: кого возьмут или не возьмут в старшие классы; что ждет тех, кто уйдет из школы? Но эти настроения могут не только разъединять, но и объединять ребят, если в классе создана атмосфера общей заботы и поддержки.

Поэтому значимой деятельностью для старших подростков нередко становятся вполне конкретные практические занятия, меняющие статус увлечения на более серьезный. К таким как раз можно отнести курсы по выбору для подготовки к экзамену. Окончание девятого класса - это не только завершение этапа общего образования, не только первые серьезные экзамены и получение первого официального документа об образовании. Это прощание с детством и отрочеством, для многих - прощание со своим классом и грядущая первая серьезная встреча со взрослой жизнью.

Курсы по выбору - учебные курсы, не обязательные для посещения, способствующие самоопределению обучающихся.

Курсы по выбору должны носить краткосрочный характер. Оптимальная продолжительность элективного курса в предпрофильной подготовке 8-12 часов. Максимальная продолжительность курса - 34 часа, по 2 часа в неделю. И это понятно, ведь ученики девятых классов находятся на пороге выбора направления дальнейшего обучения, и поэтому они должны иметь возможность попробовать свои силы на разных курсах.

Курсы по выбору в предпрофильной подготовке подразделяются на предметно-ориентированные (пробные) и межпредметные (ориентационные).

Предметно-ориентированные курсы решают следующие задачи:

-         создание условия школьнику для реализации личных познавательных интересов к учебному предмету.

-        уточнение готовности и способности осваивать предмет на повышенном уровне.

-        создание условий к сдаче экзаменов по выбору, то есть к наиболее вероятным предметам будущего профилирования.

Задачи межпредметных курсов:

-         формирование у школьников способности и умения ориентации в мире современных профессий.

-        ознакомление на практике со спецификой типичных видов деятельности, соответствующих наиболее распространенным профессиям.

-        поддерживание мотивации к тому или иному профилю.

В настоящее время не существует единой классификации элективных предпрофильных курсов. Однако большинство авторов выделяет три основных типа элективных курсов: предметные, межпредметные и ориентационные. Предметные элективные курсы построены на учебном материале одного учебного предмета, межпредметные - на учебном содержании 2-3 предметов, ориентационные призваны сориентировать ученика в мире профессий, помочь ему ответить на вопросы: «Какой я? Что я хочу? Что я могу?».

Курсы решают также ряд специфических образовательных задач:

-         удовлетворения индивидуальных образовательных интересов и потребностей каждого обучающегося;

-        развитие содержания одного или нескольких учебных предметов;

-        знакомство обучащихся с миром профессий, возможностями продолжения образования и вариантами социальной карьеры в конкретной социокультурной ситуации, формирование способности и готовности у учащихся к осознанному выбору, самоопределению;

-        создание условий для освоения способов деятельности, необходимых в том или ином профиле обучения, а также и в дальнейшей профессиональной деятельности.

В процессе изучения данных курсов учащиеся 9 классов должны иметь возможность:

-         приобрести опыт приложения усилий по освоению образовательного материала и по освоению компетентностей, востребованных в профильном обучении и послешкольном образовании;

-        получить информацию о значимости профильного обучения для дальнейшего продолжения профильного образования, жизненного, социального и профессионального самоопределения;

-        сформировать ценностные ориентации, связанные с профилем обучения и соответствующим ему направлениями будущего образования.

Курсы по выбору должны быть направлены на решение следующих задач: математический учащийся межличностный

-         способствовать самоопределению ученика и/или выбору дальнейшей профессиональной деятельности;

-        создавать положительную мотивацию обучения на планируемом профиле;

-        познакомить учащихся с ведущими для данного профиля видами деятельности;

-        активизировать познавательную деятельность школьников;

-        повысить информационную и коммуникативную компетентность учащихся.

Курсы по выбору предоставляют дополнительные возможности для развития способностей учащихся и их интересов, в том числе удачной сдачи экзамена.

История введения факультативных и элективных курсов в образование.

Существенным звеном в непрерывном обновлении содержания и методов обучения в школе является факультативное изучение некоторых предметов по выбору учащихся. Первые зачатки этого сравнительно нового явления появились после опубликования закона «Об укреплении связи школы с жизнью и о дальнейшем развитии системы народного образования в СССР», от 24 декабря 1958 г. Дальнейшее развитие этот вид организации учебного процесса получил после опубликования Постановления ЦК КПСС и Совета Министров СССР от 10 ноября 1966 г, «О мерах дальнейшего улучшения работы средней общеобразовательной школы», где сказано: «Для углубления знаний по физико-математическим, естественным и гуманитарным наукам, а также развития много сторонних интересов и способностей учащихся проводить в школах, начиная с VII класса, факультативные занятия по выбору учащихся». [38]

Министерство просвещения СССР и министерства союзных республик в конце 60-х годов уделяли много внимания этому виду работы школы. Была разработана и утверждена коллегией Министерства просвещения СССР инструкция по факультативным занятиям, на основе которой союзные республики выработали свои инструкции. В министерствах были составлены примерные тематики этих занятий и разработаны программы для целого ряда курсов. По некоторым курсам подготовлены учебники и учебные пособия, В институтах усовершенствования учителей развернулась работа по оказанию помощи учителям, преподающим факультативы.

В НИИ содержания и методов обучения АПН СССР был создан научно- методический совет по проблемам углубленного изучения предметов. Совет организовал всесоюзные конференции, на которых ученые-педагоги докладывали о своих экспериментах и обобщениях, а учителя-практики поделились своим опытом по преподаванию факультативов.

Из ученых, более длительно занимающихся изучением проблемы факультативных занятий следует отметить М.А. Мельникова. Его интересовал первоначально проблема дифференциации учебного процесса в связи с производственным обучением.

Сессия общего собрания АПН СССР в 1975 г. всесторонне обсудила доклад М.П. Кашина об итогах перехода советской школы на новое содержание обучения и дала высокую оценку значению факультативных занятий, обратив при этом внимание на серьезные недостатки в их развитии.

В 1967-68 году в учебные планы общеобразовательных школ были включены факультативные занятия.

Широкого распространения «альтернативные занятия» не получили. Видимо, поэтому в современной научно-методической литературе элективные курсы чаще сопоставляют с факультативами, которые начиная с 1966 г. были организованы практически во всех школах страны.

Второй этап в становлении факультативных занятий начался в 1980 году и был связан с переходом средней школы на новую программу по математике.

Третий этап начался с проведения съезда работников народного образования, который проходил в Москве в декабре 1988 года. Реформой предусматривалось дальнейшее развитие всех форм дифференциации, в том числе и факультативов, основной целью которой является возможность углубленного изучения отдельного предмета, в том числе и математики.

В 1990 году была опубликована новая программа факультативных курсов. (Программы средней общеобразовательной школы. Факультативные курсы. Сборник №2. Часть 1(математика, биология, химия). - М.: Просвещение). Основной целью программы является углубление знаний по основному курсу, получаемых на уроках.

В 2002 году была принята общая Концепция модернизации российского образования. Разработкой ее основных положений занимались видные ученые: Д.В. Аносов, В.И. Арнольд, Я.И. Кузьминов, В.Л. Матросов, Н.Д. Никандров, В.Д. Шадриков и др.

Анализ темы «Площадь» в учебниках геометрии 7-9

Рассмотрев следующие темы в двух учебниках Л. С. Атанасяна [4] и др. и И.М. Смирновой, В.А. Смирнова.[39], мы сделали сравнительный анализ.

1)         Параллелограмм. Площадь параллелограмма.

2)       Треугольники. Площадь треугольников.

3)         Прямоугольник. Ромб. Квадрат. Площадь прямоугольника. Площадь квадрата.

4)         Трапеция. Площадь трапеции.

Сравнительный анализ учебников.

Таблица 1

Вычисление площадей в древности.

Зачатки геометрических знаний, связанных с измерением площадей, теряются в глубине тысячелетий.

Еще в 4 - 5 тысяч лет назад вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. Квадрат издавна служит эталоном при измерении площадей благодаря многим своим замечательным свойствам: равные стороны, равные и прямые углы, симметричность и общее совершенство формы. Квадраты легко строить, или можно заполнить плоскость без пробелов. [15]

В древнем Китае мерой площади был прямоугольник. Когда каменщики определяли площадь прямоугольной стены дома, они перемножали высоту и ширину стены. Таково принятое в геометрии определение: площадь прямоугольника равна произведению его смежных сторон. Обе эти стороны должны быть выражены в одних и тех же линейных единицах. Их произведение и составит площадь прямоугольника, выраженную в соответствующих квадратных единицах. Скажем, если высота и ширина стены измерены в дециметрах, то произведение обоих измерений будет выражено в квадратных дециметрах. И если площадь каждой облицовочной Плотки составляет квадратный дециметр, то полученное произведение укажет число плиток, нужное для облицовки. Это вытекает из утверждения, положенного в основу измерения площадей: площадь фигуры, составленной из непересекающихся фигур, равна сумме их площадей.

Древние египтяне 4000 лет назад пользовались почти теми же приемами, что и мы, для измерения площади прямоугольника, треугольника и трапеции: основание треугольника делилось пополам, и умножалась на высоту; для трапеции же сумма параллельных сторон делилась пополам и умножалась на высоту и т.п. Для вычисления площади S четырехугольника со сторонами a,b, c, d. т.е. умножались полусуммы противоположных сторон.

Рис. 1.1

Эта формула явно неверна для любого четырехугольника, из нее вытекает, в частности, что площади всех ромбов одинаковы. Между тем, очевидно, что у таких ромбов площади зависят от величины углов при вершинах. Данная формула верна только для прямоугольника. С ее помощью можно вычислить приближенно площадь четырехугольников, у которых углы близки к прямым.

Для определения площади S равнобедренного треугольника ABC (рис. 1.2), в котором египтяне пользовались приближенной формулой:

 (1.2)

Рис. 1.2

Совершаемая при этом ошибка тем меньше, чем меньше разность между стороной AB и высотой AD треугольника, иными словами, чем ближе вершина B (и C ) к основанию D высоты из A . Вот почему приближенная формула (1.2) применима лишь для треугольников с сравнительно малым углом при вершине.

Но уже древние греки умели правильно находить площади многоугольников. В своих «Началах» Евклид не употребляет слова «площадь», так как он под самим словом «фигура» понимает часть плоскости, ограниченную той или иной замкнутой линией. Евклид не выражает результат измерения площади числом, а сравнивает площади разных фигур между собой.

Как и другие ученые древности, Евклид занимается вопросами превращения одних фигур в другие, им равновеликие. Площадь составной фигуры не изменится, если ее части расположить по-другому, но без пересечения. Поэтому, например, можно, исходя из формул площади прямоугольника, находить формулы площадей других фигур. Так, треугольник разбивается на такие части, из которых затем можно составить равновеликий ему прямоугольник. Из этого построения следует, что площадь треугольника равна половине произведения его основания на высоту. Прибегая к подобной перекройке, находят, что площадь параллелограмма равна произведению основания на высоту, площадь трапеции - произведению полусуммы оснований на высоту.

Когда каменщикам приходится облицовывать стену сложной конфигурации, они могут определить площадь стены, подсчитав число пошедших на облицовку плиток. Некоторые плитки, естественно, придется обкалывать, чтобы края облицовки совпали с кромкой стены. Число всех пошедших в работу плиток оценивает площадь стены с избытком, число необломанных плиток - с недостатком. С уменьшением размеров клеток количество отходов уменьшается, и площадь стены, определяемая через число плиток, вычисляется все точнее.

Одним из поздних греческих математиков - энциклопедистов, труды которого имели главным образом прикладной характер, был Герон Александрийский, живший в 1 в. н. э. Будучи выдающимся инженером, он был назван также «Герон Механик». В своем произведении «Диоптрика» Герон описывает разные машины и практические измерительные инструменты.

Одна из книг Герона была названа им «Геометрика» и является своего рода сборником формул и соответствующих задач. Она содержит примеры на вычисление площадей квадратов, прямоугольников и треугольников. О нахождении площади треугольника по его сторонам Герон пишет: « Пусть, например, одна сторона треугольника имеет в длину 13 мерных шнуров, вторая 14 и третья 15. Чтобы найти площадь, поступают вот как. Сложи 13, 14 и 15; получится 42. Половина этого будет 21. Вычти из этого три стороны одну за другой; сперва вычти 13 - останется 8, затем 14 - останется 7 и, наконец, 15 - останется 6. А теперь перемножь их: 21раз по 8 даст 168, возьми это 7 раз - получится 1176, а это еще 6 раз - получится 7056. Отсюда квадратный корень будет 84. Вот сколько мерных шнуров будет в площади треугольника».

В своем наиболее важном геометрическом произведении «Метрика» Герон излагает доказательство примененной выше формулы:

S =

где: a, b, c стороны, p - полупериметр треугольника.

Эта формула носит название «формулы Герона». На самом деле она была установлена еще в 3 в. до н. э. величайшим математиком древности Архимедом.

Практические правила Герона для вычисления площадей применялись греческими, римскими и средневековыми землемерами и техниками.

Различные подходы к изучению понятий «площадь», «многоугольник», «площадь многоугольника».

Понятие о площади. Свойства площади.

Обычно говорят, что площадь S(F) фигуры F есть число, показывающее, из скольких единиц площади составляется фигура. Однако это не определение, а только описание того, что такое площадь.

Строгое математическое определение площади можно получить с помощью палетки - прозрачной пластинки с нанесенной на нее сеткой из равных квадратов. Представим, что такая палетка лежит на плоскости. Иначе говоря, плоскость разбита на квадраты со стороной, равной 1. Если фигура F полностью помещается в фигуре, составленной, например, из81 квадрата палетки, и содержит фигуру из 43 квадратов, то: 43 ≤S(F) ≤81. [23]

Рис. 1.3

Для большей точности измерения можно каждый квадрат палетки разбить на сто квадратов и далее.

Способ измерения площадей с помощью палеток был предложен в XIX веке французским математиком Камилем Жорданом. Другой французский математик - Анри Лебег предложил более общее определение площади. Построенная выше фигура F неквадрируема по Жордану, но имеет площадь (равную), по определению Лебега, или, как говорят, измерима по Лебегу.

Если же фигура квадрируема по Жордану, то она обязательно измерима и по Лебегу (и имеет ту же площадь).

Также имеется и второе определение площади - аксиоматическое определение: площадь - функция на множестве квадрируемых фигур Q, удовлетворяющая данным аксиомам:

А. Неотрицательность. Площадь любой квадрируемой фигуры F неотрицательна:

S(F) ≥0. Не исключается нулевое значение площади, поскольку, например, любой отрезок представляет собой квадрируемую фигуру нулевой площади.

В. Аддитивность. Пусть F1 и F2 - две квадрируемые фигуры, у которых нет общих внутренних точек. Обозначим через F объединение этих фигур.

Тогда фигура F квадрируема и справедливо равенство:

(F) = S(F1) + S(F2).

То же имеет место при объединении не двух, а большего числа фигур, попарно не имеющих общих внутренних точек.

С. Инвариантность. Если две квадрируемые фигуры F1 и F2 равны, т. е. одна получается из другой с помощью движения, то площади таких фигур равны:

(F1) = S(F2).

Иначе говоря, площадь не изменяется при движениях.

D. Нормируемость. При определении площади фигуры задаётся некоторая единица площади - квадрат К, сторона которого равна единице длины:

(К) = 1.

Понятие о многоугольнике.

Термин «многоугольник» понимается в математике и, в частности, в школьном курсе математики двояко. Во-первых, многоугольник как линия. В этом случае многоугольник - это простая (т. е. без самопересечения) замкнутая ломаная, лежащая в некоторой плоскости. И, во-вторых, многоугольник, как часть плоскости, ограниченная простой замкнутой ломанной.

Понятие о площади многоугольника

В вопросе о площади многоугольник понимается как часть плоскости, ограниченная простой замкнутой ломаной. В этом смысле понятие «многоугольник» используется в дальнейшем в изложении школьного курса математики, а площадь многоугольника определяется с помощью указания её свойств:

1)     численное значение площади любого многоугольника всегда положительно;

2)   площади равных многоугольников, т. е. многоугольников, которые можно совместить с помощью движения, одинаковы;

3)      площадь многоугольника, полученного объединением двух многоугольников, не имеющих общих внутренних точек, будем называть не перекрывающимися);

4)  площадь квадрата со стороной единичной длины равна единице.

В различных учебниках по геометрии для общеобразовательных учреждений определения площади несколько отличаются друг от друга, но суть определений совпадает с указанным выше. Например, в учебнике Л.С. Атанасяна и др. площадь многоугольника определяется величиной той части плоскости, которую занимает многоугольник. А точное определение из учебника И.М. Смирновой и В.А. Смирнова говорит, что «площадь фигуры - это число, получающееся в результате измерения и показывающее, сколько раз единичный квадрат и его части укладываются в данной фигуре».

Можно рассмотреть различные формулы площадей многоугольников (см. приложение 1).

В данной главе мы рассмотрели особенности проведения курсов по выбору, выделили их задачи. Коснулись исторических аспектов проведения факультативных и элективных курсов в образовании. Сделали сравнительный анализ учебников по выбранной теме, указали различные подходы к изучению понятий «площадь», «многоугольник», «площадь многоугольника».

. Методические особенности повторения темы «Площади многоугольников» в 9 классе

Тематическое планирование темы и особенности её изучения.

Таблица 2. Тематическое планирование курса по выбору «Площади многоугольников»

Одним из важнейших вопросов, способствующих дальнейшему повышению успеваемости, достижению глубоких и прочных знаний у учеников, а также подготовка к экзамену является вопрос о повторении ранее пройденного материала.

Современные исследователи показали значительную роль при повторении изученного материала таких дидактических приёмов, как сравнение, классификация, анализ, обобщение, содействующее интенсивному протеканию процесса запоминания. При этом вырабатывается у учащихся гибкость, подвижность ума, обобщённость знаний. [2]

Необходимость повторения изученного ранее материала вызвано самой структурой программы учебного курса математики. Вот, например, учащиеся проходят по учебной программе тему: «Четырёхугольники», «Площадь» в 8 классе, а при подготовке к ОГЭ необходимо вспомнить изученную тему, для сдачи экзамена.

Правильно организованное повторение помогает ученику увидеть в старом нечто новое; помогает установить логические связи между вновь изучаемым материалом и ранее изученным; обогащает память ученика; расширяет его кругозор; приводит знания ученика в систему; дисциплинирует ученика; приучает в нем уменье находить необходимого для ответа на поставленный вопрос материал; воспитывает в ученике чувство ответственности.

Большую и серьезную ошибку допускает тот учитель, который побуждает ученика повторять материал в том порядке, в котором он изучался. Повторение в этом случае сводится и механическому воспроизведению в памяти пройденного материала.

Ушинский воспитывал против механического повторения. "Нет никакой надобности повторять выученное в том порядке, в каком оно было пройдено, а напротив, ещё полезнее повторения случайные, сводящие выученное в новые комбинации", - говорил он. [40]

Поэтому курсы по выбору по теме «Площади многоугольников» можно проводить и в 9 классе, а учитывая, что у учеников экзамен, то повторить им эту тему будет полезно.

Рассмотрим следующие виды повторения: Повторение в начале учебного года.

Текущее повторение всего, ранее пройденного:

а) повторение пройденного в связи с изучением нового материала (сопутствующие повторению);

б) повторение пройденного вне связи с новым материалом.ематичеcкoе повторение (обобщающее и систематизирующее повторение законченных тем и разделов программы).

Заключительное повторение (организуемое при окончании прохождения большого раздела программы или в конце учебного года).

Данный курс по выбору рассчитан на тематическое повторение с включением задач из банка заданий ОГЭ.

При повторении необходимо применять различные приемы и методы, сделать повторение интересным путём внесения, как в повторяемый материал, так и в методы изучения некоторых элементов новизны. Только разнообразие методов повторения может устранить то противоречие, которое возникает ввиду отсутствия желания у части учащихся повторять то, что ими усвоено однажды.

При тематическом повторении систематизируются знания учащихся по теме на завершающем этапе его прохождения или после некоторого перерыва.

Повторение на уроке проводится путем беседы с вовлечением учащихся. После этого учащиеся решают задачи, дискутируя друг с другом, также может быть в дальнейшем проведена самостоятельная работа, а при окончании курса - контрольная работа.

Контрольная работа по теме должна включать основные вопросы. После выполнения контрольной работы проводится разбор характерных ошибок и их устранение.

При тематическом повторении полезно составить вопросник, а затем логический план по теме и завершить работу составлением итоговых схем. Таблица или схема экономно и наглядно показывает общее для понятий, входящих в данную тему, их взаимосвязь в логической последовательности.

Курс будет основываться на подготовку учащихся к сдаче Основного Государственно Экзамена, в котором необходимо повторить с учащимися свойства фигур, свойства площадей и разобрать необходимые задачи, входящие в работу.

Курс по выбору разбивается на несколько этапов:

ü  Определение уровня умения решать задачи и знания теории по теме

«Треугольники» и «Четырехугольники».

ü  Курс уроков повторения с написанием самостоятельных работ.

ü  Подготовка и написание контрольной работы.

Методика проведения занятий

Представленные уроки запланированы на несколько занятий, и количество задач учитывается усвоением их учащимися. Задачи предлагаются по одному типу из вариантов ОГЭ, взятых с сайта #"895106.files/image007.gif">)

Следовательно, этот катет тоже будет равен у обоих треугольников. Тогда по признаку равенства треугольников, получается, что эти треугольники равны. Значит это утверждение верно.

Вспомним признаки равенства прямоугольных треугольников:

1)        Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.

2)       Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.

3)       Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.

17.      Если три стороны одного треугольника пропорциональны трём сторонам другого треугольника, то треугольники подобны.

Данное утверждение верно по признаку подобия.

Вспомним признаки подобия треугольников:

1)        Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.

2)       Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны, то такие треугольники подобны.

3)       Если три стороны одного треугольника пропорциональны трем сторонам другого треугольника, то такие треугольники подобны.

Встречаются и такие верные утверждения:

·         Любые два равносторонних треугольника подобны (по третьему признаку подобия).

18.      Отношение площадей подобных треугольников равно коэффициенту подобия.

Утверждение неверно по теореме об отношении площадей подобных треугольников (Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия).

19.      Треугольник со сторонами 1, 2, 4 не существует.

Утверждение верно по неравенству треугольника (в любом треугольнике каждая сторона меньше суммы двух других сторон). В данном случае: 4>1+2. То есть треугольник с такими сторонами не может существовать.

Также есть такое утверждение, которое считается верным по тому же неравенству:

·         Длина гипотенузы прямоугольного треугольника меньше суммы длин его катетов.

20.      Площадь треугольника меньше произведения двух его сторон.

Следовательно, данное утверждение верно.

21.      В прямоугольном треугольнике гипотенуза равна сумме катетов.

Утверждение неверно по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Повторение теории необходимо для понимания и решения задач. Можно провести опрос среди учащихся на данные утверждения, ввести их в дискуссию, чтобы им было интересно, но и запомнилось, сопровождая при этом презентацией или плакатами.

3. Решение задач

Для начала вспомним формулы площадей треугольников:

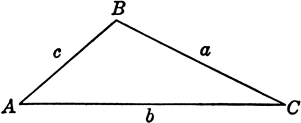
Рисс. 2.1

Через основание и высоту:

Но в прямоугольном треугольнике высота совпадает с одним из катетов, и тогда площадь прямоугольного треугольника равна половине произведения катетов.

Следовательно, для прямоугольного треугольника:

Через две стороны и угол:

Формула Герона:

Через радиусы:

Рассмотрим разные задачи из ОГЭ.

1.        На клетчатой бумаге с размером клетки 1×1 изображён треугольник. Найдите его площадь.

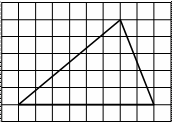
Рис. 2.2

Решение см. приложение 2 задача №1.

Данный тип задач следует решить несколько раз, применяя различные рисунки, чтобы учащиеся умели видеть и решали задачу «слету».

2.        Найдите площадь треугольника, изображённого на рисунке.

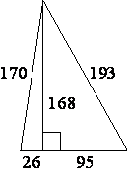
Рис. 2.3

Решение см. приложение 2 задача №2.

На этот вид задач много времени отводить необязательно. Просто прорешать несколько вариантов для ознакомления и закрепления формулы.

3.        Боковая сторона равнобедренного треугольника равна 29, а основание равно 42. Найдите площадь этого треугольника.

Рис. 2.4

Решение см. приложение 2 задача №3.

Перед решением задачи повторить свойства равнобедренного треугольника, теорему Пифагора и формулу Герона.

4.        Два катета прямоугольного треугольника равны 14 и 5. Найдите площадь этого треугольника.

Рис. 2.5

Решение см. приложение 2 задача №4.

Обратить внимание учащихся, что даны два катета, что и нужно для вычисления площади треугольника.

5.        Найдите площадь треугольника, изображённого на рисунке.

Рис. 2.6

Решение см. приложение 2 задача №5.

Задача немного усложнилась по сравнению с предыдущей. В данном случае, у нас известны длины одного катета и гипотенузы.

Поэтому необходимо обратить внимание учащихся, что даны не те стороны, а найти второй катет можно с помощью теоремы Пифагора.

6.        Сторона треугольника равна 14, а высота, проведённая к этой стороне, равна 23. Найдите площадь этого треугольника.

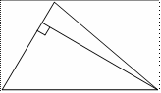
Рис. 2.7

Решение см. приложение 2 задача №6.

Обратить внимание учеников, что известны сторона и высота, проведенная к этой стороне. Что это очень важно, иначе использование формулы будет неверным.

7.         Периметр равнобедренного треугольника равен 216, а боковая сторона - 78. Найдите площадь треугольника.

Рис. 2.8

Решение см. приложение 2 задача №7.

Повторить с учащимися определение равнобедренного треугольника, периметра и формулу Герона.

8.        Площадь прямоугольного треугольника равна . Один из острых углов равен 30°. Найдите длину катета, лежащего напротив этого угла.

Решение см. приложение 2 задача №8.

Вспомнить со школьниками, что катет, лежащий против угла в 30 градусов равен половине гипотенузы. Зная это, задача решается проще с использованием переменной и теоремы Пифагора.

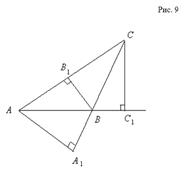
9.        В прямоугольном треугольнике один из катетов равен 4, а острый угол, прилежащий к нему, равен 45°.

Рис. 2.9

Решение см. приложение 2 задача №9.

Учитель задает наводящие вопросы и подводит учащихся к использованию теоремы о сумме углов для получения того, тчо треугольник является равнобедренным. Показывает задачу другого типа, но с похожим решением.

Подобная задача, только здесь вместо катета известна гипотенуза:

В прямоугольном треугольнике гипотенуза равна 70, а один из острых углов равен 45°.

Решение см. приложение 2 задача №9(а).

10.      Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.

Решение см. приложение 2 задача№10.

Обратить внимание учащихся, что даны не те стороны, а найти второй катет можно с помощью теоремы Пифагора.

11.      Площадь равнобедренного треугольника равна 196√3. Угол, лежащий напротив основания, равен 120°

Решение см. приложение 2 задача №11.

Ученики вспоминают свойства равнобедренного треугольника, теоремы синусов и косинусов и, используя данные находят необходимую сторону.

Задачи посложнее:

12.      В треугольнике ABC известно, что DE - средняя линия. Площадь треугольника CDE равна 9. Найдите площадь треугольника ABC.

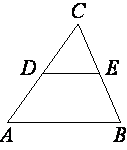
Рис. 2.10

Решение см. приложение 2 задача №12.

Учитель напоминает школьникам, что такое средняя линия треугольника и теорему о средней линии:

Средняя линия треугольника - отрезок, соединяющий середины двух его сторон.

Теорема о средней линии треугольника.

Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.

Учитель направляет учеников, на то, что нужно провести высоту, и вспомнить, что средняя линия делит высоту пополам.

13.      Через середину K медианы BM треугольника ABC и вершину A проведена прямая, пересекающая сторону BC в точке P. Найдите отношение площади треугольника ABC к площади четырёхугольника KPCM.

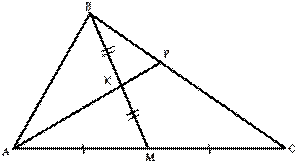
Рис. 2.11

Решение см. приложение 2 задача №13.

Учитель осуществляет вместе с учащимися поиск решения задачи, а именно, что нужно пользоваться свойством медианы (треугольники, делящиеся медианой равны и равны половине площади данного треугольника). Обратить внимание девятиклассников, что точка К - середина ВМ, следовательно, АК - медиана треугольника АВМ, что нужно провести медиану и для треугольника ВСМ, провести можно еще среднюю линию для треугольника АРС, и так разбирая средние линии треугольников, делаем вывод, что площадь маленького треугольника равна четверти площади данного треугольника. Далее разбирается все вместе с учителем.

14.      Найдите острые углы прямоугольного треугольника, если его гипотенуза равна 16, а площадь равна 32√3.

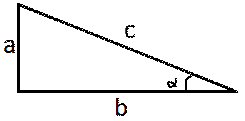
Рис. 2.12

Решение см. приложение 2 задача №14.

Школьники сначала должны выразить одну сторону через другую, зная площадь. Далее учитель направляет на поиск решения задачи, в частности, что можно, использовав теорему Пифагора и решив квадратное уравнение, найти одну сторону. Затем ученики вспоминают определение косинуса, так как надо найти углы, это пригодится. И результат получают с помощью теоремы о сумме углов треугольника.

15.      Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC относится к длине стороны AB как 9:7. Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.

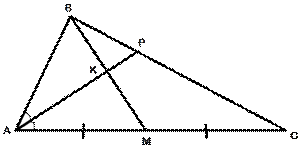
Рис. 2.13

Решение см. приложение 2 задача №15.

Задача непростая, требует долгого рассуждения. Поэтому лучше начать решать задачу в начале урока после повторенного материала. Учитель вместе с учениками осуществляет поиск решения этой задачи вместе.

Рекомендации для учителя: При повторении этой темы необходимо обратить внимание на формулу вычисления площади, так как учащиеся путают ее с формулой нахождения площади параллелограмма и какие стороны известны и какие необходимы для вычисления площади. Вспомнить с учащимися, что катет, лежащий против угла в 30° равен половине гипотенузы.

Занятие 2.

Тема: Параллелограмм. Площадь параллелограмма.

Цели: Обучающие: Повторить, обобщить и систематизировать полученные знания по темам: «Параллелограмм», «Признаки параллелограмма», «Площадь параллелограмма», повторить формулы нахождения их периметра и площади. Воспитательные: воспитание внимательности, трудолюбия, интереса к предмету, умение слушать других и высказывать свою точку зрения.

Развивающие: развить у учащихся логическое мышление, сообразительность, внимание и культуру математической речи.

Ход занятия

Организационный момент.

Приветствие.

Вспоминаем определение параллелограмма:

Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.

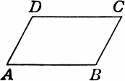
Рис. 2.14

AB||CD, BC||AD

Свойства параллелограмма:

) Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.

) В параллелограмме противоположные стороны равны и противоположные углы равны.

) Диагонали параллелограмма точкой пересечения делятся пополам.

Рис. 2.15

Признаки параллелограмма:

Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник - параллелограмм.

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник - параллелограмм.

Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник - параллелограмм. Площадь параллелограмма.

Площадь параллелограмма равна произведению его основания на высоту.

Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними.

Площадь параллелограмма равна половине произведения длин его диагоналей на синус угла между ними.

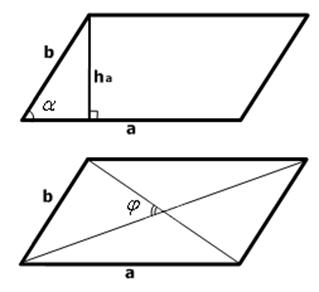
Рис. 2.16

Решение задач.

Приступаем к решению задач.

1.        Найдите площадь параллелограмма, изображённого на рисунке.

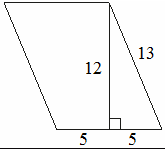
Рис. 2.17

Решение см. приложение 2 задача №16.

На этот тип задач много времени отводить не нужно, так как он больше для закрепления формулы площади.

2.        На клетчатой бумаге с размером клетки 1×1 изображён параллелограмм. Найдите его площадь.

Рис. 2.18

Решение см. приложение 2 задача №17.

Данный тип задач стоит решать побольше для того, чтобы учащиеся могли найти площадь параллелограмма, несмотря на то, как он будет повернут.

3.        Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=2 и HD=64. Диагональ параллелограмма BD равна 80. Найдите площадь параллелограмма.

Рис. 2.19

Решение см. приложение 2 задача № 18.

Обратить внимание учащихся, что внутри параллелограмма прямоугольный треугольник, и тогда школьники должны догадаться, что высоту параллелограмма можно найти как катет треугольника по теореме Пифагора. А площадь найти уже не составит труда.

Задачи посложнее:

4.        В параллелограмме ABCD диагонали AC и BD пересекаются в точке К. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.

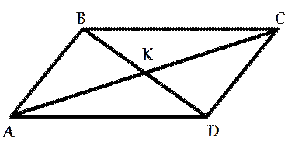
Рис. 2.20

Решение см. приложение 2 задача №19.

Учитель повторяет перед решением задачи признаки равенства треугольников. Далее он вместе с учениками обговаривает решение вместе последовательно.

5.        В параллелограмме ABCD проведена диагональ AC. Точка O является центром окружности, вписанной в треугольник ABC. Расстояния от точки O до точки A и прямых AD и AC соответственно равны 25, 8 и 7. Найдите площадь параллелограмма ABCD.

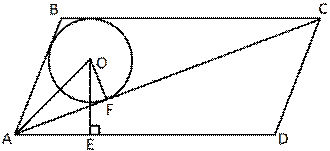
Рис. 2.21

Решение см. приложение 2 задача №20.

Учитель задает наводящие вопросы, и они вместе приходят к выводу, что АС - касательная. Тогда можно использовать свойство касательной, что ученики и делают, затем используют теорему Пифагора, свойства параллелограмма, признак равенства треугольников.

6.        Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=2, а расстояние от точки K до стороны AB равно 1.

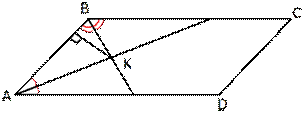
Рис. 2.22

Решение см. приложение 2 задача №21.

Вспомнить с учениками, какие углы равные есть у параллелограмма (накрестлежащие, соответственные, вертикальные). Желательно сопровождать решение задачи презентацией с последовательным дополнением к чертежу.

7.        Внутри параллелограмма ABCD выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади параллелограмма.

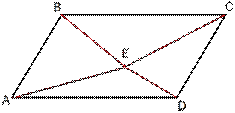
Рис. 2.23

Решение см. приложение 2 задача №22.

Учитель направляет учащихся на поиск решения задач, а именно, предлагает провести отрезок, перпендикулярный основаниям, далее рассмотреть треугольники.

8.        Теоретическая самостоятельная работа. Проверка усваивания теоретических знаний. Задание:

Выберите верные утверждения:

a.        Вокруг любого параллелограмма можно описать окружность.

b.       Любой параллелограмм можно вписать в окружность..     В параллелограмме есть два равных угла..         Площадь любого параллелограмма равна произведению длин его сторон..      Диагональ параллелограмма делит его на два равных треугольника.

f.         Площадь параллелограмма равна половине произведения его диагоналей.

Ответ: с(свойство), e(третий признак равенства треугольников).

Рекомендации для учителя: При изучении данной темы необходимо обратить внимание учащихся на возможность использования различных фигур, например, если известны диагональ и основание, то высоту можно узнать из прямоугольного треугольника, расположенного внутри параллелограмма, как катет.

Цели:

Занятие 3.

Тема: Ромб. Площадь ромба.

Обучающие: Повторить, обобщить и систематизировать полученные знания по темам: «Ромб», повторить формулы нахождения их периметра и площади.

Воспитательные: развитие навыков коммуникативного общения и диалоговой деятельности, воспитание внимательности, интереса к предмету.

Развивающие: развить у учащихся логическое мышление, сообразительность, внимание и культуру математической речи.

Ход занятия:

Организационный момент.

Приветствие. Ознакомление учащихся с ходом работы на уроке:

Заранее предложено было ученикам повторить определение, свойства и признаки ромба. Поэтому урок начинается с задания: «Найдите ошибку».

Выполнение задания - проверка знаний учащихся по теоретическому материалу.

1.        Найдите ошибку в предложенных утверждениях и аргументируйте свой ответ.

2.       Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник - ромб.

3.       Диагонали ромба точкой пересечения делятся пополам.

4.       Ромб не является параллелограммом.

5.       Диагонали ромба равны.

6.       Если диагонали параллелограмма равны, то этот параллелограмм является ромбом.

7.       Все углы ромба равны.

8.       Диагонали ромба перпендикулярны.

9.       В любой ромб можно вписать окружность.

10.     Площадь ромба равна произведению двух его смежных сторон на синус угла между ними.

11.      Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

12.      Если диагонали параллелограмма перпендикулярны, то этот параллелограмм является ромбом.

13.      Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.

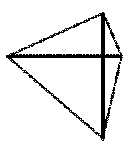
Рис. 2.24

Ответ:

1.        В данном утверждении ошибка.

Потому что не соответствует свойству ромба (Диагонали ромба взаимно перпендикулярны и делят его углы пополам). Можно привести пример, когда диагонали перпендикулярны, но это явно не ромб. Вот, например, четырехугольник, изображенный на рисунке.

2.        Так как это утверждение является свойством параллелограмма, а, по определению, ромб и есть параллелограмм (параллелограмм, у которого все стороны равны, называется ромбом), то это утверждение верно.

3.        Ошибка.

Так как противоречит определению ромба.

4.        Ошибка.

Противоречит свойствам ромба и параллелограмма.

5.        Ошибка.

Это признак прямоугольника, а не ромба.

6.        Ошибка.

Ромб - частный случай параллелограмма и обладает всеми его свойствами. Поэтому, по свойству параллелограмма: сумма углов параллелограмма, прилежащих к одной стороне, равна 180°, нельзя сделать вывода, что углы равны.

7.        Верное утверждение по признаку ромба.

8.       Верное утверждение по теореме: в любой правильный многоугольник можно вписать окружность, - а ромб - правильный четырехугольник.

9. Верно.

10. Верно.

11.      Верно по признаку ромба.

12.     Верно по свойству параллелограмма, противоположные стороны попарно равны. А раз смежные стороны равны, то и противоположные им стороны так же равны. Таким образом, все четыре стороны такого параллелограмма равны. А это и есть определение ромба. Окончательный ответ: неверны: 1, 3, 4, 5, 6

3. Решение задач.

Прежде чем перейдем к решению задач вспомним формулы для нахождения площади ромба.

Площадь ромба равна произведению стороны ромба и его высоты.

Площадь ромба равна произведению квадрата его стороны на синус угла.

Площадь ромба равна половине произведения его диагоналей.

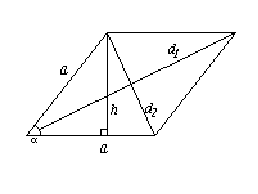
Рис. 2.25

Задачи:

1.        Найдите площадь ромба, если его диагонали равны 20 и 6.

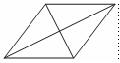
Рис. 2.26

Решение см. приложение 2 задача №23.

На задачу не нужно отводить много времени. Ее необходимо решить для закрепления формулы.

2.        Периметр ромба равен 56, а один из углов равен 30°.Найдите площадь этого ромба.

Решение см. приложение 2 задача №24.

Обратить внимание, что дан периметр, и зная, что у ромба все стороны равны, легко можно найти и сторону ромба.

3.        Высота BH ромба ABCD делит его сторону AD на отрезки AH=44 и HD=11. Найдите площадь ромба.

Рис. 2.27

Решение см. приложение 2 задача №25.

Обратить внимание школьников на треугольник ABH, и что из него можно найти катет BH, который для ромба является высотой.

4.        Площадь ромба равна 15, а периметр равен 20. Найдите высоту ромба.

Решение см. приложение 2 задача №26.

Обратить внимание учащихся, что, зная периметр ромба, можно узнать его сторону.

5.        Сторона ромба равна 74, а диагональ равна 48. Найдите площадь ромба.

Решение см. приложение 2 задача №27.

Учитель направляет учащихся найти вторую сторону с помощью теоремы Пифагора.

Задачи посложнее:

6.        Сторона ромба равна 9, а расстояние от центра ромба до неё равно.

1.       Найдите площадь ромба.

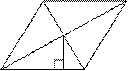
Рис. 2.28

Решение см. приложение 2 задача №28.

Учитель может предложить учащимся продлить высоту до второго основания, доказать равенство треугольников DOE и BOF, тогда высота ромба будет равна двум расстояниям от центра ромба до его стороны.

. Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и параллелограмма, если отношение диагоналей параллелограмма равно 36.

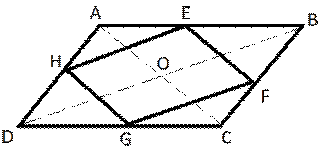
Рис. 2.29

Решение см. приложение 2 задача №29.

Вместе с учащимися учитель последовательно решают задачу, проговаривая все действия. При этом заранее повторяются свойства параллелограмма, формулы вычисления его площади, признаки подобия треугольников.

Рекомендации для учителя: Обратить внимание учащихся, что у ромба все стороны равны, потому что они на это не акцентируют внимания при решении задач.

Цели:

Занятие 4.

Тема: Прямоугольник. Квадрат . Их площадь.

Обучающие: Повторить, обобщить и систематизировать полученные знания по темам: «Прямоугольник, квадрат», «Площадь квадрата», «Площадь прямоугольника», повторить формулы нахождения их периметра и площади.

Воспитательные: воспитание внимательности, трудолюбия, интереса к предмету, умение слушать других и высказывать свою точку зрения.

Развивающие: развить у учащихся логическое мышление, сообразительность, внимание и культуру математической речи.

Ход занятия.

1. Организационный момент.

Приветствие.

2. Этап повторения.

Параллелограмм, у которого все углы прямые, называется прямоугольником.

Прямоугольник является частным случаем параллелограмма, поэтому он обладает всеми его свойствами. В частности, в прямоугольнике противоположные стороны попарно равны и диагонали в точке пересечения делятся пополам.

Признаки прямоугольника:

1)        Если в параллелограмме диагонали равны, то этот параллелограмм является прямоугольником.

2)       Если в параллелограмме один угол прямой, то этот параллелограмм - прямоугольник.

3)        Если в четырехугольнике три угла прямые, то этот четырехугольник - прямоугольник.

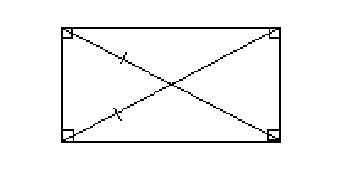
Рис. 2.30

Прямоугольник, у которого все стороны равны, называется квадратом.

Можно сказать, что квадратом является ромб, у которого все углы прямые. Квадрат обладает всеми свойствами прямоугольника и ромба.

Площадь прямоугольника и квадрата.

Площадь прямоугольника равна произведению его смежных сторон.

Площадь квадрата также равна произведению его смежных сторон, а так как стороны у квадрата равны, то формула имеет такой вид:

Площадь прямоугольника равна половине квадрата длины его диагонали на синус угла между диагоналями.

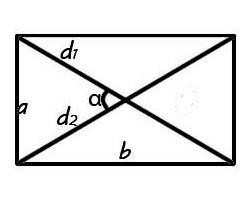
Рис. 2.31

Площадь квадрата равна половине квадрата длины его диагонали.

3. Решение задач.

1.        Площадь прямоугольного земельного участка равна 20 га, ширина участка равна 200 м. Найдите длину этого участка в метрах.

Решение см. приложение 2 задача №30.

Учитель задает наводящие вопросы: сколько в гектаре квадратных метров. Далее задача решается с использованием формулы площади.

2.        Пол комнаты, имеющей форму прямоугольника со сторонами 7 м и 8 м, требуется покрыть паркетом из прямоугольных дощечек со сторонами 10 см и 40 см. Сколько потребуется таких дощечек?

Решение см. приложение 2 задача №31.

Осуществляют поиск решения задачи, а именно, найти площадь одной дощечки, и площадь комнаты разделить на площадь одной дощечки.

3.        Аналогичная задача:

Сколько потребуется кафельных плиток квадратной формы со стороной 20 см, чтобы облицевать ими стену, имеющую форму прямоугольника со сторонами 3,4 м и 3,8 м?

4.        Из квадрата вырезали прямоугольник (см. рисунок). Найдите площадь получившейся фигуры.

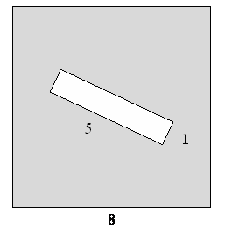
Рис. 2.32

Решение см. приложение 2 задача №32.

Обратить внимание учащихся, что площадь оставшейся фигуры - это площадь квадрата без площади прямоугольника.

5.        Картинка имеет форму прямоугольника со сторонами 14 см и 27 см. Её наклеили на белую бумагу так, что вокруг картинки получилась белая окантовка одинаковой ширины. Площадь, которую занимает картинка с окантовкой, равна 558 см2. Какова ширина окантовки? Ответ дайте в сантиметрах.

Рис. 2.33

Решение см. приложение 2 задача №33.

Обратить внимание школьников, что окантовка с двух сторон от картинки.

6.        В прямоугольнике одна сторона равна 4, а диагональ равна 5. Найдите площадь прямоугольника.

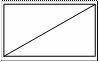
Рис. 2.34

Решение см. приложение 2 задача №34.

Обратить внимание учащихся, что прямоугольник делится на два прямоугольных треугольника.

7.        Найдите площадь квадрата, описанного около окружности радиуса 19.

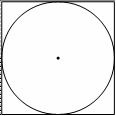
Рис. 2.35

Решение см. приложение 2 задача №35.

Продемонстрировать учащимся, что сторона квадрата равна диаметру окружности.

8.        Периметр квадрата равен 36. Найдите площадь этого квадрата.

Рис. 2.36

Решение см. приложение 2 задача №36.

Напомнить детям, что у квадрата стороны равны, и это поможет найти сторону квадрата, зная периметр.

4. Теоретическая самостоятельная работа. Проверка усваивания теоретических знаний. Задание:

Выбрать верные утверждения:

1)        Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм - квадрат.

2)       Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.

3)       Существует квадрат, который не является прямоугольником.

4)       Диагонали любого прямоугольника равны.

5)        Сумма квадратов диагоналей прямоугольника равна сумме квадратов всех его сторон.

6)        Если в ромбе один из углов равен 90°, то такой ромб - квадрат.

7)       Любой квадрат можно вписать в окружность.

8)       Любой прямоугольник можно вписать в окружность.

9)       В любом прямоугольнике диагонали взаимно перпендикулярны.

10)     Площадь квадрата равна произведению его диагоналей.

11)     В любом прямоугольнике диагонали взаимно перпендикулярны.

12)      Диагонали любого прямоугольника делят его на 4 равных треугольника.

13)      Квадрат является прямоугольником

14)     Любой квадрат является ромбом.

15)      Существует прямоугольник, который не является параллелограммом.

16)      Существует ромб, который не является квадратом.

17)     Диагонали квадрата точкой пересечения делятся пополам.

18)       Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм является квадратом.

19)      Все квадраты имеют равные площади.

20)     Площадь квадрата равна произведению двух его смежных сторон.

21)     Площадь прямоугольника равна произведению длин его смежных сторон.

Ответ: 1 (свойство), 2 (теорема Пифагора), 4 (свойство), 5 (теорема Пифагора), 6 (ромб - частный случай параллелограмма, то к нему и применимы все свойства параллелограмма, следовательно (по свойству параллелограмма), противоположный прямому углу, угол тоже равен 90°. Другие два угла по тому же свойству равны друг другу. Сумма углов многоугольника вычисляется по формуле (n-2)*180°, где n - количество углов. В нашем случае, углов - 4. Тогда сумма углов равна (4- 2)*180°=360°. Тогда получается, что сумма двух неизвестных углов равна 360°- 90°-90°=180°. А так как они равны друг другу, то каждый из них равен 180°/2=90°. Т.е. мы узнали, что все четыре угла равны по 90°), 7 (теорема о правильных многоугольниках вписанных в окружность), 8 (в любом вписанном четырехугольнике сумма противоположных углов равна 180°), 13 (определение), 16 (при значениях отличных от 90), 18 (свойство квадрата), 20 (S = a2), 21(S=ab).

Рекомендации для учителя: обратить внимание на практическую направленность при решении задач в бытовых условиях, организовать визуальное представление задачи (с паркетами, окантовкой картины).

Занятие 5.

Тема: Трапеция. Площадь трапеции.

Цели:

Обучающие: Повторить, обобщить и систематизировать полученные знания по темам: «Трапеция», «Площадь трапеции», повторить формулы нахождения их периметра и площади.

Воспитательные: развитие навыков коммуникативного общения и диалоговой деятельности, воспитание внимательности, интереса к предмету.

Развивающие: развить у учащихся логическое мышление, сообразительность, внимание и культуру математической речи.

Ход занятия

1.        Организационный момент.

Приветствие. Ознакомление учащихся с ходом работы на уроке:

Заранее предложено было ученикам повторить определение, свойства и признаки ромба. Поэтому урок начинается с задания: «Выберите верное утверждение».

2.        Выполнения задания - проверка знаний учащихся по теоретическому материалу.

1)        Площадь трапеции равна произведению средней линии на высоту.

2)       Диагональ трапеции делит её на два равных треугольника.

3)       У любой трапеции боковые стороны равны.

4)       У любой трапеции основания параллельны.

5)       Средняя линия трапеции равна сумме её оснований.

6)       Диагонали трапеции пересекаются и делятся точкой пересечения пополам.

7)       В любой прямоугольной трапеции есть два равных угла.

8)       Основания равнобедренной трапеции равны.

9)       Диагонали прямоугольной трапеции равны.

10)     Площадь трапеции равна произведению основания трапеции на высоту.

11)     Средняя линия трапеции параллельна её основаниям.

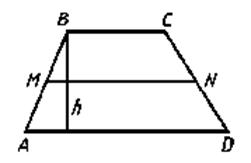
Рис. 2.37

Ответ:

1)        Верно, где - средняя линия трапеции.

2)        Во-первых, нет такого свойства трапеции. Во- вторых, если рассмотреть прямоугольную трапецию с проведенной диагональю, то становится очевидным, что один из получившихся треугольников - прямоугольный, а второй - нет. Следовательно, это утверждение неверно.

3)       Неверно. Боковые стороны равны только у равнобокой трапеции. Верно по определению трапеции (трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны). Неверно. Средняя линия трапеции равна полусумме ее оснований.

Рис. 2.38

4)        Неверно. Это свойство параллелограмма.

5)       Верно. Углы равны по 90°. См. рисунок.

Рис. 2.39

6)        Неверно. У равнобедренной трапеции равны боковые стороны.

Рис. 2.40

7)        Неверно. Только диагонали равнобокой трапеции равны, но равнобокая трапеция не может быть прямоугольной, а прямоугольная трапеция не может быть равнобокой.

8)       Неверно. Такой формулы вычисления площади трапеции нет.

9)       Верно. По теореме о средней линии трапеции: средняя линия трапеции параллельна основаниям и равна их полусумме.

Окончательный ответ: 1, 4, 7, 11.

3.        Решение задач.

Прежде чем перейдем к решению задач вспомним формулы для нахождения площади трапеции.

Площадь трапеции равна произведению полусуммы оснований на высоту.

Площадь равна произведению средней линии на высоту.

Рис. 2.41

Площадь трапеции равна половине произведения ее диагоналей на синус угла между ними.

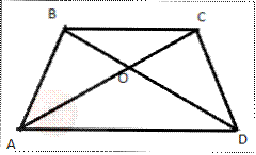
Рис. 2.42

Задачи:

1.        Найдите площадь трапеции, изображённой на рисунке.

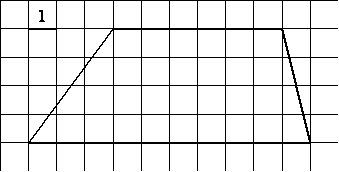
Рис. 2.43

Решение см. приложение 2 задача № 37.

Данный тип задач следует решить несколько раз, применяя различный поворот трапеции, чтобы учащиеся могли различить трапецию и в ином виде.

2.        Найдите площадь трапеции, изображённой на рисунке.

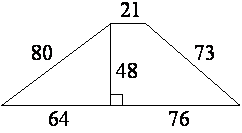
Рис. 2.44

Решение см. приложение 2 задача №38.

На этот тип задач много времени отводить необязательно, так как он просто на применение формулы площади.

3.        Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.

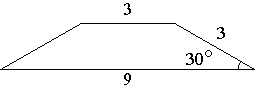
Рис. 2.45

Решение см. приложение 2 задача №39.

Обратить внимание учащихся, что можно провести высоту, и тогда получится прямоугольный треугольник с углом в 30 градусов. Далее учащимся можно напомнить, что катет, лежащий напротив угла в 30 градусов равен половине гипотенузы.

4.        Основания равнобедренной трапеции равны 5 и 17, а её боковые стороны равны 10. Найдите площадь трапеции.

Решение см. приложение 2 задача №40.

Ученики вместе с учителем осуществляют поиск решения задачи, а именно проведут две высоты и покажут, что кусочки по бокам равны. И, используя теорему Пифагора, находят высоту.

5.        В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь этой трапеции.

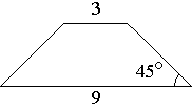
Рис. 2.46

Решение см. приложение 2 задача № 41.

Повторить с учениками теорему о сумме углов треугольника, свойства равнобедренного треугольника, признаки равенства треугольников, и вместе с ними подробно разобрать эту задачу.

6.        В трапеции ABCD известно, что AD=6, BC=2, а её площадь равна. Найдите площадь трапеции BCNM, где MN - средняя линия трапеции ABCD.

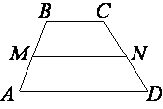
Рис. 2.47

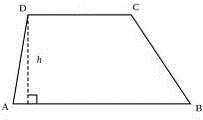
Рис. 2.48

Решение см. приложение 2 задача № 43.

Напоминает, что сумма соседних углов при боковых сторонах трапеции равна 180 градусам, определение синуса угла (синус угла А равен отношению противолежащей стороны на гипотенузу), где противолежащая сторона - высота, которую надо найти, чтобы вычислить площадь трапеции.

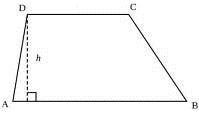
Рис. 2.49

Решение см. приложение 2 задача №44.

Последовательно решают задачу, рассуждая все вместе (можно без помощи учителя).=120° - 90° = 30°

Задачи посложнее:

7.        В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.

Рис. 2.50

Решение см. приложение 2 задача №45.

Обращает внимание, что высоту можно найти через формулу площади трапеции, и высота трапеции равна высоте треугольника

8.        В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.

Рис. 2.51

Решение см. приложение 2 задача № 46.

Учитель рассуждает вместе со школьниками, что нужно провести две высоты, далее рассмотреть треугольник с известным углом. Учитель напоминает теорему о сумме углов треугольника, определение синуса угла, определение прямоугольника, признаки равенства треугольников, определение равнобедренной трапеции, теорему Пифагора. Тогда учащиеся, пользуясь подсказками учителя, решает задачу.

9.        Площадь параллелограмма ABCD равна 56. Точка E - середина стороны CD. Найдите площадь трапеции AECB.

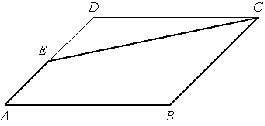
Рис. 2.52

Решение см. приложение 2 задача №47.

Можно дать данную задачу для рассуждения, так как есть несколько вариантов решение. Если задача пойдет тяжело, дать подсказку, что параллелограмм можно разделить на четыре равных треугольника, и отрезок EC будет стороной двух таких треугольников.

10.       На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку F. Докажите, что сумма площадей треугольников BFC и AFD равна половине площади трапеции.

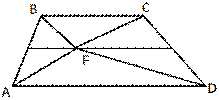
Рис. 2.53

Решение см. приложение 2 задача № 48.

Учитель направляет школьников: предлагает провести высоту через точку F. Далее учащимся задает наводящие вопросы для того, чтобы подвести их к тому, чтобы они представили сумму площадей этих треугольников и сравнили ее с площадью трапеции.

4. Самостоятельная работа.

Необходимо поставить знак «+», где утверждение верно для данной фигуры. Свойства четырехугольников

Таблица 3

Рекомендации для учителя: Обратить внимание на задачи, где изображена трапеция на клетчатой бумаге. Учащиеся часто не видят, какая именно фигура изображена, особенно, если она повёрнута не в том виде, который они привыкли видеть.

Если даны углы у трапеции, обратить внимание, что если провести высоту, то внутри трапеции будет расположен прямоугольный треугольник.

Больше решать сложные задачи, так как в основном с трапецией связаны задачи уровня посложнее. В классе всегда есть ученики, которые быстро будут решать предложенные задачи. Поэтому более сильным учащимся можно дать дополнительные задания в виде вывода различных формул фигур (см. приложение 3).

.3 Результаты опытно-экспериментальной работы

Экспериментальная проверка была проведена в школе №2123 им. М. Эрнандеса в 9 классе.

Было проведено несколько занятий, которые включали в себя: самостоятельную работу для выявления остаточных знаний с 8 класса, уроки повторения, на которых мы с учащимися вспоминали теорию: свойства многоугольников и формулы их площадей, решали задачи и ликвидировали трудности, возникшие при их решении, и контрольную работу.

Рассмотрим подробнее:

В экспериментальном классе участвовало 19 человек. Самостоятельная работа, которую писали 17 человек:

Вариант 1.

№1. Укажите номера верных утверждений.

1.       В тупоугольном треугольнике все углы тупые.

2.       В любом параллелограмме диагонали точкой пересечения делятся пополам.

.         Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.

№2. Найдите площадь треугольника, изображённого на рисунке.

Рис. 2.54

№3. На клетчатой бумаге с размером клетки 1×1 изображёна трапеция. Найдите ее площадь.

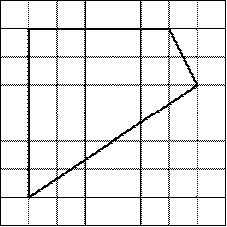
Рис. 2.55

№4. Боковая сторона трапеции равна 3, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если ее основания равны 2 и 6.

Вариант 2.

№1. Какие из данных утверждений верны? Запишите их номера.

1.   Каждая из биссектрис равнобедренного треугольника является его медианой.

2.       Диагонали прямоугольника равны.

.         У любой трапеции боковые стороны равны.

№2. Найдите площадь параллелограмма, изображённого на рисунке.

Рис. 2.56

№3. .На клетчатой бумаге с размером клетки 1×1 изображёна трапеция. Найдите ее площадь.

Рис. 2.57

№4. Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 5

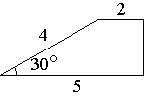
Рис. 2.58

Рис. 2.59

Проанализировав работы, мы получила такие результаты:

Таблица 4

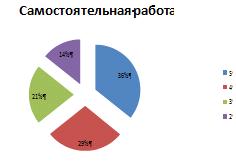
Рис. 2.60

Как видно из диаграммы на данном этапе, у учащихся хорошие знания, они многое помнят, но все же ближе к среднему.

Анализ работ показал, что наиболее сложным оказалось задание №4.

Остальные задания не вызывали особых затруднений.

Далее были проведены занятия, на которых мы разбирали теорию и решали задачи. Контрольное (закрепляющее) занятие с использованием презентации (см. приложение №4).

Контрольная работа:

Вариант 1.

№1. Укажите номера верных утверждений.

1)     Существует квадрат, который не является прямоугольником.

2)         Если два угла треугольника равны, то равны и противолежащие им стороны.

3)     Внутренние накрест лежащие углы, образованные двумя параллельными прямыми и секущей, равны.

№2. Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.

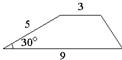
Рис. 2.61

№3. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH=8 и HD=40. Диагональ параллелограмма BD равна 50. Найдите площадь параллелограмма.

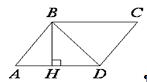
Рис. 2.62

№4. В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.

Рис. 2.63

№5. Площадь параллелограмма ABCD равна 56. Точка E - середина стороны CD. Найдите площадь трапеции AECB.

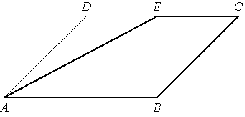
Рис. 2.64

Вариант 2.

№1. Какие из данных утверждений верны?

1)         Каждая из биссектрис равнобедренного треугольника является его высотой.

2)       Диагонали прямоугольника равны.

3)       У любой трапеции основания параллельны.

№2. В равнобедренной трапеции основания равны 3 и 5, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.

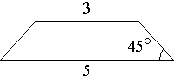
Рис. 2.65

№3. Периметр ромба равен 116, а один из углов равен 30∘. Найдите площадь ромба.

№4. Боковая сторона трапеции равна 4, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 2 и 7.

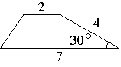
Рис. 2.66

№4. Площадь параллелограмма ABCD равна 176. Точка E - середина стороны AD. Найдите площадь трапеции AECB.

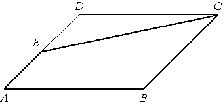
Рис. 2.67

Сначала расскажу о трудностях, возникших у учащихся при написании работы.

№1. Трудностей не возникло у большинства учащихся.

№2,4 В основном возникали сложности во втором варианте (трапеция с углом в 45 градусов). Трудности состояли в последовательности логических рассуждений, но и элементарные ошибки присутствовали: в вычислениях.

№3 (первого варианта). Особых трудностей не возникло у учащихся, но были такие, кто не приступил к выполнению данного номера.

№4 (второго варианта). Очень много учащихся даже не брались за эту задачу, они просто не стали рассуждать.

№5. Эту задачу или решали правильно учащиеся, или не решали вовсе, просто не брались или были единицы, которые придумывали «а вдруг правильно». А один школьник даже сделал предположение, что АЕ - средняя линия.

При выполнении работы присутствовали и те учащиеся, которых, к сожалению, не было на предыдущих занятиях.

Проанализировав работы, я получила такие результаты:

Результаты самостоятельной работы

Таблица 5

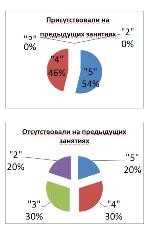
Рис. 2.68

Из диаграмм видно, что учащимся, которых не было на уроках - повторениях работа дается тяжелее, чем тем, кто присутствовал. И результаты их были похуже.

В итоге можно сказать, что изначально учащиеся подзабыли некоторый материал и есть пробелы. Поэтому повторение было им полезно. Были и такие ученики, которые даже не хотели думать и рассуждать, но большинство школьников очень стараются и решают задачу пока не дойдут до окончательного ответа.

Полученные в результате экспериментальной проверки данные позволили судить об эффективности применения повторения в 9 классе. Несмотря на то, что сроки проведения проверки были ограничены, а исследуемая проблема требует более длительного изучения, мы смогли получить необходимые данные, подтверждающие гипотезу о том, что если в 9 классе повторить изученные в 8 классе темы, то это повысит эффективность обучения математике и положительно повлияет на результаты их экзамена.

В этой главе мы представили разработанный нами курс по выбору «Площади многоугольников» в 9 классе, составили тематическое планирование курса, отметили методические особенности повторения данной темы, сделали разработки занятий, методические рекомендации к их проведению. Также подробно описали проведение опытно-экспериментальной работы и результаты её проведения.

Заключение

Прочное усвоение знаний является главной задачей процесса обучения, это очень сложный процесс. В него входят восприятие учебного материала, его запоминание и осмысление, а также возможность использования этих знаний в различных задачах.

Сформулируем основные выводы и полученные результаты проведенного исследования.

1.        На основе изученной литературы выделены психолого- педагогические особенности обучающихся в подростковом возрасте.

2.       Разработаны содержание и методика проведения курса по выбору по теме «Площади многоугольников» для 9 классов.

3.       Провели проверку эффективности разработанной методики.

4.       Доказали, что разработанная методика позволяет добиться от большинства обучающихся хорошего понимания материала, обеспечивает усвоение теоретического материала и применения его при решении задач.

5.       Выявили, что необходимость повторения темы «Площадь». Обосновали, что повторение предоставляет учащимся большую возможность сдать экзамен на высший балл. Обобщающие уроки являются итогом большой работы учащихся по повторению, оказывают им большую практическую помощь в подготовке к экзаменам. Недаром говорят: «Повторение - мать учения».

Подводя итог исследованию, можно сделать вывод, что повторение данной темы необходимо для закрепления материала и успешной сдачи ОГЭ.

Это дает основание полагать, что задачи, поставленные во введении, полностью решены.

Список литературы

1.                 Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия 7-9. Учебник для общеобразовательных учреждений.- М.: Просвещение, 2002. - 240с.

2.       Аракелян О.А. Некоторые вопросы повторения математики в средней школе. - М.: Учпедгиз, 1960. - 84с.

3.       Атанасян Л.С., Базылев В.Т. Геометрия. Для студентов педагогических институтов. - М.: Просвещение, 1987.

4.       Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И.: Геометрия 7-9. учебник для общеобразовательных учреждений.- М.: Просвещение, 2000. - 335с.

5.       Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А., Некрасов В.Б., Юдина И.И. Изучение геометрии в 7,8,9 классах: Метод. рекомендации к учеб. :Кн. Для учителя. - М.: Просвещение, 2003. - 255с.

6.       Бевз Г.П., Бевз В.Г., Владимирова Н.Г. Геометрия 7-11. Учебник для общеобразовательных учреждений. - М.: Просвещение, 1996. - 351с.

7.       Березина Л.Ю., Мельникова И. Б. Геометрия в 7-9 классах - М., 1990.

8.       Березин В.Н. и др. Сборник задач для факультативных и внеклассных занятий по математике: книга для учителя. - М.: Просвещение, 1985. - 175с.

9.       Библиотека учителя математики. Преподавание геометрии в 6-8 классах. Сборник статей / Составитель Гусев В.А. - М.: Просвещение, 1979. - 281с.

10.               Блок А.Я. Методика преподавания в школе. - М.: Просвещение, 1987.

11.               Бутурлакина Т.Ю. Методическое пособие по созданию современного урока по ФГОС. - г. Армавир, 2013 - 60с.

12.               Воропаева Р.Н. Методические советы из опыта преподавания // Математика, 2001, №35, с. 25-28.

13.               Выготский Л.С. Педагогическая психология /Под ред.В.В. Давыдова - М.: АСТ Астрель Хранитель, 2008 - 671 с.

14.               Гильберт Д. Основания геометрии. - М. - Л.: Гостехиздат, 1948. - 491с.

15.     Глейзер Г.И. История математики в школе. Пособие для учителей. М.: Просвещение, 1964. - 376с.

16.               Гусев В.А. Психолого-педагогические основы обучения математике. - М.: Вербум-М, Академия, 2003. - 360 с.

17.     Еникеева О.Б., Крупич В.И. Учить школьников учиться математике. - М., 1990.

18.     Ефимова А.И. Проблемы преподавания математики в школе. - С. - П., 1984.

19.     Жуковская Е.Н. Дидактические аспекты организации факультативов.

20.     Киселев А.И., Рыбкин Н.А. Геометрия: Планиметрия: 7-9 кл.: Учебник и задачник. - М.: Дрофа, 1995.

21.     Колмогоров А.Н. Математика в её историческом развитии. - М.: Наука, 1991. - 224с.

22.     Концепция профильного обучения на старшей ступени общего образования //Профильная школа. - 2003. - №1.

23.     Корешкова Т.А., Цукерман В.В. Многоугольники и их площадь в школьном курсе математики// Математика в школе, 2003, №9, с. 10-18.

24.     Крутецкий В.А. Психология математических способностей школьников / Под редакцией Н.И. Чуприковой. - М.: Издательство «Институт практической психологии»; Воронеж: Издательство НПО «МОДЭК», 1998. - 416 с.

25.               Крутецкий В.А., Лукин Н.С. Психология подростка. - М.: Просвещение, 1965. - 314с.

26.               Кучугурова Н.Д. Интенсивный курс общей методики преподавания математики. Учебное пособие / Н.Д. Кучугурова. - М.: МГУ, 2014. - 152с.

27.                 Кучугурова Н.Д. Курсы по выбору как средство формирования профессиональной компетентности будущих специалистов. Труды пятых Колмогоровских чтений. Ярославль: Изд-во ЯГПУ, 2007, 380 с., С.164 - 167.

28.               Кучугурова Н.Д. Организация и управление современным уроком. Современный урок: Сборник статей. - М.: МГУ, 2013. - 138с.. С. 30 -34.

29.     Леонтьев А.Н. Лекции по общей психологии. Учебное пособие. - М.: Смысл, 2000. - 509с.

30.     Макарова Н.Д. Площадь. Единицы площади// Математика, 2002, №10, с. 30-31.

31.     Математический энциклопедический словарь. - М. «Советская энциклопедия», 1988. - 847с.

32.     Перельман Я.И. Занимательная геометрия. Гос-ное изд-во технико- теоретической литературы. Москва - 1950. Ленинград. - 297с.

33.     Погорелов А.В. Геометрия 7-11. Учебник для общеобразовательных учреждений. - М.: Просвещение, 1999. - 383с.

34.     Прицнер Б.С. Площадь четырёхугольника// Математика в школе, 1989, №5, с. 21-22.

35.     Рохлин В.А. Площади и объём. Энциклопедия элементарной математики. - М.: Наука, 1966. - С. 7 - 89

36.     Рыбников К.А. История математики. - М.: МГУ, 1994. - 496с.

37.     Сефибеков С.Р. Внеклассная работа по математике: кн. Для учителя. - М.: Просвещение, 1988. - 79с.

38.     Смирнова И.М. Дипломная работа и магистерская диссертация: Учебное пособие. - М.: МГУ «Прометей», 2005. - 120 с.

39.     Смирнова И.М., Смирнов В.А. Геометрия 7-9: учебник для общеобразовательных учреждений.- М.: Мнемозина, 2007. - 376с.

40.     Ушинский К.Д. Избранные педагогические сочинения. // в 2 т. - Изд-во Педагогика, 1974. - Т. 1. Теоретические проблемы педагогики. - 584с.

41.     Хилько М.Е., Ткачёва М.С. Возрастная психология: краткий курс лекций. - М.: Издательство Юрайт, 2012. - 194с.

42.     Шевченко И. Н. Методы обучения математике // Минск. Высшая школа, 1977.

43.     Энциклопедический словарь юного математика для старшего и среднего школьного возраста. - М.: Педагогика, 1985. - 352с.

44.     Юшкевич А. П. История математики. - М., 1970. - 353с.

45.     Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования: приказ Министерства образования РФ от 09.03.2004 г. №1312 (ред. от 01.02.2012 № 74). - Режим доступа: Система Гарант.

46.     Об утверждении федерального государственного образовательного стандарта основного общего образования: приказ Минобрнауки России от 17.12.2010 г. № 1897 (в редакции приказов от 19.12.2014 г. №1644)

47.     Об утверждении федерального государственного образовательного стандарта среднего (полного) общего образования: приказ Минобрнауки России от 17.05.2012 г. № 413

48.     О методических рекомендациях по реализации элективных курсов: письмо департамента государственной политики в образовании (от 4 марта 2010 г. № 03-413) / Министерство образования и науки Российской Федерации.

Приложение 1

Различные формулы площадей многоугольников.

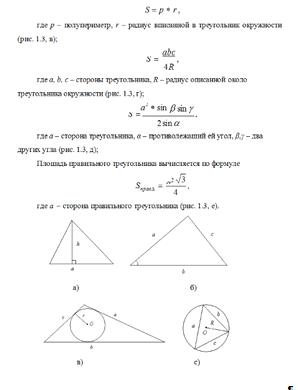
Приложение 2

Решение задач

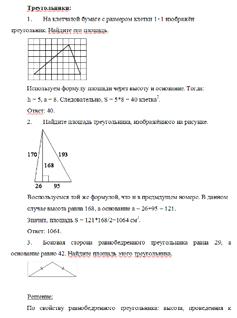
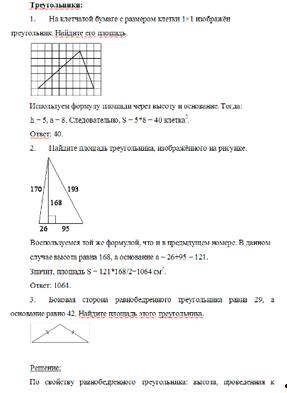
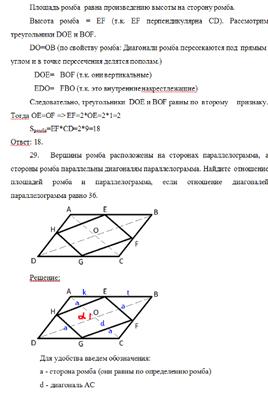
Приложение 3

Вывод формул площадей многоугольников.

Приложение 4

Тема: Подготовка к ОГЭ по теме «Площадь многоугольников», 9 класс.

Обучающие: Повторить, обобщить и систематизировать  полученные  знания по темам: «Треугольники», «Четырехугольники», «Площадь многоугольника».

Воспитательные: воспитание внимательности, интереса к предмету.

Развивающие: развить у учащихся логическое мышление, сообразительность,  внимание и культуру математической речи.

Оборудование:

Проект;

Раздаточный материал

Решение:

№1.

Площадь ромба можно найти по формуле: S=ab/2, где a и b - диагонали ромба.

Тогда: S=ab/2=39*2/2=39 Ответ: 39

№2.=AB*AC/2

Пусть угол, равный 45° будет угол В.

По теореме о сумме углов треугольника: 180°=   A+   B+ C

°=90°+45°+  C

C=45°

Следовательно, по свойству равнобедренного треугольника, треугольник ABC - равнобедренный.

Значит AB=AC.

По теореме Пифагора: BC2=AB2+AC2 BC2=AB2+AB2 702=2AB2

4900=2AB2 AB2=2450 SABC=AB*AC/2

SABC=AB2/2=2450/2=1225

Ответ: SABC=1225

№3. Р=4а а=29=а²= 841

№4.

Площадь ромба равна S=ah, где a - сторона ромба, h - высота ромба. AD=AH+HD=44+11=55.=AB=BC=CD (по определению ромба). Рассмотрим треугольник ABH.- прямоугольный (т.к. BH - высота), тогда по теореме Пифагора: AB2=BH2+AH2

=BH2+442

=BH2+1936 BH2=1089 BH=33ромба=AD*BH=55*33=1815 Ответ: Sромба=1815

№5.

Площадь трапеции равна h*(a+b)/2, где a и b - основания трапеции, h - высота трапеции. hтрапеции*(4+1)/2=35 (по условию задачи)=35/2,5=14

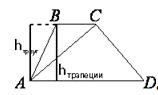
Проведем высоту треугольника ABC, как показано на рисунке. hтреугольника=hтрапеции, так как они обе перпендикулярны одним и тем же параллельным основаниям трапеции и  образуют прямоугольник.треугольника=hтреугольника*BC/2=14*1/2=7.

Ответ: Sтреугольника=7.