Задача страхователя
Введение
В рамках этой работы страхованием можно назвать определенный процесс
распределения риска между сторонами, для заключения обоюдовыгодной сделки.
Здесь страховая компания (далее страховщик) выступает в роли «покупателя» риска
и принимает ответственность по оплате потенциального ущерба клиента (далее
страхователь). Смысл этой сделки состоит в желании страхователя обезопасить
предмет страхования путем компенсации средств от страховщика при возникновении
страхового случая, оплачивая страховщику установленную сумму на определенный
период страхования. Со стороны страховщика ценность этой сделки состоит в
получении большого количества взносов и малой вероятности возникновения
страхового события, благодаря чему у страховщика будет возможность компенсировать
клиентам ущерб и покрыть свои собственные издержки. Условием совершения сделки
здесь выступает здесь выступает выгодность для обоих сторон. Решение о
принятии-непринятии сделки каждая сторона принимает, основываясь на своей
собственной системе предпочтений.
Риском здесь выступает, основываясь на математической теории страхования
потенциальный ущерб в денежном эквиваленте, являющийся случайной величиной. В
данной дипломной работе используется модель индивидуального риска, или так
называемая статическая модель. Это - базовая модель, играющая роль в построении
более массивных моделей с одной стороны, а с другой - наглядна для демонстрации
возможности математических методов в количественном анализе рисковых ситуаций,
возникающих в страховании.
Инструментами управления риском здесь являются выбор размера страховой
премии и функция дележа риска между страховщиком и страхователем. Функция
дележа определяет размер возмещения клиенту, который. в свою очередь, получает
скидку к своему страховому взносу. Эта функция оговорена в договоре и часть
риска, соответственно, переходит к клиенту.
В этой работе рассматриваются задачи минимизации издержек страхователя и
максимизацию полезности его финального капитала. Здесь функционалом полезности
является функционал экспоненциальной полезности, который зависит от показателя
неприятия риска с.
В литературе [1] показано, что с точки зрения страхователя оптимальной
формой страхования является безусловная франшиза. Цель франшизы - снижение
числа мелких страховых требований и, как следствие, снижение расходов страховой
компании. Широкое распространение этот тип страхования получил в схемах
автострахования и страхования недвижимости. В этой форме страхователь
оплачивает мелкий ущерб самостоятельно, а более крупный компенсируется страховой
компанией, основываясь на установленной функции дележа. Эту модель также можно
представить, как форму «stop-loss» дележа, где компания оплачивает
клиенту ущерб полностью, если значение ущерба не превосходит определенного
уровня k*. При значениях ущерба больше k* страховая компания выплачивает
только сумму k*. Такой тип дележа также называется
страхованием с верхним пределом. Здесь в виде страховой компании выступает сам
страхователь, оплачивающий самостоятельно мелкий ущерб и получающий возмещение
от страховой компании, если этот ущерб выше k*.
Цель этой работы - поиск оптимального дележа между страхователем и
страховой компанией. Здесь функционал экспоненциальной полезности описывает
предпочтения страхователя. Теоретические результаты этой работы проиллюстрированы
различными примерами, а также подробно описаны методы их нахождения.
Глава 1.
Теоретические материалы
Страховщик и страхователь должны прийти к взаимовыгодному решению о
величине взносов для того чтобы совершить сделку, при этом страховщика и страхователя,
принимающих суммарный риск интересуют разные величины. Несмотря на то, что цель
работы - выбор оптимального дележа с точки зрения страхователя в этой главе
механизм совершения сделки будет представлен с обоих сторон для объяснения
наличия тех или иных выражений в практической части.
Страховая компания согласится на сделку, только если ожидаемая полезность
после совершения этой сделки для нее будет не меньше чем без нее:
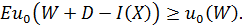
- капитал страховщика, D -
сумма страховых взносов, I(X) - сумма страховых выплат. D* будем обозначать наименьший суммарный взнос, при
котором страхование не является невыгодным для страховщика. D* и будет являться корнем уравнения
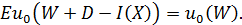
Клиент согласится на совершение этой сделки, если полезность его капитала
после сделки будет не меньше ожидаемой полезности от рисковой ситуации без
страхования
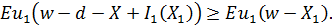
- начальный капитал клиента, d - страховой взнос, I1(X1) - страховая выплата, X1 - ущерб клиента. d* -
максимальная сумма, которую клиент может заплатить за страхование или корень
уравнения
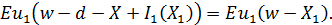
Заплатив страховой взнос d,
страхователь получает обязательство от компании погасить возможный ущерб, а его
финальный капитал равен s=w-d. Страховщик имеет суммарный взнос, полученный от всех своих
клиентов D и свой собственный капитал W. Остаточный капитал компании будет
равен S=W+D-X.
X=X1+X2+…+Xn, Xi - независимые неотрицательные
случайные величины (с.в.) ущербов отдельных клиентов в денежном эквиваленте, а F(x) и Fi(x) их функции распределения.
В математической теории страхования страховой взнос на две части D=M+L. М - рисковая
премия, а L - нагрузка. Если L зависит от M как L=αM, то α называется коэфициентом нагрузки.
Ниже приведены три самых распространенных способа расчета величины
страхового взноса.
) Формула среднего значения:
страхователь полезность управление риск
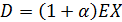
) Формула дисперсии:
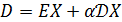
) Формула
стандартного отклонения:
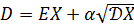
Эти формулы не являются полноценно применимыми на практике, так как в
реальности в нагрузку входят расходы страховой компании, комиссионные
брокерам, налог и надбавки на доход. Также эта модель не учитывает сторонние
факторы такие как политика компании, ситуация на рынке и т.д. В упрощенном
варианте все эти параметры вложены и зафиксированы в α.
Страховщик не имеет
права произвольно увеличивать этот коэффициент, опасаясь существенного снижения
спроса. Для некоторых видов страхования, например, для страхования жизни и
здоровья, есть законодательные ограничения на нижнее значение коэффициента
нагрузки.
Глава 2.
Постановка задачи
В представленной модели существует страховая компания и страхователь,
который хочет заключить сделку. Потенциальный ущерб клиента - неотрицательная
случайная величина X1. Функция распределения случайной
величины X1 - F1(x)=P{X1<x}.
Особенность этой функции распределения - скачок в нуле, равный вероятности
того, что страховой случай не произойдет. Таким образом, значение X характеризует тяжесть ущерба: 0 -
страховой случай не произошел, 50 - средний ущерб, 100 - катастрофический ущерб
с полной потерей имущества.
Страховщик выбирает функцию дележа I(x) на [0;∞).
С.в. I(X) - возмещаемая часть ущерба,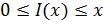 
. Размер страхового взноса
определяется формулой среднего значения D=(1+α)EI(X).
Вид страхования - безусловная франшиза.
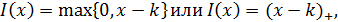
где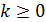 
- уровень этого дележа, называемого франшизой.
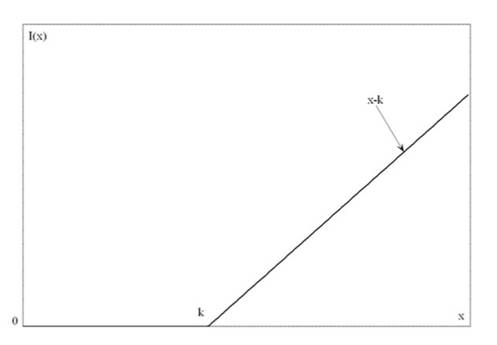
График 1
Исходя из этого определения функции I(x) ущерб X не возмещается клиенту при значениях
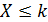и возмещается без учета суммы k, которую платит клиент. Так как I(x)<x, для
x>0, то размер взноса клиента после
введения франшизы должен быть ниже, чем размер взноса до ее введения: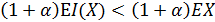 
.
Для выполнение этой работы также важно знать определение страхования с
верхним пределом или «stop-loss» страхования при котором функция
дележа равна
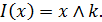
График 2
При таком виде страхования компания оплачивает ущерб полностью, если его
значение не превосходит 
, при больших значениях выплачивает только эту сумму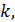 
называемую верхним пределом
ответственности страховщика.
Предпочтения страхователя описываются экспоненциальной функцией
полезности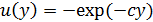 
, зависящей от показателя неприятия риска c>0.
Для решения задачи страхователя необходимо выбрать оптимальный дележ
риска с точки зрения клиента, который хотел бы максимизировать ожидаемую
полезность своего финального капитала.
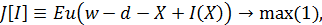
где w - начальный капитал страхователя, а d - страховой взнос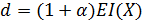 
Решение
задачи
Для решения задачи максимизации (1) сначала нужно доказать существование
и единственность оптимального дележа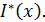 
Утверждение.
Единственным решением задачи (1) является франшиза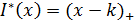 
с уровнем
Где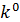 
является минимальным корнем уравнения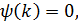 
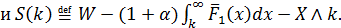
Здесь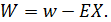 
Эта франшиза также представима в виде «stop-loss» дележа, только в роли страховой компании здесь
выступает страхователь, оплачивающий мелкие ущербы и платящий сумму k* если значение X>k*.
Доказательство.
С учетом того, что функционал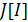 
вогнут в силу вогнутости 
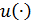, необходимое и достаточное условие
оптимальности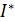 
(см. Приложение 1) имеет вид:
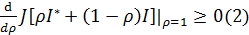
для любой допустимой функции дележа.
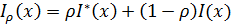
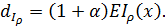
После дифференцирования неравенство (2) имеет вид:
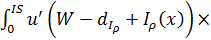
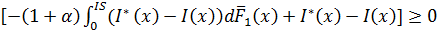
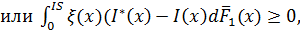
где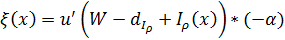 
Тогда I*(x) - решение задачи максимизации интеграла
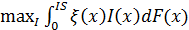
на множестве измеримых функций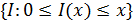 
Решение такой задачи находится обобщенной леммой Неймана-Пирсона [см.
Приложение 2].
Возвращаясь к задаче (2), получаем, что I*(x) оптимальна
тогда и только тогда, когда
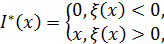(4)
с точностью до множества нулевой меры F. Отметим, что здесь сама функция ξ(x) зависит от неизвестного дележа I*(·). При возрастании x от 0 значение ξ(x) > 0 монотонно убывает в силу убывания u’(·) (при этом I*(x) = x в
силу (4)). После касания оси абсцисс в некоторой точке k0 функция ξ(x) не может принимать отрицательных значений, поскольку в
противном случае для таких x (см.
(4)) значение I*(x) = 0, и тогда приходим к противоречию: ξ(x) > 0. Возрастание ξ(x) от 0 также исключено, так как для таких x выполнено I*(x) = x, что влечет убывание, а не
возрастание ξ(x).
В итоге I*(x)=(x-k*)+. Вырожденный случай k*=IS здесь означает отказ от страхования.
Для доказательства единственности оптимальной стратегии страхования I*(x) заметим, что функционал J[I]=Eu(w-d-X+I(X)) строго вогнут
по I в силу строгой вогнутости функции
полезности u(x). Действительно, при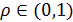 
неравенство 
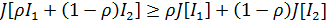обращается в равенство лишь в случае
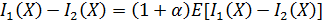, но тогда I1(X)=I2(X).
Глава 3.
Численный пример
Пусть страхователь имеет функцию полезности 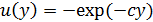заданным показателем неприятия риска
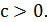Тогда уравнение 
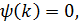можно записать как:
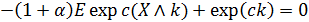
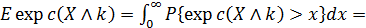
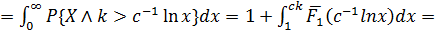
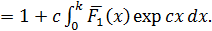
Тогда уравнение оптимальности будет:
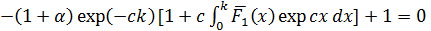
Далее предположим, что функция распределения выплат экспоненциальная,
тогда функция распределения ущерба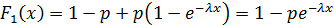 
, где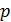 
- вероятность страхового случая.
Подставим это выражение в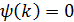 
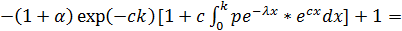
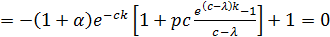
Теперь решим уравнение 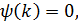подставив следующие параметры:
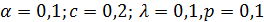
Далее попробуем поменять их и посмотреть, как значения k зависят от изменения этих параметров.
Таблица 1
|
|
|
|
|
|
|
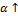
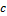
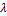
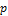
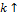
0,10
|
0,2
|
0,1
|
0,1
|
0,5307
|
|
0,11
|
0,2
|
0,1
|
0,1
|
0,5812
|
|
0,12
|
0,2
|
0,1
|
0,1
|
0,6313
|
|
0,13
|
0,2
|
0,1
|
0,1
|
0,6810
|
|
0,14
|
0,2
|
0,1
|
0,1
|
0,7303
|
|
0,15
|
0,2
|
0,1
|
0,1
|
0,7791
|
|
0,16
|
0,2
|
0,1
|
0,1
|
0,8276
|
|
0,17
|
0,2
|
0,1
|
0,1
|
0,8757
|
|
0,18
|
0,2
|
0,1
|
0,1
|
0,9233
|
|
0,19
|
0,2
|
0,1
|
0,1
|
0,9706
|
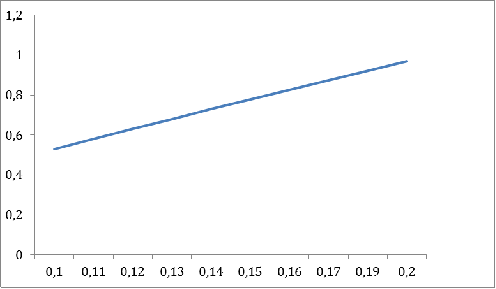
График 3
Таблица 2
|
  
|
|
|
|
|
|
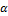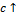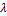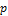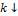
0,1
|
0,2
|
0,1
|
0,1
|
0,5307
|
|
0,1
|
0,21
|
0,1
|
0,1
|
0,5055
|
|
0,1
|
0,22
|
0,1
|
0,1
|
0,4826
|
|
0,1
|
0,23
|
0,1
|
0,1
|
0,4617
|
|
0,1
|
0,24
|
0,1
|
0,1
|
0,4425
|
|
0,1
|
0,25
|
0,1
|
0,1
|
0,4248
|
|
0,1
|
0,26
|
0,1
|
0,1
|
0,4085
|
|
0,1
|
0,27
|
0,1
|
0,1
|
0,3934
|
|
0,1
|
0,28
|
0,1
|
0,1
|
0,3794
|
|
0,1
|
0,29
|
0,1
|
0,1
|
0,3663
|
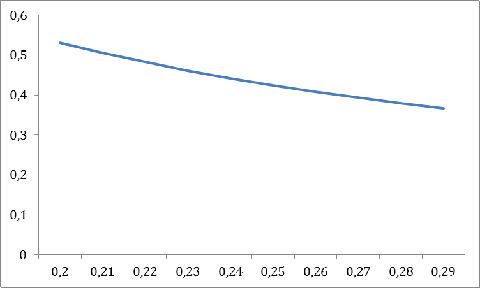
График 4
Таблица 3
|
|
|
|
|
|
|
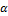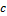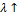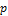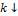
0,1
|
0,2
|
0,1
|
0,1
|
0,5307
|
|
0,1
|
0,2
|
0,11
|
0,1
|
0,5306
|
|
0,1
|
0,2
|
0,12
|
0,1
|
0,5304
|
|
0,1
|
0,2
|
0,13
|
0,1
|
0,5302
|
|
0,1
|
0,2
|
0,14
|
0,1
|
0,5301
|
|
0,1
|
0,2
|
0,15
|
0,1
|
0,5299
|
|
0,1
|
0,2
|
0,16
|
0,1
|
0,5298
|
|
0,1
|
0,2
|
0,17
|
0,1
|
0,5296
|
|
0,1
|
0,2
|
0,18
|
0,1
|
0,5295
|
|
0,1
|
0,2
|
0,19
|
0,1
|
0,5293
|
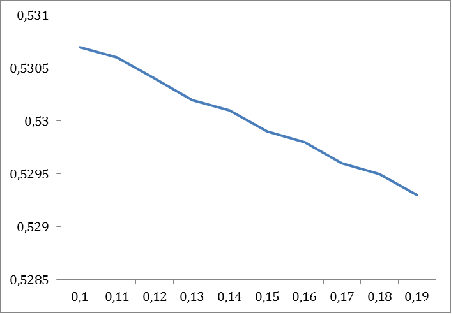
График 5
Таблица 4
|
 
|
|
|
|
|
|
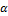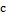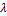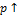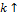
0,1
|
0,2
|
0,1
|
0,1
|
0,5307
|
|
0,1
|
0,2
|
0,1
|
0,11
|
0,5368
|
|
0,1
|
0,2
|
0,1
|
0,12
|
0,5430
|
|
0,1
|
0,2
|
0,1
|
0,13
|
0,5494
|
|
0,1
|
0,2
|
0,1
|
0,14
|
0,5559
|
|
0,1
|
0,2
|
0,1
|
0,15
|
0,5626
|
|
0,1
|
0,2
|
0,1
|
0,16
|
0,5694
|
|
0,1
|
0,2
|
0,1
|
0,17
|
0,5764
|
|
0,1
|
0,2
|
0,1
|
0,18
|
0,5835
|
|
0,1
|
0,2
|
0,1
|
0,19
|
0,5908
|
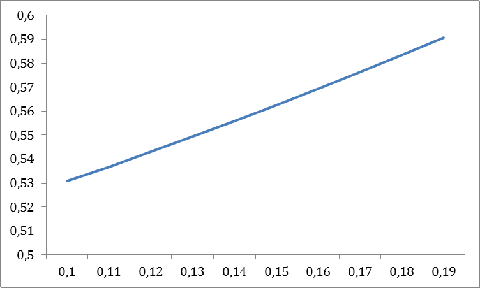
График 6
Из приведенных выше таблиц и графиков заметны прямые и обратные линейные
зависимости от наших параметров.
Прямая линейная зависимость - при увеличении одного из параметров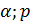 
финальное значение увеличивается. Действительно,
нетрудно дать логическое обоснование, к примеру, при увеличении вероятности
наступления страхового события
пороговое значение, которое страхователь тратит на ремонт
мелких повреждений, становится больше из-за увеличения числа этих повреждений.
Причина, по которой при увеличении суммы страхового взноса значение k тоже увеличивается, непонятна, но,
возможно, это объяснит найденная в дальнейшем ожидаемая полезность финального
капитала.
Обратная линейная зависимость: увеличение параметров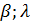 
ведет к снижению уровня верхнего
предела ответственности страхователя. Например, если страхователь является
более осторожным в выборе своей стратегии, то он увеличивает значение
коэффициента неприятия риска, соответственно принимает страховые тарифы и
условия, которые являются более выгодными для него, соответственно значение
верхнего предела ответственности снижается.
Теперь подставим найденные значения k, чтобы узнать значение функционала полезности нашего
финального капитала S.
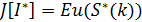
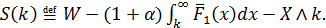
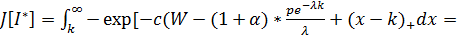
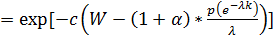
Теперь подставим все значения для нахождения J и попробуем поменять их для определения корреляции. Значение
начального капитала возьмем равным 10.
Таблица 5
|
|
|
|
|
|
|
|
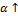
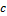
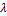
0,10
|
0,2
|
0,1
|
0,1
|
0,5307
|
0,10985
|
|
0,11
|
0,2
|
0,1
|
0,1
|
0,5812
|
0,10975
|
|
0,12
|
0,2
|
0,1
|
0,1
|
0,6313
|
0,10966
|
|
0,13
|
0,2
|
0,1
|
0,1
|
0,6810
|
0,10957
|
|
0,14
|
0,2
|
0,1
|
0,1
|
0,7303
|
|
0,15
|
0,2
|
0,1
|
0,1
|
0,7791
|
0,10939
|
|
0,16
|
0,2
|
0,1
|
0,1
|
0,8276
|
0,10930
|
|
0,17
|
0,2
|
0,1
|
0,1
|
0,8757
|
0,10922
|
|
0,18
|
0,2
|
0,1
|
0,1
|
0,9233
|
0,10913
|
|
0,19
|
0,2
|
0,1
|
0,1
|
0,9706
|
0,10904
|
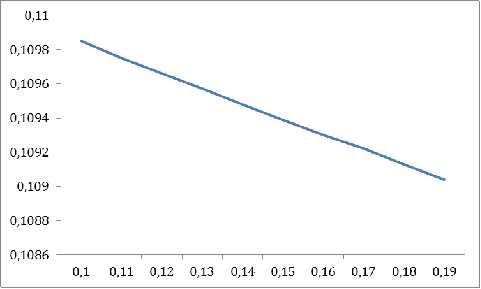
График 7
Таблица 6
|
|
|
|
|
|
|
|
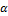
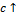
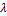
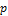
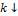
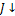
0,1
|
0,2
|
0,1
|
0,1
|
0,5307
|
0,10985
|
|
0,1
|
0,21
|
0,1
|
0,1
|
0,5055
|
0,09831
|
|
0,1
|
0,22
|
0,1
|
0,1
|
0,4826
|
0,08798
|
|
0,1
|
0,23
|
0,1
|
0,1
|
0,4617
|
0,07874
|
|
0,1
|
0,24
|
0,1
|
0,1
|
0,4425
|
0,07046
|
|
0,1
|
0,25
|
0,1
|
0,1
|
0,4248
|
0,06306
|
|
0,1
|
0,26
|
0,1
|
0,1
|
0,4085
|
0,05644
|
|
0,1
|
0,27
|
0,1
|
0,1
|
0,3934
|
0,05051
|
|
0,1
|
0,28
|
0,1
|
0,1
|
0,3794
|
0,04520
|
|
0,1
|
0,29
|
0,1
|
0,1
|
0,3663
|
0,04045
|
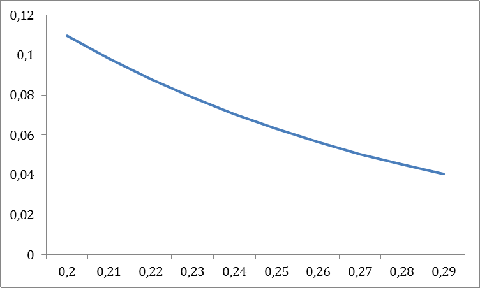
График 8
Таблица 7
|
|
|
|
|
|
|
|
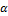
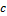
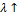
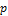
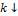
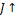
0,1
|
0,2
|
0,1
|
0,1
|
0,5307
|
0,10985
|
|
0,1
|
0,2
|
0,11
|
0,1
|
0,5306
|
0,11206
|
|
0,1
|
0,2
|
0,12
|
0,1
|
0,5304
|
0,11394
|
|
0,1
|
0,2
|
0,13
|
0,1
|
0,5302
|
0,11556
|
|
0,1
|
0,2
|
0,14
|
0,1
|
0,5301
|
0,11696
|
|
0,1
|
0,2
|
0,15
|
0,1
|
0,5299
|
0,11819
|
|
0,1
|
0,2
|
0,16
|
0,1
|
0,5298
|
0,11927
|
|
0,1
|
0,2
|
0,17
|
0,1
|
0,5296
|
0,12024
|
|
0,1
|
0,2
|
0,18
|
0,1
|
0,5295
|
0,12110
|
|
0,1
|
0,2
|
0,19
|
0,1
|
0,5293
|
0,12188
|
График 9
Таблица 8
|
|
|
|
|
|
|
|
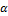
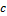
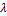
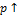
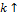
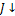
0,1
|
0,2
|
0,1
|
0,1
|
0,5307
|
0,10985
|
|
0,1
|
0,2
|
0,1
|
0,11
|
0,5368
|
0,10759
|
|
0,1
|
0,2
|
0,1
|
0,12
|
0,5430
|
0,10539
|
|
0,1
|
0,2
|
0,1
|
0,13
|
0,5494
|
0,10323
|
|
0,1
|
0,2
|
0,1
|
0,14
|
0,5559
|
0,10113
|
|
0,1
|
0,2
|
0,1
|
0,15
|
0,5626
|
0,09906
|
|
0,1
|
0,2
|
0,1
|
0,16
|
0,5694
|
0,09705
|
|
0,1
|
0,2
|
0,1
|
0,17
|
0,5764
|
0,09507
|
|
0,1
|
0,2
|
0,1
|
0,18
|
0,5835
|
0,09314
|
|
0,1
|
0,2
|
0,1
|
0,19
|
0,5908
|
0,09126
|
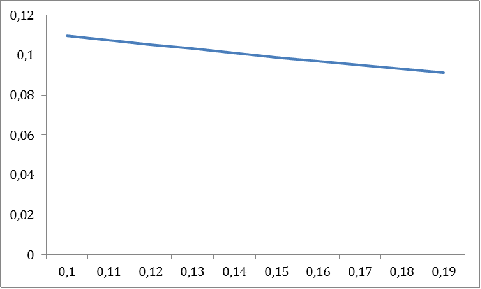
График 10
Как видно на приведенных выше графиках, результат этого анализа является
логичным - ожидаемая полезность финального капитала страхователя снижается при
увеличении размера страхового взноса(7), более осторожной стратегии при
принятии решения(8) и большей вероятности страхового события.
Заключение
В первой главе данной работы были сформулированы основные теоретические
обоснования исследуемой модели, рассмотрены ее составляющие и сделан ряд
некоторых предпосылок для дальнейшего исследования исходной задачи.
В следующей главе была поставлена задача оптимального выбора дележей
страхования и показано, что оптимальным с точки зрения страхователя является
безусловная франшиза, когда страхователь сам оплачивает ущерб, если значение
этого ущерба не превосходит определенного уровня 
В конце работы приведен численный пример, иллюстрирующий полученные в
предыдущих разделах результаты в случае экспоненциального распределения выплат.
Численные решения исследуемой задачи позволяют проследить эволюцию оптимальной
стратегий при различных значениях варьируемого параметра. Практическое
использование полученных результатов предполагает оптимизацию схем дележа риска
со страховой компанией для клиента.
Приложение 1
Пусть на выпуклом множестве А в некотором линейном пространстве определен
вогнутый функционал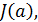 
имеющий в точке 
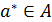производные по направлениям
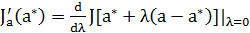
Для любого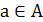 
. Точка 
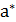есть решение 
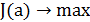, тогда и только тогда, когда 
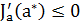для всех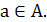 
Неположительность производных по направлениям, очевидно, можно
эквивалентно переписать как условие
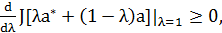
Означающее, что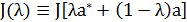 
имеет на [0,1] максимум в точке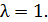 
Приложение 2
Лемма Неймана-Пирсона:
Пусть на [a,b] заданы две функции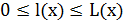 
и функция 
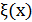, измеримые по Борелю, а также
вероятностная мера с функцией распределения F(x). Пусть
интегралы 
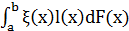и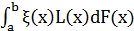 
конечны.
Функция y*(x) доставляет максимум интегралу
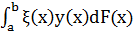
на множестве борелевских функций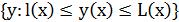 
тогда и только тогда, когда
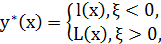
с точностью до множества нулевой меры F.
Список
используемой литературы
[1] Голубин
А.Ю. Математические модели в теории страхования: построение и оптимизация. М.: АНКИЛ, 2003.
[2]
Bowers N.L., Gerber H.U., Hickman J.C., Jones D.A., Nesbitt C.J. Actuarial
Mathematics. Itaca, Illinois: The Society of Actuaries, 1986.
[3]
Arrow K.J. Essays in the Theory of Risk Bearing. Chicago: Wyley and Sons, 1971.
[4] Голубин
А.Ю. Математические вопросы управления риском в базовых моделях страхования.
М.: АНКИЛ, 2013 C 123-137
[5] Белкина
Т.А., Чеканина С.В. Оптимальное управление инвистициями в динамической модели
страхования // В сб. «Моделирование механизмов функционирования экономики
России на современном этапе». Вып. 5. С. 101-118. М.: ЦЭМИ РАН, 2001.
[6]
Golubin A.Y. Optimal Insuranse and Rensurance Policies in the Risk Process //
ASTN Bulleten. 2008. V.
38. No. 2P. 383-398.
[7] Голубин
А.Ю., Гридин В..Н., Газов А.И. Оптимизация дележа риска в статической модели с
перестрахованием // Автоматика и телемеханика. 2009. Т. 70. В. 8 С. 133-144.
[8] Леман Э.
Проверка статистических гипотез. М.: Наука, 1964.
[9]
Golubin A.Y. Optimal Insurance and Reinsurance Policies in thr Risk Process //
ASTN Bulletin. 2008. 38(2). P. 170-179.