|
Параметр
|
Значение
|
Параметр
|
Значение
|
|
Solver
|
StepDiscrete
|
AbsTol
|
1e-6
|
|
ZeroCross
|
On
|
Refine
|
1
|
|
StartTime
|
0.0
|
InitialStep
|
auto
|
|
StopTime
|
255
|
FixedStep
|
1
|
|
RelTol
|
1e-3
|
MaxStep
|
auto
|
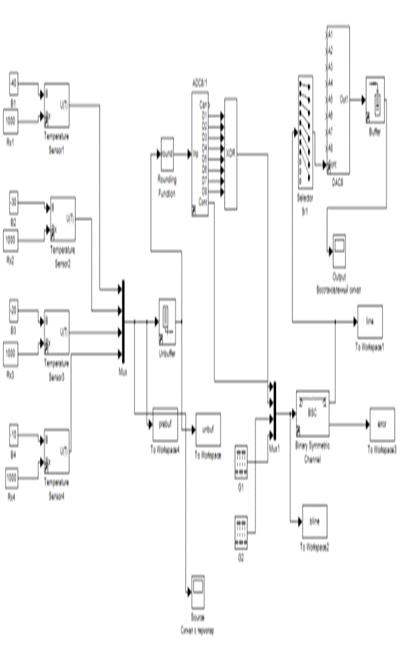
После выполнения симуляции передачи данных через канал были
получены входные и выходные осциллограммы сигналов изображенные на рисунках 5.1
и 5.2, полученные при помощи блоков Source Output.
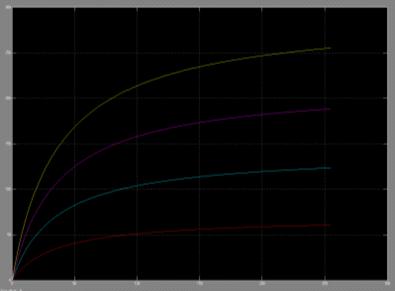
Рисунок 5.1 - Осциллограмма исходного сигнала
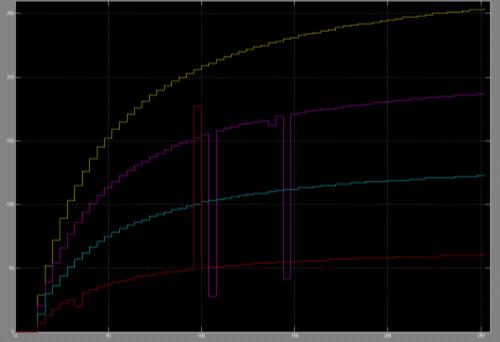
Рисунок 5.2 - Осциллограмма принятого сигнала
Для построения зависимость количества ошибок в канале связи
от вероятности возникновения ошибки параметр Error probability блока Binary Symmetric Channel следует варьировать в
диапазоне 0 до 0,1 с шагом 0,005. Для контроля возникновения ошибок
используется переменная error, формируемая на нижнем выходе блока Binary Symmetric Channel. Для подсчета числа
ошибок была использована следующая программа на языке MatLab:
clc;=0;=size(line);cRow=1:a(1);cCol=1:a(2);error
(cRow, cCol)==1=eNumb+1;
end
end
eNumb
С помощью приведенной программы произвели подсчет ошибок. Для
данной максимальной вероятности ошибок в бинарном канале связи Р=0.1 получили
число ошибок:= 336
Переменная eNumb использована как счетчик числа ошибок. В
результате выполнения программы в окне Command window выводится размер
переменной error и количество ошибок, возникших при передаче сигнала по каналу
связи. Последовательность моделирования следующая:
) задается параметр Error probability блока Binary Symmetric Channel и проводится
моделирование работы системы;
) запускается на выполнение приведенная выше программа;
) полученное значение количества ошибок заносится в массив ERRORS, имеющий 2 столбца и 16
строк. В первом столбце записываются значения вероятностей ошибок, во втором -
количество ошибок.
Последовательность 1-3 повторяется до достижения верхней
границы диапазона варьирования параметра Error probability.
Таким образом, получили зависимость числа ошибок в канале от
их вероятности, отраженную в массиве ERRORS изображенную на рисунке 5.3.
=
0
.0050 9.0000
.0100 26.0000
.0150 44.0000
.0200 68.0000
.0250 82.0000
.0300 101.0000
.0350 117.0000
.0400 141.0000
.0450 172.0000
.0500 191.0000
.0550 212.0000
.0600 229.0000
.0750 243.0000
.0800 261.0000
.0850 277.0000
.0900 301.0000
.0950 317.0000
.1000 336.0000
Рисунок 5.3 - Содержимое массива ERRORS
6. Модель кодирующего и декодирующего устройства
для инверсного кода
При построении кодирующего устройства исходными данными
является вид кода, применяемый при передаче команд управления - инверсный код.
Модель подсистемы кодирования инверсным кодом представлена на
рисунке 6.1.
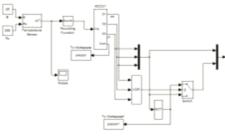
Рисунок 6.1 - Модель устройства подсистемы кодирования
инверсным кодом
Блок XOR выполняет проверку четности «1» в исходной
кодовой комбинации (когда количество «1» четно результат работы блока «0» иначе
«1»), затем кодовая комбинация дополняется при помощи блока Switch инвертированными битами,
если содержится нечетное число «1» в исходной комбинации или точной копией
исходной комбинации, если число «1» было четным.
Модель подсистемы декодирования сигнала закодированного кодом
с удвоением представлена на рисунке 6.2.
Блоки Selector применяются для выбора информационных и
поверочных бит.
При помощи блока XOR проверяется количество «1» в исходной
комбинации, если их число четное, то элементы дополнительной комбинации
принимаются в неизменном виде (через блок Switch). После этого обе части
кодовой комбинации сравниваются поэлементно. При обнаружении хотя бы одного
несовпадения кодовая комбинация считается искаженной.
Если количество «1» в исходной комбинации нечетное, элементы
дополнительной комбинации инвертируются (блок NOT). После этого производится
поэлементное сравнение обеих частей кодовой комбинации и выносится решение о
наличии или отсутствии искаженной.
Блоки Fnc и Counter используются для подсчета числа ошибок в
принимаемых битах. Блоки Fnc выполняют сравнение исходных битов с контрольными
и если они совпадают, то на блок Counter подается сигнал и его значение увеличивается на
единицу
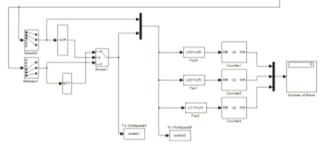
Рисунок 6.2 - Подсистема декодирования инверсного кода
Модель устройства для передачи сигнала закодированного кодом
с удвоением представлена на рисунке 6.3, в ней использованы описанные
подсистемы кодировании и декодирования сигнала.
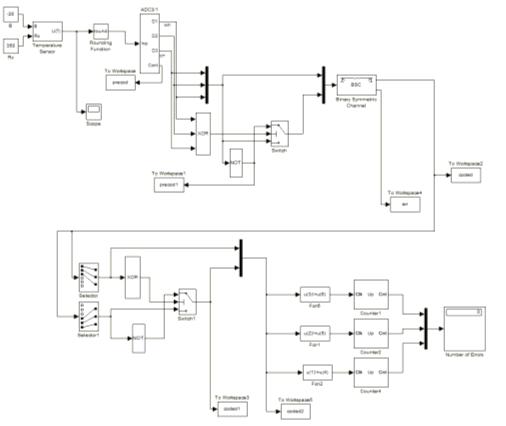
Рисунок 6.3 - Модель устройства передачи сигнала
закодированного инверсным кодом
Заключение
В ходе выполнения курсовой работы создана модель устройства
передачи данных, содержащая четыре канала передачи данных. Разработанная модель
устройства передачи данных соответствует поставленной задаче. Модель содержит
необходимый набор устройств и блоков, реализующих передачу данных и команд с
заданной вероятностью помех.
С помощью данной модели можно наглядно проследить преобразования
данных от источника информации до получателя.
Перечень ссылок
1.
Бобровников Л.З. Электроника: учебник для вузов. 5-е изд., перераб. и доп. -
СПб.: Питер, 2004. - 560 с.: ил. - (Серия «Учебник для вузов»).
.
Темников Ф.Е. и др. Теоретические основы информационной техники: Учеб. пособие
для вузов. - М: Энергия, 1979. - 512 с.
.
Черных И.В. SIMULINK: среда создания инженерных приложений / Под общ. Ред. к.т.н. В.Г.
Потемкина. - М.: ДИАЛОГ-МИФИ, 2003. - 496 с.
.
Методические указания к выполнению курсовой работы по дисциплине «Обработка
сигналов и изображений» на тему «Моделирование устройства передачи данных по
бинарному каналу». Алчевск, 2004.
Приложение А
Модель трехразрядного АЦП
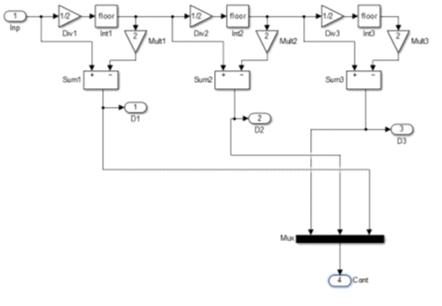
Приложение Б
Модель трехразрядного ЦАП
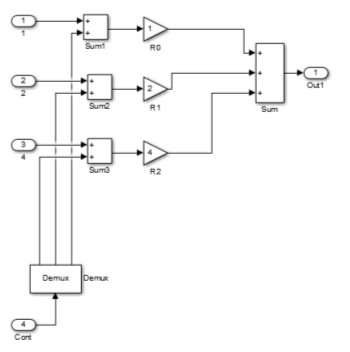
Приложение В
Модель устройства передачи данных